Effects of fiber-optic probe design and probe-to-target distance on diffuse reflectance measurements of turbid media: an experimental and computational study at 337 nm

Abstract

Fiber-optic probes are widely used in optical spectroscopy of biological tissues and other turbid media. Only limited information exists, however, on the ways in which the illumination-collection geometry and the overall probe design influence the interrogation of media. We have investigated both experimentally and computationally the effect of probe-to-target distance (PTD) on the diffuse reflectance collected from an isotropically (Lambertian) scattering target and an agar-based tissue phantom. Studies were conducted with three probes characterized by either common (single-fiber) or separate (two bifurcated multifiber probes) illumination and collection channels. This study demonstrates that PTD, probe design, and tissue scattering anisotropy influence the extent of the transport of light into the medium, the light-collection efficiency, and the sampling volume of collected light. The findings can be applied toward optimization of fiber-optic probe designs for quantitative optical spectroscopy of turbid media including biological tissues.

1. Introduction

Optical techniques are broadly investigated as potential noninvasive or minimally invasive medical diagnostic or monitoring tools. They often employ fiber-optic probes, which allow for flexible delivery and collection of light even in hard-to-reach anatomical sites. In a recent review Utzinger and Richards-Kortum¹ presented a large variety of designs for fiber-optic probes used in optical spectroscopy applications. Such applications include laser-induced fluorescence diagnostics,² Raman diagnostics,^3–5 monitoring of photosensitizer concentration,^6,7 and measurements of the optical properties of tissue.^8–10 All these measurements involve three distinct components: transfer of light from the fiber to the medium, propagation of light into the medium, and collection of the medium-reemitted light by the fiber. Whereas a significant body of research has been published on the first two components,^4,11–16 and despite this widespread use of fiber-optic probes, only limited research has been devoted to the third.

Fiber-optic probes are characterized by their overall design configuration (single-fiber, bifurcated), the number, core size, and numerical aperture (NA) of the illumination (source) and collection (detector) fibers, and the (center-to-center) source-to-detector separation (SDS). Several theoretical and experimental investigations^4,12–16 have shown that the aforementioned characteristics affect the probe’s performance with respect to light-collection efficiency (CE) and volume sampling. Those studies were focused mainly on applications involving clear solutions or other weakly absorbing, nonturbid media. Tissue examination, however, involves additional factors such as (i) the tissue’s optical properties [absorption (μ_a) and scattering (μ_s) coefficients and the anisotropy factor (g)], (ii) the tissue’s structure, heterogeneities, and intervening blood flow, and (iii) the illumination-collection geometry. These factors can significantly affect the delivery of light, CE, and sampling volume of the collected photons, which in turn can influence the signal-to-noise ratio (SNR) and determine the volume of interrogated tissue. Therefore, overall optimization of probe design and usage requires understanding of the interplay among probe design, tissue characteristics, and excitation-collection geometry.

Recently Pfefer et al. presented computational^17,18 and experimental¹⁹ studies of the performance of single- and multiple-fiber probes. The extensive computational studies have provided useful insights into the optimization of probe design: both probe design (fiber core size, NA, SDS), and probe-to-target distance (PTD) were found to significantly affect the intensity and origin of fluorescence emission. These studies were focused mainly on transport of excitation light and on the origin and collection of fluorescence. Other issues that require further investigations include the effect of probe design and PTD on the collection of excitation light alone (measurements of diffuse reflectance). An evaluation of the effects of probe design (single and multifiber probes) on depth gauging of the fluorescence of stratified epithelial tissues has been presented by Zhu et al.²⁰ These simulations were conducted with the probes in contact with the target; thus the effect of PTD was not included. Liu et al.²¹ conducted Monte Carlo validation experiments of both fluorescence and diffuse reflectance for a wide variety of tissue optical properties. The experiments were conducted with three specific bifurcated probes in direct contact with the tissue phantoms. Bargo et al.²² studied experimentally and theoretically the effect of optical properties on the CE of diffuse reflectance for a single 600-μm core-diameter fiber. The tissue scattering properties were found to influence the CE of this probe type. In those studies the probe was also assumed to be in contact with the tissue. Other studies that are relevant to various aspects of the interplay among probe characteristics, optical properties of tissue, and the resultant spectroscopic data have been conducted by Pogue and Burke⁶ and by Avrillier et al.²³ They also emphasized fluorescence measurements and did not include the effects of PTD.

All the studies mentioned above have contributed significant insight into the influence of probe design on spectroscopic applications. However, they have only lightly touched on the effect of PTD on collected light and more specifically on collected diffused light, which has been the focus of the research described in this paper. The importance of further understanding the influence of PTD on collection of light stems from the need to accommodate various practical limitations, especially in a clinical environment. For instance, it is often necessary to minimize the presence of blood or other biological fluids between the probe and the tissue, as such fluids could contaminate the probe, induce undesirable modulation of the spectroscopic signal, or both. Thus spacers or other protective shields are applied to the distal part of a probe, thus increasing the PTD. During endoscopic applications of spectroscopy, often the probe carrying the excitation light is kept at a distance from the tissue to enable it to interrogate larger tissue areas and also to facilitate the simultaneous imaging of the resultant reemitted light. The resultant PTD broadens the illumination area. The combination of the overall excitation and collection geometry along with the tissue’s optical properties can then influence the SNR, thus compromising the quality of the data. Additionally, changes in the penetration depth of the collected photons may also ensue.^17–19 Accurate knowledge of this effect is necessary for correlation of the spectroscopic signatures with the corresponding local tissue histopathology. Thus the diagnostic value of such techniques could be compromised unless further information on the effect of PTD on the volume of tissue that is actually interrogated were available.

Our study focuses on the collection of diffused reflected light rather than on fluorescence. There are a number of factors that support the investigation of the excitation light alone: (a) It is well recognized that the optical properties of tissue can differ greatly between excitation and emission wavelengths,¹¹ especially when the excitation is in the UV range. Separate examination of the excitation light reduces the computational complications that arise from considering these multiple and often greatly dissimilar values of optical properties. Thus this examination allows for a more comprehensive understanding of light–tissue interaction during the initial (excitation) phase of the fluorescence process. (b) The diffusely reflected excitation light can be used along as a diagnostic signal or in conjunction with the fluorescence signal during fluorescence spectroscopy either to enhance the diagnostic value or for estimation of the tissue’s optical properties.^24,25 (c) Lifetime fluorescence spectroscopy techniques can also be improved; i.e., as PTD increases, it induces changes in the volume of interrogation of the collected reflected signal. Such changes influence the photon path length, which in turn affects the pulse width.^26,27 Thus there could be a PTD-induced temporal dispersion of the collected pulse. Inasmuch as diffuse excitation light is often used as input to the deconvolution algorithm for estimation of tissue-fluorescence lifetime, lifetime estimations could in turn be affected. (d) Finally, estimations of lifetimes, optical properties of tissues, and other pertinent parameters can be further influenced by the experimental SNR, which is directly related to the CE of the probe.

The overall goal of this investigation was to study the effect of PTD on the light that is diffusely reflected from a turbid medium. To this end we studied the effect of PTD on the illumination volume, on the sampling volume of the collected photons, and on the CE of the collected diffuse light, defined here as the ratio of total number of collected photons to total number of photons impinging upon the target surface. The problem was addressed both experimentally by measurements of diffuse reflectance of 337-nm excitation wavelength and computationally with Monte Carlo simulation. Three specific probe designs were used as examples of designs that provide for common (single-fiber) or separate (two bifurcated multifiber probes) excitation and collection channels. Two types of target were used: an isotropically scattering target (Lambertian) and an agar-based tissue phantom. The wavelength (337 nm) was selected because it has been extensively used for tissue excitation,^2,28–30 as it is located close to absorption bands of major tissue fluorophores.

2. Materials and Methods

A. Experimental Setup

Experimental studies were carried out with a setup that allowed for making time-resolved fluorescence measurements. The overall design of the apparatus has been described in detail by Marcu et al.³¹ Briefly, the output of a nitrogen laser (Model 2100, EG&G PAR; 337.1 nm, 1.2-ns pulse width) was coupled into the illumination channel of a fiber-optic probe and aimed at the target under investigation. The diffusely reflected light from the target was collected through the collection channel of the probe and directed into a 0.25 m, f/4 monochromator (Model 77200, Oriel Instruments, Stratford, Connecticut). The signal was detected and amplified with a gated microchannel plate photomultiplier tube (Model R2024U, Hamamatsu, Bridgewater, New Jersey) and a fast, 1.0-GHz preamplifier (Model 9306, EG&G Or-tec). It was acquired at 8-bit resolution with a 1-GHz oscilloscope (TDS 680C, Tektronix) and saved on a computer for further processing. Experiments were carried out at a 5-Hz repetition rate with a probe energy output of approximately 1 μJ/pulse.

B. Fiber-Optic Probes

Three fiber-optic probes of various designs were used. Schematics of the side views and cross sections of the probes are shown in Fig. 1. The probe designs were based on either single-fiber (probe 1) or multifiber bifurcated (probes 2 and 3) architectures. The single-fiber probe (P₁) consisted of a single 600-μm-core diameter fiber (600 μm/650 μm/750 μm::core/cladding/jacket) of 1.5-m length. Illumination and reflected light were guided through the same fiber with an arrangement that employed a dichroic beam splitter (HR337/HT385–650, CVI, Albuquerque, New Mexico). The particular probe was chosen as a representative of a class of probes that allow for common illumination and collection channels (zero SDS). It is flexible and compatible with endoscopic techniques and has been used extensively in both experimental and theoretical studies.^1,22 Additionally, simulations of single-fiber probes with core size diameters of 200 and 1000 μm have also been provided to facilitate comparisons with single probes of different sizes.

Fig. 1.

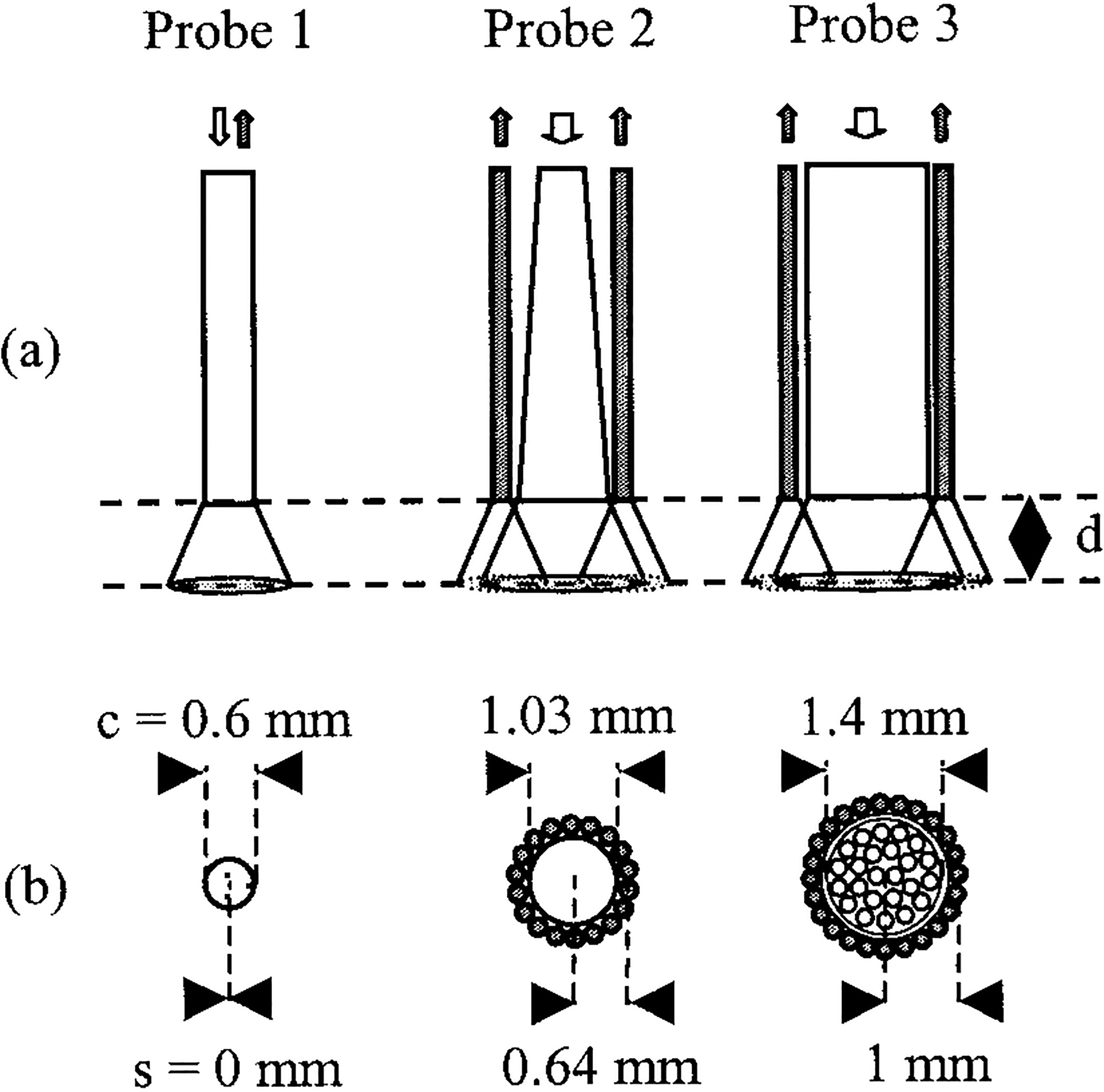
(a) Side and (b) cross-sectional views of the evaluated fiber-optic probes. Probe 1 was a dichroic beam-splitter-based single-fiber arrangement with common illumination and collection channels. Probes 2 and 3 were bifurcated, with a central illumination channel and a peripheral collection ring. The illumination channel of probe 2 consisted of a tapered fiber. The diameters of the illumination cores and the source-to-detector distances (center to center) are marked c and s, respectively. Diffuse reflectance at 337 nm was collected as a function of PTD d. Open (filled) arrows or circles indicate illumination (collection) paths. Probe views are drawn to scale.

The second probe (P₂; Polymicro Technologies LLC, Phoenix, Arizona) was custom designed. It consisted of a central illumination fiber (600 μm) that was tapered to a distal core diameter of 1025 μm. Thus the NA of the illumination channel was ~0.11. The central fiber was surrounded concentrically by a ring of 18 collection fibers, each of 200-μm core size. The SDS, which accounts for the cladding and jacket sizes and the intervening epoxy, was 0.64 mm. Both the illumination and the collection paths of the probe were 2 m long.

The third probe (P₃; Model 77558, Oriel, Stratford, Connecticut) consisted of a central excitation core of 24 closely packed fibers, each of 200-μm core size, allowing for an equivalent illumination diameter of 1.4 mm. The illumination NA was ~0.11. An equal number of peripherally arranged fibers (200 μm) formed the collection channel. The SDS for this probe was 1.0 mm. This separation accounted for the cladding and jacket sizes of the core and peripheral fibers, the intervening epoxy, and the thickness of a metal sleeve that surrounded the illumination fibers. The illumination and collection paths of this probe were also 2 m long.

The two bifurcated probes allowed for testing of the second main class of probes, which are characterized by separate illumination and excitation channels. These probes were used in previous investigations^30–32 and are currently in use in in vitro and in vivo fluorescence studies. Therefore this study provides the opportunity to enhance our understanding of previous and ongoing investigations. Future investigators can also benefit, as the probes either are already commercially available (P₃) or can be custom made (P₂). The two probes had a number of common parameters. They were characterized by the same illumination and collection NAs, and their collection fibers had the same core size. They differed only in the size of the illumination core. The probes investigated in this study were used primarily as paradigms of two main classes of probe architecture. Comprehensive investigation of each probe design was beyond the scope of this research. Finally, note that all three probes were tested over a practical range of SDSs (0, 0.64, and 1 mm).

The distal ends of the collection channels of both bifurcated probes were formed into a line to facilitate coupling into the monochromator. The light collected from all three probes entered the monochromator through f-number matching optics. All probes were constructed of UV-grade fused-silica, step-index multimode fibers with a nominal NA of 0.22. The NAs of the illumination channels were measured by far-field imaging of the probe outputs conducted with a CCD camera (Cohu Series 6400, Cohu, Inc., San Diego, California). The NAs, defined at 10% of maximum intensity, were 0.17, 0.11, and 0.11 for probes P₁, P₂, and P₃, respectively. Near-field imaging of the illumination channel of P₃ revealed output nonuniformities reflecting the distribution of the individual fibers that composed the illumination channel of this catheter. This output nonuniformity became less apparent at the far field owing to the overlap of the illumination cones of the individual fibers. Simulations did not account for this nonuniformity. Instead, uniform light distribution was assumed for the illumination channels of the three probes. The deviation of P₁ and P₃ NAs from the nominal value is attributed to the specific light-coupling conditions for these two probes: For the single-fiber probe (P₁), light was launched at a small angle with respect to the optical axis to prevent contamination of the signal by retroreflection at the (input) air–glass interface. This arrangement, compounded with bending and short fiber length, resulted in reduced higher mode distribution (i.e., lower NA). For P₃, light was coupled into the excitation channel by direct end-to-end contact with a 0.6-mm core-diameter fiber that served as an optical delay line. Coupling was achieved with a small axial separation of the two fibers such that the 0.6-mm fiber output illuminated the entire input of the P₃ illumination channel. This nonoptimal coupling helped to preserve the output diameter of probe P₃ to approximately its design diameter (~1.4 mm). It also reduced slightly the (nominal) NA. This decrease in NA, however, proved advantageous, as both bifurcated probes had the same illumination NA, which in turn facilitated interpretation of results. No axial fiber separation was applied for P₂ because the input of its illumination channel was of equal size to the core size of the fiber’s optical delay line. The measured NA for P₂ (0.11) was close to the expected NA (~0.13), owing to the taper ratio 1:1.7. For all the Monte Carlo simulations described below, the measured NAs were assumed for the illumination channels, whereas the nominal NA of 0.22 was assumed for all collection channels. These assumptions we considered reasonable, as the diffuse nature of the collected light is expected to excite the full NA of the collection fibers.

C. Reflectance Targets

The experimental targets included a white certified reflectance standard (Model SRS-99-020, Spectralon, Labsphere, Inc., North Sutton, New Hampshire) and an agar-based phantom. Because the CE of a probe is expected to depend on the angular distribution of the reemitted light,²² the two targets were chosen as paradigms of targets with different scattering properties. The white target simulated the behavior of an ideal isotropic (Lambertian) reflector (g = 0), whereas the agar-based target introduced optical turbidity, including anisotropic scattering. The former had only single backscattering, whereas the phantom had multiple scattering into 4π sr.

The phantom was prepared as follows: 2 g of ground agar (A9915, Sigma-Aldrich, St. Louis, Missouri) was slowly added, during continuous stirring, to 100 ml of buffered saline preheated to 100 °C. We then added 15 ml of stock ink solution (0.1 ml of India ink in 500 ml of deionized water) to the mixture, along with 0.6 ml of polystyrene spheres (Poly-sciences, Inc., Warrington, Pennsylvania) 0.548 μm in diameter. This mixture was poured into plastic containers (35 mm in diameter, 16 mm in depth) and allowed to cool to room temperature. Experiments were begun within 2–3 h after preparation of the phantom. We determined the optical properties of the phantom by integrating sphere measurements of diffuse reflectance and transmittance as well as collimated transmittance. We calculated them with the inverse adding doubling method³³ and verified them with Monte Carlo simulations. The following values were obtained: μ_a = 0.52 cm⁻¹, μ_s = 17.2 cm⁻¹, and g = 0.74. Based on these values the reduced scattering coefficient μ_s′ [=μ_s(1 − g)] was 4.47 cm⁻¹ and the total attenuation coefficient μ_t (=μ_a + μ_s) was 17.72 cm⁻¹. It is known³⁴ that a unique relationship exists between the diffuse reflectance and the ratio N′ (=μ_s′/μ_a) for a homogeneous semi-infinite turbid medium. This is true for a wide range of optical properties (μ_a = 0.1–1 cm⁻¹, μ_s = 1–1000 cm⁻¹, g = 0.7–0.9). All optical properties of this agar model fall within these values. Thus the ratio N′ of this phantom (=8.6) can uniquely characterize diffuse reflectance. This ratio is also representative of several tissue types.¹¹ It is actually within 5% of the corresponding value (N′= 8.3) for human meniscus at 360 nm—a wavelength that is close to the wavelength used in this study. This result suggests that the current phantom can be considered a scaled tissue model that could adequately describe the diffuse reflectance properties of some tissues such as human meniscus. In addition, as its reduced scattering coefficient μ_s′(4.48 cm⁻¹) is larger than the absorption coefficient (0.52 cm⁻¹), it does represent a scattering-dominated medium. Thus it can also represent a highly scattering turbid medium.

D. Monte Carlo Simulations

Monte Carlo simulations were performed with a customized software based on algorithms reported previously by Prahl et al.³³ and were verified against these earlier algorithms as well as against experimental tissue phantoms.^35,36 The software incorporated the Henyey–Greenstein phase function with variable photon step size, refractive mismatch at all interfaces, and variance reduction. A roulette technique was used in which 10% of the photons of very low weight were increased in weight by a factor of 10 and the rest were terminated. This approach is unbiased and conserves energy.³⁷ The algorithm allowed for simulation of several different fiber-optic sources and ideal Lambertian reflectors. It also provided detailed tracking of escaped photons in three dimensions and a detailed detector model including NA. A general model of detectors was developed to accommodate optical fibers (in both coaxial and elastic scattering spectroscopy configurations) and integrating spheres: The detector was modeled as an oriented absorbing disk with a central hole (washer shaped). Photons that escape the sample propagate to the plane of the detector, and a check of whether the photon would intersect the absorbing region is made. If it would, then we calculate the angle between the photon and the surface normal and compared it with the NA of the detector to decide whether the photon is detected.

Simulations for the white reflectance target assumed an isotropic (Lambertian) reflector (g = 0) with 99% reflectivity at the illumination wavelength. These values are supported by the bidirectional scatter distribution function (BSDF) and UV reflectivity values provided by the manufacturer (Labsphere, Inc., North Sutton, New Hampshire). For the agar phantom, a model of a semi-infinite homogenous slab was used. This choice was based on a comparison of the radial (35-mm-diameter) and axial (16-mm) dimensions of the phantom with penetration depth δ(=3.6 mm) as defined by the diffusion approximation (=1/{3μ_a[μ_a +μ_s(1 − g)]}^1/2). The phantom was assumed to be optically thick along the radial dimension because this dimension was greater than 7δ. We also considered boundary mismatch to account for the experimental conditions (layer of air between the distal parts of the probes and the phantom surface). The indices of refraction for glass (fiber tip), air, and phantom were 1.45, 1, and 1.37, respectively. The simulations accounted for both specular and diffuse reflectance off the phantom: All photons interacted with the initial air–phantom interface. Some of these photons are reflected and never enter the phantom. Reflection was calculated with the use of Fresnel equations for unpolarized light at normal incidence. We tracked these specularly reflected photons to determine whether they enter the detector within the NA cone; if they do, they are counted separately from the photons that enter the phantom and eventually scatter into the detector. All simulations were conducted in a three-dimensional Cartesian grid of 50 μm × 50 μm × 50 μm voxel size with 10⁸ photons. The statistical error for each simulation was estimated as the standard error of the mean of all photons launched.

E. Experimental Procedure

Each probe was mounted onto a precision translation stage and oriented perpendicularly to the target’s surface. The collected reflected light intensity (R) was then obtained as a function of PTD. Such measurements provided R(PTD) curves, which represented the CE profile for each probe at various PTDs. All six combinations of probe–target pairs (three probes, two targets) were evaluated. To prevent probe contamination by the phantoms, we did not take zero-distance (PTD = 0 mm) measurements for the phantoms. Rather, the probes were placed approximately 100 μm from the phantom surface. At each PTD the measured signal was calculated as the time integral of the average of 16 consecutive pulses. The probe energy output was measured with an energy meter (Model Rj-7200, Laser Precision Corporation, Utica, New York) before each experiment. Laser output variations were monitored with a reference photodiode throughout the experiments. Because of setup constraints (optics and optical hardware intervening in the optical path of the collected light), direct experimental measurements of the CE were difficult. Thus, only the corresponding simulation results allow for comparisons of the CEs for the various probe–target pairs.

The signal collected by all three probes was the total reflected light off each target. The experimental signal obtained off the Lambertian target represented diffuse reflectance, as expected from the known BSDF of such targets. However, the signal obtained from the phantom represented total reflectance, including both specular and diffuse components. These components were not separated experimentally. Rather, the total acquired reflectance of the phantom was plotted versus PTD and juxtaposed with the corresponding specular and diffuse components as they were calculated by the simulations. Measurements with the single fiber required an additional processing step. Because of the common illumination–collection path, the collected signal was contaminated by retroreflection off the silica–air interface at the fiber output. To account for this reflection we took baseline measurements without a target (blank shots). This baseline signal was then subtracted from every measurement obtained thereafter. All measurements were performed in triplicate for each probe–target combination. Data are presented as average ± 1 standard deviation (SD).

3. Results

The collection efficiency curves R(PTD) for probes P₁, P₂, and P₃ for the Lambertian reflector are shown in Figs. 2(a), 2(b), and 2(c), respectively. The curve for each probe was characterized by a distinct PTD of maximum light collection. All curves were normalized to this maximum. The single-fiber probe assumed maximum signal intensity when it was in contact with the target. Thereafter the signal decayed monotonically in a quasi-exponential fashion. The decay constants (defined as the 1/e value of the maximum intensity value) were 0.46 and 0.56 mm⁻¹ for the experimental and simulation curves, respectively. Additional simulations for probes of otherwise identical parameters with the 600-μm probe but with core size diameters of 200 and 1000 μm are also shown in Fig. 2(a). These simulations cover a wide range of single probe sizes likely to be used in practical applications. They revealed a strong relation between the probe size and the corresponding signal decay with PTD. Furthermore, these decays did not show the quasi-exponential behavior exhibited by the signal decay of the 600-μm probe.

Fig. 2.

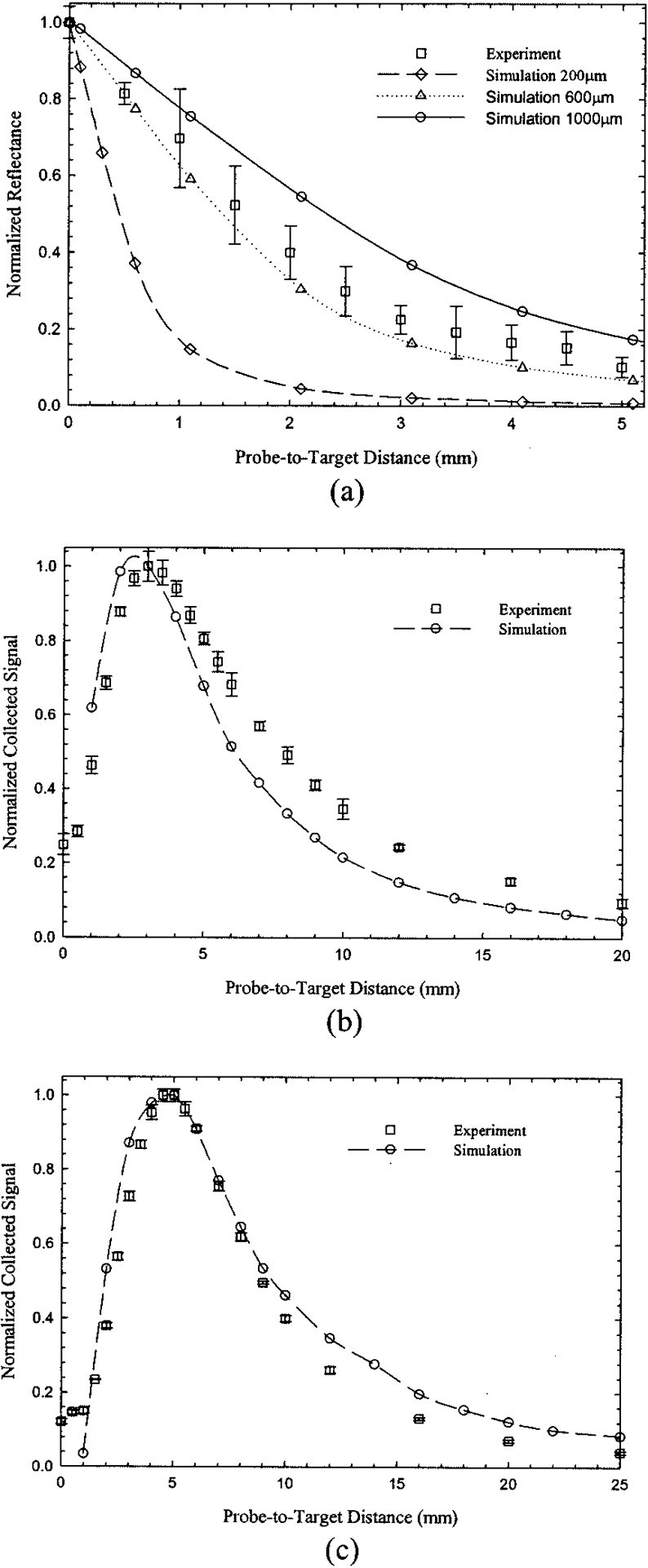
Normalized collected reflected signal versus PTD for the white Lambertian target. Experimental data and Monte Carlo simulations (open circles) are shown for (a) the 600-μm core-diameter single fiber and (b) the tapered and (c) the nontapered bifurcated probes. Additional simulations for 200-μm diameter (open diamonds) and 1000-μm diameter (open triangles) single fibers are shown in (a). Experimental error bars represent ±1 SD. Simulation error bars are not shown because they would not be discernable.

For the bifurcated probes [Figs. 2(b) and 2(c)], maximum light collection occurred several millimeters away from the target. The R(PTD) curves for both P₂ and P₃ probes resembled positively skewed bell-shaped curves with a sharp increase for small PTD’s and slower falloff past the curve’s maximum. Maximum intensity for the P₂ probe was observed at PTD ~ 3.1 mm, whereas the corresponding maximum for probe P₃ was shifted toward a longer PTD (4.7 mm). Additionally, probe P₃ had a broader R(PTD) curve profile than probe P₂. The errors for the simulations presented in Fig. 2 were less than 1.5% for all probes. Thus no error bars appear in Fig. 2, as they would have been indistinguishable from the data symbols. The Monte Carlo simulations for all three probes demonstrated good agreement with the overall shape and location of the maximum of the experimental curves. The simulated CEs (per collection fiber) for the Lambertian target are listed in Table 1 and were 2.43%, 0.097%, and 0.15% for probes P₁, P₂, and P₃, respectively. These values correspond to the maximum value for each R(PTD) curve.

Table 1.

Collection Efficiency (%) from the Monte Carlo Simulation Calculated for Each Collection Fiber at the Maximum of Each R(PTD) Curve

	Target
Probe	Lambertian, Diffused	Phantom
		Diffused	Totala
P1	2.43	0.079	2.40
P2	0.097	0.0031	0.038
P3	0.15	0.0020	0.020

^aSpecular + diffuse.

Figure 3 shows radial plots of the fluence (in joules per square centimeter) of detected photons for the Lambertian surface simulated for three PTDs of 2, 4, and 6 mm. For these plots, each data set was binned into 0.05-mm rings, normalized by the area of each ring, and finally adjusted to the unit area under the curve. The single-fiber simulations [Fig. 3(a)] indicate circular areas of high photon density at the center, which increased in diameter as the PTD increased. For the bifurcated probes the corresponding areas assume distinct shapes that were strongly dependent on the PTD. At distances close to the target (PTD = 2 mm) the maximum of the photon distribution was off center and the corresponding areas resembled a ring. At larger distances (PTD = 4 mm) the maximum of the photon distribution shifted inward towards the center (r = 0 mm), so eventually the corresponding circular areas resembled the shape of that for the single fiber. The distinct ringlike shape persisted even at 4 mm for the largest SDS probe (P₃), whereas it was not present for P₂ (the lower point at r = 0.1 mm and PTD = 6 mm of P₂ is believed to be a simulation underestimation).

Fig. 3.

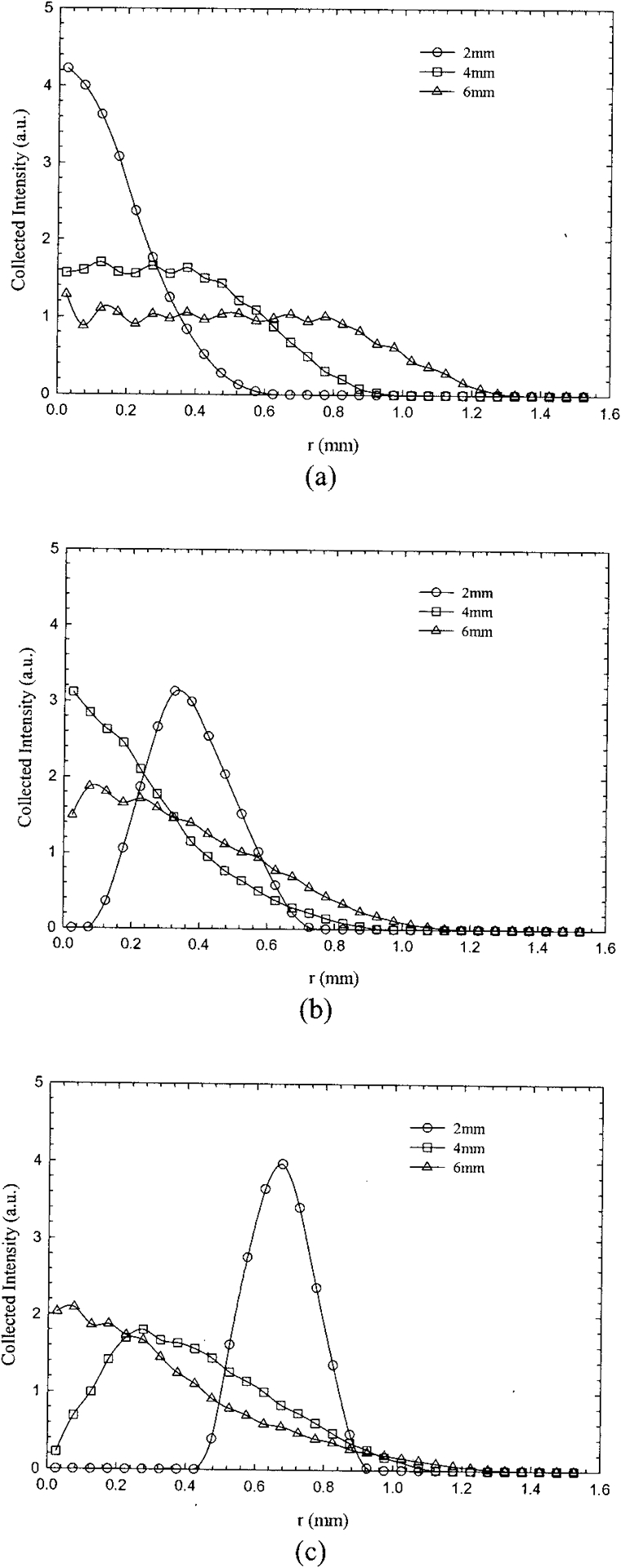
Monte Carlo simulations showing the fluence distribution of the collected diffuse signal (Lambertian target) for (a) the single fiber and probes (b) P₂ and (c) P₃. Each data set was binned into 0.05-mm radial bins, normalized by the area of each ring, and finally adjusted to unit area under the curve. The extent of the area seen by the collection fibers is shown for PTDs of 2, 4, and 6 mm.

The normalized R(PTD) curves for the agar phantom and all three probes that we studied are shown in Fig. 4. The experimental data sets represent the total collected signal, which includes both diffusely and specularly reflected photons. These data are plotted along with simulations for both the total collected signal (specular and diffuse) and the diffusely reflected signal. Overall, all probes exhibited a qualitative behavior similar to that of the Lambertian target, with monotonic decay for the single fiber [Fig. 4(a)] and asymmetric bell-shaped curves for the bifurcated probes [Figs. 4(b) and 4(c)]. The approximate decay constant for the simulated single-fiber decay was 0.39 mm⁻¹ (diffuse signal only). Maxima for curves P₂ and P₃ (total signal) were located at approximately 2.6 and 6 mm, respectively, whereas the corresponding simulation maxima were at 2.6 and 5.1 mm.

Fig. 4.

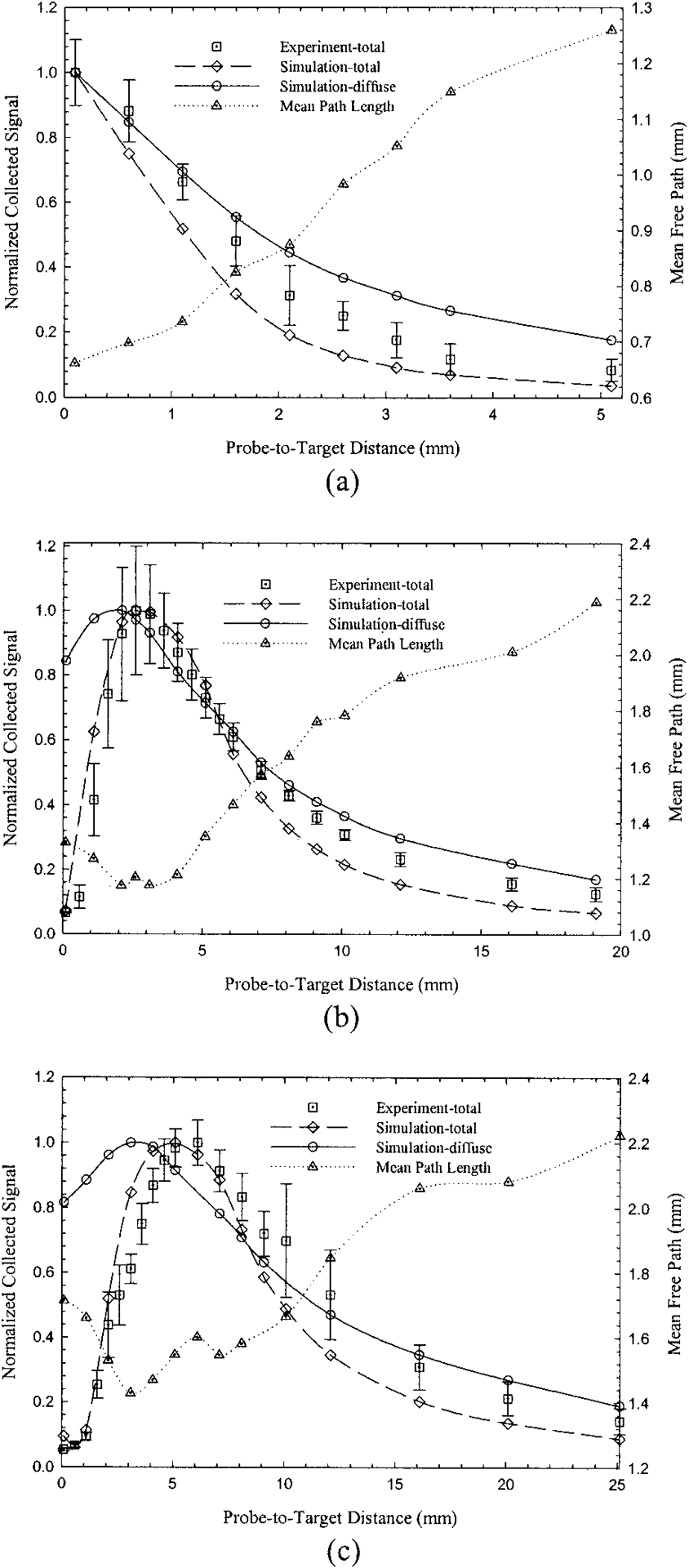
Normalized collected reflected signal versus PTD for (a) the 600-μm single fiber and (b) the tapered and (c) the nontapered bifurcated probes (agar phantom, μ_a = 0.52 cm⁻¹, μ_s = 17.2 cm⁻¹, g = 0.74). Experimental results and Monte Carlo simulations (open diamonds) represent total reflected signal (specular and diffuse). From the same simulations, but separately normalized, open circles represent collected diffuse reflected signals. Experimental error bars represent ±1 SD. Simulation error bars are not shown because they would not be discernable.

The Monte Carlo simulations (total signal) were in good agreement with the experimental curves. Comparison of simulations for the total and the diffuse-only signals revealed that the contribution of the diffuse component to the total (diffuse + specular) signal depended on the probe design, the PTD, or both. For instance, the diffuse component for P₁, as a percentage of the total signal, was 3.3%, 7.7%, and 16.4% for PTDs of 0.1, 2, and 5 mm, respectively. The corresponding percentages for PTDs of 0.1, 5, and 16 mm for probe P₂ (P₃) were 98.4% (97.7%), 7.8% (10.3%), and 20.7% (19.3%), respectively. The maxima of the simulation curves for diffuse-only signals were shifted toward shorter PTDs with respect to the curves that corresponded to the total collected signal. The simulated values of CEs for the phantom were significantly lower than the corresponding values for the Lambertian probe (Table 1) and were 0.079%, 0.0031%, and 0.0020% for P1, P₂, and P₃ respectively. The percentage errors for the simulations presented in Fig. 4 were small and ranged from 1.3% (P₁) to 2.2% (P₃). Therefore no error bars were included in the plots, as they would have been indistinguishable from the symbols.

The mean weighted path length (MPL) of the collected diffuse photons is also shown in Fig. 4 for all probes. The dependence of MPLs and CEs on PTD appeared reversed. For the single fiber the MPL increased with increasing PTD and the corresponding CE decreased. Similar behavior was observed for the bifurcated probes. Thus the minima and maxima of the MPL and the corresponding CE curves were located at approximately the same PTD.

Figures 5–7 show the Monte Carlo simulations for the internal fluence distributions (illumination volume) for all photons entering the medium (bottom) and all diffusely reflected photons collected by the three probes (sampling–detection volume; middle and top). The contours in the figures represent isofluence lines (joules per square centimeter). All data shown are normalized to the maximum value; the contours represent 20–80% of this value in increments of 20%. The lateral and axial boundaries of the illumination and sampling volumes are defined by the 20% isofluence line.

Fig. 5.

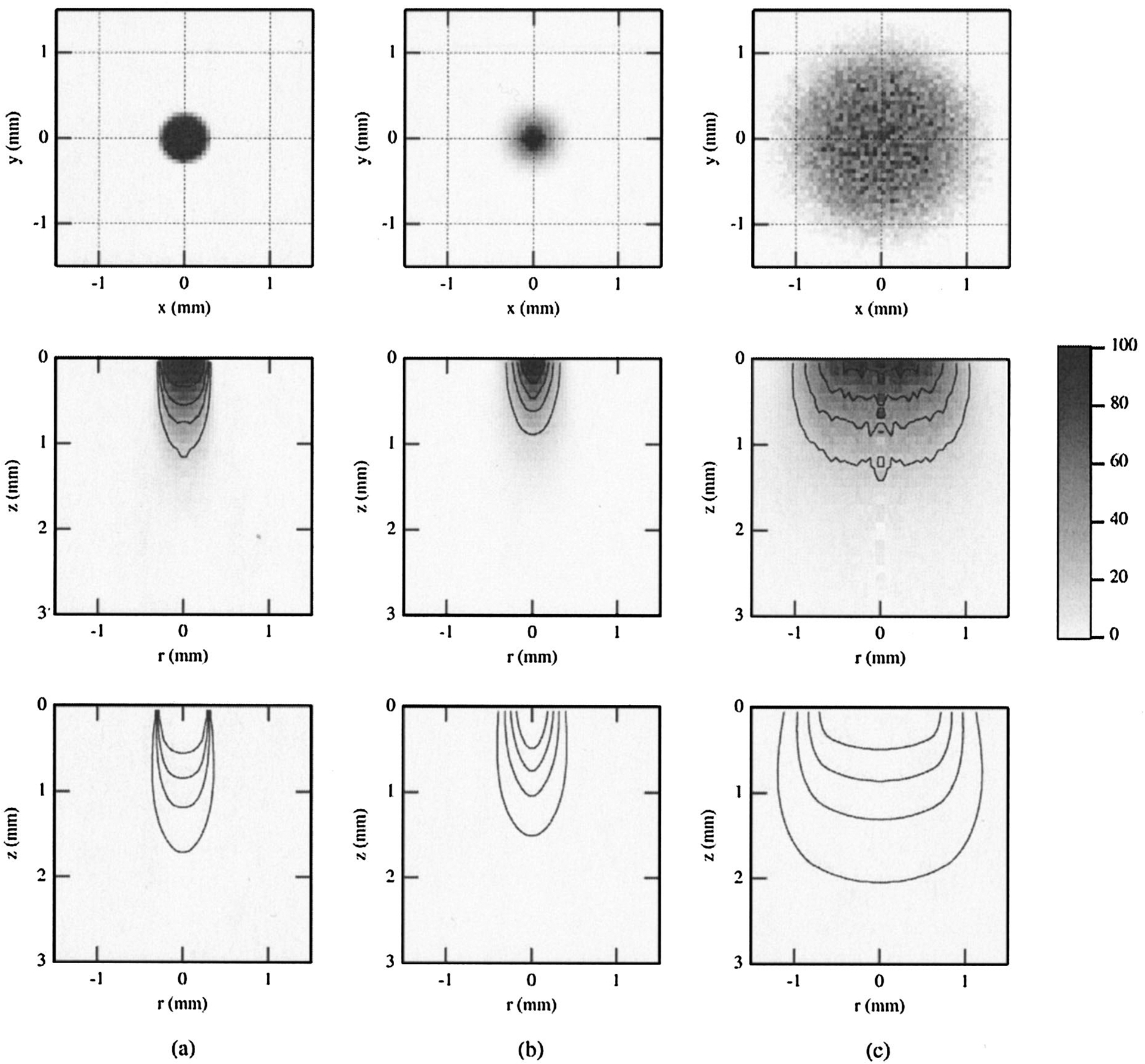
Results of Monte Carlo simulations for single-fiber probe P₁ and the agar phantom, showing the internal fluence distributions of all photons entering the medium (bottom, illumination volume) and all diffuse photons collected by the fiber (middle, sampling volume). Surface distributions for the sampling volume are shown at the top. Results are for PTDs of (a) 0.1, (b) 1, and (c) 5 mm. Contours represent isofluence lines in joules per square centimeter. All data shown are normalized to the maximum value, with the contours representing 20–80% of this value in increments of 20%.

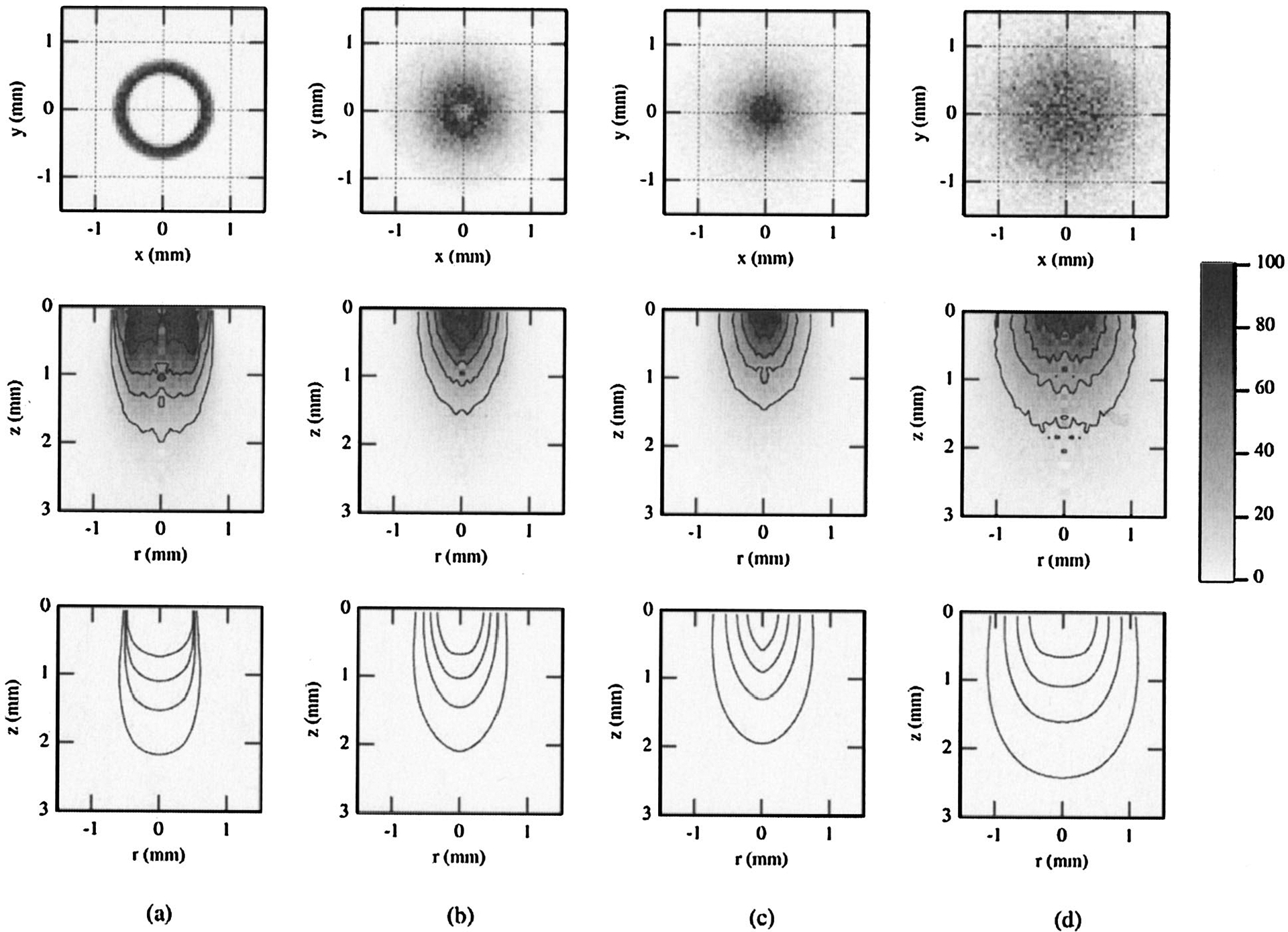
Fig. 7.

Simulations for bifurcated probe P3 and the agar phantom, showing the internal fluence distributions of all photons entering the medium (bottom, illumination volume) and all diffuse photons collected by the fiber (middle, sampling volume). Surface distributions for the sampling volume are shown at the top. Results are for PTDs of (a) 0.1, (b) 2.5, (c) 4, and (d) 7 mm. Contours represent isofluence lines in joules per square centimeter. Data are normalized to the maximum value, with the contours representing 20–80% of this value in increments of 20%.

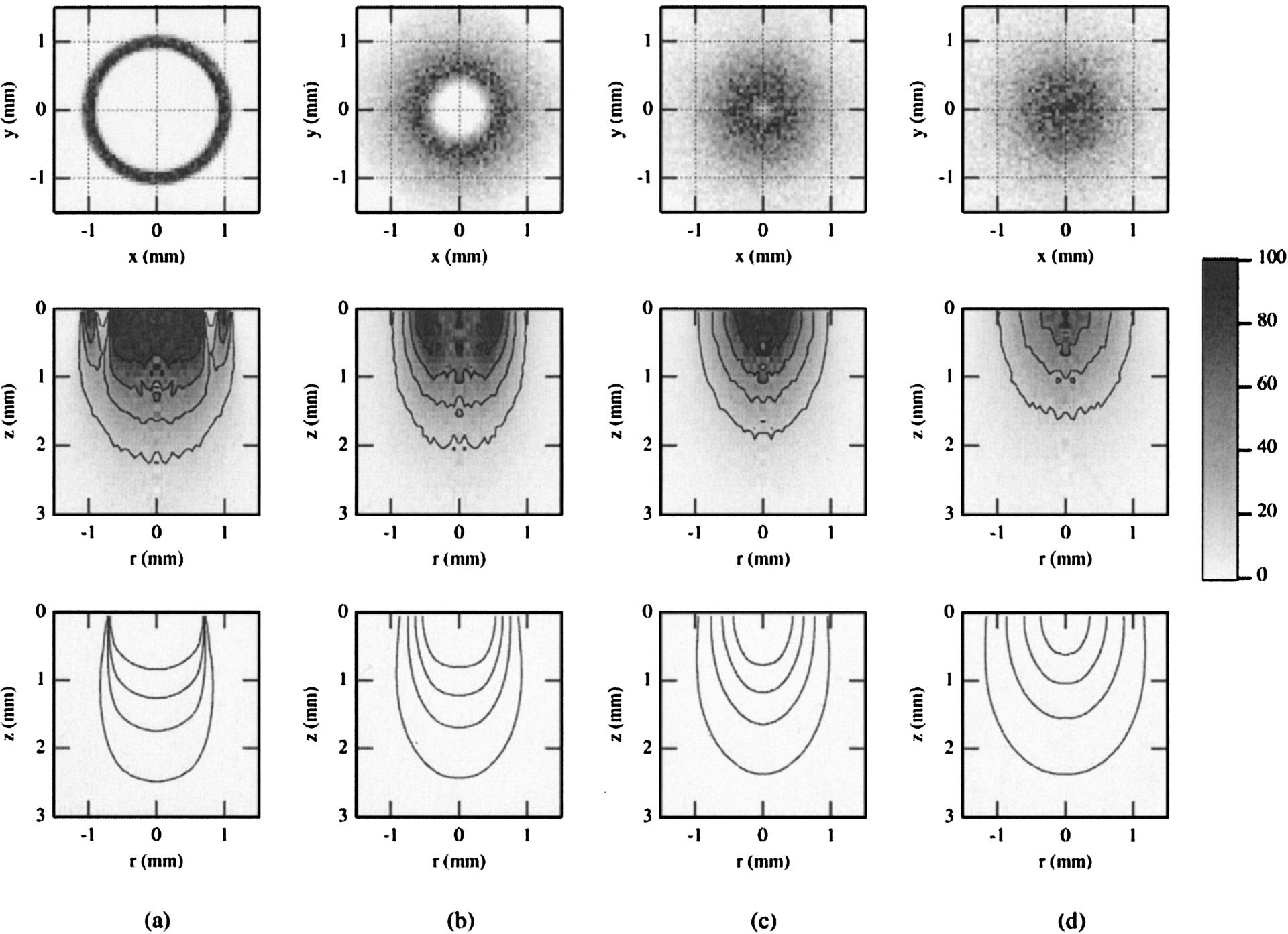
The simulations for the single fiber are shown in Figs. 5(a), 5(b), and 5(c) for PTDs of 0.1, 1, and 5 mm, respectively. Both the illumination and the sampling volumes showed dependence on PTD. This dependence was less strong at small PTDs. At larger distances (5 mm) there was an appreciable increase of the lateral and axial extents of both volumes. The corresponding fluence distributions for the bifurcated probes (Figs. 6 and 7) are shown for PTDs of 0.1, 2.5, 4.0, and 7 mm (from left to right). For P₂, at short PTDs (0.1–4 mm) there was an initial decrease of the overall extent of the sampling volumes. This trend was reversed at larger distances (7 mm). The radial extent of the illumination volume increased with increasing PTD, whereas the axial extent followed the same trend as the sampling volume. For P₃ (Fig. 7, middle), a systematic decrease of the sampling volumes was observed for all PTDs (0.1–7 mm) shown. Illumination volumes increased radially with increasing PTD. No notable change in the axial extent was observed. The superficial parts of the sampling volumes of both bifurcated probes (Figs. 6 and 7, top) had a ringlike distribution that was PTD dependent, much like the distribution of the Lambertian reflector [Figs. 3(b) and 3(c)]. This structure prevailed for short distances (<2.5 mm for P₂ and <4 mm for P₃). At contact, or very close to the target (PTD = 0.1 mm), a low-photon-density volume that coincided with the dead space between the illumination and collection channels was apparent, especially for P₃ [Fig. 7(a), middle]. Overall, for all PTDs and probes shown, the sampling volumes appeared to follow approximately the PTD-dependent modulations of the corresponding illumination volumes. The simulation results have shown that the maximum photon weight values for the illumination volumes were approximately 3 orders of magnitude higher than the values of the sampling volumes for all three probes, so the illumination and sampling volumes were not plotted on the same scale.

Fig. 6.

Results of Monte Carlo simulations for bifurcated probe P₂ and the agar phantom, showing the internal fluence distributions of all photons entering the medium (bottom, illumination volume) and all diffuse photons collected by the fiber (middle, sampling volume). Surface distributions for the sampling volume are shown at the top. Results are for PTDs of (a) 0.1, (b) 2.5, (c) 4, and (d) 7 mm. Contours represent isofluence lines in joules per square centimeter. All data shown are normalized to the maximum value, with the contours representing 20–80% of this value in increments of 20%.

Noteworthy also are the distribution differences shown at PTDs of 0.1 and 7 mm for probe P₃. These two distances correspond, approximately, to the same (diffuse) signal level [Fig. 4(c)]. Despite this signal equality, significant differences in both the illumination and the sampling volumes can be seen. These differences are more striking for the sampling volumes, for which both axial and lateral extents vary significantly. This discrepancy applies also to the overall shape of these volumes, as the ringlike structure observed at 0.1 mm was completely absent at 7 mm.

4. Discussion

A. Single Fiber

The single fiber allowed for maximum signal collection when it was in contact with [Fig. 2(a)] or very close to [Fig. 4(a)] the target. This is a direct consequence of the inherent overlap of source and detector areas for this probe type. The collected signal decayed monotonically with increasing PTD because the collection solid angle subtended by the fiber at the surface was monotonically reduced. Whereas a quasi-exponential decay was seen for the 600-μm probe, such was not the case for probes with smaller (200-μm) or larger (1000-μm) core diameters. The simulations indicate a strong influence of the fiber diameter: The CE of smaller probes decays much more rapidly than the CE of larger probes. Nevertheless, at distances of ~5 mm from the target, loss of collected signal equal to or greater than 80% of the maximum was observed for both targets and for all three experimental or simulated probe sizes or both. The results described above suggest that application of a single-fiber probe in contact with tissue allows for the highest SNR. Although such an approach is desirable, it is not always applicable because of various clinical or other anatomical restrictions discussed in Section 1. The results presented here may provide guidance in minimizing this SNR reduction. For example, and assuming that anatomical restrictions do not militate against it, the use of probes of larger diameters could partially compensate for the signal reduction.

Simulations of CE versus PTD for the agar phantom [Fig. 4(a), open circles] showed an approximately exponential decay with a constant of 0.39 mm⁻¹. This decay was slower than the corresponding simulated (0.56-mm⁻¹) decay of the Lambertian target [Fig. 2(a), 600-μm fiber]. This trend may be attributed to the difference in the angular distribution of the reemitted light between the two types of target: The relatively small reduced scattering coefficient of the phantom (μ_s′= 4.47 cm⁻¹) implies a (large) reduced mean free path (=1/μ_s′= 2.2 mm). This in turn suggests that the detected photons have a greater penetration depth and larger sampling volume compared with phantoms with larger reduced scattering coefficients. The emerging distribution of such photons is angularly biased toward the optical axis of the probe.^10,11,22 Therefore coupling of these photons into the fiber should be less sensitive with increasing PTD than coupling of the isotropically reflected photons off the Lambertian target.

As one can see from Table 1, the simulated value for the CE of the Lambertian target (at contact) was more than 30-fold higher than the value for the diffuse reflectance from the agar phantom (at PTD = 0.1 mm). The greater light collection from the Lambertian target is largely a consequence of the presence of many more reemitted photons, as this target is essentially a phantom of high scattering coefficient. Important insights into the effect of optical properties in the CE of a single fiber in contact with tissue were given by Bargo et al.²² Those authors gave a different definition of the CE from the one in this study. They define a probe CE as the ratio of coupled photons to the total number of photons impinging upon the probe input. Because of this difference in the definition of CE and because most of our measurements are performed at PTD > 0 mm, direct comparison of our results with their simulations is difficult. However, for the Lambertian target at PTD = 0 mm the two definitions are equivalent because, on contact, virtually all reflected light (R = 99%) hits the (single) probe input. In this case the CE value at high scattering (Lambertian case) was 2.66%; our corresponding simulation value of 2.43% compares favorably with it.

Optimization of the CE is important, as it is related to a favorable SNR. However, it does not by itself constitute an adequate index of optimal probe design. Of further significance is the optimal determination of the sampling depth of the collected signal. In the context of diagnostic techniques, this determination is especially important when heterogeneous targets such as tissues are encountered; a more-accurate estimation of the path of the photons that contribute to the collected signal improves the correlation of the photon path with the corresponding histopathology and thus the diagnostic value of such techniques. The simulations presented in Figs. 3(a) and 5 highlight the importance of PTD in the determination of these sampling volumes. As shown in Fig. 3(a), increasing PTD results in increasing radial sampling of the Lambertian surface. This result is consistent with the expected increase in the illumination area as dictated by the NA of the fiber. The results for the agar phantom (Fig. 5) are less consistent, at least for the range of simulated PTD’s. Decreased depth sensitivity has been observed at PTD of 1 mm, whereas tissue sampling was deeper at PTDs of 0.1 and 5 mm.

The issue of the influence of probe design and excitation–collection geometry on depth sensitivity has been of interest in a number of studies. Computational¹⁷ and experimental¹⁹ fluorescence studies of a single fiber have been reported by Pfefer et al. Their results have indicated that increased probe–tissue spacing not only reduced CE but also increased the probe’s relative sensitivity to deeper tissue layers. Our results extend these findings for diffusely scattered light and indicate a nonmonotonic behavior of depth sensitivity with PTD, at least for the range of PTDs shown in Fig. 5. The effect of PTD was more profound on the lateral extent than on the depth of the sampling volume. Elucidation of the observed depth-sensitivity modulation with PTD would, however, require further investigations with a wider range of core sizes and PTDs. Quan and Ramanujam³⁸ have suggested a variable-aperture method by which fluorescence that originates from a turbid medium can be spatially resolved. They achieved this resolution not by increasing the distance of the probe from the target but rather by increasing the diameter of the illumination beam. Their experimental and associated computational work with a stratified tissue model corroborated this suggestion. Such an increase in depth sensitivity was also observed with the equivalent approach of increasing the fiber diameter or the illumination spot size.^17,19

B. Bifurcated Probes

Signal collection by both bifurcated probes was significantly influenced by the geometrical arrangement of the illumination and detection components. Unlike the observed monotonic decay of the signal versus PTD for the single fiber, bifurcated probes showed an asymmetric signal distribution about a maximum intensity value. These findings are in agreement with results reported by Cooney et al.¹⁵ and Pfefer et al.¹⁸ The observed R(PTD) profiles are a direct consequence of the probe designs. The illumination and the collection fiber cores of a bifurcated probe are separated by dead space that comprises the intervening cladding and buffer. Thus at PTD = 0 mm there is no overlap between the illumination and the collection cones, which results in extremely low signal collection because only a very small number of laterally scattered photons are collected. At larger distances, minimal signal is also expected, as the collection fibers subtend a small solid angle with respect to the illuminated area. The extremely low signal at small PTDs is partially responsible for the mismatch of the experimental and simulation values [Figs. 2(b) and 2(c)], as it reduces the accuracy of the simulations. Another source of simulation divergence is the deviation from the assumption of uniform light distribution at the probe output. This deviation is more evident for P₃, for which at small PTD the phantom sees a nonuniform distribution that is due to the discrete spatial distribution of the individual fibers that constitute the illumination channel.

The shape of the R(PTD) profile and the location of its maximum are a result of competition of the increasing overlap between illumination and collection cones and the decay of light collection with PTD. The probe design characteristics that determine this overlap are the SDS and the fiber NAs. The R(PTD) curve’s maximum location for P₂ was shorter than the corresponding location of probe P₃ for both targets. As both the illumination and the collection fibers of probes P₂ and P₃ had the same NA, this difference in location may be due to the difference in SDS (0.64 compared with 1 mm). This separation determined the degree of overlap between illumination and collection cones: Shorter center-to-center separation (probe P₂) allows for earlier (shorter PTD) appearance of the curve maximum than longer separation (probe P₃). It is worth noting that for the Lambertian reflector the ratio of the locations of maxima of probes P₃ and P₂ was ~1.52. This ratio was close to the ratio of the center-to-center distance between the source and the detector (1.56). This was also true for the agar phantom and for the location of maxima of the (simulated) diffuse reflectance. However, this proportionality did not hold for the total signal, which was dominated by specular reflection. These findings suggest that bifurcated probe designs allow for some adjustment of the location of maximum efficiency. Thus, in applications in which anatomical or other design considerations impose restrictions on the allowed PTDs, one can still achieve maximum (but not necessarily optimum) CE by adjusting the SDS.

As with the single fiber, and for the same reasons as mentioned above, the CE (at curve maxima) of the bifurcated probes was higher for the Lambertian reflector than for the agar phantom. In this case the SDS also influenced the CE, and it was systematically lower for the probe with the larger SDS (P₃) for both targets. Photons collected by a probe with larger SDS have traveled longer (lateral and axial) distances than photons collected by a probe of shorter SDS and have experienced more attenuation. Consequently, on average, less light is available for capture and hence the CE is lower. Among the three probes tested here, the one with the least SDS, namely, the single-fiber probe, had the highest efficiency (at maximum) for both targets. In this context our results suggest a SNR advantage of the particular (600-μm) single fiber over the bifurcated probes for contact applications. For noncontact applications the relative decays will also depend on the size of the illumination–collection fibers, as is clearly indicated in Fig. 2(a), where signal decay is shown to be strongly dependent on fiber size. This finding is also supported by other simulation and experimental results.^17,19 Therefore the present results are suggestive only of the specific probe parameters used and cannot be generalized.

In the case of surface isotropic reflectance (Fig. 3) the Monte Carlo simulations indicate that the origin of captured light depends significantly on the PTD. For small PTD a ringlike structure was observed, whereas at longer PTD the origin resembled the shape of the corresponding area for the single-fiber probe. The ringlike shape is a consequence of partial overlap between the regions defined by the illumination and collection cones and of the cylindrical symmetry of the P₂ and P₃ probes. Similar results are shown for the phantom in Figs. 6 and 7. The nonmonotonic curves of the bifurcated probes show that identical collection efficiencies (equal signal) can be obtained at two different PTDs. It is important to note that equal signal intensity does not necessarily imply the same sampling volume. The simulations in Fig. 7 show a comparison of the sampling volumes for two distances (0.1 and 7 mm) that correspond to approximately identical signal levels [Fig. 4(c), open circles]. The surface areas and volumes seen by the detector are considerably different for the two equal-signal PTDs. The sampling volume was significantly more superficial at the longer PTD. Additionally, the two volume distributions were also distinct. The volume that corresponded to PTD closer to the target was substantially influenced by the structure of the distal part of the probe (collection ring, dead space), whereas the volume at the longer PTD did not reflect this and had a photon distribution similar to that of a single fiber. Our results suggest that, for bifurcated probes, the signal level obtained does not uniquely identify the sampling or illumination volumes. Rather, the signal level needs to be considered along with the appropriate PTD to allow for optimal tissue interrogation. Whereas these results may be inconsequential for homogeneous targets, they are of crucial diagnostic importance when heterogeneous targets such as tissues and other turbid media are investigated. The findings argue for careful application of the fiber-optic probes because the interrogated volumes and therefore the resultant diagnosis can depend strongly on the geometry of application. Placement of the probes at a fixed distance from the tissue could minimize the acquisition of spurious data; this is of particular importance for in vivo applications for which motion artifacts could compromise the diagnostic value of fiber-optic-based spectroscopic methods.

Finally, the observed discrepancy between sampling volumes at various PTD’s and probe designs could have possible consequences for time-resolved measurements. As our simulations indicate [Figs. 4(a) and 4(c)], the MPL of the collected photons is PTD and probe-design dependent. This in turn allows for time dispersion of the collected pulsed signal.^27,39,40 Thus various PTDs and probe designs can modulate the width of the acquired input pulse. Because this pulse is applied as input to the deconvolution algorithm for estimation of fluorescence lifetime, it is expected that this estimation can be affected by both the PTD and the probe design. In our study, no pulse stretching was observed for all probes and targets used, at least within the time resolution of the experimental setup (~0.5 ns). Nevertheless, our results provide trends in the effect of probe design and PTD on the pulse width of the collected light. For instance, a photon inside a medium of index of refraction 1.37 will travel a distance of 0.5 mm in ~10 ps. This distance is of approximately the same magnitude as the changes of MPL observed for various PTDs and probes in the simulations (Fig. 4). Thus the expected pulse modulations will be of the order of ~10 ps or less. Whereas these values are extremely low for most fluorescence studies, they could become significant in fiber-optics-based time-resolved reflectance studies involving ultrashort (picosecond and femtosecond) pulses.

Whereas the emphasis of this study has been on biological applications, our results could be useful in other areas too. For instance, in remote diffuse reflectance chemical analysis and Raman spectroscopy, media ranging from granular solids to turbid heterogeneous mixtures are encountered. It is worth noting, though, that interpretation of the results presented here cannot be freely extrapolated to other probe designs or media. The probes used here served only as paradigms; a detailed analysis of a wide range of fiber parameters with systematic changes of fiber diameter, SDS, and NAs is the subject of our planned future work. Similarly, experiments and simulations were performed with an ideal, homogeneous phantom with optical properties that were not entirely representative of tissues in the wavelength of interest. Understanding of more-realistic conditions will require construction and in vitro testing of realistic tissue phantoms, investigations that will include a wide range of optical properties, and finally in vivo validation.

5. Conclusions

We have investigated the effects of the fiber-optic probe design and excitation-collection geometry (PTD) on two important factors that pertain to biological spectroscopy: the volume of interrogated tissue and the collection efficiency and origin of collected excitation light. The problem was addressed experimentally with diffuse reflectance measurements in the UV range (near 337 nm) and computationally with Monte Carlo simulations. We studied the effects of three specific probe designs (one single-fiber probe and two bifurcated multifiber probes) and of the PTD on the collected diffuse reflectance from an isotropic reflectance target and an agar-based tissue phantom.

We have found that the probe design and the excitation-collection geometry strongly influence the illumination volume as well as the CE and the sampling volume of the collected signal. Of particular interest are the following findings: (a) For all three probes tested, the CE was both PTD and probe-design dependent. The overall probe design resulted in monotonic (single-fiber probe) or nonmonotonic (bifurcated probes) behavior of the CE with increasing PTD. Higher efficiencies were observed for the single-fiber probe than for the bifurcated probes. (b) The distributions of the illumination and sampling volumes of the collected signal were also dependent on the probe design and the PTD. Depth sensitivity was modulated by the PTD and the probe design. Increased sensitivity to superficial medium regions was observed at increased PTDs for one of the bifurcated probes (P₃), whereas for the single fiber and the second bifurcated probe (P₂) the extent of these volumes did not depend monotonically on the PTD. (c) The estimation of lifetime in time-resolved measurements could be influenced by PTD and probe-design dependence of the excitation pulse width. This effect is limited to ultrashort (picosecond and femtosecond) pulse applications.

Our findings demonstrate the significant influence of both probe design and PTD on the diagnostic value of fiber-optic-based spectroscopic techniques. Such findings can be applied toward probe-design optimization, which in turn could improve quantitative optical spectroscopy of tissue.