A Versatile Deep Learning Architecture for Classification and Label-Free Prediction of Hyperspectral Images

Abstract

Hyperspectral imaging is a technique that provides rich chemical or compositional information not regularly available to traditional imaging modalities such as intensity imaging or color imaging based on the reflection, transmission, or emission of light. Analysis of hyperspectral imaging often relies on machine learning methods to extract information. Here, we present a new flexible architecture, the U-within-U-Net, that can perform classification, segmentation, and prediction of orthogonal imaging modalities on a variety of hyperspectral imaging techniques. Specifically, we demonstrate feature segmentation and classification on the Indian Pines hyperspectral dataset and simultaneous location prediction of multiple drugs in mass spectrometry imaging of rat liver tissue. We further demonstrate label-free fluorescence image prediction from hyperspectral stimulated Raman scattering microscopy images. The applicability of the U-within-U-Net architecture on diverse datasets with widely varying input and output dimensions and data sources suggest that it has great potential in advancing the use of hyperspectral imaging across many different application areas ranging from remote sensing, to medical imaging, to microscopy.

Introduction

Computer vision techniques based on deep learning have recently demonstrated a myriad of novel applications in many disciplines. With the continuous improvement and availability of advanced computing hardware and open-source methods, deep learning is finding broader use in a wide variety of imaging, sensing, and biophotonics research^1,2. The flexibility of deep learning for image processing enables facile adoption of existing frameworks for many different imaging modalities such as transmitted light microscopy, fluorescence microscopy, X-ray imaging, magnetic resonance imaging, and many more^3–7. Often the images from such techniques are passed to a deep learning algorithm to perform tasks like classifying diseases, segmenting spatial features, improving image quality, or predicting alternate imaging modalities^8–11. However, the majority of work done so far performs deep learning on monospectral images. Such monospectral images contain only a single intensity value at each pixel. That is, there is no spectral information inherent to the imaging technique such as in black-and-white photography, X-ray imaging, or magnetic resonance imaging. Contrary to monospectral images are multispectral and hyperspectral images where multiple spectral components of a field of view can be depicted in their own image. We take “multispectral” to be a subset of “hyperspectral“ specifically pertaining to images that contain relatively few spectral channels (e.g. RGB imaging). Hyperspectral imaging combines spectroscopy and imaging such that each pixel of the image contains a wide spectral profile that allows for detailed characterization.

Linear decomposition, phasor analysis, support vector machines and other machine learning methods have indeed been used for analysis of hyperspectral imaging datasets^12–18. While many of these techniques have demonstrated promising results, such methods may suffer from limited generalizability or information loss, limiting their ultimate performance^19,20 Deep learning, in contrast, potentially offers a method for learning based on both spectral and spatial signatures and their nonlinear interplay allowing for improved performance in a variety of hyperspectral imaging analysis tasks^21,22. However, techniques for these hyperspectral stacks face unique challenges in computer vision research^23,24. For example, standard deep learning architectures that work for monospectral images (consisting of 2 or 3 spatial dimensions), may not work for hyperspectral stacks due to the extra dimension needed for spectral information. Frameworks such as Mayerich et al’s Stain-less Staining²⁵ or Behrmann et al’s work in mass spec imaging²⁶ address this by interpreting the spectra at individual pixels of hyperspectral images to produce excellent results in label-free prediction and classification, but may be missing contextual information from spatial convolutions of the whole image. Zhang et al’s recently published work bypasses the need for spectral deep learning by using machine learning to interpret spectral information and create truth maps to which spatial deep learning of images can be trained²⁷. Other frameworks for hyperspectral deep learning based on spectral-spatial convolutions also exist but are often rigid; only performing a particular task like binary pixel or multi-class label classification^28–30. Further, a convolutional framework for predicting entirely alternate imaging modalities (where the final number of spectral channels is unlikely to match the input, but spatial resolution is maintained) from hyperspectral images, to our knowledge, has not been reported. We thus present a new architecture, the U-wthin-U-Net (UwU-Net) to address these current shortcomings in hyperspectral deep learning and improve the utility of hyperspectral imaging techniques.

The UwU-Net Architecture presented here is based on the U-Net architecture developed originally by Ronneberger et al where a specialized autoencoder encodes and decodes spatial feature information in an input image to reconstruct some new output image³¹. The U-Net separates itself from a traditional autoencoder with the recontextualization of information through concatenations at equivalent encode-decode levels (noted as blue arrows in Figure 1a). This eliminates the discarding of information as in a traditional autoencoder. While the original work was concerned with image segmentation, the U-Net has seen use in a variety of applications including segmentation, label-free prediction, and denoising^9,32–34. However, most works that utilize the U-Net in this way are not concerned with images that contain multiple spectral channels. Indeed, the original U-Net is generally not applicable to hyperspectral images as the architecture is dedicated to encoding multiple spatial feature channels starting from a single spatial channel image as shown in Figure 1a. The typical 2D kernel of a U-Net is thus not well suited for hyperspectral stacks which have a third tensor dimension dedicated to spectral channels. A 3D kernel could potentially be used, but then the spatial and spectral information are being mixed during the feature encoding in a problematic fashion for image reconstruction³⁵. Modification of input and output layers to match spectral dimensions is often useful in the multispectral regime but may be too facile of a change to adequately handle spectrally complex hyperspectral images. While other recently reported modifications to the U-Net have also shown improvements with respect to the original U-Net on semantic segmentation and classification of remote sensing datasets (some of which involve multispectral datasets)^36–38, we report a robust architecture for multiple hyperspectral imaging tasks.

Fig. 1:

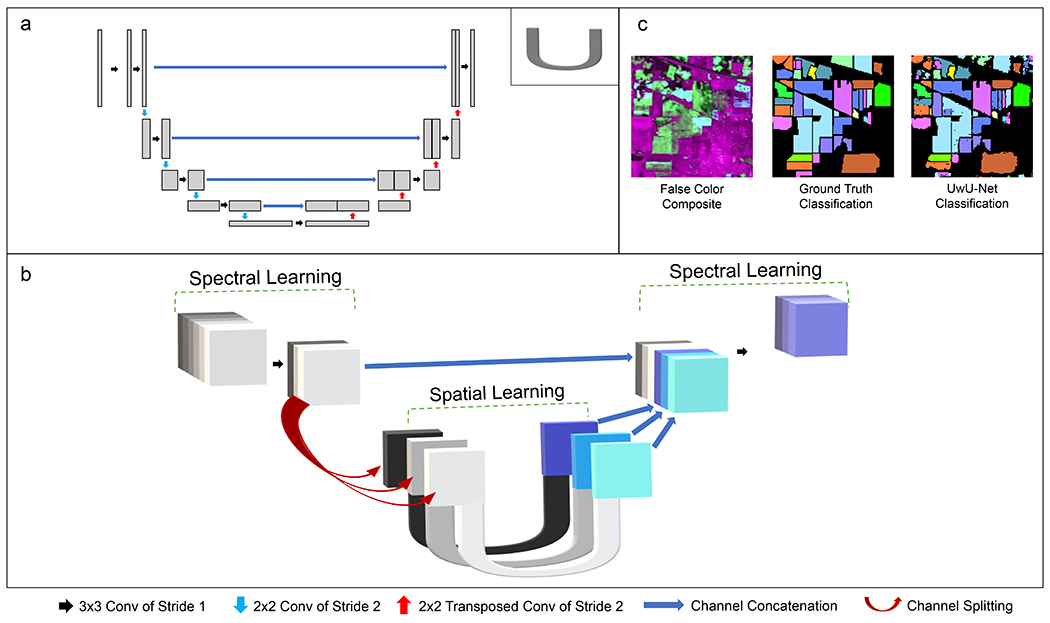
Architecture Diagrams and Indian Pines Classification.

Panel a shows a schematic representation of the traditional U-Net (adapted from Ounkomel et al.³³) where a single 2D image is convolved to encode and decode spatial features. The “U” in the upper right corner of panel a denotes its schematic representation as used in panel b. Panel b shows the schematic representation of the UwU-Net where an arbitrarily dimensioned hyperspectral stack is convolved both spectrally and spatially to produce an arbitrarily dimensioned output stack. The symbols used in panels a and b are noted at the bottom of the figure to show their operational meanings. Here, “conv” is short for convolution and the “NxN” shown describes with pixel size of the kernel used for convolution. Panel c depicts a false color composite of 3 different spectral bands from the original 200-band hyperspectral stack, the truth classifications, and predicted classifications from the UwU-net.

To create a hyperspectral deep learning architecture with the robustness and features of the traditional U-Net, we have amended the U-Net architecture such that spectral channel information is handled by a separate “U” structure “outside” of an arbitrary number of traditional spatial U-Nets as shown in Figure 1b. This UwU-Net architecture allows dedication of tunable free parameters to both spectral information (outer U) and spatial information (inner U’s). The architecture’s parameters can be empirically tuned to change the spectral layer depth, number of spatial U’s at the center, or output spectral size based on the dataset. Here we demonstrate the utility of this new architecture in 3 different tasks on 3 different types of hyperspectral imaging: feature segmentation and classification on the high altitude hyperspectral imaging Indian Pines dataset, monoisotopic drug location prediction in rat liver from mass spectrometry images, and label-free prediction of cellular organelle fluorescence in stimulated Raman scattering (SRS) microscopy.

The first task concerns segmentation and classification of the Indian Pines dataset which depicts a scene of farmland in northwest Indiana across a large range of wavelengths spanning the ultraviolet to short infrared region (400-2500 nm)³⁹. The publicly available dataset was acquired by the Airborne Visible/Infrared Imaging Spectrometer and provides a model task for hyperspectral deep learning: segmentation and classification of various crop and foliage types. The broad spectrum and spatial heterogeneity of the scene demonstrates a deep learning algorithm’s ability to correctly identify and segment features based on both spectral signatures and spatial positions. Moreover, the use of this dataset by previous work in hyperspectral deep learning allows for comparison of our proposed architecture^40–42.

The second task concerns predicting drug location in a model rat liver tissue sample from mass spectrometry imaging. Mass spectrometry imaging (MSI) is a powerful technique that provides spatially resolved, highly specific chemical information in the form of molecular ion masses. Where most deep learning computer vision work is centered around interpretation of optical images, MSI is particularly interesting to approach with deep-learning as it has an enormous spectral dimension that provides highly specific, but difficult to interpret in situ chemical information^43,44. Most MSI work follows from traditional linear decomposition and analysis that is well-developed and ubiquitous in mass spectrometry^45–49. Deep learning has been demonstrated for MSI datasets^26,43,50,51, but has been chiefly used for spectral dimensionality reduction or interpretation. To our knowledge, the simultaneous interpretation of spatial and spectral information using convolutional deep learning in MSI has yet to be reported. We demonstrate one way the UwU-Net architecture could be used in MSI by simultaneously predicting the highly specific monoisotopic peak locations of 12 drugs from low mass resolution binned images.

Finally, the third task demonstrates the capability of the UwU-Net to perform label-free prediction of fluorescence images from SRS microscopy images. SRS microscopy is a hyperspectral imaging technique where molecular vibrational bonds are coherently interrogated by two ultrashort laser pulses^52–54. While the vibrational information afforded by SRS microscopy can be specific to a given molecule, there are often many overlapping contributions to vibrational signals that confound image interpretation. In this work, we show that the specificity of SRS microscopy can be improved by deep learning to predict fluorescence images that are highly specific to an organelle. Further, we show that the trained algorithms can be multiplexed to create label-free cell organelle images in live cells.

Indian Pines Classification

To demonstrate this flexibility and to validate the architecture’s capability to classify an arbitrary number of features from hyperspectral images, a 1-U UwU-Net (where there is 1 spatial U-Net at the center of the architecture) and 17-U UwU-Net (where there are 17 spatial U-Nets at the center) were trained to classify the Indian Pines AVARIS dataset³⁹. The hyperspectral images consist of 200 spectral channels (where 20 of the original 220 bands have been removed due to water absorption) across a broad range of wavelengths (400-2500 nm) with 144 x 144 pixel images (cropped from 145 x 145 to be compatible with the spatial U-Nets) at each wavelength. The images contain a high-altitude 2 mile by 2 mile field of view of farmland in northwest Indiana. The ground truth images consist of non-mutually exclusive hand-drawn maps of the various crops and foliage depicted in the field of view. In total, there are 16 classifications shown in Figure 1c and listed in Table 1. Here, the UwU-Net is trained to predict a 17 x 144 x 144 image stack (16 classifications plus an unused background) from the 200 x 144 x 144 input image stack. The initial 200 channels are first reduced via convolution to 100 then to the final 1 (for the 1-U UwU-Net) or 17 (for the 17-U UwU-Net) before spatial learning. The output predicted images are thresholded to create a binary map to compare against the ground truth image. Looking at the results in Table 1, the 17-U UwU-Net performs well with nearly all classifications exceeding 99% accuracy. The exceptions are the classification of an untilled corn field in the upper left of the field of view that are instead identified as a mixture of the three soybean classifications. We also note the prediction of crops at the top-middle, top-right, and bottom of the field of view. While these areas contribute to the error, we note that crops do exist in these parts of the hyperspectral images (as seen in the composite image in Figure 1c) but are unidentified in the hand-drawn truth maps. To better reflect the model’s performance, especially in these cases, counts of false positive and negative pixels and the intersection over union (IOU) for each class is provided in Extended Data Table 1. The overall accuracy (99.48% ± 0.50%), however, is in concordance with state-of-the-art architectures for hyperspectral classification on the Indian Pines dataset^{41,42,55–57}. Three of these architectures’ (ResNet, Multi-Path ResNet, and Auxillary Capsule GAN) classification accuracies are shown in Table 1 for comparison with the 17-U UwU-Net demonstrating the highest accuracy. We note that the 1-U UwU-Net (with its more modest modifications to the original U-Net) performs worse than the other models suggesting that the additional spatial parameters afforded by the parallel U-Nets at the center of the UwU-Net contribute towards a more accurate model. For additional comparison, a basic U-Net (where the initial and final layers have been simply adjusted to accommodate the desired input/output channel number) was also trained. However, it was unable to classify any of the labels properly suggesting that UwU-Nets spectral layers are critical for proper identifications. A representative example of one of the basic U-Net’s errant classifications is shown in Extended Data Figure 1. These results demonstrate the UwU-Net’s ability to simultaneously segment and classify features from hyperspectral images with high accuracy. However, the UwU-Net is not limited to a binary pixel classification, like some hyperspectral architectures here compared, but can also predict intensity features as shown in the demonstrations below.

Table 1:

Classification accuracy of the Indian Pines dataset.

The individual and overall classification accuracy of the Indian Pines dataset from various hyperspectral deep learning models and the presented UwU-Net model. Note the ResNet, MPRN, and AU-Caps-GAN models are reported as produced in their respective references, the ResNet and MPRN classifications were reported without uncertainties. Reported uncertainties refer to the standard deviation among the n= 16 classifications.

Label	UwU-Net (1-U)	ResNet41	MPRN41	AU-Caps-Gan42	UwU-Net (17-U)
Alfalfa	97.40	98.33	98.89	99.15	99.96
Corn (No Till)	93.66	99.28	99.51	99.50	98.57
Corn (Min Till)	95.98	98.80	98.92	99.12	99.19
Corn	98.83	98.20	98.52	98.34	99.78
Grass (Pasture)	97.60	97.97	97.92	98.70	99.48
Grass (Trees)	98.26	98.80	99.08	99.42	99.80
Grass (Mowed Pasture)	99.98	100	98.18	98.74	99.98
Hay (Windrowed)	97.65	100	100	99.27	99.91
Oats	99.90	97.50	97.50	98.68	99.98
Soybeans (No Till)	96.35	97.99	98.14	98.45	99.18
Soybeans (Min Till)	79.37	99.27	99.38	99.12	98.49
Soybeans (Clean Till)	97.15	98.35	98.69	98.34	99.23
Wheat	99.50	99.14	98.90	98.69	99.93
Woods	94.87	99.88	99.98	99.33	99.18
Buildings (Grass/Trees/Drives)	98.07	99.55	99.68	99.41	99.18
Stone-Steel Tower	99.74	94.52	96.44	98.94	99.91
OA	96.52 ± 4.7	99.01	99.16	99.12 ± 0.25	99.48 ± 0.50

Drug Location Prediction in Mass Spectrometry Images.

To further demonstrate the utility of the UwU-Net in deep learning of hyperspectral images, we predict the location of multiple drugs (most of which are cancer treatment drugs) in a rat liver slice from publicly available mass spectrometry imaging data originally taken by Eriksson et al⁵⁸. Here, a frozen-fixed rat liver section was spiked with 5 mixtures of diluted drugs, where each mixture contains some combination of 4 of the 12 potential drugs at varying concentrations. MSI was then performed on the liver slice in the mass (m/z) range of 150 – 1000 m/z at a mass resolution of 0.001 m/z. This means that this particular raw hyperspectral dataset contains 850,000 images which is not uncommon for MSI datasets. Given this colossal spectral density, MSI datasets must be narrowed to small “windows” (e.g. only 1000 images between 300.000 m/z – 300.999 m/z are shown) and/or “binned” (e.g. all the 0.001 m/z images from 300.000 m/z – 300.999 m/z are summed together to form a single 1 m/z bin image) to be viewable. Both windowing and binning sacrifice information for interpretability. Windowing allows for only seeing a few mass components at a time while binning sacrifices the hallmark specificity of mass spectrometry⁵⁹. Analysis of these large datasets can also be cumbersome, taking potentially hours or longer to interpret per dataset.

The work we present here demonstrates a potential solution to this information trade-off issue by predicting high mass resolution drug location images (corresponding to each drug’s monoisotopic peak) from a window of hyperspectral low-resolution binned mass images of the spiked rat liver tissue. Specifically, the region of 330 – 630 m/z (a window containing all monoisotopic drug peaks) was binned into 1 m/z images and concatenated into a hyperspectral image stack. Then, the 0.001 m/z resolution images corresponding to the monoisotopic peaks of the 12 drugs (as determined in the previous publication) were isolated from the raw MSI data and concatenated to produce a stack where each image corresponds to a specific drug. The UwU-Net architecture was trained to predict 12 drug images from the 300-channel hyperspectral images. Figure 2 shows the results of these predictions and the corresponding 1 m/z bin image that contains the monoisotopic peak. While some of these low mass resolution bins are already highly correlated with the specific monoisotopic peak (e.g. Ipratropium and Vatalanib in Figures 2a and 2b, respectively), other images have strong background contributions and or conflicting drug spot signal due to fragment peaks from other drugs (e.g. Erlotinib and Gefitinib in Figures 2c and 2f, respectively). From Figure 2, it is apparent that the deep learning algorithm is able to reliably predict each drug’s location from the low resolution hyperspectral data even when there are conflicting background/fragment peaks or when the drug concentration is low (as in Lapatinib and Trametinib in Figures 2k and 2l). Even in Trametinib, where the drug is near the sensitivity limit for this MSI experiment, the UwU-Net correctly predicts the spot where the drug is present. Though the exact pixels predicted do not cleanly match (as noted by the PCC values for Trametinib in Table 2), the grouping of these sparse pixels in the correct spots suggest that the UwU-Net is picking-up the relevant spectral and spatial components for prediction.

Fig. 2:

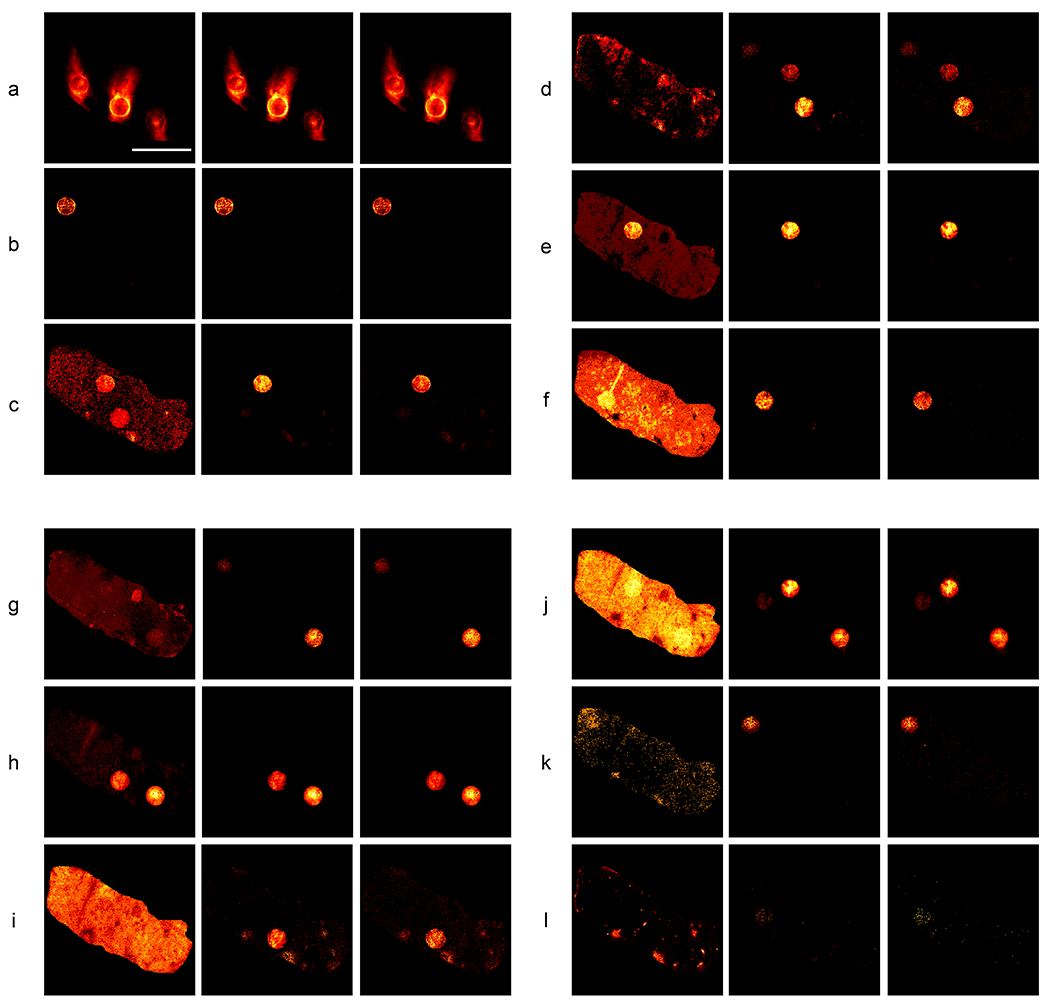
Mass spectrometry images of drug-spikes rat liver slice.

Each row (a-l) shows (from left to right) a 1 m/z bin image from the input 300 image hyperspectral stack that contains a given drug’s monoisotopic peak, the 5-U UwU-net predicted 0.001 m/z bin image of the drug, and the 0.001 m/z bin image specific to that drug’s monoisotopic peak. The following drugs are depicted in their respective panels: Ipratropium (panel a), Vatalanib (panel b), Erlotinib (panel c), Sunitinib (panel d), Pazopanib (panel e), Gefitinib (panel f), Sorafenib (panel g), Dasatinib (panel h), Imatinib (panel i), Dabrafinib (panel j), Lapatinib (panel k), Trametinib (panel l). Scalebar = 4 mm.

Table 2:

Quality metric values for the MSI dataset predictions

The table shows spiked drugs, their respective masses, and the Pearson correlation coefficients (PCC, left column under each model) and normalized root mean squared error (NRMSE, right column under each model) for the low resolution and predicted images from various models with respect to the high resolution image for the drug. U-Nets (Non-HS) refers to individual traditional U-Nets trained from a single image input of low mass resolution (i.e. non-hyperspectral images). The “only drug bins” UwU-Net was trained on a 12 image input stack of only the relevant 1m/z images that contain the drug peak. All other UwU-Nets were trained using the full 300 image stack with various numbers of spatial U-Nets at their center (1-U, 5-U, or 12-U). The uncertainty values refer to the standard deviation among the respective metrics for the given model (n=12 for all).

	1 m/z bin		U-Nets (Non-HS)		UwU-Net (12-U)		UwU-Net (1-U, only drug bins)		UwU-Net (1-U)		UwU-Net (5-U)
Drug (mass, m/z)
Ipratropium (332.223)	0.99	0.003	0.99	0.011	0.99	0.013	0.99	0.007	0.99	0.014	0.99	0.013
Vatalanib (347.107)	0.97	0.010	0.98	0.019	0.95	0.012	0.97	0.010	0.95	0.013	0.96	0.013
Erlotinib (394.177)	0.38	0.104	0.93	0.059	0.89	0.025	0.94	0.023	0.93	0.022	0.93	0.022
Sunitinib (399.220)	0.08	0.096	0.12	0.399	0.67	0.055	0.86	0.033	0.89	0.029	0.89	0.030
Pazopanib (438.171)	0.63	0.076	0.99	0.030	0.97	0.013	0.98	0.014	0.98	0.011	0.98	0.013
Gefitinib (447.160)	0.24	0.250	0.84	0.053	0.88	0.026	0.56	0.044	0.88	0.027	0.89	0.022
Sorafenib (465.094)	0.21	0.077	0.93	0.121	0.93	0.021	0.93	0.020	0.93	0.020	0.992	0.021
Dasatinib (488.267)	0.91	0.033	0.99	0.016	0.98	0.014	0.98	0.014	0.98	0.013	0.98	0.012
Imatinib (494.267)	0.25	0.240	0.72	0.096	0.59	0.057	0.73	0.042	0.78	0.040	0.75	0.039
Dabrafinib (520.143)	0.35	0.295	0.96	0.058	0.92	0.027	0.95	0.024	0.96	0.020	0.96	0.019
Lapatinib (581.143)	0.26	0.084	0.8	0.024	0.80	0.023	0.76	0.026	0.80	0.024	0.74	0.024
Trametinib (616.086)	0.05	0.047	0.11	0.023	0.12	0.030	0.03	0.024	0.10	0.025	0.24	0.023
PCC	0.44 ± 0.34		0.78 ± 0.32		0.81 ± 0.25		0.81 ± 0.28		0.85 ± 0.25		0.85 ± 0.21
NRMSE	0.110 ± 0.098		0.076 ± 0.11		0.026 ± 0.015		0.023 ± 0.012		0.021 ± 0.008		0.021 ± 0.007

To better understand the role of spectral and spatial learning in the UwU-Net, other U-Net and UwU-Net models were trained on this data with some varying parameters and compared in Table 2. To first understand the role of spectral vs spatial learning and their interplay on model accuracy, multiple basic U-Nets were trained on a single drug at a time. Here the single 1 m/z bin image and corresponding high mass resolution peak image were used for training. While some of the drugs are correctly identified and predicted (suggesting spatial learning of a single image from the hyperspectral stack may drive some drugs’ predictions), many of the drugs (sunitinib, gefitinib, sorafenib, dabrafinib, and trametinib) go partially or entirely unpredicted. A single basic U-Net modified to accept 300 channels and output 12 channels again produces unacceptable results (Extended Data Figure 1). The use of a UwU-Net with a single spatial U-Net at its center (denoted as 1-U in Table 2) allows for spectral learning of the data in addition to spatial learning. When a stack of just the 12 drug 1 m/z bins is used for training (1-U, only drug bins in Table 2), only gefitinib, dabrafinib, and trametinib were unidentified. The use of the full 300 hyperspectral stack in the 1-U UwU-Net shows further improvement leaving only one spot of dabrafenib unpredicted. This suggests additional spectral information improves the accuracy of the model in drugs where spatial information from the principal bins is insufficient for prediction. The use of a 12-U UwU-Net on the full hyperspectral data eliminates any unidentified drug spots, but errantly predicts spots in sunitinib and initinib that do not exist in the respective truth images. A 5-U UwU-Net demonstrates the most accurate prediction of drug spots with no missing or errantly predicted spots for any of the 12 drugs (as seen in Figure 2). This analysis and comparison suggest that, like “depth” in a traditional U-Net or ResNet, architecture parameters such as spectral depth or number of spatial U-Nets at center can be empirically tuned to improve model accuracy.

These results highlight a capability of the UwU-Net to mine MSI datasets for relevant features from both spatial and rich spectral features afforded in MSI in a convolutional manner. One way this is potentially useful for MSI is in the design and execution of experiments. If a priori ground-truth information is available (in this case, the masses of the drug molecules sought, their locations, and their concentrations), a UwU-Net model can be trained and utilized in other similar experiments to vastly improve analysis speed. For example, while the training of this algorithm took ~8 hours, the final prediction of all images shown takes only ~1 second. This upfront single-time investment of training then affords analysis of further samples to be performed extremely quickly in comparison to costly linear analysis of each dataset. The specific demonstration presented here could also be highly useful for the miniaturization of MSI systems for in situ use where the tradeoff of reduced mass resolution would be mitigated by a pretrained algorithm. We also note the possibility of combining MSI with an orthogonal method such as fluorescence or Raman imaging, to predict alternate imaging modalities using the UwU-Net as we demonstrate below.

Label-free Organelle Prediction from SRS Microscopy Images

Label-free prediction via deep learning has been a recent area of interest for augmenting the information acquired from a given microscopy modality⁶⁰. The label-free prediction usually involves a microscopy image, such as transmitted light or autofluorescence microscopy, being converted to an image that mimics a more complex label-requisite modality like fluorescent or histologically stained images^18,33,61. The value of this type of work is clear due to the elimination of staining protocols and the disadvantages associated with labeling the sample (photobleaching, toxicity, disruption of biological structures or functions, etc.). However, the quality of label-free prediction depends heavily on the information present in the input images⁶². For example, while transmitted-light microscopy is relatively simple to perform, it only reveals information based on light scattering due to differences in refractive index. In the context of cells and their organelles, there may not be significant enough difference between an organelle and cytosol to produce relevant information for a deep learning algorithm to reliably predict a corresponding organelle’s fluorescence.

Compared to simple bright field or autofluorescence imaging, Raman imaging is a much more information-rich, label-free alternative. The Raman spectrum of a sample reflects specific molecular vibrations quantitatively associated with the molecules within. Hyperspectral SRS imaging improves the conventional Raman imaging by significantly speeding up the image acquisition by 3-4 orders of magnitude^53,63,64. Regardless of the acquisition method, for biological samples, the Raman spectra are often congested and highly convolved due to the overlapping Raman bands from many different molecules. Principle component analysis and phasor analysis have been used to extract individual organelles from the myriad of vibrational signatures in a cell^15,18. However, the subtle variations of Raman spectra for individual organelles present significant challenges to the analysis of smaller structures such as mitochondria and endoplasmic reticulum (ER). Previous attempts to produce label-free staining based on hyperspectral Raman imaging have shown promising results for some organelles but not as rich of predictions for smaller ones¹⁸. The architecture we present here shows improved fluorescence prediction across 3 organelles. Deep learning using the rich spectral and spatial information afforded by hyperspectral SRS microscopy also outperforms previous work of label-free prediction from transmitted light microscopy³³. As shown in Figures 3a – 3c, we create label-free prediction algorithms for nuclei, mitochondria, and endoplasmic reticulum fluorescence in fixed lung cancer cells (A549, from ATCC).. The accuracy of the predictions is quantified in Table 3 by Pearson’s correlation coefficient (PCC), normalized root mean squared error (NRMSE), and feature similarity index (FSIM)^65,66. Across all computed quality metrics, we find high correlation and acceptably low error between predicted images and their respective truths. Previous work reported PCC values of 0.58, 0.69, and 0.70 for DNA (nucleus), mitochondria, and endoplasmic reticulum, respectively³³. Thus, we see a significant improvement in label-free organelle prediction with the information-rich hyperspectral SRS microscopy in comparison to bright field microscopy. A basic U-Net was again trained for comparison as seen in Extended Data Figure 1. While this task was more successful than in the previous demonstrations, unacceptable residual SRS features were also present in the image. For additional comparison to another modern architecture used for image reconstructions, a U-Net utilizing ResNet Blocks^36,67 was also trained to predict the organelles (Extended Data Figure 2 and Extended Data Table 2). While the Res-U-Net showed slightly improved organelle predictions in comparison to previously reported results, the UwU-Net predictions still outperformed across all organelles and metrics.

Fig. 3:

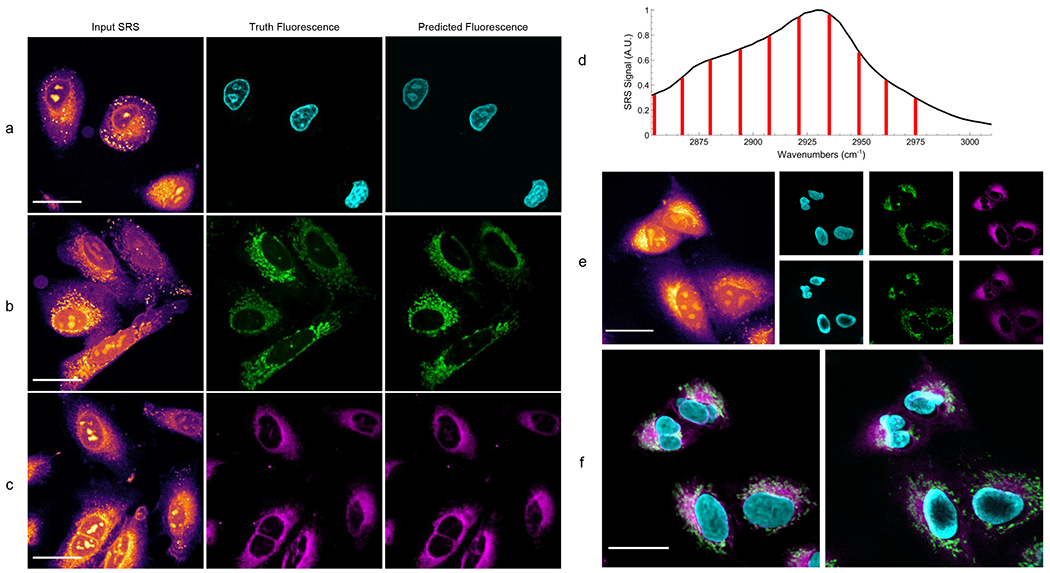
Predicted organelle fluorescence from hyperspectral SRS microscopy images.

All SRS images shown depict only the peak signal image from the hyperspectral stack. Panel a shows the prediction of nucleus fluorescence. Panel b shows the prediction of mitochondria fluorescence. Panel c shows the prediction of endoplasmic reticulum fluorescence. Panel d shows a typical cellular SRS spectrum (black) and the 10 vibrational transitions imaged and used for prediction (red). Note that the transitions marked in red represent the center of a band of probed transitions with a resolution of 19 cm⁻¹. The 15 cm⁻¹ steps between each spectral image means the entire CH vibrational region is effectively probed during hyperspectral imaging. Panel e shows an SRS image of live cells (left) that contain no dye, each algorithms predicted fluorescence (right, top row), and fluorescence images taken after the cells are stained (right, bottom row). Panel f shows an overlaid combination of each organelle prediction (left), and the same group of cells after staining (right).

Table 3:

Quality metric values for the label-free prediction of organelle fluorescence.

The table shows pearson correlation coefficients (PCC), normalized root mean squared error (NRMSE), and feature similarity index (FSIM) values for the 3 organelles predicted from hyperspectral SRS images. Numbers shown are based on the average of all withheld test images (9, 9, and 7 images for nucleus, mitochondria, and ER, respectively) of 512 x 512 pixels. Uncertainty refers to the standard deviation among the withheld test images.

Organelle Model	PCC	NRMSE	FSIM
Nucleus	0.92 ± 0.03	0.047 ± 0.022	0.89 ± 0.04
Mitochondria	0.84 ± 0.05	0.059 ± 0.019	0.93 ± 0.02
Endoplasmic Reticulum	0.94 ± 0.02	0.038 ± 0.016	0.92 ± 0.03

The utilization of both spectral and spatial information is paramount towards demonstrating utility of this architecture. This is most clearly demonstrated in the mitochondria prediction model by the differentiation of the organelle from lipid droplets in the cell. In SRS images, lipids droplets appear as bright “dots” typically ~1 μm in size. This means they have a similar size and shape to mitochondria, yet the trained models have clearly learned to exclude such similar features. This suggests that the model is not simply searching for the spatial features in the image to isolate and predict, but likely utilizing both spatial and spectral information to determine the position of the desired organelles. To confirm this, a simple 2D U-Net was trained using the single brightest SRS image to predict the fluorescence image (Extended Data Figure 3). While the PCC values demonstrated by this traditional U-Net training still outperform previous work (likely due to the higher input image quality with respect to transmitted-light microscopy), they slightly underperform the UwU-Net where spectral information augments the prediction capability (Extended Data Table 3). Moreover, the 2D U-Net models predict some spurious features such as nucleoli (Extended Data Figure 3) or lipid droplets (Extended Data Figure 4) as they are incapable of seeing the difference in vibrational spectral information for such features.

Finally, to demonstrate the multiplexing capability of the trained algorithms, hyperspectral SRS images of live A549 cells with none of the dyes present are used to predict organelle fluorescence in Figures 3e and 3f. Here new prediction models have been trained for live cells in a similar manner as in the fixed cells (Extended Data Figure 5). However, instead of predicting based on SRS images of cells where the dye is present (such as in Figures 3a – 3c and Extended Data Figure 5), the live cells are first imaged with SRS when no dye is present (Figure 3e, left). The cells are then stained while still mounted on the microscope and reimaged with two-photon fluorescence to acquire reference fluorescence images (Figure 3e, right, bottom row). The stain-free SRS images are used to predict fluorescence images using the pretrained models (Figure 3e, right, top row) and overlaid for comparison against the reference images (Figure 3f). As shown in Figure 3f, the label-free prediction in live cells matches well with the truth fluorescence images. We do, however, note slight mismatches in fields of view and cellular shape. This is due to both the sample moving and focus changing slightly during the staining process while mounted on the microscope. Additionally, organelle movement and cellular reorganization between SRS and fluorescence imaging (~10 minutes) leads to mismatch of exact spatial features. Regardless of these differences, the UwU-Net demonstrates a firm ability in predicting label-free fluorescence of organelles from SRS images of live cells.

Discussion

In this work we have presented UwU-Net, a new architecture for deep learning using hyperspectral images. The architecture is highly flexible in both the types of tasks it can perform (e.g. classification, segmentation, label-free prediction) and the types of hyperspectral images with which it is compatible (e.g. remote sensing, MSI, and SRS microscopy). Specifically, we show excellent performance of Indian Pines classification with 99.48% overall accuracy for all classifications. We also demonstrate successful drug location prediction in fixed tissue from MSI data from windowed and binned images. This highlights the capability to mine spectrally dense MSI datasets using both spectral and spatial information and offers new possibilities for deep learning in MSI. Finally, we show improved label-free prediction of organelle fluorescence by using hyperspectral SRS microscopy. We note a significant improvement in nuclear, mitochondrial, and ER prediction correlation with respect to previous work by the use of the UwU-Net to interpret spectral and spatial information.

We further note that while all models were trained using randomized starting parameters and stochastic gradient descent to minimize mean squared error (MSE) between output and truth images, the architecture is easily amenable to transfer learning methods and more complex error functions for particular tasks. We also note that the UwU-Net architecture can potentially be used in a generative adversarial network (GAN) framework to perform an even broader class of tasks^2,68. However, GAN training of a UwU-Net is not feasible currently given memory constraints.

Finally, while only a subset of tasks and imaging techniques are demonstrated here, we expect the UwU-Net to be broadly applicable or adaptable to any reasonably designed computer vision task involving a hyperspectral imaging technique with potential use in medical imaging, microscopy, and remote sensing.

Methods

The following are the methods for the label-free fluorescence prediction demonstration experiments and utilization of the UwU-Net algorithm. The methods for the publicly available datasets (Indian Pines and the MSI of Spiked Rat Liver) are briefly discussed above and details of their experimental parameters can be found in their respective original publications^39,58.

Cell Sample Preparation

A549 cells were cultured in ATCC F-12K medium with 10% fetal bovine serum at 37 °C with 5% CO2 atmosphere. Cells were seeded on coverslips 24 hours prior to imaging. Fixed cells were first dyed then fixed using 2% paraformaldehyde. Live cells were first mounted, imaged with SRS and then stained for fluorescence imaging. The fluorescent dyes used were Hoescht 33342, MitoTracker Red CMXRos, and ER-Tracker Green for nucleus, mitochondria, and ER respectively. All dye protocols were based on the provided instructions from the manufacturer.

Simultaneous SRS and Fluorescence Microscopy

SRS Microscopy was performed on a homebuilt SRS microscope as described previously. Briefly, an Insight DeepSee+ provides synchronized 798 nm and 1040 nm laser pulses which are passed through high density glass and a grating stretcher pair, respectively, to control pulse chirp. The 1040 nm bean is modulated by an electro optical modulator and polarizing beam splitter to operate in the stimulated Raman loss scheme. Time delay of the 1040 beam was controlled by a computer-controlled Zaber X-DMQ12P-DE52-KX14A delay stage. Both pulses are combined on a dichroic mirror before being directed through the microscope by a pair of scanning galvo mirrors. The microscope is a Nikon Eclipse FN1 equipped with a 40x 1.15 NA objective. The 800 and 1040 nm laser powers were set to 20 mW at focus for both beams in all experiments. Light passed through the sample is collected by a 1.4 NA condenser, filtered by a 700 nm long pass filter (to remove fluorescence light) and 1000 nm short pass filter (to remove the 1040 nm light), and finally collected on a homebuilt photodiode connected to a Zurich Instruments HF2LI lock-in amplifier. Two photon fluorescence is captured in the backwards direction by a 650 long pass dichroic towards a photomultiplier tube. SRS signal from the lock-in amplifier and fluorescence signal from the photomultiplier tube were collected simultaneously using ScanImage⁶⁹. Images were acquired with 512 x 512 pixels and a pixel dwell time of 8 μs at each of the 10 vibrational transitions as noted in Figure 3d. It is noted that the transitions noted in Figure 3d represent only the center of the probed band with 19 cm⁻¹ spectral resolution. This means that at the step size of ~15 cm⁻¹ per image in the stack, the full CH region is probed during hyperspectral imaging.

UwU-Net Functional Description

An input hyperspectral stack of dimensions (L, X, Y) is first passed to the architecture. Here, L represents the number of input channels of the hyperspectral stack (e.g. 200 for Indian Pines, 300 for MSI drug location prediction, or 10 for SRS images) and X and Y are the number of spatial pixels in the image (in all cases here X = Y). The stack is first reduced to (M, X, Y) in the channel dimension, where L > M, with a 3x3 kernel convolution of stride 1 over all L channels followed by a batch normalization and rectified linear unit (ReLU) activation function. The new stack is then reduced once more in the channel dimension by the same process to a stack of (N, X, Y) where N is the desired final number of spatial tuning channels. The stack is then split at the channel dimension (if N > 1) such that there are now N number of (X,Y) images. Each of these images is passed to its own U-Net for spatial feature learning as described previously³³. The resulting N number of images from each spatial U-Net are then reconcatenated in the channel dimension to reform a (N, X, Y) stack. This (N, X, Y) stack is then concatenated in the channel dimension to the (N, X, Y) stack from prior to splitting (mimicking the recovery of information as in the traditional U-Net) to form a stack of (2N, X, Y). This (2N, X, Y) stack is reduced to (O, X, Y) by a 3x3 kernel convolution of stride 1 over the 2N channels followed by a batch normalization and ReLU activation function. This predicted stack is then compared to the truth stack (also of dimension [O, X, Y]), a mean squared error is calculated for all channels, and parameters are tuned in a backpropagating fashion.

Training Parameters, Data Preparation, and Hardware

The models trained and shown in this paper were developed and built using the pytorch-fnet framework originally developed by Ounkomol et al³³. All models were trained using the pytorch-fnet default parameters with a few exceptions. The models were trained using randomized starting parameters on batches of randomized patches from the given dataset. Model parameters are tuned in a stochastic gradient descent manner based on minimization of mean squared error. The pytorch-fnet framework utilizes an Adam optimizer with a 0.001 learning rate and beta values of 0.5 and 0.999. The rat liver drug prediction model which was trained only for 23,000 iterations due to the satisfactory prediction accuracy and long training iteration time. The Indian Pines and rat liver drug prediction models were trained with buffer size of 6 due to the reduced number of training datasets. The Indian Pines classification and rat liver drug prediction model used patch sizes of 64 x 64 pixels for training, while all organelle prediction models utilized patch sizes of 256 x 256 pixels.

Nearly all image preparations and processing discussed below were performed using Fiji, an imageJ platform. The exception was the additional use of Datacube Explorer for initial processing of the raw MSI data.

The 200 band Indian Pines dataset was used natively from the published source. The ground truth stack was created by separating the individual labeled images via thresholding then concatenating all truth images into a TIF stack. The native pytorch-fnet cropper was used to crop the images to 144 x 144 pixels from 145 x 145 pixels to accommodate the spatial learning in the central U-Nets of the UwU-Net architectures. Training data was augmented by rotations and flips with the original dataset withheld for testing. This equated to 6 training datasets and 2 test datasets. Final predictions were recolored for each label and then overlaid into the shown prediction image (Figure 1c). The UwU-Nets reported in Table 1 use 1 (1-U) or 17 (17-U) spatial U-Nets at their center during training.

The rat liver MSI dataset was first prepared by saving the 330-630 m/z window at 1 m/z bins from the raw data using Datacube Explorer. All 300 images were concatenated into a TIF stack using Fiji. The monoisotopic images at 0.001 m/z resolution were then saved for each drug using Datacube Explorer following the m/z peaks and appropriate FWHM bins as noted by Eriksson et al⁵⁸. The 12 drug peak images were concatenated into a TIF stack using Fiji. Both stacks were padded with zeros in Fiji from their native 247 x 181 pixel size to 256 x 256 pixels to be compatible with the spatial U-Nets within the UwU-Net architecture. Training data here was also augmented by rotations and flips with the original dataset withheld for testing. There were 7 datasets used for training. The shown 1 m/z bin, truth peak, and predicted peak images for the drugs were normalized, contrast adjusted to the same level, and colored using the “Red Hot” Fiji lookup table. The UwU-Nets reported in Table 1 use 1 (1-U), 5 (5-U), or 12 (12-U) spatial U-Nets at their center.

The simultaneously collected SRS and Fluorescence images were first separated into 2 respective TIF stacks. The SRS stack was used as is for training and prediction. The fluorescence stacks were averaged to a single image and used as the truth for training and prediction. The fixed cell nucleus, mitochondria, and ER models utilized 43, 46, and 35 images, respectively, with a randomized 80%/20% train-test split for each model. Images predicted by the model were normalized, contrast adjusted to the same level, then colored using the “mpl-inferno”, “Cyan”, “Green”, and “Magenta” Fiji lookup tables for SRS, nucleus, mitochondria, and endoplasmic reticulum, respectively.

All model development, training, and prediction as well as image processing was performed on a homebuilt machine running Ubuntu 18.04. The machine is equipped with an AMD 2950X processor, Nvidia Titan RTX graphics processing unit, 64 GB memory, and a 2 TB solid state drive. All dependency software versions were based on the pytorch-fnet requirements. On our machine, trainings for Indian Pines, rat liver drug, and organelle models took ~4, ~8, and ~5 hours respectively. In all models, prediction of individual test images took 1 second or less.

Quantitative Metrics

Prediction quality was assessed by overall accuracy (OA), Intersection Over Union (IOU) Pearson’s correlation coefficient (PCC), normalized root mean squared error (NRMSE), and feature similarity index (FSIM)

OA is used to evaluate the binary pixel values assigned for each classification. Here, the number of errantly predicted pixels are counted, subtracted from the total number of pixels, then divided by the total number of pixels. A percentage score is reported here where accuracy closer to 100% indicates a more accurate prediction.

IOU also measures the segmentation and classification accuracy by taking the ratio of the intersection between predicted pixels and true pixels (i.e. true positives) and union of predicted pixels and true pixels (i.e. true positives plus false positives). The resulting ratio indicates how accurately the model segments and classifies areas where values closer to 1 indicate more accurate prediction.

PCC is used to correlate the pixels of the truth and predicted images. The covariance of the two images is divided by the standard deviation of the two images to provide a value indicating pixel-to-pixel correlation. A PCC of 1 would indicate perfect correlation while 0 would indicate no correlation.

NRMSE is used to express the accuracy of a predicted pixel versus the same pixel in the truth image. Here a value closer to 0 indicates a more accurate prediction model.

FSIM is used as an image quality assessment metric that mimics human perception of image similarity. Like the structural similarity index (SSIM), FSIM incorporates the spatially associated pixels in the images during calculation to provide a better notion of perceived similarity. However FSIM emphasizes low-level features of images to more accurately reflect the human visual system’s perception of image similarity⁶⁶. Here an FSIM of 1 indicates perfectly similar images while 0 would indicate no similarity.

Quantitative metrics were calculated using Fiji “Coloc 2” (PCC), and “SNR” (NRMSE) plugins on the normalized images produced by the trained prediction model. FSIM was calculated using the MATLAB code provided by Zhang et al⁶⁶, following the prescribed instructions.

Extended Data

Extended Data Fig. 1:

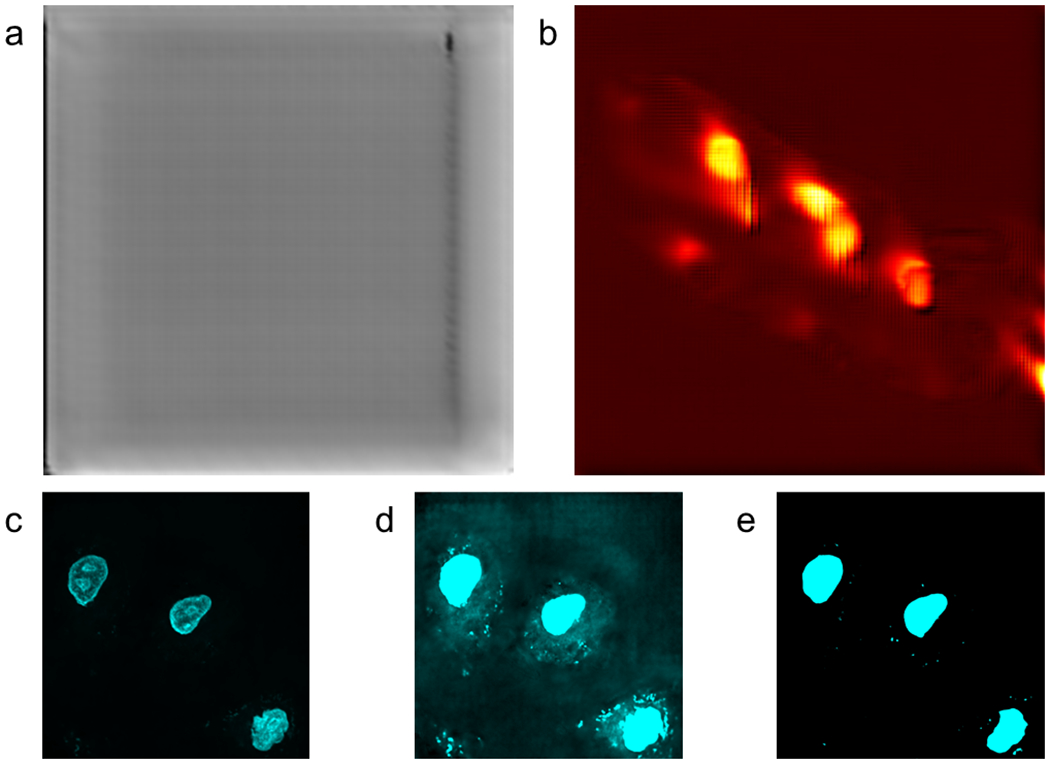
Representative predictions facile U-Nets for Hyperspectral images.

Panel a shows the Grass (Mowed Pasture) Indian Pines classification prediction with no thresholding. Panel b shows the prediction of Ipratropium from the MSI dataset. Panel c shows prediction of nuclear fluorescence from SRS images with contrast values set to mimic the images shown in Figure 3. Panel d shows the same image as Panel c with higher contrast to demonstrate the U-Net’s inability to remove non-nucleus features. Panel e shows the UwU-Net prediction from Figure 3a with high contrast demonstrating superior non-nuclear feature removal.

Extended Data Fig. 2:

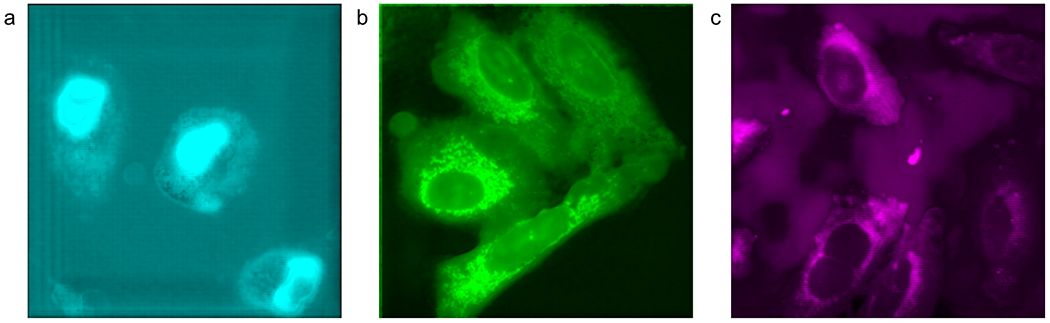
Fluorescence predictions the Modified U-Net with ResNet blocks.

Panel a shows nucleus fluorescence prediction. Panel b shows mitochondrial prediction. Panel c shows endoplasmic reticulum prediction. All truth fields of view are the same as in Figure 3.

Extended Data Fig. 3:

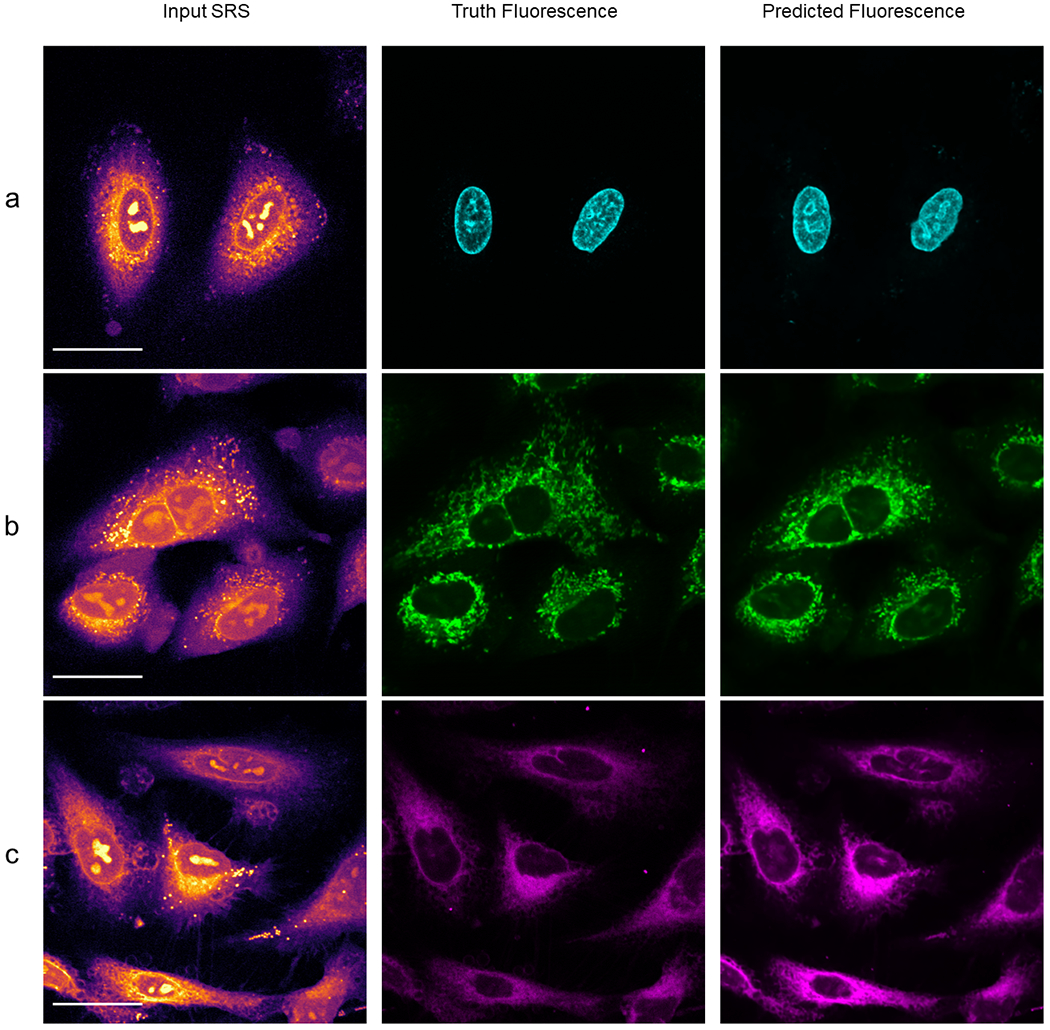
Predicted Organelle fluorescence using traditional U-Net.

Panel a shows prediction of nucleus fluorescence. Panel b shows prediction of mitochondrial fluorescence. Panel c shows prediction of endoplasmic reticulum fluorescence. We note the improper inclusion of lipid droplets in the mitochondria model and off nucleoli in both the mitochondria and endoplasmic reticulum models. The comparison between lipid droplets and mitochondria is further depicted in Extended Data Figure 4.

Extended Data Fig. 4:

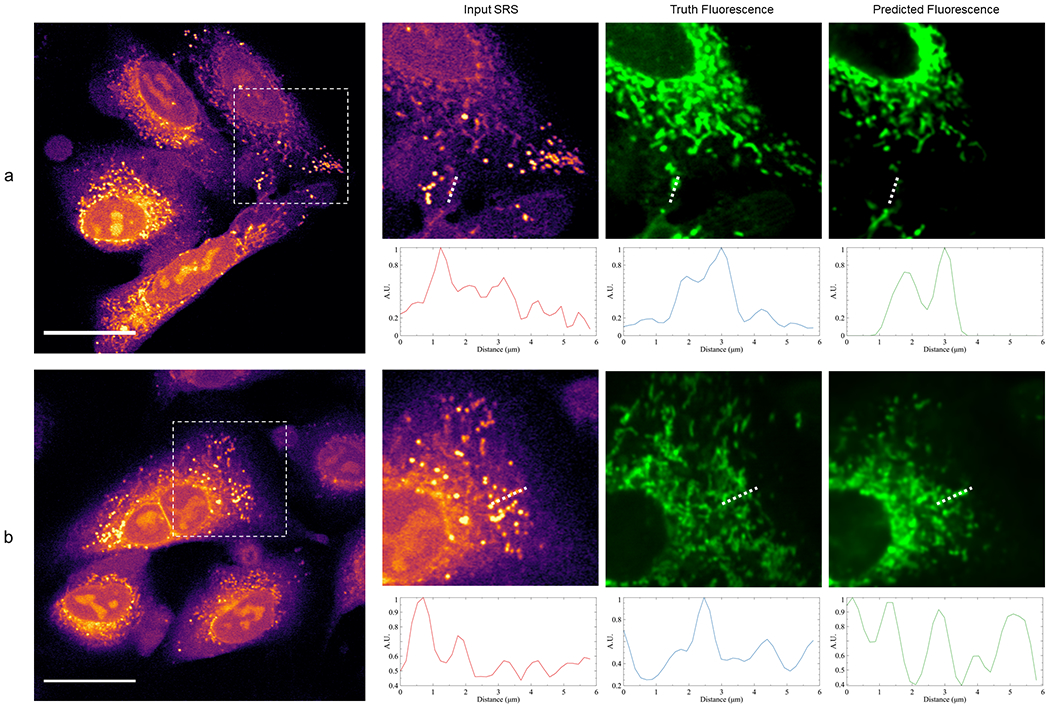
Comparison of mitochondria prediction between UwU-Net and traditional U-Net.

Panel a shows a zoomed in field of view from Figure 1b where a UwU-Net is trained to predict mitochondrial fluorescence from a hyperspectral SRS stack. The shown input SRS only corresponds to the brightest image out of the 10-image hyperspectral stack. Normalized pixel values are plotted below each image corresponding to the drawn dashed lines. In the SRS image, a strong lipid droplet is found at ~1.4 μm but is properly removed during prediction of the mitochondria at ~1.8 μm and ~3 μm. Panel b shows a zoomed in field of view from Extended Data Figure 3b where a traditional U-Net is trained to predict mitochondrial fluorescence from a single SRS image. The normalized pixel value plots beneath each zoomed-in field of view show a marked difference in how lipid droplets are handled. Here the lipid droplets at ~0.8 μm and ~1.8 μm are not removed during prediction.

Extended Data Fig. 5:

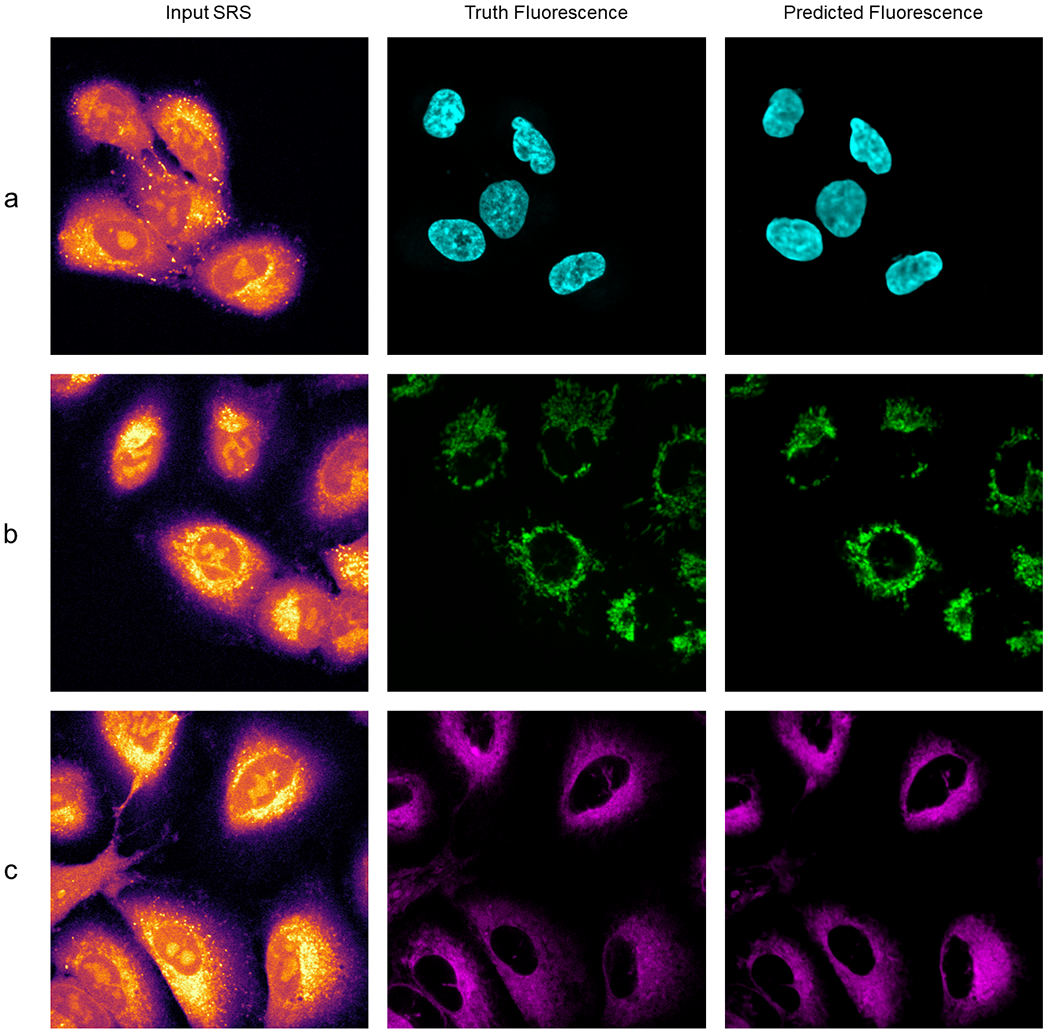
UwU-Net predicted fluorescence in live-cell SRS imaging.

Panel a shows prediction of nucleus fluorescence. Panel b shows prediction of mitochondrial fluorescence. Panel c shows prediction of endoplasmic reticulum fluorescence.

Extended Data Table 1:

Prediction Accuracy of the UwU-Net for the Indian Pines Dataset.

The table lists the count of false positive, false negative pixels, and intersection over union (IOU) per classification class.

Label	False Positive Pixels	False Negative Pixels	IOU
Alfalfa	1	8	0.836
Corn (No Till)	65	231	0.803
Corn (Min Till)	19	149	0.806
Corn	11	35	0.812
Grass (Pasture)	6	101	0.787
Grass (Trees)	9	32	0.948
Grass (Mowed Pasture)	3	2	0.828
Hay (Windrowed)	13	6	0.962
Oats	0	4	0.800
Soybeans (No Till)	59	112	0.834
Soybeans (Min Till)	210	103	0.883
Soybeans (Clean Till)	80	79	0.769
Wheat	4	10	0.935
Woods	75	96	0.875
Buildings (Grass/Trees/Drives)	9	161	0.753
Stone-Steel Tower	6	13	0.812
Overall	570	1142	0.840

Extended Data Table 2:

Quality Metrics for Res-U-Net

PCC, NRMSE, and FSIM values for the Res-U-Net trained as in Extended Data Figure 2. The number of images for used for each calculation is the same as in Table 3. Uncertainty refers to standard deviation

Organelle Model	PCC	NRMSE	FSIM
Nucleus	0.74 ± 0.04	0.379 ± 0.016	0.76 ± 0.05
Mitochondria	0.75 ± 0.15	0.172 ± 0.053	0.77 ± 0.06
Endoplasmic Reticulum	0.72 ± 0.13	0.112 ± 0.023	0.78 ± 0.03

Extended Data Table 3:

Quality Metrics for Traditional U-Net Fluorescence Prediction

PCC metrics for the organelle fluorescence prediction models trained with a traditional U-Net using a single SRS image. While still highly correlated, we note the errant prediction of spurious features in Supplementary Figures 1 and 2.

Organelle	U-Net PCC
Nucleus	0.84 ± 0.05
Mitochondria	0.81 ± 0.05
Endoplasmic Reticulum	0.93 ± 0.03