Design and testing of a microcontroller that enables alpha particle irradiators to deliver complex dose rate patterns

Abstract

There is increasing interest in using alpha particle emitting radionuclides for cancer therapy because of their unique cytotoxic properties which are advantageous for eradicating tumor cells. The high linear energy transfer (LET) of alpha particles produces a correspondingly high density of ionizations along their track. Alpha particle emitting radiopharmaceuticals deposit this energy in tissues over prolonged periods with complex dose rate patterns that depend on the physical half-life of the radionuclide, and the biological uptake and clearance half-times in tumor and normal tissues. We have previously shown that the dose rate increase half-time that arises as a consequence of these biokinetics can have a profound effect on the radiotoxicity of low-LET radiation. The microcontroller hardware and software described here offer a unique way to deliver these complex dose rate patterns with a broad-beam alpha particle irradiator, thereby enabling experiments to study the radiobiology of complex dose rate patterns of alpha particles. Complex dose rate patterns were created by precise manipulation of the timing of opening and closing of the electromechanical shutters of an α-particle irradiator. An Arduino Uno and custom circuitry was implemented to control the shutters. The software that controls the circuits and shutters has a user-friendly Graphic User Interface (GUI). Alpha particle detectors were used to validate the programmed dose rate profiles. Circuit diagrams and downloadable software are provided to facilitate adoption of this technology by other radiobiology laboratories.

Introduction

Targeted radiopharmaceutical therapies are one of most promising modalities for treating disseminated cancer cells and their resulting micrometastases (Sgouros and Goldenberg, 2014; Marcu et al., 2018). These therapies are achieved by conjugating radionuclides that emit α particles, β particles, or Auger electrons to cancer-targeting molecules such as a peptides or monoclonal antibodies (Poty et al., 2018a, b). The radiolabeled targeting molecules bind to cancer cells and the emitted particles irradiate the targeted tissue chronically. The most commonly used radionuclides emit α and β particles which differ radiobiologically in significant ways (Wheldon and O’Donoghue, 1990). The linear energy transfer (LET) of α-particles is about 100 times that of β-particles (ICRU, 1984, 1993), making these short-range high-LET particles highly effective at killing cancer cells. As a consequence, α-emitters can, in principle, deliver more localized tumor cell killing power with less damage to surrounding healthy tissue than β particle emitters (McDevitt et al., 1998).

Dose rate is a major factor in determining biological response to low-LET radiations and there is a large body of literature on the topic for constant and exponentially decreasing dose rates (Dale, 1985; O’Donoghue and Wheldon, 1989; Fowler, 1990; Baechler et al., 2008). However, little is known about how dose rate patterns that are commensurate with the uptake and clearance of radiopharmaceuticals can affect biological response (Rao and Howell, 1993; Howell et al., 1994; Howell et al., 1998; Behr et al., 1998; Sefl et al., 2016). Recently, Solanki et al. showed that cell killing with γ-rays was surprisingly sensitive to the rate of increase in dose rate (i.e. uptake half-time of radiopharmaceutical) and they attributed this to a radioadaptive phenomenon (Solanki et al., 2017). Others have shown that cells irradiated acutely with alpha particles can induce radioadaptive responses in bystander cells (Iyer and Lehnert, 2002; Choi et al., 2010; Choi et al., 2012). Furthermore, pretreatment with low-LET gamma rays can affect alpha particle induced bystander responses (Zhou et al., 2003). In contrast, early studies found that dose rate effects were not observed for cell killing with high-LET alpha particles when the radiation insult was delivered in fractions (Barendsen, 1964); a lethally irradiated (40 Gy, 250 kV x-rays) feeder layer was used in these and other early studies which may have influenced outcome. Others have demonstrated some dose rate effects when alpha particles are delivered chronically (Stevens et al., 2014; Rao et al., 1991; Miller et al., 1993). In view of these observations, and their potential importance to targeted radionuclide therapy, there is a need to study if complex dose rate patterns of alpha particles affect biological responses of tumor and normal tissues. Accordingly, in the present article we describe the design and construction of a microcontroller that facilitates the delivery of α particles with a variety of dose rate patterns; these include acute, chronic constant, exponentially increasing, exponentially decreasing, and multi-component exponential which facilitates dose rate patterns encountered in tumor and normal tissues during targeted radionuclide therapy. These dose rate patterns parallel those available on our low dose rate ¹³⁷Cs γ irradiator (Howell et al., 1997b; Pasternack and Howell, 2013).

Materials and Methods

Irradiator

The α-particle irradiator used in the present work was described in detail by Neti et al. (Neti et al., 2004). Briefly, the irradiator consists of 4 irradiation ports, each equipped with a planar source of ²⁴¹Am that serves as the source of α particles (figure 1). The ²⁴¹Am sources activities in ports 1, 2, and 3 are 20 MBq (0.34 MBq cm⁻²); port 4 has no source and is used for controls (Neti et al., 2004). The sources are rotated continuously to ensure beam uniformity, and the beam is directed vertically upward and collimated to reduce the maximum angle of incidence of α particles on the bottom of custom cell culture dishes with 1.5-μm thick Mylar™-bottoms. The collimator consists of a stainless steel honeycomb mounted on an orbital shaker to avoid dead spots above the septa of the collimator. Each port has a Copal Model DC-392 electromechanical shutter (Nidec Copal Corporation, Tokyo) to control the radiation exposure to a Mylar™-bottomed culture dish positioned above the source. In the original design, the shutters were controlled by a simple timer that facilitated the delivery of a single fraction of α particle radiation (Neti et al., 2004).

Figure 1.

Photograph of the irradiator and microcontroller.

Microcontroller

The current work was to create microcontroller hardware and software that enables a user to deliver complex dose rate patterns by manipulating the timing of opening and closing of the electromechanical shutters of the α-particle irradiator described above. All parts needed to assemble the microcontroller are detailed in Supplementary Table 1. An Arduino Uno Rev2 board with ATmega328 chip (PART#1) was implemented to control the shutters. It has a clock speed of 16 MHz, which is much faster than the rate limiting step of the 125-ms shutter speed. The Arduino 5V signal outputs were connected to optical relay modules (PART#2) to control the current from a 24V 3A DC power supply to the electromechanical shutters. This arrangement electrically decoupled the main Arduino board from the 24V power supply (PART#3) to protect the microcontroller board from the voltage surge that arise when activating the shutter. A second optical relay module (PART# 2) was used to control the 120V AC power for the collimator and rotary motors for the sources. The Arduino, relays, and connecting wires were housed inside a 17.8×12.7×7.6 cm (7×5×3 inch) aluminum enclosure (PART#4). Figure 2 shows the enclosure compartment with the corresponding electronic components.

Figure 2.

Microcontroller enclosure containing Arduino Uno R2 and optical relay modules for shutter control. A breadboard on the right has lamps that indicate circuit status; these are helpful for troubleshooting. This figure is included to assist the reader in constructing the microcontroller.

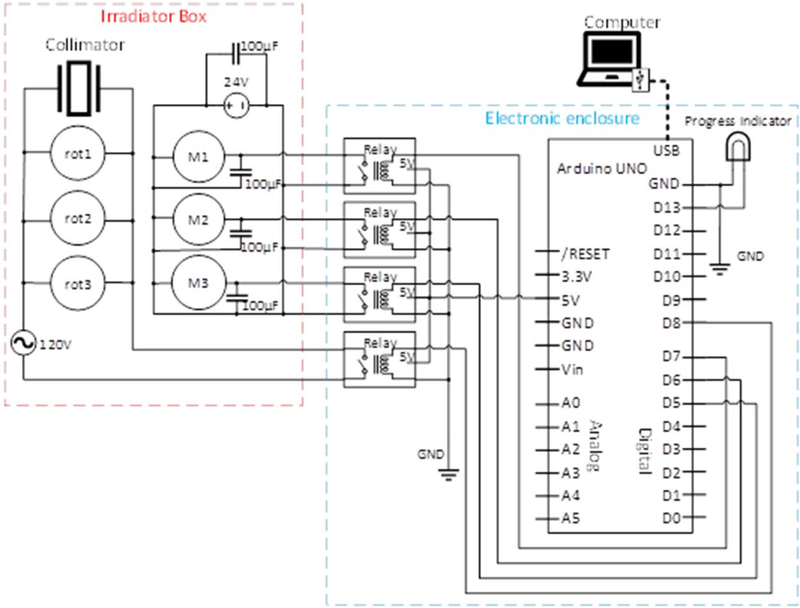
The Arduino programming language, based on C/C++, was used to write a program to accept input from a user operating a personal computer (PC) with a Windows environment. The Arduino program is provided as a supplementary file available on line to allow others to adopt this system. The Arduino receives input data from the PC via a shielded USB connector, and sends output signals in the form of 5V ON/OFF to the output pins on the Arduino board. It is essential to use a shielded USB cable to prevent signal noise created by operation of the electromagnets. As described above, the output pins are wired to the corresponding relay modules, which are in turn connected to the electromagnetic shutters. The circuit diagram is depicted in figure 3.

Figure 3.

Circuit diagram for the alpha particle irradiator microcontroller. M1, M2 and M3 are electromagnetic shutters; rot1, rot2, and rot3 are rotary motors that spin the ²⁴¹Am sources to ensure field uniformity. The 100 μF bypass capacitors (PART #5) were placed to dampen noise coming from the switching of motor states.

Graphical User Interface and Irradiator Control

Overview.

The software that controls the shutters was written in Visual Basic 2010; it is provided as a supplementary file available on line to allow others to adopt this system. The software displays a Graphic User Interface (GUI) that is user-friendly, and can be operated by users with basic computer skills. Upon loading, the software retrieves from MICROSOFT REGISTRY the most recent settings that were used by the user from prior operation. When the software is opened for the first time, default settings are used. The settings can be found in the ‘Settings’ tab (not shown), and include the mean absorbed dose rate to the cell nuclei of cultured cells adhering to the growing surface inside the Mylar™-bottomed dishes that are placed above each radiation source. This dose rate is dependent on the activity of the ²⁴¹Am sources that are placed in each of the four ports, and also on the average diameter of the cell nucleus (see Eq. 1 below). In our set up, the sources have the following mean absorbed dose rates when the default cells (AG1522) are irradiated (Neti et al., 2004): Source1: 0.082 Gy min⁻¹ (4.9 Gy h⁻¹), Source2: 0.080 Gy min⁻¹ (4.8 Gy h⁻¹), Source3: 0.073 Gy min⁻¹ (4.4 Gy h⁻¹), Source 4: 0 Gy min⁻¹ (no source present). These default values were established in our earlier publication (Neti et al., 2004), and can be changed by the user according to the activity of the sources used and the mean diameter of the cell nuclei of the irradiated cells; the software will take these changes into account when performing various calculations. Also under the ‘Settings’ tab, the user can set the mode of operation of the collimator. The collimator and rotary motors can be set to be turned on at all times during a fractionated exposure, or set to be turned on only when the shutters are open. The latter setting preserves the life of these components when irradiating chronically with a large number of fractions.

The GUI allows the user to deliver alpha particles to each of the ports in four different modes of dose rate profiles. Each mode has its own dedicated tab: ‘Single Fraction’, ‘Multiple Fractions’, ‘Exponential’, and ‘Multi-Exponential’. All the tabs have a similar interface, with checkboxes above each port header to indicate which ports will be used for the experimental run. It is important to note that each mode delivers the exposure in fractions. That is because the irradiator uses shutters, each having two discrete states - either ON or OFF. This makes the shutter-state a discrete variable as opposed to a continuous variable. Hence, discrete math was employed to manipulate the temporal pattern of the fractionation and thereby simulate different dose rate patterns.

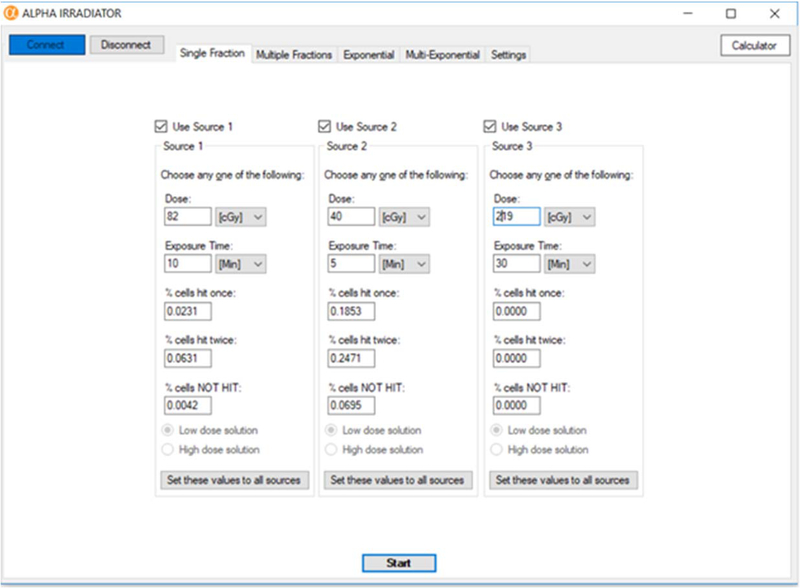
Single Fraction tab.

This tab of the GUI enables the user to specify a mean absorbed dose to each of the ports and deliver each with a single fraction (figure 4). Each source port is designated by its own panel, each with its own set of user-selectable parameters. These parameters are: ‘Dose’, ‘Exposure Time’, ‘% nuclei hit once’, ‘% nuclei hit twice’, ‘% nuclei NOT hit’. These parameters are interrelated, such that the user only needs to specify a single parameter, and the rest of the parameters are calculated by the software and automatically populated on the screen (figure 4). To describe the relationship between the parameters, the concept of traversal is in order. Charlton and Sephton quantified the absorbed dose to the cell nucleus from a single α-particle traversal, as well as the percentage of cells traversed (Charlton and Sephton, 1991). The mean dose to the cell nucleus per traversal is given by d = LET × 0.16 / A, where LET is the linear energy transfer of the alpha particle and A is the cross-sectional area of the cell nucleus (Charlton and Sephton, 1991). The percentage of cells traversed is given by a Poisson distribution:

$$P\left(D,i\right)=\frac{1}{i!}{\left(D/d\right)}^i{e}^{-\left(D/d\right)}$$ (1)

where the function P(D,i) is the percentage of cells hit by i traversals, D is the mean absorbed dose to the cell nuclei, and d is the dose to the cell nucleus per traversal. The variables and parameters in equation 1 and elsewhere in this article are summarized in Table 1. Using AG1522 cells as an example, it can be shown that for AG1522 cells flattened on our Mylar™bottomed dishes, the absorbed dose to the cell nucleus from a single α-particle traversal is d = 0.15 Gy (Neti et al., 2004); the value of d differs for other cells depending on A, LET, and culture conditions. The software provides the user with the following probabilities: ‘% nuclei hit once’ = P(D,1), ‘% nuclei hit twice’ = P(D,2), and ‘% nuclei NOT hit’ = P(D,0). Equation 1, together with the relationship Dose Rate = Dose/Time, provides the relationship among all the parameters. If P(D, 1) or P(D, 2) is specified, the inverse function P⁻¹(D,i=1 or 2) has two solutions for a given value of D. For example, when n = 1 and d = 0.15 Gy, the values of P(D,1) are equal for D = 0.050 and D = 0.336 Gy: P(0.050,1) = P(0.336,1) = 0.239. Thus, when the user chooses to modify ‘% nuclei hit once’ or ‘% nuclei hit twice’, the option of deciding between the two solutions becomes available to the user in the form of radio buttons at the bottom of the screen. The rest of the parameters will still be automatically calculated and populated on the screen.

Figure 4.

Single Fraction tab. Graphic user interface for delivering a single fraction of alpha particles.

Table 1:

Quantities and parameters.

Symbol	Units	Definition	Reference
A	µm2	Cross sectional area of the cell nucleus.
d	Gy	Absorbed dose per fraction.	(Bentzen et al., 2012)
D	Gy	Absorbed dose.	(ICRU, 2011)
Φ	-	Fluence (particles µm2)	(ICRU, 2011)
n	-	Number of fractions.	(Dale, 1985)
$\dot{N}$	particles min−1 µm2	Fluence rate.	(ICRU, 2011)
P(D,i)	-	P(D,i) is the percentage of cells hit by i traversals.	(Charlton and Sephton, 1991)
r	Gy h−1	Absorbed dose rate.	(ICRU, 2011)
r0	Gy h−1	Extrapolated initial dose rate.	(Howell et al., 1994)
tTotal		Time required to deliver the total absorbed dose.
tfraction		Time required to deliver a single fraction.
Ti	h	Dose rate increase half-time. Approximate time required for dose rate to increase to one-half of its maximum value.	(Howell et al., 1997b; Pasternack and Howell, 2013)
Td	h	Dose rate decrease half-time. Approximate time required for dose rate to decrease to one-half of its maximum value.	(Howell et al., 1997b; Pasternack and Howell, 2013)
Td1		Dose rate decrease half-times for the first component of the exponential decrease in dose rate.	(Rao and Howell, 1993; Howell et al., 1994; Howell et al., 1998; Solanki et al., 2017)
Td2		Dose rate decrease half-times for the second component of the exponential decrease in dose rate.	(Rao and Howell, 1993; Howell et al., 1994; Howell et al., 1998; Solanki et al., 2017)
Tp	h	Physical half-life of radionuclide

When ready to begin the experimental run, click the Start button at the bottom of the video monitor. This uploads the parameters for each port to the Arduino. The Arduino uses the uploaded values to control the amount of time that each shutter on the corresponding port will remain open, and synchronizes this information with the progress window on the screen in real time. The progress window has graphical representations of the exposures for each port, along with corresponding countdown timers that notify the user of the time remaining for each of the ports. If the user chooses to terminate operation, the Cancel button can be clicked during any point along the experimental run. If the experimental run is allowed to run to completion, a pop-up window informs the user of completion.

Multiple Fractions tab.

The total dose delivered can be divided into equal fractions. These fractions are equally spaced along a specified time span. The user inputs the ‘Number of Fractions (n)’, the ‘Total dose (D)’ to be equally divided into n fractions, and the ‘Overall treatment time’ (t_overall) along which the fractions will be equally distributed. When these parameters are inserted (Supplementary figure 1), a display of the characteristics about the radiation delivery is shown in sub-panels. The sub-panel with heading “TOTAL DOSE” provides the total dose to be delivered, the total exposure time corresponding to the total dose, and the percentage of nuclei hit by the total dose. The sub-panel “FRACTIONS” provides characteristics about individual fractions, such as ‘Fraction size (d)’, ‘Exposure time’ per fraction, and percent nuclei hit during a single fraction. The sub-panel with heading “TIME DEPENDENT” shows the calculated ‘Fraction rate’, which is the frequency that the fractions occur, and the ‘Interfraction interval’, which is the spacing between fractions in units of time.

When the experimental run is ready to be executed, the user clicks Start, which uploads the parameters for each port to the Arduino. A progress window provides live information about the shutters’ open/closed state for each of the ports. This information is depicted in graphs, with the vertical axis depicting open/closed state and horizontal axis depicting time. As the experimental run progresses, a vertical line scans the graphs from left to right to indicate how far along the graphs the experiment has progressed. The right hand side of the window has representations of the shutters’ state, with filled circle representing shutter closed state and unfilled circle representing shutter open state. Each port also has a countdown timer to indicate the time remaining for each of the ports.

Exponential tab.

This module simulates an exponentially increasing or decreasing dose rate (Supplementary figure 2). To simulate these time dependent dose rates, we assign the times at which the shutters open to represent the time-dependent variable. To stay consistent with our current theme, we fix the fraction size (d) (i.e. time the shutter is open to deliver a single fraction t_fraction) to a value based on the user’s input. The user enters n, D, and the ‘Overall treatment time’ (t_overall) during which the fractions will be distributed in an exponentially increasing or decreasing temporal pattern. The user may instead choose to input d and the rest of the parameters will automatically be set by the relation D = n d. It is important to note that to approximate an exponential curve, at least 3 time points must be specified. Therefore, the software will give an error message for n<2.

The software uses the following continuous function as the basis for modeling exponentially increasing or decreasing dose rates r(t):

$$r\left(t\right)={\mathrm{r}}_0{\mathrm{e}}^{\raisebox{1ex}{$\pm \mathrm{l}\mathrm{n}2\mathrm{*}t$}\!\left/ \!\raisebox{-1ex}{${\mathrm{T}}_{\mathrm{d}}$}\right.},$$ (2)

where T_d is the dose rate half-time. To be clear, r₀ is a scaling parameter and not the dose rate delivered during a single fraction which is fixed because of the long physical half-life (432 years) of the ²⁴¹Am sources. The software uses an algorithm to arrange the fractions temporally in an exponential fashion. The algorithm first assigns a fraction to occur at the beginning of the experimental run (t = 0), and another fraction to begin at a time t_fraction before the end of the experimental run (t = t_overall – t_fraction). To determine the positions of fractions within the time domain (t_min, t_overall), the algorithm first evenly divides the function’s range (r(0), r(t_overall)) into n-1 segments.

$$r\left(t_m\right)=\mathrm{m}\times \frac{r\left({\mathrm{t}}_{\mathrm{o}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}}\right)-r\left(0\right)}{n-1},m=\mathrm{1,2},\dots ,n-2$$ (3)

The algorithm takes the inverse function r⁻¹ to determine the time t_m at which the corresponding m^th fraction will occur. The functional form of the fractionation pattern, calculated by the algorithm, is previewed on a graph generated by the software. The graph also includes a plot of the fractions laid out in an exponential temporal pattern. The experimental run is initiated by clicking the Start button (Supplementary figure 2). A progress window opens up, which shows the progress of the experimental run.

Multi-Exponential tab.

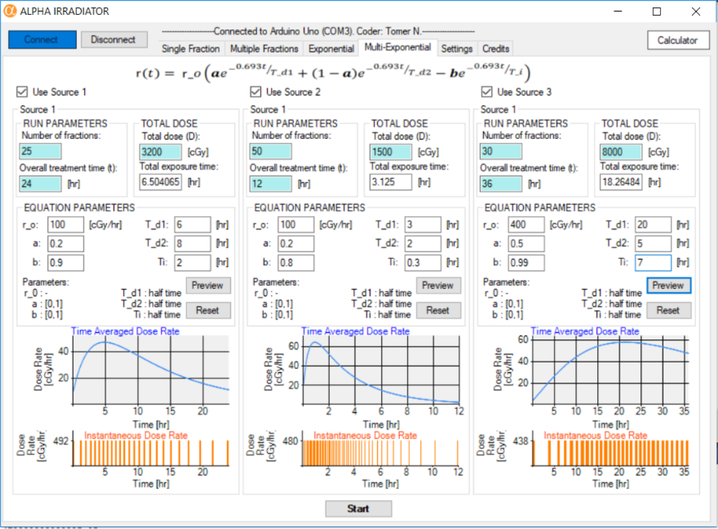
As before, the user inputs the ‘Number of fractions (n)’, the ‘Total dose (D)’ to be equally divided into n fractions, and the ‘Overall treatment time’ along which the fractions will be distributed in a multi-exponential fashion. The software simulates a multi-exponential dose rate pattern (figure 5)

$$r\left(t\right)=r_0\left(a{e}^{\raisebox{1ex}{$-\ln \left(2\right)\mathrm{\ast }t$}\!\left/ \!\raisebox{-1ex}{$T_{d1}$}\right.}+\left(1-a\right)e^{\raisebox{1ex}{$-\ln \left(2\right)\mathrm{\ast }t$}\!\left/ \!\raisebox{-1ex}{$T_{d2}$}\right.}-b{e}^{\raisebox{1ex}{$-\ln \left(2\right)\mathrm{\ast }t$}\!\left/ \!\raisebox{-1ex}{$T_i$}\right.}\right)$$ (4)

where T_i is the dose rate increase half-time, and T_d1 and T_d2 are the dose rate decrease half-times for the first and second component of the exponential decrease in dose rate (Rao and Howell, 1993; Howell et al., 1994; Howell et al., 1998; Solanki et al., 2017). As was the case for the exponential mode, an algorithm assigns a fraction to occur at the beginning of the experimental run (t = 0), and another fraction to occur at the end of the experimental run (t = t_overall –t_fraction). Because the multi-exponential function does not have an inverse function, the algorithmic method described for exponential mode cannot be used. Instead, it is recognized that the absorbed dose is the integral of the dose rate over the overall time that the experiment is conducted.

Figure 5.

Multi-Exponential tab. Graphic user interface for delivering multi-exponential dose rate patterns of alpha particles. This facilitates delivery of increasing and decreasing dose rates.

$$D\left({\mathrm{t}}_{\mathrm{o}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}}\right)={\int }_0^{{\mathrm{t}}_{\mathrm{o}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}}}r\left(t\right)dt$$ (5)

The algorithm determines the time t_m at which the percentage of the total dose delivered is equal to the m^th percentile,

$$m\times \frac{1}{n-1}={\int }_0^{t_m}r\left(t\right)dt/D\left({\mathrm{t}}_{\mathrm{o}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}}\right),\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}m=1,2,\dots ,n-2$$ (6)

Calibration of the Dose Rate Patterns

Alpha Particle Energy and LET Spectra

The energy spectrum of the alpha particle beam was measured to ensure the beam characteristics were consistent with those reported in our previous communication (Neti et al., 2004). Briefly, a Canberra (Meriden, CT) system comprising CAM300 passive implanted planar silicon (PIPS) detector with an active area of 300 mm², associated electronics, multichannel analyzer (MCA), and Genie 2000 spectroscopy software were used. The detector was calibrated for energy response in a vacuum using a Model S94–4 planar ²³⁹Pu calibration standard (427,445 cpm/2π) from Eberline (Albuquerque, NM). The irradiator box was filled with helium and the flow rate for the irradiator chamber was set to 0.5 L min⁻¹. The PIPS detector was positioned on the Mylar™ growing surface of the stainless steel culture dish and alpha particle energy spectra were acquired for each source. To determine the LET spectrum of the alpha particles incident on the cells growing in the Mylar™-bottomed culture dishes, the LET values corresponding to the energies associated with each of the 4096 channels of the MCA were calculated by interpolating the tables for liquid water in ICRU Report 49 (ICRU, 1993; Neti et al., 2004). The LET spectrum was obtained by creating bins of width 5 keV μm⁻¹ (e.g. 80–85 keV μm⁻¹, 85–90 keV μm⁻¹, etc.) and then summing counts into the appropriate bins (Neti et al., 2004).

Fluence and Absorbed Dose

The fluence rates through the Mylar™ growing surface were measured with the PIPS detector to be 0.0038, 0.0037 and 0.0034 tracks μm⁻² min⁻¹ for sources 1, 2 and 3, respectively (Neti et al., 2004). The mean absorbed dose to the nuclei of the cells adhering to the Mylar™ is calculated according to the methods in Neti et al. (Neti et al., 2004). The absorbed dose per traversal, $d=0.16\times \frac{LET}{A}$, where A is the cross sectional area of the cell nucleus. Fluence rate was then calculated according to $\dot{N}=\frac{\left(Averagecounts\right)}{t\ast \left(PIPSdetectoractivearea\right)}$(tracks μm⁻² min⁻¹) as was fluence, Φ (tracks μm⁻²) for a given irradiation time interval. Lastly, the mean absorbed dose to the cell nuclei was calculated according to the derivation of Charlton & Sephton (Charlton and Sephton, 1991):

$$D=\Phi Ad$$ (7)

Dependence of Fluence on Number of Fractions

The shutter speed of the Copal electromechanical shutters is 0.1 s. Therefore, it was anticipated that the number of fractions (n) may affect the fluence delivered for a fixed total exposure time. This was tested by conducting a series of 120 s irradiations with 0, 100, 200, 300, and 400 fractions and recording the alpha particle counts for each trial with the PIPS detector.

Continuous versus Switched Operation of the Collimator for Fractionated Exposures

Fractionated exposures that extend over time periods from hours to days can put unnecessary strain on the collimator mechanism. Each fraction requires the shutter to be open for seconds whereas the interfraction spacing may be minutes to hours. To avert wear and tear, the user can elect to have the collimator oscillate only when the shutter is in the open position. The alpha particle counts for a 180 s exposure time delivered in 100 fractions was measured with the collimator operating continuously and with the collimator operating only when the shutter was open. No significant difference in the fluences were observed.

Exponential Dose Rate Patterns

A series of measurements of alpha particle counts were made with the PIPS detector to determine that the microcontroller delivered the α particles with a multi-exponential dose rate pattern with the desired T_i and T_d. The exponential down pattern was tested by measuring the alpha particle counts over 0.5 h intervals for an overall treatment time of 18 h with T_d = 6 h. The exponential up and down pattern was tested by measuring the counts over 1.0 h intervals, for an overall treatment time of 72 h, with T_i = 16 h and T_d = 24 h. In each case, the total exposure time was fixed at 120 s (i.e. shutter was open for a total of 120 s). Measurements were made automatically using the Canberra (Meriden, CT) Genie 2000 spectroscopy software which permits repeated acquisitions over fixed time intervals.

Absorbed Dose from Gamma Rays that Leak through the Shutter

In addition to alpha particles, the ²⁴¹Am sources also emit 59 keV gamma rays. The absorbed dose to cells growing on the Mylar™ bottomed dish from gamma rays that penetrate (“leak”) through the thin metal shutter is negligible compared to the absorbed dose delivered by alpha particles when acute irradiations are conducted over a period of minutes. However, chronic irradiation over days can result in a significant absorbed dose from gamma rays. Accordingly, commercial thermoluminescent dosimeters (Landauer®) were placed in triplicate on top of each shutter and allowed to remain there for 72 h with the photographic shutter in the closed position.

Results

The measured alpha particle energy spectra for the ²³⁹Pu calibration standard Sources 1, 2, and 3 had centroids (frequency means) of 2.8, 2.7, and 2.7 MeV (Supplementary figure 3), respectively, consistent within 5% of previous measurements (Neti et al., 2004). The fluence rate of the particles (particles μm⁻² min⁻¹) that penetrated through the Mylar™ bottom of the culture dishes were consistent with previous measurements when a helium flow rate of 0.5 L min⁻¹ was used. The calculated LET values of the alpha particles in liquid water ranged from 70 to 230 keV μm⁻¹, with a mean value of 132 keV μm⁻¹ for Sources 2 and 3 of the irradiator and 128 keV μm⁻¹ for Source 1 of the irradiator. These values indicate that the beam characteristics of the alpha particle irradiator are consistent with our previous findings (Neti et al., 2004).

Table 2 shows the dependence of the alpha particle counts, acquired by the PIPS detector during the 120 s total exposure time, on the number of fractions used to deliver the 120 s exposure. As a reminder, the fraction size decreases correspondingly with increasing number of fractions. There was a linear increase in the counts as a function of the number of fractions (Counts(n) = (1 + 0.00050 n) Counts(1), where n is the number of fractions and Counts(1) is the counts when delivered in a single fraction of length 120 s). This translates to a 5% increase in fluence per 100 fractions. Accordingly, the fluence and corresponding mean absorbed dose should be corrected when large numbers of fractions are used. This is important when comparing the radiobiological impact of a fixed mean absorbed dose that is delivered with different numbers of fractions.

Table 2.

Dependence of alpha particle fluence on number of fractions^*

Number of fractions	Irradiation Time per Fraction	Counts	Increase in Fluence (%)
1	120 s	1293421	0
100	1.2 s	1357536	5.0
200	0.6 s	1421956	9.9
300	0.45 s	1487177	15
400	0.3 s	1551131	20

^*fixed total shutter-open time of 120 seconds.

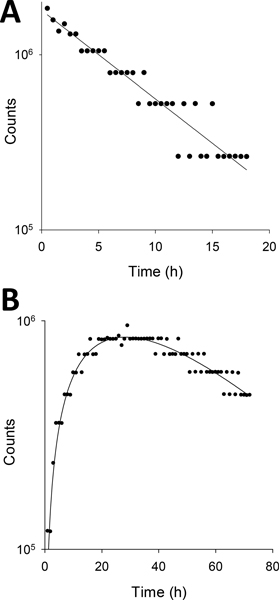
Figure 6 shows alpha particle count measurements made for exponential (T_d = 6 h) and multiexponential (T_i = 16 h, T_d = 24 h) dose rate patterns. As indicated in the Materials and Methods, the alpha particle counts were measured over 0.5 or 1.0 h intervals. Therefore, several fractions were delivered during each measurement interval and the number of counts recorded during any given measurement interval (represented by a datum point on the graph) is a multiple of the number of counts expected for a single fraction (shutter opened a fixed amount of time for each fraction). Accordingly, when a total of 100 fractions were delivered during the lengthy chronic irradiation, it was commonplace for the shutter to open the same number of times during consecutive measurement intervals such that the average number of counts recorded during consecutive intervals were often very similar. Accordingly, the data has a discretized appearance along the abscissae with a trend that matches the functional form of the expected patterns. The counts for the exponential down pattern were fit to the function y = a e^{− 0.693 t / T_d} which yielded T_d = 6.0 ± 0.3 h. The counts for the exponential up and down pattern were fit to the function Counts = a e^{− 0.693 t / T_d} – (1-a) e^{− 0.693 t / Ti} and yielded T_i = 15.9 ± 4.8 h and T_d = 24.5 ± 8.8 h.

Figure 6.

Serial measurements of alpha particle counts acquired with a PIPS detector for different dose rate patterns. A total of 100 fractions were delivered for each irradiation protocol. The counts were recorded automatically by the multichannel analyzer over contiguous 0.5 h or 1.0 h intervals, respectively, for A) exponential with T_d= 6 h, and B) multi-exponential with T_i= 16 h and T_d= 24 h.

Thermoluminescent dosimeter measurements of the absorbed dose received over 72 h from the 59 keV gamma rays emitted by the ²⁴¹Am sources yielded 0.000967 ± 0.0000058 Gy, 0.000907 ± 0.0000058 Gy, 0.000887 ± 0.0000058 Gy for sources 1, 2, and 3, respectively. The mean value is 0.000920 ± 0.000036 Gy which corresponds to an absorbed dose rate of 0.0000128 Gy h⁻¹. No significant dose (< 0.00001 Gy) was measured for the control shutter which did not have an ²⁴¹Am source below it.

Discussion

The unique capabilities of this microcontroller for shutter-controlled alpha particle irradiators can be used to acquire radiobiological data on the consequences of low dose rates of high-LET ionizing radiation delivered at constant and variable dose rates under highly controlled experimental conditions. It can facilitate delivery of a single fraction, multiple fractions equally spaced in time, or multiple fractions spaced temporally to simulate exponentially increasing and decreasing dose rates. The errors encountered in the total mean absorbed dose delivered depend on the number of fractions delivered with about a 5% increase in total dose per 100 fractions compared to a single fraction. This can be accounted for readily when setting up experiments that involve samples that receive the same mean absorbed dose delivered with different numbers of fractions. Notably, the dose rate when the shutter is open is just under 5 Gy h⁻¹. Therefore, dose rates ranging from 5 Gy h⁻¹ to very low dose rates can be accommodated depending on the fraction size and fractionation schedule. Therefore, even the in vivo absorbed dose rates required to deliver tumorcidal doses of ~ 10 Gy with alpha particle emitters with short physical half-lives (e.g. 7 h for ²¹¹At) can be simulated with this irradiator (Back et al., 2005).

When implementing this microcontroller system on shutter-controlled alpha particle irradiators, users should be aware of the potential for chronic gamma irradiation when using alpha particle sources that emit such radiations. The ²⁴¹Am sources used in our irradiator emit 59 keV gamma rays. However, the gamma ray dose rates are extremely low (0.0000128 Gy h⁻¹), delivering an average absorbed dose to the cell monolayer of approximately 1 mGy during a 72 h irradiation. A dose of 1 mGy, for instance, from ¹³⁷Cs gamma-radiation leads to an average of 2.5 energy deposition events per ng tissue; i.e., per cell in tissue (ICRU, 1983; Feinendegen, 2016). Even lower numbers may be anticipated for cells that are monolayered on the Mylar™ bottomed dishes because the number of secondary electrons arising from interactions of the upward trajectory photons with the thin 1.5-μm Mylar™ are lower than expected in solid tissue. While this low dose delivered chronically by gamma rays is not anticipated to cause observable detrimental damage compared to that caused by the alpha particles, it is possible that it may elicit some degree of adaptive protection (Azzam et al., 1996; Feinendegen, 2016; Solanki et al., 2017).

The first clinical trial on the use of α particle emitters for radiolabeled antibody therapy of cancer were reported in 2002 (Marcu et al., 2018; Jurcic et al., 2002). Subsequent trials have shown promising results in the treatment of recurrent ovarian cancer (Andersson et al., 2009), recurrent brain tumor (Cordier et al., 2010; Zalutsky et al., 2008), non-Hodgkins lymphoma (Witzig et al., 1999; Wiseman et al., 2000), myelogenous leukemia (Jurcic et al., 2002; Sgouros et al., 1999; Burke et al., 2003), and metastatic melanoma (Allen et al., 2011; Allen et al., 2005). In the meantime, the FDA-approved ²²³Ra dichloride (2013), a prolific alpha particle emitter, is having considerable success in extending the lives of patients with castrate-resistant prostate cancer metastatic to bone (Parker et al., 2013). Our GUI controlled irradiator can be utilized to study the radiobiology of this and other alpha particle emitting radiopharmaceuticals. The pharmacokinetics of radiopharmaceuticals in tumor and normal tissues conform typically to an exponential increase to a maximum followed by an exponential decrease, thereby delivering a correspondingly complex dose rate pattern (Pasternack and Howell, 2013; Solanki et al., 2017; Howell et al., 1997b). The ability to simulate these complex dose rate patterns in the laboratory may lead to new understanding of how the dose rate pattern affects the relative biological effectiveness (RBE) of radiopharmaceuticals labeled with α- versus β-particle emitters (Hobbs et al., 2014; Sgouros et al., 2010; Howell et al., 1997a; Howell et al., 1992).

There are also a number of radiobiological questions that the unique capabilities of this irradiator can help to clarify. For example, exposure to low doses of ionizing radiation has increasingly become a matter of scientific and public concern and debate. Public exposure to ionizing radiation is due mainly to chronic irradiation by “ubiquitous background” radiation from radon (Thurston, 2010). Radon is natural radioactive gas that is found in homes across the country. It is estimated that 10 to 14% of all lung cancer deaths are linked to radon gas, and radon gas is the second leading cause of lung cancer (after smoking), according to the National Cancer Institute at the NIH (Noh et al., 2016; BEIR-VI, 1998). The GUI controlled irradiator can simulate the constant or periodic dose rate patterns delivered by this high-LET background radiation. Of particular importance in this context, and other related scenarios, the GUI controlled alpha particle irradiator presented in this paper can be used to study how dose rate affects bystander effects which arise from nearby alpha-irradiated cells (Gonon et al., 2013; Nagasawa and Little, 1992; Deshpande et al., 1996; Azzam et al., 2003).

Finally, the capabilities of this microcontroller are not restricted to our irradiator. There are numerous shutter-controlled alpha particle irradiators in use around the world that can implement the hardware and software developed in this work (Inkret et al., 1990; Goodhead et al., 1991; Metting et al., 1995; Zarris et al., 1998; Esposito et al., 2009; Seideman et al., 2011; M et al., 2013; Nilsson et al., 2015; Lee et al., 2016; Soyland and Hassfjell, 2000; Søyland et al., 2000; Wang et al., 1989). The detailed table and figures in this article are intended to serve as a guide for others to build their own hardware, and our software is available as a downloadable supplement.