Dynamic Light Scattering – an all-purpose guide for the supramolecular chemist

Abstract

Dynamic light scattering (DLS) is a useful tool for the study of the solution-based behavior of colloids and molecular assemblies. The aim of this methods paper is to provide perspective on how this technique can be used by supramolecular chemists. As this technique is not extensively used within the field, we also provide a historical background of its development, summarize data interpretation and the strengths and limitations of the technique, and provide a perspective on some of the important features for supramolecular chemists that can be found in an instrument.

Introduction

In the confines of chemical analysis, light scattering refers to a collection of techniques that rely on the relationship between the scatter of light by molecules in a solution or colloidal suspension, and their translational diffusion. Within this portfolio, the two techniques of most common practice are: 1) dynamic light scattering (DLS), which provides information about the hydrodynamic size of particles in solution and; 2) static light scattering (SLS), which provides information about the molecular weight of particles in solution. Light scattering therefore offers complementary information to a technique very familiar to supramolecular chemistry: Diffusion Ordered (NMR) Spectroscopy – DOSY NMR.

Basic principles of light scattering

For an excellent, general light scattering resource see the text by Berne and Pecora.¹ Light waves are comprised of both an electrical and a magnetic component. When a polarized light source is directed towards a molecule, the oscillating electric field of the light-wave induces an oscillating polarization of the electrons in the molecule; a temporary dipole is produced which varies with time. According to classical radiation theory, a time-varying dipole emits electromagnetic radiation. Thus, the molecule acts as a secondary source of light and radiates (scatters) light. This scattered light, which is completely plane-polarized at an angle of 90° relative to the incident beam, has an intensity (I) that is proportional to the diameter (d) of the analyte (I ∝ d⁶)² and its polarizability. A single molecule is the ideal system for study by light scattering, because this eliminates the effects of secondary scattering and destructive interference. However, single molecule analysis is presently not possible. Contrastingly, in a solution at thermal equilibrium, Brownian motion dictates that all molecules are in constant motion and possess random orientations relative to each other. Therefore, upon irradiation from an incident beam, all molecules in solution scatter light and the interaction of those scattered waves will generate varying levels of both constructive and destructive interference, with the latter being more common. The outcome of these interactions is that the overall solution scattering fluctuates and has an intensity (per molecule) generally far less than the scattering intensity theoretically produced by a single molecule. The predominant light scattering techniques DLS and SLS, differ in that DLS measures these fluctuations in the scattering intensity in a time-dependent manner (see Figure 1) whereas SLS measures the time-averaged intensity of scattered light.

Figure 1:

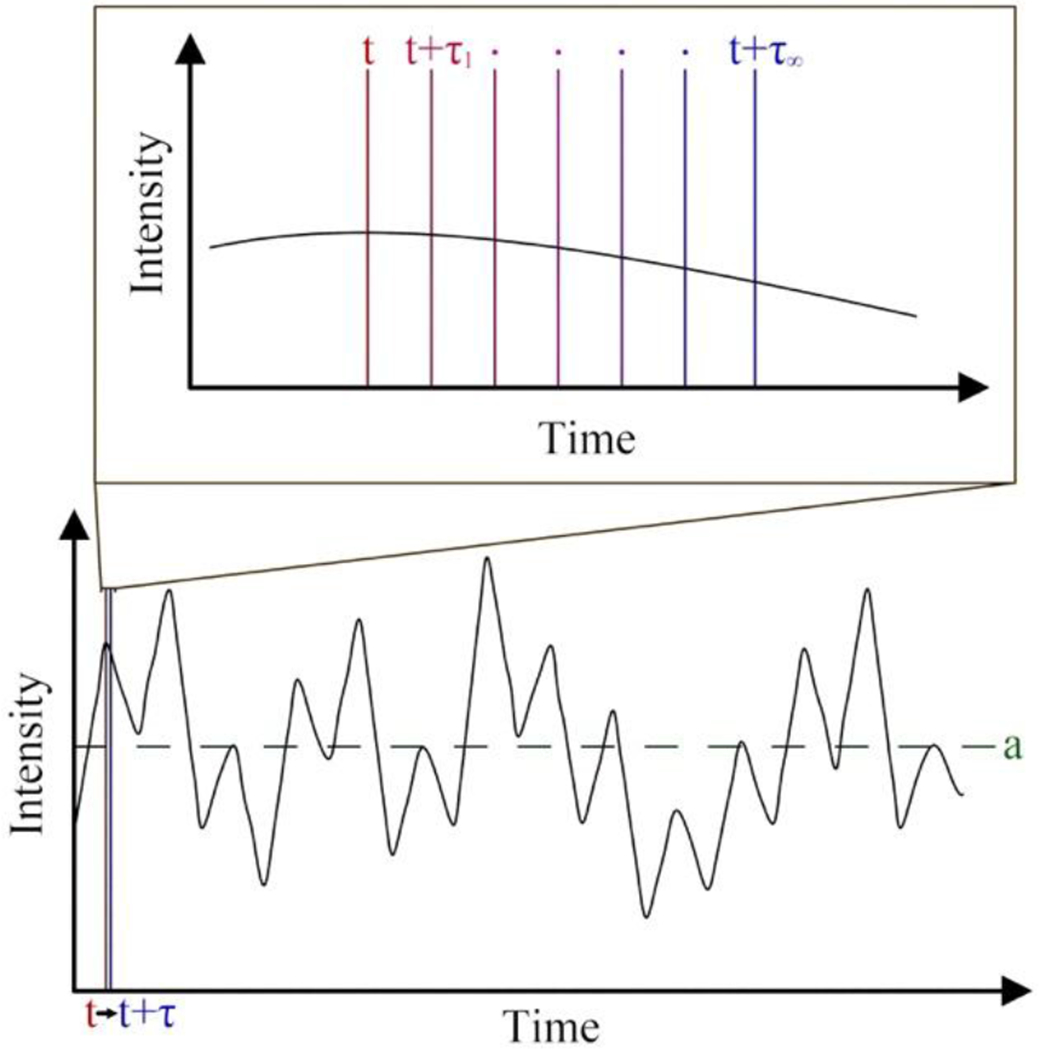
The lower portion of this figure shows the Intensity of scattered light as a function of time. SLS measures the average scattering intensity represented by ‘a’ (green). The upper portion of this figure shows a magnified region of the scattered light data. DLS determines the correlation between the intensity of light scattered at time ‘t’ (red) and some later time ‘t +τ’ (blue) as a function of ‘τ’.

History of light scattering

Optical spectroscopy in the form of light scattered from colloids is a discipline dating back at least 150 years to the initial studies of John Tyndall,³ after whom the Tyndall effect – scattering of light by particles the same size or larger than the wavelength of the incident beam – is named.⁴ Two years hence, John William Strutt,^5–7 (Lord Rayleigh), elucidated the nature of light scattered by particles smaller than the wavelength of the incident beam arising from translational and rotational degrees of freedom of molecules: Rayleigh scattering. Famously, Rayleigh scattering explained why the sky is blue when the sun is high in the sky (the intensity of scattered light is proportional to the inverse fourth power of the wavelength ($I\propto \frac{1}{{\lambda }^4}$), so the intensity of scattered blue light is much higher than that of red), but red at sunrise and sunset (the long pathlength through the atmosphere means that the scattered blue light fails to reach our eyes). DLS and SLS rely on Raleigh scattering.

Later, at the turn of the century, Smoluchowski⁸ and Einstein⁹ showed that there was a better way than trying to calculate the effects of destructive interference between wavelets scattered from different molecules as Raleigh had attempted. Instead, this difficult approach could be circumnavigated by considering the analyte solution to be a continuous medium in which thermal fluctuations led to local deviations in concentration and inhomogeneities in the refractive index, and hence to fluctuations of scattered light. This phenomenological approach to scattered light, which ignores the detailed molecular structure of the medium, raises profound questions regarding the validity of the approach.^10–11 It is also antithetical to the atomistic viewpoint of supramolecular chemists. But it works!

It is key to note that light scattering experimentation during the first two thirds of the 20^th century was relatively crude and hindered by two main problems: 1) the light sources utilized produced a broad range of wavelengths, and; 2) a general inability – both mathematically and computationally – to process the raw data (vide infra). With regard to the former, early light scattering studies relied primarily on Nernst lamps¹² or mercury vapor lamps¹³ as light sources, and it wasn’t until the twinned benefit of lasers – narrow linewidth to measure small frequency shifts in scattered light, and high intensity to probe weakly scattering molecules and particles – that scattering as it is thought of today began to develop.¹⁴ A major contribution to this development came from Gross, who showed experimentally that the scattering of light by solutions produced radiation corresponding to the wavelength of the incident beam (the Rayleigh line) as well as a “doublet” predicted by Brillouin¹⁵ that was framed symmetrically about the incident radiation.^16–17 Following on from this, the Rayleigh line was shown by Landau and Placzek to result from non-propagating entropy fluctuations,¹⁸ while the Brillouin doublet was found to be Doppler shifted by an amount proportional to the speed of sound.

Although these details were understood, without the benefits of lasers it was not possible to bridge the gap between light scattering and diffusion rates, leaving researchers mostly confined to theoretical manipulations, intensity and turbidity measurements, and molecular weight determinations.^19–24 (For an in-depth understanding of the state of light scattering prior to 1950, see the reviews by Zimm et al.²⁵ and Oster.²⁶) Progress wasn’t made until Pecora’s doctoral thesis in 1962 (relevant results published in 1964)²⁷ demonstrating that the spectral profile of the Rayleigh line broadened as a result of diffusion. Cummins et al. quickly expanded upon this work and became the first to employ the use of a laser in the study of polymer solutions.²⁸

The second major problem was one of data analysis. Standard contemporary DLS architecture – the so-called heterodyne architecture – uses a photomultiplier to gather the fluctuations in intensity of only the scattered light, which is then analyzed, or correlated by an auto-correlator. However, data analysis itself was no small task before the age of electronics. In 1969 Jakeman and Pike²⁹ laid the foundation for a digital autocorrelator (later expanded upon by Jakeman³⁰) and in 1970, Foord et al. published the first experimental results of light scattering using this method.³¹ This began to usher in a new era of light scattering that resembles the form of DLS employed today. In 1972, Koppel was the first to propose the method of cumulants – an analysis method for fitting the correlation function of a monomodal distribution.³² While the method of cumulants is straightforward and reliable, it does not accurately describe multimodal systems, and in 1985 Morrison et al. introduced non-negative least squares (NNLS) analysis for such cases.³³ We will not detail the mathematics of these methods, but suffice to say that all major manufacturers provide analysis software already built into the instrument that take advantage of a proprietary fitting method that is usually an NNLS variant (though this information is rarely disclosed).

Standard Operating Procedures

The following procedures were developed and optimized for a Nicomp ZLS Z3000 particle size analyzer (Particle Sizing Systems – Port Richey, FL), with a 50 mW laser diode (660 nm wavelength) and an avalanche photodiode (APD) detector. Measurements of scattered light were made at 90°, with data collected at 23 °C and processed using a NNLS Nicomp analysis. The procedures are, however, applicable to any modern DLS instrument.

Systems checks and sample preparation

Ensuring the performance of the instrument is the first step to collecting quality data. Most manufacturers provide a latex standard to measure the performance of their instruments. For best results, these standards typically require dilution in a salt solution prior to use.³⁴ Unlike mass spectrometry, calibration is not required prior to DLS analysis, but performance checks should be conducted on a semi-regular basis as per the manufacturer’s direction.

While some forms of analysis (e.g. NMR) can tolerate dust impurities, sedimentation and the like, optical spectroscopy such as DLS is far more sensitive to the cleanliness of the analysis environment; the I ∝ d⁶ relationship means that a typical dust particle scatters light 10¹⁸ times more strongly than a typical nano-meter sized molecule or particle. If available, a laminar-flow hood is recommended for sample preparation. Cuvettes – the primary method for sample containment in most DLS instruments (some systems utilize plate readers) – must be clean, in every sense, as an uncontaminated environment is the only way to ensure good, reproducible data. Disposable cuvettes, both glass and plastic, can be found for any instrument and are clean enough “as is” for the vast majority of purposes. If cuvettes requiring washing, it is imperative to dry them thoroughly first or risk sample dilution. Capping cuvettes, whether with disposable caps, parafilm, or some other method is also key to not only preventing evaporation but also preventing dust from entering the sample. Lastly, the exterior of the cuvette must be cleaned with a Kimwipe to remove any fingerprints or other marks that could affect optical measurements.

Centrifugation and filtration are also frequently required to minimize the presence of adventitious particles.³⁴ Typically, centrifugation for 10 minutes at 10,000 rpm is often necessary to yield high quality data. Likewise filtering samples is frequently important, and in such cases good practice necessitates the analysis of an unfiltered reference sample to ensure filtration didn’t remove aggregates of the analyte in question. Filters should be new/clean, and in some instances, it may be necessary to prewash them to ensure that residual materials from manufacture do not contaminate a sample with foreign matter. For this reason, the International Organization of Standardization (ISO) recommends that when dealing with organic solvent solutions samples should not be filtered.

Solvent effects

Solution effects are the single most important aspect to consider when preparing and analyzing a sample by DLS, and an intimate knowledge of the system is therefore critical. The density, refractive index, and viscosity of a solvent at the analysis temperature must be known prior to the experiment. These are well documented for most common solvents. All of these phenomenon are temperature dependent,³⁵ hence the presence of a Peltier temperature controller in DLS instruments. It is key, even for measurements at room temperature, to allow samples to equilibrate to the internal temperature of the instrument prior to analysis; the ISO states that for every °C departure from thermal equilibrium, the measured particle size will contain a ~2% error.³⁴

Salt effects in aqueous solutions

If one is dealing with a poly-electrolyte it is key to note that because of concentration fluctuations the normal symmetric “sphere” of counter ions around the central poly-ion can be distorted. This means that this central ion experiences a non-zero electrical force, and the resulting instantaneous force accelerates it and therefore contributes to its diffusion coefficient.¹ As a result, the particle in question appears to diffuse relatively fast and therefore be anomalously small (whilst if they could be observed, the counter ions would appear anomalously large). Another way to express this is to consider the long-range nature of Coulombic forces. As a result, poorly screened ions have large excluded volumes and therefore have relatively small volumes to move through. Regardless of the precise model, this phenomenon of anomalously fast moving (small) particles disappears if the poly-electrolytes are screened with addition of salt or buffer. Note however the macro-scale language used in these explanations (e.g., “screened”). Yet again, we must highlight here a distinct gulf between macro-scale descriptors and the atomistic level of non-covalent interactions that supramolecular chemists like to think in terms of. Commingled with these ideas, electrostatic interactions in solutions have been explained for decades by Debye-Hückel or extended Debye-Hückel theory,³⁶ but such models assume ions to be spherical, static, point charges.³⁷ In reality, and as any supramolecular chemist will readily testify to, ions come in all shapes and sizes and are often polarizable, and hence partake in many specific interactions with other solutes.^38–39 From the authors’ perspective there are major gaps in our understanding of the atomistic view of non-covalent interactions; be it with organic solutes interacting with themselves, cations and anions of salts interacting with themselves, or any combination thereof. More importantly, there are few links between these atomistic interactions and macroscale descriptors such as “screening”, “Debye length”, or “double layer”. There is much to do here.

Factors affecting the intensity of scattered light

Light scattering intensity is dependent on the concentration of a particle, its size, and its polarizability. With earlier instruments, because supramolecular chemists generally work with small organic molecules of low polarizability, DLS was not of sufficient sensitivity for it to become mainstream in the field. Even with newer technologies small organic molecules (< 5 nm) typically require concentrations in the > 1 mM range. Again, the relationship between size and scattering cannot be over emphasized: even in a scrupulously clean (dust free) sample, the Rayleigh approximation reveals a 10 nm particle will scatter one million times more strongly than a 1 nm particle (I ∝ d⁶). Thus, the small size of typical hosts or self-assembling subunits has been, and to a certain extent still is, a significant handicap to widespread adoption of the technique within the field.

Measurement angle also plays a role in the intensity of scattering. Unlike small particles which can be viewed as individual scattering centers, large particles (e.g., one twentieth the wavelength of light or larger) can be thought of as containing multiple scattering centers.²⁵ These multiple centers result in amplification and incoherence of the scattered light and lead to poorly correlated data. As a result, in these cases it is best to rely on back-scattering, i.e., light scattered back in the direction of the incident beam. Although back-scattering is relatively weak, issues from multiple scattering centers are minimal, and hence an angle of ~ 173° is ideal for such analytes. For the analysis of small particles such as those typically used by supramolecular chemists, back scattering is too weak for accurate determinations. In contrast, when the measurement angle is small, forward scattering from large species – be they endogenous or adventitious – can easily dominate the data, “swamping out” the scattering of the small analyte. As a result, the ideal scattering angle for small molecules is ~90° (side-scattering) where there is balance between maximizing sample scattering intensity and minimizing scattering from large species. It is recommended that in initial experiments, scattering angle be investigated as an independent variable to identify the ideal angle for the system in question.

Data interpretation

The autocorrelation function

There are various factors to consider when interpreting DLS data and analyzing its quality, but none are more important than the autocorrelation function. It cannot be overemphasized that the autocorrelation function is the bedrock of all DLS data; it is the equivalent of the binding isotherm of host-guest titration experiments.⁴⁰ As shown in Figure 1, the intensity of light scatter at time t is compared with the intensity after an interval τ for multiple values of τ. For very small values of τ, the signal is well correlated because the intensity has changed very little, but as τ gradually increases, the correlation of the signal will begin to decay, most commonly in an exponential manner (Figure 2a), until upon reaching τ = ∞, the signal is not correlated. Though we will not detail the derivations, the normalized intensity correlation function - g₂(τ) - is expressed in Equation 1:

Figure 2:

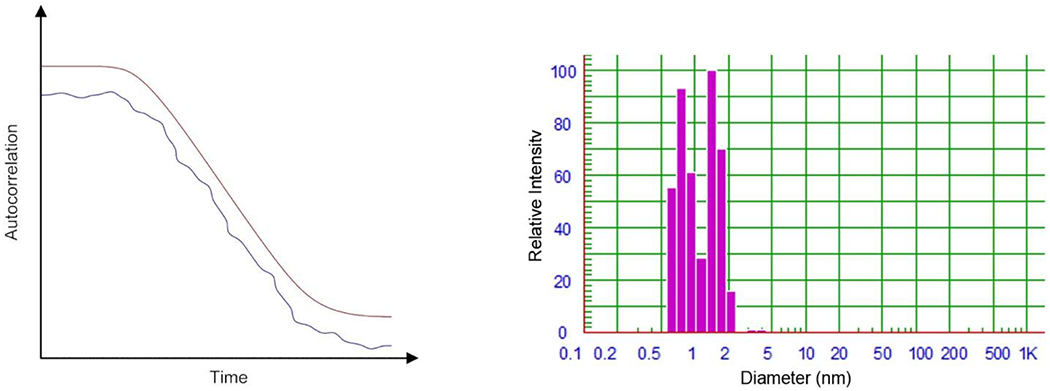
a) representative examples of a well-fit autocorrelation curve (red) and a poorly-fit autocorrelation curve (blue); b) observed size data (volume weighted) upon NNLS processing of the “raw” autocorrelation function. In this case the data shows two primarily species of 0.8 and 1.5 nm diameters.

$$g_2\left(\tau \right)=\frac{\langle I\left(t\right)I\left(t+\tau \right)\rangle }{{\langle I\left(t\right)\rangle }^2}=1+\beta e^{-2D_{\tau }{q}^2\tau }$$

where I(t) is the intensity of light scatter at time t, I(t + τ) is the intensity of light scattering at time t + τ, β is the intercept of the correlation function, D_τ is the translational diffusion constant, q is the scattering vector, and τ is the correlation delay time. As Eq. 1 shows, the diffusion constant is a direct result of the correlation function. The fitting of the correlation function using (for example) NNLS analysis yields the sought particle size data (Figure 2b).

For a number of reasons, it is possible for samples to produce an autocorrelation curve that is not well correlated (Figure 2a). Possible reasons include: an improper correlation delay time, weak scattering intensity, dust contamination, precipitation, and sedimentation. Irrespective of the cause, a poor correlation gives unreliable data. Manufacturers include a goodness-of-fit parameter for correlation curves to quantify the quality of the data. Lastly, it should be noted that some manufacturers only display a partial autocorrelation curve; a handicap that puts increased reliance on the less-visually informative goodness-of-fit parameter.

The importance of distribution

There are three common weighted (wt) distributions available for analyzing DLS data: intensity (Int-wt), volume (Vol-wt), and number (Num-wt). Int-wt distribution is the true output of the autocorrelation function and is exactly what it sounds, i.e., the ratio of each signal peak height. In contrast, the volume and number weighted distributions are simple manipulations thereof. The Vol-wt is obtained by accounting for the particular volume of the particle scattering the light, and Num-wt obtained by accounting for the number of particles responsible for each signal. For example, a sample with a 1:1 ratio of two particles of diameter 1 and 10 nm would give a Num-wt distribution of 1:1. However, because of the I ∝ d⁶ relationship, the ratio of the two peaks from the sample in an Int-wt distribution plot would be 1:1 × 10⁶. Between these two extremes, because the volume of a sphere is V = 4/3πr³, the ratio of the two signals in the Vol-wt would be ~1:1000. For a supramolecular chemist Vol-wt and Num-wt are frequently the metrics of choice.

Diameter versus volume

The diffusion constant calculated from the autocorrelation function (Eq. 1) is treated as a Stokes-Einstein diffusion coefficient. In many instruments this Stokes-Einstein diffusion coefficient is automatically converted to a particle radius by using the classical Stokes-Einstein equation relating hydrodynamic radius to diffusion coefficient (Eq. 2), where D is the diffusion constant, k_b is the Boltzmann constant, T is the temperature, η is the viscosity of the solution, and r_H is the hydrodynamic radius. For non-spherical assemblies the observed diffusion constant will not simply be the translational diffusion, but be the superposition of the rotational and translational diffusion constants of that entity.³⁴ That stated, for the small sizes typically probed by supramolecular chemists, the spherical approximation is reasonable. Note that whereas the particle size from any DLS measurement will usually be displayed either in terms of hydrodynamic radius or hydrodynamic diameter, in the context of self-assembly or general aggregation, the extent of aggregation N is usually sought. Hence hydrodynamic volume (V = 4/3πr³) is usually of more utility.⁴¹

$$D=\frac{k_{b}T}{6\pi \eta r_H}$$

Relation to other diffusion measurement methods

In supramolecular chemistry, diffusion ordered NMR spectroscopy (DOSY) is a common approach to measuring diffusion constants of molecules that provides comparable and complementary data to DLS. For the smallest of molecules that supramolecular chemists might consider, DOSY is a more sensitive technique than DLS; but the reverse is true if nanometer-sized molecules are being worked with. Furthermore, when dealing with aqueous solutions the fact that there is no background salt requirement in DOSY NMR spectroscopy can be important. In a number of ways though, DLS analysis has advantages over DOSY analysis. Thus, sample size in DLS is generally smaller (typically 10-200 μL for DLS vs ~500 μL for NMR), the required analysis time for DLS is significantly shorter (seconds as opposed to hours for DOSY), DLS does not have a calibration requirement (which effectively extends the relatively lengthy DOSY analysis time), and at higher concentrations – where aggregation becomes significant – NMR line-broadening can be an issue. Finally, plate-reader DLS instruments have a (pseudo) high-throughput advantage over NMR spectroscopy.

A word about zeta potential

Electrophoretic light scattering (ELS), more commonly known as zeta potential, is essentially a derivative of the DLS experiment. In a typical ELS experiment, a small portion of the original unscattered beam is mixed in with the scattered light fluctuations (the so-called heterodyne instrument architecture), to yield different correlation functions from the standard homodyne architecture. This subtle point noted, an ELS experiment simply probes the difference in DLS data for an analyte in the presence and absence of an applied electric field. The difference between the diffusion constants yields the zeta potential for the particle (another macro-scale descriptor). Because of the similarities of DLS and ELS, most modern instruments can perform both experiments. This is also true for plate-reader DLS instruments, which sequentially move micro-electrodes from one sample well to the next to measure zeta potential in a (pseudo) high-throughput ELS manner. One drawback of ELS is that the applied current literally electrocutes a sample. Hence depending on the nature of the molecule under study, this test can be a destructive means of analysis.

Considerations before buying

If a group is considering the purchase of a DLS instrument there are multiple points to consider. First, there are some general standards across the industry that should be confirmed. These include: minimum particle diameter requirements of 0.3 nm, proprietary fitting software to handle any form of particle distribution, and internal temperature control. Additionally, instruments can possess some less common, or unique, features of utility to supramolecular chemists. Points to consider include: 1) Is a cuvette-based system best, or could the research benefit from a plate reader that offers high through-put analysis? For example, if one is studying dynamic systems a plate reader may be undesirable because the time required between sampling the first and last wells is relatively long. 2) What is the volume required for a typical analysis? If the analyte is only available after a 10-step synthesis and in milligram quantities, a system that can operate with 10 μL is far superior to one that requires 200 μL. 3) What is the analysis time required for a single sample? Some instruments need mere seconds while others recommend several minutes per sample. 4) Is a fixed-angle system sufficient, or is it important to control the measurement angle to suit the particle size? 5) Does the system have ELS, or even SLS capabilities? 6) Does the operating software allow access to key details such as the autocorrelation function? In other words, to what extent should the instrument be a “black box.” All of these questions should be considered prior to purchasing an instrument.

Summary

This Methods Paper has served as both an entry-level summary of the theoretical and historical background of DLS, as well as a summary of the practical issues associated with purchasing an instrument and using the technique. DLS is a powerful tool that can be applied to a wide range of supramolecular systems for fast, non-destructive, and reliable sample analysis. It allows for the study of a wide range of particle sizes – both in pure samples and mixtures – and additionally can be used to study assembly/aggregation as a function of time. Moreover, most modern DLS instruments also come equipped with ELS abilities which increase their utility further. For supramolecular chemists, the key drawback of DLS is the extreme relationship between scattering intensity and particle diameter. However, modern instrument architectures combined with scrupulous sample preparation mean that measurements down to (or even below) 0.3 nm diameters are now possible. DLS is therefore a complementary and relatively inexpensive alternative to techniques such as DOSY NMR spectroscopy.