A sample size calculator for SMART pilot studies

Abstract

In clinical practice, as well as in other areas where interventions are provided, a sequential individualized approach to treatment is often necessary, whereby each treatment is adapted based on the object’s response. An adaptive intervention is a sequence of decision rules which formalizes the provision of treatment at critical decision points in the care of an individual. In order to inform the development of an adaptive intervention, scientists are increasingly interested in the use of sequential multiple assignment randomized trials (SMART), which is a type of multi-stage randomized trial where individuals are randomized repeatedly at critical decision points to a set treatment options. While there is great interest in the use of SMART and in the development of adaptive interventions, both are relatively new to the medical and behavioral sciences. As a result, many clinical researchers will first implement a SMART pilot study (i.e., a small-scale version of a SMART) to examine feasibility and acceptability considerations prior to conducting a full-scale SMART study. A primary aim of this paper is to introduce a new methodology to calculate minimal sample size necessary for conducting a SMART pilot.

1. Introduction

In the medical and behavioral health sciences, researchers have successfully established evidence-based treatments for a variety of health disorders. However, even with such treatments, there is heterogeneity in the type of individuals who respond and do not respond to treatment. Treatment effects may also vary over time (within the same individual): a treatment that improves outcomes in the short-run for an individual may not improve outcomes longer-term. Further, certain evidence based treatments may be too expensive to provide to all individuals; in such cases, health care providers may reserve these treatments for individuals who do not respond to less costly alternatives. The converse is also true: certain treatments are more ideally suited as maintenance treatments, and may be reserved for individuals who respond to earlier treatments in order to sustain improvements in outcomes. As a result, clinical researchers have recently shown great interest in developing sequences of treatments that are adapted over time in response to each individual’s needs. This approach is promising because it allows clinicians to capitalize on the heterogeneity of treatment effect. An adaptive intervention offers a way to guide the provision of treatments over time, leading to such individualized sequence of treatments.

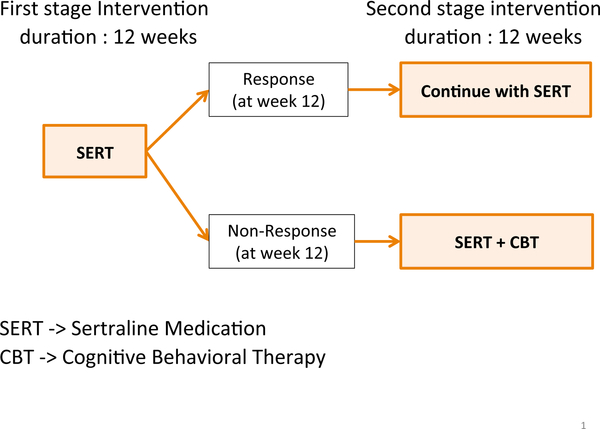
An adaptive intervention [1, 2, 3] is a sequence of decision rules that formalizes the provision of treatment at critical decision points in the course of care. In other words, an adaptive intervention is a guideline that can aid clinicians in deciding which treatment to use, for which individuals to use them, and when to use them. Figure 1 depicts a concrete example of an adaptive intervention for young children who are initially diagnosed with pediatric anxiety disorder.

Figure 1:

An example adaptive intervention for pediatric anxiety disorder patients

In this example of adaptive intervention, first, clinicians offer the medication sertraline [4] for initial 12 weeks. If the child does not show an adequate response to it at the end of week 12, the clinician offers to augment the treatment with a combination of the medication sertraline and cognitive behavioral therapy [5] for additional 12 weeks. Otherwise the clinician would continue the sertraline medication for another 12 weeks. In this adaptive intervention, response is defined based on a measure of improvement, for example, based on a cut-off of five or less on the Clinical Global Impression-Improvement Scale [6]. Change in the Pediatric Anxiety Rating Scale could also be used to define response/non-response [7]. An adaptive intervention is also known as an adaptive treatment strategy [8] or a dynamic treatment regime [9].

Recently, methodologists introduced a specific type of randomized trial design known as a Sequential Multiple Assignment Randomized Trials [1, 10, 11] to inform the development of high-quality, empirically-supported adaptive interventions. A SMART is a type of multi-stage trial where each subject is randomly (re)assigned to one of various treatment options at each stage. Each stage corresponds to a critical treatment decision point. Each randomization is intended to address a critical scientific question concerning the provision of treatment at that stage; together, these help to inform the development of a high-quality adaptive intervention. Lei et al. [1] reviews a number of SMART studies in behavioral interventions science. Also, see work by Almirall et al. [10]

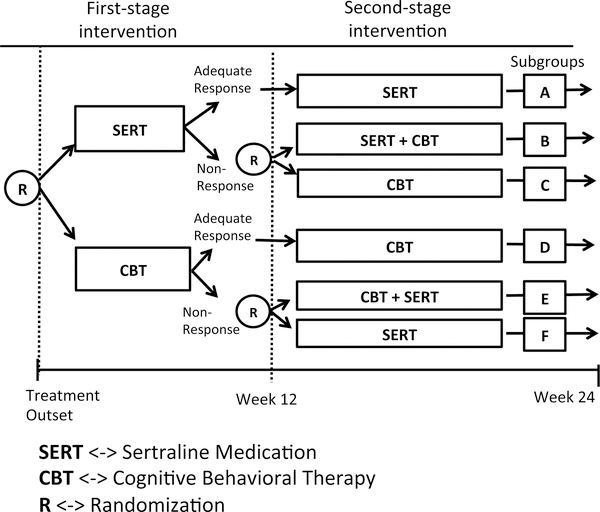
An example SMART is provided in Figure 2. This example could be used to develop an adaptive intervention for children who are diagnosed with pediatric anxiety disorder. At the first stage, there are two treatment options, sertraline medication or cognitive behavioral therapy(CBT). Each subject is randomly assigned to one of the initial treatment options and the assigned treatment is conducted for the first 12 weeks. At the end of week 12, each subject’s response to the treatment is assessed based on Clinical Global Impression-Improvement Scale [4] and categorized as a responder or as a non-responder. Based on this, those who do not respond to the initial treatment are again randomly assigned to one of two secondary treatment options: One is a switch strategy whereby the child is switched to the stage 1 treatment option they were not offered at first. The second option is the combination of both sertraline medication and cognitive behavioral therapy(CBT). For those who responded by the end of 12 weeks, continually initial intervention will be used. As with stage 1, both stage 2 treatments are provided for 12 weeks.

Figure 2:

An example SMART for pediatric anxiety disorder patients

In a SMART such as the one shown in Figure 2, research outcomes may be collected at the end of week 24 or throughout, from baseline to week 24. Research outcomes may be continuous, e.g., Pediatric Anxiety Rating Scale [4] or discrete, e.g., Clinical Global Impression-Improvement Scale [4]. Note that the measure of response versus non-response at week 12 is not necessarily a research outcome. It is purely a criterion to categorize participants of the first stage intervention into a group of responders or that of non-responders.

The SMART study described above can be used to address three key scientific questions in the development of an adaptive intervention for pediatric anxiety disorder: (1) ‘Which treatment to use in stage 1, medication or CBT?’ and (2) ‘Which tactic is best for non-responders to stage 1 treatment, switch or augment?’ Both of these questions involve randomized comparisons. Question (1) is addressed by comparing outcome measures of subgroup A, B and C in the Figure 2 with outcome measures of subgroup D,E and F in the Figure 2. Question (2) is addressed by comparing subgroup B and C when medication sertraline is stage 1 treatment and subgroup E and F when CBT is stage 1 treatment. Lastly, (3) This SMART design could also be used to compare the following four adaptive interventions contained within it.

1. First, offer sertraline medication for 12 weeks. If the patient does not respond well to initial medication at the end of week 12, augment by initiating a combination therapy (sertraline and CBT) for next 12 weeks. Otherwise continue with the medication sertraline for another 12 weeks. (Children in subgroups A and B provided data for this adaptive intervention.)

2. First, offer sertraline medication for 12 weeks. If the patient does not respond well to initial medication at the end of week 12, switch the treatment to CBT for next 12 weeks. Otherwise continue with the medication sertraline for another 12 weeks. (Children in subgroups A and C provided data for this adaptive intervention.)

3. First, offer CBT medication for 12 weeks. If the patient does not respond well to initial medication at the end of week 12, augment by initiating a combination therapy (sertraline and CBT) for next 12 weeks. Otherwise continue with the medication CBT for another 12 weeks. (Children in subgroups D and E provided data for this adaptive intervention.)

4. First, offer CBT medication for 12 weeks. If the patient does not respond well to initial medication at the end of week 12, switch the treatment to sertraline medication for next 12 weeks. Otherwise continue with the medication CBT for another 12 weeks. (Children in subgroups D and F provided data for this adaptive intervention.)

Note that the type of design used for SMART study described in Figure 2 is one of the most frequently used design. It has been used in SMART study of adolescent marijuana use [12], cocaine dependence [13, 14] and youth with conduct disorders [15]. For more recent ongoing SMART studies, visit the website: http://methodology.psu.edu/ra/smart/projects. For detailed data analysis method regarding SMART, see the work of Nahum-Shani et al. [11,16].

Despite the advantages of SMARTs, it is fairly new to clinical research. Therefore, researchers may have concerns over the feasibility or acceptability of conducting a SMART. Feasibility refers to the capability of the investigators to perform the SMART and the ability of clinical staff (i.e., staff providing treatment) to treat subjects with the adaptive interventions in the SMART. For example, psychologists or psychiatrists delivering the stage 1 treatments may have concerns about the way non-response is defined; it is important to work out these concerns prior to a full-scale SMART study. Acceptability refers to the tolerability of the adaptive interventions being studied from the perspectives of study participants, as well as the appropriateness of the decision rules from the perspective of the clinical staff. For instance, some parents may object to a switch strategy (they may, instead, prefer an augmentation or an intensification strategy). If this happens often, investigators may re-consider the acceptability of the switch strategy prior to conducting a full-scale SMART. In such cases, researchers may conduct SMART pilot study to resolve feasibility and acceptability concerns prior to performing the full-scale SMART study.

The design of any study (pilot or full-scale randomized trial) requires researchers to select an appropriate sample size in order to conduct the study. In full scale randomized trials (including SMARTs), the sample size is typically determined to ensure sufficient statistical power to detect a minimally clinically significant treatment effect. For example, in a full scale SMART study, such as the one shown in Figure 2, the sample size could be determined to provide sufficient power (e.g., 80%) to detect a minimaly clinically significant treatment effect between any two of the four embedded adaptive interventions [17].

However, because the primary aim of pilot studies centers on acceptability and feasibility considerations, the sample size for pilot studies is not based on statistical power considerations [18, 19, 20, 21]. For the SMART pilot study, the goal is to examine feasibility and acceptability of conducting a full-scale trial. One approach for selecting a sample size achieving this is to observe sufficient number of participants for each subgroup from A to E in Figure 2. This is because each subgroup corresponds to a particular sequence of treatments and if the investigator does not have an ample amount of participants in each group, they cannot detect potential problems regarding feasibility or acceptability of certain sequence of treatments prior to conducting full-scale SMART. The primary aim of this paper is to introduce a new method which calculates a minimal sample size of SMART pilot study.

In Section 2, we develop a methodology for calculating a minimal sample size for SMART pilot studies that are like the pediatric anxiety disorder SMART presented above. In Section 3, we verify the result using simulations. We also compare our proposed methodology with an pre-existing method [22]. In Section 4, we extend the method in Section 2 to other types of SMART designs (the pediatric anxiety SMART described above represents just one type of SMART design). In Section 5, we provide a summary and discussions including areas for future work.

2. A method for calculating the sample size for a SMART pilot study

2.1. The Proposed Approach

In this section, we develop a sample size calculator for SMART pilot studies. We first develop an approach for the SMART study shown in Figure 2. Note that the method we will provide can be used in any area of SMART study whose design is identical to the one in Figure 2. Later, in Section 4, we generalize the method for other types of SMART designs. The approach provides investigators planning a SMART pilot study a principled way to choose a sample size for the pilot study, such that a minimal number of participants are observed in subgroups A-F in Figure 2. This is important because if the investigators do not observe sufficient number of participants of one particular sequence of treatments, the investigator cannot judge whether the sequence of treatments is actually feasible or can be accepted. For example, suppose that to examine feasibility and acceptability concerns, an investigator wishes to observe at least three participants in each of the subgroups A-F in Figure 2: in this case, how many participants should the investigators recruit in the study? Because the exact number of non-responders is unknown ahead of the pilot study, a probabilistic argument is necessary to answer such a question.

To formalize this idea, we first define some notations. Let N denote the total sample size of the SMART pilot study. For simplicity, we assume N is always a multiple of two; later we discuss the implications of this. Let m denote the minimum number of participants that an investigator would like to observe in subgroups A-F. Let q_j denote the anticipated rate of non-response to stage 1 treatment where j = SERT or CBT and let q = min(q_SERT, q_CBT), which will be used as a common non-response rate; the implications of using the minimum will also be discussed later. Lastly, a lower bound for the probability of the event that each subgroup will have at least m number of participants is denoted as k. Note that m, q and k are all provided by the investigator planning the SMART pilot. Hence, our goal is to provide a formulae for N as a function of m, q and k. More formally, the goal is to find a smallest N which satisfies

$$\mathbb{P}(\text{all}\text{subgroups}\text{A-F}\text{have}\text{at}\text{least}m\text{participants})>k.$$

Using our notation, the above is equivalent to

$$\mathbb{P}\left(M_{\text{A}}⩾m,M_{\text{B}}⩾m,M_{\text{C}}⩾m,M_{\text{D}}⩾m,M_{\text{E}}⩾m\text{and}{M}_{\text{F}}⩾m\right)>k$$ (1)

where M_A stands for the number of participants who fall into subgroup A. M_B, M_C, M_D, M_E and M_F are defined in a similar way, respectively. Note that M_A, M_B, M_C, M_D, M_E and M_F are all discrete random variables. Next, we re-express (1) as

$$\mathbb{P}\left(M_A⩾m,M_{\text{B}}⩾m\text{and}{M}_{\text{C}}⩾m\right)\cdot \mathbb{P}\left(M_{\text{D}}⩾m,M_{\text{E}}⩾m\text{and}{M}_{\text{F}}⩾m\right)>k.$$ (2)

This is because, by the design of SMART study in Figure 2, any event of M_A, M_B and M_C is independent to that of M_D, M_E and M_F. Next let M_NS denote the number of non-responders out of N who were initially assigned to sertraline medication; and, similarly, let M_NC denote the number of non-responders initially assigned to CBT. We first consider the leftmost probability term involving M_A, M_B and M_C. Notice the event that $M_B⩾m$ and $M_C⩾m$ is equivalent to the event that $M_{\text{NS}}⩾2m$ . This is because, once the number of non-responders of sertraline medication is greater than or equal to 2m, regardless of whether M_NS is odd or even, both M_B and M_C would be at least m due to a block randomization[23] with equal probabilities. For the case, when M_NS is odd, we exclude a participant and proceed the second stage randomization. Therefore, we get

$$\mathbb{P}\left(M_A⩾m,M_{\text{B}}⩾m\text{and}{M}_{\text{C}}⩾m\right)=\mathbb{P}\left(M_{\text{A}}⩾m,M_{\text{NS}}⩾2m\right)=\mathbb{P}\left(\frac{N}{2}-M_{\text{NS}}⩾m,M_{\text{NS}}⩾2m\right).$$

A similar argument can be applied to M_D, M_E and M_F and we have

$$\mathbb{P}\left(M_{\text{D}}⩾m,M_{\text{E}}⩾m\mathrm{and}{M}_{\text{F}}⩾m\right)=\mathbb{P}\left(M_{\text{D}}⩾m,M_{\text{NC}}⩾2m\right)=\mathbb{P}\left(\frac{N}{2}-M_{\text{NC}}⩾m,M_{\text{NC}}⩾2m\right).$$

Re-expressing (2), our goal is to find the smallest N such that

$$\mathbb{P}\left(\frac{N}{2}-M_{\text{NS}}⩾m,M_{\text{NS}}⩾2m\right)\cdot \mathbb{P}\left(\frac{N}{2}-M_{\text{NC}}⩾m,M_{\text{NC}}⩾2m\right)>k$$ (3)

which is equivalent to,

$$\mathbb{P}\left(\frac{N}{2}-m⩾M_{\text{NS}}⩾2m\right)\cdot \mathbb{P}\left(\frac{N}{2}-m⩾M_{\text{NC}}⩾2m\right)>k.$$ (4)

Now note that

$${\text{M}}_{\text{NS}}={\displaystyle \sum _{\text{i}=1}^{\text{N}/2}{\text{X}}_{\text{i}}},{\text{M}}_{\text{NC}}={\displaystyle \sum _{i=1}^{\text{N}/2}{Y}_i},$$

where X_i = 1 if the ith participant assigned to sertraline medication did not respond well or X_i = 0 otherwise. Since the probability of non-response to sertraline is assumed to be q, we have that X_n has a Bernoulli distribution with success probability q [24]. Similarly, Y_n has a Bernoulli distribution with success probability q (recall the assumption that the probability of non-response is assumed to be q for both sertraline and CBT). Therefore, M_NS and M_NC have identical distributions, which we denote by the random variable Mq. Further, given the result that the sum of independent identically distributed Bernoulli random variables has a Binomial distribution [24], we have that

$$\mathbb{P}{\left(\frac{N}{2}-m⩾M_{\text{q}}⩾2m\right)}^2>k,$$ (5)

where $M_q~$ Binomial $\left(\frac{N}{2},q\right)$ or, equivalently,

$${\left(\mathbb{P}\left(\frac{N}{2}-m⩾M_{\text{q}}\right)-\mathbb{P}\left(2m-1⩾M_{\text{q}}\right)\right)}^2>k$$ (6)

holds as well.

As a side note, if we have an odd number of participants, it is impossible to assign an equal number of participants to each initial intervention. Therefore we set N to be a multiple of 2, this is because, by the design of our SMART study in Figure 2, there is a block randomization in stage 1 [23]. Setting N as a multiple of 2 allows us to assign equal number of participants to two treatment options provided at the first stage. Additionally we use a minimum value of the two non-response rate (q_SERT,q_CBT) as a common non-response rate(q). This is because, by using a minimum value of two non-response rates, we will get a robust sample size which satisfies (6).

2.1.1. Implementation

For fixed values for m, k and q(i.e., provided by the scientists designing a SMART pilot), a suitable value of N can be found by searching for the smallest N such that (6) holds true. This is possible because (6) is an inequality with respect to N assuming that m, k and q are given. This can be easily accomplished using any computer program capable of calculating upper tail probabilities for random variables with Binomial distributions(e.g., the pbinom function in R [25]).

Using the implementation outlined above, Table 1 provides values of N for a range of inputs of m, k, and q. For example, suppose an investigator wishes that at least 3(m) participants are observed in each subgroup with probability greater than 0.8(k), and assumes that the common non-response rate is 0.30(q). Based on the Table 1 below, the investigator needs to recruit at least 58 participants for the SMART pilot study. Note that in this paper, we provide sample sizes for the q values in a range between 0.2 to 0.8 because for the non-response rate values below 0.2 or above 0.8, as it may not be feasible to conduct a SMART studies.

Table 1:

Minimal sample size of SMART pilot study based on the proposed method

	Range of q :	0.20	0.30	0.40	0.50	0.60	0.70	0.80
k = 0.80	m = 3	88	58	42	34	28	32	50
k = 0.80	m = 4	112	74	54	42	36	42	64
k = 0.80	m = 5	136	90	66	52	44	50	76
k = 0.90	m = 3	100	64	48	36	32	38	60
k = 0.90	m = 4	126	82	60	46	40	48	74
k = 0.90	m = 5	150	98	72	56	48	56	86

2.1.2. A Pre-existing Approach

A similar approach to calculate the sample size for SMART pilot studies was first proposed by Almirall et al. [22]. Their proposal centered on finding the smallest sample size N which satisfies

$$\mathbb{P}\left(M_{\text{B}}>m-1,M_{\text{C}}>m-1,M_{\text{E}}>m-1\text{and}{M}_{\text{F}}>m-1\right)>k.$$

This differs from our proposed approach, which requires that all six subgroups A-F have at least m participants with probability greater than k(see (1)). The use of this objective function was based on the argument that in typical SMART studies, the rate of non-response is often not very large(i.e less than equal to 0.60). Therefore, in such settings it is highly likely that if the condition that the number of participants in subgroups B, C, E and F are respectively greater than m — 1 was required, the number of responders in subgroups A and D would also be greater than m — 1, respectively.

On top of that the pre-existing method had an assumption that the event: M_B > m — 1 & M_C > m — 1 is equivalent to the event: M_NS > 2m — 2, which may not be true. Consider the case when M_NS = 2m — 1. If M_NS = 2m — 1, either M_B or M_C should be m — 1, which violates the condition given: M_B > m — 1 & M_C > m — 1. In other words, the condition: M_B > m — 1 & M_C > m — 1 implies that M_NS > 2m — 2, but not necessarily in the other way around.

Therefore the sample size we get from the pre-existing method will not guarantee that the investigator would observe at least m number of people for each subgroup with probability greater than k. In next section, we will conduct a simulation study to check validity of the pre-existing method by comparing the simulation result of the pre-existing method with that of the new method introduced in Section 2.1.

3. Simulation

A simulation experiment is conducted (i) to verify that sample sizes obtained under the proposed approach satisfy equation (6) under a variety of realistic values for m, k and q, and (ii) to compare the performance of the proposed method with the pre-existing method by Almirall et al. [22], described above.

The simulation experiment is conducted in the following way for each combination of values of m, k and q.

1. Firstly, the values m, k and q are used to calculate the minimum suggested sample size N based on the proposed methodology.

2. Secondly, using this sample size N, we simulate the flow of participants through one realization of the SMART shown in Figure 2. Specifically, we divide the total sample size(N) by 2. Then by rbinom function [25] in R, we obtain the number of responders and non-responders for each pilot SMART simulation, which allows us to get the number of participants in each of the subgroups A-E.

3. Thirdly, we check if the number of participants in each subgroup is greater than pre-specified m or not. If the condition is met, we count it as a successful SMART pilot study. This process is repeated for 10,000 times. In the end, after 10,000 simulations, we obtain the proportion of successes out of 10,000. This represents an estimate of the left-hand side of expression (1), which we take it as a true proportion, denoted as ρ, since we are conducting 10,000 times of Monte Carlo simulation.

4. Lastly, the proportion(ρ) obtained in previous step is compared with a pre-specified lower bound for the proportion(k). If this proportion(ρ) is greater than k value, we conclude the sample size obtained from the proposed method is valid. Otherwise, the proposed sample size is invalid. The Table 2 provides the results of this experiment.

Table 2:

Simulation table of the sample sizes based on the proposed method

	Range of q :	0.20	0.30	0.40	0.50	0.60	0.70	0.80
k = 0.80	m = 3	0.807	0.816	0.821	0.860	0.809	0.810	0.815
k = 0.80	m = 4	0.810	0.828	0.814	0.820	0.834	0.844	0.821
k = 0.80	m = 5	0.811	0.825	0.820	0.835	0.838	0.830	0.813
k = 0.90	m = 3	0.911	0.902	0.921	0.903	0.931	0.912	0.910
k = 0.90	m = 4	0.906	0.911	0.921	0.913	0.925	0.920	0.912
k = 0.90	m = 5	0.903	0.906	0.915	0.918	0.926	0.902	0.901

Notice that the number of non-responsers could be an odd number. In this case, we subtract one from the number of non-responsers and divide by two. Then we use this value to check if it is greater than m or not. This is to (i) to get a conservative sample size and (ii) to avoid having non integer value of participants in each subgroup. If both values are greater than m, then we count this trial SMART pilot as a successful SMART pilot study.

From the simulation result, we can assess if the sample sizes we get from the proposed method, which are in Table 1, are valid or not. For instance, when m = 3, k = 0.80 and q = 0.30, we need to have at least 58 participants to conduct a SMART pilot study based on the Table 1. Then, from Table 2, we can see that out of 10,000 simulations, roughly in 8,160 (10,000·0.816) times, the condition that there are 3 or more people in each subgroup is satisfied. Since all the values we get from the simulation are greater than corresponding k value which is in the left end column, we can say that our new method developed in previous section is valid.

To see whether the method discussed in Section 2.1 is an improved version, a simulation study is also conducted, in a same manner, for the pre-existing method [22]. As one can see in Table 3, pre-existing method failed to prove its validity. Again, this is because of the assumptions discussed in the Section 2.1.2.

Table 3:

Simulation table of the sample sizes based on the pre-existing method

	Range of q :	0.20	0.30	0.40	0.50	0.60	0.70	0.80
k = 0.80	m = 3	0.633	0.662	0.623	0.616	0.475	0.194	0.000
k = 0.80	m = 4	0.650	0.664	0.650	0.672	0.549	0.353	0.000
k = 0.80	m = 5	0.675	0.691	0.678	0.641	0.592	0.000	0.000
k = 0.90	m = 3	0.790	0.780	0.766	0.803	0.769	0.401	0.000
k = 0.90	m = 4	0.796	0.822	0.818	0.813	0.786	0.000	0.000
k = 0.90	m = 5	0.821	0.820	0.831	0.841	0.806	0.459	0.000

4. Extensions to other SMART pilot studies

Not all SMART studies will be like the type shown in Figure 2. In the SMART in Figure 2, all non-responders were re-randomized at the second stage regardless of the initial treatment assignment; i.e., re-randomization to second-stage treatment depended only on response/non-response status. In a second type of commonly-used SMART design, re-randomization at the second stage depends on both initial treatment and response/non-response status. In a third type of commonly-used SMART design, both responders and non-responders are re-randomized at the second stage. In this section, we extend the methods of Section 2.1 to these two types of SMART designs.

4.1 Re-randomization depends on initial treatment and response status

In this section, we consider SMART studies where re-randomization to second-stage treatment depends on the choice of initial treatment as well as response/non-response status.

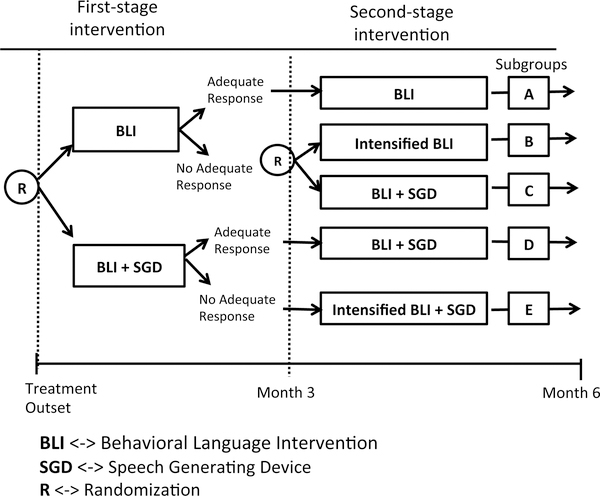
As an example, consider the SMART shown in Figure 3. This SMART study was designed to develop adaptive interventions for improving linguistic and social communication outcomes among children with autism spectrum disorders who are minimally verbal [26]. Specifically, this SMART examined the effects of three adaptive interventions involving different provisions of a speech generating device (SGD; a type of Augmentative and Alternative Communication Interventions). This SMART was facilitated to answer two scientific questions in the context of a behavioral language intervention (BLI) for children with autism [27, 28]. Initially, all children were randomized at stage 1 to BLI versus BLI+SGD for 12 weeks to answer question (1): Is providing SGD more effective at initial stage? At the end of week 12, each participant is categorized as a responder or a non-responder to stage 1 treatment based on 14 measures including: 7 communication variables from natural language sample with blinded assessor and 7 communication variables from intervention transcripts [26]. All responders continued on stage 1 treatment for an additional 12 weeks. All non-responders to BLI+SGD received intensified BLI+SGD. Non-responders to BLI were re-randomized to intensified BLI versus BLI+SGD to answer question (2): For non-responders to BLI, is providing SGD with BLI as a rescue intervention more efficacious than intensifying the initial intervention? Total number of spontaneous communicative utterances, primary outcome of the study, was collected at week 24 with a follow-up collection at week 36.

Figure 3:

An example SMART for Children with Autism

The derivation of the sample size formulae for a pilot study of a SMART of this type is similar to the derivation in Section 2.1. One difference in the notation is that in this SMART design, there are 5 subgroups, labeled A to E. Our goal is to determine the smallest N which guarantees that

$$\mathbb{P}(\text{all}\text{subgroups}\text{A-E}\text{have}\text{at}\text{least}m\text{participants})>k$$

Using arguments similar to those used in section 2.1 (see Appendix A), one can show that this inequality is identical to

$$\left[\mathbb{P}\left(\frac{N}{2}-m⩾M_{\text{q}}\right)-\mathbb{P}\left(2m-1⩾M_{\text{q}}\right)\right]\cdot \left[\mathbb{P}\left(\frac{N}{2}-m⩾M_{\text{q}}\right)-\mathbb{P}\left(m-1⩾M_{\text{q}}\right)\right]>k.$$ (7)

Notice that, unlike with the inequality given in equation (6), the left-hand-side of inequality (7) does not reduce to the square of a probability. This is due to the imbalance in the SMART design shown in Figure 3(only non-responders to one of the initial treatments are re-randomized) relative to the design shown in Figure 2(where all non-responders are re-randomized). Given k, q, and m, a solution for N in expression (7) can be found using an approach that is similar to the one described earlier to solve expression (6). Table 4 provides a minimal sample size for the type of SMART designs in Figure 3.

Table 4:

Minimal sample size of SMART pilot study for nonverbal children with autism

	Range of q :	0.20	0.30	0.40	0.50	0.60	0.70	0.80
k = 0.80	m = 3	78	52	38	30	28	32	50
k = 0.80	m = 4	100	66	48	38	34	42	64
k = 0.80	m = 5	122	80	60	48	42	50	76
k = 0.90	m = 3	90	58	42	34	30	38	60
k = 0.90	m = 4	114	74	54	42	38	48	74
k = 0.90	m = 5	138	90	66	52	46	56	86

See the work of Kilbourne et al. [29], which employs a SMART of this type to enhance outcomes of a mental disorders program.

4.2. Both responders and non-responders are re-randomized

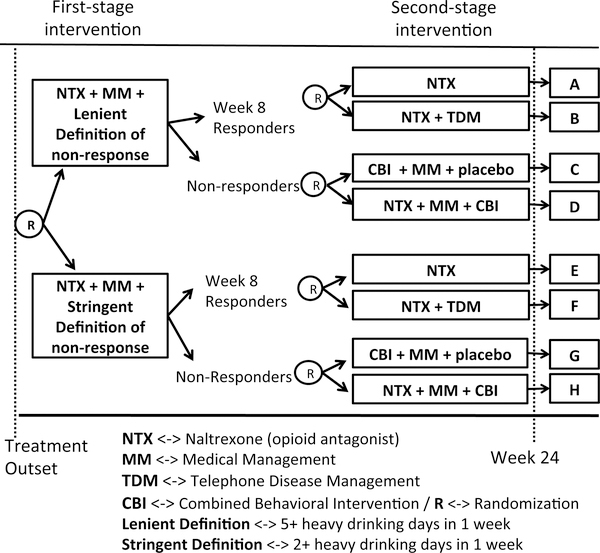
In this section, we consider a third type of SMART design where both responders and non-responders are re-randomized. As an example of this type of design, we present a study of individuals with alcoholic use disorder. The example SMART design is shown in Figure 4. The goal of this SMART study, which is reviewed in greater detail in Lei et al. [1], was to develop adaptive interventions for individuals with alcoholic use disorders. This SMART was used to answer three scientific questions regarding the use of naltrexone medication (NTX) [30], an opioid receptor antagonist, for the management and prevention of relapse among individuals with alcohol use disorder. All participants were provided NTX medication as a stage 1 treatment. Non-response to NTX was measured on a weekly basis. Participants were randomized initially to two different definitions for non-response to NTX–a lenient versus a more stringent definition–to answer the question (1): What extent of weekly drinking activity is best regarded as non-response? The lenient definition of non-response was defined as having five or more heavy drinking days per week, whereas the stringent definition of non-response was defined as having two or more heavy drinking days per week. Participants identified as non-responders to NTX were re-randomized to the combination of combined behavioral intervention (CBI) [31, 32], medical management (MM) [33] versus to the combination of NTX, CBI and MM. This randomization answers the question (2): What type of treatments would be useful for subjects who do not respond well to NTX? If participants had not been identified as non-responders by week 8, they were said to be responders to stage 1 intervention. Responders were re-randomized to the NTX versus to the combination of NTX and telephone disease management (TDM) to answer the question (3): What type of treatments would be effective for reducing the chance of relapse among people who responded well to NTX? Primary outcomes included the percentage of heavy drinking days and percentage of drinking days of the last two months of the study.

Figure 4:

An example SMART for alcoholic patients

The variables m, k, and q are defined as in Section 2.1 (see the Appendix B). In this type of SMART, there are 8 subgroups, labeled A through H. In addition, randomization occurs both for responders and non-responders. Our goal is to find a smallest N which satisfies

$$\mathbb{P}(\text{all}\text{subgroups}\text{A-H}\text{have}\text{at}\text{least}m\text{participants})>k$$

In Appendix B we show that the above equation is true if and only if

$${\left[\mathbb{P}\left(\frac{N}{2}-2m⩾M_{\text{q}}\right)-\mathbb{P}\left(2m-1⩾M_{\text{q}}\right)\right]}^2>k,$$ (8)

As you can see in expression (8), unlike in expression (7), since the design is perfectly symmetric we have two identical probability terms multiplied each other. In addition, unlike expression (6), instead of m, 2m was subtracted from $\frac{N}{2}$ . This is because, for the type of SMART designs described in Figure 4, responders were also randomized. For more detailed explanation on how this influences the method, see Appendix B. Again, given m, k and q, a solution for N in expression (8) can be found using an approach that is similar to the one described earlier to solve expression (6). Table 5 provides a minimal sample size for the type of SMART design in Figure 4.

Table 5:

Minimal sample size of SMART pilot study for alcoholic patient

	Range of q :	0.20	0.30	0.40	0.50	0.60	0.70	0.80
k = 0.80	m = 3	88	58	42	36	42	58	88
k = 0.80	m = 4	112	74	54	46	54	74	112
k = 0.80	m = 5	136	90	66	56	66	90	136
k = 0.90	m = 3	100	64	48	40	48	64	100
k = 0.90	m = 4	126	82	60	50	60	82	126
k = 0.90	m = 5	150	98	72	60	72	98	150

A number of other SMART studies are similar to the type shown in Figure 4. These studies include a SMART for developing an adaptive reinforcement-based behavioral intervention for woman who are pregnant and abusing drugs [34]; a SMART study aimed at developing an adaptive intervention involving individual and family-delivered cognitive behavioral therapy among children with depression; and a SMART designed to develop an adaptive intervention for children with autism spectrum disorders who are minimally verbal. All three of these studies are currently in the field.

5. Discussion

This manuscript presents pilot sample size calculators for three of the most common types of sequential multiple assignment randomized trial (SMART) designs. As stated in the introduction, researchers use SMARTs to inform the development of adaptive interventions. More specifically, SMART designs can be used to address critical scientific questions that need to be answered in order to construct high-quality adaptive interventions. Over the last 15 years, SMART designs have become more popular among clinical and health service researchers. However, some researchers may have concerns regarding the feasibility of conducting a full scale SMART or the acceptability of the treatments or adaptive interventions embedded in a SMART design. Such researchers may choose to conduct a smaller-scale pilot SMART prior to conducting a full-scale SMART. Specifically, a SMART pilot study is a small scale version of a full scale SMART study, where the primary purpose is to examine the acceptability and feasibility issues. See the following papers for more detailed explanations and concrete examples of SMART pilot studies [15, 22, 35].

This paper develops an approach for determining the minimum sample size necessary for conducting a pilot SMART. The number of participants for SMART pilot study should be enough to address concerns in feasibility and acceptability of full-scale SMART study. The paper introduces one way to operationalize this, which is to ensure that each subgroup corresponding to sequence of treatments to observe some minimum number(m) of participants. This approach was used to select the sample sizes for two recent SMART pilot studies: 1) SMART for developing an adaptive intervention for adolescent depression [35], 2) SMART for adolescent conduct problems [15]. Further, the methods are developed for three of the most commonly used types of SMART designs. Finally, we compare our proposed method with the pre-existing, related method to calculate a sample size for a SMART pilot [22] and explain how the proposed methodology is an improvement on the pre-existing one. In addition, the characteristics of the methodologies developed in this paper were examined thoroughly via Monte Carlo simulation. Specifically, for each type of SMART design, 10,000 simulation SMART pilot studies were conducted with different combinations of values of m,k and q via statistical software R. In all possible combinations of m,k and q, the simulation study supported that the condition imposed on the sample size(N) was met.

The method may be conservative in that, based on the way the rate of non-response is elicited from the scientist, the method may suggest a sample size that is as large or larger than the sample size actually needed to meet the constraint. Specifically, our proposed approach elicits the minimum value of the non-response rates to first-stage treatments. This was done to minimize the burden on the investigator of having to guess/provide two non-response rate. In settings where the two non-response rates differ, using the minimum for both may lead to conservative sample size requirements, relative to a method which uses both of two different non-response rates. For the future work, one can possibly develop a new methodology to calculate minimum sample size for a SMART pilot using two non-response rates. Also one can further investigate, in which circumstances (i.e. which combinations of m, k and q), a method that uses two non-response rate values results in substantially small sample size than the method introduced in this paper.

Some suggestions on choosing values for m, k and q are provided in this paragraph. Concerning q: Existing data from previous studies (not necessarily a previous SMART study) are often used to obtain estimates of q. Typical values of non-response rates for SMART ranges from 0.3 to 0.7. Concerning m: In many cases, we have found that investigators are interested in observing between 3 and 5 participants for each subgroup of a pilot SMART. Note that for typical pilot studies, resources, including the maximum number of participants that could be afforded in a pilot study, are often limited. And observing between 3 to 5 people for each subgroup is typically enough to assess feasibility and acceptability issues regarding adaptive interventions. Concerning k: typical values range from 0.8 to 0.95.

This manuscript provides a way to choose a sample size for a pilot SMART, to examine feasibility and acceptability concerns before conducting a full scale SMART study. Another possible approach is to choose a sample size so that investigators may observe an estimate of response/non-response rate with pre-specified amount of precision. Researchers may want to adopt this approach to estimate non-response rate. By using the estimate of non-response rate, researchers can implement the methodologies described in the paper. For instance, suppose we want a sample size N which allows us to estimate non-response rate(q) within the margin of error of 0.1 with significance level 0.05. Then, we estimate q by the proportion of non-responders among total sample $(\widehat{q})$ . Since the number of non-responders follows a Binomial distribution with parameters q and N [24, 36], after some calculation, we get N = 100. Note that the above example is just to illustrate another way to calculate sample size for pilot study. In this way, one can come up with an alternative way to develop a sample size calculator for SMART pilot study. For more detailed technical explanation, see Appendix C.

Appendix

A. Appendix A

Here, we provide a mathematical derivation of equation (7). All the variables used here are defined in a similar way as in Section 2.1. Recall that what we want to calculate is the smallest N such that

$$\mathbb{P}(\text{all}\text{subgroups}\text{A-E}\text{have at least}m\text{participants})>k$$

holds. Using mathematical expression, one can write it as

$$\mathbb{P}\left(M_{\text{A}}⩾m,M_{\text{B}}⩾m,M_{\text{C}}⩾m,M_{\text{D}}⩾m\text{and}{M}_{\text{E}}⩾m\right)>k.$$

By the independence of the group with behavioral language intervention and the group with both

behavioral language intervention and speech generating device, the above is same as

$$\mathbb{P}\left(M_{\text{A}}⩾m,M_{\text{B}}⩾m\text{and}{M}_{\text{C}}⩾m\right)\cdot \mathbb{P}\left(M_{\text{D}}⩾m,M_{\text{E}}⩾m\right)>k.$$

Let M_NB denote the number of non-responders of behavioral language intervention. Note that the event: $M_{\text{B}}⩾m$ and $M_{\text{C}}⩾m$ is same as the event: $M_{\text{NB}}⩾2m$ due to a block randomization with equal probabilities [23]. Therefore we get

$$\mathbb{P}\left(M_{\text{A}}⩾m,M_B⩾m\text{and}{M}_{\text{C}}⩾m\right)=\mathbb{P}\left(\frac{N}{2}-M_{\text{NB}}⩾m,M_{\text{NB}}⩾2m\right).$$

Let M_NBS denote the number of non-responders of the initial intervention which involves both behavioral language intervention and speech generating device. Then,

$$\mathbb{P}\left(M_{\text{D}}⩾m,M_{\text{E}}⩾m\right)=\mathbb{P}\left(\frac{N}{2}-M_{\text{NBS}}⩾m,M_{\text{NBS}}⩾m\right)$$

Therefore we find the smallest N, which satisfies

$$\mathbb{P}\left(\frac{N}{2}-M_{\text{NB}}⩾m,M_{\text{NB}}⩾2m\right)\cdot \mathbb{P}\left(\frac{N}{2}-M_{\text{NBS}}⩾m,M_{\text{NBS}}⩾m\right)>k,$$

One can re-write above as

$$\mathbb{P}\left(\frac{N}{2}-M_{\text{q}}⩾m,M_{\text{q}}⩾2m\right)\cdot \mathbb{P}\left(\frac{N}{2}-M_{\text{q}}⩾m,M_{\text{q}}⩾m\right)>k,$$

where M_q follows a Binomial distribution with size parameter $\frac{N}{2}$ and probability parameter q. Re-arranging M_q, we have

$$\mathbb{P}\left(\frac{N}{2}-m⩾M_{\text{q}}⩾2m\right)\cdot \mathbb{P}\left(\frac{N}{2}-m⩾M_{\text{q}}⩾m\right)>k,$$

which is analogous to

$$\left[\mathbb{P}\left(\frac{N}{2}-m⩾M_{\text{q}}\right)-\text{P}\left(2m-1⩾M_{\text{q}}\right)\right]\cdot \left[\mathbb{P}\left(\frac{N}{2}-m⩾M_{\text{q}}\right)-\text{P}\left(m-1⩾M_{\text{q}}\right)\right]>k.$$

Appendix

B. Appendix B

Here, we provide a mathematical derivation of equation (8). All the variables used here are defined in a similar way as in Section 2.1. Recall that what we want to calculate is the smallest N such that

$$\mathbb{P}(\text{all}\text{subgroups}\text{A}-\text{H}\text{have}\text{at}\text{least}m\text{participants})>k$$

holds. Using mathematical expression, one can write it as

$$\mathbb{P}\left(M_A⩾m,M_{\text{B}}⩾m,M_{\text{C}}⩾m,M_{\text{D}}⩾m,M_{\text{E}}⩾m,M_{\text{F}}⩾m,M_{\text{G}}⩾m\text{and}{M}_{\text{H}}⩾m\right)>k.$$

By design, we know that the group with the lenient definition of non-response and the group with the stringent definition of non-response are independent. Therefore, the above expression is same as,

$$\mathbb{P}\left(M_{\text{A}}⩾m,M_{\text{B}}⩾m,M_{\text{C}}⩾m\text{and}{M}_{\text{D}}⩾m\right)\cdot \mathbb{P}\left(M_{\text{E}}⩾m,M_{\text{F}}⩾m,M_{\text{G}}⩾m\text{and}{M}_{\text{H}}⩾m\right)>k$$

Let M_NL denote the number of non-responders for the initial intervention with lenient definition of non-response. Similarly we define M_NS as the number of non-responders for the initial intervention with stringent definition of non-response. Our next step is to re-express above expression in terms of M_NL, M_NS and N. Note that the event: $M_{\text{C}}⩾m$ and M_D is same as the event: $M_{\text{NL}}⩾2m$ . In addition, the event: $M_A⩾m$ and $M_B⩾m$ is same as the event: $\frac{N}{2}-M_{NL}⩾2m$ . Analogous arguments can be applied to the event involving subgroup E through H. Therefore we get,

$$\mathbb{P}\left(M_{\text{A}}⩾m,M_{\text{B}}⩾m,M_{\text{C}}⩾m\text{and}{M}_{\text{D}}⩾m\right)=\mathbb{P}\left(\frac{N}{2}-M_{\text{NL}}⩾2m\text{and}{M}_{\text{NL}}⩾2m\right)$$

and

$$\mathbb{P}\left(M_{\text{E}}⩾m,M_{\text{F}}⩾m,M_{\text{G}}⩾m\text{and}{M}_{\text{H}}⩾m\right)=\mathbb{P}\left(\frac{N}{2}-M_{\text{NS}}⩾2m\text{and}{M}_{\text{NS}}⩾2m\right).$$

Therefore our goal is to find a sample size N, which satisfies

$$\mathbb{P}\left(\frac{N}{2}-M_{\text{NL}}⩾2m\text{and}{M}_{\text{NL}}⩾2m\right)\cdot \mathbb{P}\left(\frac{N}{2}-M_{\text{NS}}⩾2m\text{and}{M}_{\text{NS}}⩾2m\right)>k$$

One can re-write above as

$$\mathbb{P}\left(\frac{N}{2}-M_{\text{q}}⩾2m,M_{\text{q}}⩾2m\right)\cdot \mathbb{P}\left(\frac{N}{2}-M_{\text{q}}⩾2m,M_{\text{q}}⩾2m\right)>k,$$

where M_q follows a Binomial distribution with size parameter N and probability parameter q. Then one can further simplify as

$$\mathbb{P}\left(\frac{N}{2}-2m⩾M_{\text{q}}⩾2m\right)\cdot \mathbb{P}\left(\frac{N}{2}-2m⩾M_{\text{q}}⩾2m\right)>k,$$

where the above is equivalent to

$${\left[\mathbb{P}\left(\frac{N}{2}-2m⩾M_{\text{q}}\right)-\text{P}\left(2m-1⩾M_{\text{q}}\right)\right]}^2>k.$$

Appendix

C. Appendix C

In this section, we provide technical explanation of finding sample size using margin of error. Recall that the number of non-responders follows a Binomial distribution with parameters q and N [24, 36]. One can show that $\widehat{q}$ , a proportion of non-responders among total sample, is an unbiased estimate of q and its variance and standard deviation are below [37]:

$$\mathrm{Var}(\widehat{q})=\frac{q(1-q)}{N}\Rightarrow \mathrm{sd}(\widehat{q})=\sqrt{\frac{q(1-q)}{N}}.$$

Then the goal is to find a sample size N which satisfies

$$2\cdot \sqrt{\frac{q(1-q)}{N}}=\mathrm{0.1.}$$

However, since we do not know the true value of q, we instead use $\frac{1}{2}$ as a value of q to find conservative sample size of N [36, 38]. By solving above formula after plugging in $\frac{1}{2}$ to q, we have

$$\frac{1}{\sqrt{N}}=0.1\Rightarrow N=100.$$