Complex 3D microfluidic architectures formed by mechanically guided compressive buckling

Mechanically guided assembly techniques yield complex 3D microvascular networks with multifunctional characteristics.

Abstract

Microfluidic technologies have wide-ranging applications in chemical analysis systems, drug delivery platforms, and artificial vascular networks. This latter area is particularly relevant to 3D cell cultures, engineered tissues, and artificial organs, where volumetric capabilities in fluid distribution are essential. Existing schemes for fabricating 3D microfluidic structures are constrained in realizing desired layout designs, producing physiologically relevant microvascular structures, and/or integrating active electronic/optoelectronic/microelectromechanical components for sensing and actuation. This paper presents a guided assembly approach that bypasses these limitations to yield complex 3D microvascular structures from 2D precursors that exploit the full sophistication of 2D fabrication methods. The capabilities extend to feature sizes <5 μm, in extended arrays and with various embedded sensors and actuators, across wide ranges of overall dimensions, in a parallel, high-throughput process. Examples include 3D microvascular networks with sophisticated layouts, deterministically designed and constructed to expand the geometries and operating features of artificial vascular networks.

INTRODUCTION

Sophisticated three-dimensional (3D) architectures are omnipresent in nearly all forms of life, where they support essential functions across multiple length scales, spanning individual cells, such as cytoskeletons for structural support and motility, to complete organisms, such as neural networks for sensing and control. Vascular systems are of particular interest, where complex, hierarchical, branching 3D constructs transport essential water and biochemical species to and from volumes of living tissue through a combination of pumped fluid flow and diffusive processes. The blood vessels, together with the heart, form a closed vascular system in vertebrates. Arteries carry blood away from the heart. Arterioles branch out from the arteries and connect to networks of capillaries that support exchange of water, nutrients, oxygen, and cellular waste between the blood and the surrounding tissues. Venules collect blood from the capillaries and pass to veins that carry blood back to the heart.

The blood flow in each organ follows unique, complex microvascular tree structures that serve particular functions. In humans, the branching of the pulmonary arterial tree adopts an ordered [>15 branch orders (1)] space-filling topology that spreads across the lungs to serve pulmonary circulation. The main pulmonary artery, ~50 mm long and ~30 mm in diameter (wall thickness, ~2 mm), carries blood from the right ventricle and branches into smaller pulmonary arteries and arterioles, where the smallest arterioles have diameters of 15 to 20 μm (1). Finer networks of thin-walled capillaries, branching out from the arterioles to surround the pulmonary alveoli, carry blood to the alveolar membrane where gas exchange occurs. The oxygenated blood returns to the left atrium through the pulmonary venules and veins. The pulmonary venular tree has a similarly ordered 3D branching geometry. The largest pulmonary venule has a diameter of ~14 mm (wall thickness, ~1 mm) and the smallest have diameters of 13 to 18 μm (1).

The unique topology of the vasculature, especially the capillaries, supports organ function. The minimum feature sizes of vasculature in almost all mammalian species lie in a range from 5 to 10 μm, somewhat larger than red blood cells, independent of mammal species or body size (2). This collection of blood vessels distributes thoroughly across the organism, in complex 3D layouts with various densities and unique topological branching geometries in different organs, such that all cells within the body lie within ~200 μm (three to four cells apart) of a capillary. In addition to their role in sustaining life mechanisms, these microfluidic systems are also important in the thermoregulation of homeothermic species, via active control over the sizes of blood vessels and, therefore, the rate of flow to and from the surfaces of organs, particularly the skin.

Access to man-made vascular systems with similar levels of complexity could be important in the development of engineered tissues and artificial organs to support human health and/or biology research and in biohybrids as emerging classes of robotic systems (3–5). New concepts in synthetic material systems lead to promising tunable and biomimetic behaviors (6–8); for example, a novel class of soft 3D network materials can offer defect-insensitive, nonlinear mechanical responses closely matched with those of biological tissues (8). Innovative artificial vascular systems would enable additional possibilities in platforms for fundamental studies of blood flow dynamics and diseases in vitro (9–11) and in essential structures for advanced microfluidic lab-on-a-chip and organ-on-a-chip technologies (12). Full control over 3D geometries, sizes, flow rates, pressure gradients, and mechanical properties of such artificial vasculature structures might create interesting and useful possibilities in revolutionary designs for these and other applications (9).

Traditional 2D microfluidic technologies (3, 13) serve important roles in artificial vascular networks (9, 11, 14) and various types of biomedical microsystems (15–17). Elaborated 3D alternatives would expand options in design and functionality, of relevance not only across the examples mentioned above but also in other areas where fluid flows can modulate electromagnetic, thermal, or other physical/chemical properties of a system. For example, certain types of 3D microfluidic structures offer potential for fast and efficient fluid mixing by folding laminar flows repeatedly to accelerate diffusive processes (18–20). Microfluidic cooling structures for 3D integrated circuits are also of interest (21–23). Paper-based analytical devices that exploit 3D stacked designs exploit capillary wicking to distribute fluids into complex arrays of detection zones, of potential use as low-cost diagnostics in resource-limited environments (24). Devices based on 3D microfluidic networks for cell cultures can promote differentiation and tissue organization at a level that is impossible with conventional 2D systems (25, 26).

A key challenge is in the development of fast, versatile methods for fabricating 3D microfluidic networks with necessary geometries and feature sizes. Recent progress includes methods for layer-by-layer stacking (27, 28) of 2D microfluidic platforms and semi-automated weaving (29) of microfluidic tubing. Some of the most versatile methods involve 3D printing techniques (14, 20, 30–38) but with limits in resolution that prevent routine construction of enclosed channels with inner diameters of less than ~50 μm (except for cases of ablation in bulk solid materials, where dimensions can reach ~10 μm, although of limited relevance here) and material constraints that prevent integration of certain types of structural components and functional devices (34, 35). Inkjet approaches, specifically, have certain capabilities in 3D fabrication, but various intrinsic features relegate their use to 2D microfluidic structures with characteristic dimensions in the range of 100 μm or larger. Microextrusion or filamentary methods, specifically exploited in scaffold removal approaches (14, 20, 31), can naturally form 3D geometries directly, but with a similar set of limitations in resolution (34, 35). Stereolithographic schemes can create microfluidic features as small as 50 μm but with increasing challenges in removal of uncured liquid resin, as these dimensions decrease. In addition, processable materials are limited to photocurable resins, for which biocompatibility and gas permeability represent additional important considerations. Some of the most impressive demonstrations exploit stereolithography in blocks of biocompatible hydrogels (30). Although optical methods based on multiphoton polymerization processes offer unmatched levels of resolution in 3D fabrication [as small as ~10 μm in fluidic structures (39)], the serial nature of this process leads to practical difficulties in realizing the types of dense structures over large areas for engineered tissues and other applications in biological research and biomedicine. Parallel variants based on holographic projection offer notably improved throughputs but with out-of-plane dimensions that are typically less than a few millimeters (40). All of the aforementioned techniques operate only with simple dielectrics or conductors, without the capacity to directly integrate semiconductor materials or functional devices.

As a complementary alternative to these approaches, this paper introduces a route to complex 3D microvascular structures that offers options in high-resolution features, large area coverage, diverse geometrical layouts, and, as a unique feature, the ability to integrate active functionality. The process, inspired by work on mechanically guided assembly techniques for 3D mechanical, electrical, and optical systems (41–53), begins with preparation of 2D microfluidic structures and integrated devices using well-established procedures of molding, bonding, lithographic processing, and other conventional and unconventional techniques in 2D micro/nanofabrication (54). The resulting microchannels, reservoirs, and valves can be readily constructed with feature sizes in the micrometer range, as described here for platforms built using the transparent elastomer poly(dimethylsiloxane) (PDMS). Integrated functional components can be realized with submicrometer resolution. Geometric transformation yields corresponding 3D architectures with complex shapes and configurations, including heterogeneous combinations of constituent materials and integrated devices in isolation or as interconnected arrays.

The following describes the procedures and demonstrates them in a range of examples, each captured in a quantitative manner using finite element analysis (FEA), with feature sizes as small as several micrometers, extending over length scales of centimeters, in individual or collected sets of structures. Schemes for pumping fluids from remote locations in isolated or arrayed collections of these 3D structures exploit interconnecting microchannels integrated into the supporting substrates. Fundamental studies highlight diffusive processes for material exchange to and from the microchannels, of potential utility in artificial microvasculature. Other demonstrations illustrate integration of metal features and devices onto and within these architectures, with capabilities in temperature and chemical sensing, thermal actuation, radio frequency communications, and others. The ideas presented here create broad opportunities in classes of 3D microfluidic systems that would be difficult or impossible to realize using other methods.

RESULTS

Mechanically guided assembly of 3D microfluidic architectures

The platforms described in the following, which we refer to as 3D microvascular systems due to their micro/millimeter scale geometries and soft mechanical properties, transform from lithographically fabricated 2D precursor structures through compressive buckling, following concepts previously demonstrated in various thin-film materials and devices in areas other than microfluidics (41, 42, 44, 50, 52, 53). This assembly approach applies across a wide range of length scales, from nanometers to meters, and it is compatible with nearly any class of material, hard or soft, organic or inorganic. Recent publications on these schemes highlight various capabilities and applications in areas ranging from microelectromechanical systems, to electronic and optoelectronic devices, to energy harvesters, and to cell scaffolds (41–53).

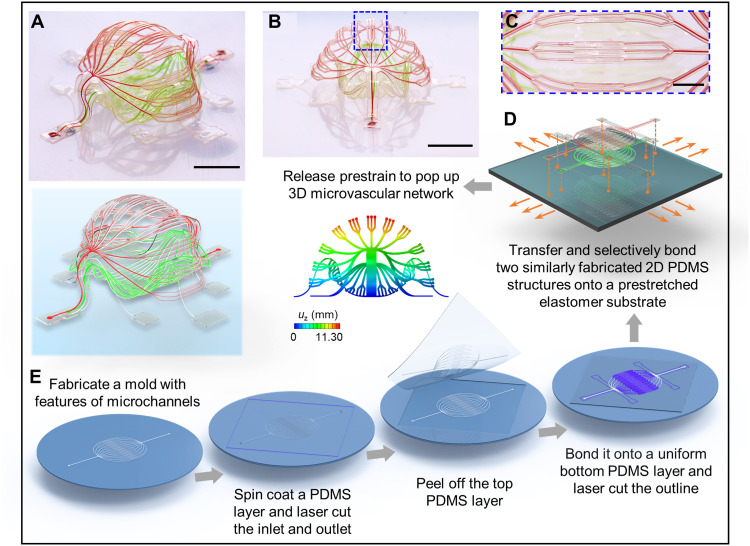
Figure 1 presents a schematic illustration of the process as implemented here, beginning with the soft lithographic preparation of 2D microfluidic precursors (geometries in fig. S1) and the subsequent controlled buckling mechanisms that convert them into 3D systems (see Materials and Methods for details; movie S1). This structure is a double-layered 3D architecture that has geometrical features comparable to those of basic biological vascular networks (Fig. 1, A and B). Specifically, the layout involves a stepwise change in the widths of the arrays of microchannels (from 100 μm to 30 μm and 10 μm, and then back to 30 μm and 100 μm) and a three-level branching configuration (Fig. 1C and figs. S2 and S3) to mimic a collection of arteries, arterioles, capillaries, venules, and veins. The narrowest channels have widths of 10 μm, comparable to the sizes of capillaries in human body. The overall 3D shape approximates a spheroid, with an enclosed internal cavity between the top and bottom layers, in resemblance to biological constructs like glomeruli and alveoli. This spheroidal configuration follows from a computationally guided design approach that includes contributions from constituent structural components bonded at a collection of sites (Fig. 1D) to an underlying elastomer substrate with a biaxial prestrain of 50% (figs. S1, S2, and S4). Note S1 (and fig. S4) summarizes key mechanical considerations in design choices.

Fig. 1. Schematic illustration of a 3D microvascular system formed by mechanically guided assembly.

A double-layer 3D microvascular network, with an enclosed internal cavity between the top and bottom layers, features a stepwise change in the width of the microchannels (from 100 μm, to 30 μm, to 10 μm, and then back to 30 μm and 100 μm) and a three-level branching structure. The narrowest microfluidic channel branches have widths of 10 μm, comparable to the sizes of capillaries in human vasculature. (A and B) Optical images and FEA predictions [with rendering in (A)] of the spheroid-shaped 3D microvascular network from a 3D view (A) and an approximate side view (B). (C) Magnified view of the blue dashed rectangle in (B). (D) Schematic illustration showing the selective locations to bond the microfluidic double layers to a prestretched elastomer substrate. (E) Procedures to fabricate 2D precursors of the microvascular network. Scale bars, 5 mm (A and B) and 2 mm (C). Photo credit: H. Luan, Northwestern University.

As described in detail in Materials and Methods, fabrication of this construct begins with formation of a 2D microfluidic system in PDMS (Fig. 1E) by casting and curing a layer of this material against a mold that consists of photodefined patterns of microchannel geometries on a silicon wafer. A laser cutting process defines inlets and outlets for fluid introduction and removal, respectively. Peeling this PDMS structure from the mold and bonding it to a flat layer of PDMS cast and cured against an unpatterned silicon wafer form a sealed 2D microchannel network. Another laser cutting process yields an open 2D architecture that follows the geometry of the microfluidic channels. Peeling this system (i.e., 2D precursor) from the wafer, bonding it at selected locations on a prestretched elastomer substrate, and then releasing this prestretch creates compressive forces that act at the bonding locations to trigger buckling processes and associated geometrical transformation into a 3D layout. The example highlighted here uses two such precursors transferred and selectively bonded to the prestretched substrate as an aligned multilayer assembly, at locations denoted as orange dots in Fig. 1D. The same processes can be applied to broad classes of materials, including not only materials for microfluidic systems but also those for electronic and photonic capabilities. On the basis of these straightforward procedures, 3D microchannel geometries with complexity and multifunctional integration are readily accessible, as described in the following sections.

Examples of basic designs in 3D microfluidics

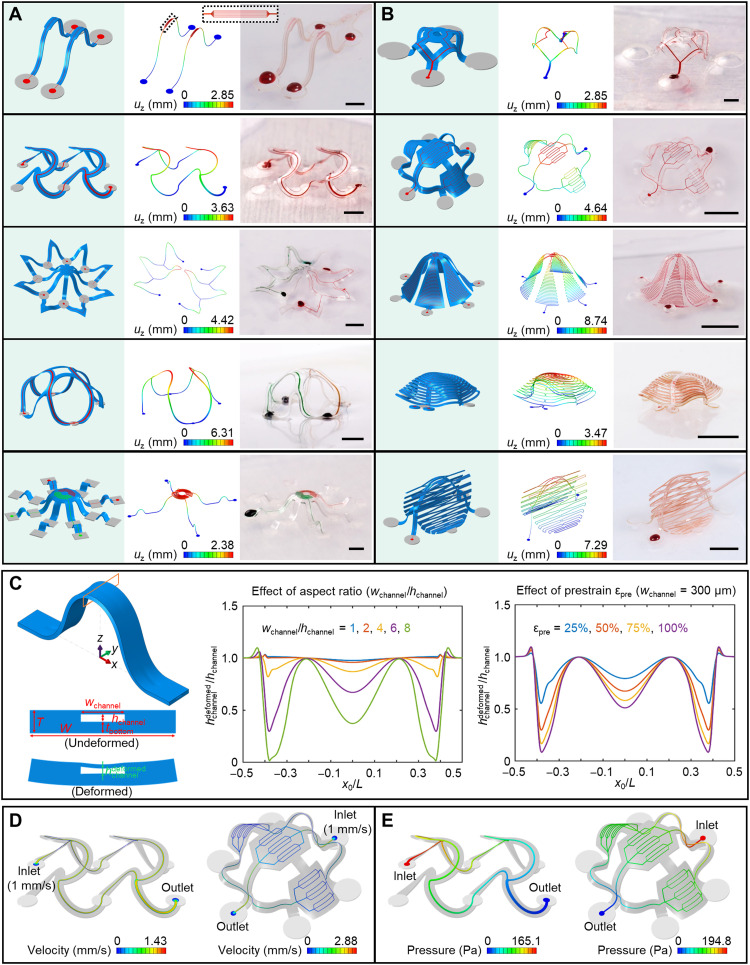
A diverse collection of 3D microfluidic systems can be achieved using these strategies (Fig. 2, A and B, and movies S2 and S3; 2D precursors in fig. S5), including both filament- and membrane-type architectures. The first example includes a pair of 3D microfluidic ribbon structures each with seven parallel microchannel branches with widths of 4 μm near the middle. The narrow microchannel branches (fig. S6) demonstrate high spatial resolution in intricate 3D microfluidic networks. Another example is a 3D “octopus” construct, shown in Fig. 2A (bottom) with two separate microfluidic channels filled with aqueous dye with different colors. A kirigami-inspired 3D architecture with a double-branched microchannel appears as the last example in Fig. 2B. This structure features a central supporting ribbon that rises above the plane of the substrate, where the two membrane components deform in a manner that involves tensile buckling modulated by strategically defined cuts (more details shown in fig. S7). Fluorescence images of selected structures filled with aqueous solutions of fluorescent dyes are in figs. S8 and S9. In some examples, the bonding sites exhibit slight deformations due to the low modulus and relatively thin geometry of the elastomer substrates.

Fig. 2. Assorted 3D microvascular structures formed by mechanically guided assembly.

(A) Ribbon-type 3D structures. The magnified inset on the top highlights seven parallel microchannel branches with widths of 4 μm after 3D assembly. (B) Membrane- and membrane/ribbon-type 3D structures. (C) FEA predictions for the deformation of a microfluidic channel after 3D assembly. Left: Schematic illustration of the 3D shape of a ribbon, highlighting the deformation that can occur in the top cover of the microfluidic channel. Illustration of the deformation of the midspan cross section after assembly. Middle: Effect of the microchannel aspect ratio on the deformation. Right: Effect of the prestrain level on the deformation. x₀/L stands for the normalized undeformed coordinate (i.e., undeformed coordinate over length) along the axial direction of the 3D structure. Distribution of fluid velocity (on middle plane) (D) and pressure (E) in the microchannels. Scale bars, 1 mm for the top two structures in (A) and the top structure in (B) and 5 mm for the others. Photo credit: H. Luan, Northwestern University.

In these cases and others, FEA serves as a convenient, rigorous method to predict the geometries and distributions of strain across all parts of these 3D microvascular systems. As shown in Fig. 2 (A and B), FEA results agree well with experiment. The effects of gravity are negligible in almost all cases. For these microfluidic structures (made of PDMS; total thickness, ~150 μm; prestrain, ~50%), global buckling dominates the 2D-to-3D shape transformation, without any noteworthy local buckling or wrinkling. The maximum strains and heights of these systems are approximately proportional to the square root of the compressive strain (ε_compr), which is related to prestrain (ε_pre) by ε_compr = ε_pre/(1 + ε_pre). Note S2 and fig. S10 summarize the relationships between applied strain ε_appl, prestrain ε_pre, and compressive strain ε_compr. As evidenced in the contour plots in fig. S11, the maximum strain in the PDMS remains well below the failure strain. Figure S11B shows that the maximum strain occurs in the top cover of the microfluidic channels near the bonding sites, due to effects in strain concentration. Generally, plastic deformation and fracture of the PDMS are not of concern, given its excellent physical toughness and high levels of elastic stretchability.

In addition to overall geometries, FEA simulations (Fig. 2C, note S3, and figs. S12 to S15) can also guide the selection of designs that avoid mechanical collapse of the microchannels, as a unique consideration for the systems reported here (55, 56). Various geometric parameters and effects of interface adhesion are important. Specifically, the width-to-height aspect ratio of the microchannel strongly influences its deformation during 3D assembly. The middle panel of Fig. 2C shows the normalized deformed channel height (i.e., deformed over undeformed value) along the length of the microchannel for different aspect ratios (with h_channel/T = 0.3125, ε_pre = 50%, t_bottom/T = 1/2). When the aspect ratio exceeds 6, the channel height decreases to less than half of its original value at certain locations (e.g., near bonding sites or at the midspan) because of deformations associated with the 3D transformation process. Figure S12 shows the 3D microfluidic structures and the microvascular channels for aspect ratios of 2, 6, and 10. The deformations of the channels increase with aspect ratio. Similar trends occur with increasing prestrain, as shown in the right panel of Fig. 2C for an aspect ratio of 6. At small aspect ratios (e.g., <2), deformations are negligible even for large prestrains, within a practically relevant range (fig. S13). At a given aspect ratio (w_channel/h_channel), reducing the size of the microchannel, measured by the ratio of its height to the total structural thickness (h_channel/T), reduces the deformation of the channel (quantified by the relative change in its height) during the 3D assembly process (fig. S14A). Positioning the microchannel at the midpoint of the PDMS through its thickness minimizes the deformations (fig. S14B). For microchannels with a given width, the total structural width (determined by the thicknesses of the PDMS side walls) has little effect on the deformation of microchannel (fig. S15). Note S3 lists the measures to prevent collapse of microchannels. Overall, for the range of design parameters explored here in this paper, collapse can be easily avoided. In extreme cases of soft microfluidic devices that include shallow and wide channels or reservoirs, support pillars (as in an irregular 3D network in the next subsection) or arch-shaped relief structures can be included (57, 58).

Computational techniques can also reveal the flow dynamics through these 3D systems. Figure 2 (D and E) shows numerical results of characteristics such as the flow velocities and the pressure differences. The velocity is highest in the centers of the channels because of no-slip boundary conditions at the inner surfaces. The total flow rate before and after the branching points remains unchanged, reflecting the conservation of mass. In the double-floor helical microvascular network (Fig. 2D, left), the cross-sectional areas of the two branches equal half of that of the main microchannel, leading to a peak flow velocity that remains the same along the microchannels. In the simplified vasculature-like network (Fig. 2D, right), the flow velocity diminishes substantially after the third-level branching structure, qualitatively like that in capillaries of the human body. In Fig. 2E, the pressure decreases gradually from the inlet to the outlet, as a result of drag consistent with the Hagen-Poiseuille law.

Extended, multilayered 3D microfluidic networks and 2D microfluidic platforms as interconnects

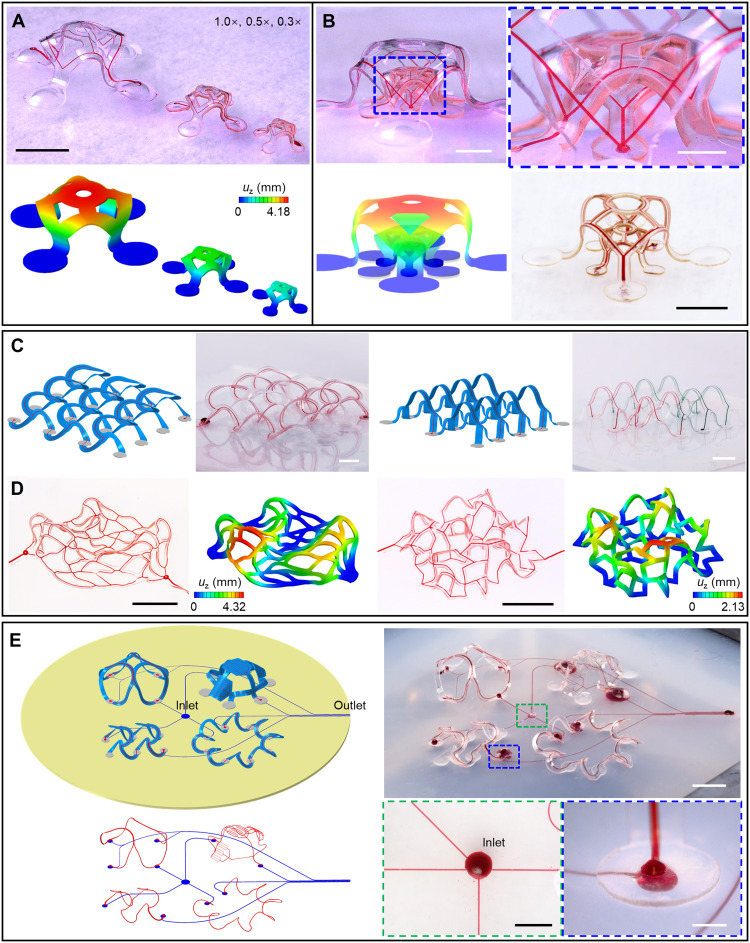
Complex, extended, and multilayered geometries are also possible, as advanced versions of the examples in Fig. 2, all guided by FEA modeling. Examples appear in Fig. 3 (A and B) and figs. S16 and S17, including a side-by-side array of three 3D microvascular structures and a multilayer array of structures with different sizes. The example in Fig. 3B (bottom right) demonstrates the capability for forming narrow filamentary elements by high-resolution laser cutting. Figure 3C shows two interconnected 3D microfluidic networks formed using 2D precursors shown in fig. S18. The 3-by-3 array of double-floor helices includes a microfluidic network that passes through every helical unit. The archway array features two branches of microfluidic channels filled with water dyed with two different colors. In all examples, experimental results agree well with FEA predictions. The FEA approaches accelerate iterative design efforts and provide detailed information on both local and global deformations. Another 4-by-4 double-floor helical array with reduced dimensions appears (see the section ‘Hybrid, multifunctional microvascular systems with integrated electronic capabilities’) as the microfluidic platform for the hybrid system described in the last section.

Fig. 3. Arrays of 3D microvascular networks.

(A) Side-by-side layout of three scalable 3D microvascular structures. (B) Multilayer layout of three/two scalable structures. The multilayer 3D array shown in the bottom right of (B) demonstrates the capability for using narrow filamentary elements. The color bar range is the same for (A) and (B). (C) Interconnected arrays of 3D microvascular networks. Left: A 3-by-3 double-floor helical array. Right: A 4-by-2 archway array with two branches of microchannels. (D) Irregular 3D microvascular networks by compressive buckling. Left: Irregular 3D microfluidic architecture assembled from a 2D simplified capillary network, with five randomly assigned bonding sites, each enclosed by a circle of constant radius. Right: Random 3D microfluidic network. (E) Integrated 3D microvascular systems on elastomer substrates with embedded microfluidic channels. Scale bars, 5 mm (A, C, and D) and (E, top right), 1 mm for the zoom-in image in (B), and 2 mm for the other two optical images in (B) and for the two magnified images in (E, bottom right). Photo credit: H. Luan, Northwestern University.

In addition, irregular 3D microfluidic architectures are fully accessible through compressive buckling of corresponding 2D shapes. Figure 3D and fig. S19 present representative designs where irregular 2D geometries similar to the projections of simplified capillary networks deterministically transform into irregular 3D architectures. One design involves two bonding sites at the ends (fig. S19C), and the other has multiple, randomly assigned bonding sites (Fig. 3D, left). More general, irregular 3D configurations are achievable following the same design rules in compressive buckling, e.g., a random 3D network in Fig. 3D (right).

Introducing 2D microfluidic channels and networks in the elastomer substrate that connect to those in the supported 3D microfluidic structures yields a complete, addressable network (Fig. 3E and fig. S20; 2D precursors in fig. S21) in assembly schemes that are otherwise identical to those described previously. This stretchable fluidic interconnect system can be used to address multiple 3D microfluidic structures simultaneously, by introducing and removing fluids through remotely located inlet/outlet ports. Various 3D architectures can be combined onto a single microfluidic elastomer substrate, as illustrated in Fig. 3E. Magnified images of the inlet of the microfluidic channels at the center of the elastomer substrate and the interface (at a bonding site) between a microchannel in a 3D structure and a substrate microchannel appear in the bottom right frame of Fig. 3E. A similarly magnified image of the microchannel outlet in the substrate is in fig. S21.

Figure S22 demonstrates a five-layer stacked design as an example of a topologically complex 3D geometry whose microfluidic channels branch across a small 3D space. An elastomer substrate with embedded microchannels serves as the assembly platform to form bilayers of 3D microfluidic structures above and beneath, respectively, as part of a 3D network of microchannels at five different height levels. The microchannels in the four 3D “dome” structures interconnect through two embedded microchannels in the substrate (marked with numbers 1 and 2 in fig. S22). Two separate 2D microchannels flow through the elastomer substrate (marked with numbers 3 and 4 in fig. S22).

Artificial 3D microvascular networks

Two 3D artificial microvascular networks, each with features comparable to biological vascular networks of arteries, arterioles, capillaries, venules, and veins, are in Fig. 4 (A to D) and movie S4. One design consists of extended and distributed 3D filaments (Fig. 4, A and B), and the other incorporates 3D filaments in nearly upright geometries (Fig. 4C), both formed using the same type of 2D microfluidic precursor, differing only in the shapes and sizes of the bonding sites. The narrowest microfluidic channel branches in these networks have widths of 10 μm, comparable to the sizes of capillaries as described previously. Together with the bilayer network in Fig. 1, these 3D microvascular networks can adopt bioinspired designs not only in geometries and characteristic dimensions but also in functionality. For example, the use of permeable/porous soft materials (standard PDMS and porous PDMS) for the channels can yield desired transport properties for chemical exchange with the surroundings. In the simplest case, the intrinsically permeable nature of PDMS allows exchange of oxygen and carbon dioxide through thin layers that define the top and bottom surfaces of the channels. Figure 4E demonstrates the delivery of oxygen through such a 3D microfluidic channel into a block of oxygen-sensitive hydrogel loaded with methylene blue (MB; also known as methylthioninium chloride). Here, in an aerobic environment, diffusion of oxygen triggers a chemical reaction that transforms leucomethylene blue (LMB) to MB, with a corresponding change from colorless to blue. In an anaerobic environment, MB tends to reduce back to LMB, changing again to a colorless state. The experiments begin with the system placed in an inert atmosphere (Fig. 4E, left). With the 3D microfluidic channel sealed, oxygen can diffuse through the elastomer substrate (Dragon Skin 10 SLOW; Fig. 4E, middle left), leading to the development of a blue color near the surface. Transport of oxygen through the 3D microfluidic channel [using air in Fig. 4E (middle right) and using an oxygen-rich perfluorocarbon liquid in fig. S23A, respectively] leads to similar, uniform color changes along the channel, here in the form of an arch-shaped structure. Computational modeling can capture the physics of the diffusion process and the associated oxygen concentration distribution, as shown in Fig. 4E, rightmost for the system. This model of oxygen diffusion is also useful in defining a parameter space for cell viability, as a guide for choices of artificial vasculature designs for application in cell culture (fig. S23B). The region filled with phosphate-buffered saline (PBS) is assumed free from advection, and the cells in the simulation correspond simply to a negative source term in the surroundings, using values for the diffusivity, solubility, cell oxygen consumption rate, cell density, and low oxygen concentration threshold from the literature (59–63). The use of microporous PDMS [pore size, 4 to 10 μm; Fig. 4F (left) and fig. S24] allows similar diffusive exchange but with enhanced rates and compatibility with a wide range of macromolecules. Figure 4F demonstrates the diffusive transport of bovine serum albumin (BSA) through a 3D microfluidic channel with a porous top layer. Fluorescent molecules bonded with BSA (Alexa Fluor 647 conjugate, Invitrogen) allow visualization of the diffusion processes. Carbon dioxide and waste can be collected and transported through the 3D microfluidic channels using such strategies, with the potential for use in tissue culture platforms, artificial organs, biorobots, and so forth.

Fig. 4. Characterization of artificial microvascular networks.

(A to D) 3D artificial microvascular system with layout comparable to a biological vascular network composed of arteries, arterioles, capillaries, venules, and veins. The narrowest microfluidic channel branches have widths of 10 μm. (A) 3D microvascular network with filaments fully spread apart. (B) Approximate front view of this 3D network. (C) 3D network with filaments oriented approximately upright. (D) Magnified optical image of the filaments, with microfluidic channels that have widths of 10 μm. (E) Images that show oxygen delivery through a 3D microfluidic channel in a block of oxygen-sensitive hydrogel that changes from colorless to blue in the presence of oxygen. Leftmost: Device in vacuum. Middle left: Device with the microfluidic channel sealed but the elastomer substrate (Dragon Skin 10 SLOW) open to air allows oxygen diffusion. A blue layer forms in the hydrogel near the substrate. Middle right: Device with the channel and the substrate open to air. An arch-shaped blue region forms in the hydrogel in regions along the channel and substrate. Rightmost: Result of an FEA diffusion model showing the oxygen concentration in the block of hydrogel with the channel and the substrate open to air (midsectional view). (F) Experimental demonstration of transport of macromolecular nutrients (e.g., BSA) through a microporous 3D microfluidic channel. Scale bars, 5 mm (A to C, E, and F, middle and right), 1 mm (D), and 50 μm (F, left). Photo credit: H. Luan, Northwestern University.

Hybrid, multifunctional microvascular systems with integrated electronic capabilities

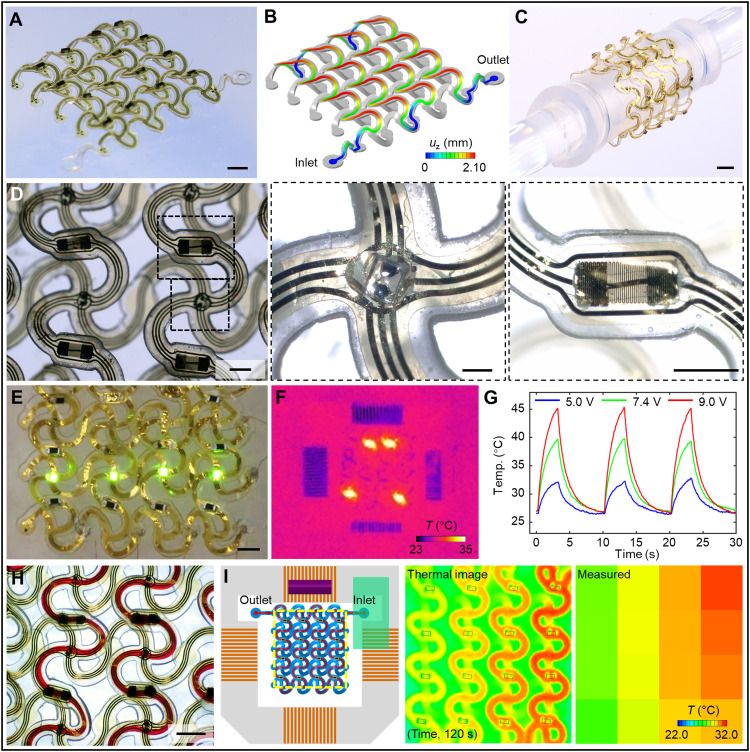
Integration of electronic/optoelectronic devices for temperature and chemical sensing, thermal actuation, radio frequency communications, and many others follow naturally from the overall fabrication process. The resultant systems create broad opportunities in 3D microfluidics that would be difficult or impossible to achieve using alternative fabrication methods. A representative 3D hybrid microfluidic and electronic system illustrated in Fig. 5 adopts the form of an interconnected 4-by-4 double-floor helical array of microvascular networks with electronic interfaces. The thin-film electronic part of the system includes two layers of gold (Au) traces insulated by polyimide (PI) films, in a stack of PI (1.5 μm)/Au (200 nm)/PI (1.5 μm)/Au (200 nm)/PI (1.5 μm), as in fig. S25. The conductive traces adopt horseshoe lattice geometries similar to those of the 2D microfluidic precursor. Integration involves alignment and selective bonding with a thin layer of optical adhesive (NOA 61, Norland Products Inc.). Under compressive buckling, the microfluidic precursor and the conductive mesh deform together to yield a 3D double-floor helical geometry (Fig. 5, A and B). The experimental results (Fig. 5A) match well with the FEA prediction (Fig. 5B). FEA results indicate that the gold traces in the hybrid system undergo purely elastic deformations during the 3D assembly process due to the selective bonding technique (fig. S26).

Fig. 5. 3D hybrid microfluidic and electronic systems in the form of extended, interconnected 4-by-4 double-floor helical arrays of 3D microvascular networks with electronic interfaces.

(A) Optical image of a 3D system with integrated electronic components (μ-ILEDs, heaters and thermistors, and electrodes). (B) FEA results for the shape of the 3D microchannel. (C) Image of a soft, stretchable hybrid system wrapped around a glass rod (6 mm in diameter). (D) Top view optical image of the system, with magnified views of a μ-ILED and a microfabricated serpentine trace, respectively. (E) Image of μ-ILEDs during operation. (F) Infrared image of local heating performance. (G) Plot of temperature versus time near a heater element during cyclic operation (10-s period and 3-s duty cycle). (H) Image of the flow of red aqueous dye in the microchannel. (I) Results of temperature mapping during injection of hot water through the 3D microchannel, captured by both an infrared thermal imaging camera (middle) and the integrated 4-by-4 array of thermistors (right). On the left panel, the yellow dashed rectangle shows the mapping region, with locations of 16 thermistors highlighted. Scale bars, 2 mm (A and C), 1 mm (E and H), 500 μm (D, left and right), and 200 μm (D, middle). Photo credit: H. Luan, Northwestern University.

The mechanics of the overall system allow bending, twisting, and other types of deformations, as demonstrated in Fig. 5C and fig. S27 for the case of wrapping around a glass rod with a diameter of 6 mm. This structure supports 16 groups of electronic components (Fig. 5D). Each group includes a microscale inorganic light-emitting diode (μ-ILED; Fig. 5D, middle) and a thermal actuator or a thermistor [microfabricated resistor in Fig. 5D (right) and fig. S28 or small-footprint 0201 (600 μm by 300 μm) commercial component in fig. S29]. Four rows and columns of gold serpentine interconnects support matrix addressing through three traces along each row and column. Additional 12 microelectrodes (100 μm in diameter) in the system serve for electrical sensing and stimulation. In this way, this system provides capabilities not only in fluid transport (figs. S30 and S31) but also in electrical, optical, and thermal actuation and in thermal sensing. All μ-ILEDs and thermal actuators (or thermistors) are individually addressable (fig. S32). Figure 5E and fig. S33 illustrate the operation of μ-ILEDs. Microfabricated serpentine gold traces (with line width of 5 or 10 μm; fig. S28) and surface-mount resistors (0201 footprint; resistance, 10 kilohms) both serve as heaters for thermal actuation, as shown in Fig. 5F and figs. S34 and S35. The inner 4 units and the peripheral 12 units feature the former and latter, respectively. Thermal imaging reveals the temperature distributions while operating multiple heating elements (Fig. 5F and fig. S34). The time-dependent change in temperature at a single actuator under different input voltages appears in Fig. 5G.

Electronic and electrochemical sensors integrated into such hybrid systems provide means to monitor variations in the physical and chemical properties (e.g., temperature and concentration of chemical species) of fluids housed within or of the immediate surroundings. In a simple example presented here, an array of thermistors (0201 NTC, 100 kilohms, TDK Corporation, Japan) distributed throughout a 3D hybrid system maps the temperature changes during the flow of hot water through the microchannels. A syringe pump (Harvard Apparatus) delivers hot water (~80°C) at a constant flow rate (~2.5 μl/s, adjustable). Figure 5I illustrates that the 4-by-4 array of thermistors (figs. S36 and S37) can capture the evolution of the resulting temperature distribution across the 3D system (figs. S38 and S39 and movie S5). The findings are consistent with those measured by thermal imaging (FLIR A615 thermal imaging camera, FLIR Systems AB, Sweden; fig. S40 and movie S6). The temperature of the injected water drops along the microchannel as heat dissipates across the channel walls. The integrated thermistors can also measure temperature gradients induced by environmental factors, such as those associated with external heating elements, as demonstrated in fig. S41. In summary, integration of high-performance electronic components (64, 65) onto complex 3D microfluidic architectures leads to complete, systematic microvascular networks with both fluid transporting and electronic sensing and regulating capabilities.

DISCUSSION

The results presented here establish a versatile and robust scheme for forming complex 3D microfluidic structures and extended 3D microvascular networks, across wide-ranging overall dimensions in a parallel, high-throughput manner. Access to micrometer-scale channel dimensions (e.g., 4 μm) and integrated functional components represent key unique aspects of this approach. Delivery of fluids into the 3D network via channels embedded in the supporting substrate and passage of molecular species through the walls of the microchannel structures represent features of relevance to the potential use of these constructs in 3D tissue cultures, biochemical analysis systems, microreactors, and others. Multifunctional platforms that include components for sensing and actuating fluid flows, light exposures, and thermal/electrical stimuli create additional possibilities. The open framework architectures of these systems allow introduction of biological or nonbiological materials into the open spaces, for hybrid configurations that have clear relevance in engineered tissue constructs and artificial organs such as organoids. Still, reproducing the extremely sophisticated, hierarchical 3D geometries of real biological systems in artificial microfluidic architectures remains challenging. Delivering fluids uniformly around the 3D microchannels or preferentially to a local domain requires alternative approaches. These and other opportunities and challenges represent meaningful directions for future work.

MATERIALS AND METHODS

Fabrication of 2D microfluidic precursors

Standard soft lithographic techniques served as the basis for fabricating the 2D microfluidic precursors. The processes began with formation of photomasks with patterns in the layouts of the microfluidic channels. Spin coating photoresist (KMPR 1010, Kayaku Advanced Materials Inc., formerly MicroChem Corp., USA) at 4000 rpm on a bare silicon wafer, followed by baking (110°C for 5 min), prepared a thin film (~8 μm) for photolithographic patterning. Exposure to ultraviolet (UV) light through a photomask, followed by hard baking (110°C for 5 min) and developing, yielded desired patterns in the photoresist. Deep reactive-ion etching (STS LpX Pegasus, SPTS Technologies Ltd., UK) removed the exposed regions of the silicon to a depth of 50 μm (adjustable) and, subsequently, the remaining photoresist. Surface functionalization of the resulting silicon molds by immersion in a solution of trichloro(octadecyl)silane (Sigma-Aldrich, USA) in hexane (0.2% v/v) for 90 s, followed by rinsing with IPA (isopropyl alcohol) and DI (deionized) water sequentially, yielded a hydrophobic surface to facilitate replication of relief structures into thin films of PDMS. Specifically, casting and curing PDMS (mix ratio 10:1; SYLGARD 184, Dow Corning, USA) against these lithographically prepared molds yielded solid elastomers with features of relief on their surfaces. A similar process performed on flat, bare silicon wafers formed films with uniform thicknesses. Bonding separate pieces of PDMS created in this manner (e.g., by oxygen plasma treatment, corona discharge, or UV-induced ozone treatment, followed by heating on a hot plate at 110°C for ~5 min) defined sealed networks of microfluidic channels. Laser cutting (ProtoLaser R, LPKF Laser & Electronics AG, Germany) defined geometric outlines and generated openings to define the inlets for fluid transport. In certain cases, separately fabricated thin electronic systems or additional microfluidic layers with open architectures were mounted on top to yield multilayered 2D precursors.

Assembly of 3D microfluidic structures

The 3D assembly process began with prestretching an elastomer substrate prepared by spin coating and curing a low-modulus silicone material (Dragon Skin 10 SLOW, mix ratio 1:1; Smooth-On, USA) against a flat surface. Exposing the bonding sites of the 2D precursors, mounted on polyvinyl alcohol (PVA) tape, through a laser-cut masking element (PI film, 75 μm; Argon Masking Inc., USA) and the entire top surface of the prestretched elastomer substrate to UV-induced ozone yielded hydroxyl termination on their surfaces. Laminating the precursors face down onto the substrate followed by baking in an oven at 70°C for ~10 min formed strong covalent bonds. Washing with hot water for 2 min removed the PVA tape. Gradually releasing the prestretched elastomer substrate induced controlled buckling of the PDMS precursors into 3D geometries. Injection of fluid using a syringe, controlled manually or with a syringe pump, completed the assembly and filling of 3D microfluidic structures.

Finite element analysis

3D FEA performed using the commercial software package Abaqus captured the nonlinear deformations of the elastomer substrates and defined the postbuckling behaviors of the 2D precursor structures. Eight-node solid elements and four-node shell elements were chosen for the substrates and the 2D precursor structures, depending on the analysis specifics. Linear buckling analyses for the 2D precursor structures under compression were performed to determine the critical buckling strain and corresponding buckling mode, implemented as initial geometric imperfections in postbuckling simulations. Deformed configurations and strain distributions at different levels of prestrain for the 2D precursor structures were thus obtained.

In finite element simulations, the Mooney-Rivlin strain energy potential model was used for elastomeric materials with hyperelastic behavior. PDMS (10:1) was modeled as incompressible, with an elastic modulus E_PDMS = 1.8 MPa. Dragon Skin 10 SLOW was modeled as incompressible, with an elastic modulus E_DragonSkin = 166 kPa. PI for 3D electronics was modeled with linear elastic behaviors. The elastic modulus (E) and Poisson’s ratio (ν) were E_PI = 2.5 GPa and ν_PI = 0.34 for PI. Metal materials, such as gold (Au) and copper (Cu), have elastoplastic material behavior. An idealized elastoplastic model (without hardening) was used in simulations, and the yield strain was chosen as 0.3%. The elastic modulus (E) and Poisson’s ratio (ν) were E_Au = 78 GPa and ν_Au = 0.44 for Au and E_Cu = 119 GPa and ν_Cu = 0.34 for Cu.

Simulations on diffusion of oxygen through solid and liquid materials used the mass diffusion analysis in Abaqus, with governing equations based on Fick’s laws of diffusion. Henry’s law defines the relationship between the mass concentration of oxygen and its partial pressure. Both 3D and 2D mass diffusion models were used depending on the analysis specifics.

Formation of microporous PDMS thin films

The process for making microporous PDMS thin films began with preparing 100 ml of a supersaturated aqueous solution of sodium chloride (NaCl) at 75°C and 1000 ml of ethanol at −80°C. Stirring the solution on a hot plate (PC-420D, Corning Inc., USA) at 800 rpm and subsequently adding an excess amount of cold ethanol (−80°C) caused precipitation and recrystallization of NaCl. The recrystallized NaCl particles were then separated from liquids by vacuum filtration and dried in an oven for 15 min. Grinding the recrystallized NaCl particles for 10 min and thoroughly mixing the resulting material with uncured PDMS (mix ratio 10:1; SYLGARD 184, Dow Corning, USA) and hexane (Thermo Fisher Scientific, USA) with a weight ratio of 5:10:2 prepared a precursor to the microporous PDMS elastomer. Spin coating or blade coating the mixture to a desired thickness and curing it at 75°C yielded PDMS thin films with uniformly distributed microparticles of NaCl. Dissolving the embedded NaCl by immersion in DI water and then freeze drying the PDMS yielded the desired microporous structure.

Fabrication of electronic structures in open mesh geometries

The fabrication procedures started with formation of a thin sacrificial layer of copper (80 nm) on a glass slide (75 mm by 50 mm by 1.2 mm; Thermo Fisher Scientific, USA) by sputter deposition (ATC Orion series magnetron sputtering system, AJA International Inc., USA). Spin coating a precursor to PI (PI2545, HD MicroSystems, USA) at 6000 rpm, followed by baking (110°C for 3 min and 155°C for over 5 min) and curing (265°C in a vacuum convection oven; Yield Engineering Systems, USA) yielded a thin (~1.5 μm) coating of PI. Spin coating a primer (MicroChem primer 80/20; Kayaku Advanced Materials Inc., formerly MicroChem Corp., USA) at 2000 rpm on a bare glass slide followed by baking at 110°C for 1 min and subsequently spin coating a negative photoresist (nLOF 2035) at 2000 rpm followed by baking at 110°C for 90 s formed a thin film of photoresist for photolithographic patterning. Exposure to UV light (dose, 180 mJ/cm²) through a photomask with geometric features of the first layer of gold traces, followed by postexposure baking (110°C for 90 s) and developing (exactly 45 s in AZ300 MIF developer), transferred the patterns onto the photoresist. Plasma cleaning (Samco PC-300 plasma cleaner, Samco-UCP Ltd., Liechtenstein) removed the residual photoresist in the exposed and developed regions. Electron-beam evaporation (ATC-E series, AJA International Inc., USA) yielded a uniform bilayer of chromium (10 nm) and gold (200 nm). Washing in acetone (45°C on a hot plate for 30 min) removed the photoresist in a lift-off process, thereby completing the fabrication of the first layer of gold traces. Repeating these steps yielded another layer of gold traces on PI, on top of the first. Similar processes yielded an overcoat of PI with a patterned thin layer of copper (80 nm) as a mask. Reactive ion etching (Samco RIE-10NR system, Samco-UCP Ltd., Liechtenstein) defined the outline of the PI layers. Submerging the sample in copper etchant removed the top and bottom copper sacrificial layers. Carefully transferring the samples onto a piece of water-soluble tape (with PVA backing) finished the fabrication of PI/Au/PI/Au/PI thin-film electronic structures with an open mesh geometry. The microfabricated resistors consisted of serpentine gold traces formed in a similar manner in a configuration of 1.5-μm PI/10-nm Cr/80-nm Au/1.5-μm PI.

Preparation of 2D precursors for 3D hybrid microfluidic/electronic systems

The 2D precursor for the 4-by-4 double-floor helical microfluidic array and the thin-film PI/Au/PI/Au/PI electronic structure in a matching double-floor helical geometry (referred to as the PI-Au sample in the following description) were prepared separately according to previously described methods. The first step involved aligning the 2D microfluidic precursor with the 2D PI-Au sample. This procedure began with laminating a PDMS thin film (~300 μm) on a glass slide (75 mm by 50 mm by 1.2 mm), temporarily bonding the PI-Au sample together with the PVA tape onto the surface of the PDMS, and then laminating a transparent film (~75 μm) of polyethylene terephthalate (PET) on top. Alignment of the 2D microfluidic precursor over the PET film with the PI-Au sample occurred under a microscope. Transferring the aligned 2D microfluidic precursor using a piece of transparent water-soluble tape (Ultra Solvy water-soluble stabilizer, Sulky, USA) prepared it for later use.

The second procedure bonded the 2D microfluidic precursor to the PI-Au sample. This process began with peeling away the PET film and carefully applying ~5 nl of UV-curable adhesive (NOA 61, Norland Products Inc., USA) using the tip of a needle at the joints and midspan points of the PI-Au. Aligning and laminating the microfluidic precursor onto the PI-Au and curing the glue under UV light for 5 min securely bonded the two as a hybrid system. Submerging the bonded samples in warm DI water dissolved the water-soluble tape. Retrieving the hybrid system using a sheet of polytetrafluoroethylene from the water prepared it for integration with electronic components.

Silver conductive epoxy (Chemtronics CircuitWorks CW2400, Illinois Tool Works Inc., USA) bonded commercially available components (e.g., 0201 surface-mount resistors, thermistors, and μ-ILEDs) and microfabricated resistors in the form of gold serpentine traces to the hybrid array. Applying a small amount (~2 nl) of UV-curable adhesive onto the μ-ILEDs, followed by UV curing for 5 min, reinforced the connections. Curing the silver conductive epoxy at room temperature for ~6 hours completed the microfluidic-electronic hybrid array as a 2D precursor. A combination of jump wires, a customized flexible printed circuit board (PCB) connector, ACF (anisotropic conductive film) cables, and a rigid PCB connector connected the array to an external power supply.

Supplementary Materials

This PDF file includes:

Supplementary Text

Legends for movies S1 to S6

Figs. S1 to S41

Other Supplementary Material for this manuscript includes the following:

Movies S1 to S6