Passive Cavitation Mapping by Cavitation Source Localization from Aperture-Domain Signals –Part 2: Phantom and in vivo Experiments

Abstract

Passive cavitation mapping (PCM) techniques typically utilize a time-exposure acoustic (TEA) approach, where the received radio-frequency data is beamformed, squared, and integrated over time. Such PCM-TEA cavitation maps typically suffer from long tail artifacts and poor axial resolution with pulse-echo diagnostic arrays. Here, we utilize a recently developed PCM technique based on cavitation source localization (CSL), which fits a hyperbolic function to the received cavitation wavefront. A filtering method based on the root-mean-squared error (rmse) of the hyperbolic fit is utilized to filter out spurious signals. We apply a wavefront correction technique to the signals with poor fit quality to recover additional cavitation signals and improve cavitation localization. Validation of the PCM-CSL technique with rmse filtering and wavefront correction was conducted in experiments with a tissue-mimicking flow phantom and an in vivo mouse model of cancer. It is shown that the quality of the hyperbolic fit, necessary for the PCM-CSL, requires an rmse <0.05mm² in order to accurately localize the cavitation sources. A detailed study of the wavefront correction technique was carried out and it was shown that, when applied to experiments with high noise and interference from multiple cavitating microbubbles, it was capable of effectively correcting noisy wavefronts without introducing spurious cavitation sources, thereby improving the quality of the PCM-CSL images. In phantom experiments, the PCM-CSL was capable of precisely localizing sources on the therapy beam axis as well as off-axis sources. In vivo cavitation experiments showed that PMC-CSL showed a significant improvement over PCM-TEA and yielded acceptable localization of cavitation signal in mice.

I. INTRODUCTION

ULTRASOUND-guided and microbubble-mediated drug delivery is a promising therapeutic approach to enhance the local drug delivery rate to various tissues, including cancer tumors [1]–[4]. This approach involves insonating gas-filled microbubbles (MB) to create small pores in tumor capillaries through microbubble cavitation, thereby increasing penetration of drugs into the extravascular compartment [5]. Using therapeutic ultrasound, microbubbles undergo either repeated expansions and contractions (a process called stable cavitation) at moderate acoustic pressure amplitudes or explosive growth and collapse (inertial cavitation) at high pressure amplitudes [6]–[8]. Microbubble oscillations, along with associated fluid flow, create strain on the cell membranes, thus modifying the permeability of these membranes by making small pores [5]. This permeability allows uptake of large therapeutic agents for improved drug penetration [1], [2], [9]. Combined with image guidance, this approach can deliver therapeutics in a spatially localized manner while minimizing systemic drug toxicity. For example, therapeutics such as drug-loaded nanoparticles with limited extravascular penetration (e.g. particles larger than 100nm) have been shown to benefit from this drug delivery strategy [4]. For clinical use, an ultrasound-based drug delivery platform requires both image guidance, for accurate spatial location of the treatment field (e.g. a tumor), and quantitative mapping of the therapeutic acoustic dose, for effective microbubble cavitation and downstream treatment effects.

It has been shown that there is a significant correlation between cavitation strengths and therapeutic outcomes [10]–[14], where increased broadband emissions, typical of inertial cavitation, corresponds to in an increased ultrasound ablation volume [10], [11]. In addition, in vivo studies have shown that drug delivery rate to the solid tumors can be increased by using higher inertial cavitation doses. For example, it was shown that more drug is delivered deeper in the tumor as the the inertial cavitation dose is increased [12]. However, most studies typically use a single element transducer as a passive cavitation detector, resulting in cavitation signals spatially averaged within the focal volume. For accurate therapy guidance of ultrasound and microbubble-mediated drug delivery, cavitation signal mapping is desired. Such cavitation signal mapping must be capable of providing real-time mapping of sources of acoustic emissions from microbubbles induced by therapeutic ultrasound. These maps will be able to provide spatial and temporal images of therapeutic dose delivered to the tissues. Recently, passive cavitation mapping (PCM) with an array of transducers has been introduced [13], [15], [16], allowing for both real-time mapping and quantification of cavitation sources producing nonlinear acoustic emissions. PCM has shown promise in therapy monitoring, which has been successfully implemented for monitoring lesion formation by HIFU in excised bovine livers [17], drug delivery to tumors [18], and transcranial therapies in the brain [19].

There are several ways to reconstruct cavitation maps, including time-exposure acoustics based method (TEA) [20]–[22] or passive cavitation mapping with cavitation source localization (PCM-CSL) [23]. PCM-TEA utilizes fixed-focus delay-and-sum or robust Capon beamforming on a grid of points, followed by the time-averaging of the squared data. In a companion paper, we have introduced PCM-CSL, which is capable of localizing cavitation sources based on the arrival-times of the acoustic emission relative to the transducer geometry [23]. Briefly, the PCM-CSL utilizes cross-correlation of the received radio-frequency (RF) channel data with a sliding window in the aperture domain to estimate the arriving wavefronts from cavitation emissions. Because these cavitation wavefronts are expected to have a hyperbolic shape when received by a linear transducer array, a hyperbolic function is fit to the arrival time profile. The coefficients of the hyperbolic fit and their confidence values are then used to estimate the cavitation source location and its uncertainty region and generate a passive cavitation map. A wavefront correction technique was proposed in this paper to mitigate localization errors due to noise or interfering cavitation signals. The wavefront correction is accomplished by analyzing the derivative of the arrival times and “re-aligning” the wavefronts at points of discontinuity. In a simulation study, PCM-CSL was shown to have better axial and lateral resolution, and more accurate source localization compared to the conventional PCM-TEA technique [23]. In the following, we apply the PCM-CSL technique proposed in [23] to phantom and in vivo cavitation experiments and compare its performance to PCM-TEA. In addition, we introduce a filtering technique based on hyperbolic fit quality to further remove spurious signals from the PCM-CSL process and improve localization and image performance.

II. EXPERIMENTAL METHODS

A. Experimental System

In order to separate inertial cavitation signals from stable cavitation signals, a dual-transducer system was utilized. The ultrasound therapy and imaging system was constructed using two commercially-available transducer arrays, which were fixed at a 40° angle relative to each other in a custom 3D-printed fixture, as shown in Fig. 1 in order to overlap the imaging planes of the two transducers (note the difference in the transducer orientation compared to Part 1 [23], where a 0° angle configuration was used, as Field II was unable to simulate the 40° angle between transducers). The two transducers include a low frequency transducer for therapy (ATL P4–1, Philips Healthcare, Netherlands) and a high frequency transducer for B-mode imaging and passive cavitation mapping (ATL L11–5, Philips Healthcare). The P41 transducer was selected for therapy application to achieve high MI for inertial cavitation while allowing for the therapy beam to be electronically steered over a region of interest. A transmit frequency of 1.78 MHz was used for therapy pulses (wavelength of λ₀ = 837μm). The L11–5 was used for passive cavitation mapping and B-mode imaging using a conventional focused transmit sequence at 7.8MHz. Because the frequency band of the L11–5 does not overlap with the P4–1, no additional filtering was used to separate microbubble reflections from inertial cavitation emissions. The transducer parameters are shown in Table I. Both transducers were simultaneously connected to and controlled by a Verasonics Vantage 256 research platform (Verasonics, Inc., Kirkland, WA). The custom 3D-printed fixture was used to align and fix each transducer’s xz-plane in elevation [24], [25]. The therapy beam’s pressure field was measured for a range of voltages using an Acoustic Intensity Measurement System (AIMS III, Onda, Sunnyvale, CA) and a hydrophone (HNR-0500, Onda, Sunnyvale, CA) in a water tank. To confirm the alignment of the two probes, both transducers were laterally co-focused at three different points in a plane and the elevation beam profiles of the two transducers were measured.

Fig. 1:

The dual-transducer setup consisting of a lowfrequency therapy transducer and a high-frequency imaging transducer aligned and held together with a 3D printed fixture (size is approximately 20cm × 8cm × 8cm).

TABLE I:

Transducer & System Parameters

	Therapy	B-Mode Imaging	PCM
Transducer	P4–1	L11–5	L11–5
Frequency, MHz	1.78	7.8	n/a
Elements	96	128	128
F/#	2	2	n/a
Element spacing, μm	295	260	260
Receive sample rate, MHz	n/a	31.2	31.2
Cycles per pulse	5	1	n/a
Excitation	Focused	Plane waves	n/a

For experimental confirmation of the PCM-CSL technique with a wire target, a single linear array transducer (L12–3v, Mindray, Mahwah, NJ) with 192 elements and a pitch of 200μm was used. A transmit frequency of 4MHz (wavelength of λ₀ = 374μm) was used in a pulse-echo format, similar to the simulation configuration in [23].

B. Phantom Experiments

Cavitation detection experiments were performed in an agar tissue-mimicking vessel phantom containing a 1mm (1.2λ₀) diameter vessel, which was connected to a flow pump (Reglo Digital, Ismatec, Wertheim, Germany), circulating Definity microbubbles (Lantheus Medical Imaging, North Billerica, MA, USA) with a 1.2×10⁷ MBs/mL concentration in saline (Sigma Aldrich, St. Louis, MO) and a peak flow velocity of 4.35mm/s. All experiments were performed at 25° C. The mean speed of sound of the phantom was measured using a pulse-echo technique [26] and was combined with the corresponding speed of sound in water at 25° C (1497m/s, [27]) using the mixing equation [28]. The resulting speed of sound was then used in scanner pulse sequencing and for PCM reconstruction. The dual-transducer ultrasound system was used to apply therapeutic pulses and record the RF channel signals for passive cavitation mapping while providing live B-mode imaging. Therapy pulses utilized 5 transmit cycles at f₀ = 1.78MHz frequency and were applied at a pulse repetition frequency (PRF) of 10Hz. Cavitation signals were passively detected by the L11–5 transducer with a sampling frequency of 31.2MHz (Fig. 2 (a)). A series of experiments were carried out with transducers placed transverse and longitudinal to the vessel with circulating microbubbles, as shown in Fig. 2(b–d).

Fig. 2:

(a) Schematic of the dual-transducer system and vessel phantom. The therapy transducer can electronically steer its focus while the imaging transducer is used for concurrent B-mode image guidance and detection of cavitation signals (red). (b)–(d): B-mode images of three experimental configurations (15dB dynamic range) used for passive cavitation mapping experiments. Microbubbles are continuously circulated through the vessel, and the six therapy regions (No1–No6) are shown in cyan. (b) Therapy region No4 is aligned with the vessel cross-section. (c) Therapy region No1 is aligned with the vessel cross-section. (d) The therapy regions are placed along the longitude of the vessel.

Therapy pulses were electronically steered to 6 different treatment regions in the vessel phantom, with the therapy beams separated 1.2mm apart laterally. Each therapy region received 100 therapy pulses for a combined total of 600 pulses over the 6 regions. Each experiment was repeated with different applied peak negative pressures (PNP) of 2.5, 4, and 5.4MPa (free field measurements, see Section III.A: System Calibration). The synchronized dual-probe system allowed passive signal recording immediately after the therapy pulses were transmitted. RF channel signals from the imaging transducer were recorded after every therapy pulse. B-mode imaging was paused during cavitation acquisition. Matlab (R2015b, MathWorks, Natick, MA) was used for offline image formation and cavitation mapping.

Wire target experiments were performed using an L12–3v transducer in order to test localization of a known target. In this case, a single transducer was used in order to capture the reflected signals because the out-of-band reflections in the dual-transducer setup were below the noise floor and thus undetectable. A 200μm wire was placed in degassed and deionised water and aligned with the elevation axis of the L12–3v transducer. Therapeutic beams (at 4MHz frequency) focused at 12.5mm with a PRF of 10Hz, 5 cycles per pulse, and applied voltage of 10V (PNP of 1.5 MPa) were used to insonify eleven target regions spaced laterally by 0.6mm about the wire target. A total of 100 pulses were applied at each target region and the resulting echoes were acquired on 128 elements. Five cycles per therapeutic pulse were used.

C. In Vivo Animal Experiments

Animal experiments were approved by the Stanford University Institutional Administrative Panel on Laboratory Animal Care. In vivo experiments were performed on subcutaneous hepatocellular carcinoma (HCC) tumors established in a nude mouse, using the protocol described in [25], with HepG2 cells subcutaneously injected into both flanks of mice and allowed to grow to approximately 5mm in diameter.

Mice were positioned on a scanning table (37° C with a temperature control unit) and anesthetized with 2% isoflurane in 2L/min of oxygen. A catheter (MicroMarker Tail Vein Access Cannulation kit; VisualSonics, Toronto, Ontario) was inserted into a lateral tail vein for administration of microbubbles. A test solution of 3.5×10⁸ BR38 microbubbles (Bracco Research, Geneva, Switzerland) in 450μL saline was used, resulting in a microbubble concentration of 7.8×10⁸MBs/mL necessary to achieve a strong inertial cavitation signal, as previously described by Wang et al [12]. The in vivo microbubble concentration was higher compared to the in vitro experiments to account for the rapid clearance of microbubbles in animals relative to their dissolution in vitro. The ultrasound therapy beam was electronically steered over six locations during five 1-minute treatment cycles, as described previously [12]. In each treatment cycle, the microbubbles were administered for 1min prior to therapy using continuous infusion at a constant flow rate of 70μL/min by an automated infusion pump (GeniePlus, Kent Scientific, Torrington, CT).

The therapy regions had a lateral spacing of 1.5mm, leading to an effective sonicated volume of 6 regions ×1.4 mm × 8.8 mm ×15.6 mm = 604 mm³ based on the beamwidths (approximately 1.4 mm, 8.8 mm, and 15.6 mm in lateral, elevation, and axial dimensions, respectively) measured at the focal point of the ultrasound therapy beam. This volume allowed complete anatomical coverage of the tumor. Each therapy region received 1000 pulses (a total of 10s) before electronically steering to the next therapy region. This procedure was repeated 5 times, so that the total therapy (regions No1–No6) was applied for a total of 5 min (10s × 6 locations × 5 times). A PNP of 5.4MPa was used in the in vivo experiments.

D. Passive Cavitation Mapping

1). Source Localization Technique:

Passive cavitation mapping based on cavitation source localization described in a companion paper [23] was utilized on the recorded RF channel signals from the imaging transducer. Briefly, the received RF channel signals from the imaging transducer were upsampled by a factor of 8 (F_s = 249.6 MHz) using cubic spline interpolation. A sliding cross-correlation window was applied to the upsampled RF channel signals to obtain the arrival-time profiles of the cavitation acoustic emissions. Hyperbolic functions were fit to the arrival-time profiles and the resulting fit coefficients were used to estimate the location of the cavitation sources. A threshold on the fit quality (R² > 0.9) was used to exclude spurious and corrupted signals from source localization and cavitation mapping. The 68% confidence intervals of the hyperbolic fit were used as the standard deviation in the Gaussian shaped uncertainty function for cavitation mapping. The wavefront correction technique described in [23] was used to improve the localization of the multiple sources. The resulting PCM-CSL images show the accumulated cavitations detected over the entire therapeutic pulse sequence and thus display a spatio-temporal map of cavitation energy.

PCM-TEA images were reconstructed to compare with PCM-CSL. PCM-TEA images were reconstructed using delay-and-sum beamforming with fixed-focus over a grid of points, followed by the time-averaging of the squared beamformed data [20].

2). rmse Thresholding:

To eliminate further spurious signals and noise that bypassed the fit quality threshold, an additional filtering process was introduced after the R² threshold. This second filter was applied as a threshold on the root-mean-square error (rmse, units of mm²) between the hyperbolic fit and the estimated arrival-time profile.

The “optimal” threshold for the rmse error was selected based on an analysis of the number of cavitation signals detected inside the assumed boundaries of a phantom vessel containing circulating microbubbles (see Section II-B). Two parameters, γ₀ and γ₁, were computed as quality measures for the analysis. γ₀ is the ratio of cavitation sources with an rmse below the threshold localized inside the vessel (N_in) to the total number of sources (N_all) in the entire image with an rmse below the threshold; thus, γ₀ represents the percentage of sources appearing inside the vessel for any given rmse threshold. γ₁ is the ratio of the number of sources detected inside the vessel to the total number of sources detected inside the vessel with a rmse less than 0.5 mm² (N_in(rmse<0.5)). Thus, γ₁ represents the percentage of sources appearing inside the vessel from the subset of sources most likely to be cavitation sources. γ₀ and γ₁ were computed for rmse thresholds in the range from 0.012 to 0.5 mm² as

$$\begin{gathered} {\gamma }_0=\frac{N_{in}}{N_{all}}, \\ {\gamma }_1=\frac{N_{in}}{N_{in(rmse<0.5)}}. \end{gathered}$$ (1)

The range of the rmse threshold was limited to 0.5 mm² because a larger rmse does not adequately represent the correct physical model of a cavitation signals in the aperture domain and served to decrease the computational load in the rmse analysis.

Receiver operating characteristic (ROC) plots were computing using (N_in/N_in(rmse<0.5)) and (1 − N_out/N_{out(rmse<0.5)}) as the sensitivity and specificity, respectively, where N_out is the number of sources detected outside of the vessel boundaries. The optimal rmse threshold value was estimated from the ROC curves using the squared root distance to the (0,1) point (d_(0,1)) as well as the Youden index (J).

3). Wavefront Correction:

The wavefront correction technique is intended to correct wavefront discontinuities by evaluating the time derivative of the arrival-time profile and correcting the outliers. Wavefront correction was applied only to arrival-time profiles that had no more than 5 outliers. Outliers are the points in the derivative that are greater than k times the standard deviation (Σ) from the derivative’s mean (M) [23]. Outliers with k =3 and 5 were evaluated in the phantom experiments.

The performance of the wavefront correction was determined by evaluating the likelihood of the cavitation source to be localized inside the vessel, as well as sensitivity and specificity of the technique with different k. For sensitivity and specificity analysis, signals remaining after rmse filtering and localized inside the vessel were considered true positives, while those localized outside the vessel were considered false positive. Signals that were rejected after applying the rmse filtering but localized inside the vessel were considered as false negative, while those localized outside the vessel were considered true negatives.

III. RESULTS

A. System Calibration

Elevation profiles of the P4–1 therapy and L11–5 imaging transducers co-focused at the three different points are shown in Fig. 3. Good elevation alignment is achieved, with a maximum peak amplitude misalignment of only 0.5mm. The elevation peak of the imaging beam is well within the −3dB region of the therapy beam.

Fig. 3:

Verification of alignment of the elevation planes of the two transducers. The two transducers were co-focused at three different points on the elevation plane. The peak amplitude of the L11–5 transducer was aligned with that of the P4–1 transducer to a tolerance of less than 0.5mm.

The measured PNP as a function of applied voltage was measured, and a linear dependence of PNP vs. voltage was observed. Voltage amplitude applied in cavitation experiments was selected to be 30, 50, and 70 V, resulting in a PNP of 2.5, 4.0, and 5.4 MPa, respectively, and an MI of 1.9, 3.0, and 4.0, respectively.

The measured speed of sound in the agar phantom was 1488 m/s. A speed of sound of 1495 m/s was computed based on a propagation path that was approximately 75% in water at 25 ° C and 25% in the agar phantom; this speed of sound was subsequently used in all experiments for pulse sequencing and PCM reconstruction.

A plot of the frequency spectrum from the cavitation signals (not shown) reveals that the majority of the energy is from inertial cavitation with only minor superharmonics leakage associated with stable cavitation. This spectrum is expected due to the differences in the transducer bandwidths.

B. Cavitation Detection: Phantom Studies

1). Rmse Threshold Validation:

Fig. 4(a–c) plots both γ₀ and γ₁ as a function of rmse threshold for the phantom experiments for each PNP. The corresponding location of the vessel with microbubbles with respect to the therapy beams is shown in Fig. 2(b). γ₀ peaks at an rmse threshold around 0.015 – 0.05 mm², and then decreases gradually as rmse is increased. γ₁ increases rapidly with rmse threshold value and plateaus in the region of 0.015–0.05 mm².

Fig. 4:

(a-c) The dependence of γ₀ (blue line) and γ₁ (red line) on the rmse threshold for cavitation emissions inside a 1-mm vessel. Plots are shown for three applied peak negative pressures. (d-f) ROC curves for the three applied pressures. The optimal rmse threshold, 0.05 mm², is indicated by a red circle. Several other rmse threshold values are shown for reference.

ROC curves are shown in Fig. 4(d–f) and suggest that 0.05mm² is the optimal rmse threshold given [d_(0,1), J] values of [0.12, 0.85], [0.17, 0.77], and [0.13, 0.83] for PNPs of 2.4, 3.5, and 5.4MPa, respectively. This rmse threshold value most frequently resulted in the lowest d_(0,1) and largest J across all ROC curves. Thus, an rmse threshold of 0.05mm² was selected for further experimentation unless otherwise specified.

Sources having higher fit qualities and optimal rmse errors (R² >0.9 and rmse <0.05 mm²) are shown as blue dots in Fig. 5(a–c). These sources are mostly located within the 1mm diameter vessel (black line). Sources filtered out by the rmse thresholding (R² >0.9 and 0.05 < rmse <0.5mm²) are shown as red dots and are mostly located outside the vessel. Because microbubbles should be located only within the vessel, the sources with higher rmse values clearly show incorrect localization.

Fig. 5:

(a-c) The location of the detected scatterers with rmse threshold values of 0.5 mm² (red) and 0.05 mm² (blue). The vessel is outlined in black, with the vessel positioned as shown in Fig. 2(b). (d-f) PCM-CSL image of the sources identified in (c) with rmse <0.5 mm² (d), rmse <0.05 mm² (e), and 0.05 < rmse <0.5 mm² (f). The vessel is shown in cyan, and the colorbar indicates cavitation energy, E_n, in dB.

The PCM-CSL image for the experimental configuration in Fig. 2(b) with a PNP of 5.4MPa and thresholding values of R² > 0.9 and rmse < 0.5mm² is shown in Fig. 5(d). The same PCM-CSL image is divided into constituent parts using only those wavefronts passing the rmse threshold (rmse < 0.05mm²; Fig. 5(e)) and using only those wavefronts rejected by the rmse threshold (0.05 < rmse < 0.5 mm²; Fig. 5(f)).

2). Wavefront Correction:

Out of a total 6,340 detected cavitation sources from Fig. 5(d) (i.e. 10.6 cavitations detected per pulse from the 600 pulses applied over the 6 therapy spots), 2,150 (3.6 per pulse) had an rmse < 0.05mm². Applying the wavefront correction process (using outliers with k = 5) to the remaining 4,190 sources, 1,288 sources (2.1 per pulse) were successfully corrected and 902 (1.5 per pulse) of the 1,288 sources were localized within the vessel boundaries. The “realigned” wavefronts were then used to reconstruct the image in Fig. 6(a). The final PCM-CSL image using the combined corrected wavefronts and those from Fig. 5(e) is shown in Fig. 6(b).

Fig. 6:

PCM-CSL images after applying wavefront correction (experimental configuration as in Fig. 2(b) at 5.4MPa PNP). (a) Reconstructed PCM-CSL image after applying wavefront correction to wavefronts with 0.05 < rmse <0.5mm² in Fig. 5(f). (b) Final PCM-CSL image combining the wavefronts with rmse <0.05 mm² (Fig. 5(e)) and the corrected wavefronts in (a)). The vessel is shown in cyan and the color map indicates cavitation energy E in dB.

Using k =3 to define the outliers resulted in a similar PCM-CSL image with 1,493 corrections (2.5 per pulse) and 971 (1.6 per pulse) of the 1,493 sources were localized within the vessel boundaries. Applying wavefront correction with k =3 resulted in a greater cavitation intensity observed at the center of the vessel.

The total number of detected cavitation sources (N_sources; sources with R² >0.9 and rmse <0.05mm²) with and without wavefront correction, the percentage of the scatterers localized inside the vessel, and the sensitivity and specificity of the technique, are shown in Table II. The values of N_sources and N_inside are presented separately for sources with and without wavefront correction and therefore represent mutually exclusive sources. For example, in the case of 2.5MPa PNP and the experimental configuration in Fig. 2(d), 1,981 cavitation sources (3.3 per pulse) passed all filtering stages and did not require wavefront correction. Using k = 5, an additional 1,692 sources (2.8 per pulse) were captured with wavefront correction. To obtain a final PCM-CSL image, the 1,981 cavitation sources (3.3 per puslse) with no wavefront correction are combined with the 1,692 cavitation sources (2.8 per pulse with wavefront correction, and results in 63% of the sources localized inside the vessel (total 6.1 cavitation sources per pulse).

TABLE II:

Total number of detected sources (N_sources), percentage of sources localized withing the vessel boundaries (N_inside), sensitivity, and specificity of the technique for all experimental configurations, with and without wavefront correction.

		Wavefront correction applied: No if Not, k value if Yes
Setup	PNP, MPa							Sensitivity and Specificity
		N sources			Ninside, %			Separately						Combined
		No	k = 3	k = 5	No	k = 3	k = 5	No		k = 3		k = 5		k = 3		k = 5
								Sen	Spe	Sen	Spe	Sen	Spe	Sen	Spe	Sen	Spe
	2.5	1,867	2,004	1,168	71	38	56	60	99	100	20	100	17	92	80	94	91
Fig. 2(b)	4	1,756	1,428	973	65	50	58	78	99	100	16	100	21	97	84	97	90
	5.4	2,150	1,493	1288	74	65	70	81	98	100	13	100	22	98	80	99	90
	2.5	1,624	2,029	1,561	52	45	48	58	97	100	10	100	9	94	65	95	77
Fig. 2(c)	4	1,178	1,628	1,179	47	38	39	45	97	100	13	100	7	92	65	92	74
	5.4	869	1,196	818	54	35	37	54	98	100	19	100	7	88	73	90	82
	2.5	1,981	2,318	1,692	55	75	73	9	96	91	1	92	0	64	75	53	71
Fig. 2(d)	4	469	2,053	1,453	43	51	49	5	97	68	0	93	0	37	82	28	82
	5.4	264	1,995	1,444	27	35	33	2	98	41	1	94	0	22	75	16	80

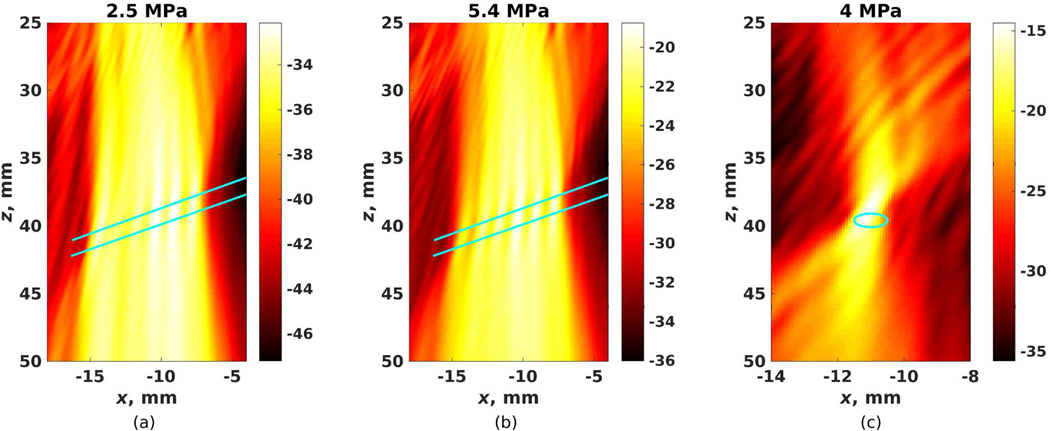
The PCM-CSL images of the experimental configuration in Fig. 2(d) at 5.4MPa PNP before and after wavefront correction are shown in Fig. 7. Applying the wavefront correction with a larger margin for outliers (k = 5) results in 1,444 (out of 4,459 wavefronts with rmse >0.05 mm², or 2.4 per pulse) corrected source locations, while a narrower margin for outliers (k =3) corrects 1,995 sources locations (3.3 per pulse). An outlier definition of k =5 was selected for further experimentation due to the higher likelihood of cavitation sources being localized inside the vessel (Table II).

Fig. 7:

PCM-CSL images for the experimental configuration in Fig. 2(d) at 5.4MPa PNP with an rmse threshold of 0.05 mm² and (a) no wavefront correction, (b) wavefront correction with outliers defined by k =3, and (c) wavefront correction with outliers defined by k =5. The vessel is shown in cyan and the color map indicates cavitation energy E_n in dB.

The sensitivity varied from 45% to 81% with rmse threshold filtering but no wavefront correction for the experimental setup as in Fig. 2(b,c), but was significantly lower (2% - 9%) with the vessel geometry placed within the imaging plane. The specificity was very high (96–99%) for all configurations with no wavefront correction. The wavefront corrected data generally had high sensitivity and low specificity. The combined sources with and without the wavefront correction resulted in high sensitivity with a moderate to high specificity for the experimental setup as in Fig. 2(b,c). Low to moderate sensitivity and moderately-high specificity were observed for the combined sources for the experimental setup of Fig. 2(d).

3). Passive Cavitation Mapping:

PCM-CSL images are shown for all pressures and vessel configurations in Fig. 8. The PCM-CSL images here include rmse filtering (R² >0.9, rmse <0.05 mm²) and wavefront correction. The number of sources used in the image (i.e. sources with rmse <0.05mm² plus the successfully corrected sources) and the total number of detected sources with R² >0.9 and rmse <0.5 mm² are provided at the top of each panel in Fig. 8. For example, in the PCM-CSL image in Fig. 8(a), there were 5,954 sources (9.9 per pulse) with R² >0.9, but only 3,035 sources (1,867 with rmse <0.05 mm² added to the 1,168 corrected sources, resulting in an overall 5.1 cavitation sources per pulse) were used for image reconstruction.

Fig. 8:

PCM-CSL images for all phantom experiments. The vessel location with circulating microbubbles is shown in cyan. (a-c) The cross section of the vessel is centered on therapy beam No4 (Fig. 2(b)). (d-f) The cross section of the vessel is centered on therapy beam No1 (Fig. 2(c)). (g-i) The vessel is align it parallel to the imaging plane (Fig. 2(d)). The number of sources used (i.e. sum of sources with rmse <0.05 mm² and wavefront-corrected sources) and total number of detected sources (i.e. sources with R² >0.9 and rmse <0.5 mm²) are shown at the top of each image. Color bars indicate the cavitation energy, E_n, in dB.

PCM-CSL images for each individual therapy beam from the 4MPa PNP case are shown in Fig. 9. Good localization of cavitation is seen for all individual beams (except region No2 in Fig. 9, bottom row), with most of the cavitation energy localized inside or near the vessel, even for the cases where the therapy beam was focused laterally away from the vessel.

Fig. 9:

PCM-CSL images for individual therapy beams for the phantom experiments at 4MPa PNP. The vessel location is shown in white and the focal regions are shown in cyan. Top row: the vessel cross section is centered on therapy beam No4. Middle row: the vessel cross section is centered on therapy beam No1. Bottom row: all 6 beams are placed along the long axis of the vessel. The number of sources used for image reconstruction (i.e. sources with rmse <0.05 mm² plus the wavefront-corrected sources) and the total number of detected sources (i.e. sources with R² >0.9 and rmse <0.5 mm²) are shown at the top of each image.

Several examples of passive cavitation maps created using the time exposure acoustics (PCM-TEA) are shown in Fig. 10 for comparison. Individual therapy regions can be distinguished, although long tail artifacts are observed with significant spreading of the cavitation energy.

Fig. 10:

Passive cavitation mapping with time exposure acoustics for several example microbubble cavitation experiments. Images are shown on a dB scale.

4). Wire Target Experiments:

PCM-CSL applied to the wire target (with rmse threshold of 0.05 mm² and wavefront correction with k =5) and the corresponding B-Mode image are shown in Fig. 11 with a dynamic range of 45dB. A total of 7,750 sources (7.0 per pulse) were detected, and the final PCM-CSL image was reconstructed using 5,482 sources (5.0 per pulse) after rmse filtering and wavefront correction (2,414 sources, or 2.2 per pulse, after initial rmse filtering plus an additional 3,068 sources, or 2.8 per pulse, after wavefront correction). As seen in the zoomed regions of the images (Fig. 11(c,d)), the wire target location in the PCM-CSL image is the same as the location in the B-Mode image. The wire in PCM-CSL image has a tighter axial and lateral localization, and additional ”sources” are seen distal to the wire due to the extended pulse-echo signal (observed in the B-mode image). Assuming the peak of the B-Mode image to be the ground truth location of the wire target, the localization error was 0.19±0.15 mm (0.51±0.40λ₀).

Fig. 11:

B-Mode (a,c) and PCM-CSL (b,d) images of the 200μm wire target. A zoomed region, outlined in white in (a,b), is shown in (c,d). Images are shown on a dB scale with 45dB dynamic range. The location of the 11 therapy beams is shown in cyan in (a)

The computational effort necessary to reconstruct the PCM-CSL image in Fig. 11, using unoptimized Matlab code, took roughly 150ms for each cavitation extraction and source localization (total time of 30 minutes) and 3.75sec for each wavefront correction (total time of 35 minutes) using parallel execution on 4 CPU cores. The reconstruction involved 7,750 sources captured from 11 therapy regions and 100 pulses per region.

5). Cavitation Energy:

Cavitation energies for the combined and individual therapy beams for a PNP of 2.5MPa for the three vessel configurations are shown in Fig. 12. Kernel density estimation (KDE) was used to calculate the probability density function of the cavitation energy. Cavitation sources not requiring wavefront correction (R² >0.9 and rmse <0.05 mm²) are shown in blue, while corrected wavefronts with k = 5 are shown in red. For each sub-figure, the leftmost violin pair shows cavitation energy for all therapy regions combined, while the other pairs show the cavitation energy for each individual therapy region.

Fig. 12:

Violin plots of the cavitation energy, E_n, in dB for the phantom experiments with PNP = 2.5 MPa, with the median value shown as a white circle. The cavitation energy is shown for all therapy regions combined and for each individual region separately. Cavitation sources not requiring wavefront correction are shown in blue, while those requiring wavefront correction are shown in red. The number of detected sources in each case is shown on top. The sub-figures (a,b,c) show data for the experimental configurations shown in Fig. 2(b,c,d), respectively.

Increasing cavitation energy as a function of applied PNP is observed for all vessel configurations (see Fig. 8). For vessel cross-section configurations, the highest cavitation energy is observed when the therapy beam is centered directly on the vessel, as seen for the therapy beams No3 and No4 in Fig. 12(a) and No1 in Fig. 12(b). Cavitation energy from the sources requiring wavefront correction was approximately the same as the cavitation energy from the sources not requiring wavefront correction. In addition, the cavitation energy for the adjacent therapy regions has a shape roughly similar to the lateral beam profile of the therapy excitation. Similar findings were observed for experiments with PNPs of 4 and 5.4MPa.

The cavitation energy from wavefronts with low rmse values typically showed a Gaussian distribution. Examples of the cavitation energy distribution before and after applying the wavefront correction are shown in Fig. 13. Applying 5.4MPa to therapy region No2 resulted in a mean cavitation energy of E_n =1.7±0.3mJ. Fitting a Gaussian distribution to the cavitation energy of the individual sources resulted in μ =1.7mJ and σ =0.4mJ. For the cavitation sources requiring wavefront correction (with outliers having k = 5), the resulting energy was E_n =1.6±0.4mJ and the Gaussian fit had μ =1.6mJ and σ =0.4mJ (Fig. 13(a)). For therapy region No4, only a single source was localized with E_n = 11.1mJ (Fig. 13(b)). After wavefront correction, the mean E_n was 9.5±2.8mJ. TheE_n values for the corrected sources are relatively close to the initial E_n value, but there are too few sources to properly represent a Gaussian distribution.

Fig. 13:

Examples of cavitation energy distribution for sources not requiring wavefront correction (top row, blue) and sources after wavefront correction (bottom row, red). Cavitation energies are shown with a histogram, and the Gaussian probability density function calculated using KDE is shown with a solid line. The mean cavitation energy, E_n, and Gaussian distribution parameters are shown at the top of each subplot. (a) E_n for sources from therapy region No2 in Fig. 12(c). The energy shows a Gaussian distribution and was observed in most of the therapy beams. (b) The E_n for therapy region No4 for Fig. 12(c) has only a single cavitation source not requiring wavefront correction. 22 sources with wavefront correction had a mean E_n close to the single detected cavitation.

C. In vivo Animal Experiments

Fig. 14(a) shows the B-mode image of the tumor site in the mouse with the locations of the applied therapy beams and Fig. 14(b) shows the corresponding PCM-TEA image having significant tail artifacts. Fig. 14(c) shows the same PCM-TEA as in Fig. 14(b), but on a decibel scale. The PCM-CSL images without wavefront correction with rmse <0.5 mm² and rmse <0.05 mm² are shown in Figs. 14(d,e), respectively. The PCM-CSL image after wavefront correction is shown in Fig. 14(f). The total number of detected sources before applying the rmse threshold filter was 144,727 (24.1 per pulse). Using a threshold value of 0.05 mm² resulted in 9,506 detected cavitation sources (1.6 per pulse), which is 6.6% of all detected cavitation sources having R² >0.9 and rmse <0.5mm². However, after applying wavefront correction (with outliers having k = 5; number of outliers ≤ 5), the number of corrected cavitation sources included in the final PCM-CSL image reconstruction was 54,830 (9.1 per pulse, i.e. an additional 38% of possible cavitation sources). The corrected PCM-CSL image shows that a significant amount of cavitation signals were localized within or in close proximity to the tumor margin (dashed white circle), with stronger cavitation occurring in the center of the tumor.

Fig. 14:

Passive cavitation maps of the in vivo mouse experiment. (a) B-mode image of the mouse’s tumor. The center of the treatment region is placed at the center of tumor. (b) Passive cavitation map based on time-exposure acoustics on a linear scale. (c) The same PCM-TEA image using a decibel scale. (d) PCM-CSL using wavefronts with rmse <0.5 mm² and no wavefront correction. (e) PCM-CSL using wavefronts with rmse <0.05 mm² and no wavefront correction. (f) PCM-CSL with wavefront correction. The colorbars for the PCM-CSL images indicate cavitation energy E_n in dB. The tumor boundary is outlined with a dashed line.

IV. DISCUSSION

A. Phantom Studies

To avoid noise and spurious signals, the arrival-time profiles with poor hyperbolic fit (R² <0.9) and poor rmse values (rmse >0.5mm²) were filtered out. Next, arrival-time profiles were subjected to a threshold on the rmse between the fit and the arrival-time profiles. An analysis in a phantom vessel showed that a threshold of 0.05mm² yielded retains most of the sources (up to 92%, Fig. 4(a–c)) that were localized inside the vessel (blue colored dots in Fig. 5(a–c)) and rejects the majority of those detected outside the vessel (red colored dots in Fig. 5(a–c)). Those arrival-time profiles with an rmse between 0.05mm² and 0.5mm² were then subjected to wavefront correction. Because the number of cavitation sources can be large, this proposed filtering approach attempts to minimize the number of sources that require additional computational processing. However, because the imaging conditions in the phantoms have low noise, the optimal rmse threshold observed here may not directly translate to all in vivo conditions, although it appeared to translate well for our in vivo experiment. Because the vast majority of wavefronts with a large rmse are localized outside of the vessel and do not have arrival-time profiles representative of cavitation sources, we believe it unnecessary to explore thresholds greater than 0.5mm² for optimization purposes.

The PCM-CSL images reconstructed after rmse filtering show good identification of sources that require wavefront correction (see Fig. 5(d–f)). In Fig. 5(f) the PCM-CSL image was reconstructed using only the cavitations with poor rmse values and shows poor source localization. Applying wavefront correction permits these sources to be correctly remapped, as seen in Fig. 6(a). This previously discarded data was able to be used in the PCM-CSL image reconstruction and resulted in higher cavitation energy with clearer visualization of cavitation sources (e.g. Fig. 7).

Wavefront correction was particularly useful in Fig. 7 where greater interference occurs from cavitation sources spread over a wider area. The original PCM-CSL image without wavefront correction (Fig. 7(a)) was reconstructed using only 264 cavitation sources that had sufficient fit quality and low rmse. Applying wavefront correction resulted in an additional 1,981 and 1,493 localized cavitations for outliers with k = 3 and k = 5, respectively. After the wavefront correction was applied, the cavitation locations were better localized (Fig. 7(b,c)) and showed stronger cavitation energy per image pixel.

Utilizing outliers with k = 3 resulted in a higher number of corrected sources compared to outliers with k = 5, which can be explained by the fit quality of the arrival-time profile’s derivative. For k = 5, the derivative can be noisy even after outlier correction, so that fitting Equation 6 from [23] to the derivative may still result in a poor quality fit, which will exclude the wavefront from further consideration. Unexpectedly, applying the wavefront correction with k = 5 frequently resulted in more sources localized inside the vessel than with k =3 (see Table II). In addition, the sensitivity and specificity were higher for the wavefront correction with k =5 compared to k =3 for the case of simple vessel geometry as in Fig. 2(b,c). Assuming that the complex microvasculature in tumors is unlikely to be as ideal as the vessel phantom, a selection of k =5 was used as a definition of an outlier for further phantom and in vivo experiments. A detailed study on parameter selection for wavefront correction, such as k or the maximum number of outliers allowed for wavefront correction, was beyond the scope of this paper.

We have observed in a few instances, such as therapy beam No2 in the bottom row of Fig. 8, that the localization appears to be incorrect, even after wavefront correction. At this time, we are unable to explain this problem, as this occurrence was not reliably reproduced.

The resulting PCM-CSL maps (Fig. 8) show good localization of the cavitation sources within the vessel without the tail artifacts present in PCM-TEA (Fig. 10). In fact, the reconstructed PCM-CSL images show a significant improvement compared to PCM-TEA for all experiments. Although the proposed PCM-CSL approach improves localization of the cavitation sources to within the boundaries where cavitation should be expected (i.e. within the vessel region), the filtering method based on R² and rmse threshold may still eliminate valid cavitation sources, such as cavitation from large bubble clouds, or interference from multiple cavitating microbubbles.

Reconstructing the PCM-CSL with combined and separate therapy regions confirms that the proposed technique is able to accurately localize cavitation sources, with approximately 80% of the detected cavitation sources located inside the vessel (Figs. 12 and 9, Table II). For example, moving the focal region laterally away from the vessel and inducing cavitation with the sidelobes (e.g. Fig. 9, middle row, therapy regions No2–No6) show proper localization of the cavitation sources.

However, the longitudinal vessel configuration (Fig. 2(d)) showed poorer sensitivity and specificity than the cross-sectional vessel configurations (Fig. 2(b,c)). This is likely due to the greater amount of interference from cavitation sources induced by the sidelobes in an extended target, as worse sensitivity and specificity is observed with the higher PNPs (Table II). In this case, stronger off-axis sources can interfere with the cross-correlation process, increase the localization error, and can manifest as a narrowing of the detected cavitation region. This would indicate that decomposition methods, such as the DORT method [29] or principle component analysis, may be useful in separating on- and off-axis cavitation sources for proper localization, especially when weaker off-axis sources may not be detected and localized in the image.

As shown in Part I [23], a microbubble cloud, within the diffraction limit of the transmitted beam, is mapped by a few cavitation sources. A similar observation is encountered in the phantom experiments, where thousands of microbubbles present within the therapy region are represented by 2 and 6 cavitation sources per therapy pulse (approximately 1,500 to 3,500 cavitation sources captured over 100 pulses in each of 6 therapy regions).

The proposed technique has shown a significant improvement over PCM-TEA while localizing cavitating microbubbles in a homogeneous phantom. Because the technique assumes the sound speed is known, aberrations may degrade the localization. While this may necessitate the re-optimization of the rmse threshold, the Anderson and Trahey [30] showed that the technique is relatively robust to sound speed inhomogeneity. In addition, speed of sound estimation techniques (such as the Anderson-Trahey technique itself [30]) may be used to estimate the global average speed of sound in the medium, which may be used with the proposed PCM-CSL technique.

As seen from the results with the wire target (Fig. 11), the proposed technique is capable of localizing the wire target with high accuracy. The result is promising given that the rmse threshold and the applied wavefront correction were optimized for cavitation sources in a vessel and not reflective targets (even though they have similarities).

The total number of detected (R² >0.9, rmse <0.5 mm²) and filtered (rmse <0.05 mm²) sources varies for each experiment. However, the number of detected sources before wavefront correction tends to be lower when the therapy beam is placed directly on the vessel than when the vessel is placed laterally away from the focal region. We speculate that this is due to the higher PNP where the therapy pulse is applied directly to the microbubbles, thereby causing most of the microbubbles to collapse at roughly the same time and yield strongly interfering signals. When the therapy pulse is focused away from the microbubbles, the sidelobes have a lower PNP and only the smaller microbubbles collapse [31]. Because there are fewer microbubbles collapsing, there is less signal interference, allowing the proposed method to capture multiple cavitation events.

For most of the phantom experiments, the cavitation energy had a Gaussian distribution shape for sources not requiring wavefront correction, as shown in Fig. 13(a). Typically, applying wavefront correction increased the number of detected cavitation sources, but did not introduce any significant changes to the μ and σ of the Gaussian distribution of the cavitation energy (Fig. 13(a)), and was able to localize the sources inside the vessel. In some experiments, such as a strong therapeutic beam placed directly on the site of the microbubbles, only a few cavitation sources with good fit quality were initially extracted (Fig. 13(b)). In such cases, additional wavefronts were corrected, but the cavitation energy after correction still did not have a clear Gaussian distribution due to the low number of cavitation sources. However, the mean E_n value after correction did not change significantly.

Based on this analysis, the wavefront correction technique corrects for errors in arrival-time profiles of cavitation wavefronts but does not introduce significant spurious cavitation signals or artifacts. In addition, the wavefront correction is not only able to properly localize cavitation sources but also measure consistent cavitation energies across experiments. One limitation in this study is that while the use of a dual transducer setup to separate frequency bands was sufficient to capture significant inertial cavitation, there is still stable cavitation signal present in these experiments (approximately 25% in power). However, the technique itself is not intended to separate inertial from cavitation signal and will work in conjunction with signal processing or other methods designed to separate inertial and stable cavitation signals.

B. In vivo Experiments

The cavitaion maps based on PCM-CSL show a significant improvement over the PCM-TEA maps by reducing the tail artifacts. The PCM-CSL images without rmse filtering show a significant spread of cavitation energy over the image (Fig. 14(d)). Applying an rmse threshold of 0.05mm² rejects most of the spurious cavitation events and only permits those with high hyperbolic fit quality, which are localized inside or in close proximity to the tumor margins (Fig. 14(e)). Applying wavefront correction permits much of the previously rejected events to be re-mapped to similar locations inside or near the tumor (Fig. 14(f)). Even though the rmse threshold of 0.05mm² was optimized in phantoms, the value resulted in an acceptable localization in vivo.

Applying the wavefront correction technique to the sources above the rmse threshold restored approximately 38.0% of the detected cavitation sources, a significant increase from the initial 6.6% detected based on R² and rmse thresholding alone. Without wavefront correction, 38% of the cavitation sources are localized incorrectly and cause spreading of the cavitation energy in the PCM reconstruction. This is a potential explanation for why the PCM-TEA maps have significant tail artifacts as well as potentially underestimating the amount of cavitation energy occuring. With wavefront correction, the cavitation energy is increased significantly while localizing it to the inside of the tumor area (Fig. 14(f)). There is cavitation energy present outside the tumor margins, but this is due to the location of therapy beam No1 located outside of the tumor (Fig. 14(a)) and proximal to blood vessels in normal tissue, which is a potential source of this cavitation energy. An alternative explanation is that the phantom experiments did show elongated cavitation energy in the axis of the imaging transducer outside of the phantom vessel, which is not unlike that observed here. For comparison, region No6 is also outside the tumor, and it is noted that this region does not contain tissues or blood vessels, and therefore does not yield any cavitation energy.

V. CONCLUSION

We have demonstrated a high-resolution passive cavitation mapping technique, described in a companion paper, using two aligned transducer arrays in phantom and in vivo studies. The mapping was done passively using a hyperbolic fit to the received cavitation signal wavefront. A filtering technique was introduced that applies a threshold on the root-mean-squareerror of the cavitation’s arrival-time profile compared to its hyperbolic fit. The optimal threshold was determined to be 0.05mm² based on an experimental analysis in a phantom vessel. It was shown that the wavefront correction technique with a higher threshold for outliers (k =5) results in a higher likelihood of cavitation sources localized inside the vessel and lower weighted localization error, compared to a lower threshold for outliers (k =3). Applying wavefront correction yielded 6-fold more cavitation wavefronts that were previously rejected by rmse filtering in vivo. The cavitation mapping technique based on cavitation source localization showed a significant advantage over the time exposure acoustic method both in phantoms and in vivo experiments.