Abstract
This work aims at a better understanding and the optimal control of the spread of the new severe acute respiratory corona virus 2 (SARS-CoV-2). A multi-scale model giving insights on the virus population dynamics, the transmission process and the infection mechanism is proposed first. Indeed, there are human to human virus transmission, human to environment virus transmission, environment to human virus transmission and self-infection by susceptible individuals. The global stability of the disease-free equilibrium is shown when a given threshold is less or equal to 1 and the basic reproduction number is calculated. A convergence index is also defined in order to estimate the speed at which the disease extincts and an upper bound to the time of infectious extinction is given. The existence of the endemic equilibrium is conditional and its description is provided. Using Partial Rank Correlation Coefficient with a three levels fractional experimental design, the sensitivity of , and to control parameters is evaluated. Following this study, the most significant parameter is the probability of wearing mask followed by the probability of mobility and the disinfection rate. According to a functional cost taking into account economic impacts of SARS-CoV-2, optimal fighting strategies are determined and discussed. The study is applied to real and available data from Cameroon with a model fitting. After several simulations, social distancing and the disinfection frequency appear as the main elements of the optimal control strategy against SARS-CoV-2.
Keywords: SARS-CoV-2, Multi-scale modeling, Estimation of parameter, Stability analysis, Time of extinction, Sensitivity analysis, Optimal control
Introduction
According to the World Health Organization1 (WHO), the severe acute respiratory syndrome corona virus 2 (SARS-CoV-2) previously known as new corona virus 2019 (2019-nCoV) is responsible of an infectious disease called Covid-19 [67]. In 1937, corona viruses were first identified as infectious bronchitis viruses with which birds suffered, that could devastate poultry stocks. Today, the viruses are the cause of the common cold in to of all cases. In the past 70 years, researchers have found camels, cattle, cats, dogs, horses, mice, pigs, rats and turkeys that were infected with corona viruses.2 Older people, and those with underlying medical problems like cardiovascular diseases, diabetes, chronic respiratory diseases and cancer are more likely to develop serious illness. The Centers for Disease Control and Prevention3 (CDC) affirm that the most common ways the virus spreads from an infected person to healthy people around them is when they cough or sneeze and release viral particles into the air and through touching, hands shaking and other forms of close personal contact. When healthy people touch objects or surfaces on which there are viral particles, then touch their eyes, nose or mouth before washing their hands, the virus can spread. In some rare cases, fecal contamination can cause the virus to spread as well. The best way to prevent and slow down transmission is being well informed about the SARS-CoV-2, the disease, its causes and how it spreads. Each person protects himself and others from infection by hands washing or using an alcohol-based rub frequently and not touching his face. The SARS-CoV-2 spreads primarily through droplets of saliva or discharge from the nose when an infected person coughs or sneezes, so it is important to also practice respiratory etiquette (for example, by coughing into a flexed elbow). Depending on its location, the SARS-CoV-2 can leave up to 7 days out of human body [17]. Several promising vaccines have recently emerged even though their efficiency is not fully established [43]. However, their adoption by populations is very partial, especially in the case of Cameroon where awareness is a major challenge. This slow uptake of vaccine solutions can be explained in part by the fact that vaccination is not a substitute for the application of barrier measures, even for those who are vaccinated. In this context, modeling, analyzing models, estimating risks and forecasting the potential spread of the disease in population remain very useful for decision makers [42].
Recently, numerous papers (published or not) appeared in order to contribute to the fight against the pandemic Covid-19. Those papers can be organized in three groups. The first group addressed the problem of forecasting the disease in order to help decision makers to better evaluate the logistic challenges they will face [3, 8, 9, 23, 24, 32, 34, 37, 38, 50, 52, 53, 55, 62, 65, 66, 69, 83, 84]. The second category of papers focused on evaluating the effectiveness of mitigations measures prescribed by the WHO and different governments in order to define better fighting strategies [10, 16, 19, 21, 22, 33, 38, 45, 46, 50, 55, 61–63, 68, 71–75, 77, 82, 84]. The last set of papers studied the social and the economical impacts of the pandemic [47, 81]. As we can observe in the literature, the wide part of models only considers person to person disease transmission. Of course it is important, but indirect transmission by environment may also be considered. On the other hand, the virus population dynamics appears also important and should be explicitly studied.
Indeed, when an individual gets in contact with the virus he is not directly exposed. According to the classic epidemiological literature, an exposed person refers to an infected person who cannot yet transmit the disease [7, 14, 51]. In the context of Covid-19, it refers to an individual whose virus is present in his body, but the level of reproduction has not yet reached the stage where the individual is shedding virus through various channels (coughing and sneezing). Hence, to become exposed the virus has to penetrate in the organism by oral or respiratory ways. Therefore, the exposition is mainly indirect in terms of human-to-human, or human-to-environment contacts. This consideration justifies the regular disinfection of individuals and the environment as recommended by public health agencies.
Following the authors in [27–31, 57], it is important to build and understand models that link the within-host dynamics and population-level dynamics of infectious. The prediction of the behavior of Covid-19 is very difficult because mitigation strategies are permanently changing. So it could be more efficient given an initial situation to propose optimal control strategies that will lead to disease extinction at a time to be determined. Hence, this work proposes efficient and low-cost control strategies against Covid-19.
The paper is organized as follows. A model is described in Sect. 2.2 according to the notations given in Sect. 2.1 and its asymptotic behavior is studied in Sect. 2.3 depending on some critical thresholds we define. In Sect. 3.1, we estimate the parameters of the model according to the real available data from Cameroon. A sensitivity analysis of critical thresholds depending on some control parameters is carried out in Sect. 3.2. Section 4 is devoted to the design and the computation of optimal control strategies according to different constraints. Illustrative simulations are carried out in Sect. 4.2. The algorithm which computes the optimal control is given in appendix B. The proofs of different theoretical result in “Appendix A.” The paper ends with a conclusion in Sect. 5.
The model and its general features
Definition of parameters
In this short section, different parameters are presented in order to make easier the understanding of the model to be proposed and studied later.
Description of the model
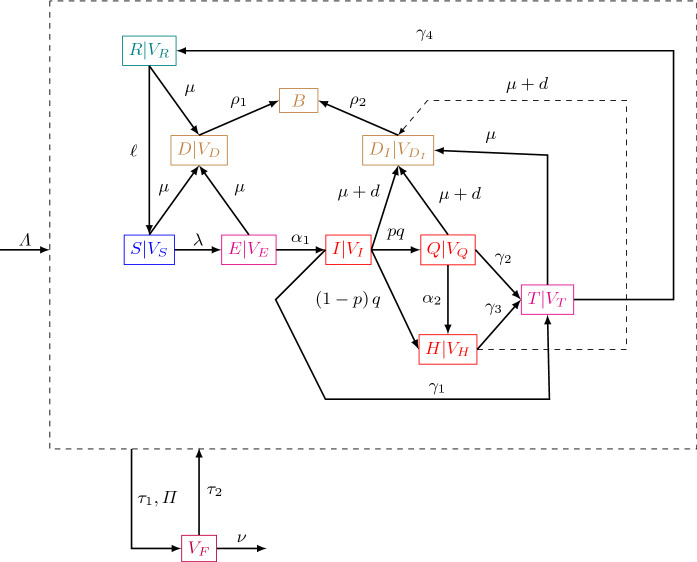
We can summarize the dynamics of Covid-19 by Fig. 1.
Fig. 1.
Flowchart of the compartmental model
The disease dynamics can be viewed under two angles. Indeed, there are human dynamics on the first hand and the viruses dynamics on humans or in the environment on the other. According to the Cameroonian context, we consider ten compartments in the human population per unit area:
Susceptible : Public health institutions refer to a susceptible person as a person who is not a carrier of the virus and has no immunity to the disease. Such a person may become infected if he or she does not comply with the barrier measures prescribed by the government.
Exposed (Infected but not contagious) : public health institutions refer to an exposed person as a person who has the virus in his or her body but is not contagious in the sense that the virus has not yet reproduced sufficiently in the body to be present in the body’s secretions such as saliva and nasal secretions. Such a person has no symptoms and will test negative for Corona virus.
Infectious : public health institutions refer to an infectious person as anyone who is a carrier of the disease and contagious (the virus has reproduced sufficiently in the body to be present in the body’s secretions such as saliva and nasal discharge), but who has not yet been identified as such, probably because he or she does not manifest symptoms (asymptomatic case) or has not yet been tested. People who are infectious from this point of view are very often free to move around and represent a great risk of contamination.
Quarantined : public health institutions refer to a person in quarantine as any person isolated (at home or in a specialized center) after having been identified or suspected as a carrier of the disease and contagious (infectious), but not presenting a serious form of the disease endangering his or her life (no respiratory assistance for example). The follow-up of these people being particular (at least because of their isolation, even it cannot be perfect due to contacts with health agents who are also in contact with the rest of the population), it seems important to distinguish them explicitly by a compartment. This distinction allows on the one hand to take into account the effect of isolation on the dynamics of the disease. On the other hand, it allows the economic impact of quarantine to be explicitly evaluated.
Hospitalized : public health institutions refer to a hospitalized person as any infectious person (infectious or in quarantine) who manifests severe forms of the disease to the point of requiring special medical attention (such as respiratory assistance and oxygen).
Treated : public health institutions refer to a treated person as any person who, after having been in the infectious phase (and possibly the quarantine or hospitalization phases), returns to a state where he or she is out of danger and is less contagious: even if the viruses remain in low concentration in the body, their reproduction rate decreases due to the body’s resistance or to any treatment. It is important to note that despite the controversy about the existence of a treatment, several treatment protocols are proposed either by conventional medicine, called modern medicine, or by local or traditional medicine using herbal teas (for those who do not go to the hospital and practice self-medication without having tested their serological status). It is common for a treated person to be sent back to his usual daily life (home) if he was followed in a health facility (out of quarantine or hospitalization). This is due to the limited resources available to monitor large numbers of patients.
Recovered : public health institutions refer to a cured person as anyone who, after having been in the treated phase, no longer has the virus in his or her body and has possibly developed a resistance (a priori temporary) to the virus. He/she is no longer contagious in the sense that he/she does not participate in the reproduction of the virus and his/her nasal or oral discharge is healthy.
Non-infectious dead : public health institutions refer to a non-infectious decedent as anyone who died for reasons unrelated to the Corona virus. The funeral procedures for such persons are classic and entrusted to their families (more or less long stay in the morgue, wake with the body, transfer of the body to its village and festive burial4 [40]).
Infectious dead : Public health institutions refer to a deceased infectious person as a person who has died from Covid-19. Funeral procedures for such persons are very fast and ensured by public services: the body is sealed and is not given to the family to avoid any risk of secondary contamination in the handling of the corpse. Even if it is not proven that the corpses of these people are not contagious, no study to our knowledge shows the contrary. As recommended in [43], taking into account the effect of the deceased follow-up policy in the dynamics of the disease and the impacts of the disease and the economic aspects requires the explicit introduction of the compartments of the deceased in the modeling.
Buried : The buried compartment makes it possible to count burials and assess the impact of the rapid burial of infectious dead on the dynamics of the disease. It also makes it possible to assess the economic impact of deaths due to Covid-19.
WHO and the Government of Cameroon recommend several control measures that can be explicitly listed here as follows:
Limiting direct contacts with others through a control parameter : obviously, direct contact with a person who is contaminated with viruses leads to being contaminated as well.
Limiting movements through a control parameter : multiplying movements increases the risk of being in contact with the virus from environment or from a person after a direct contact.
Social distancing which is implemented through limitation of group size per unit area to a maximum value : social distancing limits not mobility but the density of people per unit area. For example, guaranteeing a distance of one meter between individuals means that on a disk of radius 1 meter there is exactly one person. The implementation of social distancing does not affect the size of the total population but rather its spatial distribution. To our knowledge, no existing epidemiological model has implemented social distancing using a concept similar to “carrying capacity” which is rather common in ecological models.
Limiting the area of movements through a lock-down ratio : the disease is better contained if its spatial spreading is limited by lock-down. Social distancing is not to be confused with lock-down. In the lock-down ratio , denotes the “effective area” while is the global geographic area of study where people are living. The concept of effective area, which we also newly introduced, designates the surface of the spatial domain in which an individual is allowed to move in order to respect the rules of Lock-down. Indeed, lock-down results in small subpopulations that can be geographically delimited and do not interact. This is expected to facilitate the control of the disease.
Frequently hands washing and disinfection through a control parameter : by frequently hands washing and avoiding to touch the face (especially eyes, nose and mouth), the probability to get infected is clearly reduced.
Wearing mask and avoiding to touch the face through a control parameter : Wearing mask reduces both the risk of infection and the release of viruses by infectious, quarantined, hospitalized and treated individuals.
One of the specificities of our modeling is based on the fact that each individual regardless of his compartment of belonging is potentially a reservoir since the outside part of his body (including his clothes) can carry viruses that he would have acquired in contact with the contaminated environment or a contaminated person. On the other hand, the amount of virus available in a human “reservoir” depends on its compartment since people who are contagious beyond transporting viruses taken elsewhere also produce them. This consideration makes it possible to explicitly assess the impact of barrier and disinfection measures. Again, we emphasize on the fact that getting in contact with viruses does not mean to be infected, but the infection occurs when the viruses penetrate the organism by oral or respiratory ways. Thus, we have ten compartments for virus population per individual status group located in a unitary surface or per unit area of environment : global viral load in susceptible compartment , global viral load in infected compartment , global viral load in infectious compartment , global viral load in quarantined compartment , global viral load in hospitalized compartment , global viral load in treated compartment , global viral load in recovered compartment , global viral load in non-infectious dead compartment , global viral load in infectious dead compartment , global free load of viruses in the environment . The viral load is transferred from an individual being in compartment i to the environment (transfer of type I: ) or conversely from the environment to an individual being in compartment i (transfer of type II: ). In addition, there are transfers of external viral load (available on the body and clothing) between individuals when there are direct contacts (transfer of type III: ). Under the simplifying assumption of mass action, it can be assumed that the amount of free virus lost by an individual from one compartment after contact is distributed to the other compartments in proportion to their different fractions in the population. It is likely that the balance of viruses received and lost is deficient in compartments I, Q and H since they participate in the reproduction of viruses. Infectious, quarantined, hospitalized and treated individuals produce new viruses at a rate with i indexing a specific compartment. A susceptible individual becomes infected when a virus passes from the outside of his body to the inside (transfer of type IV: ). Infected persons die at a rate or become infectious with a rate . An infectious case is reported at a rate q and dies at a rate . The probability that a person identified as infectious does not immediately develop a severe form of the disease and is therefore quarantined is p, otherwise he is admitted to hospital. With a rate a quarantined person develop a severe form of the disease and is therefore admitted to hospital. Infectious, quarantined and hospitalized individuals die at a rate or become treated (partially recovered) at the respective rates of , and . A treated individual is out of danger but is still infectious and can die at a rate . Treated persons recover completely and become immune at a rate . A recovered person losses his immunity at a rate or dies at a rate . Indeed, Recovered people may die from natural death or from causes unrelated to Covid-19. Potentially acquired immunity has certainly been considered in several modeling articles but no precise study on its effectiveness and duration exists to our knowledge. It is therefore more appropriate, as is the case in the literature, to assume that it is not definitive [42]. Moreover, despite the advent of vaccines, barrier measures remain strongly recommended for everyone, including those who have been vaccinated. With a rate , a non-infectious dead person is buried while an infectious dead individual is buried at a rate . Indeed, infectious dead persons are potentially very contagious and it is recommended to bury them rapidly in order to limit contacts.
Let be the vector of human population densities per unit area in each compartment, be the vector of virus population densities per unit area in each compartment,
be the vector of horizontal immigration rates in each compartment of the human population, be the vector of vertical immigration rates (through births) in each compartment of the human population, be the vector of the release rates of viruses by contagious humans (via their nasal or oral discharge) into the environment, and be, respectively, the density of the living human population per unit area and the density of the living or deceased (but not yet buried) human population per unit area. A mathematical model corresponding to Fig. 1 can be described as
- A mesoscopic model (intermediate scale of human gatherings):
The first term to the right of the equality in equation (1) corresponds to horizontal recruitment (immigration at rate ) and vertical recruitment (birth at rates ) in the susceptible human population. Population density per unit of surface is restricted by logistic expression which reduce the population growth when N is near to . The limiting capacity models social distancing which reduces the number of individuals per unit of area. The second term represents the exposition () and the natural death at rate . The last term corresponds to the lost of immunity at rate . Considering all those features in the same model are not common and it makes the analysis of the model more difficult.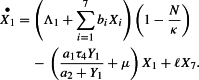
1
The first term to the right of the equality in equation (2) corresponds to horizontal recruitment in the exposed human population. The second term represents the arrival of new exposed. The last term corresponds to the natural death at rate and the worsening of the disease at rate .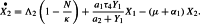
2
The first term to the right of the equality in equation (3) corresponds to horizontal recruitment in the infectious human population. The second term represents the arrival of new infectious. The last term corresponds to the death at rate , the detection of the disease by screening test (at rate q) and the treatment at rate .3
The first term to the right of the equality in equation (4) corresponds to horizontal recruitment in the quarantined human population. The second term represents the arrival of new quarantined after testing an infectious at rate pq. The last term corresponds to the death at rate , the worsening of the disease (at rate and the treatment at rate ).4
The first term to the right of the equality in equation (5) corresponds to horizontal recruitment in the hospitalized human population. The second and third terms represent the arrival of new hospitalized after testing an infectious (at rate ) and disease worsening for quarantined (at rate ). The last term corresponds to the death at rate and the treatment at rate .5
The first term to the right of the equality in equation (6) corresponds to horizontal recruitment in the treated human population. The second, the third and the fourth terms represent the respective treating rates from the infectious (), quarantined () and hospitalized (). The last term corresponds to the death at rate and the recovering at rate .6
The first term to the right of the equality in equation (7) corresponds to horizontal recruitment in the recovered human population. The second term represents the recovering rates of treated (). The last term corresponds to the death at rate and the lost of immunity at rate .7
The first term to the right of the equality in equation (8) corresponds to horizontal recruitment in the non-infectious dead human population. That recruitment could correspond to transportation or transfer of dead individuals for burial ceremonies like it is common in Cameroon or other valuable reasons. The second term represents the death of individuals in susceptible, exposed and treated compartment at rate . The last term corresponds to the burying at rate .8
The first term to the right of the equality in equation (9) corresponds to horizontal recruitment in the infectious dead human population. As in equation (8) that recruitment could correspond to transportation or transfer of dead individuals for burial ceremonies like it is common in Cameroon or other valuable reasons. The second term represents the death of individuals in infectious, quarantined, hospitalized at rate . The third term represents the death of individuals in recovered compartment . The last term corresponds to the burying at rate .9
The first and the second terms in Eq. (10) correspond the burying of dead individuals at respective rates and . The horizontal migrations (represented by the s) in the different compartments can be explained by the movements of travelers who sometimes prefer to return to their countries of origin (as has been mentioned by the media about citizens of several African countries including Cameroonians residing in China), medical evacuations for more competent health centers, or repatriation of human remains. Thus, if the geographical area of study is limited, horizontal recruitments are possible in practically all the compartments.10 - A microscopic model (virus scale):
The first term to the right of the equality in equation (11) represents the recruitment of viruses in susceptible population after a contact with environment (at rate ) and individuals of other compartments (at respective rates ). The second term corresponds to the disappearing of viruses by natural death (at rate ), by the death of the human host (at rate ), by disinfection measures applied by the host (at rate ), by the exchange of viruses with environment (at rate ) and other compartments (at rate ), and by the transition of the host from the susceptible compartment to the exposed compartment.11
The first term to the right of the equality in equation (12) represents the recruitment of viruses in exposed population after a contact with environment (at rate ) and individuals of other compartments (at respective rates ). The second term corresponds to the update in population of viruses due to the transition from susceptible status to exposed status at rate . The third term represents the disappearing of viruses by natural death (at rate ), by the death of the human host (at rate ), by disinfection measures applied by the host (at rate ), by the exchange of viruses with environment (at rate ) and other compartments (at rate ), and by the transition of the host from the susceptible compartment to the exposed compartment at rate .12
The first term to the right of the equality in equation (13) represents the release of internal viruses by infectious individuals on themselves. The second term corresponds to the recruitment of viruses in infectious population after a contact with environment (at rate ) and individuals of other compartments (at respective rates ). The third term corresponds to the update in population of viruses due to the transition from exposed status to infected status at rate . The fourth term represents the disappearing of viruses by natural death (at rate ), by the death of the human host (at rate ), by disinfection measures applied by the host (at rate ), by the exchange of viruses with environment (at rate ) and other compartments (at rate ), by the transition of the host from the infectious compartment to the treated compartment at rate , and by the transition of the host from the infectious compartment to the quarantined or the hospitalized compartment at screening rate q.13
The first term to the right of the equality in equation (14) represents the release of internal viruses by quarantined individuals on themselves. The second term corresponds to the recruitment of viruses in quarantined population after a contact with environment (at rate ) and individuals of other compartments (at respective rates ). The third term corresponds to the arrival of new quarantined from the infectious compartment at rate pq. The last term represents the disappearing of viruses by natural death (at rate ), by the death of the human host (at rate ), by disinfection measures applied by the host (at rate ), by the exchange of viruses with environment (at rate ) and other compartments (at rate ), by the transition of the host from the quarantined compartment to the hospitalized compartment at rate , and by the transition of the host from the quarantined compartment to the treated compartment at rate .14
The first term to the right of the equality in equation (15) represents the release of internal viruses by hospitalized individuals on themselves. The second term corresponds to the recruitment of viruses in hospitalized population after a contact with environment (at rate ) and individuals of other compartments (at respective rates ). The third term corresponds to the arrival of new hospitalized from the infectious compartment at rate . The fourth term materializes the arrival of new hospitalized from the quarantined compartment at rate . The last term represents the disappearing of viruses by natural death (at rate ), by the death of the human host (at rate ), by disinfection measures applied by the host (at rate ), by the exchange of viruses with environment (at rate ) and other compartments (at rate ), and by the transition of the host from the hospitalized compartment to the treated compartment at rate .15
The first term to the right of the equality in equation (16) represents the release of internal viruses by treated individuals on themselves. The second term corresponds to the recruitment of viruses in treated population after a contact with environment (at rate ) and individuals of other compartments (at respective rates ). The third, the fourth and the fifth terms correspond to the update in viruses population due to the transition from infectious, quarantined and hospitalized compartments, respectively. The last term represents the disappearing of viruses by natural death (at rate ), by the death of the human host (at rate ), by disinfection measures applied by the host (at rate ), by the exchange of viruses with environment (at rate ) and other compartments (at rate ), and by the transition of the host from the treated compartment to the recovered compartment at rate .16
The first term to the right of the equality in equation (17) corresponds to the recruitment of viruses in recovered population after a contact with environment (at rate ) and individuals of other compartments (at respective rates ). The second term corresponds to the update in viruses population due to the transition from treated compartment. The last term represents the disappearing of viruses by natural death (at rate ), by the death of the human host (at rate ), by disinfection measures applied by the host (at rate ), by the exchange of viruses with environment (at rate ) and other compartments (at rate ), and by the transition of the host from the recovered compartment to the susceptible compartment at rate .17
The first term to the right of the equality in equation (18) corresponds to the recruitment of viruses in non-infectious dead population after a contact with environment (at rate ) and individuals of other compartments (at respective rates ). The second term corresponds to the update in viruses population due to the death of individuals belonging to susceptible, exposed and recovered compartments. The last term represents the disappearing of viruses by natural death (at rate ), by the burial of the dead host (at rate ), by disinfection measures applied on the dead host (at rate ), and by the exchange of viruses with environment (at rate ) and other compartments (at rate ).18
The first term to the right of the equality in equation (19) corresponds to the recruitment of viruses in infectious dead population after a contact with environment (at rate ) and individuals of other compartments (at respective rates ). The second and the third terms correspond to the update in viruses population due to the death of individuals belonging to infectious, quarantined, hospitalized and treated compartments. The last term represents the disappearing of viruses by natural death (at rate ), by the burial of the dead host (at rate ), by disinfection measures applied on the dead host (at rate ), and by the exchange of viruses with environment (at rate ) and other compartments (at rate ).19
The first term to the right of the equality in equation (20) corresponds to the release of virus in the environment by infectious, quarantined, hospitalized and treated populations. The second terms represents the recruitment of viruses in environment after a contact with individuals of each compartment (at respective rates ). The last term represents the disappearing of viruses by natural death (at rate ), by disinfection measures (at rate ) and by the exchange of viruses from the environment to human hosts (at rate ).20
The Monod5 type infection force is the product of the mass action factor , the adequate contact probability (the probability that viruses reach critical parts of the body like nose, mouth and eyes), the transfer rate and the susceptible body virus population size .
The parameters of the model (1 )–(20) are described in Table 1. Although we focus explicitly on microscopic and mesoscopic scales, there is also a macroscopic scale of the global human population
| 21 |
Hence, equation at the macroscopic scale can be derived easily from the equation at the mesoscopic scale. Since the variables of the model (1 )–(20 ) are densities per unit area, the effect of lock-down is evaluated by multiplying these densities by the effective area instead of the total area like in (21). As mentioned before, lock-down allows the disease to be managed independently in small subpopulations. As we will see in Theorem 3, lock-down accelerates the extinction of the disease.
Table 1.
Description of the parameters of the model (22)
| Parameter | Formula or range | Description | Unit |
|---|---|---|---|
 |
Density of human population belonging | ||
| To compartment i | |||
 |
Density of virus population belonging | ||
| To compartment i | |||
 |
Mass action factor | ||
 |
Semi-saturation constant | virus | |
| Probability of wearing a mask in | |||
| Probability of being in movement in | |||
 |
Maximal size of group of individual | ||
| Per unit area | |||
| Proportion of free viruses released from | |||
 |
Rate at which new free viruses are | ||
| Produced from | |||
| Transfer rate of viruses from | |||
| To the environment | |||
| Transfer rate of viruses from the | |||
| Environment to the | |||
| Transfer rate of viruses from to | |||
| Other compartments | |||
| Rate at which viruses enter inside susceptible body | |||
| And start their internal replication | |||
| Infection force of viruses on susceptible individuals | |||
 |
Natural death rate of viruses | ||
 |
Additional death rate of viruses due to disinfection | ||
 |
Natural death rate of humans | ||
| d |  |
Additional death rate of humans due to disease | |
 |
Reproduction rate of humans in | ||
 |
Horizontal immigration rate of humans in | ||
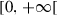 |
Transition rate from infected to infectious | ||
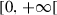 |
Transition rate from quarantined to hospitalized | ||
| q | 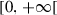 |
Reporting/screening rate of infectious | |
| p | 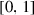 |
Probability of being asymptomatic infectious | |
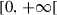 |
Transition rate from infectious to treated | ||
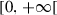 |
Transition rate from quarantined to treated | ||
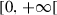 |
Transition rate from hospitalized to treated | ||
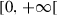 |
Transition rate from treated to recovered | ||
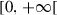 |
Transition rate from recovered to susceptible | ||
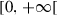 |
Burial rate of a non-infectious dead | ||
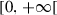 |
Burial rate of an infectious dead |
The model (1)–(20) can be written in the form
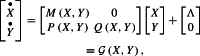 |
22 |
with M,Q Metzler and P having all its coefficients nonnegative.
Proposition 1
Let , , , , and . is an attractor of the invariant positive orthant with respect to the system (22).
Proposition 1 shows the validity of the model ( 1)–(20). It shows the boundedness of the population density () due to the social distancing. It also allows us to consider separately the microscopic dynamics (of viruses) and the macroscopic dynamics (of humans). Indeed, control strategies at the microscopic level concern the individual precautions to be applied (social distancing, mobility, disinfection of people and surfaces, mask wearing and treatment). At the macroscopic level, the global health policies are considered (social distancing, wearing mask, screening, rapid burying of infectious dead, isolation and treatment of infectious). Of course there are measures that act at both levels.
Equilibriums and asymptotic behaviors
Omitting the compartment of buried (B or ), we can address the issue of existence of equilibriums. We are particularly interested in the ’Disease Free Equilibrium’ () and other feasible ’Endemic Equilibrium’ (). It is clear that immigration in the infectious compartments with a constant positive rate makes impossible the existence of the DFE. It should be noted, however, that if horizontal immigration is proportional to the population, then a disease-free balance is still possible.
If the geographical area of study extends to the planet ( the model and the strategy of disease control are on a planet level) or a systematic control is applied at all the territorial frontiers (spatial isolation or lock-down). Of course, the latter possibility is less realistic than the former. Indeed, the concept of horizontal immigration is defined when there is a transition of material from one delimited geographical area to another delimited area. Therefore, if we consider the global population we will have only one area (global) and no horizontal immigration (ie ).
If then there is no horizontal recruitment and the only possibility of recruitment of new individuals is only from new births. That last consideration will be adopted here for simplicity.
Proposition 2
Assume that . Then the following statements hold.
-
(i)
The trivial null equilibrium always exists : ,
-
(ii)If , then the non-trivial disease-free equilibrium (DFE) exists :
-
(iii)If and there is an endemic equilibrium (EE) then where
the s are given as follows:
Let us consider the Jacobian matrix of (22) given by
with
Proposition 3
Assume that .
-
(i)
The null invariant set is locally asymptotically stable (LAS) if .
-
(ii)
The null equilibrium is globally asymptotically stable (GAS) if .
-
(iii)
The disease-free equilibrium is locally asymptotically stable (LAS) if and only if and is Metzler stable.
-
(iv)
If and then the disease-free equilibrium for the macroscopic model () is GAS.
Let denote the vector of flows due to infectious contacts between humans an viruses in the disease associated compartments (E, I, Q, H, T, , , , , , , , , , and ). Similarly, let denote the vector of flows in the disease associated compartments but which are not due to infectious contacts:
| 23 |
with given in 22).
If F and V are the respective Jacobian matrix of and evaluated at the DFE, then the basic reproduction number is given by the spectral radius of the next generation matrix (Van Den Driessche and Watmough method [78–80]). In this context, F is a matrix given such as , and otherwise. V is a matrix given such as , if , if , , if , if , if , if , if and if . Although the calculation of the inverse of V is nontrivial, we have the particular formula
| 24 |
The effective reproduction number can also be computed by multiplying by the proportion of susceptible individuals [70]. can be biologically interpreted in this context as the average number of new viruses generated by an introduced virus during its lifespan.
The infection force plays an important role on the disease spreading. Subsequently, regarding the expression of in Table 1, we can see that the use of mask and avoiding to touch the face is crucial to limit disease spreading. The control u can be viewed as the fraction of time the mask is well used. can vary with time depending on individual human habits. It is interesting to depict how the disease behaves if is a decreasing function of time (). We start by stating a useful result which is a particular case of very useful theorems in [36, 58, 76], about -limit sets of asymptotic autonomous systems.
Lemma 1
Let us consider a linear differential system
| 25 |
| 26 |
where A is a constant Metzler stable matrix, B is a constant Metzler matrix, C is a constant matrix and v is a positive numeric function of the time. Assume that the solution of (25)–( 26) is bounded and 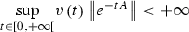 . Then . This will happen in particular if , where denotes the spectral radius of A.
. Then . This will happen in particular if , where denotes the spectral radius of A.
Instead of using the technical approaches in [36, 58, 76], Lemma 1 is proved here in a simple contextual manner in the appendix. The remaining results of the paper are original and so are their proofs. Although the latter combine fairly general results on dynamical systems, their implementation is non-trivial according to the structure of the model ( 1)–(20).
Theorem 1
If and then the DFE is GAS.
Theorem 1 gives us a first way to limit disease spreading.
Theorem 2
Assume that and . Let D denotes a diagonal matrix such that is the sum of absolute values of only negative terms in the expression of , , and . Then the DFE is GAS if
| 27 |
Theorem 2 provides a sufficient condition that ensures the stability of the disease free equilibrium. Moreover, it shows that avoiding to touch the face and the frequency of wearing mask by susceptible population ( via ), the mobility (m via different contact rate among people , and with the environment ), the disinfection (washing of hands included in) by susceptible population () and social distancing (reducing ) are crucial parameters in order to stop the spreading of the disease. The biological interpretation of is the following. During its lifespan a virus infects a susceptible individual at the adequate rate . Once the susceptible individual is infected he becomes infectious with a probability and will produce , , and viruses during its respective stays in compartments of infectious, quarantined, hospitalized and treated.
By setting
we can see using the boundedness of , that . Hence, Theorem 2 also permits us to evaluate given , u and m the minimum frequency at which the disinfection should occur. For example, if probably due to the management of death persons, then the condition is satisfied when
| 28 |
Notice that by disinfection we mean a global action on the body, so it would be necessary to evaluate the specific contribution of hands washing.
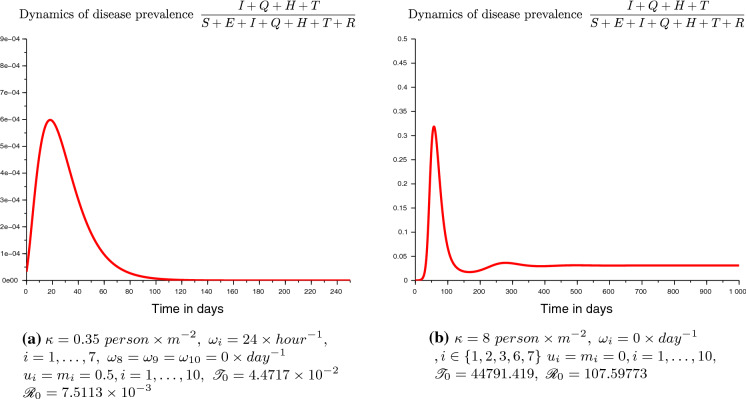
Figure 2 is an illustration of the asymptotic behavior of cumulative infectious individuals depending on the relative position of with respect to 1. The smaller is, the smaller is the amplitude of the peak and the earlier it occurs. If the mask is never adopted then the disease prevalence can pass above and stabilize around .
Fig. 2.
Asymptotic behavior of infectious dynamics depending on
We end the section with a theorem giving an upper bound to the time of extinction of the disease. By the time of extinction we mean the first time where there is neither infectious and nor virus. That is there is less than one infectious and less than one virus.
Theorem 3
Let , and denotes the effective area of the spatial study zone in (ie the area of the zone each individual is allowed to move in during the lock-down). Assume that , . Then
| 29 |
where , is the probability to die during the stay in infected or infectious compartments (E, I, Q, H, T) and the s denote the average times spent in those compartments. Moreover, if then
| 30 |
Furthermore, if , then
| 31 |
and the respective first times and such that, respectively, and satisfy
As we can see in the expressions of and that the higher , , , and are, the longer the time of disease extinction is. If the lock-down is applied, then the effective global population to consider is which represents the number of living persons admitted in a given closed area. Hence, the lock-down level can be expressed by the ratio , where denotes the real area of the physical study zone (town, district, department, region, country, continent, or the whole world).
A focus on Cameroonian context
Early estimation of the parameters of the disease dynamics
This section aims to determine values of the parameters of the model ( 1)–(20) in such a way that its predicted dynamics is close to the Corona’s observed data in Cameroon, from March 2 to June 7, 2020. That is estimation of parameters also known in the literature as fitting the model. We used the daily data available on the website https://www.data.gouv.fr/fr/datasets/coronavirus-covid19-evolution-par-pays-et-dans-le-monde-maj-quotidienne/www.data.gouv.fr for our estimates. We also used the situation reports on Covid-19 in Cameroon available on the website https://www.humanitarianresponse.info/en/operations/cameroon/health/documentshttps://www.humanitarianresponse.info. It corresponds to the beginning of the epidemic, when the natural dynamics of the disease were less complex to predict since control measures were simpler and secondary approaches (e.g. periodic containment and vaccine) had not yet taken place. The data consist of daily counts of infections, recoveries, deaths, quarantines and hospitalizations. Following the reference [52, 53], we set , , , and to be, respectively, the cumulative numbers of reported infectious cases, of reported quarantined, of reported hospitalized (active cases), of reported recovery and of reported dead at time , where denotes the date of the first introduction of an infectious to be evaluated. Note that these values will be divided by the cumulative area of populated areas () to match the model ( 1–(20) for which variables are expressed in density per unit area. There are several approaches for the estimation of the parameters of a model. A first method is to discretize the differential equation model with respect to available time series and to fit unknown parameters by reducing the distance between the numerical solution and observed time series [13]. Another method consists of empirical estimating function linking the state of the system with the time using times series and after in estimation through the considered model [12, 24, 54, 65].
Here we use a semi-empirical method using statistical regressions based on empirical models according to data (the upcoming model ( 40) for example) and key relations derived from the main model (1)–(20). In the global population (as defined in (21)), those relations are the following :
| 32 |
| 33 |
| 34 |
| 35 |
| 36 |
According to certain cultural practices in Cameroon6 (See [40]), we will assume that the average time that elapses between the death of an individual not identified as infectious (i.e., he or she dies without being quarantined or hospitalized) and his or her burial is 3 days (), while burial takes place within 24 hours of the death of an individual considered infectious (). According to the literature, we will assume that the transition rate from the infected compartment (E) to the infectious compartment (I) is , the transition rates from the infectious compartments (I,Q,H) to the treated compartment (T) are and the transition rate from the treated compartment (T) to the recovered/immune compartment (R) is [52, 53]. It is not clearly established in the literature that there is a real immunity, but according to [42], we will suppose that . The recommended social distancing parameter in Cameroon is but we will estimate the real value of according to available data and the model (1)–( 20).
The data on CRQ, CRQ being available in situation reports only for the 30 firsts days contrarily to the data on CRI, CRD and CRR which cover the whole period of study. Hence we divide the estimation in two steps :
- Step 1: Use of data from March 2 to April 1, 2020. Summing equations (32), (33) and (34), we have
being the greater time where . The mathematical expectation approximated by the empirical average is used here to contain uncertainties causing variation on . Such as statistical approach could also permit to evaluate a confidence interval assuming adequate hypotheses on the distribution of the noises. Commonly, large numbers law and central limit theorem are used for large dataset [48]. Due to their relatively rapid growth, we suppose as in the references [52, 53] that and can be approximated through log-linear models as follows37 38 39
The coefficients , , , , , were estimated through log-linear regression with the software R. Among the above coefficient only was found not statistically different from zero during the regression analysis of variance. The adopted empirical models were highly significant with all the adjusted s between and , and the probability-values (commonly called p-values) between and . A negative means that the first infectious case occurs probably before the origin date of the study. The same holds for and . Since CRI was given by (32) it was easy to determine the expression of , in particular . The statistical approach we adopted is justified by the uncertainties. , p, q, d and other estimated values are available in Table 2.
Table 2.
Estimation and baseline values of parameters of the model (22)
| Parameter | Value | Unit | Source |
|---|---|---|---|
| Assumed | |||
| virus | [42] | ||
| 0 | Percentage | Assumed | |
| 1 | Percentage | Assumed | |
| https://www.populationdata.net/pays/cameroun/www.populationdata.net | |||
| Percentage | Assumed | ||
| 1 | Percentage | Assumed | |
| [42] | |||
| [42] | |||
| 0 | Assumed | ||
| [42] | |||
| 0 | Assumed | ||
| [42] | |||
| 0 | Assumed | ||
| 1 | [42] | ||
| [17] | |||
| 0 | Assumed | ||
| https://www.populationdata.net/pays/cameroun/www.populationdata.net | |||
| d | Fitted | ||
| https://www.populationdata.net/pays/cameroun/www.populationdata.net | |||
| 0 | Assumed | ||
| [53] | |||
| Fitted | |||
| q | Fitted | ||
| p | percentage | Fitted | |
| [53] | |||
| [53] | |||
| [53] | |||
| [53] | |||
| [42] | |||
| Assumed | |||
| 1 | Assumed | ||
| Fitted | |||
| Fitted | |||
| 7.987228 | https://www.populationdata.net/pays/cameroun/www.populationdata.net | ||
| Fitted | |||
| Fitted | |||
| 0 | Assumed | ||
| 0 | Assumed | ||
| 0 | Assumed | ||
| Fitted | |||
| Assumed | |||
| 0 | Assumed |
It appeared more difficult to explicitly estimate , , , , , , , , , and using available data. Regarding public transport conditions in Cameroon the maximum value of can be fixed to . According to the density of population per unit of surface7 the minimum value of is fixed to . Without social distancing at the disease outbreak, we have and the infection term is proportional to the global population (say ) due to the mass action. S being bounded from above by according to the model, we have . Notice that and are non decreasing functions of . Thus, we can simplify by assuming that is definitely a constant given by . It is possible to estimate and (global population of alive or dead except buried individuals) similarly to and . Under the hypothesis of homogeneity of the population the values of S, E and I can be estimated by multiplying the respective proportions in the global population by the threshold (for example ). The term can be estimated using the relations
| 47 |
| 48 |
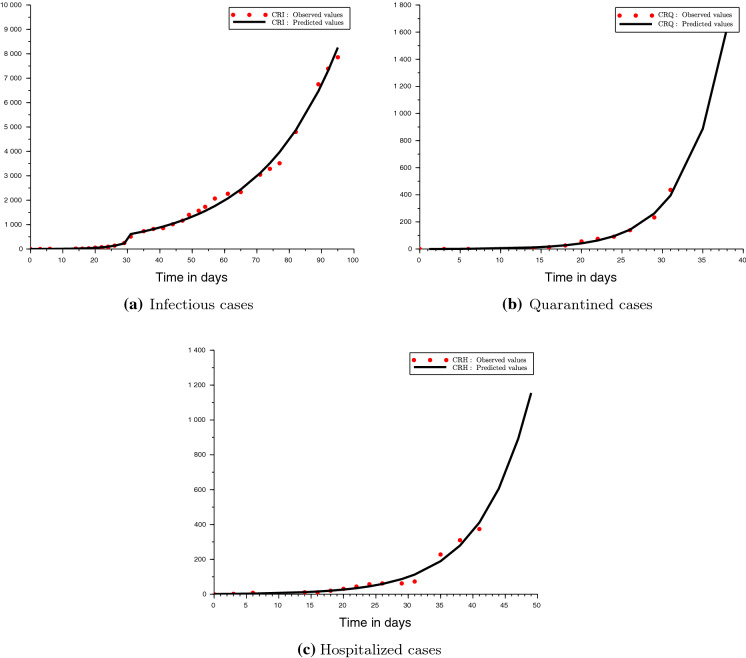
Figure 3 shows the cumulative reported infectious cases in Cameroon from the 2nd of March to the 7th of June 2020. When studying the dynamics of cumulative reported infectious cases we noticed a change approximatively around the thirtieth days. Indeed, the growth of the cumulative number of reported infectious appeared to be higher during the first thirty days. This is likely due to the delay in the implementation of the barrier measures (which were announced by the Cameroonian government only as of March 20, 2020) and the delay in their effects on the disease dynamics.8 Thus, to capture this apparent change, we split the empirical modeling into two periods: those of the first 30 days and those of the days after. This splitting also allowed for a better fit of the model. Parameters concerning the disease outbreak (starting time, initial values of state variables) have been estimated using the first dataset. The other parameters have been fitted using the whole sample. The estimates are given in Table 2.
Fig. 3.
Cumulative reported cases from the 2nd of March to the 07th of June 2020
According to the values in Table 2, relation (28 ) and Theorem 2, if people never wear a mask, no social distancing is applied and only susceptible individuals disinfect themselves, then the rate of complete disinfection () should not be less than (ie about once every 72 minutes) in order to have and . If at least the social distancing of is respected then the lower bound value of drops to (ie about once every 8 hours) in order to have and . Thus, a complementary application of all mitigation measures is mandatory.
Effects of controls on disease dynamics
This section aims at evaluating first the sensitivity of different control parameters with respect to the thresholds and . The second fold of this section is to survey the effect of some control parameters on the asymptotic behavior of the disease dynamics. Following Theorem 1, we define the convergence index
| 49 |
is an indicator of the rate of the potential convergence of the disease dynamics toward an equilibrium. Indeed, if then there is an exponential convergence to the disease free equilibrium. If then there is an endemicity of the disease, in particular if is near to zero then we are in the neighborhood of an endemic equilibrium. is an estimation of the key parameter which permits according to Theorem 3, to bound the average time the disease is expected to disappear.
There are several methods for sensitivity analysis in the literature (see [18, 56] for example). The normalized forward sensitivity index (of variable u with respect to parameter p) defined in [18] provides an idea on effect of a local perturbations around a given situation in terms of the values of the parameter p. Paper [56] presents several alternative methods of assessing the global effect of variation on coefficients: Pearson correlation coefficient (CC), Spearman rank correlation coefficient (RCC), partial correlation coefficient (PCC), standardized correlation coefficient (SCC), standardized rank correlation coefficient (SRCC), partial rank correlation coefficient (PRCC) and Extended Fourier amplitude sensitivity test (eFAST). The authors in [56] recommended PRCC and eFAST as robust sensitivity indexes to be used, respectively, in cases of monotonic and non-monotonic sensitivities. These indexes are based on samples obtained through latin hyper cube sampling, Monte-Carlo sampling or any other appropriate experimental design [11, 20, 35]. Hence, there are statistics and confidence intervals or region can be provided in order to decide on their significance.
We adopt the PRCC with a three levels9 (, 0, ) fractional experimental design with the factors , q, , and , . Such an experimental design allows us to get a statistical approximation of optimal parameters based on a quadratic model obtained by regression. Ideally, strategies should be specific to different compartments. However, since it is difficult to know the status of people, it is reasonable to apply the same strategies for similar” compartments. Thus, we reduce the factors by considering the classes , , and . We also assume that . Finally, we have 10 factors with two responses and . We consider a fractional experimental design with a sample size 81. The experimental matrix is computed using Box calculus for the aliases with second order interactions. Table 3 provides us with the codification of factors values that have been arbitrarily chosen but appear realistic.
Table 3.
Codification of factors values
| Parameter | Level | Level 0 | Level |
|---|---|---|---|
| 1 | 4.5 | 8 | |
| q | 0 | 24 | 48 |
| 0 | |||
| 0 | 1 | ||
| 0 | 24 | 48 |
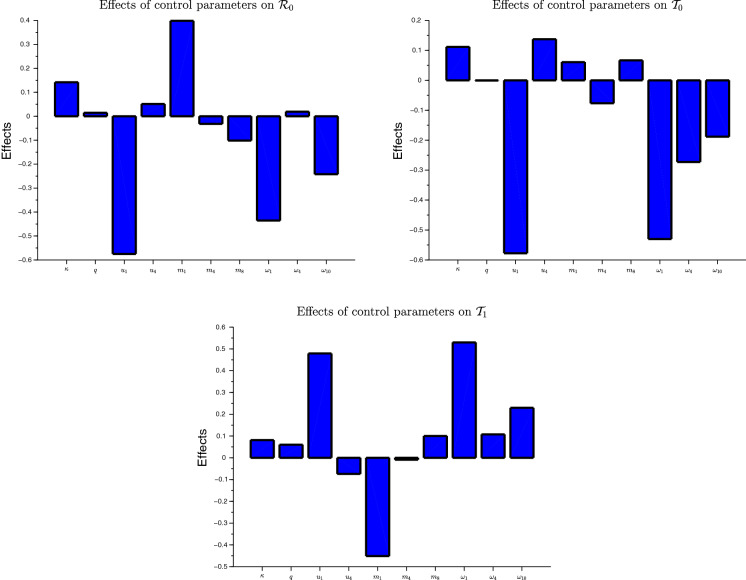
Figure 4 shows graphically the effects of control parameters on , and . , , and are in decreasing order the more sensitive parameters with respect to . Thus, an efficient control strategy should prioritize the usage of mask, the reduction of mobility and the disinfection in class compartment, and the disinfection of the environment. , , and are in decreasing order the more sensitive parameters with respect to . Thus, an efficient control strategy based on should prioritize the usage of mask in class , and disinfection in classes , and the environment. , , , and are in decreasing order the more sensitive parameters with respect to . Thus, to accelerate the convergence toward the disease free equilibrium the fighting policies should prioritize the reduction of mobility in class , the frequent usage of mask, the disinfection of people in class and the disinfection of the environment.
Fig. 4.
Effects of control parameters on , and
Globally, the usage of mask in class compartment is the most sensitive control followed by the reduction of mobility and the disinfecting in class , and the disinfection of the environment. As we can observe, the effects of the social distancing and the screening, the effect of using masks in class , and the mobility in classes and are not very significant. However, as we will observe in Sect. 4, those controls have influence on the economical point of view.
An optimal control analysis
Design of the control strategy
There are several works tackling the issue of optimality of fighting strategies against Covid-19 [19, 46, 47, 61, 68, 72]. The objective function to optimize is commonly expressed in the literature by the sum of a positive linear combination of disease states and a positive quadratic combination of control parameters. Such a formulation is a penalization approach to solve the multiple objective problem which is to reduce both the population size of disease compartments and the control energy. The quadratic dependence of the objective functional with respect to control parameters makes easier the optimization procedure since the problem has better chances to be convex [4, 49]. Unfortunately, the choice of penalization coefficients is very often not justified and there is no specific interpretation. Only few papers tried a practical optimization in terms of social and the economical impacts of the pandemic [47, 81]. We follow the references [47, 81] to define a realistic new economical objective function since the main issue of the fight against Covid-19 pandemic seems to eradicate it with limited existing resources. We highlight the contradictory costs, respectively, due to disease spreading and disease containment strategies.
The control parameters we consider here are mainly the limit density of population , the probability of mobility m, the proportion of time spent on wearing a mask u, the disinfection rate and the reporting rate of infectious (through screening test especially) q. Indeed, those controls appear explicitly in the expression of the threshold which will play a similar role to the basic reproduction number. Since the threshold appears important for the asymptotic behavior of the disease, it could be interesting to minimize an analog to the effective reproduction number : . Unfortunately, the expression of is very complex and it is not differentiable with respect to all its parameters. This irregularity involves an additional complexity in the optimization procedure. Thus, we will consider the infection rate instead of . takes into consideration the dynamics of viruses.
The medical monitoring of a patient during his infectious period has an economical cost c that can be evaluated depending on the time spent before recovery and on the expenses during each stay in a disease compartment. The expression of c should depend on , the daily revenue of a person in health which will be lost due to the disease. The application of each control involves an economical cost proportional to the size of the population and to the time. We will note the cost per unit of time and per individual for u and for . Reducing m and involves a relative reduction in economical activities and subsequently a reduction of gross domestic product assumed proportional to ( in 2018.10) A screening test has a cost which is not clearly defined according to the media. We will assume that in average. Since it is difficult to really estimate unreported infectious, it seems better to define general measures to be applied by everyone independently of the status. Thus, we will assume here that , , , , , , . Let . We consider the following functional cost per area :
| 50 |
where denotes the usual average density of population per unit of surface, and is the rate of hands washing corresponding to spending the half of time for disinfection. The negative term in the expression of Z represents the reduction of economic losses when people are free to move around in their various economic activities. A negative value of the cost means that globally the losses due to Covid-19 are not greater than the production of wealth.
We assume that an efficient hands washing takes about 30s. Thus, if the time spent on hands washing is half of the time between two consecutive washes. On the other hand, when tends to then the proportion of time spent to wash hands is 1. A function of displaying the behavior explained above is with . We suppose that the disinfection costs is in average. We also assume that after using a mask for a given time (4 h) it is systematically changed for a new mask having a certain unitary cost (). Hence, .
Let and denote, respectively, the time spent by an individual in the compartment and the cost generated by unit of time. According to probabilistic properties of Poisson processes [15, 25, 44], we have
| 51 |
| 52 |
| 53 |
| 54 |
| 55 |
One can associate a cost per person which is related to his burial ceremony. The probability to die during the stay in disease compartments I, Q and H is given by
| 56 |
Hence,
| 57 |
Table 4 summarizes the different unit costs we mentioned above.
Table 4.
Baseline values of elementary costs
| Parameter | Value | Unit | Source |
|---|---|---|---|
| 0 | Assumed | ||
| 2.83 | https://fr.numbeo.com/prix-de-l%27immobilier/pays/Camerounwww.numbeo.com | ||
| 500 | Assumed | ||
| 1600 | Assumed | ||
| 3.9 | http://www.journaldunet.com/business/salaire/cameroun/pays-cmrwww.journaldunet.com | ||
| 145 | https://blogs.mediapart.fr/edition/transparence-dans-les-politiques-du-medicament/article/140320/covid-19-la-transparence-sur-le-prix-des-diagnosticswww.mediapart.fr | ||
| 6 | Assumed | ||
| Assumed | |||
| g | 4.183562 | https://www.populationdata.net/pays/cameroun/www.populationdata.net |
Let us consider the Hamiltonian
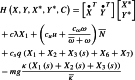 |
58 |
where the adjoint state satisfies
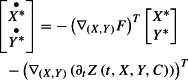 |
59 |
and
| 60 |
The optimal control will be given by the optimality condition
| 61 |
Notice that is projected into the admissible set where (persons are tested in average every 30 minutes), , , . The existence of a unique optimal strategy is guaranteed by the fact that the strict convexity of the Hamiltonian with respect to C and the regularity of the optimal feedback strategy . For more details on the determination of optimal control we refer to the books [4, 49] and references therein.
Theorem 4
There is a unique piecewise continuous optimal control for the model (1)–(20 ) characterized by Algorithm 1–.
Numerical simulations and discussion
In order to numerically determine the optimal control strategy, we implement the forward-backward sweep method described in Chapter 3, page 101 of [4]. It is an iterative approach that consists of replacing the feedback by a guess value first, solving the forward state problem, solving the backward adjoint problem and then updating the feedback using the gradient direction with a step length obtained by the golden section method. The algorithm stops when the updates of the control does not significantly change its values according to a chosen threshold. That method is similar to the one given into the Chapter 3 of [49], but it permits to better control the convergence. Notice that one could also envisage a method which minimizes the distance between the final condition of the adjoint problem obtained for a guess initial condition and the reference final condition. That method could be a multidimensional variant of the secant algorithm [26, 39].
We found after several simulations that, if we globally consider the economic losses and gains then, no specific control effort is needed additionally to take care of hospitalized patients and putting in quarantine of infectious reported individuals as it is already done. Probably that is a consequence of the high recovery rate of patients and the relatively small death probability. However, since the logistic resources for quarantine and hospitalization are limited, the economical losses in terms of gross domestic product (due to social distancing, reduction of mobility and lock-down) can be penalized in the cost functional Z. That is done in the rest of the section.
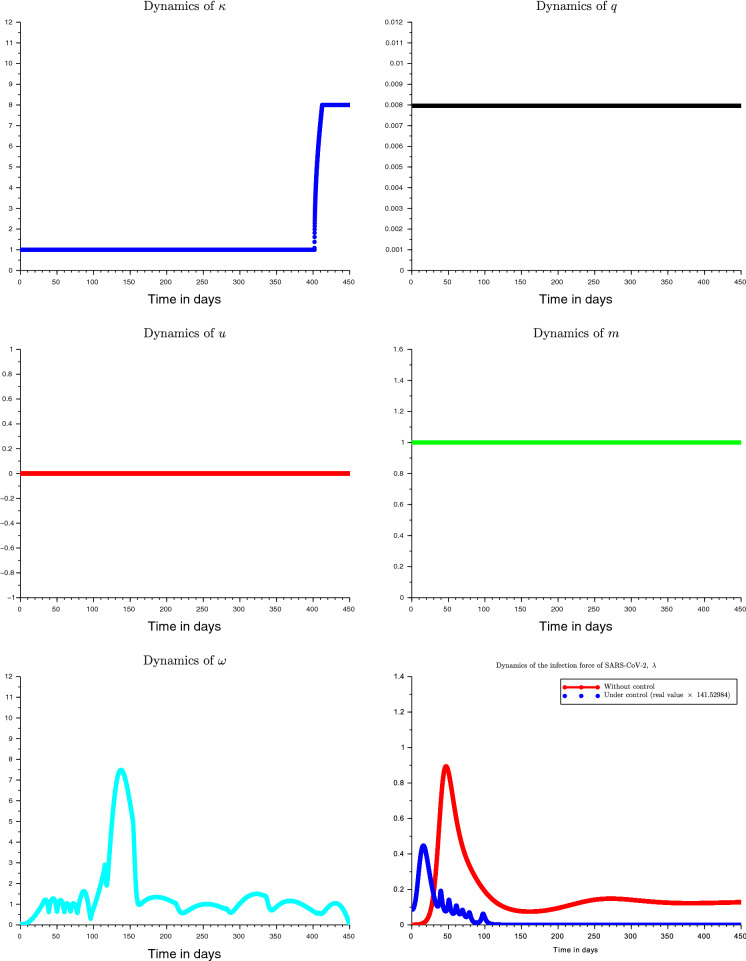
Figure 5 is an illustration of the optimal control strategy against Covid-19 and the evolution of the infection force . We can observe that social distancing and disinfection frequency are the main elements of the optimal control strategy. The frequent oscillations of can be explained by the sensitivity of the controlled system behavior with respect to . Social distancing permits to have no restriction on mobility. The use of mask is useful but not necessary when social distancing and regular disinfection are respected. Notice that if the mask is misused it is useless, and it can promote other respiratory complications. As the sensitivity analysis showed the screening has no significant effect on disease behavior and it is economically better to keep q at its minimal value corresponding to self decision to be tested or the hospitalization of severe disease cases.
Fig. 5.
Optimal control dynamics of Covid-19 prevalence
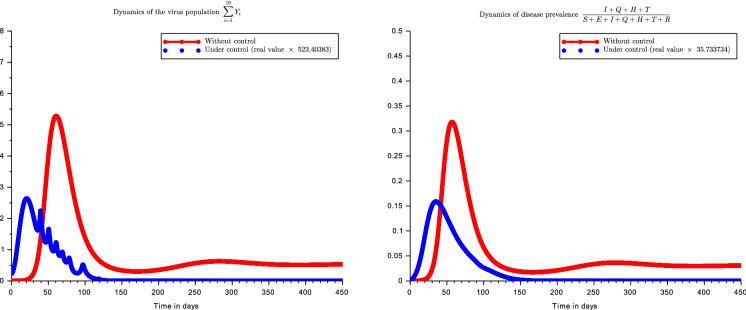
Figure 6 shows the progression of the SARS-CoV-2 population (in terms of number of viruses per ) and the disease prevalence either the optimal control is applied or not. Relative prevalence of disease is preferred over absolute prevalence because it is more appropriate for scaling up. The peak of the disease occurs earlier and with smaller values under optimal control policy. We also observe that without control there is a possibility to observe several peaks of the disease. Without control, the peak of the disease ( prevalence) occurs after 57 days (about 8.5 weeks) while under control it occurs after 26.37 days (about 4 weeks) with a weaker magnitude ( prevalence). With the initial compartmental population sizes given in Table 2 and under the optimal control strategy, the disease extinction in the human population is reached after while it occurs in the virus population after . If we consider the maximal disease prevalence and the virus population size () is equal to its upper bound given in Proposition 1, then the disease extinction in the human population is reached after . Similarly, the extinction in virus population is reached after . Thus, the sooner the control measures are taken, the sooner the disease can disappear. The dependence of the disease extinction time with respect to the surface clearly highlights the importance of lock-down. As we can observe, the extinction can be very slower in the virus population than in the human population. The cost of the optimal strategy has been computed for 180 days corresponding to half of the year. It has been evaluated at which corresponds on average to .
Fig. 6.
Controlled dynamics of Covid-19 prevalence
Conclusion
This work is concerned with the mathematical modeling of the severe acute respiratory corona virus 2. According to governmental data and World Health Organization, the corona virus made several millions of dead in the world. It spreads very rapidly and affects not only the public health sector, but also the global economy. The transmission of the disease can occur through direct contact with an infectious individual or through indirect contacts via the environment. The high complexity of the disease spreading suggested numerous modeling activities. Indeed, through a mathematical model it is possible to rigorously study fighting policies against corona. Hence, the goals we aimed to achieve were to propose a realistic model for the Covid-19 dynamics, to estimate the parameters of the proposed model according to the available real data, to study asymptotic behaviors depending on some featured control parameters related to WHO and governmental recommendations, and to design control strategies that are optimal with regards to socio-economical constraints.
We have constructed a two scale compartmental model with 20 classes corresponding to 10 human population states (macroscopic scale) and 10 viruses locations (microscopic scale). Indeed, we considered Susceptible , Infected , Infectious , Quarantined , Hospitalized , Treated , Recovered , Non-Infectious dead , Infectious dead , Buried . Each individual was assumed to have an external viral load on his body while there were free viruses in the environment. The model has been labeled as described graphically in Fig. 1. To better access the effects of social distancing, the units of state variables have been taken in terms of person per unit area and virus per unit of surface. The parameters of the model have been successfully fitted using a Cameroonian dataset and a semi-empiric procedure. Additionally to the quantitative study of the system, we carried out a qualitative analysis of the model.
The existence of equilibriums has been studied. Contrarily to the endemic equilibrium, the disease free equilibrium (DFE) exists unconditionally. The DFE is globally asymptotically stable if a threshold is less or equal to one. We also provided a formula for the basic reproduction number which has a biological interpretation regarding the model: the average number of new viruses generated by an introduced virus during its lifespan. has a similar biological interpretation. A convergence index has been defined. Under an exponential convergence hypothesis, the times of disease extinction respectively in human population () and virus population () are determined. A sensitivity analysis of , and have been done using the partial rank correlation coefficient (PRCC). We found that the sensitive parameters are in descending order the proportion of time of wearing mask, the proportion of time spent on disinfecting people and the environment, and the mobility probability. Through a concept of specific area , the importance of lock-down is highlighted. Indeed, the times of extinction are proportional to knowing that is the lock-down level. Since the disease and the application of the different control strategies generate economical costs, an optimal control analysis has been already carried out.
In order to guarantee effectiveness of control strategies and to reduce the expenses generated by Covid-19, we defined a functional cost to be minimized. The existence and the uniqueness of the optimal control is established and its characterization is given. By the sweep decent method the optimal strategies are computed according to some practical constraints materialized by an admissible control set. We found that if one globally considers the economical losses and gains, then no specific control effort is needed additionally to take care of hospitalized patients and putting in quarantine of infectious reported individuals as it is already done. However, since the logistic resources for quarantine and hospitalization are limited, the economical losses in terms of gross domestic product (due to social distancing, reduction of mobility and lock-down) can be penalized in the functional cost. That has been done and we computed new optimal strategies.
According to the simulations, we observed that social distancing and disinfection frequency are the main elements of the optimal control strategy. Social distancing permits to have no restriction on mobility. The use of mask is useful but not necessary when social distancing and regular disinfection are respected. Screening has no significant effect on disease behavior and it is economically better to keep q at its minimal value corresponding to self decision to be tested or the hospitalization of severe disease cases. Under the optimal control policy, the peak of the disease occurs earlier and with smaller values.
The current work has several perspectives. The first one is to take into consideration the effects of the available vaccine against Covid-19 both in the asymptotic behavior analysis and in the optimization of the control strategy. Another aspect is to consider the spatial heterogeneity in terms of available logistic resources, population densities, attractiveness of specific places at given periods of a day, cultural and religious habits, and others significant factors. An ongoing work is trying to tackle the problem regarding those aspects. The model can also be extended using the promising theory of fractional calculus [1, 2, 5, 6, 59, 60, 64].
Acknowledgements
The authors would like to thank the anonymous editors and reviewers for their comments, which considerably improved the quality of the work.
Proofs of different results
Proof
(Proof of Proposition 1 )
Assume that the initial condition is taken in . Using Cauchy=-Lipschitz Theorem there exists a maximal solution of the system (22) . Assume that the solution is defined and remains nonnegative on a set . Then, on , N satisfies
| 62 |
Thus, the orbit of N is clearly converges to the set . , and satisfy respectively
| 63 |
| 64 |
| 65 |
Hence, and the orbits of , converge, respectively, to the sets and . On the other hand,
| 66 |
Looking carefully the system (1)–(20), we can see that , (respectively, ) is nonnegative when (respectively, ). This proves the positivity of the solution which is finally global since it is bounded by the attractiveness of .
Proof
(Proof of Proposition 2)
-
(i)
Regarding the form of the model (22), it is plain that it admits the equilibrium given by .
-
(ii)
Again, regarding the form of the model (22) the DFE exists if and only if and . Indeed, at the equilibrium . So it is necessary to have .
-
(iii)Once more, regarding the form of the model (22) the EE exists only if and
Solving the last equation leads to the expression of given above. The linear relation come from matrix M.
Proof
(Proof of Proposition 3)
-
(i)
Looking at the expression of J in , we can see that and both matrices and have all their eigenvalues negative except which is null (the compartment of buried individuals is a sink). This shows that the set is locally asymptotically stable (LAS) if .
-
(ii)If then it suffices to look at the equation of to get that the null equilibrium is GAS. Indeed,
Since the s are nonnegative, if then converges to 0 and necessarily X and Y converge to zero by construction of the model. -
(iii)
From other equilibrium than the null equilibrium is unstable if . So, it is necessary to have . The disease free equilibrium is locally asymptotically stable (LAS) if J is Metzler stable. That is the case if , and are all Metzler stable (see Proposition 3.1 in [41]). and are unconditionally Metzler stable. So it remains the stability of the matrix .
-
(iv)
Assume that and . Due to the linear form of Eqs. ( 2)–(7), ( 9) we can easily see that tends to zero. Hence, regarding equations ( 1) and (8) we can check that tends to while tends to .
Proof
(Proof of Lemma 1) The solution of (25)–( 26) is given by
| 67 |
| 68 |
Let denote the stability modulus of the matrix A. We have
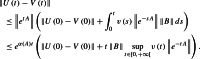 |
69 |
The results follows.
Proof
(Proof of Theorem 1) From Proposition 3, if and then the DFE is GAS. Using Lemma 1 the result is immediate.
Proof
(Proof of Theorem 2) The proof is based on the quasilinear form of the model (22). Indeed, the model 22) can be rewritten as
| 70 |
where , , , , , . The model has an almost triangular form and is Metzler with a negative diagonal. The matrix is Metzler stable by its particular form ( is a negative eigenvalue and the complementary diagonal block is triangular and Metzler stable). The matrix Q is Metzler and stable since its transpose is strictly diagonal dominant. Using Proposition 3.1 in [41], the stability is ensured if is Metzler stable. We have , and otherwise. Hence, and otherwise. G is therefore a Metzler. The stability of G is equivalent to the one of the sub-matrix due to the particular form of G. Again, using Proposition 3.1 in [41], the stability is ensured if
| 71 |
We have
| 72 |
Thus, the stability holds if
| 73 |
Using the boundedness of and , we have and we get the sufficient condition . Since and , the stability holds if .
Proof
(Proof of Theorem 3) Let , and assume that , . From the model (1)–(20 ) we have according to probabilistic properties of Poisson processes [15, 25, 44],
| 74 |
Indeed, the real phenomenon is a tuple of Poisson processes which jumps with rates given by different transition rates. The average time between two consecutive jumps is the inverse of the jumping rate and almost surely only one process in the tuple jumps at a given time. Hence, the average time spent by an individual from his entry in the compartment E to his exit from the compartment T is the sum of average times he spent in of each the compartment E, I, Q, H and T respectively. If then using the resolvent operator we have ,
| 75 |
| 76 |
| 77 |
The last inequality comes from the fact that for and . Since , , we have
| 78 |
Let and . We have
| 79 |
Again, using the Gronwall’s Lemma we have
| 80 |
Hence, the respective first times and such that, respectively, and satisfy
| 81 |
and
| 82 |
Proof
(Proof of Theorem 4) The existence of the optimal control is guaranteed by the boundedness of the solution of (1)–(20) and subsequently, the boundedness of the functional cost Z which is continuously differentiable with respect to its parameters. The rest of the proof is essentially based on the study of the gradient of the Hamiltonian. Indeed, the minimization consists in moving according to the opposite direction of the gradient of the Hamiltonian while it is possible and necessary. Precisely, when the gradient is the null vector then a singular point is reached. If the gradient is not zero but it is not possible to move again, then the optimum is reached at the boundary of the eligible region.11 We have
| 83 |
| 84 |
| 85 |
| 86 |
| 87 |
| 88 |
If the optimal control exists then Algorithm 1– describes it such as a piecewise continuous feedback which is locally Lipschitz with respect to the state variable and the adjoint state variable. Thus, by the Cauchy–Lipschitz Theorem the optimal control is unique.
Computation of the optimal control
Data Availability Statement
The datasets generated and/or analyzed during the current study are available in the websites https://www.data.gouv.fr/fr/datasets/coronavirus-covid19-evolution-par-pays-et-dans-le-monde-maj-quotidienne/www.data.gouv.fr and https://www.humanitarianresponse.info/en/operations/cameroon/health/documentshttps://www.humanitarianresponse.info.
Declaration
Conflict of interest
The authors declare that they have no conflict of interest.
Footnotes
https://www.who.int/emergencies/diseases/novel-coronavirus-2019, https://www.who.int/emergencies/diseases/novel-coronavirus-2019.
See https://medicalaid.org/coronavirus-what-you-need-to-know/?gclid=CjwKCAjw26H3BRB2EiwAy32zhaqJLCeU-KplWm3AoMmsgUuDNRssM9pChnoM_KPDhJ4K6NawLSPfexoCreUQAvD_BwE , https://medicalaid.org.
See https://www.lassurance-obseques.fr/deuil-afrique-rituels/, https://www.lassurance-obseques.fr/deuil-afrique-rituels/ and https://www.obseques-infos.com/actualites/23264-le-deuil-au-cameroun, https://www.obseques-infos.com/actualites/23264-le-deuil-au-cameroun.
See the book [36] for more details.
See https://www.lassurance-obseques.fr/deuil-afrique-rituels/, https://www.lassurance-obseques.fr/deuil-afrique-rituels/ and https://www.obseques-infos.com/actualites/23264-le-deuil-au-cameroun, https://www.obseques-infos.com/actualites/23264-le-deuil-au-cameroun.
https://www.lemonde.fr/afrique/article/2020/06/04/coronavirus-au-cameroun-la-gestion-de-la-pandemie-severement-critiquee_6041729_3212.html, https://www.lemonde.fr/afrique/.
See the book [4] for more details.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Ahmad S, Ullah A, Al-Mdallal QM, Khan H, Shah K, Khan A. Fractional order mathematical modeling of covid-19 transmission. Chaos Solitons Fractals. 2020;139:112256. doi: 10.1016/j.chaos.2020.110256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Ahmad S, Ullah A, Shah K, Salahshour S, Ahmadian A, Ciano T. Fuzzy fractional-order model of the novel coronavirus. Adv. Differ. Equ. 2020;2020(1):1–17. doi: 10.1186/s13662-020-02934-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Alberti T, Faranda D. On the uncertainty of real-time predictions of epidemic growths: a Covid-19 case study for china and Italy. Commun. Nonlinear Sci. Numer. Simul. 2020;90:105372. doi: 10.1016/j.cnsns.2020.105372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Anita S, Capasso V, Arnautu V. An Introduction to Optimal Control Problems in Life Sciences and Economics: From Mathematical Models to Numerical Simulation with MATLAB. Berlin: Springer; 2011. [Google Scholar]
- 5.Arqub OA. Computational algorithm for solving singular Fredholm time-fractional partial integrodifferential equations with error estimates. J. Appl. Math. Comput. 2019;59(1):227–243. doi: 10.1007/s12190-018-1176-x. [DOI] [Google Scholar]
- 6.Arqub OA, Rashaideh H. The rkhs method for numerical treatment for integrodifferential algebraic systems of temporal two-point bvps. Neural Comput. Appl. 2018;30(8):2595–2606. doi: 10.1007/s00521-017-2845-7. [DOI] [Google Scholar]
- 7.Auger P, Magal P, Ruan S. Structured Population Models in Biology and Epidemiology. Berlin: Springer; 2008. [Google Scholar]
- 8.Batista, M.: Estimation of the final size of the second phase of Coronavirus epidemic by the logistic model. MedRxiv (2020)
- 9.Bekiros S, Kouloumpou D. SBDiEM: a new mathematical model of infectious disease dynamics. Chaos Solitons Fractals. 2020;136:109828. doi: 10.1016/j.chaos.2020.109828. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Belgaid Y, Helal M, Venturino E. Analysis of a model for Coronavirus spread. Mathematics. 2020;8(5):820. doi: 10.3390/math8050820. [DOI] [Google Scholar]
- 11.Berger PD, Maurer RE, Celli GB. Experimental Design: With Application in Management, Engineering, and the Sciences. Berlin: Springer; 2017. [Google Scholar]
- 12.Bowong S, Kurths J. Modeling and parameter estimation of Tuberculosis with application to Cameroon. Int. J. Bifurc. Chaos. 2011;21(07):1999–2015. doi: 10.1142/S0218127411029598. [DOI] [Google Scholar]
- 13.Bowong S, Mountaga L, Bah A, Tewa J, Kurths J. Parameter and state estimation in a Neisseria meningitidis model: a study case of Niger. Chaos Interdiscip. J. Nonlinear Sci. 2016;26(12):123115. doi: 10.1063/1.4971783. [DOI] [PubMed] [Google Scholar]
- 14.Brauer F, Castillo-Chavez C, Castillo-Chavez C. Mathematical Models in Population Biology and Epidemiology. Berlin: Springer; 2012. [Google Scholar]
- 15.Britton T, Pardoux E, Ball F, Laredo C, Sirl D, Tran VC. Stochastic Epidemic Models with Inference. Berlin: Springer; 2019. [Google Scholar]
- 16.Castilho C, Gondim JA, Marchesin M, Sabeti M. Assessing the efficiency of different control strategies for the Covid-19 epidemic. Electron. J. Differ. Equ. 2020;64(2020):1–17. [Google Scholar]
- 17.Chin, A., Chu, J., Perera, M., Hui, K., Yen, H.-L., Chan, M., Peiris, M., Poon, L.: Stability of SARS-CoV-2 in different environmental conditions. MedRxiv (2020) [DOI] [PMC free article] [PubMed]
- 18.Chitnis N, Hyman JM, Cushing JM. Determining important parameters in the spread of malaria through the sensitivity analysis of a mathematical model. Bull. Math. Biol. 2008;70(5):1272. doi: 10.1007/s11538-008-9299-0. [DOI] [PubMed] [Google Scholar]
- 19.Djidjou-Demasse, R., Michalakis, Y., Choisy, M., Sofonea, M.T., Alizon, S.: Optimal COVID-19 epidemic control until vaccine deployment. MedRxiv (2020)
- 20.Easterling RG. Fundamentals of Statistical Experimental Design and Analysis. New York: Wiley; 2015. [Google Scholar]
- 21.Eikenberry, S.E., Mancuso, M., Iboi, E., Phan, T., Eikenberry, K., Kuang, Y., Kostelich, E., Gumel, A.B.: To mask or not to mask: Modeling the potential for face mask use by the general public to curtail the COVID-19 pandemic. Infect. Dis. Modell. (2020) [DOI] [PMC free article] [PubMed]
- 22.Espinoza B, Castillo-Chavez C, Perrings C. Mobility restrictions for the control of epidemics: When do they work? PLoS ONE. 2020;15(7):0235731. doi: 10.1371/journal.pone.0235731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Fanelli D, Piazza F. Analysis and forecast of COVID-19 spreading in China, Italy and France. Chaos Solitons Fractals. 2020;134:109761. doi: 10.1016/j.chaos.2020.109761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Faranda D, Castillo IP, Hulme O, Jezequel A, Lamb JS, Sato Y, Thompson EL. Asymptotic estimates of SARS-CoV-2 infection counts and their sensitivity to stochastic perturbation. Chaos Interdiscip. J. Nonlinear Sci. 2020;30(5):051–107. doi: 10.1063/5.0008834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Foata, D., Fuchs, A.: Processus stochastiques: Processus de Poisson, chaînes de Markov et martingales (2002)
- 26.Fortin, A.: Analyse numérique pour ingénieurs. Presses inter Polytechnique (2011)
- 27.Garabed, R.B., Jolles, A., Garira, W., Lanzas, C., Gutierrez, J., Rempala, G.: Multi-scale dynamics of infectious diseases (2020)
- 28.Garira W. A complete categorization of multiscale models of infectious disease systems. J. Biol. Dyn. 2017;11(1):378–435. doi: 10.1080/17513758.2017.1367849. [DOI] [PubMed] [Google Scholar]
- 29.Garira W. The research and development process for multiscale models of infectious disease systems. PLoS Comput. Biol. 2020;16(4):1007734. doi: 10.1371/journal.pcbi.1007734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Garira W, Mafunda MC. From individual health to community health: towards multiscale modeling of directly transmitted infectious disease systems. J. Biol. Syst. 2019;27(01):131–166. doi: 10.1142/S0218339019500074. [DOI] [Google Scholar]
- 31.Garira W, Mathebula D, Netshikweta R. A mathematical modelling framework for linked within-host and between-host dynamics for infections with free-living pathogens in the environment. Math. Biosci. 2014;256:58–78. doi: 10.1016/j.mbs.2014.08.004. [DOI] [PubMed] [Google Scholar]
- 32.Gilbert M, Pullano G, Pinotti F, Valdano E, Poletto C, Boëlle P-Y, dOrtenzio E, Yazdanpanah Y, Eholie SP, Altmann M, et al. Preparedness and vulnerability of African countries against importations of COVID-19: a modelling study. The Lancet. 2020;395(10227):871–877. doi: 10.1016/S0140-6736(20)30411-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Giordano G, Blanchini F, Bruno R, Colaneri P, Di Filippo A, Di Matteo A, Colaneri M. Modelling the Covid-19 epidemic and implementation of population-wide interventions in Italy. Nat. Med. 2020;26(6):855–860. doi: 10.1038/s41591-020-0883-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Götz T, Heidrich P. Early stage COVID-19 disease dynamics in Germany: models and parameter identification. J. Math. Ind. 2020;10(1):1–13. doi: 10.1186/s13362-020-00088-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Goupy, J., Creighton, L.: Introduction aux plans d’expériences, vol. 3. Dunod Paris (2006)
- 36.Harmand J, Lobry C, Rapaport A, Sari T. The Chemostat: Mathematical Theory of Microorganism Cultures. New York: Wiley; 2017. [Google Scholar]
- 37.Hilton J, Keeling MJ. Estimation of country-level basic reproductive ratios for novel Coronavirus (SARS-CoV-2/COVID-19) using synthetic contact matrices. PLoS Comput. Biol. 2020;16(7):1008031. doi: 10.1371/journal.pcbi.1008031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Hu Z, Cui Q, Han J, Wang X, Wei E, Teng Z. Evaluation and prediction of the COVID-19 variations at different input population and quarantine strategies, a case study in Guangdong province, China. Int. J. Infect. Dis. 2020;95:231–240. doi: 10.1016/j.ijid.2020.04.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Jedrzejewski F. Introduction aux méthodes numériques. Berlin: Springer; 2005. [Google Scholar]
- 40.Kaffo, C., Noubactep, C., Akamba Bekono, J.C., Tchekote, H.: Les cérémonies funéraires à l’Ouest-Cameroun: Entre mutations des pratiques sociétales, reconstruction des économies locales et aménagement de l’espace. Géographie et cultures, (110):13–32 (2019)
- 41.Kamgang JC, Sallet G. Computation of threshold conditions for epidemiological models and global stability of the disease-free equilibrium (DFE) Math. Biosci. 2008;213(1):1–12. doi: 10.1016/j.mbs.2008.02.005. [DOI] [PubMed] [Google Scholar]
- 42.Kassa SM, Njagarah JB, Terefe YA. Analysis of the mitigation strategies for COVID-19: from mathematical modelling perspective. Chaos Solitons Fractals. 2020;138:109968. doi: 10.1016/j.chaos.2020.109968. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Khajanchi, S., Sarkar, K., Mondal, J., Nisar, K.S., Abdelwahab, S.F.: Mathematical modeling of the covid-19 outbreak with intervention strategies. Results Phys. 104285 (2021) [DOI] [PMC free article] [PubMed]
- 44.Kingman J. Poisson Processes. Oxford: Oxford University Press; 1993. [Google Scholar]
- 45.Kouakep Y, Tchoumi S, Fotsa D, Kamba F, Ngounou D, Mboula E, Kamla V, Kamgang J. Modelling the anti-Covid19 individual or collective containment strategies in Cameroon. Appl. Math. Sci. 2021;15(2):63–78. [Google Scholar]
- 46.Kouidere, A., Khajji, B., El Bhih, A., Balatif, O., Rachik, M.: A mathematical modeling with optimal control strategy of transmission of COVID-19 pandemic virus. Commun. Math. Biol. Neurosci. (2020) Article–ID, 2020
- 47.La Torre D, Malik T, Marsiglio S. Optimal control of prevention and treatment in a basic macroeconomic-epidemiological model. Math. Soc. Sci. 2020;108:100–108. doi: 10.1016/j.mathsocsci.2020.03.005. [DOI] [Google Scholar]
- 48.Lejeune M. Statistique: La théorie et ses applications. Berlin: Springer; 2004. [Google Scholar]
- 49.Lenhart S, Workman JT. Optimal Control Applied to Biological Models. London: CRC Press; 2007. [Google Scholar]
- 50.Li M-T, Sun G-Q, Zhang J, Zhao Y, Pei X, Li L, Wang Y, Zhang W-Y, Zhang Z-K, Jin Z. Analysis of COVID-19 transmission in Shanxi province with discrete time imported cases. Math. Biosci. Eng. 2020;17(4):3710. doi: 10.3934/mbe.2020208. [DOI] [PubMed] [Google Scholar]
- 51.Liu X, Stechlinski P. Infectious Disease Modeling: A Hybrid System Approach. Berlin: Springer; 2017. [Google Scholar]
- 52.Liu Z, Magal P, Seydi O, Webb G. A COVID-19 epidemic model with latency period. Infect. Dis. Model. 2020;5:323–327. doi: 10.1016/j.idm.2020.03.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Liu Z, Magal P, Seydi O, Webb G. Understanding unreported cases in the COVID-19 epidemic outbreak in Wuhan, China, and the importance of major public health interventions. Biology. 2020;9(3):50. doi: 10.3390/biology9030050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Magal P, Webb G. The parameter identification problem for SIR epidemic models: identifying unreported cases. J. Math. Biol. 2018;77(6–7):1629–1648. doi: 10.1007/s00285-017-1203-9. [DOI] [PubMed] [Google Scholar]
- 55.Mandal M, Jana S, Nandi SK, Khatua A, Adak S, Kar T. A model based study on the dynamics of COVID-19: Prediction and control. Chaos Solitons Fractals. 2020;136:109889. doi: 10.1016/j.chaos.2020.109889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Marino S, Hogue IB, Ray CJ, Kirschner DE. A methodology for performing global uncertainty and sensitivity analysis in systems biology. J. Theor. Biol. 2008;254(1):178–196. doi: 10.1016/j.jtbi.2008.04.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Martcheva M, Tuncer N, StMary C. Coupling within-host and between-host infectious diseases models. Biomath. 2015;4(2):1510091. doi: 10.11145/j.biomath.2015.10.091. [DOI] [Google Scholar]
- 58.Mischaikow K, Smith H, Thieme HR. Asymptotically autonomous semiflows: chain recurrence and Lyapunov functions. Trans. Am. Math. Soc. 1995;347(5):1669–1685. doi: 10.1090/S0002-9947-1995-1290727-7. [DOI] [Google Scholar]
- 59.Momani S, Abu Arqub O, Maayah B. Piecewise optimal fractional reproducing kernel solution and convergence analysis for the Atangana-Baleanu-Caputo model of the Lienards equation. Fractals. 2020;28(08):2040007. doi: 10.1142/S0218348X20400071. [DOI] [Google Scholar]
- 60.Momani S, Maayah B, Arqub OA. The reproducing kernel algorithm for numerical solution of van der pol damping model in view of the Atangana-Baleanu fractional approach. Fractals. 2020;28(08):2040010. doi: 10.1142/S0218348X20400101. [DOI] [Google Scholar]
- 61.Nah K, Chen S, Xiao Y, Tang B, Bragazzi N, Heffernan J, Asgary A, Ogden N, Wu J. Scenario tree and adaptive decision making on optimal type and timing for intervention and social-economic activity changes to manage the Covid-19 pandemic. Eur. J. Pure Appl. Math. 2020;13(3):710–729. doi: 10.29020/nybg.ejpam.v13i3.3792. [DOI] [Google Scholar]
- 62.Ngonghala CN, Iboi E, Eikenberry S, Scotch M, MacIntyre CR, Bonds MH, Gumel AB. Mathematical assessment of the impact of non-pharmaceutical interventions on curtailing the: novel Coronavirus. Math. Biosci. 2019;325:108364. doi: 10.1016/j.mbs.2020.108364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Ngonghala, C.N., Iboi, E.A., Gume, A.B.: Could masks curtail the post-lockdown resurgence of COVID-19 in the US? MedRxiv (2020) [DOI] [PMC free article] [PubMed]
- 64.Nisar KS, Ahmad S, Ullah A, Shah K, Alrabaiah H, Arfan M. Mathematical analysis of sird model of covid-19 with caputo fractional derivative based on real data. Results Phys. 2021;21:103772. doi: 10.1016/j.rinp.2020.103772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Nkwayep CH, Bowong S, Tewa J, Kurths J. Short-term forecasts of the COVID-19 pandemic: study case of Cameroon. Chaos Solitons Fractals. 2020;140:110106. doi: 10.1016/j.chaos.2020.110106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Prem K, Cook AR, Jit M. Projecting social contact matrices in 152 countries using contact surveys and demographic data. PLoS Comput. Biol. 2017;13(9):1005697. doi: 10.1371/journal.pcbi.1005697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Rabi FA, Al Zoubi MS, Kasasbeh GA, Salameh DM, Al-Nasser AD. SARS-CoV-2 and Coronavirus disease 2019: what we know so far. Pathogens. 2020;9(3):231. doi: 10.3390/pathogens9030231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Richard, Q., Alizon, S., Choisy, M., Sofonea, M.T., Djidjou-Demasse, R.: Age-structured non-pharmaceutical interventions for optimal control of COVID-19 epidemic. MedRxiv (2020) [DOI] [PMC free article] [PubMed]
- 69.Roda WC, Varughese MB, Han D, Li MY. Why is it difficult to accurately predict the COVID-19 epidemic? Infect. Dis. Model. 2020;5:271–281. doi: 10.1016/j.idm.2020.03.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Rothman KJ, Greenland S, Lash TL. Modern Epidemiology. London: Lippincott Williams & Wilkins; 2008. [Google Scholar]
- 71.Sardar T, Nadim SS, Rana S, Chattopadhyay J. Assessment of lockdown effect in some states and overall India: a predictive mathematical study on COVID-19 outbreak. Chaos Solitons Fractals. 2020;139:110078. doi: 10.1016/j.chaos.2020.110078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Sasmita NR, Ikhwan M, Suyanto S, Chongsuvivatwong V. Optimal control on a mathematical model to pattern the progression of coronavirus disease 2019 (covid-19) in indonesia. Global Health Res Policy. 2020;5(1):1–12. doi: 10.1186/s41256-020-00163-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Serhani, M., Labbardi, H.: Mathematical modeling of COVID-19 spreading with asymptomatic infected and interacting peoples (2020) [DOI] [PMC free article] [PubMed]
- 74.Tchoumi S, Diagne M, Rwezaura H, Tchuenche J. Malaria and covid-19 co-dynamics: a mathematical model and optimal control. Appl. Math. Model. 2021;99:294–327. doi: 10.1016/j.apm.2021.06.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Tchoumi S, Kouakep Y, Fotsa Mbogne D, Kamgang J, Kamla V, Bekolle D. Covid-19 modeling with caution in relaxing control measures and possibilities of several peaks in Cameroon. Appl. Appl. Math. Int. J. (AAM) 2021;16(1):37. [Google Scholar]
- 76.Thieme HR. Convergence results and a Poincaré–Bendixson trichotomy for asymptotically autonomous differential equations. J. Math. Biol. 1992;30(7):755–763. doi: 10.1007/BF00173267. [DOI] [Google Scholar]
- 77.Ud Din R, Seadawy AR, Shah K, Ullah A, Baleanu D. Study of global dynamics of covid-19 via a new mathematical model. Results in Phys. 2020;19:103468. doi: 10.1016/j.rinp.2020.103468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.van den Driessche P. Reproduction numbers of infectious disease models. Infect. Dis. Model. 2017;2(3):288–303. doi: 10.1016/j.idm.2017.06.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Van den Driessche P, Watmough J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002;180(1–2):29–48. doi: 10.1016/S0025-5564(02)00108-6. [DOI] [PubMed] [Google Scholar]
- 80.Van den Driessch, P., Watmough, J.: Further notes on the basic reproduction number. In: Mathematical Epidemiology, pp. 159–178. Springer (2008)
- 81.Volpert, V., Banerjee, M., d’Onofrio, A., Lipniacki, T., Petrovskii, S., Tran, V.C.: Coronavirus-Scientific insights and societal aspects (2020)
- 82.Wang, Q., Xie, S., Wang, Y., Zeng, D.: Survival-convolution models for predicting COVID-19 cases and assessing effects of mitigation strategies. MedRxiv (2020) [DOI] [PMC free article] [PubMed]
- 83.Zhang X, Ma R, Wang L. Predicting turning point, duration and attack rate of COVID-19 outbreaks in major Western countries. Chaos Solitons Fractals. 2020;135:109829. doi: 10.1016/j.chaos.2020.109829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Zhou L, Wu K, Liu H, Gao Y, Gao X. CIRD-F: spread and influence of COVID-19 in China. J. Shanghai Jiaotong Univ. (Sci.) 2020;25:147–156. doi: 10.1007/s12204-020-2168-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The datasets generated and/or analyzed during the current study are available in the websites https://www.data.gouv.fr/fr/datasets/coronavirus-covid19-evolution-par-pays-et-dans-le-monde-maj-quotidienne/www.data.gouv.fr and https://www.humanitarianresponse.info/en/operations/cameroon/health/documentshttps://www.humanitarianresponse.info.