Abstract
Polycyclic aromatic hydrocarbons (PAHs) play an important role in interstellar chemistry and are subject to high energy photons that can induce excitation, ionization, and fragmentation. Previous studies have demonstrated electronic relaxation of parent PAH monocations over 10–100 femtoseconds as a result of beyond-Born-Oppenheimer coupling between the electronic and nuclear dynamics. Here, we investigate three PAH molecules: fluorene, phenanthrene, and pyrene, using ultrafast XUV and IR laser pulses. Simultaneous measurements of the ion yields, ion momenta, and electron momenta as a function of laser pulse delay allow a detailed insight into the various molecular processes. We report relaxation times for the electronically excited PAH*, PAH+* and PAH2+* states, and show the time-dependent conversion between fragmentation pathways. Additionally, using recoil-frame covariance analysis between ion images, we demonstrate that the dissociation of the PAH2+ ions favors reaction pathways involving two-body breakup and/or loss of neutral fragments totaling an even number of carbon atoms.
Subject terms: Chemical physics, Reaction kinetics and dynamics, Atomic and molecular interactions with photons
Polycyclic aromatic hydrocarbons play an important role in interstellar chemistry, where interaction with high energy photons can induce ionization and fragmentation reactions. Here the authors, with XUV-IR pump-probe experiments, investigate the ultrafast photoinduced dynamics of fluorene, phenanthrene and pyrene, providing insight into their preferred reaction channels.
Introduction
Polycyclic aromatic hydrocarbons (PAHs) are abundant molecules in the interstellar medium (ISM), accounting for ~10% of the total galactic carbon, according to infrared (IR) emission spectra measured by the Spitzer Space Telescope1,2. PAHs undergo a variety of processes upon irradiation, including ionization, dehydrogenation, fragmentation, and isomerization, and the influence of PAHs on the thermodynamics and chemistry of the ISM has motivated laboratory research for many decades3,4. The conditions of low temperature, low density, and strong photon radiation mean that these unimolecular reactions become more important compared to a terrestrial environment and are key to the structure and evolution of the ISM5–7.
Previous studies into the ionization and fragmentation of PAHs have employed synchrotron and rare gas lamps as photon sources up to the extreme ultraviolet (XUV) and X-ray wavelengths8–12. Photoelectron photoion photoion coincidence (PEPIPICO) experiments demonstrated that the interaction of PAHs with XUV photons yielded a PAH2+/PAH+ ratio of ~0.25 for naphthalene at the highest photon energy of 40.8 eV13. These studies also investigated the decay mechanisms of doubly charged PAHs (naphthalene-d8, naphthalene-h8, and azulene), revealing prominent dissociation channels into two monocations where zero, two, and four carbon atoms were lost in neutral co-fragments14,15. Such experiments provide important information on the photofragmentation products and give an insight into molecules that may exist in the ISM but have not yet been assigned by spectral features.
PAHs, with their extended electron system, also provide a framework to explore ultrafast dynamics and beyond-Born-Oppenheimer effects. Within the Born-Oppenheimer approximation, electrons are assumed to move much faster than the nuclei, and the electronic and nuclear frameworks can therefore be treated separately. If the electronic and nuclear motion are instead strongly coupled, this can result in the ultrafast energy transfer from electronic excitation into nuclear motion, and the Born-Oppenheimer approximation breaks down16–20. Non-adiabatic electronic relaxation has been demonstrated in recent ultrafast time-resolved studies on a series of small PAHs revealing electronic lifetimes of the monocation in the range 30–55 fs21. Theoretical calculations suggest the presence of conical intersections facilitating rapid electronic relaxation. Further experiments indicate that the electronic lifetimes increase with both the molecular size and the cationic excitation energy, and that multi-electronic and non-Born-Oppenheimer effects must be accounted for to provide accurate theoretical calculations22–24.
Here, we present femtosecond XUV-IR pump-probe experiments from the free-electron laser (FEL) FLASH in Hamburg25, studying the ultrafast photoinduced dynamics of fluorene (FLU), phenanthrene (PHE), and pyrene (PYR). The structures of these molecules are shown in Fig. 1. This comparative study using 30.3 nm (40.9 eV) XUV photons, corresponding to the He II emission line, a dominant spectral line in the interstellar environment, provides valuable insight into the stability and the accessible reaction pathways of these complex molecules26. The time-resolved photodynamics of the PAHs are investigated by concurrently recording the photoelectrons using velocity-map imaging (VMI) and the photoions by VMI and time-of-flight (TOF) mass spectrometry. In addition to determining PAH+* excited state lifetimes similar to those reported in the high-harmonic generation (HHG) study by Marciniak et al.21, our measurements demonstrate ultrafast relaxation for the PAH* and PAH2+* species. Furthermore, the application of recoil-frame covariance analysis to the ion images provides a detailed mechanistic insight into the fragmentation pathways of the PAH2+ ions, demonstrating a strong preference for dissociation into two monocations, where neutral co-fragments contain an even number of carbon atoms27–31. Theoretical calculations, reported in Supplementary Notes 1 and 8, support both the electronic relaxation times and the fragmentation channels observed.
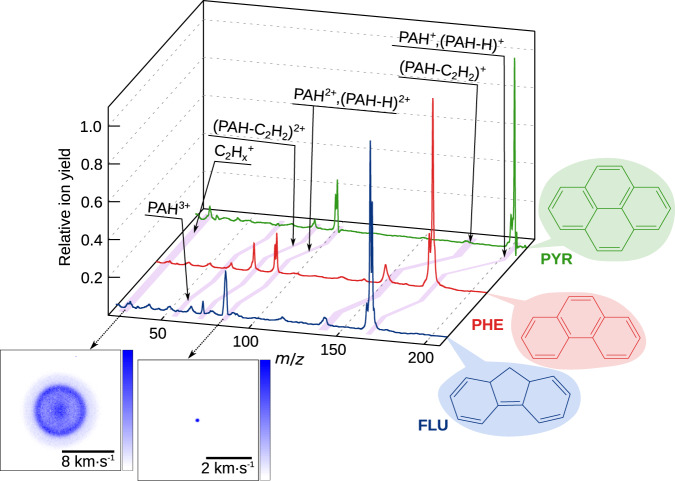
Fig. 1. XUV pulse only data.
Ion mass spectra for the three PAH molecules, pyrene (PYR), phenanthrene (PHE), and fluorene (FLU), after irradiation with the XUV pulse at 30.3 nm, in green, red, and blue respectively. Intensities are normalized on the height of the respective parent ion PAH+. Insets show the velocity-map images for the PAH2+ dication and C2H for FLU (four-fold symmetrization about the laser polarization and vertical axis applied).
Results
Time-independent results
The mass spectra obtained following irradiation of FLU, PHE, and PYR with 30.3 nm FEL light are shown in Fig. 1. The spectra are dominated by the cations (PAH+) and dications (PAH2+) of the respective parents, with small signals from triply ionized molecules also visible. Multiple fragment ions are also seen. The FEL power was set to minimize the formation of PAH2+ and PAH3+ ions whilst maximizing the PAH+ ion yield to avoid multi-photon interactions. In line with the results of previous studies, fragmentation is more pronounced for the two smaller PAHs, FLU and PHE, than for PYR32. The parent ion peaks are generally much sharper than the fragment peaks as a result of peak broadening associated with kinetic energy release during the fragmentation process. To illustrate this further, the insets to Fig. 1 show the symmetrized velocity-map ion images for the PAH2+ dication and one of the fragmentation products, C2H, for FLU. The velocity distribution of the dication reflects that of the neutral parent molecule within the molecular beam, which is essentially unaffected by the loss of two electrons, while the fragment ion (C2H) possesses significant recoil velocity as a result of the kinetic energy released during the parent ion dissociation. The nomenclature of, for example, C2H and C8H, is used throughout this discussion to refer to all monocations with two and eight carbon atoms, respectively, where x and y encapsulate the possible hydrogen atom values for the fragment.
The velocity-map images provide the 2D projection of the velocity distribution of each detected fragment. Because the velocity distributions for all fragments are recorded simultaneously for each laser pulse, a covariance analysis of the data set allows statistical correlations between the velocities of two or more fragments to be investigated27. This provides the correlated velocity distributions of two fragments from the data set, which is a powerful tool for determining the fragmentation processes occurring. The covariance-mapping procedure has been described in previous publications28–31,33 and is detailed further in the Methods section. To the authors’ knowledge, the PAHs studied here are the largest molecules that recoil-frame covariance map imaging has been applied to. Briefly, in a covariance image, cov(A, B), one of the two fragments is chosen to be the ‘reference’ ion (B), and the covariance map image reveals the velocity distribution of the ion of interest (A) relative to the trajectory direction of the reference ion. In the simplest example, for a parent dication undergoing unimolecular dissociation into two monocations, A and B, the trajectories of A and B will always be directly opposed due to conservation of momentum. Therefore, assuming no other formation pathways, the appearance of cov(A, B) would strongly resemble a single point directly opposite the reference direction. Due to rotational freedom of the molecule in and out of the detector plane, signal leading from the point to the center of the covariance image would also be expected.
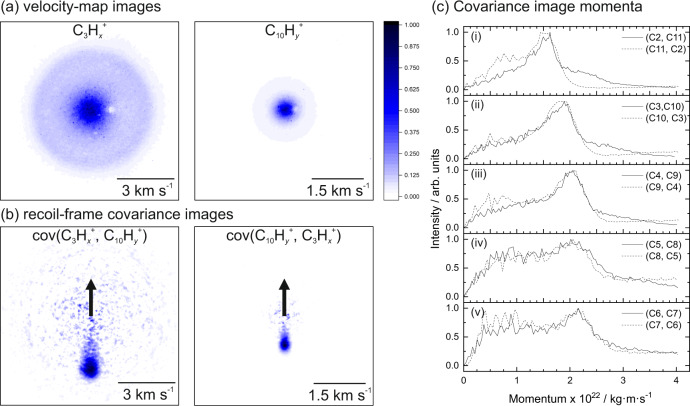
In this experiment, as hydrogen loss is difficult to resolve using ion imaging (limited by the phosphor screen decay time and the time resolution of the PImMS sensor), the discussion focuses on the fragmentation of the carbon framework. Figure 2a shows the raw velocity-map images recorded for the C3H and C10H fragments of the dissociative ionization of FLU, C13H10. The two images potentially contain contributions from the dissociation of singly charged, doubly charged, and more highly charged parent ions. Performing the covariance analysis isolates the fragmentation of the doubly charged parent ion to form two monocations, which corresponds to the higher velocity ring component seen in the velocity-map images. Figure 2b shows the recoil-frame covariance images of C3H relative to the C10H reference ion (left), and vice versa (right), with black arrows indicating the direction of the reference ion. As expected for a two-body dissociation, the two fragments recoil in opposite directions, i.e., the covariance signal is seen 180∘ from the reference direction, due to conservation of momentum, as described above. The relative speeds of the two fragments are determined by their individual masses: the heavier C10H recoils more slowly than the lighter C3H fragment, yielding a covariance signal closer to the center of the image. Converting the spatial coordinates in the covariance images to momentum units and performing an angular integration gives the momentum profiles shown in Fig. 2(c)(ii). As expected, there is excellent agreement between the momentum profiles obtained from the cov(C3H,C10H) and cov(C10H,C3H) covariance maps.
Fig. 2. Ion images, covariance images, and momentum comparisons.
a Velocity-map images and b covariance map images for the C3H and C10H fragment ions arising from dissociative ionization of FLU, C13H10. Each image is individually normalized. The velocity-map images are presented without symmetrization or Abel-inversion to provide a better comparison to the covariance images. The small areas lacking signal near the center of the velocity-map images are attributed to damage in the MCP/phosphor detector. Black arrows in the covariance images indicate the direction of the reference ion. c Momentum profiles of the ion pairs resulting from the two-body dissociative ionization of fluorene. An angular integration is performed on the covariance images, and the spatial coordinates are converted to momentum units. Cov(A, B) refers to the covariance of ion A with B as the reference ion. Discrepancies between the plots in (i) are attributed to physical defects in the detector and background ions affecting the ion images differently.
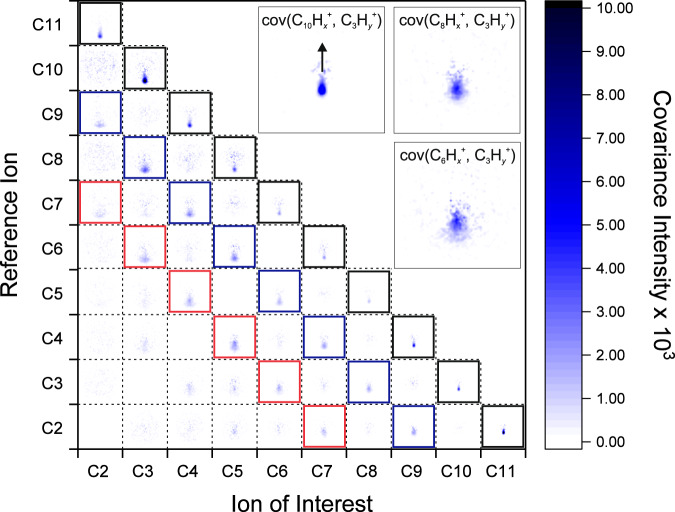
Further to this, the recoil-frame covariance analysis can be performed between all CnH species for the PAHs. The resulting covariance maps for the FLU fragment ions are plotted as a matrix in Fig. 3, providing a rich basis for elucidating the formation mechanisms for each fragment. The initial focus is on the covariance maps along the main diagonal of the matrix, highlighted by black squares in Fig. 3. These correspond to the two-body dissociations of the doubly charged parent, similar to the reaction FLU2+ → C3H + C10H discussed above. Clear covariance signals can be seen for each of the ion pairs, demonstrating that, except for the loss of a single carbon atom, all two-body dissociation processes of the carbon framework resulting in two monocations are possible from the PAH2+ parent. This may seem surprising given the extensive rearrangement of the carbon backbone that must occur for several of the dissociation pathways. Calculated dissociation energies for various channels of PAH+ and PAH2+, resulting in neutral, singly, and doubly charged fragments, are shown in Supplementary Note 1. These energies were calculated using a rigid approximation for simplicity. Pathways that correspond to a doubly charged parent ion fragmenting into two singly charged ions, for example, C10H + C3H or C9H + C4H, are predicted to have relatively low dissociation energies (8.3 and 10 eV, respectively), which are energetically consistent with the observation of many such fragmentation channels in the covariance map images. Each of the two-body dissociation processes also shows excellent momentum matching in the covariance maps, as plotted in Fig. 2c(i)-(v).
Fig. 3. Full recoil-frame covariance map images.
The covariance map images between all ion species produced from FLU. Axis labels refer to the number of carbons in the monocationic species and omit the number of hydrogen atoms. Fragment ion pairs that have a total number of carbons greater than that of the parent ion, for example, between C8H and C9H, show no covariance as they cannot be formed as partners from the same parent molecule; these have been omitted for clarity. Any ion species will also always show covariance with itself (autocovariance), and these entries have also been omitted. Notably, signal in the cells along the main diagonal of the matrix (highlighted in black) corresponds to the two-body dissociation pathways from the FLU2+ ion. In addition, the cells highlighted in blue and red correspond to the dissociation pathways where two and four carbon atoms, respectively, are lost in neutral co-fragments. Inset: expansions for the maps corresponding to cov(C10H, C3H), cov(C8H, C3H), cov(C6H, C3H) showing increased blurring as more carbon atoms are lost in neutral co-fragments. The black arrow indicates the direction of the reference ion in all covariance maps.
In addition to seeing covariances between the ion pairs that have masses totaling the molecular mass of the parent ion, prominent covariances are seen between ion pairs that are an even number of carbon units deficient from the parent mass. Ion pairs that are two and four carbon units deficient from the parent mass are highlighted with blue and red squares, respectively, in Fig. 3. The covariance signal between C3H and C8H in Fig. 3 demonstrates a dissociation pathway that is consistent with the reaction C13H → C3H + C8H + C2H2, and the velocities of the C3H and C8H ions match the Coulombic repulsion expected between two monocations. Similarly, the covariance signals between C3H and C6H demonstrate two-body dissociation from the parent dication with four carbon atoms lost in neutral fragments. Previous PEPIPICO studies investigating the dissociative ionization of PAH molecules at XUV wavelengths have attributed similar observations to the loss of one or more neutral acetylene (C2H2) molecules13,14.
It is observed that as more carbon atoms are lost in neutral molecules, the covariance maps become successively more blurred, e.g., as shown in the insets in Fig. 3 comparing cov(C10H, C3H), cov(C8H, C3H), and cov(C6H, C3H). Assuming that the two carbons are lost as a neutral C2H2 molecule, this may result either from secondary fragmentation (PAH2+ → + → + + C2H2) or from deferred charge separation reactions (PAH2+ → C2H2 + → C2H2 + + ). In both cases, blurring in the covariance images would be expected. These pathways would usually be differentiated by observing the gradient of the regression line in an ion-TOF ion-TOF covariance plot34, as previously performed for naphthalene-d8, demonstrating deferred charge separation14. The ion-TOF ion-TOF partial covariance plots for the PAH molecules in our study are shown in Supplementary Note 2, following correction for the FEL and IR shot-to-shot intensity fluctuations. Some two-body dissociation pathways from the parent dication are visible, but three-body dissociations (two ions and one neutral fragment) cannot be discerned above the noise level, preventing this technique from being applied. There is currently ongoing work exploring the use of the ion images to create an ion-momentum ion-momentum covariance plot to differentiate the dissociation pathways.
The recoil-frame covariance results for PHE and PYR are shown in Supplementary Note 3. These similarly demonstrate a propensity for dissociation pathways from the parent dication into two monocations, with either zero or an even number of carbon atoms lost in neutral co-fragments. The signal levels for PYR2+ fragmentation are notably lower than for FLU2+ and PHE2+, matching previous studies commenting that larger PAH molecules such as PYR tend to form stable parent cations and undergo less dissociative ionization compared to smaller PAHs35,36.
Time-dependent results
In this section, we present the effect of applying a 30.3 nm XUV pulse and 810 nm pulse at various delays on the three PAHs. This analysis integrates the electron VMI, ion VMI, and ion TOF measurements. Analysis of the helium carrier gas photoelectron sideband lines in the electron images provides an independent and accurate measurement of when the two laser pulses overlap in time (t0), outlined in more detail in Supplementary Note 4. For the PAHs in this investigation, there are two major two-color reaction pathways depending on which laser pulse arrives first, as shown in the schematic in Fig. 4b:
Scenario 1: The XUV pulse interacts with the PAH to produce an electronically excited charged molecule, which can rapidly decay to produce a vibrationally hot parent species. Absorption of one or more IR photons before electronic relaxation can cause electronic excitation and/or promote the molecule to the next charge state. If further ionization is induced, the ejected electron typically has low kinetic energy (LKE), as each IR photon is low in energy. In this analysis, LKE electrons are defined as having a kinetic energy lower than 2 eV, compared to the 1.53 eV of the IR photons. Increasing the delay between the XUV and the IR pulse allows the molecule to electronically relax, thus increasing fragmentation caused by the IR pulse through loss of H, C2H2 or other neutral or charged species.
Scenario 2: The IR pulse interacts with the PAH first, producing a vibrationally and electronically excited neutral molecule by multiphoton excitation. In the excited state, absorption of an XUV photon has an increased probability of leading to ionization or dissociative ionization. Evidence for this scenario is demonstrated in the analysis of the time-dependent PAH parent ions described below, where the fits were significantly improved by introducing a channel representing this pathway, i.e., before t0. Note that the IR pulse is strong enough to produce PAH+ ions directly but in a negligible quantity compared to the XUV pulse. Comparative TOF spectra are shown in Supplementary Note 5.
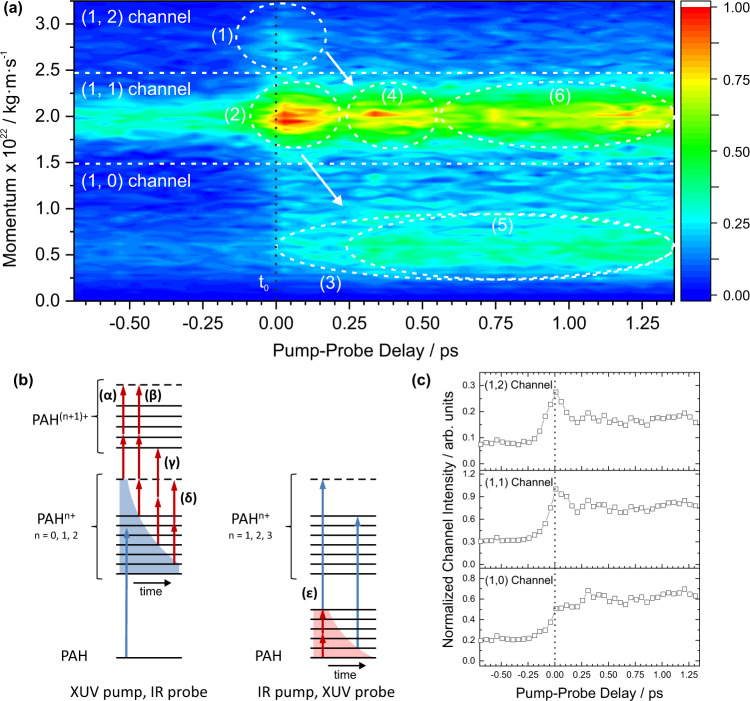
Fig. 4. Time-dependent fragmentation channels.
a The C3H momentum profile formed from FLU as a function of XUV-IR laser pulse delay. The IR pulse interacting with the molecular beam before the XUV pulse gives negative pump-probe delay values, whereas for positive pump-probe values, the XUV pulse interacts first. The vertical black dotted line indicates t0 determined by the helium electron sidebands. Channels and numbered features are described in detail in the text. Briefly, (1) and (2) show the increase in C3H ions formed by dissociative ionization from the PAH3+ and PAH2+ ion, respectively, around t0. (3) shows the increase in C3H ion signal after t0 due to the XUV pulse creating PAH+ ions that are dissociated by the IR pulse. (4) and (5) show the increase in signal in the (1, 1) and (1, 0) channels following relaxation of the PAH2+ and PAH+ ions, respectively, and dissociation by the IR laser pulse. (6) highlights the general increase in signal after t0 compared to before t0, even after a long pump-probe delay, in this case, due to the XUV pulse creating PAH2+ ions which are dissociated by the IR pulse. White arrows highlight the shift in channel yields from pathway β and γ to pathway δ, as denoted in (b). b Schematic of the PAH states involved in this experiment. Solid black lines and dashed lines represent bound and dissociative electronic states, respectively. Blue and red arrows represent the effects of the XUV laser and IR laser pulses, respectively. The pump pulses are able to populate a multitude of electronic states, as represented by the blue and red shaded areas for the XUV and IR pulses, respectively. Electronic relaxation of the wavepacket over time is represented by the curvature in the shaded areas. The change in electronic states due to relaxation alters the product of the probe pulse. c Integrated plots of the (1, 0), (1, 1), and (1, 2) channels from (a). Plots are normalized to the maximum signal detected in the (1, 1) channel, and t0 is represented by the dotted black line.
For all PAHs, the XUV/IR laser regime creates significant quantities of both fragment and parent ions. The delay-dependent yields of these are considered separately in the following sections.
Fragment Ions
The XUV/IR pump-probe experiments create all possible singly charged ions from the carbon framework with the exception of CH, consistent with previous studies13,14. For each fragment ion, a velocity-map image was extracted from the PImMS data and Abel-inverted using the polar onion-peeling method37. After performing an angular integral, the velocity distribution was converted to momentum and plotted as a function of pump-probe delay. This discussion focuses on the C3H ion formation from FLU, shown in Fig. 4a, which had strong signal levels across the three PAHs studied. Momentum plots for C3H from PHE and PYR are shown in Supplementary Note 3, and other fragments will be discussed in a follow-up publication. The momentum plot can be divided into three regions:
high momentum, referred to as the (1, 2) channel, with the C3H ion primarily recoiling against a dication.
medium momentum, referred to as the (1, 1) channel, where C3H recoils against a monocation.
low momentum, referred to as the (1, 0) channel, where there is no charged partner in the dissociation.
The (1, 2) and (1, 1) channels were confirmed by performing a covariance analysis between ion pairs, as described above. The integrated channel yields are plotted in Fig. 4c.
A transient increase in signal around t0 is highlighted as feature (1) in Fig. 4a. At negative pump-probe delays, the IR pulse arrives before the XUV pulse, creating vibrationally and electronically excited PAH* molecules. If the pump-probe delay is short (−100 to 0 fs), the PAH* molecules remain in an excited state and the XUV pulse can induce ionization to PAHn+ (n = 1, 2, 3) states, as represented by path ϵ in Fig. 4b. Dissociation from the PAH3+ states produces fragments in the (1, 2) channel, explaining the increase in signal in feature (1) before t0. After t0, the XUV pulse precedes the IR pulse, and the XUV-only mass spectrum in Fig. 1 demonstrates that the primary products are PAH+ and PAH2+ ions. The IR pulse can induce dissociative ionization of the electronically hot PAH2+*, producing fragments from PAH3+, represented by pathways α and β in Fig. 4b. This pathway also produces ions in the (1, 2) channel.
Electronic relaxation following the initial laser pulse is represented in Fig. 4b by the curvature in the blue and red shaded areas for the XUV pulse and IR pulse, respectively. Electronically excited PAH2+* molecules produced by the XUV pulse relax during the time of the pump-probe delay; as the delay is increased, more energy is required from the IR pulse to initiate dissociative ionization. Consequently, the (1, 2) channel yield diminishes, and the IR pulse begins to favor dissociating the PAH2+ ion instead of promoting it to a PAH3+ state. This is represented in Fig. 4b by pathways α, β, and γ converting to pathway δ as the molecule relaxes and is similar to the wavepacket evolution identified for the PAH2+ ion in a previous HHG study21. This causes a signal increase in the (1, 1) channel after ~250 fs, labeled as feature (4) in Fig. 4a.
In the (1, 1) channel, an increase in signal can be seen around t0, labeled feature (2). As noted for the (1, 2) channel, prior to t0, the IR pulse primarily creates PAH* molecules. Whilst electronically excited, the XUV pulse can more easily promote PAH* to a dissociative PAH2+ state, as represented by pathway ϵ with n = 2. At positive pump-probe delay values, the XUV pulse creates significant quantities of PAH+ and PAH2+, which are subsequently promoted to a dissociative PAH2+ state by the IR pulse. These processes are represented by pathways β and δ with n = 1 and 2, respectively.
Two increases in signal are visible in the (1, 0) channel, one beginning at t0, labeled feature (3), and one beginning after ~250 fs, labeled feature (5). Feature (3) is attributed primarily to the XUV pulse creating excited PAH+*, which is dissociated by the IR pulse. This is represented by pathway δ with n = 1. Notably, the signal increase only begins after t0, implying that the IR-pump, XUV-probe regime contribution to this channel is negligibly small. Feature (5) has a similar origin to feature (4)—the XUV pulse initially creates an ensemble containing highly excited PAH+* ions, which can be readily promoted to a PAH2+ state by the IR laser pulse at short pump-probe delays. However, at longer delay values, the ions electronically relax causing the IR laser to induce dissociation rather than ionization. Again, this can be represented as a shift from pathways α, β, and γ to δ.
An overall increase in signal is seen when the IR pulse arrives after the XUV pulse, even for very long pump-probe delays; for example, the signal level in feature (6) compared to the signal before t0. This is attributed to the XUV pulse creating excited parent ions PAH+*, PAH2+*, and PAH3+*, which relax to their ground electronic states. The IR pulse induces dissociation in a fraction of the molecules so the PAH+, PAH2+, and PAH3+ ions contribute to the (1, 0), (1, 1), and (1, 2) fragment channels, respectively. This is shown by pathway δ in Fig. 4b.
Parent Ions
The delay-dependent formations of all ions can be plotted by integrating the appropriate arrival times of the TOF spectrum recorded from the MCP current. This provides a more accurate quantification of the ion signal compared to the ion images, which are susceptible to saturation, particularly for parent ions, which are always incident in the center of the detector. In addition, the behavior of LKE electrons can be monitored using the electron velocity-map images. Yields for the LKE electrons, the PAH2+ parent, and the (1, 2) C3H ions extracted from the ion images for FLU, PHE, and PYR are shown in Fig. 5. A Monte Carlo sampling procedure was used to obtain the relaxation times of the excited PAH, PAH+, and PAH2+ species38. The pump pulses are able to populate a multitude of electronic states and the measured relaxation times are those averaged over the populated states following the pump laser pulse that are excited to the relevant ionic or dissociative state by the probe pulse. A summarized description of the analysis is detailed below, and the analysis procedure is described briefly in the Methods section and in full in Supplementary Note 6. The relaxation constants for all PAH species are given in Table 1.
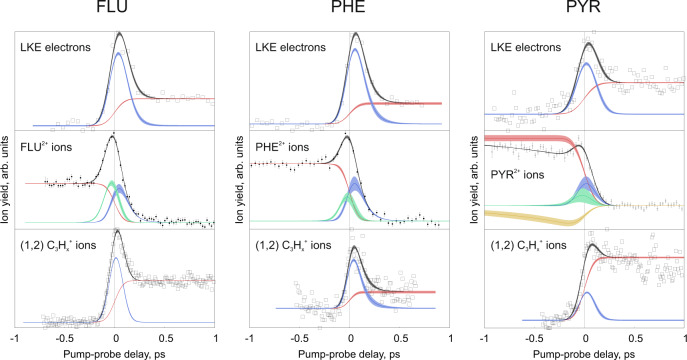
Fig. 5. Delay dependent yields and fits.
Delay-dependent yields of the LKE electrons, PAH2+, and C3H ions from the (1, 2) channel formed from FLU, PHE, and PYR. The vertical black line represents t0. LKE electrons are defined as having a kinetic energy below 2 eV. Details for the fitting procedure are described in the Methods section. The blue and green peak functions represent the XUV-pump, IR-probe and the IR-pump, XUV-probe laser regimes, respectively. The red sigmoidal curves represent the change in signal due to different PAH ionization states populated by the pump laser. The PYR2+ curve additionally contains another peak function (in yellow) to account for slowly changing IR-pump dynamics reproduced over multiple measurements. The black curves show the sum of the peak functions and sigmoidal. Each data point in the PAH2+ plots results from averaging 1300 ± 200, 2000 ± 400, and 900 ± 400 measurements for FLU, PHE, and PYR, respectively (variation arises from sorting and filtering according to jitter in the FEL pulse timing).
Table 1.
Electronic decay lifetimes.
| Exponential Lifetime/fs | ||||
|---|---|---|---|---|
| Charge State | FLU | FLU (Theory) | PHE | PYR |
| PAH* | 35 ± 8 | 54 ± 2 | 29 ± 17 | 62 ± 71 |
| PAH+* | 57 ± 13 | 42 ± 8 | 76 ± 14 | 24 ± 11 |
| PAH2+* | 17 ± 5 | – | 74 ± 19 | 28 ± 10 |
Exponential electronic decay lifetimes for the various charged parent species. The listed error values refer to the fit errors. The pump laser pulses are expected to populate an ensemble of electronic states, as described and modeled in Supplementary Note 6.
PAH+* lifetime
When the IR pulse induces ionization, the molecule absorbs IR photons until the ionization energy is reached and the electron is ejected. As each photon is low in energy, the electron typically has LKE, defined in this study as below 2 eV. The relatively low IR intensity (1 × 1013 W/cm2) prevents any significant contribution from above-threshold ionization, which would produce higher-energy electrons. Figure 1 demonstrates that PAH+ is the dominant product after interaction with the XUV pulse. This suggests that the transient increase in the LKE electron yield is primarily due to the ionization of PAH+* to PAH2+ by the IR pulse. By fitting the LKE electron yield, the PAH+* lifetime can be extracted for each PAH.
PAH* lifetime
There are a significant number of possible processes leading to both the creation and depletion of the PAH2+ ion. For example, the XUV photon may form PAH2+* directly, which is depleted by further ionization or dissociation by the IR pulse. However, as the yields of the other parent and fragment species are comparatively low, it is reasonable to fit the transient behavior using two major pathways, namely (i) the absorption of an XUV photon to form PAH+* followed by ionization to PAH2+ by the IR pulse; and (ii) the IR pulse interacting with the molecule to generate an excited neutral PAH*, which is ionized by the XUV pulse to generate PAH2+. The transient behavior is therefore dependent on the relaxation times of both the PAH+* and PAH* species. By using the values for t0 and the PAH+* relaxation lifetimes determined from the electron data, the fitting procedure can isolate the PAH* relaxation times. The PYR2+ trace was found to have a slow decrease in signal at t0 (visible in Fig. 5) that was reproduced over multiple scans. An additional peak function was used to fit this trace in order to produce the associated PYR* lifetime.
PAH2+* lifetime
As discussed above in the Fragment Ions section, the transient signal increase for C3H in the (1, 2) channel is dependent upon two pathways. Firstly, before t0, the IR pulse creates an excited neutral PAH* species, which undergoes dissociative ionization with an XUV photon to a PAH3+ state. Secondly, after t0, the XUV laser pulse induces the formation of PAH2+*, which the IR laser pulse promotes to a dissociative PAH3+* state. The time dependence of the C3H ions in the (1, 2) channel is therefore governed by the lifetimes of the PAH* and PAH2+* states, which can be determined from the fitting procedure. The transient increase showed a good fit using a single Gaussian representing XUV-pump, IR-probe (centered after t0), indicating the IR-pump, XUV-probe contribution to be small. Therefore, the (1, 2) channel for C3H was fitted using only the XUV-pump, IR-probe channel, allowing the PAH2+* lifetime to be extracted.
Theoretical model
Extensive theoretical calculations were performed to support the experimental results. These are compared in Table 1. Due to the computational requirements, these studies were restricted to calculating the FLU* and FLU+* electronic lifetimes. The approaches are described in the Methods section and in more detail in Supplementary Note 8.
To calculate the FLU* lifetime, the effect of the IR laser pulse on an ensemble of molecules in various orientations was simulated explicitly. Following this, DFT-based trajectory surface hopping molecular dynamics (TSH-MD) calculations were used to track the dynamics of the states formed over 400 fs. The photoionization cross section of each electronic state was calculated to simulate the XUV laser pulse probing these states. Combining the population of the states and the photoionization cross section allows the time-dependent change in FLU+ yield to be estimated at 54 ± 2 fs.
For the FLU+ lifetimes, the effect of the XUV pulse on a ground state FLU molecule was simulated. 480 FLU+ electronic states can be populated by an XUV photon, of which 180 are high enough in energy to be further ionized to FLU2+ by a 810 nm photon. This matches our experimental conditions where the experimental cross-correlation times and electron images indicate that single-photon processes are dominant for the IR probe pulse. Given the high number of states and the complicated potential energy surface topology, a linear vibronic coupling (LVC) model was used to perform TSH-MD simulations over 50 fs. The population that can be ionized by a 810 nm photon decreases as the population decays over time, thus giving rise to a decay constant of 42 ± 8 fs for the FLU+ ion.
Discussion
The PAHs studied are different sizes with different levels of bonding between the carbon rings; nonetheless, ultrafast electronic relaxation in the range 10–100 fs was observed for all molecules in all charge states, indicating that electronic relaxation on this timescale is likely to be ubiquitous across PAHs. Theoretical calculations show that with the high range of accessible electronic states, the populations resulting from IR or XUV excitation undergo ultrafast relaxation within this time range. Our value of 24 ± 11 fs for the PYR+* lifetime (Table 1) roughly matches the measurement of 37 ± 3 fs by Marciniak et al.21, with discrepancies primarily attributed to the difference in XUV photon energy (16–20 eV compared to 40.9 eV in this study).
Overall, our results provide a comprehensive view of the electronic and fragmentation dynamics of PAH molecules under irradiation of 30.3 nm photons, corresponding to the He II emission line. The propensity for molecules to fragment with neutral fragments containing zero or an even number of carbon atoms provides valuable information for modeling the ISM, both in terms of the species that might be detected and potential reagents for interstellar chemistry. The abundance of accessible dissociation pathways consistent with the loss of one or more neutral C2H2 echoes the widely accepted model for PAH growth called the hydrogen abstraction C2H2 addition (HACA) model39–41. Our work showcases the potential for the novel technique of recoil-frame covariance map imaging to unravel the dynamics of large molecules with multiple competing fragmentation channels. Furthermore, the ubiquity of ultrafast relaxation times determined experimentally and theoretically indicates that electronically excited PAHs are generally short lived and such molecules in the ISM can be assumed to be in the electronic ground state. This greatly simplifies interstellar chemical modeling involving PAHs by reducing the number of accessible reaction pathways. Our work demonstrates how ultrafast XUV experiments can be used to simultaneously investigate the dissociation and ionization dynamics of complex systems and provide a more complete picture of the molecular processes.
Methods
Experiment
The time-resolved pump-probe experiments were performed at FLASH42 using the CFEL-ASG Multi Purpose (CAMP) endstation43 at beamline 1 (BL1). The CAMP endstation houses a double-sided VMI spectrometer for simultaneous measurement of the electron and ion kinetic energy and angular distributions. The FEL provided 30.3 nm (40.9 ± 0.4 eV) XUV pulses, which, from the electron pulse durations, were estimated to be 90 fs FWHM with a pulse energy of 14 μJ. Two aluminum filters, thicknesses 100.9 and 423.4 nm, were used to reduce the FEL pulse energy to ~3.3 μJ. In addition, to perform pump-probe measurements, the present study used 60 fs FWHM IR laser pulses at 810 nm. By measuring the IR laser pulse intensity and the focal spot size before the beam enters the chamber, the intensity of the IR laser pulse is estimated to be 1 × 1013 W/cm2. The intensity was tuned so that the IR laser pulse was strong enough to induce a small level of single ionization of the parent molecules without causing significant fragmentation or double ionization (see Supplementary Note 5). An overview of the laser settings is given in Supplementary Note 7, and the laser is described by Redlin et al.44.
The sample molecules FLU (C13H10, melting point (mp) = 116 ∘C), PHE (C14H10, mp = 101 ∘C), and PYR (C16H10, mp = 145 ∘C) were purchased from Sigma-Aldrich with 98% purity and used without further purification. The structures of these molecules are shown in Fig. 1. The samples were placed in an in-vacuum reservoir and heated to ~220–230 ∘C to increase their respective vapor pressures. Using helium as a carrier gas (1.5–2 bar backing pressure), the molecules were then introduced into vacuum via a supersonic expansion produced by an Even-Lavie high-temperature pulsed valve45, using valve opening times of a few tens of microseconds. The resulting molecular beam was skimmed twice to yield well-collimated pulses of isolated PAH molecules.
In terms of the laser pulses employed, two experiments were performed: (a) irradiating the molecules with the XUV light only, in order to explore its effect on the molecules and to allow the FEL pulse intensity to be tuned to minimize multi-photon effects by the FEL and (b) time-resolved pump-probe experiments employing both the 30.3 nm FEL and 810 nm laser pulses. In the pump-probe experiments, the two laser pulses interacting with the molecules have a defined, adjustable time delay with respect to each other. The pump-probe delay is derived by subtracting the arrival time of the XUV pulse from the arrival time of the IR pulse; hence a positive pump-probe delay refers to the XUV pulse interacting with the molecules first, while a negative pump-probe delay refers to the IR pulse interacting with the molecules first. All pump-probe data were sorted into delay bins according to the bunch arrival monitors of the FLASH FEL in order to account for the FEL jitter46.
Ions were velocity-mapped onto a position-sensitive detector comprising a pair of microchannel plates (MCPs) coupled to a P47 phosphor screen47,48. The ion TOF spectra were recorded by coupling out the voltage drop at the back side of the MCP with a 2 GHz ADC (ADQ412AC-4G-MTCA) through a resistor-capacitor circuit. The ion images from the phosphor screen were captured by a Pixel Imaging Mass Spectrometry 2 (PImMS2) multi-mass imaging sensor housed within a PImMS camera49,50, enabling images to be acquired for all fragment ions on each laser cycle. Data from the PImMS2 sensor was processed to obtain TOF mass spectra and two-dimensional projections of the three-dimensional momentum distribution for each detected product. These were analyzed to extract their kinetic energy and angular distributions37. A conversion curve from spatial coordinates to kinetic energy was created by modeling the instrument using SIMION51.
Electrons were velocity-mapped onto a separate position-sensitive detector mounted opposite to the ion detector. This comprised a pair of MCPs and a P20 phosphor screen. Electron images on the phosphor screen were recorded with a CCD camera (PIKE F145B). Following background correction, the 2D projections of the electron momentum distributions were fully symmetrized (top/bottom/left/right), corrected for ellipticity, and Abel-inverted to obtain time-resolved electron kinetic energy spectra52.
Recoil-frame covariance analysis
Details of the covariance-mapping procedure have been provided in previous publications28–31. Performing this analysis requires the data for each species of interest to be recorded for each experimental cycle, in this case, using the PImMS sensor to record the ion image for each species for every laser pulse. Applying recoil-frame covariance analysis to the ion-imaging data allows the investigation of channels producing two or more cations. Covariance analysis is optimal for regimes such as FLASH1, where the FEL operates at 10 Hz with each laser pulse producing significant quantities of ions (e.g. >100). Conversely, lasers operating in the 1 kHz or faster regime generally produce better results under coincidence conditions, in which fewer than one event is detected per laser pulse.
Briefly, the covariance between two variables A and B is defined as the product of their deviations from their mean values:
| 1 |
where 〈〉 indicates a mean. Here, A and B are the velocities of the two fragments of interest, and 〈AB〉 and 〈A〉〈B〉 are referred to as the ‘coincidence image’ and ‘false covariance image’, respectively. The covariance of a two-dimensional ion image with another two-dimensional ion image produces a four-dimensional covariance dataset; however, such a data set is generally difficult to interpret. In practice, for each laser pulse, the signal for ion A is rotated relative to the reference ion B and summed into the coincidence term. In the common case where more than one A or B ion associated with that laser pulse is detected, the process is repeated for each B ion and a proportionate signal for A is added to the covariance image. The false covariance image is constructed in a similar manner using the mean A and B ion images from the whole data set, i.e., 〈A〉 and 〈B〉. For each pixel in the 〈B〉 image that contains signal, the 〈A〉 image is rotated to the reference direction, and a proportional amount of signal is added to the false covariance image. Subtracting the false covariance image from the coincidence image yields the covariance image. The covariance images shown in this study are referred to as ‘positive covariance images’ where negative values have been set to 0 for clarity.
Fitting of the delay dependent yields
The equations used to derive the PAHn+* relaxation lifetimes are given in Supplementary Note 6. Briefly, the functions used to approximate the LKE electrons, PAH2+, and (1, 2) C3H ions consist of the following components:
A sigmoidal curve centered at t0. t0 is independently determined from the He(1s) photoelectron line, described in more detail in Supplementary Note 4. The sigmoidal curves represent the change in the signal due to the pump pulse altering the molecular charge state; for example, as demonstrated in Fig. 5, the yield of PAH2+ for the PAHs studied is always greater at a pump-probe delay of −0.5 ps compared to +0.5 ps. Before t0, this is interpreted as the IR pulse primarily causing internal excitation and the XUV pulse promoting the excited neutral PAH to PAH2+. After t0, the XUV pulse interacts with the PAH first and can generate PAH2+. Following electronic relaxation to the PAH2+ ground state, the IR pulse can induce dissociation causing the PAH2+ yield to be depleted.
A transient peak function representing electronic relaxation following excitation by the XUV-pump pulse, probed by the IR pulse. Specifically, the XUV pulse is expected to initiate ionization and electronic excitation, and the peak function accounts for the change in IR-probe yield as electronic relaxation takes place. The maximum of this transient appears after t0.
A transient peak function representing electronic relaxation following excitation by the IR-pump pulse, probed by the XUV pulse. The IR pulse primarily creates electronically excited neutral PAH molecules; electronic relaxation will change the effect of the XUV pulse. This maximum of this transient appears before t0, and it is only used when fitting PAH2+.
The model sampled two types of non-linear parameters: relaxation lifetimes of the intermediate PAH species and cross-correlation time, which accounts for the finite duration of the pump and probe pulses, the number of pump and probe photons involved in creating the observed product, and the jitter between the pulses. The parameter distributions were obtained using Monte-Carlo sampling of the likelihood function with the Metropolis algorithm53. The sampling procedure also sampled the determined uncertainty in t0, with the initial t0 value determined by analysis of the helium photoelectrons (see Supplementary Note 4).
Dissociation energies computations
For all three PAHs, structural optimizations on the ground electronic states of the neutral species were performed. Based on these geometries, we calculated the vertical ionization potentials (VIP) and estimated bounds for the dissociation energy corresponding to reactions of the types PAH(PAH-X)X, where q and m are the charge and multiplicity of the species, X = H, C2H2, C3H3, and C4H4, and (PAH-X) refers to a fragment where the moiety X has been removed from the PAH. For this purpose, single-point energy calculations of the PAHs, (PAH-X), and X fragments at the geometries of the ground state optimized PAHs were performed. All calculations were performed at the UKS-DFT/def2-TZVPP level using the ORCA 4.0 software54 with ωB9755 and M06-2x56 functionals. The latter functionals have been shown to reproduce various properties of PAHs and aromatic allotropes of carbon57,58.
Simulation of the beyond-Born-Oppenheimer internal conversion
TSH-MD simulations59 of FLU were done with the SHARC software60–62 interfaced with Orca 454. All the simulations were performed with or based on calculations at the PBE/def2-SV(P) level of theory63,64. Excited states were calculated with TD-DFT at the chosen level of theory using the Tamm-Dancoff approximation (TDA). To speed up the TD-DFT calculations, the resolution-of-identity (RI) approximation was used65–67. Simulations of the FLU+ dynamics excited to the correlation bands were done using a LVC model68 as implemented in SHARC69. More details on the correlation bands can be found in Herve et al.22. The initial conditions for trajectories were sampled from the Wigner distribution of the ground vibrational state. A full description of the procedure including the calculation of the photoionization cross-sections is available in Supplementary Note 8.
Supplementary information
Acknowledgements
This work was supported by the ERC Starting Grant ASTROROT, grant number 638027, and the project CALIPSOplus under the grant agreement 730872 from the EU Framework Programme for Research and Innovation HORIZON 2020. The experimental parts of this research were carried out at beamline BL1 FLASH at DESY, a member of the Helmholtz Association (HGF). We acknowledge the Max Planck Society for funding the development and the initial operation of the CAMP end-station within the Max Planck Advanced Study Group at CFEL and for providing this equipment for CAMP@FLASH. The installation of CAMP@FLASH was partially funded by the BMBF grants 05K10KT2, 05K13KT2, 05K16KT3, and 05K10KTB from FSP-302. We acknowledge financial support by the European Union’s Horizon 2020 research and innovation program under the Marie Skłodowska-Curie Grant Agreement 641789 “Molecular Electron Dynamics investigated by Intense Fields and Attosecond Pulses” (MEDEA), the Clusters of Excellence “Center for Ultrafast Imaging” (CUI, EXC 1074, ID 194651731), the “Advanced Imaging of Matter” (AIM, EXC 2056, ID 390715994) of the Deutsche Forschungsgemeinschaft (DFG), and the Helmholtz Gemeinschaft through the “Impuls-und Vernetzungsfonds”. In addition, the project was supported by The Netherlands Organization for Scientific Research (NWO) and is part of the Dutch Astrochemistry Network (DAN) II (Project No. 648.000.029). S.M., J.L., J.P., and P.E.-J. acknowledge support from the Swedish Research Council and the Swedish Foundation for Strategic Research. The authors are additionally thankful for support from the following funding bodies: the UK EPSRC (M. Brouard and C.V. - EP/L005913/1 and EP/V026690/1; M. Burt - EP/S028617/1), STFC (PNPAS award and mini-IPS Grant No. ST/J002895/1), the Chemical Sciences, Geosciences, and Biosciences Division, Office of Basic Energy Sciences, Office of Science, US Department of Energy (F.Z. - DE-FG02-86ER13491); the National Science Foundation (D. Rolles - PHYS-1753324); and the Helmholtz Initiative and Networking Fund through the Young Investigators Group Program (S.B.). This research was supported in part through the Maxwell computational resources operated at Deutsches Elektronen-Synchrotron DESY, Hamburg, Germany.
Author contributions
B.M. and M.S. conceived and designed the experiments. J.W.L.L., P.C., S.M., A.L.S., S.G., F.A., R.B., X.C., S.D, B.E., L.H., D.H., M.J., M.M.K., H.K., J.L., A.L., D.L., R.M., E.M., T.M., P.O., C.P., J.P., D. Ramm, D. Rompotis, N.S., S. Trippel, J.W., F.Z., S.B., M. Burt, D. Rolles, S. Techert, P.J., B.M., and M.S. performed the experiments. J.W.L.L., D.S.T., P.C., S.M., A.L.S., S.G., D.G., and E.M. analyzed the data. D.S.T. performed the theoretical simulations. J.W.L.L., D.S.T., P.C., S.M., A.S., S.G., F.A., M. Burt, J.K., A.R., D. Rolles, P.E.-J., M. Brouard, C.V., B.M., and M.S. performed detailed discussions of the results. J.W.L.L., D.S.T., B.M., and M.S. wrote the manuscript.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author (M.S.) upon reasonable request.
Code availability
New custom codes were used to fit the experimental data and to generate the theoretical results in this manuscript. The source codes are available in the following link: https://stash.desy.de/projects/CFA/repos/pahscriptsanddata/browse.
Competing interests
The authors declare no competing interests.
Footnotes
Peer review information Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
These authors contributed equally: J. W. L. Lee, D. S. Tikhonov.
Contributor Information
B. Manschwetus, Email: bastian.manschwetus@desy.de
M. Schnell, Email: melanie.schnell@desy.de
Supplementary information
The online version contains supplementary material available at 10.1038/s41467-021-26193-z.
References
- 1.Joblin C, Tielens A. 25 years of pah hypothesis. Eur. Astronomical Soc. Publ. Ser. 2011;46:3–10. [Google Scholar]
- 2.Lagache G, et al. Polycyclic aromatic hydrocarbon contribution to the infrared output energy of the universe at z ≈ 2. Astrophys. J. Suppl. Ser. 2004;154:112. doi: 10.1086/422392. [DOI] [Google Scholar]
- 3.Leach S. Laboratory studies of polycyclic aromatic hydrocarbons, fullerenes and linear carbon chains in an astrophysical context. Planet. Space Sci. 1995;43:1153–1164. doi: 10.1016/0032-0633(95)00046-8. [DOI] [Google Scholar]
- 4.Dabestani R, Ivanov IN. A compilation of physical, spectroscopic and photophysical properties of polycyclic aromatic hydrocarbons. Photochem. Photobiol. 1999;70:10–34. [Google Scholar]
- 5.Herbst E, van Dishoeck EF. Complex organic interstellar molecules. Annu. Rev. Astron. Astrophys. 2009;47:427–480. doi: 10.1146/annurev-astro-082708-101654. [DOI] [Google Scholar]
- 6.Tielens A. 25 years of pah hypothesis. EAS Publ. Ser. 2011;46:3–10. doi: 10.1051/eas/1146001. [DOI] [Google Scholar]
- 7.Snow TP, Le Page V, Keheyan Y, Bierbaum VM. The interstellar chemistry of pah cations. Nature. 1998;391:259–260. doi: 10.1038/34602. [DOI] [PubMed] [Google Scholar]
- 8.Jochims H, Baumgärtel H, Leach S. Photoionization quantum yields of polycyclic aromatic hydrocarbons. Astron. Astrophys. 1996;314:1003–1009. [Google Scholar]
- 9.Jochims H, Rühl E, Baumgärtel H, Tobita S, Leach S. Vuv peaks in absorption spectra and photoion yield curves of polycyclic aromatic hydrocarbons and related compounds. Int. J. Mass Spectrom. Ion-. Process. 1997;167:35–53. doi: 10.1016/S0168-1176(97)00031-1. [DOI] [Google Scholar]
- 10.Jochims H, Baumgärtel H, Leach S. Structure-dependent photostability of polycyclic aromatic hydrocarbon cations: laboratory studies and astrophysical implications. Astrophys. J. 1999;512:500. doi: 10.1086/306752. [DOI] [Google Scholar]
- 11.Boschman L, Cazaux S, Spaans M, Hoekstra R, Schlathölter T. H2 formation on pahs in photodissociation regions: a high-temperature pathway to molecular hydrogen. Astron. Astrophys. 2015;579:A72. doi: 10.1051/0004-6361/201323165. [DOI] [Google Scholar]
- 12.Reitsma G, et al. Near edge x-ray absorption mass spectrometry on coronene. J. Chem. Phys. 2015;142:024308. doi: 10.1063/1.4905471. [DOI] [PubMed] [Google Scholar]
- 13.Leach S, Eland J, Price S. Formation and dissociation of dications of naphthalene, azulene and related heterocyclic compounds. J. Phys. Chem. 1989;93:7575–7583. doi: 10.1021/j100359a013. [DOI] [Google Scholar]
- 14.Leach S, Eland J, Price S. Formation and dissociation of dications of naphthalene-d8. J. Phys. Chem. 1989;93:7583–7593. doi: 10.1021/j100359a014. [DOI] [Google Scholar]
- 15.Ruehl E, Price SD, Leach S. Single and double photoionization processes in naphthalene between 8 and 35 ev. J. Phys. Chem. 1989;93:6312–6321. doi: 10.1021/j100354a011. [DOI] [Google Scholar]
- 16.Domcke W, Yarkony DR. Role of conical intersections in molecular spectroscopy and photoinduced chemical dynamics. Annu. Rev. Phys. Chem. 2012;63:325–352. doi: 10.1146/annurev-physchem-032210-103522. [DOI] [PubMed] [Google Scholar]
- 17.Joalland B, Mori T, Martínez TJ, Suits AG. Photochemical dynamics of ethylene cation c2h4+ J. Phys. Chem. Lett. 2014;5:1467–1471. doi: 10.1021/jz500352x. [DOI] [PubMed] [Google Scholar]
- 18.Galbraith M, et al. Few-femtosecond passage of conical intersections in the benzene cation. Nat. Commun. 2017;8:1–7. doi: 10.1038/s41467-016-0009-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Bazzi S, Welsch R, Vendrell O, Santra R. Challenges in xuv photochemistry simulations: a case study on ultrafast fragmentation dynamics of the benzene radical cation. J. Phys. Chem. A. 2018;122:1004–1010. doi: 10.1021/acs.jpca.7b11543. [DOI] [PubMed] [Google Scholar]
- 20.Curchod BF, Martínez TJ. Ab initio nonadiabatic quantum molecular dynamics. Chem. Rev. 2018;118:3305–3336. doi: 10.1021/acs.chemrev.7b00423. [DOI] [PubMed] [Google Scholar]
- 21.Marciniak, A. et al. XUV excitation followed by ultrafast non-adiabatic relaxation in PAH molecules as a femto-astrochemistry experiment. Nat. Commun.6, 7909 (2015). [DOI] [PMC free article] [PubMed]
- 22.Hervé, M. et al. Ultrafast dynamics of correlation bands following xuv molecular photoionization. Nat. Phys.17, 327–331 (2021).
- 23.Reitsma G, et al. Delayed relaxation of highly excited cationic states in naphthalene. J. Phys. Chem. A. 2019;123:3068–3073. doi: 10.1021/acs.jpca.8b10444. [DOI] [PubMed] [Google Scholar]
- 24.Marciniak A, et al. Electron correlation driven non-adiabatic relaxation in molecules excited by an ultrashort extreme ultraviolet pulse. Nat. Commun. 2019;10:1–8. doi: 10.1038/s41467-018-08131-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ackermann WA, et al. Operation of a free-electron laser from the extreme ultraviolet to the water window. Nat. Photonics. 2007;1:336–342. doi: 10.1038/nphoton.2007.76. [DOI] [Google Scholar]
- 26.Craig N, et al. TheExtreme ultraviolet ExplorerStellar spectral atlas. Astrophys. J. Suppl. Ser. 1997;113:131–193. doi: 10.1086/313052. [DOI] [Google Scholar]
- 27.Frasinski LJ. Covariance mapping techniques. J. Phys. B: At., Mol. Optical Phys. 2016;49:152004. doi: 10.1088/0953-4075/49/15/152004. [DOI] [Google Scholar]
- 28.Slater CS, et al. Covariance imaging experiments using a pixel-imaging mass-spectrometry camera. Phys. Rev. A. 2014;89:011401. doi: 10.1103/PhysRevA.89.011401. [DOI] [Google Scholar]
- 29.Slater CS, et al. Coulomb-explosion imaging using a pixel-imaging mass-spectrometry camera. Phys. Rev. A. 2015;91:053424. doi: 10.1103/PhysRevA.91.053424. [DOI] [Google Scholar]
- 30.Allum F, et al. Coulomb explosion imaging of ch3i and ch2cli photodissociation dynamics. J. Chem. Phys. 2018;149:204313. doi: 10.1063/1.5041381. [DOI] [PubMed] [Google Scholar]
- 31.Amini K, et al. Alignment, orientation, and coulomb explosion of difluoroiodobenzene studied with the pixel imaging mass spectrometry (pimms) camera. J. Chem. Phys. 2017;147:013933. doi: 10.1063/1.4982220. [DOI] [PubMed] [Google Scholar]
- 32.Hagan D, Eland J. Formation and decay of doubly charged ions in n-alkanes from methane to triacontane. Org. Mass Spectrom. 1992;27:855–863. doi: 10.1002/oms.1210270803. [DOI] [Google Scholar]
- 33.Vallance C, Heathcote D, Lee JW. Covariance-map imaging: a powerful tool for chemical dynamics studies. J. Phys. Chem. A. 2021;125:1117–1133. doi: 10.1021/acs.jpca.0c10038. [DOI] [PubMed] [Google Scholar]
- 34.Eland J. The dynamics of three-body dissociations of dications studied by the triple coincidence technique pepipico. Mol. Phys. 1987;61:725–745. doi: 10.1080/00268978700101421. [DOI] [Google Scholar]
- 35.West B, et al. Unimolecular reaction energies for polycyclic aromatic hydrocarbon ions. Phys. Chem. Chem. Phys. 2018;20:7195–7205. doi: 10.1039/C7CP07369K. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.West BJ, Lesniak L, Mayer PM. Why do large ionized polycyclic aromatic hydrocarbons not lose c2h2? J. Phys. Chem. A. 2019;123:3569–3574. doi: 10.1021/acs.jpca.9b01879. [DOI] [PubMed] [Google Scholar]
- 37.Roberts G, Nixon J, Lecointre J, Wrede E, Verlet J. Toward real-time charged-particle image reconstruction using polar onion-peeling. Rev. Sci. Instrum. 2009;80:053104. doi: 10.1063/1.3126527. [DOI] [PubMed] [Google Scholar]
- 38.Vishnevskiy YV, Schwabedissen J, Rykov AN, Kuznetsov VV, Makhova NN. Conformational and bonding properties of 3, 3-dimethyl-and 6, 6-dimethyl-1, 5-diazabicyclo [3.1. 0] hexane: a case study employing the monte carlo method in gas electron diffraction. J. Phys. Chem. A. 2015;119:10871–10881. doi: 10.1021/acs.jpca.5b08228. [DOI] [PubMed] [Google Scholar]
- 39.Bockhorn H, Fetting F, Wenz H. Investigation of the formation of high molecular hydrocarbons and soot in premixed hydrocarbon-oxygen flames. Ber. der Bunsenges. f.ür. physikalische Chem. 1983;87:1067–1073. doi: 10.1002/bbpc.19830871121. [DOI] [Google Scholar]
- 40.Richter H, Howard JB. Formation of polycyclic aromatic hydrocarbons and their growth to soot–a review of chemical reaction pathways. Prog. Energy Combust. Sci. 2000;26:565–608. doi: 10.1016/S0360-1285(00)00009-5. [DOI] [Google Scholar]
- 41.Shukla B, Koshi M. A novel route for pah growth in haca based mechanisms. Combust. flame. 2012;159:3589–3596. doi: 10.1016/j.combustflame.2012.08.007. [DOI] [Google Scholar]
- 42.Feldhaus J. FLASH—the first soft x-ray free electron laser (FEL) user facility. J. Phys. B: At., Mol. Optical Phys. 2010;43:194002. doi: 10.1088/0953-4075/43/19/194002. [DOI] [Google Scholar]
- 43.Erk B, et al. CAMP@FLASH: an end-station for imaging, electron- and ion-spectroscopy, and pump–probe experiments at the FLASH free-electron laser. J. Synchrotron Radiat. 2018;25:1529–1540. doi: 10.1107/S1600577518008585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Redlin H, et al. The FLASH pump–probe laser system: setup, characterization and optical beamlines. Nucl. Instrum. Methods Phys. Res. Sect. A: Accelerators, Spectrometers, Detect. Associated Equip. 2011;635:S88–S93. doi: 10.1016/j.nima.2010.09.159. [DOI] [Google Scholar]
- 45.Even U. The even-lavie valve as a source for high intensity supersonic beam. EPJ Tech. Instrum. 2015;2:17. doi: 10.1140/epjti/s40485-015-0027-5. [DOI] [Google Scholar]
- 46.Savelyev E, et al. Jitter-correction for ir/uv-xuv pump-probe experiments at the flash free-electron laser. N. J. Phys. 2017;19:043009. doi: 10.1088/1367-2630/aa652d. [DOI] [Google Scholar]
- 47.Eppink AT, Parker DH. Velocity map imaging of ions and electrons using electrostatic lenses: application in photoelectron and photofragment ion imaging of molecular oxygen. Rev. Sci. Instrum. 1997;68:3477–3484. doi: 10.1063/1.1148310. [DOI] [Google Scholar]
- 48.Parker DH, Eppink AT. Photoelectron and photofragment velocity map imaging of state-selected molecular oxygen dissociation/ionization dynamics. J. Chem. Phys. 1997;107:2357–2362. doi: 10.1063/1.474624. [DOI] [Google Scholar]
- 49.Clark AT, et al. Multimass velocity-map imaging with the pixel imaging mass spectrometry (pimms) sensor: an ultra-fast event-triggered camera for particle imaging. J. Phys. Chem. A. 2012;116:10897–10903. doi: 10.1021/jp309860t. [DOI] [PubMed] [Google Scholar]
- 50.Amini K, et al. Three-dimensional imaging of carbonyl sulfide and ethyl iodide photodissociation using the pixel imaging mass spectrometry camera. Rev. Sci. Instrum. 2015;86:103113. doi: 10.1063/1.4934544. [DOI] [PubMed] [Google Scholar]
- 51.Dahl D, Delmore J, Appelhans A. Simion pc/ps2 electrostatic lens design program. Rev. Sci. Instrum. 1990;61:607–609. doi: 10.1063/1.1141932. [DOI] [Google Scholar]
- 52.Vrakking MJ. An iterative procedure for the inversion of two-dimensional ion/photoelectron imaging experiments. Rev. Sci. Instrum. 2001;72:4084–4089. doi: 10.1063/1.1406923. [DOI] [Google Scholar]
- 53.Press, W. H., Teukolsky, S. A., Vetterling, W. T. & Flannery, B. P. Numerical Recipes 3rd edition: The Art of Scientific Computing (Cambridge university press, 2007).
- 54.Neese F. The orca program system. Wiley Interdiscip. Rev.: Computational Mol. Sci. 2012;2:73–78. [Google Scholar]
- 55.Chai J-D, Head-Gordon M. Systematic optimization of long-range corrected hybrid density functionals. J. Chem. Phys. 2008;128:084106. doi: 10.1063/1.2834918. [DOI] [PubMed] [Google Scholar]
- 56.Zhao Y, Truhlar DG. The m06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four m06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008;120:215–241. doi: 10.1007/s00214-007-0310-x. [DOI] [Google Scholar]
- 57.Rayne S, Forest K. Benchmarking semiempirical, hartree–fock, dft, and mp2 methods against the ionization energies and electron affinities of short- through long-chain [n]acenes and [n]phenacenes. Can. J. Chem. 2016;94:251–258. doi: 10.1139/cjc-2015-0526. [DOI] [Google Scholar]
- 58.Zhou B, et al. Benchmark study of ionization potentials and electron affinities of armchair single-walled carbon nanotubes using density functional theory. J. Phys.: Condens. Matter. 2018;30:215501. doi: 10.1088/1361-648X/aabd18. [DOI] [PubMed] [Google Scholar]
- 59.Tully JC, Preston RK. Trajectory surface hopping approach to nonadiabatic molecular collisions: The reaction of h+ with d2. J. Chem. Phys. 1971;55:562–572. doi: 10.1063/1.1675788. [DOI] [Google Scholar]
- 60.Mai, S. et al. Sharc2.1: Surface hopping including arbitrary couplings – program package for non-adiabatic dynamics, sharc-md.org. https://sharc-md.org/?page_id=286 (2019).
- 61.Richter M, Marquetand P, González-Vázquez J, Sola I, González L. SHARC: ab initio molecular dynamics with surface hopping in the adiabatic representation including arbitrary couplings. J. Chem. Theory Comput. 2011;7:1253–1258. doi: 10.1021/ct1007394. [DOI] [PubMed] [Google Scholar]
- 62.Mai S, Marquetand P, González L. Nonadiabatic dynamics: The sharc approach. WIREs Comput. Mol. Sci. 2018;8:e1370. doi: 10.1002/wcms.1370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Perdew JP, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996;77:3865–3868. doi: 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- 64.Weigend F, Ahlrichs R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005;7:3297–3305. doi: 10.1039/b508541a. [DOI] [PubMed] [Google Scholar]
- 65.Weigend F. Accurate Coulomb–fitting basis sets for H to Rn. Phys. Chem. Chem. Phys. 2006;8:1057–1065. doi: 10.1039/b515623h. [DOI] [PubMed] [Google Scholar]
- 66.Neese F, Wennmohs F, Hansen A, Becker U. Efficient, approximate and parallel Hartree–Fock and hybrid DFT calculations. A ‘chain-of-spheres’ algorithm for the Hartree–Fock exchange. Chem. Phys. 2009;356:98–109. doi: 10.1016/j.chemphys.2008.10.036. [DOI] [Google Scholar]
- 67.Izsák R, Neese F. An overlap fitted chain of spheres exchange method. J. Chem. Phys. 2011;135:144105. doi: 10.1063/1.3646921. [DOI] [PubMed] [Google Scholar]
- 68.Köuppel, H., Domcke, W. & Cederbaum, L. S. Multimode Molecular Dynamics Beyond the Born-Oppenheimer Approximation, 59–246 (John Wiley & Sons, Ltd, 1984).
- 69.Plasser F, Gómez S, Menger MFSJ, Mai S, González L. Highly efficient surface hopping dynamics using a linear vibronic coupling model. Phys. Chem. Chem. Phys. 2019;21:57–69. doi: 10.1039/C8CP05662E. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data that support the plots within this paper and other findings of this study are available from the corresponding author (M.S.) upon reasonable request.
New custom codes were used to fit the experimental data and to generate the theoretical results in this manuscript. The source codes are available in the following link: https://stash.desy.de/projects/CFA/repos/pahscriptsanddata/browse.