Simulation is an important tool within epidemiology for both learning and developing new methodology (1–5). Unfortunately, few epidemiology training programs teach basic simulation methods. Briefly, when conducting a simulation experiment, we generally follow the same basic steps. We first decide which variables to include, as well as their distributions and associations—often aided by a causal diagram. We then generate those variables by sampling from their specified distributions and estimate whatever target parameter is of interest (e.g., sample average or causal effect). We finally repeat the process multiple times, building a distribution for the target parameter from the estimates obtained in each replicate.
Table 1.
Estimated Marginal Probabilities Under Different Simulation Specifications, in a Single Simulation of 10,000 Units
| Simulationa | Y Model Intercept | X Model Intercept | L Model Intercept |
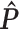 (L=1)
(L=1) |
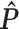 (X=1)
(X=1) |
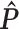 (Y=1)
(Y=1) |
|---|---|---|---|---|---|---|
| Generate Y | 0.3 | N/A | N/A | N/A | N/A | 0.295 |
| Generate X and Y | 0.3 | 0.5 | N/A | N/A | 0.490 | 0.400 |
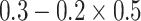
|
0.5 | N/A | N/A | 0.490 | 0.288 | |
| Generate L, X, and Y | 0.3 | 0.5 | 0.8 | 0.799 | 0.577 | 0.497 |
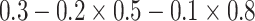
|
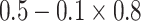
|
0.8 | 0.799 | 0.501 | 0.301 |
Abbreviations: 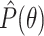 , estimated
probability of
, estimated
probability of 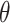 ; NA, not
applicable.
; NA, not
applicable.
a Variables generated: Y, outcome; X, exposure; L, confounder.
Here, we briefly demonstrate one key simulation practice: the balancing intercept, which allows us to specify in the first step above the marginal mean of a variable and see that mean preserved (in expectation) in the simulated sample. This is attractive because the marginal probability is an easily interpretable quantity. Additionally, if the simulation is designed to mimic real data, the marginal probability of a variable is often a known, reported characteristic of the data (although, conversely, there could be areas in which researchers know more about the conditional probability of that variable). Use of a balancing intercept also makes validation of simulation code simple; regardless of how other simulation parameters change, as long as the balancing intercept is specified correctly, the marginal probability of a variable in the simulated data set should match the desired marginal probability.
Suppose we were only interested in generating a binary outcome 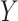 for
for
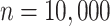 simulated individuals, from
a Bernoulli distribution with probability
simulated individuals, from
a Bernoulli distribution with probability  . We can express
this probability in terms of an intercept-only model:
. We can express
this probability in terms of an intercept-only model: 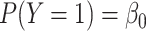 , where
, where
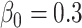 . It is then relatively
easy to use any software program of one’s choosing to generate
. It is then relatively
easy to use any software program of one’s choosing to generate 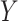 (see
Web Table 1 and the Web Appendix, available at https://www.doi.org/10.1093/aje/kwab039, for example code). Although
here we focus on binary
(see
Web Table 1 and the Web Appendix, available at https://www.doi.org/10.1093/aje/kwab039, for example code). Although
here we focus on binary 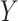 , much of the discussion below also
applies to continuous
, much of the discussion below also
applies to continuous 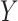 .
.
The simulation becomes slightly more complicated when we expand our simulation to include
a binary exposure 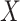 (with
(with 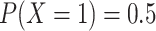 ), which affects
), which affects
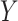 . Now, when we generate
. Now, when we generate
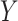 , we need to account for the
association
, we need to account for the
association 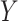 has with
has with 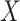 . This
is commonly done by specifying a model for the conditional probability of
. This
is commonly done by specifying a model for the conditional probability of
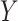 given
given 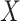 ,
,
 , rather than
, rather than
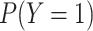 . One could also model the
joint distribution directly. For example, we can use the linear model (specifically, fit
with an identity link function):
. One could also model the
joint distribution directly. For example, we can use the linear model (specifically, fit
with an identity link function):
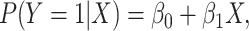 |
where 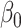 is the probability of
is the probability of
 when
when 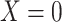 and
and
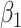 is the risk difference for
is the risk difference for
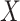 , which we set to be
, which we set to be
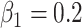 . The question here is:
How should we determine the appropriate value of
. The question here is:
How should we determine the appropriate value of 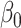 in this model? One approach would be to add
in this model? One approach would be to add 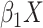 to the
intercept-only model above:
to the
intercept-only model above:
 |
This is intuitive because when 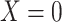 in the above formula,
in the above formula,
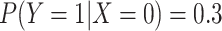 . We will refer to this
intercept as the “standard intercept.”
. We will refer to this
intercept as the “standard intercept.”
The main drawback of the standard intercept is that the marginal probability of
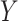 in our simulated sample,
in our simulated sample,
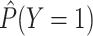 , will not be the same as
the desired
, will not be the same as
the desired 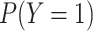 as long as
as long as
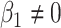 . We see this in our
simulation (Table 1). In the scenario where
. We see this in our
simulation (Table 1). In the scenario where 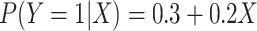 ,
,
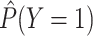 was 0.400, rather than
the desired 0.3. We can show why this occurs using the law of total probability:
was 0.400, rather than
the desired 0.3. We can show why this occurs using the law of total probability:
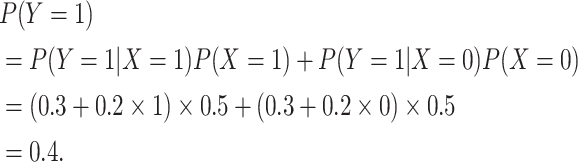 |
If we do wish to preserve the specified marginal probability, we can replace the standard
intercept with what we refer to here as the “balancing intercept.” To do this, we could
specify in the model for 
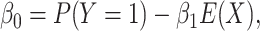 |
where 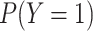 is the desired marginal
probability of
is the desired marginal
probability of 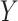 . This intercept balances out the
influence of the effect of
. This intercept balances out the
influence of the effect of 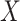 on
on 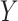 on the
expectation of
on the
expectation of 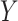 by including an offset that
multiplies the effect size for
by including an offset that
multiplies the effect size for 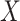 by the expected value of
by the expected value of
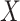 . For binary variables, the expected
value of
. For binary variables, the expected
value of  is the marginal probability,
is the marginal probability,
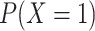 ; if
; if 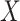 were
continuous, the expected value would be the mean. Note that the sign is opposite of that
in the formula for the conditional probability; that is, for (positive)
were
continuous, the expected value would be the mean. Note that the sign is opposite of that
in the formula for the conditional probability; that is, for (positive)
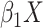 , we include the term
, we include the term
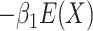 . In the simulation
scenario in which
. In the simulation
scenario in which 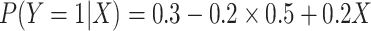 , we
estimated that
, we
estimated that 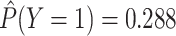 , which is closer
to the
, which is closer
to the 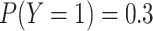 we desired. The difference
here is largely due to random error, which decreases if we increase
we desired. The difference
here is largely due to random error, which decreases if we increase
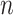 .
.
The approach presented here can be extended to account for more variables. Let us add to
our simulation a binary confounder 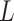 , with
, with
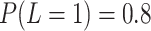 , which affects the
exposure
, which affects the
exposure 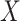 and the outcome
and the outcome
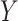 . Accordingly, in our simulation, we
model the conditional probabilities of
. Accordingly, in our simulation, we
model the conditional probabilities of 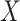 and
and
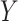 given
given 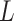 , as
follows:
, as
follows:
 |
 |
Note that we first simulate 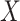 based on
based on 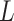 , then
, then
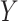 based on
based on 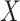 and
and
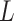 together. Furthermore, each
equation includes a balancing intercept:
together. Furthermore, each
equation includes a balancing intercept:
 |
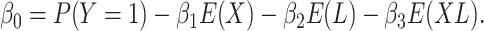 |
In our simulation, we specified 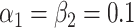 and
and
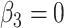 (i.e., no interaction
between
(i.e., no interaction
between 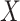 and
and 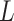 on the
additive scale) and estimated that
on the
additive scale) and estimated that 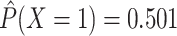 and
and
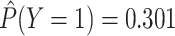 .
.
We can model the conditional probabilities using functions other than the linear model.
In fact, when simulating a binary variable, we might prefer to use the inverse of the
logit function (expit function), which will guarantee that
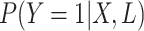 will fall between (0, 1).
A linear model, on the other hand, could lead to probabilities falling outside this
range (e.g., a probability of 1.04). The expit model (see Web Table 2
and the Web Appendix for code) takes the form:
will fall between (0, 1).
A linear model, on the other hand, could lead to probabilities falling outside this
range (e.g., a probability of 1.04). The expit model (see Web Table 2
and the Web Appendix for code) takes the form:
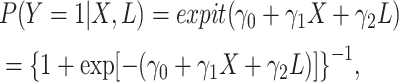 |
where 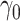 is the intercept,
is the intercept,
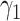 is the conditional log
odds ratio (log(OR)) for
is the conditional log
odds ratio (log(OR)) for 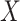 , and
, and 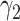 is the conditional log(OR) for
is the conditional log(OR) for
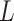 . The standard intercept for this
model would be the marginal log odds of
. The standard intercept for this
model would be the marginal log odds of 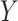 :
:
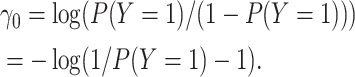 |
We can instead specify a balancing intercept, as follows:
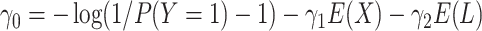 |
The balancing intercept allows a researcher to set a desired marginal probability for
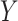 and then see that same probability
manifested in the resulting simulation (in expectation). We should note, though, that
the balancing intercept approach is an approximation and could fail as the model for the
conditional probability of
and then see that same probability
manifested in the resulting simulation (in expectation). We should note, though, that
the balancing intercept approach is an approximation and could fail as the model for the
conditional probability of 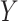 becomes extreme (e.g., when
variables in the model have complex distributions). Even so, we believe that using a
balancing intercept is a best practice for simulation design that deserves wider
attention and adoption.
becomes extreme (e.g., when
variables in the model have complex distributions). Even so, we believe that using a
balancing intercept is a best practice for simulation design that deserves wider
attention and adoption.
Supplementary Material
ACKNOWLEDGMENTS
All authors contributed equally to this work.
This work was supported in part by National Institutes of Health grants R01 HD093602 and K01 AI125087.
We thank Dr. Stephen Cole for his insightful and thoughtful feedback on a draft of this paper. We also thank Dr. Tim Morris for providing STATA code to match our R and SAS code.
Conflicts of interest: none declared.
REFERENCES
- 1.Hodgson T, Burke M. On simulation and the teaching of statistics. Teach Stat. 2000;22:91–96. [Google Scholar]
- 2.Westreich D, Cole SR, Schisterman EF, et al. A simulation study of finite-sample properties of marginal structural cox proportional hazards models. Stat Med. 2012;31(19):2098–2109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Lesko CR, Lau B. Bias due to confounders for the exposure-competing risk relationship. Epidemiology. 2017;28(1):20–27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Jurek AM, Greenland S, Maldonado G, et al. Proper interpretation of non-differential misclassification effects: expectations vs observations. Int J Epidemiol. 2005;34(3):680–687. [DOI] [PubMed] [Google Scholar]
- 5.Rudolph JE, Cole SR, Eron JJ, et al. Estimating human immunodeficiency virus (HIV) prevention effects in low-incidence settings. Epidemiology. 2019;30(3):358–364. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


