Abstract
ALL MODELS ARE WRONG, SOME ARE USEFUL, AND OTHERS ARE NOT AS USEFUL AS THEY SEEM
In observational studies, confounding is a fundamental threat to causal inference. Consider an epidemiologic study of the causal effect of exposure X on disease, D. Further, consider another risk factor, F. If F is unrelated to X, we might characterize F as a “nonconfounding risk factor for disease.” Intuitively, we might expect that conditioning on nonconfounding risk factor, F, will have no impact on our effect estimates for exposure. However, this intuition has been demonstrated to be incorrect and, in some cases, dramatically so (1, 2). Specifically, models of the odds ratio conditioned on very strong nonconfounding risk factors can result in gross differences between unadjusted and adjusted estimates because of “noncollapsibility” of the odds ratio and not due to control for confounding. Noncollapsibility is a long-standing point of confusion. In this paper, we describe noncollapsibility and clarify how it can occur and influence epidemiologic research.
CONFOUNDING, NONCOLLAPSIBILITY, AND THE CHANGE-IN-ESTIMATE APPROACH
For a given population, we define confounding and causal effects of exposure
X using counterfactuals; consider a summary parameter
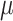 (e.g., risk) in the population if everyone were
exposed (
(e.g., risk) in the population if everyone were
exposed ( ), if everyone were unexposed
(
), if everyone were unexposed
( ), and a comparison thereof as a causal
effect (say, a counterfactual risk difference, as
), and a comparison thereof as a causal
effect (say, a counterfactual risk difference, as  ). Confounding by
disease risk factor F occurs when this risk difference is unequal to the
observed difference in risk between the exposed (
). Confounding by
disease risk factor F occurs when this risk difference is unequal to the
observed difference in risk between the exposed ( ) and unexposed
(
) and unexposed
(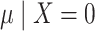 ) because of a correlation between
X and F.
) because of a correlation between
X and F.
Noncollapsibility refers to the circumstance where the measure of association conditioned on
some factor is unequal to the marginal measure collapsed over strata of that factor, and is a
property of the model (i.e., a population-level phenomenon) rather than the estimation process.
Mathematically, noncollapsibility can be described in terms of expectation, as in the
circumstance when 
In practice, control for confounding by a variable F often entails consideration of models conditional on F (by stratification, or regression-based adjustment) and models collapsed across F. The change-in-estimate approach for evaluating confounding by F compares estimates from these two approaches to evaluate the difference between them. This comparison is premised on noncollapsibility being equivalent to confounding; indeed, the change-in-estimate approach has been called the “collapsibility definition of confounding” (2). However, as noted above (1, 2), and as we show here, there is a problem with this approach because noncollapsibility can occur in the absence of confounding. In this paper, we describe conditions that lead to noncollapsibility in the absence of confounding and illustrate this phenomenon under additive and multiplicative risk models.
MODELS THAT ARE WRONG AND NOT SO USEFUL
Noncollapsibility of the odds ratio in the absence of confounding under additive risk
As described above, examples have been described that illustrate how conditioning on nonconfounding risk factors can cause the appearance of substantial confounding based on the change-in-effect approach, given that expected values from marginal and conditional models can be significantly different. However, these examples are based on unlikely, extreme relationships among X, F, and D (1, 2). These extreme scenarios do not provide information about how large the magnitude of noncollapsibility might be in the absence of confounding more generally. To address this question, we generated summary data with dichotomous exposure X, nonconfounding risk factor F, and outcome, Y, using additive risk as the causal data generating mechanism:
 |
We considered a range of baseline risks (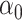 = 1%–50%) and causal risk
differences for X (
= 1%–50%) and causal risk
differences for X ( = 0.5%–30%) and for F
(
= 0.5%–30%) and for F
( = 0.5%–30%), and we calculated expected
conditional and unconditional measures in order to address noncollapsibility as a population
level phenomenon. Circumstances where risks exceeded 100% were not considered. Results under a
subset of these conditions are shown in Table 1 (for
additional results, see Web Figures 1–3, available at https://doi.org/10.1093/aje/kwaa267).
= 0.5%–30%), and we calculated expected
conditional and unconditional measures in order to address noncollapsibility as a population
level phenomenon. Circumstances where risks exceeded 100% were not considered. Results under a
subset of these conditions are shown in Table 1 (for
additional results, see Web Figures 1–3, available at https://doi.org/10.1093/aje/kwaa267).
Table 1.
Noncollapsibility in the Absence of Confounding Under Additive Risk: Unadjusted, Stratum-Specific, and Adjusted Odds Ratios and Risk Ratios for the Effect of Exposure X With and Without Consideration of a Nonconfounding Risk Factor F
| Simulation Parameters—Risk | OR Estimates | RR Estimates | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| RD X | RD F |

|
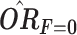
|
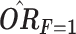
|

|

|
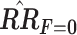
|

|

|
P int a |
| Baseline = 0.01 b | ||||||||||
| 0.04 | 0.94 | 1.17 | 5.21 | 5.21 | 5.21 | 1.08 | 5.00 | 1.04 | 1.08 | 0.04 |
| 0.04 | 0.90 | 1.24 | 5.21 | 1.88 | 3.16 | 1.17 | 5.00 | 1.04 | 1.17 | <0.01 |
| Baseline = 0.10 c | ||||||||||
| 0.30 | 0.50 | 3.60 | 6.00 | 6.00 | 6.00 | 2.13 | 4.00 | 1.50 | 2.13 | <0.01 |
| 0.30 | 0.30 | 4.27 | 6.00 | 0 | 5.00 | 2.71 | 4.00 | 1.75 | 2.71 | <0.01 |
| Baseline = 0.01 | ||||||||||
| 0.20 | 0.20 | 5.50 | 26.32 | 2.61 | 6.42 | 4.33 | 21.00 | 1.95 | 4.33 | <0.01 |
| 0.20 | 0.10 | 8.47 | 26.32 | 3.64 | 9.03 | 6.71 | 21.00 | 2.82 | 6.71 | <0.01 |
| 0.20 | 0.01 | 21.32 | 26.32 | 13.82 | 21.36 | 17.00 | 21.00 | 11.00 | 17.00 | <0.01 |
| 0.10 | 0.20 | 2.98 | 12.24 | 1.69 | 3.33 | 2.67 | 11.00 | 1.48 | 2.67 | <0.01 |
| 0.10 | 0.10 | 4.30 | 12.24 | 2.15 | 4.52 | 3.86 | 11.00 | 1.91 | 3.86 | <0.01 |
| 0.10 | 0.01 | 10.01 | 12.24 | 6.68 | 10.03 | 9.00 | 11.00 | 6.00 | 9.00 | <0.01 |
| 0.05 | 0.20 | 1.94 | 6.32 | 1.32 | 2.09 | 1.83 | 6.00 | 1.24 | 1.83 | <0.01 |
| 0.05 | 0.10 | 2.56 | 6.32 | 1.54 | 2.66 | 2.43 | 6.00 | 1.45 | 2.43 | <0.01 |
| 0.05 | 0.01 | 5.27 | 6.32 | 3.69 | 5.27 | 5.00 | 6.00 | 0 | 5.00 | 0.02 |
| 0.01 | 0.20 | 1.18 | 2.02 | 1.06 | 1.21 | 1.17 | 2.00 | 1.05 | 1.17 | <0.01 |
| 0.01 | 0.10 | 1.30 | 2.02 | 1.10 | 1.32 | 1.29 | 2.00 | 1.09 | 1.29 | 0.01 |
| 0.01 | 0.01 | 1.82 | 2.02 | 1.52 | 1.82 | 1.80 | 2.00 | 1.50 | 1.80 | 0.40 |
| Baseline = 0.10 | ||||||||||
| 0.20 | 0.20 | 3.05 | 3.86 | 2.33 | 3.22 | 2.33 | 3.00 | 1.67 | 2.33 | <0.01 |
| 0.20 | 0.10 | 3.37 | 3.86 | 2.67 | 3.42 | 2.60 | 3.00 | 2.00 | 2.60 | <0.01 |
| 0.20 | 0.01 | 3.80 | 3.86 | 3.64 | 3.80 | 2.95 | 3.00 | 2.82 | 2.95 | 0.50 |
| 0.10 | 0.20 | 1.89 | 2.25 | 1.56 | 1.95 | 1.67 | 2.00 | 1.33 | 1.67 | <0.01 |
| 0.10 | 0.10 | 2.03 | 2.25 | 1.71 | 2.05 | 1.80 | 2.00 | 1.50 | 1.80 | <0.01 |
| 0.10 | 0.01 | 2.22 | 2.25 | 2.15 | 2.22 | 1.98 | 2.00 | 1.91 | 1.98 | 0.68 |
| 0.05 | 0.20 | 1.42 | 1.59 | 1.26 | 1.44 | 1.33 | 1.50 | 1.17 | 1.33 | 0.01 |
| 0.05 | 0.10 | 1.48 | 1.59 | 1.33 | 1.49 | 1.40 | 1.50 | 1.25 | 1.40 | 0.09 |
| 0.05 | 0.01 | 1.58 | 1.59 | 1.54 | 1.58 | 1.49 | 1.50 | 1.45 | 1.49 | 0.81 |
| 0.01 | 0.20 | 1.08 | 1.11 | 1.05 | 1.08 | 1.07 | 1.10 | 1.03 | 1.07 | 0.55 |
| 0.01 | 0.10 | 1.09 | 1.11 | 1.06 | 1.09 | 1.08 | 1.10 | 1.05 | 1.08 | 0.70 |
| 0.01 | 0.01 | 1.11 | 1.11 | 1.10 | 1.11 | 1.10 | 1.10 | 1.09 | 1.10 | 0.96 |
Abbreviations: MH, Mantel-Haenszel adjusted; OR, odds ratio; RD, risk difference; RR, risk ratio.
a Pint = P value from Breslow Day test of homogeneity of stratum-specific RR estimates.
b The scenario presented by Miettinen and Cook (1) with n = 400.
c The scenario presented by Newman (2) with n = 600. For all other cases: n = 20,000, exposure prevalence = 10%, factor F prevalence = 25%.
Extreme scenarios presented previously (1, 2) illustrate how conditioning on a very strong nonconfounding risk factor can cause the appearance of confounding of the odds ratio when there is not actually confounding based on causal considerations, and as a property of the model, not the estimation process. Notably, the F conditional odds ratio is not adjusted for confounding but nor is it biased per se. Instead, it is a valid measure of the odds ratio conditional on F (3, 4). However, the interpretation of this measure is not straightforward, and these conditional estimates are hard to compare across different studies, even using marginal standardization. Also notably, the risk ratio and risk difference are not similarly affected. The odds ratio is inherently noncollapsible, whereas the same is not true for the risk ratio and risk difference. In less-extreme scenarios included in Table 1, noncollapsibility of the odds ratio from conditioning on nonconfounding risk factors can be seen to be small. Nevertheless, these small effects occurred frequently for the odds ratio but not the risk ratio. Concern about the potential impact of noncollapsibility might motivate use of alternatives to logistic regression, as we have described previously in the AJE Classroom (5).
Unequal stratum-specific risk ratio in the absence of effect modification under additive risk
Unlike the odds ratio, the risk ratio is not noncollapsible. The weighted average of the risk ratio in strata of nonconfounding risk factors equals the unconditional risk ratio. However, estimates in the two strata of the nonconfounding risk factor will be unequal in many scenarios (Table 1). Because the weighted averages of the risk ratio are equal to the unconditional risk ratio, but the stratum-specific estimands are not, the risk ratio is considered to be “not fully collapsible” (3). The reason for this is effect modification, which occurs when an exposure has different causal effects in subgroups of the effect modifier. But effect modification is known to depend on scale (i.e., additive vs. multiplicative): No effect modification on the additive scale implies that there must be effect modification on the multiplicative scale, and vice versa. Because our data were generated on the additive scale, and because effect modification is an effect-measure–specific phenomenon, valid conclusions depend on choosing the correct model scale. Next, we consider the circumstance when data are generated by a multiplicative risk process, and consider measures of association conditioned on a nonconfounding risk factor to evaluate noncollapsibility in the context of multiplicative risk. We also note that, although not considered here, the hazard ratio is also noncollapsible in a manner similar to the odds ratio.
“OMITTED VARIABLE BIAS”: NONCOLLAPSIBILITY UNDER LOGIT RISK
In the two sections above, we considered noncollapsibility under an additive risk process, but other data-generating mechanisms are possible. Prior work has considered data generated via logistic regression, whereby odds are determined in multiplicative fashion and causal effects are correctly specified as ratios of odds (6). In this setting, noncollapsibility takes a surprising and underappreciated form. In the logit case, noncollapsibility in the absence of confounding will occur when nonconfounding risk factors are excluded from the model. As a result, unadjusted logistic regression models yield estimates unequal to those that that correctly specify all risk factors for the outcome regardless of confounding. This is in contrast to the additive risk scenario, where inclusion of nonconfounding risk factors in a logistic model results in noncollapsibility of the odds ratio. This “omitted variable bias” (6) can be shown mathematically using a data-generating process that is additive on the logit scale:
 |
which is multiplicative on the odds scale:
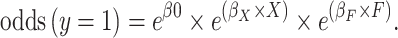 |
Evaluating unadjusted, stratum-specific, and adjusted odds ratios, risk ratios, and risk differences, as in the additive risk case, we find that collapsibility results in slightly different properties when data are generated on the logit scale.
As shown in Table 2, given the data-generating mechanism shown above, the odds ratio from unadjusted models omitting the risk factor F are consistently different from the true causal odds ratio due to noncollapsibility. Stratum-specific and adjusted odds ratios are all equal and all correct. Failure to include nonconfounding risk factors in logistic regression models creates this apparent “omitted variable bias” that results from noncollapsibility of the odds ratio even when the odds ratio is the appropriate measure of association for data generated using a logit process. In contrast, unadjusted and adjusted estimates of the risk ratio and risk difference are equivalent, demonstrating the collapsibility of these measures. And, as shown in Web Table 1, noncollapsibility of the odds ratio and collapsibility of the risk ratio and risk difference holds when risk is determined by a multiplicative risk process, also.
Table 2.
Effects of Adjusting for a Nonconfounding Risk Factor When Outcomes Are Determined by a Multiplicative Odds (i.e., Logit) Data-Generating Mechanism: Unadjusted, Stratum-Specific, and Adjusted Exposure (X) Effect Estimates of the Odds Ratio, Risk Ratio, and Risk Difference
| Simulation Parameters | Estimated OR | Estimated RR | Estimated RD | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
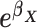 a
a
|
RR b | RD b |
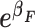 a
a
|
Unadjusted | F = 0 | F = 1 | Adjusted c | Unadjusted | F = 0 | F = 1 | Adjusted c | Unadjusted | F = 0 | F = 1 | Adjusted c |
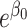 a = 0.01 a = 0.01
| |||||||||||||||
| 1.5 | 1.49 | 0.005 | 1.5 | 1.50 | 1.50 | 1.50 | 1.50 | 1.49 | 1.49 | 1.49 | 1.49 | 0.006 | 0.005 | 0.007 | 0.006 |
| 1.5 | 1.49 | 0.005 | 3.0 | 1.50 | 1.50 | 1.50 | 1.50 | 1.49 | 1.49 | 1.48 | 1.49 | 0.007 | 0.005 | 0.014 | 0.007 |
| 1.5 | 1.49 | 0.005 | 10.0 | 1.47 | 1.50 | 1.50 | 1.50 | 1.45 | 1.49 | 1.43 | 1.45 | 0.014 | 0.005 | 0.040 | 0.014 |
| 3.0 | 2.94 | 0.019 | 1.5 | 3.00 | 3.00 | 3.00 | 3.00 | 2.93 | 2.94 | 2.91 | 2.93 | 0.022 | 0.019 | 0.029 | 0.022 |
| 3.0 | 2.94 | 0.019 | 3.0 | 2.97 | 3.00 | 3.00 | 3.00 | 2.89 | 2.94 | 2.83 | 2.89 | 0.028 | 0.019 | 0.054 | 0.028 |
| 3.0 | 2.94 | 0.019 | 10.0 | 2.78 | 3.00 | 3.00 | 3.00 | 2.64 | 2.94 | 2.53 | 2.64 | 0.050 | 0.019 | 0.141 | 0.050 |
| 10.0 | 9.17 | 0.082 | 1.5 | 9.97 | 10.00 | 10.00 | 10.00 | 9.06 | 9.17 | 8.82 | 9.06 | 0.090 | 0.082 | 0.117 | 0.090 |
| 10.0 | 9.17 | 0.082 | 3.0 | 9.64 | 10.00 | 10.00 | 10.00 | 8.55 | 9.17 | 7.91 | 8.55 | 0.112 | 0.082 | 0.203 | 0.112 |
| 10.0 | 9.17 | 0.082 | 10.0 | 7.69 | 10.00 | 10.00 | 10.00 | 6.39 | 9.17 | 5.48 | 6.39 | 0.164 | 0.082 | 0.411 | 0.164 |
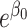 = 0.11 = 0.11
| |||||||||||||||
| 1.5 | 1.43 | 0.043 | 1.5 | 1.50 | 1.50 | 1.50 | 1.50 | 1.42 | 1.43 | 1.40 | 1.42 | 0.046 | 0.043 | 0.057 | 0.046 |
| 1.5 | 1.43 | 0.043 | 3.0 | 1.48 | 1.50 | 1.50 | 1.50 | 1.39 | 1.43 | 1.33 | 1.39 | 0.053 | 0.043 | 0.083 | 0.053 |
| 1.5 | 1.43 | 0.043 | 10.0 | 1.37 | 1.50 | 1.50 | 1.50 | 1.28 | 1.43 | 1.19 | 1.28 | 0.057 | 0.043 | 0.099 | 0.057 |
| 3.0 | 2.50 | 0.150 | 1.5 | 2.98 | 3.00 | 3.00 | 3.00 | 2.45 | 2.50 | 2.33 | 2.45 | 0.160 | 0.150 | 0.190 | 0.160 |
| 3.0 | 2.50 | 0.150 | 3.0 | 2.85 | 3.00 | 3.00 | 3.00 | 2.27 | 2.50 | 2.00 | 2.27 | 0.175 | 0.150 | 0.250 | 0.175 |
| 3.0 | 2.50 | 0.150 | 10.0 | 2.35 | 3.00 | 3.00 | 3.00 | 1.84 | 2.50 | 1.46 | 1.84 | 0.173 | 0.150 | 0.243 | 0.173 |
| 10.0 | 5.26 | 0.426 | 1.5 | 9.86 | 10.00 | 10.00 | 10.00 | 4.98 | 5.26 | 4.38 | 4.98 | 0.440 | 0.426 | 0.482 | 0.440 |
| 10.0 | 5.26 | 0.426 | 3.0 | 8.92 | 10.00 | 10.00 | 10.00 | 4.27 | 5.26 | 3.08 | 4.27 | 0.450 | 0.426 | 0.519 | 0.450 |
| 10.0 | 5.26 | 0.426 | 10.0 | 6.38 | 10.00 | 10.00 | 10.00 | 3.02 | 5.26 | 1.74 | 3.02 | 0.418 | 0.426 | 0.391 | 0.418 |
Abbreviations: OR, odds ratio; RD, risk difference; RR, risk ratio.
a  , baseline odds;
, baseline odds;
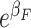 , OR (F = 1 vs.
F = 0);
, OR (F = 1 vs.
F = 0); 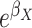 , OR (X = 1 vs.
X = 0).
, OR (X = 1 vs.
X = 0).
b RR calculated from simulation parameters for odds and OR for exposure.
c Adjusted estimates are Mantel-Haenszel–weighted averages of stratum-specific estimates.
CONCLUSIONS: NONCOLLAPSIBILITY IN PRACTICE
As described above, noncollapsibility has an impact on population-level estimands that depends upon the true data-generating mechanism. Notably, this mechanism is generally unknown and cannot be determined from data. If risk is truly logit in nature, the potential issues due to omitting risk factors from models are justification for caution in interpreting results. When risk is additive, the odds ratio is noncollapsible, although the impact on estimates could be small. Still, models of the risk ratio or risk difference are alternatives to models of the odds ratio like logistic regression to avoid issues of noncollapsibility, and which might be more “useful.”
Supplementary Material
ACKNOWLEDGMENTS
Author affiliations: Department of Biostatistics and Epidemiology, University of Massachusetts Amherst, Amherst, Massachusetts, United States (Brian W. Whitcomb); and Department of Epidemiology, Rollins School of Public Health, Emory University, Atlanta, Georgia, United States (Ashley I. Naimi).
The authors acknowledge funding support from the National Institutes of Health (grants R01HD093602 and R01HD098130 (to A.I.N.) and R21ES029686 (to B.W.W.)).
REFERENCES
- 1.Miettinen OS, Cook EF. Confounding: essence and detection. Am J Epidemiol. 1981;114(4):593–603. [DOI] [PubMed] [Google Scholar]
- 2.Newman SC. Commonalities in the classical, collapsibility and counterfactual concepts of confounding. J Clin Epidemiol. 2004;57(4):325–329. [DOI] [PubMed] [Google Scholar]
- 3.Greenland S, Robins JM, Pearl J. Confounding and collapsibility in causal inference. Statist Sci. 1999;1(14):29–46. [Google Scholar]
- 4.Pang M, Kaufman JS, Platt RW. Studying noncollapsibility of the odds ratio with marginal structural and logistic regression models. Stat Methods Med Res. 2016;25(5):1925–1937. [DOI] [PubMed] [Google Scholar]
- 5.Naimi AI, Whitcomb BW. Estimating risk ratios and risk differences using regression. Am J Epidemiol. 2020;189(6):508–510. [DOI] [PubMed] [Google Scholar]
- 6.Neuhaus JM, Jewell NP. A geometric approach to assess bias due to omitted covariates in generalized linear models. Biometrika. 1993;80(4):807–815. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


