Social distancing enhanced automated optimal design of physical spaces in the wake of the COVID-19 pandemic

Abstract

As the COVID-19 pandemic unfolds, manually enhanced ad-hoc solutions have helped the physical space designers and decision makers to cope with the dynamic nature of space planning. Due to the unpredictable nature by which the pandemic is unfolding, the standard operating procedures also change, and the protocols for physical interaction require continuous reconsideration. Consequently, the development of an appropriate technological solution to address the current challenge of reconfiguring common physical environments with prescribed physical distancing measures is much needed. To do this, we propose a design optimization methodology which takes the dimensions, as well as the constraints and other necessary requirements of a given physical space to yield optimal redesign solutions on the go. The methodology we propose here utilizes the solution to the well-known mathematical circle packing problem, which we define as a constrained mathematical optimization problem. The resulting optimization problem is solved subject to a given set of parameters and constraints – corresponding to the requirements on the social distancing criteria between people and the imposed constraints on the physical spaces such as the position of doors, windows, walkways and the variables related to the indoor airflow pattern. Thus, given the dimensions of a physical space and other essential requirements, the solution resulting from the automated optimization algorithm can suggest an optimal set of redesign solutions from which a user can pick the most feasible option. We demonstrate our automated optimal design methodology by way of a number of practical examples, and we discuss how this framework can be further taken forward as a design platform that can be implemented practically.

1. Introduction

In the wake of the COVID-19 pandemic, social distancing has become one of the crucial elements of our present day lifestyle. In fact, the pandemic has changed much in terms of the way we conduct our lives, including how we work, how we conduct meetings and how we manage social gatherings. Like many other unpleasant elements the crisis has brought upon us, the need to arrange and re-arrange physical spaces with the appropriate level of safety measures have become essential.

The aim of optimized physical space modeling is to design or reconfigure a given physical environment so as the risk of infection is minimized while pursuing an optimal level of physical interaction among people. For instance, the work in Zhang et al. (2019) explored the distribution of droplet aerosols generated by mouth coughing and nose breathing – considered to be two important transmission vectors for COVID-19 – in an air-conditioned room. Interestingly, this work was published some months prior the emergence of the COVID-19 pandemic. The motivation in this case was based on the strong association between ventilation systems and airborne pathogen infection, as observed in several previous epidemics associated with respiratory diseases, such as SARS (2003) and H1N1 (2009), for which breathing, coughing or sneezing were also routes of transmission. The work in Leng, Wang, and Liu (2020) analyzed the sustainable design of courtyards, a public space with a strong social interaction, from the point of view of airborne diseases control and human health. The results showed that optimal architectural design can improve air quality and safety against airborne diseases and mitigate the risk of infection. The work presented in Ge et al. (2020) analyzed the exposure risk to SARS-CoV-2 (the virus that caused the COVID-19 disease) in hospital environments. They found evidence of viral nucleic acid in air samples and surfaces of the environments in hospitals during the COVID-19 pandemic, suggesting potential infection risks. The study further showed the importance of air ventilation in buildings, and other measures for disease prevention, to reduce the potential risk of infection among healthcare workers and patients. An artificial intelligence assisted ventilation control system using fast prediction models incorporating data from ZigBee-based monitoring systems was proposed in Ren and Cao (2020). Interestingly this work was also carried out prior to the present COVID-19 pandemic. Similarly, a recent paper analyzed the efficacy of social distancing and ventilation in preventing the transmission of COVID-19 by introducing two new indices (social distance probability and ventilation effectiveness) in the Wells-Riley model – one of the most classical and popular methods to predict the probability of infection by an airborne virus (Sun & Zhai, 2020).

Social distancing – i.e., keeping a safe distance between people to reduce the number of short-range physical interactions – has been one of the strongest measures that help minimize the infection rates arising from the COVID-19 disease. Given that, face to face communication is an essential element for humans to thrive and to perform optimally, there is a need to seek a balanced compromise between maintaining a safe physical distance and an efficient medium of interaction for effective communication. For instance, non-verbal communication requires an environment which is well lit with a relatively neutral background, absence of excessive noise, and a relatively short physical distance between subjects, e.g., 2 m or less between subjects (Albert, 2019). It is also important to note that an optimal arrangement of physical space can also result in enhanced productivity (Travers, 2020).

As the COVID-19 pandemic unfolds, manually intervened, ad-hoc solutions have helped to cope with the dynamic nature of space planning, i.e., from social distancing enabled rearrangements of office spaces, shop floors, restaurants, cafes and other such public areas. Due to the unknown nature in which the pandemic is unfolding, the standard operating protocols (SOPs) which often get issued by the authorities are very dynamic in nature. This includes the physical distancing requirements between people in social spaces – which appear to be changing dynamically depending on our knowledge of the COVID-19 disease, functional requirements placed by the authorities and the economic requirements prescribed based on the resources available. For further information and insight, the reader is referred to Rahmani and Hosseini (2021) for a very recent systematic literature review about prevention and treatment methods for the COVID-19 disease.

Several computer-based solutions have been released during the last few months to deal with different aspects of the COVID-19 pandemic. Some authors applied deep learning techniques for object and people detection in video sequences recorded by video surveillance systems of public areas in order to control and enforce social distancing between people (Ahmed, Ahmad, Rodrigues, Jeon, & Din, 2021; Shorfuzzaman, Shamim Hossain, & Alhamid, 2021). The work in Zhou, Qiu, Pu, Huang, and Ge (2020) introduced a user-friendly software, named BioAider, for sequence annotation and mutation analysis of large-scale genoma-sequencing data. This software can be applied to track SARS-CoV-2 transmission, thus providing a helpful tool for prevention and control of COVID-19 and similar viral driven infectious diseases. Other computer tools are being deployed for tasks such as predicting the spread of the disease, tracking the genetic evolution and potential mutations of the virus during the transmission among human hosts, enhancing and accelerating the diagnosis, or performing simulations on the impact of different preventive measures to assist health authorities and policy makers in putting in place more effective strategies to fight against the disease. We remark, however, that none of these computational solutions we have come across addresses the problem of social distancing enhanced optimal design of physical spaces.

As a result, a computer based solution that can help decision makers and planners to quickly input design requirements and the necessary constraints in order to generate feasible social distancing enhanced space arrangements has become essential. To do this, in this paper, we propose an optimal design platform which could take the dimensions, the constraints and other essential requirements of a given physical space. The optimal design or redesign of the chosen physical space can then be defined as a constrained mathematical optimization problem. Thus, given a physical space, one can identify the various physical dimensions of the space and the relevant constraints, such as the physical distancing required between people, air circulation requirements, the position of doors and windows, and humidity and lighting levels to pose a feasible constraint based optimization problem which can then be solved to obtain potential optimal design solutions. Clearly, a framework of this nature will prove to be novel in that it can cater towards the daunting task of physical space planning within situations in which the SOPs are ever changing as the COVID-19 pandemic unfolds.

This paper is organized as follows. In Section 2, we discuss the general problem of computer aided design of optimal physical spaces and the essential criteria and parameters one must consider in addressing the problem at hand. In Section 3, we discuss our proposed methodology, which is based on posing a constrained optimization problem which is then solved using the circle packing technique. In Section 4, we provide a comprehensive set of examples through which we show how our proposed methodology can be used to design or redesign social distancing enhanced physical spaces. Finally, in Section 5, we provide a general discussion while, in Section 6, we conclude the paper.

2. Computer aided design of optimal physical spaces

The design of physical spaces can be inferred as the arrangement of a given physical environment by taking into account the various requirements or variables that are associated with the design. These may include, the number of people to whom it should be accessible to, the arrangement of various pieces of furniture, structural elements such as beams and partitions doors and windows, the airflow pattern and the location of lights, among others. The physical environments themselves can range from classrooms, offices, shopping malls, factory floors or similar social spaces. The optimal designs of these physical spaces involve the identification of feasible configurations taking into account the relevant requirements.

When it comes to computer based optimal physical design, the problem can be defined as a constrained optimization problem. Consequently, the problem then requires efficient search strategies to obtain feasible solutions for a given set of constraints (Kumar, 2019). Thus, the chosen form of optimization requires to maximize or minimize a cost function subject to a set of chosen constraints. The cost function often considers variables or constraints relating to the ergonomics, functionality and aesthetics (Kán & Kaufmann, 2017).

Common techniques to solve such optimization problems include those based on either emergence or graph theory approaches where planar graphs are used to arrange spaces or quadratic assignment problem approaches where a cell- matrix is used for the assignment of entities (El-Baz, 2004, Pourvaziri and Naderi, 2014). Other methods such as the slicing tree approach divides a space using vertical and horizontal lines to generate new sub-zones (Aiello, Scalia, & Enea, 2012; Azevedo, Crispim, & Sousa, 2017; Dou, Zong, & Nan, 2016; Hasda, Bhattacharjya, & Bennis, 2016; Hosseini-Nasab, Fereidouni, Ghomi, & Fakhrzad, 2018; Kulturel- Konak & Konak, 2013; Petrone & Meruane, 2017; Shayan & Chittilappilly, 2004; Wu & Appleton, 2002). The slicing tree approach can, however, be limited in its application to a given geometric configuration (Leno, Sankar, & Ponnambalam, 2016; Lin & Yingjie, 2019; Palomo-Romero, Salas-Morera, & García-Hernández, 2017; Wang, Hu, & Ku, 2005).

Other than that, hybrid approaches (Singh & Sharma, 2006) can be used to handle complex configuration geometry where the technique of space-filling curves and genetic algorithms can be used to define an arrangement of a given space over a matrix (Buscher, Mayer, & Ehrig, 2013; Leno et al., 2016; Lin & Yingjie, 2019; Palomo-Romero et al., 2017; Wang et al., 2005). Such algorithms can handle hierarchical organization (Koenig & Schneider, 2012) of layout elements and multi-level space allocation using evolutionary approaches (Rodrigues, Gaspar, & Gomes, 2013). Examples of such approaches include the design of rectangular shapes to handle objects, doors and windows (Yang, Li, Song, Jiang, & Ling, 2019) which can be further enhanced using semantic parent–child approaches where the relationship between furniture objects can be arranged according to an optimized plan (Eppner & Brock, 2015; Germer & Schwarz, 2009). Similarly, heuristic agent-based approaches can also be employed to obtain optimal design solutions for spatial configuration arrangements (Abdelmohsen, Assem, Tarabishy, & Ibrahim, 2016; Eppner & Brock, 2015; Germer & Schwarz, 2009; Kán & Kaufmann, 2017; Leno et al., 2016).

Likewise, in Fischetti, Fischetti, and Stoustrup (2020) the authors applied a recent approach of wind farm layout design to produce optimized facility layouts with strict physical distancing requirements between the individual turbines. This is similar to solving the physical space planning problem with the social distancing constraint requirements arising from the present case of the COVID-19 pandemic. The authors proposed parallelism between this problem and locating wind turbines in an offshore area. It is emphasized in this work that both problems require fitting facilities (turbines or people) in a given area while ensuring a minimum distance between them. Similarly, like people who are in close proximity can infect each other, the turbines, if close by, can “infect” each other by casting wind shadows that cause production losses. In both problems, the desired goal is to minimize the interference/infection.

The same problem arises in several industrial applications. For instance, Fraser and George (1994) considers the container loading problem, developed for the paper and pulp industry, where products are delivered as reels of different diameters, which are assumed to stand on end when being transported. Similarly, the authors in George, George, and Lamar (1995) consider the problem of packing pipes of different diameters into a shipping container, while in Drezner and Erkut (1995) the p-dispersion problem (i.e., how to select p points from set of n > p objects in order to maximize the smallest distance between two chosen objects) for optimal location of facilities or fast-food franchises in a fixed area. Other similar problems are the robot communication problem (i.e., how to locate a swarm of robots with circular coverage communication of a maximum and minimum range of R and r meters, respectively), the indoor wireless communication network layout problem (locating the transceivers in the layout for full coverage with the minimum number of devices), and the container loading problem (in which equal cylinders need to packed into a rectangular container), described in Martin (2004), Adickes et al. (2002) and Birgin, Martinez, and Ronconi (2005), respectively. In all cases, the resulting optimization problem in the two-dimensional plane becomes equivalent to the so-called circle packing problem (see Section 3 for details).

Furthermore, the space planning techniques such as that discussed in Acharyya, Losalka, Gupta, and Panda (2012) can also be used for object arrangements – in this case assigning seats to students in exams – within a selected set of criteria. However, these systems are used for seating arrangements without dynamically generating space models. Such approaches use a set of rules where different possibilities of student arrangements are explored heuristically, e.g., no two students who are attempting the same exam paper should be seated together. Similarly, the authors in Tutenel, Bidarra, Smelik, and Kraker (2009) proposed a hierarchical optimization approach for multi criteria building performance problem. They presented a rigorous simulation based optimization framework that enables concurrent and consistent decision making in building design. The framework facilitates computational decision support for meeting building performance goals, allows autonomy of specialized design tasks with timely and efficient use of analysis tools, and preserves dependencies between possibly competing building performance goals.

It is important to highlight that there exist a wide array of methods and techniques that can be adopted to solve the optimization problem involving the layout of structures minimizing a given cost function subject to a given set of constraints. Though these techniques may appear to be different, there also exist many analogies between them (Alyaqout & Alyaqout, 2020).

2.1. Essential elements and parameters for social distancing enhanced physical spaces

As mentioned before, physical space modeling needs to take into account a set of parameters in order to achieve the best or one of the best possible solutions in terms of layout configuration and arrangement. These parameters can come in the form of safety guidelines, physical disposition of the place and pre-existing structures or elements, the requirements on the ventilation systems or other considerations such as the number of people and any special accessibility arrangements that must be in place.

It is clear that physical distancing has become a key element of our daily lives. Before the COVID-19 pandemic, this factor was not even considered beyond the normal, and it was a lightly prescribed social convention. However, nowadays, according to the governments and the guidelines of various health authorities, a physical distance of at least 2 m within social spaces should be maintained among all participants at any time (Pearce, 2020). Other parameters that need to be considered are related to the physical settings themselves. Before the COVID-19 pandemic, the physical arrangements, including lighting and ventilation, were optimized for people to stay in close proximity. However, now it is known that the airflow pattern can become a vector of transmission for the virus, and hence, there is a need to make adjustments in the physical spaces to take into account the pre-existing physical structures and airflow patterns (COVID-19; Qian & Zheng, 2018). Naturally, lighting conditions should also be adapted to the new configuration of the physical environment. Similarly, the environmental conditions, including the temperature and humidity, can also play an important role in the transmission of the infectious disease, as they affect the survival rate of the virus. Therefore, these parameters should be maintained at optimum levels as much as possible (Huang et al., 2020).

In addition to the above elements, social factors are also a fundamental aspect that must be taken into account. For example, typically, physical spaces were designed to promote social interactions so that people are able to be close to each other in a natural way. In such scenarios, communication was fluent, and both the body language and speech can be smoothly perceived. On the other hand, the new enforcements regarding physical distancing make it harder to keep the original communication proximities. Parameters such as the level of voice volume and inference of facial expressions must be taken into account in order to enhance communication while keeping safety measures in place (Zahorik & Kelly, 2007). In Table 1 , we outline the essential design parameters that must be taken into account when rearranging or redesigning physical spaces with a view to having them social distancing enabled.

Table 1.

Examples of essential parameters that should be considered for social distancing enabled rearrangement of physical spaces.

Settings	Constraints to be considered
Physical distance	A prescribed physical distance, e.g., 2 m
Accessibility	Ease of access for people movement
Health and safety	Locations of health and safety equipment
Airflow	Direction and pattern of airflow
Social factors	Ease of visual contact and level of voice

From the discussions above, one can see that there are a number of constraints and parameters one must consider when attempting to create an optimal design. One can also see that, in principle, there exist a variety of methods and techniques that can be potentially applied to solve the social distancing enabled space re-arrangement problem. However, for a problem of the nature discussed here, computational efficiency and ease of use are key factors to consider. Thus, in the following section, we present an effective methodology to address the problem at hand.

3. Our proposed approach

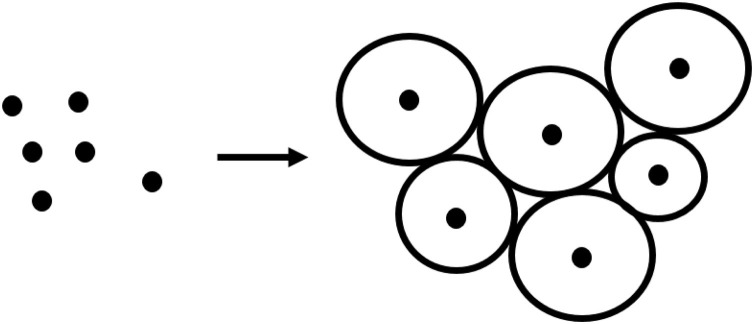
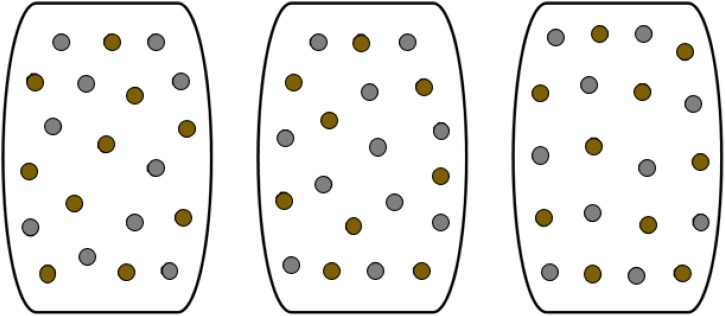
We postulate that the problem of arranging or re-arranging elements in a given physical space boils down to determining the optimal configuration such that it enables circles of given radii to be neatly arranged within the configuration. Thus, given a configuration K and the appropriate boundary ∂K, we can compute circles of radii R _i for the corresponding circle packing for K. Fig. 1 shows how this can be done, in which the set of unarranged points on the left – corresponding to entities or objects – have been arranged with given distances between them, as shown on the right hand of the figure.

Fig. 1.

An example showing how a given set of points can be optimally re-arranged through circle packing.

Given a configuration K, and the conditions on K as well as on ∂K, then there exist sufficient mathematical theory to determine both the existence and the uniqueness of the circle packing configuration with circles of radii R _i that arise as a solution to our problem (Dubejko & Stephenson, 1995; Hodgson & Rivin, 1993). In fact, this problem is closely connected to the well- known Dirichlet problem displaying the characteristics of the discrete Laplace equations with properties such as convexity, conserved geometric qualities and the existence of minimal energy. Furthermore, one could consider the following theorem.

Theorem: Let K be a planar topological configuration in ${\mathbb{R}}^2$. Let A be a function in K spanning the circles with radii R _i such that g _i : ∂K is a function defined on the boundary of K. Then, there exist a unique Euclidean packing of circles with R _i such that $R(w_i)=g(w_j)$ for each chosen boundary point $w_j$. Furthermore, the solution for R _i satisfies a non-linear system of N equations such that ∑_i α (R _i) = A _j with j = 1 … N, where α is the unique interior angle formed by the triangle T _i defined by the pack of circles corresponding to the circle with radius R _i.

This theorem statement and its proof can be derived from the classical Dirichlet problem for harmonic problems of which the Laplace equation is a special case (Dubejko, 1999; Elmahmudi & Ugail, 2019).

3.1. Solving the circle packing problem

3.1.1. The circle packing problem as an optimization problem

In the current context of re- arranging elements with appropriate social distancing parameters in physical spaces the circle packing becomes a two-dimensional geometrical form for a domain K with the corresponding boundary ∂K. The domain of interest in this particular case often is a square, a rectangle or a general polygonal form.

Here, the circle packing problem is solved based on the logic that a given number of circles in a two- dimensional space must be arranged with the condition that none of them must overlap with each other – this is equivalent to, for example, prescribing a certain social distance that must be adhered to.

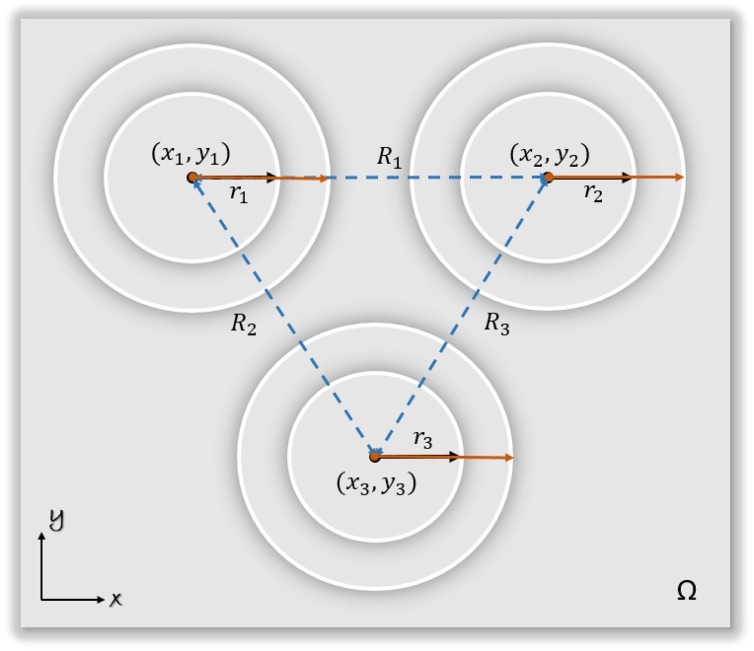
Fig. 2 represents a simple example showing the conditions corresponding to a generic room, where a set of entities need to be arranged so that a certain minimum distance (e.g., R ₁ = R ₂ = R ₃ = 2 m) must be guaranteed.

Fig. 2.

An example showing how the circle packing arrangement is carried out with a given distance constraint between the center of each circle.

Thus, considering the above case, given a region Ω being a general polygonal form, our problem is to define circles in that region such that all those circles do not overlap with each other. Suppose we denote the center of a given circle i and radius of the circle by (x _i, y _i) and r _i, respectively, as shown in Fig. 2, and since any of the given circles i and j must not overlap, we have,

$$(r_i+r_j)\le \sqrt{{(x_i-x_j)}^2+{(y_i-y_j)}^2}.$$ (1)

Note that, if two circles appear in the same order, then the centers of these circles i and j satisfy the condition such that,

$$x_i\le x_j,y_i\le y_j.$$ (2)

If two circles appear in the opposite order in y direction, then the centers of circles i and j satisfy the conditions,

$$x_i\le x_j,y_j\le y_i.$$ (3)

Thus, the nonlinear problem, as above, can be formulated as follows.

• •Place n identical non-overlapping circles in the region, with the Cartesian origin (0, 0) as the center.
• •Construct a variable r.
• •Let r be the minimal distance between all the points, i.e r ≤ || p _i − p _j||, where p _i is the coordinate vector in ${ℝ}^2$ for point i.
• •Maximize r – which is equivalent to minimize −r.

Now, the above algorithmic form can be formulated into an optimization problem with non-negative constraints on x = (x, y) such that,

$$\begin{array}{cc}\underset{\text{x}}{\mathrm{minimize}}\hfill & -r,\hfill \\ \mathrm{subject}\mathrm{to}\hfill & r\le ||p_i-p_j||,i=1,\dots ,n,\hfill \end{array}$$ (4)

where $p_i=(x_i,y_i)\in {ℝ}^2,\forall i$ and || · || is the Euclidean distance.

Since the circles cannot overlap, an important constraint arises. That is, the distance between the centers of any two adjacent circles cannot exceed the diameter. Hence, the constraint becomes, 2r ≤ || p _i − p _j||.

As an example, we shall imagine our domain to be the unit square centered at origin. Then, a constraint is that no circle should cross over the boundaries of the square. Thus, the optimization formulation for maximizing the distances of objects within a unit square becomes,

$$\begin{array}{cc}\underset{\text{x}}{\mathrm{minimize}}\hfill & -r,\hfill \\ \mathrm{subject}\mathrm{to}\hfill & 2r\le ||p_i-p_j||,\hfill \\ \hfill & r-0.5\le x_i\le 0.5-r,\hfill \\ \hfill & r-0.5\le y_i\le 0.5-r,\hfill \\ \hfill & i,j=1,\dots ,n,i<j.\hfill \end{array}$$ (5)

3.1.2. Solving the unconstrained nonlinear optimization problem

The circle packing algorithm, as described above, can be solved numerically through a nonlinear programming solver. In this work, we apply a method for constrained minimization problems involving both equality and inequality constraints. The approach, called interior-point method, consists of solving the constrained minimization by a sequence of approximate minimization problems (Byrd, Hribar, & Nocedal, 1999). The main idea behind the interior-point optimization algorithm is to take the original constrained minimization problem,

$$\begin{array}{c}\underset{x}{min}f(x),\hfill \\ h(x)=0,g(x)\le 0,x>0,\hfill \end{array}$$ (6)

where f (x) is the original cost function to be minimized on x, and h(x) and g (x) are vector functions representing respectively all the equality and inequality constraints (either boundary, linear or nonlinear constraints) and convert it to a new system (7), without the inequality constraints,

$$\begin{array}{c}\underset{x,s}{min}{f}_{\mu }(x,s)=\underset{x,s}{min}f(x)-\mu \sum _{i}ln(s_i),\hfill \\ h(x)=0,g(x)+s=0,s_i\ge 0,\hfill \end{array}$$ (7)

where s is a vector of slack variables s _i (as many as the inequality constraints g _i), and the scalar μ > 0 is a multiplier of the barrier function called barrier parameter (Byrd, Gilbert, & Nocedal, 2000). Note that all s _i must be positive for the expression ln (s _i) to be bounded. Eq. (7) is then solved iteratively through a series of Newton steps and conjugate gradient steps (Andrei, 2020; Yuan, Li, & Hu, 2020) as follows. At each iteration, one of the following steps is chosen such that,

• (8)
  a direct step in (x, s), also called a Newton step. It consists of solving the Karush–Kuhn–Tucker (KKT) equations ${\nabla }_x\mathcal{L}(x,\lambda )=0$, where $\mathcal{L}(x,\lambda )$ is the Lagrangian function given by,

  $$\mathcal{L}(x,\lambda )=f(x)+\sum _i{\lambda }_i^g{g}_i(x)+\sum _i{\lambda }_h^h{h}_j(x)$$ (8)

  and λ is the vector formed by the ${\lambda }_i^g$ and ${\lambda }_j^h$, called the Lagrange multiplier vector, and whose length is the total number of constraints of the problem,

• (9)
  a conjugate gradient step, to solve Eq. (7) adjusting both x and s. For this purpose, a quadratic approximation using a trust region is considered (Steihaug, 1983). The core idea of the this approach is to use an approximation of the function f (x) to be minimized around a given point x through a simpler function providing a relatively accurate description of the behavior of f(x) in the neighborhood of x, denoted as N _x and called the trust region (Byrd et al., 2000). In particular, if R denotes the radius of the trust region, the algorithm computes the Lagrange multipliers by solving the KKT equations,

  $${\nabla }_{x}f(x)+\sum _i{\lambda }_i^g\nabla g_i(x)+\sum _i{\lambda }_h^h\nabla h_j(x)$$ (9)

  in the least-squares sense. Then, the algorithm applies minimization subjected to linearized constraints, by minimizing the norm of such constraints inside the region of radius R (see Byrd et al., 2000; Waltz, Morales, Nocedal, & Orban, 2006 for further details).

After each iteration, the value of the barrier parameter μ is reduced (Waltz et al., 2006). This enables the final value obtained to become closer to that desired result.

3.1.3. Pseudocode of the proposed algorithm

We describe this algorithm further using the pseudocode as given in Algorithm 1.

Algorithm 1

Pseudocode for the proposed algorithm

Note that the description of the Algorithm 1 is such that it is based on the domain being a rectangle and objects in it being circles. The domain types can conveniently be changed using the following considerations.

• •The initial solution (x _i, y _i), i = 1, …, n is generated by randomly placing n circles in the rectangular domain.
• •Then, the correction procedure correct(X, Y) ensures that the centers of the circles (x _i, y _i) from the optimizer are inside the domain. Essentially, this will correct the maximum radius of the circle that can be placed in the domain without any overlapping.
• •Thus, one of the advantages of this heuristic based algorithm is that it is easy to adapt it to encompass a variety of different domains.

3.1.4. Two illustrative examples

We now describe our algorithm and the optimization process by way of a further example. Consider arranging a number of chairs n in a rectangular room where we prescribe a certain distance r between every chair. This quadratically constrained nonlinear optimization problem for a given n > 1 integer value is written as,

$$\begin{array}{cc}\underset{\text{x}}{\mathrm{minimize}}\hfill & -r,\hfill \\ \mathrm{subject}\mathrm{to}\hfill & 2r\le ||p_i-p_j||,\hfill \\ \hfill & x_i,y_i\in [r,1-r],\hfill \\ \hfill & 1\le i<j\le n,r\in (0,1/2).\hfill \end{array}$$ (10)

And, more specifically, for a rectangular room the optimization problem is written as,

$$\begin{array}{cc}\underset{\text{x}}{\mathrm{minimize}}\hfill & -r,\hfill \\ \mathrm{subject}\mathrm{to}\hfill & 2r\le ||p_i-p_j||,\hfill \\ \hfill & x_i\in [r,L-r],y_j\in [r,W-r],\hfill \\ \hfill & 1\le i<j\le n,\hfill \end{array}$$ (11)

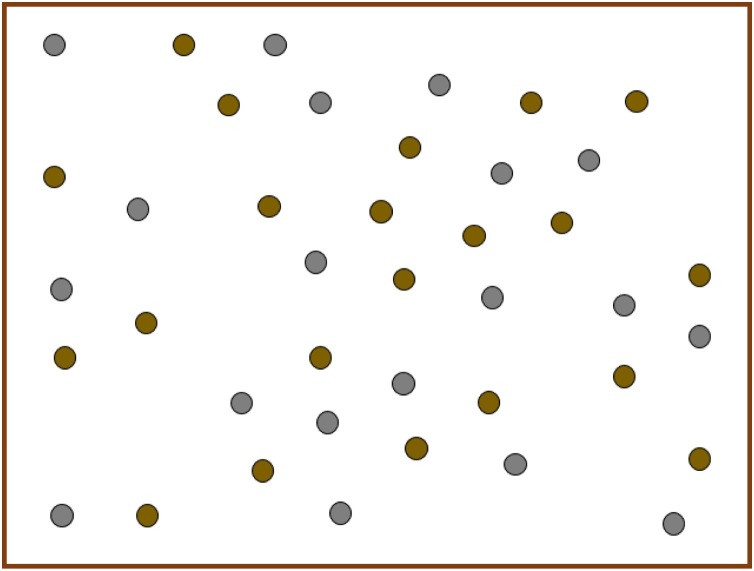
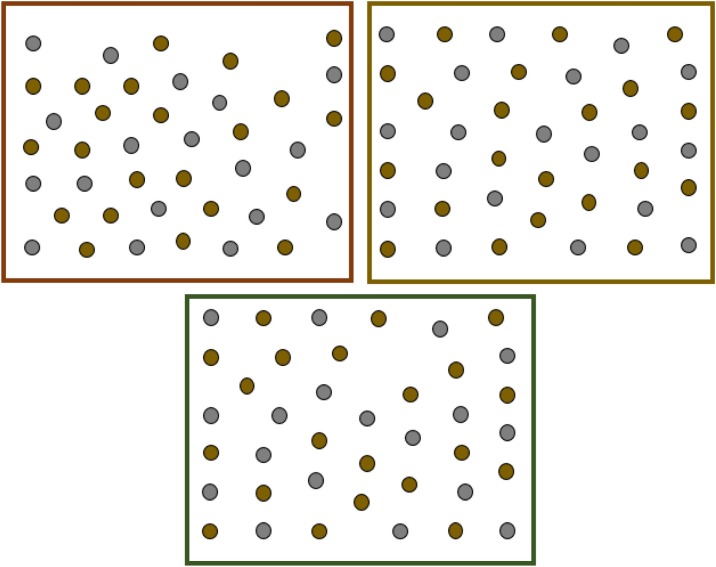
where L and W are the length and the width of the room. Fig. 3 shows an initial arrangement of 40 chairs, which is fed as a random seed to the optimization algorithm. The algorithm then comes up with a set of optimized arrangements for the chairs in the room. In Fig. 4 , we show some sample optimal solutions for the arrangement of chairs in the room. As one can see, all the arrangements that are shown in Fig. 4 are feasible. However, the most aesthetically pleasing solution in this particular case is probably the option shown at the top right image in Fig. 4.

Fig. 3.

An initial arrangement of chairs which is taken as a random seed for input to the optimization algorithm.

Fig. 4.

Example optimal arrangements of chairs, with a prescribed distance r between them, in a room.

The above problem can easily be recast to simulate the arrangement of chairs within a room of different shape. For example, if the room shape is triangular like type, we can write down the optimization as,

$$\begin{array}{cc}\underset{\text{x}}{\mathrm{minimize}}\hfill & -r,\hfill \\ \mathrm{subject}\mathrm{to}\hfill & 2r\le ||p_i-p_j||,\hfill \\ \hfill & 6x_i+2\sqrt{3}{y}_i\le 3L-4\sqrt{3}r,\forall i,\hfill \\ \hfill & -6x_i+2\sqrt{3}{y}_i\le 3L-4\sqrt{3}r,\forall i,\hfill \\ \hfill & 1\le i<j\le n.\hfill \end{array}$$ (12)

Fig. 5 shows an optimal result for arranging the chairs with a prescribed physical distance of r for the triangular shaped room with length L.

Fig. 5.

Example optimal arrangements of chairs, with a prescribed distance r between them, in a triangular like room.

3.2. Implementation details

The architecture of the software prototype used in this work consists of two layers organized hierarchically in a bottom-up sequence such that,

• •the first layer, at the bottom, is derived by the computing layer. It is responsible for the mathematical computations according to the methods described in the previous section. The input of this layer is provided by the user and consists of a constrained nonlinear minimization problem involving the cost function, and the set of all linear and nonlinear constraints (e.g., positions of doors, windows, furniture, walkways, variables related to the indoor airflow patterns, and others, including the boundary conditions of the problem), formulated as equality and inequality equations. The output of this layer is fed into the second (upper) layer for visualization purposes.
• •a second layer, at the top, derived by the visualization layer. It takes the output data from the first layer as the input and displays the 3D scene of the obtained solution in a graphical viewport, thus returning a graphical output.

On the implementation itself, the first layer has been implemented using the software package Matlab, version 2020a. Matlab is a very popular multiplatform scientific program for numerical computation, with versions for all major computer operating systems (Windows, Mac, and Linux), widely used in many areas of science and engineering and particularly recognized by its sophisticated numerical routines for optimization. The circle packing algorithm for our optimization problem is implemented as an standard Matlab m-file, where the dimensions of a given physical space, the description of the entities in the space and the physical requirements in terms of constraints can be entered (as inputs). The algorithm then automatically finds (a set of) feasible optimal solutions which can be then presented to the user to choose from or stored in files for further processing.

Thus, to obtain the optimal solution, we make use of the well-known Matlab function fmincon, which is based on the use of a barrier function and the concept of trust region, explained above. This method essentially finds the minimum value of a multivariate nonlinear function numerically over values that obey a given set of inequality or equality constraints. The fmincon function has four different algorithms for optimization, namely, the interior-point algorithm (Roode, 2015), Sequential Quadratic Programming (SQP) (Andrei, 2017), active-set algorithm (Yuan, Wei, & Zhang, 2014) and trust-region reflective algorithm (Le, Fatahi, Khabbaz, & Sun, 2017), based on the interior-reflective Newton method (Coleman & Li, 1994). Throughout the work discussed in this paper, we have used the interior-point algorithm (Byrd et al., 1999, Byrd et al., 2000), because it can handle large, sparse problems, as well as small dense problems (Waltz et al., 2006). It also ensures to satisfy the bound conditions at all iterations: with this algorithm, the components of x that are outside the bounds, or are equal to the bounds, are moved inside the bounded region. Finally, the method also satisfies bounds at all iterations and is robust against NaN or Inf results.

Some practical situations might allow the constraints to be relaxed, particularly regarding the boundaries. For instance, in Eq. (5), we imposed that no circle should cross over the boundaries of the square, a constraint that could be too strict in some real cases. Individuals may arguably sit against a wall while still keeping enough social distance with other individuals. This would imply that more individuals could be accommodated within the same interior space. These cases are not discussed in this work, but the methodology presented here can still handle them by considering algorithms other than the interior-point algorithm for the corresponding optimization problem. For example, the trust-region reflective algorithm moves the components that go outside the boundaries back into the region, but the components on the boundaries can stay there. The other two algorithms, SQP and active- set, go even further, i.e., the components of x falling outside the boundaries are actually moved to the closest boundaries. In general, as often happens in many optimization problems, there is no such thing as one algorithm that outperforms the rest in all scenarios, and the choice of the most suitable algorithm depends on the problem at hand. However, we suggest to select the interior-point algorithm as the default option, and change to other algorithms only in case the problem requires so.

Once the solution is obtained, it is displayed in the Matlab graphical environment and the corresponding output data is stored in files for further processing. In this work, we use CSV files, a widely used and popular format for exchanging data between different applications. These CSV files are subsequently invoked in Unity 3D for visualization purposes. Unity 3D is a popular multi-platform game engine available not only for all personal computer operating systems but also for video game consoles, and most of mobile devices (smartphones, tablets), and even the most popular websites. Unity 3D comes with many different features and tools for accurate simulation of 3D scenes, including high-quality graphics for advanced photo-realistic rendering (e.g., lighting, shadows, textures, and materials), an advanced physics engine, powerful navigation tools, advanced algorithms for collision detection, and an intuitive graphical editor with different windows and workspaces for the project, scene view, game view, hierarchy, toolbars, inspector, and many other features. It supports the programming languages C# and JavaScript. The programming code in Unity 3D for this work has been created in C# using Atom, a free and open source multiplatform code editor. The source code consists of a set of C# scripts to read the output CSV files from Matlab, extract the relevant data, such as geometric coordinates of the physical spaces of our problem and elements within, such as doors, windows, walkways, other structural elements (walls, beams, room partitioners, etc.), furniture, and so on, and finally display the generated 3D scenes (with all these graphical elements) on a computer screen. These graphical scenes are fully metric, in the sense that they correspond to the real measurements (with a scaling factor chosen by the user) provided as the input in Matlab.

The communication protocol between Matlab and Unity 3D is carried out through CSV files, which are simple to read and manipulate through LINQ queries using the open-source library LINQtoCSV, a popular API to handle CSV files. We also remark the excellent integration of Matlab and Unity 3D, the selected tools for the two layers of our architecture. Both programs are multiplatform and keep a similar user interface for all versions, thus ensuring a high and smooth cross-platform portability. Although other programs might be used for each layer, our choice guarantees wide availability, easy and smooth portability, and high numerical and graphical performance.

4. Examples of social distancing enhanced optimal designs

In this section, we discuss a number of examples whereby we show how our proposed approach for the design or the re-design of physical spaces with social distancing and other crucial factors can be incorporated through automated optimal design. We show examples of how various types of meeting rooms and other social spaces can be laid out. We also show how optimal designs in which essential factors such as the airflow within the physical environments can be factored into the design process.

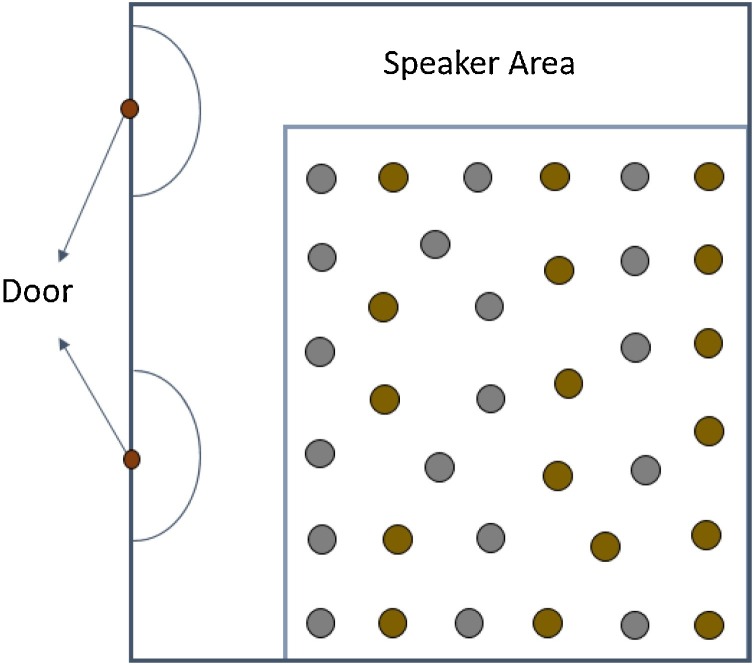
As a first example, we start with the arrangements discussed in Eq. (11) and the rectangular arrangement shown in Fig. 3. With this initial design, we generate a meeting environment in which an audience is facing one direction. This could be a get-together, a lecture or a classroom environment. In this particular case, the requirements are to allocate sufficient space at the front for the speaker(s), and space for the walkways with an arrangement. Specifically, for this example, we require an audience of 35 participants in the room whereby the size of the room is considered to be 12.9 m × 15.8 m and the social distancing requirement is considered to be 2 m between the participants. Fig. 6 , shows an optimal arrangement for this.

Fig. 6.

An example optimal design showing a front facing audience of 35 people within a room size of 12.9 m × 15.8 m.

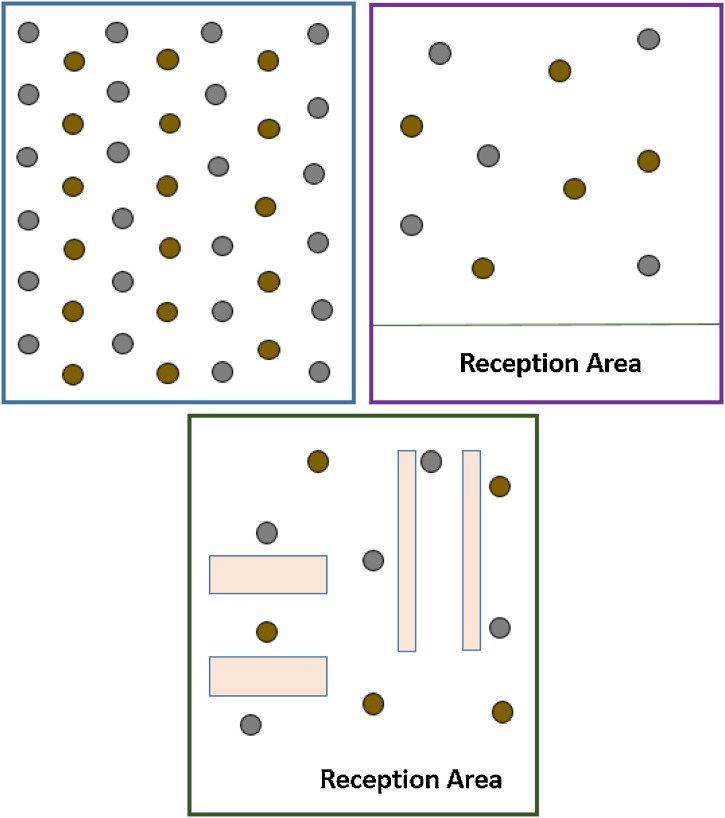
Similarly, Fig. 7 shows a variation in the design for a rectangular room environment which can be utilized as common areas – whereby we show how they can be arranged combined space allocation for people, furniture and administrative areas. The problem is formulated using similar parameters and design constraints, as discussed in Eq. (11).

Fig. 7.

Examples social distancing enabled optimal designs of common areas.

Thus, with the formulation we have set up, variations in the shape of the physical spaces can be conveniently incorporated. This can range from square rooms to circular rooms. For example, suppose we want to arrange social distancing enabled chairs in a circular room, the optimization can be set up as,

$$\begin{array}{cc}\underset{\text{x}}{\mathrm{minimize}}\hfill & -r,\hfill \\ \mathrm{subject}\mathrm{to}\hfill & 2r\le ||p_i-p_j||,\hfill \\ \hfill & x_i^2+y_i^2\le {(1-R)}^2,\hfill \\ \hfill & -R+r\le x_i\le R-r,\hfill \\ \hfill & -R+r\le y_i\le R-r,\hfill \\ \hfill & 1\le i<j\le n,R>0,\hfill \end{array}$$ (13)

where R is the radius of the circular room and r is the radius of the objects that need to be placed within the circular domain.

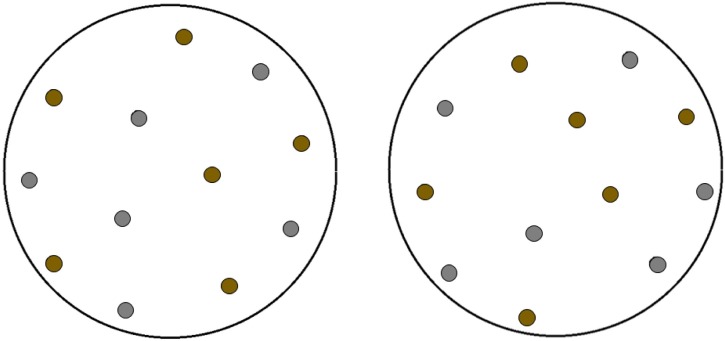
Fig. 8 shows example arrangements of chairs in a circular room in which the optimization problem highlighted in the Eq. (13) is solved subject to the constraints of the circular boundary and a given distance between the chairs inside the circular domain.

Fig. 8.

Optimal arrangements of chairs in a circular room with a prescribed distance between the chairs.

In a similar fashion, Fig. 9 shows example seating arrangements inside an airplane. Here we assume the fuselage area is a general elliptic shape (with a as major axis and b as minor axis) and with flat ends such that the length is L and width is W. This design optimization problem can be written as,

$$\begin{array}{cc}\underset{\text{x}}{\mathrm{minimize}}\hfill & -r,\hfill \\ \mathrm{subject}\mathrm{to}\hfill & 2r\le ||p_i-p_j||,\hfill \\ \hfill & r\le \frac{{(x_1-x_i)}^2}{a^2}+\frac{{(y_1-y_i)}^2}{b^2}-D^2,\hfill \\ \hfill & 1\le i<j\le n,a\le b,\hfill \\ \hfill & x_i\in [r,L-r],y_i\in [r,W-r],\hfill \end{array}$$ (14)

where D is the depth of the fuselage, which can be changed accordingly.

Fig. 9.

Example social distancing enabled optimal seating arrangements inside an airplane.

We note that unlike common airplane seating arrangements where the seats are placed along straight lines with fixed distances, the optimization provides interesting feasible arrangements with appropriate social distancing requirements in place.

4.1. Optimization with multi object constraints

In the discussions above, we have shown how it is possible to set up and solve design optimization problems in order to arrange a given type of object (in this case chairs for people to sit on). Here we show how multiple objects can be optimally placed inside the design environment with the appropriate constraints in place.

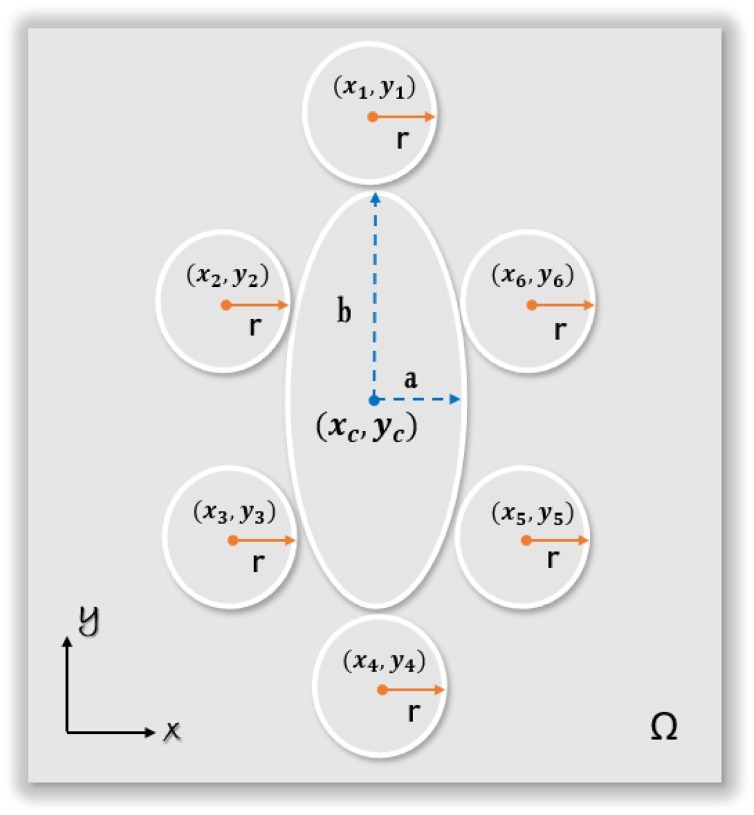
Let us suppose that we have a number of tables whose positions are fixed inside a room. In this case, we require a certain number of chairs to be arranged around the table so that the placement of chairs are social distance enabled. Unlike the previous examples, here we need to consider some extra constraints consisting of a distance measure from tables to the chairs and walls. For instance, considering an elliptic table with the fixed position at center p _C =  (x _C, y _C), where a is the major axis and b is the minor axis of the ellipse, as shown in Fig. 10 , we can write down the optimization problem as,

$$\begin{array}{cc}\underset{\text{x}}{\mathrm{minimize}}\hfill & -r,\hfill \\ \mathrm{subject}\mathrm{to}\hfill & 2r_i\le ||p_i-p_j||,\hfill \\ \hfill & r\le \frac{{(x_C-x_i)}^2}{a}+\frac{{(y_C-y_i)}^2}{b},\hfill \\ \hfill & x_i\in [r,L-r],y_j\in [r,W-r],\hfill \\ \hfill & 1\le i<j\le n.\hfill \end{array}$$ (15)

Fig. 10.

Consideration of social distancing enabled chair arrangements around an elliptic shaped table.

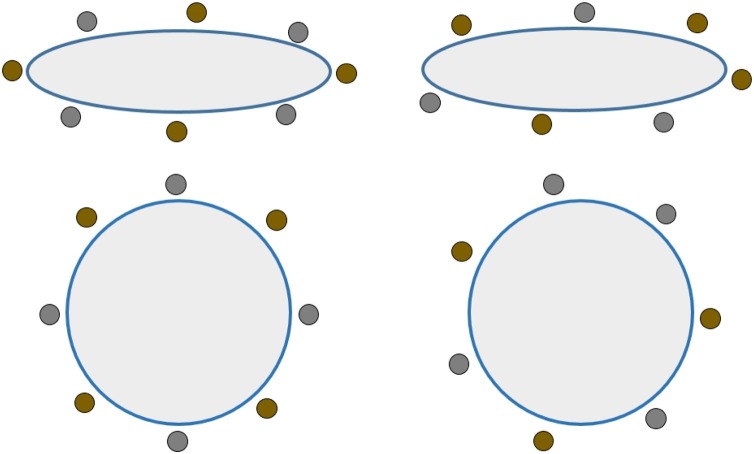
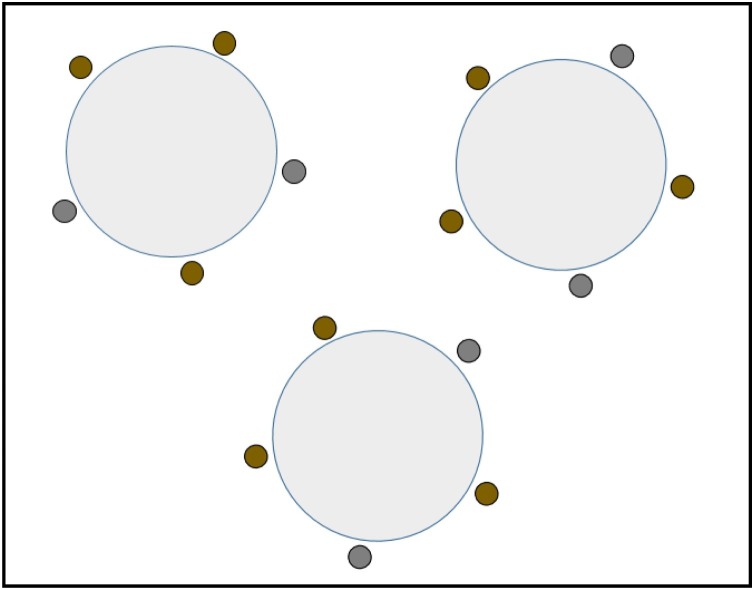
Fig. 11 shows examples of social distance enabled optimal arrangement of 7 and 8 chairs around an elliptical and a circular table. Similarly, Fig. 12 shows optimal arrangement of chairs and circular tables in a banquet style inside a rectangular room.

Fig. 11.

Social distance enabled optimal arrangement of chairs around an elliptical and a circular table.

Fig. 12.

Social distance enabled optimal arrangement of chairs around circular tables in a banquet style.

4.2. Constraints for airflow

In the redesign of physical spaces, to optimize for the health and safety aspects in the wake of the COVID-19 pandemic, one important parameter that must be borne in mind is the flow of air around a closed environment in which people are required to interact socially. As far as possible, the circulation of air around the given environment must be minimized so that the chances of spread of the disease are decreased. Here, we show how the parameters relating to airflow inside a closed environment can be taken into account when formulating the optimal design problem.

The airflow pattern, though occurs in a three dimensional physical environment which is under consideration, can be projected into a two dimensional plane. The flow itself inside an environment can be circular or rectangular. Considerations must also be given to the location of the source from which the air flows, the speed at which the air is flowing and also the position of any windows and doors.

For example, if the source of airflow is a fan then the pattern of flow would vary depending on the location of the fan. We can write this as an optimization problem such that,

$$\begin{array}{cc}\underset{\text{x}}{\mathrm{minimize}}\hfill & -r,\hfill \\ \mathrm{subject}\mathrm{to}\hfill & 2r\le ||p_i-p_j||,\hfill \\ \hfill & p_i\in [r,L-r],p_j\in [r,W-r],\hfill \\ \hfill & x_i-x_j<a,y_i-y_j<ba,b\in ℝ,\hfill \\ \hfill & 1\le i<j\le n,\hfill \end{array}$$ (16)

where L is the length, W is the width of the room/domain, a and b are the adjustable parameter, chosen according to the flow type. The constraints in the problem shown in Eq. (16) can be added or subtracted according to the specific need of the user.

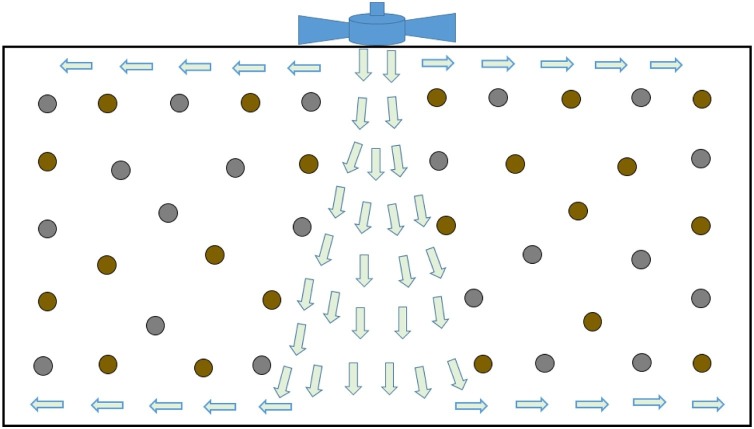
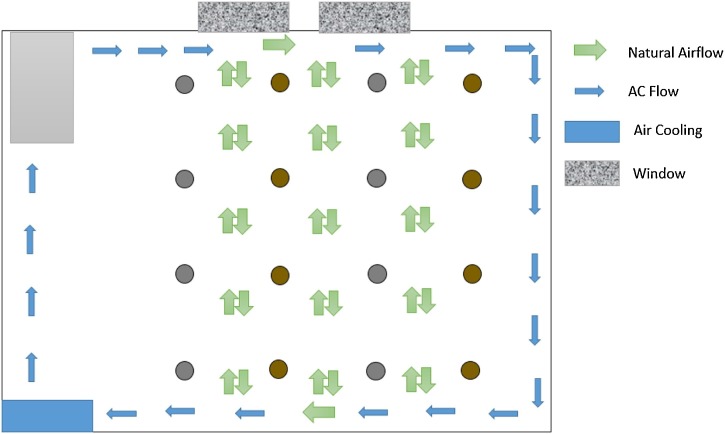
Thus, one must note that this case is highly dependent on the user's requirement and the setup. However, it is easy to detect the pattern and consider the constraint from the problems defined above and get the space rearranged. Fig. 13 shows the optimal solution for the airflow pattern with a fan fixed in the middle of one end of the room whereby the fan is assumed to be running at a constant speed. This kind of physical systems can be often found in meeting rooms. Fig. 14 shows airflow pattern with an air-conditioner. We also consider the position of windows and doors here. This kind of systems can be used for designing meeting rooms, common rooms, waiting areas, as well as similar such public areas.

Fig. 13.

An example optimal seating arrangement with airflow pattern from a fan taken into account.

Fig. 14.

An example optimal seating arrangement with airflow pattern from an air conditioner along with the position of windows are taken into account.

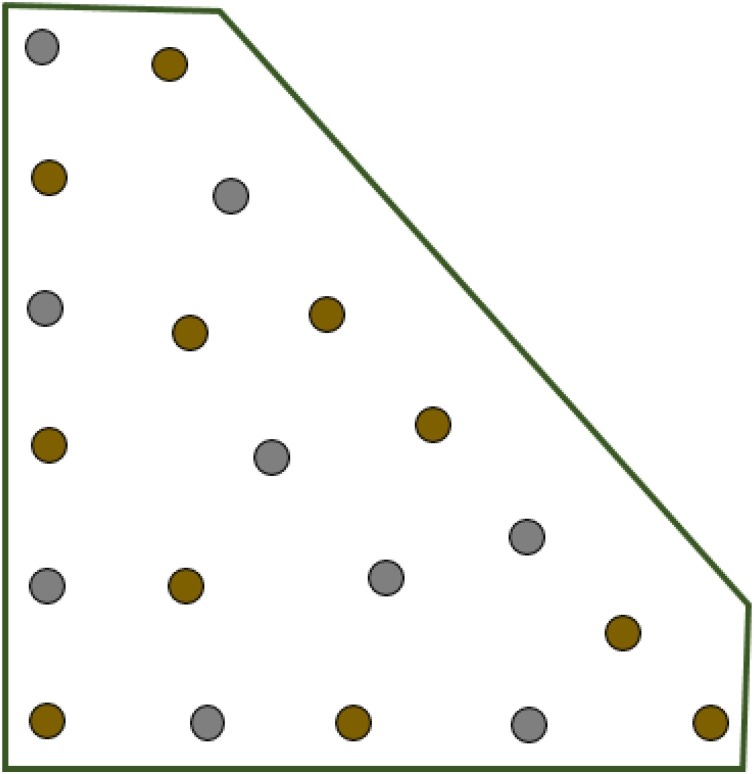
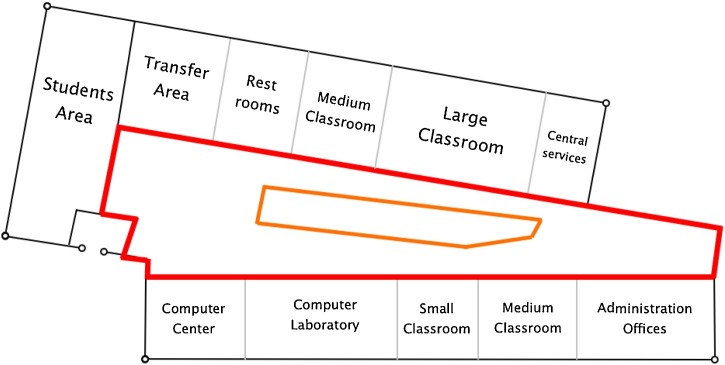
4.3. Example – the atrium area of a university campus building

The final example is aimed at showing the performance of our method for a more compelling (and perhaps more challenging) practical problem. Here the atrium area of a large university building is considered, as shown in Fig. 15 . This example is based on, and very similar (although not totally identical) to a project design of a future School of Business building in the campus of a western coast Canadian university. The atrium, enclosed by a red polyline in Fig. 15, is a large public area connecting several space areas for various uses, i.e., classrooms of several sizes, a computer lab, a student's area, administrative offices, storage rooms, transfer areas, and others. As the reader can appreciate, it has a complex geometry, with several walls at different angles, and several shapes of convexity. Mathematically, this non- convex convoluted geometry leads to a large set of constraints in the resulting optimization problem. In addition, there is a fixed closed structure in the middle (enclosed in orange in the figure) that includes some meeting rooms, a rest area, and a meeting point for students and visitors. This area adds a new set of constraints to the problem. As a result, this practical example is, by far, more challenging and difficult to solve than the previous (more academic) examples.

Fig. 15.

2D design of the first floor of a university campus building, with the atrium area enclosed in red. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

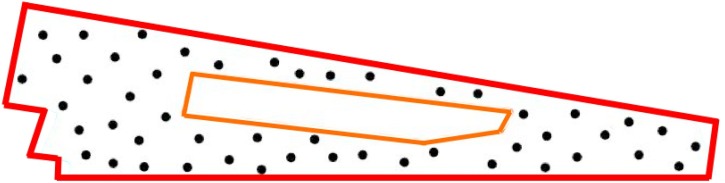
Fig. 16 shows the proposed arrangement of people with 2 m social distancing obtained with our method. Fig. 17 displays three different views of this solution as obtained graphically from our visualization tool Unity 3D.

Fig. 16.

Proposed arrangement of people with 2 m social distancing in the atrium area.

Fig. 17.

Three different 3D views of the obtained solution for the atrium example.

5. Discussions

Clearly, the examples discussed above provide good grounds to suggest that our proposed methodology for social distancing enhanced automated optimal design of physical spaces is feasible. We have shown examples of physical space layouts taking on board considerations such as the requirement on the physical distancing and other physical constraints such as the position of doors, windows, walkways and the conditions on airflow within the spaces. Fig. 18 shows examples of rendered images for various optimal physical space layouts resulting from our optimization platform. These renderings have been performed using the Unity 3D software whereby the final (optimized) coordinates for the positions of the objects from the optimizer are fed to Unity 3D.

Fig. 18.

Examples of optimal physical layouts rendered using the Unity 3D software environment.

Our methodology, based on the idea of the circle packing problem, assumes a given physical space and the constraints can be modeled using basic mathematical shapes such as circles, squares, rectangles and ellipses. This is a reasonable assumption since most of the common physical spaces and the design constraints one can consider can be very closely modelled using a combination of such basic mathematical shapes. In Table 2 , we show the number of variables and constraints needed for the basic nonlinear model for different domain types with N being the number of objects. Of course, if more constraints are added, then these numbers will change accordingly. Furthermore, the aim here is to seek a global optimal solution to the proposed nonlinear programming model. We run our solver starting with an initial (often random) seed and iteratively proceed until we obtain a set of optimal solutions according to the user requirements.

Table 2.

Basic modelling shapes utilized in the optimizer along with the variables and constraints considered.

Domain	Model constraints	No. of variables	No. of constraints
Square	Problem (10)	2N + 1	4N + 1
Rectangle	Problem (11)	2N + 2	4N + 1
Triangle	Problem (12)	2N + 1	3N + 1
Ellipse	Problem (15)	2N + 1	N + 2
Circle	Problem (13)	2N + 1	N + 2

It is important to highlight that the examples we have provided in this paper are geared to show the working principles of the methodology we have proposed. The parameters and constraints are also chosen to demonstrate this methodology. In practice, aside from the strict social distancing requirements, there can be many other constraints and variations in the design one could consider, especially when it comes to solving problems which are of practical significance. For example, in the case of the optimal seating arrangement for the airplane example, given in Fig. 9, although it is a feasible solution, in certain circumstances, this might not be practical. In this particular case, for example, there might be a need to have sufficient arrangements for the food trolley to be moved around with ease – the optimal designs proposed in Fig. 9 may not be well suited for this requirement. Nonetheless, using the recipe provided here, with the correct formulation of the optimization, such complex constraints can be conveniently added.

Furthermore, on the circle packing algorithm proposed here, it is important to note that the objective function to be minimized and the constraints must be continuous and real valued for the Algorithm 1 to be feasible. However, as discussed above, it is worth noting that many of the layout design problems involving the design or redesign of physical spaces can be defined or closely approximated – without compromising the practical applicability – using such formulations.

6. Conclusions

We have proposed a methodology that utilizes the solution of the well-known circle packing problem to address the current challenge of reconfiguring common physical environments with appropriate physical distancing measures as needed. Given the dimensions of a physical space and other essential requirements such as the social distancing requirements and the position of non-movable physical objects as well as the airflow pattern, the solution resulting from the automated optimization algorithm can suggest an optimal set of design alternatives from which a user can pick the most feasible option. Thus, we have shown that the chosen optimization problem can be solved using circle packing with the use of interior-point minimization. This formulation can handle not only large and sparse problems but also small dense problems making it feasible and efficient to set up and solve the optimization problem.

Much of the current design/redesign of physical spaces, in the wake of the present COVID-19 pandemic, is undertaken manually in an ad-hoc manner. On the other hand, the methodology we have proposed could be implemented as a solution to efficiently arrange physical spaces with given social distancing and other physical constraints.

By way of a number of practical examples, we have shown how our proposed solution can be utilized for social distancing enabled automated optimal design of physical spaces. Our system, if implemented as a practical tool, would be easy to use in which the dimensions and constraints can be entered by the user. The system will then provide a number of feasible solutions from which the user can pick the most desirable option. As a next step, we are presently working in developing a web based platform so that designers and decision makers can utilize it for use in real life scenarios.

Declaration of Competing Interest

The authors report no declarations of interest.