Factors determining training-induced changes in V̇O_2max, critical power, and V̇O₂ on-kinetics in skeletal muscle

Abstract

Computer simulations, using the “P_i double-threshold” mechanism of muscle fatigue postulated previously (the first threshold initiating progressive reduction in work efficiency and the second threshold resulting in exercise intolerance), demonstrated that several parameters of the skeletal muscle bioenergetic system can affect maximum oxygen consumption (V̇O_2max), critical power (CP), and oxygen consumption (V̇O₂) on-kinetics in skeletal muscle. Simulations and experimental observations together demonstrate that endurance exercise training increases oxidative phosphorylation (OXPHOS) activity and/or each-step activation (ESA) intensity, the latter, especially in the early stages of training. Here, new computer simulations demonstrate that an endurance training-induced increase in OXPHOS activity and decrease in peak P_i (Pi_peak), at which exercise is terminated because of exercise intolerance, result in increased V̇O_2max and CP, speeding of the primary phase II of V̇O₂ on-kinetics, and decreases V̇O₂ slow component magnitude, consistent with their observed behavior in vivo. It is possible, but remains unknown, whether there is a contribution to this behavior of an increase in the critical P_i (Pi_crit), above which the additional ATP usage underlying the slow component begins, and a decrease in the activity of the additional ATP usage (k_add). Thus, we offer a mechanism, involving P_i accumulation, Pi_crit and Pi_peak, of the training-induced adaptations in V̇O_2max, CP, and the primary and slow component phases of V̇O₂ on-kinetics that was absent in the literature.

NEW & NOTEWORTHY A mechanism of the training-induced changes in V̇O_2max, critical power, and V̇O₂ on-kinetics in skeletal muscle reported in the literature is postulated. It involves the self-driving “P_i double-threshold” mechanism of muscle fatigue underlying exercise inefficiency, the slow component of the V̇O₂ on-kinetics, and termination of exercise. It is proposed that an increase in OXPHOS activity and decrease in peak P_i at which exercise terminates are responsible for the training-induced changes in the muscle bioenergetic system.

INTRODUCTION

Endurance training changes several kinetic properties of the skeletal muscle bioenergetic system. It elevates maximum oxygen consumption (V̇O_2max) (1–14), increases critical power (CP) (5, 8, 10), speeds the primary phase II of the oxygen consumption (V̇O₂) on-kinetics (1, 9, 13–15), and lowers the slow component of the V̇O₂ on-kinetics (1–3, 16). It was shown that training-induced increase in oxidative phosphorylation (OXPHOS) activity and each-step activation (ESA) intensity (the activation of all OXPHOS complexes and the NADH supply block, in parallel with the activation of ATP usage) leads to speeded V̇O₂ on-kinetics (17). However, the mechanisms underlying the rest of the observed intramuscular kinetic changes following endurance training are still not well understood.

Muscle performance during exercise is reduced by both peripheral and central fatigue mechanisms (18–22). Inorganic phosphate (P_i) is proposed as the main metabolite involved with peripheral fatigue, whereas other metabolites, for instance, H⁺ ions and ADP, as well as depletion of glycogen stores, play a less important role in peripheral fatigue (18).

Muscle fatigue is associated with changes in V̇O₂ on-kinetics, and the emergence of the V̇O₂ slow component (rev. ref. 22), but no quantitative cellular mechanism for this association was proposed until the recent development of “P_i double-threshold” mechanism of muscle fatigue and inefficiency (23). This hypothesis postulated that 1) additional ATP usage, underlying the slow component of the V̇O₂ and intramuscular metabolic on-kinetics, appears when P_i exceeds a certain critical value, termed Pi_crit; 2) muscle work is terminated because of exercise intolerance when P_i reaches another, greater, peak value, termed Pi_peak; and 3) P_i increase and additional ATP usage form a self-driving, reciprocal mechanism of positive feedback (23, 25), which, if sustained, leads to attainment of Pi_peak, peripheral fatigue, and exercise intolerance. It was demonstrated that these assumptions could generate various, apparently unrelated, system properties, comprising (23): time courses of muscle V̇O₂, cytosolic ADP, pH, PCr, and P_i during rest-to-work transition; end-exercise constancy of these variables at various power outputs; hyperbolic shape of the power-duration curve with critical power (CP) as an asymptote; and hyperoxia-induced increase in CP and acceleration of the principal phase II V̇O₂ on-kinetics (decrease in the characteristic transition time t_0.63, related to τ_p) observed in knee extension or supine cycling exercise (26, 27).

These previous simulations provide the first model of cellular events that determine whether a power output exceeds CP (the power output where a metabolic steady-state is lost). To test this model, here we use a computer simulation of the entire muscle bioenergetic system to test the hypothesis that changes in several parameters related to OXPHOS activity (rate constants of OXPHOS complexes and ESA intensity) and muscle fatigue (Pi_crit, Pi_peak, and k_add), of the order observed or estimated following endurance exercise training, result in anticipated adaptations of the kinetic system properties of skeletal muscle. We aim to identify whether a simulated increase in OXPHOS activity (rate constants of OXPHOS complexes) and/or ESA intensity (in the early stages of training), as well as decrease in the Pi_peak, are the main factors responsible for (the size of) the training-induced increase in V̇O_2max, increase in CP, acceleration of the primary phase II of the V̇O₂ on-kinetics, and reduction of the V̇O₂ slow component. We also aim to identify whether simulated increases in Pi_crit and additional ATP usage activity (k_add) contribute to training-induced adaptations of the muscle kinetic system behavior. Overall, this study postulates a plausible mechanism of the training-induced increase in V̇O_2max and CP, as well as acceleration of the phase II of the V̇O₂ on-kinetics and reduction of its slow component that was absent in the literature.

THEORETICAL METHODS

Ethical Approval

This is a purely theoretical study that did not involve any experiments on humans or animals.

Computer Model

The computer model of OXPHOS and the entire bioenergetic system in intact skeletal muscle was used (23, 28–33). The model involves the ESA (or parallel activation) concept, according to which not only ATP usage but also the NADH supply block and all OXPHOS complexes are directly activated by some cytosolic factor/mechanism (probably involving cytosolic Ca²⁺ ions) during rest-to-work or low- to high-work transition in skeletal muscle and heart (28, 34). The complete model description is given in Korzeniewski’s study (25) and is located at http://awe.mol.uj.edu.pl/∼benio/.

This model was able to reproduce a wide range of, apparently unrelated, kinetic properties of the skeletal muscle bioenergetic system during exercise and was used for numerous theoretical studies (see ref. 34 for review; 23, 25, 29, 30).

Rate constants appear in kinetic equations for all OXPHOS complexes (complex I, complex III, complex IV, ATP synthase, ATP/ADP carrier, P_i carrier) and NADH supply block within the computer model. All these rate constants (k_C1, k_C3, k_C4, k_SN, k_EX, k_PI, k_DH) are individually represented in the model and can be grouped into a single rate constant (activity) of OXPHOS: k_OX, notionally proportional to the volume-density of mitochondria and concentration and activity of OXPHOS enzymes. In the standard model version, corresponding to moderately trained (physically active) individuals, the relative k_OX is scaled to 1.

The intensity of ESA A_OX determines how much OXPHOS is directly activated, or how many times k_OX is elevated, during the rest-to-work transition. A_OX is within the model, a function of the relative ATP usage activity A_UT (29):

$${\text{A}}_{\text{OX}}={1+\text{A}}_{\text{OXmax}}\left(\frac{{\text{A}}_{\text{UT}}\mathrm{ }-\mathrm{ }1}{\left({\text{A}}_{\text{UT}}\mathrm{ }-\mathrm{ }1\right)+{\text{K}}_{{\text{A}}_{\text{UT}}}}\right)$$ (1)

where A_OXmax (unitless) is the maximum ESA activity minus one, A_UT (unitless) is the relative (fold) increase in the activity (rate constant) of ATP usage during rest-to-work transition, and K_Aut (unitless) is the saturation constant for A_UT. In the standard model version (23, 25, 29) A_OXmax = 5 and K_Aut = 5.

During high-intensity exercise, an additional ATP usage is observed, which is in excess of regular ATP usage, proportional to power output (PO) for any given type of exercise. This additional ATP usage is the basis for the V̇O₂ slow component. The kinetics of additional ATP usage is described by the following formula (23):

$${\text{v}}_{\text{add}}=k_{add}\times {\text{v}}_{\text{UT}}\times {\left({\text{P}}_{\text{i}}-{\text{P}}_{{\text{i}}_{\text{crit}}}\right)}^{0.5}\times {10}^{-{\text{t}}_{\text{a}}/{\text{t}}_{\text{ex}}}$$ (2)

where v_add is the rate of additional ATP usage (mM·min⁻¹), k_add is the “rate constant” of the additional ATP usage (mM⁻¹), v_UT is the rate of the regular ATP usage (mM·min⁻¹), P_i is the current inorganic phosphate concentration (mM), Pi_crit is the critical P_i for the initiation of the additional ATP usage (mM), t_a is the characteristic time of the activation of the additional ATP usage (min), and t_ex is the time after the onset of exercise (min). In the standard model version, additional ATP usage starts when P_i exceeds Pi_crit = 18 mM, k_add = 0.2 mM⁻¹, t_a = 2 min (23), and muscle work is terminated because of exercise intolerance when P_i reaches Pi_peak = 25 mM (25).

The total absolute ATP usage flux v_UTtot (in mM·min⁻¹) is equal to the sum of the regular and additional absolute ATP usage rate:

$${\text{v}}_{\text{UTtot}}={\text{v}}_{\text{UT}}+{\text{v}}_{\text{UTadd}}$$ (3)

Simulation Procedures

Power-duration relationships for different selected parameter values were obtained by subsequent running of simulations for increasing values of the ATP usage activity (A_UT, corresponding to power output) at a given set of parameter values. The effect of the following parameters was studied: OXPHOS activity (k_OX), ESA intensity (A_OXmax), peak P_i (Pi_peak), critical P_i (Pi_crit), and activity (rate constant) of the additional ATP usage (k_add). Power-duration curves for “standard” values of these parameters (see previous section) and for these values decreased or increased by 10% were simulated.

The standard version of the model (23), where the characteristic transition time of V̇O₂ on-kinetics (t_0.63, corresponding to τ_p) is equal to ∼25 s, corresponds to physically active, “moderately trained” individuals. To represent untrained (sedentary) individuals, the relative OXPHOS activity k_OX was decreased to 0.8 of the standard value. On the other hand, in two sets of simulations representing well-trained individuals, k_OX was increased to 1.1 of the standard value. Thus, the simulation of training of untrained individuals involved an increase in k_OX from 0.8 to 1.1 (by 37.5%). In the first simulation (simulation set A), Pi_peak = 25 mM was unchanged, whereas in the second simulation (simulation set B), Pi_peak was decreased from 25 mM to 22 mM to reproduce more closely observations from experimental data (for justification see discussion).

The training-induced increase in OXPHOS activity by 37.5% (from 0.8 to 1.1) conforms well with the size of the training-induced increases in skeletal muscle mitochondrial volume-density or OXPHOS activity encountered in experimental studies as a result of long-term endurance training (4, 6, 12, 35).

Rest-to-work transitions at different ATP usage activities for voluntary constant-power exercise were simulated as described by Korzeniewski (29). The relative activity of ATP usage A_UT (relative increase in its rate constant k_UT in relation to rest) between 110 (maximum A_UT) and A_UT below the critical A_UT (A_UTcrit) was used in computer simulations. One A_UT unit corresponds to ∼3 W during cycle ergometer exercise (29). This value may vary between ∼2 and 4 W, depending on, for example, working muscle mass and type of exercise.

THEORETICAL RESULTS

Our initial findings from simulating the effect of changes in selected parameter values on V̇O_2max, A_UTcrit (CP) and t_0.63 are shown in Figs. 1 and 2 and Table 1. Parameters were manipulated in isolation to determine their effects on a range of system variables and kinetics.

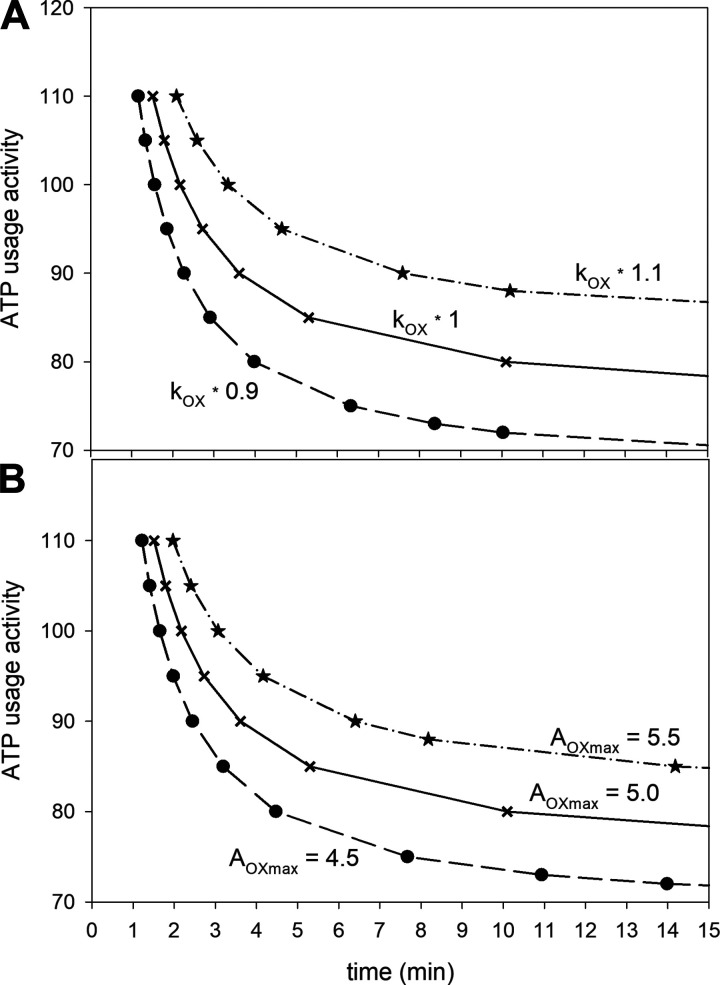
Figure 1.

A: simulated ATP usage activity-exercise duration curves (corresponding to power-duration curves) for “standard” oxidative phosphorylation (OXPHOS) activity k_OX (k_OX *1), k_OX diminished by 10% (k_OX * 0.9), and k_OX enlarged by 10% (k_OX * 1.1); B: simulated ATP usage activity-exercise duration curves for “standard” each-step activation (ESA) intensity A_OXmax (A_OXmax = 5), A_OXmax diminished by 10% (A_OXmax = 4.5), and A_OXmax enlarged by 10% (A_OXmax = 5.5).

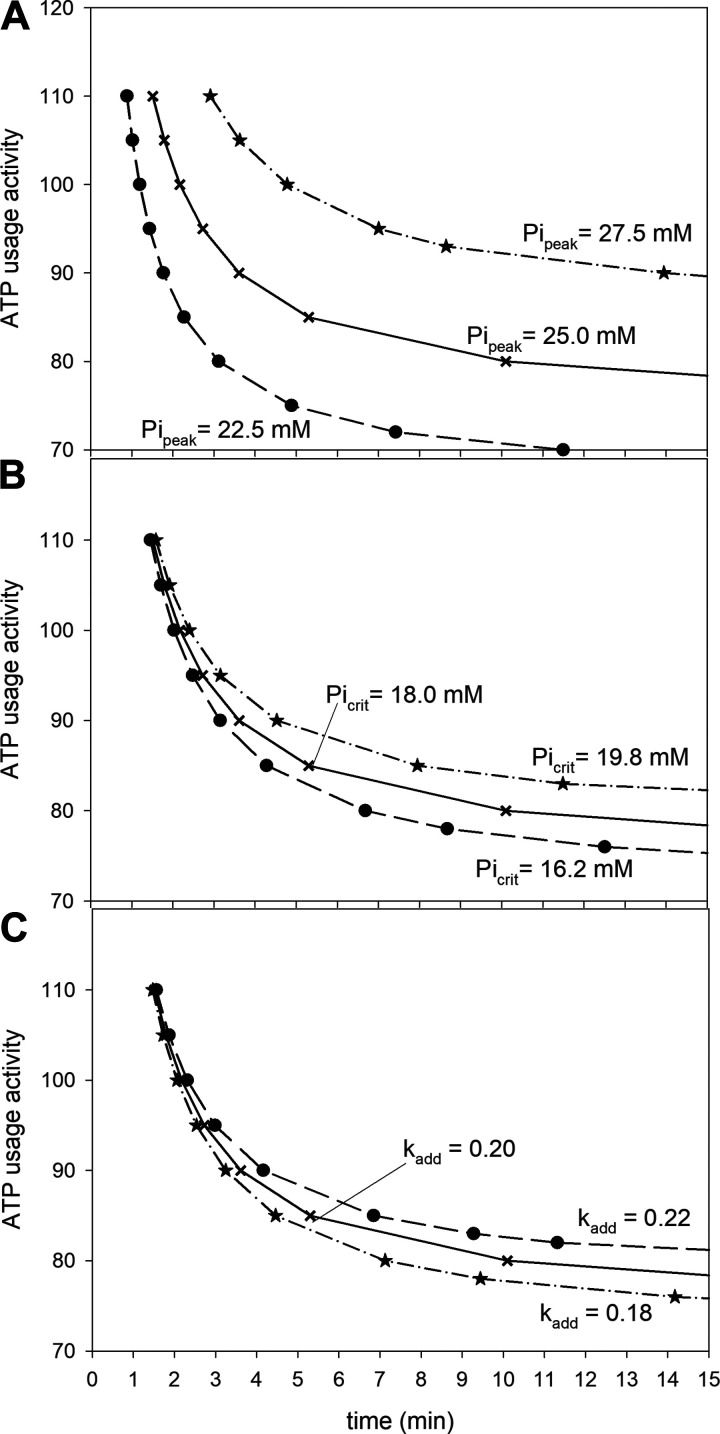
Figure 2.

A: simulated ATP usage activity-exercise duration curves (corresponding to power-duration curves) for “standard” peak inorganic phosphate (P_i) at which exercise is terminated Pi_peak (Pi_peak = 25.0 mM), Pi_peak diminished by 10% (Pi_peak = 22.5 mM), and Pi_peak enlarged by 10% (Pi_peak = 27.5 mM); B: simulated ATP usage activity-exercise duration curves for “standard” critical P_i (Pi_crit) at which the additional ATP usage [and thus slow components of the oxygen uptake (V̇O₂) and metabolites on-kinetics] is initiated Pi_crit (Pi_crit = 18 mM), Pi_crit diminished by 10% (Pi_crit = 16.2 mM), and Pi_crit enlarged by 10% (Pi_crit = 19.8 mM); C: simulated ATP usage activity-exercise duration curves for “standard” activity (rate constant) of the additional ATP usage k_add (k_add = 0.20), k_add diminished by 10% (k_add = 0.18), and k_add enlarged by 10% (k_add = 0.22).

Table 1.

Simulated effect of a decrease or increase in chosen parameter values by 10% in relation to “standard” (100%) values on selected variables

Parameter	Relative Parameter Value	V̇O2max, mM·min−1	AUTcrit, unitless	t0.63, s
kOX	−10%	11.9 (–10.2%)	67.1 (–10.2%)	26.5 (+8.2%)
	100%	13.3	74.7	24.5
	+10%	14.7(+10.5%)	83.3 (+10.5%)	22.8 (–6.9%)
AOXmax	−10%	12.2 (–8.4%)	69.4 (–7.1%)	26.8(+9.4%)
	100%	13.3	74.7	24.5
	10%	14.4 (+8.6%)	81.0 (+8.4%)	22.5 (–8.2%)
Pipeak	−10%	11.1 (–16.2%)	66.6 (–10.8%)	24.5 (--)
	100%	13.3	74.7	24.5
	+10%	15.7 (+18.1%)	84.5 (+13.1%)	24.5 (--)
Picrit	−10%	13.3 (--)	71.5 (–4.3%)	24.5 (--)
	100%	13.3	74.7	24.5
	+10%	13.3 (--)	78.7 (+5.4%)	24.5 (--)
kadd	−10%	13.3 (--)	72.1 (–3.5%)	24.5 (--)
	100%	13.3	74.7	24.5
	+10%	13.3 (--)	77.5(+3.7%)	24.5 (--)

t_0.63 was simulated for ATP usage activity A_UT = 40 (moderate exercise). A_OXmax, each-step activation (ESA) intensity; A_UTcrit, critical ATP usage activity (corresponding to critical power); k_add, activity (rate constant) of the additional ATP usage; k_OX, oxidative phosphorylation (OXPHOS) activity; Pi_crit, critical P_i at which the additional ATP usage (and thus the slow component of the V̇O₂ and metabolites) appears; Pi_peak, peak P_i at which exercise is terminated because of exercise intolerance; V̇O_2max, maximal V̇O₂; t_0.63, characteristic transition time of the V̇O₂ on-kinetics (analogous to τ_p).

In the simulations shown in Fig. 1, the values of parameters related to OXPHOS activity (OXPHOS activity, k_OX, and ESA intensity, A_OXmax) were either decreased or increased by 10% in relation to “standard” values, and the effect of this manipulation on the power-duration relationship was studied. Solid lines in Fig. 1 correspond to “standard” parameter values. Reducing k_OX by 10% decreased V̇O_2max by 10.2%, decreased A_UTcrit by 10.2%, and lengthened t_0.63 by 8.2% (Fig. 1A and Table 1). An increase in k_OX by 10%, increased V̇O_2max by 10.5%, increased A_UTcrit by 10.5%, and shortened t_0.63 by 6.9% (Fig. 1A and Table 1). On the other hand, a decrease in A_OXmax by 10% decreased V̇O_2max by 8.4% and A_UTcrit by 7.1% and lengthened t_0.63 by 9.4%, whereas an increase in A_OXmax by 10% increased V̇O_2max by 8.4% and A_UTcrit by 8.4% and shortened t_0.63 by 8.2% (Fig. 1B and Table 1). Therefore, while a change in the value of k_OX has a slightly greater effect on V̇O_2max and A_UTcrit, a change in A_OXmax has a slightly greater effect on t_0.63.

All of the three tested parameters related to the additional ATP usage and muscle fatigue influenced A_UTcrit (CP), but only one influenced V̇O_2max and none influenced t_0.63. This is demonstrated in Fig. 2 and Table 1. In Fig. 2 the values of Pi_peak, Pi_crit, and k_add, were independently decreased or increased by 10%, and the effect of this manipulation on the power-duration relationship was studied. Solid lines in Fig. 2 correspond to “standard” parameter values. A decrease in Pi_peak by 10% decreased V̇O_2max by 16.2%, decreased A_UTcrit by 10.8%, and did not affect t_0.63, whereas an increase in Pi_peak by 10% increased V̇O_2max by 18.1%, increased A_UTcrit by 13.1%, and did not affect t_0.63 (Fig. 2A and Table 1). A decrease in Pi_crit by 10% did not affect V̇O_2max, decreased A_UTcrit by 4.3%, and did not affect t_0.63, whereas an increase in Pi_crit by 10% did not affect V̇O_2max, increased A_UTcrit by 5.4%, and did not affect t_0.63 (Fig. 2B and Table 1). Finally, a decrease in k_add by 10% did not affect V̇O_2max, decreased A_UTcrit by 3.5%, and did not affect t_0.63, whereas an increase in k_add by 10% did not affect V̇O_2max, increased A_UTcrit by 3.7%, and did not affect t_0.63 (Fig. 2C and Table 1). Therefore, although the relative impact of the value of Pi_peak on A_UTcrit (CP) and V̇O_2max is the strongest of all the parameters tested, the impact of the value of Pi_crit and k_add is rather small or none at all.

Overall Figs. 1 and 2 and Table 1 demonstrate that ±10% alterations in key system parameters (e.g., as in response to training or detraining) have very diverse magnitudes of effect on V̇O_2max, A_UTcrit, and t_0.63.

In the first set of simulations of the effect of endurance training (set A), where only the activity of OXPHOS (k_OX) was increased from 0.8 (untrained state) to 1.1 (trained state) of the “standard” value (37.5% increase), V̇O_2max increased by ∼40%, A_UTcrit (corresponding to CP) increased by ∼35%, and the characteristic transition time of the phase II of the V̇O₂ on-kinetics (t_0.63) decreased by ∼22%. This is demonstrated in Table 2 Although qualitatively appropriate, set A simulations of the training-induced increase in k_OX alone produced changes in V̇O_2max and A_UTcrit (CP) that were quantitatively too large compared with in vivo observations (see discussion), and therefore, a second set of simulations was carried out.

Table 2.

Simulated effect of training when only OXPHOS activity is elevated (set A of simulations)

Parameter	Untrained	Trained
OXPHOS activity, kOX	0.8	1.1 (↑37.5%)
(in relation to standard)
Variable
V̇O2max, mM·min−1	10.43	14.61 (↑40.1%)
AUTcrit, unitless	60.6	82.0 (↑35.3%)
t0.63, s	29.2	22.8 (↓21.9%)

The change in the parameter value causes changes in variable values. A_UTcrit, critical ATP usage activity (corresponding to critical power); k_OX, oxidative phosphorylation (OXPHOS) activity; V̇O_2max, maximal V̇O₂; t_0.63, characteristic transition time of the V̇O₂ on-kinetics (analogous to τ_p).

In the second set of simulations of the effect of endurance training (set B), the activity of OXPHOS (k_OX) was increased from 0.8 (untrained state) to 1.1 (trained state) of the “standard” value (37.5% increase) and peak P_i (Pi_peak) was simultaneously decreased from 25 mM (untrained state) to 22 mM (trained state) (12% decrease). This resulted in increased V̇O_2max by ∼13% and A_UTcrit by ∼22% and the characteristic transition time of the phase II of the V̇O₂ on-kinetics (t_0.63) decreased by ∼22%. The decrease in Pi_peak was chosen to lower the training-induced rise in V̇O_2max and A_UTcrit (CP), as the effect of an increase in Pi_crit and increase in k_add on these variables was too small or none at all (compare Fig. 2 and Table 1).

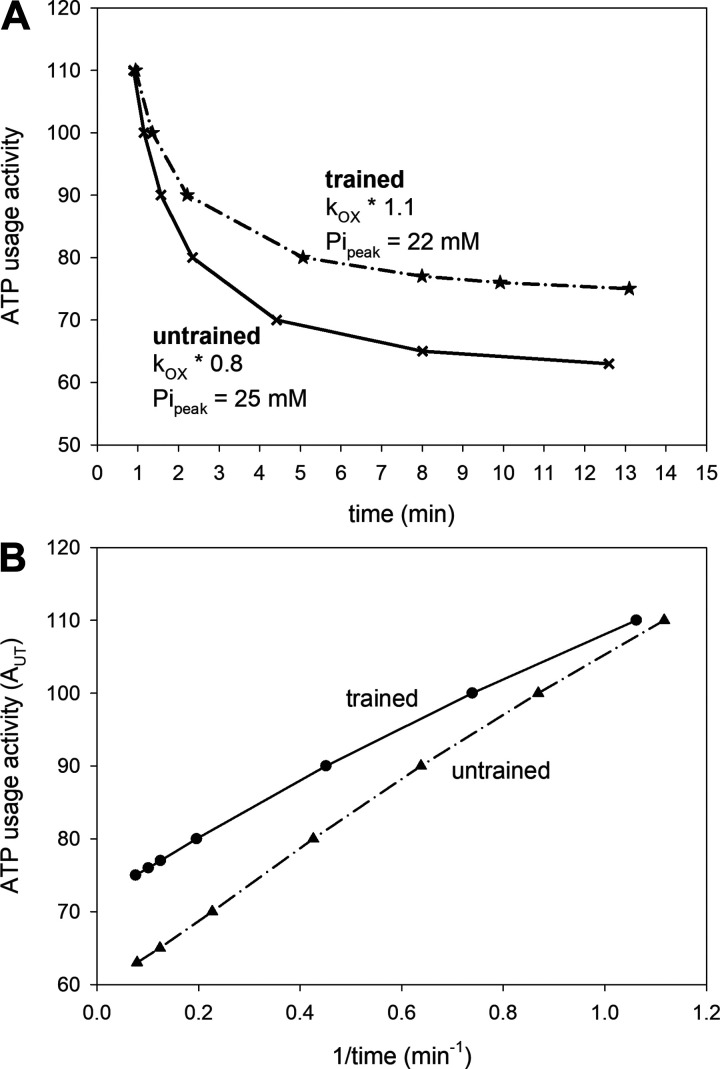
Using set B of simulation parameters, the ATP usage activity-duration of exercise (time) relationship was very close to hyperbolic, both before and after training. This is shown in Fig. 3A; at the same time, the critical ATP usage activity (corresponding to CP) increased significantly as a result of training (by ∼22%; compare Table 3). Consequently, the dependence of the critical ATP usage on 1/time (exercise duration) was near-linear, and the line representing this dependence for trained muscle was situated above the line representing the dependence for untrained muscle (Fig. 3B). Also of note, the slope of this relationship in the trained state is somewhat shallower (Fig. 3B). This represents a smaller W′ (the curvature constant of the power-duration relationship) by ∼22% in the trained state.

Figure 3.

A: simulated ATP usage activity-exercise duration curves (corresponding to power-duration curves) for untrained muscle and trained muscle under the assumption that training causes an increase in oxidative phosphorylation (OXPHOS) activity (k_OX) from 0.8 to 1.1 of the standard value and a decrease of the peak P_i at which exercise is terminated (Pi_peak) from 25 mM to 22 mM (setB of simulations); B: simulated ATP usage activity minus 1/duration curves (corresponding to power minus 1/duration curves) for untrained muscle and trained muscle constituting transformed data from A.

Table 3.

Simulated effect of training when OXPHOS activity is increased and peak P_i is decreased (set B of simulations)

Parameter	Untrained	Trained
OXPHOS activity, kOX	0.8	1.1 (↑37.5%)
(in relation to standard)
Peak Pi (Pipeak), mM	25	22 (↓12%)
Variable
V̇O2max, mM·min−1	10.50	11.83 (↑12.7%)
AUTcrit, unitless	59	72 (↑22%)
t0.63, s	29.2	22.8 (↓21.9%)

The changes in the parameter values cause changes in variable values. A_UTcrit, critical ATP usage activity (corresponding to critical power); V̇O_2max, maximal V̇O₂; t_0.63, characteristic transition time of the V̇O₂ on-kinetics (analogous to τ_p).

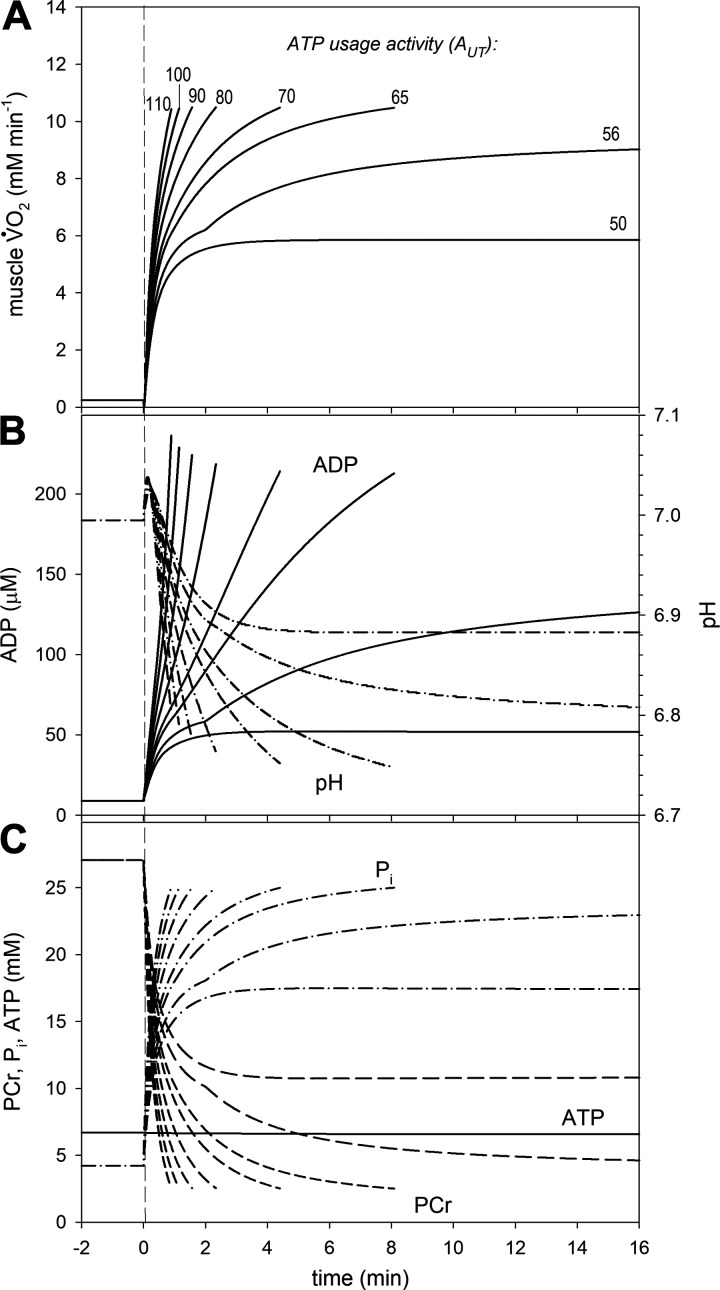
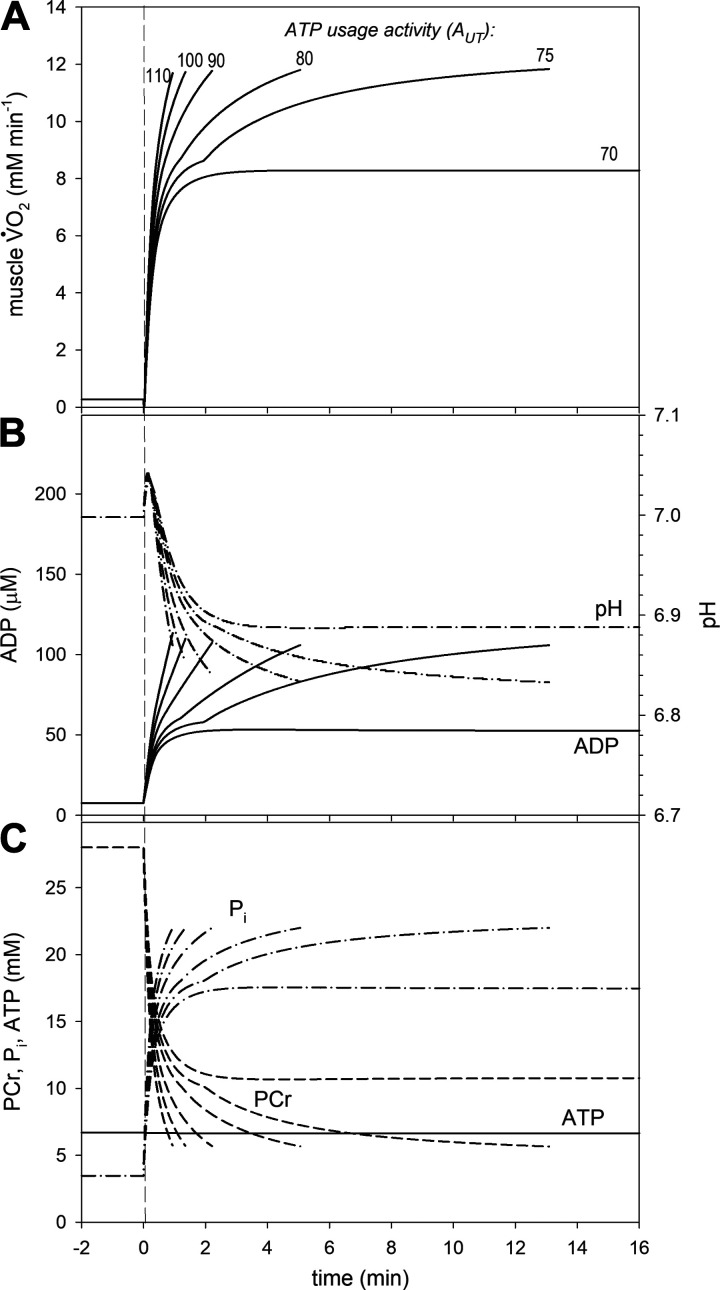
The simulated time courses of V̇O₂ and metabolites during the on-transient over a range of ATP usage activities for the untrained state and trained state generally agree well with experimental data (see refs. 23, 25 for a detailed discussion of the “standard” state). They are presented in Figs. 4 and 5. Generally speaking, identical V̇O_2max, PCr, and P_i (by definition) were present at the end of exercise in both cases (but significantly different between cases), whereas the levels of ADP and pH were similar, but not identical in each case. A characteristic “notch” in time-course of simulated variables was observed for some values of the ATP usage, encountered in several experimental studies (see ref. 23 for discussion). The “notch” appears at the point in time when P_i exceeds Pi_crit. The characteristic transition time t_0.63 for the phase II of the V̇O₂ on-kinetics for A_UT = 40 (moderate exercise) equaled ∼29 s for untrained state and ∼23 s for trained state (compare Table 3). A steady-state, without a V̇O₂ or metabolite slow component, was quickly reached for ATP usage activities corresponding to moderate exercise, whereas a slow component appeared for higher ATP usage activities that corresponded to heavy and very heavy (and severe) exercise. In untrained muscle, for A_UT = 56, which is below the critical ATP usage activity A_UTcrit = 59, the slow component appeared, but a delayed steady-state was observed without reaching V̇O_2max. Therefore, this simulation corresponded to heavy exercise. None of the A_UT values above A_UTcrit resulted in a steady-state, and variable values continued to change up to the termination of exercise. Thus, these simulations represented very heavy and severe exercise. On the other hand, in simulations of well-trained muscle, the range of A_UT values that represented heavy intensity was greatly diminished. At A_UT = 70, which was just below A_UTcrit = 72, there was no V̇O₂ or metabolite slow component observed (moderate exercise), whereas above A_UTcrit, V̇O₂ increased progressively toward V̇O_2max (very heavy and severe exercise).

Figure 4.

Simulated muscle oxygen uptake (V̇O₂) and metabolites on-kinetics for various ATP usage activities (A_UT) in untrained muscle (k_OX * 0.8, Pi_peak = 25 mM). A: time courses of muscle V̇O₂; B: time courses of cytosolic free ADP and pH; C: time courses of cytosolic phosphocreatine (PCr), inorganic phosphate (P_i), and ATP.

Figure 5.

Simulated muscle oxygen uptake (V̇O₂) and metabolites on-kinetics for various ATP usage activities (A_UT) in trained muscle (k_OX * 1.1, Pi_peak = 22 mM). A: time courses of muscle V̇O₂; B: time courses of cytosolic free ADP and pH; C: time courses of cytosolic phosphocreatine (PCr), inorganic phosphate (P_i), and ATP.

The metabolic perturbations caused by simulated exercise were smaller in the trained than in the untrained state. The magnitude of changes in metabolites relative to ATP usage activity (increase in ADP and Pi, decrease in PCr, and decrease in pH after an initial increase), and the values for these metabolites at end-exercise when exercise was terminated were much smaller in trained muscle than in untrained muscle (Fig. 5 versus Fig. 4).

Training simulations demonstrated that the same ATP usage activity (and therefore, PO) can result in very different states of metabolic strain. This is demonstrated in Fig. 6, which represents the simulated V̇O₂ on-kinetics for ATP usage activity A_UT = 65 before and after training. The principal phase II of the V̇O₂ on-kinetics in untrained muscle is also presented. Training principally changes the behavior of the system. Although before training a clear slow component can be observed and no steady-state can be achieved before reaching V̇O_2max, there is no slow component and a steady-state is quickly reached after training at the same A_UT activity. Therefore, whereas in untrained muscle this power output clearly corresponds to very heavy-intensity exercise, in trained muscle, the same power output results in moderate-intensity metabolic behavior. In addition, training causes a clear acceleration of the primary phase II of the V̇O₂ on-kinetics. Therefore, at this particular A_UT (PO), training brings the system from nonsteady (very heavy-exercise) to steady-state (moderate exercise)-like behavior.

Figure 6.

Simulated oxygen uptake (V̇O₂) on-kinetics for ATP usage activity A_UT = 65 in untrained and trained muscle. In untrained muscle, the V̇O₂ primary phase II component and the slow component are distinguished.

DISCUSSION

This theoretical study postulates that the changes in V̇O_2max, CP, and V̇O₂ on-kinetics in skeletal muscle induced by long-term endurance training can be caused by an increase in OXPHOS activity and a decrease in the peak P_i, at which exercise is terminated because of exercise intolerance. No such mechanism that unifies the training-induced increase in these muscle bioenergetic behaviors had been proposed in the literature.

Comparison with Experimental Data

Endurance training programs typical of research studies lead to an average increase in V̇O_2max (and maximal work) in the region of 10%–15%, increase in CP by 15%–20%, decrease in t_0.63 by ∼25%, and significant decrease in the slow component of the V̇O₂ on-kinetics (1–16). Therefore, the increase in V̇O_2max by 40% and increase of A_UTcrit (corresponding to CP) by 35% obtained in set A of simulations (solely resulting from a 37.5% increase in OXPHOS activity) differ significantly from experimental data. On the other hand, the increase in V̇O_2max by 13%, increase of A_UTcrit by 22%, and decrease in t_0.63 by 22% obtained in set B of simulations (37.5% increase in OXPHOS activity and decrease in Pi_peak from 25 mM to 22 mM) agree well with experimental data. This leads to the prediction that long-term endurance training leads to not only an increase in mitochondrial volume-density and oxidative activity but also a decrease of the peak P_i at which exercise is terminated.

Within the computer model used, the training-induced increase in V̇O_2max is caused by the attenuation of P_i accumulation during exercise owing to an increased OXPHOS activity (and/or ESA intensity). This, is turn, delays P_i reaching Pi_peak. The increase in CP is also related to a slower P_i accumulation, as this delays attainment of Pi_crit and also reduces the magnitude of the V̇O₂ slow component for any given ATP usage activity above CP. The increase in A_UTcrit (CP) causes some POs that were unsustainable before training to reach steady-state after training, where Pi_peak is not reached at all. On the other hand, the decrease in Pi_peak in the trained state exerts an opposite effect to the increase of OXPHOS activity: this has the action of suppressing an increase in both V̇O_2max and CP, as it somewhat accelerates the reaching by P_i of Pi_peak. The lowering Pi_peak has the effect of reducing A_UTcrit (CP), as P_i reaches Pi_peak sooner at POs that cause [P_i] to exceed Pi_crit, and also reduces the range of supra-CP POs over which [P_i] can stabilize at a steady-state (heavy-intensity exercise).

To the best of our knowledge, no direct experimental data exist concerning the end-exercise changes in metabolites in the same individuals before and after training. An indirect cue can be found in the study by McCully at al. (36), who showed that in ramp exercise of the wrist flexors that was terminated because of exercise intolerance, the end-exercise, H₂PO₄⁻ is over two times higher (13.0 mM vs. 5.7 mM) in controls than in trained rowers. Also, the finding by Sundberg et al. (37) that in maximum-intensity kicking exercise associated with fatigue (decline of generated force during exercise), P_i increases significantly more in old versus young individuals. In our simulations, the exact molar values of Pi_crit and Pi_peak were chosen to obtain system kinetics that best represented the experimental observations. However, their values are likely to vary among individuals or fiber types, and their range remains to be determined. Nevertheless, the chosen exact molar values representing these thresholds do not qualitatively influence simulations results (23, 25).

Significantly different end-exercise [PCr] (and thus, as it can be inferred, end-exercise [P_i]), during exercise terminated because of exercise intolerance were encountered in different experimental conditions using (an identical model of) single-leg knee extension exercise in the prone position. Although in Vanhatalo et al.’s study (27), end-exercise [PCr] fell to 5%–12% of the rest value in subjects with a single leg knee-extensor CP of 16 W, it was only diminished to 26% of the rest value in Jones et al.’s study (38), in subjects who had 25% greater CP. This suggests a much lower end-exercise [P_i] in the latter case, where subjects had a greater CP (and presumably V̇O_2max).

It has been proposed that in the early stage of training the acceleration of the V̇O₂ on-kinetics is caused by an increase in ESA intensity, rather than in OXPHOS activity (13). However, it is likely that after longer-term training, the former is replaced by and/or supplemented with the latter, as long-term training causes an increase in OXPHOS activity, as discussed above.

Mechanisms Underlying Training-Induced Changes in the Bioenergetic System

Several factors, including O₂ supply limitations (and thus lowered myocyte O₂ concentration) or OXPHOS capacity for ATP synthesis, and central fatigue contribute to task-specific V̇O_2max in vivo. The greater the muscle mass involved in the exercise, the greater is the likelihood that an individual will be limited less by peripheral fatigue (intramuscular limitations) and more by convective or diffusive O₂ delivery or motor-neural mechanisms (11, 24). In isolated muscle exercise, for example, forearm flexion, plantar flexion, or perhaps single-leg knee extension, according to the concept presented, the “P_i double-threshold” mechanism defines the response, kinetics, and limitations of the muscle system. A “direct peripheral” mechanism of action of P_i is not known, although some possibilities have been proposed (see ref. 25 for discussion). In larger muscle mass exercise, or in environmental or pathologic conditions that alter O₂ delivery, it is proposed that system behavior also acts through the “P_i double-threshold” mechanism (and perhaps other associated factors, for instance H⁺ ions). In these situations, earlier exercise limitation would occur because of more rapid P_i accumulation, earlier attainment of Pi_crit, and greater V̇O₂ slow component, resulting in earlier attainment of Pi_peak (determined, among others, by factors related to muscle training). An “indirect peripheral” (or central) control loop, involving P_i (or some related factor, e.g., H⁺), which can participate in both control operations—peripheral (direct) and central (indirect) control—is unknown. For this, neural feedback loops would need to sense (e.g., through metaboreceptors) wide-ranging effects of enhanced intramuscular P_i accumulation for any given A_UT and exacerbate central fatigue contributions to exercise limitation. Although other models of central control could explain the observed system behavior, independent of the muscle metabolic state, the “P_i double-threshold” mechanism reproduces to a startling degree a broad range of diverse system properties (including time courses of V̇O₂ and metabolites, constancy of end-exercise V̇O_2max and metabolites, the origin and form of the slow component, the hyperbolic shape of the power-duration relationship, the dependence of CP and t_0.63 on oxygen concentration and the effect of endurance training on the system properties), at least for exercise durations up to 20 min (23, 25; current data).

According to the proposed “P_i double-threshold” mechanism, moderate exercise can be described as exercise in which Pi_crit is not exceeded, heavy exercise as exercise in which Pi_crit is exceeded, but Pi_peak is not reached, whereas very heavy (and severe) exercise as exercise in which Pi_crit is exceeded and Pi_peak is reached (in severe exercise there is too little time for the slow component to fully develop, which is demonstrated by our simulations).

Computer simulations show that while the space (the range of A_UT values) for heavy exercise between moderate exercise and very heavy exercise is wide in untrained muscle (Fig. 4), this becomes smaller in the “standard” state of moderately trained muscle (23), and there is little or no space for heavy exercise in well-trained muscle (Fig. 5). This is because, for power outputs just below critical power, moderate exercise-like behavior is observed. This is caused by an increased metabolite, especially P_i, stability for a given power output as a result of elevated OXPHOS activity (17). The analogue of this in vivo is a greater influence of exercise training on the lactate threshold than on CP, i.e., with endurance training, the lactate threshold (LT) becomes a greater fraction of CP. This concept is supported in a recent meta-analysis, which found that LT varies between 57% and 83% of CP among subjects (39).

Endurance training can shift the relative intensity of a given power output from very heavy-intensity exercise to moderate-intensity exercise. This is shown in Fig. 6, where the V̇O₂ on-kinetics for A_UT = 65 for untrained and trained muscle is presented (also the primary component of the V̇O₂ on-kinetics for untrained muscle is presented). The slow component of the V̇O₂ on-kinetics, which is present and large in untrained muscle, vanishes completely in trained muscle. One can also see that training leads to acceleration of the primary phase of the V̇O₂ on-kinetics. A very similar effect of training for the same absolute work intensity was shown by Casaburi et al. (3) (see Fig. 1D therein).

Simulations for very heavy/severe exercise also showed that W′ was reduced following endurance training. Lower W′ after endurance-training is not a consistent finding in vivo. Nevertheless, W′ is typically unchanged or reduced, rather than increased by training (5, 8, 10). In our simulations, W′ (like CP) constitutes an emergent property of the system, and therefore, its decrease in response to training does not have a simple physiological interpretation. The combination of increase in in OXPHOS activity (k_OX) and lower Pi_peak in the trained state would predispose toward a reduced W′ following endurance training. W′ can also depend on Pi_crit and k_add that are kept constant in computer simulations of the effect of training, but they can be affected by training in real systems.

It should be stressed that all these simulated adaptations of the system behavior following training are consequences only of increased OXPHOS activity. Decreased Pi_peak only diminishes effects on V̇O_2max and CP. In other words, changes in other parameters are in principle not necessary to induce the considered effects observed by endurance training, although some contribution of an increase in Pi_crit and decrease in k_add cannot be excluded. Training-induced decrease in the additional ATP usage activity (k_add) and/or increase in the critical P_i (Pi_crit), would also have the effect of decreasing the magnitude of the slow component (not shown). However, at this time, it is not clear whether endurance muscle training actually causes these effects.

V̇O₂ at task failure (V̇O_2max) is influenced by any factor delaying or accelerating the reaching of Pi_peak by P_i. V̇O_2max is increased by the increase in OXPHOS activity, as this delays the reaching of Pi_peak by P_i, and decreased by the decrease in Pi_peak, as this accelerates the reaching Pi_peak by P_i.

It has been proposed that the greater vulnerability of skeletal muscle than heart to mitochondrial diseases caused by OXPHOS complex deficiencies elicited by mutations in mitochondrial or nuclear DNA is caused by a greater maximum increase in P_i in the former than in the latter (40). This conforms well with the “P_i double-threshold” mechanism of muscle fatigue postulated in this article and previously (23, 25).

These theoretical predictions concerning training-induced decrease in Pi_peak could be tested experimentally, for example, by measurement of end-exercise P_i in constant-power exercise or ramp-incremental exercise before and after training. Thus, this theoretical study can stimulate and direct future experimental studies. The effect of the training-induced increase in OXPHOS activity (and/or ESA intensity) is sufficiently supported by the experimental studies discussed in this article. Further research is needed to identify whether training alters Pi_crit (or k_add), and therefore, whether these parameters form part of the adaptations that improve muscle metabolic stability and enhanced exercise tolerance in the trained state.

Study Limitations

Of course, this model, as any model of this kind, has limitations.

First, the model involves explicitly only P_i as a fatigue-generating factor and fixed P_i concentrations representing the “P_i double-threshold.” These are recognized simplifications of the fatigue process, which most probably includes action of other variables, especially H⁺ and alteration in Ca²⁺ release and sensitivity, and which also differ among fiber types. However, for instance, pH changes in parallel with P_i (Figs. 4 and 5). Central fatigue also contributes to reducing maximal muscle force and/or velocity, and may contribute to, or cause, intolerance at the limit of whole-body exercise. Central fatigue is not a component of this single-cell model. On the other hand, P_i as a trigger of fatigue may act either directly within the cell or indirectly through central nervous system, for example, through metaboreceptors. The model involves constant cellular O₂ concentration and, therefore, does not take into account potential O₂ transport limitations. This undoubtedly constitutes a significant simplification, as O₂ concentration changes during rest-to-work transition are well described. Nevertheless, this is a limitation of the model. It was shown in our previous article (23) that lowered/elevated O₂ can affect CP (and V̇O_2max) through an elevation or lowering of P_i accumulation, but it is by no means the only factor determining (“limiting”) these variables.

Despite these simplifications, the model was able to explain diverse behaviors of the whole muscle bioenergetic system during exercise in the trained and deconditioned state, providing a cellular mechanism by which fatigue acts as a mediator of CP, inefficiency, and intolerance. The precise concentration where the P_i “thresholds” occur is not the primary focus, rather the novelty of our findings is contained in the observed behavior of the system when the proposed mechanism is simulated.

Second, the model uses typical values of training-induced changes in the OXPHOS activity, V̇O_2max, and PO. Although the experimental studies report a wide range of adaptive response to endurance training, we used an average of these training-induced changes to inform model parameter values. For example, in one extreme, Wibom et al. (35) found that cytochrome-c oxidase activity (a major component of OXPHOS activity) increased by 78% (although complex III activity increased by only 18%), whereas whole-body V̇O_2max increased by only 9% in response to training; a disconnect that could reflect regional adaptations in biopsied muscle and/or the active muscle mass, but it can also be explained in our simulations through reduced Pi_peak. Thus, the variability among experimental studies can be emulated by appropriate manipulation of parameter values used in the model.

Third, the model used is a one-compartment model that does not consider different muscle fiber types. However, the model is compared with “one-compartment” experimental data of whole-muscle V̇O₂, cytosolic PCr, P_i, pH, and ATP using MRS and biopsy studies that themselves represent responses of multiple cells of a range of fiber types. Therefore, we selected parameter values representing a “chimeric” muscle cell with lumped parameter values representative of a large human working muscle complex, such as the quadriceps.

Fourth, the model assumes that the training-induced increase in the activity of all OXPHOS complexes is identical. However, this can be only an approximation: the activity of some complexes increases more, whereas the activity of other complexes increases less. Therefore, the assumed increase in the OXPHOS activity by 37.5% represents only an average increase in complex activity. This does not affect significantly the predictions made in this study.

Conclusions

This theoretical study postulates a simple mechanism underlying the training-induced increase in V̇O_2max, increase in critical power, and changes in the V̇O₂ on-kinetics (acceleration of its principal phase II and reduction of the slow component) in skeletal muscle. According to this mechanism, these changes are mostly caused by an increase in OXPHOS activity and decrease in the peak P_i, at which exercise is terminated because of exercise intolerance (in fact, the latter simply lessens the changes). An increase in ESA activity can play an important role in early stages of training. There may also be some minor role played by an increase in the critical P_i, above which the additional ATP usage, underlying the slow component, appears, and decrease of the additional ATP usage activity; however, further research is needed to identify contribution of these mechanisms. Therefore, the “P_i double-threshold” mechanism can explain a wide range of training-induced changes in skeletal muscle behavior during exercise. No such mechanism that quantitatively unifies the training-induced increase in muscle bioenergetic behaviors had been postulated in the literature.

GRANTS

No specific funding was received.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTION

B.K. conceived and designed research; B.K. performed computer simulations; B.K. and H.B.R. analyzed data; B.K. and H.B.R. interpreted results of experiments; B.K. prepared figures; B.K. and H.B.R. drafted manuscript; B.K. and H.B.R. edited and revised manuscript; B.K. and H.B.R. approved final version of manuscript.