Estimation and removal of spurious echo artifacts in single-voxel MRS using sensitivity encoding

Abstract

Purpose:

In localized MR spectroscopy, spurious echo artifacts commonly occur when unsuppressed signal outside the volume-of-interest is excited and refocused. In the spectral domain, these signals often overlap with metabolite resonances and hinder accurate quantification. Since the artifacts originate from regions separate from the target MRS voxel, this work proposes that sensitivity encoding based on receive coil sensitivity profiles may be used to separate these signal contributions.

Methods:

Numerical simulations were performed to explore the effect of sensitivity encoded separation for unknown artifact regions. An imaging-based approach was developed to identify regions that may contribute to spurious echo artifacts, and tested for sensitivity-based unfolding of signal on 6 datasets from 3 brain regions. Spectral data reconstructed using the proposed method (‘ERASE’) were compared to standard coil combination.

Results:

The method was able to fully unfold artifact signals if regions were known a priori. Mismatch between estimated and true artifact regions reduced the efficiency of removal, yet metabolite signals were unaffected. Water suppression imaging (WSI) was able to identify regions of unsuppressed signal and ERASE (from up to 8 regions) led to visible removal of artifacts relative to standard reconstruction. Fitting errors across major metabolites were also lower; for instance CRLBs of myo-inositol were 13.7% vs. 17.5% for ERASE vs. standard reconstruction, respectively.

Conclusion:

The ERASE reconstruction tool was demonstrated to reduce spurious echo artifacts in single voxel MRS. ERASE may be incorporated into standard workflows to improve spectral quality when hardware limitations or other factors result in out-of-voxel signal contamination.

Introduction

Robust quantification of metabolite concentrations in single-voxel (SV) MR spectroscopy (MRS) of the brain is critically dependent on spectral quality. However, spectra are often observed to contain a number of artifacts (1) which can lead to poor metabolite fitting, rejection of datasets based on quality criteria, and ultimately lowers the value of MRS for either research or clinical use. One commonly observed artifact is the spurious echo. In the spectral domain, the spurious echo manifests as an oscillatory or ‘beating’ signal spanning a range of frequencies and often overlaps with metabolite resonances and is also referred to as ‘ghosting artifact’. A rigorous description of the origin of spurious echoes in MRS has been provided in terms of coherence pathways (2) and later k-space formalism within a PRESS localization sequence (3). Essentially, spurious echoes arise from spins outside the voxel of interest which are excited at some point during the pulse sequence, e.g. due to imperfections in slice localization and coherence pathway selection, and then subsequently refocused by sequence elements or magnetic field gradients, generating an echo during signal reception. On Fourier transformation, this signal usually has a large first order phase error because it occurs at some variable time point in the free induction decay. Given the sizeable concentration difference between water and metabolites in ¹H-MRS of brain (~10⁴), the main contribution to the spurious echo artifact arises from regions of unsuppressed water signal (3), although lipid resonances may also form spurious echoes.

It has been shown that when slice localization overlaps with air-filled cavities such as the frontal sinuses, the likelihood of observing spurious echo artifacts is increased (4). Susceptibility differences at these air-water interfaces causes local B₀-field perturbation and hence the water resonance can be shifted outside of the bandwidth of the water suppression pulses. It has also been shown that localized higher-order shimming on small volumes-of-interest, as is commonly performed in MRS, generates an inhomogeneous B₀ field outside the VOI which leads to regions of poor water suppression (4).

A number of methods to remove these artifacts have been proposed. The use of outer-volume suppression pulses (5) can reduce the artifact intensity, as well as improved RF pulses for spatial localization (i.e. minimizing excitation of out-of-voxel magnetization) (6,7). Phase cycling schemes are used to eliminate unwanted coherence pathways and therefore reduce presence of these artifacts. However, phase cycling is often performed with a small number of steps and is susceptible to subject motion. Crusher gradients also dephase unwanted coherences, however their efficacy may be limited if gradient strengths (and/or durations) are constrained by scanner hardware or sequence design (8). An early study showed that the order of the slice selective pulses (and hence cumulative crusher effect) could be used to minimize artifact intensity (4), although the optimum order would likely vary depending on the voxel location and subject. Recent work has introduced mathematically optimized crusher schemes for different localization sequences (DOTCOPS) (9). In this way, unwanted coherences could be reduced. Nevertheless, crushing power is always limited by hardware constraints, acquisition geometry and the minimum TE desired. Recently, a method to remove spurious echoes in MR spectra has examined the use of deep learning techniques, which were trained on simulated datasets (10). The flexibility of applying deep learning to in vivo datasets, however, depends on the nature and extent of the training data.

The separation of aliased signal components based on their spatial position has been demonstrated in MRS using sensitivity-based techniques akin to SENSE acceleration (11,12). One study showed that lipids aliased into a spectroscopic imaging grid could be separated from brain metabolite signals using coil sensitivity information (13). In another study, after performing dual-voxel excitation, reconstruction of separate signals from the left and right hemispheres could be performed based on the sensitivity weighting of the receive coils, thereby accelerating the MRS acquisition by a factor of 2 compared to the sequential acquisition of spectra from each hemisphere (14). It has also been previously proposed to add phase-encoding gradients to SV MRS acquisitions followed by spatial Fourier transformation, in order to separate the desired ROI signal from out-of-voxel artifacts (15–17). The separation of spectral components from anatomical regions using receive coil information has also been shown using the SPLASH technique (18).

In the current study, it was hypothesized that sensitivity information from multiple receive coils could be used to separate spurious echo artifacts from metabolite signal during a single-voxel acquisition, given that spurious echoes arise from regions outside of the volume-of-interest. A requirement for this method is that the location of the artifact region must be known in order to successfully separate it from the actual region of interest. Here, potential regions of artifact (regions with unsuppressed water signal) were estimated by prepending a water suppression module to a conventional imaging sequence. The combination of water suppression imaging with SENSE MRS reconstruction is termed Estimation and Removal of Artifacts using Sensitivity Encoding (‘ERASE’).

Theory

Signal unfolding

To separate spurious echo signals, arising from distinct spatial regions, from desired signal, the SENSE unfolding approach is used (11–14). In a K-channel receive array, the time-domain signal measured in the kth channel, $C_k$, can be expressed as a weighted sum of desired metabolite signal, $x_V$, from the voxel, V, and artifact signals, $x_{A_j}$, assumed to arise from N distinct regions, $(A_1,A_2,\dots , A_N)$, such that

$$C_k=S_{V,k}{x}_V+\sum _{j=1}^N{S}_{A_j,k} x_{A_j}+{\eta }_k\text{,}$$ (Eq.1)

Where ${\eta }_k$ is the noise observed in channel k and $S_{A_j,k}$ is the integrated receive sensitivity of the kth channel over the spatial region, $A_j$, defined as

$$S_{A_j,k}=\underset{\text{region} A_j}{\int }{s}_k\left(\overrightarrow{r}\right) d^3\overrightarrow{r}.$$ (Eq.2)

Here, $s_k\left(\overrightarrow{r}\right)$ is the complex sensitivity of the kth channel at position, $\overrightarrow{r}$. Eq. 2 is also used to define $S_{V,k}$, calculated over the region encompassed by the voxel, $V$. In the unfolding approach, signals are assumed to be spatially homogeneous, i.e. a single signal component in each region. Eq. 1 can then be extended to a linear system of equations for all $K$ receive channels, such that

$$\mathit{C} = \mathit{S}\mathit{x}$$ (Eq.3)

Where $\mathit{x}={\left(x_V,x_1,\dots x_N\right)}^T$ are the signal components and $\mathit{S}$ is the $K \times \left(N+1\right)$ sensitivity matrix. To separate the aliased signals, Eq. 3 can be solved using the unfolding matrix, $\mathit{U}$, given by (11)

$$\mathit{U}={\left({\mathit{S}}^H{\mathbf{\Psi }}^{-1}\mathit{S}\right)}^{-1}{\mathit{S}}^H{\mathbf{\Psi }}^{-1}\text{.}$$ (Eq.4)

Here, $\mathbf{\Psi }$ is the $K\times K$ noise covariance matrix of the receive array and ${\mathit{S}}^H$ is the conjugate transpose of the sensitivity matrix. Effective separation of multiple signals using receive coil sensitivities relies on a unique weighting of each receive channel, at each location. Regions with similar channel sensitivities lead to poorly-conditioned signal unfolding and noise amplification which is dependent on the coil geometry. The SNR penalty of unfolding relative to the separate reconstruction of region, j, is expressed as the geometry factor (g-factor), g, such that,

$$g_j^2={\left({\mathit{S}}^H{\mathbf{\Psi }}^{-1}\mathit{S}\right)}_{j,j}^{-1}{\left({\mathit{S}}^H{\mathbf{\Psi }}^{-1}\mathit{S}\right)}_{j,j}.$$ (Eq.5)

Eq. 5 is identical to previous SENSE approaches to multi-voxel MRS (14,19) since the unfolding of artifact and metabolite signals can be considered as a form of accelerated parallel reconstruction of simultaneously excited signals.

Quantifying removal

Similar to previous sensitivity-based approaches (12,18), a spatial response function, SRF, can be defined by applying the unfolding matrix (Eq. 4) to each spatial point. In this way, the amount of signal (phase and amplitude) at $\overrightarrow{r}$ contributing to the unfolded spectrum from $V$, can be calculated, such that,

$${\text{SRF}}_V\left(\overrightarrow{r}\right)=\sum _{k=1}^K{U}_{k,V} s_k\left(\overrightarrow{r}\right).$$ (Eq.6)

By integrating Eq. 6 over some spatial region, R, a metric, ${\vartheta }_R$, for assessing the total signal contribution to the unfolded spectrum at V from spatial region R is defined as,

$${\vartheta }_R={\int }_{\text{region} R}{\text{SRF}}_V\left(\overrightarrow{r}\right) d^3\overrightarrow{r}.$$ (Eq.7)

It can be shown that when region R is identical to region V in Eq. 7 then ${\vartheta }_V=1$ (see ref. (18)). In other words, there is perfect reconstruction of signal from V. If region R is defined by artifact region, $A_j$, then it can be shown that ${\vartheta }_{A_j}=0$ for $j = 1\dots N$, indicating perfect removal of signal from these regions in the reconstructed spectrum. These results hold provided that the regions are known and coil sensitivities can be estimated. In addition, the signal model (Eq. 1) assumes a single component in each region.

In practice, $A_j$ is not known a priori thus the calculated unfolding matrix does not capture the sensitivities of the true artifact regions, in which case some degree of artifact signal will remain in the reconstructed spectrum, ${\vartheta }_{A_j}>0$. Furthermore, due to the nature of the spurious echo artifact there is likely heterogeneity in the signal in each estimated artifact region. However, the aim of this work is the removal of spurious echo contribution from the reconstructed metabolite spectrum, rather than accurately reconstructing each artifact signal. Thus, provided that the proposed method is effective in reducing the artifact signal contribution in metabolite spectra, it may prove sufficiently powerful for MRS even when signal unfolding assumptions are not fully met. Thus, to assess the influence of these effects on artifact removal, the performance of the method is examined in simulation experiments and in vivo acquisition.

Methods

Simulation of artifact removal

In order to assess the feasibility of the proposed sensitivity-based artifact removal method, simulations of SV MRS acquisition with the addition of spurious echo artifact were performed. A set of complex sensitivity maps were simulated using the Biot-Savart law using a freely available toolbox for parallel MRI written in MATLAB (MathWorks, Natick, MA, USA) (20). Signal reception was simulated using a 16-channel circular array of 30 cm diameter, and 4 cm coil radius, over a 2D spatial grid of 256x256 mm² with 1x1 mm² resolution. A ‘ground truth’ metabolite signal was modelled by density matrix simulations for a STEAM localized acquisition (TE = 14 ms) arising from a 2x2cm² voxel. A single artifactual signal component was simulated as an echo-based complex exponential signal at a chemical shift value of 3.9 ppm, with a refocused echo occurring 164 ms after the start of signal reception and a transverse decay time, T₂ = 20 ms. The off-diagonal components of the simulated noise covariance were zero. For a list of simulation parameters used to generate the spurious echo artifact see Supporting Information Text S1.

For data acquired in vivo, the spatial origin of spurious echo artifacts may not be known accurately, so it is important to understand how a mismatch between the estimated and actual artifact location affects the performance of the proposed method. Therefore, three sets of simulation experiments (Experiment 1–3) were performed with different configurations of artifact- and estimated reconstruction regions. In all cases, the location of the MRS voxel was fixed and assumed to be known. In Experiment 1, the shape, size and position of the artifact region was varied and subsequently reconstructed assuming exact knowledge. In Experiment 2, the shape, size and position of the artifact region was fixed, while the ‘estimated’ region for reconstruction (for calculation of Eq. 2) was systematically varied across the whole 2D spatial grid. At each grid position, the signal contribution arising from the true artifact location was calculated using Eq. 7. A total of 63,273 reconstructions were performed (excluding region estimates which overlapped with the MRS region). In Experiment 3, an additional ground truth artifact was simulated in a region adjacent to the first with different signal characteristics (3.5 ppm, T₂ = 2 ms, occurring 492 ms into signal reception). The removal performance was compared using knowledge of all regions, using only one region, and using a single estimated region encompassing both ground truth artifact regions to simulate the effect of non-uniformity within a region.

MRS acquisition

Experimental data were acquired with five healthy volunteers (mean age = 33 years, 1 female, 4 male) on a 3T Philips Ingenia Elition MR system with 32-channel receive array head coil. All participants provided written informed consent as approved by the Johns Hopkins Medicine Institutional Review Board. A total of 6 datasets (R01–06) were obtained from three brain regions; two in occipital cortex (OCC; 15x15x15 mm³, R04,R06), one in putamen (30x15x15 mm³, R02) and three in anterior cingulate cortex (ACC; 20x20x20 mm³ for R03,R05 and 15x15x15 mm³ for R01). A T₁-weighted MPRAGE acquisition (TR = 13 ms, TE = 3.5 ms, 1 mm in-plane resolution) was additionally acquired for voxel placement.

MR spectra were acquired using standard PRESS localization (TE/TR = 30/2000 ms) with VAPOR water suppression (bandwidth = 100 Hz). The pulse sequence diagram is shown in Supporting Information Figure S2. For test purposes, in order to increase the presence of spurious echo artifacts, no phase cycling was performed. In addition, projection-based shimming was carried out using up to 2^nd order corrections, optimized over the same spatial extent as the observed voxel; this is known to increase field inhomogeneity in parts of the sample remote from the voxel, leading to increased spurious echoes. A total of 64 transients were acquired.

For assessment of the efficacy of the proposed ERASE method, comparisons were made to conventionally reconstructed multi-channel data (here termed ‘standard reconstruction’), which were calculated using the coil sensitivity information at the target voxel and the measured noise covariance (equivalent to a SENSE-based weighted combination). After coil-combination, individual transients were frequency and phase-corrected before being averaged.

Calculation of coil sensitivities

Individual channel sensitivity maps were determined using a 3D gradient echo acquisition (TE/TR = 0.97/4.1 ms, 3.5 mm isotropic resolution, acquisition time 43 s). Complex channel sensitivities were calculated using ESPIRiT (21) as part of the BART Toolbox for computational MRI (22), using the raw k-space data exported from the scanner. The complex noise covariance between the 32 receive channels was calculated using raw noise samples obtained on each channel as part of the scanner’s preparation steps before acquisition of the gradient echo image data. For the unfolding of spectral and artifact signals from multiple regions, coil sensitivities were calculated as the sum of the sensitivities within the MRS voxel or estimated artifact ROIs (Eq. 2).

Spectral fitting

To compare the performance of artifact removal using either the ERASE method or standard coil combination, spectra were fit using LCModel (23). A basis set was generated using 2D density matrix simulations of PRESS acquisition (TE = 30 ms) of 19 commonly observed metabolites, namely: alanine, ascorbate, aspartate, creatine, GABA, glutamine, glutamate, myo-inositol, lactate, phosphocholine, phosphocreatine, phenylethyanolamine, scyllo-inositol, taurine, glucose, glycerophosphocholine, glutathione, N-acetylaspartate and N-acetylaspartyl-glutamate. Estimated concentrations and Cramér–Rao Lower Bounds (CRLBs) of fitting were compared on spectra reconstructed using ERASE and standard coil combination. Since estimated concentration values were not the focus of this study, no corrections for T₂ relaxation times were applied. Datasets R04, R03 and R06 were fit over the range 1.8 to 4.2 ppm due to severe lipid contamination, whereas the remaining datasets were fit over the range 0.5 to 4.2 ppm.

Raw SNR was measured in the spectral domain as the height of the NAA peak at 2.01 ppm divided by the standard deviation of the noise in the range 15 – 20 ppm using the FID-A toolbox (24). In addition, LCModel reported SNR values were compared between ERASE and standard coil combinations.

Water-Suppression Imaging (WSI)

The artifact is believed to originate in most cases from regions of the head where B₀-field inhomogeneity has shifted the water resonance outside of the bandwidth of the water suppression pulses. Thus, in order to identify the location of the artifact signal in vivo, water suppression imaging (WSI) maps were acquired using a modified sequence similar to that described in reference (4). WSI maps were acquired after MRS using a 2D turbo spin echo sequence (64 slices, 3.5mm isotropic resolution, TE = 160 ms, TR = 3s, acquisition time 2 m 27 s) and included a VAPOR water suppression preparation module (RF pulse bandwidth = 100 Hz). Importantly, WSI was performed with the identical first- and second-order shim settings, in addition to water suppression parameters, as those used to acquire the MRS signal. In addition, a whole-brain B₀ fieldmap (TR = 8.2, TE = 3.3 and 5.6 ms, 3.5 mm isotropic, acquisition time 1 m 6 s) was acquired after MRS acquisition using identical shim settings for validation of the WSI method.

Estimation of artifact regions

In order to determine regions which are solely influenced by water suppression, and to remove tissue contrast from the images, a residual WSI (rWSI) approach was developed by normalizing the WSI images to an identical acquisition acquired without water suppression (non-WSI). An automated algorithm was developed to subsequently partition binary rWSI maps (thresholded at the mean image intensity of non-zero voxels) into separate artifact regions for reconstruction. Regions were segmented and labeled by iteratively eroding the rWSI maps and then applying a watershed transform (25) to generate unique contiguous regions based on nearest neighbor distances. The watershed transform was chosen since it is able to segment connected regions into smaller sub-regions. The region segmentation algorithm was implemented in MATLAB (MathWorks, Natick, MA, USA). This iterative process continued until 8 or fewer possible artifact regions were identified. Regions were also constrained to be bigger than a single image voxel however no constraint was placed on the maximum region size.

Results

Effect of artifact size and location

A demonstration of the proposed method for artifact removal is shown in a numerical phantom (Fig. 1) for regions of different size, shape and location (Experiment 1). The phantom contained a simulated metabolite signal originating from MRS region (V) and a single simulated spurious echo artifact component (centered on 3.9 ppm) originating from a region (A). The center of A was varied to lie (a) 6.5 cm (b) 10 cm and (c) 5.3 cm from V and its total area was calculated to be 7.2 cm², 49.7 cm² and 1 cm², respectively. Coil combination of the resulting multi-channel data using standard reconstruction resulted in considerable contamination of the metabolite spectrum by the spurious echo in all cases (Fig. 1a–c). Under ideal simulated conditions of a single uniform artifactual signal and exact knowledge of the artifact region, A, the proposed ERASE reconstruction method resulted in unfolded signal components with clear separation of metabolite and artifact signal (Fig. 1h–j), thereby completely removing artifact from the metabolite spectrum. Maps of the spatial response function of the reconstructed metabolite signal (${\text{SRF}}_V$) (Fig. 1e–g) show the signal weighting over the numerical phantom during unfolding. In particular, there was a $2\pi$ phase cancellation of signal over region A, in addition to a lower signal magnitude at the center of A. As a result, the integral of ${\text{SRF}}_V$ (Eq. 7) calculated over A, $\left|{\vartheta }_A\right|$, was 0 for all configurations.

Fig. 1:

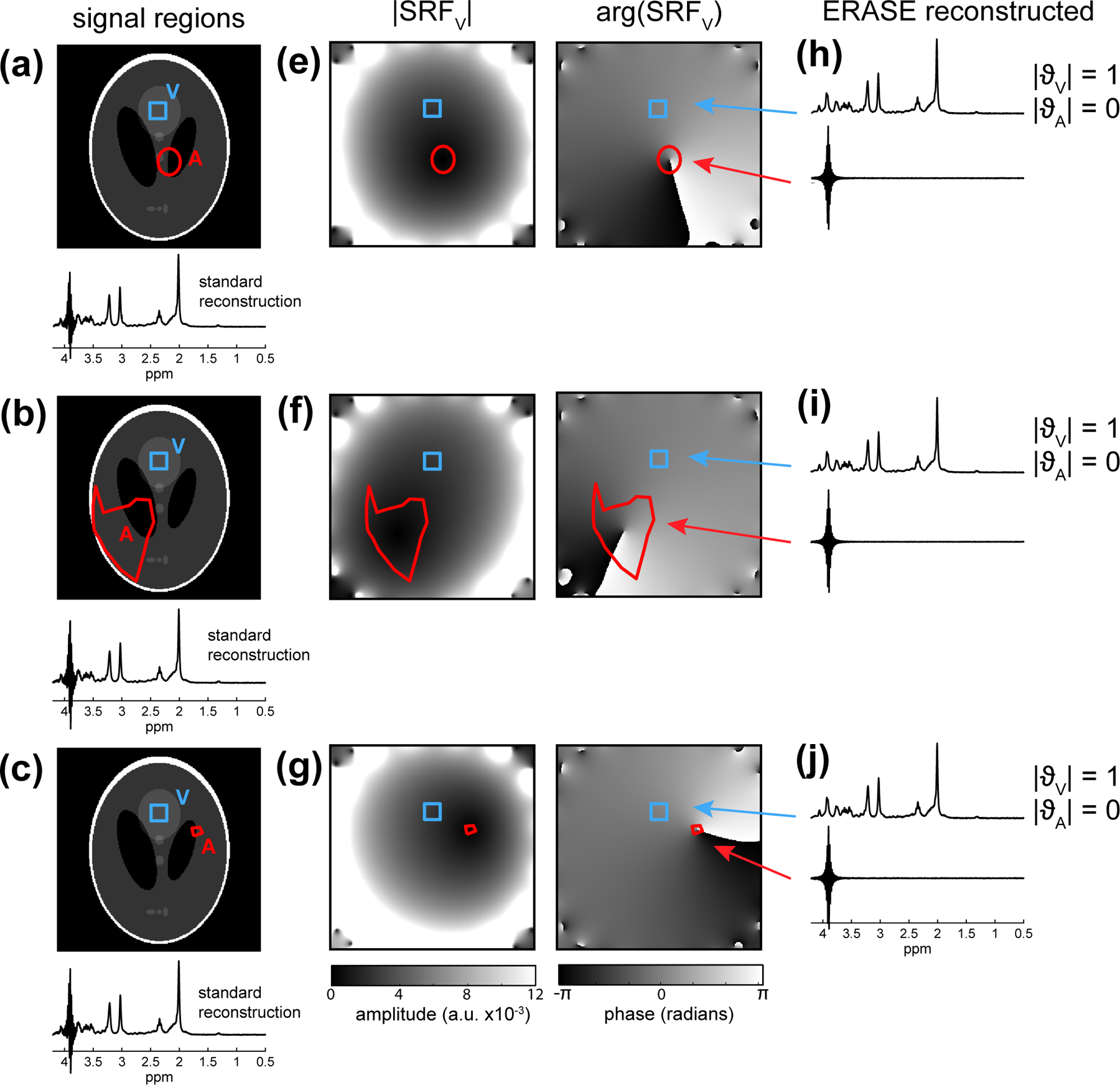
Numerical phantom simulations of the proposed artifact removal method for different sizes and locations of artifact regions (Experiment 1). A metabolite spectrum (STEAM, TE=14ms) was simulated to arise from an MRS region (V; blue) and a spurious echo artifact (at 3.9 ppm) from region (A; red). In (a-c), the artifact support region is varied and the coil-combined data using standard reconstruction is shown. Images (e-f) show the corresponding complex valued spatial response function (${\text{SRF}}_V$) (Eq. 6) resulting from ERASE reconstruction and spectra (h-j) show the corresponding unfolded spectra using ERASE reconstruction. In all cases, there was complete removal of artifact from the metabolite spectrum as indicated by the integral of the ${\text{SRF}}_V$ over A, $\left|{\vartheta }_A\right|=0$.

Effect of region estimation

For data acquired in vivo, the spatial origin of spurious echo artifacts may not be known accurately, so it is important to understand how mismatch between the estimated and actual artifact region affects the performance of the ERASE method. Fig. 2 shows numerical phantom results obtained after varying the location of the reconstruction region while keeping the size and position of the true artifact region fixed (Fig. 2a). As the ‘estimated’ region moved further from the true region, A, the removal performance deteriorated. The proportion of artifact signal in the unfolded metabolite spectrum (Fig. 2b) was below 1 for small errors in the estimated region, indicating partial removal. In extreme cases, when the reconstruction region was positioned far from the true artifact region, there was worse performance than standard combination ($\left|{\vartheta }_A\right|=1.77$, Fig. 2c,d) leading to an increase in the proportion of artifact signal. These simulations illustrate the importance of accurately identifying the location of the artifact signal in order for it to be successfully eliminated using ERASE. Importantly, even when the reconstruction location was not aligned with the ground truth, there was still a perfect reconstruction of metabolite signal from V, i.e. $\left|{\vartheta }_V\right|=1$ in all cases.

Fig. 2:

Simulations of the effect of estimating the position of the artifact region on removal performance (Experiment 2). The simulated ground-truth configuration of MRS voxel (V; blue) and artifact region (A; red) is shown in (a) together with standard reconstruction. The heatmap (b) shows the magnitude of the signal contribution in the metabolite spectrum from the true artifact region A as the reconstruction region is placed at each point in the phantom. The white contour line shows where there is no removal, i.e. $\left|{\vartheta }_A\right|=1$. The ${\text{SRF}}_V$ and reconstructed spectra from 3 points in the phantom are shown in plots (c and d). The ‘estimated’ reconstruction region is shown in yellow.

Effect of multiple artifacts

With the inclusion of an additional artifact (centred at 3.5 ppm) from a second region, $A_2$, standard reconstruction led to considerable contamination from both artifacts (Fig. 3a). As expected, removal of artifact signal was complete $\left(\left|{\vartheta }_V\right|=1, \left|{\vartheta }_{A_1}\right|=0, \left|{\vartheta }_{A_2}\right|=0\right)$ when both true artifact regions were used for reconstruction (Fig. 3b,e). If only a single artifact component was assumed by reconstructing at $A_1$, then the additional artifact at $A_2$ was partially removed (Fig 3c,f) in the ERASE-reconstructed metabolite spectrum $\left(\left|{\vartheta }_{A_2}\right|=0.25\right)$. Finally, when a single reconstruction region encompassed both true artifact regions then ERASE reconstruction was able to partially remove contributions from $A_1$ and $A_2$ with $\left|{\vartheta }_{A_1}\right|=0.26$ and $\left|{\vartheta }_{A_2}\right|=0.16$, and generated a considerably cleaner metabolite spectrum than standard reconstruction (Fig. 3d,g).

Fig. 3:

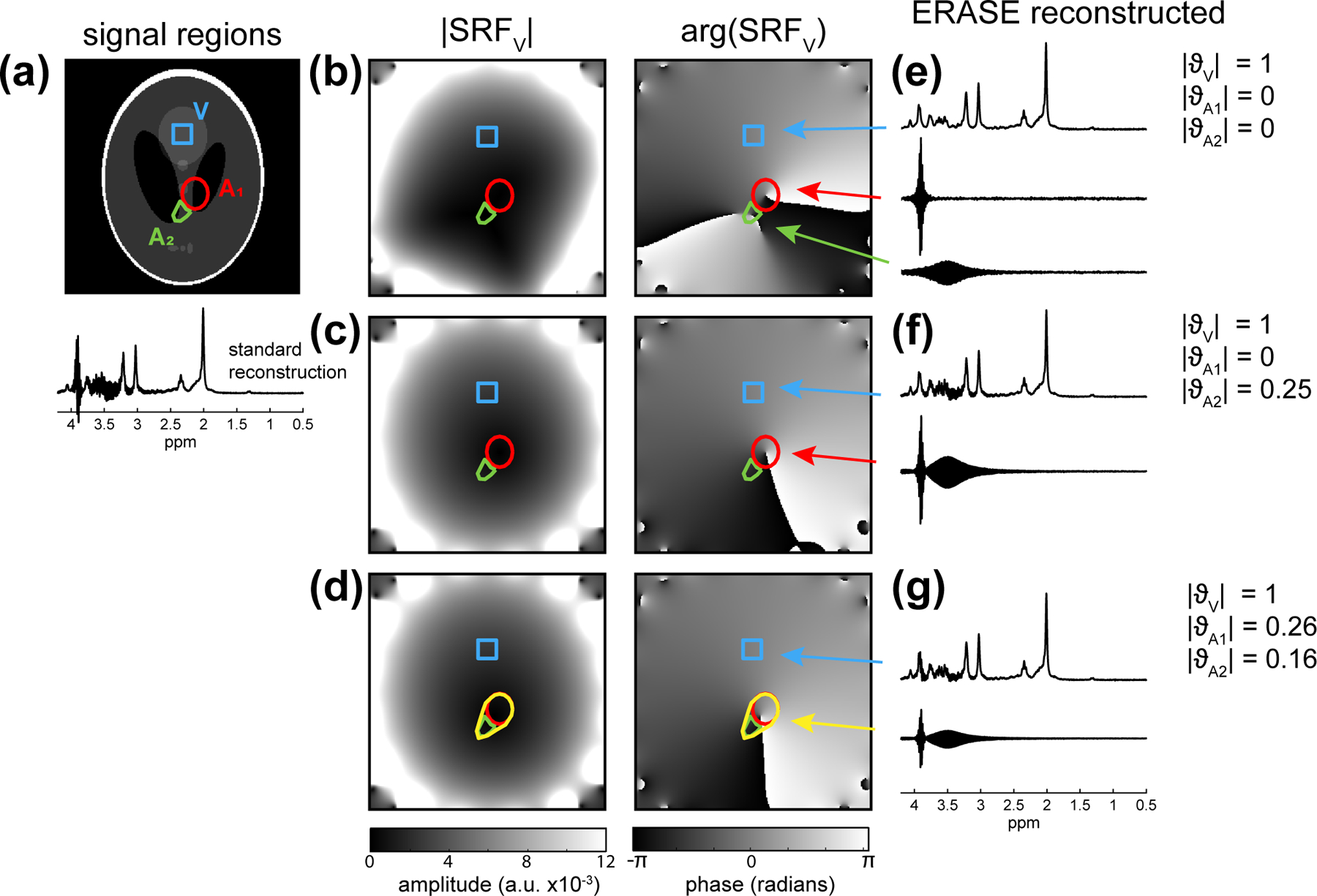
Simulations of the effect of multiple artifact signals on removal performance (Experiment 3). The ground-truth configuration (a) contains 2 adjacent artifact regions ($A_1$; red, $A_2$; green) and shows standard reconstruction with contamination of spectra between 3–4 ppm. Three different reconstructions are shown with ${\text{SRF}}_V$ maps (b-d) and corresponding ERASE-reconstructed spectra (e-g). Reconstruction using 3 signal components with precise knowledge of regions (b,e) shows perfect removal of artifact. Using a single region ($A_1$) in the reconstruction (c,f) resulted in the complete removal of one artifact $\left|{\vartheta }_{A1}\right|=0$ and partial removal of the other, $\left|{\vartheta }_{A2}\right|=0.25$. Using a single region (yellow) containing both artifacts (d,g) resulted in partial removal of both spurious echo artifacts.

Water suppression imaging (WSI) and artifact region estimation

For the estimation of spatial origin of artifacts in vivo, water suppression imaging (WSI) maps were acquired in each volunteer. The WSI maps and corresponding residual water suppression imaging (rWSI) maps, showing regions of unsuppressed water, are shown for two volunteers in Fig. 4. WSI, acquired using identical second order shims to the MRS acquisition, was found to very clearly show regions of poor water suppression indicated by higher signal intensity. In all acquisition geometries, there was unsuppressed signal in the oral cavity and adjacent structures, infratentorial regions and other regions distal from the MRS acquisition voxel. Peri-cranial lipid signal was visible in all WSI images, since it lies outside the water suppression bandwidth and is unaffected by the water suppression module. Placing the MRS voxel in an anterior region (Fig. 4A) led to large regions of unsuppressed water in the cerebellum and above the frontal sinus. Conversely, for the voxel positioned in the occipital region (Fig. 4B), the frontal lobe contained a large area of unsuppressed water. The spatial distribution of the WSI images was observed to correspond strongly with the B₀ distribution after localized shimming. When normalized to the image acquired without water suppression and masked, rWSI maps could accurately reveal unsuppressed regions, without the underlying grey and white matter contrast observed in the WSI maps themselves.

Fig. 4:

Water-suppression imaging (WSI) for identification of spurious echo artifact regions. Data shown for datasets in ACC (a) and OCC (b). The MRS voxel position is the white box overlaid onto the anatomical T₁-weighted scan, B₀-fieldmap, WSI, with and without water suppression (non-WSI). The residual WSI (rWSI) is formed by normalizing the WSI to non-WSI and masking. Note the high similarity between rWSI and B₀-fieldmap.

The automated thresholding and segmentation procedure used in this work (Fig. 5), resulted in separate contiguous regions of potential spurious echo artifact for each MRS region. The algorithm led to estimation of between 2 and 8 regions. There was a large variation in estimated region volume (mean ± standard deviation: 57±111 cm³, minimum: 0.086 cm³, maximum: 573 cm³).

Fig 5:

Flowchart outlining the steps (i - vi) in the artifact region segmentation algorithm using the residual water suppression imaging maps (rWSI) acquired in vivo. After filtering and thresholding, images are eroded and segmented into separate regions using the watershed transform. This process is repeated until the number of estimated regions, N, is less than or equal to 8. Intermediate steps are shown using an example transverse slice (R02). In practice, the image processing steps are applied to the 3 dimensional image data.

Spectral quality of reconstruction in vivo

Individual channel sensitivity maps, acquired in vivo and processed offline, were smoothly varying as expected: representative data is provided in Supporting Information Figure S3. The ERASE reconstruction method in 3 datasets (R03, R06, R02) is shown in Fig. 6. The remaining 3 datasets are provided in Supporting Information Figure S4. Spurious echo artifacts were observed in all datasets and regions (apart from R05), and were largely centered over the 3–4 ppm region of the spectra.

Fig 6:

In vivo demonstration of the ERASE method in 3 datasets acquired in ACC (A), OCC (B) and putamen (C). Segmented artifact regions are overlaid in color and labelled (a-f) on the rWSI maps for each dataset for different transverse image slices. The MRS voxel (V) is shown in blue. In each dataset the standard reconstruction is shown above the ERASE reconstructed data for the voxel, V (blue). Alongside the metabolite spectra, the artifact spectra reconstructed in each region (a-f) is plotted.

Fig. 6A shows artifact estimation and removal results for a voxel placed in the ACC (R03). The rWSI maps revealed unsuppressed water signals in temporoparietal regions of both hemispheres which were automatically segmented into two regions (a, b) and contributed relatively little artifact signal to the spectrum. Two further regions (c and d) adjacent to the frontal sinus were segmented and led to the largest reconstructed artifactual signal components dominated by a signal around 3 ppm. The reconstructed spectrum from the MRS voxel (V) using the ERASE method was visibly improved compared to the standard method, particularly in 3–4 ppm region. The appearance of the mI peaks was visibly improved.

Fig. 6B shows results for a voxel in the occipital cortex (R06). The rWSI maps revealed an area of unsuppressed water in the frontal lobe which was automatically segmented into three regions (a,b,c) in addition to a small region near frontal sinus (d) and two more regions inferior to the MRS region in temporal lobe (e) and cerebellum (f). The reconstructed MRS spectrum using the ERASE method was much cleaner than the standard reconstruction. In particular, there was a cleaner appearance of the mI peaks, and complete removal of a spurious peak around 3.3 ppm. The difference between both reconstructions (labeled ‘residual’ in Figure 6) showed no removal of metabolite peaks with ERASE. Lipid contamination was equally present in both the standard and ERASE reconstructions as expected, since no attempt was made to unfold pericranial lipid signals. The temporal lobe region (e) contained relatively little artifactual signal, whereas frontal regions (a) had larger high-frequency artifactual component (>3.5 ppm).

Fig. 6C shows the voxel acquired in the putamen (R02). Standard reconstruction resulted in severe contamination around the choline peak at 3.2 ppm and total creatine peak at 3.9 ppm. Artifactual components were mainly estimated to arise from regions (a and b) both anterior and posterior to the MRS voxel, with large signal over the 3–4 ppm range. ERASE reconstruction revealed a cleaner spectrum over this range, as shown by the improved shape of the choline and creatine peaks.

g-factor and SNR

The MRS voxel with the largest associated g-factor (Eq. 5) of reconstruction was dataset R01 (g = 2.75) in the frontal region with 8 artifact regions estimated. This dataset also had the largest spectral SNR penalty of reconstruction measured in the spectral domain (54.6 vs. 25.3, standard vs. ERASE), however, still performed well in terms of artifact removal (see Supporting Information Figure S4). A complete list of g-factors and corresponding measured spectral SNR is provided in Table 1. As expected, there was a linear relationship between the calculated g-factor for the MRS voxel and the measured SNR penalty following ERASE reconstruction (SNR_standard/SNR_ERASE) as measured using a regression analysis but this was less than unity (R² = 0.73, $\beta =0.6$, p=0.03). LCModel reported SNR (which accounts for residual unfitted signal in its noise estimation) was significantly improved for ERASE reconstructed spectra than standard combination (8.8 vs. 6.8, p = 0.02, paired t-test).

Table 1:

Measured signal-to-noise (SNR) of the metabolite spectrum using standard reconstruction and ERASE reconstruction for all datasets. The ratio of SNR_standard/ SNR_ERASE is provided alongside the calculated g-factor associated with the MRS voxel (Eq. 5).

Dataset	Location	Regions	SNRstandard	SNRERASE	SNRstandard/ SNRERASE	g-factor
R01	Frontal	8	54.6	25.3	2.16	2.75
R02	Putamen	3	28.6	23.2	1.23	2.32
R03	Frontal	5	87.2	74.4	1.17	1.79
R04	Occipital	2	42.9	39.5	1.09	1.16
R05	Frontal	4	76.3	89.6	0.85	1.14
R06	Occipital	6	42.5	36.8	1.15	1.56

Metabolite fitting

Spectra processed with standard combination and ERASE were fit using the LCModel. The difference in the CRLBs between reconstructing with ERASE and standard reconstruction are shown in Fig. 7A for five major metabolites. Across all 6 datasets, CRLBs for tNAA, tCho, tCr, Glx and mI using ERASE were less than or equivalent to standard combination. Fitting errors were significantly lower using ERASE compared to the standard combination for all major metabolites apart from Glx (11.7% vs. 14.7%, p=0.06), which was very close to significance; tNAA (5.6% vs. 7.0%, p=0.03), tCho (10.7% vs. 14.1%, p=0.019), tCr (7.0% vs. 9.2%, p=0.04) and mI (13.7% vs. 17.5%, p=0.03). The difference in estimated metabolite concentrations is also provided in Fig. 7B. There was no clear difference in the metabolite concentrations after using ERASE reconstruction for the major metabolites across datasets, which was also confirmed statistically using a paired t-test. One dataset (R05) saw no reduction in CRLBs and very little change in estimated concentration after ERASE. This dataset also contained no clear spurious echo signal in its metabolite spectrum following standard reconstruction.

Fig. 7:

LCModel fitting results for major metabolite signals using standard- and ERASE reconstructed spectra for all 6 in vivo datasets (R01-R06). (a): Difference in the errors of fitting (CRLBs) between ERASE and standard reconstructed data. Lower values indicate smaller CRLBs for ERASE. (b): Difference in the estimated concentration values between ERASE and standard calculated relative to internal water reference. Values are in institutional units (i.u). (*) indicates p<0.05 after paired t-test.

Discussion

An approach for the removal of spurious echo artifacts from single voxel MR spectra is presented, based on receive coil sensitivity profiles. As demonstrated by numerical simulations, the method works best when the spatial origin of spurious echoes is accurately known. In this study, rWSI was used to identify regions likely to contribute artifactual signal; under the conditions used here, frontal regions and the cerebellum were often found to have large amounts of residual water shifted outside the bandwidth of the water suppression pulses. Across 6 in vivo datasets acquired in 3 different brain regions, the proposed ERASE method visibly improved spectral quality compared to standard reconstruction of multi-channel MRS data, in particular over the 3–4 ppm region. Spectra reconstructed using ERASE showed lower fitting errors for all major metabolite resonances, reaching statistical significance for tNAA, tCr, tCho, mI (p<0.05, Fig. 7). Despite the fact that sensitivity-encoding has a g-factor related penalty in SNR, the amount of any SNR reduction was below that attributed to the g-factor alone and did not hinder metabolite fitting in the current examples. It is anticipated that this method will be particularly useful for improving the quality of spectroscopic data when either gradient crushing power is limited, or other factors lead to significant out of voxel magnetization.

In theory, the ERASE method requires only receiver-coil sensitivity maps, which are frequently acquired as a calibration step during a standard MR protocol. Thus, the method could be applied post-hoc to data where this information is available. However, unlike previous methods exploiting sensitivity-based unfolding in MRS, such as lipid removal in MRSI (13), multi-voxel localization (14) and SPLASH (18), the spatial origin of the artifact signal is unknown a priori. In order for aliased signal components to be fully reconstructed (Eq. 4), the spatial origin of signals must be known (Eq. 2). The numerical phantom simulations confirmed that when the estimated reconstruction region intersects fully with the true artifact region, signal separation was complete as in the case of PRIAM (14). Critically for the success of ERASE, partial removal of artifact signal was achieved even when the reconstruction region did not fully overlap with artifact origin (Fig. 2d), and when more than one signal component was present in a single region (Fig. 3g). Importantly, the full metabolite signal from the MRS voxel was reconstructed in all cases, as measured using the SRF ($\left|{\vartheta }_V\right|=1$), even when the artifact regions were not estimated correctly - thereby indicating no loss of metabolite signal using ERASE. This was also apparent in the in vivo data, whereby after applying ERASE reconstruction, there was no clear difference in estimated concentrations (Fig. 7) or residual metabolite signal in the unfolded components (Fig. 6). Under certain conditions, the true location of acquired metabolite signal may deviate slightly from the prescribed MRS voxel used for reconstruction due to localization inaccuracy from chemical shift displacement or imperfect excitation profiles. This effect may have a small influence on reconstructed metabolite signals, yet is present in all image-based techniques for MRS data reconstruction.

The WSI technique was relatively straightforward to implement and successfully mapped signal that was not suppressed by the water suppression scheme, revealing potential regions of artifactual signal, similar to data presented in reference (4). Scan time for WSI with whole head coverage was about 2.5 minutes, mainly limited by the TR needed to incorporate the lengthy VAPOR sequence. Together with the non-water suppressed image needed for calculating rWSI maps, the total WSI time was therefore 5 minutes. This could be dramatically reduced in future work, for instance by reducing spatial resolution and using SENSE acceleration. In an MRS study involving multiple spectral locations (and hence multiple high order shim settings), the WSI sequence will need to be repeated for each location. The WSI approach was chosen as a direct measurement of unsuppressed water, potentially accounting for differences in T₁ relaxation and B₁ transmit field across the brain. However, other approaches could also be considered for identifying regions of unsuppressed water, for instance based on B₀ maps which showed good concordance with rWSI (e.g. Fig. 4), and could be used if rWSI were not available on a particular scanner.

Across 6 datasets, independent of voxel geometry, unsuppressed water outside the VOI was often observed in frontal regions. This finding, reflects previous work pointing to frontal sinuses and oral cavity as the main culprit for spurious echo artifacts (8). In addition, due to the use of localized high-order shimming, brain regions remote from the target voxel location often showed large amounts of unsuppressed water, often including the frontal or parietal lobes, and posterior fossa. These regions could potentially be reduced by the use of dynamic B₀ shimming, with a globally optimized shim set used during water suppression, and a regionally optimized shim set during data acquisition (26,27). WSI could potentially also be used online during scanning to plan acquisition-specific parameters such as order of slice selection gradients or OVS bands, to further reduce these artifacts. Removal of lipid signals was not considered in this work, since spurious echoes were anticipated to largely arise from unsuppressed water. However, by including known locations of lipid signal into the ERASE algorithm, their contribution to the spectrum could be removed similar to previous work using MRSI (13).

The intensity thresholding and segmentation algorithm applied to rWSI maps generated a small number of volumes for ERASE reconstruction which was limited to a maximum of 8 regions. The theoretical maximum number of regions which can be reconstructed is limited by the total number of receive elements. However, a large number of volumes will generally decrease the conditioning of the unfolding matrix, hence incur larger g-factor penalties associated with each region. This was observed in dataset R01, where 8 regions were identified (g = 2.75). In this work, low g-factors were measured for reconstruction of the MRS volume, presumably because artifact regions were generally far away from the target MRS volume. A linear relationship was found between g-factors and the ratio of SNR measured using ERASE and standard reconstructions ($\beta =0.6$, p = 0.03), yet the influence of g-factor on reconstructed SNR was below the value predicted from SENSE unfolding alone ($\beta =1$). This is likely due to two factors: some of the ‘noise’ in the standard reconstruction actually results from very broad residual out-of-voxel signals which are removed by ERASE (e.g. Fig. 3). In addition, the height of the NAA peak used to determine SNR may be altered between reconstructions, and in particular an increase may occur if overlapping signal contributions with opposite phase are removed by ERASE.

As with similar compartment-based reconstruction methods, an assumption of unfolding is that of a single homogenous signal in each region. Unlike other methods (18), however, accurate reconstruction of the artifact signals themselves is not required, solely their removal from the metabolite spectrum. Our phantom results show that partial removal still occurs if the estimated region encompasses more than one unwanted signal. However, large region estimates are likely to contain multiple unwanted signals and worsen the g-factor penalty. In this work, the in vivo automated region estimation algorithm did not constrain maximum size, which led to large variation in region volumes (0.09–573 cm³). Furthermore, the iterative erosion and watershed transform (Fig. 5) led to heterogeneity in artifact size and shape across datasets. It is suggested that more sophisticated algorithms for region estimation could be implemented, based on a combination of region-growing and optimization by iterating ERASE reconstruction. Constraints could be placed on the total volume size, larger volumes split into sub-volumes, and removal of regions found to contribute no artifact signal. Additionally, prior knowledge could be incorporated, such as the location of the slice selection planes for each axis and sequence-specific coherence generation (9), to improve region estimation.

This study has several limitations, including a lack of comparison to other methods for removing out-of-voxel artifacts in MRS data, such as the use of optimal crusher gradient schemes, or phase-cycling. Future work will be required to establish if the ERASE reconstruction method may be useful for data recorded in conjunction with such acquisition-related strategies.

In conclusion, a new method for reconstruction and removal of spurious echo signals arising from out-of-voxel magnetization is demonstrated. Estimation of the artifact regions was achieved using an imaging-based method and overlapping signal contributions was separated using sensitivity-based reconstruction. This method may improve quantification of metabolites when hardware limitations and voxel geometries lead to contamination of spectra, and could be modified in the future to be run as part of a standard MRS pre-scan.

Supplementary Material

supinfo

Text S1: Description of the simulation parameters used to generate spurious echo artifact signals.

Figure S2: Pulse sequence diagram of the single voxel symmetric PRESS sequence used for the in vivo acquisitions. Sequence parameters were as follows: TE/TR = 30 / 2000 ms; samples = 2048, spectral width = 5 kHz. Around each refocusing pulse, the spoiler gradient pairs are shown.

Figure S3: Example 32-channel receive sensitivity maps acquired and processed for one dataset in one subject (R06); a single axial slice at the level of the MRS voxel is shown. Data were processed with BART toolbox and are smoothly varying. Absolute values of the complex sensitivities are shown.

Figure S4: ERASE reconstruction from remaining 3 datasets showing estimated artifact regions and reconstructed artifact spectra compared to standard reconstruction.