Factor investing: A stock selection methodology for the European equity market

Abstract

This paper uses European high capitalization corporate data for the 1991–2019 period to demonstrate that a systematic active management portfolio based on the identification of value, profitability, and momentum factors can outperform competing benchmark strategies. Factor investment methodologies received significant attention in the literature in the U.S. market but their application to European corporates is more limited. The authors construct several systematic investment strategies combining different metrics measuring the three factors. Reported results show that a) combined (mixed/conditional) strategies deliver positive alphas and significantly outperform their pure strategy counterparts and b) while there exists a time changing performance of selected metrics the iterative combination of factors delivers the highest performance with average annualized compounded returns of up to about 17%.

Three Key Takeaways:

 1. This paper documents the existence of alpha-generating factor strategies based on a combination of value, profitability, and momentum metrics. Combined (mixed/conditional) portfolios significantly outperform their pure strategy counterparts.

 2. The iterative combination of factors delivers the highest performance with annualized compounded returns of up to 17%.

 3. In line with the recent literature, we find decaying returns to factor strategies.

Factor investing; Value; Profitability; Momentum; Alpha; Active management.

1. Introduction

Over the 2007–2017 period, 87.4% of the European Equity funds investing in European equities did not beat the market.1 This underperformance triggered a significant flow out of active and into passively managed funds.2 “Stock picking” and paying higher fees for active management, therefore, seems to be a less attractive option for institutional and retail investors.

The underperformance of active portfolio management has been addressed in the mutual funds industry (see Gennaioli et al., 2015 and references therein). In a related paper Cremers et al. (2016) use a multi-country sample of equity mutual funds and ETFs to demonstrate empirically that actively managed funds are more active and charge lower fees when they face more competitive pressure from low cost indexed funds. A similar concern has been addressed in the factor investing literature. For instance, evidence shown in Kao (2002) and Bird and Casavecchia (2007) points towards the reduced capacity of long-only strategies to consistently generate abnormal returns (alpha). Arnott et al. (2019) underline the process by which an increasing number of investors exploit factor-based trading opportunities until the mispricing disappears.

This study contributes to this literature by unveiling the existence of positive and statistically significant alphas of up to 5,3% and long-term returns of up to 16,78% over different periods, for long-only factor strategies applied to European corporates.3 We exploit for this purpose a series of algorithms that rely on fundamental and momentum factors. The stock-picking process is automatized, and human bias, as underlined in Barberis et al. (1998) and Daniel et al. (1998), is ruled out from the investment process.4

Traditional factor investment techniques of portfolio selection rely on the analysis of company fundamentals or static metrics. These strategies were initially designed using the concept of value investing introduced by Graham and Dodd (1934). The value factor has been extensively studied by academic researchers, mainly using the book-to-market ratio as the key measure to segregate value from growth stocks (Fama and French, 1993). Investment strategies based on a profitability factor were introduced by Novy-Marx, 2013a, Novy-Marx, 2013b. Profitability relates to the company's ability to generate gross profits (i.e., revenues minus cost of goods sold) in relation to its asset base. The inclusion of profitability allows value investors to distinguish between stocks that trade at prices well below fundamentals (underpriced stocks) and those that are cheap due to low intrinsic values (value traps). By including price signals, quality investors can detect good firms that are already fully priced. As underlined by Novy-Marx, 2013a, Novy-Marx, 2013b trading on the basis of value and profitability signals brings the double benefit of increasing expected returns while decreasing volatility and drawdown size.

Momentum strategies are used in the literature to address the influence of past relative returns on portfolio performance. Jegadeesh and Titman (1993) identified the existence of positive persistence in stock returns that can be exploited to generate positive additional abnormal returns in the future. Momentum was considered by Fama and French (2008) as the “premier anomaly” and is now one of the most extensively studied factors in the literature.

The main objective of the paper is to evaluate the performance of the combined portfolios using first value, second profitability and third momentum metrics. Applied to 28 years of European data, the paper focuses on determining the extent to which the mixed or iterative combination of the three factors enhances performance. While our results are highly consistent with those reported in the literature, they show that mixed and iterative portfolios provide positive alphas relative to the corresponding pure strategy benchmarks. The iterative combination of different criteria yields improved performance relative to the mixed portfolio algorithm.

The iterative (or recursive)5 combination of factors follows the spirit of Gray and Carlisle (2012), who applied this mechanism to value and quality portfolios. In this context, this paper uses the iterative combination for the three factors and the portfolio selection algorithm incorporates the cheapest stocks in step one, the most profitable stocks in step two,6 and the stocks driven by the highest momentum (higher return) in step three.7 The iterative methodology involves a comprehensive fundamental analysis that includes an ordered selection of criteria that designs the critical steps required in the portfolio construction process.8 This allows the ordered combination of a significant number of signals such as first value then quality and then momentum.

This paper also contributes by analyzing the evolution of individual and combined factor performance over time. We find that the documented alpha-generating performance diminishes over time. A standardized factor approach based on Z-scores demonstrates that there is time-changing factor profitability over our sample period.

The rest of the paper is organized as follows. In section 2 discusses data collection and methodology. In section 3 we provide results under the application of pure, mixed and iterative algorithms. A series of spanning tests are provided in subsection G. We report results from the proposed Z-score estimations in subsection H. We conclude in section 4.

2. Data and methodology

2.1. Data

This study uses final year European corporate accounting data and end of the month market prices from the FactSet dataset for the period ranging from July 1991 to July 2019.9 Banks, insurance, REITS, financial holdings, dually listed companies, as well as companies not reporting complete accounting data, are excluded from the analysis. This is consistent with the work of Novy-Marx, 2013a, Novy-Marx, 2013b which also excludes financial firms from the sample. Finally, companies are sorted yearly in decreasing order according to market capitalization (in USD) as recorded on the 31^st of December. We select the top 600 to replicate the number of stocks used by one of the benchmark indexes in Europe such as the Stoxx Europe 600. By concentrating on blue chips, we guarantee the liquidity of the proposed long-only strategies and minimize transaction costs. Filtering by market capitalization allows us to address the problem of vanishing profitability raised by Novy-Marx and Velikov (2016), guaranteeing that reported profitability does not rely on illiquid microcap names (see Hou et al., 2017).

Our sample constitutes a balanced panel of 17.400 observations corresponding to 1.830 different companies, which represent 90% of the total market cap of the European investment universe distributed amongst 29 countries and 19 different economic sectors.10. This sample includes live as well as dead companies, which constitute 1.4% of our data set. We thus avoid survivorship bias. Following Leippold and Lohre (2008), we label as “dead” those companies that are in extreme distress or those being merged, delisted, or converted.

2.2. Building portfolios

Once our sample of corporate data is constructed, we proceed to build different metrics corresponding to the value, profitability, and momentum factors.

This way, four different metrics are employed to measure value: 1) Book-to-market ratio (BTM), 2) Price-to-earnings (PER), 3) Total enterprise value to EBIT ratio (EVEBIT) and 4) Total enterprise value to EBITDA ratio (EVEBITDA thereafter). BTM is the most common ratio used to measure value in the academic literature (see Fama and French, 1993; Lakonishok et al., 1994). Then, PER ratio, applied by Graham and Dodd (1934) and Graham (1949), and the group of EVEBIT and EVEBITDA, more recently applied by Greenblatt (2010), Gray and Vogel (2012) and Gray and Carlisle (2012), are extensively utilized by practitioners in both public and private equity markets.11

Profitability is, then, measured through three different metrics: 1) Gross profit on total assets (GPA), 2) Return on capital (ROC_Green), as defined by Greenblatt (2010). 3) Return on capital (ROC_Det) including intangible assets. While the GPA has received wide attention in the academic literature, following the contribution of Novy-Marx, 2013a, Novy-Marx, 2013b, the use of ROC metrics is more extended among institutional investors.

The role of intangibles has been addressed in this literature in recent years due to the so called “value conundrum” phenomena that followed the Great Financial Crisis. While some studies (see Urionabarrenetxea et al., 2017) present intangibles as corporate risk and default probability impounders, some others (see Amenc et al., 2020) highlight their capacity to produce a better representation of value when properly incorporated in the corresponding metric. This paper differs from the previous literature in that it addresses the effect of intangibles from a profitability perspective. We contend that including intangible assets allows greater assessment of corporate efficiency of financial resources delivering a more precise measure of their return on capital.

Finally, we select those firms that have exhibited a positive price trend over their recent history. For this purpose, and to avoid reversal effects,12 we follow Lehmann (1990), Jegadeesh (1990) and Jegadeesh and Titman (1993) and use a metric of 12 months momentum which excludes the most recent one (“12_1 momentum”) in its calculation.

To build our long-only portfolios, the 30^th of June of each year, following Novy-Marx, 2013a, Novy-Marx, 2013b, we proceed as follows:

• 1.First, we rank companies according to every single factor (value, profitability and momentum) metrics: when using a value metric, companies are ranked from cheaper to more expensive; when applying a profitability metric, companies are ranked from higher to lower profitability. Finally, the momentum ranking is obtained by sorting, for each year, companies from higher to lower accumulated returns. Portfolios built solely according to each of these single rankings are denoted as “pure”.
• 2.To investigate the performance of the proposed factor strategies, an equally weighted (EW) benchmark portfolio is built from the entire universe of 600 European companies. This index also illustrates the returns that arise from passive management. The natural market traded benchmark, i.e., the Stoxx Europe 600 index, is not used because this contains banks, insurance companies and REITS, which are excluded from our sample.
• 3.We next find the best performing factor metric within each category and analyze the statistical significance of the selected tier 1 (or top 5%) constructed portfolios.
• 4.An additional set of rankings (denoted as “mixed”) is constructed by averaging each value ranking with a profitability/Momentum one and sorting the result in descending order. This type of analysis was previously used by Greenwald et al. (2004), Greenblatt (2010), and Novy-Marx, 2013a, Novy-Marx, 2013b among others.
• 5.A final set of rankings (denoted as “conditional”) is obtained by iteratively classifying stocks according to value, then profitability and then momentum indicators. This requires us to combine the three factors into a single portfolio, following the spirit of Gray and Carlisle (2012) in their combination of value and profitability. Conditional value-based (pure) sub-portfolios are split according to each quality metric and, further, decomposed according to the momentum indicator. For example, we create portfolios of thirty stocks using the following procedure: out of the 600 stocks, the first quintile (top 20%) is selected by a metric of value (120 stocks), subsequently, we select the top 50% by a metric of profitability (60 stocks) and finally we choose the top 50% by momentum to select a portfolio with thirty-stocks.13All the results in the main text correspond to equally weighted (EW) portfolios. Portfolio performance remains qualitatively unchanged when a value weighed (VW) scheme is applied.14

Therefore, the total number of different rankings considered in this study amounts to 40: 8 pure rankings, 16 mixed rankings and 16 conditional rankings.15

As previously discussed, our analysis focuses on traditional long-only portfolio management strategies applied to high cap liquid corporates and does not apply long-short strategies. As shown by Novy-Marx and Velikov (2016) almost no factor constructed on a long-short basis exhibits positive returns after accounting for transaction costs.

By concentrating on long-only active portfolio management, we exclude hedge fund strategies from our portfolios. Long-only investment funds and hedge funds are exposed to significantly different investment constraints and structures.16 While hedge funds do not exhibit short-selling restrictions, traditional active asset management in Europe was subject to substantial short-selling constraints, arising mainly due to limitations imposed by the regulation. These restrictions were even stronger before the introduction of the Euro currency and, in consequence, the process of applying life trading to paper long-short portfolios over our sample period is complicated. A secondary purpose in this paper is thus to demonstrate that actively managed long-only portfolios remain profitable in the long run, despite the fierce competition arising from hedge fund activity and passively managed funds.

2.3. Characterizing the impact of value, profitability and momentum strategies: the Z-Score

To assess the impact on the relative performance of each factor individually, every metric or factor exposure, i, corresponding to the company j is standardized each year, t, to retrieve its corresponding Z-score:

$$Z_{i,j,t}=\frac{V_{j,i,t}-{\overline{V}}_{i,t}}{{\sigma }_{i,t}}$$ (1)

where $V_{j,i,t}-{\overline{V}}_{i,t}$ is the distance from its mean of each specific metric, and ${\sigma }_{i,t}$ denotes the yearly dispersion (standard deviation) of the values of that criterion. This standardization provides a set of “universe neutral scores” where each factor Z-score exhibits zero mean and unit standard deviation across the universe of securities. This standardization allows reliable comparison among the different factors, which becomes important when assessing relative performance in terms of financial ratios (see Altman, 1968). Note that this methodology has recently been applied in the factor investing literature (see Clarke et al., 2014) who perform multivariate regressions and scaling of stock characteristics to unit standard deviations (i.e., Z-scores).

To assess the impact of company characteristics, while avoiding sampling bias, every feasible combination of the factor metrics is considered to generate 5% top tier conditional portfolios. In doing so, we first split the sample into five quintiles (120 stocks) according to one of our eight metrics. The resulting portfolios are then separated into two according to the same, or an alternative metric, to obtain ten portfolios of 60 companies. Each of those portfolios are again divided in two according to any candidate factor metric. This procedure leaves us with 10.240 (20 × 8³) different portfolios, each one including 5% of the original universe (30 stocks).

For each sub-portfolio yearly returns are obtained as the simple average of company return values.17 The portfolio Z-score, ${\overline{Z}}_{i,t}$, is obtained by averaging individual factor Z-scores for every corporate under all portfolios. Excess returns of the market portfolio benchmark are denoted as $R_{m,t}$ while $R_{p,t}$ denotes excess portfolio returns. The 1-year Libor is subtracted from annualized returns in order to obtain excess returns.

A time series-panel data regression is then used to estimate the coefficients of the extended CAPM equation:

$$R_{p,t}={\overline{\alpha }}_m+\sum _{w=0}^t{\beta }_w{R}_{m,t-w}+\sum _{i=1}^8{\gamma }_i{\overline{Z}}_{i,t-1}+controls+u_{m,t}$$ (2)

The Z-score loadings, ${\gamma }_i,$ and the drift parameter, ${\overline{\alpha }}_m$ , represent factor sensitivities and the abnormal return generated by the stock selection for each sub-portfolio class, respectively. Controls include Fama and French (1993) smb, hml and rmw factors. The use of the three Fama and French factors has recently been supported by Arnott et al. (2019) as well as Lewellen (2014).

3. Results

In what follows, we present the results produced by the proposed strategies. We first analyze the performance of pure and mixed strategies. In a later section, we analyze the extent to which conditional rankings improve the stock selection process of pure and mixed strategies. Afterward, a panel data approach is utilized to quantify the individual impact of value, profitability, and momentum metrics in portfolio excess returns.

3.1. The value of systematic factor investing

Table 1 presents descriptive statistics reported in local currency delivered by the different quintile portfolios in terms of a) final index values which represent final portfolio value achieved by an investment index with an initial value equal to one (corresponding to the initial investment allocated to a given portfolio) and b) portfolio returns compounded annually.18

Table 1.

Final value and compounded return for pure factor portfolios 1990–2019.

	Benchmark	BTM	PER	EVEBIT	EVEBITDA	GPA	ROC_	ROC_	MOM
							Green	Det
Final Index Value Portfolio 1 (Best)	12.95	16.53	24.49	25.21	22.39	26.43	18.85	20.90	25.49
Final Index Value Portfolio 2		12.59	13.64	12.93	15.70	13.75	17.21	18.25	14.98
Final Index Value Portfolio 3		12.16	14.83	11.99	11.19	13.85	12.08	14.89	13.10
Final Index Value Portfolio 4		10.55	11.41	11.95	13.30	10.27	13.42	10.04	10.09
Final Index Value Portfolio 5 (Worst)		11.73	5.49	6.75	7.41	9.24	6.51	6.67	6.60
Annualized Return Portfolio 1 (Best)	9.15%	9.94%	11.20%	11.21%	10.67%	11.38%	10.42%	10.76%	11.56%
Annualized Return Portfolio 2		9.01%	9.26%	9.14%	9.69%	9.36%	10.06%	10.34%	9.47%
Annualized Return Portfolio 3		8.84%	9.58%	8.76%	8.61%	9.24%	8.87%	9.61%	9.09%
Annualized Return Portfolio 4		8.39%	8.65%	8.83%	9.16%	8.17%	9.24%	8.10%	8.22%
Annualized Return Portfolio 5 (Worst)		8.65%	5.78%	6.00%	5.87%	7.20%	6.43%	6.24%	6.58%

This exhibit presents final values and compounded returns for each equally weighted portfolio formed according to a pure metric ranking. Each portfolio includes 20% (120) of the companies in the total sample. Individual Company financial Accounts and Absolute Return data are collected from FactSet database.

Results reported in Table 1 show that the upper quintile (portfolio 1) outperforms the market benchmark under all reported factor metrics. As expected, quintile 5 (portfolio 5) underperforms the market benchmark under all strategies and returns exhibit an ordered structure in all metrics under most tiers considered apart from three cases.19 This confirms that, on average, the proposed methodology effectively discriminates corporates.

It is also important to highlight the outperformance, in terms of final index values and annualized compounded returns, of the Momentum and GPA factors with respect to the other metrics. Other value measures, PER and EVEBIT, also stand out with favorable performance.

3.2. Pure and mixed rankings

This subsection concentrates on the performance of tier 1 portfolios (Top hereafter). As already mentioned, top portfolios incorporate the upper 5% of companies under each of the combinations considered.20

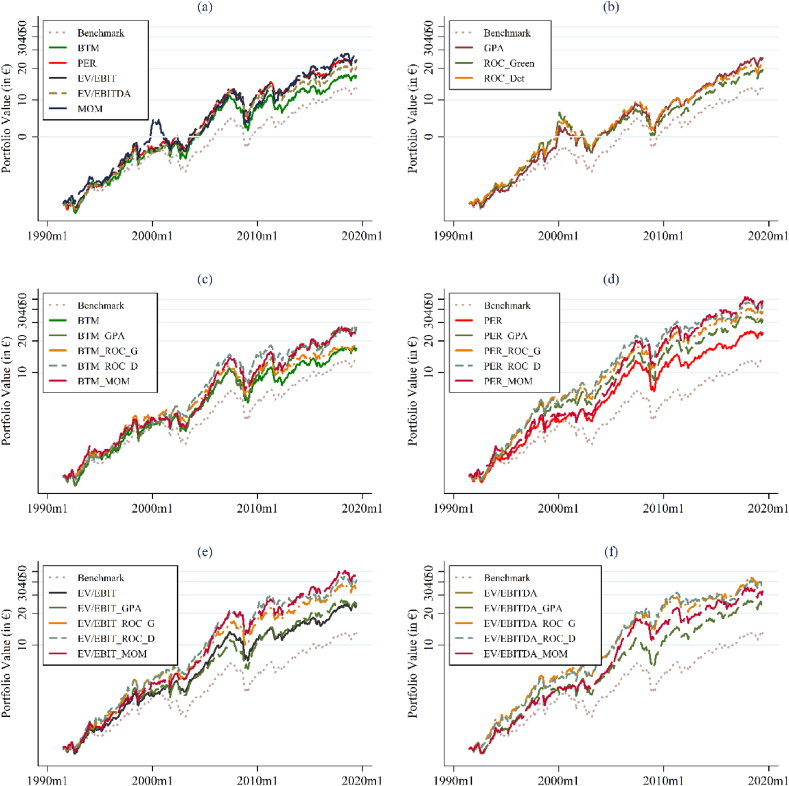
Figure 1 (a)-(f) present the evolution of cumulative returns for each of the constructed Top and benchmark portfolios under the assumption that 1€ was invested in 1991. A final figure of 25, observed for some of the mixed momentum strategies, implies that the value of the initial investment multiplies by 25 times during the investment period. Results corresponding to the pure value, momentum, and profitability portfolios are depicted in Figure 1(a) and (b). Mixed portfolios combining value and profitability, and value and momentum are provided in Figure 1 (c)–(e).

Figure 1.

Evolution of Pure and Mixed Portfolios 1990–2019. This exhibit depicts the evolution over the 1990–2019 period of portfolios built with the upper 5% companies sorted according to Pure and Mixed criterium. Company Accounting and Absolute Return data from FactSet database.

A close inspection of each graph shows that Top portfolios exhibit higher accumulated returns than the 600-stock benchmark, facing significant market drawdowns during the 2000 dot-com crash and the global financial crisis. Out of the single factor strategies GPA, Momentum, and EVEBITDA remain the most profitable in terms of final index values. These are followed very closely by the PER based pure strategy. Within the value strategies depicted in 2(a), the BTM metric underperforms each of its value counterparts. Figure 1(b) demonstrates that ROC_Det and GPA measures outperform ROC_Green. The outperformance of ROC_Det is more evident from 2002 onwards, maybe reflecting an increased importance of intangibles during the second part of our sample. The relevance of such assets is further discussed in the final section.

Similarly, Figure 1(c)–(e) demonstrate the extent to which average mixed factor strategies return exceeds that of single factor strategies. Value-momentum and Value-profitability as measured by PER_MOM and EVEBITDA_ROC_Green stand out with favorable cumulative returns before and after 2002. This is consistent with Novy-Marx, 2013a, Novy-Marx, 2013b (NM hereafter) where large profitable value stocks are shown to outperform alternative benchmark strategies.

This highlights the importance of filtering value portfolios with profitability measures and momentum. While the former requires considering value and profitability in the selection process, the later strategy requires investing in a value stock when there is also a positive market sentiment for the underlying corporates.

Table 2 reports performance metrics for the best performing Top portfolios within each category (pure, mixed value-profitability and mixed value-momentum) under two main measures:21 a) final compounded returns, and b) average portfolio returns annually compounded.

Table 2.

Performance metrics of top portfolios 1991–2019 (pure and mixed).

	1Y Libor	Benchmark	PER	GPA	MOM	EVEBITDA	EVEBITDA_ROC_Green	PER_MOM
Annualized Compounded Return (Final)	3.56%	9.15%	12.06%	11.73%	11.71%	12.00%	12.17%	12.54%
Annualized Compounded Return (Average)	2.51%	9.61%	13.52%	12.43%	15.18%	12.96%	14.95%	14.43%
Annualized Compounded Return Volatility	4.80%	14.84%	15.19%	15.31%	20.90%	15.05%	16.68%	19.61%
Sharpe Ratio		0.62	0.79	0.77	0.56	0.80	0.74	0.66
CAPM Beta			87.62%	92.64%	118.78%	88.24%	96.22%	111.12%
CAPM Beta (Std. Dev.)			0.04	0.03	0.06	0.03	0.04	0.05
Jensen's Alpha			3.97%	3.26%	2.20%	3.84%	3.66%	3.42%
T-statistic			8.91	8.48	3.62	9.11	7.91	6.66
Alpha (FF3)			0.93%	4.23%	1.54%	1.10%	4.51%	2.05%
T-stat (FF3)			1.95	10.88	2.62	2.30	9.52	3.95

This exhibit presents performance metrics for best performing portfolios within each Pure and Mixed category over the 1991–2019 period. Categories are Pure Value, Pure Profitability, Pure Momentum, Mixed Value_Profitability and Mixed Value_Momentum. Company accounting data and Absolute Returns from the FactSet database. Fama and French factors are European Factors downloaded from Kenneth French website: https://mba.tuck.dartmouth.edu/pages/faculty/ken.french/data_library.html. The dollar value of the portfolio is converted into Euros using the conversion factor specified in Appendix A.

Results demonstrate that there is an average premium over the benchmark (risk-free) equal to 4.2% (11.30%). This delivers positive risk-adjusted returns as measured by reported Sharpe ratios, which on average improve by 0.11 points when compared to the market benchmark.22

Moreover, Sharpe Ratios reported in Table 2 are consistent with those found in the literature. While Asness et al. (2013) report values ranging from 0.42 to 0.91 for European Top value and momentum portfolios, our strategies deliver average Sharpe Ratios of 0.73 and with the exception of the momentum portfolio, always exceed the market benchmark. Performance is also evaluated against the simple and Fama and French three-factor (FF3, hereafter) versions of the CAPM model. To this end, the European FF3 factors reported on FF web page are used.23 Given that those are denominated in USD, we use the conversion formula specified in the last row of Appendix A to retrieve their Euro denominated counterparts. Alphas are estimated using the Fama-MacBeth estimator using a 12-month rolling window (see Jegadeesh et al., 2019). Estimates and corresponding t-statistics in Table 2 demonstrate that the proposed strategies generate positive and statistically significant alphas that are consistent with those reported in Fama and French (2017).24

CAPM betas are significant and lower than one in all cases but for those including the momentum metric.25 This suggests that the proposed stock selection method generates systematic risk-adjusted returns without exacerbating the exposure to the market component (levered strategies). These results are important for systematic active portfolio management, as they demonstrate that the proposed portfolios are defensive in all cases but under the momentum metric.

Reported figures in Table 2 also show that the mixed strategies EVEBITDA_ROC_Green and PER_Momentum (PER_MOM, hereafter) stand out with superior performance in terms of annualized compounded returns, while the EVEBITDA_ROC_Green delivers the highest alpha after controlling for the FF3. Results for the EVEBITDA_ROC_Green strategy can be compared with those provided for the long side of joint value and profitability strategies in NM. We see that reported Sharpe Ratios and alphas for the selected value profitability strategy are higher than those yielded under the Long Side universe in NM. For instance, our EVEBITDA-ROC_Green strategy delivers an alpha of 4.51% while NM reports 2.5% and 2.2% for long-large and long-small portfolios, respectively. A comparison of the performance of the PER-Momentum with the long side of the joint value and momentum in NM shows that the proposed value-momentum portfolio also outperforms NM.26 While NM reports insignificant alpha for the long-small caps strategy and a significant alpha of 1.1% for the long-large cap portfolio the selected PER-Momentum strategy yields an alpha of 2.05%.

Results for value weighed portfolios are provided in Exhibit 3 in Appendix C. We can see that performance is moderately reduced in terms of Sharpe Ratios and alphas when compared to that delivered by equally weighted portfolios. Value weighted strategies are expected to deliver lower volatility (see Fama and French, 1993) but may also yield lower average returns (see Chen et al., 2017). Their performance in terms of Sharpe-Ratios relative to equally weighted strategies will thus depend on the average return volatility trade-off. The outperformance of equal-weighted portfolios has been documented in the literature: see for example DeMiguel, Garlappi, and Uppal (2009) or more recently, Malladi and Fabozzi (2017) who argue that equal weighting makes economic sense. Plyakha et al. (2012) show that the differences in performance of value and equal weighed portfolios arise partly due to divergences in exposure to systematic risk factors. They also document how factors with extremely high reversal contribute to the higher alpha of the equal-weighted portfolio.

3.3. The 2002 effect

The emergence of the Euro in January 2002 constituted one of the major political and financial events of the current century and led to significant changes in Europe's financial structure. As discussed in Galati and Tsatsaronis (2003), this event resulted in stock prices increasingly reflecting risk factors specific to industrial sectors rather than individual countries.

During the same period, there were important regulatory reforms worldwide aimed to increase the reliability of accounting information. These included the introduction of the Sarbanes-Oxley Act (SOX) in July 2002 (see Espahbodi et al., 2015) and the Global Analyst Research Settlement (GARS) in the US, both designed to restore investor's confidence and improve the quality of information available to market participants. Parallel changes were performed in the European Union between 2001 and 2003 such as the Financial Services Action Plan (FSAP) or the introduction of amendments of the 7^th directive of consolidated accounts.27

While regulatory changes contributed to a reduction of exchange rate risks in the common currency area, they did not lead to the reduction of country specific risk sources for firms. Under the presence of common financial shocks, the lack of monetary autonomy aggravates sovereign debt problems which eventually affect credit risk for individual corporates (see Bianchi and Mondragon, 2018). For instance, during the 2010–2012 European Sovereign Debt Crisis, Portugal and Spain faced increased difficulties when trying to avoid corporate defaults despite exhibiting low debt-GDP ratios compared to other economies not in the currency union. Hence, the effect of global shocks under a common currency area could have a significant impact on the return distribution of the proposed strategies.

We explore in greater depth the effect of macroeconomic shocks and regulatory changes in Figure 2, which presents the graphical evolution of our Top performing pure and mixed portfolios and Benchmark over the 2002–2019 period.28 Table 3 reports coefficient estimates and performance metrics.29

Figure 2.

Evolution of Pure and Mixed Portfolios 2002–2019. This exhibit depicts the evolution from 2002 to 2019 of best performing portfolios within each Pure and Mixed category. Company Accounting and Absolute Return data from FactSet database.

Table 3.

Performance metrics of top portfolios 2002–2019 (pure and mixed).

	Benchmark	PER	GPA	MOM	EVEBITDA_ ROC_Green	PER_MOM
Annualized Compounded Return (Final)	16.19%	21.02%	15.23%	20.48%	18.70%	21.96%
Annualized Compounded Return (Average)	6.40%	12.83%	3.61%	9.78%	12.58%	16.49%
Annualized Compounded Return Volatility	14.68%	17.35%	14.70%	19.61%	15.39%	18.48%
Sharpe Ratio	0.58	0.64	0.55	0.55	0.61	0.60
CAPM Beta		105.79%	92.72%	115.11%	93.54%	102.87%
CAPM Beta (Std. Dev.)		0.039	0.03	0.064	0.035	0.047
Jensen's Alpha		2.85%	0.16%	1.93%	1.43%	2.39%
T-statistic		5.12	3.97	2.77	7.2	10.22
Alpha (FF3)		0.08%	1.06%	1.53%	1.21%	1.59%
T-stat (FF3)		0.16	2.65	2.26	2.77	3.78

This exhibit presents performance metrics for best performing portfolios within each Pure and Mixed category over the 2002–2019 period. Categories are Pure Value, Pure Profitability, Pure Momentum, Mixed Value_Profitability and Mixed Value_Momentum. Company accounting data and Absolute Returns from the FactSet database. Fama and French factors are the European Factors from Kenneth French website: https://mba.tuck.dartmouth.edu/pages/faculty/ken.french/data_library.html

The Euro value of the factors is obtained using the conversion factor in Appendix A.

Figure 2 suggests that on average results are consistent with those reported for the full sample period. The performance reported for the profitability based (GPA) portfolio is the only exception. This only over-performs the market benchmark for a short period after 2014. The remaining strategies exhibit outperformance with respect to the market benchmark. While the market portfolio multiplied its value by approximately 4 times, the mixed EVEBITDA_ROC_Green portfolio and the pure PER and Momentum portfolios rose by a seven-fold while the mixed PER_MOM driven portfolio rose by an eleven fold.

The effects of the Global Financial Crisis on the time series of cumulative returns are visually more evident when the 2002–2019 period is considered. During this timeframe the Momentum portfolio only just replicates the market benchmark while mixed and pure PER strategies outperform the market portfolio. As documented in Bretschger and Lechthaler (2018) and Amenc et al. (2019), results of the profitability-factor-driven portfolios are statistically associated with economic growth and strongly affected by common macroeconomic exposures.

The first and second rows of Table 3 show that the strategy based on the mixed combination of value and momentum (PER_MOM) is the best performer in terms of final and average compounded returns. As in Bird and Casavecchia (2007), returns of value strategies are enhanced with the introduction of the momentum filter. PER and Momentum pure portfolios outstand for their outperformance in terms of final compounded returns.

Final annual return estimates reported in the first row of Table 3 are on average 7.4 percentage points higher than those in the first row of Table 2. Outperformance with respect to the full sample estimates is however not as evident when analyzing average return estimates. In fact, only the mixed strategy PER_MOM outperforms the full sample estimate. Moreover, the gap between final compounded returns and average compounded returns widens when considering the 2002–2019 period suggesting that there may be return distributional asymmetries. The latter possibly arise due to extraordinary movements in prices seen during the 2007–2009 Global Financial Crisis and the 2010–2012 European Sovereign Debt Crisis. As underlined by Arnott et al. (2019) factor returns can exhibit distributions consistent with tail behavior. The latter could be enhanced under the introduction of a monetary union.

The drop in average returns is paired with a lower fall in return volatility, which explains the moderate reduction of average Sharpe ratios from 0.72 to 0.59 when comparing the 2002–2019 estimates with those reported for the whole sample period. As was the case in Table 2, the highest value for this ratio is reported for the PER strategy, closely followed by EVEBITDA_ROC_Green. The latter metric exhibits the highest and statistically significant FF3 alpha as it reported under full sample estimates. Value-momentum (PER_MOM) and value-profitability (EVEBITDA_ROC_Green) mixed criterion outperform in terms of average and final compounded returns.

Results for value weighted portfolios are provided in Exhibit 5 in Appendix C. They are consistent with those yielded under equal-weighted portfolios.

3.4. Time series evolution of factor outperformance

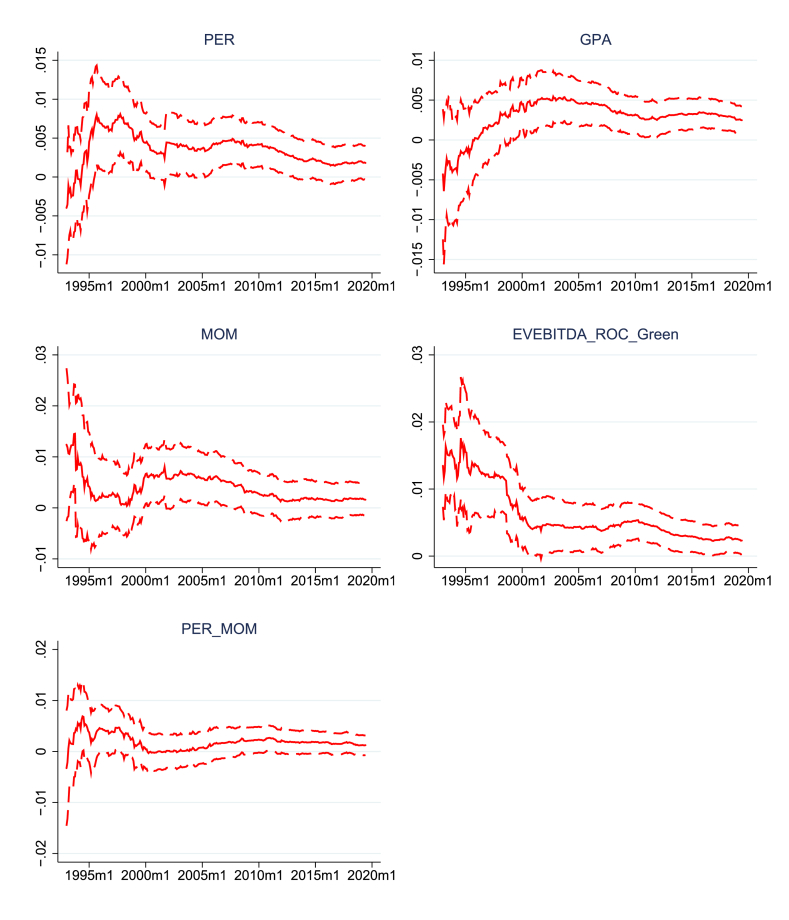
In what follows, the time changing nature of factor outperformance is analyzed in greater depth. Figure 3 presents the evolution of abnormal returns (alphas) obtained when the selected strategies (PER, GPA, MOM, EVEBITDA_ROC_Green, PER_MOM) are benchmarked against the FF3 model. Alphas are monthly rolling estimates computed using a 12-month window.

Figure 3.

Average Excess Return (Alpha) for Top Portfolios 1992–2019 (Pure and Mixed). This exhibit presents the evolution of alpha and its 95% confidence interval for the 3 factors Fama-French model when applied to returns on best performing portfolios. Alphas are estimated over a 12- month rolling window using the Fama-Macbeth estimator. Company accounting data and Absolute Returns from the FactSet database. Fama and French factors are from Kenneth French website: https://mba.tuck.dartmouth.edu/pages/faculty/ken.french/data_library.html.

The time series plot of the alpha parameter is depicted by the solid line while the 95% confidence interval is represented by the dotted lines. A close look at Figure 3 shows that in the early stages of our sample, reported alphas exhibited wide confidence interval bands, due to a high variation of the return premiums. For instance, the return premium of the GPA strategy oscillated between -10% and +10% until 2000. During the 2000–2012 period, the estimated alphas fall in absolute value but remain positive and exhibit higher statistical significance than in the early or final stages of our sample. As a result, the confidence interval bands narrow.

In the aftermath of the European Sovereign Debt crisis estimated alphas decrease further, and approach zero. This is consistent with the fall in the average of estimated alphas, from 2.39% to 1.09%, observed when comparing Tables 2 and 3. The decay in the value of alpha is especially notable for the GPA and EVEBITDA_ROC_Green strategies and is consistent with the existence of factor crowding widely discussed in the literature: see Linnainmaa et al. (2018), Arnott et al. (2019), and Fama and French (2020) among others. As addressed by Cerniglia and Fabozzi (2018) returns from factor strategies decay as investors learn about factor mispricings.30

3.5. Conditional rankings

This subsection analyzes the screening capacity of the iterative mechanism based on the successive application of value, profitability and momentum criteria.

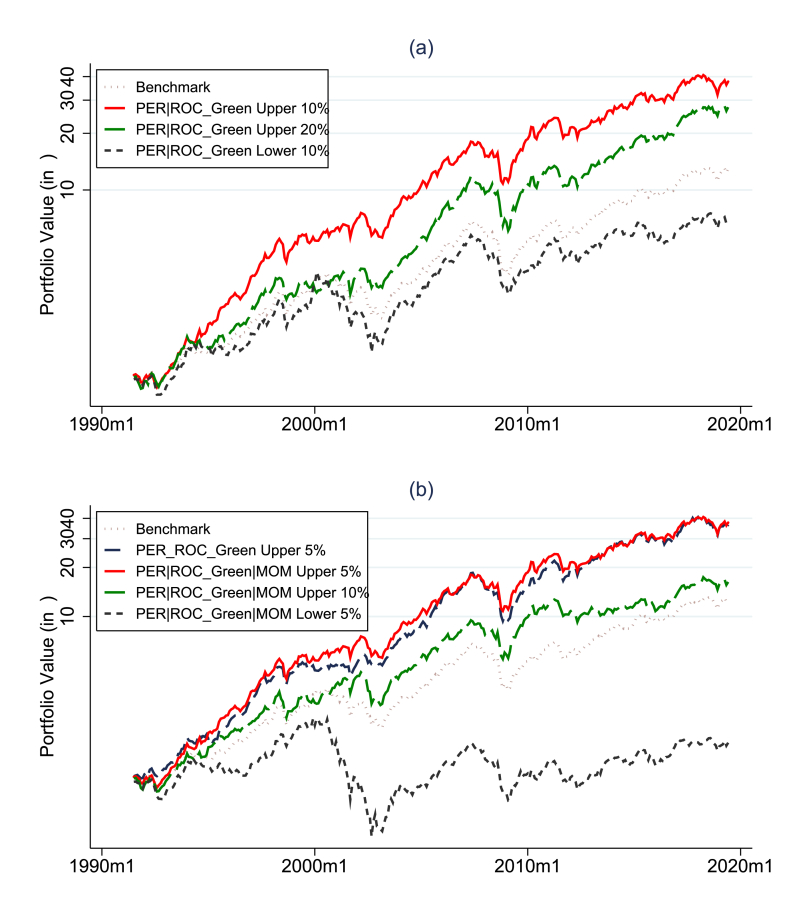
Figure 4(a) depicts portfolio performance when using an iterative value and then profitability filter while Figure 4 7(b) presents the evolution of cumulative returns when an additional momentum-based filter is applied. A close look at Figure 4 7(b) allows us to see the benefits that arise from double screening iterative portfolios as final portfolio values more than double when comparing upper 5% and 10% portfolios, respectively.

Figure 4.

A Recursive Strategy, an Illustration. This exhibit depicts the evolution of a recursive strategy comparing it with its benchmark and the corresponding mixed strategy over the 1990–2019 period. Company financial information and Absolute Returns from the FactSet database.

Figure 4(b) also shows that applying a momentum-based criterion to a value-then-profitability selected portfolio allows outperformance with respect to the single and mixed portfolios. For the PER|ROC_Green|MOM portfolio considered, selecting the Top 5% portfolios allows portfolio value to increase by 40-fold, delivering superior performance than its PER_ROC mixed portfolio counterpart. It is however noted that the difference in performance diminishes in the aftermath of the 2010–2012 European Sovereign Debt Crisis.

Performance results for the complete set of strategies are available upon request. They demonstrate that similar improvements in terms of returns are achieved when applying conditional rankings regardless of the metric used to define value and profitability. Conditional rankings, therefore, outperform on average mixed and pure rankings in terms of cumulative returns.

Table 4 provides summary statistics of the best portfolios generated combining PER and EVEBITDA value portfolios with each profitability and momentum metric. A comparison of the first and second rows of Tables 2 and 4, shows that PER and EVEBITDA based conditional portfolios present, an average increase in final annualized returns of 1.09 and 1.22 percentage points respectively over their corresponding pure counterparts.31 A close comparison of Tables 2 and 4 allows us to see the outperformance of iterative strategies, in terms of Sharpe Ratios, with respect to pure strategies. Specifically, ratios reported in Table 4 are on average 0.12 points higher than those presented in Table 2.

Table 4.

Performance metrics of top iterative portfolios 1991–2019 (recursive strategies).

	Benchmark	EVEBITDA				PER
		GPA	ROC_Green	ROC_Det	MOM	GPA	ROC_Green	ROC_Det	MOM
		MOM	MOM	MOM	MOM	MOM	MOM	MOM	MOM
Annualized Compounded Return (Final)	9.15%	12.61%	13.38%	13.76%	12.42%	12.86%	12.84%	13.62%	13.80%
Annualized Compounded Return (Average)	9.61%	14.65%	16.05%	16.54%	13.83%	14.31%	15.95%	16.78%	15.70%
Annualized Compounded Return Volatility	14.84%	15.68%	14.79%	14.67%	15.42%	15.95%	15.64%	15.79%	16.58%
Sharpe Ratio	0.62	0.80	0.90	0.94	0.81	0.81	0.82	0.86	0.83
CAPM Beta		95.08%	88.21%	87.08%	93.96%	97.48%	92.79%	91.80%	99.75%
CAPM Beta (Std. Dev.)		3.09%	2.93%	2.98%	3.08%	2.97%	3.31%	3.65%	3.47%
Jensen's Alpha		4.01%	5.19%	5.65%	3.87%	4.12%	4.42%	5.31%	5.00%
T-statistic		10.28	13.42	14.37	10.27	10.74	10.52	11.68	11.55
Alpha (FF3)		0.87%	2.06%	2.42%	1.27%	1.09%	0.18%	1.34%	1.49%
T-stat (FF3)		2.23	5.33	5.96	3.37	2.84	2.43	2.96	3.72

This exhibit presents performance metrics for Top 5% portfolios obtained sorting and discarding companies recursively according to value, profitability and momentum factors. Value and profitability factors are selected to match those of best performing mixed strategies. Company accounting data and Absolute Returns from the FactSet database. Fama and French factors European Factors from Kenneth French website: https://mba.tuck.dartmouth.edu/pages/faculty/ken.french/data_library.html

The Euro value of the factors is obtained using the conversion factor in Appendix A.

Moreover, estimated CAPM beta coefficients are on average a 4.5% lower than those in Table 2 while reported t-statistics for CAPM and FF3 alphas illustrate a high statistical significance of the strategies considered. Our results are therefore consistent with Blitz and Vidojevic (2019) who claim that pure factor strategies are suboptimal when compared with those that combine factors on a conditional basis.

Results also show that while the best performance in terms of average return arises under the iterative use of EVEBITDA|ROC_Det|MOM and PER|MOM|MOM criteria, the best Sharpe Ratio is reported under the EVEBITDA|ROC_Det|MOM portfolio. Our results are therefore consistent with Novy-Marx, 2013a, Novy-Marx, 2013b who demonstrates that accounting for quality improves the performance of strategies that combine momentum as well as price signals.

In line with findings in Amenc et al. (2020), the absolute outperformance of ROC_Det iterative portfolios when compared with results under ROC_Green, highlights the gains in the value premium that arises with the inclusion of intangible capital in working capital computation.

Average return and performance measures are consistent with those reported in the literature. We can compare the performance of conditional value, profitability, and momentum portfolios with those reported with the long side strategies of NM. We see that our selected value-profitability and momentum iterative portfolios yield higher alphas and Sharpe ratios. For instance, the conditional EVEBITDA/ROC_Green/MOM portfolio delivers a Sharpe ratio of 0.90 and alpha of 5.19% while NM reports an average Sharpe-Ratio and alpha of 0.59 an 2.6% for the long large cap and small cap strategies.

Exhibit 8 in Appendix C reports results when iterative strategies are used to build value weighted portfolios. While results are qualitatively consistent with those corresponding to the EW portfolios, they also present a moderately lower performance in terms of Sharpe ratio and Alpha. Lower average compounded returns are reported for the PER/MOM/MOM strategy as well as for the three EVEBITDA/ROC-Det/MOM, EVEBITDA/ROC-GREEN/MOM, and EVEBITDA/MOM/MOM when compared to the equally weighted counterparts. As it is the case under the equally weighted analysis value weighted iterative strategies outperform mixed strategies.

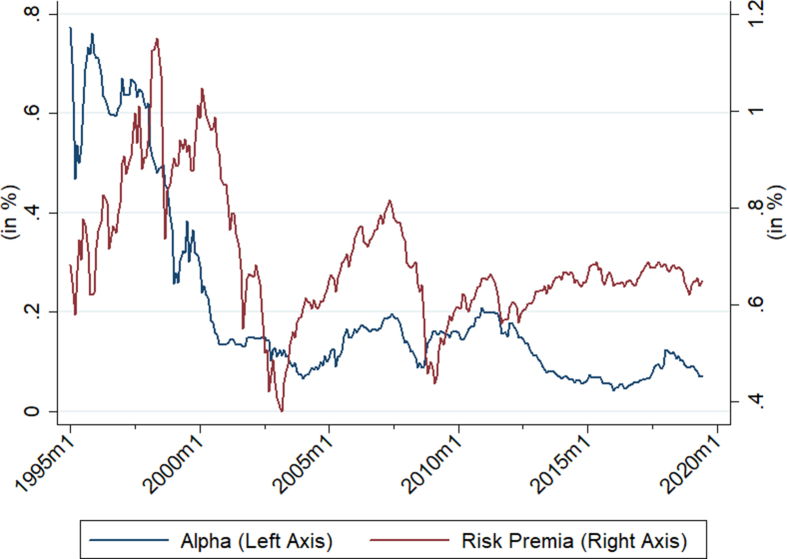
Figure 5 depicts a comparison between the average time series evolution of 12 month rolling window alphas (blue line) and their respective beta weighted risk premia, $\beta \left(R\_BMK-RF\right)$, (red line) for the best conditional portfolios. We can see that both metrics commove over our sample period. Alphas and risk premia are significantly higher during the 1995–2000 dot.com episode, the 2007–2008 global financial crisis and the 2010–2012 European Sovereign Debt Crisis. It is however evident that outperformance and the extra return demanded by investors decreases during our sample period. In fact, the share that the scaled risk premium represents on total portfolio return raises from approximately 50%–85%. While factor overcrowding may explain the observed diminishing alphas, the documented stable risk premiums over the 2014–2020 period may relate to the stable growth in company valuations under European Quantitative Easing policies.

Figure 5.

Average Excess Return (Alpha) and Risk premia for Top Portfolios 1995–2019. This exhibit depicts the evolution of the average alpha and the average beta scaled risk premia over the 1995–2019 period. The average alpha and risk premia are computed as simple means of their portfolio counterparts.

3.6. Spanning tests

Reported results suggest that mixed and iterative strategies outperform pure strategies. In this subsection, we formally investigate the extent to which mixed or/and combined strategies improve the pure strategies. We use for this purpose the Mean-Variance spanning intersection tests: see Huberman and Kandel (1987), Fama and French (2017) and Novy-Marx, 2013a, Novy-Marx, 2013b. In this framework, we test whether there is an improvement of the mixed or iterative strategies over combinations of the pure portfolios. A rejection of the spanning will indicate that the mixed/combined strategies contribute to the generation of abnormal returns.

Results from the spanning tests for the whole sample period are provided in Exhibit I of Appendix E. This reports three panels with 16 regressions in which pure factors explain the variability of mixed (Panel A) and iterative (Panel B) portfolios. In Panel C we test whether there is any additional performance of iterative portfolios relative to mixed portfolios.

The first column in each panel reports estimated intercept values and corresponding standard errors. These are the key estimates for the spanning test. Reported results in panel A show that we can reject the null hypothesis that mixed factor strategies are spanned by their pure counterparts at the 5% level in 9 out of 16 cases. The hypothesis is rejected at the 10% level in five regressions. We are however unable to reject spanning in the PER_GPA and the EVEBIT_ROC_Detailed mixed combinations. This implies that the PER, GPA and EVEBIT, ROC-DETAILED pure strategies can price their corresponding mixed portfolios. The under-performance of PER_GPA with respect to the pure portfolios may be explained by the strong results, in terms of Sharpe ratio and alpha, reported for the GPA pure portfolio in Table 2. The PER portfolio is also selected among the best pure performers with higher Sharpe Ratios than their mixed portfolio counterparts. We are unable reach the same conclusion regarding the EVEBIT_ROC_Green portfolio.

Panel B shows estimated coefficients for the regressions of iterative portfolios on combinations of pure portfolio counterparts. For instance, the first row of this panel reports intercepts and slope coefficients of a regression where the returns of the iterative BTM-GPA and then MOMENTUM are explained by the returns of the pure BTM, GPA and MOMENTUM portfolios. We find that regression alphas are significant at the 5% level in 11 out of 16 cases. We can therefore conclude that for these cases the iterative portfolios are not redundant relative to their pure portfolio counterparts. There are only two exceptions seen in the EVEBITDA_GPA and the EVEBITDA_ROC green. We recall again the strong outperformance exhibited by the GPA and EBITDA pure portfolios to explain this result. Note that under iterative strategies EVEBITDA_ROC_DETAILED and EBITDA_MOM are only significant at the 10% while under the mixed combinations this was the case for five portfolios (see EVEBIT_ROC_Green, EVEBITDA_GPA, EVEBITDA_ROC_Green, EVEBITDA_ROC_Detailed and EVEBITDA_MOM). There is, therefore, some evidence suggesting that the outperformance of the iterative portfolios with respect to their pure counterparts is stronger relative to the mixed combinations.

We formally analyze the extent to which iterative portfolios relatively outperform mixed ones in Panel C of the same table. This reports regression results when mixed portfolios returns are considered relative to their iterative counterparts. Reported alphas are significant at the 5% level in 11 out of the 16 cases analyzed. The estimated alpha is only significant at the 10% level for the BTM/ROC_Detailed/MOM case and not significant for the BTM_MOM/MOM portfolio.32 This confirms the outperformance of iterative strategies when compared with the mixed strategies.

Exhibit II in Appendix E reports conditioning tests. These tests are more appropriate under conditional frameworks where portfolio returns are seen to be predictable. In this paper, Z-score regressions are estimated in section H where portfolio returns are regressed against value profitability and momentum scaled metrics. When portfolio returns are conditionally modeled using standardized factors it becomes natural to apply conditional spanning and intersection tests with scaled returns (see also Cochrane, 1996). We use the conditional framework with scaled returns described in De Roon, Nijman and Werker (2001) and apply a pooled regression approach that allows testing the extent to which momentum and profitability are conditioning variables for spanning. The pooled regression is estimated using the returns of mixed and iterative portfolios as independent variables. The joint significance of GPA, ROC_GREEN, ROC_DETAILED and MOMENTUM is then tested using an F-test and the three FF factors as control variables. The p-value of the F-test statistic shows that the profitability and momentum factors are jointly significant in explaining mixed and iterative portfolio variability.

3.7. Results for Z-score regressions

In what follows, the evolution of the contribution of each of the investment value, profitability, and momentum metrics to portfolio outperformance is quantified in a framework in which all metrics are jointly considered.

As a preliminary analysis, we investigate the relationship between different variables. We report for this purpose in Appendix G (see Exhibit 11) estimated coefficients of (pooled) OLS regressions performed between each of the different standardized value, profitability and momentum metrics used in the analysis.

Estimated coefficients are relatively high for those variables that are by construction related such as (EVEBIT and EVEBITDA, ROC and ROC_det). However, correlations remain low but mostly significant across value and profitability metrics as well as momentum and profitability variables.

Note that reported results are consistent with those found in the literature (see Fama and French, 2015), FF5 hereafter, in which high correlations are reported for different versions of the same factors while correlations that are low but significantly different from zero are reported across different factors such as HML (book to market), CMA (Investment) and RMW (profitability).

Results also show that there is a highly negative correlation reported for the BTM-MOM variables. This is consistent with the literature (see Asness et al., 2013) who find for a sample of European Equity markets similar magnitudes of negative correlations for the BTM-MOM variables.

We next analyze several sub-samples that are determined by the previously discussed events: the 2002 Euro introduction, the 2007–2009 global financial crisis, and the 2010–2012 European sovereign risk crisis. We use for this purpose the framework specified in Eq. (2) We include for completeness in the analysis FF3 factors as well as the market factor. The optimal lag length has been selected on the basis of AIC, BIC and HIC criteria.33 The lag order chosen is that which would deliver the minimum value of the statistic among the three criteria.

The top panel of Table 5 presents Z-score parameter estimates. The second panel reports FF3 coefficient estimates while the third panel presents results with respect to the market factor. Finally, the last panel reports alpha coefficient estimates. Clustered robust standard errors are reported in parenthesis to take account of factor cross correlations.

Table 5.

Z-score analysis of excess returns for the full sample, 2002–2019, 2007–2019 and 2012–2019 subperiods.

	1991–2019		1991–2001	2002–2019	1991–2006	2007–2019	1991–2011	2012–2019
Z_BTM	0.0299∗∗∗	0.0320∗∗∗	0.0243∗∗∗	0.0416∗∗∗	0.0338∗∗∗	0.0368∗∗∗	0.0383∗∗∗	0.0192∗∗∗
	(0.001)	(0.001)	(0.002)	(0.001)	(0.001)	(0.001)	(0.001)	(0.001)
Z_PER	-0.0258∗∗∗	-0.0230∗∗∗	-0.0325∗∗∗	-0.0096∗∗∗	-0.0366∗∗∗	-0.0008	-0.0269∗∗∗	-0.0089∗∗∗
	(0.001)	(0.001)	(0.002)	(0.001)	(0.001)	(0.001)	(0.001)	(0.001)
Z_EVEBIT	-0.0021∗∗∗	-0.0047∗∗∗	-0.0130∗∗∗	-0.0108∗∗∗	-0.002	0.0121∗∗∗	0.0002	-0.0014
	(0.001)	(0.001)	(0.002)	(0.001)	(0.002)	(0.001)	(0.001)	(0.001)
Z_EVEBITDA	-0.0079∗∗∗	-0.0067∗∗∗	0.0331∗∗∗	-0.0211∗∗∗	0.0183∗∗∗	-0.0191∗∗∗	0.0094∗∗∗	-0.0063∗∗∗
	(0.001)	(0.001)	(0.002)	(0.001)	(0.002)	(0.001)	(0.001)	(0.001)
Z_GPA	0.0468∗∗∗	0.0478∗∗∗	0.0906∗∗∗	0.0310∗∗∗	0.0664∗∗∗	0.0299∗∗∗	0.0567∗∗∗	0.0200∗∗∗
	(0.001)	(0.001)	(0.003)	(0.001)	(0.002)	(0.001)	(0.002)	(0.001)
Z_ROC_Green	-0.0081∗∗∗	-0.0082∗∗∗	-0.0955∗∗∗	0.0117∗∗∗	-0.0287∗∗∗	0.0068∗∗∗	-0.0096∗∗∗	0.0025∗∗∗
	(0.001)	(0.001)	(0.004)	(0.000)	(0.002)	(0.000)	(0.001)	(0.000)
Z_ROC_Det	-0.0035∗∗∗	-0.0035∗∗∗	0.0348∗∗∗	-0.0063∗∗∗	0.0024	-0.0041∗∗∗	0.0113∗∗∗	-0.0037∗∗∗
	(0.001)	(0.001)	(0.004)	(0.000)	(0.002)	(0.000)	(0.001)	(0.000)
Z_MOM	0.0258∗∗∗	0.0267∗∗∗	0.0561∗∗∗	0.0061∗∗∗	0.0383∗∗∗	0.0155∗∗∗	0.0270∗∗∗	0.0291∗∗∗
	(0.001)	(0.001)	(0.002)	(0.001)	(0.001)	(0.000)	(0.001)	(0.000)
SMB		0.0122	0.417∗∗∗	0.0917∗∗∗	0.0573∗∗	0.230∗∗∗	0.0409∗	0.0909∗∗∗
		(0.015)	(0.025)	(0.017)	(0.018)	(0.018)	(0.017)	(0.023)
HML		-2.052∗∗∗	-3.247∗∗∗	-0.0598∗∗∗	-3.134∗∗∗	-0.150∗	-2.547∗∗∗	-0.147∗
		(0.107)	(0.147)	(0.005)	(0.139)	(0.065)	(0.124)	(0.062)
RMW		0.0530	1.508∗∗∗	-0.350∗∗∗	1.232∗∗∗	0.224∗∗∗	0.526∗∗∗	-0.137∗∗
		(0.058)	(0.085)	(0.069)	(0.093)	(0.053)	(0.070)	(0.048)
R_BMK-RF	1.110∗∗∗	1.120∗∗∗	1.173∗∗∗	1.052∗∗∗	1.144∗∗∗	1.055∗∗∗	1.141∗∗∗	1.024∗∗∗
	(0.002)	(0.003)	(0.005)	(0.002)	(0.004)	(0.002)	(0.003)	(0.002)
Alpha	0.0277∗∗∗	0.0316∗∗∗	0.0620∗∗∗	0.0203∗∗∗	0.0559∗∗∗	0.0151∗∗∗	0.0405∗∗∗	0.0172∗∗∗
	(0.000)	(0.000)	(0.001)	(0.001)	(0.001)	(0.000)	(0.001)	(0.000)

Clustered robust standard errors in parenthesis. ∗ Significant at 95%, ∗∗ significant at 99%, ∗∗∗ significant at 99.9%

This exhibit illustrates the impact of different factors on annualized monthly portfolio excess returns over different time windows. Portfolios are built iteratively for each feasible combination of metrics. Model coefficients were estimated using a GLS-Random effects estimator. Company accounting data and Absolute Returns underlying portfolio construction come from the FactSet database. Fama and French smb, hml and rmw factors obtained in Kenneth French website: https://mba.tuck.dartmouth.edu/pages/faculty/ken.french/data_library.html

Our findings for the whole sample can be summarized as follows: First, one standard deviation from sample average values for BTM, GPA, and Momentum Z-scores leads to improvements in returns, while the same variation in PER, EVEBIT and EVEBITDA ROC_Green and ROC_Det, delivers a negative effect on performance. Estimated parameters do therefore exhibit the expected sign in all cases but under the ROC_Green and ROC_Det measure.34 In what follows, the evolution of factor impact over time is analyzed.

Second, the impact of different factors on portfolio returns changes over time. Columns 3 and 4 of Table 5 show that, before the introduction of the Euro, one standard deviation in the EVEBITDA Z-score increases excess returns in 3.31%, while upper 5% portfolios exhibit a beta equal to 1.17. After the introduction of the Euro, the same increase in the EVEBITDA Z-score leads to a reduction in excess returns to 2.11% and a fall of the estimated beta to 1.05. The effect of EVEBITDA on portfolio profitability takes the expected sign within the second sample considered.

Third, we see that for some of the factor metrics analyzed the impact of factor Z-scores on portfolio profitability decreases over time. For instance, the GPA metric exhibits an important drop in coefficient estimates, which becomes evident when comparing estimates for the 1991–2001 and 2002–2019 samples (see columns 4 and 5 of Table 5). This is consistent with the drop in performance of GPA based strategies reported in Table 2. The second raw of Table 5 also shows that the impact of the PER based strategies on portfolio profitability decreases over time. The observed decreasing factor premiums are in line with the results documented in Figure 3 under the analysis of recursive alpha parameters and support the existence of factor crowding in the aftermath of the Euro introduction. Results can be evaluated against a simple regression with the market risk premium and the 3 FF factors (see Exhibit 9 in Appendix D). While coefficients for the 3 FF factors are very close to those reported in the main text, we can see that the lack of consideration of individual Z-scores delivers marginally larger (and significant) alphas.

Fourth, reported results for different sub-samples also demonstrate that there is a change in the sign of the reported ROC_Det and ROC_Green coefficients. While the effect of ROC_Green on profitability becomes positive for later sub-samples, the impact of ROC_Det becomes negative. Given that the only difference between both metrics is defined by the size of intangibles and that the coefficients of the two metrics are estimated jointly, reported results can only be interpreted by analyzing the evolution of intangibles over our sample period.

Exhibit 1 in Appendix B presents the time series plot of total capital and total tangible capital, respectively. Overall, total capital increased by more than 9 over our whole sample period fold (from 3,011.55 to 27,297 million € in 2019), while tangible capital grew at a relatively slower rate (2,826 million € to 19,499 million €). This droves the ratio of intangibles over total capital from 6% to 30%. Total capital was raised fourfold before 2007 and slightly decreased during 2008. Growth was recovered in the aftermath of the Global Financial Crisis and the gap between total capital and tangible capital widened, reaching its maximum in 2019. The documented growth of intangibles jointly considered with our panel regression results suggests that intangibles become an important determinant of portfolio profitability. A further analysis, which can be provided upon request, shows that the growth of intangibles can partly be explained by a substantial rise in the weight of technological firms during our sample period from 9% to 23% with the value of their reported market cap rising from 15% to 27%.

The overall conclusion of this section is that the influence of different factor metrics on portfolio performance significantly evolves, with some factor metrics changing coefficient size and others also changing coefficient sign and statistical significance. Reported results are consistent with those in Table 3, which suggests that the emergence of the common currency played a determinant role in portfolio profitability and risk, which was shaped under a common regulatory framework. Our findings, therefore, offer relevant implications for portfolio management.

4. Conclusions

In this paper, the authors analyze whether systematic active portfolio management strategies based on factor investing criteria have been profitable over the past 28 years in Europe. The purpose is to quantify the extent to which long term factor strategies remain profitable over time. This question is important as there is a large strand of recent literature that documents vanishing factor risk premia (see Arnott et al., 2019). In doing this, we also address whether the currently observed decrease in active management profitability can be explained by the decay of the performance in traditional management practices.

We propose a factor-based approach to long-term investing which involves a simultaneous combination of value, profitability and momentum metrics. Applied to a long span of European equity data, we show that the proposed strategies beat the benchmark models commonly used in the literature. Different metrics are used to measure the proposed factors.

Reported results demonstrate that risk-adjusted returns achieved by individual factors can be improved by the combination of factors into single portfolios. Top performing mixed portfolios, composed of two different factors (value + profitability/momentum), yield significant and risk-adjusted returns that outperform similar strategies in the literature (see Novy-Marx, 2013a, Novy-Marx, 2013b). We also show how the investor can iteratively combine value, profitability and momentum factors in top quintile value portfolios to increasingly improve the risk-adjusted returns of those portfolios. A series of spanning tests demonstrate that mixed and iterative strategies generate positive alpha relative to the pure portfolio benchmarks. Those portfolios that incorporate the three factors iteratively (value first, profitability second and momentum third) can significantly outperform mixed combinations. We, therefore, demonstrate the ordered structure of the filtering process contributes to portfolio management.

To our knowledge, this is the first paper that uses European corporate data to analyze portfolio performance using a combination of three factors (defined by different metrics) following both iterative and mixed approaches. Moreover, our paper also contributes by showing via estimation of Z-score regressions that factor performance changes over time. While some metrics such as momentum gain importance over our sample period reported factor sensitivities for most factors considered decrease but remain significant over time. While we document that on average there is a diminishing alpha across our sample period, our findings suggest factor mispricing is positive across Europe for the samples considered.

Average return and performance measures are consistent with those reported in the literature. The three drawdowns documented over our sample period suggest that business cycle characteristics play a role in portfolio return determination.

Declarations

Author contribution statement

All authors listed have significantly contributed to the development and the writing of this article.

Funding statement

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Data availability statement

Data will be made available on request.

Declaration of interests statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.

Appendix A. Supplementary data

The following is the supplementary data related to this article: