Abstract
The theoretical (Freebase, Cationic species) and experimental investigations on the molecular structural, spectroscopic characterization, and electronic properties of N2M5MB are reported. The most stable structure of the N2M5MB was analysed by employing Density Functional Theory (DFT) at different functional such as B3LYP, PBEPBE, TPSSTPSS and IEF-PCM (Freebase) and Cationic (B3LYP, IEF-PCM)/ 6–311++G (d,p) basis set level. The Potential Energy Scan (PES) analysis has been employed to investigate the conformational preference of the title molecule. The optimized molecular geometry, vibrational assignments (FT-IR, FT-Raman) of wavenumbers have been performed for freebase, cationic species (Gas, PCM) for the individual modes of vibration. The experimental UV-Vis absorption spectrum was obtained and compared with the simulated (Freebase, Cationic species) Time-Dependent (TD-DFT-M062X) method. The FMO's, electron-hole distributions, HOMA, FLU, Hirshfeld surface analysis, Electrostatic potential surface (ESP), Fukui functions, and topological parameters were discussed. Molecular docking studies were performed for the N2M5MB (ligand) into the active site of targeted proteins (1H22, 4DTL, 5OV9) which belong to AChE inhibitors with the minimum binding energy was detected.
Keywords: DFT, Hirshfield surface analysis, Topology, Molecular docking
DFT; Hirshfield surface analysis; Topology; Molecular docking.
1. Introduction
Benzamide pharmacophores are essential bioactivities in drug discovery methods and have pharmacological and biological applications. Benzamide and its derivatives involved as antimicrobial, analgesic anticancer, carbonic anhydrase inhibitory and a cholinesterase inhibitor [1,2,3]. According to the National Institute of Aging, Alzheimer's disease (AD) is the most common cause of death in the United States of America [4]. The neuropsychiatric symptoms of diseases such as AD have developed health problems predominantly among aging people and categorized by a low concentration of acetylcholine (ACh) in the hippocampus (region of the brain that is associated primarily with memory) and cortex [5]. Further, Alzheimer's diseases (AD) are the loss of cholinergic neurons and a decreasing quantity of neurotransmitter acetylcholine (ACh) in synapses (central role in the processes of memory formation). Cholinesterase (an important enzyme involved in the function of the nervous system) has a crucial part in the process of Alzheimer's disease that regulates synaptic levels of ACh [6]. Besides, the main category of cholinesterase is AChE (acetylcholinesterase) inhibitor has a decisive target for AD to surge the acetylcholine (ACh) level in the brain. Further, Kratky et al [7] reported the benzamide derivatives with significant activity against AChE inhibitors and Malose J. Mphahlele et al [8] added that a combination of sulphoamide derivative exhibit inhibitory properties against different types of enzymes including AChE inhibitors. Also, koksal et al [9] reported a sulphonamide derivative exhibit biological effects and also used for symptomatic treatment of AD. Based on the above facts and continuation of the investigation on sulphonylbenzamides derivatives shows an interesting sign for AD drug target. Thus, the header compound was envisaged to further exploit in the development of AChE inhibitors.
According to the detailed review of the available literature, it is pointed out that no theoretical (DFT) of freebase structure and experimental work was reported on the N-[2-(diethylamino) ethyl]-2-methoxy-5-methylsulfonyl benzamide (N2M5MB). Therefore, in the present investigation, spectroscopic measurements were carried out for and compared with the simulated (Freebase and Cationic species) interpretation employing DFT computations as B3LYP/6–311++G (d,p) basis set. Further, Hirshfield surface and two-dimensional finger plots were analyzed to elucidate the complete exploration of the intermolecular interactions in N2M5MB. The molecular orbitals (HOMO and LUMO), Harmonic Oscillator Model of Aromaticity index (HOMA), and fluctuation index (FLU) indices were obtained. Electron excitation, QTAIM, ELF, LOL, and IGM analyses were obtained using a Multiwfn 3.7 software program. Electrostatic Potential (ESP) map and Fukui function descriptors were discussed to attain information about the chemical and site selectivity of N2M5MB. Molecular docking analyses were executed to confirm the inhibitory nature of N2M5MB (as a ligand) with AChE inhibitors as targeted protein receptors.
2. Experimental details
The header compound “N-[2-(diethylamino)ethyl]-2-methoxy-5-methylsulfonyl benzamide” (Freebase structure) was procured from Toronto research chemicals Ltd. The Fourier Transform-Infrared spectrum of the N2M5MB with a spectral resolution of 1.0 cm−1 was observed in the range of 4000-400 cm−1 equipped with a Potassium bromide (KBr) pellet technique. The BRUKER RFS 27: MultiRAM using Nd: YAG (1064 nm) as laser source was used to record the FT-Raman spectrum in the scan range of 4000-100 cm−1 with a resolution of 0.8–4 cm−1. Ultra-Violet absorption (UV-Vis) spectrum of N2M5MB (DMSO as solvent) was studied in the range 200–700 nm using the PerkinElmer LAMBDA 950 UV-Visible spectrometer instrument. The Fourier Transform-Infra-Red (FT-IR), FT-Raman, and Ultraviolet (UV-Vis's) absorption spectral measurements were achieved at IIT, Chennai, India.
3. Computational details
The optimized molecular geometrical parameters were implemented in the gas phase (Freebase, Cationic species) using the Gaussian 09W program using a set of approximations using DFT/ B3LYP (Becke-3-LYP)/PBEPBE (Perdew-Burke-Ernzerhof)/TPSSTPSS (Tao, Perdew, Staroverov, and Scuseria) functionals with 6–311++G (d,p) basis set [10,11,12,13,14]. The structural conformational behavior was employed using Potential Energy Scan (PES) studies by the DFT approach. The potential energy distribution (PED) and individual vibrational assignments (theoretical approach) were calculated using the vibrational energy distribution analysis VEDA 4 program for freebase and cationic species (N6–H47) for both Gas (B3LYP) and IEF-PCM (Integral equation-formalism polarizable continuum model) of N2M5MB [15]. The unique feature of the VEDA 4 package is a prospect for automatic optimization of PED contributions of the N2M5MB. To compute the theoretical UV-Vis spectra, electron transition energies, and oscillator strength have been achieved by M06-2X functional using DMSO as a solvent with 6–311++G (d,p) basis set in Time-Dependent density functional theory (TD-DFT) approach [16,17,18,19,20]. The Hirshfeld surface analysis was achieved to quantify and envisage the closed intermolecular atomic contacts and energy frameworks were determined using the Crystal Explorer 17.5 (intended to visualization of interactions in crystal structures) program [21]. Besides the investigation of reactive sites in electrostatic potential (EPS) map was plotted using a molecular visualization program VMD 1.9.1 [22]. The topology analyses such as QTAIM, ELF, LOL, and IGM were obtained from the output file of B3LYP/ 6–311++G (d,p) basis set using the Multiwfn – a wave functional analyser [23]. Molecular docking process (ligand-protein interactions) using AutoDock Suite software 4.2.1 [24] graphical user interface. In AutoDock 4.0 software, the polar hydrogens were added to the selected protein, and atomic charges were calculated by the Kollman method and the Lamarckian genetic Algorithm (LGA) was employed using for the docking process.
4. Result and discussion
4.1. Potential Energy Surface (PES) and Molecular geometry
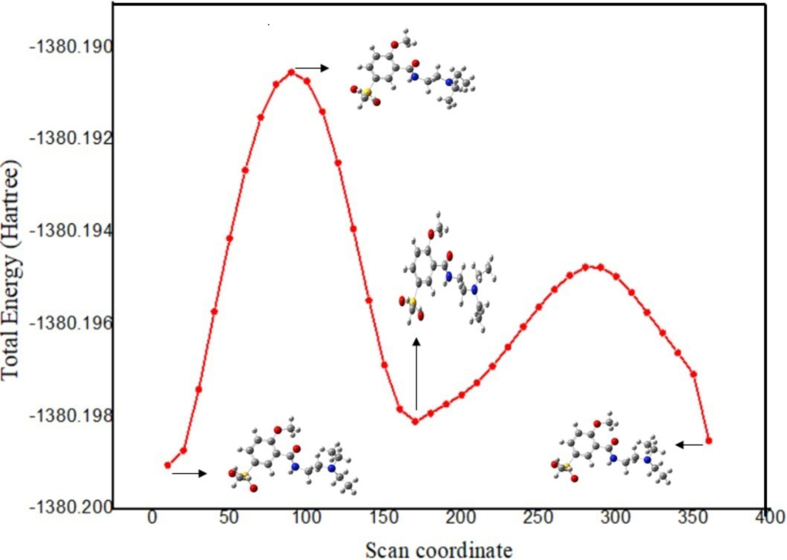
The minimum energy conformers for N2M5MB on the Potential Energy Surface (PES) scan are shown in Figure 1 at a free base with basis set B3LYP/6–311++G (d,p) level. The determination of PES was obtained at the selected torsion angle of C15–N7–C9–C8. In this analysis, all the geometric parameters were equally relaxed whereas the selected angle C15–N7–C9–C8 was rotated in the range of 0°–360° at every step of 10° around the bond respectively. The most minimum (stable configuration) conformer is shown in Figure 1. The parameters such as bond lengths and bond angles were calculated using the afore-mentioned basis set level and the optimized geometrical structure of the N2M5MB with the atom numbering scheme freebase and cationic species were represented in Figures 2(a) and 2(b). Houttemane et al. [25] reported that the experimental XRD details for N2M5MB belong to the orthorhombic crystal system as Pbca space lattice with lattice parameter values as a = 25.380 Å, b = 12.620 Å, c = 10.470 Å. The theoretical (B3LYP/PBEPBE/TPSSTPSS) parameters (bond length, bond angle) for the free base and cationic (N6–H47) structures show a good correlation with the values obtained by the experimental method and are presented in Table 1a and 1b. The benzene in a regular hexagon with bond lengths for C–C in the range of 1.382–1.414, 1.390–1.425, 1.389-1.423,1.395-1.380,1.433-1.380,1.462-1.382 Å well agreed with the experimental values for N2M5MB. Lukose et al. [26] stated the C=O bond length value as 1.2486 Å. In this study, the bond length values of C15–O3 as 1.224–1.311 (freebase/ cationic species) and 1.230 for the experimental and it agrees well with each other. Houttemane et al. [25] further reported the bond lengths in the ranges of S–O = 1.441Å, S–C = 1.753–1.760 Å, C–C = 1.506–1.386 Å, C–N = 1.469–1.324 Å, the equivalent values observed in the present case are S1–O4 = 1.488–1.456 Å, S1–O5 = 1.488–1.456 Å, S1–C21 = 1.822–1.778 Å, S1–C16 = 1.801–1.746 Å, C–C = 1.537–1.382, 1.541–1.390, 1.542-1.389,1.522-1.395,1.535-1.402,1.540-1.414 Å, C–N = 1.469–1.363, 1.471–1.372, 1.477-1.372,1.462-1.390, 1.489–1.394, 1.522–1.418 Å respectively. For N2M5MB, the simulated bond angles such as O4–S1–C16 = 108.9°–107.7°, O4–S1–C21 = 106.9°–107.2°, O5–S1–C16 = 107.5°–109.6°, S1–C16–C19 = 120.2°–118.9°, C18–O2–C22 = 123.1–115.2°, C8–N6–C11 = 110.5°–113.0° and N6–C8–C9 = 110.3°–112.8° were in close agreement with experimental (XRD) values. At the S1 position, the bond angle values O4–S1–C16, O4–S1–C21, O5–S1–C16, O5–S1–C21, C16–S1–C21 between the ranges of 108.9°–107.7°, 106.9°–107.4°,109.6°–107.5° and the bond angle (O4–S1–O5) values are 121.7°–117.5° (freebase and cationic species) increased because of oxygen atoms substitution in the sulfonyl region of the N2M5MB respectively [27]. Besides, for freebase, the RMSD value for bond length ranges from 0.029 to 0.013, and for cationic species, the RMSD values range from 0.019 to 0.011, respectively. The free base presents the bond angles between 0.505 to 0.635, while for cationic species the RMSD bond angle values from 0.645 to 0.648 respectively. From Table-1b, the RMSD bond angle values of freebase in solution (DMSO) show the lowest value when compared to corresponding cationic (-NH) species. As a result, the optimized parameters (bond lengths, bond angles) are nearly similar to crystallographic literature values but the values are much closer to the parameters calculated by the freebase (Gas) simulated method.
Figure 1.
Potential energy surface (PES) curve of N2M5MB.
Figure 2.
Optimised molecular geometry structure with the atom numbering (a) freebase, (b) cationic species of N2M5MB.
Table 1a.
Optimized geometrical parameter bond length (Å) for N2M5MB with experimental (∗), theoretical Free base (B3LYP, PBEPE, TPSSTPSS, IEF-PCM) and Cationic (B3LYP, IEF-PCM) with 6–311++G (d,p) basis set approach.
| Bond length (Å) | |||||||
|---|---|---|---|---|---|---|---|
| Bonds | Freebase |
Cationic |
Exp∗ | ||||
| B3LYP | PBEPBE | TPSSTPSS | PCM | B3LYP | PCM | ||
| S1–O4 | 1.468 | 1.485 | 1.483 | 1.456 | 1.456 | 1.488 | 1.441 |
| S1–O5 | 1.469 | 1.486 | 1.484 | 1.456 | 1.456 | 1.488 | 1.441 |
| S1–C16 | 1.796 | 1.801 | 1.800 | 1.746 | 1.746 | 1.781 | 1.753 |
| S1–C21 | 1.810 | 1.818 | 1.822 | 1.778 | 1.778 | 1.806 | 1.760 |
| O2–C18 | 1.350 | 1.357 | 1.359 | 1.363 | 1.363 | 1.386 | 1.350 |
| O2–C22 | 1.433 | 1.435 | 1.442 | 1.426 | 1.426 | 1.434 | 1.437 |
| O3–C15 | 1.224 | 1.240 | 1.24 | 1.228 | 1.228 | 1.266 | 1.230 |
| N6–C8 | 1.462 | 1.465 | 1.471 | 1.462 | 1.462 | 1.518 | 1.461 |
| N6–C10 | 1.469 | 1.471 | 1.477 | 1.462 | 1.462 | 1.522 | 1.465 |
| N6–C11 | 1.469 | 1.472 | 1.478 | 1.463 | 1.463 | 1.522 | 1.469 |
| N7–C9 | 1.461 | 1.459 | 1.466 | 1.438 | 1.438 | 1.448 | 1.461 |
| N7–C15 | 1.363 | 1.372 | 1.372 | 1.39 | 1.39 | 1.418 | 1.324 |
| N7–H31 | 1.008 | 1.017 | 1.014 | 1.015 | 1.015 | 1.012 | |
| C8–C9 | 1.537 | 1.541 | 1.542 | 1.522 | 1.522 | 1.540 | 1.506 |
| C8–H23 | 1.105 | 1.116 | 1.109 | 1.098 | 1.098 | 1.092 | |
| C8–H24 | 1.091 | 1.102 | 1.096 | 1.095 | 1.095 | 1.088 | |
| C9–H25 | 1.090 | 1.101 | 1.094 | 1.096 | 1.096 | 1.094 | |
| C9–H26 | 1.092 | 1.102 | 1.097 | 1.093 | 1.093 | 1.094 | |
| C10–C12 | 1.528 | 1.53 | 1.534 | 1.519 | 1.519 | 1.522 | 1.502 |
| C10–H27 | 1.093 | 1.104 | 1.099 | 1.093 | 1.093 | 1.090 | |
| C10–H28 | 1.106 | 1.117 | 1.110 | 1.097 | 1.097 | 1.092 | |
| C11–C13 | 1.528 | 1.53 | 1.534 | 1.519 | 1.519 | 1.522 | 1.505 |
| C11–H29 | 1.092 | 1.103 | 1.097 | 1.095 | 1.095 | 1.090 | |
| C11–H30 | 1.106 | 1.116 | 1.110 | 1.097 | 1.097 | 1.092 | |
| C12–H32 | 1.094 | 1.102 | 1.098 | 1.096 | 1.096 | 1.093 | |
| C12–H33 | 1.093 | 1.101 | 1.096 | 1.096 | 1.096 | 1.095 | |
| C12–H34 | 1.093 | 1.102 | 1.097 | 1.094 | 1.094 | 1.093 | |
| C13–H35 | 1.094 | 1.102 | 1.098 | 1.096 | 1.096 | 1.093 | |
| C13–H36 | 1.093 | 1.101 | 1.096 | 1.095 | 1.095 | 1.095 | |
| C13–H37 | 1.093 | 1.103 | 1.097 | 1.094 | 1.094 | 1.093 | |
| C14–C15 | 1.509 | 1.510 | 1.509 | 1.486 | 1.486 | 1.441 | 1.514 |
| C14–C17 | 1.402 | 1.411 | 1.411 | 1.381 | 1.381 | 1.436 | 1.384 |
| C14–C18 | 1.414 | 1.425 | 1.423 | 1.380 | 1.38 | 1.462 | 1.378 |
| C16–C17 | 1.386 | 1.395 | 1.394 | 1.395 | 1.395 | 1.382 | 1.386 |
| C16–C19 | 1.396 | 1.405 | 1.405 | 1.395 | 1.395 | 1.419 | 1.396 |
| C17–H38 | 1.083 | 1.094 | 1.088 | 1.085 | 1.085 | 1.083 | |
| C18–C20 | 1.407 | 1.417 | 1.415 | 1.395 | 1.395 | 1.383 | 1.411 |
| C19–C20 | 1.382 | 1.390 | 1.389 | 1.395 | 1.395 | 1.414 | 1.382 |
| C 19-H39 | 1.083 | 1.093 | 1.088 | 1.086 | 1.086 | 1.083 | |
| C20–H40 | 1.083 | 1.093 | 1.087 | 1.087 | 1.087 | 1.087 | |
| C21–H41 | 1.089 | 1.099 | 1.093 | 1.092 | 1.092 | 1.091 | |
| C21–H42 | 1.089 | 1.098 | 1.093 | 1.092 | 1.092 | 1.09 | |
| C21–H43 | 1.090 | 1.100 | 1.094 | 1.092 | 1.092 | 1.092 | |
| C22–H44 | 1.089 | 1.100 | 1.093 | 1.095 | 1.095 | 1.093 | |
| C22–H45 | 1.089 | 1.099 | 1.093 | 1.093 | 1.093 | 1.092 | |
| C22–H46 | 1.094 | 1.104 | 1.098 | 1.095 | 1.095 | 1.098 | |
| N6–H47 | - | - | - | 1.000 | 1.026 | ||
| RMSDb | 0.022 | 0.028 | 0.029 | 0.013 | 0.019 | 0.011 | |
Table 1b.
Optimized geometrical parameter bond angle (°) for N2M5MB with experimental (∗), theoretical Free base (B3LYP, PBEPE, TPSSTPSS, IEF-PCM) and Cationic (B3LYP, IEF-PCM) with 6–311++G (d,p) basis set approach.
| Bond Angle (°) | |||||||
|---|---|---|---|---|---|---|---|
| Bonds | Freebase |
Cationic |
Expa | ||||
| B3LYP | PBEPBE | TPSSTPSS | PCM | B3LYP | PCM | ||
| (O4–S1–O5) | 121.0 | 121.6 | 121.7 | 119.8 | 119.8 | 117.5 | |
| (O4–S1–C16) | 107.9 | 107.7 | 107.7 | 107.9 | 107.9 | 108.9 | 108.0 |
| (O4–S1–C21) | 107.2 | 107.4 | 107.3 | 107.9 | 107.9 | 106.9 | 108.2 |
| (O5–S1–C16) | 107.7 | 107.6 | 107.5 | 108.9 | 108.9 | 109.6 | 109.2 |
| (O5–S1–C21) | 107.2 | 107.3 | 107.2 | 106.9 | 106.9 | 107.2 | 108.2 |
| (C16–S1–C21) | 104.8 | 103.8 | 104 | 104.4 | 104.4 | 106.1 | 104.9 |
| (S1–C16–C17) | 119.4 | 119.3 | 119.2 | 120 | 120 | 118.2 | 119.6 |
| (S1–C16–C19) | 120.2 | 120.2 | 120.2 | 120 | 120 | 118.9 | 120.0 |
| (S1–C21–H41) | 109.0 | 109.1 | 109 | 109 | 109 | 108.7 | |
| (S1–C21–H42) | 109.0 | 109.1 | 109 | 109 | 109 | 108.5 | |
| (S1–C21–H43) | 105.9 | 106.2 | 106.1 | 108.1 | 108.1 | 106.7 | |
| (C18–O2–C22) | 123.1 | 121.9 | 122 | 117 | 117 | 115.2 | |
| (O2–C18–C14) | 127.3 | 127.6 | 127.6 | 121.9 | 121.9 | 122.0 | 122.4 |
| (O2–C18–C20) | 113.2 | 112.9 | 112.8 | 119.1 | 119.1 | 116.3 | |
| (O2–C22–H44) | 110.9 | 111.2 | 110.8 | 110.9 | 110.9 | 111.1 | |
| (O2–C22–H45) | 105.0 | 105.1 | 104.6 | 108.2 | 108.2 | 106.4 | |
| (O2–C22–H46) | 110.7 | 110.9 | 110.5 | 110.4 | 110.4 | 110.3 | |
| (O3–C15–N7) | 122.7 | 122.6 | 122.4 | 124.6 | 124.6 | 117.6 | 122.2 |
| (O3–C15–C14) | 122.0 | 122.7 | 122.8 | 119.2 | 119.2 | 125.8 | 122.4 |
| (C8–N6–C10) | 112.0 | 111.7 | 111.4 | 110.5 | 110.5 | 111.8 | 113.3 |
| (C8–N6–C11) | 112.6 | 112.2 | 112.1 | 110.5 | 110.5 | 111.8 | 113.0 |
| (N6–C8–C9) | 111.5 | 111.2 | 110.6 | 110.3 | 110.3 | 112.8 | 112.4 |
| (N6–C8–H23) | 111.7 | 112.4 | 112.3 | 111.5 | 111.5 | 106.5 | |
| (N6–C8–H24) | 109.4 | 109.4 | 109.2 | 111.3 | 111.3 | 107.6 | |
| (C10–N6–C11) | 112.6 | 112.5 | 112.3 | 110.5 | 110.5 | 111.5 | 112.4 |
| (N6–C10–C12) | 113.5 | 113.1 | 112.7 | 111.2 | 111.2 | 112.8 | 113.6 |
| (N6–C10–H27) | 107.8 | 107.6 | 107.4 | 111.4 | 111.4 | 106.8 | |
| (N6–C10–H28) | 110.8 | 111.5 | 111.4 | 112.1 | 112.1 | 106 | |
| (N6–C11–C13) | 113.1 | 112.6 | 112.2 | 111.2 | 111.2 | 106.9 | 112.4 |
| (N6–C11–H29) | 107.8 | 107.7 | 107.6 | 110.6 | 110.6 | 112.8 | |
| (N6–C11–H30) | 110.8 | 111.4 | 111.4 | 112 | 112 | 106.6 | |
| (C9–N7–C15) | 122.7 | 121.6 | 121.7 | 122.7 | 122.7 | 106 | 121.7 |
| (C9–N7–H31) | 118.9 | 119.5 | 119.3 | 116.7 | 116.7 | 119.7 | |
| (N7–C9–C8) | 112.9 | 112.8 | 112.7 | 111.2 | 111.2 | 114.6 | 112.4 |
| (N7–C9–H25) | 108.4 | 108.2 | 108 | 109.2 | 109.2 | 111.9 | |
| (N7–C9–H26) | 107.7 | 108.1 | 107.8 | 103.7 | 103.7 | 108.4 | |
| (C15–N7–H31) | 118.3 | 118.5 | 118.6 | 120.5 | 120.5 | 108 | |
| (N7–C15–C14) | 115.2 | 114.6 | 114.7 | 116.1 | 116.1 | 117.1 | 113.0 |
| (C9–C8–H23) | 109.8 | 110 | 110.1 | 110.1 | 110.1 | 116.6 | |
| (C9–C8–H24) | 107.5 | 106.8 | 107.3 | 106.3 | 106.3 | 111.9 | |
| (C8–C9–H25) | 108.9 | 108.4 | 108.7 | 111 | 111 | 108.5 | |
| (C8–C9–H26) | 110.9 | 111.1 | 111.1 | 112.9 | 112.9 | 109.1 | |
| (H23–C8–H24) | 106.8 | 106.7 | 107.2 | 107.1 | 107.1 | 111.1 | |
| (H25–C9–H26) | 108.0 | 108 | 108.4 | 108.5 | 108.5 | 109.4 | |
| (C12–C10–H27) | 108.2 | 108.3 | 108.5 | 104.2 | 104.2 | 108.2 | |
| (C12–C10–H28) | 110.1 | 110.2 | 110.3 | 109.9 | 109.9 | 110.4 | |
| (C10–C12–H32) | 110.1 | 110.4 | 110.2 | 109.6 | 109.6 | 112.3 | |
| (C10–C12–H33) | 110.4 | 110.3 | 110.2 | 111.8 | 111.8 | 108.2 | |
| (C10–C12–H34) | 112.2 | 112.2 | 112 | 112.5 | 112.5 | 111.4 | |
| (H27–C10–H28) | 106.0 | 105.8 | 106.3 | 107.7 | 107.7 | 112.9 | |
| (C13–C11–H29) | 108.5 | 108.6 | 108.7 | 105.7 | 105.7 | 108.3 | |
| (C13–C11–H30) | 110.1 | 110.3 | 110.4 | 109.6 | 109.6 | 110.4 | |
| (C11–C13–H35) | 110.1 | 110.5 | 110.3 | 109.4 | 109.4 | 112.3 | |
| (C11–C13–H36) | 110.4 | 110.3 | 110.1 | 111.9 | 111.9 | 108.1 | |
| (C11–C13–H37) | 112.3 | 112.2 | 112 | 112.6 | 112.6 | 111.4 | |
| (H29–C11–H30) | 106.2 | 106 | 106.4 | 107.6 | 107.6 | 112.8 | |
| (H32–C12–H33) | 108.6 | 108.7 | 108.8 | 107.3 | 107.3 | 108.4 | |
| (H32–C12–H34) | 107.4 | 107.3 | 107.5 | 106.4 | 106.4 | 107.7 | |
| (H33–C12–H34) | 107.9 | 107.8 | 108 | 109 | 109 | 107.6 | |
| (H35–C13–H36) | 108.6 | 108.7 | 108.8 | 107.2 | 107.2 | 108.9 | |
| (H35–C13–H37) | 107.6 | 107.5 | 107.7 | 106.3 | 106.3 | 107.7 | |
| (H36–C13–H37) | 107.8 | 107.6 | 107.8 | 109.1 | 109.1 | 107.7 | |
| (C15–C14–C17) | 116.9 | 116.9 | 116.9 | 118.1 | 118.1 | 106.8 | |
| (C15–C14–C18) | 124.5 | 124.7 | 124.7 | 119.8 | 119.8 | 106 | 126.3 |
| (C17–C14–C18) | 118.2 | 118 | 118 | 122.1 | 122.1 | 106.9 | 118.2 |
| (C14–C17–C16) | 121.4 | 121.5 | 121.5 | 118.9 | 118.9 | 112.8 | 121.6 |
| (C14–C17–H38) | 119.6 | 119.5 | 119.5 | 122 | 122 | 106.6 | |
| (C14–C18–C20) | 119.4 | 119.5 | 119.6 | 118.9 | 118.9 | 106 | 120.0 |
| (C17–C16–C19) | 120.4 | 120.5 | 120.6 | 120 | 120 | 119.7 | 120.4 |
| (C16–C17–H38) | 119.0 | 119.0 | 119.0 | 119 | 119 | 114.6 | |
| (C16–C19–C20) | 118.9 | 118.9 | 118.9 | 120 | 120 | 111.9 | 118.2 |
| (C16–C19–H39) | 120.2 | 120.0 | 120.1 | 121.3 | 121.3 | 108.4 | |
| (C18–C20–C19) | 121.5 | 121.6 | 121.5 | 120 | 120 | 108 | |
| (C18–C20–H40) | 117.4 | 117.2 | 117.3 | 120.4 | 120.4 | 117.1 | |
| (C20–C19–H39) | 120.8 | 121.1 | 121.0 | 118.7 | 118.7 | 116.6 | |
| (C19–C20–H40) | 121.0 | 121.2 | 121.2 | 119.6 | 119.6 | 111.9 | |
| (H41–C21–H42) | 111.4 | 111.2 | 111.3 | 110.9 | 110.9 | 108.5 | |
| (H41–C21–H43) | 110.6 | 110.5 | 110.6 | 109.9 | 109.9 | 109.1 | |
| (H42–C21–H43) | 110.7 | 110.5 | 110.7 | 109.9 | 109.9 | 111.1 | |
| (H44–C22–H45) | 110.8 | 111 | 111.4 | 108.6 | 108.6 | 109.4 | |
| (H44–C22–H46) | 110.0 | 109.2 | 109.8 | 110 | 110 | 108.2 | |
| (H45–C22–H46) | 109.3 | 109.4 | 109.7 | 108.6 | 108.6 | 110.4 | |
| (C8–N6–H47) | - | - | - | 108.5 | 112.3 | ||
| (C10–N6–H47) | - | - | - | 108.5 | |||
| (C11–N6–H47) | - | - | - | 108.5 | |||
| RMSDb | 0.603 | 0.561 | 0.635 | 0.505 | 0.645 | 0.648 | |
4.2. Vibrational assignments
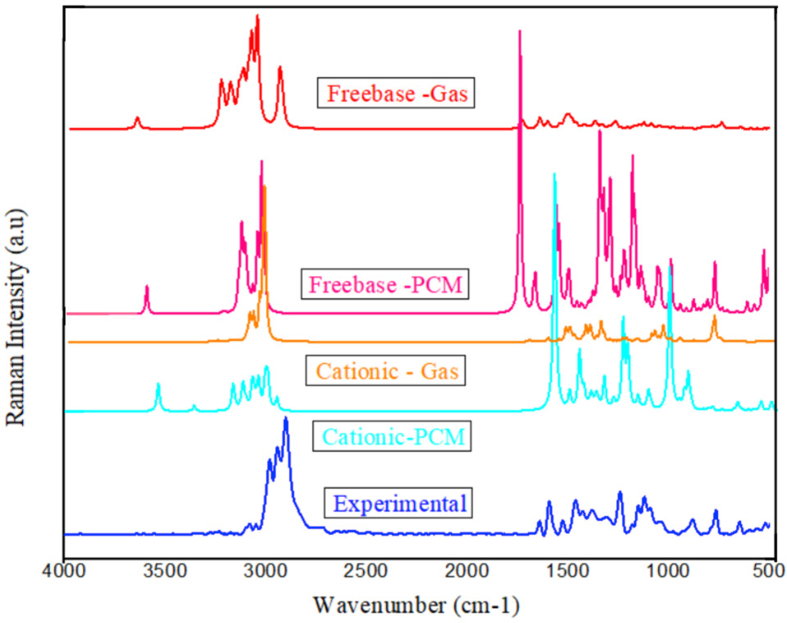
The N2M5MB consists of 46 atoms with C1 point group symmetry give rise to 132 (freebase) and 135 (cationic) normal modes of vibrations. The recorded and simulated (freebase and cationic) FT-IR and FT-Raman spectra of N2M5MB were depicted in Figures 3 and 4 respectively. The detailed assignments (freebase and cationic media) obtained through PED values using VEDA software are tabulated in Table S1. The theoretical vibrational assignments (freebase, cationic species) are scaled with a scaling factor of 0.961 [28], to compensate for the deviations arising from the measured values due to vibrational anharmonicity effects being neglected. The brief discussions of some assignments are presented below.
Figure 3.
Compared B3LYP/6–311++G (d,p) (Freebase, Cationic) and Experimental FTIR spectrum of N2M5MB.
Figure 4.
Compared B3LYP/6–311++G (d,p) (theoretical) and Experimental FT-Raman spectrum of N2M5MB.
4.2.1. N–H vibrations
The heteroaromatic molecules exhibit N–H vibrations in the array of 3500-3000 cm−1 [29]. In this study, the N7–H31 in freebase structure (B3LYP(Gas) and IEF-PCM) phases with symmetric stretching were observed at 3496, 3446, 3437, and 3463 cm−1 respectively. The corresponding experimental wavenumber was observed at 3390 cm−1 in the FT-IR spectra. The N6–H47 with stretching modes were noted at 3437, 3463 cm−1 from the cationic phases (B3LYP(Gas) and IEF-PCM). In general, the in-plane and out of plane N–H deformations are stated in the region of 1444-1114 cm−1 and 693-550 cm−1 respectively. For N2M5MB, the computed N–H in-plane (scissoring) vibrations in free base media (Gas and IEF-PCM) phases such as 1483 (1495),1370,1307 (1320),1244(1250),1113, 976 cm−1, 1338 cm−1 in cationic (IEF-PCM) mode and their equivalent experimental values were matches with each other. As K. Karrouchi et al. reported the out of plane N–H vibrations scaled between 734 and 501 cm−1, here in header compound the simulated out of plane (wagging and twisting) vibrations were assigned as 820, 776, and 777 cm−1 in cationic (IEF-PCM) phase, 645 cm−1 respectively [29]. These vibrations were found to be analogous with the closely related compound [30] and agreeable with the experimental wavenumbers respectively.
4.2.2. Methyl vibrations
Socrates [31] proposed that C–H bending vibrations detected around 1283-909 cm−1. Here, in the header compound, the scaled wavenumbers in freebase phase (Gas, IEF-PCM) modes such as 1370, 1244,1250 cm−1 (rocking modes) achieved a well-suited correlation with the experimental FT-IR and FT-Raman values. The in plane bending C–H vibrations noticed at 1463 and 1113 cm−1 with the equivalent experimental wavenumbers [30] were noted. In the current study, the out of plane C–H deformations has occurred in the span of 1100-600 cm−1. The scaled wavenumbers in freebase and cationic structures were noticed at 760,777 and 570 cm−1. Corresponding experimental peaks were observed as FT-Raman (766 cm−1) and FT-IR (560 cm−1) respectively.
4.2.3. Methylene and methyne vibrations
The methylene (-CH2) asymmetric stretching vibrations are generally noticed in the vicinity of 3000-2900 cm−1. In title compound, the simulated CH2 asymmetric vibrations in freebase and cationic media such as 3061,3055,3063,3065, 3042,3011,3059, 2956,2973,2997 and 2947,2942,2984 cm−1 and their corresponding experimental peaks were observed at 2996 cm−1 (FT-IR) and 3070, 3049,2955,2948 cm−1 (FT-Raman) respectively. The methylene (-CH2) scissoring in plane H–C–H modes are expected in the array of 1445 ± 35 cm−1 [32,33]. The computed freebase and cationic modes of frequency in H–C–H scissoring mode has appeared at 1454,1439,1437,1446,1438,1448,1434,1433,1430,1431,1420 and 1417 cm−1 which is consistent with both FT-IR and FT-Raman experimental modes [30]. The simulated out-of-plane twisting modes of vibrations were detected at 1160,1126 cm−1 is suited with the experimental values at 1148 (FT-IR), 1147 (FT-Raman), and 1125 (FT-Raman) respectively. In header composite, the CH3 asymmetric and symmetric stretching vibrations for freebase and cationic species were computed at 2990,2976,2978,3015, 2988,2970,2978,3009 cm−1 (asymmetric stretching vibrations) and symmetric stretching modes such as 2923, 2917, 2923, 2954 cm−1. The corresponding experimental FT-IR (2984 cm−1), FT-Raman (2990 cm−1), and symmetric stretching vibrations such as FT-IR (2919 cm-1) and FT-Raman (2902 cm-1) with PED contributions as 88,86 and 92 % were observed. The symmetric and asymmetric bending modes of CH3 modes generally fall in the range of 1390-1360 cm-1 and 1485-1400 cm-1 respectively [34]. Further, Ajaz Hussian et al. [35], reported the C–H scissoring vibration frequencies in the array of 1636-1400 cm−1. In Table S1, the computed wavenumbers in freebase and cationic with both Gas and IEF-PCM phases such as 1483,1495,1463,1446,1438,1448,1434 cm−1 were dependable with the experimental values noticed at 1472,1442 cm−1, and 1463 cm−1 in the FT-IR, FT-Raman regions.
4.2.4. C–C, S–O and C–S vibrations
The ring C–C stretching mode is measured in the wide range from 1600-1400 cm−1 [35]. The stretching C–C vibrations generate complex modes using the combination of several added deformational modes of vibration. In the title composite, computed C–C stretching vibrations in freebase and cationic media were noticed at 1659, 1655,1576,1601,1572, 1538,1592,1558,1500, 1079, 1089, 1043, 1063,1022,1007,1024,1048,1007,967,993,977,892,621 cm−1, showed excellent agreement with the experimental wavenumbers [30]. The S–O stretching vibrations appear in the region 1360–1310 cm−1 [36]. In freebase and cationic structures, the asymmetric stretching S–O has been noticed at 1226,1303 cm−1 with the equivalent experimental wavenumber in FT-Raman was noted at 1221 cm−1 respectively. The C–S stretching vibrations occur at lower wavenumber ranges, where vibrational modes are much more susceptible to coupling effects. In general, the stretching C–S vibrations exhibit in the range 780-510 cm−1 [37]. Here, the theoretical (freebase and cationic) C21–S1 symmetrical stretching mode at 708 cm−1 with a closely related experimental wavenumber as 706 cm−1(FT-IR) was assigned to this mode [38]. The bending deformation (H–C–S) was computed theoretically (free base and cationic) at 1297,1317 cm−1 with an equivalent experiment FT-IR value of 1290 cm−1 respectively.
4.2.5. Other vibrations
The computed wavenumbers in freebase and cationic phases were observed at 1392,931, 1275,901,792,1143, 837,905,901,478,560,788,502 cm−1 are ascribed to the torsion vibrations viz., HCSO, HCNC, HCNH, CCOC, HCCS, HCCC and HNCC. These modes were agreed with the recorded (FT-IR and FT-Raman) spectral data values respectively.
4.3. Electronic properties
4.3.1. Frontier molecular orbital
The Frontier Molecular Orbital (FMO) theory plays a significant part in the electrical and optical properties, chemical reactivity, intermolecular charge transfers, and molecular charge distributions within the compound. The frontier molecular orbital electron theory emphasizes the reactivity preferences on the HOMO and LUMO molecular orbitals. Further, FMO assumes that the reaction rates influence the energy separation of HOMO (electron-rich component) and LUMO (electron-deficient) orbitals. The FMO's and the energy parameters were obtained using the DFT method with the above-stated basis set levels (B3LYP/PBEPBE/TPSSTPSS). A pictorial representation of the frontier orbital's energy level is depicted in Figure 5a. Using the Koopman's theorem [39], the global reactivity parameters were calculated, Ionization potential (I) = 6.145, 4.740, 4.845 eV Electron affinity (A) = 1.483, 1.812,1.718 eV, Energy gap (ΔE) = 4.660, 2.928, 3.127 eV, Electronegativity (χ) = 3.814, 3.276, 3.281 Global hardness (ղ) = 2.331, 1.464, 1.564, Chemical potential (μ) = -3.814, -3.276, -3.281, Chemical softness (S) = 0.214, 0.341, 0.319 and Electrophilicity index (ω) values are 3.121, 3.665, 3.444, Nucleophilicity index (N) ev−1 = 0.320, 0.273, 0.290 which are described herein terms of molecular orbital theory [40,41,42]. The HOMO-LUMO energy difference between these orbitals (B3LYP/PBEPBE/TPSSTPSS) interprets high chemical reactivity. The global chemical descriptors parameters as ω – (electron donating) = 5.318, 5.486, 5.276 and ω + (electron accepting) = 1.504, 2.210, 1.998 were tabulated in Table 2. In the present investigation, ionization potential values are found much higher than the electron affinity, strengthens the findings of more electron donor capability (ω−) as compared to the values of electron acceptor (ω+) capability [43,44]. The electrophilicity index values determine the biological nature of N2M5MB. The HOMA index interprets the geometrical aromaticity of heterocyclic compounds. The FLU aromaticity calculates the electron delocalization divergences for aromatic types of molecules. A HOMA index is estimated as the mentioned ring is aromatic if it is equal to one [45]. For zero, the chosen ring is nonaromatic. If HOMA has a substantial negative value, then it shows anti-aromaticity features. In the present study, the calculation of HOMA (geometric), FLU (electronic) aromaticity criteria were assessed using Multiwfn 3.7 wave function analyzer program [23]. The calculated HOMA index for three B3LYP, PBEPBE, TPSSTPSS methods is 0.923,0.868, 0.881 (equals one) in the ring (C14, C17, C16, C19, C20, and C18) structure, smaller FLU values (0.007,0.008,0.008) reveal strong aromaticity of N2M5MB.
Figure 5.
(a) Frontier molecular orbital -HOMO-LUMO energy plots, (b) Comparative UV-Vis spectra by using TD-DFT (MO62X) level and experimental approach, (c) Electron-hole contributions for the three excited states of N2M5MB.
Table 2.
Calculated Energy and Global Chemical Descriptors values of N2M5MB by B3LYP, PBEPBE, TPSSTPSS/6–311++G (d,p) methods.
| Parameters | B3LYP | PBEPBE | TPSSTPSS |
|---|---|---|---|
| EHOMO (eV) | -6.145 | -4.740 | -4.845 |
| ELUMO (eV) | -1.483 | -1.812 | -1.718 |
| Harmonic Oscillator Model of Aromaticity (HOMA) index | 0.923 | 0.868 | 0.881 |
| Aromatic Fluctuation Index (FLU) | 0.007 | 0.0081 | 0.008 |
| Ionization potential (I) | 6.145 | 4.740 | 4.845 |
| Electron affinity (A) | 1.483 | 1.812 | 1.718 |
| Energy gap (eV) (ΔE) | 4.660 | 2.928 | 3.127 |
| Electronegativity (χ) | 3.814 | 3.276 | 3.281 |
| Chemical potential (μ) | -3.814 | -3.276 | -3.281 |
| Global hardness (ղ) | 2.331 | 1.464 | 1.564 |
| Chemical softness (S) | 0.214 | 0.341 | 0.319 |
| Electrophilicity index (ω) | 3.121 | 3.665 | 3.444 |
| Nucleophilicity index (N) ev−1 | 0.320 | 0.273 | 0.290 |
| Electron donating capability (ω -) | 5.318 | 5.486 | 5.276 |
| Electron accepting capability (ω +) | 1.504 | 2.210 | 1.998 |
4.3.2. UV-Vis analysis & charge transfers due to excitation
UV-Vis's absorption spectrum signifies the physiochemical characteristics of molecular electronic transitions in the organic compound. The theoretical electronic energy for freebase and cationic (-NH) species of the N2M5MB were measured using the TD-DFT/M06-2X (DMSO-solvent) method. Figure 5b depicted the computed (freebase, cationic) and experimental UV-Vis's absorption spectra (DMSO-solvent) of N2M5MB. The calculated wavelength (λmax), bandgap energies, oscillator strength (f) (measure the intensity of an electronic transition state) with corresponding major assignments contributions tabulated in Table 3. The two bandgap energies of 5.179 eV, 4.455 eV (freebase) and 2.476 eV (Cationic) were compared with the experimental absorption peaks at 286 nm involved nonbonding molecular orbital (n) to anti-bonding π orbital (π∗) transitions, another peak observed at 247 nm transition from bonding pi orbital π to anti-bonding pi orbital (π∗). The computed (freebase) absorption peak at 279 nm is contributed to the transition from HOMO-1 to LUMO with 43%, and at 240 nm at major contributions of HOMO-3 to LUMO+1 with 40%. The absorption peaks at 501nm for cationic in DMSO solvent (-NH) the major contributions as HOMO to LUMO+2 with 88% was observed. These results interpreted that the cationic species (-NH) absorption could be attributed to the intense band at 501 nm (longer wavelength) as n to (π∗) transitions, using DMSO as solvent [33], whereas the freebase in DMSO solvent values was well agreed with experimental absorptions.
Table 3.
Experimental and TD-DFT-MO62X (Freebase, Cationic species) - UV-Vis's characteristics of N2M5MB.
| TD-DFT |
Experimental |
Assignments | ||||
|---|---|---|---|---|---|---|
| λmax (nm) | Band gap (eV) | f (Osc. strength) | Major contributions | λmax (nm) | ||
| Freebase (DMSO) | 240 | 5.179 | 0.0542 | HOMO-4- > LUMO (29%), HOMO-3- > LUMO+1 (40%) | 247 | π→π∗ |
| 279 | 4.455 | 0.0247 | HOMO-1- > LUMO (43%), HOMO-1- > LUMO+1 (22%) | 286 | n→π∗ | |
| Cationic (DMSO) | 501 | 2.476 | 0.2132 | HOMO- > LUMO+2 (88%) | n→π∗ | |
The intuitive visual effect of representing the electron-hole (green-blue) isosurface distribution map for three excited states was obtained using the Multiwfn 3.7 software program [23] is shown in Figure 5c. The obtained values of Excitation energy E (eV), Charge transfer (D) length index, t index, an overlap (S) of electron-hole distribution for the three excitation modes (output from TD-DFT method) are tabulated in Table 4. The D index value (charge-transfer length) is 2.906 for the second excitation mode in N2M5MB interprets the large charge transfer (CT) excitation. Besides, from the positive t index value (0.038), the high degree of electron and hole separation is evident and the S index value of 0.1879 compute the overlap of holes and electrons distributions [46].
Table 4.
Excitation energy, Charge transfer length, Overlap integral, t index for different excited states for N2M5MB.
| Parameters | First excited state | Second excited state | Third excited state |
|---|---|---|---|
| Excitation energy E (eV) | 4.807 | 5.233 | 5.625 |
| Charge transfer length D index (A°) | 0.695 | 2.906 | 0.953 |
| Overlap of electron-hole distribution (S) | 0.1287 | 0.1879 | 0.3443 |
| t index | -0.976 | 0.038 | -0.486 |
4.4. Electrostatic potential map
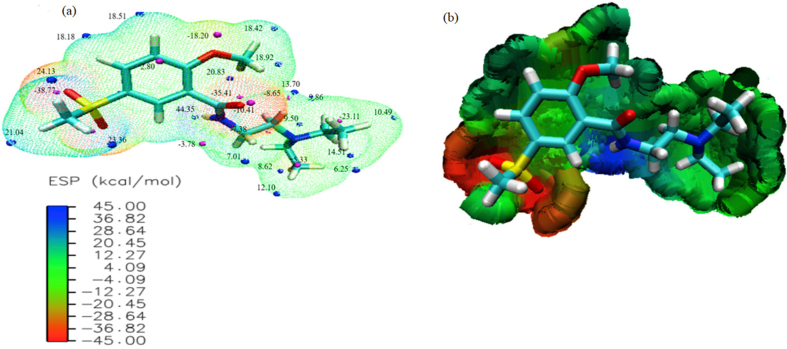
The electrostatic potential (ESP) map is highly informative concerning the charge distributions of the compound. The ESP map elucidates the reactivity sites using electrophiles and nucleophiles attack regions. An ESP map is an effective tool in the field of biological phenomenon [47]. The reactive sites and surface extrema for the N2M5MB are computed based on the earlier mentioned method, depicted in Figure 6a. The values of ESP at different points on the electron density isosurface regions are interpreted as red regions as the lowest electrostatic (attractive) and blue regions as the highest electrostatic (repulsive) potential energy values were shown in Figure 6b. The green color corresponds to intermediate between the two extremes (red and blue) regions shown in Figure 6b. The color scale of the map ranges from -45.00 to 45.00 kcal/mol. The maxima and minima values in the blue and magenta spheres of the ESP map generated using VMD software [22] shown in Figure 6a. In N2M5MB, the oxygen atom (O4) leads to a negative value (favorable site for interacting with positively charged) is surface minima corresponds to hydrogen bond acceptors with the value of -38.77 kcal/mol reveals the most suitable region for an electrophilic attack. Maximum value from the positively charged H31 (44.35 kcal/mol) can behave as a hydrogen bond donor group.
Figure 6.
(a), (b) Electrostatic potential (ESP) at the basis level of B3LYP/6–311++G (d,p) of N2M5MB.
4.5. Hirshfeld surface analysis
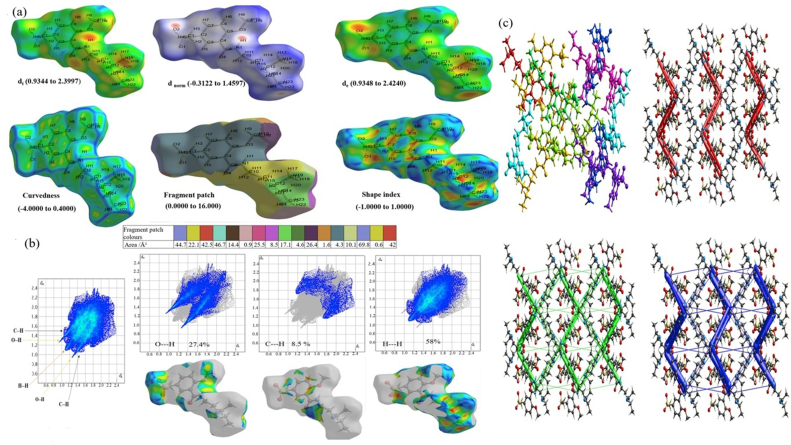
Hirshfeld surface analysis is to envisage the existence of molecule packing detected in crystal structures. The structural 3D environment with different properties as d norm (−0.3122 to 1.4597), di (0.9344–2.3997), shape index (−1.0000 to 1.0000), de (0.9348–2.4240), curvedness (−4.0000 to 0.4000), and color patch fragment ranges from 0.0000 to 16.0000 affords an appropriate method of detecting the adjacent coordination in N2M5MB. The 2D finger plots contribution (in percentage) was plotted within the atoms on the molecular surface depicted in Figure 7 (a, b). The di is the internal surface estimates the distance from a point on the surface to the nearest interior atom and the de for the external distance from the surface to the exterior, and d norm function is the normalized contact measurement based on the di and de interactions. The di and de afford a piece of evidence on the existence of intermolecular contacts in the N2M5MB. The red spots (high electron density) over the surface specify the contact points shorter than the sum of van Der Waals with negative dnorm and the positive dnorm with lower electron density (blue regions) values representing long range than the sum of the van Der Waals radii. In Figure 7a, a red color spot regions represent the shorter contacts over O–H in the hirshfeld surface region. A large area denoted in blue edges with flat green on the curvedness surface signifies the π---π stacking interactions of N2M5MB [48]. Major H..H/H..H interactions exhibit contributions of 58 % to the entire crystal packing region. The influence from the H⋯O/O⋯H contacts are signified by a pair of sharp spikes with 27.4% respectively. The H⋯C/C⋯H contacts in the structure have a wing shape distribution with an 8.5% along with reciprocal contacts depicted in Figure 7b. The energy frameworks offer a remarkable way to envision the interaction energy between the pairs of molecular crystal structures. Energy framework interactions were calculated using a cluster radius value of 3.8Å. The energy frameworks envisaged as red (electrostatic), green (dispersion), and blue (total interaction) cylinders were generated (using .cif file) shown in Figure 7c. The radius of the cylinders directly related to the amount of interaction level between the neighbouring atoms. The globularity value was obtained as G = 0.698 (less than one) visualizes that the N2M5MB has well defined molecular structure.
Figure 7.
(a) Hirshfeld surface of N2M5MB with a different view (di, dnorm, de, curvedness, fragment patch, shape index) mapped onto the surface,(b) 2-D finger plots of percentage contributions from all, O–H, C–H, H–H contacts (reciprocal included),(c) Energy framework diagram for all the pairs, Red = electrostatic (Coulomb), green = dispersion, blue = total interaction energies.
4.6. Topological analysis
4.6.1. Quantum Theory of Atom in molecules
Quantum Theory of Atom in molecules (QTAIM) analysis affords the new dimensions and accounts for the degree of covalency of hydrogen bonding interactions. The concept of bonding through bond paths (BP) and critical points (CP) of interacting atoms have been delineating using the topological properties of electron density (gradient vector field) and its derivatives [49]. The critical points are the points at which the gradient function value is zero (excepting at the point of infinity). BCP (Bond Critical Point) provides a good measure of interaction between two molecular systems (+3, -1). The topological parameters of the critical points (CP) associated with the interaction for the title compound were achieved using the Multiwfn software program [23]. The molecular graph of N2M5MB revealed by QTAIM analysis is visualized in Figure 8a. Large magenta spheres (+3, -3) are nuclear critical point (NCP), small orange spheres (+3, -1) are BCP, and yellow spheres (+3, +1) in the center of the RCP (Ring Critical Point) respectively. The brown line indicates the intramolecular interaction between H44–O3 atoms in the bond path shown in Figure 8b. The positive value of Laplacian electron density (0.05469) corresponds to local depletion with closed is shell type of interaction. As Rozas, Alkorta et al. reported [50], N2M5MB is recognized with partial covalent nature, with H-bonds having moderate strengths when Laplacian electron density values (∇2ρ > 0) and the H (total energy density) value of BCP is less than zero. Further, Espinosa et al reported [51], the calculated kinetic energy density G(r) (0.01226) and the potential energy density V (r) (−0.0108) values that reveal the types of interaction. The positive value of H (0.001412) reflects a dominant covalence (ie. excess of potential energy) with closed shell or hydrogen bond interaction types in N2M5MB.
Figure 8.
(a)AIM- Molecular graph of N2M5MB, NCP-Large violet spheres, BCP-small orange spheres and RCP-yellow spheres in the centre of the ring. Brown lines represent the bond path (H44–O3), (b) Laplacian electron density - bond between H44–O3 depicted in brown dashed line.
4.6.2. ELF, LOL and IGM
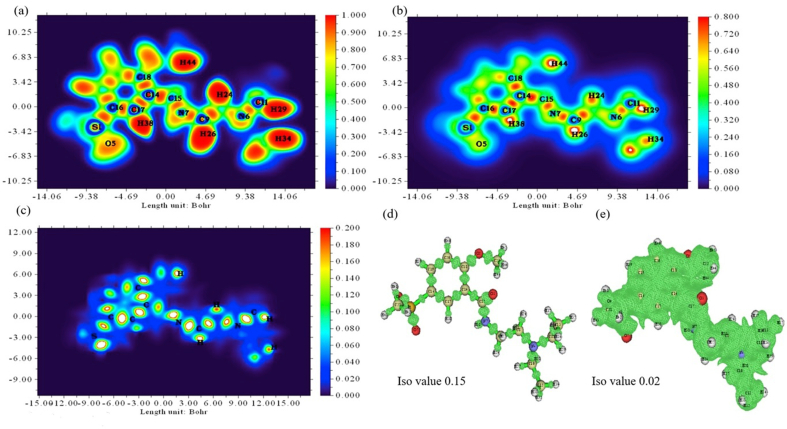
The topological parameters and validation of the Electron localization descriptors as Electron Localization Function (ELF) and Localized Orbit Locator (LOL) analyses were accomplished in confirming the chemical concepts with the colour scale representation [52]. From Figure 9a in ELF analysis, the blue region (represents more probability for parallel spins) carbon, nitrogen corresponds to highly delocalized electron density. Further, the red colour region substantially around hydrogen atoms depicts the electron localization nature in the bonding regions. In general, the smaller LOL value appears in the boundary region (blue), the high LOL value (red) appeared in the inner space of the localized orbitals. The white spots in the LOL map (Figure 9b.) indicate the electron density exceeding the upper limit value. The independent gradient model (IGM) investigates the interactions (strong and weak) in molecules using a wavefunction scheme. Further, IGM affords a method to detect and enumerate the total electron density gradient attenuation due to interaction between the atoms. The IGM analysis was carried out using the Multiwfn software program 3.7 [23]. The chemical bonded regions have high δg values (i.e, the value greater than 0.2 depicted in white) represented in Figure 9c and the regions with isosurface with iso values of 0.15 and 0.02 in Figures 9d and 9e respectively.
Figure 9.
Colour filled map of N2M5MB (a) ELF, (b) LOL, (c) IGM - with isovalue of (d) 0.15, and (e) 0.02.
4.7. Fukui functions
Fukui functions investigate the precise nature of the atom's reactivity and selectivity in a molecule. The local reactivity parameters for N2M5MB using a mentioned basis set of computation. It is conceivable to label the corresponding condensed or aromatic Fukui functions on the rth atom site as [53],
| f+(r) = ρN+1 (r) - ρN (r) for nucleophilic attack |
| f−(r) = ρN (r) - ρN-1 (r) for electrophilic attack |
| fo(r) = [ρN+1 (r) - ρN-1 (r)]/2 for radical attack |
| Δf(r) = [(f +(r) - (f -(r)] dual descriptor |
The dual descriptor was calculated using the electrophilic f−(r) and nucleophilic f+(r) values. Perez et al. [54], proposed a multiphilic descriptor using the philicity concept, an index of selectivity towards nucleophilic attack (ωr+) and electrophilic attack (ωr -). The multiphilic parameter has been calculated by the following equation,
| Δωr = [ωr + - ωr -] = ω [Δƒr] multiphilic parameter |
In the present study, dual descriptor Δf(r), multiphilic descriptor (Δωr), and local parameters reveal the more positive value of carbon atoms viz., C18, C19, C10, C9 is favored for a nucleophilic attack (electron donor) and they are presented in Table 5.
Table 5.
Condensed fukui functions, local parameters, dual descriptor and multiphilic parameters for N2M5MB.
| Atoms | Condensed fukui functions |
Local parameters |
Dual descriptor |
Multiphilic parameter |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | N +1 | N-1 | fr + | fr - | fr 0 | sr+ ƒr+ | sr-ƒr- | sr0 ƒr0 | ωfr+ | ωfr- | ωfr0 | Δ f(r) | Δωr | |
| S1 | 2.088 | 1.118 | 1.104 | -0.971 | -0.984 | 0.007 | -0.208 | -0.211 | 0.001 | -3.029 | -3.072 | 0.021 | 0.014 | 0.043 |
| O2 | -0.556 | -0.283 | -0.197 | 0.272 | 0.358 | -0.043 | 0.058 | 0.077 | -0.009 | 0.849 | 1.119 | -0.135 | -0.086 | -0.269 |
| O3 | -0.604 | -0.308 | -0.147 | 0.295 | 0.457 | -0.081 | 0.063 | 0.098 | -0.017 | 0.921 | 1.426 | -0.253 | -0.162 | -0.505 |
| O 4 | -0.933 | -0.496 | -0.466 | 0.437 | 0.467 | -0.015 | 0.094 | 0.100 | -0.003 | 1.364 | 1.457 | -0.047 | -0.030 | -0.093 |
| O5 | -0.939 | -0.499 | -0.476 | 0.440 | 0.463 | -0.012 | 0.094 | 0.099 | -0.002 | 1.372 | 1.445 | -0.036 | -0.023 | -0.072 |
| N6 | -0.568 | -0.272 | 0.162 | 0.296 | 0.730 | -0.217 | 0.063 | 0.156 | -0.046 | 0.924 | 2.280 | -0.678 | -0.434 | -1.356 |
| N7 | -0.641 | -0.345 | -0.326 | 0.296 | 0.315 | -0.009 | 0.063 | 0.067 | -0.002 | 0.925 | 0.983 | -0.029 | -0.019 | -0.058 |
| C8 | -0.185 | -0.141 | -0.162 | 0.044 | 0.023 | 0.011 | 0.009 | 0.005 | 0.002 | 0.139 | 0.070 | 0.034 | 0.022 | 0.068 |
| C9 | -0.192 | -0.140 | -0.145 | 0.052 | 0.047 | 0.002 | 0.011 | 0.010 | 0.000 | 0.162 | 0.147 | 0.007 | 0.005 | 0.014 |
| C10 | -0.182 | -0.137 | -0.163 | 0.045 | 0.019 | 0.013 | 0.010 | 0.004 | 0.003 | 0.139 | 0.059 | 0.040 | 0.026 | 0.080 |
| C11 | -0.181 | -0.136 | -0.163 | 0.045 | 0.018 | 0.013 | 0.010 | 0.004 | 0.003 | 0.141 | 0.057 | 0.042 | 0.027 | 0.083 |
| C12 | -0.583 | -0.352 | -0.361 | 0.231 | 0.223 | 0.004 | 0.050 | 0.048 | 0.001 | 0.722 | 0.695 | 0.014 | 0.009 | 0.027 |
| C13 | -0.586 | -0.354 | -0.362 | 0.233 | 0.224 | 0.004 | 0.050 | 0.048 | 0.001 | 0.726 | 0.700 | 0.013 | 0.008 | 0.026 |
| C14 | -0.164 | -0.079 | -0.077 | 0.085 | 0.087 | -0.001 | 0.018 | 0.019 | 0.000 | 0.266 | 0.270 | -0.002 | -0.001 | -0.004 |
| C15 | 0.663 | 0.353 | 0.332 | -0.309 | -0.331 | 0.011 | -0.066 | -0.071 | 0.002 | -0.966 | -1.032 | 0.033 | 0.021 | 0.066 |
| C16 | -0.319 | -0.170 | -0.170 | 0.149 | 0.149 | 0.000 | 0.032 | 0.032 | 0.000 | 0.465 | 0.466 | 0.000 | 0.000 | -0.001 |
| C17 | -0.161 | -0.105 | -0.091 | 0.055 | 0.070 | -0.007 | 0.012 | 0.015 | -0.002 | 0.173 | 0.220 | -0.023 | -0.015 | -0.047 |
| C18 | 0.374 | 0.259 | 0.178 | -0.115 | -0.197 | 0.041 | -0.025 | -0.042 | 0.009 | -0.359 | -0.614 | 0.127 | 0.081 | 0.254 |
| C19 | -0.162 | -0.016 | -0.088 | 0.147 | 0.074 | 0.036 | 0.031 | 0.016 | 0.008 | 0.458 | 0.232 | 0.113 | 0.072 | 0.226 |
| C20 | -0.220 | -0.170 | -0.116 | 0.050 | 0.104 | -0.027 | 0.011 | 0.022 | -0.006 | 0.156 | 0.325 | -0.085 | -0.054 | -0.170 |
| C21 | -0.799 | -0.468 | -0.470 | 0.332 | 0.330 | 0.001 | 0.071 | 0.071 | 0.000 | 1.036 | 1.029 | 0.003 | 0.002 | 0.007 |
| C22 | -0.194 | -0.145 | -0.164 | 0.049 | 0.030 | 0.009 | 0.010 | 0.006 | 0.002 | 0.152 | 0.094 | 0.029 | 0.019 | 0.058 |
4.8. Molecular docking analysis
Molecular docking is an effective method to foresee the best binding interactions of ligand (header compound) and targets (enzyme/protein). Acetylcholinesterase (Ache) inhibitors have been linked to increasing the acetylcholine concentration level in the brain. Further, Acetylcholinesterase (AChE) inhibitors have a promising role in the process of effective encounter in neurotransmitter diseases [55]. In this connection, the molecular docking analysis explores the binding interactions of the header composite (ligand) confirmations with AChE inhibitors (protein). The N2M5MB (ligand) was selected to be docked into the AChE inhibitors-protein receptors such as 1H22,4DTL,5OV9. The Autodock software tool [24] envisages ligand-protein binding energetics. The N2M5MB was docked in the suitable sites of the target receptors and the least binding energy value was observed. The binding energies (kcal/mol), bond distance, bonded residues, and inhibition constant (μm) values were enlisted in Table 6. The minimum binding energy values are vital for rational drug discovery. According to the results, N2M5MB (ligand) exhibited good binding affinity values ranges from -5.62 to -6.45 (kcal/mol), in comparison with the Tacrine (AChE inhibitors) [56] depicted in Figure 10. Thus, N2M5MB validates a good binding affinity towards the targeted receptors and could be considered as an Alzheimer's disease treatment.
Table 6.
Molecular Docking analysis and hydrogen bonding interactions of N2M5MB and Tacrine with target proteins 1H22,4BTL,5OV9.
| Target protein | Ligand | Binding energy (kcal/mol) | Bonded residues | Bond distance (Å) | Estimated inhibition constant (μm) |
|---|---|---|---|---|---|
| 1H22 | N2M5MB | -6.45 | PHE288 | 2.0 | 18.59 |
| ARG289 | 2.6 | ||||
| Tacrine∗ | -6.38 | GLU199 | 2.2 | 20.94 | |
| 4BTL | N2M5MB | -6.44 | PHE295 | 2.0 | 19.10 |
| Tacrine∗ | -6.11 | TYR341 | 2.2 | 33.09 | |
| 5OV9 | N2M5MB | -5.62 | ARG296 | 2.4 | 75.43 |
| PHE295 | 2.2 | ||||
| TYR72 | 3.2 | ||||
| Tacrine∗ | -6.02 | ARG296 | 2.1 | 38.95 | |
| SER293 | 2.0 |
Tacrine - AChE inhibitor (reference drug).
Figure 10.
The docked ligand (N2M5MB) with different protein targets (a) 1H22, (b) 4BTL, (c) 5OV9; Targeted proteins in 3D mode (d) 1H22, (e) 4BTL, (f) 5OV9 and the docked ligand (Tacrine) with different protein targets (g) 1H22, (h) 4BTL, (i) 5OV9.
5. Conclusion
In this study, the theoretical structures of freebase, cationic species of N2M5MB have been determined using DFT/B3LYP 6–311++G (d,p).The stable structure confirmations have been achieved using Potential energy scan (PES) analysis of the N2M5MB. The vibrational assignments for freebase (Gas, IEF-PCM) and Cationic (Gas, IEF-PCM) have been performed along with PED (Potential Energy Distribution) values and compared with recorded FT-IR and FT-Raman spectral analysis were compatible with calculated values. The optimized molecular geometrical values (bond length, bond angle) for different simulated basis set such as B3LYP, PBEPBE and TPSSTPSS, IEF-PCM in Freebase and B3LYP, IEF-PCM in Cationic media were agreed with the reported XRD values and RMSD values (bond length and bond angle) for both the species (Freebase, Cationic) were also mentioned. The calculated FMO parameters (HOMO-LUMO Energy gaps E = 4.660,2.928,3.127 eV) imply the electron density delocalization within the molecule. In the UV-Vis analysis, the absorption peak values are in good conformity with both simulated (279, 240 nm) in Freebase structure and 501 nm in Catioinc (-NH) species using IEF-PCM method (DMSO solvent). The experimental (286, 279 nm) values show good concordance with the Freebase structure. The cationic species (-NH) of N2M5MB reveals a higher absorbance peak compared with freebase structure. Besides, calculated HOMA (0.923,0.8686,0.8807) and FLU (0.0075,0.0081,0.0082) indices values have been calculated for three functional combinations which indicate the aromaticity of the heterocyclic ring in N2M5MB. The nucleophilic and electrophilic regions were interpreted using ESP map, Fukui functions (fr+, fr- and fr0), multiphilic (Δωr), and dual descriptors (Δfr). The molecular graph was plotted using critical points in QTAIM analysis along with a Laplacian electron density map that highlighted the path between two atoms as H44–O3 in N2M5MB. The ELF, LOL, and IGM (two isosurfaces) were obtained and Hirshfeld surface analysis (various fragments) and corresponding 2D fingerprint plots were computed to accomplish insight into the molecular interactions of N2M5MB. Molecular docking methods to underline the binding interactions of header composite (ligand) using AChE protein targets and the minimum binding energy (−6.45), bond distances (2.0,2.6Å), bonded residues (PHE288, ARG289) were compared with Tacrine, a standard drug on AChE inhibitors. Thus, N2M5MB capitalizes in AChE inhibitors to be a potent candidate for future Alzheimer's disease (AD) therapy.
Declarations
Author contribution statement
S. Janani: Conceived and designed the experiments; Contributed reagents, materials, analysis tools or data; wrote the paper.
Hemamalini Rajagopal: Conceived and designed the experiments; Contributed reagents, materials, analysis tools or data.
S. Muthu; S. Aayisha: Performed the experiments.
M. Raja; Ahmad Irfan: Analyzed and interpreted the data.
Funding statement
This work was supported by Deanship of Scientific Research at King Khalid University (KKU), Saudi Arabia for funding through research groups program under grant number R.G.P.1/110/42.
Data availability statement
Data included in article/supplementary material/referenced in article.
Declaration of interests statement
The authors declare no conflict of interest.
Additional information
No additional information is available for this paper.
Appendix A. Supplementary data
The following is the supplementary data related to this article:
References
- 1.Sener E.A., Bingol K.K. Synthesis and microbiological activity of some N-(2-hydroxy-4-substituted phenyl) benzamides, phenylacetamides and furamides as the possible metabolites of antimicrobial active benzoxazoles. Il Farmaco. 2002;57:451–456. doi: 10.1016/s0014-827x(02)01226-0. [DOI] [PubMed] [Google Scholar]
- 2.Pau A., Boatto G., Palomba M., Asproni B., Cerri R. Synthesis of N-[4-(alkyl)cyclohexyl]-substituted benzamides with anti-inflammatory and analgesic activities. Il Farmaco. 1999;54:524–532. doi: 10.1016/s0014-827x(99)00057-9. [DOI] [PubMed] [Google Scholar]
- 3.Asif M. Pharmacological potential of benzamide analogues and their uses in medicinal chemistry. Mod. Chem. Appl. 2016:4. [Google Scholar]
- 4.Karlawish J., Jack C.R., Rocca W.A., Snyder H.M., Carrillo M.C. Alzheimer’s disease: the next frontier-special report 2017. Alzheimer's Dementia. 2017;13:374–380. doi: 10.1016/j.jalz.2017.02.006. [DOI] [PubMed] [Google Scholar]
- 5.Lu S.H., Wu J.W., Liu H.L. The discovery of potential acetylcholinesterase inhibitors: a combination of pharmacophore modelling, virtual screening, and molecular docking studies. J. Biomed. Sci. 2011;18 doi: 10.1186/1423-0127-18-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Brodaty H., Breteler M.M.B., DeKosky T.S., Dorenlot P., Fratiglioni L., Hock C., Kenigsberg P.A., Scheltens P., Strooper B.D. Vol. 59. 2011. The World of Dementia beyond 2020; pp. 923–927. [DOI] [PubMed] [Google Scholar]
- 7.Kratky M., Stepankova S., Houngbedji N.H., Vosatka R. 2-Hydroxy-N-phenylbenzamides and their esters inhibit acetylcholinesterase and butyrylcholinesterase. Biomolecules. 2019;9(11):698–714. doi: 10.3390/biom9110698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Mphahlele M.J., Agbo E.N., More G.K., Gildenhuys S. In vitro enzymatic and kinetic studies, and in silico drug-receptor interactions, and drug-like profiling of the 5-styrylbenzamide derivatives as potential cholinesterase and β-secretase inhibitors with antioxidant properties. Antioxidants. 2021;10:647. doi: 10.3390/antiox10050647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Köksal Z., Alim Z., Bayrak S. Investigation of the effects of some sulfonamides on acetylcholinesterase and carbonic anhydrase enzymes. J. Biochem. Mol. Toxicol. 2019;33:22300. doi: 10.1002/jbt.22300. [DOI] [PubMed] [Google Scholar]
- 10.Becke A.D. A new mixing of Hartree–Fock and local density-functional theories. J. Chem. Phys. 1993;98(2):1372–1377. [Google Scholar]
- 11.Lee C., Yang W., Parr R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B. 1988;37(2):785–789. doi: 10.1103/physrevb.37.785. [DOI] [PubMed] [Google Scholar]
- 12.Frisch M.J., Trucks G.W., Schlegel H.B., Scuseria G.E. Gaussian, Inc; Walling-ford CT: 2010. Gaussian 09, C3 Revision B.01. [Google Scholar]
- 13.Araújo R.L., Lima Neto J.X., Henriques J.M., Tromer R.M., Barboza C.A., Oliveira J.I.N., Fulco U.L. Insights into solid-state properties of dopamine and L-Dopa hydrochloride crystals through DFT calculations. Chem. Phys. Lett. 2020:138033. [Google Scholar]
- 14.Kanai Y., Wang X., Selloni A., Car R. Testing the TPSS meta-generalized-gradient-approximation exchange-correlation functional in calculations of transition states and reaction barriers. J. Chem. Phys. 2006;125(23):234104. doi: 10.1063/1.2403861. [DOI] [PubMed] [Google Scholar]
- 15.Jamroz M.H. Vol. 4. 2013. Vibrational Energy Distribution Analysis VEDA; pp. 2004–2010. Warsaw. [DOI] [PubMed] [Google Scholar]
- 16.Casida M.E., Jamorski C., Casida K.C., Salahub D.R. Molecular excitation energies to high-lying bound states from time-dependent density-functional response theory:Characterization and correction of the time-dependent local density approximationionization threshold. J. Chem. Phys. 1998;108(11):4439–4449. [Google Scholar]
- 17.Scalmani G., Frisch M.J., Mennucci B., Tomasi J., Cammi R., Barone V. Geometries and properties of excited states in the gas phase and in solution: theory and application of a time-dependent density functional theory polarizable continuum model. J. Chem. Phys. 2006;124(9) doi: 10.1063/1.2173258. [DOI] [PubMed] [Google Scholar]
- 18.Van Caillie C., Amos R.D. Geometric derivatives of excitation energies using SCF and DFT. Chem. Phys. Lett. 1999;308(3-4):249–255. [Google Scholar]
- 19.Adamo C., Jacquemin D. The calculations of excited-state properties with time-dependent density functional theory. Chem. Soc. Rev. 2013;42(3):845–856. doi: 10.1039/c2cs35394f. [DOI] [PubMed] [Google Scholar]
- 20.Improta R., Ferrante C., Bozio R., Barone V. The polarizability in solution of tetra-phenyl-porphyrin derivatives in their excited electronic states: a PCM/TD-DFT study. Phys. Chem. Chem. Phys. 2009;11(22):4664. doi: 10.1039/b902521a. [DOI] [PubMed] [Google Scholar]
- 21.Wolff S.K., Grimwood D.J., McKinnon J.J., Turner M.J., Jayatilaka D., Spackman M.A. University of Western Australia; 2012. Crystal Explorer. (Version 3.1) [Google Scholar]
- 22.Humphrey W., Dalke A., Schulten K. VMD: visual molecular dynamics. J. Mol. Graph. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- 23.Lu Tian, Chen Feiwu, Multiwfn A multifunctional wavefunction analyzer. J. Comput. Chem. 2012;33:580–592. doi: 10.1002/jcc.22885. [DOI] [PubMed] [Google Scholar]
- 24.Morris G.M., Goodsell D.S., Halliday R.S., Huey R., Hart W.E., Belew R.K., Olson A.J. Automated docking using a lamarckian genetic algorithm and empirical binding free energy function. J. Comput. Chem. 1998;19:1639–1662. [Google Scholar]
- 25.Houttemane P.C., Boivin J.C., Nowogrocki G., Thomas D.J. N-(Diethylamino-2 6thyl) Methoxy-2 Methylsulfonyl-5 Benzamide (Tiapride), C15H24N204S: etudes & 203 et 298 K. Acta Crystallogr. 1983;C39:585–586. [Google Scholar]
- 26.Lukose J., Panicker C.Y., Nayak P.S., Naryana B., Sarojini B.K., Van Alsenoy C., Al-Saadi A.A. FT-IR, NBO, HOMO–LUMO, MEP analysis and molecular docking study of MethylN-({[2-(2-methoxyacetamido)-4-(phenylsulfanyl)phenyl]amino}[(methoxycarbonyl)imino]methyl)carbamate. Spectrochim. Acta. 2015;135:608–616. doi: 10.1016/j.saa.2015.03.064. [DOI] [PubMed] [Google Scholar]
- 27.Muthu S., Rajamani T., Karabacak M., Asiri A.M. Vibrational and UV spectra, first order hyperpolarizability, NBO and HOMO–LUMO analysis of 4-chloro-N-(2-methyl-2,3-dihydroindol-1-yl)-3-sulfamoyl-benzamide. Spectrochim. Acta Mol. Biomol. Spectrosc. 2014;122:1–14. doi: 10.1016/j.saa.2013.10.115. [DOI] [PubMed] [Google Scholar]
- 28.Abraham C.S., Prasana J.C., Muthu S., Rizwana B.F., Raja M. Quantum computational studies, spectroscopic (FT-IR, FT Raman and UV-Vis) profiling, natural hybrid orbital and molecular docking analysis on 2,4 Dibromoaniline. J. Mol. Struct. 2018;1160:393–405. [Google Scholar]
- 29.Karrouchi Khalid, Brandan Silvia A., Sert Yusuf, El-marzouqi Hakima, Radi Smaail, Ferbinteanu Marilena, Faouzi My El Abbes, Garcia Yann, Ansar M’hammed. Synthesis, X-ray structure, vibrational spectroscopy, DFT, biological evaluation and molecular docking studies of (E)-N’-(4-(dimethylamino)benzylidene)-5-methyl-1H-pyrazole-3-carbohydrazide. J. Mol. Struct. 2020;1219:128541. [Google Scholar]
- 30.Brizuela A.B., Raschi A.B., Castillo M.V., Davies L., Romano E., Brandán S.A. Structural and vibrational investigation on species derived from the cyclamic acid in aqueous solution by using HATR and Raman spectroscopies and SCRF calculations. J. Mol. Struct. 2014;1074:144–156. [Google Scholar]
- 31.Socrates G. third ed. Wiley; Chichester: 2001. Infrared and Raman Characteristic Group Frequencies, Table and Charts. [Google Scholar]
- 32.Prabakaran A., Muthu S. Normal coordinate analysis and vibrational spectroscopy (FT-IR and FT-Raman) studies of (2S)-2-amino-3-(3,4-dihydroxyphenyl)-2-methylpropanoic acid using ab initio HF and DFT method. Spectrochim. Acta. 2012;99:90–96. doi: 10.1016/j.saa.2012.09.014. [DOI] [PubMed] [Google Scholar]
- 33.Manzur M.E., Brandán S.A. S(-) and R(+) species derived from antihistaminic promethazine agent: structural and vibrational studies. Heliyon. 2019;5 doi: 10.1016/j.heliyon.2019.e02322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Hidalgo J.R., Brandan S.A. Theoretical DFT studies on free base, cationic and hydrochloride species of narcotic tramadol agent in gas phase and aqueous solution. Biointerfaces Res. Appl. Chem. 2021;11:13064–13088. [Google Scholar]
- 35.Hussain A., Khan M.U., Ibrahim M., Khalid M., Ali A., Hussain S., Saleem M. Structural parameters, electronic, linear and nonlinear optical exploration of thiopyrimidine derivatives: a comparison between DFT/TDDFT and experimental study. J. Mol. Struct. 2020;1201:127183. [Google Scholar]
- 36.Parimala K., Balachandran V. Vibrational spectroscopic (FTIR and FT Raman) studies, first order hyperpolarizabilities and HOMO, LUMO analysis of p-toluenesulfonyl isocyanate using ab initio HF and DFT methods. Spectrochim. Acta. 2011;81:711–723. doi: 10.1016/j.saa.2011.07.011. [DOI] [PubMed] [Google Scholar]
- 37.Prasath M., Govindammal M., Sathya B. Spectroscopic investigations (FT-IR and FT-Raman) and Molecular docking analysis of 6-[1-methyl-4-nitro-1H-imidazole-5-yl) sulfonyl]-7H-purine. J. Mol. Struct. 2017;1146:292–300. [Google Scholar]
- 38.Raja M., Raj Muhamed R., Muthu S., Suresh M. Synthesis, spectroscopic (FT-IR, FT-Raman, NMR, UV–Visible), NLO, NBO, HOMO-LUMO, Fukui function and molecular docking study of (E)-1-(5-bromo-2-hydroxybenzylidene)semicarbazide. J. Mol. Struct. 2017;1141:284–298. [Google Scholar]
- 39.Koopmans T. About the assignment of wave functions and eigenvalues to the individual electrons of an atom. Physica. 1934;1:104–113. [Google Scholar]
- 40.Parr R.G., Szentpály L.V., Liu S. Electrophilicity index. J. Am. Chem. Soc. 1999;121(9):1922–1924. [Google Scholar]
- 41.Parr R.G., Pearson R.G. Absolute hardness: companion parameter to absolute electronegativity. J. Am. Chem. Soc. 1983;105(26):7512–7516. [Google Scholar]
- 42.Pearson R.G. Absolute electronegativity and hardness correlated with molecular orbital theory. Proc. Natl. Acad. Sci. Unit. States Am. 1986;83(22):8440–8441. doi: 10.1073/pnas.83.22.8440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Gázquez J.L., Cedillo A., Vela A. Electrodonating and electroaccepting powers. J. Phys. Chem. 2001;111(10):1966–1970. doi: 10.1021/jp065459f. [DOI] [PubMed] [Google Scholar]
- 44.Gómez B., Likhanova N.V., Domínguez-Aguilar M.A., Martínez-Palou R., Vela A., Gázquez J.L. Quantum chemical study of the inhibitive properties of 2-pyridyl-azoles. J. Phys. Chem. B. 2006;110(18):8928–8934. doi: 10.1021/jp057143y. [DOI] [PubMed] [Google Scholar]
- 45.Yu D., Rong C., Lu T., Chattaraj P.K., De Proft F., Liu S. Aromaticity and antiaromaticity of substituted fulvene derivatives: perspectives from the information-theoretic approach in density functional reactivity theory. Phys. Chem. Chem. Phys. 2017;19:18635–18645. doi: 10.1039/c7cp03544f. [DOI] [PubMed] [Google Scholar]
- 46.Rizwana B.F., Prasana J.C., Muthu S. Spectroscopic investigation (FT-IR, FT-Raman, UV, NMR), Computational analysis (DFT method) and Molecular docking studies on 2-[(acetyloxy) methyl]- 4-(2-amino-9h-purin-9-yl) butyl acetate. Int. J. Mater. Sci. 2017;12:973–4589. [Google Scholar]
- 47.Geesi M.H., Riadi Y., Kaiba A., El Hassane A., Ouerghi O., Ibnouf E.O., Guionneau P. Synthesis, antibacterial evaluation, Raman, Crystal Structure and Hirshfeld Surface analysis of a new 3-(4-fluorophenyl)-6-methyl-2-(propylthio)quinazolin-4(3H)-one. J. Mol. Struct. 2020;1215:128265. [Google Scholar]
- 48.Shruthi C., Ravindrachary V., Guruswamy B., Prasad D., Goveas J., Kumara K., Lokanath N.K. Molecular structure, hirshfeld surface and density functional theoretical analysis of a NLO active chalcone derivative single crystal – a quantum chemical approach. Mol. Struct. 2021;1228:129739. [Google Scholar]
- 49.P.S.V. Kumar, V. Raghavendra, &V. Subramanian, Bader’s theory of atoms in molecules (AIM) and its applications to chemical bonding, J. Chem. Sci.. 128 (10) 1527–1536.
- 50.Rozas I., Alkorta I., Elguero J. Bifurcated hydrogen bonds:three -Centered interactions. J. Phys. Chem. 1998;102:9925–9932. [Google Scholar]
- 51.Espinosa E., Alkorta I., Elguero J., Molins E. From weak to strong interactions: a comprehensive analysis of the topological and energetic properties of the electron density distribution involving X–H⋯F–Y systems. J. Chem. Phys. 2002;117:5529–5542. [Google Scholar]
- 52.Silvi B., Savin A. Classification of chemical bonds based on topological analysis of electron localization functions. Nature. 1994;371:683–686. [Google Scholar]
- 53.Chattaraj P.K., Maiti B., Sarkar U. Philicity: a unified treatment of chemical reactivity and selectivity. J. Phys. Chem. 2003;107:4973–4975. [Google Scholar]
- 54.Perez P., Labbe A.T., Aizman A., Contreras R. Comparison between experimental and theoretical scales of electrophilicity in benzhydryl cations. J. Org. Chem. 2002;67:4747–4752. doi: 10.1021/jo020255q. [DOI] [PubMed] [Google Scholar]
- 55.Gulcin I., Abbasova M., Taslimi P. Synthesis and biological evaluation of aminomethyl and alkoxymethyl derivatives as carbonic anhydrase, acetylcholinesterase and butyrylcholinesterase inhibitors. J. Enzym. Inhib. Med. Chem. 2017;32:1174–1182. doi: 10.1080/14756366.2017.1368019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Alonso D., Dorronsoro I., Rubio L., Munoz P., Palomero E.G., Monte M.D. Donepezil-tacrine hybrid related derivatives as new dual binding site inhibitors of AChE. Bioorg. Med. Chem. 2005;13:6588–6589. doi: 10.1016/j.bmc.2005.09.029. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data included in article/supplementary material/referenced in article.