Mathematical modeling reveals quantitative properties of KEAP1-NRF2 signaling

Abstract

Under oxidative and electrophilic stresses, cells launch an NRF2-mediated transcriptional antioxidant program. The activation of NRF2 depends on a redox sensor, KEAP1, which promotes the ubiquitination and degradation of NRF2. While a great deal has been learned about this duo, its quantitative signaling properties are largely unexplored. Here we examined these properties, including half-life, maximal activation, and response steepness (ultrasensitivity) of NRF2, through mathematical modeling. The models describe the binding of KEAP1 and NRF2 via ETGE and DLG motifs, NRF2 production, KEAP1-dependent and independent NRF2 degradation, and perturbations by different classes of NRF2 activators. Simulations revealed at the basal condition, NRF2 is sequestered by KEAP1 and the KEAP1-NRF2 complex is distributed comparably in an ETGE-bound (open) state and an ETGE and DLG dual-bound (closed) state. When two-step ETGE binding is considered, class I–V, electrophilic NRF2 activators shift the balance to a closed state incompetent to degrade NRF2, while the open and closed KEAP1-NRF2 complexes transition from operating in cycle mode to equilibrium mode. Ultrasensitive NRF2 activation (a steep rise of free NRF2) can occur when NRF2 nearly saturates KEAP1. The ultrasensitivity results from zero-order degradation through DLG binding and protein sequestration through ETGE binding. Optimal abundances of cytosolic and nuclear KEAP1 exist to maximize ultrasensitivity. These response characteristics do not require disruption of DLG binding as suggested by the hinge-latch hypothesis. In comparison, class VI NRF2 activators cause a shift to the open KEAP1-NRF2 complex and ultimately its complete dissociation, resulting in a fast release of NRF2 followed by stabilization. However, ultrasensitivity is lost due to decreasing free KEAP1 abundance. In summary, by simulating the dual role of KEAP1, i.e., sequestering and promoting degradation of NRF2, our modeling provides novel quantitative insights into NRF2 activation, which may help design novel NRF2 modulators and understand the oxidative actions of environmental stressors.

Graphical abstract

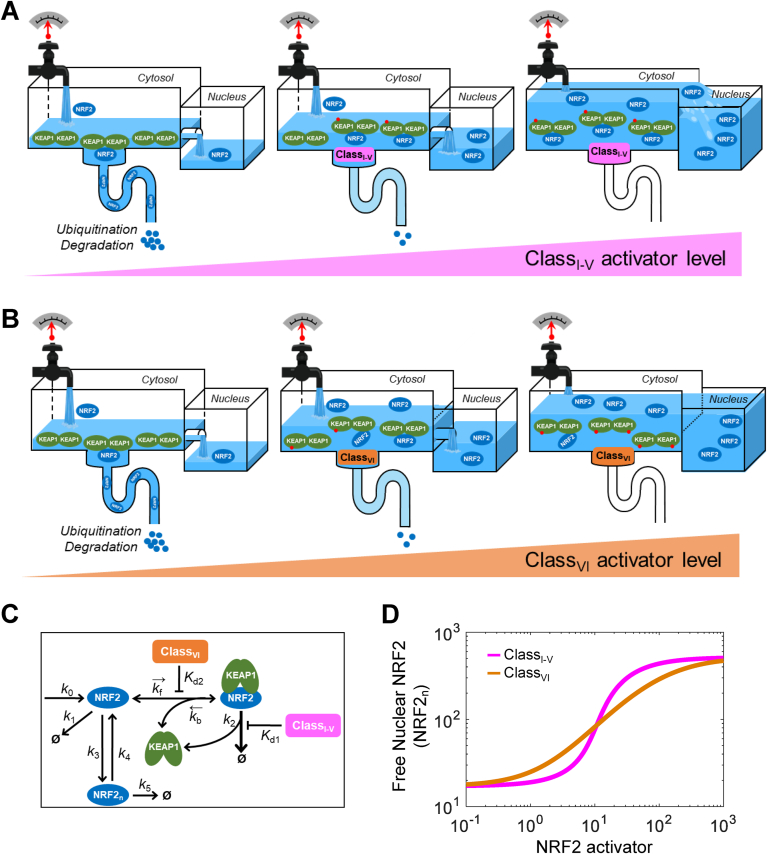
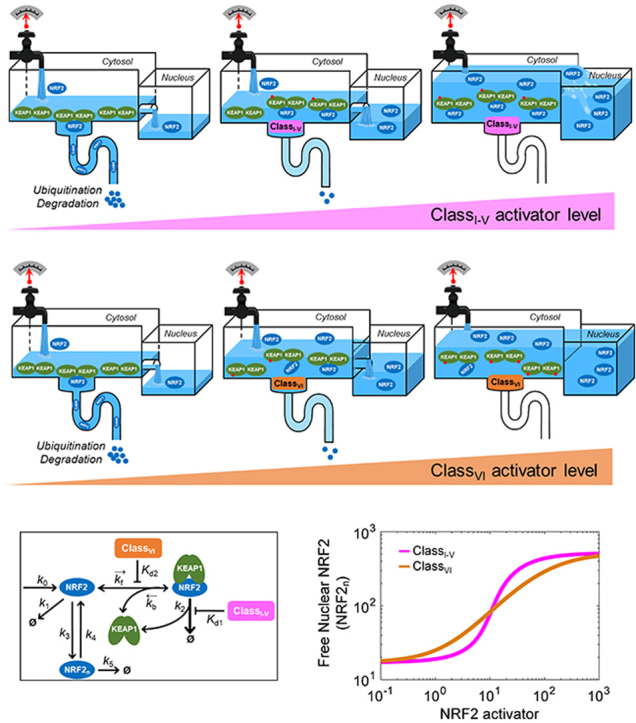
Class I–V electrophilic compounds induce increased formation of closed KEAP1-NRF2 complex and an abrupt increase in nuclear NRF2. By titrating KEAP1, class VI protein-protein interaction inhibitors induce dissociation of NRF2 from KEAP1 and a gradual increase in nuclear NRF2. Mathematical modeling captures the two different NRF2-activating mechanisms and predicts quantitatively different dose-response profiles of NRF2 activation.

Highlights

• •Steep (ultrasensitive) NRF2 activation can occur when it rises to saturate KEAP1.
• •Ultrasensitivity results from zero-order degradation and protein sequestration.
• •Optimal cytosolic and nuclear KEAP1 abundances exist for maximal ultrasensitivity.
• •Open and closed KEAP1-NRF2 complexes transition in cycle and equilibrium mode.
• •NRF2 activation by KEAP1-NRF2 interaction inhibitors is more gradual.

1. Introduction

Under oxidative and electrophilic stresses, the antioxidant capacity of cells is upregulated to meet the increasing demand for reactive species removal to maintain cellular redox homeostasis and limit cellular damage [1]. Similar to many other cytoprotective responses, this adaptive antioxidant response is underpinned by a complex molecular circuitry of primarily negative feedback and incoherent feedforward nature, involving both posttranslational and transcriptional regulations [2,3]. In mammalian cells, the main circuit mediating the transcriptional part of the antioxidant response is the KEAP1-NRF2-ARE pathway [4]. KEAP1 (Kelch ECH associating protein 1) is a thiol-based molecular sensor of ROS and other reactive species, which detects the redox status inside the cell and relays it to NRF2 (nuclear factor erythroid 2-related factor 2) [[5], [6], [7]]. As the master transcription factor, NRF2 partners with small Maf (sMaf) proteins to recognize promoter consensus sequences containing AREs (antioxidant response element) and induce a suite of target genes participating in antioxidant and detoxification reactions [[8], [9], [10], [11], [12]].

As the essential components for the transcriptional induction of antioxidant genes, the KEAP1 and NRF2 proteins and their interactions have been studied in great details in the past two decades [[13], [14], [15], [16]]. Tethered to the perinuclear actin cytoskeleton in the cytosol, KEAP1 functions as a homodimer [[17], [18], [19]]. The KEAP1 peptide is composed of 624 amino acid residues forming five functional domains: NTR (N-terminal region), BTB (Broad complex, Tramtrack, and Bric-a-Brac), IVR (intervening region), DGR (double glycine repeat) or Kelch-repeat, and CTR (C-terminal region) [20,86]. The BTB domain at the N-terminal is responsible for the formation of KEAP1 homodimer [22]. The neighboring DGR and CTR domains (collectively termed as DC region) are responsible for the interaction of KEAP1 with NRF2 [23,24]. As a redox sensor, KEAP1 contains 27 cysteine residues distributed across the five domains, many of which can be modified or conjugated on the thiol group by oxidants and electrophiles [5,25,26].

The NRF2 protein is composed of 589 amino acids forming six functional domains, Neh1 through Neh6 [12,27]. The Neh2 domain on the N-terminal is responsible for the binding with the KEAP1 dimer [28]. Within Neh2, there exist two conserved motifs: DLG and ETGE in the N-to-C direction, with an intervening sequence containing 7 lysine residues that can be ubiquitinated [29,30]. Both motifs are involved in mediating the association between NRF2 and KEAP1 dimer. The ETGE motif can bind to the DC region of one of the monomeric subunits of KEAP1 dimer, and the DLG motif of the same NRF2 molecule binds to the DC region of the other subunit [17]. Therefore, the KEAP1-NRF2 complex exists at an internal molar ratio of 2:1 [29,31]. The binding affinities between ETGE and KEAP1 and between DLG and KEAP1 are substantially different, with ETGE nearly 100-fold higher than DLG [24,[32], [33], [34], [35]]. It is therefore expected that the binding between KEAP1 and NRF2 occurs primarily in two sequential events: an initial ETGE-mediated association forming an “open” KEAP1-NRF2 complex, and a subsequent DLG-mediated intra-complex association forming a “closed” KEAP1-NRF2 complex [29].

By interacting with CUL3 (Cullin 3) via its BTB and IVR domains, KEAP1 is an adaptor of the KEAP1-CUL3-RBX1 E3 ubiquitin ligase complex [36]. When KEAP1 is associated with NRF2 in the closed state, KEAP1 is able to enable the transfer of ubiquitin molecules from the E2-ubiquitin conjugating enzyme bound to RBX1 (RING-box protein 1) to the 7 lysine residues in the intervening region between the DLG and ETGE motifs of NRF2 [29,30,37]. Once ubiquitinated, NRF2 is rapidly degraded by the proteasomal pathway [38]. Therefore, at basal conditions, NRF2 in the cytosol has a very short half-life, mostly ranging between 6 and 20 min [21,36,[39], [40], [41], [42], [43], [44]]. Under oxidative stress, certain sensor cysteine residues on KEAP1 are modified, which disables KEAP1's capability of mediating NRF2 ubiquitination [7,25,26]. As a result, NRF2 is stabilized and accumulates via de novo synthesis in the cytosol. Rising NRF2 then translocates into the nucleus where it induces antioxidant and detoxification genes [9,12,13].

Despite the molecular details of KEAP1 and NRF2 interactions have been revealed to a great extent, the quantitative signaling properties of the duo, culminating in NRF2 accumulation and nuclear translocation, are still poorly understood. It has been demonstrated that the binding between KEAP1 and NRF2 is not altered by oxidative stress, such that NRF2 does not dissociate from KEAP1 [38,43,45]. Since the discovery of the two-site sequential binding scheme for KEAP1-NRF2 interaction, i.e., first through ETGE and then through DLG, a hinge-latch model has been proposed [29,30,35]. The model considers that the ETGE-mediated association (the hinge) between KEAP1 and NRF2 is always engaged regardless of the presence of oxidative stressors. However, oxidative stressors may disrupt the weaker DLG-mediated association (the latch), rendering the closed KEAP1-NRF2 complex to revert to the open configuration [17,19]. In the open state, KEAP1 can no longer mediate the ubiquitination of NRF2, resulting in NRF2 stabilization. However, the validity of the hinge-latch model for KEAP1 cysteine-modifying, electrophilic oxidants has been challenged as emerging evidence suggests that these classes of compounds do not disrupt DLG binding [31]. Studies using Förster resonance energy transfer (FRET) revealed that the association between KEAP1 and NRF2 may become even stronger when cells are exposed to KEAP1 cysteine-modifying compounds [46].

The ETGE-mediated binding affinity between KEAP1 and NRF2 is high relative to their cellular abundances, with the dissociation constant (K_d) ranging between 5 and 26 nM, as summarized in Table S1 footnote [24,29,[33], [34], [35]], and the intracellular concentrations of KEAP1 dimer and NRF2 in the order of hundreds of nM as observed in a variety of cell types [47]. This suggests that when KEAP1 is in excess relative to NRF2, as often the case at the basal condition, NRF2 molecules are largely sequestered by KEAP1, leaving free NRF2 only a very small fraction of its total abundance. Such binding kinetics suggests that under oxidative stress, newly synthesized NRF2 molecules will be first sequestered by the remaining free KEAP1 reservoir, and only when the reservoir is nearly all filled by NRF2, will NRF2 becomes more available for nuclear translocation. Therefore, the magnitude of effective NRF2 activation is in part regulated by the KEAP1 reservoir capacity. This mode of NRF2 activation is recently suggested in the floodgate hypothesis [7,14,47]. If total NRF2 never accumulates to a level that can saturate existing KEAP1 molecules, nuclear NRF2 translocation and gene induction will remain muted. However, from a quantitative signaling prospective, if total NRF2 can rise to a higher level that nearly saturates KEAP1, KEAP1-dependent NRF2 degradation will operate near zero order and simultaneously NRF2 begins to escape KEAP1 sequestration, both of which are robust ultrasensitive mechanisms that can potentially produce a steep rise in free NRF2 levels [[48], [49], [50]]. This amplified, nonlinear NRF2 activation can in turn induce antioxidant genes strongly. Therefore, the kinetic parameters governing the interactions between KEAP1 dimer and NRF2 seem to be critical to the quantitative behaviors of KEAP1-NRF2-ARE-mediated redox signal transduction.

As far as effectively restoring redox homeostasis is concerned, the induction of antioxidant genes needs to be launched timely and to levels that are sufficient to counteract the oxidative impacts exerted by the stressors [2]. Strong antioxidant induction would require signal amplification, i.e., ultrasensitivity, by which a small percentage change in the redox status can be transduced to induce a larger percentage change in the expression of antioxidant genes [49,51]. A number of ultrasensitive mechanisms, including multistep signaling, homomultimerization, and autoregulation, have been revealed in the KEAP1-NRF2-ARE mediated transcriptional pathway [2,52]. They operate collectively to ensure that the cellular antioxidant capacity can be adequately induced to levels matching the intensity of the oxidant insult.

Mathematical modeling plays a crucial role in understanding and predicting the quantitative behavior of redox pathways [53,54]. Earlier modeling work including our own has included the KEAP1-NRF2 module in the larger context of NRF2-mediated antioxidant response pathways [44,52,[55], [56], [57], [58], [59]]. However, in most of these studies the KEAP1-NRF2 module was treated as simplified degradation network motifs, the details of KEAP1-NRF2 interactions and especially the likely nonlinearity in signaling have not been explicitly and fully explored. In the present study, we developed a suite of mathematical models of detailed KEAP1-NRF2 interactions to explore the quantitative properties of NRF2 activation. With these models we examined the roles of open and closed states of the KEAP1-NRF2 complex for the hinge-latch and floodgate hypotheses. Our simulation predicts that ultrasensitive NRF2 activation may occur via zero-order protein degradation and protein sequestration by KEAP1 under certain circumstances. Our mathematical models provide key quantitative insights into the signaling properties of the KEAP1-NRF2 module of the adaptive cellular antioxidant response pathway.

2. Methods

2.1. Model structure

In keeping with the principle of parsimony while exploring the importance of molecular details, we started with a minimal model capturing the basic interactions between KEAP1 and NRF2, and then progressively built more complexity into the model based on more recent quantitative knowledge about the interactions. As a result of this evolution, a total of 6 models were explored and summarized in Table 1. The models differentiate the two main categories of NRF2 activators: class I–V electrophilic compounds and class VI non-electrophilic KEAP1-NRF2 interaction inhibitors [16]. Specifically, class I–V activators conjugate or modify different redox-sensing cysteine residues of KEAP1, resulting in inhibition of KEAP1 as an E3 ligase adaptor, and consequently, stabilization of NRF2. Class VI activators directly compete with NRF2 for binding to KEAP1, thus disrupting KEAP1-NRF2 association. Table S12 summarizes the different classes of electrophilic compounds and their preferred cysteine residues as well as class VI activators. For all models, the following assumptions were made.

• (i)KEAP1 is treated as a single entity of homodimer with two binding sites for NRF2 as the dimeric structure is required for NRF2 binding and destabilization [22].
• (ii)Total KEAP1 abundance is a constant which is not altered by oxidative stress as extensively demonstrated in experimental studies [47], and thus KEAP1 turnover (synthesis and degradation) is not considered.
• (iii)Since the binding affinity between KEAP1 and the ETGE motif of NRF2 is much higher than the binding affinity between KEAP1 and the DLG motif of NRF2 (>100-fold), as summarized in Table S1 [24,29,[33], [34], [35]], for simplicity and following the concept of hinge-latch hypothesis [14], the initial interaction between KEAP1 and NRF2 is assumed to always start with the binding between KEAP1 and ETGE while the binding between KEAP1 and DLG occurs subsequently, as an intramolecular event.
• (iv)Oxidation or conjugation of one monomeric subunit of the KEAP1 dimer by a class I–V NRF2 activator is sufficient to cause KEAP1 to lose its ability to mediate NRF2 degradation. The oxidation or conjugation can occur on either free KEAP1 dimer or KEAP1 dimer complexed with NRF2.
• (v)For the Models (4a and 4b) with nuclear NRF2 translocation, cytosolic KEAP1 and nuclear KEAP1 are kept as separate pools.

Table 1.

KEAP1-NRF2 model features.

Model #	Model structure	Cycle mode of operation	Two-step ETGE binding	NRF2 nuclear translocation	Class of NRF2 activator
1	Fig. 1				I–V
2	Fig. 1	X			I–V
3a	Fig. 2A	X	X		I–V
3b	Fig. 6A	X	X		VI
4a	Fig. 7A	X	X	X	I–V
4b	Fig. 8A	X	X	X	VI

Note: X denotes that a model has the corresponding feature. The structure of each model is illustrated in the Figures indicated.

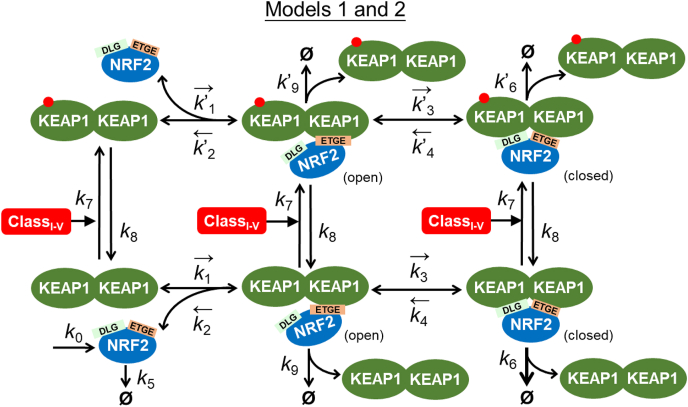
Model 1 is the most basic model, which captures the known essence of interactions between KEAP1 and NRF2 in the cytosol as shown in Fig. 1. In this model, NRF2 is synthesized at a constant rate of k₀. Free NRF2 (NRF2_free) is degraded with a first-order rate constant of k₅, reflecting KEAP1-independent degradation such as the one mediated by the Neh6 domain involving the GSK-3, β-TrCP and Cul1 system [[60], [61], [62], [63]]. NRF2_free first binds to one monomeric subunit of the KEAP1 dimer through ETGE with a second-order association rate constant k₁ and first-order dissociation rate constant k₂, forming an intermediate complex KEAP1_NRF2_open (termed open state here). Since KEAP1 in the open state of the complex cannot execute its E3 ligase adaptor function [29,30,37], NRF2 in KEAP1_NRF2_open is assumed to be degraded with a first-order rate constant of k₉ that is equal to k₅. As NRF2 is degraded, KEAP1 is recycled, joining the free KEAP1 dimer (KEAP1_free) pool. The NRF2 molecule in KEAP1_NRF2_open then further associates with the other unoccupied monomeric subunit of the KEAP1 dimer through the DLG motif with a first-order association rate constant k₃ and a first-order dissociation rate constant k₄, forming the final complex KEAP1_NRF2_closed (termed closed state here). NRF2 in KEAP1_NRF2_closed is degraded with a first-order rate constant of k₆ which is much higher than k₅ and k₉, reflecting KEAP1-mediated ubiquitination and accelerated degradation of NRF2, and KEAP1 dimer is recycled to the KEAP1_free pool. Class I–V oxidants and electrophiles can oxidize or conjugate KEAP1 [7,25,26]. In the model a class I–V compound (Class_I-V) converts KEAP1 to an oxidized form, KEAP1_o, with a second-order rate constant k₇. Besides on KEAP1_free, the same oxidation reaction is assumed to occur on the KEAP1 molecule in KEAP1_NRF2_open and KEAP1_NRF2_closed as well, forming KEAP1_o_NRF2_open and KEAP1_o_NRF2_closed respectively. KEAP1_{o_free}, KEAP1_o_NRF2_open, and KEAP1_o_NRF2_closed can be reduced back to the respective original states with a first-order rate constant k₈. The same values of k₇ and k₈ were used across all three oxidation/reduction reaction pairs for most of the simulations, however, we also explored the situations when the open and closed configurations of KEAP1-NRF2 complexes may affect the rates of oxidation or conjugation of the reactive cysteines of KEAP1 by oxidants. Since the alteration of NRF2 stability only occurs in the closed state, NRF2 in KEAP1_o_NRF2_open is degraded with a first-order rate constant of k’₉ that is equal to k₉. NRF2 in KEAP1_o_NRF2_closed is degraded with a first-order rate constant of k’₆ that is much lower than k₆, reflecting the well-established fact that cysteine-modified KEAP1 in the closed state loses its capability to mediate the ubiquitination and degradation of NRF2 [29,30,37]. In both the k’₉ and k’₆ steps, KEAP1_o is recycled, joining the free KEAP1_{o_free} pool. The binding between NRF2_free and KEAP1_o through the ETGE motif is described by the second-order association rate constant k’₁ and first-order dissociation rate constant k’₂, which are kept the same as k₁ and k₂ respectively since class I–V oxidants do not alter the binding affinity between KEAP1 and NRF2 [38,43,45]. The association and dissociation rate constants k’₃ and k’₄ for the intramolecular DLG binding between KEAP1_o_NRF2_open and KEAP1_o_NRF2_closed are also kept the same as k₃ and k₄ respectively, however, their values were varied to explore the behavior of the hinge-latch hypothesis.

Fig. 1.

Structure of KEAP1-NRF2 Models 1 and 2. The models feature one-step ETGE binding and interaction with class I–V activator. Short arrow bars next to a parameter symbol denote the direction of the reversible binding described by the parameter. Φ denotes degradation. These denotations apply to all other model structures.

The detailed structures of Models 2, 3a, 3b, 4a, and 4b are presented in Fig. 1, Fig. 2, Fig. 6, Fig. 7, Fig. 8A, respectively. Briefly, in Model 2, the DLG-mediated internal binding kinetics (k₃ and k₄) between KEAP1_NRF2_open and KEAP1_NRF2_closed is modified from Model 1 to simulate the situation that the transitioning between the two states occurs in a cycle mode rather than an equilibrium mode, as observed experimentally [46]. In Models 3a and 3b, the ETGE-mediated binding between KEAP1 and NRF2 is modified from the one-step mode as in Models 1 and 2 to a two-step mode to simulate the situation that ETGE-mediated binding involves an initial fast binding event followed by a subsequent slow binding event observed experimentally [35]. This modification allows us to achieve the cycle mode of operation without altering the DLG-mediated binding kinetics dramatically as done in Model 2. Models 3a and 3b consider class I–V and VI NRF2 activators as separate cases respectively. Lastly, in Models 4a and 4b, translocation of NRF2 to the nucleus and its interaction with nuclear KEAP1 in the nucleus are considered, and the two models consider class I–V and VI NRF2 activators as separate cases.

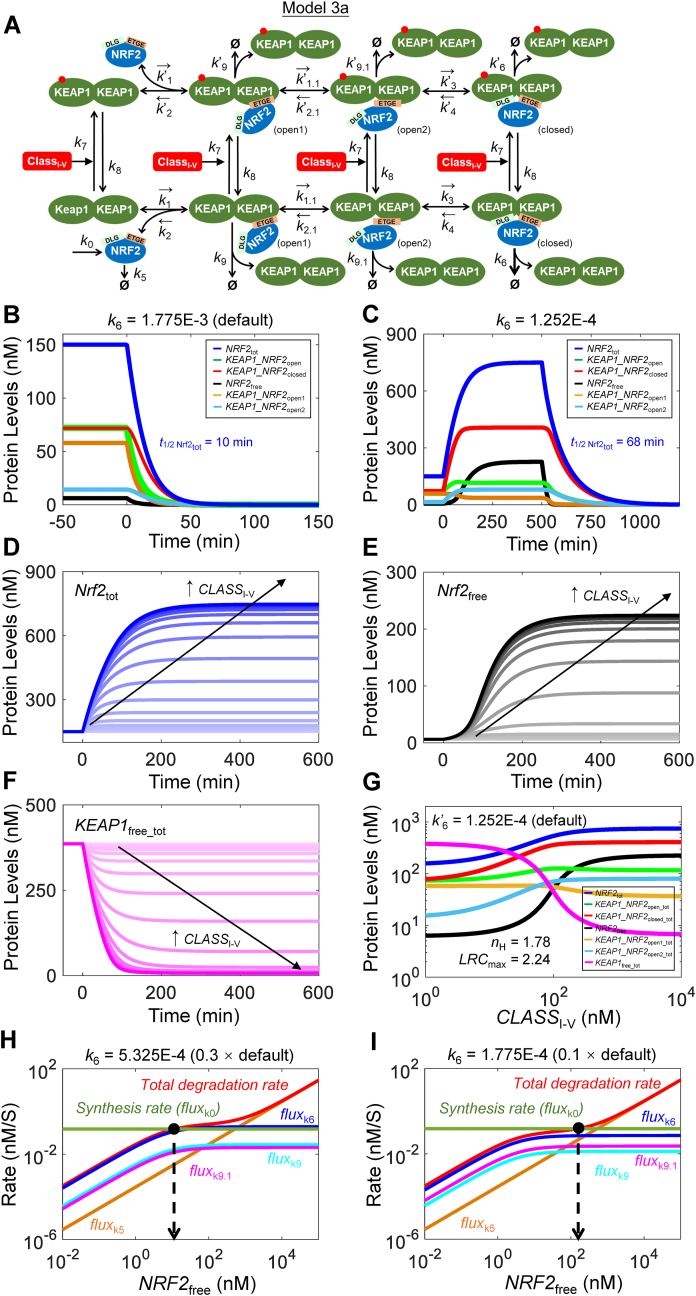
Fig. 2.

Structure, and dynamical and steady-state behaviors of Model 3a. (A) Structure of Model 3a featuring two-step ETGE binding and interaction with class I–V activator. (B) Dynamical changes of basal NRF2_free, KEAP1_NRF2_open1, KEAP1_NRF2_open2, KEAP1_NRF2_closed, and NRF2_tot in response to termination of NRF2 synthesis (by setting k₀ = 0) starting at 0 min with k₆ at default value. (C) Dynamical changes of various NRF2 species in response to stabilization of NRF2 in KEAP1_NRF2_closed by setting k₆ = 1.252E-4 starting at 0 min and in response to termination of NRF2 synthesis (by setting k₀ = 0) starting at 500 min. For simulations in (B) and (C), CLASS_I-V level is kept at zero. Dynamical changes of (D)NRF2_tot, (E)NRF2_free, and (F)KEAP1_{free_tot} in response different levels of CLASS_I-V with k’₆ at default value. (G) Steady-state dose-response curves of various NRF2 species and KEAP1_{free_tot} on double-log scale with k’₆ at default value. Shown are n_H and LRC_max for NRF2_free; n_H and LRC_max for NRF2_total are 1.22 and 0.42 respectively (not shown). (H–I) Flux analyses for conditions when NRF2 in KEAP1_NRF2_closed is stabilized by setting k₆ to 30% (H) and 10% (I) of default value.

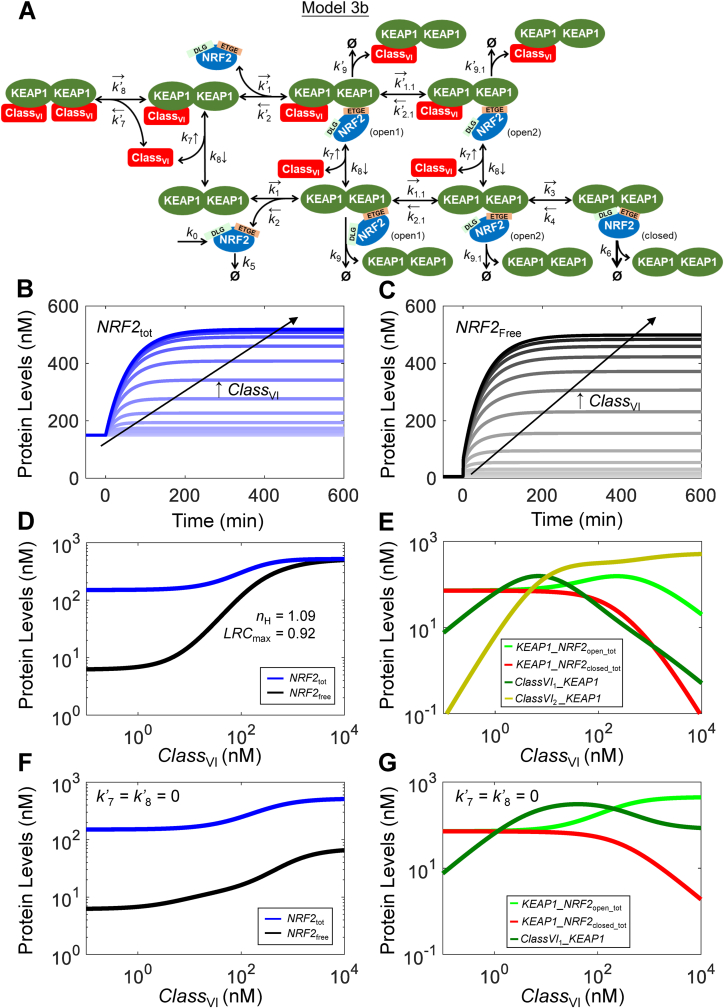
Fig. 6.

Structure, and dynamical and steady-state behaviors of Model 3b. (A) Structure of Model 3b featuring two-step ETGE binding and interaction with class VI activator. Dynamical changes of (B)NRF2_tot and (C)NRF2_free in response different levels of CLASS_VI. (D) Steady-state dose-response curves of NRF2_tot and NRF2_free. Shown are n_H and LRC_max for NRF2_free; n_H and LRC_max for NRF2_total are 1.35 and 0.35 respectively (not shown). (E) Steady-state dose-response curves of KEAP1_NRF2_{open_tot}, KEAP1_NRF2_{closed_tot}, ClassVI₁_KEAP1 (Class VI activator-KEAP1 complex containing one activator molecule) and ClassVI₂_KEAP1 (containing two activator molecules). (F–G) Steady-state oxidant-response curves of NRF2_tot, NRF2_free, KEAP1_NRF2_{open_tot}, KEAP1_NRF2_{closed_tot}, and ClassVI₁_KEAP1 under condition when only one class VI activator molecule is allowed to bind to KEAP1 by setting k’₇ = k’₈ = 0.

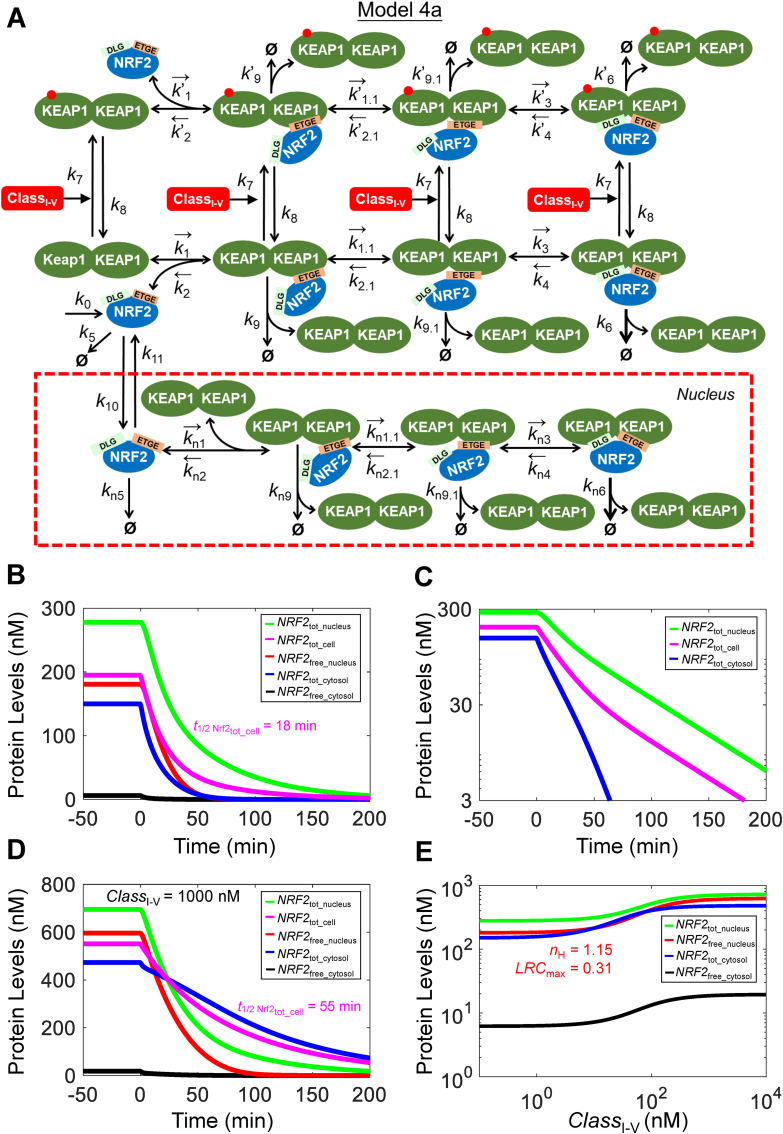
Fig. 7.

Structure, and dynamical and steady-state behaviors of Model 4a. (A) Structure of Model 4a featuring two-step ETGE binding, nuclear NRF2 translocation, and interaction with class I–V activator. (B) Dynamical changes of basal NRF2_{tot_cell}, NRF2_{tot_nucleus}, NRF2_{tot_cytosol}, NRF2_{free_nucleus}, and NRF2_{free_cytosol} in response to termination of NRF2 synthesis (by setting k₀ = 0) starting at 0 min. (C)NRF2_{tot_cell}, NRF2_{tot_nucleus}, and NRF2_{tot_cytosol} in (B) shown in log Y scale. (D) Dynamical changes of various NRF2 species previously induced by a high level of CLASS_I-V at 1000 nM in response to termination of NRF2 synthesis (by setting k₀ = 0) starting at 0 min. E) Steady-state dose-response curves of various NRF2 species. n_H and LRC_max of NRF2_{free_nucleus} curve are indicated.

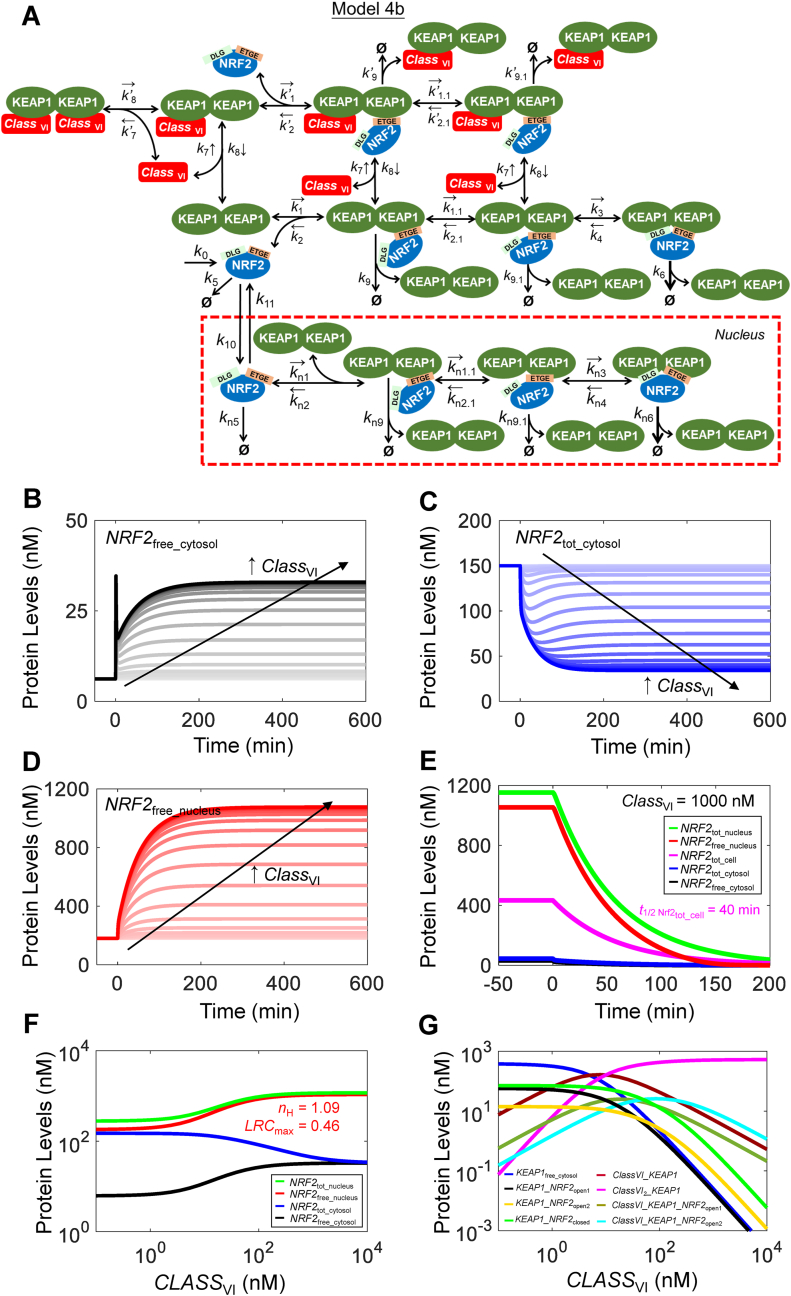
Fig. 8.

Structure, and dynamical and steady-state behaviors of Model 4b. (A) Structure of Model 4b featuring two-step ETGE binding, nuclear NRF2 translocation, and interaction with class VI activator. Dynamical changes of (B)NRF2_{free_cytosol}, (C)NRF2_{tot_cytosol}, and (D)NRF2_{free_nucleus} in response to different levels of CLASS_VI.(E) Dynamical changes of various NRF2 species previously induced by a high level of CLASS_VI at 1000 nM in response to termination of NRF2 synthesis (by setting k₀ = 0) starting at 0 min. (F–G) Steady-state dose-response curves of various NRF2 species and KEAP1 species respectively.

2.2. Model parameters and ordinary differentiation equations (ODEs)

The values of most of the model parameters, including binding rate constants, degradation rate constants, and abundances (concentrations) of KEAP1 and NRF2, were obtained or derived from the literature. For those unknown parameter values, they were estimated based on other constraints of the modeled system. The values of all parameters in all 6 models are presented in Table S1 and the references and details of determination and calculation of the parameter values are provided in the footnote. The unit of concentration of the state variables is nM and time is second (S). The ODEs are presented in Tables S2–S6 and algebraic equations calculating the concentrations of state variables in various combinations are presented in Table S7. The steady-state concentrations of state variables at the basal and maximally induced conditions are in Tables S8 and S9 respectively, and the steady-state turnover fluxes of reactions at the basal and maximally induced conditions are in Tables S10 and S11 respectively.

2.3. Modeling tools

The models were constructed and simulated in Berkeley Madonna (version 8.3.18, University of California, Berkeley, CA) using the “Rosenbrock (stiff)” ODE solver. All model codes in Berkeley Madonna format as well as in R format are available as additional Supplemental files and can also be accessed at the GitHub repository https://github.com/pulsatility/Mathematical-Modeling-of-KEAP1-NRF2.git.

2.4. Metrics of ultrasensitivity

In the present study, all dose-response (DR) curves were obtained once the simulation has achieved steady state. The degree of ultrasensitivity of a steady-state DR curve were evaluated with two related metrics. First, the Hill coefficient, n_H, is approximated from the equation

$$n_{\mathrm{H}}=\frac{\ln 81}{\ln {\displaystyle \frac{X_{0.9}}{X_{0.1}}}},$$ (1)

where X_0.9 and X_0.1 are the concentrations of an NRF2 activator that produce 90% and 10% of the maximal NRF2 response respectively (after subtracting the basal NRF2 levels) [49]. n_H represents the overall steepness or global degree of ultrasensitivity of a DR curve. Second, we evaluate the local response coefficient (LRC) of a DR curve by calculating all slopes of the curve on dual-log scales, which are equivalent to the ratios of the fractional change in response (R) to the fractional change in dose (D) [64]:

$$LRC=\frac{\text{dln}R}{\text{dln}D}.$$ (2)

The maximal |LRC| of a DR curve, LRC_max, represents the maximal amplification capacity of KEAP1-NRF2-mediated signaling. Typical ultrasensitive responses have LRC_max values substantially above 1. The comparison between n_H and LRC_max is important as these two metrics are not necessarily equivalent and depend on the basal response level and the shape of the DR curve; n_H alone can misrepresent the actual degree of signal amplification [49,65,66].

3. Results

3.1. Models 1 and 2

In-depth analyses of the properties and response behaviors of the two basic models (1 and 2) are provided in the Supplemental Material. Simulations of these two models produced the initial findings that the KEAP1-NRF2 interaction is capable of producing ultrasensitive activation of free NRF2 by class I–V compounds (Figs. S1C, S1D, and S3F), and the ultrasensitivity results from saturation of KEAP1 by NRF2 where both zero-order degradation and protein sequestration of NRF2 occur (Figs. S3G–S3H).

In Model 1, however, the abundance ratio of the open and closed KEAP1-NRF2 complexes remains constant at 1:1 at all times in all conditions (Figs. S1A-S1C and S2), indicating these two states are always at equilibrium to each other. Using FRET to track the open and closed states of KEAP1-NRF2 complex, Baird et al. observed that the two states diverge and do not follow an equilibrium mode of operation in a variety of chemically perturbed conditions [46]. Rather, a “cyclic sequential attachment and regeneration” (abbreviated as “cycle”) mode of operation was suggested. In this mode, because of the rapid degradation of NRF2 in the closed KEAP1-NRF2 complex, KEAP1 is quickly released (or regenerated) to join the free KEAP1 dimer pool and able to sequester newly synthesized NRF2 again, thus completing a global cycle for KEAP1. Under oxidative stress, this cycle is blocked as the NRF2 degradation-coupled release of KEAP1 from the closed KEAP1-NRF2 complex is inhibited, leading to accumulation of the closed state and depletion of free KEAP1 dimer. Flux analysis indicated that Model 1 operates in equilibrium mode because of the much higher association and dissociation fluxes through the DLG-binding step than the connected NRF2 turnover fluxes (Tables S10–S11). We thus evolved Model 1 into Model 2 by dramatically reducing the parameter values of k₃ and k₄ (the rate constants for DLG binding), which indeed successfully made Model 2 behave in a cycle mode with divergent responses of the open and closed KEAP1-NRF2 complexes (Figs. S3A-S3B, and S4). However, this “success” was achieved by setting k₄, the dissociation rate constants for DLG binding, to a value that is hundreds-fold lower than experimentally measured [35]. Importantly, in the same study, it was also demonstrated that the first binding event, i.e., between KEAP1 and the ETGE motif of NRF2, is a thermodynamically two-step process, involving an initial fast binding step to form a transient, intermediate complex (termed KEAP1_NRF2_open1 here) first, followed by a much slower second step that leads to a more stable configuration of the open complex (termed KEAP1_NRF2_open2 here). As a minimal model, Models 1 and 2 only considered single-step ETGE binding. We hypothesized that this second, slow ETGE-binding step may account for the experimentally observed cycle mode of operation. We next set out to test this hypothesis with Model 3a.

3.2. Model 3a (two-step ETGE-Binding for class I–V activators)

In Model 3a we added an extra, reversible step, k_1.1 and k_2.1, to account for the intramolecular state transition between KEAP1_NRF2_open1 and KEAP1_NRF2_open2 (Fig. 2A), with k₄ restored to the high value measured in Ref. [35]. As detailed in Table S1 footnote, we then iteratively adjusted the values of k₀, k₃ and k₆ such that the basal NRF2_tot level is still at 150 nM and half-life at 10 min, and the basal open (KEAP1_NRF2_open = KEAP1_NRF2_open1 + KEAP1_NRF2_open2):closed (KEAP1_NRF2_closed) state ratio remains at 1:1 (Fig. 2B). NRF2 in KEAP1_NRF2_open1 and KEAP1_NRF2_open2 were assumed to degrade with the same rate constants (k₉ = k_9.1 = k₅).

At the basal condition, with the default parameter setting of Model 3a, the second step of ETGE binding (k_1.2 and k_2.1) does not operate in equilibrium mode. This is because flux_k1.1 = 0.133 and flux_k2.1 = 1.73E-3 nM/S, thus only a tiny fraction of KEAP1_NRF2_open2 is returned to KEAP1_NRF2_open1 (Table S10). Another small fraction is degraded through flux_k9.1 at 4.1E-3 nM/S. Over 95% of KEAP1_NRF2_open2 is moved forward to become KEAP1_NRF2_closed at a net flux (flux_k3 - flux_k4) of 0.127 nM/S. In contrast, both the first step of ETGE binding (k₁ and k₂) and the step of DLG binding (k₃ and k₄) operate in equilibrium mode, with flux_k1 and flux_k2 at 16.48 and 16.33 nM/S respectively, and flux_k3 and flux_k4 at 14.19 and 14.07 nM/S respectively, all of which are >100 fold higher than their connected turnover fluxes (Table S10). As a result, the NRF2_free:KEAP1_NRF2_open1 ratio, which is 1:9.4, is largely determined by the k₂:(2×k₁×KEAP1_free) ratio, and the KEAP1_NRF2_open2:KEAP1_NRF2_closed ratio, which is 1:5, is largely determined by the k₄:k₃ ratio. At 58 and 14 nM respectively, KEAP1_NRF2_open1 dominates KEAP1_NRF2_open2, accounting for 80% of the total open KEAP1-NRF2 complex (Fig. 2B and Table S8).

When setting k₀ = 0 to examine the decay of NRF2 species from their basal steady states, NRF2_free:KEAP1_NRF2_open1 and KEAP1_NRF2_open2:KEAP1_NRF2_closed remain at the same equilibrium ratios as above as all NRF2 species decrease (Fig. 2B). NRF2_free and KEAP1_NRF2_open1 decrease quickly with a half-life of about 4–5 min, due primarily to the depletion of KEAP1_NRF2_open1 through flux_k1.1, which is about 8-fold greater than flux_k9. In contrast, KEAP1_NRF2_open2 and KEAP1_NRF2_closed do not decrease as fast because of the continued supply of KEAP1-NRF2 complex through flux_k1.1. Because of the differential decay rates, the relative abundance of KEAP1_NRF2_open1 and KEAP1_NRF2_open2 switches positions over time, with KEAP1_NRF2_open2 becoming the dominant form eventually. Furthermore, the levels of KEAP1_NRF2_open and KEAP1_NRF2_closed diverge quickly from the basal ratio of 1:1 to 1:2.5 by 15 min, and to about 1:4.5 eventually. This 1:4.5 ratio closely reflects the equilibrium ratio of KEAP1_NRF2_open2:KEAP1_NRF2_closed, which is determined primarily by the k₄:k₃ ratio.

To examine the behavior of Model 3a when NRF2 in KEAP1_NRF2_closed is stabilized, we first lowered k₆ to different values, while keeping CLASS_I-V = 0. As k₆ decreases from the default 1.775E-3 S⁻¹ (equivalent t_1/2 = 6.5 min) to 1.252E-4 (which is the default value of k’₆, equivalent t_1/2 = 92 min), all NRF2 species (except KEAP1_NRF2_open1) increase and reach steady states in about 400 min (Fig. 2C). The open:closed ratio decreases and reaches about 1:2.8 at 1 h, and settles to 1:3.5 (approaching the k₄:k₃ ratio) at steady state, with KEAP1_NRF2_open2 switching to the dominant form of the open-state complex. When reaching steady states, NRF2_tot increases by 5-fold, while NRF2_free increases by a much greater fold, from 6.2 to 227 nM (36.6-fold). At this activated state, by setting k₀ = 0, all NRF2 species decrease, with a half-life of 68 min for NRF2_tot, while NRF2_free disappears much more quickly (Fig. 2C). By setting k₆ to even lower values, the maximal levels of both NRF2_free and NRF2_tot increase but only to a limited extent and the half-life of NRF2_tot lengthens to 126 min in the extreme case when k₆ = 0. (Figs. S5A and S5C).

The temporal behaviors of NRF2_tot (Fig. 2D), NRF2_free (Fig. 2E), and KEAP1_free (Fig. 2F) in response to a class I–V activator are similar to Model 2. With increasing CLASS_I-V levels, it takes a longer time for NRF2_tot to reach steady states, while the NRF2_free response, although initially delayed, rises increasingly faster. For steady-state dose-response relationships, KEAP1_NRF2_{open2_tot} (KEAP1_NRF2_open2 + KEAP1_o_NRF2_open2) and KEAP1_NRF2_{closed_tot} (KEAP1_NRF2_closed + KEAP1_o_NRF2_closed) both increase with increasing CLASS_I-V levels, while remaining at a constant equilibrium ratio (Fig. 2G). In contrast, steady-state KEAP1_NRF2_{open1_tot} (KEAP1_NRF2_open1 + KEAP1_o_NRF2_open1) first increases slightly then decreases (Fig. 2G). Steady-state NRF2_free exhibits an ultrasensitive, sigmoidal dose-response with respect to CLASS_I-V levels, with an n_H of 1.78 and LRC_max of 2.24 (Fig. 2G).

Flux analysis shows that the total degradation rate curve of NRF2 exhibits an S-shape, as in Model 2 (Fig. 2H and I). However, because of the two-step ETGE binding implemented in Model 3, higher concentrations of NRF2_free are required to support turnover flux levels that are similar to Model 2, which results in a right shift of the flux_k6 and flux_k9 curves toward the flux_k5 curve. This shift leads to a shorter second phase of the S-shaped total degradation rate curve, and the second phase is not as flat as in Model 2. As the k₆ value is varied mimicking different stress levels, the intersection point between the synthesis rate and total degradation rate curves still swings quite dramatically. When k₆ is lowered from 5.325E-4 to 1.775E-4, a 3-fold decrease, the corresponding steady-state NRF2_free concentration increases by 13-fold (Fig. 2H and I), indicating clearly there is some signal amplification.

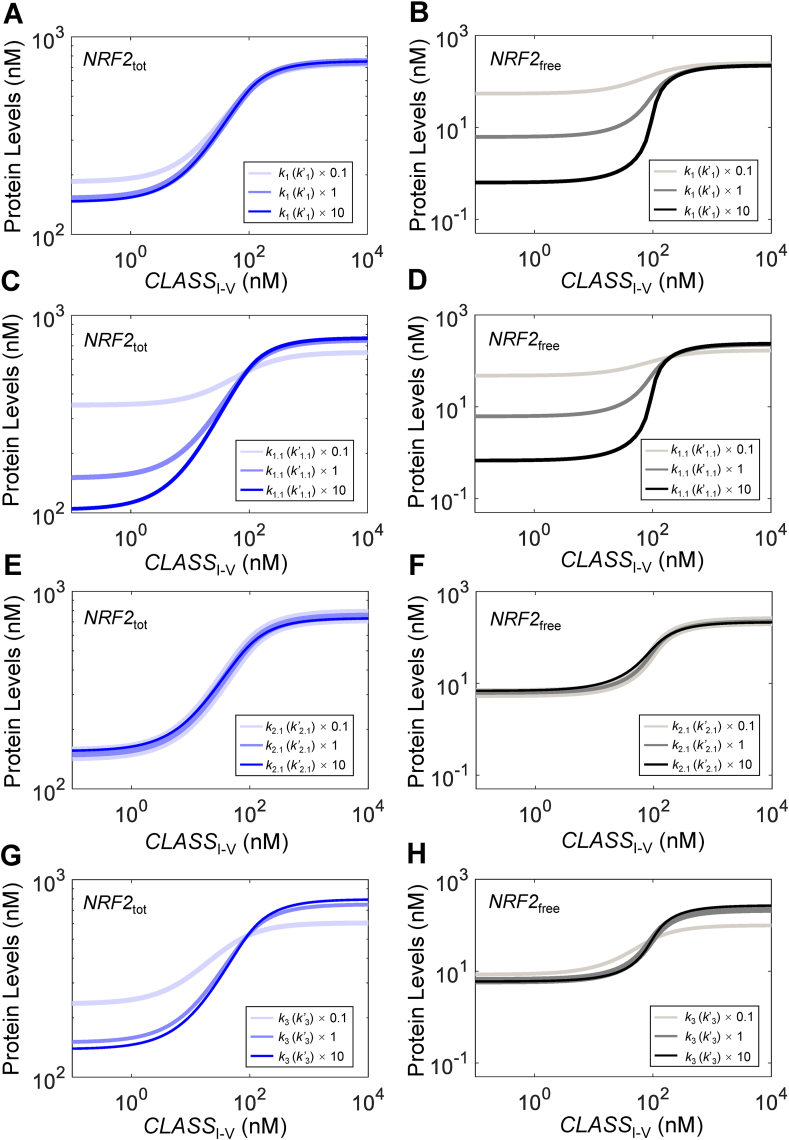
3.2.1. Effects of k₁(k’₁) and k₂ (k’₂)

We next examined the effects of different parameters on the NRF2 response in Model 3a. Enhancing the ETGE-mediated first-step binding affinity between free KEAP1 and free NRF2, by increasing k₁ and k’₁ by 10-fold, only marginally decreases the basal NRF2_tot level and half-life (Fig. S6A) with nearly no effect on the steady-state dose-response curve (Fig. 3A). Neither the basal levels of different open and closed KEAP1-NRF2 complexes nor their steady-state dose-response curves are affected (Figs. S6E–S6H). In contrast, the basal NRF2_free level decreases dramatically and the ultrasensitivity of the dose-response curve is enhanced markedly without much change in the maximal level (Fig. 3B). Decreasing k₁ and k’₁ by 10-fold appears to have slightly larger albeit opposite effects on the various NRF2 species (Figs. 3A and S6), and dramatically increases the basal NRF2_free level and reduces its ultrasensitivity (Fig. 3B). The time delay in the NRF2_free response disappears with decreasing k₁ and k’₁ (Fig. S6C) and is further increased with increasing k₁ and k’₁ (Fig. S6D). Varying k₂ and k’₂ has opposite effects as varying k₁ and k’₁ (simulation results not shown).

Fig. 3.

Effects of KEAP1-NRF2 binding parameters on NRF2 responses in Model 3a. Effects of varying (A–B)k₁ (k’₁), (C–D)k_1.1 (k’_1.1), (E–F)k_2.1 (k’_2.1), and (G–H)k₃ (k’₃) on steady-state dose-response curves of NRF2_tot (left panels) and NRF2_free (right panels). Note k_i = k'_i for i = 1, 1.1, 2.1, or 3; ×0.1, ×1, and ×10 denote 0.1, 1, and 10 times default values.

3.2.2. Effects of k_1.1(k’_1.1) and k_2.1 (k’_2.1)

We next examined the effects of the ETGE-mediated second-step binding, which is much slower than the first step and is the key step for making Model 3a behave in a cycle mode at the basal condition. Increasing k_1.1 and k’_1.1 shifts the balance between the two open states, causing a reduction in KEAP1_NRF2_{open1_tot} (Fig. S7E) but only a slight increase in KEAP1_NRF2_{open2_tot} (Fig. S7F) and KEAP1_NRF2_{closed_tot} (Fig. S7H), resulting in a net decrease of the total open state KEAP1_NRF2_{open_tot} (Fig. S7G). As a result, the basal level of NRF2_tot is reduced with a slight decrease in its half-life (Fig. S7A) and the steady-state dose-response curve becomes steeper (Fig. 3C). In comparison, the basal level of NRF2_free is considerably reduced and the ultrasensitivity of the dose-response curve is dramatically enhanced with little change in the maximal response level (Fig. 3D). Decreasing k_1.1 and k’_1.1 has the opposite but generally larger effects. It causes an increase in KEAP1_NRF2_{open1_tot} (Fig. S7E) and a decrease in KEAP1_NRF2_{open2_tot} (Fig. S7F) and KEAP1_NRF2_{closed_tot} (Fig. S7H), resulting in a net increase of KEAP1_NRF2_{open_tot} which seems to have a flat response to CLASS_I-V (Fig. S7G). As k_1.1 and k’_1.1 are decreased by 10-fold, the basal level of NRF2_tot is dramatically increased with its half-life lengthened (Fig. S7A) and the steady-state dose-response curve becomes much shallower (Fig. 3C). The basal level of NRF2_free is considerably elevated and the ultrasensitivity of its dose-response curve is dramatically reduced (Fig. 3D). The time delay in the NRF2_free response disappears with decreasing k_1.1 and k’_1.1 (Fig. S7C) and is further increased with increasing k_1.1 and k’_1.1 (Fig. S7D). Varying k_2.1 and k’_2.1, especially when lowering the values, seems to affect KEAP1_NRF2_{open1_tot} the most, with a minimal effect on all other NRF2 species (Fig. 3E-F and S7I–S7P), which is consistent with the low backward flux nature of this second-step ETGE binding, where the backward flux (flux_k2.1 + flux_k’2.1) is only a tiny fraction of the forward flux (flux_k1.1 + flux_k’1.1).

3.2.3. Effects of k₃(k’₃) and k₄ (k’₄)

We next examined the effects of DLG-mediated binding. Increasing k₃ and k’₃ by 10-fold reduces the KEAP1_NRF2_{open2_tot} level dramatically across the range of CLASS_I-V levels as expected (Fig. S8F). However, it only marginally decreases the basal KEAP1_NRF2_{open1_tot} (Fig. S8E) and increases the basal KEAP1_NRF2_{closed_tot} (Fig. S8H) levels. At high CLASS_I-V levels, KEAP1_NRF2_{open1_tot} is suppressed considerably and KEAP1_NRF2_{closed_tot} increases to higher levels. These changes have only slight effects on the basal NRF2_tot level and its half-life (Fig. S8A), and the steady-state dose-response curve (Fig. 3G). The basal NRF2_free level decreases marginally and the ultrasensitivity of the steady-state dose-response curve barely increases with a slightly higher maximal level (Fig. 3H). Decreasing k₃ and k’₃ by 10-fold has opposite but larger effects on the various species. With KEAP1_NRF2_{open2_tot} at higher levels (Fig. S8F), KEAP1_NRF2_{open1_tot} (Fig. S8E) becomes higher and KEAP1_NRF2_{closed_tot} (Fig. S8H) becomes lower. Both basal NRF2_tot and NRF2_free levels increase and maximal response levels decrease, reducing their ultrasensitivity (Fig. 3G and H). The time delay in the NRF2_free response does not appear to be affected by k₃ and k’₃ (Figs. S8B–S8D). Varying k₄ and k’₄ has opposite effects as varying k₃ and k’₃, and reducing k₄ and k’₄ to zero thus making the DGL-mediated binding irreversible has a similar effect to reducing k₄ and k’₄ by 10-fold (simulation results not shown).

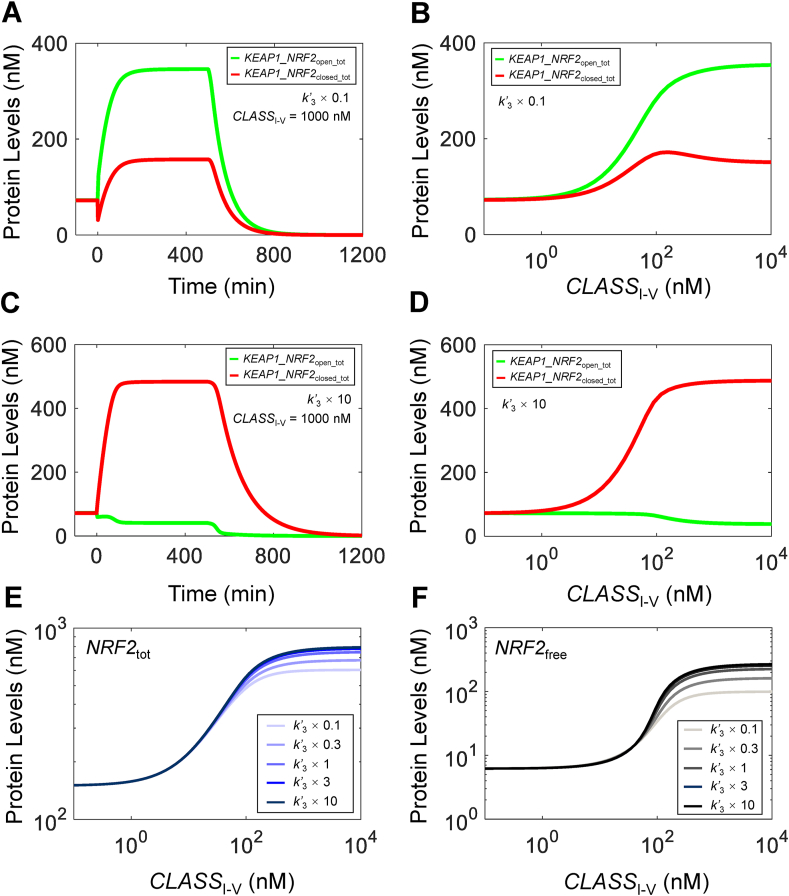
3.2.4. Effects of hinge-latch mode of operation

The hinge-latch hypothesis states that under oxidative stress by class I–V NRF2 activators, the DLG-mediated binding is weakened, likely due to the cysteine modification on KEAP1 in various domains, and the level of the closed KEAP1-NRF2 complex is reduced so that NRF2 is no longer destabilized by KEAP1 [29,30,35]. Here we used Model 3a to explore the effects of the hinge-latch hypothesis. When setting k’₃ (which is the association rate constant for the intramolecular binding between oxidized/modified KEAP1 and DLG motif) to a lower value (1/10 of default) to mimic a hinge-latch mode of operation, a high CLASS_I-V level leads to increases in both the open and closed states (Fig. 4A and B). However, the open state level is higher than the closed state, which runs counter to the decreasing open:closed ratio under oxidative stress as expected [46]. The hinge-latch simulation also predicts more muted maximal responses of NRF2_tot (Fig. 4E) and NRF2_free (Fig. 4F). Interestingly, increasing k’₃ to simulate strengthened DLG binding under oxidative stress has the opposite effect: the open:closed ratio further increases (Fig. 4C and D) and the NRF2_tot (Fig. 4E) and NRF2_free (Fig. 4F) dose-response curves exhibit higher maximal levels and enhanced ultrasensitivity, although these changes approach a limit as k’₃ is increased by > 10-fold. Changing the DLG binding affinity by varying k’₄ has opposite effects as varying k’₃ (simulation results not shown). Therefore, with current parameter settings, the hinge-latch mode of operation is predicted to be less effective in activating NRF2 by class I–V compounds.

Fig. 4.

Effects of varying parameter k’₃alone on NRF2 responses in Model 3a to test hinge-latch hypothesis - with k’₆at default value. Dynamical changes of KEAP1_NRF2_{open_tot} and KEAP1_NRF2_{closed_tot} in response to a high level of CLASS_I-V at 1000 nM starting at 0 min and in response to termination of NRF2 synthesis (by setting k₀ = 0) starting at 500 min, when k’₃ is (A) 0.1 and (C) 10 times of default value. Steady-state dose-response curves of KEAP1_NRF2_{open_tot} and KEAP1_NRF2_{closed_tot} when k’₃ is (B) 0.1 and (D) 10 times of default value. (E–F) Effects of varying k’₃ on steady-state dose-response curves of NRF2_tot and NRF2_free respectively.

3.2.5. Effects of k₇ and k₈

It is possible that the structural alignment of reactive cysteine residues of KEAP1 is altered in the open and closed KEAP1-NRF2 complex, relative to that in free KEAP1. As a result, the ease with which the cysteines are modified by electrophilic compounds or de-modified by reducing enzymes may change, depending on whether KEAP1 is free or complexed with NRF2. To explore this scenario, the values of parameters k₇ and k₈ individually associated with KEAP1_NRF2_open1, KEAP1_NRF2_open2 and KEAP1_NRF2_closed were varied relative to those for free KEAP1. In general, increasing k₇ or decreasing k₈ shifts the NRF2_tot and NRF2_free dose-response curves to the left and decreasing k₇ or increasing k₈ does the opposite, without affecting the maximal levels (Fig. S10). In some cases, there are small changes in the ultrasensitivity of the curves. Interestingly, k₇ and k₈ governing the modification of KEAP1_NRF2_closed play a dominant role in shifting the NRF2 dose responses, while k₇ and k₈ for the open states have a minimal effect. This result is consistent with the notion that only the stability of NRF2 in the closed KEAP1-NRF2 complex is altered by the modifications of reactive cysteine residues of KEAP1.

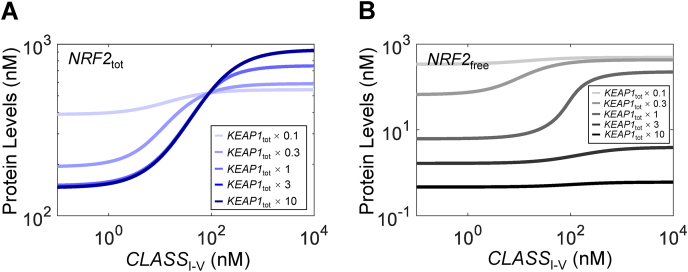
3.2.6. Effects of KEAP1 abundance

The relative abundance of KEAP1 and NRF2 can have important effects on NRF2 activation. The current default basal NRF2_tot:KEAP1_tot ratio is about 1:4. Increasing KEAP1_tot by up to 10-fold has little effect on the basal NRF2_tot level and its half-life (Fig. S11A). This lack of effect is because at the default KEAP1_tot level, there is already sufficient KEAP1 to sequester the majority of NRF2, so increasing KEAP1_tot further does not alter the fraction of NRF2 in complex with KEAP1 much, including the closed state which is actively degraded. But the maximal level of the dose-response curve of NRF2_tot increases (Fig. 5A) and this occurs because NRF2 in KEAP1_o_NRF2_closed is not degraded as readily as NRF2_free and NRF2 in the open state. Increasing total KEAP1 abundance reduces basal NRF2_free and the maximal response levels dramatically (Fig. 5B). The muted response is mostly due to the increased sequestering effect of higher KEAP1 abundance. When KEAP1_tot is reduced from its default value, basal NRF2_tot levels and its half-life increase (Fig. S11A), and the dose-response curve becomes shallower with lower maximal response levels (Fig. 5A). Basal NRF2_free increases dramatically with little further increase in response to CLASS_I-V at higher levels, indicating constitutive activation of NRF2 (Fig. 5B). These results suggest that there is an optimal NRF2:KEAP1 ratio that can maximize the dynamic range of free NRF2 in response to oxidative stress.

Fig. 5.

Effects of total KEAP1 abundance on NRF2 responses in Model 3a. Steady-state dose-response curves of (A)NRF2_tot and (B)NRF2_free under different values of total KEAP1 abundance relative to default value.

3.3. Model 3b (two-step ETGE-Binding for class VI activators)

Since Model 3a represents the most updated biology of KEAP1 and NRF2 interactions, the remaining Models (3b, 4a and 4b) are based on this model. In Model 3b, we simulated class VI NRF2 activators, which activate NRF2 by competing with NRF2 for binding to the DC domain of KEAP1 [[67], [68], [69]]. Model 3b keeps the interactions between KEAP1 and NRF2 at the basal condition as in Model 3a, but differ in how the activator interacts with KEAP1 (Fig. 6A). We assume that a CLASS_VI molecule can bind equally to either of the two monomeric subunits in KEAP1 dimer that is not occupied by NRF2. It is thus possible that a KEAP1 dimer can be occupied by 2 molecules of a CLASS_VI compound such that no NRF2 is able to bind to this KEAP1 dimer. This assumption is well justified as it has been recently demonstrated that NRF2 can be progressively and ultimately completely liberated off KEAP1 by increasing concentrations of p62 and other KEAP1-NRF2 interaction inhibitors [31].

Unlike the case with CLASS_I-v activators, in response to CLASS_VI, NRF2_free increases immediately without delay, followed by a slower rise over time to reach the steady state in about 300 min (Fig. 6C). The initial rapid response of NRF2_free results from immediate liberation of NRF2 from the KEAP1-NRF2 complexes. The subsequent slow NRF2_free rise occurs because more KEAP1-NRF2 complex shifts away from the rapidly-degrading closed state, resulting in NRF2 stabilization (Fig. 6E). Contrary to Model 3a for CLASS_I-v, the higher the CLASS_VI level, the longer it takes for NRF2_free to reach the steady state (Fig. 6C). NRF2_tot has a similar temporal profile to NRF2_free except lacking the initial fast-rising phase (Fig. 6B). The steady-state dose-response of NRF2_free exhibits an n_H of 1.09 and LRC_max of 0.92 (Fig. 6D). The NRF2_free and NRF2_tot responses to low CLASS_VI levels are nearly flat, as CLASS_VI molecules are first sequestered away by free KEAP1. Contrary to the decreasing open:closed ratio of KEAP1-NRF2 complexes under CLASS_I-V, this ratio increases by CLASS_VI (Fig. 6E). At high CLASS_VI levels, the half-life of NRF2_tot approaches 40 min, which is also the half-lives of NRF2_free and KEAP1_NRF2_{open_tot} (Fig. S12). We also explored the situation when only one KEAP1 monomeric subunit can be occupied by class VI activators by setting both k’₇ and k’₈ to zero. As shown in Fig. 6F and G, this configuration does not affect NRF2_tot, but weakens the NRF2_free response as its maximal level cannot reach as high as when both KEAP1 monomeric subunits can be occupied by class VI activators. This more muted response is because without class VI activators blocking both binding sites on KEAP1 dimer, NRF2 can still be sequestered by KEAP1 through the ETGE motif, resulting in lower NRF2_free levels.

3.4. Model 4a (with nucleus for class I–V activators)

Since NRF2 that translocates to the nucleus is what ultimately drives target gene expression, we next explored the situation when a nuclear compartment is added. The following assumptions were made regarding NRF2 translocation between the cytosol and nucleus (Fig. 7A). (i) The binding kinetics between free nuclear NRF2 (NRF2_{free_nucleus}) and free nuclear KEAP1 dimer (KEAP1_{free_nucleus}) are the same as in the cytosol. (ii) KEAP1-mediated NRF2 ubiquitination and degradation does not occur in the nucleus, thus the degradation rate constants of various NRF2 species in the nucleus are the same as in the cytosol, except for the closed KEAP1-NRF2 complex, which is degraded with the same rate constant as other NRF2 species. (iii) NRF2 activators do not modify KEAP1 in the nucleus to regulate NRF2 stability.

At the basal condition, total nuclear NRF2 (NRF2_{tot_nucleus}) is at 278 nM as observed in RAW 264.7 cells [47] and a significant fraction of which is titrated by KEAP1 such that NRF2_{free_nucleus} is at 180 nM (Table S8). When setting k₀ = 0, NRF2_{tot_cytosol}, NRF2_{tot_nucleus}, and NRF2_{tot_cell} all decay but at different paces, with corresponding half-lives of about 11, 28, 18 min, respectively (Fig. 7B). When viewed on log scale, it is apparent that NRF2_{tot_cell} decays in two phases, a fast phase followed by a slow one (Fig. 7C). This two-phase decay profile is caused by the fast cytosolic and slow nuclear NRF2 decay and has been observed experimentally in a variety of cell lines [44]. Under high stress when CLASS_I-V = 1000 nM, the half-life of NRF2_{tot_cell} markedly lengthens to 55 min (Fig. 7D). In response to a range of CLASS_I-v levels, free and total NRF2 in both cytosol and nucleus rise and reach steady states in about 300 min (Fig. S13). In contrast to Model 3a which does not have the nucleus compartment, NRF2_{free_cytosol} rises to much lower levels (Fig. S13A) as most of it translocates into the nucleus (Fig. S13C). The steady-state dose-response relationship for NRF2_{free_nucleus} exhibits a shallow response, with n_H of 1.15 and of LRC_max of 0.31 (Fig. 7E). The maximal response levels of NRF2_{tot_nucleus} and NRF2_{free_nucleus} increase by 2.6 and 3.5-fold respectively, while those of NRF2_{tot_cytosol} and NRF2_{free_cytosol} both increase by about 3.2 and 3.1-fold, respectively (Tables S8 and S9). Thus, with a nuclear load, NRF2 activation is not as robust as when the action is limited to the cytosol only. The overall muted response of NRF2 is due to the following reasons. At the basal condition, the net influx of NRF2 from the cytosol to nucleus is flux_k10 - flux_k11 = 0.0434 nM/s, which is about 22% of k₀ (0.1933), the NRF2 synthesis rate in the cytosol. Therefore, even if a CLASS_I-V activator can divert all synthesized NRF2 into the nucleus, the total nuclear NRF2 can only increase by a maximal 4.45-fold (0.1933/0.0434) assuming a constant nuclear NRF2 half-life.

We wondered the relative abundance of nuclear KEAP1 and NRF2 may play a role in determining the magnitude of the nuclear NRF2 response. When the KEAP1_{tot_nucleus} abundance is increased (with k₁₀ adjusted simultaneously to maintain the same basal NRF2_{tot_cytosol} and NRF2_{tot_nucleus} concentrations), the simulations showed that both the basal and maximally-induced levels of NRF2_{free_nucleus} decease because of the sequestering effect of KEAP1 (Fig. S14C). However, the degree of ultrasensitivity of the NRF2_{free_nucleus} dose-response curve seems to be optimal when KEAP1_{tot_nucleus} is at an intermediate abundance. Increasing KEAP1_{tot_nucleus} also leads to changes in the maximal levels of NRF2_{tot_cytosol}, NRF2_{free_cytosol}, and NRF2_{tot_nucleus} (Fig. S14), but the fold-increase of NRF2_{tot_nucleus} remains relatively low. These results suggest that other mechanisms, as to be described in the Discussion, may operate in vivo to produce a more robust nuclear NRF2 response.

3.5. Model 4b (with nucleus for class VI activators)

We next considered the situation of class VI activators which compete with NRF2 for binding to KEAP1 in Model 4b (Fig. 8A). The model assumptions are similar to Model 4a and the class VI activator only operates in the cytosol. Model 4b exhibits an interesting dynamic response. In response to a range of CLASS_VI levels, there is a quick spike in NRF2_{free_cytosol} within a couple of minutes followed by a slow rise (Fig. 8B). Correspondingly, NRF2_{tot_cytosol} decreases immediately followed by a slower increase before setting to steady states (Fig. 8C). The rapid increase in NRF2_{free_cytosol} results from the immediate liberation of NRF2 from the KEAP1-NRF2 complex, and the liberated NRF2 moves quickly into the nucleus, causing NRF2_{free_nucleus} (Fig. 8D) and NRF2_{tot_nucleus} to rise quickly, which is followed by a slower increase to steady states. Under high stress when CLASS_VI = 1000 nM, the half-life of NRF2_{tot_cell} lengthens to 40 min (Fig. 8E), shorter than that in Model 4a. However, the steady-state NRF2_{free_nucleus} and NRF2_{tot_nucleus} levels can increase to higher levels, maximally by 6 and 4.2-fold from their basal levels, respectively (Tables S8 and S9). This is because by outcompeting NRF2 for KEAP1, CLASS_VI can drive more NRF2 into the nucleus (Fig. 8D vs. Fig. S13C). The steady-state dose-response curve of NRF2_{free_nucleus} is shallow, with an n_H of 1.09 and LRC_max of 0.46 (Fig. 8F). Interestingly, the steady-state dose-response curve of NRF2_{tot_cytosol} monotonically decreases, from the basal 150 nM–33 nM for higher levels of CLASS_VI. This decrease occurs because KEAP1 dimer is gradually titrated away by CLASS_VI activator, leaving fewer NRF2 in the KEAP1-bound form (Fig. 8G), and more NRF2 translocates to the nucleus. As in Model 4a, varying nuclear KEAP1 can also improve the magnitude and ultrasensitivity of NRF2_{free_nucleus} (Fig. S17).

4. Discussion

NRF2 activation is mediated via a unique mechanism of protein stabilization where KEAP1 functions as both a redox sensor and regulator. In the present study, we explored the steady-state and dynamic behaviors of the KEAP1-NRF2 interactions through a series of mathematical models of increasing complexity. Our simulations demonstrated that the kinetic details of the molecular interactions between KEAP1 and NRF2 play critical roles in determining the redox signaling properties.

4.1. Basal NRF2 half-life in relation to different NRF2 states

The E3 ligase adaptor function of KEAP1 to promote NRF2 ubiquitination and degradation is critically dependent on the configuration of the KEAP1-NRF2 complex. It is well-established that for the ubiquitination and degradation of NRF2 to occur, the KEAP1-NRF2 complex has to be in the closed state, i.e., the two binding sites in the cysteine-unmodified KEAP1 dimer have to be engaged by the ETGE and DLG motifs of the same NRF2 molecule, respectively. Therefore, the fraction of this closed state and the rate at which NRF2 within this closed KEAP1-NRF2 complex is ubiquitinated and degraded are key determinants for the half-life of NRF2 in the cytosol.

In the confine of the present model structure, NRF2 exists in three forms: free, open and closed KEAP1-NRF2 complex. The relative abundances of these forms at the basal steady state are determined by the binding kinetics as well as the degradation rate constant of each NRF2 form. Given the high binding affinity between KEAP1 and ETGE, it is expected in theory and shown by our simulation that when KEAP1 is not limiting, the fraction of free cytosolic NRF2 is very small, and NRF2 exists predominantly in the complex forms at the basal condition. Using FRET to track the open and closed states of the KEAP1-NRF2 complex, Baird et al. showed that, at least in HEK293 cells, the open:closed ratio of the KEAP1-NRF2 complex is near 1:1 under nonstressed conditions [46]. The half-life of total NRF2 in whole cells at basal conditions is short, mostly ranging between 6 and 20 min depending on cell types [21,36,[39], [40], [41], [42], [43], [44]]. Since nuclear NRF2 is relatively more stable than cytosolic NRF2 [41,70] and often constitutes a considerable fraction of total NRF2 at the basal condition [44,47], it is expected that cytosolic NRF2 is actually degraded at even faster rates than measured in whole cells. The comparable basal abundance of open and closed KEAP1-NRF2 complexes suggests that NRF2 in the closed form has to be degraded very fast with a half-life of its own that is much shorter than the averaged half-life of total NRF2. In our models, parameter k₆ governs the degradation of this NRF2 form. With an apparent half-life of cytosolic total NRF2 around 10 min at the basal condition, the default values of k₆ across the six models correspond to a half-life of 5.7–6.6 min. In comparison, the half-lives of free NRF2 and NRF2 in the open KEAP1-NRF2 complex, as determined by parameters k₅ and k₉ (and k_9.1 in the case of two-step ETGE binding) respectively, are much longer, which is 40 min here, as reported for COS-1 and HEK293T cells [60,61]. If k₅, k₉, and k_9.1 are set lower than the current default value, k₆ needs to be even higher to maintain the same basal total NRF2 half-life. Therefore, the turnover of basal NRF2 is predominantly routed through the closed KEAP1-NRF2 complex, and the apparent half-life of cytosolic total NRF2 is determined by the fraction of the closed complex. In Model 1 which operates in an equilibrium mode, this fraction remains constant at 50% at all times (Fig. S1A), therefore the instantaneous half-life of total NRF2 is fixed at any given moment during the decay. In the remaining models which operate in a cycle mode at the basal condition, the fraction increases dynamically and the closed KEAP1-NRF2 complex becomes dominant over other NRF2 forms during the decay process (Figs. S3A and 2B), resulting in a nonlinear degradation of total NRF2 with shortening instantaneous half-life. In Models 4a and 4b, which has the nuclear compartment, cellular total NRF2 decays with a two-phase profile, which has been observed experimentally in a variety of cell types [44], reflecting the differential half-lives of cytosolic and nuclear NRF2.

4.2. Equilibrium vs cycle mode of operation

The comparable abundance of the open and closed states of the KEAP1-NRF2 complex at the basal condition can be achieved in theory in two ways, depending on the transition fluxes (flux_k3 and flux_k4) between the two states relative to other turnover fluxes (flux_k5, flux_k6, flux_k9 and flux_k9.1). If the transition fluxes are much higher than the turnover fluxes, then the open and closed states of the KEAP1-NRF2 complex operate in an equilibrium mode, which means that the ratio of the two states is predominantly determined by the k₃:k₄ ratio regardless of other parameter values. Parameters k₃ and k₄ describe the DLG-mediated KEAP1 and NRF2 binding. In the literature, its binding kinetics was determined in vitro by using mouse KEAP1-DC fragment and NRF2-Neh2 domain fragment [29] or extended DLG motif peptide (DLGex) [35]. However, in vivo the DLG binding is mostly an intra-molecular event within the open KEAP1-NRF2 complex, since the ETGE-mediated binding almost always occurs first to form the open-state complex due to its much higher binding affinity [42]. Thus, in an in vivo scenario, k₃ is actually a first-order, as opposed to a second-order, association rate constant while k₄ remains as a first-order dissociation rate constant. It is unclear whether in the open state, the DLG binding is enhanced since the DLG is in a closer vicinity to the unoccupied KEAP1 binding site than the DLG in a free NRF2 molecule not yet attached to KEAP1.

In Model 1 we used the k₄ value measured in vitro [35] and adjusted k₃, as detailed in Table S1 footnote, to achieve a 1:1 ratio for the basal open:closed states. Examining the fluxes clearly revealed that with these parameter settings, flux_k3 and flux_k4 are absolutely dominant over other turnover fluxes (Table S10). As shown in Fig. S1, the open and closed KEAP1-NRF2 complexes remain at a 1:1 ratio in all perturbed conditions (Figs. S1A–S1C), demonstrating that Model 1 definitely operates in an equilibrium mode. However, the experimental study by Baird et al. clearly demonstrated that under various perturbations similar to above, the closed KEAP1-NRF2 state will eventually dominate over the open state, which is inconsistent with an equilibrium mode of operation [46]. It was further suggested that the KEAP1-NRF2 interaction may operate instead in a global cycle mode where KEAP1 in the closed complex moves predominantly forward to exit the complex along with NRF2 degradation to join the free KEAP1 dimer pool as opposed to returning to the open state complex.

When parameters k₃ and k₄, which govern the open-closed state transition, were lowered as in Model 2, it indeed exhibits the behavior consistent with the cycle mode, where the open:closed ratio decreases in all perturbed conditions (Figs. S3A, S3B, and S3F). The issue with Model 2 is that k₄, which describes the dissociation rate constant of DLG binding, is 1.0E-4 S⁻¹, only about 1/2000 of the in vitro measured value (Table S1). This value translates into an average lifetime of 167 min for the closed state before it can revert back into the open state, which is considered too long for such weak binding [35]. In the same study it was also demonstrated that ETGE-mediated binding is actually a two-step process, involving an initial fast binding step followed by a subsequent slow binding step. We therefore wondered whether the slow binding here may be responsible for the cycle mode behavior. When this idea was implemented in Model 3, simulations indeed showed such effects on the open:closed ratio under all perturbed conditions, including shutdown of NRF2 synthesis (Fig. 2B), stabilization of NRF2 in the closed state (Fig. 2C), and under a wide range of CLASS_I-V levels (Fig. 2G). With the current parameter setting for the second-step, slow ETGE binding (k_1.1 and k_2.1), flux_k1.1 is much greater than flux_k2.1 (Table S10). KEAP1_NRF2_open1 is the dominant form of the open state at the basal condition (Fig. 2B and Table S8), and is not in equilibrium with KEAP1_NRF2_open2 (Fig. 2C and G). In contrast, KEAP1_NRF2_open2 is always in equilibrium with KEAP1_NRF2_closed at an approximate 1:5 ratio as determined by the k₄:k₃ ratio (Fig. 2G). During CLASS_I-V perturbation, KEAP1_NRF2_open1 decreases while KEAP1_NRF2_open2 increases and becomes the dominant open form, resulting in an overall open:closed ratio that is close to 1:3.5. Therefore, although Model 3 behaves globally in a cycle mode at the basal condition with KEAP1_NRF2_open1 as the dominant open form, upon perturbation KEAP1_NRF2_open2 becomes the dominant open form and the system switches to operate largely in equilibrium mode as far as the relationship between open and closed KEAP1-NRF2 complexes is concerned.

4.3. Hinge-latch hypothesis and class I–V vs. class VI NRF2 activators

An important theory of NRF2 activation is the hinge-latch hypothesis which postulates that the ETGE-mediated association (i.e., the open-state complex) is always there functioning as a hinge between KEAP1 dimer and NRF2, while the weaker DLG-mediated association can be latched on (i.e., forming the closed-state complex) or off (i.e., reverting to the open state complex) by oxidative stressors [14]. With Model 3a we tested the effects of hinge-latch mode of operation on NRF2 activation by altering the k’₃:k’₄ ratio which governs the intramolecular DLG binding affinity between oxidized/conjugated KEAP1 and NRF2. Our simulations showed that when the DLG binding affinity is lowered to mimic a hinge-latch, the maximally induced steady-state levels of total NRF2 and particularly free NRF2 is tangibly reduced (Fig. 4E and F). In contrast, when the k’₃:k’₄ ratio is made higher, i.e., a strengthening of the latched-on state under oxidative stress, there is an increase, albeit limited, in the maximal NRF2 levels. These results suggest that a hinge-latch mode of operation may lead to a lessor NRF2 response to class I–V compounds. The reason for the less robust response in our model is because under oxidative stress, the closed KEAP1-NRF2 complex in which the KEAP1 molecule is modified on the sensor cysteine residues, i.e., KEAP1_o_NRF2_closed, has a half-life (determined by k’₆) longer than those of NRF2 in the free or open complex forms. Therefore, KEAP1 here reverses the normal role of promoting NRF2 degradation as at the basal condition, and becomes instead protective of the NRF2 molecule. We also examined the situation when KEAP1_o_NRF2_closed is not protective of NRF2 by setting k’₆ equal to k₅ such that it degrades with the same half-life as free NRF2 and as open complex. In this case, the hinge-latch mode of operation slightly improves the ultrasensitivity of free NRF2 and total NRF2 (Figs. S9E and S9F). But regardless, when in the hinge-latch mode of operation, the open:closed ratio of KEAP1-NRF2 complexes increases in response to high CLASS_I-V levels (Fig. 4A-B and S9A-S9B), as opposed to the expected decreases, suggesting that the hinge-latch hypothesis may not be valid for class I–V compounds. Indeed, using titration NMR spectroscopy, the most recent study by Yamamoto group clearly demonstrated that modifications of reactive cysteines of KEAP1 by class I–V oxidants and electrophiles, including CDDO-Im and sulforaphane targeting Cys151 and 15d-PGJ2 targeting Cys288, do not break the DLG binding [31].

Class VI compounds are those that can bind to the DC region of KEAP1 and thus disrupt DLG-mediated, and also potentially, ETGE-mediated NRF2 binding. Therefore, the NRF2-stabilizing effect of class VI compounds is indirect, by shifting KEAP1-NRF2 complex away from the ubiquitinatible closed state. An endogenous ligand is p62, which has a KEAP1-interacting region (KIR) containing a DPSTGE motif that is similar to the ETGE motif of NRF2 [71,72]. The motif has similar or even higher binding affinities for KEAP1 than the DLG motif of NRF2, depending on its phosphorylation status [34,73]. Small-molecule compounds have also been identified recently as disruptors of the protein-protein interaction between KEAP1 and NRF2, such as Cpd16 [68] and several others [69,74,75]. By displacing DLG binding preferentially, these compounds make the KEAP1-NRF2 complex function as a hinge-latch as recently demonstrated experimentally [31]. Our Model 3b captures the hinge-latch behavior in response to class VI NRF2 activators (Fig. 6), and shows that the open:closed ratio of KEAP1-NRF2 complex actually increases with increasing class VI activator concentrations (Fig. 6E). Simulations of Model 3b also suggest that when the two monomeric subunits of KEAP1 dimer can both be occupied by a class VI compound, NRF2 activation is more robust because of total blockade of the two binding sites (Fig. 6D vs. 6F). Horie et al. indeed showed that with high enough concentrations, p62 and small-molecule class I–V compounds can completely dissociate NRF2 from KEAP1 dimers, breaking the ETGE-mediated hinge [31]. A recently identified endogenous protein, FAM129B, has both DLG and ETGE motifs on the C terminal and can compete with NRF2 for KEAP1 binding [76]. FAM129B is found to be upregulated in many cancers which have poor prognosis by promoting NRF2 activation and thus chemoresistance.

4.4. Maximal NRF2 activation, ultrasensitivity, and floodgate hypothesis

The maximal fold increase of total NRF2 is determined by the differential half-lives at the basal vs. severely stressed conditions. With a basal half-life of about 10 min in the cytosol in our models, and the lengthening of the half-life to over an hour under simulated oxidative stress such as in Model 3a, total NRF2 increases by 5-fold (Fig. 2D and Tables S8–S9). As discussed above, under oxidative stress, this model switches from KEAP1-mediated degradation to KEAP1-mediated stabilization of NRF2, therefore the fold-increase can be even higher when parameter k’₆ is of lower values (Figs. S5B and S5D). Conversely, the fold-increase becomes smaller when k’₆ is higher (Fig. S5F). It is likely that by reacting with and thus modifying different cysteine residues of KEAP1, different electrophilic class I–V compounds may inhibit the E3 ligase adaptor function of KEAP1 to different extent, which will result in quantitatively different stability of NRF2, as simulated with different values of k’₆ here. This would translate into different maximal fold-increase in NRF2 activation for different compounds. In contrast, as we demonstrated with varying parameters k₇ and k₈ (Figs. S10 and S16), if different electrophilic compounds only differ in how fast they react with a cysteine residue of KEAP1, only the potency is altered without affecting the efficacy (as demonstrated by the horizontal shifting of the NRF2 dose-response curve without changes in the maximal levels). It is also evident that at the basal condition when there is a higher fraction of the closed KEAP1-NRF2 complex that is rapidly degraded, the system is poised to produce higher levels of NRF2 in response to stresses, as the closed complex becomes stabilized by a class I–V compound or dissociated by a class VI compound. In Model 3b which simulates class VI compounds, because there is no closed KEAP1-NRF2 complex with a CLASS_VI molecule attached, the maximal fold-increase of total NRF2 is limited by the half-lives of free NRF2 and NRF2 in the open KEAP1-NRF2 complexes. In our study parameters k₅, k’₅, k₉, k’₉, k_9.1 and k’_9.1 govern the degradation of these NRF2 species, which have an equal half-life of 40 min. As a result, the maximal fold-increase of total NRF2 in Model 3b cannot exceed 40/10 = 4-fold (Fig. 6B and Tables S8–S9).

As aforementioned in Introduction, for an adaptive stress response, it is ideal that some degree of signal amplification, i.e., ultrasensitivity, can be embedded in the feedback circuit to ensure robust resistance to perturbation. In Models 1, 2, and 3a, free NRF2 exhibits some decent ultrasensitivity. Molecular mechanisms producing ultrasensitivity can arise from six common ultrasensitive motifs [49]. In the KEAP1-NRF2 module here, it appears that both zero-order degradation and protein sequestration (molecular titration) are at play simultaneously to produce NRF2 ultrasensitivity, where the sequestration is mediated by ETGE binding and zero-order degradation is mediated by saturation of DLG binding. As shown in Figs. S3G–S3H and 2H–2I, KEAP1-mediated degradation of NRF2 in the closed KEAP1-NRF2 complex will eventually saturate when all KEAP1 dimers are occupied by NRF2. Around this saturation point, KEAP1-mediated NRF2 degradation becomes zero order such that any additional increase in NRF2 will have to rely on KEAP1-independent mechanism to degrade. As a result of the nonlinear, zero-order degradation, the steady-state total NRF2 abundance may experience some steep changes around the point of KEAP1 saturation than when no saturation occurs. Indeed, for Models 1–3b, the n_H of total NRF2 is between 1.17 and 1.35, but with LRC_max between 0.35 and 0.42, total NRF2 does not exhibit overt ultrasensitivity because of the high basal level. From the perspective of free NRF2, this KEAP1 saturation point is also a juncture when free NRF2 can no longer be sequestered by KEAP1, and as a result any additional NRF2 synthesized de novo will remain as free NRF2, leading to a steep increase in its abundance. Therefore, both zero-order degradation (by providing more NRF2 overall) and protein sequestration are at play simultaneously to produce the ultrasensitivity of free NRF2.

Conceivably, the abundance of total KEAP1 and whether NRF2 can accumulate to a level that surpasses this abundance play a critical role in quantitative NRF2 activation. If total NRF2 can never increase to a level higher than KEAP1 dimer, then NRF2 cannot escape the sequestration by KEAP1 and there will be no ultrasensitivity of free NRF2. This is first illustrated by setting k’₆ to a higher value such that total NRF2 can only barely match the level of total KEAP1 (Figs. S4F and S5F). The intracellular NRF2:KEAP1 ratio at basal conditions varies among different cell types, which can be lower or higher than 1:1 [44,47]. Since nuclear NRF2 often constitutes a considerable fraction of total NRF2 at basal conditions [44,47], the cytosolic NRF2:KEAP1 ratio can be actually even lower than the values reported for the whole cells. Varying the abundance of KEAP1 in the models has some interesting results. By increasing KEAP1, its role in further destabilizing Nrf2 is limited because it is already in excess, and as a result total NRF2 does not increase further (Fig. 5A). But increasing KEAP1 will be more effective as a sequester to inhibit Nrf2. There seems to be an optimal KEAP1 abundance that can produce the steepest NRF2_free response (Fig. 5B). When KEAP1 is too low, NRF2 is constitutively activated, but when KEAP1 is too high, free NRF2 is constitutively suppressed. That an optimal KEAP1 abundance exists for maximal NRF2 ultrasensitivity also seems to apply to nuclear KEAP1 (Figs. S14 and S17).

This sequestering role of KEAP1 is consistent with the floodgate hypothesis which postulates that stabilization of NRF2 due to loss of KEAP1 activity as an E3 ligase adaptor protein is not sufficient to initiate NRF2 nuclear translocation; NRF2 has to accumulate to a higher level to overflood the KEAP1 gate to move to the nucleus [14]. A potential caveat of this mechanism is that it takes some time to produce enough NRF2 to saturate KEAP1, therefore the free NRF2 response can be delayed as we demonstrated with our models. However, it is likely that at the basal condition, the cytosolic NRF2:KEAP1 ratio is near parity in some cells such that KEAP1 is near saturation. As a result, the system is at a tipping point, poised to respond evenly to a slight increase in oxidative stress to overwhelm KEAP1 and cause an immediate and steep increase in free NRF2 [46].

The ultrasensitivity of free NRF2 exhibited by Model 3a, which has two-step ETGE binding, is somehow weaker than Model 2. As described in Results, this is partly because a higher free NRF2 level is required to maintain the same turnover fluxes through different NRF2 species (Fig. 2H and I) at the basal steady state in Model 3a, resulting in a lesser zero-order degradation effect. A higher basal level will always reduce the degree of ultrasensitivity [49], despite that Models 2 and 3a have comparable maximally induced free NRF2 levels (Table S9). The apparent dissociation constant for the ETGE-mediated two-step binding is 7.54 nM, which is lower than the 20 nM used in Model 2. However, at the basal condition, as a result of the two-step binding and slow fluxes through the second-step binding, free NRF2 is higher in Models 3a than Model 2. By increasing the binding affinity of ETGE, e.g., through increasing k₁ and k_1.1, to reduce basal free NRF2, the ultrasensitivity of Model 3a is improved dramatically (Fig. 3B and D).

With both n_H and LRC_max of free NRF2 close to unity, the ultrasensitivity for class VI compounds as in Model 3b is basically absent. In contrast to class I–V compounds, a class VI compound does not need to induce total NRF2 to a level that exceeds total KEAP1 to produce tangible increase in free NRF2. This is because when a class VI compound can bind to both of the monomeric subunits of KEAP1 dimer, it would titrate free KEAP1 away, essentially lowing the amount of available KEAP1 that can sequester NRF2. This lowering of the “floodgate” can result in a much higher maximal level of free NRF2 that can be induced by class VI compounds than class I–V compounds (Fig. 6D vs. 2G and Table S9). However, because of the reduced sequestration by KEAP1, the ultrasensitivity of free NRF2 is lost for class VI compounds.

4.5. Response of nuclear NRF2

The flux of nuclear translocation constitutes a load to the cytosolic NRF2. At a constant NRF2 production rate in the cytosol, this nuclear load is expected to alter the dynamics of NRF2 activation. With higher abundance of nuclear NRF2 than KEAP1, as observed in RAW 264.7 cells and potentially many other cell types [47], nuclear KEAP1 is nearly saturated by NRF2, resulting in low basal free nuclear KEAP1 dimer and high free nuclear NRF2 levels. These configurations result in a net nuclear influx of NRF2 that is 22% of the NRF2 production rate in the cytosol (Table S10). Therefore, net nuclear importing of NRF2 constitutes a significant load to NRF2 production. It can thus be estimated that even under oxidative stress that completely terminates cytosolic NRF2 degradation and all cytosolic NRF2 translocates into the nucleus, total nuclear NRF2 cannot increase by > 5-fold. Our simulations confirmed this prediction (Fig. 7, Fig. 8F, Tables S8–S9), and the fold-increase of nuclear free NRF2 is only slightly higher than the total. Class VI activators seem to has a larger effect on maximal nuclear NRF2 (4.2-fold) than class I–V activators (2.6-fold). This is due to the KEAP1-titrating effects of a class VI activator, which reduces free cytosolic KEAP1, pushing more NRF2 into the nucleus. Nonetheless these lessor responses contrast with the nearly 10-fold increase in nuclear NRF2 under exposure to DEM at 100 μM for 3 h in RAW 264.7 cells which our model is partially based upon [47]. For nuclear NRF2 to increase to higher levels, additional mechanisms have to be at play which are not included in our models. These include (i) increased NRF2 production through transcriptional autoregulation, which has been confirmed in many cell types including RAW 264.7 cells [39,77,78]; (ii) reduced nuclear exporting of NRF2 due to redox-sensitive cysteine modification of the nuclear export signal (NES) sequence in the Neh5 domain of NRF2 [79]; (iii) stabilization of nuclear NRF2 under oxidative stress; and (iv) lower nuclear NRF2 load at the basal condition such that there is still more reserve capacity for nuclear NRF2 accumulation. For the last possibility, our simulations indeed showed that reducing the basal nuclear load and thus level of nuclear NRF2 considerably improves the magnitude of both NRF2_{tot_nucleus} and NRF2_{free_nucleus} responses (Figs. S15 and S18).

Free nuclear NRF2 does not exhibit overt ultrasensitivity in either of the two models. Part of the reason is due to its high basal level and smaller fold increase of total nuclear NRF2 discussed above. However, a number of mechanisms that can potentially contribute to ultrasensitivity have been confirmed in the KEAP1-NRF2 system. These mechanisms include (i) positive transcriptional autoregulation of both NRF2 and sMaf [39,80], (ii) molecular titration of sMaf by inhibitor Bach1 [81], (iii) positive feedback through NRF2 induction of p62 which can titrate KEAP1 away from NRF2 and also promote KEAP1 autophagy [82], and (iv) multi-step signaling through (a) enhanced nuclear NRF2 accumulation due to redox modification of NES as mentioned above [79] and (b) redox-sensitive nuclear exporting of Bach1 [83,84]. It is highly likely that these mechanisms converge to produce ultrasensitive free NRF2 accumulation in the nucleus.

5. Limitations

The KEAP1-NRF2 module has been modeled mathematically as part of larger networks. We have constructed NRF2-mediated pathways of antioxidant induction and phase II enzyme induction, containing negative feedback, incoherent feedforward, and a variety of ultrasensitive motifs to understand the nonlinear dose-response relationship under oxidative stress [52,55]. Blis and his colleagues adapted these models to interpret and predict antioxidant gene induction in human renal cells in response to cyclosporine [56], and glutathione depletion in liver microfluidic chips in response to flutamide [57]. Khalil et al. constructed a model of KEAP1-NRF2/sMaf-ARE activation and its interaction with the peroxiredoxin and thioredoxin antioxidant enzymes in controlling intracellular H₂O₂ levels and regulating the reduction of KEAP1, in which one-step ETGE binding was considered [44]. Xue et al. observed a basal NRF2 cytosol-nucleus oscillation behavior in cells with a period of about 2 h for which they constructed a mathematical model of negative feedback through NRF2 phosphorylation and dephosphorylation without involving changes in the abundance [58]. Kolodkin et al. has recently incorporated the KEAP1-NRF2 component into an ROS dynamic network to explore the design principles relevant to network-based therapies for Parkinson disease [59]. Compared to the previous work, our present study provided a much more detailed analysis of the KEAP1-NRF2 module itself, which can be adapted and included in future systems-level models of antioxidant and detoxification responses.

There are several limitations of the present study, however. In the models we have limited the action of class I–V and VI compounds on the KEAP1 molecules in the cytosol only, however it is possible that these compounds, especially class VI, may still compete for KEAP1 in the nucleus to further drive NRF2 activation. We have assumed separate pools of cytosolic and nuclear KEAP1 without exchange. However, it has been shown that KEAP1 may also control post-induction repression of the NRF2-mediated antioxidant response by escorting NRF2 out of the nucleus [85]. The DLG-mediated binding kinetics has been measured in vitro with peptide fragments of KEAP1 and NRF2 as inter-molecular event following the law of mass action. Measuring the binding kinetics as an intra-molecular event as occurring with full-length dimers will help reduce the uncertainty of model parameterization. It is also unclear whether the modification of cysteine residues of both KEAP1 subunits of the dimer will have any differential effects on NRF2 ubiquitination than when only one subunit is modified. Lastly, the parameterization and calibration of our models are based on experimental measurements from multiple cell types, such as RAW 264.7 and HEK293 cells, and under various experimental conditions. Therefore, the parameter values and model responses do not necessarily represent an ideal “average” cell. However, we systemically varied the parameters where applicable in our study to explore their effects on NRF2 response. All in all, future iterations of the KEAP1-NRF2 model should address these limitations as more quantitative information, such as binding and degradation kinetics of all NRF2 forms in complex with KEAP1, is obtained.

6. Conclusions

KEAP1 plays a dual role in repressing NRF2 – promoting its degradation to keep its total abundance low and sequestering to keep its free abundance low. The floodgate hypothesis captures some of the dual actions of KEAP1 [7,47]. Our modeling revealed here that the quantitative aspect of protein stabilization of NRF2 and nuclear translocation can be better understood as a water tank model that overflows due to drain closure (Fig. 9A and B), which we believe is an improvement over the floodgate analogy. Here, the water is poured into the large water tank at a constant rate, just as NRF2 is produced in the cytosol. Since the drain is open, most of the water will leave the tank with a small amount remaining and leaking to the small tank (nucleus). The draining event is analogous to NRF2 being actively degraded by KEAP1, resulting in low cytosolic and nuclear NRF2 levels. If a stopper is partially put in place, the water will drain slowly, and the water level in the large tank will rise, however it is still being held in the large tank without going into the small tank much. This is like under mild stress, KEAP1-dependent NRF2 degradation is partially inhibited, total NRF2 will increase but because of the sequestration by KEAP1, it still remains largely in the cytosol. Therefore, the height of the interface between the large and small tanks here is equivalent to the total cytosolic KEAP1 dimer available for sequestering NRF2. When the stopper is further pushed in to completely block the drain, the water level will rise and eventually overflow the large tank and flood the small tank. This is like under severe oxidative stress, KEAP1-mediated NRF2 degradation is totally shut down, NRF2 accumulates to a level exceeding available cytosolic KEAP1 dimer, and free NRF2 rises sharply and translocates into the nucleus. Modification of KEAP1 cysteine by class I–V compounds is analogous to slowing the drain without affecting the height of the interface between the large and small tanks, thus causing a waterfall effect (Fig, 9A), while binding of class VI compounds to both of the two subunits of KEAP1 dimer is analogous to simultaneously slowing the drain and lowering the height of the interface without causing much of a waterfall (Fig. 9B). The differential actions of this water-tank model can be captured by a reduced mathematical model of KEAP1-NRF2 interaction (Fig. 9C). The free nuclear NRF2 response to class I–V compounds is potentially more ultrasensitive than that to class VI compounds, while at lower concentrations class VI compounds may lead to more nuclear NRF2 than class I–V compounds (Fig. 9D).

Fig. 9.

Water-tank analogy and reduced KEAP1-NRF2 mathematical model. Schematic illustrations of the water-tank analogy for KEAP1-dependent NRF2 degradation, sequestration, and nuclear translocation for (A) class I–V and (B) class VI activators. Large tank: cytosol, Small tank: nucleus, Height of the interface wall between large and small tanks: abundance of available cytosolic KEAP1 (note in B the height is lowered as class VI activator level increases to titrate more KEAP1 away), Water: NRF2, Tap: NRF2 production, Drain: KEAP1-dependent NRF2 degradation, Stopper: class I–V or class VI NRF2 activator. To reduce clutter for clarity, KEAP1-independent NRF2 degradation and nuclear NRF2 degradation are not shown. (C) Reduced KEAP1-NRF2 mathematical model for NRF2 activation by class I–V and class VI activators. (D) Predicted differential free nuclear NRF2 dose-response for class I–V and class VI activators.

Quantitative understanding of NRF2 activation can have many implications. A detailed kinetic model like the one we presented here can help to explore the systems-level behavior of cellular oxidative stress responses. It may help to better understand cancer chemoresistance, where mutation in either NRF2 or KEAP1 can lead to constitutive NRF2 activation or a more prompt and robust activation in response to chemo-drugs. Our modeling suggests that threshold concentrations may exist for certain class I–V compounds and at suprathreshold concentrations they can readily activate NRF2, while to finely control NRF2 activation with precision, class VI compounds are preferred. The model may thus help with using a synthetic biology approach to improve current and design novel classes of NRF2 activators or inhibitors. The mechanistically-based KEAP1-NRF2 model can also help to understand common and differential toxic actions of environmental oxidative stressors.

Declaration of competing interest

The authors declare no conflict of interest.

Appendix A. Supplementary data

The following are the Supplementary data to this article: