Abstract
Microsimulation models (MSMs) are used to inform policy by predicting population-level outcomes under different scenarios. MSMs simulate individual-level event histories that mark the disease process (such as the development of cancer) and the effect of policy actions (such as screening) on these events. MSMs often have many unknown parameters; calibration is the process of searching the parameter space to select parameters that result in accurate MSM prediction of a wide range of targets. We develop Incremental Mixture Approximate Bayesian Computation (IMABC) for MSM calibration, which results in a simulated sample from the posterior distribution of model parameters given calibration targets. IMABC begins with a rejection-based ABC step, drawing a sample of points from the prior distribution of model parameters and accepting points that result in simulated targets that are near observed targets. Next, the sample is iteratively updated by drawing additional points from a mixture of multivariate normal distributions and accepting points that result in accurate predictions. Posterior estimates are obtained by weighting the final set of accepted points to account for the adaptive sampling scheme. We demonstrate IMABC by calibrating CRC-SPIN 2.0, an updated version of a MSM for colorectal cancer (CRC) that has been used to inform national CRC screening guidelines.
Keywords: Adaptive ABC, Agent-based models, Colorectal cancer
1. Introduction.
Microsimulation models (MSMs) are used to inform policy by predicting population-level outcomes under different policy scenarios. MSMs are characterized by simulation of agents that represent individual members of an idealized population of interest. For each agent, the model simulates event histories that catalog landmarks in the disease process. In general, disease processes modeled are not directly observable, though outcomes from these processes may be observed. For example, the process of developing colorectal cancer (CRC) cannot be observed, but the prevalence of both precursor lesions (adenomas) and preclinical (asymptomatic) CRC can be estimated from screening trials, and CRC incidence can be observed from national registry data.
Model calibration involves selecting parameter values that result in model predictions that are consistent with observed data and expected findings. Once parameters are selected, MSMs can be used to make predictions about population trends in disease outcomes, effectiveness of interventions, and the comparative effectiveness of interventions, especially those without direct empirical comparisons. For example, models have been used to inform U.S. Preventive Services Task Force screening guidelines for breast (Mandelblatt et al., 2016), cervical (Kim et al., 2017), colorectal (Knudsen et al., 2016), and lung cancer (de Koning et al., 2014) by comparing the effectiveness of different screening regimens.
MSM calibration involves searching a high dimensional parameter space to predict many targets. Several approaches have been proposed. The simplest calibration method involves perturbing parameters one at a time and evaluating the goodness of fit to calibration data, but this is only feasible when calibrating a few parameters. Directed searches, such as the Nelder-Mead algorithm (Nelder and Mead, 1965), provide a derivative free hill-climb to identify a single best value for each parameter. Kong, McMahon and Gazelle (2009) used search algorithms from engineering (simulated annealing and a genetic algorithm) for model calibration. Bayesian calibration methods estimate the joint posterior distribution of MSM parameters, which provides information about parameter uncertainty and enables estimation of functions of parameters. Rutter, Miglioretti and Savarino (2009) used Markov Chain Monte Carlo (MCMC) to simulate draws from the posterior distribution of MSM parameters given calibration targets. However, MCMC can be difficult and costly to apply to MSM calibration and because MCMC is based on a process of sequentially updating draws, it is not easy to parallelize the process to take advantage of modern computing resources.
Approximate Bayesian Computation (ABC) offers an alternative approach to MSM calibration. ABC is a likelihood-free technique for simulating draws from the posterior distribution that approximates likelihood-based algorithms by choosing parameters that produce a close match to data rather than calculating the likelihood (Marin et al., 2012; Conlan et al., 2012). The validity of ABC algorithms, in the sense that they result in samples from the approximate posterior distribution, relies on the validity of the corresponding exact algorithms (Sisson, Fan and Tanaka, 2007). The idea underlying ABC is simple. For a parameter θ with prior distribution π(θ) and observed data y, we can write the posterior probability as p(θ∣y) = p(y∣θ)π(θ) implying that we can approximate p(θ∣y) by sampling θ from π(·) and retaining only points with p(y∣θ) ≈ 1. However, ABC is inefficient and can fail when the parameter space is high dimensional, when there are many calibration targets, or when the prior distributions are very different from the posterior distributions. McKinley et al. (2018) found that popular ABC variants that improve the algorithm’s efficiency were not computationally feasible for calibrating stochastic epidemiological models. We propose an Incremental Mixture ABC (IMABC) approach for MSM model calibration that begins with a basic rejection-sampling ABC step (e.g., Pritchard et al., 1999) and then incrementally adds points to regions where targets are well predicted.
In the next sections we describe the CRC-SPIN MSM for the natural history of colorectal cancer (CRC) (§2), calibration targets used to inform CRC-SPIN model parameters (§3), the IMABC calibration approach (§4), and results of CRC-SPIN model calibration based on IMABC (§5). We conclude with general remarks about the proposed approach and discussion of future work (§6).
2. Microsimulation Model for the Natural History of Colorectal Cancer.
The ColoRectal Cancer Simulated Population Incidence and Natural history model (CRC-SPIN) (Rutter, Miglioretti and Savarino, 2009; Rutter and Savarino, 2010) describes the natural history of CRC based on the adenoma-carcinoma sequence (Muto, Bussey and Morson, 1975; Leslie et al., 2002). Four model components describe the natural history of CRC: 1) adenoma risk; 2) adenoma growth; 3) transition from adenoma to preclinical cancer; and 4) transition from preclinical to clinical cancer (sojourn time).
CRC-SPIN has been used to provide guidance to the Centers for Medicare and Medicaid Services (CMS) (Zauber et al., 2009) and to inform U.S. Preventive Services Task Force CRC screening guidelines (Knudsen et al., 2016). Model validation, based on comparison of model predictions to observed outcomes, revealed that while CRC-SPIN predicted many aspects of CRC well (including clinically detected cancer, cancer mortality, and the effectiveness of screening), it predicted detection of too few preclinical cancers at screening, indicating that the simulated times spent in the preclinical cancer phase (sojourn times) were too short (Rutter et al., 2016). In this paper we present CRC-SPIN 2.0, an update to the original CRC-SPIN 1.0. CRC-SPIN 2.0 contains 21 calibrated parameters (Table 1). Because this is a model recalibration, prior distributions are based on results from the previous calibration of CRC-SPIN 1.0 (Rutter, Miglioretti and Savarino, 2009). In this section, we provide an overview of the model. Additional details are provided in Appendix §A and online at cisnet.cancer.gov (National Cancer Institute, 2018).
Table 1.
Summary of CRC Microsimulation Model Components. Calibrated parameters associated with the 4 components of the natural history model, including parameter notation, associated equations, prior distributions and posterior estimates (mean and 95% credible interval). TN[a,b] (μ,σ) denotes a truncated normal distribution with mean μ and standard deviation σ, restricted to the interval (a,b). U(a,b) denotes a Uniform distribution over (a,b). Refer to section 2 for details of the 4 model components.
| Prior | Posterior Estimates | ||
|---|---|---|---|
| Component | Distribution | Mean | 95% CI |
| Adenoma Risk (eqn 1) | |||
| Baseline log-risk | A ~ TN[−6.7,−6.1](−6.4,0.25) | −6.36 | (−6.65,−6.03) |
| Standard deviation, baseline log-risk | σα ~ U(0.75,1.75) | 1.28 | (0.86,1.69) |
| Female | α1 ~ TN[−0.7,−0.3](−0.5,0.1) | −0.61 | (−0.69,−0.49) |
| Age effect, age ∈ [20, 50) | α20 ~ TN[0.02,0.05](0.04,0.06) | 0.041 | (0.033,0.049) |
| Age effect, age ∈ [50, 60) | α50 ~ TN[0.01,0.05](0.03,0.01) | 0.028 | (0.012,0.046) |
| Age effect, age ∈ [60, 70) | α60 ~ TN[−0.01,0.05](0.03,0.01) | 0.013 | (−0.007,0.039) |
| Age effect, age ≥ 70 | α70 ~ U(−0.02,0.03) | 0.008 | (−0.016,0.028) |
| Time to 10mm (eqn 2) | |||
| Shape, colon | β1C ~ U(1.1,5) | 1.32 | (1.12,1.57) |
| Shape, rectum | β1R ~ U(1.1,5) | 3.30 | (1.68,4.84) |
| Scale, colon* | β2C ~ U(10.7,40) | 38.1 | (35.6,39.9) |
| Scale, rectum* | β2R ~ U(10.7,40) | 16.4 | (13.5,19.3) |
| Intercept | γ0 ~ TN[2.6,3.6] (3.1,0.25) | 3.23 | (3.07,3.42) |
| Female (versus male) | γ1 ~ TN[−0.3,0.3](−0.06,0.2) | −0.17 | (−0.26,−0.09) |
| Rectal (versus colon) | γ2 ~ U(−0.25,0.25) | −0.07 | (−0.24,0.15) |
| Female & rectal | γ3 ~ U(−0.25,0.25) | 0.12 | (−0.03,0.23) |
| Age at initiation | γ4 ~ TN[−0.024,0.002](−0.008,0.004) | −0.009 | (−0.014,−0.004) |
| Female & age at initiation | γ5 ~ U(−0.004,0.004) | 0.001 | (−0.003,0.004) |
| Rectal & age at initiation | γ6 ~ U(−0.004,0.004) | 0.000 | (−0.004,0.003) |
| Female, rectal, & age at initiation | γ7 ~ U(−0.004,0.004) | 0.000 | (−0.004,0.004) |
| Mean Sojourn Time (eqn 4) | |||
| Colon | τC ~ U(1.5,5.0) | 1.91 | (1.52,2.65) |
| Rectum | τR ~ U(1.5,5.0) | 2.32 | (1.55,3.55) |
Scale parameters, β2, were also restricted to range from 10(−ln(0.25))1/β1 to (−ln(0.0001))1/β1, corresponding to the probability of an adenoma reaching 10mm within 10 years ranging from 0.0001 to 0.25.
2.1. Adenoma Risk Model.
The occurrence of adenomas is modeled using a non-homogeneous Poisson process with a piecewise age-effect. We assume zero risk before age 20. We focus on CRC in adults because CRC is very rare before age 20, with incidence of about one in 10 million (Koh et al., 2015). The ith agent’s baseline instantaneous risk of an adenoma at age a = 20 years is given by ψi(20) = exp(α0i + α1femalei) where α0i ~ N(A, σα) and α1 captures the difference in risk for women (femalei = 1 indicates agent i is female). Adenoma risk changes over time, generally increasing with age, a process we model using a linear change-point for log-risk with knots at ages 50, 60, and 70.
| (1) |
2.2. Adenoma Growth Model.
For each adenoma, we simulate a hypothetical time to reach 10mm, t10mm, which may exceed the agent’s lifespan. We assume that t10mm has a Frèchet distribution with shape parameter β1, scale parameter β2, and cumulative distribution function given by
| (2) |
for t ≥ 0, with E(t10mm) = β2Γ(1 − 1/β1) and median(t10mm) = β2 ln(2)−1/β1. Prior distributions for adenoma growth parameters specify that most adenomas grow very slowly. We allow different scale and shape parameters for adenomas in the colon and rectum.
Adenoma size at any point in time is simulated using a von Bertalanffy growth curve model (Tjørve and Tjørve, 2010, see also §A). The simulated time to reach 10mm is used in combination with the growth curve model to calculate the adenoma growth rate parameter.
2.3. Model for Transition from Adenoma to Preclinical Invasive Cancer.
For the jth adenoma in the ith agent the size at transition to preclinical cancer (in mm) is simulated using a lognormal distribution; the underlying (exponentiated) normal distribution is assumed to have standard deviation 0.5 and mean
| (3) |
Where rectumij is an indicator of rectal versus colon location and ageij is the age at adenoma initiation. Based on this model, the probability that an adenoma transitions to preclinical cancer increase with increasing size. The expected size at transition is given by exp(μγ + 0.125), with median exp(μγ) and variance 0.28 exp(2μγ + 0.25). Most adenomas do not reach transition size and small adenomas are unlikely to transition to cancer. For example, if μγ = 3.5 then the probability of transition to preclinical cancer is less than 1 × 10−5 at 10mm, 0.008 at 15mm and 0.16 at 20mm.
2.4. Model for Sojourn Time.
Sojourn time is the time from the transition to preclinical (asymptomatic) CRC and clinical (symptomatic and detected) cancer. We simulate sojourn time using a Weibull distribution with shape parameter fixed at 5:
| (4) |
so that E(x) = τΓ(1.2) and Var(x) = τ2 (Γ(1.4)−Γ(1.2)2. By fixing the shape parameter, we focus on distributions with a limited range of skewness to disallow distributions with heavy right tails while retaining enough flexibility to model plausible sojourn time distributions. We allow different values of τ for cancers in the colon and rectum. Prior distributions for sojourn time parameters allow the mean (and standard deviation) of sojourn time to range from 1.4 (sd 0.32) to 6.4 years (sd 1.5).
2.5. Simulation of Lifespan and Colorectal Cancer Survival.
Once a cancer becomes clinically detectable, we simulate stage and size at clinical detection and survival. Stage and tumor size at clinical detection are based on SEER data from 1975 to 1979, prior to diffusion of CRC screening (National Cancer Institute, 2004). Simulated survival time after CRC diagnosis is based on a Cox proportional hazards model, estimated using SEER data from individuals diagnosed with CRC from 1975 through 2003 (Rutter et al., 2013). CRC survival is based on the first diagnosed CRC and depends on sex, age at diagnosis, cancer location (colon or rectum) and stage at diagnosis.
Other-cause mortality is modeled using survival probabilities based on product-limit estimates for age and birth-year cohorts from the National Center for Health Statistics Databases (National Center for Health Statistics, 2000).
3. Calibration Data.
Calibration data are derived from published studies, and typically take the form of summary statistics with known distributions, such as binomial, multinomial, and Poisson. We calibrate to 37 targets from six sources: SEER registry data (National Cancer Institute, 2004, 16 targets, §3.1) and five published studies (21 targets, §3.2). We also bounded adenoma growth parameters, based on information from a recent study of repeated screening colonoscopies (Ponugoti and Rex, 2017), so that the probability of an adenoma reaching 10mm within 10 years ranged from 0.0001 to 0.25, by requiring 10(−ln(0.25))1/β1 ≤ β2 ≤ 10(−ln(0.0001))1/β1.
Calibration targets are based on individual-level data that is reported in aggregate. Calibration requires simulating targets by simulating a set of agents with risk that is similar to the study population based on age, gender, and prior screening patterns, and the time period of the study, which may affect both overall and cancer-specific mortality.
3.1. SEER Registry Data.
SEER colon and rectal cancer incidence rates in 1975-1979 are a key calibration target (Table 2). Incidence rates reported are per 100,000 individuals. These rates are based on the first observed invasive colon or rectal cancer during the years 1975-1979, the most recent period prior to dissemination of CRC screening tests. We assume that given the SEER population size, the number of incident CRC cases in any year follows a binomial distribution.
Table 2.
Observed and Predicted Annual Incidence of Clinically Detected Cancers in 1975-1979, per 100,000 individuals.
| Observed | Tolerance | Posterior Predicted | ||||
|---|---|---|---|---|---|---|
| Location | Gender | Age | Mean | Interval | Mean | 95% CI |
| Colon | Female | 20-49 | 4.8 | (2.8, 6.8) | 3.5 | (2.8, 4.8) |
| 50-59 | 43.3 | (31.3, 55.2) | 46.3 | (37.0, 54.2) | ||
| 60-69 | 100.7 | (79.7, 121.7) | 106.0 | (89.8, 119.9) | ||
| 70-84 | 216.7 | (185.6, 247.8) | 210.1 | (187.7, 239.3) | ||
| Colon | Male | 20-49 | 4.5 | (2.5, 6.5) | 3.4 | (2.6, 4.7) |
| 50-59 | 45.9 | (33.2, 58.6) | 51.0 | (41.4, 58.1) | ||
| 60-69 | 121.4 | (96.6, 146.2) | 126.2 | (107.0, 143.5) | ||
| 70-84 | 268.4 | (224.6, 312.2) | 261.6 | (228.7, 301.4) | ||
| Rectal | Female | 20-49 | 1.9 | (0.6, 3.1) | 1.7 | (0.7, 2.8) |
| 50-59 | 20.4 | (12.2, 28.6) | 20.4 | (13.8, 27.3) | ||
| 60-69 | 42.5 | (28.9, 56.1) | 41.9 | (31.7, 53.1) | ||
| 70-84 | 73.9 | (55.7, 92.1) | 73.2 | (58.1, 89.7) | ||
| Rectal | Male | 20-49 | 2.3 | (0.9, 3.7) | 2.4 | (1.3, 3.5) |
| 50-59 | 30.0 | (19.7, 40.3) | 31.7 | (23.1, 39.5) | ||
| 60-69 | 71.4 | (52.4, 90.4) | 67.9 | (54.5, 83.4) | ||
| 70-84 | 128.0 | (97.7, 158.3) | 120.5 | (100.0, 146.9) | ||
To simulate SEER incidence rates, we generate a population of individuals from 20 to 100, with an age- and sex-distribution that matches the SEER 1978 population (to capture risk-levels within each age category), who are free from clinically detected CRC. Model-predicted CRC incidence is based on the number of people who develop CRC in the next year.
3.2. Other Published Targets.
Table 3 summarizes calibration targets from five studies. To simulate these targets, we generated separate populations for each target that match the age and gender distribution of study participants during the time-period of the study. One study (Church, 2004) describing the pathology of lesions (i.e., adenomas and preclinical cancers) did not provide information about the age or sex of patients, and so we simulated a population that was 50% male with an average age of 65 (standard deviation of 5), and an age range of 20 to 90 years.
Table 3.
Observed and Predicted Calibration Targets from Published Studies
| Tolerance | Posterior Predicted | |||
|---|---|---|---|---|
| Target | Mean | Interval | Mean | 95% CI |
| Corley et al. (2013) | ||||
| Adenoma Prevalence, Women 50-54 | 15 | (12.9, 20.8) | 16.8 | (14.1, 19.9) |
| Adenoma Prevalence, Women 55-59 | 18 | (15.5, 25.0) | 20.3 | (17.4, 23.6) |
| Adenoma Prevalence, Women 60-64 | 22 | (19.4, 30.1) | 23.8 | (20.6, 27.1) |
| Adenoma Prevalence, Women 65-69 | 24 | (20.6, 33.4) | 27.0 | (23.5, 30.4) |
| Adenoma Prevalence, Women 70-74 | 26 | (21.5, 37.0) | 29.9 | (26.1, 33.4) |
| Adenoma Prevalence, Women ≥75 | 26 | (20.8, 37.7) | 33.2 | (29.0, 37.2) |
| Adenoma Prevalence, Men 50-54 | 25 | (22.1, 34.2) | 26.0 | (22.7,29.6) |
| Adenoma Prevalence, Men 55-59 | 29 | (25.6, 39.7) | 30.7 | (26.8,34.6) |
| Adenoma Prevalence, Men 60-64 | 31 | (27.5, 42.3) | 35.1 | (30.9,39.3) |
| Adenoma Prevalence, Men 65-69 | 34 | (29.6, 46.9) | 39.2 | (34.4,43.8) |
| Adenoma Prevalence, Men 70-74 | 39 | (33.2, 54.6) | 42.7 | (37.4,47.7) |
| Adenoma Prevalence, Men ≥75 | 38 | (31.6, 53.9) | 46.6 | (40.4,52.1) |
| Pickhardt et al. (2003) * | ||||
| Percent of Detected Adenomas ≥ 10mm | 9.2 | (5.2, 13.2) | 12.2 | (10.7, 13.2) |
| Imperiale et al. (2000) | ||||
| Detected Preclinical Cancers per 1,000 People | 6.0 | (0.3, 117.1) | 2.4 | (1.8, 5.3) |
| Lieberman et al. (2008) * | ||||
| Preclinical CRCs per 1,000 Lesions 6 – 9mm | 2.5 | (0.0, 8.4) | 4.7 | (2.1, 7.6) |
| Preclinical CRCs per 1,000 Lesions ≥ 10mm | 32.8 | (11.6, 54.0) | 41.4 | (29.2, 52.9) |
| Church (2004) | ||||
| Preclinical CRCs per 1,000 Lesions [6, 10)mm | 2.4 | (0.0, 10.3) | 5.6 | (2.5,9.0) |
| Preclinical CRCs per 1,000 Lesions ≥ 10mm | 42.3 | (12.6, 72.1) | 36.7 | (24.3, 49.0) |
Size was reported categorically as ≤ 5mm, 6 to 9mm, and ≥ 10mm. We operationalized these categories as: [1, 5.5) mm, [5.5, 9.5) mm and ≥ 9.5 mm
Simulation of targets in Table 3 also requires simulating the detection of lesions (adenomas and preclinical cancers). Sensitivity is a function of lesions size, and is informed by back-to-back colonoscopy studies (Hixson et al., 1990; Rex et al., 1997, additional details provided in §A). We assume that study participants are free from symptomatic (clinically detectable) CRC and have not been screened for CRC prior to the study. This is a reasonable assumption because studies used for model calibration were conducted prior to widespread screening, or were based on minimally screened samples. CRC screening guidelines have been in place since the late 1990s (Winawer et al., 1997), and screening rates have since risen steadily (Meissner et al., 2006; Centers for Disease Control & Prevention, 2011).
4. Posterior Inference via Incremental Mixture Approximate Bayesian Computation (IMABC).
The basic rejection-based ABC algorithm (Tavare et al., 1997; Pritchard et al., 1999) generates model parameter vectors θ from the prior distribution, π(θ), then uses the model to simulate data, y*. Draws that result in simulated data that are similar to observed data, y, are accepted. Similarity between y* and y is based on user-defined summary statistics, a distance metric, and a tolerance level that defines the distance of acceptable points.
In practice, simulating θ from the prior distribution can be very inefficient because the prior and posterior distributions are often poorly aligned. Many versions of ABC have been developed to address inefficiencies. Two popular variants are ABC-MCMC (Marjoram et al., 2003) and sequential Monte Carlo ABC (ABC-SMC, Sisson, Fan and Tanaka, 2007; Toni et al., 2009). ABC-MCMC involves proposing a new value of θ by sampling u from a user-specified jumping distribution, q(·), that is centered at zero with θ(t+1) = θ(t) + u. If simulated data based on θ(t+1) are within tolerance levels for observed data then, similarly to MCMC, θ(t+1) is accepted with a probability equal to the minimum of 1 and . Drawbacks of ABC-MCMC include the usual problems with MCMC, such as correlated samples, low acceptance rates, the possibility of getting stuck in low posterior probability regions, and slow mixing requiring simulation of very long chains. ABC-SMC is based on importance sampling with the prior used as the proposal distribution. ABC-SMC starts by simulating a set of draws from the prior distribution. Each subsequent set of draws is simulated by drawing an (importance) weighted sample from the previous set of draws and for each sampled point adding a random deviate u that is drawn from a user-specified jumping distribution. For each sampled point this process is repeated until the perturbed point is accepted (i.e., falls within the tolerance interval). When using the ABC-SMC approach, users specify the total number of iterations, T, and a sequence of T increasingly stringent tolerance intervals, which require accepted points to be nearer to targets as the algorithm proceeds. After T iterations, draws from the posterior distribution are simulated by drawing a weighted sample of θ’s using final importance weights that are based on the sequence of jumping distributions. The population Monte Carlo ABC algorithm (ABC-PMC) is closely related to ABC-SMC, and also draws on importance sampling (Beaumont et al., 2009; Marin et al., 2012). ABC-PMC uses a multivariate normal jumping distribution with covariance matrix that is based on prior draws.
In general, ABC and its variants can be impractical or can fail when the parameter space is high dimensional, or there are many summary statistics that the simulated data must approximate (Blum and Francois, 2010). We propose a new ABC approach that we call incremental mixture approximate Bayesian computation (IMABC), which is well-suited to MSM calibration which involves both high dimensional parameter spaces and many calibration targets. IMABC is an approximate Bayesian version of adaptive importance sampling, similar to IMIS (Steele, Raftery and Edmond, 2006; Raftery and Bao, 2010), with samples drawn from the parameter space using a proposal distribution that is a mixture of normal distributions. Posterior estimates are based on accepted draws that are weighted to account for differences between the prior and proposal distrbutions. IMABC is most similar to the ABC-PMC approach (Beaumont et al., 2009). IMABC adds new points in regions near a subset of points that produce simulated targets closest to observed targets, whereas ABC-PMC samples points based on an approximation to the joint distribution using importance weights.
4.1. The IMABC algorithm.
The IMABC algorithm begins with a rejection-sampling ABC step, and updates this initial sample by adding points near a set of “best” points that result in simulated targets that are closest to corresponding observed targets.
Let O1,…,OJ denote the J calibration targets, which we assume are summary statistics. We specify tolerance bounds around targets based on (1−αj)×100% confidence intervals, for j = 1, …, J. Let α = (α1, α2, …, αJ). The IMIS algorithm updates tolerance intervals so they become more stringent in later iterations. Let α(0) be the alpha-levels used for tolerance intervals for the initial ABC step, α(t) are alpha-levels for the tth iteration, and α* are the final (user-specified) alpha-levels, corresponding to convergence of the IMABC algorithm. When searching a high dimensional parameter space, it is practical to begin with very wide tolerance intervals, corresponding to small values of α. Final alpha-levels used to calculate tolerance intervals may vary across targets depending on the quality of and confidence in calibration targets.
Let Sij denote the jth simulated target (corresponding to Oj) for the ith sampled point, and let δj (θi, αj) = 1 if Sij falls within the (1 − αj) × 100% confidence interval for target Oj. We use an intersection criterion for acceptance (Conlan et al., 2012; Ratmann et al., 2014), with θi is accepted when all Sij lie within ABC tolerance bounds, so that .
At the first IMABC step, a sample of N0 points is drawn from the prior distribution of model parameters, π(θ). The algorithm then enters an updating phase. The (t + 1)st iteration in the IMABC algorithm proceeds as outlined below:
Step 1: Identify the best points and sample new points nearby
-
1A.
Calculate p-values, ρij, for each accepted θi, based on two-sided tests of H0: Sij = Oj versus HA: Sij ≠ Oj for j = 1, …, J, treating Sij as fixed and Oj as estimated with error. Often, as in our application, Oj is a summary statistic, and is approximately normally distributed. We summarize model fit across multiple targets with ρi· = mini(ρij), the worst fit across the J targets.
-
1B.
Select the N(c) points with the largest ρi·. When there are ties, calculate the distance between the simulated and observed targets, where and select points with the largest ρi· and smallest di·.
-
1C.
Simulate B new draws around each of the , k = 1, …, N(c) best points by sampling from a normal distribution with mean and covariance .
Let p be the dimension of θ (i.e., the number of calibrated parameters). If there are fewer than 5p accepted points, then is set to a diagonal covariance matrix with standard deviation set to half the prior distribution standard deviation for each parameter. If there are at least 5p and up to 25p accepted points, is calculated using all accepted points. If there are more than 25p accepted points, is calculated using the 25p accepted points nearest to . This means that until the algorithm accepts 25p points, the the same covariance matrix is used for all normal mixtures.
-
1D.
Simulate calibration targets, Sij, for each new draw, and resimulate targets at center points, . Accept or reject new draws and previously sampled center points based on δ(θi, α(t)). Resimulation of targets at center points enables the algorithm to move away from center points with Sij that are, by chance, similar to Oi.
Step 2: Update Tolerance Intervals
If any and there are 50p or more accepted points, check to see if the tolerance can be updated. Identify i′ associated with the median ρi·, with di· as a tie breaker. For each potentially updated tolerance level, set , then update the accepted θ’s, so that they are based on δ(θi, α(t+1)), removing up to half of the previously accepted points that are furthest from the targets.
Step 3: Evaluate Stopping Criteria
If α(t+1) = α*, calculate sampling weights and the corresponding effective sample size (ESS). Sampling weights account for sampling of points from the normal mixture rather than the prior distribution, wi = π(θi)/qt(θi). The mixture sampling distribution, qt, is given by where is the kth normal distribution at iteration s, given by , and Nt = N0 + N(c)Bt, the total number of draws through iteration t.
The ESS for the N(t+1) draws is , where wi = 0 if δ(θi, α(t+1)) = 0 (Kish, 1965; Liu, 2004). The algorithm stops when ESS ≥ Npost, having obtained the desired number of draws from the posterior distribution. If α(t+1) = α* and ESS < Npost the algorithm continues to iterate, but without further updates to tolerance intervals.
Once the IMABC algorithm is complete, independent draws from the posterior distribution are simulated by taking a weighted sample from accepted points with replacement, using the wi. Alternatively, posterior means and 95% credible intervals (CIs) can be estimated using weighted means and percentiles based on all accepted draws.
When implementing the IMABC algorithm, we recommend using a large initial sample size, N0, to ensure exploration of the parameter space and because few initially sampled points may lie in high posterior probability regions. The number of normal mixtures used to draw new points at each step, N(c), can be selected to optimize use of computing resources. The effective sample size of the final set of accepted points, Npost, will depend on the planned uses of the calibrated targets. For example, 2, 000 is a good choice when the goal is to provide interval estimates of model predictions based on percentile intervals, but larger samples may be desired when estimating functions of parameters.
Using IMABC to calibrate an MSM requires multiple model evaluations at each parameter draw and the user needs to specify mj, the size of the simulated sample used to obtain Sij. mj may be smaller for common outcomes (such as adenoma prevalence), and larger for rare outcomes (such as cancer incidence). Setting m too low will result in too much stochastic variation in Sij and inaccurate identification of acceptable θi. Setting m too high will unnecessarily slow the algorithm.
5. CRC-SPIN 2.0 Calibration Results.
5.1. IMABC Implementation.
To calibrate CRC-SPIN 2.0, we used N0 = 21,000 with Latin hypercube sampling from the prior distribution to ensure coverage of the parameter space at the initial draw. With the exception of the SEER target, we began with α(0) = 0.0001 and worked toward α* = 0.001. For SEER targets we began with α(0) = 0, accepting all points regardless of nearness to SEER targets, and worked toward α* = 1 × 10−9, which results in narrow bands around these registry-based incidence rates. Tolerance intervals are wider for study-derived targets because of the smaller sample sizes. These wider tolerance intervals also reflect the greater uncertainty in these targets due to a range of factors related to their simulation, including uncertainty about population characteristics, sensitivity of lesion detection, and lesion size measurement and categorization. Because the Corley et al. (2013) study is based on insured patients who underwent colonoscopies from 1/1/2006 to 12/31/2008, the observed adenoma incidence rates may be lower than expected because of prior screening and removal of adenomas. Therfore, we specified asymetric tolerance limits for the Corley et al. (2013) target, extending the upper tolerance range by adding 0.25Oj to the upper tolerance limit.
To take advantage of high performance computing and parallel processing (Appendix §B), we used N(c) = 10, drawing B = 1, 000 points from each normal mixture so that 10, 000 new points were evaluated at each updating iteration. We assumed a normal distribution for sample statistics when estimating (1 − α) × 100% confidence intervals and p-values. We set the final effective sample size, Npost, to 5, 000.
When simulating target data, we used mj equal to 5×104 for Pickhardt et al. (2003); 2×105 for Corley et al. (2013) and Imperiale et al. (2000); 3×105 for Church (2004), 5×105 for Lieberman et al. (2008) and 5×106 for the SEER registry data. To improve efficiency of the IMABC algorithm, we sequentially calculated Sij for each new θi in Step 1 of the algorithm, working from targets that are least to most computationally intensive. After calculating each target, we evaluated δj(θi, αj) and once δj(θi, αj) = 0, the point is rejected without simulating the remaining, more computationally intensive, targets.
Both the IMABC algorithm and the CRC-SPIN 2.0 model were implemented in the R programming language (R Core Team, 2014). They were coupled to produce an integrated, dynamic, high-performance computing workflow with the use of the Extreme-scale Model Exploration with Swift (EMEWS) framework (Ozik et al., 2016). Further details about the computing environment are provided in Appendix B.
5.2. Posterior Estimates.
The IMABC algorithm completed 8 iterations, obtaining 5,253 parameter draws within tolerance limits, with an effective sample size of 5, 168 draws from the joint posterior distribution. Sampling weights ranged from 1.3 × 10−4 to 3.20 × 10−4, with a mean and median of 1.9 × 10−4.
Posterior estimated means and 95% CIs of model parameters were based on weighted means and percentiles of accepted draws from the joint posterior distribution (shown in Table 1). We estimated that adenoma risk is higher for men than women, increases with age, and increases more rapidly at younger (than older) ages. Parameters that govern the time for an adenoma to reach 10mm were tightly estimated, with the exception of β1R. Consistent with prior limitations, the model predicted that 0.4% of adenomas in the colon reach 10mm within 10 years (95% CI (0.4%, 1.0%)) and 1.8% of adenomas in the rectum reach 10mm within 10 years (95% CI (0.002%, 9.8%)). The predicted percent of adenomas reaching 10mm within 20 years rises to 9.6% (95% CI (6.8%, 12.3%)) for adenomas in the colon and 59.7% (95% CI (38.8%, 83.3%)) for adenomas in the rectum. We estimated that adenomas transition to preclinical cancer at smaller sizes for women, for adenomas in the rectum, and for adenomas initiated at later ages. The gender effect was stronger for adenomas in the colon than for adenomas in the rectum. We did not find evidence of differential effects of age at adenoma initiation on size at transition by adenoma location or agent sex (based on interaction terms γ5, γ6, and γ7). We estimated shorter sojourn times for preclinical cancers in the colon relative to the rectum. The estimated posterior mean sojourn time is 1.75 years with 95% CI (1.39, 2.44) for preclinical cancers in the colon and 2.13 with 95% CI (1.42, 3.26) for preclinical cancers in the rectum.
By simulating draws from the posterior distribution, we were able to examine correlations and relationships among model parameters. For example, Figure 1 displays the bivariate posterior distributions of baseline log-adenoma risk (A) and the annual increase in risk between the ages of 20 and 50 years (α20). When baseline risk is lower, risk increases more rapidly from 20 to 50 years to accurately predict observed adenoma prevalence, which largely is based on prevalence after age 50 when guidelines recommend initiation of CRC screening (correlation is −0.61). Adenoma growth parameters also show negative correlation, as demonstrated by the bivariate distribution of β1R and β2R (correlation is −0.55).
Fig 1:
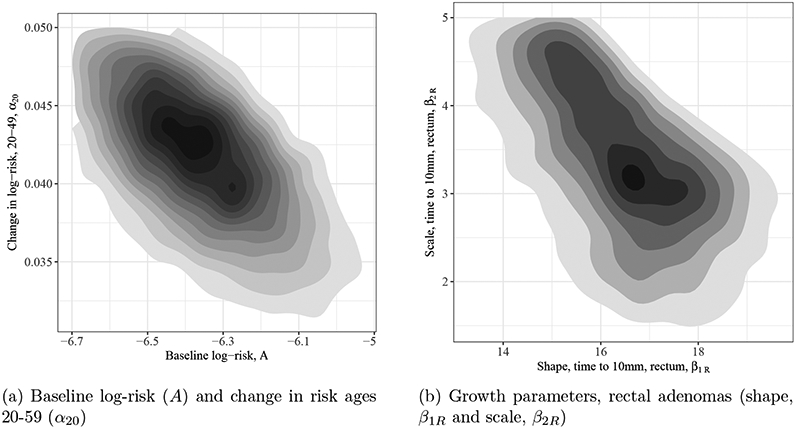
Joint posterior distribution of model parameters associated with adenoma risk, and the growth and sojourn time in the colon.
The posterior predicted means of SEER targets were near observed rates and posterior 95% CIs include SEER targets (Table 2). Posterior 95% CI do not always include other targets (Table 3). The model predicted higher adenoma prevalence than observed by Corley et al. (2013), especially at older ages, acknowledging the possibility of prior screening. The model also predicted a larger number of adenomas ≥10mm than observed by Pickhardt et al. (2003). The probability of detecting preclinical cancer came from 3 studies, and the accuracy of model predictions demonstrates how the IMABC calibration approach combines information across potentially conflicting targets.
6. Discussion.
We addressed the problem of calibrating microsimulation models by developing IMABC, an ABC algorithm based on the ideas of incremental mixture importance sampling (IMIS) (Steele, Raftery and Edmond, 2006; Raftery and Bao, 2010), an adaptive Sampling Importance Resampling algorithm (SIR; Rubin, 1987). We illustrate our approach by calibrating CRC-SPIN 2.0, an MSM for colorectal cancer, a problem that involves a relatively high dimensional parameter space and multiple targets.
Like IMIS, the IMABC algorithm iteratively updates the proposal distribution at each iteration to obtain samples from regions of the parameter space that are consistent with calibration targets. The resulting mixture of normal distributions with locally adaptive covariance matrices is a very flexible distribution, and the algorithm can sample from a distribution that is multimodal to better approximate the posterior distribution. In terms of ABC algorithms, IMABC uses a new approach to selecting tolerance levels, based on α-levels associated with a test of equality between the simulated and observed targets, which implicitly incorporates the precision of calibration targets. IMABC also provides an automated approach to tuning these tolerance intervals, requiring users to specifiy only the initial and final values whereas ABC-SMC requires prespecification of the sequence of tolerance intervals.
Other advantages of IMABC include clear stopping rules based on the effective sample size, the ability to specify which targets are most important through final tolerance intervals, and the ability to take advantage of parallelized code. A limitation of the IMABC algorithm, especially as applied to MSM calibration, is that IMABC can be computationally demanding. Evaluation of a very large number of points may be necessary, and calibration targets must be simulated for each point. The computational expense can be reduced through the ordering of target evaluations, and ceasing evaluation of a point when the first set of targets fails to fall within tolerance bounds. We implemented IMABC as a dynamic high-performance computing (HPC) workflow via the EMEWS framework (Ozik et al., 2016). While the HPC environment was advantageous for development of the IMABC approach, we found that it was not ultimately necessary for its application.
Future work will explore the release of publicly available code to allow others to utilize IMABC. In addition, because calibration to summary statistics requires simulation of a large number of model evaluations, each with a large number of agents, we plan to explore ways to improve the efficiency of IMABC model calibration. We also plan to examine efficient approaches to parameter updating when new targets become available, and sequential calibration approaches that can be used to efficiently build from simpler to more complex models.
ACKNOWLEDGEMENTS
This publication was made possible by financial support provided by NIH. Drs. Rutter and DeYoreo were supported by a grant from the National Cancer Institute (U01-CA-199335) as part of the Cancer Intervention and Surveillance Modeling Network (CISNET). Drs. Ozik and Collier were supported by the NIH (grants 1R01GM115839, 1S10OD018495), the NCI-DOE Joint Design of Advanced Computing Solutions for Cancer program, and through resources provided by the Computation Institute and the Biological Sciences Division of the University of Chicago, the University of Chicago Research Computing Center, and Argonne National Laboratory. This material is based upon work supported by the U.S. Department of Energy, Office of Science, under contract number DE-AC02-06CH11357. The contents of this article are solely the responsibility of the authors and do not necessarily represent the official views of the National Cancer Institute.
Appendix
APPENDIX A: CRC-SPIN 2.0: ADDITIONAL MODEL INFORMATION
This appendix provides information about the CRC-SPIN 2.0 model that that may be useful for understanding the model, but is not essential to understanding the calibration approach. Complete model description can be found on the cancer.cisnet.gov (National Cancer Institute, 2018), in the section describing model profiles.
A.1. Adenoma Risk Model.
Once adenomas are initiated, they are assigned a location. The distribution of adenomas throughout the large intestine follows a multinomial distribution based on data from 9 autopsy studies (Blatt, 1961; Chapman, 1963; Stemmermann and Yatani, 1973; Eide and Stalsberg, 1978; Rickert et al., 1979; Williams, Balasooriya and Day, 1982; Bombi, 1988; Johannsen, Momsen and Jacobsen, 1989; Szczepanski, Urban and Wierzchowski, 1992). The probabilities associated with six sites in the large intestine (from distal to proximal) are: P(rectum) = 0.09; P(sigmoid colon) = 0.24; P(descending colon) = 0.12; P(transverse colon) = 0.24; P(ascending colon) = 0.23; and P(cecum) = 0.08. For many purposes it is important to distinguish between colon and rectal locations; more detailed location information is sometimes used for determining screening test accuracy.
A.2. Adenoma Growth Model.
The diameter of the jth adenoma in the ith agent at time t after onset is given by
where d∞ = 50 is the maximum adenoma diameter in millimeters (mm), d0 = 1mm is the minimum adenoma diameter, p = 3, corresponding to the von Bertalanffy growth model, and λij is the growth rate for the jth adenoma within the ith agent. CRC-SPIN 1.0 specified p = 1, corresponding to the negative exponential model, but this resulted in relatively faster early adenoma growth and too few small adenomas.
We parameterized the growth model in terms of the time it takes for the adenoma diameter to reach 10mm to improve our ability to relate adenoma growth to observable data and clinical knowledge. The growth rate, γij, can easily be calculated given the time to reach 10mm.
A.3. Model for Transition from Adenoma to Preclinical Invasive Cancer.
The CRC-SPIN 2.0 model for adenoma transition is a reparameterized version of the CRC-SPIN 1.0 model for adenoma transition, restated as a regression model to better evaluate differences based on agent and adenoma characteristics.
A.4. Model for Sojourn Time.
CRC-SPIN 2.0 uses a Weibul for sojourn times. This allows longer sojourn times and better aligns with findings from previous studies than the log-normal model used in Version 1.0. For example, data from the TAMACS study (Chen et al., 1999), reported an estimated mean sojourn time of 2.85 years with a 95% confidence interval (2.15, 4.30).
A.5. Simulation of Lifespan and Colorectal Cancer Survival.
The CRC-SPIN 2.0 model first simulates the stage at clinical detection given sex and age at detection, and then simulates size at detection conditional on stage. (In contrast, the CRC-SPIN 1.0 model simulated size, and then stage conditional on size.)
A.6. Simulated Screening.
Colonoscopy sensitivity for adenoma and preclinical CRC detection is based on a quadratic function of lesion size (s) that was successfully used in the CRC-SPIN 1.0 model. For adenomas, we assume P(miss∣size = s ≤ 15mm) = 0.34 − 0.0349s + 0.0009s2, P(miss∣size = 15 < s ≤ 30mm) = 0.01, P(miss∣size = 30 < s ≤ 40mm) = 0.005 and P(miss∣size = s ≥ 40mm) = 0.001. This function results in sensitivity that is consistent with observed findings from the 1990’s (Hixson et al., 1990; Rex et al., 1997): sensitivity is 0.76 for a 3mm adenoma, 0.87 for a 7.5mm adenoma, and 0.95 for a 12mm adenoma. For preclinical cancers, we assume sensitivity that is the maximum of 0.95 and sensitivity based on adenoma size, so that colonoscopy sensitivity is 0.95 for preclinical cancers 12mm or smaller, and sensitivity is greater than 0.95 for preclinical cancers larger than 12mm.
Participants in the Pickhardt et al. (2003) study underwent both CT colonography (CTC) and colonoscopy for the purposes of evaluating the accuracy of CTC, primarily for adenomas 6mm and larger. The sensitivities reported by Pickhardt et al. (2003) are consistent with those used for onetime colonoscopy.
APPENDIX B: PROGRAMMING AND COMPUTING ENVIRONMENT
We utilized the EMEWS framework (Ozik et al., 2016) to implement a dynamic HPC workflow controlled by the IMABC algorithm. EMEWS, built on the general-purpose parallel scripting language Swift/T (Wozniak et al., 2013), allows for the direct integration of multi-language software components, in this case IMABC and CRC-SPIN 2.0, and can be used on computing resources ranging from desktops and campus clusters to supercomputers. The resulting IMABC EMEWS workflow is driven directly by the IMABC R source code, obviating the need for porting the code to alternate programming languages or platforms for the sole purpose of running large-scale computational experiments.
The experiments were performed on the Cray XE6 Beagle at the University of Chicago, hosted at Argonne National Laboratory. Beagle has 728 nodes, each with 2 AMD Operton 6300 processors, each having 16 cores, for a total of 32 cores per node; the system thus has 23,296 cores in all. Each node has 64 GB of RAM. Experiments were also run on the Midway2 cluster at the University of Chicago Research Computing Center. Midway2 is a hybrid cluster, including both CPU and GPU resources. For this work, the CPU resources were used, consisting of 370 nodes of Intel E5-2680v4 processors, each with 28 cores and 64 GB of RAM. Swift/T, with the underlying EMEWS workflow engine, allows for the abstraction of resource specific settings (e.g., scheduler type and compute layouts) for a variety of target computing resources. Thus, once the IMABC EMEWS workflow was developed, it could be run on both the Beagle and Midway2 clusters with only minimal configuration modifications.
The experiment reported here used 80 nodes on Beagle with 4 worker processes per node (to account for the memory footprint of CRC-SPIN 2.0) for a total of 320 worker processes, each of which could concurrently execute an individual model run. The total compute time was 29.4 hours or 2,352 node-hours.
REFERENCES
- Beaumont MA, Corneaut JM, Marin JM and Robert CP (2009). Adaptive approximate Bayesian computation. Biometrika 96 983–990. [Google Scholar]
- Blatt LJ (1961). Polyps of the colon and rectum: Incidence and distribution. Diseases of the Colon and Rectum 4 277–282. [Google Scholar]
- Blum M and Francois O (2010). Non-linear regression models for Approximate Bayesian Computation. Statistics and Computing 20 63–73. [Google Scholar]
- Bombi JA (1988). Polyps of the colon in Barcelona, Spain. Cancer 61 1472–1476. [DOI] [PubMed] [Google Scholar]
- Chapman I (1963). Adenomatous polypi of large intestine: Incidence and distribution. Annals of Surgery 157 223–226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen THH, Yen MF, Lai MS, Koong SL, Wang CY, Wong JM, Prevost TC and Duffy SW (1999). Evaluation of a selective screening for colorectal carcinoma: The Taiwan Multicenter Cancer Screening (TAMACS) Project. Cancer 86 1116–1128. [PubMed] [Google Scholar]
- Church JM (2004). Clinical Significance of Small Colorectal Polyps. Dis Colon Rectum 47 481–485. [DOI] [PubMed] [Google Scholar]
- Conlan AJK, McKinley TJ, Karolemeas K, Pollock EB, Goodchild AV, Mitchell AP, Birch CPD, Clifton-Hadley RS and Wood JLN (2012). Estimating the Hidden Burden of Bovine Tuberculosis in Great Britain. PLOS Computational Biology 8 1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corley DA, Jensen CD, Marks AR, Zhao WK, De Boer J, Levin TR, Doubeni C, Fireman BH and P QC (2013). Variation of Adenoma Prevalence by Age, Sex, Race adn colon Location in a Large Population: Implications for Screening and Quality Programs. Clinical Gastroenterology and Hepatology 11 172–180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Koning HJ, Meza R, Plevritis SK, Ten Haaf K, Munshi VN, Jeon J, Erdogan SA, Kong CY, Han SS, van Rosmalen J et al. (2014). Benefits and harms of computed tomography lung cancer screening strategies: a comparative modeling study for the US Preventive Services Task Force. Annals of internal medicine 160 311–320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eide TJ and Stalsberg H (1978). Polyps of the large intestine in Northern Norway. Cancer 42 2839–2848. [DOI] [PubMed] [Google Scholar]
- Centers for Disease Control & Prevention (2011). Vital signs: Colorectal cancer screening, incidence, and mortality–United States, 2002-2010. Morbidity and mortality weekly report 60 884. [PubMed] [Google Scholar]
- National Center for Health Statistics (2000). US Life Tables.
- Hixson L, Fennerty M, Sampliner R, McGee D and Garewal H (1990). Prospective study of the frequency and size distribution of polyps missed by colonoscopy. J Natl Cancer Inst 82 1769–1772. [DOI] [PubMed] [Google Scholar]
- Imperiale TF, Wagner DR, Lin CY, Larkin GN, Rogge JD and Ransohoff DF (2000). Risk of Advanced Proximal Neoplasms in Asymptomatic Adults According to the Distal Colorectal Findings. NEJM 343 169–174. [DOI] [PubMed] [Google Scholar]
- National Cancer Institute (2004). Surveillance, Epidemiology, and End Results (SEER) Program. Technical Report, National Cancer Institute, DCCPS, Surveillance Research Program, Cancer Statistics Branch. released April 2004, based on the November 2003 submission. [Google Scholar]
- National Cancer Institute (2018). Cancer INtervention and Surveillance Modeling Network (CISNET) Technical Report.
- Johannsen LGK, Momsen O and Jacobsen NO (1989). Polyps of the large intestine in Aarhus, Demark. An autopsy study. Cancer 24 799–806. [DOI] [PubMed] [Google Scholar]
- Kim JJ, Burger EA, Regan C and Sy S (2017). Screening for Cervical Cancer in Primary Care: A Decision Analysis for the U.S. Preventive Services Task Force Technical Report, Agency for Healthcare Research and Quality. Contract No. HHSA-290-2012-00015-I. [PubMed] [Google Scholar]
- Kish L (1965). Survey sampling. John Wiley and Sons, New York, USA. [Google Scholar]
- Knudsen AB, Zauber AG, Rutter CM, Naber SK, Doria-Rose VP, Pabiniak C, Johanson C, Fischer SE, Lansdorp-Vogelaar I and Kuntz KM (2016). Estimation of benefits, burden, and harms of colorectal cancer screening strategies: modeling study for the US Preventive Services Task Force. Jama 315 2595–2609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koh K-J, Lin L-H, Huang S-H and Wong J-U (2015). CARE - pediatric colon adenocarcinoma: a case report and literature review comparing differences in clinical features between children and adult patients. Medicine 94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kong CY, McMahon PM and Gazelle GS (2009). Calibration of Disease Simulation Model Using an Engineering Approach. Value in Health 12 521–529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leslie A, Carey FA, Pratt NR and Steele RJC (2002). The colorectal adenoma–carcinoma sequence. British Journal of Surgery 89 845–860. [DOI] [PubMed] [Google Scholar]
- Lieberman D, Moravec M, Holub J, Michaels L and Eisen G (2008). Polyp Size and Advanced Histology in Patients Undergoing Colonoscopy Screening: Implications for CT Colonography. Gastroenterology 135 1100–1105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu J (2004). Monte Carlo Strategies in Scientific Computing. Springer Verlag, New York. [Google Scholar]
- Mandelblatt JS, Stout NK, Schechter CB, Van Den Broek JJ, Miglioretti DL, Krapcho M, Trentham-Dietz A, Munoz D, Lee SJ, Berry DA et al. (2016). Collaborative modeling of the benefits and harms associated with different US breast cancer screening strategies. Annals of internal medicine 164 215–225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marin J-M, Pudlo P, Robert CP and Ryder RJ (2012). Approximate Bayesian computational methods. Statistics and Computing 22 1167–1180. [Google Scholar]
- Marjoram P, Molitor J, Plagnol V and Simon T (2003). Markov chain Monte Carlo without likelihoods. Proceedings of the National Academy of Sciences 100 15324–15328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKinley TJ, Vernon I, Andrianakis I, McCreesh N, Oakley JE, Nsubuga RN, Goldstein M and White RG (2018). Approximate Bayesian Computation and simulation-based inference for complex stochastic epidemic models. Statistical science 33 4–18. [Google Scholar]
- Meissner HI, Breen N, Klabunde CN and Vernon SW (2006). Patterns of colorectal cancer screening uptake among men and women in the United States. Cancer Epidemiology and Prevention Biomarkers 15 389–394. [DOI] [PubMed] [Google Scholar]
- Muto T, Bussey HJR and Morson BC (1975). The Evolution of Cancer in the Colon and Rectum. Cancer 36 2251–2270. [DOI] [PubMed] [Google Scholar]
- Nelder JA and Mead R (1965). A simplex method for function minimization. Computer Journal 7 308–313. [Google Scholar]
- Ozik J, Collier NT, Wozniak JM and Spagnuolo C (2016). From desktop to Large-Scale Model Exploration with Swift/T,. In Proceedings of the 2016 Winter Simulation Conference(WSC) 206–220. IEEE Press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pickhardt PJ, Choi R, Hwang I, Butler JA, Puckett ML, Hildebrandt HA, Wong RK, Nugent PA, Mysliwiec PA and Schindler WR (2003). Computed Tomographic Virtual Colonocopy to Screen for Colorectal Neoplasia in Asymptomatic Adults. NEJM 349 2191–2200. [DOI] [PubMed] [Google Scholar]
- Ponugoti PL and Rex DK (2017). Yield of a second screening colonoscopy 10 years after an initial negative examination in average-risk individuals. Gastrointestinal endoscopy 85 221–224. [DOI] [PubMed] [Google Scholar]
- Pritchard JK, Seielstad MT, Perez-Lezaun A and Feldman MW (1999). Population growth of human Y chromosomes: a study of Y chromosome microsatellites. Molecular Biology and Evolution 16 1791–1798. [DOI] [PubMed] [Google Scholar]
- Raftery A and Bao L (2010). Estimating and Projecting Trends in HIV/AIDS Generalized Epidemics Using Incremental Mixture Importance Sampling. Biometrics 66 1162–1173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratmann O, Camacho A, Meijer A and Donker G (2014). Statistical modelling of summary values leads to accurate approximate Bayesian computations. ArXiv arXiv:1305.4283. [Google Scholar]
- Rex D, Cutler C, Lemmel G, Rahmani E, Clark D, Helper D, Lehman G and Mark D (1997). Colonoscopic miss rates of adenomas determined by back-to-back colonoscopies. Gastroenterology 112 24–28. [DOI] [PubMed] [Google Scholar]
- Rickert RR, Auerbach O, Garfinkel L, Hammond EC and Frasca JM (1979). Adenomatous lesions of the large bowel. An autopsy survey. Cancer 43 1847–1857. [DOI] [PubMed] [Google Scholar]
- Rubin D (1987). The calculation of posterior distributions by data augmentation: Comment: A noniterative sampling/importance resampling alternative to the data augmentation algorithm for creating a few imputations when fractions of missing information are modest: The SIR algorithm. Journal of the American Statistical Association 82 543–546. [Google Scholar]
- Rutter CM, Miglioretti DL and Savarino JE (2009). Bayesian Calibration of Microsimulation Models. JASA 104 1338–1350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rutter CM and Savarino JE (2010). An Evidence-Based Microsimulation Model for Colorectal Cancer: Validation and Application. Cancer Epidemiology Biomarkers and Prevention 19 1992–2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rutter CM, Johnson EA, Feuer EJ, Knudsen AB, Kuntz KM and Schrag D (2013). Secular trends in colon and rectal cancer relative survival. Journal of the National Cancer Institute 105 1806–1813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rutter CM, Knudsen AB, Marsh TL, Doria-Rose VP, Johnson E, Pabiniak C, Kuntz KM, van Ballegooijen M, Zauber AG and Lansdorp-Vogelaar I (2016). Validation of Models Used to Inform Colorectal Cancer Screening Guidelines: Accuracy and Implications. Medical Decision Making 36 604–614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sisson SA, Fan Y and Tanaka MM (2007). Sequential Monte Carlo without likelihoods. Proceedings of the National Academy of Sciences 104 1760–1765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steele R, Raftery A and Edmond M (2006). Computing Normalizing Constants for Finite Mixture Models via Incremental Mixture Importance Sampling (IMIS). Journal of Computational and Graphical Statistics 15 712–734. [Google Scholar]
- Stemmermann GN and Yatani R (1973). Diverticulosis and polyps of the large intestine. A necropsy study of Hawaii Japanese. Cancer 31 1260–1270. [DOI] [PubMed] [Google Scholar]
- Szczepanski W, Urban A and Wierzchowski W (1992). Colorectal polyps in autopsy material. Part I. Adenomatous polyps. Pat Pol 43 79–85. [PubMed] [Google Scholar]
- Tavare S, Balding D, Griffiths R and Donnelly P (1997). Inferring Coalescence Times from DNA Sequence Data. Genetics 145 505–518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Core Team (2014). R: A Language and Environment for Statistical Computing R Foundation for Statistical Computing, Vienna, Austria. [Google Scholar]
- Tjørve E and Tjørve KM (2010). A unified approach to the Richards-model family for use in growth analyses: why we need only two model forms. Journal of theoretical biology 267 417–425. [DOI] [PubMed] [Google Scholar]
- Toni T, Welch D, Strelkowa N and Stumpf M (2009). Approximate Bayesian computation scheme for parameter inference and model selection in dynamical systems. Journal of the Royal Society Interface 6 187–202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams AR, Balasooriya BAW and Day DW (1982). Polyps and cancer of the large bowel: A necropsy study in Liverpool. Gut 23 835–842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winawer SJ, Fletcher RH, Miller L, Godlee F, Stolar M, Mulrow C, Woolf S, Glick S, Ganiats T, Bond J et al. (1997). Colorectal cancer screening: clinical guidelines and rationale. Gastroenterology 112 594–642. [DOI] [PubMed] [Google Scholar]
- Wozniak JM, Armstrong TG, Wilde M, Katz DS, Lusk E and Foster IT (2013). Swift/T: Large-Scale Application Composition via Distributed-Memory Dataflow Processing. In 2013 13th IEEE/ACM International Symposium on Cluster, Cloud, and Grid Computing 95–102. IEEE. [Google Scholar]
- Zauber AG, Knudsen AB, Rutter CM, Lansdorp-Vogelaar I, Savarino JE, van Ballegooijen M and Kuntz KM (2009). Cost-Effectiveness of CT Colonography to Screen for Colorectal Cancer: Report to the Agency for Healthcare Research and Quality from the Cancer Intervention and Surveillance Modeling Network (CISNET) for MISCAN, SimCRC, and CRC-SPIN Models Technical Report. Project ID: CTCC0608. [PubMed] [Google Scholar]


