Building a three-dimensional model of early-stage zebrafish embryo brain

Abstract

We introduce a computational approach to build three-dimensional (3D) surface mesh models of the early-stage zebrafish brain primordia from time-series microscopy images. The complexity of the early-stage brain primordia and lack of recognizable landmarks pose a distinct challenge for feature segmentation and 3D modeling. Additional difficulty arises because of noise and variations in pixel intensity. We overcome these by using a hierarchical approach in which simple geometric elements, such as “beads” and “bonds,” are assigned to represent local features and their connectivity is used to smoothen the surface while retaining high-curvature regions. We apply our method to build models of two zebrafish embryo phenotypes at discrete time points between 19 and 28 h post-fertilization and collect measurements to quantify development. Our approach is fast and applicable to building models of other biological systems, as demonstrated by models from magnetic resonance images of the human fetal brain. The source code, input scripts, sample image files, and generated outputs are publicly available on GitHub.

Why it matters

Building geometric surface models of biological structures can enable quantitative measurements of corresponding morphological features. However, this is a nontrivial task, especially for early-stage embryos of model organisms that lack salient features to use as landmarks and when images are noisy. This work introduces a computational approach that builds surface mesh models by progressively eliminating effects of noise and by assigning geometric elements such as beads and bonds that comprise a mesh. These structural elements add a new dimension to image-based model building. Our approach is generally applicable and will complement existing approaches.

Introduction

The physical and molecular mechanisms underlying tissue rearrangements during neural tube formation have been the subjects of intense study (1, 2, 3, 4). Modeling presumptive vertebrate brain structures from the early embryo is a nontrivial task and depends on the proper construction of physical boundaries. Of particular interest is the midbrain-hindbrain boundary (MHB), or isthmic organizer, located between the midbrain and hindbrain neuromeres (5). The MHB is characterized structurally by a constriction in the neural tube (6) and functionally by its role in cell fate patterning (7) and as a local signaling center (5,8). Although studies have established a relationship between aberrant gene expression and anomalous MHB formation (6,9), the direct effects of gene expression on tissue morphology that yield the characteristic isthmic constriction remain unclear (10).

The zebrafish is a widely used model organism for studying vertebrate brain development and MHB formation (6,11, 12, 13). To quantify how aberrant phenotypes lead to MHB changes during neuroepithelial folding, it is necessary to measure the three-dimensional (3D) morphology of the early-stage brain at time points surrounding MHB formation, around 24 h post-fertilization (hpf). However, a lack of clearly distinguishable features and noisy images pose a challenge in segmenting the neuroepithelium. For embryos older than 1 or 2 days, salient anatomical features, such as the eyes or spinal cord, are typically used as landmarks to segment multiple embryos (14,15). However, before 24 hpf, the embryo does not have features easily recognizable by existing software; thus, image segmentation needs to be based on the general shape (e.g., Fig. 1 A). Furthermore, variations in uneven fluorescence intensity within the image make it difficult to apply only intensity-based thresholding to extract regions of interest. To our knowledge, measurable surface models of the zebrafish embryo brain between the segmentation and pharyngula periods (19–28 hpf) have not been built.

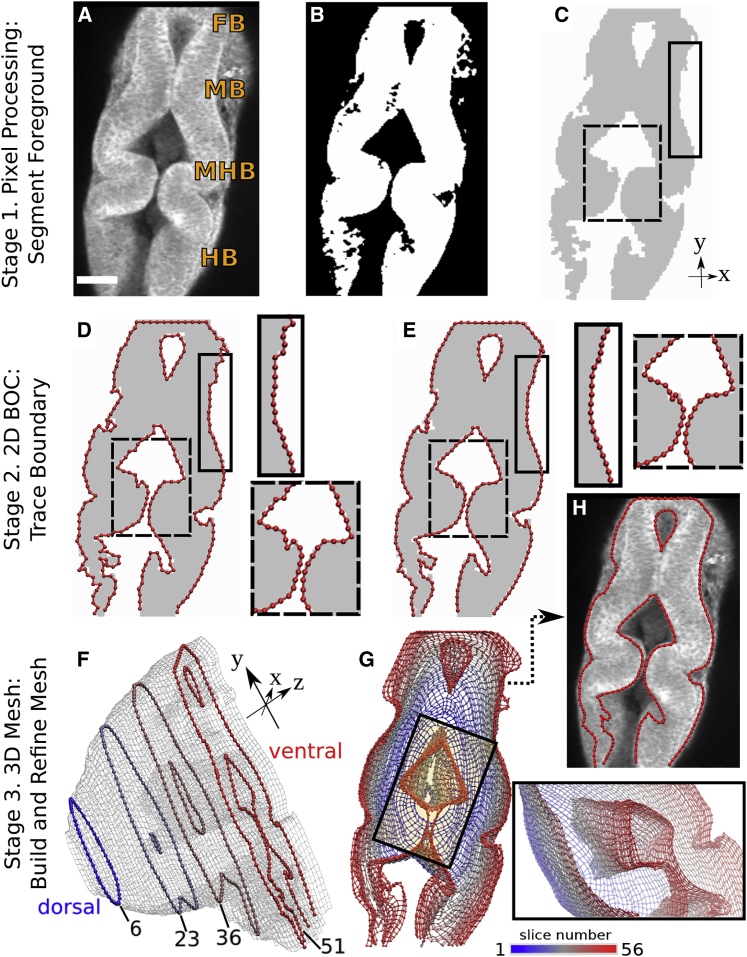
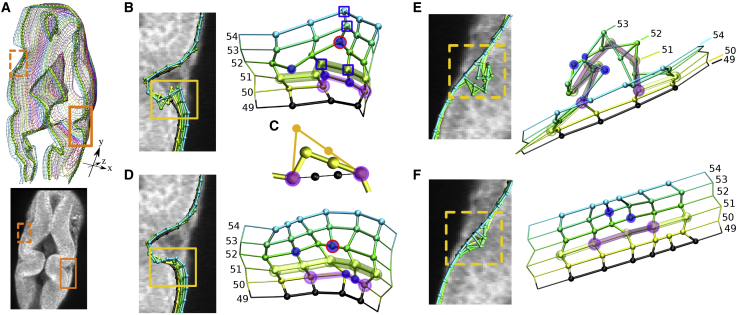
Figure 1.

Methodology overview. (A) Image slice 51 (150 μm from the dorsal plane, shown in F) from WT zebrafish embryo time-lapse set at 24 hpf obtained via multiphoton microscopy. FB, forebrain; MB, midbrain; HB, hindbrain; MHB, midbrain-hindbrain boundary. Scale bars, 50 μm. (B) Binary filtering. (C) Image after noise removal and region extraction; colors are inverted and intensity is adjusted for presentation. (D) Initial 2D BOC (linearly connected red spheres). Note the rough outline. (E) After refinement, contour is smoother. Insets correspond to solid and dashed rectangles in (C). (F) Refined 3D mesh. There are 56 slices, imaged 3 μm apart. The z dimension is exaggerated to show the 2D BOC of slices 6, 23, 36, and 51. (G) Mesh in (F) viewed from the ventral side. Color scale from 1 to 56 corresponds to slice number from dorsal to ventral planes. Inset is view of the rectangle looking into the mesh from the top left corner. View is rotated 130° counterclockwise about the y axis. Part of the outer mesh is hidden in the viewing plane to reveal the inner mesh. (H) 2D BOC of slice 51 after stage 3 refinement. Note the further refined regions compared to (E). BOC is overlaid onto the original image in (A) for comparison.

Here, we develop a procedure to construct models of the neuroepithelium surface, focusing near the MHB (Fig. 1). The resulting geometric model is used to measure structural features that span multiple imaging planes and vary depending on the orientation of each embryo. There are three main stages in our approach. The first is pixel processing, in which a series of operations are carried out to reduce small-scale noise and yield processed images that more faithfully capture larger-scale features of interest. In the second stage, a linear “beads-on-chain” (BOC) model is assigned to outline features in each 2D image. The third stage assigns “z-bonds” between BOC models of successive image slices to generate the 3D mesh. Because of noise, BOC models may not faithfully follow the target shape identified by human observers. Refinement of the BOC model is carried out by imposing continuity and smoothness of contours and surfaces so that holes in the mesh and irregular protrusions are automatically located and corrected. To demonstrate the utility of our approach in a morphometric analysis of developing brains, we carry out BOC-based automated measurements of the MHB structure at several time points during the development of two zebrafish phenotypes, which agree well with image-based manual measurements.

Our method for building 3D models is fast and requires only a small number of parameters, without any need for mouse-clicking operations on individual images. It can also build and combine models based on image sets obtained from different imaging channels of a sample. To demonstrate its general applicability, we build 3D BOC models based on magnetic resonance (MR) images of the human fetal brain. Being script based, we expect our method to be complementary to voxel-based approaches and useful for quickly building 3D models from image stacks, particularly when individual images are too noisy to apply common pixel intensity-based processing or when target structures lack clear features for use as landmarks for image segmentation.

Materials and methods

Overview of the approach

The basis of our approach is that features vary smoothly over length scales greater than pixel dimensions in an image. This allows the reduction of small-scale noise and correcting “missing parts” when building the 3D BOC model. Yet, relatively sharp corners in the contour that occur consistently across image slices are retained, as in the constriction in the MHB (Fig. 1 H).

The main goal of stage 1 is to reduce noise and make features of interest more clearly defined (Fig. 1, A–C). For example, in Fig. 1 A, the tube-shaped neuroepithelium is embedded in the embryo, with a blurry boundary due to pixels with nonuniform brightness. Although it is not difficult for a human observer to trace the neuroepithelium outline, it is nontrivial to capture computationally. Conversion from the original to the binary image (Fig. 1, A–C) is achieved by multistep operations.

In stage 2, we construct 2D BOC models of each image slice by tracing the binary thresholded image (Fig. 1, D and E). Beads carry coarse-grained positional information of the boundaries, and chains provide connectivity information. We refer to the BOC model of a 2D image simply as “BOC,” a segment of the BOC as “chain,” and a connection between two beads as “bond.” Note that a BOC may consist of multiple disconnected chains. In stage 3, z-bonds are assigned between nearby beads in successive slices to generate a 3D mesh of the surface (Fig. 1, F and G). As with stage 1, assigning the 2D and 3D BOC involves multistep operations. The resulting model is examined using a 3D viewing software and can be used for subsequent structural measurement and analysis.

Pixel processing

Thresholding and noise removal

The goal of pixel processing is to generate binary images with more defined regions of interest (e.g., the neuroepithelium contour; Fig. 1, A–C). We first apply a Gaussian blur with a 3 × 3 pixel rolling window and a three-pixel kernel to achieve slight blurring. We then apply binary thresholding to retain the main outline of the neuroepithelium. Because successive image slices are similar in intensity profile, we process the 56-slice stack in four groups and apply the same pixel intensity threshold to each.

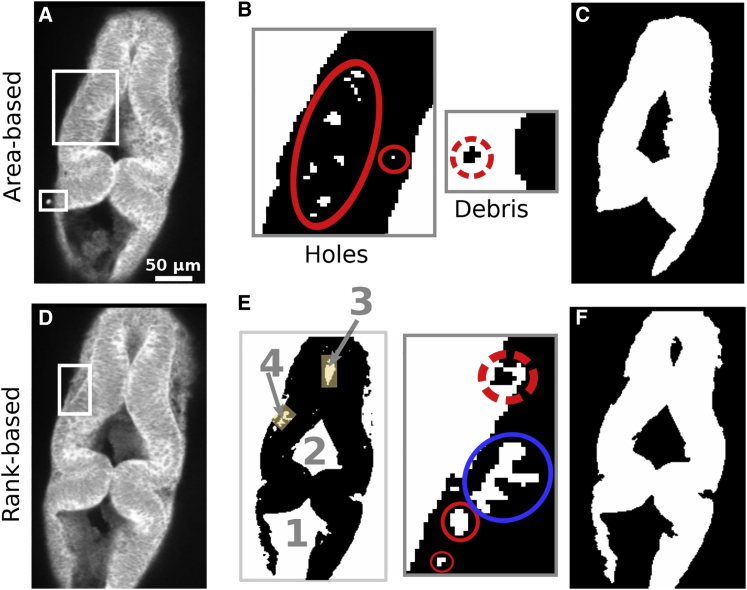
The thresholded image contains two types of “noisy” regions: 1) “holes” within the neuroepithelium and 2) outside “debris” (Fig. 2 B). Because debris becomes holes in an inverted image, the hole-removal method can be used to remove debris as well. Our approach starts by identifying clusters of contiguous high-intensity pixels. In most cases, holes are much smaller than the feature of interest, so they constitute the smallest clusters. We thus remove clusters (set their pixel intensity to 0) if their area (number of pixels belonging to the cluster) is less than a cutoff value (we used 20 pixels for all slices). However, some slices, especially toward the ventral side (e.g., cluster 4 in Fig. 2 E), contain larger noise clusters. Increasing the area size cutoff to remove them is not desirable because it involves estimating the size of particular clusters, which is time consuming. To remove such noisy regions, we apply rank-based cluster removal, in which a given number of largest clusters are kept and all other lower-ranked ones are removed. For example, in Fig. 2 E, the four largest clusters are marked (the ventricle on the lower side is connected to the background). Keeping the three largest clusters will remove the noise cluster (labeled 4) and other smaller clusters. In images in which the lower ventricle is disconnected from the background, such as in Fig. 3 A, we keep the four largest clusters. Compared to the area cutoff, the cluster rank order cutoff can be assigned by a quick visual inspection, which takes less time.

Figure 2.

Pixel noise removal. (A–C) Area-based noise removal of slice 36. (B) Two areas after binary thresholding and inverting. (C) After removing holes and debris using a 20-pixel area cutoff. The same area size cutoff was used for all slices. (D–F) Rank-based cluster removal of slice 45. (E) After binary thresholding and inverting. Four largest clusters are ranked by size (1 is the largest and includes all the background in this slice). Inset shows enlarged view of the rectangle in (D); the cluster ranked number 4 is circled in blue. Holes and debris are marked by red circles, as in (B). (F) Binary image after rank-based noise removal. The three largest clusters were kept.

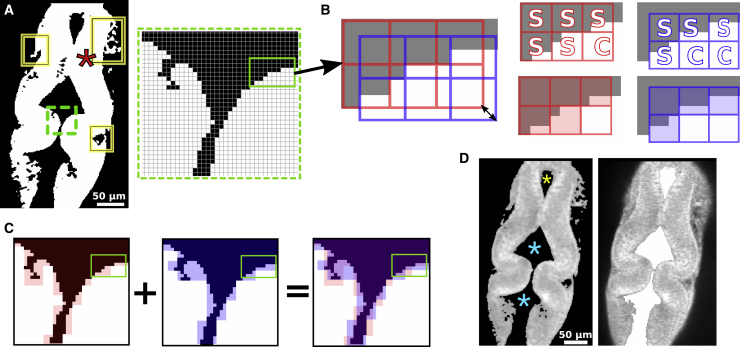
Figure 3.

Contiguous region extraction. (A) Binary thresholded image from Fig. 1B. Solid rectangles mark irregular protrusions. Inset is a magnified view of the area marked by the dashed rectangle. A star marks the point for initiating region extraction. (B) Positions of two 3 × 3 pixel grids for the area within the solid rectangle in the inset of (A). Black was changed to gray for presentation. Double-headed arrow denotes the diagonal shift of grids (additional two grid shifts are not shown for clarity). Panels on the right show labeling each 3 × 3 window based on the intensity of pixels it contains. Checked windows (labeled “C”) are set to 255 intensity, and the sealed windows (labeled “S”) are filled with the background intensity (represented by semitransparent red or blue). (C) AND operation of the extracted foreground from two grid variations. Because red and blue represent the background, pixels where they overlap are set to 0, and pixels for which only one color is present are not changed. (D) Ventricle extraction using a 2 × 2 pixel window. The left panel is the filtered grayscale image used for ventricle extraction; stars mark the points for initiating ventricle extraction. The right panel shows the extracted ventricle (area filled in white) overlaid onto the original image for comparison.

Most slices do not have large-area noise, so the rank order cutoff only needs to be used for the last 20 slices. Thus, area-based noise removal followed by rank-based removal requires the least parameter manipulation. Even after this, a small number of noisy clusters may still remain in a few images, as they were not selected under the criteria we used. These are later removed in the BOC assignment procedure below.

Removing protrusions

For the last 14 images on the ventral side, in which the mesenchyme surrounding the neuroepithelium is more visible, binary filtering leaves irregular protrusions (Fig. 3 A, solid rectangles). Thresholding with a higher intensity cutoff cannot be used to remove these because pixels in other parts of the actual neuroepithelium will also be removed. We applied a method to extract contiguous regions with the same pixel intensity, in which small protrusions that do not fit within a running window of a given size are omitted. For this, we select a pixel (star in Fig. 3 A) inside the region to extract. The exact location of this pixel does not affect the result, which allows us to use the same point for all slices. Next, a three-pixel square grid is generated, in which a positional reference pixel is at the top left corner of the grid (Fig. 3 B, red grid). If all pixels within this window have the same reference intensity (255 in the binary thresholded image), it is marked as checked, and the search moves to a neighboring window. In each new window, if all pixels have the same reference intensity, it is again marked as checked, and the process continues by spawning new windows in the unchecked area. On the other hand, if any pixel in a given window has an intensity different from the reference, the window is marked sealed, and no new neighboring windows spawn from it. The search continues until no unchecked windows neighbor the window being checked. For the panels on the top row of Fig. 3 B, sealed windows are labeled “S” and checked windows “C.” We fill the extracted region by setting all checked windows to the foreground intensity and sealed windows to the background intensity. In this way, the extracted region excludes protrusions not large enough to accommodate the running window.

A downside of this approach is that it makes a window either sealed or checked in a binary manner, which makes the outline of the extracted region coarser, effectively reducing its resolution by the size of the running window. To mitigate this, we generate a total of four grids, in which each is shifted by one pixel in four diagonal directions such that the windows of each grid tile the image differently (Fig. 3 B). We merge regions obtained from the four grids by applying an AND operation, which results in a smoothing effect (Figs. 3 C and S1).

Ventricle extraction

We separately extracted ventricles proximal to the MHB (Fig. 3 D, cyan stars) because their 3D models provide additional information on MHB structure. We adjusted the pixel intensity cutoffs for thresholding because the ventricle regions had intensity profiles different from the neuroepithelium. We also applied the contiguous region extraction method to the ventricles using a smaller grid size (2 × 2 pixel window). This was possible because the ventricle did not have any large protrusions to eliminate, and a smaller running window more finely captures the narrow MHB (Fig. 3 D). In image slices in which the narrowest point of the region connecting two ventricles is thinner than the grid used for region extraction, we used two reference positions (Fig. 3 D, cyan stars). We also extracted the forebrain ventricle (Fig. 3 D, yellow star).

Constructing 2D BOC

Initial BOC assignment

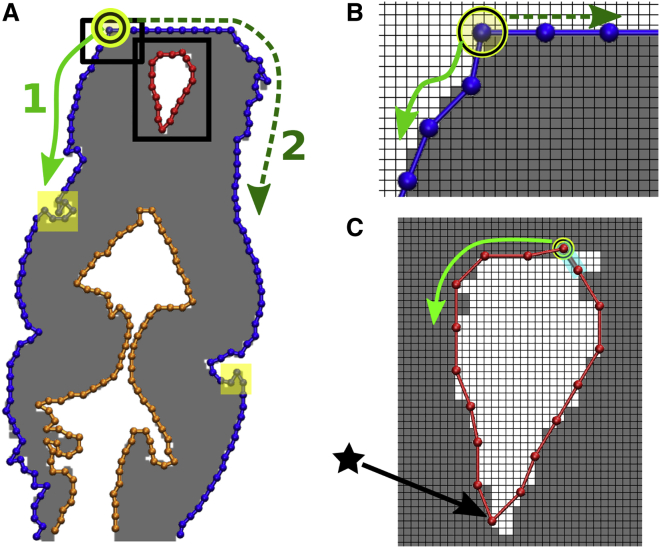
For each image slice, we represent boundaries of the foreground using BOCs. First, clusters of foreground (high-intensity) pixels are identified from the binary image. In each cluster, a boundary pixel that neighbors background pixels is chosen randomly. The boundary pixel as a square has at least one edge that neighbors a background pixel and another that neighbors a pixel belonging to the same cluster. At a corner of the former, a “seed” bead is assigned (Fig. 4, circled beads). The trace then moves along the boundary edges of the cluster in a counterclockwise direction (Fig. 4, solid arrows). As each new edge is visited, the distance between its end and the previously added bead is calculated. If it is greater than a bond length cutoff b₀ (= 5 pixel distance was used), a new bead is added, and a bond with the previously added bead is assigned to connect the two. This continues until all cluster boundary pixels are visited.

Figure 4.

Assign beads and bonds. (A) BOC from Fig. 1D. Individual chains are colored differently. Solid and dashed arrows (paths 1 and 2) denote counterclockwise and clockwise search directions along the bead boundary from the arbitrarily chosen seed bead (circled) to construct the outer chain. (B and C) Zoomed-in views of the rectangles in (A). One grid window represents one pixel. Beads and bonds are added as new edges meet the bond length cutoff b₀. Beads are assigned at pixel corners. (C) For boundary forming a closed contour, only one search direction is needed. The last bond added to close the contour is marked in cyan. Note that the sharp bend marked by a star is retained after smoothing (cf. Fig. S2).

There are different scenarios in which BOC assignment terminates. For a closed contour such as a ventricle, the BOC assignment terminates as the last bead is within 2.5 b₀ from the seed bead. After, a pixel along another unvisited boundary is randomly selected, and a new chain begins. For a cluster that spans to the boundaries of the image, the BOC that started from a seed somewhere in the middle of the outline (Fig. 4 A, circled bead) will reach the image boundary before returning to the seed bead. If this happens, a clockwise search starts from the seed to build the BOC for the rest of the contour (Fig. 4, A and B, dashed arrows).

Refining 2D BOC

Direct contour tracing results in a jagged outline and sharp corners. We smoothened the contour by using the average of linear fits from overlapping four-bead segments along the chain. For every bead, there are up to four such fits, in which the bead is located from the first to fourth positions in four consecutive four-bead segments (Fig. S2). Projections of the bead to these four fits were found and averaged to obtain the new smoothened position. This method avoids smoothing structural features such as sharp bends (Fig. 4 C, star).

After smoothing, beads were evenly spaced within the BOC. Then we closed a contour by adding a bond between two end beads if they were located within 2.5 b₀ (Fig. 4 C, bond highlighted in cyan). Two types of spurious BOC noise include isolated beads that do not belong to any chain and chains less than five beads in length, both of which were removed. These are from pixel noise that was not removed during the hole and debris removal procedures in stage 1. With error checks in subsequent stages, the output from each processing step does not have to be perfect to execute the next stage. The refined BOC consists of chains smoothly tracing the contour of the binary image (Fig. 1 E). However, discrepancies may still occur in regions where the binary thresholded image does not faithfully represent the feature (e.g., lower left side in Fig. 1 E and yellow squares in Fig. 4 A). These can be corrected when building the 3D BOC based on better-defined contours in neighboring slices (cf. Fig. 1 H), as explained below.

Constructing 3D mesh

Assigning z-bonds and closing mesh holes

We connect the BOCs of image slices to build the 3D mesh model of the zebrafish neuroepithelium surface. Similarly as describing contours in an image slice as 2D chains, we construct the surface in 3D by adding “z-bonds” between beads in neighboring image slices. The initial criterion for assigning a z-bond is that the 2D distance (projected distance on the xy plane) of a pair of beads in two neighboring slices is less than or equal to the cutoff b₀ used for the 2D BOC assignment. If there are multiple pairs of beads within b₀, a z-bond is assigned between the shortest distance pair so that a bead has at most one z-bond with each of its neighboring slices (Fig. 5 A).

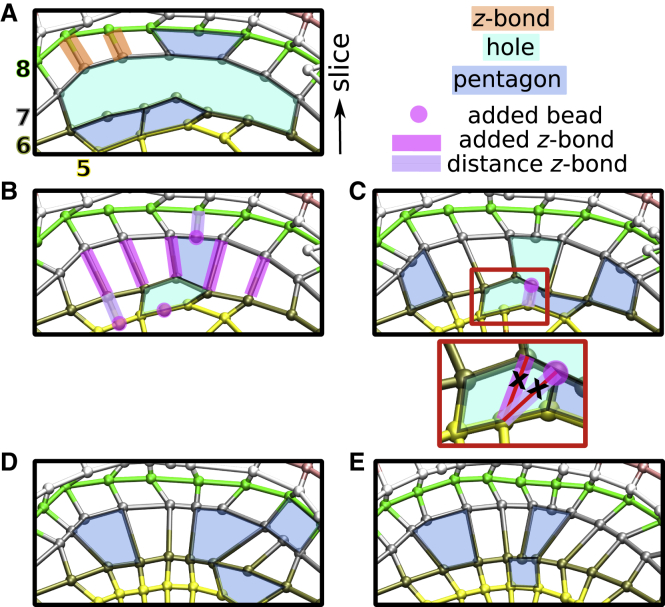
Figure 5.

Close mesh holes. (A) z-bond assignment. Mesh from Fig. 1 before refinement. Slice numbering follows Fig. 1F. Mesh elements are labeled. Holes and pentagons of slices 5–8 are shown. Mesh after first (B) and second iterations (C) of the hole closing procedure and z-bond updates is shown. Added beads, added z-bonds, and new distance-based z-bonds pertaining to the holes in (A) are marked. Inset of (C) is zoomed view of area in the red rectangle. z-bonds marked by X were removed after the procedure to limit z-bonds to one per bead for each neighboring slice. (D) Mesh after depressing protrusions (see Fig. 6 for further detail). Note the lack of holes. (E) Mesh after final refinement steps (smoothen BOC and equalize bond length). Note decrease in the number and size of pentagons.

A bead lacks a z-bond if it does not satisfy the b₀ cutoff. Also, if multiple beads on one slice share the same closest bead on the neighboring slice, only the shortest z-bond is kept, leaving the rest of the beads not z-bonded. Beads without z-bonds create “holes” and “pentagons” in the 3D mesh (Fig. 5; these holes are different from noise holes in binary thresholded images as in Fig. 2 B). At a large hole, the spatial relationship between BOC segments of two successive slices is not well defined. We thus apply a procedure aimed at reducing the size and number of holes on the mesh. Although a hole can, in principle, span more than two slices, in our study this does not occur because the BOC of each slice consists of either closed chains or chains ending at the image boundary. In the absence of open chain ends to allow formation of multislice holes, we deal only with holes confined between two slices. Pentagons are treated as holes in that we use them to add beads to initially refine the mesh, but small pentagons may remain in the final mesh because we deem them sufficient as a local descriptor of the surface.

A hole is bound by two z-bonds and can have multiple beads without z-bonds on either or both slices (Fig. 5 A). To close it, we first assign z-bonds sequentially to pairs of beads starting from one end, even if the 2D distance of the pair is greater than b₀ (Fig. 5 B, “added z-bond”). If the number of beads on the two slices enclosing the hole are not equal, this will leave beads without z-bonds on one slice. Similarly, in a pentagon there is one bead without a z-bond on one slice. In both cases, we add a bead to the opposing slice at the midpoint of the two neighboring z-bonded beads (Fig. 5, B and C, “added bead”). A z-bond is then placed between this new bead and the closest bead on the other side. This is done by imposing the 2D distance cutoff (Fig. 5, B and C, “distance z-bond”), which is stricter compared to “added z-bonds” that initially reduced the size of the hole. This way, added z-bonds are for initially closing holes without changing the cutoff parameter for distance z-bonds.

In case the added bead is closer to a bead that has an existing z-bond, a new z-bond with the added bead replaces the existing one (Fig. 5 C, inset). Also, the newly added bead does not have a z-bond with the slice on the opposite side of the hole under consideration. To remove most of the large holes and build a mesh with similarly spaced z-bonds, we thus apply the hole closing procedure twice (Fig. 5, B and C). Because the program runs in seconds, repeated operations do not incur any significant burden on the processing time.

Handling mesh protrusions

On noisy parts of the image, bead locations vary greatly across slices, and the method described above does not generate a well-defined mesh. We call these segments mesh “protrusions” (Fig. 6; these are different from pixel protrusions, as in Fig. 3 A). Mesh protrusions are identified as BOC segments containing one or more beads lacking z-bonds to a neighboring slice. Protrusions are processed slice by slice starting from slice 1. For this, the line connecting the two beads flanking a protrusion is determined, and evenly spaced points on the line are used as guides for depressing the protruding segment. The midpoint between the protruding bead and the corresponding guiding point is the new bead position (Fig. 6 C). This results in smoothing the mesh (Fig. 6, B versus D and E versus F).

Figure 6.

Depress mesh protrusions. (A) Mesh from Fig. 1G colored by slice. Autofluorescence image below and in all panels corresponds to slice 51. Before (B and E) and after (D and F) mesh refinement images are shown. Insets are side views for the rectangles. Protruding beads are marked in blue. (B) Intervening beads are marked with blue squares. (C) Depressing the protrusion on slice 50 of (B) (purple highlight) using guiding points (black) on the line between the flanking beads (purple). Chain before smoothing the protrusion is shown in orange. (E) A protruding segment on slice 51 is highlighted in purple. (F) During final refinement, some beads were deleted for the equalize bond length procedure. Also see Fig. S3.

Protruding segments often span multiple slices, which may include beads with and without z-bonds (Fig. 6 E). In such cases, within the protruding segment, beads without any z-bonds (Fig. 6 E, beads in blue) will vary more in position from beads in neighboring slices than the z-bonded beads. Thus, adjusting bead positions in a protrusion solely based on flanking beads of individual slices may not be effective. To impose z-directional persistence in depressing protrusions, after encountering a protrusion and adjusting bead positions, two beads on the next slice that are z-bonded to the flanking beads of the current slice are identified. Positions of intervening beads between these two beads on the next slice are similarly adjusted, regardless of whether they form a protrusion or not. For example, in Fig. 6 B, slice 50 has a two-bead protrusion (beads in blue) bound by two flanking beads (beads in purple). After adjusting the positions of the protruding beads on slice 50, the positions of the beads marked by blue squares on slice 51 are also adjusted, even though they do not themselves form a protrusion. This is because they are intervening beads to the two beads z-bonded to the purple flanking beads on slice 50.

We propagate the effect of z-bonded flanking beads up to two slices. As another example, slice 52 in Fig. 6 B has two individual protrusions, marked by the blue beads without and with a red circle. For the former, as we follow the beads on slices 53 and 54 z-bonded to its flanking beads, there are no intervening beads, and thus, only the blue protruding bead is moved. For the latter, slices 53 and 54 do contain intervening beads (blue squares). The positions of these beads are adjusted based on the neighboring beads in respective slices z-bonded to the flanking beads of the red-circled protrusion on slice 52. A similar operation is performed on the case shown in Fig. 6 E, in which z-bonded intervening beads on slices 52 and 53 are moved after depressing the protrusion highlighted in purple on slice 51. Because the blue beads in slices 52 and 53 are not z-bonded to the previous slice, they are treated as separate single-bead protrusions. Although we can propagate the z-directional persistence to more than two slices, the procedure alters the positions of beads in nonprotruding regions only slightly, so propagating up to two slices was sufficient (see also Fig. S3).

Final refinement

After depressing protrusions, sharp local changes between BOC contours are reduced, but beads may not be evenly distributed, and z-bonds need to be adjusted. For the final refinement, we remove all z-bonds and reapply 2D smoothing to the BOC of each slice, as described previously. We then make spacing between beads (bond lengths) within a BOC approximately equal, with extra beads being deleted. Using the updated BOCs, we rebuild the 3D mesh as described, excluding depressing protrusions. Sections of the final mesh are shown in Figs. 5 E, 6, D and F, and S3 C and the complete mesh in Fig. 1 G. Table 1 is a summary of each procedure and rationale for parameters used.

Table 1.

Summary of procedures

	Procedure	Purpose	Parameter
Pixel processing	binary filtering	remove background noise while retaining salient structural features	∗pixel intensity cutoff
	pixel noise removal: area-based	remove holes and debris that are distinctly smaller than feature areas	∗pixel area cutoff (20 pixels)
	pixel noise removal: rank-based	remove larger holes	∗cluster rank order cutoff (three to four clusters)
	contiguous region extraction	remove irregular and narrow pixel protrusions and segment contiguous areas	∗reference position (anywhere in the region to be extracted)
			∗running window size (two to three pixels)
2D BOC	assign beads and bonds	generate BOC along structure boundaries	∗bond length cutoff b0 (three to five pixels)
	smoothen BOC	reduce jagged outline	number of beads used for local linear fit (four beads)
	equalize bond length	evenly space beads within a BOC	none
3D mesh	assign z-bonds	connect beads between slices	b0
	close mesh holes	add beads and z-bonds to reduce number and size of holes	none
	depress mesh protrusions	smoothen irregular regions missing z-bonds	number of slices to propagate (two slices)

Distance-based 2D and 3D parameters are scaled based on the distance cutoff b₀ for contour tracing. Typical values for parameters are in parentheses. Six parameters require manual adjustment between sets (marked by ∗). “None” indicates no user input value is needed.

Implementation

Program source code and execution

The source code for our program is written in C++. For reading and writing image files, we used the GraphicsMagick C++ API (www.graphicsmagick.org), which supports C++ Standard Template Library functions and a wide range of image formats. We only used C++ Standard Template Library functions without relying on any compiler or operating system-specific functions. Hence, the code can be compiled and run on all major operating systems.

For batch processing and user-friendly execution, the program uses an input script file consisting of text commands with a small number of adjustable parameters. To assist with understanding command flow, simplified input scripts are included in the Supporting material; full scripts are available on GitHub. Among the parameters listed in Table 1, only those regarding pixel processing (pixel intensity, debris size, and rank cutoffs) need fine adjustment. This is done for groups of slices per stack, rather than on individual slices. Parameters for BOC-related procedures require minimal adjustment. The main parameter is the distance cutoff b₀ for assigning beads which is determined based on the size of the smallest feature to extract, such as the neuroepithelium MHB. Other distances in BOC assignment and refinement steps are proportional to b₀.

The BOC data (positions of beads and their connectivity) are written to protein structure file and coordinate file formats of the CHARMM (Chemistry at HARvard Macromolecular Mechanics) program (16). These are visualized using existing molecular structure rendering programs. We used VMD (Visual Molecular Dynamics) (17) because its ability to select and view individual beads or slices was convenient for code development and debugging. We included a utility to save the 3D mesh as an STL (stereolithography) file to enable visualization using CAD software, such as MeshLab (18) or 3D Slicer (19). For quick examination of the image stack in 3D, we also wrote a utility in which voxels are saved into the Mdical Research Council electron density format file and used UCSF Chimera (20) for visualization.

Sample data

Live multiphoton microscopy images of early-stage zebrafish embryo brain primordia were used to test our methodology (21, 22, 23). Each image slice was 256 × 256 pixels, with one pixel equaling 1.6 × 1.6 μm². Slices were imaged every 3 μm. Total number of slices varied depending on image stack, for which we used ∼50 from each. Regions of interest are defined where neuroepithelium autofluorescence is higher than local background of the mesenchyme. A wild-type (WT) phenotype at 24 hpf with distinctive midbrain, hindbrain, and MHB is used to demonstrate step-by-step methodology (Fig. 1). For time-lapse zebrafish images (Figs. 7 and 8), we used a WT and an fgf8a loss of function mutant embryo called acerebellar or ace. The ace phenotype is characterized by a loss of the cerebellum and MHB constriction (24). The spatial distribution of the wnt1 gene expression is related to proper MHB formation (10). We used the GFP channel of the images from the time-lapse set, which marks wnt1 expression, to visualize the distribution of gene expression relative to the structural BOC.

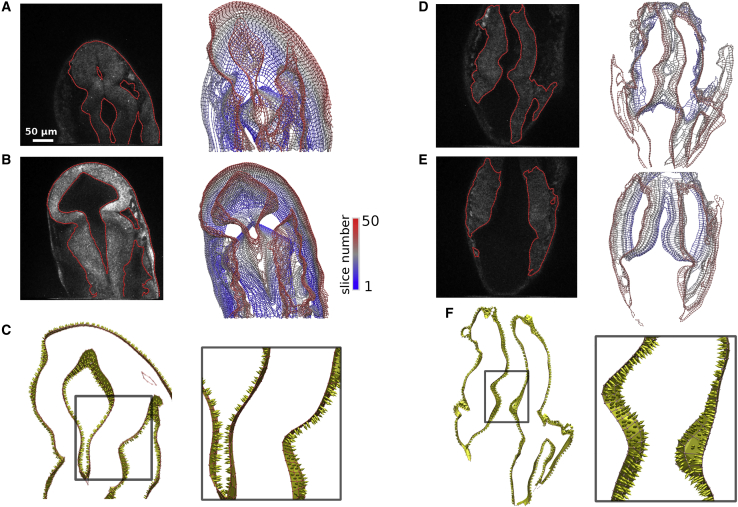
Figure 7.

3D models of images from live zebrafish embryos. WT embryos are at 20 (A and C) and 27.5 hpf (B). Mutant ace embryos are at 20.5 (D and F) and 27.5 hpf (E). For each set, the BOC of slice 35 is overlaid on the respective autofluorescence image. Mesh color scale corresponds to slice number from dorsal to ventral planes. For ace, only slices 18–42 are shown for clarity. Surface and normal vectors are shown in yellow for slices 47–50 of the WT (C) and 35–38 of the ace embryos (F). Normal vectors (arrows) point to the outside of the neuroepithelium. Fig. S4 shows models for other time points.

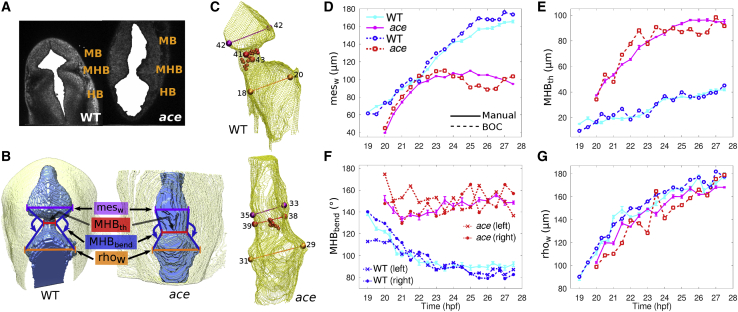
Figure 8.

Measuring phenotype characteristics. (A) Extracted ventricle (solid white) from one slice of WT and ace embryos at 25 hpf. (B) 3D rendering of extracted ventricle images (blue) and embryo outline (yellow) visualized using UCSF Chimera (20). Renderings were manually oriented such that the dorsal side is facing out of the page. Measured structures are labeled. (C) 3D meshes of WT and ace embryo ventricles. Measured widths are colored in the same way as in (B). Positions marked by spheres are automatically located. MHB positions are denoted by small red spheres. Larger spheres mark the ventricles and MHB constriction. The number next to each sphere corresponds to the slice on which the sphere is located. See Fig. S5 for a detailed illustration of the automated measurement procedure. (D–G) Plots comparing voxel-based manual measurements (thick solid lines) and automated BOC-based (dashed) measurements for the two phenotypes. Manual measurements of MHB_bend (F) were taken for the right side only. BOC-based MHB_bend is measured between the vectors formed from the MHB constriction to the mesencephalic ventricle position and from the MHB constriction to the rhombencephalic ventricle position on each respective side. Error bars represent standard deviation of five manual measurements. Some error bars may be covered by marker symbols.

Code and data availability

The source code, example sets used in this work, and input scripts to produce binary images and BOC models are available for download from GitHub (https://github.com/hwm2746/brain-mesh-builder) or Zenodo (https://doi.org/10.5281/zenodo.4698489).

Results

3D models for WT and ace zebrafish at discrete developmental time points

The image stack we used to explain the method (Figs. 1, 2, 3, 4, 5, and 6) was for a formaldehyde-fixed embryo at 24 hpf. Compared to a live embryo, compaction of the tissue due to fixation leads to higher pixel intensity (25). We apply the method to live embryo images (Figs. 7 and S4). Because slices in all sets (fixed or live) were imaged every 3 μm and one pixel equals 1.6 × 1.6 μm², the z-coordinate of the BOC for successive image slices was set 3.0/1.6 = 1.875 units apart. The resulting 3D BOC models contain between 8000 and 30,000 beads.

We compared the 2D BOC of each slice with the corresponding image. Although our method effectively reduced much of the background noise and captured the general shape of the neuroepithelium for both WT and ace embryos, areas where local high-intensity noise blended with the foreground resulted in sections of the background being included in the BOC (Figs. 7 and S4). Because this noise is not uniform across all slices, extensive presence of background segments in some slices cannot be corrected by our protrusion-correcting operations and results in poor mesh construction. However, for most of the extracted neuroepithelium, the 3D models are defined well enough to describe the surfaces, especially around the MHB region (Fig. 7, C and F). To properly segment noisier areas, an intensity-based analysis alone is insufficient. Instead, a ground-truth model constructed based on many training sets may be used to fit a test set. In such cases, our approach of building the 3D mesh will be useful for constructing the ground truth.

Another common issue in handling large image stacks is the processing time. For a 50-slice stack, the total computational time for all processing steps was less than 20 s on a PC with Intel Core i7 CPU (3.00 GHz). Computational time depends on the total number of voxels at stage 1 and the total number of beads at stages 2–3 (Fig. 1). We typically spent ∼30 min per image stack to determine the parameters in Table 1, mostly for producing binary thresholded images. Because these parameters are similar between sets imaged under the same experimental conditions, our approach is scalable to multiple stacks.

Quantitative comparison of zebrafish embryo phenotypes

As an application of the method, we quantified structural changes of the zebrafish neuroepithelium during MHB formation by collecting measurements from the built 3D models and comparing with manual voxel-based measurements (Fig. 8, D–G, dashed and solid lines, respectively). Four quantities were measured: two ventricle widths (mesencephalic, mes_w and rhombencephalic, rho_w), MHB thickness (MHB_th), and MHB bend angle (MHB_bend). These characterize the structural changes on the apical side of the neuroepithelium about the MHB during brain ventricle morphogenesis (Fig. 8, A and B). Morphological changes of the ace mutant have been related to failures of MHB-proximal cells to carry out normal morphogenesis. However, in these mutants the associated genes are properly activated, but not maintained; thus, the timing of gene expression patterns is important (10).

Because the live embryo is in an arbitrary orientation relative to the z-direction (imaging axis), measuring features in 3D is not easily done from individual images. For a manual measurement of the structures before building BOC models, we wrote a utility to save the binary segmented image into an electron density map file (grayscale images can be saved as well). After loading the file in an electron density map viewer (UCSF Chimera (20)), we rotated the set to a desired orientation, took a screenshot of the cross section of the embryo (Fig. 8 B), and used ImageJ (26) to measure distances and angles. We repeated this five times per set, each time reselecting reference positions that lie on different slices (cf. Fig. 8 C).

In contrast to voxel-based manual measurements, because the 3D BOC contains positional information of the structure, automated measurements can be performed. The code works by orienting the BOC such that its longest axis is along the y axis. A sagittal plane containing the y axis is used to measure transverse distances (parallel to the xz plane; Fig. S5). In roughly 5 μm intervals along the y direction, transverse widths of the 3D BOC were measured. From these values, the location of the MHB in each slice (Figs. 8 C and S5, red spheres) is identified as the narrowest position excluding the top and bottom ends of the ventricle, which can be narrower than the MHB constriction, yielding MHB_th. The widest positions above and below this position are located to measure mes_w and rho_w, from which MHB_bend follows. For some sets, the automatically generated sagittal plane does not pass through the narrow MHB. For these cases, we manually correct the plane orientation by assigning three points to define a new plane. Computation time ranged from 1 to 3 min per set to locate positions and collect measurements.

Structural changes expected by visual inspection of each phenotype are reflected in the manual and BOC-based measurements (Fig. 8, D–G). During the maintenance phase of MHB formation in a WT embryo, wnt1 expression is restricted to the anterior side of the MHB. In the ace mutant, this boundary restriction is lost (10). The loss of MHB definition of the mutant is notable comparing the wider and faster growing MHB intersection width versus that of the WT phenotype (Fig. 8 E). Interestingly, the steady growth of the rhombencephalic ventricle is comparable between the two phenotypes during these time points (Fig. 8 G). In contrast, around 22 hpf the growth of the mesencephalic ventricle of the ace mutant stalls, reaching around 100 μm, whereas the WT mesencephalic ventricle continues to grow (Fig. 8 D). This suggests that the midbrain is established but does not fully form in the mutant, as has been previously observed (10). To measure MHB bend angle from the BOC, we used the positions of the two ventricles and of the MHB intersection on each side of the sagittal plane (Fig. 8 F, left and right distinction). The progressive MHB compression in the WT embryo, as noted by the sharpening of the MHB bend angle to ∼90°, compared to the lack of sharpening of the ace mutant MHB bend angle, hovering around 150°, is likewise a characteristic of the mutant related to changes in gene expression patterning (Fig. 8 F). Taken together, our measurements provide a quantitative insight into the spatiotemporal differences of these two phenotypes.

3D models from MR scans of the human fetal brain

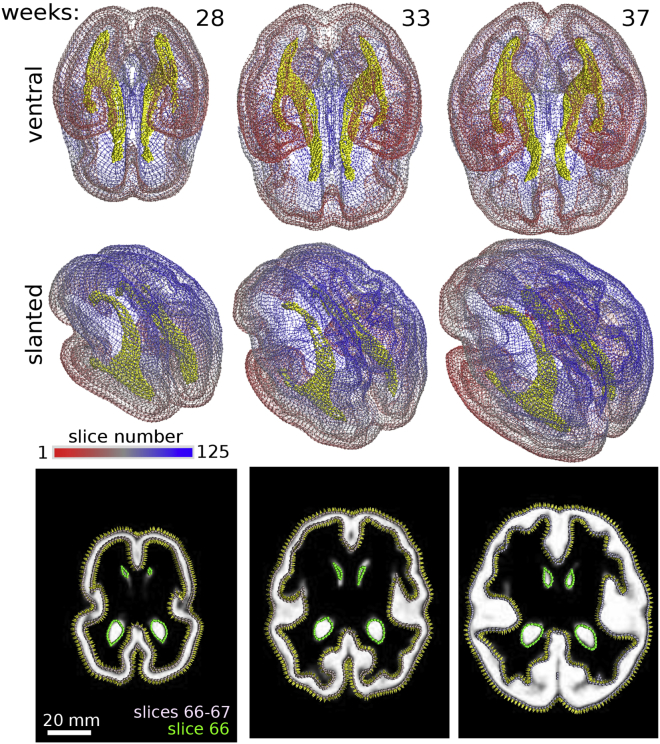
Although our method was developed using multiphoton microscopy images of zebrafish embryos, the geometric modeling approach works regardless of imaging modality. To demonstrate, we built 3D models of the human fetal brain cortex and ventricle from MR images (Fig. 9). The images used were from a Fetal Brain Atlas (brain-development.org) (27), in which the cortex and ventricles were already segmented and stored as separate images. Image stack size is 117 × 159 × 125 voxels, where each voxel is 1.18³ mm³. Because of uniform contrast, we used a single pixel intensity cutoff to get binary images for all slices in each set. Neither Gaussian blurring nor image noise removal were needed. For 2D BOC contour tracing, we used b₀ = 2 pixels to capture cortex folds. All other parameters and the order of procedures were the same as those for the zebrafish embryo sets. Computational time was ∼15 s per set to build the BOC and construct the surface. Because of the high contrast of the preprocessed MR images, surface construction was easier than for the zebrafish embryo. To further demonstrate the ability to perform quantitative measurement using 3D BOC, we measured the local surface curvature (Fig. S6).

Figure 9.

3D BOC of human fetal brain. The cortex (slices colored based on color scale) and ventricles (yellow) are modeled at three gestational ages (weeks 28, 33, and 37). Ventral and slanted views of each structure are shown. Bottom row shows sample input image slices with BOC overlaid on the merged images of the cortex and ventricles (green BOC) for each respective time point. Normal vectors denoting the orientation of the constructed surface between slices 66 and 67 are shown. Surface curvature measurements are in Fig. S6.

Conclusions

The computational method in this study to build surface BOC models from 3D image stacks requires minimal user input, is tolerant to noise, and is applicable to a broad range of imaging data. A strength of our approach lies in casting data from pixels to a BOC. Although the former varies widely depending on imaging modality, the type of system, and imaging condition, once a BOC is built, the rest of the operations do not require pixel data. Hence, setting the binary filtering pixel intensity cutoff and noise removal criteria during stage 1 is the most time-consuming step. Yet even this takes relatively little time because the parameters are set for image slices in groups rather than individually. Furthermore, because of the multistep progressive refinement, a perfectly clean binary image is not required, which is especially important for processing noisy images where complete elimination of the effects of noise in a single-pass operation is difficult. Because the total bead count is far less than the number of voxels in an image stack, BOC processing is very fast. Combined with command-based execution (see sample input scripts in the Supporting material), our program is amenable to batch processing of a large number of image stacks obtained under similar conditions. Furthermore, as demonstrated in the comparative analysis between WT and ace embryos (Fig. 8), the 3D model can be used for automated morphometric measurements.

To the extent that beads are used, our approach is conceptually similar to the ball-pivoting algorithm (BPA) (28). To generate a mesh using BPA, a ball of a given radius “rolls” over a separately determined point cloud representing an image stack. An issue we found with the BPA method, particularly with building the mesh of the human brain embryo (Fig. 9), was with the highly curved cortex folds or between separate gyri layers where the pivoting ball does not fit. Decreasing the radius of the pivoting ball can mitigate this issue, but it also requires more points to build a continuous surface, a process that has to be done separately. Moreover, the BPA method relies on predetermined estimates of the surface normal to determine the rolling direction of the mesh, which likely contributes to erroneous mesh assignment in narrow regions. In our approach, we utilize connectivity among beads by assigning bonds, which eliminates these issues. Although there are other landmark-based methods to fill a hole with a mesh (29), to our knowledge, automated identification and correction of defects (e.g., Figs. 5 and 6) by addition, removal, and adjustments of beads and bonds have not been implemented previously.

Whereas stage 1 (Fig. 1, A–C) is pixel-level processing, the main core of our approach lies in the next two stages, assigning and manipulating BOCs in 2D and 3D. Our method can thus be used in combination with other image processing software, in which pixel-based noise removal and preparation of images for BOC assignment can be performed. More broadly, other than building models of surfaces and volumes as described in our study, the BOC-based approach can be used for studying filamentous systems as well, which we demonstrated previously for collagen fibrils in atomic force microscopy images (30,31).

If image slices are too noisy to yield a faithful representation of the surface (e.g., Fig. 7), a model-based approach may be necessary. For example, one may manually remove noisy background to reveal features of interest for one stack and apply the 3D model building procedure to construct a “clean” mesh of the system. The resulting reference or ground-truth model can be used to compare with 3D models of test sets. Noisy regions that deviate largely from the reference can then be identified and corrected by utilizing better defined regions within the 3D stack.

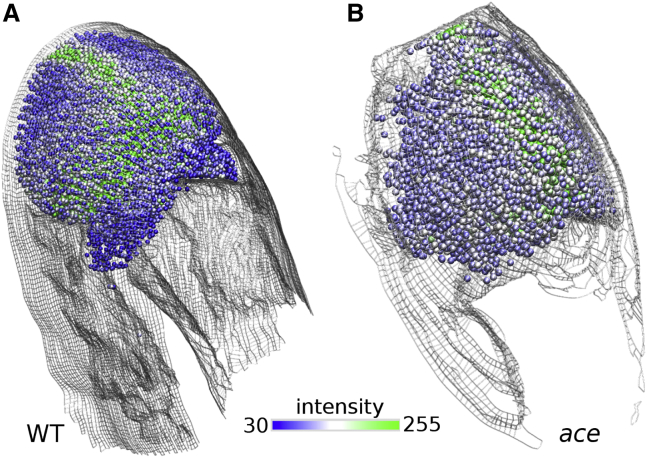
Another advantage of our approach is the ease of combining models from different imaging channels. As an example, for the sets shown in Fig. 7, we separately processed images of the fluorescent reporter of the wnt1 gene that reinforces the anterior boundary of the MHB (10). The spatially distributed wnt1 signal is represented by a collection of beads and the result is overlaid with the surface model of the tissue (Fig. 10). A combined analysis of the distribution of the gene reporter and the neuroepithelium morphology will yield a quantitative description of the genetic effect on brain ventricle morphogenesis.

Figure 10.

Combining models from two imaging channels. Spatial distribution of wnt1 expression from the GFP channel autofluorescence image over BOC of WT (A) and ace embryos at 27.5 hpf (B). One bead represents a 6 × 6 pixel area. Bead color represents the intensity of the wnt1 reporter fluorescence. Beads are not assigned to areas with pixel intensity below 30.

In conclusion, we have developed an efficient and broadly applicable method to build 3D surface models from image stacks. Refinement of the method for specific systems and further development of quantitative measurements are subjects of future studies.

Author contributions

A.C.C.-G., H.C.G., A.C.L., A.T.Y., and W.H. designed research and wrote the manuscript. H.C.G., A.C.L., and A.T.Y. carried out experiment. A.C.C.-G. and W.H. developed the computational method, analyzed data, and wrote the initial draft of the manuscript.

Editor: Shi-Wei Chu.