Unnuclear physics: Conformal symmetry in nuclear reactions

Significance

Symmetry plays a key role in modern physics as a guiding principle for fundamental theories of nature. We use the nonrelativistic conformal symmetry to predict universal energy spectra of final states in reactions of quantum particles at vastly different length scales. Our work extends Georgi’s “unparticle” proposal to nonrelativistic spin-1/2 fermions in the unitary regime of strong interactions. These systems form so-called unparticles, which behave characteristically different from normal particles. They can be engineered with ultracold atoms and occur naturally in nuclear reactions with multiple neutrons—a situation we dub “unnuclear physics.” We present the general scenario of unnuclear physics, apply it to identify unnuclei in nuclear reactions, and highlight the opportunity to measure unnuclei at radioactive beam facilities.

Abstract

We investigate a nonrelativistic version of Georgi’s “unparticle physics.” We define the unnucleus as a field in a nonrelativistic conformal field theory. Such a field is characterized by a mass and a conformal dimension. We then consider the formal problem of scatterings to a final state consisting of a particle and an unnucleus and show that the differential cross-section, as a function of the recoil energy received by the particle, has a power-law singularity near the maximal recoil energy, where the power is determined by the conformal dimension of the unnucleus. We argue that unlike the relativistic unparticle, which remains a hypothetical object, the unnucleus is realized, to a good approximation, in nuclear reactions involving emission of a few neutrons, when the energy of the final-state neutrons in their center-of-mass frame lies in the range between about 0.1 MeV and 5 MeV. Combining this observation with the known universal properties of fermions at unitarity in a harmonic trap, we predict a power-law behavior of an inclusive cross-section in this kinematic regime. We verify our predictions with previous effective field theory and model calculations of the ⁶He$\left(p,p\alpha \right)2n$, ³H$\left({\pi }^{-},\gamma \right)3n$, and ³H$\left({\mu }^{-},{\nu }_{\mu }\right)3n$ reactions and discuss opportunities to measure unnuclei at radioactive beam facilities.

The concept of symmetry plays a key role in modern physics (1). On the one hand, many phenomena in elementary particle physics are governed by the symmetries of the unitary Lie groups. On the other hand, statistical systems at a critical point possess a symmetry not realized in particle physics—the conformal symmetry. In a 2007 paper (2), Howard Georgi put forward the proposal (called “unparticle physics”) that beyond the Standard Model of elementary particle physics there is a hidden conformal symmetry sector. This sector would consist not of particles but of fields belonging to a conformal field theory. In general, correlation functions of fields in conformal field theory do not have poles, but only cuts, so the “unparticles” that correspond to these fields, if they exist, would leave collider signals distinct from those of the normal particles. Georgi’s proposal has attracted considerable activity in theoretical particle physics, but, despite intensive search, so far the unparticle has failed to turn up at the Large Hadron Collider (3–5).

In this paper, we consider a nonrelativistic analog of the unparticle, which we call the “unnucleus.” Formally, the unnucleus corresponds to a field in a nonrelativistic conformal field theory (6). In contrast to the relativistic unparticle, which is characterized solely by its conformal dimension, the nonrelativistic counterpart is characterized by two parameters—its mass $\mathrm{M}$ and dimension $\mathrm{\Delta }$. We use the term “unnucleus” because, as we will argue later, this object appears in a certain regime in nuclear reactions involving several neutrons in the final state. Thus, in contrast to the unparticle, the unnuclei already exist in nature, although only as an approximation.

Our result can be summarized as follows. Consider a nuclear reaction with a few final-state neutrons, besides one other product which we call $B$, for example

$$A_1+A_2\to B+\underset{N\hspace{0.17em}\text{neutrons}}{\underbrace{n+n+\cdots }}.$$ [1]

The number of final-state neutrons $N$ can be $\mathrm{2,3,4},\dots$. We register only the energy of $B$, but not of the neutrons, measuring the inclusive differential cross-section as the function of the energy $E$ of $B$ and its direction $\mathrm{\Omega }$, $d^2\sigma /dEd\mathrm{\Omega }$. In the center-of-mass frame the rate does not depend on the direction of $B$, so what is measured is $d\sigma /dE$. The energy spectrum of $B$ is continuous and has a cutoff at some maximal value $E_0$. We predict that

$$\frac{d\sigma }{dE}\sim {\left(E_0-E\right)}^{\nu }$$ [2]

with some exponent $\nu$ that depends on the number of final-state neutrons, in the regime where

$$\frac{{\hslash }^2}{m{a}^2}\ll \left(1+\frac{M_B}{Nm}\right)\left(E_0-E\right)\ll \frac{{\hslash }^2}{m{r}_0^2},$$ [3]

where $\mathrm{m}$ is the mass of the neutron, $M_B$ the mass of the nucleus $B$, while $a$ and $r_0$ are the neutron–neutron scattering length and effective range. If $M_B$ is not too large compared to $Nm$, this means $E_0-E$ is between 0.1 MeV and a few megaelectron volts.

The exponent $\nu$ is predicted to be

$$\nu =\left\{\begin{array}{cc}-1/2\hspace{1em}\hfill & N=2,\hfill \\ 1.77\hspace{1em}\hfill & N=3,\hfill \\ 2.5-2.6\hspace{1em}\hfill & N=4.\hfill \end{array}\right.$$ [4]

In general, $\nu$ is equal to the ground-state energy of a system of $N$ fermions at unitarity in a harmonic trap with unit frequency, minus $\frac{5}{2}$.

The structure of this paper is as follows. In The Unnucleus we introduce the notion of an unnucleus and review the properties of the unnucleus propagator that follow from nonrelativistic conformal field theory. In Rate of Processes Involving an Unnucleus we compute rates for reactions with an unnucleus in the final state. We argue that multineutron final states can approximate unnuclei in Multineutron Final States as Unnuclei. In Comparison with Multineutron Spectra we compare our prediction with previous model calculations for several nuclear reactions. Finally, Conclusion contains concluding remarks.

The Unnucleus

We will start our discussion at a rather formal level and transition to real nuclear processes later.

The unnucleus is a nonrelativistic field with mass $M_{\mathcal{U}}$ and dimension $\mathrm{\Delta }$. There is a unitarity bound on $\mathrm{\Delta }$: $\mathrm{\Delta }\ge \frac{3}{2}$, where the lower bound corresponds to a free field. (In our convention, the dimensions of momentum and energy are 1 and 2, respectively.) According to the general formalism, the two-point function of a primary operator $\mathcal{U}$ in nonrelativistic conformal field theory is completely fixed (up to an overall factor), so the propagator of an unnucleus is (6)

$$G_{\mathcal{U}}\left(t,\mathbf{x}\right)=-i⟨T\mathcal{U}\left(t,\mathbf{x}\right){\mathcal{U}}^{†}\left(0,\mathbf{0}\right)⟩=C\hspace{0.17em}\frac{\theta \left(t\right)}{{\left(it\right)}^{\mathrm{\Delta }}}\exp \left(\frac{i{M}_{\mathcal{U}}{x}^2}{2t}\right),$$ [5]

where $C$ is a normalization factor. For $\mathrm{\Delta }=\frac{3}{2}$ (the dimension of a free field), the unnucleus becomes a nucleus (a nonrelativistic particle).

One example of the unnucleus is a collection of noninteracting particles,

$$\mathcal{U}={\psi }_1{\psi }_2\dots {\psi }_N.$$ [6]

Assuming the masses of all fields ${\psi }_i$ are equal, the mass and the dimension of this operator are

$$M_{\mathcal{U}}=N{m}_{\psi },\hspace{1em}\mathrm{\Delta }=\frac{3}{2}N.$$ [7]

The propagator of $\mathcal{U}$ is then the $N$th power of the propagator of a single particle.

For diagrammatic calculation we need the unnucleus propagator in momentum space. Taking the Fourier transform of Eq. 5 we get

$$G_{\mathcal{U}}\left(\omega ,\mathbf{p}\right)=-C{\left(\frac{2\pi }{M_{\mathcal{U}}}\right)}^{3/2}\mathrm{\Gamma }\left(\frac{5}{2}-\mathrm{\Delta }\right){\left(\frac{p^2}{2M_{\mathcal{U}}}-\omega \right)}^{\mathrm{\Delta }-\frac{5}{2}}.$$ [8]

In Fourier space the imaginary part of the propagator of an unnucleus is

$$\mathrm{I}\mathrm{m}{G}_{\mathcal{U}}\left(\omega ,\mathbf{p}\right)\sim \left\{\begin{array}{cc}\delta \left(\omega -\frac{p^2}{2M_{\mathcal{U}}}\right),\hspace{1em}\hfill & \mathrm{\Delta }=\frac{3}{2},\hfill \\ {\left(\omega -\frac{p^2}{2M_{\mathcal{U}}}\right)}^{\mathrm{\Delta }-\frac{5}{2}}\theta \left(\omega -\frac{p^2}{2M_{\mathcal{U}}}\right),\hspace{1em}\hfill & \mathrm{\Delta }>\frac{3}{2}.\hfill \end{array}\right.$$ [9]

Only for free fields ($\mathrm{\Delta }=\frac{3}{2}$) the propagator has a pole; otherwise it has a cut. For the composite operator in Eq. 6, $\mathrm{I}\mathrm{m}{G}_{\mathcal{U}}$ is proportional to the final-state phase space available when an initial state carrying energy $E$ and momentum p becomes $N$ final particles. Similar to the relativistic case, an unnucleus of dimension $\mathrm{\Delta }$ can be thought of as $N=\frac{2}{3}\mathrm{\Delta }$ (which is, in general, a fractional number) particles. The imaginary part of the unnucleus propagator can be interpreted as the phase space volume of a fractional number of particles.

Rate of Processes Involving an Unnucleus

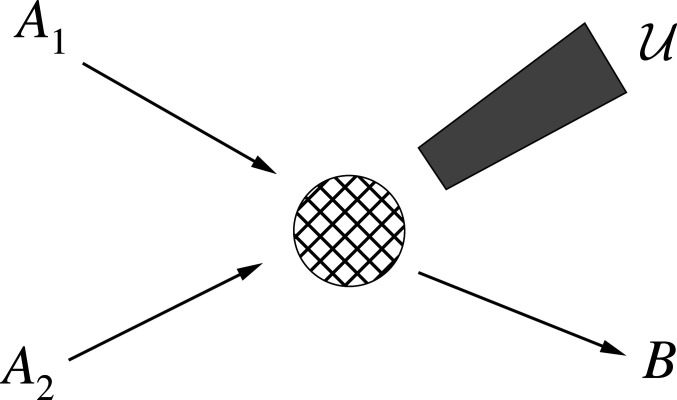
To illustrate the physical consequences of the existence of an unnucleus, consider the following reaction (see Fig. 1):

$$A_1+A_2\to B+\mathcal{U},$$ [10]

where $A_1$ and $A_2$ are some initial particles, $B$ is a particle, and $\mathcal{U}$ is the unnucleus. For simplicity, we assume all particles involved in the reaction are nonrelativistic, though our main conclusion requires that only $\mathcal{U}$ is. While on-shell scattering amplitudes in relativistic conformal theories are typically ill-defined because of infrared divergences associated with massless particles, they are well-defined in nonrelativistic theories even in the conformal limit (7). Therefore, no special procedure is required to calculate this process.

Fig. 1.

A nuclear reaction with an unnucleus $\mathcal{U}$ (represented by the shaded region) in the final state.

We work in the center-of-mass frame. The total kinetic energy available to final products is

$$E_{\text{kin}}=\left(M_{A_1}+M_{A_2}-M_B-M_{\mathcal{U}}\right)c^2+\frac{p_{A_1}^2}{M_{A_1}}+\frac{p_{A_2}^2}{M_{A_2}}.$$ [11]

Unless $\mathcal{U}$ is a particle, the energy spectrum of $B$ is continuous. Let $E$ and $\mathbf{p}$ be the energy of the particle $B$, $E=p^2/2M_B$. We are interested in the differential cross-section $d\sigma /dE$. We can think about a term in the effective Lagrangian

$${\mathcal{L}}_{\text{int}}=g\hspace{0.17em}{\mathcal{U}}^{†}{B}^{†}{A}_1{A}_2+\text{h.c.},$$ [12]

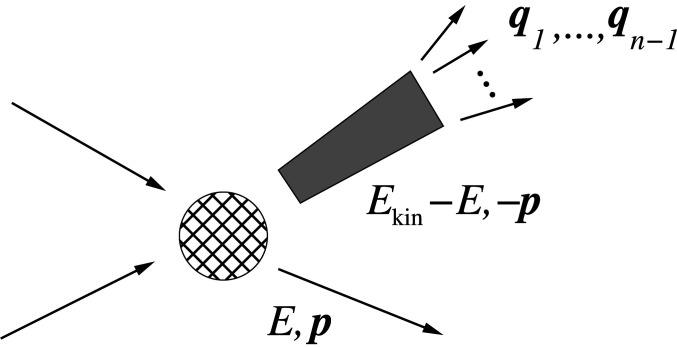
where $g$ is some coupling constant, such that the unnucleus is produced at a point. For definiteness, we assume the unnucleus to represent an interacting $n$-particle state with total mass $M_{\mathcal{U}}$ and total momentum $-\mathbf{p}$. The Jacobi momenta and reduced masses of the particles are denoted by ${\mathbf{q}}_i$ and ${\mu }_i$ with $i=1,..,n-1$, respectively (see Fig. 2).

Fig. 2.

Kinematics for the production of an unnucleus $\mathcal{U}$ (indicated by shaded region) representing an interacting $n$-particle state in the reaction of Eq. 10.

The differential cross-section can then be written as

$$\begin{array}{ccc}\hfill & \hfill & d\sigma \sim g^2|G_{\mathcal{U}}\left(E_{\text{kin}}-E,\mathbf{p}\right){|}^2\hspace{0.17em}{d}^3\mathbf{p}\hspace{0.17em}\prod _{i=1}^{n-1}{d}^3{\mathbf{q}}_i\hfill \\ \hfill & \hfill & \hspace{1em}\times \delta \left(E_{\text{kin}}-E-\frac{{\mathbf{p}}^2}{2M_{\mathcal{U}}}-\sum _{i=1}^{n-1}\frac{{\mathbf{q}}_i^2}{2{\mu }_i}\right),\hfill \end{array}$$ [13]

where the incoming flux factor and factors of $2\pi$ have been suppressed. We rewrite $d^3\mathbf{p}\sim d{\mathrm{\Omega }}_p\sqrt{E}dE$ and perform the trivial integration over $d{\mathrm{\Omega }}_p$. Further integrating over the Jacobi momenta of the final state particles ${\prod }_{i=1}^{n-1}{d}^3{\mathbf{q}}_i$ and using the optical theorem, we obtain

$$d\sigma \sim g^2\hspace{0.17em}\sqrt{E}\hspace{0.17em}\mathrm{I}\mathrm{m}{G}_{\mathcal{U}}\left(E_{\text{kin}}-E,\mathbf{p}\right)\hspace{0.17em}dE.$$ [14]

Thus, the differential cross-section for a general production amplitude $\mathcal{M}$ can be written as

$$\frac{d\sigma }{dE}\sim |\mathcal{M}{|}^2\sqrt{E}\hspace{0.17em}\mathrm{I}\mathrm{m}{G}_{\mathcal{U}}\left(E_{\text{kin}}-E,\mathbf{p}\right).$$ [15]

In principle $\mathcal{M}$ can contain dependence on the momenta of the incoming and outgoing particles. The statement of Eq. 15 is that the cross-section can be factorized into two parts, one (encoded by $\mathcal{M}$) corresponding to the primary process $A_1+A_2\to B+\mathcal{U}$, the other (encoded by $\mathrm{I}\mathrm{m}{G}_{\mathcal{U}}$) corresponding to the final-state interaction between the constituents of $\mathcal{U}$. Such a factorization requires that the energy scale of the primary scattering process is much larger than that of the interaction between the neutrons and is the essence of the Watson–Migdal approach to final-state interaction (8, 9).

According to Eq. 9,

$$\begin{array}{ccc}\hfill \mathrm{I}\mathrm{m}{G}_{\mathcal{U}}\left(E_{\text{kin}}-E,\mathbf{p}\right)& \sim \hfill & {\left(E_{\text{kin}}-E-\frac{p^2}{2M_{\mathcal{U}}}\right)}^{\mathrm{\Delta }-\frac{5}{2}}\hfill \\ \hfill & =\hfill & {\left[E_{\text{kin}}-\left(1+\frac{M_B}{M_{\mathcal{U}}}\right)E\right]}^{\mathrm{\Delta }-\frac{5}{2}}.\hfill \end{array}$$ [16]

Denote the maximal value of the recoil energy received by the particle $B$ as

$$E_0={\left(1+\frac{M_B}{M_{\mathcal{U}}}\right)}^{-1}{E}_{\text{kin}}.$$ [17]

In the regime $E_0-E\ll E_0$, ignoring the energy dependence of all other factors, we can write

$$\frac{d\sigma }{dE}\sim {\left(E_0-E\right)}^{\mathrm{\Delta }-\frac{5}{2}}.$$ [18]

Thus, a characteristic feature of processes involving an unnucleus is the power-law dependence of the differential cross-section on the recoil energy near the end point.

Multineutron Final States as Unnuclei

So far the search for relativistic unparticles has been unsuccessful (3–5). In nuclear physics, however, there are natural approximate unnuclei due to the fortuitous occurrence of fine tuning in several nuclear systems. In particular, neutrons have a large $\mathrm{s}$-wave scattering length: $a\approx -19$ fm, compared to the effective range $r_0\approx 2.8$ fm. A system of neutrons can be considered as an unnucleus if the relative momentum between any two neutrons in the system is between $\hslash /a$ and $\hslash /r_0$. If this is the case, they are described by a well-known nonrelativistic conformal field theory—the theory of fermions at unitarity.

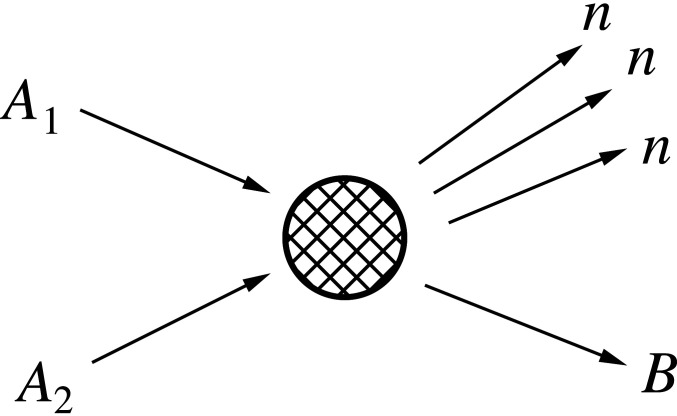
Thus, the real-world realizations of the reaction pictured in Fig. 1 are reactions with a few neutrons in the final state. A typical reaction with three final-state neutrons is schematically depicted in Fig. 3. The differential cross-section $d\sigma /dE$ considered above is now an inclusive cross-section, where the momenta of the neutrons are left unmeasured. Reactions of this type are abundant in nuclear physics. Some examples are

$${}^3\text{H}+{}^3\text{H}\to {}^4\text{He}+2n,$$ [19]

$${}^7\text{Li}+{}^7\text{Li}\to {}^{11}\text{C}+3n,$$ [20]

$${}^4\text{He}+{}^8\text{He}\to {}^8\text{Be}+4n.$$ [21]

The final-state neutrons can be considered as forming an unnucleus when the kinetic energy of the system of neutrons in its center-of-mass frame (neutron kinetic energy) is between ${\epsilon }_0={\hslash }^2/m{a}^2\sim 0.1$ MeV and ${\hslash }^2/m{r}_0^2\sim 5$ MeV. Only in this kinematic regime, our prediction, Eq. 18, for $d\sigma /dE$ applies. Physically, in this regime the neutrons travel together and keep interacting with each other until the distance between them becomes larger than $a$. If the total kinetic energy of the final scattering products $E_{\text{kin}}$ is much larger than ${\hslash }^2/m{r}_0^2$, then the power-law behavior of the differential cross-section, Eq. 18, is expected in a region near, but not too close to, the maximal recoil energy.

Fig. 3.

A nuclear reaction with three neutrons in the final state.

According to the general formalism (6) the dimension of an operator is equal to the energy of the corresponding state in the harmonic potential with unit oscillator frequency. This leads to a nontrivial connection between the few-body physics of fermions at unitarity and the physics of nuclear reactions. Namely, the spectrum of fermions at unitarity in a harmonic trap determines the behavior of the processes involving emission of neutrons in a certain kinematic regime.

For emission of two neutrons, the ground state of two unitary fermions in a harmonic trap (with opposite spins) is known exactly, and corresponds to the “dimer” operator of conformal dimension $\mathrm{\Delta }=2$. The differential cross-section thus grows toward the endpoint

$$\frac{d\sigma }{dE}\sim \frac{1}{\sqrt{E_0-E}}.$$ [22]

This growth stops very close to the endpoint when the neutron kinetic energy is of order ${\epsilon }_0$, after which, the two neutrons become effectively noninteracting, and the unnucleus now becomes an operator in free field theory $n_{\downarrow }{n}_{\uparrow }$ with dimension $\mathrm{\Delta }=3$, and the differential cross-section decreases as $\sqrt{E_0-E}$. This nonmonotonic behavior of $d\sigma /dE$ is well known (8, 9). In fact, the whole behavior of the differential cross-section in the cross-over region can be read off from the propagator of the dimer field in effective field theory,

$$G_d\left(\omega ,0\right)\sim \frac{1}{\frac{1}{a}+i\sqrt{m\omega }}\Rightarrow \mathrm{I}\mathrm{m}{G}_d\left(\omega ,0\right)\sim \frac{\sqrt{\omega }}{{\epsilon }_0+\omega },$$ [23]

so

$$\frac{d\sigma }{dE}\sim \frac{\sqrt{E_0-E}}{E_0-E+{\left(1+\frac{M_B}{M_{\mathcal{U}}}\right)}^{-1}{\epsilon }_0}.$$ [24]

which reaches a maximum at $E_0-E={\left(1+M_B/M_{\mathcal{U}}\right)}^{-1}{\epsilon }_0$.

For the problem of three final-state neutrons, we know that the ground state of three fermions at unitarity in a harmonic trap is a state with $S=\frac{1}{2}$, $L=1$ and energy $\mathrm{\Delta }\approx 4.27272$ in units of the trap frequency (10, 11). Thus, the differential cross-section behaves as

$$\frac{d\sigma }{dE}\sim {\left(E_0-E\right)}^{1.77272}.$$ [25]

The first excited state of three neutrons in the trap is a $S=\frac{1}{2}$, $L=0$ state with $\mathrm{\Delta }\approx 4.66622$, corresponding to a contribution ${\left(E_0-E\right)}^{2.1662}$. This is suppressed compared to the contribution from the ground state, but, due to the relatively small difference between the exponents, may need to be taken into account to describe real data.

At very small $E_0-E$ there is a cross-over from Eq. 25 to the free-neutron behavior, controlled by the dimension of the operator $nn\nabla n$ in free field theory (with one derivative because of the Pauli exclusion principle): ${\left(E_0-E\right)}^3$. This behavior can also be obtained by multiplying the three-particle phase space ${\left(E_0-E\right)}^2$ and a suppression factor $E_0-E$ coming from the fermionic statistics of the neutrons.

For four final-state neutrons, different approaches have given the ground-state energy of four trapped unitary fermions between 5.0 and 5.1 oscillator frequencies (12–18), which means

$$\frac{d\sigma }{dE}\sim {\left(E_0-E\right)}^{\alpha },\hspace{1em}\alpha \approx 2.5-2.6.$$ [26]

The excited state of the four-fermion system has $\mathrm{\Delta }\approx 6.6$ (18) and thus is much more separated from the ground state compared to the three-fermion case. The behavior crosses over to the free-particle behavior ${\left(E_0-E\right)}^{5.5}$ at very low $E_0-E$.

We will not consider larger numbers of final-state neutrons, except to point out that differential cross-section will fall off with larger and larger exponent as $E\to E_0$ with increasing number of neutrons.

Comparison with Multineutron Spectra

Ideally, one should compare our predictions with experimental measurements. However, since at present there are no sufficiently precise experimental spectra in the endpoint region to identify a multineutron unnucleus we compare our predictions to realistic theoretical calculations. For convenience, we consider the neutron energy distribution in their center of mass instead of the energy distribution of the recoil particle. This makes it possible to consider reactions with more than one particle besides the neutrons in the final state and also makes the relevant energy scales more transparent. We expect that a comparison to low-energy multineutron spectra from experiments at radioactive beam facilities will become possible in the near future. In particular, precise low-energy two- and four-neutron spectra will be measured at the Rare Isotope Beam Facility at RIKEN in the reactions ⁶He$\left(p,p\alpha \right)2n$ and ⁸He$\left(p,p\alpha \right)4n$ in inverse kinematics with all final state particles being detected.*

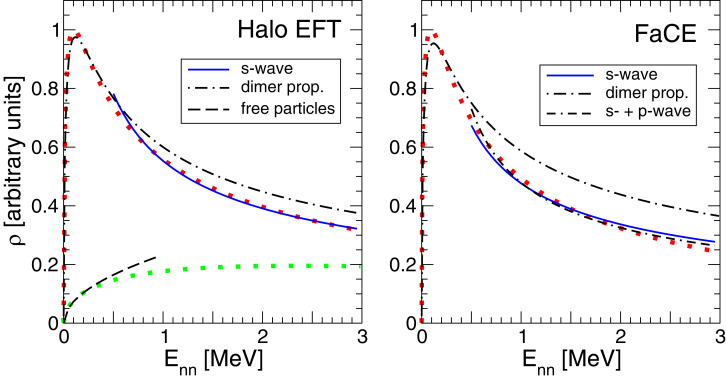
In ref. 19, a novel method to measure the neutron-neutron scattering length using the ⁶He$\left(p,p\alpha \right)2n$ in inverse kinematics at high energies was proposed. It uses the final state interaction of the neutrons after the sudden knockout of the $\alpha$ particle in ⁶He. The authors showed that the scattering length can be extracted from the spectrum of the neutrons at very low relative energies. Here we use the two-neutron spectra calculated in ref. 19 to search for the two-neutron unnucleus. Once the data from the experiment* are available, the analysis can be repeated using the measured spectrum. In Fig. 4, we analyze the calculations of ref. 19 with respect to signatures of the two-neutron unparticle. In that paper, calculations within two effective three-body approaches for the wave function of the initial ⁶He nucleus are carried out: 1) a leading order Halo effective field theory (Halo EFT) calculation which includes $nn\hspace{0.17em}s$-wave interactions, $n\alpha p$-wave interactions, and a short-range $nn\alpha$ three-body force (20) (Fig. 4, Left) and 2) a model calculation using the three-body code FaCE (21) which has $n\alpha$ interactions in the $\mathrm{s}$-, $p$- and $d$-wave and a longer ranged three-body force (Fig. 4, Right). The two-neutron distribution from Halo EFT (upper red dotted line) is well-described by the unnucleus behavior, $1/\sqrt{E}$, above 0.5 MeV as indicated by the solid line. In fact, even the full energy distribution up to 3 MeV can reasonably well be described by the dimer propagator, Eq. 23 (dash-dotted line), by just fitting the prefactor to the data below 0.5 MeV. If the propagator is fit to the whole energy range, a better description at higher energies can be achieved at the expense of a somewhat worse description of the peak. The deviations are due to the initial ⁶He wave function, which also enters into the description of the reaction. This can be seen by the lower green dotted curve which gives the energy distribution without the $nn$ final state interaction. This distribution is well-described by the free-neutron behavior $\sqrt{E}$ up to about 0.5 MeV. At this energy scale, it seems that structure effects from the ⁶He wave function become important and the neutron distribution starts to differ from the free case. This is consistent with the intrinsic scale generated by the two-neutron separation energy of ⁶He, which is of order 1 MeV. A similar behavior is observed in the FaCE calculation in the Fig. 4, Right (dotted curve). However, in this case the description of the FaCE calculation for energies beyond 0.5 MeV can be improved by also including the $p$-wave contribution which falls off as $1/E^{3/2}$ (dash-dash-dotted line). We expect this to be due to the more complicated structure of the ⁶He wave function in FaCE.

Fig. 4.

Center-of-mass energy spectrum of two neutrons in the reaction ⁶He$\left(p,p\alpha \right)2n$ at high energies. Halo EFT calculations from Göbel et al. (19) with/without final state interaction of the neutrons are given by the upper red/lower green dotted lines (Left). FaCE calculations with final state interaction are given by the dotted line (Right). Different fits are explained in the key and in the main text.

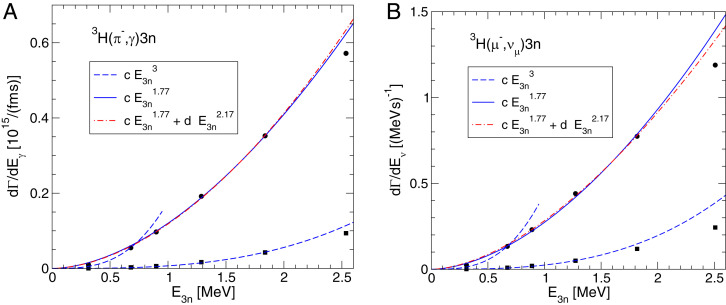
Next, we turn to the case of a three-neutron final state. A precise photon spectrum near the kinematical endpoint for radiative capture of stopped pions on tritium was measured by Miller et al. (22). While unnucleus behavior is consistent with the spectrum of Miller et al., we cannot unambiguously extract the power behavior from these data. Therefore, we turn to the theoretical calculation of Golak et al. (23). They have carried out a realistic model calculation of the capture rate for the reaction ³H$\left({\pi }^{-},\gamma \right)3n$ using the AV18 two-nucleon potential and a Urbana IX three-body force. Their results are shown in Fig. 5, Left for the full calculation (circles) and the plane wave impulse approximation (squares). We have converted the calculated photon spectra to three-neutron spectra for convenience. As expected, the free neutron behavior, $E^3$ (dashed line), can describe the full calculation (circles) only at the lowest energies. However, the plane wave impulse approximation (squares) can be described up to about 2.5 MeV. The full calculation including final state interaction displays clear unnucleus behavior, $E^{1.77}$ (solid line) for energies also up to about 2.5 MeV, where it starts to deviate from the prediction. This is somewhat smaller than the value 5 MeV expected from the effective range. We suspect that this is due to the wave function of the triton, which has finite extent, making the reaction a less than ideal “point source” of the neutrons and causing the factorization formula, Eq. 15, to break down earlier than expected. The description cannot be significantly improved by including the next state which behaves as $E^{2.17}$ (dash-dotted line). Analogous behavior is exhibited by the theoretical spectra for the reaction ³H$\left({\mu }^{-},{\nu }_{\mu }\right)3n$ calculated by Golak et al. (24) using the same interaction model (see Fig. 5, Right). In this reaction, the energy scale of the primary scattering process is slightly smaller such that the corrections to factorization are larger.

Fig. 5.

Center-of-mass energy spectrum of three neutrons in the reaction ³H$\left({\pi }^{-},\gamma \right)3n$ (A) and ³H$\left({\mu }^{-},{\nu }_{\mu }\right)3n$ (B). The circles/squares give the full/plane wave calculations by Golak et al. (23, 24). Different fits are explained in the key and in the main text.

A four-neutron spectrum was recently measured by Kisamori et al. in the reaction ⁴He (⁸He,⁸Be)$4n$ (25), but the number of events is too low to extract evidence of unnucleus behavior. It may, however, be possible to observe unnucleus behavior in the four-neutron spectrum of a new experiment using the reaction ⁸He$\left(p,p\alpha \right)4n$, which has higher statistics and is currently being analyzed.

Conclusion

We have suggested that nuclear processes involving a few neutrons in the final state may be well described, in a certain kinematic regime, as the production of an unnucleus, defined as an object corresponding to a field in a nonrelativistic conformal field theory. Using this observation, we predict power-law behaviors of the differential cross-section in a certain range of the neutron kinetic energy, or equivalently, of the recoil energy of the particle that emits the neutrons, with the value of the exponent determined by the universal physics of fermions at unitarity.

The power-law behavior breaks down when the relative momentum between the neutrons is less than $\hslash /a$, crossing over to the regime of free neutrons. The transition between the two regimes is well known in the case of two-neutron final state. For final states containing more than two neutrons, this cross-over can be, in principle, studied within the effective field theory approach.

The problem can be formalized as the calculation of the imaginary part of the two-point Green’s function of an operator $\mathcal{U}$ in the nonrelativistic conformal field theory of unitary fermions, deformed by a relevant deformation corresponding to a finite scattering length $a$. The theory therefore flows from an ultraviolet fixed point of fermions at unitarity to an infrared free-fermion fixed point. We expect that in such a theory

$$\mathrm{I}\mathrm{m}{G}_{\mathcal{U}}\left(\omega ,\mathbf{0}\right)=\theta \left(\omega \right){\omega }^{\mathrm{\Delta }-\frac{5}{2}}{F}_{\mathcal{U}}\left(\frac{\omega }{{\epsilon }_0}\right),$$ [27]

where $F_{\mathcal{U}}\left(\omega /{\epsilon }_0\right)$ are universal functions, one for each primary operator $\mathcal{U}$, which are expected to have the following asymptotic behavior:

$$F_{\mathcal{U}}\left(x\right)\to \left\{\begin{array}{cc}{c}_1\hspace{1em}\hfill & x\gg 1,\hfill \\ c_2{x}^{{\mathrm{\Delta }}_{\text{free}}-\mathrm{\Delta }}\hspace{1em}\hfill & x\ll 1,\hfill \end{array}\right.$$ [28]

where $c_1$ and $c_2$ are constant, and ${\mathrm{\Delta }}_{\text{free}}$ is the dimension of the operator that $\mathcal{U}$ becomes in the free-fermion infrared fixed point. For example, for the dimer operator we have $F_d\left(x\right)=x/\left(x+1\right)$. The functions $F_{\mathcal{U}}\left(x\right)$ are properties of a well-defined renormalization group flow. Once they have been calculated, the behavior of the differential cross-section of the process in Eq. 10 in the cross-over region is then

$$\frac{d\sigma }{dE}\sim {\left(E_0-E\right)}^{\mathrm{\Delta }-\frac{5}{2}}\hspace{0.17em}{F}_{\mathcal{U}}\left[\left(1+\frac{M_B}{M_{\mathcal{U}}}\right)\frac{E_0-E}{{\epsilon }_0}\right].$$ [29]

There may be contributions from more than one operator $\mathcal{U}$ to a given process.

It may be important to investigate the correction to the power law coming from effects beyond the large scattering length, e.g., the effective range or the three-body force. This too, hopefully, could be accomplished using techniques of effective field theory.

Nuclear reactions involving three and four neutrons in the final states have been investigated in the searches for bound trineutron and tetraneutrons or narrow resonances (see, e.g., refs. 25–27). Our prediction is made under the assumption that there is no narrow resonance with energy comparable to or less than the kinetic energy of the neutrons in the frame of their center of mass. We have analyzed the two- and three-neutron spectra of realistic calculations for the reactions ⁶He$\left(p,p\alpha \right)2n$ (19), ³H$\left({\pi }^{-},\gamma \right)3n$ (23), and ³H$\left({\mu }^{-},{\nu }_{\mu }\right)3n$ (24). These spectra show clear evidence of unnucleus behavior. An analysis of experimental two- and four-neutron spectra for unnucleus behavior will become possible in the near future.^†

Other types of unnuclei may be interesting to consider. The scattering length between two $\alpha$ nuclei is also large, so one can consider processes where two or three $\alpha$ particles are knocked out from a nucleus. The unnucleus formed by three $\alpha$ particles is where the Efimov effect takes place (28–30). The dimension of the unnucleus operator is complex: $\mathrm{\Delta }=\frac{5}{2}\pm i{s}_0$ with $s_0\approx 1.006$, so the differential cross-section should have a weak log-periodic dependence on $\left(E_0-E\right)$, crossing very near the endpoint to ${\left(E_0-E\right)}^2$. However, the presence of the long-range Coulomb repulsion complicates these systems (31). Unnuclear physics may also play a role in the three-nucleon system where different regions with approximate scale invariance exist (32).

Finally, cold atoms with fine-tuned interaction may provide another avenue for the investigation of the universal aspects of the unnuclear physics considered in this paper (33).

Data Availability

There are no data underlying this work.