Optimized delay of the second COVID-19 vaccine dose reduces ICU admissions

Significance

Shortages of COVID-19 vaccines hampered efforts to fight the current pandemic, leading experts to argue for delaying the second dose to provide earlier first-dose protection to twice as many people. We designed a model-based strategy for identifying the optimal second-dose delay using the hospitalization rate as the key metric. While epistemic uncertainties apply to our modeling, we found that the optimal delay was dependent on first-dose efficacy and vaccine mechanism of action. For infection-blocking vaccines, the second dose could be delayed $\ge$8 weeks if the first-dose efficacy was $\ge$50%. For symptom-alleviating vaccines, this delay duration is recommended if the first-dose efficacy was $\ge$70%. These results suggest that delaying the second vaccine dose is a feasible option.

Abstract

Slower than anticipated, COVID-19 vaccine production and distribution have impaired efforts to curtail the current pandemic. The standard administration schedule for most COVID-19 vaccines currently approved is two doses administered 3 to 4 wk apart. To increase the number of individuals with partial protection, some governments are considering delaying the second vaccine dose. However, the delay duration must take into account crucial factors, such as the degree of protection conferred by a single dose, the anticipated vaccine supply pipeline, and the potential emergence of more virulent COVID-19 variants. To help guide decision-making, we propose here an optimization model based on extended susceptible, exposed, infectious, and removed (SEIR) dynamics that determines the optimal delay duration between the first and second COVID-19 vaccine doses. The model assumes lenient social distancing and uses intensive care unit (ICU) admission as a key metric while selecting the optimal duration between doses vs. the standard 4-wk delay. While epistemic uncertainties apply to the interpretation of simulation outputs, we found that the delay is dependent on the vaccine mechanism of action and first-dose efficacy. For infection-blocking vaccines with first-dose efficacy $\ge$50%, the model predicts that the second dose can be delayed by $\ge$8 wk (half of the maximal delay), whereas for symptom-alleviating vaccines, the same delay is recommended only if the first-dose efficacy is $\ge$70%. Our model predicts that a 12-wk second-dose delay of an infection-blocking vaccine with a first-dose efficacy $\ge$70% could reduce ICU admissions by 400 people per million over 200 d.

Immunization of a large proportion of the worldwide population against the severe acute respiratory syndrome coronavirus 2 (COVID-19) is the most pressing current public health concern globally. Despite the unprecedented speed at which safe and effective vaccines were developed, tested, and approved, slower than anticipated vaccine production and distribution have hampered efforts to curtail the ongoing pandemic (1–3). The delays have not only resulted in an alarming number of potentially preventable deaths but also, contributed to the emergence of more virulent strains that could reduce the efficacy of current vaccines (4). Of the eight COVID-19 vaccines currently authorized around the globe, most have a recommended schedule of two doses separated by 3 to 4 wk. While awaiting replenishment of vaccine supplies, some governments are considering or have implemented delayed administration of the second vaccine dose in order to increase the proportion of the population with at least partial protection from a single dose. Recent debates argue in favor of such delay strategies (1–3), but there are no guidelines as to how the optimal delay duration should be determined, and this has yet to be tested in clinical trials. Two major questions are the extent to which delaying the second dose would impact hospitalization rates and alleviate mitigation measures when compared with the standard 3- to 4-wk second-dose delay.

Here, we report a model-based strategy for identifying the optimal delay time between vaccine doses using intensive care unit (ICU) hospitalizations as the key metric. We show that the optimal time is influenced by both the first-dose efficacy and whether the vaccine prevents infection or alleviates symptoms. The decision to delay the second vaccine dose is therefore not trivial because single doses of infection-blocking and disease-modifying vaccines are unlikely to have an equivalent impact on curbing the pandemic (5), and a large number of infection scenarios and their effect on disease evolution must also be taken into account.

To assist in decision-making about the optimal time to delay the second COVID-19 vaccine dose, we extended the susceptible, exposed, infectious, and removed (SEIR) model to include vaccination campaigns with two doses across populations. The epidemiological dynamic is used to predict ICU bed occupancy as a stochastic process that follows the disease trajectory. This information feeds a larger model that maintains the ICU occupancy within the operational capacity by restricting population circulation when needed. This is a unique feature of our approach, as other efforts to determine optimal dosing schedules for the COVID-19 vaccines do not take into account social distancing (6–8). We describe an optimization algorithm to find the best vaccination regimen that does not increase hospitalization rates while successfully alleviating social distancing and travel restrictions, thereby accelerating a return to “normality” as soon as possible.

1. Results

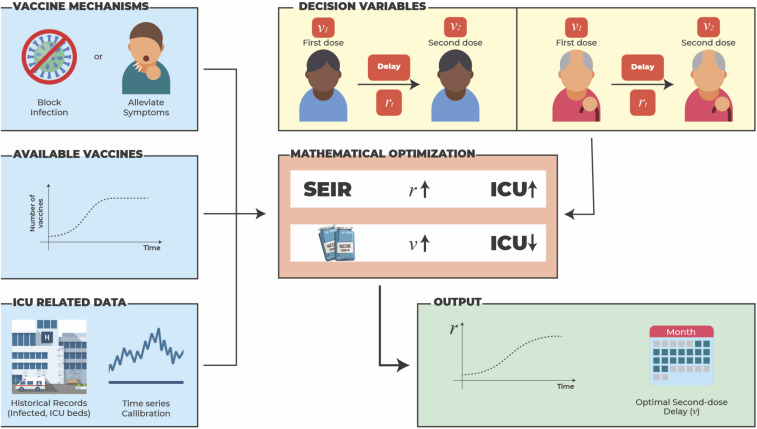
The algorithm explores multiple scenarios to obtain the best profile for delaying the second vaccine dose while safeguarding the health care system and lessening mitigation measures. The second-dose delay mechanism is not explicit but emerges from the solution of the optimization, and the solver decides when to administer the second dose. As illustrated in Fig. 1, several factors are taken into account: age, mechanism of vaccine action (symptom alleviation vs. infection prevention), vaccine availability, ICU capacity and its variability, and ICU hospitalization rates among different age groups.

Fig. 1.

A mathematical model combines data and optimization to obtain an optimal delay for administration of a vaccine second dose. The optimal second-dose delay emerges from the solution of the optimization model. The model blends ICU usage data, the vaccine mechanism of action, vaccine availability, and population demographics into an epidemiological model to predict future ICU admissions by age group. The model is solved using an optimization algorithm that considers multiple scenarios and iteratively adjusts the decision variables to find the optimal delay between the first and second vaccine doses and the target control reproduction number. The graphics used to prepare Fig. 1 are extracted from Freepik.

To illustrate, consider a single age group. At each incremental change in delay time, there are three decision variables: 1) the reproduction number $r_t$, 2) the number of first doses currently administered, and 3) the number of second doses currently administered. Reducing mitigation measures (i.e., increasing $r_t$) increases the number of ICU admissions, whereas increasing the vaccination rate has the opposite effect. However, a certain time delay between first and second doses may be beneficial depending on the protection level conferred by the first dose. Each iteration of the solution method adjusts the control variables taking into account the dynamics, the logistic constraints, and the ICU capacity. The adjustment is performed in a manner that favors large reproduction numbers $r_t$. We can then compute a second-dose delay for all time steps to obtain the optimal delay.

1A. Multiple Subpopulation SEIR Model with Two Vaccine States.

We extend the SEIR model to include individuals receiving vaccines.

Given a subpopulation $p$, the proportions of the susceptible subpopulation that have received zero, one, and two vaccine doses are $S_{p,1},S_{p,2}$, and $S_{p,3}$, respectively. The other SEIR states, $E,$ $I$, and $R$, were also similarly split. The parameters $a_1,a_2\in \left[\mathrm{0,1}\right]$ decrease the probability that a vaccinated individual will be infected when exposed to an infected individual, considering one and two doses, respectively, while $v_{p,1}$ and $v_{p,2}$ represent the proportions of individuals who have received first and second doses. The model is presented in Methods, and the interactions are illustrated in Fig. 1. The main elements of our optimization model are described below.

1A.1. Groups in the population.

We stratify the population into subgroups with specific demands on health care. We considered four age groups of 0 to 19, 20 to 49, 50 to 64, and 65 to 90 y in groups 1, 2, 3, and 4, respectively. The contact matrix $C$ between age groups is presented in Methods. We set the initial condition as $S_0=68.5$%, $E_0=1.0$%, $I_0=0.6$%, and $R_0=29.9$%, corresponding to typical values for multiple countries at the beginning of February 2021. The algorithm was run with basal reproduction number $r_0$ ranging between 1.8 and 3.0 without observing a significant change in the output decisions. The subpopulation breakdown by age is 30, 48, 14, and 8% for groups 1, 2, 3, and 4, respectively.

Given a reproduction number $r_0$, the reproduction number of the subpopulation $p$ is the product $b_p{r}_0$, where factor $b_p$ represents subpopulation susceptibility that is greater than or equal to that of the overall population. This factor is one except for $b_2=1.3$, which takes into account the increased mobility and thus, contribution to disease transmission by the 20- to 49-y-old age group.

1A.2. Objectives.

To prevent collapse of the health care system, the reproduction number must be decreased. This can be achieved by restricting circulation and implementing a vaccination campaign: that is, deciding for each day $t$ and subpopulation $p$ the values of $v_{p,1}\left(t\right)$ and $v_{p,2}\left(t\right)$ (9, 10) until the reproduction number reaches a target value $r\left(t\right)$.

Rather than performing simulations of known case studies defined by experts (1, 2) in our model, the optimization algorithm drives selection of the best strategy by considering implicitly all possible combinations of social distancing and vaccination profiles. Accordingly, the optimization model casts $r\left(t\right)$, $v_{p,1}\left(t\right)$, and $v_{p,2}\left(t\right)$ as decision variables to be selected by the algorithm among all scenarios that combines mitigation measure and vaccine administration to save ICU admissions. The choices range from complete lockdown $\left(r\left(t\right)=0\right)$ to free circulation $\left(r\left(t\right)=r_0\right)$ in combination with single-dose administration to any or no portion of a population ($v_{p,1}\left(t\right)\in \left[\mathrm{0,1}\right]$), and similarly for the second dose ($v_{p,2}\left(t\right)\in \left[\mathrm{0,1}\right]$). To determine the best strategy, the optimization process is guided by its objective function that encourages higher values of $r\left(t\right)$ and translates into a more freely circulating population. For logistic reasons, the objective function also includes a term that promotes smooth changes in the vaccination profile.

The optimization model also takes into account ICU occupancy and maintains it below maximum capacity with a 95% probability. The number of ICU patients on day $t$ follows a stochastic process calibrated as a time series for the proportion of infected individuals who will need intensive care on day $t$. We estimate that the average stay in the ICU is 7 d (11). Using official records for Brazil for the last quarter of 2020, we computed the mean number of patients in the ICU for each day t between day $t-7$ and day $t$ and divided that by the number of new cases reported in day t. After the time series is calibrated for the ratio, knowing the number of infected individuals in the SEIR dynamics at day $t$ gives a stochastic trajectory of ICU bed occupancy from which we derive a probabilistic constraint. The considered ICU bed capacity is 17.5 per 100,000 inhabitants, and the mean ICU bed demand is 1.2% (SD 0.64%) of the infected population, distributing the values among the age groups.

1A.3. Vaccine mechanisms.

We consider two types of vaccine (5): infection blocking and symptom alleviating. An infection-blocking vaccine can prevent infection by decreasing the likelihood of becoming infected from an encounter with an infectious individual by one minus the dose efficacy. This is modeled by multiplying the respective reproduction number by this factor, represented by the parameters $a_1$ and $a_2$ in the model. In the case of a vaccine that alleviates symptoms, we keep $a_1=a_2=1$ and assume that the effect of the vaccine is only to decrease the likelihood of an infected individual requiring ICU admission. This is modeled by multiplying the estimate of ICU beds needed for vaccinated individuals by one minus the dose efficacy.

1A.4. Profile of available doses.

Available dose numbers are given as a proportion of the population size, with an initial number of 0.1% ramping up linearly to 1.0% over 150 d and remaining constant thereafter. Small modifications to this profile do not affect the main results.

1B. Standard Vaccination by Age Groups as Baseline.

For both types of vaccine mechanisms over a period of 364 d, we first performed a simulation in which the standard two-dose vaccination strategy is administered to the most at-risk age group (65 to 90 y) first. As a “baseline” strategy, the second dose is automatically reserved for administration 4 wk later, and subpopulations are parsed in order of decreasing age. To evaluate the benefits of postponing the second dose, we used the number of ICU admissions as a measure of benefit gained by optimization of the vaccination strategy compared with the baseline strategy. A complementary metric is to assess the closeness of the reproduction number $r_t$ to the maximum value $r_0$ = 2.5. Since a value of 2.5 represents no circulation restriction, closeness to $r_0$ reflects proximity to an “open society” without enforced mitigation measures.

1C. Delaying the Second Dose.

To address whether delaying the second vaccine dose is desirable, the optimization model determines the best combination of target reproduction number $r\left(t\right)$ and vaccine distribution among the age groups. In our model, the second dose can be administered at any time up to 12 wk after the first dose.

1C.1. Impact of first-dose efficacy and the vaccine mechanism.

We fixed the second-dose efficacy at $a_2=82.4$%, as observed for the AstraZeneca Oxford vaccine (AZD1222) (12), and let the first-dose efficacy $a_1$ vary from 0 to $80\%$ in steps of 5%. The goals are 1) to determine if an optimal delay exists (other than the standard 4 wk) and 2) to determine if a threshold exists that would trigger a switch in the best delay time from the recommended (i.e., 4 wk) to as late as possible (12 wk).

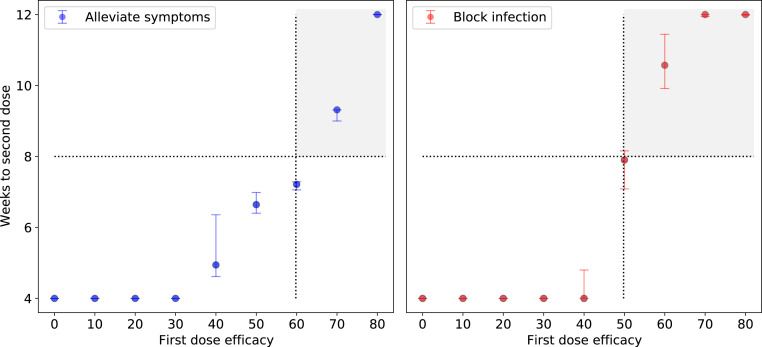
The results for infection-blocking and symptom-alleviating vaccines are shown in Fig. 2, where the dotted lines mark the delay at $r_0=2.5$ and the whiskers correspond to all possible values when $r_0$ is varied from 1.8 to 3 in 0.2 steps. For $r_0$ across this range, the threshold efficacy to obtain herd immunity (defined as the point at which the effective reproduction number is below one) ranges from 44.4 to 66.6%. For example, for $r_0=1.8$, the model predicts that a fully open society can be reached by week 5, well before the maximum allowed delay for the second dose (12 wk). In contrast, for $r_0=3.0$, the model predicts that mitigation measures will still be required beyond 12 wk. The decision to postpone the second dose is robust across the considered reproduction numbers. These results show that the vaccine mechanism plays a major role in the decision. Thus, when the vaccine blocks infections, the algorithm suggests that the second dose can be delayed by $\ge$8 wk if the first-dose efficacy is $\ge$ 50% and by the maximum delay of 12 wk if the first-dose efficacy is $\ge$ 70%, whereas a delay $\ge$ 8 wk is advisable for symptom-alleviating vaccines only when the first-dose efficacy is $\ge$ 70%.

Fig. 2.

Optimization of the delay between the first and second doses of a COVID-19 vaccine based on first-dose efficacy and vaccine mechanism. The shaded areas represent the first-dose efficacy that results in doubling the time to second dose from the baseline (4 wk). Left shows the second-dose delay when the vaccine alleviates symptoms; in this case, the best strategy delays the second dose for $\ge$8 wk when the first-dose efficacy is $\ge$70%. Right shows the second-dose delay when the vaccine blocks infection; here, the best strategy delays the second dose for $\ge$8 wk when the first-dose efficacy is $\ge$50%. For both vaccine types, the second-dose efficacy reaches 82.4%. The filled circles show the time to the second dose for $r_0=2.5$, and the bars represent the variability across simulations when $r_0$ is varied from 1.8 to 3 in 0.2 steps.

1C.2. Effect of augmented transmission in a subpopulation.

Individuals within specific age groups may play a more active role than other age groups in spreading the disease due to a higher degree of social activity or less stringent attention to sanitary measures. For this analysis, we considered people in the 20- to 49-y-old age group, most of whom would be working and socially active. We fix $r_0$ at 2.5 and compute the second-dose timing as a function of the first-dose efficacy for $b_2$ ranging from 1 to 1.6. We observed only a small variability in the optimal time to second dose; in fact, all curves fell within the shaded area of Fig. 2. Thus, postponing the second dose is robust with respect to changes in both $r_0$ and the reproduction number of specific subpopulations.

1C.3. Comparison between the optimally delayed second dose and baseline strategy.

We let $r_0=2.5$ for all age groups except the 20- to 49-y-old group, where $r_0$ was set 30% higher. We fixed the first- and second-dose efficacies at 76 and 82.4%, respectively, as estimated for the AZD1222 vaccine (12).

To quantify the effect of delaying the second dose on health, we computed the difference in ICU demand when comparing the optimization model and baseline strategies. We varied the efficacy of the first dose from 0 to 80% and determined the impact on COVID-19–related ICU admissions over a specific period, which we set here as 200 d. The algorithm finds an optimal second-dose delay in which social distancing values are no worse than those with the baseline strategy. To achieve this, the model includes the mean baseline $r_t$ as a lower bound and runs the optimization problem with a metric that decreases the overall ICU usage.

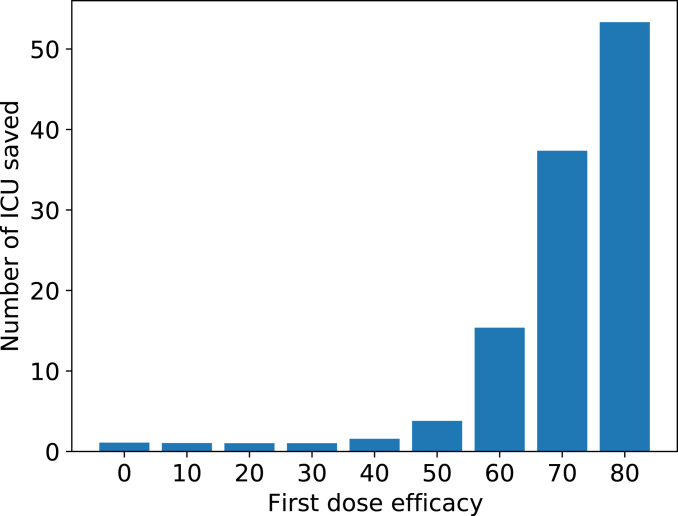
The results for the first 200 d are reported in Fig. 3. The data show that a second-dose delay beyond the standard 4 wk will result in a progressive reduction in ICU admissions as the first-dose efficacy increases, with a threshold of 50%. As a comparison, this model would predict that for an infection-blocking vaccine such as AZD1222, which has an actual first-dose efficacy of about 76%, an optimized second-dose delay would save 45 ICU admissions per 100,000 individuals compared with the baseline strategy.

Fig. 3.

Reduction in ICU occupancy using the optimized second-dose delay strategy compared with the standard delay strategy. The graph shows the predicted reduction in ICU admissions when the first-dose efficacy is varied from 0 to 80% in 5% increments and is normalized to the baseline strategy of 4 wk between doses.

Assuming a first-dose efficacy of $\ge$50%, the optimization model indicates that each 6% increase in first-dose efficacy reduces the number of ICU admissions by 10 per 100,000 individuals for infection-blocking vaccines and 8 per 100,000 individuals for symptom-alleviating vaccines.The optimized second-dose delay strategy is also supported by complementary metrics that examine the extent to which the vaccination campaign leads progressively to a fully open society. Whereas the baseline strategy results in three periods of 2 wk each of strict lockdown, an optimized second-dose delay of 12 wk results in a single initial lockdown of 2 wk followed by a gradual relaxation of social distancing measures. Thus, the optimization model predicts that a second-dose delay would be beneficial not only in reducing the burden on the health care system but also, in accelerating the return of society to a normal lifestyle.

2. Discussion

We developed a model to examine the impact of optimizing the delay between doses of a two-dose COVID-19 vaccine on ICU admissions and societal restrictions compared with a standard delay of 4 wk. Our study demonstrates that the mechanism of vaccine action has a profound effect on the delay. Thus, if the vaccine blocks infection with a first-dose efficacy of $\ge$50%, the second dose can be delayed by at least 8 wk after the first dose (half of the maximal delay allowed). In contrast, the same delay would be advisable for a symptom-alleviating vaccine only if the first-dose efficacy is at least 70%.

Strategies to extend the reach of available vaccine supplies, such as halving the dose or increasing the delay interval between doses as considered here, could have a significant beneficial effect on disease transmission and mortality until vaccine supplies increase (1, 2). Critics of these strategies fear that induced immunity may wane before the second dose can be administered or result in weak immunity that would favor the emergence of variant strains with higher virulence (13). However, even partial immunity may reduce disease and/or infection and concomitantly lessen the opportunity for viral mutation and propagation (14–17).

Our findings suggest that several societal benefits can be obtained by delaying the second dose of a vaccine, especially if the first-dose efficacy is high (e.g., 76% for AZD1222). First, an optimized delay could lead to a massive reduction in the number of ICU admissions. Given that ICU mortality rates for COVID-19 have reached about 60% in some countries (18), our findings suggest that an optimized second-dose delay for infection-blocking and symptom-alleviating vaccines could save 90,000 and 40,000 lives, respectively, over 200 d in a country with 300 million inhabitants. The second benefit obtained by an optimized second-dose delay is the extent to which it reduces mitigation measures. Our model predicts a reduction in full lockdowns from three 2-wk lockdowns when using the standard second-dose delay of 4 wk to a single 2-wk lockdown followed by a gradual social distancing relaxation with the optimized delay. Thus, a second-dose delay can save lives and accelerate the return to free circulation.

3. Methods

3A. SEIR Model with Multiple Doses of Vaccine.

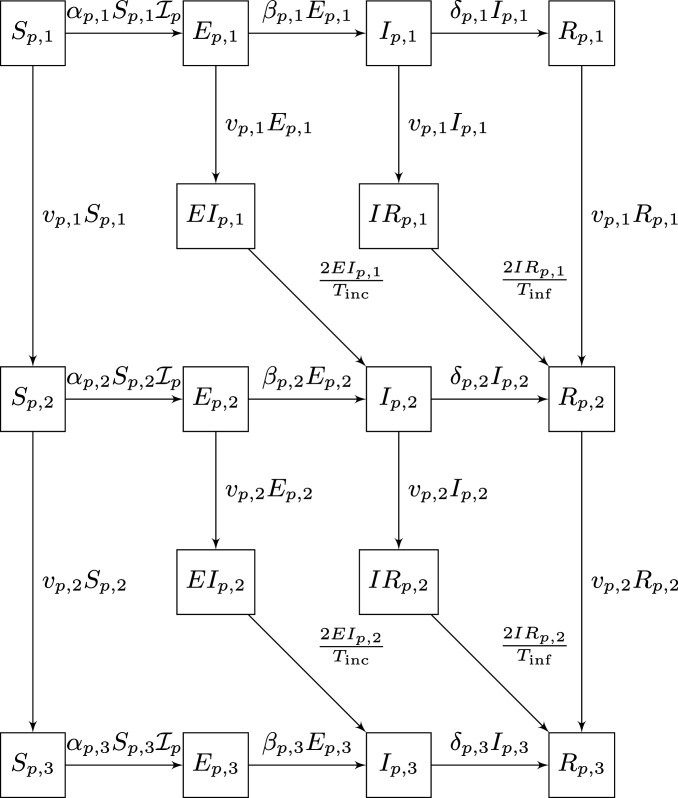
First, we discuss the SEIR dynamic when a two-dose vaccination campaign is put in place. For a fixed population $p$ and a vaccine mechanism that blocks transmission, we consider the diagram represented by Fig. 4.

Fig. 4.

SEIR model for age group $p$ with a two-dose vaccine that blocks infection.

The mean incubation and infectious times are $T_{\mathrm{i}\mathrm{n}\mathrm{c}}$ and $T_{\text{inf}}$, respectively. The variable $S_{p,1}$ represents the proportion of the subpopulation $p$ that is in the first stage of the vaccination process: that is, susceptible individuals in age group $p$ who did not receive any dose of the vaccine yet or who have been recently inoculated and the first-dose immunity is still building up. Likewise, $S_{p,2}$ is the proportion of susceptible individuals who are already protected by the effect of the first dose while still waiting for the second dose to be inoculated or become effective. Finally, $S_{p,3}$ represents the fraction of susceptible already protected by the full effect of the two doses. The meaning of the other compartments, $E_{p,i},I_{p,i},R_{p,i}=1,\dots ,3$, is similar. The intermediate states $E{I}_{p,i}$ and $I{R}_{p,i}$ represent individuals in $E_{p,i-1}$ and $R_{p,i-1}$ for whom the $i$th vaccine dose has just made effect and who are transitioning to the new states $I_{p,i}$ and $R_{p,i}$, respectively. Note that they spend only half of the time in this state, as they have already spent some time in the original state before moving to the next stage.

The variable $v_{p,i},i=\mathrm{1,2}$, models the number of people from the level $i-1$ for which the $i$th dose of the vaccine made effect at a given moment in time, afterwards their state changes and they move to the next level $i$. Other transition relations can be found in Table 1, where $a_1,a_2$ stands for the level achieved in attenuating the infection after receiving one and two doses of the vaccine. The factor $b_p$ models the effect that behavioral patterns of the subpopulation $p$ have on the chances of getting infected when encountering infectious individuals (for instance, younger and active individuals being more prone to agglomerate have an increased risk of infection). The variable $r\left(t\right)$ denotes the target reproduction number that is needed at time $t$ to control the spread of the disease with nonpharmaceutical measures, such as social distancing or mask wearing. Also, we note that the diagram in Fig. 4 has no transitions from $E{I}_{p,1}$ and $I{R}_{p,1}$ to the lower levels because we are assuming that the meantime in these states, $T_{\mathrm{i}\mathrm{n}\mathrm{c}}/2$ and $T_{\text{inf}}/2$, is significantly lower than the time required for a vaccine dose to make an effect.

Table 1.

Transition ratios for levels in the diagram in Fig. 4

	${\alpha }_{p,i}$	${\beta }_{p,i}$	${\delta }_{p,i}$
$i=1$	$\frac{b_p{r}_t\left(1-v_{p,1}\right)}{T_{\text{inf}}}$	$\frac{1-v_{p,1}}{T_{\mathrm{i}\mathrm{n}\mathrm{c}}}$	$\frac{1-v_{p,1}}{T_{\text{inf}}}$
$i=2$	$\frac{a_1{b}_p{r}_t\left(1-v_{p,2}\right)}{T_{\text{inf}}}$	$\frac{1-v_{p,2}}{T_{\mathrm{i}\mathrm{n}\mathrm{c}}}$	$\frac{1-v_{p,2}}{T_{\text{inf}}}$
$i=3$	$\frac{a_2{b}_p{r}_t}{T_{\text{inf}}}$	$\frac{1}{T_{\mathrm{i}\mathrm{n}\mathrm{c}}}$	$\frac{1}{T_{\text{inf}}}$

Finally, the variable ${\mathcal{I}}_p$ binds all the subpopulations together by a contact matrix that describes how the different age groups interact. This is a square matrix $C$ of dimension $\#\text{subpopulations}\times \#\text{subpopulations}$ in which the entry $C_{p,p^{\prime }}$ represents the proportion of contacts the subpopulation $p$ makes with individuals of the subpopulation $p^{\prime }$. In particular, the sum by rows equals 1.0. Using this matrix, we define

$$I_p≔\frac{I_{p,1}+I_{p,2}+I_{p,3}+I{R}_{p,1}+I{R}_{p,2}}{\text{proportion}\hspace{0.17em}\text{of}\hspace{0.17em}\text{the}\hspace{0.17em}\text{overall}\hspace{0.17em}\text{population}\hspace{0.17em}\text{that}\hspace{0.17em}\text{belongs}\hspace{0.17em}\text{to}\hspace{0.17em}p}.$$

Additionally,

$${\mathcal{I}}_p=\sum _{p^{\prime }=1}^{\#\text{populations}}{C}_{p,p^{\prime }}{I}_{p^{\prime }},$$

for which the contact matrix is

$$C=\left(\begin{array}{cccc}0.57\hfill & \hfill 0.27\hfill & \hfill 0.10\hfill & \hfill 0.06\hfill \\ 0.20\hfill & \hfill 0.59\hfill & \hfill 0.15\hfill & \hfill 0.06\hfill \\ 0.15\hfill & \hfill 0.46\hfill & \hfill 0.27\hfill & \hfill 0.12\hfill \\ 0.18\hfill & \hfill 0.24\hfill & \hfill 0.18\hfill & \hfill 0.39\hfill \end{array}\right).$$

3B. ICU Occupation.

Since the percentage of the infected population that needs intensive care at time $t$ is represented by a stochastic process, a probabilistic constraint keeps the ICU bed usage below the maximum capacity, $v_t^{max}$. The use of a time series for the stochastic process makes it possible to reformulate the probabilistic constraint into an equivalent deterministic inequality. The detailed procedure is explained in ref. 19; here, we mention a few key points only.

Suppose infected individuals spend on average $\nu =7$ days in intensive care (20). At time $t$, if the bed usage for a given age group $p$ is $v_p^t$, then the fraction of infected individuals who need ICU beds at time $t$ can be estimated by the ratio $v_p^t/{\mathcal{J}}_p^t$, where ${\mathcal{J}}_t^p$ corresponds to individuals in the subpopulation $p$ moving to the compartment $R$ at time $t$. In our setting, this is equal to $1/T_{\text{inf}}\left({\sum }_{k=t-\nu }^t{\sum }_d\left(I_{pd}^k+2I{R}_{pd}^k\right)\right)$ . The total ICU demand is distributed proportionally among the age groups using a correcting factor ${\gamma }_p$ that represents the proportion of the age group that uses ICU beds, when compared with its demography. Table 2 reports the corresponding data for 2010 in São Paulo state, which has 44 million inhabitants.

Table 2.

ICU demand by age for the state of São Paulo, Brazil

$\begin{array}{c}\hfill \text{Population}\hfill \\ \hfill \text{group,}p\hfill \end{array}$	$\begin{array}{c}\hfill \text{Age}\hfill \\ \hfill \text{group,}\hspace{0.17em}\text{y}\hfill \end{array}$	Demography, %	$\begin{array}{c}\hfill \text{Actual}\hspace{0.17em}\text{ICU}\hfill \\ \hfill \text{usage},\hspace{0.17em}\%\hfill \end{array}$	$\begin{array}{c}\hfill \text{Correcting}\hfill \\ \hfill \text{factor,}{\gamma }_p\hfill \end{array}$
1	0–19	29	2	0.06
2	20–49	48	28	0.58
3	50–64	14	30	2.06
4	65–90	8	40	5.16

To obtain the time series parameters, we computed the history of ratios from the last quarter of 2020 until the end of January 2021 using official records of São Paulo state. Autoregressive models with lag up to two and no trend appeared as the best ones in terms of Bayesian information criterion. Back testing over January gave mean absolute percentage error values of 1.88, 2.02, and 9.84% for the lags two, one, and zero, respectively, with an approximate normal-looking shape for the residual histograms. When performing out of sample simulations until May 2021, we noticed that both trajectories with positive lags stabilized at the same value as those with zero lag. Since the mean absolute percentage error accuracy of the latter model was acceptable and the optimization problem covers a long time horizon, we chose the simplest time series, with lag zero, for the constraint. After scaling back, this procedure gave the following simple model, ${\mathrm{i}\mathrm{c}\mathrm{u}}^t\left(\omega \right)\sim \hspace{0.17em}\mathcal{N}\left(c_0,{\sigma }_{\omega }^2\right)$ for $c_0=0.01$ and ${\sigma }_{\omega }=0.002$. After these parameters are known, the pro rata per subpopulation is done as explained above to make explicit the probabilistic constraints

$$\mathbb{P}\left[{\mathrm{i}\mathrm{c}\mathrm{u}}^t\left(\omega \right)\sum _{p=1}^4{\gamma }_p{\mathcal{J}}_p^t\le v_{max}^t\right]\ge \delta ,$$

which ensure the hospital capacity will not be exceeded, with $\delta$ probability. In the experiments, we used $\delta =95\%$. The deterministic equivalent of the chance constraint is an affine inequality of the form $c_0{\sum }_p{\gamma }_p{\mathcal{J}}_p^t\le v_{max}^t+\mathrm{\Delta }$, where the term $\mathrm{\Delta }$ involves the inverse cumulative function of the standard Gaussian distribution. Ref. 19 has more details.

3C. Optimizing on Multiple Populations.

Given the models for ICU demand and vaccine supplies, the optimization algorithm finds the best strategy for vaccination and social distancing that simultaneously avoids the collapse of the health care infrastructure and controls the pandemic in the shortest amount of time. To achieve these goals we initially use an objective function $f$ that encourages large values of the reproduction number $r_t$. The optimization is done over the decision variables $r_t$, $v_{p,1}$, and $v_{p,2}$ that control the trajectories of the state variables, defined by the different SEIR compartments. The system of differential equations of the modified SEIR dynamic illustrated by the diagram in Fig. 1 is discretized using central finite differences over a horizon of $K$ days ($K=364$ in the simulations). Letting $c$ denote the vector whose components are the control variables $r_t^i,v_{p,1}^i$, and $v_{p,2}^i$, for $i=1,\dots ,K$ and $p=1,\dots ,\#\text{subpopulations}$, and letting $\mathrm{s}$ denote the state vector, with all the SEIR compartments for all subpopulations, the optimization problem has the abstract form

$$\begin{array}{ll}\hfill \underset{c,s}{max}& \hspace{1em}f\left(c\right)\hfill \\ \hfill \text{s.t.}& \hspace{1em}s\in \text{Discretization}\hspace{0.17em}\text{of}\hspace{0.17em}\text{SEIR}\left(c\right)\hfill \\ \hfill & \hspace{1em}c\in \text{logistic}\hspace{0.17em}\text{bounds}\hfill \\ \hfill & \hspace{1em}s\in \text{ICU}\hspace{0.17em}\text{usage},\hfill \end{array}$$

where the latter set represents the reformulation of the probabilistic constraint defined in Section 3B. Logistic relations on the control variables refer to the number of vaccines available each day taking into account both vaccine availability and the inoculation capacity. Specific time windows for giving the second dose, say $\left[t_{min},t_{max}\right]$, are enforced by requiring the total number of second doses applied up to day $t$ to be smaller than or equal to the total number of first doses administered up to the day $t-t_{min}$. This constraint ensures that no second doses are given before possible. On the other hand, we also limit the total number of second doses given until $t$ to be at least the total number of first doses administered up to $t-t_{max}$, ensuring that the second doses are applied within the desired time window. In our implementation, $t_{min}=28$ and $t_{max}=84$.

The objective function to minimize is the sum of differences ${\sum }_{i=1}^K{r}_0-r_t^i$, where $r_0=2.5$ is the basal reproduction number of the virus used in the simulation (21, 22). The rationale is to allow the population to circulate freely. To discourage bang-bang controls, we add to the objective a total quadratic variation term for the number of doses applied at each population each day. This term results in vaccination profiles that are easier to visualize and understand. After this first optimization step, we perform a second optimization that tries to minimize ICU usage without deteriorating the computed $r_t^{*}$ profile. To achieve this, we add the constraint

$$\sum _{i=1}^K{r}_t^i\ge \sum _{i=1}^K{\left(r_t^{*}\right)}^i,$$

and we switch the objective to minimize the estimated ICU usage.

These problems are large-scale nonconvex quadratic optimization problems. They are formulated using the JuMP (23) modeling language and solved using the nonlinear optimization solver Ipopt (24). The typical solution time is around 5 min on a desktop computer with a Ryzen 1700X processor.

Data Availability

Input files or sets of input parameters as well as the source code have been deposited in GitHub (https://github.com/pjssilva/Robot-vaccine).