Significance
The motion of granular materials, e.g., sand or catalytic particles, underlies many natural and industrial processes. Granular dynamics are difficult to understand and model because of transitions between solid-, liquid-, and gas-like behavior, and prior continuum models have struggled to capture these transitions. Bubble-like voids normally rise chaotically through grains suspended by upward gas flow. We create structured bubble formations by vibrating the system at a resonant frequency, independent of particle properties or system size, and we identify salient physics using a harmonic oscillator model. We propose a constitutive relationship that enables continuum models to predict structured bubbling a priori by capturing fluid–solid transitions. The continuum model and controlled bubble patterning can advance scale-up and optimization of industrial processes.
Keywords: granular material, bubbles, fluidization, rheological modeling
Abstract
The dynamics of granular materials are critical to many natural and industrial processes; granular motion is often strikingly similar to flow in conventional liquids. Food, pharmaceutical, and clean energy processes utilize bubbling fluidized beds, systems in which gas is flowed upward through granular particles, suspending the particles in a liquid-like state through which gas voids or bubbles rise. Here, we demonstrate that vibrating these systems at a resonant frequency can transform the normally chaotic motion of these bubbles into a dynamically structured configuration, creating reproducible, controlled motion of particles and gas. The resonant frequency is independent of particle properties and system size, and a simple harmonic oscillator model captures this frequency. Discrete particle simulations show that bubble structuring forms because of rapid, local transitions between solid-like and fluid-like behavior in the grains induced by vibration. Existing continuum models for gas–solid flows struggle to capture these fluid–solid transitions and thus cannot predict the bubble structuring. We propose a constitutive relationship for solids stress that predicts fluid–solid transitions and hence captures the experimental structured bubbling patterns. Similar structuring has been observed by oscillating gas flow in bubbling fluidized beds. We show that vibrating bubbling fluidized beds can produce a more ordered structure, particularly as system size is increased. The scalable structure and continuum model proposed here provide the potential to address major issues with scale-up and optimal operation, which currently limit the use of bubbling fluidized beds in existing and emerging technologies.
Granular materials can behave like liquids when subject to external forcing, as seen in lizards “swimming” through sand (1), wavy instabilities forming under shear (2), Faraday waves in granular layers (3, 4), Rayleigh–Taylor fingering (5, 6), and droplets of grains forming in tapped plates (7) and hourglass streams (8). Gaseous voids resembling bubbles in liquids can rise through grains suspended in a fluid-like state by upward gas flow (9) or vertical vibration (10). These gas voids are not conventional bubbles because there is no surface tension between the voids and surrounding fluid-like grains, and gas can pass freely between voids and the interstices between granular particles. Voids or bubbles are instead formed in grains typically due to gas channeling through small spaces between particles, which causes the spaces to grow into a bubble and more gas to channel through the bubble. A bubble typically grows until the drag force from gas channeling through the bubble can no longer support the roof of particles above the bubble. These bubbles are typically at least an order of magnitude larger in size than the particles. Despite the differences in governing physics compared to conventional bubbles, bubbles in suspended grains coalesce and break up in a manner similar to conventional bubbles and adopt shapes and rise velocities closely resembling those seen in Newtonian liquids (11).
In engineering applications including pharmaceutical production (12), polymer recycling (13), carbon capture (14), coal combustion (15), and biomass gasification (16), granular particles are suspended by upward gas flow, forming rising voids, which act to mix the particles in devices known as “bubbling fluidized beds” (9). These systems are often used to promote mixing and heat transport among particles. The dynamics of bubbles in these fluidized beds are mathematically chaotic (17–19), and thus bubble and particle dynamics can change dramatically with changes in system size or particle size in ways that are often unpredictable. As such, scale-up, optimization, and operation of bubbling fluidized beds often create engineering challenges, which then limit their adoption despite their favorable properties in heat transport and mixing (20). Prior studies have shown that oscillating gas flow rate can suppress chaos (17) and create structuring (19) in bubbles in fluidized beds with bubble sizes and separation distances and solids circulation controllable based on gas flow oscillation conditions (21). Granular beds fluidized by upward gas flow can also be vibrated, often to reduce the effects of cohesive forces between particles (22), and vibrating gas-fluidized beds has been shown to reduce the minimum fluidization velocity (5, 23, 24) and suppress bubbling in some cases (5, 23, 25). Currently, vibrated gas-fluidized beds are used extensively in industry (26, 27), largely to improve drying processes and break up agglomerates of cohesive particles, and thus the use of vibration to promote structuring has potential for industrial applications.
Here, we demonstrate that vibrating bubbling fluidized beds (Fig. 1) at a resonant frequency creates a periodic triangular structuring of bubbles, which persists across different particle properties and system sizes, providing the potential to address major issues in current bubbling fluidized beds. The resonant frequency can be captured by a harmonic oscillator model, and the length scale for this model can be predicted analytically. Discrete particle modeling shows that structure emerges due to rapid yet controlled transitions between fluid-like and solid-like behavior in the particle system. We propose a continuum stress model that can predict structuring by capturing fluid–solid transition behavior, addressing a major issue (21, 28) in current continuum models of granular flow.
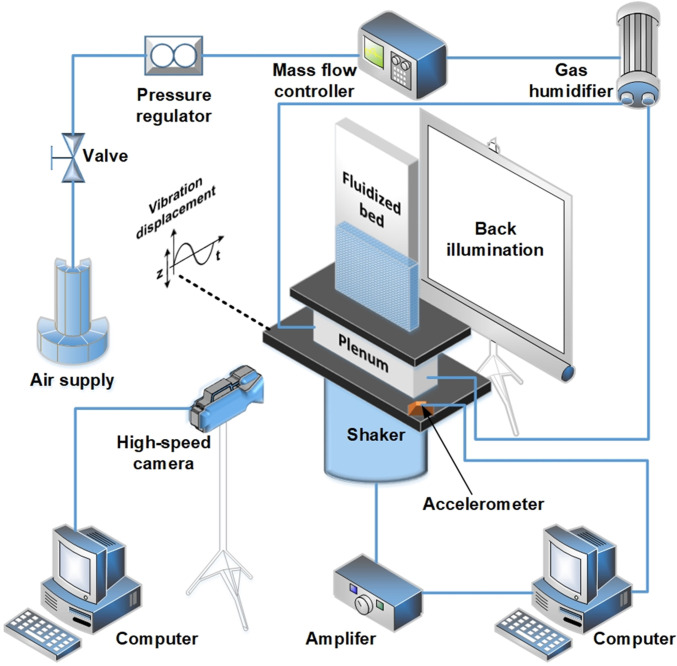
Fig. 1.
Schematic of the experimental setup.
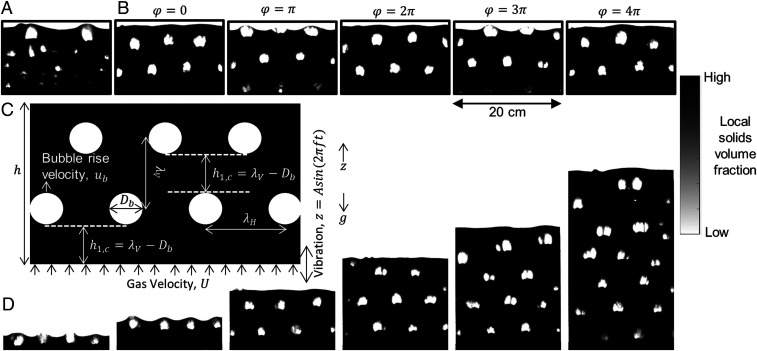
The ability of vibration to transform normally chaotic bubble dynamics into structured arrays of rising bubbles that repeat in form periodically is shown in Fig. 2 and Movie S1. Under conditions without vibration, bubbles of a wide range of shapes and sizes rise, coalesce, and split (Fig. 2A). When the system is vibrated, shown schematically in Figs. 1 and 2C, bubbles of uniform size form and rise in a regularly spaced triangular arrangement without coalescing or splitting (Fig. 2B). A new row of bubbles forms with each vibration cycle. Bubbles originate at horizontal positions centered in-between the positions of bubbles in the row above them, such that the structure in the bubble array repeats itself every two vibration cycles (Fig. 2B). The structuring persists as bed height is increased (Fig. 2D); however, structure is somewhat diminished higher in the system in taller beds. This feature of bubble structure persisting, albeit in a somewhat diminished manner, to taller system heights is also observed in fluidized beds with oscillating gas flow (21). Since bubble dynamics strongly influence particle and gas motion (11), structuring the bubbling effectively structures particle and gas conveyance and mixing in these systems.
Fig. 2.
Vibration-induced structured bubbling: Optical images of bubbling patterns under different flow conditions: (A) Bubbling with no system vibration and (B) bubbling with system vibration with an initial bed height of 10 cm. C shows schematically how gas flow and vibration are used, as well as the relevant length scales in the system. D shows optical images of bubbling with system vibration with different initial bed heights. The particles used are glass beads with ρp = 2,500 kg/m3 and dp = 212–300 μm. The time interval between two consecutive images in B is 0.1 s, half of the vibration period. From Left to Right, the initial bed height in D is 2.5, 5, 10, 15, 20, and 30 cm. The vibration frequency is 5 Hz and the vibration amplitude is 4.5 mm for B and D. U/Umf is 1.42 for A, B, and D.
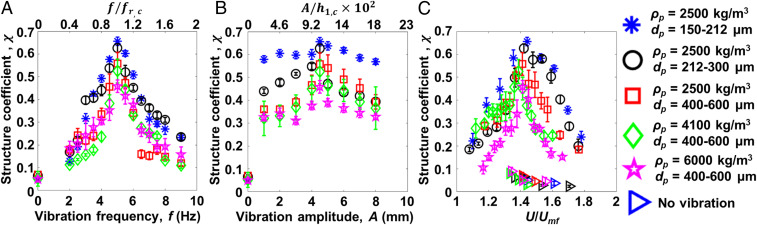
Structured bubbling is optimized at a specific vibration frequency and amplitude as well as a specific ratio of inlet gas velocity (U) to that needed to suspend the particles (Umf), and these conditions for flow structuring are independent of particle properties (Fig. 3). The extent of bubble structuring can be quantified by comparing images of the bubble structure separated by two vibration cycles for each image collected over the duration of the experiment. Here, we quantify this structure using Pearson’s correlation coefficient (29), , which has a value = 1 for exact periodic repetition of structure and = 0 for no periodic repetition of structure. In this equation, N is the number of pixels in the image, i is the pixel index, and are the intensity at pixel in the current frame and in the frame after two vibration periods, respectively, and and are the average of and over the entire system in space at the time of interest, respectively. Upon varying vibration frequency (f) while keeping vibration amplitude (A) and U/Umf constant, the correlation coefficient achieved a maximum at frequency of 5 Hz (Fig. 3A). Similarly, when f and U/Umf were held constant and A was varied, a maximum correlation coefficient was achieved at an amplitude of 4.5 mm (Fig. 3B). Maximal bubble structuring was achieved at U/Umf = 1.4 when vibration conditions were kept constant (Fig. 3C). For all of these cases, the vibration and gas flow conditions needed to achieve maximal structure did not change when particle diameter and density were varied. In addition to producing the most repeatable structure, these optimal flow and vibration conditions produced the smallest variations in bubble diameter (SI Appendix, Fig. S1). These conditions also optimize structure and produce approximately the same amount of quantitative structure and bubble properties when the system width is doubled (SI Appendix, Fig. S2 and Table S1).
Fig. 3.
Vibration and flow conditions needed to produce structured bubbling: Correlation coefficient versus (A) vibration frequency, (B) vibration amplitude, and (C) U/Umf. Each panel of images varies a property while keeping other properties constant: (A) Constant properties: vibration amplitude = 4.5 mm, U/Umf = 1.4. (B) Constant properties: vibration frequency = 5 Hz, U/Umf = 1.4. (C) Constant properties: vibration frequency = 5 Hz, vibration amplitude = 4.5 mm. The initial bed height is 10 cm in A–C. The right-pointing triangles in C denote experiments without system vibration.
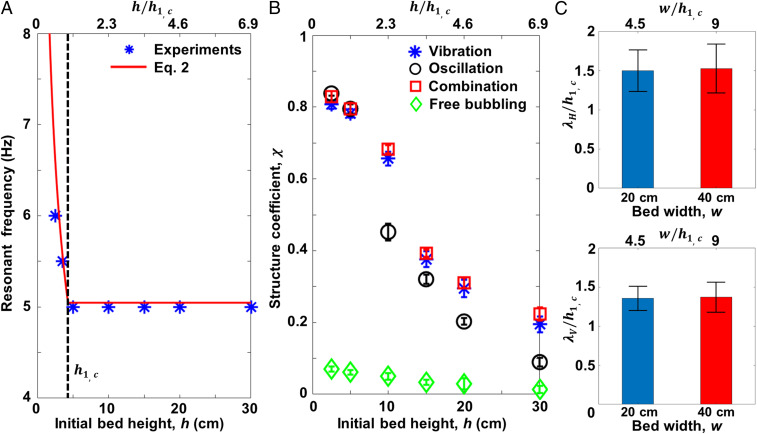
The vibration frequency that produces maximal structure decreases with increasing bed height at low bed heights before becoming independent of bed heights above a critical bed height, (Fig. 4A). The frequency that produces the maximal structure can be predicted analytically based on a harmonic oscillator derived from a balance between drag and gravitational force on particles. We ultimately identify the critical length scale, , for this model and relate it to two measured properties, bubble diameter () and solids volume fraction (), which do not vary significantly with changing particle properties.
Fig. 4.
Effects of scale-up on structured bubbling: (A) Resonant frequency for structure formation via vibration versus initial bed height, showing , the critical bed height above which the resonant frequency becomes constant. (B) Correlation coefficient versus initial bed height for vibration, gas flow oscillation, the combination of vibration and gas flow oscillation, and free bubbling. (C) Horizontal and vertical separation distances ( and ) between bubbles for vibrated gas-fluidized beds with different widths. The fluidized particles in A and B are glass beads with ρp = 2,500 kg/m3 and dp = 150–212 μm. The fluidized particles in C are glass beads with ρp = 2,500 kg/m3 and dp = 212–300 μm. The initial bed height is 10 cm in C. The vibration frequency and amplitude are 5 Hz and 4.5 mm, respectively, for A–C. The U/Umf is 1.44 in A and in the vibration and free bubbling cases in B. U/Umf = in the gas flow oscillation and combination cases in B. U/Umf = 1.42 in C.
Prior studies (30, 31) have shown that small harmonic oscillations in pressure drop occur in shallow layers of particles fluidized by gas flow, and these pressure oscillations are concurrent with small oscillations in bed height. Verloop and Heertjes (31) showed that based on the balance of drag and gravitational forces in a fluidized bed and the dependencies of these forces on and layer height, , small changes in layer height lead to restoring forces proportional to change in layer height. Damping is negligible due to the low density and viscosity of the gas, and thus the system can be modeled as an undamped harmonic oscillator with resonant frequency:
| [1] |
Verloop and Heertjes found that these harmonic compressions and expansions resulted in porosity waves rising through the system. If the layer height is tall enough, a new wave can form before the prior wave passes through the system; as such, the particles no longer oscillate in phase and the layer breaks up, causing multiple waves of multiple frequencies to form in the system. Such waves ultimately manifest in the bubbles of various sizes forming and moving chaotically through fluidized beds.
Vibration at a resonant frequency can be viewed as an external force driving the harmonic oscillator to prevent porosity waves of different frequencies forming and thus suppress chaotic bubbling. We find that Eq. 1 predicts the sharp decrease in vibration frequency, which produces maximal structure with increasing bed height at low bed heights (Fig. 4A), but cannot predict the height-independent behavior above . Our experiments show that this critical height is equal to the bed height at which one row of bubbles starts to form before the previous row of bubbles fully passes through the system. is thus analogous the critical height for layer breakup in the Verloop and Heertjes (31) model, except in this case the void waves are now externally forced to form uniformly at the vibration frequency. Since we find that bubbles rise at a constant velocity, is equal to , where is the vertical spacing between bubbles and is the bubble diameter (Fig. 2C). Now, we can view the regions of particles vertically in-between rows of bubbles as the fluidized layers of grains described by Verloop and Heertjes (31). As such, we can modify the resonant frequency predicted by the harmonic oscillator to the following:
| [2] |
Here, is the height of contiguous particles above the base of the bed when a new row of bubbles is forming:
| [3] |
Eq. 2 matches experimental results across a range of bed heights above and below (Fig. 4A). Furthermore, the resonant frequency, , for bed heights above is well matched by the equivalent prediction from Eq. 2, , across a range of particle properties (Table 1). Harmonic oscillator models have been able to capture resonant phenomena in short fluidized beds structured by oscillating gas flow rate (32), and in our own experiments with oscillating gas flow, we have noticed that resonant frequency also levels off above a critical height. Therefore, the modification in Eq. 2 is an attempt to capture the leveling off of resonant frequency in taller beds with external driving forces.
Table 1.
Comparison between experiments and theoretical models for the bubble rise velocity, resonant frequency, and , the bed height above which resonant frequency becomes constant with increasing bed height
| Particle type | Particle size, μm | Particle density, kg/m3 | Db, mm | , m/s | , m/s | , Hz | , Hz | , mm | , mm |
| Glass beads | 150–212 | 2,500 | 17 ± 3 | 0.29 ± 0.04 | 0.29 | 5 | 5.05 | 43 ± 3 | 35 |
| Glass beads | 212–300 | 2,500 | 20 ± 3 | 0.31 ± 0.04 | 0.31 | 5 | 4.98 | 44 ± 4 | 41 |
| Glass beads | 400–600 | 2,500 | 20 ± 5 | 0.30 ± 0.06 | 0.31 | 5 | 5.17 | 41 ± 4 | 41 |
| Ceramic beads | 400–600 | 4,100 | 22 ± 5 | 0.32 ± 0.05 | 0.33 | 5 | 5.05 | 43 ± 3 | 45 |
| Ceramic beads | 400–600 | 6,000 | 23 ± 4 | 0.33 ± 0.05 | 0.34 | 5 | 4.88 | 46 ± 4 | 47 |
The critical bed height, , can be predicted analytically using only two measured properties and , which do not change significantly with varying particle properties. We find experimentally that bubble diameter, , and rise velocity, , do not change as bubbles rise through the bed. Furthermore, bubble rise velocity is predicted well (Table 1) by a semiempirical relationship:
| [4] |
The semiempirical model (33) in Eq. 4 starts with a relationship to gravity and bubble diameter that comes from theory for bubble rise in conventional liquids (34). The constant = 0.71 comes from prior experiments in conventional bubbling fluidized beds (33). One row of bubbles forms per vibration period, and thus the vertical separation distance between bubbles is . As seen schematically in Fig. 2C, the height of contiguous particles between rows of bubbles and thus the height of the layer of particles below the first row of bubbles when the next row of bubbles forms is . Thus, combining equations, we can predict the critical bed height above which the resonant frequency becomes constant as follows:
| [5] |
Combining Eqs. 2, 4, and 5, we can achieve an equation for , which is only dependent on two measured properties, and :
| [6] |
| [7] |
| [8] |
Based on the measured value of = 0.63, the value of is ∼2 from Eq. 7. The predicted value of (Eq. 6) matches experimental measurements well across a range of particle properties (Table 1).
In all, the analytical modeling conducted here demonstrates an ability to predict the resonant vibration frequency for producing maximum bubble structure as well as the bed height above which this frequency is independent of bed height. Importantly, this model, verified by experiments, captures that this frequency and critical bed height do not change significantly with changing system size or particle diameter or density. Since particle packing fraction can be easily measured and does not change significantly with changing system size or particle diameter or density, the bubble diameter is the only significant empirical input to the analytical model. Our experiments further show that bubble diameter does not change significantly with system size or particle diameter or density. As such, the combination of experimental results of bubble size, critical bed height, and optimal vibration frequency not changing significantly with system size or particle properties and analytical modeling that captures the scientific underpinning of this structuring creates design rules for industrial practitioners to structure flow and optimize their systems.
Vibrating fluidized beds at a resonant frequency provides structure that is scalable as system size is increased (Fig. 4 B and C, and SI Appendix, Table S1). When system width is increased, the spacing between bubbles in the vertical and horizontal directions is unchanged (Fig. 4C and SI Appendix, Table S1). The correlation coefficient decreases with increasing bed height (Fig. 4B) due to degradation of structuring caused by bubble coalescence higher in the bed (Fig. 2D). However, the structuring in the case of a vibrated fluidized bed is approximately an order of magnitude higher than that of a conventional fluidized bed at all bed heights, and it is significantly higher than that of a fluidized bed with oscillating gas flow rate at taller bed heights (Fig. 4B). Results for combined gas oscillation and system vibration show that, especially at higher bed heights, vibration dominates over gas flow oscillation in producing structure, and thus the combined gas flow oscillation and system vibration produces correlation coefficients similar to those for vibration alone. The better scaling of structure in vibrated beds is attributed to system vibration persisting more through the entire height of the bed, while gas oscillation effects are more dissipated higher in the bed due to percolating gas motion through bubbles and interstices between particles.
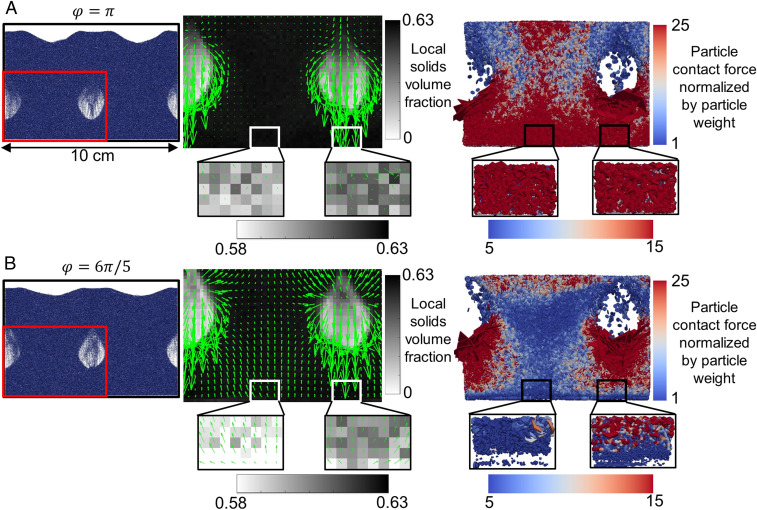
Discrete particle simulations predict the experimental triangular structure in resonantly vibrated fluidized beds, and demonstrate that this structure arises due to rapid, local transitions between fluid-like and solid-like behavior in the particles (Fig. 5, SI Appendix, Fig. S3, and Movie S1). Computer simulations (35) that model the motion of each individual particle using the discrete element method (36) and gas motion using computational fluid dynamics with gas–solid interaction modeled using a drag law (37) were used to simulate a vibrated fluidized bed with the same particle properties used experimentally. Due to the downward velocity of particles surrounding bubbles, the solids volume fraction is greater at the base of the system below bubbles than at the base of the system in-between bubbles (Fig. 5, second column). As the next row of bubbles is about to form, strong particle contact forces are seen at the base of the bed just below bubbles as well as in-between the bubbles (Fig. 5A, third column). However, due to particle concentration and convection patterns (Fig. 5, second column), contact forces are smaller between bubbles than directly below the bubbles as the next row of bubbles starts to form (Fig. 5B, third column). Thus, particles are in a densely packed, solid-like state below bubbles and in a less densely packed, fluid-like state between bubbles as the next row of bubbles forms. As a result, the bubbles form at the most favorable positions, locations halfway horizontally in-between the positions of bubbles in the row above, leading to the formation of the triangular structure. This local solidification persists surrounding bubbles as they rise (SI Appendix, Fig. S3 and Movie S1), indicating how structure can propagate high in the bed without coalescence of bubbles. Prior discrete particle simulations have also indicated that local solidification of particles leads to similar bubble structuring in fluidized beds with oscillating gas flow (38). The importance of this local solidification in causing structure formation and persistence is further evidenced by experiments we have conducted with viscous, Newtonian fluids in which combined vibration and gas flow could not produce structured bubbling (SI Appendix, Fig. S4).
Fig. 5.
Discrete particle simulation results of the structured bubbling with vibration at two different time instances (A and B), showing fluid–solid transitions in particles at the base of the system. First column: Snapshots of discrete particles, marking in red the region used for the zoomed-in view in the second and third columns. Second column: Zoomed-in local solids volume fraction with arrows indicating particle velocity. Third column: Zoomed-in particle contact force normalized by particle weight. The time interval between A and B is 0.02 s, 1/10th of the vibration period. The simulated particles have properties ρp = 2,500 kg/m3 and dp = 238 μm. The vibration frequency and amplitude are 5 Hz and 8 mm, respectively. The U/Umf is 1.39.
The insights of this study have a number of important parallels to those from studies considering oscillating gas flow rate, together with key physical understanding. A recent review paper summarizes prior work using oscillating gas flow to induce structured bubbling patterns (21). In contrast to this recent thinking (21), here we show that vibration can induce structured bubbling patterns, and that vibration-induced patterning (Fig. 4B) persists through higher system heights than when oscillating gas flow is used, demonstrating scalability. The importance of “natural frequencies” for governing structured versus unstructured bubbling regimes has been noted in an oscillating gas flow study (32). Here, we show that for vibration-induced structuring, the frequency predicted by a harmonic oscillator model is in fact a resonant frequency for maximizing structure (Fig. 3A), and this resonant frequency is independent of bed height above a critical bed height, which we can capture analytically (Table 1). Discrete particle simulations have reproduced triangular structured bubbling patterns in oscillating gas flow and shown that structure forms due to local solidification of particles below bubbles (38), as we have shown here for vibration (Fig. 5). Importantly, prior reviews (21, 28) have noted the inability for continuum models to predict the triangular structured bubbling pattern and that this inability stems from the rheological models being incapable of accurately predicting fluid–solid transitions in grains, a wide-reaching modeling need and effort in predicting granular flows. In the remainder of this paper, we describe our development of a continuum model, which can predict structured bubbling a priori by capturing fluid–solid transitions in grains as a final important insight with the potential to impact a variety of future work.
Fully continuum simulations (37) of gas–solid flows treat particles as a fluid, and thus are significantly more computationally efficient than discrete particle simulations, but require complex rheological models to formulate the solids stress. Prior studies (39–41) have attempted to use fully continuum simulations to predict structured bubbling with alternating bubble rows seen experimentally in systems with oscillating gas flow. However, these prior works have not successfully reproduced the highly regular patterns observed in experiments and discrete particle simulations. Here, we propose a frictional solids stress model, which enables fully continuum models to predict the triangular structured bubbling pattern a priori.
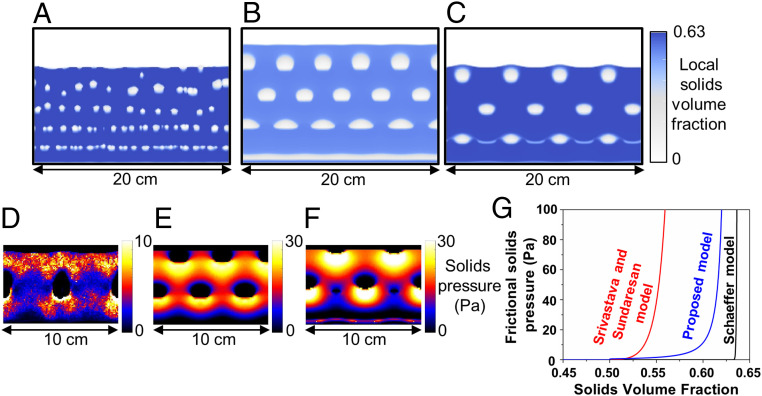
Herein, we use fully continuum models to simulate the structured bubbling patterns produced by vibration. Two predominantly used frictional solids stress models, the Schaeffer model (42) and the Srivastava and Sundaresan model (43), were first tested. The Schaeffer model couples the frictional solids pressure formulation of Syamlal et al. (42) and the frictional solids viscosity formulation of Schaeffer (44). The Srivastava and Sundaresan model (43) uses the frictional solids pressure at the critical state of Johnson and Jackson (45) and modifies the Schaeffer viscosity formulation (44) to take into account the effect of strain rate fluctuations. The Schaeffer model (42) cannot predict the structured bubbling pattern (Fig. 6A) across a wide range of vibration and superficial gas velocity conditions. The Srivastava and Sundaresan model (43) can produce structured bubbling with alternating rows (Fig. 6B); however, the gas flow conditions needed to achieve structuring as well as the size and separation between bubbles are different from those observed experimentally. The model proposed here predicts a priori the alternating bubble row structure with greater accuracy in bubble size and separation distance, while also utilizing the gas flow conditions used experimentally (Fig. 6C, SI Appendix, Fig. S5, and Movie S1). In further simulations, we found that the proposed model predicts structured bubbling induced by oscillating gas flow accurately, while the other models tested cannot predict structured bubbling induced by oscillating gas flow with the same level of accuracy as the proposed model (SI Appendix, Fig. S6).
Fig. 6.
Continuum modeling of structured bubbling: (A–C) Snapshots of local solids volume fraction predicted by continuum simulations using different constitutive models: (A) Schaeffer model (42), (B) Srivastava and Sundaresan model (43), and (C) the proposed model. (D) Solids pressure produced in discrete particle simulations of structured bubbling. (E and F) Solids pressure produced in continuum simulations of structured bubbling using (E) Srivastava and Sundaresan model (43) and (F) the proposed model. (G) Plot of frictional solids pressure versus solids volume fraction for different constitutive models in continuum simulations for flow conditions observed in structured bubbling. The simulated solids phase has properties ρp = 2,500 kg/m3 and dp = 238 μm. The vibration frequency and amplitude are 5 Hz and 4.5 mm, respectively. U/Umf = 1.37 for the Schaeffer model (42) and the proposed model, and U/Umf = 1.25 for the Srivastava and Sundaresan model (43).
The frictional solids stress model proposed here considers a shear-induced dilation law developed independently from structured bubbling experiments or simulations. Prior discrete particle simulation studies without gas flow have proposed a dilation law to capture how a granular assembly dilates under shear (46–48). These studies have shown that, starting from the solids volume fraction at maximum packing, , the solids concentration, , decreases linearly with increasing the inertial number I:
| [9] |
where is the lowest solids concentration at which frictional contacts affect particle-phase stress. The inertial number I is defined by the following:
| [10] |
where is the shear rate, is the solids pressure, is particle diameter, and is the particle density.
The solids pressure at a critical state in which the granular assembly deforms without volume change, (49), is needed to determine frictional solids pressure and solids viscosity. We treat the pressure in the inertial number as pc because both pressures occur at high volume fractions when particles are transitioning between fluid- and solid-like behavior. By combining Eqs. 9 and 10, we propose a critical state solids pressure formulation:
| [11] |
As shown in SI Appendix, we apply a transition factor to ensure continuity in across solids volume fraction, we add the solids pressure of the Schaeffer (42) model at to prevent overpacking of particles, and we combine this formulation of with the equations of Srivastava and Sundaresan (43) to model frictional solids pressure and solids viscosity.
Discrete particle simulations (Fig. 6D) and continuum models using the Srivastava and Sundaresan stress model (43) (Fig. 6E) and the proposed stress model (Fig. 6F) all predict high particle-phase pressure below bubbles, indicating local solidification. This local solidification is key to the formation of the triangular pattern (Fig. 5) as well as its propagation higher in the bed (SI Appendix, Fig. S3) because the solidification prevents bubbles from moving sideways and bubbles from accelerating to coalesce with bubbles above them. Similar behavior has been observed previously in discrete particle simulations with oscillating gas flow (28, 38).
Different continuum models have different curves for the frictional solids pressure versus solids volume fraction (Fig. 6G). We attribute the failure of the Schaeffer model (42) to capture the alternating structured bubbling pattern to the fact that this model only accounts for frictional solids stress above . Thus, this model cannot capture solidifying particle behavior in the intermediate particle packing regime ( < < ) typically observed surrounding bubbles in a fluidized bed. In contrast, the proposed model and that of Srivastava and Sundaresan (43) show a gradually increasing frictional particle stress in this intermediate regime with increasing solids volume fraction, allowing particles to exhibit local solidification below bubbles while having fluid-like behavior above and to the sides of bubbles. We attribute the better quantitative accuracy of the proposed model to that of the Srivastava and Sundaresan (43) model to the subtle differences in the curves in Fig. 6G arising from the specific formulation of the proposed constitutive model. In separate simulations, we shifted the curves of the Srivastava and Sundaresan (43) and Schaeffer (42) models by adjusting the values of and to have significant frictional solids stress begin at a solids volume fraction of 0.6 to more closely match the curve of the proposed model. However, even in these cases, these two prior models could not match the accuracy of the proposed model for producing structured bubbling, further indicating that the accuracy of the proposed model comes from the particular details of its formulation.
Thus, vibrating granular systems with upward gas flow at a resonant frequency can create structured arrays of bubble-like voids rising through the particles, suppressing the mathematical chaos in bubble dynamics observed when the system is not vibrated. Since bubble motion is directly tied to overall gas and particle motion, structuring bubbling effectively structures particle mixing and gas–solid contact. The resonant frequency can be captured by a harmonic oscillator model, and discrete particle simulation demonstrates that structure forms due to rapid, local transitions between solid-like and fluid-like behavior in the grains. These fluid–solid transitions are difficult to capture in continuum models, making the structures formed a testbed for challenging continuum models. We show that existing continuum gas–solid flow models cannot fully capture the bubbling structures observed experimentally, yet our proposed constitutive relationship for frictional solids stress can predict the alternating bubble structure. The bubble structure formed remains largely unchanged across changing system sizes and particle properties, with more robust structure than that created by oscillating gas flow rate, opening opportunities to address key issues in bubbling fluidized beds needed in industry.
Materials and Methods
Fluidized beds were constructed using polymethyl methacrylate (PMMA) sheets with a sintered bronze plate with an average pore size of 15 μm (HENGKO Technology) used to create a uniform gas flow through the distributor at the base of the fluidized bed. The beds were vibrated (Fig. 1) using an electrodynamical shaker (Labworks; ET-140). Particles were fluidized using fully humidified air; the tops of the fluidized beds were open to the air at atmospheric pressure. Gas flow was controlled using a mass flow controller (Alicat; MCP-50 slpm or MCP-250 slpm), and the mass flow controller was used to oscillate gas flow rate for experiments involving oscillating gas flow rate. Spherical particles were used with the density and size specifications given in the figures as quoted by the manufacturer; glass beads (Ceroglass) had a density of 2,500 kg/m3, while ceramic beads (Ceroglass) were used for the higher density particles. The solids volume fraction was measured by filling the system with particles of known density () and measured total weight () to a known total volume () and calculating the solids volume fraction as . Minimum fluidization velocities were determined by slowly decreasing the gas velocity with no vibration from a bubbling state until no bubbles or particle motion were observed. Optical images were obtained using a high-speed camera (AOS Technologies AG; PROMON U750 monochrome camera). Digital image analysis was conducted using MATLAB to quantify correlation coefficient, bubble diameter, separation distance between bubbles, and bubble rise velocity. Bubble diameter was determined by binarizing images into particulate and bubble regions, evaluating the area of bubbles and determining the diameter of a circle with the same area. Horizontal and vertical distance between bubbles were determined, respectively, as the horizontal distance between the center of two horizontally neighboring bubbles formed in the same row and as the vertical distance between the center of two vertically neighboring bubbles, respectively. Bubble rise velocity was determined as the slope of a linear regression through the plot of the vertical center position of a bubble versus time.
Discrete particle gas–solid flow simulations were conducted using CFDEM coupling software (50). Images of particle velocity and volume fraction of these simulations were rendered using MATLAB. Images of force chains from these simulations were rendered using ParaView. Continuum gas–solid simulations were conducted using MFiX software (51). The proposed constitutive model was built into MFiX as a user-defined function. Images of these simulations were rendered using MATLAB.
Supplementary Material
Acknowledgments
K.X. acknowledges support from the China Scholarships Council. A.P. acknowledges support from the Bakhmeteff Fellowship for Fluid Mechanics.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2108647118/-/DCSupplemental.
Data Availability
All study data are included in the article and/or supporting information.
References
- 1.Maladen R. D., Ding Y., Li C., Goldman D. I., Undulatory swimming in sand: Subsurface locomotion of the sandfish lizard. Science 325, 314–318 (2009). [DOI] [PubMed] [Google Scholar]
- 2.Goldfarb D. J., Glasser B. J., Shinbrot T., Shear instabilities in granular flows. Nature 415, 302–305 (2002). [DOI] [PubMed] [Google Scholar]
- 3.Melo F., Umbanhowar P. B., Swinney H. L., Hexagons, kinks, and disorder in oscillated granular layers. Phys. Rev. Lett. 75, 3838–3841 (1995). [DOI] [PubMed] [Google Scholar]
- 4.Melo F., Umbanhowar P., Swinney H. L., Transition to parametric wave patterns in a vertically oscillated granular layer. Phys. Rev. Lett. 72, 172–175 (1994). [DOI] [PubMed] [Google Scholar]
- 5.McLaren C. P., Kovar T. M., Penn A., Müller C. R., Boyce C. M., Gravitational instabilities in binary granular materials. Proc. Natl. Acad. Sci. U.S.A. 116, 9263–9268 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Vinningland J. L., Johnsen Ø., Flekkøy E. G., Toussaint R., Måløy K. J., Granular Rayleigh-Taylor instability: Experiments and simulations. Phys. Rev. Lett. 99, 048001 (2007). [DOI] [PubMed] [Google Scholar]
- 7.Duran J., Rayleigh-Taylor instabilities in thin films of tapped powder. Phys. Rev. Lett. 87, 254301 (2001). [DOI] [PubMed] [Google Scholar]
- 8.Royer J. R., et al., High-speed tracking of rupture and clustering in freely falling granular streams. Nature 459, 1110–1113 (2009). [DOI] [PubMed] [Google Scholar]
- 9.Davidson J. F., Harrison D., Fluidised Particles (Cambridge University Press, 1963). [Google Scholar]
- 10.Pak H. K., Behringer P. R., Bubbling in vertically vibrated granular materials. Nature 371, 231–233 (1994). [Google Scholar]
- 11.Davidson J. F., Harrison D., Guedes de Carvalho J. R. F., Liquidlike behavior of fluidized beds. Annu. Rev. Fluid Mech. 9, 55–86 (1977). [Google Scholar]
- 12.Muzzio F. J., Shinbrot T., Glasser B. J., Powder technology in the pharmaceutical industry: The need to catch up fast. Powder Technol. 124, 1–7 (2002). [Google Scholar]
- 13.Mastellone M. L., Perugini F., Ponte M., Arena U., Fluidized bed pyrolysis of a recycled polyethylene. Polym. Degrad. Stabil. 76, 479–487 (2002). [Google Scholar]
- 14.Abanades J. C., Anthony E. J., Lu D. Y., Salvador C., Alvarez D., Capture of CO2 from combustion gases in a fluidized bed of CaO. AIChE J. 50, 1614–1622 (2004). [Google Scholar]
- 15.Basu P., Combustion of coal in circulating fluidized-bed boilers: A review. Chem. Eng. Sci. 54, 5547–5557 (1999). [Google Scholar]
- 16.Gómez-Barea A., Leckner B., Modeling of biomass gasification in fluidized bed. Pror. Energy Combust. Sci. 36, 444–509 (2010). [Google Scholar]
- 17.Pence D. V., Beasley D. E., Chaos suppression in gas-solid fluidization. Chaos 8, 514–519 (1998). [DOI] [PubMed] [Google Scholar]
- 18.Daw C. S.et al.; van Goor NA , Self-organization and chaos in a fluidized bed. Phys. Rev. Lett. 75, 2308–2311 (1995). [DOI] [PubMed] [Google Scholar]
- 19.Coppens M. O., van Ommen J. R., Structuring chaotic fluidized beds. Chem. Eng. J. 96, 117–124 (2003). [Google Scholar]
- 20.Merrow E. W., Linking R&D to Problems Experienced in Solids Processing (RAND Corporation, 1984). [Google Scholar]
- 21.Francia V., Wu K., Coppens M.-O., Dynamically structured fluidization: Oscillating the gas flow and other opportunities to intensify gas-solid fluidized bed operation. Chem. Eng. Process. 159, 108143 (2021). [Google Scholar]
- 22.Noda K., Mawatari Y., Uchida S., Flow patterns of fine particles in a vibrated fluidized bed under atmospheric or reduced pressure. Powder Technol. 99, 11–14 (1998). [Google Scholar]
- 23.McLaren C. P., Metzger J. P., Boyce C. M., Müller C. R., Reduction in minimum fluidization velocity and minimum bubbling velocity in gas-solid fluidized beds due to vibration. Powder Technol. 382, 566–572 (2021). [Google Scholar]
- 24.Mawatari Y., Tatemoto Y., Noda K., Prediction of minimum fluidization velocity for vibrated fluidized bed. Powder Technol. 131, 66–70 (2003). [Google Scholar]
- 25.Beeckmans J. M., Macwilliam K., Stabilization of a fluidized bed by horizontal vibrations. Powder Technol. 45, 177–181 (1986). [Google Scholar]
- 26.Zhao Y., et al., Industrial application of a modularized dry-coal-beneficiation technique based on a novel air dense medium fluidized bed. Int. J. Coal Prep. Util. 37, 44–57 (2017). [Google Scholar]
- 27.Lehmann S. E., et al., Fluidization characteristics of cohesive powders in vibrated fluidized bed drying at low vibration frequencies. Powder Technol. 357, 54–63 (2019). [Google Scholar]
- 28.Wu K., Francia V., Coppens M.-O., Dynamic viscoplastic granular flows: A persistent challenge in gas-solid fluidization. Powder Technol. 365, 172–185 (2020). [Google Scholar]
- 29.Pearson K., Henrici O. M. F. E., VII. Mathematical contributions to the theory of evolution.—III. Regression, heredity, and panmixia. Philos. Trans. R. Soc. Lond. Ser. Contain. Pap. Math. Phys. Character 187, 253–318 (1896). [Google Scholar]
- 30.Hiby J. W., “Periodic phenomena connected with gas–solid fluidization” in Proceedings of the International Symposium on Fluidization (Netherlands University Press, 1967), pp. 99–112. [Google Scholar]
- 31.Verloop J., Heertjes P. M., Periodic pressure fluctuations in fluidized beds. Chem. Eng. Sci. 29, 1035–1042 (1974). [Google Scholar]
- 32.de Martín L., Ottevanger C., van Ommen J. R., Coppens M.-O., Universal stability curve for pattern formation in pulsed gas-solid fluidized beds of sandlike particles. Phys. Rev. Fluids 3, 034303 (2018). [Google Scholar]
- 33.Clift R., Grace J. R., “Continuous bubbling and slugging” in Fluidization, Davidson J. F., Clift R., Harrison D., Eds. (Academic Press, ed. 2, 1985). [Google Scholar]
- 34.Davies R. M., Taylor G., The mechanics of large bubbles rising through extended liquids and through liquids in tubes. Proc. R. Soc. Lond. Ser. Math. Phys. Sci. 200, 375–390 (1950). [Google Scholar]
- 35.Tsuji Y., Kawaguchi T., Tanaka T., Discrete particle simulation of two-dimensional fluidized bed. Powder Technol. 77, 79–87 (1993). [Google Scholar]
- 36.Cundall P. A., Strack O. D. L., A discrete numerical model for granular assemblies. Geotechnique 29, 47–65 (1979). [Google Scholar]
- 37.Ding J., Gidaspow D., A bubbling fluidization model using kinetic theory of granular flow. AIChE J. 36, 523–538 (1990). [Google Scholar]
- 38.Wu K., de Martín L., Coppens M.-O., Pattern formation in pulsed gas-solid fluidized beds—The role of granular solid mechanics. Chem. Eng. J. 329, 4–14 (2017). [Google Scholar]
- 39.Ding Z., Tiwari S. S., Tyagi M., Nandakumar K., Computational fluid dynamic simulations of regular bubble patterns in pulsed fluidized beds using a two-fluid model. Can. J. Chem. Eng., in press. [Google Scholar]
- 40.Wu K., de Martín L., Mazzei L., Coppens M.-O., Pattern formation in fluidized beds as a tool for model validation: A two-fluid model based study. Powder Technol. 295, 35–42 (2016). [Google Scholar]
- 41.Bakshi A., Altantzis C., Bershanska A., Stark A. K., Ghoniem A. F., On the limitations of 2D CFD for thin-rectangular fluidized bed simulations. Powder Technol. 332, 114–119 (2018). [Google Scholar]
- 42.Syamlal M., Rogers W., O’Brien T. J., “MFIX documentation theory guide” (Technical Report, DOE Technical Note, DOE, 1993).
- 43.Srivastava A., Sundaresan S., Analysis of a frictional–kinetic model for gas–particle flow. Powder Technol. 129, 72–85 (2003). [Google Scholar]
- 44.Schaeffer D. G., Instability in the evolution equations describing incompressible granular flow. J. Differ. Equ. 66, 19–50 (1987). [Google Scholar]
- 45.Johnson P. C., Jackson R., Frictional–collisional constitutive relations for granular materials, with application to plane shearing. J. Fluid Mech. 176, 67–93 (1987). [Google Scholar]
- 46.Forterre Y., Pouliquen O., Flows of dense granular media. Annu. Rev. Fluid Mech. 40, 1–24 (2008). [Google Scholar]
- 47.Pouliquen O., Cassar C., Jop P., Forterre Y., Nicolas M., Flow of dense granular material: Towards simple constitutive laws. J. Stat. Mech. Theory Exp. 2006, P07020 (2006). [Google Scholar]
- 48.da Cruz F., Emam S., Prochnow M., Roux J. N., Chevoir F., Rheophysics of dense granular materials: Discrete simulation of plane shear flows. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 72, 021309 (2005). [DOI] [PubMed] [Google Scholar]
- 49.Dsouza P. V., Nott P. R., A non-local constitutive model for slow granular flow that incorporates dilatancy. J. Fluid Mech. 888, R3 (2020). [Google Scholar]
- 50.Kloss C., Goniva C., Hager A., Amberger S., Pirker S., Models, algorithms and validation for opensource DEM and CFD–DEM. Prog. Comput. Fluid Dyn. Int. J. 12, 140–152 (2012). [Google Scholar]
- 51.Musser J. M., Carney J. E., “Theoretical review of the MFIX fluid and two-fluid models” (Technical Report, DOE/NETL, 2020).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All study data are included in the article and/or supporting information.