Mathematical analysis for the effect of voluntary vaccination on the propagation of Corona virus pandemic

Abstract

In this manuscript, a new nonlinear model for the rapidly spreading Corona virus disease (COVID-19) is developed. We incorporate an additional class of vaccinated humans which ascertains the impact of vaccination strategy for susceptible humans. A complete mathematical analysis of this model is conducted to predict the dynamics of Corona virus in the population. The analysis proves the effectiveness of vaccination strategy employed and helps public health services to control or to reduce the burden of corona virus pandemic. We first prove the existence and uniqueness and then boundedness and positivity of solutions. Threshold parameter for the vaccination model is computed analytically. Stability of the proposed model at fixed points is investigated analytically with the help of threshold parameter to examine epidemiological relevance of the pandemic. We apply LaSalle’s invariance principle from the theory of Lyapunov function to prove the global stability of both the equilibria. Two well known numerical techniques namely Runge–Kutta method of order 4 (RK4), and the Non-Standard Finite Difference (NSFD) method are employed to solve the system of ODE’s and to validate our obtained theoretical results. For different coverage levels of voluntary vaccination, we explored a complete quantitative analysis of the model. To draw our conclusions, the effect of proposed vaccination on threshold parameter is studied numerically. It is claimed that Corona virus disease could be eradicated faster if a human community selfishly adopts mandatory vaccination measures at various coverage levels with proper awareness. Finally, we have executed the joint variability of all classes to understand the effect of vaccination strategy on a disease dynamics.

Introduction

Corona virus disease (COVID-19) is a severe pandemic with an extremely high fatality rate caused by an infectious respiratory virus called SARS-CoV-2. The virus spreads uniformly among individuals and affecting people worldwide through direct and indirect physical contact. The first and overall third outbreak of novel Corona virus disease was experienced at the end of December 2019 in the Wuhan City of China. The outbreak spreads rapidly in different parts of China and then worldwide in almost $223$ countries of Asia, Australia, America and Europe [1]. World Health Organization (WHO) reported that there are more than $232,636,622$ confirmed cases with $4,762,089$ deaths by September $29$, $2021$. It is remarkable that WHO reported $18,325,098$ new infected cases including 90,529 serious or critical cases to date while the number of confirmed cases are continuing to increase. However, almost $210,951,891$ people have been recovered. A total of $6,136,962,861$ vaccine doses have been administered by $29$ September, $2021$. Currently, the number of highest positive cases encountered in United States of America followed by India, Brazil and Spain respectively.

The current evidence suggests that the main source of Corona virus transmission among individuals are the respiratory droplets through sneezing, coughing and spitting of an infected person [2]. During the treatment of Corona patients, health care staff can also get infected. Incubation period for the Corona virus disease normally varies from $2$ to $14$ and on average $5$-$6$ days. Every individual can get Corona infection at any age and time instant and become seriously ill or die. It is observed that people $60$ years and older and people who develop severe diseases like heart disease, obesity or cancer, diabetes or lung disease are at higher risk of getting seriously sick with Corona virus and can be infectious for longer. People with a variety of symptoms like fever, dry cough, sneezing, red eyes, shortness of breath, muscle pain, fatigue, severe headache, new loss of smell or taste, persistent pain in the chest, sore throat, runny nose, sleep disorders, vomiting, and diarrhea, may have Corona virus disease [3]. It may create to intense acute multi-organ failure, respiratory torture progression, blood clots, and septic shock, among other conditions [4], [5]. Without needing hospital treatment, about 80% among the people who create these indications may recover from the viral infirmity. About 15% turn critically ill and want oxygen. About 5% turn seriously sick and need medical care. They may face a rapid progression to death due to their ill condition. The virus may spread on a large scale if the pandemic is not restricted. It will threaten the entire human population. Therefore, to take care of infected patients, it is inevitable to take comprehensive preventive measures.

Public health experts worldwide are continuously learning and monitoring the dynamics of novel Corona virus these days. They always look for multiple solutions to control the pandemic. The first important step is to develop appropriate community engagement, awareness campaign and protection measures among individuals. For instance, appropriate careful steps, for example, wearing proper clothes and gloves, and washing hands subsequent to visiting the patients ought to be dealt with. To protect yourself and other people, we should wear a surgical mask that especially covers our mouth and nose. Keep a distance of at least $6$ feet from other peoples who do not live with you, especially in crowded areas. Keep away from indoor spaces however much as could be expected, especially ones that are not all around ventilated. Clean up your hands with soap and water for $20$ s. This trial should be repeated throughout the day. Use hand sanitizer with basically 60% liquor content. Everyone takes these actions to help slow down COVID-19. The other rigorous measures are the use of vaccination, public quarantine facilities, lock down, isolation or treatment of infected humans. This also includes raising the awareness like public health education, laboratory testing, risk communication, start of antiviral drugs, designed special hospitals and health screening at boarders. It is remarkable that antibiotics do not work against COVID-19. There is no licensed medicine which is used to cure pandemic.

The best method to control the pandemic is the prospective vaccination of human population. The vaccine is a safe and effective way to produce an immune response in the human body without causing illness. Execution of various vaccination strategies in human communities is a significant public health measure, generally been utilized to control the spread of all communicable infections. Some genuine endeavors to acquire a vaccine for COVID-19 sickness have been made after the $2019$ Corona infection episode in China. No less than seven unique vaccines have been carried out in different countries by $18$ February $2021$. Physically weak populations from all nations are the most noteworthy need for vaccination. Throughout $2021$, more potential vaccines for Corona virus disease will become available. Therefore, recommendations of vaccination strategies will expand to include more people in the whole world.

To assess the standard and safety of vaccines is the highest priority of World Health Organization (WHO). To check the efficacy, WHO works closely with researchers around the world to ensure that global standards and norms are developed and implemented during the vaccine developing process. To control the spread of epidemic diseases, numerous scientists are drawn to create different models [6], [7], [8], [9], [10] dealing with vaccination strategies while other people have analyzed stochastic delay differential models for COVID-19 pandemic [11], [12]. Recently, a group of researchers [13], [14], [15], [16] studied the stability pattern of Ebola virus epidemic models by introducing vaccination strategies in a host population. A several number of articles [17], [18], [19], [20], [21], [22] have been published recently on the efficacy of implemented vaccines. According to our little knowledge, a least number of research articles [17], [23] have been published to understand the effect of voluntary vaccination on the propagation of Corona virus epidemic. No one did a complete mathematical analysis of Corona pandemic through a vaccination model. We will move in this direction.

In this manuscript, an SVEIR pandemic model is developed to predict class wise transmission dynamics of Corona infection in a population. Mathematical modeling of COVID-19 shall work confidentially to predict and comprehend how virus spread. These predictions will likewise assist with seeing how the Corona contamination might diminish or increment later on. We incorporate a class of those susceptible humans who have vaccinated through a proper vaccination programme. For this study, we assumed that any universally available vaccine is not 100% effective, means that the people will get tainted during vaccination period and can be sound toward the finish of this period. We have assessed the effect of vaccine programme on human community with the assistance of proposed model. Using some known techniques, we have presented a complete mathematical analysis of the proposed Corona model with an aim of controlling the pandemic. Additionally, we shall study the correlation between vaccinated class and the remaining classes.

In Chaos theory, an important area of research is to study various mathematical models with different descriptions and requirements for their numerical stability. Recently, the stability of various epidemic models with respect to the involved parameters was obtained [13], [24], [25]. Some appropriate reliable numerical techniques [26], [27], [28], [29], [30], [31], [32], [33], [34], [35], [36], [37], [38], [39], [40] to solve the governing equations were employed. The dynamics of epidemic diseases was examined with the help of numerical simulations. We tend to expect that our projected model also contains all vital self-propelling properties, for example, well-posedness of the problem and, boundedness and positivity of solutions. It is ascertained that most of the traditional standard methods including Euler, RK schemes sometimes become unbounded divergent when implemented to a system. Implementation of these numerical methods could cause major problems such as generating oscillations, bifurcations, chaos, negative solutions, or solutions converging to false equilibrium states as time grid size increased [13], [24], [25], [28], [29]. Subsequently, the best approach to solve our model herein is to develop NSFD scheme [30]. We have demonstrated the dynamic consistency of the developed NSFD scheme alongside a few examinations with RK4 scheme by performing detailed mathematical investigation of the given model.

The numerical examination highlights the impact of vaccination strategy on the dynamics of Corona virus disease at different levels of proposed vaccination. The effect of vaccine on susceptible and exposed class is executed reveals that number of susceptible and the exposed humans are decreased consistently with the increase in levels of vaccination. A rapid regress in the population of infected humans is observed when vaccination rates are high. It is noticed that infectivity will approach to zero as time goes to infinity. However, a quick increment in the number of recovered individuals is observed whenever the levels of vaccination are continuously increased. An addition in the number of recovered individuals and the decrease in the population of infected individuals essentially diminish the danger of Corona infection sickness. As a result, the host population will become healthy if the coverage level and effectiveness of implemented vaccination strategy is high. Furthermore, it has been observed that threshold parameter is being affected by the vaccination programme. We have discussed statistically the joint variability among all populations.

The paper is organized as follows: The derivation of the compartmental model is outlined in Section “Derivation of Corona model”. In Section “Theoretical analysis”, the existence of a unique global solution for the derived model is investigated. The positivity and boundedness of solutions is proved. Two main equilibrium points of the underlying model are obtained and the threshold parameter ${\mathcal{R}}_0$ is computed analytically. Stability of the SVEIR model is analyzed analytically. Numerical stability of the model to confirm the main theoretical results along with graphical illustrations and necessary discussions is performed in Section “Numerical simulations”. We discuss the computational advantages of NSFD scheme by comparing it with RK4 method. We conclude the present work in Section “Conclusions”.

Derivation of Corona model

There is a series of various mathematical models in the existing literature [23], [24], [41], [42], [43], [44], [45], [46], [47], [48] with different assumptions depending on the propagation mechanism of Corona virus disease. These models assist the public health planners and policy makers in lots of ways. In this section, we have developed a new real world SVEIR COVID-19 pandemic model by incorporating a class of vaccinated human. For the proposed model, all of our efforts will be to study the effect of proposed vaccination on the dynamical behavior of Corona virus disease. The variables used to model out the transmission dynamics of Corona pandemic among the individuals are given below:

We divide the total population $N\left(t\right)$ at time $t$ into five disjoint classes. The first class includes number of susceptible humans which is denoted by $S\left(t\right)$. Note that there will be a limited supply of Corona virus vaccine for the host population for a while. Hence, not everyone will be able to be vaccinated right away. The second class denoted by $V\left(t\right)$ gives the number of susceptible individuals who have been vaccinated at time instant $t$. The third class which represents the number of exposed humans at time instant $t$ is denoted by $E\left(t\right)$. The fourth epidemic class denoted by $I\left(t\right)$ characterizes all infected people who are able to spread the infection further. Ultimately, people who have developed complete immunity from the COVID-19 are going to the fifth class of recovered humans, denoted by $R\left(t\right)$. We assume that the recovered people will stay in the class $R\left(t\right)$ throughout their life. Thus the variables for the Corona model (1) are $S$, $V$, $E$, $I$ and $R$ respectively. All these variables are assumed to be real valued continuously differentiable functions defined on the interval $[0,1)$ of $t$ values.

Fig. 1 describes a graphical representation the flow pattern of Corona virus in the host population. The physical relevance and description of the employed parameters is provided in Table 1.

Fig. 1.

A schematic of the Corona virus disease in a compartmental model (1).

The following SVEIR mathematical model represents the flow pattern of Corona virus in a community:

$$\frac{dS}{dt}=\Omega -{\alpha }_{1}SE-({\alpha }_3+\mu )S,$$ (1a)

$$\frac{dV}{dt}={\alpha }_{3}S-({\alpha }_6+\mu )V-{\alpha }_{4}VE-{\alpha }_{5}VI,$$ (1b)

$$\frac{dE}{dt}={\alpha }_{4}VE+{\alpha }_{1}SE-{\alpha }_{2}EI-(k+\mu )E,$$ (1c)

$$\frac{dI}{dt}={\alpha }_{5}VI+{\alpha }_{2}EI-(d+r+\mu )I,$$ (1d)

$$\frac{dR}{dt}={\alpha }_{6}V+rI+kE-\mu R,$$ (1e)

We have assumed that all the initial conditions and involved parameters of the system are non-negative.

Table 1.

Representation of involved parameters with their estimated values.

Symbol	Description	Value	Source
$\Omega$	Recruitment rate of humans into susceptible class	0.5000	[24]
$\mu$	Natural death rate of each class	0.5000	[24]
$d$	Death rate of infected class due to corona virus disease	0.0047876	[24]
$k$	Rate of transfer of exposed humans into recovered class	0.00398	[24]
$r$	Rate of transfer of infected humans into recovered class	0.09871	[24]
${\alpha }_1$	Rate of transfer of susceptible humans into exposed class	0.005	[24]
${\alpha }_2$	Rate of transfer of exposed humans into infected class	0.085432	Assumed
${\alpha }_3$	Transition of susceptible humans into vaccinated class	0.6000	Assumed
${\alpha }_4$	Rate of transfer of vaccinated humans into exposed class	0.2807	Assumed
${\alpha }_5$	Rate of transfer of vaccinated humans into infected class	0.3813	Assumed
${\alpha }_6$	Rate of transfer of vaccinated humans into recovered class	0.9092	Assumed

Theoretical analysis

In this section, we prove some important properties such as well-posedness of the problem (1) followed by the positivity and boundedness of all solutions for $t\ge 0$. Threshold parameter and the equilibrium points for the prescribed model along with their stability analysis have been presented. All these computations are done in the following steps.

Existence of a unique solution

In a compact form, the system (1) can be put into the form

$$\frac{d\mathbf{x}}{dt}=F\left(\mathbf{x}\right),\mathbf{x}\left(\mathbf{0}\right)={\mathbf{x}}_0,$$ (2)

where $\mathbf{x}$ is a column vector of state variables in ${\mathbb{R}}^5$ and defines a mapping from $[0,+\infty )$ to ${\mathbb{R}}^5$. However, $F\left(\mathbf{x}\right)={(F_1\left(\mathbf{x}\right),F_2\left(\mathbf{x}\right),F_3\left(\mathbf{x}\right),F_4\left(\mathbf{x}\right),F_5\left(\mathbf{x}\right))}^T\in {\mathbb{R}}^5$, is a vector valued function from ${\mathbb{R}}^5$ to ${\mathbb{R}}^5$ with components

$$F_1\left(\mathbf{x}\right)=\Omega -{\alpha }_{1}SE-({\alpha }_3+\mu )S,$$

$$F_2\left(\mathbf{x}\right)={\alpha }_{3}S-({\alpha }_6+\mu )V-{\alpha }_{4}VE-{\alpha }_{5}VI,$$

$$F_3\left(\mathbf{x}\right)={\alpha }_{1}SE+{\alpha }_{4}VE-{\alpha }_{2}EI-(k+\mu )E,$$

$$F_4\left(\mathbf{x}\right)={\alpha }_{5}VI+{\alpha }_{2}EI-(d+r+\mu )I,$$

$$F_5\left(\mathbf{x}\right)={\alpha }_{6}V+rI+kE-\mu R,$$

The function $F$ in (2) is Lipschitz continuous in $\mathbf{x}$ [49]. Hence by existence and uniqueness theorem [50], the solution of problem (2) is unique. This solution will be realistic and epidemiologically meaningful if it is nonnegative and bounded. We prove these properties in the following subsections.

Positivity of solutions

In this subsection, we have proved that all the state variables are non-negative for any $t>0$, that is the solution will remain positive forever corresponding to any non-negative initial data in ${\mathbb{R}}_{+}^5$. This property is required to show our model physically realizable.

Theorem 1

The solutions of system (1) will remain positive forever with any positive initial costs.

Proof

First equation of the model (1) is rearranged to give,

$$\frac{dS}{dt}=\Omega -H\left(t\right)S\left(t\right).$$ (3)

where

$$H\left(t\right)=({\alpha }_3+\mu )+{\alpha }_{1}E\left(t\right).$$

On multiplying $exp\left({\int }_0^{t}H\left(s\right)ds\right)>0$ to both sides of  Eq. (3), we get

$$exp\left({\int }_0^{t}H\left(s\right)ds\right)\ast \frac{dS}{dt}=\left[\Omega -H\left(t\right)S\left(t\right)\right]\ast exp\left({\int }_0^{t}H\left(s\right)ds\right),$$

which further implies that

$$\frac{d}{dt}\left[S\left(t\right)\ast exp\left({\int }_0^{t}H\left(s\right)ds\right)\right]=\Omega \ast exp\left({\int }_0^{t}H\left(s\right)ds\right).$$

Integration of both sides with respect to $s$ from $0$ to $t$ will leads to

$$S\left(t\right)\ast exp\left({\int }_0^{t}H\left(s\right)ds\right)-S\left(0\right)=\Omega \ast {\int }_0^t\left[exp\left({\int }_0^{w}H\left(s\right)ds\right)\right]dw.$$ (4)

Multiplication of both sides of Eq. (4) with $exp\left(-{\int }_0^{t}H\left(s\right)ds\right)$ gives

$$S\left(t\right)=S\left(0\right)\ast exp\left(-{\int }_0^{t}H\left(s\right)ds\right)+\Omega \ast exp\left(-{\int }_0^{t}H\left(s\right)ds\right)\ast {\int }_0^t\left[exp\left({\int }_0^{w}H\left(s\right)ds\right)\right]dw\ge 0.$$

Implies that the solution $S\left(t\right)$ is positive for all $t>0$. Similarly, it can be shown that $V\left(t\right)\ge 0$, $E\left(t\right)\ge 0$, $I\left(t\right)\ge 0$, $R\left(t\right)\ge 0$ for all $t>0$ corresponding to any non-negative initial data. Thus the solution $(S,V,E,I,R)$ in ${\mathbb{R}}_{+}^5$ remain positive forever.  □

Invariant region

In this subsection, we determine the boundary of solutions of the nonlinear system (1) with an initial data $S\ge 0$, $V\ge 0$, $E\ge 0$, $I\ge 0$, $R\ge 0$. Our main target is to show that the obtained feasible region in ${\mathbb{R}}_{+}^5$ is positively invariant for the proposed model (1).

Theorem 2

The solutions of system (1) given in Theorem 1 are bounded.

Proof

Addition of all the five equations in model (1) gives

$$\frac{dN}{dt}=\Omega -\mu S-\mu V-\mu E-(d+\mu )I-{\mu }_{6}R\le \Omega -\mu N,$$

provided that $\mu <d+\mu$, where $N\left(t\right)=S\left(t\right)+V\left(t\right)+E\left(t\right)+I\left(t\right)+R\left(t\right)$, $t\ge 0$, is the total population under consideration. It follows that $\frac{dN}{dt}\le 0$ whenever $N\left(t\right)\ge \frac{\Omega }{\mu }$. By using Gronwall’s inequality [51], it can be shown that

$$N\left(t\right)=\frac{\Omega }{\mu }\left[1-exp(-\mu t)\right]+N\left(0\right)exp(-\mu t),$$

where $N\left(0\right)$ is the initial population size. In particular, $N\left(t\right)\ge \frac{\Omega }{\mu }$ whenever $N\left(0\right)\ge \frac{\Omega }{\mu }$. Thus $N$ and all other variables of the model (1) are bounded in a region

$$\Pi =\left\{(S,V,E,I,R)\in {\mathbb{R}}_{+}^5:0\le N\left(t\right)\le \frac{\Omega }{\mu };S,V,E,I,R\ge 0\right\}.$$ (5)

The solution remains $\mathbf{x}=0$ for all $t>0$ if ${\mathbf{x}}_0=0$. Moreover, for any nonnegative set of initial conditions in $\Pi$, every solution of model (1) in ${\mathbb{R}}_{+}^5$ approach asymptotically in finite time $t$, enters and remains in the region $\Pi$. Implies the set $\Pi$ is closed and positively invariant for our system [1]. Whenever $N\left(0\right)>\frac{\Omega }{\mu }$, either $N\left(t\right)$ approaches $\frac{\Omega }{\mu }$ asymptotically or the solution enters $\Pi$. Hence the region $\Pi$ attracts all solutions in ${\mathbb{R}}_{+}^5$. Hence, the problem (2) or equivalently (1) is mathematically well-posed.

Equilibrium points

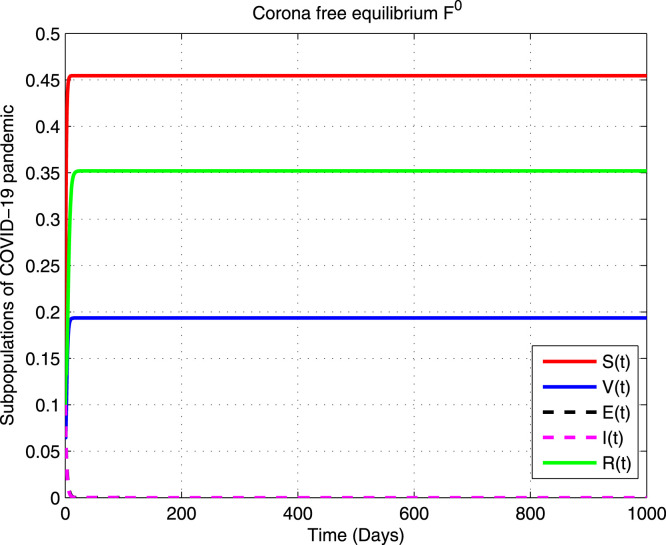
A unique non-negative Corona free equilibrium for the model (1) exists at the point

$$F^0=(S^0,V^0,E^0,I^0,R^0)=\left(\frac{\Omega }{{\alpha }_3+\mu },\frac{\Omega {\alpha }_3}{({\alpha }_6+\mu )({\alpha }_3+\mu )},0,0,\frac{\Omega {\alpha }_3{\alpha }_6}{\mu ({\alpha }_6+\mu )({\alpha }_3+\mu )}\right),$$

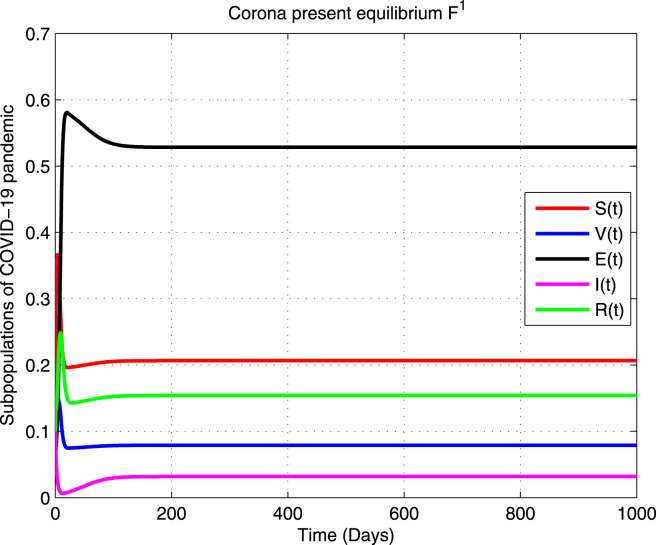
and a unique non-negative Corona present equilibrium exists at the point given by

$$F^1=(S^1,V^1,E^1,I^1,R^1),$$

in the epidemiological region $\Pi$, where

$$S^1=\frac{\Omega }{\pi +{\alpha }_3+\mu }>0,$$

$$V^1=\frac{1}{{\alpha }_4}\left[(k+\mu )+{\alpha }_2{I}^1-\frac{\Omega {\alpha }_1}{\pi +{\alpha }_3+\mu }\right]>0,$$

$$E^1=\frac{1}{{\alpha }_2}(d+r+\mu )-\frac{{\alpha }_5}{{\alpha }_4}\left[\frac{1}{{\alpha }_2}(k+\mu )+I^1\right]+\frac{\Omega {\alpha }_1{\alpha }_5}{{\alpha }_2{\alpha }_4(\pi +{\alpha }_3+\mu )}>0,$$

$$I^1=\frac{C_1(\pi +{\alpha }_3+\mu )-{\Omega }^2{\alpha }_1^2{\alpha }_5+C_2{(\pi +{\alpha }_3+\mu )}^2}{{\alpha }_2(\pi +{\alpha }_3+\mu )C_3}>0,$$

$$R^1=\left(\frac{{\alpha }_2{\alpha }_6+r{\alpha }_4-k{\alpha }_5}{\mu {\alpha }_4}\right)I^1+C_4-C_5>0,$$

along with

$$\pi ={\alpha }_1{E}^1,$$

$$C_1=\Omega \left[2{\alpha }_1{\alpha }_5(k+\mu )-{\alpha }_2{\alpha }_3{\alpha }_4-{\alpha }_1{\alpha }_4(d+r+\mu )\right],$$

$$C_2=(k+\mu )\left[{\alpha }_2({\alpha }_6+\mu )+{\alpha }_4(d+r+\mu )-{\alpha }_5(k+\mu )\right]-\Omega {\alpha }_1{\alpha }_2({\alpha }_6+\mu ),$$

$$C_3={\alpha }_2{(\pi +{\alpha }_3+\mu )}^2\left[{\alpha }_5(k+\mu )-{\alpha }_2({\alpha }_6+\mu )-{\alpha }_4(d+r+\mu )\right]-\Omega {\alpha }_1{\alpha }_2{\alpha }_5(\pi +{\alpha }_3+\mu ),$$

$$C_4=\frac{{\alpha }_6(k+\mu )}{\mu {\alpha }_4}+\frac{k(d+r+\mu )}{\mu {\alpha }_2}+\frac{\Omega k{\alpha }_1{\alpha }_5}{\mu {\alpha }_2{\alpha }_4(\pi +{\alpha }_3+\mu )},$$

$$C_5=\frac{\Omega {\alpha }_1{\alpha }_6}{\mu {\alpha }_4(\pi +{\alpha }_3+\mu )}+\frac{k{\alpha }_5(k+\mu )}{\mu {\alpha }_2{\alpha }_4}.$$

Threshold parameter ${\mathcal{R}}_0$

We can determine the dynamics of mathematical models by computing the value of threshold parameter, usually denoted by ${\mathcal{R}}_0$. The spread of any infectious disease begins when an infected person enters into a class of completely susceptible humans. Therefore, ${\mathcal{R}}_0$ gives the total number of new infections produced by an infected human at $t\ge 0$. It works confidentially to predict the dynamical behavior of a model. We can study the future spread of any disease in details by computing this number. Therefore, for the model (1), the value of ${\mathcal{R}}_0$ is computed by using the standard next generation matrix approach [13], [14], [25], [52].

We assume $\xi ={(E,I,V,S,R)}^T$ and the system (1) becomes

$$\frac{d\xi }{dt}=\mathcal{F}\left(\xi \right)-\mathcal{G}\left(\xi \right)$$

where

$$\mathcal{F}\left(\xi \right)=\left[\begin{array}{c}\hfill {\alpha }_{4}VE+{\alpha }_{1}SE-{\alpha }_{2}EI\hfill \\ \hfill {\alpha }_{5}VI+{\alpha }_{2}EI\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right]=\left[\begin{array}{c}\hfill {\mathcal{F}}_1\hfill \\ \hfill {\mathcal{F}}_2\hfill \\ \hfill {\mathcal{F}}_3\hfill \\ \hfill {\mathcal{F}}_4\hfill \\ \hfill {\mathcal{F}}_5\hfill \end{array}\right]$$

and

$$\mathcal{G}\left(\xi \right)=\left[\begin{array}{c}\hfill (k+\mu )E\hfill \\ \hfill (d+r+\mu )I\hfill \\ \hfill -{\alpha }_{3}S+({\alpha }_6+\mu )V+{\alpha }_{4}VE+{\alpha }_{5}VI\hfill \\ \hfill -\Omega +({\alpha }_3+\mu )S+{\alpha }_{1}SE\hfill \\ \hfill -{\alpha }_{6}V-rI-kE+{\mu }_{6}R\hfill \end{array}\right]=\left[\begin{array}{c}\hfill {\mathcal{G}}_1\hfill \\ \hfill {\mathcal{G}}_2\hfill \\ \hfill {\mathcal{G}}_3\hfill \\ \hfill {\mathcal{G}}_4\hfill \\ \hfill {\mathcal{G}}_5\hfill \end{array}\right]$$

We only focus on the dynamics of classes $E$ and $I$, since they are contributing to new infections. The matrix $\mathfrak{F}$ representing the appearance rate of new cases is given by

$$\mathfrak{F}=\left[\begin{array}{c}\hfill {\alpha }_{4}VE+{\alpha }_{1}SE-{\alpha }_{2}EI\hfill \\ \hfill \hfill \\ \hfill {\alpha }_{5}VI+{\alpha }_{2}EI\hfill \end{array}\right],$$

whereas the matrix $\mathfrak{G}$ representing the transition rate of existing or transported cases is computed as follows:

$$\mathfrak{G}=\left[\begin{array}{c}\hfill (k+\mu )E\hfill \\ \hfill \hfill \\ \hfill (d+r+\mu )I\hfill \end{array}\right].$$

The jacobian of the matrices $\mathfrak{F}$ and $\mathfrak{G}$ evaluated at point $F^0$ are

$$\overline{\mathfrak{F}}=\left[\begin{array}{cc}\hfill \frac{\partial {\mathcal{F}}_1}{\partial E}\hfill & \hfill \frac{\partial {\mathcal{F}}_1}{\partial I}\hfill \\ \hfill \hfill \\ \hfill \frac{\partial {\mathcal{F}}_2}{\partial E}\hfill & \hfill \frac{\partial {\mathcal{F}}_2}{\partial I}\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill \frac{\Omega ({\alpha }_1({\alpha }_6+\mu )+{\alpha }_3{\alpha }_4)}{({\alpha }_6+\mu )({\alpha }_3+\mu )}\hfill & \hfill 0\hfill \\ \hfill \hfill \\ \hfill 0\hfill & \hfill \frac{\Omega {\alpha }_3{\alpha }_5}{({\alpha }_6+\mu )({\alpha }_3+\mu )}\hfill \end{array}\right],$$

$$\overline{\mathfrak{G}}=\left[\begin{array}{cc}\hfill \frac{\partial {\mathcal{G}}_1}{\partial E}\hfill & \hfill \frac{\partial {\mathcal{G}}_1}{\partial I}\hfill \\ \hfill \hfill \\ \hfill \frac{\partial {\mathcal{G}}_2}{\partial E}\hfill & \hfill \frac{\partial {\mathcal{G}}_2}{\partial I}\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill k+\mu \hfill & \hfill 0\hfill \\ \hfill \hfill \\ \hfill 0\hfill & \hfill d+r+\mu \hfill \end{array}\right].$$

Thus the value of threshold parameter, that is

$${\mathcal{R}}_0=\frac{\Omega \left[{\alpha }_1({\alpha }_6+\mu )+{\alpha }_3{\alpha }_4\right]}{({\alpha }_5+\mu )({\alpha }_3+\mu )(k+\mu )}$$

is the spectral radius of the product matrix $\overline{\mathfrak{F}}{\overline{\mathfrak{G}}}^{-1}$.

Stability analysis

In this subsection, we analyze the stability of the model (1) at both the steady states with the help of ${\mathcal{R}}_0$ theoretically. Theorem 3, Theorem 5 are dealing with equilibrium point $F^0$ whereas Theorem 4, Theorem 6 describe the nature of $F^1$. Global stability of the given model is established by employing LaSalle’s invariant principle [13], [24], [25], [53], [54].

Local behavior of the vaccination model

Theorem 3

A Corona free equilibrium $F^0$ is locally asymptotically stable (LAS) when ${\mathcal{R}}_0<1$ . If ${\mathcal{R}}_0>1$ , it is unstable.

Proof

For system (1), the Jacobian $J$ at $F^0$ can be written as

$$J\left(F^0\right)=\left(\begin{array}{ccccc}\hfill -({\alpha }_3+\mu )\hfill & \hfill 0\hfill & \hfill -\frac{\Omega {\alpha }_1}{{\alpha }_3+\mu }\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \hfill \\ \hfill 0\hfill & \hfill -({\alpha }_6+\mu )\hfill & \hfill Q\hfill & \hfill -\frac{\Omega {\alpha }_3{\alpha }_5}{({\alpha }_6+\mu )({\alpha }_3+\mu )}\hfill & \hfill 0\hfill \\ \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill (k+\mu )({\mathcal{R}}_0-1)\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{\Omega {\alpha }_3{\alpha }_5}{({\alpha }_6+\mu )({\alpha }_3+\mu )}-(d+r+\mu )\hfill & \hfill 0\hfill \\ \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -\mu \hfill \end{array}\right),$$

where

$$Q=-\frac{\Omega {\alpha }_3\left[{\alpha }_4({\alpha }_3+\mu )+{\alpha }_1({\alpha }_6+\mu )\right]}{({\alpha }_6+\mu ){({\alpha }_3+\mu )}^2}.$$

Jacobian matrix $J\left(F^0\right)$ has the following eigenvalues:

$${\lambda }_1=-({\alpha }_3+\mu ),$$ (6)

$${\lambda }_2=-({\alpha }_6+\mu ),$$ (7)

$${\lambda }_3=(k+\mu )({\mathcal{R}}_0-1),$$ (8)

$${\lambda }_4=\frac{\Omega {\alpha }_3{\alpha }_5}{({\alpha }_6+\mu )({\alpha }_3+\mu )}-(d+r+\mu ),$$ (9)

$${\lambda }_5=-\mu .$$ (10)

It is to be noted that the parameters in the proposed model are assumed to be positive. Therefore, the eigenvalues ${\lambda }_1$, ${\lambda }_2$ and ${\lambda }_5$ are negative. Indeed the quantities ${\alpha }_3+\mu$, ${\alpha }_6+\mu$, $\mu$ are strictly positive. Now consider Eq. (8), that is ${\lambda }_3=(k+\mu )({\mathcal{R}}_0-1)$. Hence ${\lambda }_3<0\iff {\mathcal{R}}_0<1$. From Eq. (9), ${\lambda }_4<0$ if and only if

$$\Omega {\alpha }_3{\alpha }_5<(d+r+\mu )({\alpha }_6+\mu )({\alpha }_3+\mu ),$$

which is obviously true. Thus all the eigenvalues of $J\left(F^0\right)$ when ${\mathcal{R}}_0$ is less than unity, are negative and hence $F^0$ is locally asymptotically stable. Once the dynamical system is stable at disease free point $F^0$, then there will be no pandemic threat. For the later case, if ${\mathcal{R}}_0>1$,

$$(k+\mu )({\mathcal{R}}_0-1)>0,$$

which implies that ${\lambda }_3>0$ and thus $F^0$ is unstable.  □

Theorem 4

A Corona present equilibrium $F^1$ is locally asymptotically stable (LAS) whenever ${\mathcal{R}}_0>1$ . Whenever ${\mathcal{R}}_0<1$ , it is unstable.

Proof

The Jacobian for the system (1) at $F^1$ can be written as

$$J\left(F^1\right)=\left(\begin{array}{ccccc}\hfill J_{11}\hfill & \hfill 0\hfill & \hfill -{\alpha }_1{S}^1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \hfill \\ \hfill {\alpha }_3\hfill & \hfill J_{22}\hfill & \hfill -{\alpha }_4{V}^1\hfill & \hfill -{\alpha }_5{V}^1\hfill & \hfill 0\hfill \\ \hfill \hfill \\ \hfill {\alpha }_1{E}^1\hfill & \hfill {\alpha }_4{E}^1\hfill & \hfill J_{33}\hfill & \hfill -{\alpha }_2{E}^1\hfill & \hfill 0\hfill \\ \hfill \hfill \\ \hfill {\alpha }_5{I}^1\hfill & \hfill {\alpha }_2{I}^1\hfill & \hfill J_{44}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \hfill \\ \hfill 0\hfill & \hfill {\alpha }_6\hfill & \hfill k\hfill & \hfill r\hfill & \hfill -\mu \hfill \end{array}\right),$$

where

$$J_{11}=-{\alpha }_1{E}^1-({\alpha }_3+\mu ),$$

$$J_{22}=-({\alpha }_6+\mu )-{\alpha }_4{E}^1-{\alpha }_5{I}^1,$$

$$J_{33}={\alpha }_4{V}^1+{\alpha }_1{S}^1-{\alpha }_2{I}^1-(k+\mu ),$$

$$J_{44}={\alpha }_5{V}^1+{\alpha }_2{E}^1-(d+r+\mu ).$$

The eigenvalues of $J\left(F^1\right)$ are as follows:

$${\lambda }_1=-\mu ,$$ (11)

$${\lambda }_2=J_{11}=-{\alpha }_1{E}^1-({\alpha }_3+\mu ),$$ (12)

$${\lambda }_3=J_{22}=-({\alpha }_6+\mu )-{\alpha }_4{E}^1-{\alpha }_5{I}^1,$$ (13)

$${\lambda }_4=\frac{1}{J_{11}{J}_{22}}\left[J_{22}(J_{11}{J}_{33}+{\alpha }_1^2{S}^1{E}^1)-{\alpha }_4{E}^1({\alpha }_1{\alpha }_3{S}^1+{\alpha }_4{J}_{11}{V}^1)\right],$$ (14)

$${\lambda }_5=\frac{1}{Q_3}(Q_1-Q_2).$$ (15)

where

$$Q_1=J_{22}{J}_{44}(J_{11}{J}_{33}+{\alpha }_1^2{S}^1{E}^1)+J_{11}{V}^1(J_{44}{\alpha }_4^2{E}^1+J_{33}{\alpha }_5^2{I}^1)+E^1{I}^1({\alpha }_1^2{\alpha }_5^2{S}^1{V}^1+{\alpha }_2^2{J}_{11}{J}_{22}),$$

$$Q_2={\alpha }_1{\alpha }_3{S}^1{E}^1({\alpha }_4{J}_{44}+{\alpha }_2{\alpha }_5{I}^1),$$

$$Q_3=J_{11}{J}_{22}{J}_{33}+{\alpha }_4^2{J}_{11}{V}^1{E}^1+{\alpha }_1{S}^1{E}^1({\alpha }_1{J}_{22}-{\alpha }_3{\alpha }_4),$$

Clearly from Eq. (11), Eq. (12), and Eq. (13), ${\lambda }_1$, ${\lambda }_2$, ${\lambda }_3$ are negative. Since the product $J_{11}{J}_{22}$ is positive, so it is clear that ${\lambda }_4<0\iff J_{22}(J_{11}{J}_{33}+{\alpha }_1^2{S}^1{E}^1)<{\alpha }_4{E}^1({\alpha }_1{\alpha }_3{S}^1+{\alpha }_4{J}_{11}{V}^1)$, which has been verified. As $Q_3$ is positive, so ${\lambda }_5<0\iff Q_1<Q_2$ which is also true. Hence $F^1$ is LAS.  □

Global behavior of the vaccination model

Theorem 5

A Corona free equilibrium $F^0$ is globally asymptotically stable (GAS) in the domain $\Pi$ when $R_0<1$ .

Proof

Let $S^0=\frac{\Omega }{{\alpha }_3+\mu }$. We construct a candidate [55] Lyapunov function $U_0:\Pi \to \mathbb{R}$ such that,

$$U_0=S-S^0-S^{0}ln\frac{S}{S^0}+V-V^0-V^{0}ln\frac{V}{V^0}+E+I.$$

Differentiating $U_0$ with respect to time $t$ yields

$${\dot{U}}_0=(S-S^0)\frac{\dot{S}}{S}+(V-V^0)\frac{\dot{V}}{V}+\dot{E}+\dot{I}.$$

Substituting the values of derivatives from the system (1), we have

$${\dot{U}}_0=\left(1-\frac{S^0}{S}\right)\left[(S^0-S)\mu -{\alpha }_{1}SE+({\alpha }_6+\mu )V^0\left(1-\frac{S^0}{S}\right)\right]+\left(1-\frac{V^0}{V}\right)\left[({\alpha }_6+\mu )V^0\frac{S}{S^0}-({\alpha }_6+\mu +{\alpha }_{4}E+{\alpha }_{5}I)V\right]+({\alpha }_{5}V-d-r-\mu )I+({\alpha }_{1}S+{\alpha }_{4}V-k-\mu )E,=-\frac{\mu }{S}{(S-S^0)}^2+(k+\mu )({\mathcal{R}}_0-1)E+\left[\frac{\Omega {\alpha }_3{\alpha }_5}{({\alpha }_6+\mu )({\alpha }_3+\mu )}-(d+r+\mu )\right]I+({\alpha }_6+\mu )\left(3-\frac{S^0}{S}-\frac{V}{V^0}-\frac{V^0}{V}\frac{S}{S^0}\right)$$

Since ${\alpha }_3{\alpha }_5<(d+r+\mu )({\alpha }_6+\mu )({\alpha }_3+\mu )$ and employing Arithmetic–Geometric inequality, it can be shown that

$$3-\frac{S^0}{S}-\frac{V}{V^0}-\frac{V^0}{V}\frac{S}{S^0}\le 0.$$

Implies ${\dot{U}}_0\le 0$ whenever ${\mathcal{R}}_0<1$, and ${\dot{U}}_0=0$  $\iff$  $S=S^0$, $V=V^0$, $E=E^0=0$, $I=I^0=0$. The system (1) with these substitutions gives $S\to S^0$, $V\to V^0$, $I\to 0$, $E\to 0$ and $R\to R^0$ as $t\to \infty$. Implies $\left\{F^0\right\}$ is the maximal invariant set contained in

$$N_0=\left\{(S,V,E,I,R)\in \Pi :{\dot{U}}_0=0\right\}.$$

whenever ${\mathcal{R}}_0<1$. Hence by LaSalle’s invariance principle [53], $F^0$ is globally asymptotically stable in $\Pi$. Subsequently, COVID-19 disappears from the human population.  □

Theorem 6

A Corona present steady state $F^1$ is globally asymptotically stable (GAS) in the feasible region $\Pi$ if ${\mathcal{R}}_0>1$ .

Proof

To show the global stability of a Corona present steady state $F^1$, we construct a proposed [55] Lyapunov function $U_1:\Pi \to \mathbb{R}$ such that

$$U_1=S-S^1-S^{1}ln\frac{S}{S^1}+V-V^1-V^{1}ln\frac{V}{V^1}+E-E^1-E^{1}ln\frac{E}{E^1}+I-I^1-I^{1}ln\frac{I}{I^1}.$$

Now, time derivative of $U_1$ can be written as

$${\dot{U}}_1=(S-S^1)\frac{\dot{S}}{S}+(V-V^1)\frac{\dot{V}}{V}+(E-E^1)\frac{\dot{E}}{E}+(I-I^1)\frac{\dot{I}}{I}.$$

Using equations given in the model (1), we obtain that

$${\dot{U}}_1=\left(1-\frac{S^1}{S}\right)\left[\mu (S^1-S)+{\alpha }_1(S^1{E}^1-SE)\right]+V^1\left(1-\frac{S^1}{S}\right)\left[{\alpha }_4{E}^1+{\alpha }_5{I}^1+({\alpha }_6+\mu )\left(1-\frac{S}{S^1}\right)-({\alpha }_4{E}^1+{\alpha }_5{I}^1)\frac{S}{S^1}\right]+\left(1-\frac{V^1}{V}\right)\left[({\alpha }_6+\mu +{\alpha }_{4}E+{\alpha }_{5}I)(V^1-V)+({\alpha }_6+\mu +{\alpha }_4{E}^1+{\alpha }_5{I}^1)\times \frac{V^1}{V}\frac{S}{S^1}(V-V^1)\right]+(E-E^1)\left[{\alpha }_4(V-V^1)+{\alpha }_1(S-S^1)-{\alpha }_2(I-I^1)\right]+(I-I^1)\left[{\alpha }_5(V-V^1)+{\alpha }_2(E-E^1)\right].$$

After a simple calculation, we get

$${\dot{U}}_1=S^1(\mu +{\alpha }_1{E}^1)\left(2-\frac{S}{S^1}-\frac{S^1}{S}\right)+V^1({\alpha }_6+\mu +{\alpha }_4{E}^1+{\alpha }_5{I}^1)\times \left(3-\frac{S^1}{S}-\frac{V}{V^1}-\frac{S}{S^1}\frac{V^1}{V}\right)$$ (16)

where Arithmetic–Geometric mean inequality yields

$$2-\frac{S}{S^1}-\frac{S^1}{S}\le 0,$$

$$3-\frac{S^1}{S}-\frac{V}{V^1}-\frac{S}{S^1}\frac{V^1}{V}\le 0.$$

Therefore the expression (16) implies that ${\dot{U}}_1\le 0$. Particularly, ${\dot{U}}_1=0$ $\iff$  $S=S^1$, $V=V^1$. Implies $\left\{F^1\right\}$ is the greatest invariant set contained in

$$N_1=\left\{(S,V,E,I,R)\in \Pi :{\dot{U}}_1=0\right\}.$$

Hence by LaSalle’s invariance principle [53], it is concluded that $F^1$ is GAS in $\Pi$. Global stability of $F^1$ enables that COVID-19 will persist in the community and eventually lead to pandemic.  □

Numerical simulations

The aim of this section is to analyze and predict the numerical stability of the system (1). We have developed two well-known numerical schemes namely RK4 and NSF D method to solve the system (1). Development of these schemes helps us to observe dynamical behavior of COVID-19 over time $t$ through numerical simulations shown by graphs. We observe that solutions are in good agreement with the dynamical behavior of the continuous model. Numerical values of involved parameters are given in Table 1. The impact of proposed vaccine on human population is studied using NSFD scheme. Moreover, the correlation between model variables is computed numerically. Numerical analysis proves the reliability and dynamic consistency of NSFD scheme even for larger time step size when it compared with RK4 scheme.

RK4 scheme

To construct an explicit numerical scheme of RK4 method [13], [25], [26], [49], let us denote by $S^n$, $V^n$, $E^n$, $I^n$, and $R^n$ the approximations of solutions $S$, $V$, $E$, $I$, and $R$ respectively, for $n=0,1,2,3,4,\dots$, and time step size $h$. With these substitutions, RK4 scheme may be constructed as follows:

$$k_1=h\left[\Omega -{\alpha }_1{S}^n{E}^n-({\alpha }_3+\mu )S^n\right]$$

$$w_1=h\left[{\alpha }_3{S}^n-({\alpha }_6+\mu )V^n-{\alpha }_4{V}^n{E}^n-{\alpha }_5{V}^n{I}^n\right]$$

$$l_1=h\left[{\alpha }_1{S}^n{E}^n+{\alpha }_4{V}^n{E}^n-{\alpha }_2{E}^n{I}^n-(k+\mu )E^n\right]$$

$$m_1=h\left[{\alpha }_5{V}^n{I}^n+{\alpha }_2{E}^n{I}^n-(d+r+\mu )I^n\right]$$

$$n_1=h\left[{\alpha }_6{V}^n+r{I}^n+k{E}^n-\mu R^n\right]$$

$$k_2=h\left[\Omega -{\alpha }_1\left(S^n+\frac{k_1}{2}\right)\left(E^n+\frac{l_1}{2}\right)-({\alpha }_3+\mu )\left(S^n+\frac{k_1}{2}\right)\right]$$

$$w_2=h\left[{\alpha }_3\left(S^n+\frac{k_1}{2}\right)-({\alpha }_6+\mu )\left(V^n+\frac{w_1}{2}\right)-{\alpha }_4\left(V^n+\frac{w_1}{2}\right)\left(E^n+\frac{l_1}{2}\right)-{\alpha }_5\left(V^n+\frac{w_1}{2}\right)\left(I^n+\frac{m_1}{2}\right)\right]$$

$$l_2=h\left[{\alpha }_1\left(S^n+\frac{k_1}{2}\right)\left(E^n+\frac{l_1}{2}\right)+{\alpha }_4\left(V^n+\frac{w_1}{2}\right)\left(E^n+\frac{l_1}{2}\right)-{\alpha }_2\left(E^n+\frac{l_1}{2}\right)\left(I^n+\frac{m_1}{2}\right)-(k+\mu )\left(E^n+\frac{l_1}{2}\right)\right]$$

$$m_2=h\left[{\alpha }_5\left(V^n+\frac{w_1}{2}\right)\left(I^n+\frac{m_1}{2}\right)+{\alpha }_2\left(E^n+\frac{l_1}{2}\right)\left(I^n+\frac{m_1}{2}\right)-(d+r+\mu )\left(I^n+\frac{m_1}{2}\right)\right]$$

$$n_2=h\left[{\alpha }_6\left(V^n+\frac{w_1}{2}\right)+r\left(I^n+\frac{m_1}{2}\right)+k\left(E^n+\frac{l_1}{2}\right)-\mu \left(R^n+\frac{n_1}{2}\right)\right]$$

$$k_3=h\left[\Omega -{\alpha }_1\left(S^n+\frac{k_2}{2}\right)\left(E^n+\frac{l_2}{2}\right)-({\alpha }_3+\mu )\left(S^n+\frac{k_2}{2}\right)\right]$$

$$w_3=h\left[{\alpha }_3\left(S^n+\frac{k_2}{2}\right)-({\alpha }_6+\mu )\left(V^n+\frac{w_2}{2}\right)-{\alpha }_4\left(V^n+\frac{w_2}{2}\right)\left(E^n+\frac{l_2}{2}\right)-{\alpha }_5\left(V^n+\frac{w_2}{2}\right)\left(I^n+\frac{m_2}{2}\right)\right]$$

$$l_3=h\left[{\alpha }_1\left(S^n+\frac{k_2}{2}\right)\left(E^n+\frac{l_2}{2}\right)+{\alpha }_4\left(V^n+\frac{w_2}{2}\right)\left(E^n+\frac{l_2}{2}\right)-{\alpha }_2\left(E^n+\frac{l_2}{2}\right)\left(I^n+\frac{m_2}{2}\right)-(k+\mu )\left(E^n+\frac{l_2}{2}\right)\right]$$

$$m_3=h\left[{\alpha }_5\left(V^n+\frac{w_2}{2}\right)\left(I^n+\frac{m_2}{2}\right)+{\alpha }_2\left(E^n+\frac{l_2}{2}\right)\left(I^n+\frac{m_2}{2}\right)-(d+r+\mu )\left(I^n+\frac{m_2}{2}\right)\right]$$

$$n_3=h\left[{\alpha }_6\left(V^n+\frac{w_2}{2}\right)+r\left(I^n+\frac{m_2}{2}\right)+k\left(E^n+\frac{l_2}{2}\right)-\mu \left(R^n+\frac{n_2}{2}\right)\right]$$

$$k_4=h\left[\Omega -{\alpha }_1(S^n+k_3)(E^n+l_3)-({\alpha }_3+\mu )(S^n+k_3)\right]$$

$$w_4=h\left[{\alpha }_3(S^n+k_3)-({\alpha }_6+\mu )(V^n+w_3)-{\alpha }_4(V^n+w_3)(E^n+l_3)-{\alpha }_5(V^n+w_3)(I^n+m_3)\right]$$

$$l_4=h\left[{\alpha }_1(S^n+k_3)(E^n+l_3)+{\alpha }_4(V^n+w_3)(E^n+l_3)-{\alpha }_2(E^n+l_3)(I^n+m_3)-(k+\mu )(E^n+l_3)\right]$$

$$m_4=h\left[{\alpha }_5(V^n+w_3)(I^n+m_3)+{\alpha }_2(E^n+l_3)(I^n+m_3)-(d+r+\mu )(I^n+m_3)\right]$$

$$n_4=h\left[{\alpha }_6(V^n+w_3)+r(I^n+m_3)+k(E^n+l_3)-\mu (R^n+n_3)\right]$$

Hence

$$S^{n+1}=S^n+\frac{1}{6}(k_1+2k_2+2k_3+k_4)$$ (17a)

$$V^{n+1}=V^n+\frac{1}{6}(w_1+2w_2+2w_3+w_4)$$ (17b)

$$E^{n+1}=E^n+\frac{1}{6}(l_1+2l_2+2l_3+l_4)$$ (17c)

$$I^{n+1}=I^n+\frac{1}{6}(m_1+2m_2+2m_3+m_4)$$ (17d)

$$R^{n+1}=R^n+\frac{1}{6}(n_1+2n_2+2n_3+n_4)$$ (17e)

where $n=0,1,2,3,\dots$ and the discretization time step is denoted by $h$.

Non-standard finite difference scheme

After RK4 technique, we now demonstrate a non-standard finite difference (NSFD) scheme for the model (1) presented herein. The scheme is based on Micken’s theory [30], [31], [32], [33] of non-standard finite difference numerical modeling. The proposed NSFD scheme has been efficiently applied to solve numerous problems [34], [35], [36], [37], [38], [39], [40], [55] in physical sciences and engineering where it is basically required that the obtained numerical solutions preserve all the properties of a dynamic model. It is shown that NSFD scheme provides more accurate solutions as compared to RK4 method for larger step sizes. For the proposed model (1), we construct NSFD numerical scheme as follows:

$$S^{n+1}=\frac{S^n+h\Omega }{1+h{\alpha }_1{E}^n+h({\alpha }_3+\mu )},$$ (18a)

$$V^{n+1}=\frac{V^n+h{\alpha }_3{S}^n}{1+h{\alpha }_4{E}^n+h{\alpha }_5{I}^n+h({\alpha }_6+\mu )},$$ (18b)

$$E^{n+1}=\frac{E^n+h{\alpha }_4{V}^n{E}^n+h{\alpha }_1{S}^n{E}^n}{1+h{\alpha }_2{I}^n+h(k+\mu )},$$ (18c)

$$I^{n+1}=\frac{I^n+h{\alpha }_5{V}^n{I}^n+h{\alpha }_2{E}^n{I}^n}{1+h(d+r+\mu )},$$ (18d)

$$R^{n+1}=\frac{R^n+h{\alpha }_6{V}^n+hr{I}^n+hk{E}^n}{1+h\mu }.$$ (18e)

where $n=0,1,2,3,\dots$ and the discretization time step is denoted by $h$.

Theorem 7

The only fixed points of the scheme (18) are either the $F^0$ or $F^1$ of the dynamic model (1) . Moreover, fixed points of proposed scheme (18) has the same stability properties as that of $F^0$ and $F^1$ of the given model.

Theorem 8

Whenever${\mathcal{R}}_0<1$, the NSFD scheme (18) has a globally asymptotically stable equilibrium point $F^0$ and a globally asymptotically stable endemic point $F^1$ whenever ${\mathcal{R}}_0>1$ . For the later case, $F^0$ will become unstable.

Analysis through comparisons

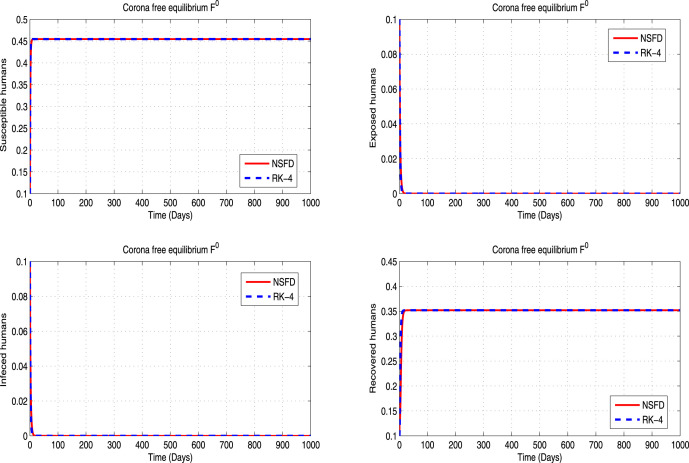
In the current section, the comparison of the nonstandard computational method with well known standard computational method is presented. In Fig. 2, Fig. 3, Fig. 4, Fig. 5, Fig. 6, Fig. 7, we can observe that RK4 method converge for small time step sizes. Although for larger time step sizes, RK4 scheme fails to restore the desired properties like positivity and boundedness of solutions. As time increases, RK4 method also loses dynamical consistency of the continuous model (1). By this property, all the fixed points of an implemented numerical scheme should be the same as the continuous model for the any set of parameter values. For details, we will refer the Fig. 9, Fig. 10, Fig. 11. To check the validity of analytical results, We first solve the system (1) using both RK4 and NSFD method with time step sizes $h=1.0$ and $h=1.2$ respectively. In Fig. 2, Fig. 3, Fig. 4, Fig. 5, Fig. 6, Fig. 7, both the numerical schemes are seen to be convergent to the same equilibrium states $F^0$ (whenever ${\mathcal{R}}_0<1$) and $F^1$ (whenever ${\mathcal{R}}_0>1$) of the model. Furthermore, both the numerical schemes exhibit positive and bounded solutions in the region $\Pi$ for these step sizes. Additionally, if we increase the value of $h$, for example $h=1.5$ and $h=2.0$, it is observed that RK4 method do not converge to both $F^0$ and $F^1$. Moreover, for these values of $h$, RK4 scheme exhibit unexpected negative solutions as observed in Fig. 9, Fig. 10, Fig. 11. However, the NSFD scheme converges to true states with the same set of condition applied on ${\mathcal{R}}_0$, and preserves all the essential properties of the model (1). For comparisons, see Fig. 2, Fig. 3, Fig. 4, Fig. 5, Fig. 6, Fig. 7, Fig. 8, Fig. 9, Fig. 10, Fig. 11. We have presented four numerical experiments for NSFD and RK4 scheme respectively using different values of $h$, and the obtained results are given in Table 2.

Fig. 2.

Graphical behavior of NSFD scheme at $F^0=(0.4545,0.1935,0,0,0.3519)$ of the model (1) with $h=1.0$.

Fig. 3.

Graphical behavior of NSFD scheme at $F^1=(0.2066,0.07896,0.5283,0.03185,0.1541)$ of the model (1) with $h=1.0$.

Fig. 4.

Graphical behavior of RK4 scheme at $F^0=(0.4545,0.1935,0,0,0.3519)$ of the model (1) with $h=1.0$.

Fig. 5.

Graphical behavior of RK4 scheme at $F^1=(0.2066,0.07896,0.5283,0.03185,0.1541)$ of the model (1) with $h=1.0$.

Fig. 6.

The solutions are obtained by NSFD and RK4 techniques with step size $h=1.2$. It is seen that both techniques converge numerically to the point $F^0=(0.4545,0.1935,0,0,0.3519)$.

Fig. 7.

The solutions are obtained by NSFD and RK4 techniques with step size $h=1.2$. It is seen that both techniques converge numerically to the point $F^1=(0.2066,0.07896,0.5283,0.03185,0.1541)$.

Fig. 9.

The solutions are obtained by NSFD and RK4 techniques with step size $h=1.5$. It is observed that RK4 scheme diverges and gives unexpected negative solutions whereas NSFD converges to the true equilibrium point $F^1=(0.2066,0.07896,0.5283,0.03185,0.1541)$.

Fig. 10.

The solutions are obtained by NSFD and RK4 techniques with step size $h=2.0$. It is observed that RK4 scheme diverges and gives unexpected negative solutions whereas NSFD converges to the true equilibrium point $F^0=(0.4545,0.1935,0,0,0.3519)$.

Fig. 11.

The solutions are obtained by NSFD and RK4 techniques with step size $h=2.0$. It is observed that RK4 scheme diverges and gives unexpected negative solutions whereas NSFD converges to the true equilibrium point $F^1=(0.2066,0.07896,0.5283,0.03185,0.1541)$.

Fig. 8.

The solutions are obtained by NSFD and RK4 techniques with step size $h=1.5$. It is seen that both techniques converge numerically to the point $F^0=(0.4545,0.1935,0,0,0.3519)$.

Table 2.

Convergence of numerical schemes vs. time step size $h$.

Step size	$h=1.0$	$h=1.2$	$h=1.5$	$h=2.0$
RK4	Convergent	Convergent	Divergent	Divergent
NSFD	Convergent	Convergent	Convergent	Convergent

Projected scheme and its computational advantages

This section is dedicated to showing the numerical advantages and dynamic consistency of the proposed NSFD technique. The numerical comparisons discussed in Section “Analysis through comparisons” demonstrates that the RK4 scheme is not always convergent, rather conditionally convergent and stable. It is very sensitive to the time step size $h$ and fails to converge especially for larger step sizes. In contrast with other widely utilized standard numerical strategies including RK4, our proposed NSFD scheme is seen to be convergent for any step size used. It is clear from Table 2 that the adopted NSFD scheme is more competitive in terms of numerical stability of the model (1) at fixed points. The Fig. 2, Fig. 3, and Fig. 6, Fig. 7, Fig. 8, Fig. 9, Fig. 10, Fig. 11, Fig. 12, Fig. 13, Fig. 14, Fig. 15 illustrate the potential of NSFD scheme. Furthermore, it is concluded that the developed NSFD scheme is unconditionally convergent and stable, gives positive and bounded solutions, convergence to the equilibrium points and maintains its dynamical consistency with the vaccination model.

Fig. 12.

Behavior of the population proportion of susceptible humans at corona present point $F^1$ for different coverage levels (%) of voluntary vaccination. Numerical results are obtained by NSFD scheme using $h=0.1$.

Fig. 13.

Behavior of the population proportion of exposed humans at corona present point $F^1$ for different coverage levels (%) of voluntary vaccination. Numerical results are obtained by NSFD scheme using $h=0.1$.

Fig. 14.

Behavior of the population proportion of infected humans at corona present point $F^1$ for different coverage levels (%) of voluntary vaccination. Numerical results are obtained by NSFD scheme using $h=0.1$.

Fig. 15.

Behavior of the population proportion of recovered humans at corona present point $F^1$ for different coverage levels (%) of voluntary vaccination. Numerical results are obtained by NSFD scheme using $h=0.1$.

Vaccination effect on human populations

In this subsection, the effect of voluntary vaccination on the human population is studied, just to handle the spread of Corona virus pandemic in a community. The study indicates that susceptibility of humans decreases with the increase in proportion of vaccinated humans. It is observed that the number of exposed and infected humans are significantly reduced with the increase in the rate of vaccination. However, the number of recovered individuals is increased by increasing the number of vaccinated humans. As time $t\to \infty$, an increment in vaccination levels $\left(\text{\%}\right)$, will help automatically all populations approach $F^0$, see Fig. 12, Fig. 13, Fig. 14, Fig. 15. The analysis proves that the spread of Corona virus disease could be controlled if people adopt proper vaccination strategies at least up to the level of 60%. The dynamical behavior of Corona virus disease in all populations through a vaccination programme is observed in Fig. 12, Fig. 13, Fig. 14, Fig. 15. These profiles are illustrated in Table 3, Table 4, Table 5, Table 6 respectively.

Table 3.

Rate of vaccination versus proportion of susceptible humans at $F^1$.

Vaccination rate (%)	Proportion of susceptible humans
0	0.4985
20	0.4896
40	0.4720
60	0.4546

Table 4.

Rate of vaccination versus proportion of exposed humans at $F^1$.

Vaccination rate (%)	Proportion of exposed humans
0	0.4365
20	0.2561
40	0.0785
60	0.0000

Table 5.

Rate of vaccination versus proportion of infected humans at $F^1$ .

Vaccination rate (%)	Proportion of infected humans
0	0.1072
20	0.0603
40	0.0209
60	0.0000

Table 6.

Effect of vaccination on the proportion of recovered humans at $F^1$ .

Vaccination rate (%)	Proportion of recovered humans
0	0.0034
20	0.1340
40	0.2624
60	0.3519

Effect of vaccination on ${\mathcal{R}}_0$

Our goal is to lift up the proportion of recovered humans and to decrease the number of humans in susceptible, exposed and the infected compartments by adopting proper vaccination measures. It is important to compute the value of ${\mathcal{R}}_0$ at different levels of voluntary vaccination to get the better understanding of the problem. Therefore, the effectiveness of voluntary vaccination on threshold parameter ${\mathcal{R}}_0$ has been examined in Fig. 16. We saw that increment in the level of vaccination diminishes the value of ${\mathcal{R}}_0$. It is likewise seen that the Corona virus disease will remain continue in the community at all vaccination levels goes from 0% to 60%. Indeed, for this range, the value of ${\mathcal{R}}_0$ is greater than one. However, from 60% onward, the value of threshold parameter ${\mathcal{R}}_0$ will become less than one as given in Table 7 and the infectivity goes to zero as illustrated in Fig. 13, Fig. 14 already. This shows that Corona virus disease will be eliminated from the host population if we vaccinate around 60% of the human population, which legitimizes the title of our manuscript.

Fig. 16.

Portrait of threshold parameter ${\mathcal{R}}_0$ plotted against vaccination coverage levels. It is observed that ${\mathcal{R}}_0$ gives a small decease in its value by increasing the levels of voluntary vaccination.

Table 7.

Threshold parameter ${\mathcal{R}}_0$ under the effect of persistent vaccination.

Vaccination levels (%)	Threshold parameter ${\mathcal{R}}_0$
0	$1.9860>1$
20	$1.4750>1$
40	$1.1910>1$
60	$1.0110>1$
61	$0.9991<1$

Covariance

In the current subsection, the joint variability [40] of all classes is studied numerically. For each pair of populations, we have elaborated the consequences of relationship quantity $\rho$ as illustrated in Table 8. A numerical study performed in Fig. 12, Fig. 13, Fig. 14 authentically justified the inverse relationship among susceptible, exposed, infected and the vaccinated humans. However, it is noticed that there is a direct correlation between the recovered and vaccinated class as demonstrated in Fig. 15. Subsequently, a continuous rapid increment in the recovered class will lead the total population to $F^0$.

Table 8.

Joint variability of populations.

Populations	$\rho$	Relationship
$(V,S)$	−0.8842	Inverse
$(V,E)$	−0.6574	Inverse
$(V,I)$	−0.6971	Inverse
$(V,R)$	0.6765	Direct

Conclusions

In this research article, we proposed a mathematical model for COVID-19 that provides a good description about the spread of a Corona virus within the community. Dynamical behavior of Corona virus disease is investigated through this dynamic model using some comprehensive mathematical techniques. First, we proved existence and uniqueness and then positivity and the boundedness of solutions. Subsequently, our problem is well-posed and solutions are physically realizable.

We evaluated two main equilibrium states of the proposed model respectively. The value of threshold parameter ${\mathcal{R}}_0$ was computed using the method of next generation to study the dynamics of the vaccination model. Existence of a Corona free point $F^0$ is proved for the condition ${\mathcal{R}}_0<1$ in the local and global sense. When ${\mathcal{R}}_0>1$, it is also proved that $F^1$ exists and is locally and globally stable, where $F^0$ got unstable. LaSalle’s invariance principle from the theory of Lyapunov functions was established to carry out the proofs of global stability.

Furthermore, we have investigated stability analysis of COVID-19 within the community numerically by employing NSFD and RK4 methods. We have made this effort to solve the system and to validate our obtained analytical results. Numerical simulations show that RK4 is not suitable especially when the time step size is large. It produces non-physical oscillations, fails to preserve positivity of solutions and converges to false steady states and diverges. On the other hand, the projected NSFD scheme is reliable and consistent with the SVEIR model and preserves all the essential properties of solutions. Moreover, the developed NSFD scheme is unconditionally convergent and stable.

We also discussed graphically the dynamical behavior of the Corona model under the effect of four vaccination levels. It is proved that the disease can be controlled efficiently if the level of voluntary vaccination is increased in susceptible, exposed, and infected population. We also studied the effect of vaccination on the value of ${\mathcal{R}}_0$. As time goes to infinity, the value of ${\mathcal{R}}_0$ regresses with the increase in levels of voluntary vaccination. It is found that Corona virus disease will persist in the community if the susceptible humans are vaccinated up to the level of 60%. An increase in this percentage significantly reduces the risk of Corona virus disease.

Covariances among susceptible, exposed, infected, recovered and the vaccinated humans is computed to check the statistical relationship between all the classes. We have discussed the corresponding joint variability.

CRediT authorship contribution statement

W. Ahmad: Conceptualization, Methodology, Computations, Writing – original draft. M. Abbas: Supervision, Visualization, Investigation, Validation. M. Rafiq: Project administration, Resources, Data curation, Revision of original draft, Formal analysis. D. Baleanu: Writing – review & editing, Software.

Uncited references

[56], [57], [58], [59], [60], [61], [62], [63], [64], [65], [66], [67], [68], [69]

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.