Abstract
Earth’s surface environment is largely influenced by its budget of major volatile elements: carbon (C), nitrogen (N), and hydrogen (H). Although the volatiles on Earth are thought to have been delivered by chondritic materials, the elemental composition of the bulk silicate Earth (BSE) shows depletion in the order of N, C, and H. Previous studies have concluded that non-chondritic materials are needed for this depletion pattern. Here, we model the evolution of the volatile abundances in the atmosphere, oceans, crust, mantle, and core through the accretion history by considering elemental partitioning and impact erosion. We show that the BSE depletion pattern can be reproduced from continuous accretion of chondritic bodies by the partitioning of C into the core and H storage in the magma ocean in the main accretion stage and atmospheric erosion of N in the late accretion stage. This scenario requires a relatively oxidized magma ocean ( , where is the oxygen fugacity, is , and is at the iron-wüstite buffer), the dominance of small impactors in the late accretion, and the storage of H and C in oceanic water and carbonate rocks in the late accretion stage, all of which are naturally expected from the formation of an Earth-sized planet in the habitable zone.
Subject terms: Planetary science, Core processes, Early solar system, Geochemistry, Geodynamics, Inner planets
Introduction
Earth’s major volatile elements—carbon (C), nitrogen (N), and hydrogen (H)—are the main components of the atmosphere and oceans and the key elements for life. The budget of these major volatiles in the bulk silicate Earth (including the atmosphere, oceans, crust, and mantle: hereafter BSE) influences the volume of the oceans and the atmospheric inventory of C () and N (), and consequently, Earth’s habitable environment1–3. Similar isotopic compositions of volatiles in Earth and chondrites suggests that delivery was made chiefly by chondritic materials4. In contrast, although their absolute abundances are largely uncertain, the abundances of C–N–H in BSE relative to chondrites are known to have a V-shaped depletion pattern5,6. Owing to this discrepancy, the origin of the major volatile elements on Earth remains unclear5.
The composition of major volatiles in the BSE should have been modified by element partitioning processes, including removal by core-forming metals and by atmospheric escape (Fig. 1). Although the origins and timing of volatile delivery are still debated, the delivery during the main accretion stage is expected based on the planet formation theory, which involves large-scale dynamic evolution, such as the Grand Tack model7. Recent isotopic analyses point to the late-accreting bodies being composed of enstatite chondrites8 or carbonaceous chondrites9, suggesting that volatile delivery continued into the late stage. On the growing proto-Earth with planetesimal accretion and several giant impacts, the formation of magma oceans allowed volatiles to be stored within the magma ocean10. Core-forming metal could have removed some of the iron-loving elements (siderophiles) from the magma ocean during the main accretion stage11. Volatiles partitioned into the atmosphere (atmophiles) were continuously removed via atmospheric erosion caused both by small planetesimal accretion12 and giant impacts13. The successive late accretion after the solidification of the magma ocean further removed and replenished volatile elements14.
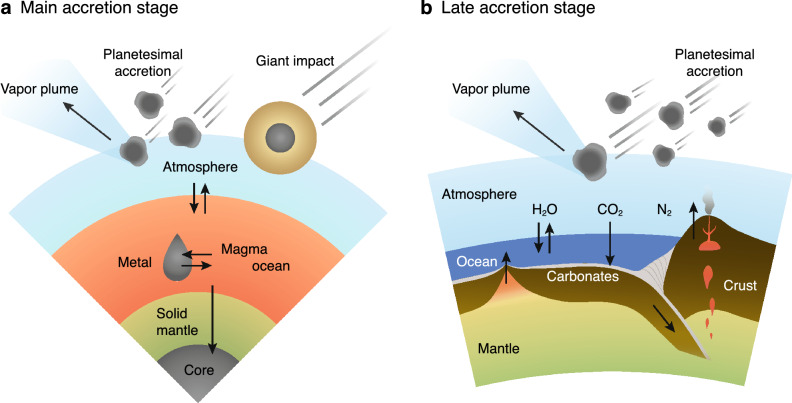
Figure 1.
Cartoon of element partitioning processes during Earth’s accretion according to our model. Accreting planetesimals and giant impactors deliver volatiles and simultaneously form a vapour plume eroding the atmosphere. (a) Model for the main accretion stage (10% to 99.5% of the Earth’s mass). Equilibration among the magma ocean (silicate melt), liquid metal droplets transiting to the core, and the overlying atmosphere are achieved according to each metal silicate partitioning coefficient and solubility. (b) Model for the late accretion stage after the solidification of the magma ocean (the last 0.5%). We consider the liquid water oceans and the carbonate-silicate cycle to be driven by plate tectonics on the surface. In this stage, most H and C on Earth are stored in the oceans and carbonate rocks, respectively. Numerous impactors can selectively erode N.
Alhough several previous studies have attempted to explain the depletion patterns of major volatile elements in BSE5,15,16, the evolution of the volatile composition through the full accretion history has not been simulated. The previous studies employed ad hoc models where a single-stage metal-silicate equilibration event and complete/negligible atmospheric loss were assumed. Hirschmann5 showed that the combination of core segregation and atmospheric blow off would leave BSE with low C/H and C/N ratios compared with accreted material, and he concluded that the BSE’s high C/N ratio requires late accreting bodies with elevated C/N ratios compared with chondrites. Other works have attributed the discrepancy largely to the accretion of thermally processed or differentiated, non-chondritic bodies15,16, which are hypothetical and may not satisfy the isotopic constraints8. Here, we consider another mechanism that can fractionate C/N: the preferential loss of N relative to C and H by impacts during the late accretion stage, where N is partitioned into the atmosphere, while C and H are partitioned into the oceans and carbonate rocks14. This work builds on previous studies5,15,16 in terms of volatile element partitioning, but makes improvements to simulate core formation and atmospheric loss as continuous processes rather than single stage events.
In this study, we aimed to reproduce the V-shaped C–N–H pattern by considering realistic processes to the extent of today’s observational uncertainties. We modelled the evolution of the volatile abundances in the atmosphere, oceans, crust, mantle, and core through the full accretion by taking elemental partitioning and impact erosion into account. Figure 1 shows a schematic image of our model setting. The main and late accretion stages were modelled separately, and the masses of C, N, and H in each reservoir were computed using a multiple-boxes model (“Methods”). We assumed the existence of the oceans and the active carbonate-silicate cycle in the late accretion stage; the validity of this assumption is discussed. We explored the plausible accretion scenarios that reproduce the current BSE’s C–N–H composition pattern from the accretion of chondritic bodies. The major parameters were the size distribution of planetesimals in each stage; the number of giant impacts; the redox state of the magma ocean, which controls the solubility and metal-silicate partitioning coefficient of volatiles; the composition of impactors; and the total mass of the late accretion. Our nominal model, which is a successful case, assumes a volatile supply from CI chondrite-like building blocks, an oxidized magma ocean ( IW+1, where is the oxygen fugacity, is defined hereafter as , and is at the iron-wüstite buffer), a single giant impact, and a change in planetesimal size distribution with time, and 0.5 wt% late accretion. Figures 2 and 3 show the evolution of major volatile abundances for this successful case. As the composition of building blocks, a mixture of CI chondrite-like impactors (12 wt%) and dry objects (88 wt%) was fixed by exploring the best fit homogeneous accretion (see Supplementary Information). In order to understand the physical behaviours of the volatile element partitioning, we also calculated the evolution for other cases with different impactor size distributions, accretion scenarios, amounts of late accretion, and redox states of the magma ocean (Fig. 4). In the Supplementary Information, we show the results for the cases where we assume a different source for volatile elements (enstatite chondrites) and the range of partitioning coefficients and solubilities. We confirmed that other parameters such as the magma ocean depth, metal/silicate ratio, surface temperature during the magma ocean stage, and efficiency of impact erosion by a giant impact had only minor effects (Fig. S1). The uncertainties in the final volatile abundances in BSE caused by these minor parameters, except for the magma ocean depth, are smaller than 10%. As to the magma ocean depth, the uncertainties differ by species and the redox state of the magma ocean: a factor of 2 for H in the oxidized model, 40% for N and 15% for H in the reduced model, and smaller than 10% for the others (Fig. S1 for the oxidized model and the figure not shown for the reduced model).
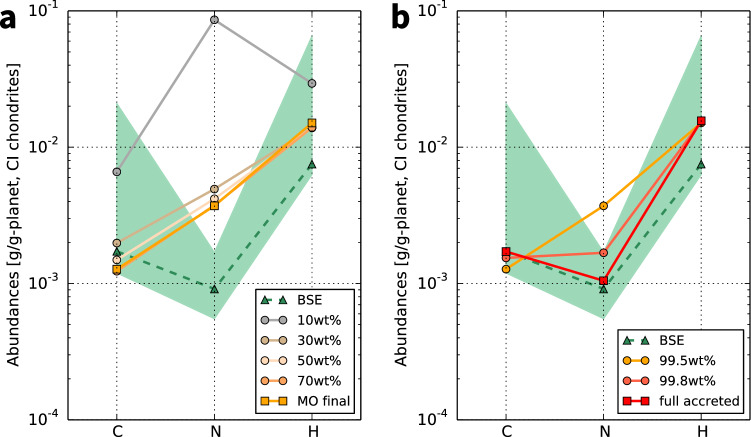
Figure 2.
Evolution of major volatile abundances in the bulk silicate Earth (BSE) scaled by those of CI chondrites in the nominal model. The abundances are normalized by each planetary mass at each time for (a) the main accretion stage, from 10 to 99.5% of Earth’s accretion, and (b) the late accretion stage defined as the last 0.5% of accretion after the magma ocean solidification. The time sequence is shown by lines from top to bottom with snapshots. The thick orange and red lines correspond to the end of main and late accretion stages, respectively. The range in the current BSE composition estimate4,5,17 is shown for comparison (green area). The mean value of Hirschmann5 is shown as a reference for the relative depletion pattern (green line). See Table 1 for the composition of BSE and chondrites.
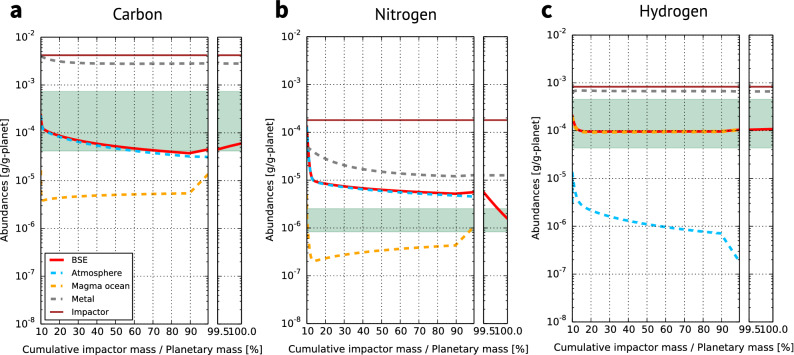
Figure 3.
Evolution of the abundances of C, N, and H in the surface and interior reservoirs over the full accretion obtained from the nominal model. Dashed lines correspond to the amounts in the atmosphere (light-blue), magma ocean (orange), and metallic core (grey) for the main accretion phase and in the surface reservoirs (the atmosphere, oceans, and carbonate rocks: red solid line) for the late accretion phase. Solid lines mean the net cumulated into the bulk silicate Earth (BSE; red) and delivered by impactors (brown). The green areas denote the amounts in the current BSE. Plotted abundances are scaled by the planetary mass at a given time.
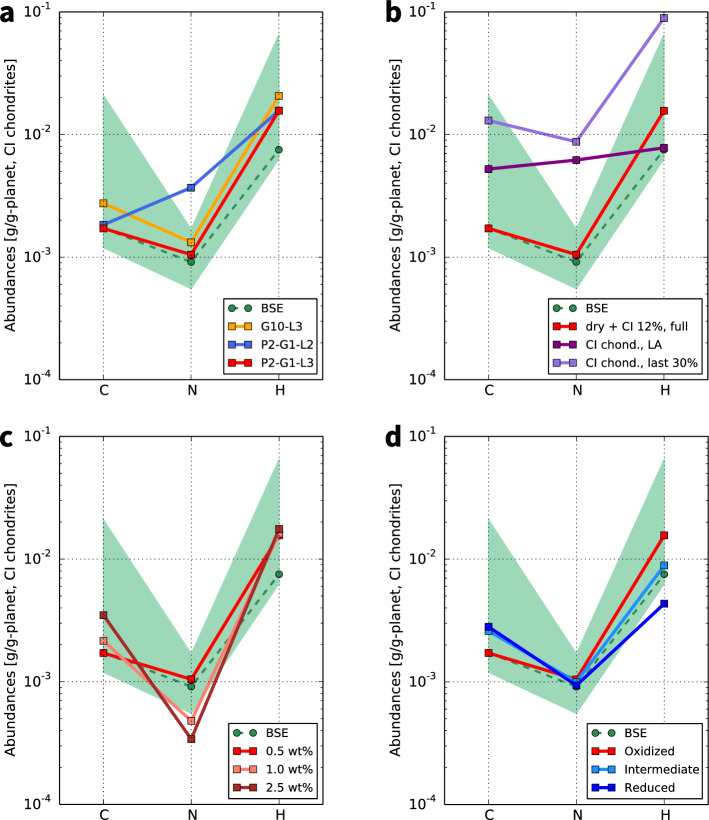
Figure 4.
Dependence of final volatile composition of the bulk silicate Earth (BSE) on the accreting conditions. (a) Effects of the impactor’s size distribution. P2-G1-L3 (the nominal model, red line): planetesimal accretion ( and for in the main and late accretion stages, respectively) and one giant impact. G10-L3 (orange line): ten giant impacts and the late accretion of planetesimals . P2-G1-L2 (blue line): shallower planetesimal size distribution ( throughout the full accretion) and one giant impact. Here we assumed , where N(D) is the number of objects of diameter smaller than D, and q is the power law index. (b) Dependence on volatile accretion scenarios. Late volatile accretion (dark-purple): volatiles are delivered only by late accretion with CI chondrite-like bodies. Heterogeneous accretion model (purple): volatiles are supplied in the last 30 wt% accretion with CI chondrite-like bodies. (c) Dependence on the late accretion mass. The mass of late accretion was varied from 0.5 wt% (brown) to 2.5 wt% (orange). (d) Dependence on the redox state of the magma ocean. Oxidized (the nominal model, red line), intermediate (light blue line), and reduced (blue line) conditions are compared. The solubilities and partitioning coefficients are summarised in Table 1.
Origin of the V-shaped C–N–H depletion pattern
The V-shaped C–N–H depletion pattern compared with chondrites in the current BSE (Fig. 2) can be successfully reproduced from chondritic building blocks by considering both the element partitioning between reservoirs and the impact-induced atmospheric erosion simultaneously over all accretion stages. The successful case (the nominal model) assumed three conditions: an oxidized magma ocean (IW+1), a change in impactor size distribution with time, and the storage of H and C in oceanic water and carbonate rocks after magma ocean solidification. The nominal model assumed CI chondrite-like building blocks, but enstatite chondrite-like impactors’ case, where a smaller amount of H is present in the building blocks, also successfully reproduced the BSE composition under more limited conditions (see Supplementary Fig. S2, Fig. S3, Fig. S4, and Fig. S5). Element partitioning among the overlying atmosphere, magma ocean, and suspended metal droplets during the main accretion phase led to a subtle C deficit, N excess, and an adequate amount of H at the end of the main accretion stage (Fig. 2a). In the late accretion stage after solidification, the interplay of H and C storage in oceanic water and carbonate rocks and the preferential loss of N due to atmospheric erosion finally solved the remaining issue: N excess (Fig. 2b).
Earth’s C and H abundances were set chiefly during the main accretion stage (Fig. 3). Although the first kink of volatile abundances in each reservoir is set by the initial conditions (see “Methods”), the system soon evolves towards a quasi-steady state between the gain and loss of volatile elements. The highly siderophile property of C18 and high solubility of H19 in silicate melt under the oxidized condition in the nominal model caused those elements to be removed by core segregation. As the remaining part of C was partitioned into the atmosphere owing to its low solubility20, the atmospheric erosion led to C being more depleted than H in BSE. The low solubility of N21 in magma led to almost all N in BSE being partitioned into the atmosphere soon after the magma ocean solidification. For N, the impact-induced erosion governs the abundance evolution14, while the transport to the core governs for C and H. N also has a siderophile property, which has been proposed to cause N depletion in the BSE16,22,23. However, we found that partitioning into the core is less important compared with the atmospheric escape, even considering the uncertainty in the partitioning coefficient (see Supplementary Information). A Mars-sized, moon-forming giant impact24 was assumed in the nominal model, which corresponds to the kink at 90% Earth mass, but it did not modify the BSE volatile abundances significantly. We considered a completely molten mantle25 in the element partitioning after the giant impact, while a smaller molten fraction of 30 wt% was assumed for the planetesimal accretion. Thus, the larger mass of the magma ocean after the giant impact allowed increases in the abundances of all volatile elements in the magma ocean.
The abundance of N was decreased by approximately one order of magnitude during the late accretion phase owing to impact-induced atmospheric escape. The formation of oceans and the initiation of the carbonate-silicate cycle right after the solidification of the magma ocean trapped H and C into the surface reservoirs, and subsequently facilitated preferential N erosion from the atmosphere. Since N neither condense nor become incorporated into any solid or liquid reservoirs in our model, the final N abundance is determined by the balance between the supply by impactors and the loss by atmospheric erosion. From this result, we argue that the presence of oceans and carbonate formation in the late accretion stage are requirements to explain the current high C/N and H/N ratios of the BSE.
The exact timing of the ocean formation and the initiation of the carbonate-silicate cycle are unknown, but these assumptions are supported by theoretical, geological, and geochemical studies. As the timescale for the magma ocean solidification is short (0.2–7 Myrs after the last giant impact26–28), the oceans would have persisted in the late accretion stage. Archean sediments imply that the oceans29 and plate tectonics30 already existed at least 3.8 Gyr ago. Geochemical studies of Hadean zircons suggest the existence of oceans and the active plate boundary interactions in the Hadean31,32. Although plate tectonics might not have started on the Hadean Earth33, the storage of C by carbonate precipitation is possible even without plate tectonics as long as liquid water is present34. The continental crust, which releases water-soluble cations such as and on modern Earth, might not be present in the Hadean, but efficient carbonate formation is possible owing to seafloor weathering35. However, the presence of liquid water which allows silicate weathering to occur is required to drive the carbonate-silicate cycle3. Furthermore, if marine pH was neutral to alkaline (7), most of the total atmosphere plus ocean C inventory (90%) would have dissolved into the oceans as bicarbonate and carbonate ions36, as proposed for the preferential N loss by a giant impact37. We note, however, that a giant impact will vaporize the oceans, which could end up losing some C.
Another key assumption of our model is the slow (negligible) N fixation compared to C on early Earth during late accretion, which led to the preferential erosion of atmospheric N. A combined model of atmospheric and oceanic chemistry determined the lifetime of molecular N in anoxic atmospheres to be years38. After Earth’s accretion ceased, N cycling between the atmosphere and mantle over a billion-year timescale39 would lead to lower N partial pressures in the later period (e.g., those recorded in the Archean40). In contrast, the timescale of carbonate precipitation even in the cation supply-limited regime ( years3) is shorter than the duration of late accretion (– years41).
Size distribution of impactors and accretion models
Our results suggest the dominance of small (km-sized) impactors during the late accretion. The nominal model assumed a change in the size distribution of impactors from shallower ( in , where N(D) is the number of objects of diameter smaller than D, and q is the power law index) for the main accretion phase to steeper (, main asteroid belt-like) for the late accretion phase (see “Methods”, Fig. 4a). The impact erosion by the late accretion which has a shallow size distribution is not sufficient to reproduce the BSE’s N-depletion because km-sized small bodies are the most efficient in ejecting the atmosphere per unit mass of the impactor12,42.
The case where Earth formed by multiple giant impacts followed by late accretion also reproduced the current BSE volatile composition (Fig. 4a); however, atmospheric erosion by small bodies during late accretion is needed to obtain the V-shaped C–N–H pattern anyway. Since atmospheric loss per unit impactor mass is less efficient in giant impacts than in planetesimal accretion, larger amounts of volatiles remained in the BSE. In addition, incomplete mixing between the impactor’s core and magma ocean lowered the storage in the core.
The combination of a moon-forming giant impact with continuous planetesimal accretion in our nominal model is a plausible accretion scenario for Earth. The dominance of planetesimal accretion and the change in the size distribution with time are naturally expected from the planet formation models. The giant impact stage was set in the time when the total mass in planetesimals remained comparable to the mass in protoplanets42–44. About half of giant impacts are not accretionary, but hit-and-run collisions which produce many fragments45. The change in size distribution from shallower to steeper is consistent with the inference that asteroids are born big and evolved through collisional cascades46,47. A size distribution of late accretion impactors shallower than that of our nominal model ( vs. ) has been proposed as the origin for the lunar depletion of highly siderophile elements (HSE) relative to Earth48, but the long-lived magma ocean on the Moon also serves alternative explanation41. Our scenario, in which Earth chiefly formed from a swarm of planetesimals, is in contrast to the pebble accretion model49 and the idea that attributes the Late Veneer to a single big impact50, although impact fragments may act as small “planetesimals” to eject atmospheric N efficiently in those cases.
The timing of the volatile delivery onto the accreting terrestrial planets remains an open question51. We assumed homogeneous accretion of CI chondritic building blocks combined with dry objects in the nominal model and investigated the dependence on the variety of Earth’s accretion models for both the volatile-rich late accretion9,52 and the heterogeneous accretion model53–55 (Fig. 4b). The latter two models, which assumed later addition of 100% CI chondrites accretion, result in much larger amounts of volatiles, especially for N, than the current BSE inventory. This means that the volatile content fraction of the late accretion impactors appears more significant factor than the total accumulated amount for explaining Earth’s N depletion. The uncertainty in the late accretion mass (0.5–2.5 wt%56) is considered in Fig. 4c. Greater late accretion can erode more N and accumulate more C, but V-shaped patterns were obtained over the range of mass estimates.
Magma ocean redox state
We explored how the redox state of the magma ocean affects the final volatile composition by considering oxidized (IW+1), intermediate (IW-2), and reduced (IW-3.5) conditions5 (see “Methods”). The current C–N–H depletion pattern can be obtained under the oxidized or intermediate magma ocean, while we ruled out the reduced condition (Fig. 4d). The redox state of the magma ocean, which successfully reproduces the BSE’s abundance of major volatile elements, has a relatively oxidized condition (). In the reduced model, the final amount of H corresponding to 1.15 ocean mass (0.15 ocean mass in the mantle) was obtained; this is even smaller than the minimum estimate for present-day Earth’s mantle water content of > 0.56 ocean masses4,5,17,57,58. The behaviour of element partitioning during the main accretion stage is determined by solubilities in the magma ocean and the partitioning coefficients between silicate melt and metal liquid, both of which depend on the pressure-temperature- conditions of the magma ocean. According to what is currently understood, C becomes soluble and less siderophile, N becomes insoluble, and H becomes far more soluble in silicate liquids under oxidized conditions compared with reduced conditions5,21,22,59,60. We note that assuming enstatite chondrites as volatile sources fits only with the oxidized model (Fig. S5).
Since the flux from the atmosphere to the core is proportional to the product of solubility and partitioning coefficient (see “Methods”), their influences on the resulting C cancelled each other out. The change in molecular masses (e.g., = 44 amu in the oxidized model to = 16 amu in the reduced model) also influences partial pressure and, consequently, effective solubility slightly, but the influence is not significant. For H, the storage in the magma ocean is important to reproduce the current BSE abundance and so high solubility under oxidizing conditions is required. We emphasize that even when we employed smaller values for the partitioning coefficient of H as argued by a few previous high-pressure metal-silicate partitioning experiments61,62, the final H amount does not increase under the reduced magma ocean (see Supplementary Fig. S6, case ’m’) because the low solubility in silicate melt limits the influence of partitioning into metal on the BSE’s budget, supporting the idea of a relatively oxidized magma ocean during Earth’s accretion.
The oxidizing magma ocean has been proposed by several studies and mechanisms to oxidize the magma ocean as Earth grew have been suggested63–65. Crystallization of perovskite at the depth of the lower mantle induces disproportion of ferrous to ferric iron plus iron metal, the latter of which would then sink to the core, with the remnant in the mantle being oxidized (named self-oxidation66). The pressure effect on a fixed / ratio leads to a redox gradient where the surface becomes more oxidized than the depth65,67. Both are natural outcomes of the formation of an Earth-sized planet. An increase in the mantle oxygen fugacity on growing Earth has been proposed by many heterogeneous accretion models to explain Earth’s bulk composition of refractory and moderately siderophile elements54,66,68,69. As shown in Fig. 3, the volatile distribution between the atmosphere, magma ocean, and metal soon converged towards quasi-steady state balancing of in/out fluxes of volatile elements within the first 20 wt% accretion. Given 20 wt% accretion being the mass required to reach the steady state for a give condition, the requirement for the redox state of the magma ocean () should be considered as that for the final 20 wt% planetesimal accretion before the giant impact. This result does not contradict the initial reduced condition followed by a more oxidized state.
Volatile predictions for Earth’s core, bulk Venus, and Mars
Our scenario for the origin of Earth’s volatile depletion pattern is testable with the further constraints of the composition of light elements in the core. The final mass fractions in the metallic core in our nominal model, assuming an oxidized magma ocean (IW+1), were 0.9 wt%, 0.004 wt%, and 0.2 wt%for C, N, and, H, respectively. These predicted contents of light elements are within the range of each element’s content allowance and account for approximately 30% of the Earth’s core density deficit70. Therefore, other light elements such as oxygen, silicon, and sulphur should also contribute to the core density deficit. The relatively oxidized magma ocean required from our results may support the large contribution of oxygen64. With upcoming data of solubilities and partitioning coefficients, this model will provide a more accurate estimate of Earth’s core composition (see also Supplementary Information).
Our model also predicts the different depletion patterns of major volatile elements in bulk Venus and Mars. Venus might never experience the condensation of liquid water and, consequently, carbonate precipitation on the surface28. The lack of H and C storage leads to atmospheric loss of these elements as well as N. If atmospheric is the dominant C reservoir of bulk Venus, the total amount of C for Venus is 0.4 times the value for Earth71, supporting the model prediction. In contrast, the formation of O and ice on early Mars72 allows the preferential loss of atmospheric N by impact erosion in the same manner as Earth14. From the analysis of SNC meteorites73,74, the Martian mantle is thought to be very reduced with (IW-1), and previous models have predicted a more reduced magma ocean for Mars than for Earth75,76. The reduced mantle would lead to a smaller storage of H in the magma ocean and a subsequent deficit of bulk H.
Methods
We calculated the abundances of C, N, and H in Earth growing from a Mars-sized embryo via accretion of planetesimals and protoplanets with a box model considering the partitioning between reservoirs and atmospheric erosion caused by impacts. We defined two stages: main accretion and late accretion stages (e.g., the growth from 10% to 99.5% and the final 0.5% of current Earth mass, respectively) in our nominal model. The former is also called the magma ocean stage. For each finite mass step of planetesimal accretion, we solved the deterministic differential equations formally given by,
| 1 |
where , , , and are the total mass of element i in BSE, planetary mass, the abundance of volatiles in impactors, and outflux per unit mass accretion by the process k, respectively. As the volatile loss processes (sinks), we considered the atmospheric escape through the full accretion and the core segregation only for the magma ocean stage. For each accretion step, the element partitioning between surface and interior reservoirs is calculated by the mass balance modelling,
| 2 |
where the atmosphere, silicate melt, and suspended metal in the magma ocean in the main accretion stage, the atmosphere, ocean, and sedimentary carbonate rocks in the late accretion stage are considered as reservoirs j (see below for details). Each giant impact is treated separately from the statistically averaged planetesimal accretion. We note that we confirmed numerical convergence by changing the step size of the cumulative accreted mass in our simulations.
Accretion model
In our model, Earth grows by accreting planetesimals and protoplanets during the main accretion phase, followed by late accretion composed only of planetesimals. For planet growth, we considered a change in the bulk density caused by pressure by using Eq. (3), which expresses the mass-radius relationship for planets with an Earth-like composition. Seager et al.77 showed a power-law relation between the masses and radii of solid planets by modelling their interior structures. They provided fitted formulas for rocky planets with 67.5 wt% + 32.5 wt% Fe as,
| 3 |
where and are the normalized radius and mass of terrestrial planets, is the fitting constants ( = 0.20945, 0.0804, 0.394), and r and are the conversion factors obtained as and ; we used modified in our study to match Earth’s mass and radius without changing the power-law index. The growth by planetesimal accretion was investigated by a statistical method14 where the contribution of each impact was averaged over their size and velocity distributions. The size distribution is given by a single power-law , where N(D) is the number of objects of diameter smaller than D and the index q is a parameter. We assumed a shallow size distribution with for the main accretion phase and a steep size distribution with , which corresponds to that of the present-day main belt asteroids46, for the late accretion phase in the nominal model, and investigated the dependence of the results by changing the power-law index (see main text). The minimum and maximum sizes are assumed to be km and km, respectively. We assumed a Rayleigh distribution for the random velocity of impactors as modelled by Sakuraba et al.14, which corresponds to the Gaussian eccentricity distribution for impactors from the terrestrial planet feeding zone excited by a protoplanet78. Each giant impact is included in a discrete way separately from continuous planetesimal accretion.
Volatiles have been delivered by the accreted bodies that have formed Earth. The building blocks of Earth are not fully understood and so we treat the abundance of volatiles in an impactor as an unknown parameter. We considered CI chondrites containing volatile elements which accreted with dry planetesimals11. CI chondrites contain 2–5 wt% C79–81, 500–2000 ppm N79–81, and 0.47–1.01 wt% ppm H79,80,82, and their atomic ratio of C/N is 17.0 ± 3.015. Enstatite chondrites contain 0.2–0.7 wt% C80,81, 100–500 ppm N81, and 90–600 ppm H83,84, and their C/N is 13.7 ± 12.115. In our model, we assumed the reference abundances as listed in Table 1. The fraction of CI chondrites was used as a parameter and set to be 12 wt% in the nominal model (Supplementary Fig. S2). The results for cases where enstatite chondritic impactors are considered as volatile sources are also shown in the Supplementary Information (Supplementary Fig. S3 and Fig. S4).
Table 1.
List of key parameters for the model calculations.
| C | N | H | C/N | C/H | |
|---|---|---|---|---|---|
| BSE [μg/g-Earth] | 42–730 | 0.83–2.5 | 44–450 | 40 ± 8 | 1.3 ± 0.3 |
| CI chondrites [ppm] | 20,000–50,000 | 500–2,000 | 4,700–10,500 | 14.5 ± 2.5 | 2–8 |
| CI model [ppm] | 35,000 | 1,500 | 6,900 | 23 | 5 |
| Enstatite chondrites [ppm] | 2,000–7,000 | 100–500 | 90–600 | 13.7± 12.1 | |
| EC model [ppm] | 4,000 | 250 | 400 | 16 | 10 |
| Oxidised model | |||||
| 1.6 | 1.0 | M98 model | |||
| 500 | 20 | 6.5 | |||
| Intermediate model | |||||
| 0.55 | 5.0 | M98 | |||
| 1000 | 20 | 6.5 | |||
| Reduced model | |||||
| 0.22 | 50 | 5.0 | |||
| 3,000 | 20 | 6.5 | |||
Observational data and model reference values for the abundances of C, N, and H in the bulk silicate Earth (BSE) and chondrites (assumed as building blocks, CI chondrites and enstatite chondrites). We set CI chondritic model, solubilities (the units are for reduced and for the others, where is the partial pressure of each molecule ), and the partitioning coefficients under each redox state by following Hirschmann5. (a) Hirschmann5, (b) Marty4, (c) Hirschmann17, (d) Bergin et al.15, (e) Hirschmann and Dasgupta124, (f) Grady and Wright81, (g) Vacher et al.82, (h) Kerridge79, (i) Piani et al.84, (j) Stolper and Holloway123, (k) Pan et al.20, (l) Libourel et al.114, (m) Moore et al.19, (n) Chi et al.100, (o) Armstrong et al.101, (p) Roskosz et al.103, (q) Okuchi102, (r) Wetzel et al.112, (s) Hirschmann et al.67.
Giant impactors would have experienced core-mantle differentiation and volatile loss by atmospheric erosion. We calculated the abundances of C, N, and H in protoplanets by running our model for the growth by planetesimal accretion in advance from 0.05 to 0.1 Earth masses and then adapted the result to the compositions of giant impactors.
We assumed that 32.5 wt% of the impactor mass is added to Earth as metallic iron regardless of the impactor type to reproduce the mass fraction of Earth’s core. The metal mass fraction is not necessarily equal to that of impactors because the former would be controlled by redox reactions (namely, the oxygen fugacity of the magma ocean), which are not explicitly modelled in our study.
Atmospheric erosion and loss of impactors
Atmospheric erosion and loss of the impactors themselves through planetesimal accretion are computed as compiled by Sakuraba et al.14. The net impact-induced escaping flux per unit impactor mass is given by
| 4 |
where is the abundance of volatiles in the impactor, is the erosion efficiency of the atmosphere, and is the escaping efficiency of the impactor vapor, and calculated for each element i. The erosion and escaping efficiencies for a single impact can be estimated from input impactor’s size and impact velocity. We calculated the efficiencies statistically-averaged over both impactor’s size and velocity distributions assumed in the above accretion model. We adopted the scaling laws obtained by numerical simulations for the atmospheric escape and for loss of an impactor’s vapour. Realistic numerical simulations of atmospheric erosion were given in 3D geometry by Shuvalov85, and in 2D cylindrical geometry by Svetsov86. In Sakuraba et al.14, the Svetsov model86,87 and Shuvalov model85 are adopted for the atmospheric erosion efficiency (Equation 5 in Sakuraba et al.14) and the impactor’s escaping efficiency (Equation 8 in Sakuraba et al.14), respectively. The effect of oblique impacts that enhance the impact erosion is considered by including the angle-averaged factor estimated by Shuvalov model85. The volatiles in the fraction of impactors that avoided the loss are released to the atmosphere and then partitioned into other reservoirs. Since the atmospheric loss mass is proportional to the abundance of each species in the atmosphere, element partitioning between the atmosphere and the other solid or liquid reservoirs is important for atmospheric erosion14. We used the surface temperatures, 1,500 K for the main accretion stage and 288 K for the late accretion stage, given below to compute the atmospheric density and scale height, but we confirmed that the results are insensitive to the atmospheric temperature (Supplementary Fig. S1a).
For each giant impact, we calculated the atmospheric loss from the mixture of the proto-atmosphere and the impactor’s atmosphere caused by the global ground motion by using the model of Schlichting et al.42. We assumed Mars-sized (0.1 Earth masses) impactors whose impact velocity is 1.1 times the mutual escape velocity as commonly considered for the Moon-forming impact (see, for example, Hosono et al.88). We note that the estimates for the giant impact velocity has uncertainty from 1.0 to 1.2 times the escape velocity89. We also note that recent 3D smoothed particle hydrodynamics simulations90,91 suggest a lower erosion efficiency than that of Schlichting model by a factor of 3. However, we found that the dependence on the atmospheric erosion efficiency by a giant impact was negligible even if the atmospheric erosion was more or less efficient by a factor of three (Supplementary Fig. S1b) owing to the range in uncertainty arising from the velocity of a giant impact and/or the model dependency.
Core segregation
We considered the core segregation under the solidified mantle in the magma ocean stage by excluding the segregated metal from the equilibrium partitioning calculation. Core-forming liquid metal droplets carry volatile elements from the magma ocean to the metal pond, and consequently, to the core. We assumed the suspended metal fraction in the magma ocean to be constant; then, the net segregation flux per unit impactor mass is given by
| 5 |
where , , , and are the volatile concentration in the metal, the metal fraction of the newly accreted mass (assumed to be 32.5 wt%), the melting fraction of the planet, and the metal mass fraction in the magma ocean, respectively. Our model is based upon previous studies5,15 that assumed that core-mantle separation is a single stage event as a simplification, but we improved the model to track time evolution through accretion, where core formation is a contentious process.
During growth by planetesimal accretion, the mass fraction of the molten magma ocean was fixed to 30 wt% of the planetary mass. This was derived from the estimated depth of the magma ocean (30%-40% of the mantle) constrained from the abundance of refractory siderophile elements (Ni and Co) in the present-day mantle66. A deeper magma ocean is also suggested68, but we confirmed that the results do not change significantly even if we consider a deeper magma ocean of up to 60 wt% (see Supplementary Fig. S1c).
As the Earth grows, the metal droplets descend through the deep magma ocean, continuously equilibrating with the silicate liquid92. Metal droplets that have reached the base of the magma ocean forms metal ponds and subsequently descend as large diapirs to the growing core without further equilibration with the surrounding silicate66. The metal in the magma ocean is assumed to be in equilibrium with the entire magma ocean and the mass fraction of the suspended metal is fixed to . This reference value is estimated from the typical timescales of metal droplets settling ( years93) and accretion of the Earth ( years94) by,
| 6 |
The settling timescale of the metal droplets was estimated from the magma ocean depth –10 km divided by the settling velocity 0.5 cm/s92. In fact it evolves with time, but we confirmed that the results do not depend on the suspended metal fraction unless it exceeds 10 because metal droplets carry almost the same mass of volatiles in total anyway (Supplementary Fig. S1d). The sum of remaining fraction of metal is assumed to have segregated from the magma ocean into the metal pond and, subsequently, into the core and are treated as one isolated reservoir.
In contrast to planetesimal accretion, giant impacts lead to a deeper magma ocean and incomplete mixing between the magma ocean and the core of the impactor. Since the Mars-sized moon-forming giant impact is thought to have delivered enough energy to completely melt the whole mantle95, we assumed a fully molten mantle after the giant impacts (see, for example, Canup25). Moreover, we confirmed that assuming partial melting for a giant impact does not change our results significantly (Supplementary Fig. S1c). For metal–silicate mixing in re-equilibration between the impactor’s core and proto-magma ocean, we considered turbulent entrainment by applying the formula of the metal fraction in the metal-silicate mixture to the completely molten mantle (Equation 6 in Degen et al.96).
The solidified mantle is assumed to be volatile free and is not considered as a reservoir because of its low capacity compared with the magma ocean (see, for example, Elkins-Tanton10). In terms of H and C, it is suggested that considerable amounts could be retained in the residual solid mantle as melt inclusions upon magma ocean solidification97, but this would not affect the final BSE inventory estimates. While we did not consider the volatile trapping by the solid silicate reservoir during the crystallization of the magma ocean, we did consider efficient trapping of outgassed H and C into the oceans and the crustal carbonate reservoirs as well as the mantle, respectively, which are included as BSE abundances. Whether H and C are trapped in the mantle or in the surface reservoirs does not affect the evolution of the BSE volatile contents. In the case of N, since the N partitioning coefficient between mantle minerals and silicate melt is smaller than unity by orders of magnitude even under high temperature98, almost all N would have been enriched in the melt during the crystallization and subsequently outgassed to form the early atmosphere. Hier-Majumder and Hirschmann97 showed that owing to extremely low solubility of , N retention into the residual mantle is inefficient. For these reasons, the incorporation of volatiles into the solidified mantle does not change our conclusions.
Equilibrium partitioning in magma ocean
We calculated the partitioning of elements between the magma ocean, core-forming alloy, and overlying atmosphere (Fig. 1a), assuming equilibrium partitioning. For the element partitioning between these three reservoirs, the mass balance equation (Eq. 2) can be written as,
| 7 |
where is the partial pressures, g is the gravitational acceleration given by , where G is the gravitational constant, is the mean molecular mass of the atmosphere, is the molecular mass of the volatile species, is the mass ratio of the volatile species to the element of interest (e.g., for C, for N, for H in the oxidized condition), is the mass concentration in the silicate and metal, and and are the masses of the magma ocean and the metal liquid in the magma ocean. The partition coefficient which characterizes elemental partitioning between silicate and metal can be written as,
| 8 |
Equilibrium between the atmosphere and the underlying silicate melt is given by a solubility law, that in many cases can be approximated by a Henrian constant,
| 9 |
where x is the ratio of the number of atoms between gas and solute phases for the element of interest (e.g., for C and N, for H, see below).
We defined three models for the redox state of the magma ocean: the oxidized (), intermediate (IW-2), and reduced (IW-3.5) conditions5, where is the oxygen fugacity, is defined hereafter as , and is at the iron-wüstite buffer. We call the redox state of an ’intermediate’ condition because it corresponds to that estimated for a single stage core formation scenario99. As proposed by several studies64,65, we assumed an oxidized magma ocean in the nominal model, and investigated the dependence of the results by changing the redox state. The conditions for the metal-silicate equilibrium at the bottom of Earth’s magma ocean were estimated to be at 40 GPa from Ni and Co partitioning, and at 3750 K from V and Cr partitioning54. We assumed the partitioning coefficients thought to be applicable to these high P-T conditions mentioned above for each redox state model (Refs.100–103) as tabulated by Hirschmann5 (see Table 1). Since the dependence of the partitioning coefficients on P-T- conditions has not been fully understood, we additionally investigated the sensitivity of our model by varying partitioning coefficients for a wide range suggested from the literature: = 0.5–567018,22,59,62,100,101,104,105, = 0.003–15016,22,23,103,106–108 , and = 0.2–10061,62,102,109–111 (Supplementary Text, Supplementary Table S1 and Supplementary Fig. S6).
We considered different atmospheric components and used the constant solubilities and partitioning coefficients for each redox state model: , , and O for the nominal oxidized model; CO, , and for the intermediate model; and , , and for the reduced model. All these species of molecules in the atmosphere are assumed by following Hirschmann5. As summarised in Table 1, we fixed solubilities for C and N and used the Moore model19 for H by following Hirschman5. Considering the range of solubilities reported by experimental studies, we also tested the model sensitivity for = (0.002–8) ppm20,60,101,112,113, = (0.2–46) ppm21,114,115. For , we tested for more and less soluble cases than the Moore model by a factor of two (Supplementary Text, Supplementary Table S1, and Fig. S6). By substituting Eq. (8) and (9) to Eq. (5), we can get the relationship of which means that the volatile flux of core segregation is proportional to the product of solubility and the partitioning coefficient of each element i5.
Late accretion stage surface environment
As we defined the late accretion as the last 0.5 wt% accretion, we examined whether the surface could melt again after the magma ocean solidification by roughly estimating the energy balance between the gravitational accretion and the planetary radiation from the oceanic surface during late accretion. The input accretional energy is estimated by , where is 0.5 wt% of the Earth mass and years48 is the timescale of the late accretion. The maximum outgoing planetary radiation flux is estimated by assuming the radiation limit from the saturated atmosphere (300 W/116–118). As a result, the latter exceeded the former by 2 orders of magnitude and confirmed that the planetary surface would not melt again during the late accretion.
We assumed the formation of the oceans and onset of the carbonate-silicate cycle (Fig. 1b) as modelled by Sakuraba et al.14. For the surface conditions, it is suggested that the oceans have formed within the several Myrs after the Moon-forming giant impact by calculating the timescale of the magma ocean solidification26–28. Furthermore, voluminous oceans underlain by a dry mantle, like that right after the magma ocean solidification, create an ideal situation to drive plate tectonics33,119. The carbonate-silicate cycle is believed to have stabilized the Earth’s climate over a long geological timescale against the increase in solar luminosity over the past 4 billion years120. As long as its negative feedbacks of temperature-dependent continental and seafloor weathering has been driven throughout Earth history as assumed here, the early climate was likely temperate, with temperatures on Earth is estimated to be 273–370 K35,121. Since we confirmed that dependence on the temperature within this range is negligible (the figure not shown), we assumed the present-day global mean temperature of T = 288 K as the reference value. We calculated the partitioning of elements between the atmosphere, oceans, and crust plus mantle. The vapour-liquid equilibrium sets an upper limit to the partial pressure of O in the atmosphere, 122, calculated for the assumed surface temperature of 288 K. We impose the negative feedback of the carbonate-silicate cycle by simply setting an upper limit to the partial pressure of bar, as expected for the steady state121. Neglecting the time lag to reach the steady state is justified by considering the short timescale of carbonate precipitation compared with the duration of late accretion (see main text). Atmospheric H and C in excess from the upper limits are partitioned into oceans and crust plus mantle reservoirs, respectively.
Initial condition
We prepared the initial condition for the elemental abundances by assuming a chondritic bulk composition the same as planetesimal impactors and equilibrium partitioning between the atmosphere, the fully molten magma ocean, and the core. While this is a crude assumption that neglects the complexity of how planetary embryos formed, we have confirmed that the results are insensitive to the initial condition because the system soon evolves towards the quasi-steady state between the gain and loss of volatile elements.
Supplementary information
Acknowledgements
This work was supported by JSPS KAKENHI Grant No. 19J21445, 18K13602, and MEXT KAKENHI Grant No. JP17H06457.
Author contributions
H.S., H.K., H.G., and K.O. designed the project; H.S. performed the numerical simulations and analysed the results; H.S. and H.K. interpreted the results and wrote the manuscript.
Code availability
The codes used to generate these results and the data that support the findings of this study are available at http://www.geo.titech.ac.jp/lab/okuzumi/sakuraba/Contents.html.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
The online version contains supplementary material available at 10.1038/s41598-021-99240-w.
References
- 1.Abbot DS, Cowan NB, Ciesla FJ. Indication of insensitivity of planetary weathering behavior and habitable zone to surface land fraction. Astrophys. J. 2012;756:178. doi: 10.1088/0004-637X/756/2/178. [DOI] [Google Scholar]
- 2.Wordsworth, R. & Pierrehumbert, R. Hydrogen-nitrogen greenhouse warming in Earth’s early atmosphere. Science339, 64–67 (2013). [DOI] [PubMed]
- 3.Foley BJ. The role of plate tectonic-climate coupling and exposed land area in the development of habitable climates on rocky planets. Astrophys. J. 2015;812:36. doi: 10.1088/0004-637X/812/1/36. [DOI] [Google Scholar]
- 4.Marty B. The origins and concentrations of water, carbon, nitrogen and noble gases on Earth. Earth Planet. Sci. Lett. 2012;313:56–66. doi: 10.1016/j.epsl.2011.10.040. [DOI] [Google Scholar]
- 5.Hirschmann, M. M. Constraints on the early delivery and fractionation of Earth’s major volatiles from C/H, C/N, and C/S ratios. Am. Mineral.101, 540–553 (2016).
- 6.Halliday AN. The origins of volatiles in the terrestrial planets. Geochim. Cosmochim. Acta. 2013;105:146–171. doi: 10.1016/j.gca.2012.11.015. [DOI] [Google Scholar]
- 7.Walsh, K. J., Morbidelli, A., Raymond, S. N., O’brien, D.P. & Mandell, A. M. A low mass for Mars from Jupiter’s early gas-driven migration. Nature475, 206–209 (2011). [DOI] [PubMed]
- 8.Dauphas, N. The isotopic nature of the Earth’s accreting material through time. Nature541, 521–524 (2017). [DOI] [PubMed]
- 9.Fischer-Gödde, M. et al. Ruthenium isotope vestige of Earth’s pre-late-veneer mantle preserved in Archaean rocks. Nature579, 240–244 (2020). [DOI] [PMC free article] [PubMed]
- 10.Elkins-Tanton LT. Linked magma ocean solidification and atmospheric growth for Earth and Mars. Earth Planet. Sci. Lett. 2008;271:181–191. doi: 10.1016/j.epsl.2008.03.062. [DOI] [Google Scholar]
- 11.Dasgupta, R. & Grewal, D. S. Origin and early differentiation of carbon and associated life-essential volatile elements on earth. In Deep Carbon, 4–39 (Cambridge University Press, 2019).
- 12.de Niem D, Kührt E, Morbidelli A, Motschmann U. Atmospheric erosion and replenishment induced by impacts upon the Earth and Mars during a heavy bombardment. Icarus. 2012;221:495–507. doi: 10.1016/j.icarus.2012.07.032. [DOI] [Google Scholar]
- 13.Genda H, Abe Y. Enhanced atmospheric loss on protoplanets at the giant impact phase in the presence of oceans. Nature. 2005;433:842–844. doi: 10.1038/nature03360. [DOI] [PubMed] [Google Scholar]
- 14.Sakuraba H, Kurokawa H, Genda H. Impact degassing and atmospheric erosion on Venus, Earth, and Mars during the late accretion. Icarus. 2019;317:48–58. doi: 10.1016/j.icarus.2018.05.035. [DOI] [Google Scholar]
- 15.Bergin EA, Blake GA, Ciesla F, Hirschmann MM, Li J. Tracing the ingredients for a habitable earth from interstellar space through planet formation. Proc. Natl. Acad. Sci. 2015;112:8965–8970. doi: 10.1073/pnas.1500954112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Grewal DS, Dasgupta R, Sun C, Tsuno K, Costin G. Delivery of carbon, nitrogen, and sulfur to the silicate Earth by a giant impact. Sci. Adv. 2019;5:eaau3669. doi: 10.1126/sciadv.aau3669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Hirschmann MM. Comparative deep Earth volatile cycles: The case for C recycling from exosphere/mantle fractionation of major (O, C, N) volatiles and from O/Ce, /Ba, and /Nb exosphere ratios. Earth Planet. Sci. Lett. 2018;502:262–273. doi: 10.1016/j.epsl.2018.08.023. [DOI] [Google Scholar]
- 18.Dasgupta R, Chi H, Shimizu N, Buono AS, Walker D. Carbon solution and partitioning between metallic and silicate melts in a shallow magma ocean: Implications for the origin and distribution of terrestrial carbon. Geochim. Cosmochim. Acta. 2013;102:191–212. doi: 10.1016/j.gca.2012.10.011. [DOI] [Google Scholar]
- 19.Moore G, Vennemann T, Carmichael I. An empirical model for the solubility of O in magmas to 3 kilobars. Am. Mineral. 1998;83:36–42. doi: 10.2138/am-1998-1-203. [DOI] [Google Scholar]
- 20.Pan V, Holloway JR, Hervig RL. The pressure and temperature dependence of carbon dioxide solubility in tholeiitic basalt melts. Geochim. Cosmochim. Acta. 1991;55:1587–1595. doi: 10.1016/0016-7037(91)90130-W. [DOI] [Google Scholar]
- 21.Miyazaki A, Hiyagon H, Sugiura N, Hirose K, Takahashi E. Solubilities of nitrogen and noble gases in silicate melts under various oxygen fugacities: implications for the origin and degassing history of nitrogen and noble gases in the Earth. Geochim. Cosmochim. Acta. 2004;68:387–401. doi: 10.1016/S0016-7037(03)00484-8. [DOI] [Google Scholar]
- 22.Dalou C, Hirschmann MM, von der Handt A, Mosenfelder J, Armstrong LS. Nitrogen and carbon fractionation during core-mantle differentiation at shallow depth. Earth Planet. Sci. Lett. 2017;458:141–151. doi: 10.1016/j.epsl.2016.10.026. [DOI] [Google Scholar]
- 23.Grewal DS, Dasgupta R, Hough T, Farnell A. Rates of protoplanetary accretion and differentiation set nitrogen budget of rocky planets. Nat. Geosci. 2021;14:369–376. doi: 10.1038/s41561-021-00733-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Canup, R. M. & Asphaug, E. Origin of the Moon in a giant impact near the end of the Earth’s formation. Nature412, 708–712 (2001). [DOI] [PubMed]
- 25.Canup RM. Simulations of a late lunar-forming impact. Icarus. 2004;168:433–456. doi: 10.1016/j.icarus.2003.09.028. [DOI] [Google Scholar]
- 26.Salvador, A. et al. The relative influence of HO and CO on the primitive surface conditions and evolution of rocky planets. J. Geophys. Res. Planets (2017).
- 27.Nikolaou A, et al. What factors affect the duration and outgassing of the terrestrial magma ocean? Astrophys. J. 2019;875:11. doi: 10.3847/1538-4357/ab08ed. [DOI] [Google Scholar]
- 28.Hamano K, Abe Y, Genda H. Emergence of two types of terrestrial planet on solidification of magma ocean. Nature. 2013;497:607–610. doi: 10.1038/nature12163. [DOI] [PubMed] [Google Scholar]
- 29.Appel PW, Fedo CM, Moorbath S, Myers JS. Early Archaean Isua supracrustal belt, West Greenland: pilot study of the Isua multidisciplinary research project. Geol. Greenl. Surv. Bull. 1998;180:94–99. doi: 10.34194/ggub.v180.5092. [DOI] [Google Scholar]
- 30.Komiya T, et al. Plate tectonics at 3.8–3.7 Ga: Field evidence from the Isua accretionary complex, southern West Greenland. J. Geol. 1999;107:515–554. doi: 10.1086/314371. [DOI] [PubMed] [Google Scholar]
- 31.Wilde SA, Valley JW, Peck WH, Graham CM. Evidence from detrital zircons for the existence of continental crust and oceans on the Earth 4.4 Gyr ago. Nature. 2001;409:175–178. doi: 10.1038/35051550. [DOI] [PubMed] [Google Scholar]
- 32.Hopkins M, Harrison TM, Manning CE. Low heat flow inferred from 4 Gyr zircons suggests Hadean plate boundary interactions. Nature. 2008;456:493–496. doi: 10.1038/nature07465. [DOI] [PubMed] [Google Scholar]
- 33.Korenaga J. Initiation and evolution of plate tectonics on Earth: Theories and observations. Annu. Rev. Earth Planet. Sci. 2013;41:117–151. doi: 10.1146/annurev-earth-050212-124208. [DOI] [Google Scholar]
- 34.Foley BJ. Habitability of Earth-like stagnant lid planets: Climate evolution and recovery from snowball states. Astrophys. J. 2019;875:72. doi: 10.3847/1538-4357/ab0f31. [DOI] [Google Scholar]
- 35.Krissansen-Totton, J., Arney, G. N. & Catling, D. C. Constraining the climate and ocean pH of the early Earth with a geological carbon cycle model. Proc. Natl. Acad. Sci. 201721296 (2018). [DOI] [PMC free article] [PubMed]
- 36.Pierrehumbert RT. Principles of Planetary Climate. Cambridge University Press; 2010. [Google Scholar]
- 37.Tucker JM, Mukhopadhyay S. Evidence for multiple magma ocean outgassing and atmospheric loss episodes from mantle noble gases. Earth Planet. Sci. Lett. 2014;393:254–265. doi: 10.1016/j.epsl.2014.02.050. [DOI] [Google Scholar]
- 38.Hu R, Diaz HD. Stability of nitrogen in planetary atmospheres in contact with liquid water. Astrophys. J. 2019;886:126. doi: 10.3847/1538-4357/ab4cea. [DOI] [Google Scholar]
- 39.Stüeken, E. E., Kipp, M. A., Koehler, M. C. & Buick, R. The evolution of Earth’s biogeochemical nitrogen cycle. Earth-Science Reviews160, 220–239 (2016).
- 40.Catling DC, Zahnle KJ. The Archean atmosphere. Sci. Adv. 2020;6:eaax1420. doi: 10.1126/sciadv.aax1420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Morbidelli A, et al. The timeline of the lunar bombardment: Revisited. Icarus. 2018;305:262–276. doi: 10.1016/j.icarus.2017.12.046. [DOI] [Google Scholar]
- 42.Schlichting HE, Sari R, Yalinewich A. Atmospheric mass loss during planet formation: The importance of planetesimal impacts. Icarus. 2015;247:81–94. doi: 10.1016/j.icarus.2014.09.053. [DOI] [Google Scholar]
- 43.Goldreich P, Lithwick Y, Sari R. Final stages of planet formation. Astrophys. J. 2004;614:497. doi: 10.1086/423612. [DOI] [Google Scholar]
- 44.Kenyon SJ, Bromley BC. Terrestrial planet formation. I. The transition from oligarchic growth to chaotic growth. Astron. J. 2006;131:1837. doi: 10.1086/499807. [DOI] [Google Scholar]
- 45.Kokubo E, Genda H. Formation of terrestrial planets from protoplanets under a realistic accretion condition. Astrophys. J. Lett. 2010;714:L21. doi: 10.1088/2041-8205/714/1/L21. [DOI] [Google Scholar]
- 46.Bottke WF, et al. The fossilized size distribution of the main asteroid belt. Icarus. 2005;175:111–140. doi: 10.1016/j.icarus.2004.10.026. [DOI] [Google Scholar]
- 47.Bottke W, et al. Dating the Moon-forming impact event with asteroidal meteorites. Science. 2015;348:321–323. doi: 10.1126/science.aaa0602. [DOI] [PubMed] [Google Scholar]
- 48.Bottke WF, Nesvornỳ D, Vokrouhlický D, Morbidelli A. The irregular satellites: The most collisionally evolved populations in the Solar System. Astron. J. 2010;139:994. doi: 10.1088/0004-6256/139/3/994. [DOI] [Google Scholar]
- 49.Levison HF, Kretke KA, Walsh KJ, Bottke WF. Growing the terrestrial planets from the gradual accumulation of submeter-sized objects. Proc. Natl. Acad. Sci. 2015;112:14180–14185. doi: 10.1073/pnas.1513364112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Brasser R, Mojzsis S, Werner S, Matsumura S, Ida S. Late veneer and late accretion to the terrestrial planets. Earth Planet. Sci. Lett. 2016;455:85–93. doi: 10.1016/j.epsl.2016.09.013. [DOI] [Google Scholar]
- 51.Albarede F. Volatile accretion history of the terrestrial planets and dynamic implications. Nature. 2009;461:1227–1233. doi: 10.1038/nature08477. [DOI] [PubMed] [Google Scholar]
- 52.Chou, C. L. Fractionation of siderophile elements in the Earth’s upper mantle. Lunar Planet. Sci.IX, 219–230 (1978).
- 53.Wänke, H., Dreibus, G. & Jagoutz, E. Mantle chemistry and accretion history of the Earth. In Archaean geochemistry, 1–24 (Springer, 1984).
- 54.Wade J, Wood B. Core formation and the oxidation state of the earth. Earth Planet. Sci. Lett. 2005;236:78–95. doi: 10.1016/j.epsl.2005.05.017. [DOI] [Google Scholar]
- 55.Schönbächler M, Carlson R, Horan M, Mock T, Hauri E. Heterogeneous accretion and the moderately volatile element budget of earth. Science. 2010;328:884–887. doi: 10.1126/science.1186239. [DOI] [PubMed] [Google Scholar]
- 56.Marchi S, Canup R, Walker R. Heterogeneous delivery of silicate and metal to the Earth by large planetesimals. Nat. Geosci. 2018;11:77. doi: 10.1038/s41561-017-0022-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Korenaga, J., Planavsky, N. J. & Evans, D. A. Global water cycle and the coevolution of the Earth’s interior and surface environment. Philos. Trans. R. Soc. A375, 20150393 (2017). [DOI] [PMC free article] [PubMed]
- 58.Peslier, A. H., Schönbächler, M., Busemann, H. & Karato, S.-I. Water in the Earth’s interior: distribution and origin. Space Science Reviews212, 743–810 (2017).
- 59.Tsuno K, Grewal DS, Dasgupta R. Core-mantle fractionation of carbon in Earth and Mars: The effects of sulfur. Geochim. Cosmochim. Acta. 2018;238:477–495. doi: 10.1016/j.gca.2018.07.010. [DOI] [Google Scholar]
- 60.Bureau H, Pineau F, Métrich N, Semet M, Javoy M. A melt and fluid inclusion study of the gas phase at Piton de la Fournaise volcano (Réunion Island) Chem. Geol. 1998;147:115–130. doi: 10.1016/S0009-2541(97)00176-9. [DOI] [Google Scholar]
- 61.Clesi V, et al. Low hydrogen contents in the cores of terrestrial planets. Sci. Adv. 2018;4:e1701876. doi: 10.1126/sciadv.1701876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Malavergne V, et al. Experimental constraints on the fate of H and C during planetary core-mantle differentiation. Implic. Earth. Icarus. 2019;321:473–485. doi: 10.1016/j.icarus.2018.11.027. [DOI] [Google Scholar]
- 63.Siebert J, Badro J, Antonangeli D, Ryerson FJ. Terrestrial accretion under oxidizing conditions. Science. 2013;339:1194–1197. doi: 10.1126/science.1227923. [DOI] [PubMed] [Google Scholar]
- 64.Badro J, Brodholt JP, Piet H, Siebert J, Ryerson FJ. Core formation and core composition from coupled geochemical and geophysical constraints. Proc. Natl. Acad. Sci. 2015;112:12310–12314. doi: 10.1073/pnas.1505672112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Armstrong, K., Frost, D. J., McCammon, C. A., Rubie, D. C. & Ballaran, T. B. Deep magma ocean formation set the oxidation state of Earth’s mantle. Science365, 903–906 (2019). [DOI] [PubMed]
- 66.Wood BJ, Walter MJ, Wade J. Accretion of the Earth and segregation of its core. Nature. 2006;441:825. doi: 10.1038/nature04763. [DOI] [PubMed] [Google Scholar]
- 67.Hirschmann M, Withers A, Ardia P, Foley N. Solubility of molecular hydrogen in silicate melts and consequences for volatile evolution of terrestrial planets. Earth Planet. Sci. Lett. 2012;345:38–48. doi: 10.1016/j.epsl.2012.06.031. [DOI] [Google Scholar]
- 68.Fischer RA, et al. High pressure metal-silicate partitioning of Ni Co, V, Cr, Si, and O. Geochim. Cosmochim. Acta. 2015;167:177–194. doi: 10.1016/j.gca.2015.06.026. [DOI] [Google Scholar]
- 69.Rubie DC, et al. Accretion and differentiation of the terrestrial planets with implications for the compositions of early-formed Solar System bodies and accretion of water. Icarus. 2015;248:89–108. doi: 10.1016/j.icarus.2014.10.015. [DOI] [Google Scholar]
- 70.Hirose K, Labrosse S, Hernlund J. Composition and state of the core. Annu. Rev. Earth Planet. Sci. 2013;41:657–691. doi: 10.1146/annurev-earth-050212-124007. [DOI] [Google Scholar]
- 71.Dauphas, N. & Morbidelli, A. 6.1 - Geochemical and Planetary Dynamical Views on the origin of Earth’s Atmosphere and Oceans. In Holland, H. D. & Turekian, K. K. (eds.) Treatise on Geochemistry (Second Edition), 1–35 (Elsevier, Oxford, 2014).
- 72.Forget F, et al. 3d modelling of the early Martian climate under a denser atmosphere: Temperatures and ice clouds. Icarus. 2013;222:81–99. doi: 10.1016/j.icarus.2012.10.019. [DOI] [Google Scholar]
- 73.Wadhwa, M. Redox state of Mars’ upper mantle and crust from Eu anomalies in shergottite pyroxenes. Science291, 1527–1530 (2001). [DOI] [PubMed]
- 74.Herd CD, Borg LE, Jones JH, Papike JJ. Oxygen fugacity and geochemical variations in the Martian basalts: Implications for Martian basalt petrogenesis and the oxidation state of the upper mantle of Mars. Geochim. Cosmochim. Acta. 2002;66:2025–2036. doi: 10.1016/S0016-7037(02)00828-1. [DOI] [Google Scholar]
- 75.Hirschmann MM, Withers AC. Ventilation of from a reduced mantle and consequences for the early Martian greenhouse. Earth Planet. Sci. Lett. 2008;270:147–155. doi: 10.1016/j.epsl.2008.03.034. [DOI] [Google Scholar]
- 76.Zhang H, Hirschmann M, Cottrell E, Withers A. Effect of pressure on Fe/Fe ratio in a mafic magma and consequences for magma ocean redox gradients. Geochim. Cosmochim. Acta. 2017;204:83–103. doi: 10.1016/j.gca.2017.01.023. [DOI] [Google Scholar]
- 77.Seager S, Kuchner M, Hier-Majumder C, Militzer B. Mass-radius relationships for solid exoplanets. Astrophys. J. 2007;669:1279. doi: 10.1086/521346. [DOI] [Google Scholar]
- 78.Ida S, Makino J. N-body simulation of gravitational interaction between planetesimals and a protoplanet: I. Velocity distribution of planetesimals. Icarus. 1992;96:107–120. doi: 10.1016/0019-1035(92)90008-U. [DOI] [Google Scholar]
- 79.Kerridge JF. Carbon, hydrogen and nitrogen in carbonaceous chondrites: Abundances and isotopic compositions in bulk samples. Geochim. Cosmochim. Acta. 1985;49:1707–1714. doi: 10.1016/0016-7037(85)90141-3. [DOI] [PubMed] [Google Scholar]
- 80.Pepin RO. On the origin and early evolution of terrestrial planet atmospheres and meteoritic volatiles. Icarus. 1991;92:2–79. doi: 10.1016/0019-1035(91)90036-S. [DOI] [Google Scholar]
- 81.Grady MM, Wright IP. Elemental and isotopic abundances of carbon and nitrogen in meteorites. Space Sci. Rev. 2003;106:231–248. doi: 10.1023/A:1024645906350. [DOI] [Google Scholar]
- 82.Vacher LG, et al. Hydrogen in chondrites: Influence of parent body alteration and atmospheric contamination on primordial components. Geochim. Cosmochim. Acta. 2020;281:53–66. doi: 10.1016/j.gca.2020.05.007. [DOI] [Google Scholar]
- 83.Robert F. The D/H ratio in chondrites. Space Sci. Rev. 2003;106:87–101. doi: 10.1023/A:1024629402715. [DOI] [Google Scholar]
- 84.Piani, L. et al. Earth’s water may have been inherited from material similar to enstatite chondrite meteorites. Science369, 1110–1113 (2020). [DOI] [PubMed]
- 85.Shuvalov V. Atmospheric erosion induced by oblique impacts. Meteorit. Planetary Sci. 2009;44:1095–1105. doi: 10.1111/j.1945-5100.2009.tb01209.x. [DOI] [Google Scholar]
- 86.Svetsov V. Atmospheric erosion and replenishment induced by impacts of cosmic bodies upon the Earth and Mars. Sol. Syst. Res. 2007;41:28–41. doi: 10.1134/S0038094607010030. [DOI] [Google Scholar]
- 87.Svetsov V. On the efficiency of the impact mechanism of atmospheric erosion. Solar Syst. Res. 2000;34:398–410. [Google Scholar]
- 88.Hosono, N., Karato, S.-I., Makino, J. & Saitoh, T. R. Terrestrial magma ocean origin of the Moon. Nat. Geosci. 1 (2019).
- 89.Kaib NA, Cowan NB. The feeding zones of terrestrial planets and insights into Moon formation. Icarus. 2015;252:161–174. doi: 10.1016/j.icarus.2015.01.013. [DOI] [Google Scholar]
- 90.Kegerreis J, et al. Planetary giant impacts: convergence of high-resolution simulations using efficient spherical initial conditions and swift. Mon. Not. R. Astron. Soc. 2019;487:5029–5040. doi: 10.1093/mnras/stz1606. [DOI] [Google Scholar]
- 91.Kegerreis JA, et al. Atmospheric erosion by giant impacts onto terrestrial planets: A scaling law for any speed, angle, mass, and density. Astrophys. J. Lett. 2020;901:L31. doi: 10.3847/2041-8213/abb5fb. [DOI] [Google Scholar]
- 92.Rubie D, Melosh H, Reid J, Liebske C, Righter K. Mechanisms of metal-silicate equilibration in the terrestrial magma ocean. Earth Planet. Sci. Lett. 2003;205:239–255. doi: 10.1016/S0012-821X(02)01044-0. [DOI] [Google Scholar]
- 93.Rubie, D., Nimmo, F. & Melosh, H. Formation of Earth’s Core. Treatise on Geophysics. V. 1/Ed. in Chief G. Schubert (Elsevier B.V., 2015).
- 94.Kleine T, Münker C, Mezger K, Palme H. Rapid accretion and early core formation on asteroids and the terrestrial planets from hf-w chronometry. Nature. 2002;418:952. doi: 10.1038/nature00982. [DOI] [PubMed] [Google Scholar]
- 95.Pritchard M, Stevenson D. Thermal aspects of a lunar origin by giant impact. Orig. Earth Moon. 2000;1:179–196. doi: 10.2307/j.ctv1v7zdrp.16. [DOI] [Google Scholar]
- 96.Deguen R, Olson P, Cardin P. Experiments on turbulent metal-silicate mixing in a magma ocean. Earth Planet. Sci. Lett. 2011;310:303–313. doi: 10.1016/j.epsl.2011.08.041. [DOI] [Google Scholar]
- 97.Hier-Majumder, S. & Hirschmann, M. M. The origin of volatiles in the Earth’s mantle. Geochem. Geophys. Geosyst.18, 3078–3092 (2017).
- 98.Li Y, Wiedenbeck M, Shcheka S, Keppler H. Nitrogen solubility in upper mantle minerals. Earth Planet. Sci. Lett. 2013;377:311–323. doi: 10.1016/j.epsl.2013.07.013. [DOI] [Google Scholar]
- 99.Palme, H. & O’Neill, H. Cosmochemical Estimates of Mantle Composition. Planets, Asteriods, Comets and The Solar System, Volume 2 of Treatise on Geochemistry. Edited by Andrew M. Davis (2014).
- 100.Chi H, Dasgupta R, Duncan MS, Shimizu N. Partitioning of carbon between Fe-rich alloy melt and silicate melt in a magma ocean-implications for the abundance and origin of volatiles in Earth, Mars, and the Moon. Geochim. Cosmochim. Acta. 2014;139:447–471. doi: 10.1016/j.gca.2014.04.046. [DOI] [Google Scholar]
- 101.Armstrong LS, Hirschmann MM, Stanley BD, Falksen EG, Jacobsen SD. Speciation and solubility of reduced C-O-H-N volatiles in mafic melt: Implications for volcanism, atmospheric evolution, and deep volatile cycles in the terrestrial planets. Geochim. Cosmochim. Acta. 2015;171:283–302. doi: 10.1016/j.gca.2015.07.007. [DOI] [Google Scholar]
- 102.Okuchi, T. Hydrogen partitioning into molten iron at high pressure: implications for Earth’s core. Science278, 1781–1784 (1997). [DOI] [PubMed]
- 103.Roskosz M, Bouhifd MA, Jephcoat A, Marty B, Mysen B. Nitrogen solubility in molten metal and silicate at high pressure and temperature. Geochim. Cosmochim. Acta. 2013;121:15–28. doi: 10.1016/j.gca.2013.07.007. [DOI] [Google Scholar]
- 104.Li Y, Dasgupta R, Tsuno K, Monteleone B, Shimizu N. Carbon and sulfur budget of the silicate Earth explained by accretion of differentiated planetary embryos. Nat. Geosci. 2016;9:781–785. doi: 10.1038/ngeo2801. [DOI] [Google Scholar]
- 105.Fischer RA, Cottrell E, Hauri E, Lee KK, Le Voyer M. The carbon content of Earth and its core. Proc. Natl. Acad. Sci. 2020;117:8743–8749. doi: 10.1073/pnas.1919930117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.Li, Y.-F., Marty, B., Shcheka, S., Zimmermann, L. & Keppler, H. Nitrogen isotope fractionation during terrestrial core-mantle separation. Geochem. Perspect. Lett.2 (2016).
- 107.Speelmanns IM, Schmidt MW, Liebske C. The almost lithophile character of nitrogen during core formation. Earth Planet. Sci. Lett. 2019;510:186–197. doi: 10.1016/j.epsl.2019.01.004. [DOI] [Google Scholar]
- 108.Grewal DS, et al. The fate of nitrogen during core-mantle separation on Earth. Geochim. Cosmochim. Acta. 2019;251:87–115. doi: 10.1016/j.gca.2019.02.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Shibazaki Y, Ohtani E, Terasaki H, Suzuki A, Funakoshi K. Hydrogen partitioning between iron and ringwoodite: Implications for water transport into the Martian core. Earth Planet. Sci. Lett. 2009;287:463–470. doi: 10.1016/j.epsl.2009.08.034. [DOI] [Google Scholar]
- 110.Li, Y., Vočadlo, L., Sun, T. & Brodholt, J. P. The Earth’s core as a reservoir of water. Nat. Geosci.13, 453–458 (2020).
- 111.Tagawa, S. et al. Experimental evidence for hydrogen incorporation into Earth’s core. Nat. Commun.12, 1–8 (2021). [DOI] [PMC free article] [PubMed]
- 112.Wetzel DT, Rutherford MJ, Jacobsen SD, Hauri EH, Saal AE. Degassing of reduced carbon from planetary basalts. Proc. Natl. Acad. Sci. 2013;110:8010–8013. doi: 10.1073/pnas.1219266110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113.Stanley BD, Hirschmann MM, Withers AC. Solubility of C-O-H volatiles in graphite-saturated Martian basalts. Geochim. Cosmochim. Acta. 2014;129:54–76. doi: 10.1016/j.gca.2013.12.013. [DOI] [Google Scholar]
- 114.Libourel G, Marty B, Humbert F. Nitrogen solubility in basaltic melt. Part I. Effect of oxygen fugacity. Geochim. Cosmochim. Acta. 2003;67:4123–4135. doi: 10.1016/S0016-7037(03)00259-X. [DOI] [Google Scholar]
- 115.Boulliung J, et al. Oxygen fugacity and melt composition controls on nitrogen solubility in silicate melts. Geochim. Cosmochim. Acta. 2020;284:120–133. doi: 10.1016/j.gca.2020.06.020. [DOI] [Google Scholar]
- 116.Abe Y, Matsui T. Evolution of an impact-generated HO-CO atmosphere and formation of a hot proto-ocean on Earth. J. Atmos. Sci. 1988;45:3081–3101. doi: 10.1175/1520-0469(1988)045<3081:EOAIGH>2.0.CO;2. [DOI] [Google Scholar]
- 117.Kasting JF. Runaway and moist greenhouse atmospheres and the evolution of Earth and Venus. Icarus. 1988;74:472–494. doi: 10.1016/0019-1035(88)90116-9. [DOI] [PubMed] [Google Scholar]
- 118.Nakajima, S., Hayashi, Y.-Y. & Abe, Y. A study on the “runaway greenhouse effect” with a one-dimensional radiative-convective equilibrium model. J. Atmos. Sci.49, 2256–2266 (1992).
- 119.Kurokawa, H., Foriel, J., Laneuville, M., Houser, C. & Usui, T. Subduction and atmospheric escape of Earth’s seawater constrained by hydrogen isotopes. Earth Planet. Sci. Lett.497, 149–160 (2018).
- 120.Walker, J. C., Hays, P. & Kasting, J. F. A negative feedback mechanism for the long-term stabilization of Earth’s surface temperature. J. Geophys. Res. Oceans86, 9776–9782 (1981).
- 121.Kasting, J. F. Earth’s early atmosphere. Science259, 920–926 (1993). [DOI] [PubMed]
- 122.Murphy DM, Koop T. Review of the vapour pressures of ice and supercooled water for atmospheric applications. Q. J. R. Meteorol. Soc. 2005;131:1539–1565. doi: 10.1256/qj.04.94. [DOI] [Google Scholar]
- 123.Stolper E, Holloway JR. Experimental determination of the solubility of carbon dioxide in molten basalt at low pressure. Earth Planet. Sci. Lett. 1988;87:397–408. doi: 10.1016/0012-821X(88)90004-0. [DOI] [Google Scholar]
- 124.Hirschmann MM, Dasgupta R. The H/C ratios of Earth's near-surface and deep reservoirs and consequences for deep Earth volatile cycles. Chemical Geology. 2009;262(1-2):4–16. doi: 10.1016/j.chemgeo.2009.02.008. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The codes used to generate these results and the data that support the findings of this study are available at http://www.geo.titech.ac.jp/lab/okuzumi/sakuraba/Contents.html.