Cardiac Alternans Occurs through the Synergy of Voltage- and Calcium-Dependent Mechanisms

Abstract

Cardiac alternans is characterized by alternating weak and strong beats of the heart. This signaling at the cellular level may appear as alternating long and short action potentials (APs) that occur in synchrony with alternating large and small calcium transients, respectively. Previous studies have suggested that alternans manifests itself through either a voltage dependent mechanism based upon action potential restitution or as a calcium dependent mechanism based on refractoriness of calcium release. We use a novel model of cardiac excitation-contraction (EC) coupling in the rat ventricular myocyte that includes 20,000 calcium release units (CRU) each with 49 ryanodine receptors (RyR2s) and 7 L-type calcium channels that are all stochastically gated. The model suggests that at the cellular level in the case of alternans produced by rapid pacing, the mechanism requires a synergy of voltage- and calcium-dependent mechanisms. The rapid pacing reduces AP duration and magnitude reducing the number of L-type calcium channels activating individual CRUs during each AP and thus increases the population of CRUs that can be recruited stochastically. Elevated myoplasmic and sarcoplasmic reticulum (SR) calcium, [Ca²⁺]_myo and [Ca²⁺]_SR respectively, increases ryanodine receptor open probability (P_o) according to our model used in this simulation and this increased the probability of activating additional CRUs. A CRU that opens in one beat is less likely to open the subsequent beat due to refractoriness caused by incomplete refilling of the junctional sarcoplasmic reticulum (jSR). Furthermore, the model includes estimates of changes in Na⁺ fluxes and [Na⁺]_i and thus provides insight into how changes in electrical activity, [Na⁺]_i and sodium-calcium exchanger activity can modulate alternans. The model thus tracks critical elements that can account for rate-dependent changes in [Na⁺]_i and [Ca²⁺]_myo and how they contribute to the generation of Ca²⁺ signaling alternans in the heart.

1. Introduction

The alternating strong and weak beats in the left ventricle are known as pulsus alternans or mechanical alternans which was first described in the 19th century by Traube [1]. Another type is electrical alternans (or T-wave alternans) which describe the beat-to-beat variation in direction, amplitude, and duration of any components in an ECG waveform [2]. The two are distinguished, yet they may both coexist [3,4].

Pulsus alternans is associated with different pathophysiological conditions, e.g., aortic stenosis, tachycardia, ischemia, acidosis and hypertrophic cardiomyopathy [5]. Other tested conditions that may lead to cellular or subcellular alternans include, but are not limited to: decrease RyR2 open probability (P_o) to increase the variability of Ca²⁺ transient between the different areas of the cell, metabolic deficiencies, e.g., acidosis, and/or abnormal calcium handling [4,6,7]. Pulsus alternans may lead to pulseless activity, i.e., when there is an electrical activity, but the heart either does not contract, or the contraction is not strong enough to produce a sufficient cardiac output to generate a pulse [8].

It has been suggested that a voltage-dependent mechanism underlies cardiac alternans. Under this hypothesis, action potential restitution is the underlying cause of cardiac alternans [9,10,11,12,13]. With the shorter diastolic interval with faster pacing rates, the sarcolemmal ion channels do not completely recover from one beat to the next. Therefore, after a large/long action potential, since ion channels have not fully recovered, they are not available to participate in the next action potential resulting in a small/short action potential. In these studies, a steep restitution curve is the primary requirement, and pathological conditions or experimental manipulations can increase the slope of this restitution curve making alternans more likely.

Other studies have suggested, that modified intracellular calcium cycling plays a role in occurrence of mechanical and electrical alternans [14,15,16,17,18,19]. In fact, many studies have found that it is possible to have alternans in calcium release without requiring action potential alternans [18,20,21]. Calcium alternans is a beat-to-beat variation in intracellular Ca²⁺ transient amplitude. Typically, calcium alternans occurs at high heart rates, yet the frequency threshold varies by different conditions such as ischemia or ionic disturbances that disturb the bidirectional coupling between the membrane potential and intracellular calcium. This has been identified as a potential precursor to the dangerous reentrant arrhythmias and SCD; yet the mechanism is not well understood [22]. Current computational models are unable to recreate this phenomenon; unless certain modifications to the ionic currents were made [9,23].

Newer studies have suggested that both mechanisms are possible under different conditions [24,25]. Those studies used computational models to suggest specific model configuration that can produce alternans by either a calcium-dependent or voltage-dependent mechanism. They then used rapid pacing in guinea-pig ventricular myocyte and observed calcium-dependent alternans under conditions of control of action potential alternans. They suggested that in these myocytes, a voltage-driven mechanism was possible due to the steep action potential duration restitution curves.

In this study we use our local-control model of the rat ventricular myocyte to study the interplay of calcium-dependent and voltage-dependent mechanisms to give rise to rapid pacing induced alternans. Through dissection of calcium dynamics and sarcolemmal ion channel activity at the release site level we demonstrate that for alternans brought about by increased pacing rate, there is a synergy between these two mechanisms. The modeling suggests that restitution of the action potential due to incomplete recovery of the Na⁺ channels that sets the stage for alternans by a calcium dependent mechanism. Here the small action potential reduces the number of L-type calcium channels that are activated creating the substrate for stochastic activation of the ryanodine receptors that is favored by elevated myoplasmic calcium.

2. Materials and Methods

2.1. The Model

In order to study the mechanisms of alternans, we developed a novel local-control model for excitation-contraction coupling in the rat ventricular myocytes with 20,000 Ca²⁺ release sites that improves upon our previous work [26,27,28] (Figure 1). Notable improvements of this model over previous work include the following: (1) explicit buffer dynamics in the subspace, (2) an improved L-type calcium channel that incorporate calcium-bound calmodulin dependent inactivation, (3) updated formulation of Ito, and (4) updated parameters based on newer experimental data from rat ventricular myocytes [29]. In addition, by using our patented Ultra-fast Monte Carlo Method and GPU technology, it now allows us to do larger scale simulations that provide insights into calcium dynamics. The model equations are detailed in Appendix B.

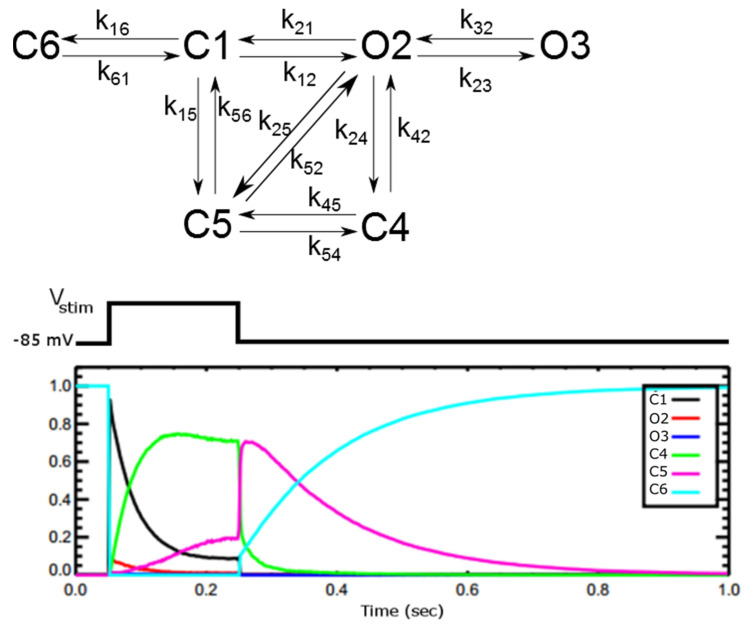
Figure 1.

Schematic diagram of a ventricular cell that shows only 2 T-tubule branches with 4 or the 20,000 Ca²⁺ release units. Abbreviations: jSR—junctional sarcoplasmic reticulum; nSR—network sarcoplasmic reticulum; ryr—ryanodine receptor; T-tubule—transverse tubule; NCX—sodium-calcium exchanger; Na/K—sodium-potassium ATP ase; PMCA—plasmalemmal calcium ATPase; SERCA—sarcoplasmic and endoplasmic reticulum calcium ATPase; I_Na—sodium current; I_Kss—steady-state (sustained) potassium current; I_Ktof—fast transient outward potassium current; I_tos—slow transient outward potassium current; I_K1—inward rectifier potassium current; I_bCa = background calcium current; I_bK—background potassium current; I_bNa—background sodium current.

2.1.1. Calcium Release Site (CRU)

A calcium release site is formed by the dyadic subspace and contains a cluster of 49 RyR2 channels and 7 LCCs channels. At each calcium release site, dynamic calcium buffering is implemented for three different endogenous buffers: calmodulin (CaM), sarcolemmal (SL) buffer and sarcoplasmic reticulum (SR) buffer rather than using the rapid buffering approximation or fixed buffering [27,30].

2.1.2. Ryanodine Receptor Type-2 Model

The 2-state ryanodine receptor model incorporates cytosolic calcium-dependent and luminal calcium dependent gating as described previously with only a small modification to the luminal dependence function to match spark characteristics [27]. The states are with the transition rate $k_{ryr}^{+}$ being increased by subspace Ca²⁺ (${\left[{\mathrm{Ca}}^{2+}\right]}_{ds}^i$) and junctional SR Ca²⁺ (${\left[{\mathrm{Ca}}^{2+}\right]}_{jsr}^i$) and $k_{ryr}^{+}$ being a constant. The RyR2s are arranges in a cluster and display coupled gating as using our previous formulation [27].

$$C\begin{array}{c}\stackrel{k_{ryr}^{+}}{\to }\\ \underset{k_{ryr}^{-}}{\leftarrow }\end{array}O$$ (1)

2.1.3. L-Type Ca²⁺ Channel Model

The 6-state L-type Ca²⁺ channel (LCC) model, Figure 2, is derived from 5-state LCC model for rat ventricle myocyte from Sun and co-workers with parameters adjusted for the new spark model [31,32]. The Sun model was developed to work in the range of −30 mV + 30 mV of the transmembrane potential reproducing single channel dwell times and currents from populations of channels matched to experiments. As Sun and co-workers suggested in their original paper, the 6-th state C6 was added to work with stronger depolarization (<−40 mV), so that all the channels stay in this state when the cell is at rest.

Figure 2.

Schematic diagram of the model (top) for the L-type calcium channel (DHPR channel) from [29]. C1 and C6 are closed states with C6 the resting state. O2 and O3 are the open states that conduct Ca²⁺ ions with equal conductance. C4 is Ca²⁺-dependent inactivated state. C5 is the voltage-dependent inactivated state. The fraction of LCC channels in different states during the voltage-clamp of V_stim = +10 mV for 200 ms (bottom).

The inactivation of the LCC was modelled via 2 separate pathways: VDI (voltage-dependent inactivation (O2→C5)) and CDI (Ca²⁺-dependent inactivation (O2→C4)). At each release site, the Ca²⁺ level that controls the inactivation is the subspace calcium. The source of contributing calcium to this microdomain is the influx of calcium via LCC and the release of calcium from SR via RyR. The much higher level of calcium in this subspace, i.e., ~100-fold compared to cytosolic bulk calcium, enhances the rate of inactivation of LCC and thereby preventing calcium overload.

The endogenous buffer CaM bound to Ca²⁺ (CaCaM) is the effector for Ca²⁺-dependent inactivation (CDI) of L-type Ca²⁺ channel. The calcium-free CaM is called apo calmodulin (apo-CaM) with two homologous domains, known as lobes [31]. For each apo-CaM molecule, there are four different calcium binding sites: two at the E-F hand motifs of the N-terminal (N-lobe) and two at the E-F hand motifs of the C-terminal (C-lobe) of CaM (for review see [32]). In L-type Ca²⁺ channels (Cav1.2), CDI is triggered by the binding of two Ca²⁺ ions to the C-lobe of CaM [33,34,35]. It means that to model CDI, two Ca²⁺ binding at C-lobe is necessary. This differs from the original Sun model, which used the Hill coefficient as 3 based upon earlier data [36]. In addition, the original model didn’t incorporate the loss of calcium in the subspace due to binding to calmodulin (CaM). This is important as the level of free [Ca²⁺]_ds control the gating of RyR2 channels. This was also corrected in our modified model. Experiments suggest the existence of non-junctional DHPR (10–20%), located on the external sarcolemma and not forming the release sites with RyR2 [37,38]. Hence the contribution of calcium from a small fraction of DHPR I_dhpr,nj (15%) was also added.

2.1.4. Na⁺ Channel Model

The rapid inward Na⁺ current in the cardiac cells exhibits a bi-phasic time courses for recovery during inactivation and one activation gating variable [39]. We have modified the Pandit model so that the model more closely simulates data for the adult rat ventricular myocyte than does the more commonly used Luo-Rudy model as shown in Figure 3 [40,41,42,43,44]. The new model better simulates the correct upstroke velocity for rat as 213.8 ± 6.6 V/s with the overshoot is 48.76 ± 1.09 (mV). Experiments estimate the velocity range as 150–190 V/s at 23 °C V/s in Wistar rat heart which is calculated to be 184–233 V/s using a Q10 of 1.23 [42,45,46]. The new model also better estimates the value of h∞ to be 0.812 at −80 mV at body temperature. This value of h_∞ has been experimentally estimated as 0.7–0.8 at −80 mV in rat and mice [39,47]. In contrast, the value of h∞ in Pandit is 0.6; and the value in Luo-Rudy is 0.97. Our estimate takes into consideration the temperature dependence for recovery kinetics with the Q10 ranging from 1.7 to 2.3 for membrane potential in the range −76 mV to −62 mV, and 1.5 to 1.8 for the membrane potential in the range −84 mV to −65 mV [43]. The maximum current conductance is 8 mS/cm² which is in the range 3–25 mS/cm² [39,48].

Figure 3.

(A) steady-state inactivation curve (B) steady-state activation curve; (C) voltage dependence of slow inactivation gate time constant (D) voltage dependence of activation gate time constants at different voltages. (E) I-V curve, (F) dynamics of gating variables of the proposed model during an AP—activation gate m (red), inactivation gate h (blue), and slow inactivation gate j (green).

2.1.5. K⁺ Channel Models

There are four different K⁺ channel currents (I_tof, I, I_K1, and I_Kss). The formula for fast and slow transient outward currents (I_Ktof, I_Ktos, respectively) are based on the model based on experimental data observed in mice [49].

2.1.6. Sarcoplasmic Reticulum Ion Pumps

The sarco (endo)plasmic reticulum Ca²⁺-ATPase (SERCA) pump re-sequesters Ca²⁺ back to the SR/ER during each excitation-contraction cycle to facilitate muscle relaxation by pumping two calcium ions per ATP molecule hydrolyzed [50]. We used the 2-state formulation by Tran and co-workers developed because it is constrained both by the thermodynamic and kinetic data for the SERCA pump [51].

2.1.7. Calcium Buffers

The three endogenous buffers of calmodulin (CaM), troponin (Trpn), and the phospholipids of the SR membrane (SRbuf) are used for the bulk myoplasm. The troponin complex consists of three different subunits. The troponin complex as modeled includes the binding of calcium (troponin C), the inhibition of actomyosin interaction (troponin I), and the binding to tropomyosin (troponin T).

2.1.8. Membrane Potential

During AP, the dynamics of the membrane voltage V_m are governed by the ionic currents described above.

2.2. Numerical Methods

We used our patented Ultra-fast Monte Carlo Simulation Method to solve for the states of the RyR2 and L-type Ca²⁺ channels in each release unit [52]. Using this method the RyR2 channels at each release site are modeled as a single stochastic cluster, and the L-type channels are modeled similarly. Rather than keeping track of individual channel’s state, we used a mean-field approach in which we assume all channels in the cluster see the same local calcium concentration in the dyadic subspace [53,54]. Thus, the individual channel’s states are ignored, and only the number of channels in each state is important. Each release site is fed with a different sequence of pseudo-random numbers. These Monte-Carlo simulations are computed on Fermi-GPU cards, with pseudo-random numbers were derived from the Saru PRNG algorithm implemented on GPU provided by Steve Worley (Private communication at GTC’12) [55]. Instead of using a fixed timestep, an adaptive time-step strategy is used. When the channel fires, a smaller time-step is selected; first to ensure numerical stability, second to limit maximum 10% of the CRUs having state changes to occur at a time [56,57]. This limits Type II error with the hypothesis that there is only channel state transition in the cluster per time step. In fact, when a full Monte Carlo Simulation is performed there are two channels undergoing state transitions in each timestep <0.6% of the time.

The system of ordinary differential equations comprising the model is solved using the explicit Euler method. The small and adaptive timestep (10–100 ns) which is required to simulate the fast and stochastic gating of DHPR and RyR2 channels is sufficient to ensure numerical stability.

3. Results

The model integrates the complex mechanisms involved in excitation-contraction coupling by describing the 20,000 stochastic calcium release units. In the model components were validated in the model described above and the model dynamics below in the results section. For example, the model demonstrates the same mechanism of release as our previous work and fully accounts for the SR Ca²⁺ visible and invisible leak by flux through the RyR2 channels in the forms of Ca²⁺ sparks and non-spark openings, respectively (Figure A1) [27,58,59]. Details of the ionic currents are shown in Figure A2.

3.1. Dynamics of Calcium during a Twitch-Relaxation Cycle

Figure 4 shows for 1 Hz pacing the time courses for a train of action potentials, myoplasmic calcium transients, network, and SR calcium transients. In our model, the ratio of SR calcium release over the influx of calcium during a twitch is 10.0 ± 0.3. It means that, on average, the SR-release contributes about 90.07% and calcium influx contributes 9.03%. This approximates the value 92% of SR contribution estimated for rat ventricular myocytes [9,60]. During one cycle, our model produced a total extrusion of calcium of about 11.5 µM/cell/s. Among this, ~1 µM is extruded by the PMCA and ~10.5 µM is extruded by the NCX. This is in agreement with the value given above by [61]. The ionic currents during a twitch-relaxation cycle are given in Figure A2. The model also simulates pacing, with APD20 ~10.69 ms, APD50 ~22.57 ms and APD90 ~78.3 ms as is evident in Figure 4.

Figure 4.

A long trace of calcium dynamics in the (A) myoplasmic [Ca²⁺], (B) network SR [Ca²⁺], and (C) Action Potential, (D) L-type current density, and (E) Sodium current density.

3.2. Mechanisms of Alternans

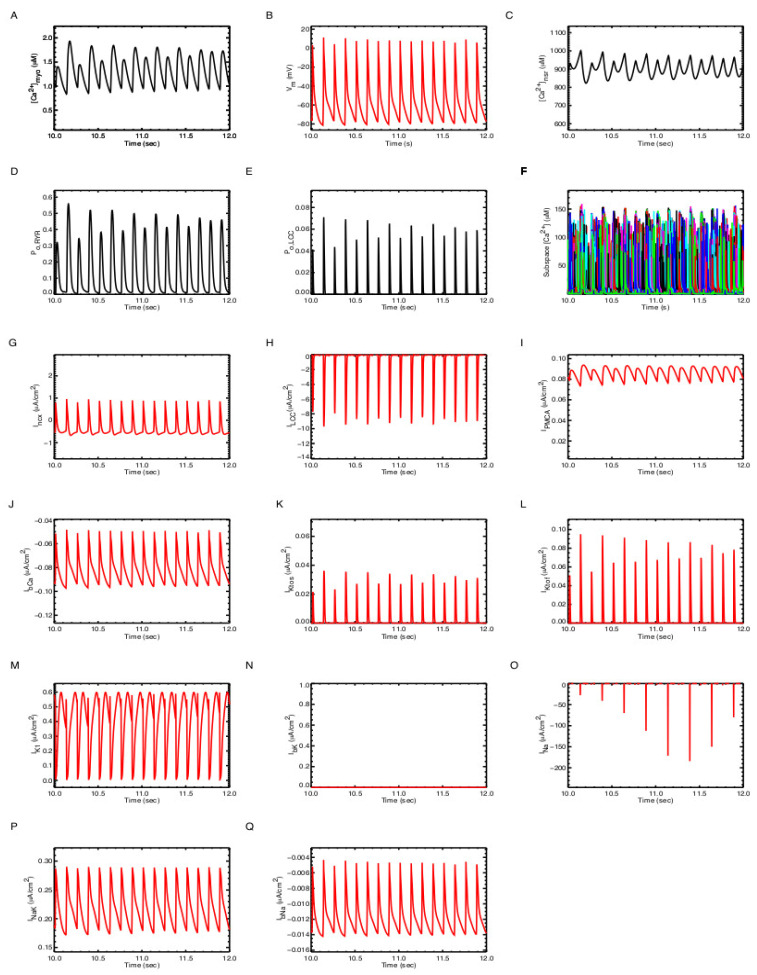
The model produces stable action potential and calcium transient trains below 8 Hz, however, above 8 Hz pacing frequency, periods of alternans are observed. One such period of AC concordant alternans is shown in Figure 5 with both [Ca²⁺]_myo and V_m alternating in phase. There are also alternating small and large amplitude and duration of other observable quantities such as [Ca²⁺]_SR, RyR P_O, and I_Ca. It is also important to note that the amplitude of I_Na and I_CaL are greatly reduced.

Figure 5.

Calcium alternans at 8 Hz: (A) Cytosolic calcium, (B) RyR open probability Po (RyR2), (C) membrane potential V_m, (D) L-type Ca²⁺ current I_CaL, (E) Sodium current I_Na.

Note that both the [Ca²⁺]_myo and [Ca²⁺]_SR fail to recover back to the normal diastolic level between systoles.

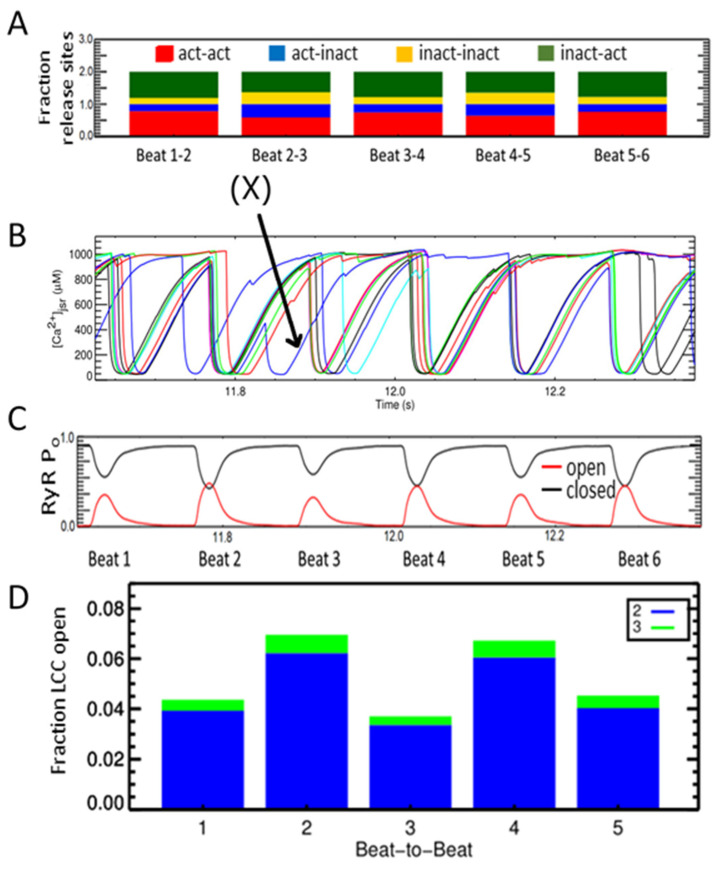
Many studies have suggested that alternans is a defect of the calcium subsystem. The conceptual framework of refractoriness, randomness, and recruitment has been used to understand alternans [62]. To study the refractoriness of calcium release beat-to-beat changes of the CRU’s states were analyzed. A CRU is activated if a Ca²⁺ spark occurs. The CRUs are grouped into either activated or inactivated at each beat. Therefore, when considering a pair of beats, there are 4 groups: act-act, act-inact, inact-act, and inact-inact.

In the transition from beat-1 to beat-2, there is a large fraction of CRUs changing from Inactivated to Activated (green), and also a large fraction of CRUs which are Activated in beat-1 continue to Activate in beat-2 (red)–the beat that has a strong contraction. For example, the number of activated release sites increases from Beat1-2 as indicated by the increased green and red. Corresponding to this, Figure 6B shows that beat 2 has a higher RyR open probability than beat-1. This suggests that alternans might originate at the level of the CRU. Figure 6C tracks the [Ca²⁺]_jsr local depletion for individual CRUs as shows that the CRUs (red, blue, green, and black) activate at alternating beats.

Figure 6.

Alternans occurs at 8 Hz pacing rate. (A) An example that show a CRU that fires at two contiguous beats, e.g., (X) marks an individual release site that is Act-Act. (B) Alternans in the calcium release seen by the changing amplitude and duration of the [Ca²⁺]_myo. Beat-to-beat variation in CRU’s states where we examine act-act—the fraction of CRU that activate in beat (i) (red) and continue to activate in beat (i + 1), similarly with act-inact (blue), inact-inact (yellow), and inact-act (dark green). (C) The probability of RyR opening at each beat (red = open, black = closed). (D) The fraction of LCC open (states O2-blue and O3-green) during each beat.

However, a Chi-squared test with the 2 × 2 contingency table shown in Figure 7A did not support this hypothesis (p < 0.61). Even though there are more L-type Ca²⁺ channels assuming the Ca²⁺ dependent inactivated state during 8 Hz pacing, their number does not exceed 2 or 3 per CRU out of the 7 available channels. This leaves sufficient number of channels in a state to be activated during the subsequent beat. The next hypothesis is that after a CRU has been triggered it is less likely to activate again in the following beat. To quantify this hypothesis, whether or not a spark occurred in the first beat versus whether or not a spark occurred in the second beat, we used a Chi-squared test with a 2 × 2 contingency table (Figure 7B). With a Chi-squared statistic of 55.6 and a p-value of p < 0.001, this showed that if a spark occurred in the first beat for a given CRU, there was a slightly lower probability that it would occur in the next. Figure 6B depicts the explanation for this. The jSR depletes after a CRU triggers and does not fully recover until the next beat. This lowers the likelihood of CRU activation both through the effects of jSR calcium on RyR open probability and in the event if a RyR does open, the reduced flux will be insufficient to trigger adjacent RyRs. As a result, the model suggests that refractoriness in jSR is an important component of alternans.

Figure 7.

Contingency Tables for Spark Analysis. (A) Does L-type Ca²⁺ channels (LCC) opening effect LCC opening in the subsequent beat? (B) Does a Ca²⁺ spark in one beat affect Ca²⁺ spark occurrence in the subsequent beat?

These results suggest that the recovery of junctional SR Ca²⁺ after a release event can contribute to the development of alternans. To assess the SR Ca²⁺ content, we split the CRUs at each beat in two groups: those that are activated (Act) and those are not activated (Inact) and investigated two things: (1) the values of [Ca²⁺]_jSR at these release sites, right at before the next beat to start, (2) the nadir of [Ca²⁺]_SR during calcium release (Figure 8). Larger SR [Ca²⁺] comes with larger Ca²⁺ release and the beats with larger release have more activated CRUs. We can see that the ensemble initial [Ca²⁺]_SR is not an indicator of alternans formation. If we look at the nadir [Ca²⁺]_SR, the result shows a similar small beat-to-beat alternation, in agreement with the study of [16].

Figure 8.

(A) The diastolic [Ca²⁺]_jSR right before the stimulus from CRUs in two groups: red = Act, blue = Inactivate. (B) The upper black line shows the average [Ca²⁺]SR level right before the Istim is applied, and the lower red line shows the nadir of average [Ca²⁺]SR level at the corresponding beat.

The mechanism by which randomness of calcium release arises in the system is also explained by the model. The reduction in I_Na current which reduced the action potential magnitude contributed a huge effect in reducing the number of L-type channels opening that opens the gateway for alternans (Figure 5). When there is less I_Na (Figure 5E), there is a smaller AP (Figure 5C) and reduced L-type current (Figure 5D). These beat also have a smaller RyR open probability (Figure 5B) and Ca²⁺ transient (Figure 5A) This is in agreement with the result in which a small depolarizing potential under voltage clamp can induce alternans [16], and confirms the hypothesis that SR Ca²⁺ release is graded with the beat-to-beat alternation in I_CaL [63,64]. The reduction in L-type opening reduces the synchronization of activation of the CRUs. Furthermore, the elevated myoplasmic [Ca²⁺] increases the stochastic activation of Ca²⁺ sparks. At the normal quiescent condition, as shown in our previous study, the activation of a CRU is the result of 8–10 RyR2 opening [27]. During field-stimulus simulation with high pacing, this number reduces to 5, where Ca²⁺ alternans is observed (Figure 9). During the large beat, there can be up to 80% of CRUs activated, though the time to peak of activation is slower, e.g., 60%.

Figure 9.

The fraction of CRUs that has 1 or more RyR openings during each beat (black = beat-1, red = beat-2, blue = beat-3, yellow = beat-4, green = beat-5).

We then explored the hypotheses that a high level of [Na⁺]_i increases the likelihood of alternans through the modulation of Na⁺/Ca²⁺ exchanger activity (NCX). The normal function of NCX is to extrude one calcium ion in exchange for three sodium ions. It has been hypothesized that at high level of [Na⁺]_i, it may fail to extrude calcium, thus maintaining a high diastolic cytosolic [Ca²⁺]. In other words, increasing Na⁺ lead to more reverse mode NCX, leading to increases [Ca²⁺]_myo and [Ca²⁺]_SR. With 8 Hz pacing simulation with our model, alternans were observed at [Na⁺]_i at ~10.2 mM. We tested the effect of high sodium concentration by fixing the sodium level with [Na⁺]_i = 15 mM. Under this condition, alternans were also observed yet the levels of cytosolic calcium, at both basal and peak, are higher (Figure 10).

Figure 10.

8 Hz pacing with [Na⁺]_i = 15 mM: (A) The average of [Ca²⁺]_jSR right before the stimulus from CRUs in two groups: red = Act, blue = Inactivate, and the nadir value. (B) Alternans in the myoplasmic calcium transient.

Simulations were performed with [Na⁺]_i held at 1 mM, 12 mM, and 20 mM. As [Na⁺]_i increase the diastolic (peak) [Ca²⁺]_nsr and the [Ca²⁺]_myo both increase (Figure 11A,B). As expected, with increasing [Na⁺]_i the reverse NCX current increases bringing more Ca²⁺ into the cell (Figure 11C). The forward NCX (Ca²⁺ extrusion) also increases due to the higher [Ca²⁺]_myo. When the NCX rate is increased intracellular [Ca²⁺] falls due to the increase extrusion (Figure 11D). Increasing [Na⁺]_i also attenuates alternans (Figure A4 and Figure A5).

Figure 11.

Tables for analyzing the dependence of Calcium dynamics on [Na⁺]_i and Na⁺/Ca²⁺ exchanger activity (NCX). (A) Peak network SR Ca2 concentration ([Ca²⁺]_nsr) at different myoplasmic Na⁺ concentrations ([Na⁺]_i). (B) Peak myoplasmic Ca²⁺ concentration ([Ca²⁺]_myo) at different values of [Na⁺]_i and (C) Peak forward and reverse Na⁺/Ca²⁺ exchanger (NCX) current at different values of [Na⁺]_i. (D) Peak [Ca²⁺]_NSR at different Na⁺/Ca²⁺ exchanger (NCX) activity levels.

If reduction of NCX activity by high Na⁺ is crucial for the formation of alternans, NCX upregulation should reduce alternans. Consistent with this hypothesis, high expression levels of NCX reduces SR calcium, along with cytosolic [Ca²⁺] and thus reduce alternans amplitude (Figure 12C). Large reduction of NCX (to 50% control) still generates alternans, however, the calcium alternations are attenuated. It again confirms that there is a range of changes that can be critical for the arrhythmogenesis to occur. When the temperature is reduced (23 °C), the alternans become more prominent (Figure 12). In this test case, the simulation was done using a stochastic model for the Na⁺ current developed by [40]. This is in agreement with many other experiments that low-temperature increases the likelihood of alternans development [65,66,67], and we anticipated that Na⁺ current plays an important role here.

Figure 12.

Alternans at high pacing rate (8Hz) using a stochastic Na⁺ current model at 23 °C, (A) action potential. (B) I_CaL current. (C) cytosolic calcium. (D) opening probability of whole-cell ryanodine receptors.

4. Discussion

Cellular alternans in cardiac myocytes have been shown in experiments and modeling to have a mechanism that depends both on the membrane currents and on the Ca²⁺ subsystem. This modeling study demonstrates that for alternans produced at high pacing rates, both mechanism act synergistically to produce alternans. Under the hypothesis that relies on membrane currents, action potential restitution is the underlying cause of cardiac alternans [9,10,11,12,13]. Studies that have suggested that modified intracellular calcium cycling plays a role in occurrence of mechanical and electrical alternans have found that it is possible to have alternans in calcium release without requiring action potential alternans [14,15,16,17,18,19,20,21]. Current computational models are unable to recreate this phenomenon; unless certain modifications to the ionic currents were made [9,23]. Newer studies have suggested that both mechanisms are possible under different conditions [24,25].

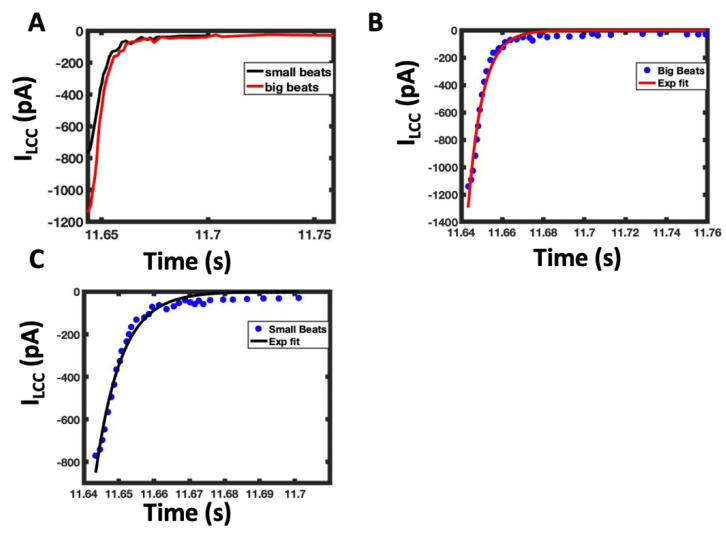
Computational studies have suggested that the randomness of Ca²⁺ sparks; recruitment of a Ca²⁺ spark by neighboring Ca²⁺ sparks; and refractoriness of Ca²⁺ release units are the important factors required for cardiac alternans [68]. The work here is consistent with this idea. While we take into account the stochastic nature of ionic channel gating at individual release site, the subspace area is treated as a single compartment and thus all ion channels (RyRs and LCCs) in the same calcium release site sense the same level of calcium. The potential spatial distribution of the receptors that may govern the allosteric interaction between them, underlying the long- or short-range correlation mechanism between receptors is approximated using a mean-field approach which governs the non-linearity via a non-linear coupling function as shown in Appendix B.2. One question that can be probed using the model is how Ca²⁺-dependent inactivation of the L-type Ca²⁺ channel varies beat to beat during alternans. Figure 6D shows more L-type Ca²⁺ during large beats than small beats during alternans. If this is caused by increased Ca²⁺ dependent inactivation, it would be expected that there be a faster rate of decay of the L-type current during the large currents. The rate of L-type current decay is shown in the Figure A6 in Appendix A by overlapping the currents at a big and small beat during alternans. Fitting an monoexponential curve (f(x) = a × exp(−x/b)) to the decay yielded a = −9.37 pA and b = 0.21 s for the large beat and a = −55.8 pA and b = 0.46 s for the small beat with a R2 = 0.977 and R2 = 0.980, respectively. The large beat where Ca²⁺ is more elevated displays a faster decay than the small beat.

Refractoriness in Ca²⁺ release is demonstrated to be crucial to alternans by our statistical analysis of sparks at each release site (Ca²⁺ release unit). Our studies also show that an uncoupling of depolarization to Ca²⁺ release occurs as the L-type current is reduced both through Ca²⁺-dependent inactivation and smaller action potential amplitude due to reduced Na⁺ current. Our model is not a spatial model and hence does not model neighboring sparks. However, we do see recruitment as elevated bulk myoplasmic Ca²⁺ during rapid pacing, in part produced by more sparks, promotes Ca²⁺ sparks at additional Ca²⁺ release units.

Previous studies have shown that block of NCX by ORM-10962 has been shown to attenuate alternans in experiments [69]. In our model with decreasing NCX activity the NSR Ca²⁺ load increases and NCX attenuates alternans. The model suggests that large reduction of NCX (to 50% control) still generates alternans, however, the calcium alternations are attenuated. This suggests that there is a range of conditions that can be critical for the occurrence of alternans. Other studies have shown that blocking late Na⁺ current by ranolazine attenuates alternans, presumably by reduction of reverse NCX although this has not been proven [70,71]. While reduction of NCX, can reduce Ca²⁺ entry through reverse-NCX, it will suppress the greater role of Ca²⁺ extrusion leading to more calcium overload. The rat ventricular myocyte does not have a late component of the Na⁺ current so we cannot test this directly. In our simulations, increasing intracellular Na⁺ to 12, 15, and 20 mM, the NSR Ca²⁺ load increases, yet alternans are attenuated. There is a decrease in the action potential duration with increasing [Na⁺]_i as shown in the Figure A3, Figure A4 and Figure A5 allowing for recovery of the Na⁺ current and production of a regularization of the action potential. It suggests that blocking late Na⁺ current allows the Na⁺ channels to recover to open in the next beat resulting in attenuated alternans.

Calcium sensitive K⁺ channels (SK channels) have been found in rat ventricular myocytes. These channels activate and allow hyperpolarizing outward current when [Ca²⁺]_myo is elevated with a K_0.5 = 0.5 µM [72]. The SK channel conductance in rat peaks at 1–2 pA/pF [73]. This Ca²⁺ sensitivity is conferred though the binding of Ca²⁺ with calmodulin with experimental studies suggesting calmodulin variants can alter SK channel function and potentially lead to arrhythmia [74]. Furthermore, SK channel expression has been observed to increase during heart failure or after myocardial infarction and have been suggested to contribute to arrhythmia [75,76]. Computational rabbit ventricular myocyte models have suggested that when these channels are blocked, a mild to moderate action potential prolongation occurs depending on the conductance level assigned to the channel [73,76]. However, at the physiological conductance levels, these models predict a very small effect. Additionally, experimental studies have und AP clamp suggested that blocking the K⁺ using Cs under AP clamp, resulted in no change in the difference current between beats in alternans suggesting little role for the SK current alternans. The same study however found that the Ca²⁺-activated Cl⁻ current did play a role [77]. For this reason, we did not include them in the current model and left them for future studies of arrhythmia and disease.

Calmodulin has high and low affinity Ca²⁺ binding sites. Experiments have measured high affinity sites in the C-lobe to have a K_d = 1 µM and the low affinity sites in the N-lobe to have a K_d = 12 µM [78,79]. We have chosen to only include the low affinity N-lobe site because in the microdomain near the L-type channel upon L-type opening that high affinity site will saturate rapidly leaving the low affinity site to play the regulatory role. This is supported by the role the N-lobe has been found to play in Ca²⁺ dependent inactivation of the L-type Ca²⁺ channel [80]. Furthermore, at high pacing rates where Ca²⁺ is elevated, it even more likely that the C-lobe is saturated and plays less of a regulatory role. We did not choose to use the model by Limpitikul et al., which uses a C-lobe K_d = 1.15 µM and a N-lobe K_d = 0.9 µM as it would not be appropriate for a model which explicitly models the dyadic subspace [81]. According to Uniprot, the D96V, D130G and F142L variants are implicated in LQTS. While located in the C-terminus, molecular dynamics simulations show that they affect the positional relation between the lobes such as the linker distance and dihedral angles between the lobes, so the effect of the variants is not simply an effect on Ca²⁺ binding affinity [82]. Including the low affinity sites would not affect the model results presented here. However, to model LQTS all four sites would need to be considered. This is left for future work.

The model is a set non-linear differential equations with stochastic elements. The conversion to alternans is period doubling behavior and has been observed both in experiments and in other models of the cardiac action potential [83,84,85]. For example, with rapid pacing the dog heart can develop alternans. With increasing pacing rate there is period doubling, a repeating sequence of four beat amplitudes. With further increases, fibrillation or chaos occurs. We have also observed this behavior in our previous Guinea pig model and this model (at 12 Hz) [86].

Ca²⁺ oscillations have been observed in cardiac ventricular myocytes under Ca²⁺ overload conditions. Similar to deterministic systems such as our previous model, this model is capable of Ca²⁺ oscillations due to the dynamics of the Ca²⁺ subsystem because it is a non-linear excitable system [86]. However, the cardiac ventricular myocyte is a driven system with a periodic applied current to trigger action potentials similar to experiment that mimic the periodic excitation of a ventricular myocytes by adjacent cells during the heartbeat. If the rapid pacing is abruptly ceases, there will be some spontaneous Ca²⁺ release events (calcium oscillations) similar to experiment [87]. Furthermore, we have developed a spatial model of the rat ventricular myocyte that displays oscillatory Ca²⁺ waves under calcium overload conditions with no depolarization stimulus similar to the phenomena observed in isolated rat cardiac ventricular myocytes [88,89].

Anomalous diffusion has been proposed to explain the spatial diffusion of Ca²⁺. Anomalous diffusion by definition is a diffusion where the mean squared displacement does not depend linearly on time [90]. This is different from the Fickian diffusion that causes Brownian motion which has been observed in cells. Other modeling studies have invoked anomalous diffusion to create Ca²⁺ spark models because existing models using Fickian diffusion have only achieved FWHM of 1.0 µm compared to the experimentally observed FWHM of 1.8 µm [91]. With their anomalous diffusion model (subdiffusion) it is possible to get a FWHM of 2.0 µm. However, we have shown previously that with our model that includes Fickian diffusion we can get a FWHM of 1.8 µm [89]. In our modeling efforts there has been no need to invoke novel diffusion formulations to reproduce experimentally observed phenomena.

5. Conclusions

In conclusion, we presented here a study using a stochastic computational model to study the cellular mechanism underlying cardiac alternans in rat ventricular myocyte. The model helps to explain a modest role of [Ca²⁺]_jSR in forming alternans, while it’s suggested that disturbing I_Na, I_CaL and membrane potential plays a dominant role in the forming of pulsus alternans. In addition to this, the model was able to reproduce results at conditions that have been known for alternans like lowering the temperature, high [Na⁺]_i or reducing alternans amplitude by up/down regulation of NCX. The limitation of the model is the inability to investigate the spatial effect on the generation of cardiac alternans, i.e., subcellular Ca²⁺ alternans or calcium waves in alternans. This will be the next step in our study with a full-scale spatio-temporal model of the cardiac ventricular myocyte to investigate subcellular Ca²⁺ alternans [92,93,94].

Appendix A

Appendix A.1. Spark Termination

The termination of Ca²⁺ sparks involves the combination of luminal calcium depletion, which reduce the driving force for the Ca²⁺ flux; the stochastic closing of the channels and their failure to re-open due to less subspace and jSR Ca²⁺, and the effect of the increasing number of closed channels on the open ones through allosteric coupling, as in our previous model (Figure 8) [27,58]. Clearly, this predates the concept of pernicious attrition and induction decay in which the smaller Ca²⁺ flux at each RyR2 due to local luminal calcium depletion devastates inter-RyR2 CICR [95]. In fact, the idea the reduced Ca²⁺ flux through the RyR2s in the dyad are insufficient to sustain CICR as suggested in pernicious attrition has been suggested previously [53,86].

Appendix A.2. Dynamics of Calcium Sparks and Calcium Leak

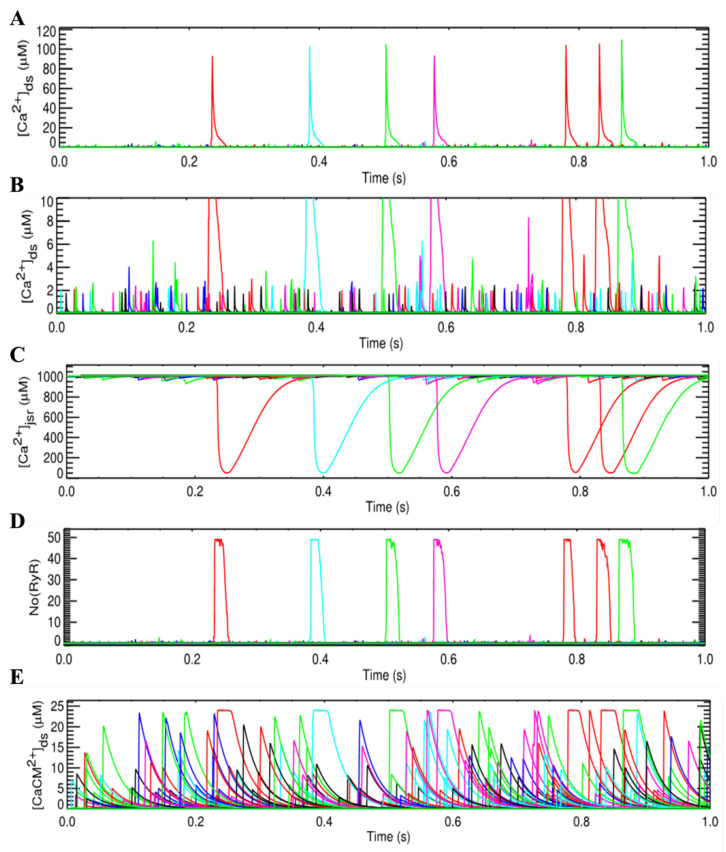
The model predicts three possible mechanisms of the SR Ca²⁺ leak that are sufficient to account for balancing Ca²⁺ uptake via SERCA2a during the diastolic phase, similar to our previous work [27]. They are visible Ca²⁺ sparks (~120 sparks/cell/s under quiescent), invisible Ca²⁺ leaks known as Ca²⁺ quarks (~4300 quarks/cell/s under quiescent) and calcium leak via a small population of RyRs at a distance from the release sites, known as non-junctional RyR or ‘rogue’ RyR (Figure 8) [96]. The so-called non-spark events or invisible Ca²⁺ quarks are the result of one or a few RyR channels opening whose signals cannot be detected using standard confocal imaging microscopies [97].

The visible leak i.e., 120 Ca²⁺ sparks per cell per second is in the physiological range (100–200 sparks/cell/s) and accounts for 75% of the leak. Part of the invisible leak results from the stochastic gating of one or a few RyR2 channels, accounting for 25% of the leak. This yields a spark fidelity of ~2.8% which is the ability a single calcium release to trigger the Ca²⁺ spark. The total quiescent leak rate was ~1.2 µmol/(L cyt.)/s which is in the range 0.5–5 µM [98]. The Ca²⁺ spark peak was ~100.1 µM (Figure A1), which is in agreement with the estimate that due to the small subspace, the elevation of free calcium can be two orders of magnitude larger than the resting value [99]. The plateau in the spark profile of free calcium explains the energy coupling effect between the closed and open channels, before the Ca²⁺ spark is completely terminated. Similar to the study of [27], the effect of IP₃R has not been incorporated in this model study. Thus, the involvement of other leak pathways like via IP₃-receptors (IP3R) has not been excluded, though the functional role of IP₃R at rest has not been confirmed. As shown in Figure A1D, the higher frequency of [Ca²⁺/CaM] elevation in the quiescent cell model provided the evidence of non-spark events where calcium release via the opening of one or a few RyRs bind to calmodulin buffer, as well as SR and SL buffers.

Figure A1.

Calcium in the subspaces during (A) Ca²⁺ sparks and (B) Ca²⁺ quarks, (C) Dynamics of jSR Ca²⁺ release, (D) Number of RyR openings, (E) Ca²⁺-bound calmodulin complex.

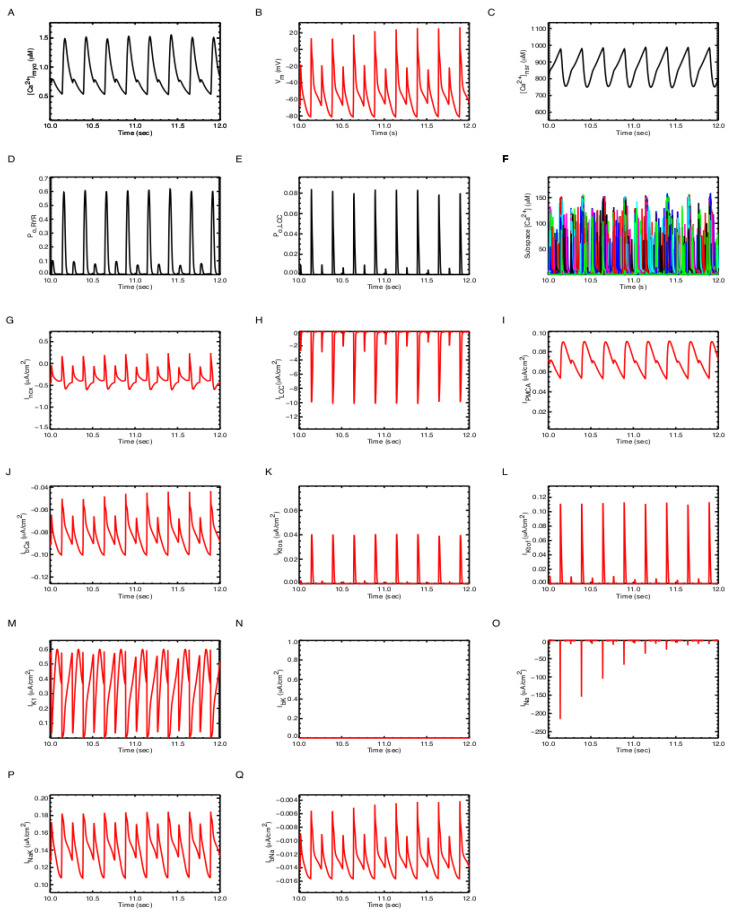
Figure A2.

A single action potential at 1 Hz pacing. To emulate the excitation-contraction of the cell, a stimulus current Istim = −6.5189 µA/cm² was given during 5.0 ms second [40]. (A) [Ca²⁺]_myo, (B) Membrane potential (V_m); (C) Network SR Ca²⁺ concentration ([Ca]_nsr); (D) RyR2 open probability (P_O,RyR); (E) L-type Ca²⁺ channel open probability (P_O,LCC); (F) subspace free Ca²⁺ concentration ([Ca²⁺]_ds); (G) L-type Ca²⁺ current (I_LCC); (H) NCX current (I_ncx); (I) PMCA current (I_PMCA); (J) Ca²⁺ current (I_Na); (K) Na/K exchanger current; (L) K₁ current; (M) slow component of transient-outward K⁺ current; (N) fast-component of transient-outward K⁺ current; (O) Na⁺ current; (P) Na⁺-K⁺ ATPase current; (Q) Background Na⁺ current.

Figure A3.

The amount of Ca²⁺/CaM complex in the subspace is greater during pacing at 8 Hz compared to acing at 1 Hz pacing leading to increased Ca-dependent inactivation of the L-type channel.

Figure A4.

Pacing at 8 Hz pacing produces alternans and a diastolic [Na⁺]_i of 10.2 mM. To emulate the excitation-contraction of the cell, a stimulus current I_stim = −6.5189 µA/cm² was given during 5.0 ms second [40]. (A) [Ca²⁺]_myo; (B) Membrane potential (V_m); (C) Network SR Ca²⁺ concentration ([Ca²⁺]_nsr); (D) RyR2 open probability (P_O,RyR); (E) L-type Ca²⁺ channel open probability (P_O,LCC); (F) subspace free Ca²⁺ concentration ([Ca²⁺]_ds); (G) L-type Ca²⁺ current (I_LCC); (H) NCX current (I_ncx); (I) Plasmalemmal Ca²⁺-ATPase current (I_PMCA); (J) background Ca²⁺ current (I_Cab); (K) slow transient outward current (I_tos); (L) fast transient outward current (I_tof); (M) K₁ current (M) slow component of transient-outward K⁺ current; (N) Background K⁺ current; (O) Na⁺ current; (P) Na⁺-K⁺ ATPase current; (Q) Background Na⁺ current.

Figure A5.

Pacing at 8 Hz pacing produces alternans with diastolic [Na⁺]I = 20 mM. To emulate the excitation-contraction of the cell, a stimulus current I_stim = −6.5189 µA/cm² was given during 5.0 ms second [40]. (A) [Ca²⁺]_myo; (B) Membrane potential (V_m); (C) Network SR Ca²⁺ concentration ([Ca²⁺]_nsr); (D) RyR2 open probability (P_O,RyR); (E) L-type Ca²⁺ channel open probability (P_O,LCC); (F)subspace free Ca²⁺ concentration ([Ca²⁺]_ds); (G) L-type Ca²⁺ current (I_LCC); (H) NCX current (I_ncx); (I) PMCA current (I_PMCA); (J) Ca²⁺ current (I_Na); (K) Na/K exchanger current; (L) K1 current; (M) slow component of transient-outward K⁺ current; (N) fast-component of transient-outward K⁺ current; (O) Na⁺ current; (P) Na⁺-K⁺ ATPase current; (Q) Background Na⁺ current.

Figure A6.

Ca²⁺-dependent inactivation of the L-type channel occurs at different rates in large and small beats during alternans. (A) The decay in the L-type Ca²⁺ current for large (red) and small (blue) beats. (B) Fitting an monoexponential curve (f(x) = a × exp(−x/b)) to the decay yielded a = −9.37 pA and b = 0.21 s for the large beat with a R2 = 0.977. (C) Fitting an monoexponential curve (f(x) = a × exp(−x/b)) to the decay yielded a = −55.8 pA and b = 0.46 s for the small beat with a R2 = 0.980, respectively.

Appendix B. Model Equations and Parameters

Appendix B.1. Calcium Release Site (CRU)

The differential equations describing Ca²⁺ at the release site are as follows:

$$\frac{d{[Ca]}_{ds}^{\left(i\right)}}{dt}=\frac{(J_{ryr}^{\left(i\right)}-J_{efflux}^{\left(i\right)}+J_{dhpr}^{\left(i\right)})}{{\lambda }_{ds}}-2\frac{d{\left[CaM\right]}^{\left(i\right)}}{dt}-\frac{d{\left[CaSL\right]}^{\left(i\right)}}{dt}-\frac{d{\left[CaSR\right]}^{\left(i\right)}}{dt}$$ (A1)

$$\frac{d{\left[CaM\right]}^{\left(i\right)}}{dt}=k_{CaM}^{+}{({\left[Ca\right]}_{ds}^{\left(i\right)})}^2({\left[CM\right]}_T-{\left[CaM\right]}_{ds}^i)-k_{CM}^{-}{\left[CaM\right]}_{ds}^i$$ (A2)

$$\frac{d{\left[CaSL\right]}^{\left(i\right)}}{dt}=k_{SL}^{+}({\left[Ca\right]}_{ds}^i)({\left[SL\right]}_T-{\left[CaSL\right]}_{ds}^i)-k_{SL}^{-}{\left[CaSL\right]}_{ds}^i$$ (A3)

$$\frac{d{\left[CaSR\right]}^{\left(i\right)}}{dt}=k_{SR}^{+}({\left[Ca\right]}_{ds}^i)({\left[SR\right]}_T-{\left[CaSL\right]}_{ds}^i)-k_{CM}^{-}{\left[CaSR\right]}_{ds}^i$$ (A4)

where (i) is an index indicating the ith specific CRU, ${\lambda }_{ds}=V_{ds}/V_{myo}$ is the volume fraction that scale the fluxes, defined based on myoplasmic volume, to the subspace volume compartment. The membrane buffers used here are similar to those used previously [58,100].

Appendix B.2. Ryanodine Receptor Type-2 Model

The states of the RyR2 are

$$C\begin{array}{c}\stackrel{k_{ryr}^{+}}{\to }\\ \underset{k_{ryr}^{-}}{\leftarrow }\end{array}O$$ (A5)

with the transition rates

$$k_{ryr}^{+}=12{({\left[{\mathrm{Ca}}^{2+}\right]}_{ds}^i)}^2·(2.8\times {10}^{-4}{\left[{\mathrm{Ca}}^{2+}\right]}_{jsr}^i+0.02)$$ (A6)

$${\left[{\mathrm{Ca}}^{2+}\right]}_{ds}^i=500$$ (A7)

Coupling of the RyR2 channels in the cluster uses allosteric coupling energies: ${\epsilon }_{OO}, {\epsilon }_{CC}$ as before [27]. At each release site, the transition between two cluster states Si and Sj is represented as

$$S_i\begin{array}{c}\stackrel{{\chi }_{CO}{k}_{ryr}^{+}{N}_{C\to O}}{\to }\\ \underset{{\chi }_{OC}{k}_{ryr{N}_{O\to C}}^{-}}{\leftarrow }\end{array}{S}_j$$ (A8)

where $N_{O\to C}\left(N_{C\to O}\right)$ represents the number of channels in cluster state Si (Sj) that can be switched from Open to Closed (Closed to Open). The coupling gating in the cluster is given by the formula

$${\chi }_{co}=\exp \left(-{\overline{a}}_j\times 0.5\times \left(N_{closed}{\epsilon }_{cc}-\left(N_{open}-1\right){\epsilon }_{oo}\right)\right)$$ (A9)

$${\chi }_{oc}=\exp \left(-{\overline{a}}_j\times 0.5\times \left(N_{open}{\epsilon }_{oo}-\left(N_{closed}-1\right){\epsilon }_{cc}\right)\right)$$ (A10)

with $\overline{a_j}$ is the average allosteric connectivity for each RyR based on mean-field approach [54]. The variables $N_{closed}$ and $N_{open}$ represent the current number of non-conducting, and conducting channels in the cluster state Si, respectively.

The non-junctional or ‘rogue’ RyR is modelled deterministically using the formula

$$J_{ryr-nj}=P_{O,ryr-nj}·({\left[{\mathrm{Ca}}^{2+}\right]}_{nsr}-{\left[{\mathrm{Ca}}^{2+}\right]}_{myo})$$ (A11)

$$v_{ryr-nj}=v_{ryr}^T\times \left[{\mathrm{fraction}}_{\mathrm{nj}-\mathrm{RyR}} \right]$$ (A12)

$$\frac{d{P}_{o,ryr-nj}}{dt}=k_{ryr-nj}^{+}\left(1-P_{o,ryr-nj}\right)-k_{ryr-nj}^{-}{P}_{o,ryr-nj}$$ (A13)

$$\frac{d{P}_{o,ryr-nj}}{dt }=k_{ryr-nj}^{+}\left(1-P_{o,ryr-nj}\right)-k_{ryr-nj}^{-}{P}_{0,ryr-nj}$$ (A14)

$k_{ryr-nj}^{+}$ has the same functional form as $k_{ryr}^{+}$, except the subspace calcium [Ca²⁺]_ds in the formula of is now replaced by [Ca²⁺]_myo. In the model, the fraction of non-junctional RyRs (ryr-nj) is 5%.

Appendix B.3. L-Type Ca²⁺ Channel Model

The 6-state L-type Ca²⁺ channel (LCC) model, Figure 2, is derived from 5-state LCC model for rat ventricle myocyte from Sun and co-workers with parameters adjusted for the new spark model [29]. Permeation of the L-type Ca²⁺ channel used the Goldman-Hodgkin-Katz (GHK) formalism was used [101]

$$I_{dhpr}^{\left(i\right)}=N_{open, dhpr}^{\left(i\right)}\frac{P_{dhpr}{z}_{Ca}^2{V}_m}{\frac{RT}{F^2}}\frac{{\left[C{a}^{2+}\right]}_{ds}^{\left(i\right)}\exp \left(\frac{z_{Ca}{V}_m}{\frac{RT}{F}}\right)-\frac{{\beta }_o}{{\beta }_I·{\left[C{a}^{2+}\right]}_o}}{\exp \left(\frac{z_{Ca}{V}_m}{\frac{RT}{F}}\right)-1}$$ (A15)

with (i) represents the index of a release site $N_{open, dhpr}^{\left(i\right)}$ is the number of open DHPR channels, ${[{\mathrm{Ca}}^{2+}]}_{ds}^{(i)}$ is the calcium concentration in a dyadic subspace), ${[{\mathrm{Ca}}^{2+}]}_o$ is the extracellular calcium concentration; P_dhpr is the single channel permeability; z_Ca = 2 is the valence of Ca²⁺ ion; R is the universal gas constant, T is the temperature and F is the Faraday constant. The partition coefficients are ${\beta }_0=0.341, {\beta }_1=1$ in the case of Ca²⁺ channel [102,103]. NOTE: If V_m = 0, this formula is used instead

$$I_{dhpr}^{\left(i\right)}=N_{open, dhpr}^{\left(i\right)}{P}_{dhpr}{z}_{Ca}F({\left[C{a}^{2+}\right]}_{ds}^{\left(i\right)}-{\left[C{a}^{2+}\right]}_o)$$ (A16)

Even though the role of extracellular calcium was not investigated in this study, the model also considered the effect of extracellular calcium [Ca²⁺]_o on the model by modulating single channel current and shifting the half-activation voltage V1/2.

$$\begin{gathered} V_{\frac{1}{2}}=-40.344+13.31\times \exp \left(-{\left[Ca\right]}_o\times \frac{{10}^{-3}}{0.053}\right)+31.65 \\ \hspace{1em}\hspace{1em}\hspace{1em}\times \exp \left(-{\left[Ca\right]}_o\times \frac{{10}^{-3}}{11.305}\right)+3 \end{gathered}$$ (A17)

It has been suggested that CaM tethers to a region of C-terminal between an EF and IQ domain of LCC [104,105], with 2 different segments (A and C sequences) within the pre-IQ motif of LCC have been indicated to be critical for CDI [106], and this tethering occurs at very low level of calcium concentration (20–100 nM) [35]. This is the range of resting calcium level; thus, it is assumed that all CaM tethers to the channels all the time. So, the total [CaM] is assumed fixed in the subspace, and calcium-dependent inactivation of LCC (k2→4) is modelled via calcium-Calmodulin (CaCaM) complex. In the model, similar to the experimental data, it is assumed that a single bound Ca²⁺/CaM complex is both necessary and sufficient for CDI [107]. Hence, the transition rate for CDI is formulated as k24 = c24 [Ca²⁺/CaM].

Not only Ca²⁺, but also other ions can also permeate via LCC [108,109]. However, due to the large permeability of Ca²⁺ compared to other ions (e.g., PCa/PNa > 1000), in this study, only Ca²⁺ current is modelled. Due to the nonlinearity in the I-V curve and based on the assumption of independent permeation between ion species and constant-field theory, the Goldman-Hodgkin-Katz (GHK) formalism was used [101].

The equations for the LCC model are given in Table A1. The fraction of LCC channels in each state during a +10 (mV) voltage clamp is shown in Figure 2B. State 2 and 3 are open states; while State 4 is calcium-dependent inactivation and State 5 is voltage-dependent inactivation.

Appendix B.4. Na⁺ Channel Model

The whole-cell Na⁺ current was derived from the formula

$$I_{Na}=g_{Na}{m}_{Na}{h}_{Na}^3{j}_{Na}\left(V_m-E_{Na}\right)$$ (A18)

with the ODE for gating variable follows the first-order differential equation [108]

$$\frac{d{x}_{Na}}{dt}=\frac{x_{\infty }-x_{Na}}{{\tau }_x}$$ (A19)

where x_Na represents the dimensionless gating variables, either m, h, or j, in the range between 0 and 1.0 and $x_{\infty }$ is the steady-state value for the gating variable. The unit for the time constants is in seconds.

$$h_{\infty }=\frac{1}{1+\exp \left(\frac{V_m+76.1}{6.07}\right)}$$ (A20)

$$j_{\infty }=h_{\infty }$$ (A21)

$$m_{\infty }=\frac{1}{1+\exp \left(\frac{V_m+48}{-6.5}\right)}$$ (A22)

$${\tau }_m=\frac{0.00136}{0.32\left(V_m+47.13\right)/(1-\exp \left(-0.1\left(V_m+47.13\right)\right)+0.08\times \exp \left(-\frac{V_m}{11}\right))}$$ (A23)

If V_m >= −40

$${\tau }_h=0.0004537\left(1+\exp \left(\frac{V_m+10.66}{-11.1}\right)\right)$$ (A24)

$${\tau }_j=\frac{0.01163\left(1+\exp \left(-0.1\left(V_{m+32}\right)\right)\right)}{\exp \left(-2.535\times {10}^{-7}{V}_m\right)}$$ (A25)

If V_m < −40

$${\tau }_h=\frac{0.00349}{0.81\exp \left(\frac{V_m+80}{-6.8}\right)+3.56\exp \left(0.079V_m\right)+3.1\times {10}^5\exp \left(0.35V_m\right)}$$ (A26)

$${\tau }_j=\frac{0.00349}{\begin{array}{c}\frac{5\left(V_m+37.78\right)}{1+\exp \left(0.311\left(V_m+79.23\right)\right)}(-\mathrm{12,714}\exp \left(0.2444V_m\right)-3.474\times {10}^{-5}\exp \left(-0.04391V_m\right))+\\ \frac{0.1212\exp \left(-0.01052V_m\right)}{1+\exp \left(-0.1378\left(V_m+40.14\right)\right)}\end{array}}$$ (A27)

$$h_{\infty }=\frac{0.135\exp \left(\frac{V_m+80}{-6.8}\right)}{0.135\exp \left(\frac{V_m+80}{-6.8}\right)+3.56\exp \left(0.079V_m\right)+3.1\times {10}^5\exp \left(0.35V_m\right)}$$ (A28)

$$j_{\infty }=\frac{\frac{V_m+37.78}{1+\exp \left(0.311\left(V_m+79.23\right)\right)}(-\mathrm{12,714}\exp \left(0.2444V_m\right)-3.474\times {10}^{-5}\exp \left(-0.04391V_m\right))}{\begin{array}{c}\frac{V_m+37.78}{1+\exp \left(0.311\left(V_m+79.23\right)\right)}(-\mathrm{12,714}\exp \left(0.2444V_m\right)-3.474\times {10}^{-5}\exp \left(-0.04391V_m\right))+\\ \frac{0.1212\exp \left(-0.010527V_m\right)}{1+\exp \left(-0.1378\left(V_m+40.14\right)\right)}\end{array}}$$ (A29)

Appendix B.5. K⁺ Channel Models

There are four different K⁺ channel currents (I_tof, I, I_K1, and I_Kss). The formula for fast and slow transient outward currents (I_Ktof, I_Ktos, respectively) are based on the model developed using data observed in mouse [49].

$$I_{K1}=g_{K1}\times \frac{{\left[K\right]}_o}{{\left[K\right]}_o+210}\times \frac{\left(V_m-E_K-1.73\right)}{1+\exp \left(0.0896\left(V_m-E_{K-1.73}\right)\right)}$$ (A30)

$$I_{kss}=g_{Kss}\times a_{Kss}\ast i_{Kss}\left(V_m-E_K\right)$$ (A31)

$$I_{ksf}=g_{Ktof}\times a_{Ktof}\ast i_{Ktof}\left(V_m-E_K\right)$$ (A32)

$$I_{ktos}=g_{Ktos}\times a_{Ktos}\ast i_{Ktos}\left(V_m-E_K\right)$$ (A33)

$$\frac{d{a}_{Kss}}{dt}={10}^3\frac{\frac{1.0}{1.0+\exp \left(-\frac{V_m+22.5}{7.7}\right)}-a_{Kss}}{0.13+0.393\times 0.393\times \exp \left(-0.0862V_m\right)}$$ (A34)

$$\begin{gathered} \frac{d{a}_{Ktof}}{dt}={10}^3\times \left[0.18064\exp \left(\left(V_m+30\right)\times 0.3577\right)\times \left(1-a_{Ktof}\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-0.3956\exp \left(-\left(V_m+30\right)\times 0.06237\right)\times a_{Ktof}\right] \end{gathered}$$ (A35)

$$\begin{gathered} \frac{d{a}_{Ktof}}{dt}={10}^3\times [\frac{\left(0.000152\exp \left(-\frac{V_m+13.5}{7}\right)\right)}{1+0.067083\exp \left(-\frac{(V_m+33.5)}{7}\right)}\times \left(1-a_{ktof}\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\frac{0.00095\exp (\frac{V_m+33.5}{7})}{1+0.051335\exp \left(\frac{(V_m+33.5)}{7}\right)}\times i_{Ktof}] \end{gathered}$$ (A36)

$$\frac{d{a}_{Ktos}}{dt}={10}^3\frac{\frac{1.0}{1.0+\exp \left(-\frac{V_m+22.5}{7.7}\right)}-a_{Ktos}}{2.058+0.493\times \exp \left(-0.0629V_m\right)}$$ (A37)

$$\frac{d{i}_{Ktos}}{dt}={10}^3\frac{\frac{1.0}{1.0+\exp \left(\frac{V_m+45.20}{5.70}\right)}-i_{Ktos}}{270.0+1050/(1+\exp \left(\frac{V_m+45.2}{5.70}\right))}$$ (A38)

with $g_{K1}=0.15;g_{Kss}=0.0421;g_{Ktof}=0.0798;g_{Ktos}=0.00629;g_{bK}=1.38\times {10}^{-7}$.

The initial values are given in Table A2.

Appendix B.6. Sarcolemmal Pumps/Exchangers

The two extrusion pathways for calcium via SL are plasma-membrane Ca²⁺/ATP-ase (PMCA) and Na⁺/Ca²⁺ exchanger (NCX).

$$J_{ncx}=\frac{-A_m{I}_{ncx}}{F{V}_{myo}}$$ (A39)

with A_m is the SL surface area and V_myo is the myoplasmic volume

The NCX is given by the formula

$$\begin{gathered} I_{\frac{N{a}^{+}}{K^{+}}}={\overline{I}}_{\frac{N{a}^{+}}{K^{+}}}\frac{1}{(1+0.01245\exp \left(-0.1\left(V_m\frac{F}{RT}\right)\right)\times 0.0365\left(\frac{1}{7}\exp \left(\frac{{\left[Na\right]}_o}{\mathrm{67,300}}\right)-1\right)\exp \left(-V_m\frac{F}{RT}\right))} \\ \times \frac{1}{1+{\left(\frac{\mathrm{21,000}}{{\left[Na\right]}_i}\right)}^{1.5}\frac{{\left[K\right]}_o}{{\left[K\right]}_o+1500}} \end{gathered}$$ (A40)

with ${\overline{I}}_{ncx}$ is the maximal NCX current. The parameters are given in Table A3.

$$I_{pmca}={\overline{I}}_{pmca}\frac{{({\left[{\mathrm{Ca}}^{2+}\right]}_{myo})}^{{\eta }_{pmca}}}{{\left(K_{m,pmca}\right)}^{{\eta }_{pmca}}+{({\left[{\mathrm{Ca}}^{2+}\right]}_{myo})}^{{\eta }_{pmca}}}$$ (A41)

In the case of sodium and potassium pumps, we have

Appendix B.7. Background Currents

The background currents follow the linear Ohm-law

$$I_{bX}=g_X\left(V_m-E_X\right)$$ (A42)

The three different background currents were used in the model

$$I_{bCa}=g_{bCa}\left(V_m-E_{Ca}\right)$$ (A43)

$$I_{bNa}=g_{bNa}\left(V_m-E_{Na}\right)$$ (A44)

$$I_{bK}=g_{bK}\left(V_m-E_K\right)$$ (A45)

with the reversal potentials are derived from Nernst equation.

$$E_X=\frac{RT}{F{z}_X}\ln \left(\frac{{\left[X\right]}_i}{{\left[X\right]}_o}\right)$$ (A46)

with z_x is the valance of ion X.

Appendix B.8. Sarcoplasmic Reticulum Ion Pumps

The 2-state reduced model of the Tran-Crampin model was chosen with parameters selected so that the maximum pumping rate per pump molecule, max (v_serca), is 5 s⁻¹.

$$J_{serca}=2\times v_{serca}$$ (A47)

$$v_{serca}=\frac{3.24873\times {10}^{12}{\left(K_{myo}\right)}^2+K_{myo}\left(9.17846\times {10}^6-\mathrm{11,478.2}{K}_{sr}\right)-0.329904K_{sr}}{D_{cycle}}$$ (A48)

$$\begin{gathered} D_{cycle}=0.104217+17.923K_{sr}+K_{myo}\left(1.75583\times {10}^6+7.61673K_{sr}\right)+ \\ {\left(K_{myo}\right)}^2\left(6.08463\times {10}^{11}+4.50544\times {10}^{11}{K}_{sr}\right) \end{gathered}$$ (A49)

and

$$K_{myo}={\left(\frac{{\left[Ca\right]}_{myo}}{{10}^{-3}{K}_{d,myo}}\right)}^2; K_{sr}={\left(\frac{{\left[Ca\right]}_{nsr}}{{10}^{-3}{K}_{d,sr}}\right)}^2$$ (A50)

Appendix B.9. Sarcoplasmic Reticulum Ion Pumps

The three endogenous buffers of calmodulin (CaM), troponin (Trpn), and the phospholipids of the SR membrane (SRbuf) are used for the bulk myoplasm. The buffering parameters are listed in Table A4.

$$\frac{d\left[Ca;CaM\right]}{dt}=k_{CM}^{+}({\left[Ca\right]}_{myo}^2)({\left[CM\right]}_T-{\left[Ca;CaM\right]}_{myo})-k_{CM}^{-}{\left[Ca;CaM\right]}_{myo}$$ (A51)

$$\begin{gathered} \frac{d\left[Ca;SRbuf\right]}{dt}=k_{SR}^{+}({\left[Ca\right]}_{myo})({\left[SRbuf\right]}_T-{\left[Ca;SRbuf\right]}_{myo}) \\ -k_{SR}^{-}{\left[Ca;SRbuf\right]}_{myo}\hspace{1em}\hspace{1em} \end{gathered}$$ (A52)

$$\begin{gathered} \frac{d\left[Ca;Trpn\right]}{dt}=k_{Trpn}^{+}({\left[Ca\right]}_{myo})({\left[Trpn\right]}_T-{\left[Ca;Trpn\right]}_{myo}) \\ -k_{Trpn}^{-}{\left[Ca;Trpn\right]}_{myo}\hspace{1em}\hspace{1em} \end{gathered}$$ (A53)

Appendix B.10. Membrane Potential

During AP, the dynamics of the membrane voltage V_m is governed by the equation

$$\frac{d{V}_m}{dt}=-\frac{{10}^3}{C_{sc}}\left(\begin{array}{c}\frac{\left(I_{dhpr}^T\right)}{A_m}+I_{Na}+I_{NCX}+I_{NaK}+I_{pmca}+I_{K1}+I_{Kss}+I_{Ktof}+\\ I_{Ktos}+I_{background}+I_{app}\end{array}\right)$$ (A54)

with NSFU is the number of Ca²⁺ release sites, and

$$I_{dhpr}^T={\displaystyle \sum }_{i=1}^{N_{SFU}}{I}_{dhpr}^i$$ (A55)

$$I_{background}=I_{bCa}+I_{bNa}+I_{bK}$$ (A56)

NOTE: The units: membrane potential and reversal potential are in mV, while other parameters are given in the form of unit-density, e.g., the specific membrane capacitance C_sc = 1 µF/cm², the ionic currents are given in (µA/cm²), except the L-type currents are measured at whole-cell level (µA) which needs to be converted to current density by dividing the membrane surface area A_m (cm²).

Appendix B.11. Parameters

The rat ventricular cell volume was chosen 25 pL to match to the number 20,000 CRUs per cell with Cm/Vcell = 7.12 pF/pL [99,100]. The schematic diagram of the compartmental model of the rat ventricular myocyte with all the ionic currents is given in Figure A1.

Table A1.

Parameters for L-type Ca²⁺ channel model.

$P_{o2}=\frac{-1}{1+e^{\frac{v-v_{\frac{1}{2}}}{S}}}+1$

$V_{\frac{1}{2}}=-40.344+13.31\times e^{\left(-\frac{{\left[Ca\right]}_o}{53.0}\right)}+31.65\times e^{\left(-\frac{{\left[Ca\right]}_o}{\mathrm{11,305}}\right)}+3$

$S=(0.632+0.368\times e^{(\frac{-{\left[Ca\right]}_0}{{10}^3}-0.1)/0.784)})\times (-\frac{3.792}{1+e^{(\frac{{\left[Ca\right]}_0}{{10}^3}-0.0469)/0.011)}+6.39})$

$att=130+\frac{-129}{1+e^{\frac{V_m-60}{8}}}+\frac{0.76}{1+e^{\frac{V_m-5}{3.14}}}$

${\tau }_{P_{02}}=0.00025+0.00305\times e^{-0.0045{\left(V_m+7\right)}^2}+0.00105\times e^{-0.002{\left(V_m-18\right)}^2}$

$inc{h}_{Ca}=0.89+\frac{-0.888}{1+e^{\frac{V_m-43.066}{2.289}}}\times \left(1.004+\frac{-1.199}{1+e^{\frac{\frac{{\left[Ca\right]}_o}{{10}^3}-0.259}{0.164}}}\right)$

$k_{1,5}=\frac{k_{5,1}{k}_{1,2}{k}_{2,5}}{k_{5,2}{k}_{2,1}}$

$k_{5,4}=\frac{k_{4,5}{k}_{5,2}{k}_{2,4}}{k_{4,2}{k}_{2,5}}$

$d_{dhpr}=d_{dhpr,\left({\left[Ca\right]}_0=1.8\mathrm{mM}\right)}\left(1+\frac{-1}{1+e^{\frac{\frac{{\left[Ca\right]}_o}{{10}^3}-0.08}{0.0159}}}\right)$

$k_{1,2}=0.115\times \frac{P_{O2}}{{\tau }_{O2}}$

$k_{2,1}=0.115\times \frac{1-0.155\times P_{O2}}{{\tau }_{O2}}\times att$

$k_{2,3}=0.7\times (987.3+\frac{-903.53}{1+e^{\frac{V_m-51.23}{6.785}}}$)

$k_{3,2}=500$

$k_{2,5}=0.5\times (32+\frac{-18.46}{1+e^{\frac{V_m-30}{5.746}}})\times (1-in{h}_{Ca})$

$k_{5,2}=1.0\times \left(32+\frac{-5.03}{1+e^{(V_m-30)/0.787}}\right)+\left(0.95+\frac{-0.93}{1+e^{\frac{V_m+40}{0.787}}}\right)$

$k_{2,4}=8\times \left[CaM\right]$

$k_{4,2}=1$

$k_{5,1}=6.9$

$k_{4,5}=600$

$k_{3,2}=500$

$k_{6,1}=1\times (0.0022+\frac{2998.978}{1+e^{-\left(Vm+45\right)\times 0.71428}})$

$k_{1,6}=1\times (3000+\frac{2998.978}{1+e^{-\left(Vm+45\right)\times 0.6667}})$

Table A2.

Initial values.

Variables	Value	Unit
mNa	0.0015d0	Unitless
hNa	0.9849d0	Unitless
jNa	0.9849d0	Unitless
aKss	0.0021d0	Unitless
inKss	1.d0	Unitless
aKtof	0.0021d0	Unitless
inKtof	1.d0	Unitless
aKtos	2.9871d-04	Unitless
inKtos	0.9994d0	Unitless
[Ca2+]myo	0.08769	µM
[Ca2+]nsr	1.00737d3	µM
[Na+]i	1.02d4	µM
[K+]i	1.4372d5	µM

Table A3.

Constant data and whole-cell level data.

Variables	Value	Unit
Faraday constant (F)	9.6485d4	C/mol
Universal gas constant (R)	8.314d3	mJ/(mol.K)
Temperature (T)	310	K
[Na]o	1.4d5	µM
[Ca]o	1.8d3	µM
[K]o	5.4d3	µM
Cell volume (Vcell)	25.0	pL
Myoplasmic volume (Vmyo)	12.5	pL
Network SR volume ($V_{nsr}^{}$)	0.762d0	pL
Junctional SR volume ($V_{jsr}^T$)	1.25d-1	pL
Subspace volume ($V_{ds}^T$)	1.55d-2	pL
Concentration [SERCA] Kd,myo Kd,sr	300 900 2150	µM µM µM
RyR release rate ($v_{ryr}^T$)	56.4279	1/s
Percent nj-RyR	0.5	Unitless
Transfer rate from subspace to bulk myoplasm ($v_{efflux}^T$)	300	1/s
Refill rate from nSR to jSR ($v_{refill}^T$)	2.4	1/s
NCX maximum current density ($\overline{I_{ncx}}$) Kd,ncxNa Kd,ncxCa	520 8750 1380	µA/µF
PMCA maximum current density ($\overline{I_{pmca}}$) Kd,pmca	0.12 0.5	µA/µF
Na/K maximum current density ($\overline{I_{Na/K}}$)	0.88	µA/µF

Table A4.

Calcium buffers.

Variables	Value	Unit
General buffer in myoplasm Kd	1.23d2 0.96	µM µM
General buffer in jSR (e.g., Calsequestrin) Kd	1.4d4 6.38d2	µM µM
High-affinity Troponin C $k_{CM}^{+}$  $k_{CM}^{-}$	1.40d2 2.37 3.2d-2	µM 1/(µM.s) 1/s
Calmodulin $k_{SR}^{+}$  $k_{SR}^{-}$	2.4d1 3.0d1 7.14d1	µM 1/(µM.s) 1/s
SL buffer $k_{SL}^{+}$  $k_L^{-}$	250 115 1000	µM 1/(µM.s) 1/s
SR buffer $k_{SR}^{+}$ $k_{SR}^{-}$	47 115 100	µM 1/(µM.s) 1/s

Author Contributions

Conceptualization, M.S.J. and M.T.H.-T.; methodology, M.S.J. and M.T.H.-T.; software, M.T.H.-T.; validation, M.S.J., A.U., W.J.L. and M.T.H.-T.; formal analysis, M.T.H.-T.; investigation, M.T.H.-T.; resources, M.S.J.; data curation, M.T.H.-T.; writing—original draft preparation, M.T.H.-T.; writing—review and editing, M.S.J., A.U., W.J.L. and M.T.H.-T.; visualization, M.T.H.-T. and A.U.; supervision, M.S.J.; project administration, M.S.J.; funding acquisition, M.S.J. and A.U. All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by the National Institutes of Health (NIH) grant no. 5R01HL105239 (W.J.L. & M.S.J.), 5R01HL106059 (W.J.L.), 5U01HL116321 (M.S.J. & W.J.L.), and R01 HL142290 (W.J.L.).

Institutional Review Board Statement

No human subjects were involved.

Informed Consent Statement

No human subjects were involved.

Data Availability Statement

Model codes are publicly available at the Mason Archival Repository Service (MARS) at the following link: available online: https://hdl.handle.net/1920/11957 (accessed on 5 October 2021).

Conflicts of Interest

The authors declare that there is no conflict of interest.