Pandemic fatigue impact on COVID-19 spread: A mathematical modelling answer to the Italian scenario

Abstract

The COVID-19 outbreak has generated, in addition to the dramatic sanitary consequences, severe psychological repercussions for the populations affected by the pandemic. Simultaneously, these consequences can have related effects on the spread of the virus. Pandemic fatigue occurs when stress rises beyond a threshold, leading a person to feel demotivated to follow recommended behaviours to protect themselves and others. In the present paper, we introduce a new susceptible–infected–quarantined–recovered-dead (SIQRD) model in terms of a system of ordinary differential equations (ODE). The model considers the countermeasures taken by sanitary authorities and the effect of pandemic fatigue. The latter can be mitigated by fear of the disease’s consequences modelled with the death rate in mind. The mathematical well-posedness of the model is proved. We show the numerical results to be consistent with the transmission dynamics data characterising the epidemic of the COVID-19 outbreak in Italy in 2020. We provide a measure of the possible pandemic fatigue impact. The model can be used to evaluate the public health interventions and prevent with specific actions the possible damages resulting from the social phenomenon of relaxation concerning the observance of the preventive rules imposed.

Introduction

The year 2020 will be remembered. The COVID-19 virus pandemic has spread unprecedented around the world. Governments, institutions, economic systems, scientific research, and entire populations have faced the challenges of an anti-epidemic battle. Very many families and individuals have been subjected to sanitary risks and tremendous psychological pressure.

The World Health Organization (WHO) declared the 2019-nCoV ARD outbreak as a “Public Health Emergency of International Concern” on 30 January 2020, specifically to enhance the level of preparedness of countries that required additional support [1].

On 11 February 2020, the WHO gave the name COVID-19 (Coronavirus Disease 2019) [2] to the epidemic, which consists of a severe acute respiratory syndrome caused by the coronavirus 2 (SARS-CoV-2) and was detected in December 2019 in Wuhan, China [3]. This novel virus belongs to the large coronavirus family responsible for several respiratory illnesses, including the Middle East Respiratory Disease (MERS) and the Severe Acute Respiratory Syndrome (SARS). However, COVID-19 is characterised by a particular aggressiveness: its high reproductive rate [4], and grave mortality rate [5]. Common symptoms are fever, dry cough, sore throat, headache, fatigue, myalgia, and breathlessness. Some patients can suffer acute respiratory distress syndrome, and multiorgan dysfunction [6].

The COVID-19 contagion is due to human transmission through respiratory droplets or contact with surfaces contaminated by an infected person. For this reason, non-pharmaceutical interventions have been adopted with variable measures implemented according to the severity of the situation, from the use of personal protection such as breathing masks and hand protective/disposable gloves to social distancing and public health measures, including the lockdown of entire regions or countries [7], [8]. Such measures were essentially the primary means of preventing and mitigating the spread of the epidemic. Despite these interventions, on 31 December 2020, the WHO reported $81,475,053$ confirmed cases and $1,798,050$ deaths for COVID-19 in the world.

On 11 March 2020, the WHO declared COVID-19 a pandemic, emphasising its global character, and countries were urged to take actions and make evidence-based decisions [9]. This emergency represents a challenge for mathematicians called to build models capable of predicting the course of the disease and suggesting appropriate countermeasures.

Despite the scarce information on the virus and the availability of insufficient data, the mathematical modelling community did not fail to produce efforts to assist the health authorities [10], [11]. Many significant papers have been published, ranging from statistical approaches [12], [13], [14], [15], to deterministic compartmental models [16], [17], [18], [19], [20], [21], [22], [23], [24], [25] to stochastic procedures [26], [27]. Some aim to estimate the transmission risk [28], others to estimate the number of unreported cases [29], or to consider both the age and social contact structure [30].

One common question is to understand to what extent significant public policies restricting social movements, such as social distancing, “stay-at-home” measures, quarantine, and public closings, can mitigate the epidemic spread. The idea is not only to predict outbreak behaviour, such as its final size and its peak time [31] but also to help in planning effective control strategies and public health interventions [32]. Specifically, mathematical models based on dynamic equations have the advantage of clearly identifying the mechanisms behind the dynamics of the epidemic [33], [34], [35], [36], [37].

Although COVID-19’s epidemiological characteristics are yet to be fully elucidated and the introduction of a certain degree of estimation error is unavoidable [38], ordinary differential equation (ODE) models can give a general description of the spread of the virus.

Although deterministic, ODE models provide information on the dynamics of quantities such as the number of cases, recoveries, and deaths averaged at the regional level [39]. Such models allow the identification and definition of a set of parameters characterising the dynamics of the epidemic that can be estimated on a rational basis and then tuned to fit the available experimental data. Consequently, changes in the values of these parameters can simulate the system’s response to political strategies and social–environmental features. Therefore, despite their drastic simplifications, their flexibility might make them more valuable than models that are more complex [40], [41], [42].

The psychological repercussions for the population are a general and impactful side effect of COVID-19. The relevant effects of the pandemic on the mental health of quarantined persons, hospital and front-line staff, and their relatives and the general population have been the object of extensive studies in various contexts, not to mention the changes induced in social behaviour. These aspects are outside the scope of this paper. However, psychological effects have also had a direct impact on the spread of the pandemic.

“Pandemic fatigue” is a term coined by the WHO to indicate the psychological response to the prolonged public health crisis. This kind of distress is due to invasive measures having unprecedented impacts on people’s daily lives. Pandemic fatigue can express itself as a gradually emerging demotivation to engage in protection behaviours [43]. Many countries reported an increase in collective fatigue, evident by the fact that “people are feeling demotivated about following recommended behaviours to protect themselves and others from the virus” [44]. Although there are some sporadic conflicting ideas on the subject [45], [46], there is no doubt that this social phenomenon can affect our behaviour and, therefore, consequently, the evolution of the pandemic. Pandemic fatigue becomes a vital factor in the COVID-19 spread. In the book “The Psychology of Pandemics”, Steven Taylor states that: “remarkably little attention has been devoted to the psychological factors that influence the spread of pandemic infection and the associated emotional distress and social disruption. Psychological factors [...] play a role in non-adherence to vaccination and hygiene programs, and play an important role in how people cope with the threat of infection” [47].

The tiredness of living with the discomforts induced by the health regulations imposed, including a heightened state of distrust towards these measures, can easily lead a considerable number of individuals to let their guard down and to unjustifiably minimise the danger and vulnerability to the virus [48].

On the other hand, the fear of the consequences of the disease can counteract fatigue. It can push the population to better comply with the measures imposed by the government. This feeling of vulnerability can reasonably be related to the rate of deaths due to the pandemic.

In this paper, we consider and introduce the non-negligible role of pandemic fatigue and the sense of vulnerability, since human behaviour appears to be central to the virus transmission [49]. We opt for a simple mean-field model for a general quantitative picture of epidemic spreading, including restrictive public health interventions and the social and emotional population response. There are attempts to consider the individual reaction, but they are rare [50]; the merit of our mathematical model compared to the other existing works is to add and mimic the averaged pandemic fatigue impact into COVID-19 spread. This novel study aims to explain the pandemic behaviour concerning the public’s relaxation and resistance to comply with public health restrictions and, therefore, albeit with a certain degree of approximation, to evaluate how much the pandemic fatigue and fear of the disease affected the COVID-19 outbreak in Italy in 2020. The mathematical model consists of a susceptible–infected–quarantined–recovered–dead (SIQRD) system of ordinary differential equations (ODEs). We apply the model to the Italian context during 2020 (already the subject of other publications [40], [51], [52]) to test the consistency of the hypotheses applied to the results obtainable with the model simulations and compared with the epidemiological data.

The paper contents are organised as follows. In Section “Model” we describe the assumptions adopted, develop the mathematical model, and prove its mathematical well-posedness. Section “The case of Italy: numerical results” contains the numerical results of the simulations performed with our model, where the Italian preventive actions acquire the calibration of the parameters during 2020. The comparison of the data collected by the competent authorities on the evolution of positive cases, quarantined people, and dead is also presented. Subsequently, the model is used predictively to evaluate the hypothetical results based on different administrative choices and the population’s more or less virtuous behaviour. The estimated cost of infected people and deaths due to the harmful effects of pandemic fatigue is reported. Finally, in Section “Conclusions and future perspectives” we provide a brief discussion on the achievements of this work and its implications in terms of measures to contain or prevent the adverse effects of pandemic fatigue. We include some comments on possible future developments and applications of the model.

Model

Let us propose to study the evolution dynamics of the COVID-19 outbreak with respect to time $t\ge t_0$, $t_0$ representing the initial time. We assume that the entire population is divided into five compartments. We denote by $S\left(t\right)$ the number of individuals susceptible to infection at time $t$ and by $I\left(t\right)$ the number of infected people who, at time $t$ is still in an asymptomatic state. We apply the simplifying hypothesis that, after an average time of virus incubation, each infected person presents symptoms and consequently is placed in quarantine. We indicate by $Q\left(t\right)$ the number of infected people at time $t$, who have symptoms and are automatically isolated, that is, from the point of view of the model, they are no longer able to infect susceptible persons. Finally, every quarantined person can die or recover. $D\left(t\right)$ counts the total number of deaths and $R\left(t\right)$ recovered individuals at time $t$. We suppose that a recovered person does not go back to being susceptible to the virus. We assume also that the whole population is constant and equal to $N$. This approximation is justifiable because the pandemic outbreak covers a period of time in which the variation in the total number of individuals, including the deaths because of the disease, is negligible. The model can also take into account vaccination (i.e., direct passage from compartment $S\left(t\right)$ to $R\left(t\right)$) and relapse (from $R\left(t\right)$ to $S\left(t\right)$).

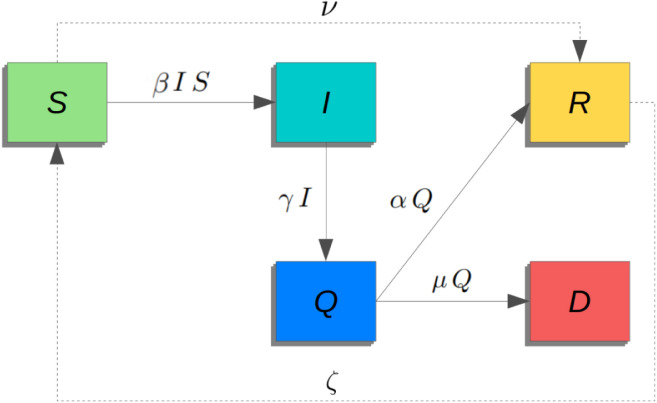
The dynamics between these compartments are illustrated in the flow diagram of Fig. 1 and governed by some parameters. Setting the time unit, we define $\gamma \ge 0$ the inverse of the average period during which an infected individual becomes symptomatic, i.e. the average incubation time. Then, we use the parameters $\alpha \ge 0$ and $\mu \ge 0$ to rule the transition from the compartment of symptomatically ill and quarantined persons to the compartment of those who are healed or dead, respectively. We note that $\alpha$ and $\mu$ are given by the combination of the average time to exit the quarantined class and the probability of defeating or not the disease. Concerning the transition between the susceptible to the infected population, we introduce $\beta$ transmission rate obeying to the mass action law. The definition of $\beta$ deserves particular attention, because it must have the information content suitable for describing (i) the virus contagiousness, (ii) the effect of the social isolation measures and, at the same time, (iii) the population response due to the combined effect of pandemic fatigue and feeling of vulnerability.

Fig. 1.

Schematic flow diagram representation of the model.

In absence of lockdown and of any social distancing measures $\beta$ has a value ${\beta }_0$ that can be considered to be the product of the contagiousness of the viral agent and by a term representing the average “connection” of the society in the pre-epidemic period. We remark that ${\beta }_0$ can be taken as a constant since in the period we will consider no significant variants of the virus were observed.

Any intervention of the public health authorities that includes specific health prevention measures and/or directives such as “stay-at-home” or lockdown directly affects the value of this factor. We express this fact by multiplying ${\beta }_0$ by a factor $(1--\phi )$ where $\phi \in [0,1)$ denotes the intensity of the measures taken. At this point, we include the degree of compliance of the population with these measures, which we express by a multiplicative factor $(1-G)$ where $G$ is the result of fatigue and the feeling of vulnerability. We assume the following form

$$G=f\left(t\right)exp(-k{D}^{\prime }\left(t\right)),$$ (1)

where $f\left(t\right)\in [0,1]$ is the fatigue and the exponential factor modulates fatigue in terms of the death rate $D^{\prime }=\mu Q$, and $k\ge 0$ denotes the sensitivity to the occurrence of deaths. Summing up

$$\beta =\beta (t,Q\left(t\right))={\beta }_0[1--\phi (1--f\left(t\right)exp(-k\mu Q\left(t\right)))].$$ (2)

Based on the above considerations and neglecting vaccination and relapse ($\nu =\zeta =0$), we obtain the mathematical model consisting of the following system of nonlinear ODEs,

$$\left\{\begin{array}{c}{S}^{\prime }\left(t\right)=-\beta (t,Q\left(t\right))I\left(t\right)S\left(t\right),\hfill \\ I^{\prime }\left(t\right)=\beta (t,Q\left(t\right))I\left(t\right)S\left(t\right)-\gamma I\left(t\right),\hfill \\ Q^{\prime }\left(t\right)=\gamma I\left(t\right)-(\alpha +\mu )Q\left(t\right),\hfill \\ R^{\prime }\left(t\right)=\alpha Q\left(t\right),\hfill \\ D^{\prime }\left(t\right)=\mu Q\left(t\right),\hfill \end{array}\right)$$ (3)

where, $t\ge t_0$. The system is supplemented by the initial conditions

$$S\left(t_0\right)=S_0>0,I\left(t_0\right)=I_0\ge 0,Q\left(t_0\right)=Q_0\ge 0,$$ (4)

$$R\left(t_0\right)=R_0\ge 0,D\left(t_0\right)=D_0\ge 0.$$

We remark that it is immediately seen that, since $S^{\prime }\left(t\right)+I^{\prime }\left(t\right)+Q^{\prime }\left(t\right)+R^{\prime }\left(t\right)+D^{\prime }\left(t\right)=0$, the total population is constant and equal to $N=S_0+I_0+Q_0+R_0+D_0$. We may also note that in the case of Italy and whenever populations have a number of inhabitants of several orders of magnitude higher than the other variables, a possible reasonable simplification consists in considering the number of susceptible people constant. Here, we will keep the complete model in which vaccination and relapse could be easily taken into account.

In order to prove the well-posedness of the formulation, we proceed to rewrite the model (3), considering the new normalised variables $s\left(t\right)=S\left(t\right)/N$, $i\left(t\right)=I\left(t\right)/N$, $q\left(t\right)=Q\left(t\right)/N$, $r\left(t\right)=R\left(t\right)/N$, and $d\left(t\right)=D\left(t\right)/N$. With a little abuse of notation, we redefine ${\beta }_0={\beta }_{0}N$ and $k=kN$. Now, under the new normalised formulation, $s\left(t\right)+i\left(t\right)+q\left(t\right)+r\left(t\right)+d\left(t\right)=1$, $\forall t\ge t_0$; therefore we can remove the first equation of the system (3) and obtain the following new system of 4 ODEs,

$$\left\{\begin{array}{c}{i}^{\prime }\left(t\right)=\beta (t,q\left(t\right))(1-i\left(t\right)-q\left(t\right)-r\left(t\right)-d\left(t\right))i\left(t\right)-\gamma i\left(t\right),\hfill \\ q^{\prime }\left(t\right)=\gamma i\left(t\right)-(\alpha +\mu )q\left(t\right),\hfill \\ r^{\prime }\left(t\right)=\alpha q\left(t\right),\hfill \\ d^{\prime }\left(t\right)=\mu q\left(t\right),\hfill \end{array}\right)$$ (5)

with the corresponding initial conditions

$$i\left(t_0\right)=i_0\ge 0,q\left(t_0\right)=q_0\ge 0,r\left(t_0\right)=r_0\ge 0,d\left(t_0\right)=d_0\ge 0.$$ (6)

Expressed in a compact form, the feasible domain of the system (5) is

$$\Gamma =\{(i,q,r,d)\in {\mathbb{R}}_{+}^4:i+q+r+d\le 1\}.$$ (7)

A initial-value problem for a ODEs system is mathematically well-posed when a solution exist, the solution is unique, and it depends continuously on the data. By well-know classical methods, we prove that $\Gamma$ is positively invariant, yielding the well-posedness of the model under the regularity assumptions on the coefficients (see e.g. [53]).

Let us denote $x\left(t\right)={(i\left(t\right),q\left(t\right),r\left(t\right),d\left(t\right))}^T$. The system (3) is equivalent to the system (5), which can be seen as

$$\frac{dx\left(t\right)}{dt}=f\left(x\left(t\right)\right),t\ge t_0,$$ (8)

where

$$\begin{array}{cc}f\left(x\left(t\right)\right)=\hfill & \beta (t,q\left(t\right))(1-i\left(t\right)-q\left(t\right)-r\left(t\right)-d\left(t\right))i\left(t\right)-\gamma i\left(t\right),\hfill \\ \hfill & {\gamma i\left(t\right)-(\alpha +\mu )q\left(t\right),\alpha q\left(t\right),\mu q\left(t\right)]}^T.\hfill \end{array}$$ (9)

To prove that $\Gamma$ is positively invariant, we observe that $\Gamma$ is a compact set. We need to prove that if $x\left(0\right)\in \Gamma$, then $x\left(t\right)\in \Gamma \forall t\ge 0$. Let us consider the boundary $\delta \Gamma$ that consists of 5 plane domains, as follows

$$P_1=\{(i,q,r,0):(i,q,r)\in {\mathbb{R}}_{+}^3,i+q+r\le 1\},$$ (10)

$$P_2=\{(i,q,0,d):(i,q,d)\in {\mathbb{R}}_{+}^3,i+q+d\le 1\},$$ (11)

$$P_3=\{(i,0,r,d):(i,r,d)\in {\mathbb{R}}_{+}^3,i+r+d\le 1\},$$ (12)

$$P_4=\{(0,q,r,d):(q,r,d)\in {\mathbb{R}}_{+}^3,q+r+d\le 1\},$$ (13)

$$P_5=\{(i,q,r,d)\in {\mathbb{R}}_{+}^4:i+q+r+d=1\}.$$ (14)

In addition, let us consider the corresponding outer normal vector to these plane domains, i.e., $v_1=(0,0,0,-1)$, $v_2=(0,0,-1,0)$, $v_3=(0,-1,0,0)$, $v_4=(-1,0,0,0)$, and $v_5=(1,1,1,1)$. We can prove that the scalar products of $f\left(x\right)$ and the normal vectors $(v_1,v_2,v_3,v_4,v_5)$ of the boundary planes are less or equal to zero in order to conclude that $x\left(0\right)\in \Gamma$, then $x\left(t\right)\in \Gamma \forall t\ge 0$. These are easily verifiable, as reported below,

$$〈f\left(x\left(t\right)\right){|}_{x\in P_1},v_1〉=-\mu q\left(t\right)\le 0,$$ (15)

$$〈f\left(x\left(t\right)\right){|}_{x\in P_2},v_2〉=-\alpha q\left(t\right)\le 0,$$ (16)

$$〈f\left(x\left(t\right)\right){|}_{x\in P_3},v_3〉=-\gamma i\left(t\right)\le 0,$$ (17)

$$〈f\left(x\left(t\right)\right){|}_{x\in P_4},v_4〉=0,$$ (18)

$$〈f\left(x\left(t\right)\right){|}_{x\in P_5},v_5〉=0.\square$$ (19)

A few analytical considerations

We can verify the existence of the disease-free equilibria $E^0(S^0,0,0,R^0,D^0)$, with $S^0+R^0+D^0=N$, corresponding to steady state solutions of the system (3) in the absence of infected people.

An important epidemiological indicator is the basic reproduction number ${\mathcal{R}}_0$, which indicates the number of new infections an infected individual causes during the infectious period in a susceptible population. Mathematically, we can establish ${\mathcal{R}}_0$ using the next generation matrix method presented by Van den Driessche [54], [55], [56]. In particular, we can consider the equation of system (3) for the compartment $I$ expressed as

$$I^{\prime }\left(t\right)={\mathcal{F}}_j-{\mathcal{V}}_j=\beta (t,Q\left(t\right))I\left(t\right)S\left(t\right)-\gamma I\left(t\right),$$ (20)

i.e., with ${\mathcal{F}}_j=\beta (t,Q\left(t\right))I\left(t\right)S\left(t\right)$ and ${\mathcal{V}}_j=\gamma I\left(t\right)$. Being $F$ the Jacobian of ${\mathcal{F}}_j$ at $E^0$ and $V$ the Jacobian of ${\mathcal{V}}_j$ at $E^0$ we can evaluate ${\mathcal{R}}_0$ as the spectral radius $\rho$ of the next generation matrix $F{V}^{-1}$. Thus, we obtain

$${\mathcal{R}}_0=\rho \left(F{V}^{-1}\right)=\frac{\beta S^0}{\gamma }\le {\mathcal{R}}_0^{\ast }=\frac{{\beta }_{0}N}{\gamma }.$$ (21)

We can prove that the disease-free equilibria $E^0$ are locally asymptotically stable if ${\mathcal{R}}_0^{\ast }<1$. To this goal, we can compute the Jacobian matrix of system (3) and find the characteristic polynomial

$$P\left(\lambda \right)=-{\lambda }^3(\alpha +\mu +\lambda )(-\beta S^0+\gamma +\lambda )=0,$$ (22)

form which we get 5 eigenvalues: ${\lambda }_1={\lambda }_2={\lambda }_3=0$ with linearly independent eigenvectors, ${\lambda }_4=-(\alpha +\mu )<0$, and ${\lambda }_5=\beta S_0-\gamma$ that it is negative if ${\mathcal{R}}_0^{\ast }<1$. From the epidemiological point of view, this means that the virus spread can be eliminated if the initial data are in the basin of attraction of $E^0$ and ${\mathcal{R}}_0^{\ast }<1$.

Nevertheless, we can provide an even stronger result about effective control of the infected population that it is independent of the initial size in the most unfavourable case, i.e., when the infectivity parameter $\beta$ has constantly its maximum value ${\beta }_0$. Indeed, if we consider the Lyapunov function $\mathcal{G}={\beta }_{0}I\left(t\right)S\left(t\right)-\gamma I\left(t\right)$ and we differentiate it in the solutions of system (3), we obtain

$$\dot{\mathcal{G}}=I({\beta }_0^2{S}^2-{\beta }_0^{2}IS-2{\beta }_0\gamma S+{\gamma }^2)\le I{({\beta }_{0}S-\gamma )}^2.$$ (23)

As we can see, $\dot{\mathcal{G}}<0$ whenever ${\mathcal{R}}_0^{\ast }<1$. According to this result, we can affirm that if ${\mathcal{R}}_0^{\ast }<1$ the virus spread will die out from the community.

A brief sensitivity analysis of ${\mathcal{R}}_0^{\ast }$ can suggest some considerations. In particular, we give the following indices

$${\mathcal{I}}_{\beta }^{{\mathcal{R}}_0^{\ast }}=\frac{\partial {\mathcal{R}}_0^{\ast }}{\partial {\beta }_0}\times \frac{{\beta }_0}{{\mathcal{R}}_0^{\ast }}=1,{\mathcal{I}}_{\gamma }^{{\mathcal{R}}_0^{\ast }}=\frac{\partial {\mathcal{R}}_0^{\ast }}{\partial \gamma }\times \frac{\gamma }{{\mathcal{R}}_0^{\ast }}=-1.$$ (24)

As expected, the parameter ${\beta }_0$ has a positive influence on the basic reproduction number ${\mathcal{R}}_0^{\ast }$. For this reason one strategy is to apply measures in order to decrease $\beta$. On the other hand, an increase in $\gamma$ implies a decrease in ${\mathcal{R}}_0^{\ast }$. This evidence supports the strategy to subject suspected diseased individuals to swab tests as soon as possible, to reduce the stationing of individuals in compartment $I$.

The case of Italy: numerical results

During 2020, one of the most severely affected countries by the pandemic was Italy and can be considered as a case study for the reaction of public health authorities through containment measures and also with respect to the psychological/behavioural response of the general population. On January 31, 2020, the Italian Council of Ministers declares a state of emergency as a result of the health risk associated with the spread of the epidemic. On 31 December 2020, Italy counted 2,107,166 positive cases since the emergency began and 74,159 victims. The data of surveillance for COVID-19 are managed and communicated by the Italian Civil Protection Department and they are publicly available. They are collected in a dataset published in the GitHub repository [57] and presented in [58]. We refer to these data to test our model in the Italian scenario during 2020.

The Italian government has established various interventions and it is possible to consult their detailed list. An overview of Italian government initiatives to prevent and restrain the COVID-2019 pandemic is available in [59]. However, for modelling purposes, we resume the anti-contagion policy with the following main events:

• •9 March 2020: National lockdown. “Stay-at-home” requirements enacted and commercial businesses halted as well as schools and universities throughout the national territory;
• •23 March 2020: Tightening of lockdown rules. Closure of production, industries and commercial services considered non-essential. Reduction of the possibility of transport, even of a private nature;
• •7 June 2020: Reopening of the Country. Activities and mobility are allowed. The authorities issued a series of measures to reopen the activities in the Italian regions: for simplicity, we consider this date as indicative;
• •6 November 2020: Restrictive lockdown measures, on a national scale, for the second wave of contagion.

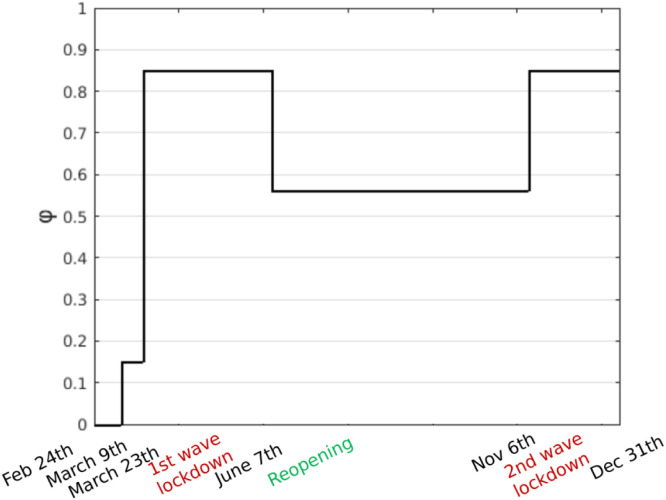
From the point of view of the model and system dynamics, these interventions are reflected in the value of the parameter $\phi$. The qualitative graph in Fig. 2 visually represents how these events can be taken into account in the setting of $\phi$. For example, the two evident jumps to the upside correspond to the first national lockdowns on 9 and 23 March 2020, respectively. The actual values to be given to $\phi$ in the four periods of interest will be deduced a posteriori from the epidemiological data.

Fig. 2.

Values of $\phi$ according to the main Italian Government COVID-19 preventive measures.

In order to choose the values of the other parameters entering the system, we take 1 day as a unit time and we consider 24 February 2020 as the starting day $t_0$ because it is the first day with the data recording. The initial conditions (4) can be taken from the data published by the Italian government [57] and are: $S_0=6.0\times 10^7$, $I_0=3.5\times 10^4$, $Q_0=221$, $R_0=30$, and $D_0=7$.

In the sequel, we will discuss how to determine the values of the following parameters/functions:

• •the constants $\gamma$ and ${\beta }_0$;
• •the recovering and death rate $\alpha$ and $\mu$;
• •the degree $f\left(t\right)$ of fatigue of the population with negligible effects of fear;
• •the sensitivity $k$ of the population to the death rate, to include the fear effect.

Being 1 day the time unit, we can fix $\gamma =0.07$, meaning that the virus has an incubation period of 2 weeks; we may note that the value of $\gamma$ is opinionable because the average length of 14 days is not accepted by all researchers [60], [61] and surely the average time between the infection and the quarantine can be lowered by an extensive practice of antigenic swabs. However, we observe that this practice was not so frequent in the period under consideration. As a general remark, we may outline the fact that the choice of the values of the parameters are hypothetical and the result of averages and simplifying choices; but on the other hand, a conceptual model is a simplified picture of a phenomenon that is, per se, extremely complex. Another example of this complexity, is the fact that a COVID-19 infected person is not homogeneously contagious during the infectious period and possibly begins to be able to transmit the virus after a few days. This fact and other time delays are not incorporated in the model. But any mathematical model is a compromise between simplicity and detailed description and not always a more general model, with a large number of parameters to be chosen is more useful to describe a phenomenon and/or to possess a forecasting ability.

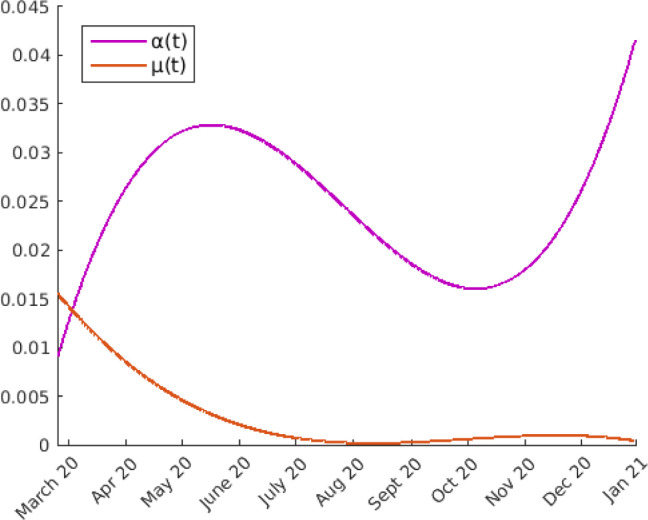
The estimate of parameters $\alpha$ and $\mu$ can be made using the statistical data. Recording the daily variations of the recovered and of the dead persons and dividing these values by the average number of the quarantined people in the same period, after least squares polynomial approximation, we obtain the graphs of Fig. 3.

Fig. 3.

Estimation of parameters $\alpha$ and $\mu$ using least squares polynomial approximation of the statistical data.

In any case, we will take these experimental values for the functions $\alpha \left(t\right)$ and $\mu \left(t\right)$.

Also ${\beta }_0$ can be deduced by the statistical data fitting the curve of the quarantined individuals in the initial period of 30 days with the solution of the system (3) where both $\phi$ and $f$ are taken to be zero because the first isolation measures were taken only at $t=t_0+15$. Accordingly, we will take ${\beta }_0=0.2/(6\times 10^7)$. With these values, the basic reproduction number is ${\mathcal{R}}_0\approx 2.85$.

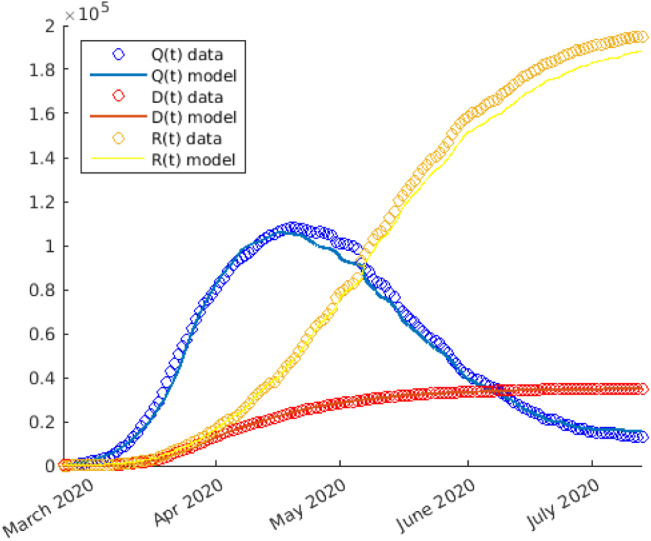
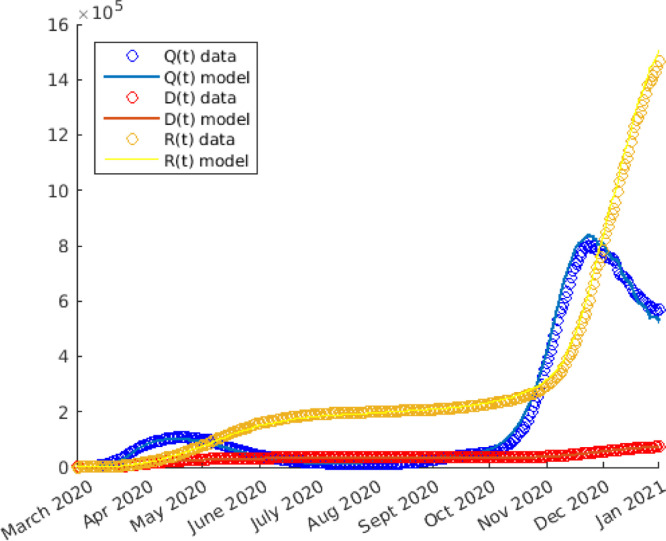
The trend of the pandemic during 2020 in Italy can be macroscopically divided into 2 phases, the first and the second wave, to indicate a significant increase in cases in two distinct moments. The first wave took place between the months of February and May. Let us primarily focus on this first phase and proceed to numerically solve the system (3). We opt to use the Matlab’s solver for ordinary differential equations based on Runge–Kutta method with a variable time step for efficient computation. The code developed to generate the following simulation is available in the GitHub repository [62].

According to the experience, during the whole period from February 24th to September 20th, the compliance of people with the measures taken was practically total, so we put the fatigue term $f\left(t\right)=0$. At this point the only function that has to be fitted with the data is the piecewise constant function $\phi$.

From Fig. 4 we can see that setting, as in Fig. 2,

Fig. 4.

Numerical solutions (solid line) of the simulation of the first phase of COVID-19 spread in Italy during 2020. The statistical data (circle) are also reported.

• •$\phi =0$ from February 24th to March 9th, i.e., for $0=t_0\le t<16$,
• •$\phi =0.15$ from March 9th to March 23rd, i.e., for $16\le t<29$,
• •$\phi =0.85$ from March 23rd to June 7th, i.e., for $29\le t<105$,
• •$\phi =0.56$ from June 7th onwards, i.e,. for $t\ge 105$,

the fitting between the computed curves (solid line) and the reported experimental data (circle) is good. We remark that $\phi$ during the re-opening phase does not assume again the same value as before the lockdown; this fact is justified because of the acquisition by people of good habits, such as the use of masks or better hygiene.

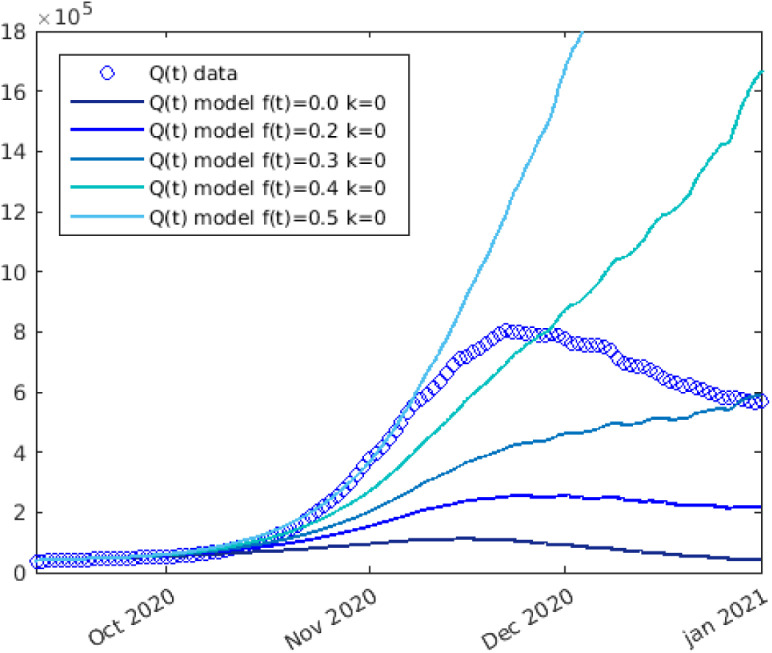
Let us now turn our attention to the second wave phase. By maintaining the same parameters setup (without introducing fatigue effects), the results of our model would deviate significantly from the statistical data. We observe that taking into account the various preventive measures and thus the values of $\phi$ already set (the measures taken from November 6th onwards were the same as the ones taken between March 23rd and June 7th), the progress of the epidemic is exceedingly faster (Fig. 5) than the results of the model (with $f\left(t\right)=0$) that described in a satisfactory way the phenomenon in the months from March 2020 to September 2020.

Fig. 5.

Numerical solutions (solid line) of the simulation of COVID-19 spread in Italy during the second phase, neglecting the fatigue ($f\left(t\right)=0$). The statistical data (circle) are also reported.

Comparing the numerical results with the pandemic data, it is evident that, neglecting the fatigue term ($f\left(t\right)=0$), the solution of the system (3) does not suit well the reality of the COVID-19 outbreak during the second part of 2020 in Italy. Indeed, the model without taking fatigue into account, foresees the number of deaths at the end of 2020 as 42,000 versus the statistical data of 74,000.

This fact confirms the arguments we displayed in Section “Model”: there is evidence that prolonged exposure to a pandemic and to rules that affect daily life exerts a strain on the individual that can lead to a more or less gradual loss of diligence in complying with anti-contagion measures. In terms of the model, this means that we have to introduce the function expressing “fatigue”. As we can observe in Fig. 6, applying a certain fatigue from mid-September 2020 ($t\ge 210$) we obtain an increase in the dimension of the second wave of diseased person. Nevertheless, if we confine ourselves to the consideration of fatigue and do not include the term expressing the reaction of people to the danger perception induced by an increase in deaths. (i.e. setting $k=0$) we cannot fit the experimental data.

Fig. 6.

Numerical solutions (solid line) of the simulation of COVID-19 spread in Italy during 2020, performed by our model applying a certain degree of fatigue $f\left(t\right)$ (neglecting the perception of the increase of deaths ($k=0$)) from the mid-September 2020 ($t\ge 210$). The statistical data (circle) are also reported.

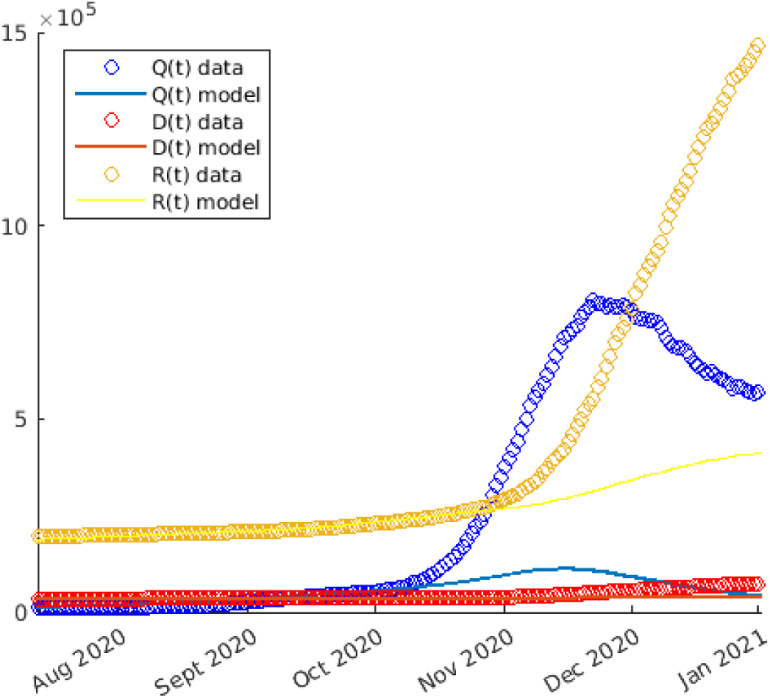
Let us therefore perform a final test, where we introduce both social responses: the pandemic fatigue and the reaction to the fear of the consequences of the disease. In Figure Fig. 7 we display the numerical results of the simulation, in which starting from mid-September ($t\ge 210$) we set $f\left(t\right)=0.65$ and $k=3\times 10^{-3}$.

Fig. 7.

Numerical solutions of the simulation of COVID-19 spread in Italy during 2020, performed by the complete model (including pandemic fatigue and the reaction to the fear of consequences of COVID-19), and with $f\left(t\right)=0.65$ and $k=3\times 10^{-3}$ for $t\ge 210$. The statistical data are also reported.

The graphs in Figure Fig. 7 show that, although the results obtained with our model are not exactly identical to the data, they are nevertheless close enough to accept that the dynamics described by the system reflect what may occur during COVID-19 outbreak in real life. If the theory presented in this study is consistent, this means that the model could be used to hypothesise with a certain degree of confidence not only a possible justification for the size of the second wave but to provide an estimate of the impact of pandemic fatigue in terms of deaths. Concerning Italy, according to our results the impact of the pandemic fatigue may have cost 32,000 lives at the end of 2020.

This model, although with simplifications and inevitable limitations, can be used not only for a posteriori analysis of Covid-19 or epidemic scenarios, but also preventively to make containment and precautionary decisions, giving a tool to measure possible future impacts due to pandemic fatigue.

Conclusions and future perspectives

Strategies to face the COVID-19 pandemic must be identified. The fight against this novel virus has called for countless people from various fields of knowledge to propose studies and evidence. In this paper, we have presented an ODE mathematical model to describe the epidemic’s dynamics, including the measures put in place by public health authorities and individual behavioural responses.

Our model is nonlinear but relatively simple; in addition to being space-independent and giving information on the averages of the quantities in each region, it considers the essential epidemiological elements. Some of the parameters entering the model can be directly calculated by the data recorded, while others are chosen by fitting the experimental curve. Data from the Italian epidemic in 2020 was used for model testing, and the results show an excellent fit with the numerical simulations and the data released by the Italian government. It can easily simulate the dynamics resulting from applying measures affecting the transmission rate and demonstrate how they were instrumental in controlling the COVID-19 outbreak. The key feature of our model is to incorporate a possible lowering of the guard and negligence in observing precautionary practices for the emotional pressure of the emergency perpetration and the social discomforts resulting from a different and, in some cases, hostile daily life. According to the model, in Italy, the population’s decreased sensitivity to the state of alarm could have caused 32,000 more deaths by the end of 2020.

Our study involves the (i) formulation and well-posedness proof of the mathematical model, (ii) a consistency test with publicly accessible data sources, and (iii) the availability of the numerical code. Our Matlab implementation is freely downloadable and utilisable from the GitHub repository [62].

A challenging future opportunity could consist of introducing the spatial dependence of variables and parameters. This development may lead to a considerable complication of the model, introducing partial differential equations. Other modelling choices, such as an agent-based model or cellular automata, could turn out to be viable and simultaneously relevant options [63], [64]. Some study objectives may be represented by identifying an optimal preventive strategy under a territorial basis, studying the mutual behavioural influences of different populations, and the effects of the restrictions on internal and international mobility.

Our study underlines the importance of developing beyond directly restrictive strategies. Such measures are vital. Nonetheless, positive impacting results can be achieved by promoting indirect strategies oriented to alleviate the sense of fatigue felt by the population. For example, promoting the idea that physical distancing does not imply emotional detachment from others is beneficial. Social connections can potentially buffer against adverse physical and mental health outcomes [65]. In addition, advertising opportunities for reduced academic and work stress, increased time with family, or other advantages of the new situation can encourage positive attitudes [43], [66]. A more acute containment strategy coupled with an effort to improve social responsibility and resilience can mitigate the terrible consequences of the COVID-19 pandemic.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.