Abstract
Hot compression experiments of annealed 7075 Al alloy were performed on TA DIL805D at different temperatures (733, 693, 653, 613 and 573 K) with different strain rates (1.0, 0.1, 0.01 and 0.001 s−1.) Based on experimental data, the strain-compensated Arrhenius model (SCAM) and the back-propagation artificial neural network model (BP-ANN) were constructed for the prediction of the flow stress. The predictive power of the two models was estimated by residual analysis, correlation coefficient (R) and average absolute relative error (AARE). The results reveal that the deformation parameters including strain, strain rate, and temperature have a significant effect on the flow stress of the alloy. Compared with the SCAM model, the flow stress predicted by the BP-ANN model is in better agreement with experimental values. For the BP-ANN model, the maximum residual is only 1 MPa, while it is as high as 8 MPa for the SCAM model. The R and AARE for the SCAM model are 0.9967 and 3.26%, while their values for the BP-ANN model are 0.99998 and 0.18%, respectively. All these reflect that the BP-ANN model has more accurate prediction ability than the SCAM model, which can be applied to predict the flow stress of the alloy under high temperature deformation.
Keywords: 7075 Al alloy, flow stress, strain-compensated Arrhenius, BP-ANN
1. Introduction
The 7000 series aluminum alloys can be strengthened by heat treatment, used for many high-end fields such as aerospace and transportation because of their high strength toughness, low density and excellent stress corrosion resistance [1,2,3]. The 7075 aluminum alloy is the earliest ultra-high strength aluminum alloy and is mainly used for the load-bearing parts of aircraft [1]. Similar to most alloys [4,5,6], the 7000 series aluminum alloys are generally produced by various thermoplastic processes, including extrusion, forging and rolling. However, their thermoplastic forming is complicated, because the deformation behavior is controlled by deformation conditions including strain, strain rate and temperature [7,8]. Therefore, investigating the hot deformation behavior of the 7075 Al alloy under different conditions is helpful to optimize process parameters for obtaining excellent microstructure and mechanical properties.
As an important means to characterize the relationship between the flow stress of materials and deformation parameters, the constitutive model is widely used, and also can provide great convenience for the study of hot deformation characteristics in finite element simulation [4]. Reliable simulation results require an accurate constitutive model, which is always pursued by scholars [9,10,11]. Many scholars have devoted themselves to establishing various constitutive models to describe the mechanical behavior of materials during hot working. Some typical models are proposed, including phenomenological model, physical model and artificial neural network (ANN) model [12,13]. Recently, in the prediction of high temperature flow stress in aluminum alloys, a phenomenological constitutive model called the strain-compensated Arrhenius model (SCAM) has been extensively employed [4,14,15,16,17,18,19,20]. Meanwhile, some statistical methods such as correlation coefficient (R) and average absolute relative error (AARE) are often employed to characterize the predictive power of the constitutive model. Rezaei Ashtiani et al. [16], predicted the flow stress of the AA1070 alloy at high temperature by the SCAM model. As the R value reached 99.2%, they believed that a considerable prediction effect had been achieved. Haghdadi et al. [17], developed a SCAM model for flow stress prediction of the A356 alloy, and obtained a satisfactory R value of 0.991 and an AARE value of 8.1%, respectively. In predicting the flow stress of the 7050 alloy, Li et al. [18], also adopted the SCAM model, and achieved good prediction results, with the R and AARE of 0.9922 and 6.28%, respectively. In addition, Gan et al. [19] and Dai et al. [20], predicted the flow stress of the 6063 and the AA5083 alloys, respectively, based on the SCAM model. In their respective studies, the AARE for the models were 4.65% and 4.52%, respectively. In summary, the SCAM model is suitable for predicting the flow stress of aluminum alloy in the process of hot deformation to a certain extent. Although the AARE obtained using the SCAM model was almost in the range of 4.5–8.5%, it can be further improved [12]. Generally, the flow behavior of the alloy is nonlinear, so the linear fitting method used in the establishment of the SCAM model is easy to produce a fitting error, and leads the constitutive model obtained to be not ideal.
In recent years, the ANN model has been developed as an artificial intelligence method to simulate brain neural information transmission and applied to predict thermal deformation flow stress of metal materials [21,22,23,24]. Compared with other models, the ANN model does not require repeated regression calculation. It relies on the characteristics of self-organization, self-learning and self-adaptation. It can effectively couple multiple variables, solve the nonlinear problem, and greatly improve the prediction accuracy [25,26], such as the prediction of flow stress of aluminum alloy. Li et al. [27], constructed the ANN constitutive model for the 6082 alloy, and proved that the model has a very satisfactory prediction accuracy by R and AARE being 0.99824 and 0.8%, respectively. Luo et al. [28], established a BP-ANN model to predict the thermal deformation behavior of the 7055 alloy, and confirmed that the model has a high prediction accuracy, with an average relative error of only 0.813%. It should be known that the AARE obtained by the artificial neural network model is almost less than 1%, which indicated that the ANN model had high prediction accuracy of the flow stress for aluminum alloys.
In our study, hot compression tests of the annealed 7075 Al alloy were carried out to study the flow behavior in different conditions (strain rates: 1.0, 0.1, 0.01, 0.001 s−1; temperature: 733, 693, 653, 613, 573 K). Based on the test data, the SCAM and BP-ANN models were derived to predict the flow stress of the alloy during hot deformation. Then, the predictive power of the two models for flow stress was evaluated and compared by residual analysis, correlation analysis and prediction error analysis.
2. Materials and Experiments
The chemical composition of the annealed 7075 Al alloy used in this study is shown in Table 1.
Table 1.
Chemical composition of the annealed 7075 Al alloy (wt. %).
| Fe | Si | Cr | Mn | Ti | Cu | Mg | Zn | Al |
|---|---|---|---|---|---|---|---|---|
| 0.20 | 0.07 | 0.21 | 0.06 | 0.02 | 1.54 | 2.68 | 5.76 | Bal. |
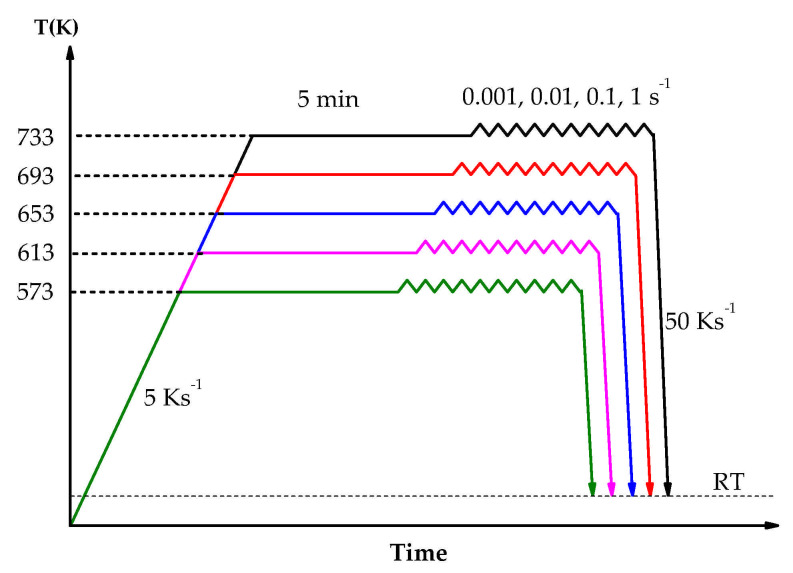
The cylindrical samples had a diameter of 10 mm and a height of 5.0 mm. Hot compression tests were performed on a TA DIL805D at the temperatures (733, 693, 653, 613 and 573 K) with strain rates (1.0, 0.1, 0.01 and 0.001 s−1.) Each sample was heated from room temperature to the target temperature at a rate of 5 K s−1, and then they were kept for 5 min. The compression stopped when the true strain was up to 0.8, and the samples were immediately cooled to room temperature at a rate of 50 K s−1. Figure 1 shows the detailed experimental scheme. The stress and strain data were obtained by the acquisition system. A total of 300 data points were selected from the hot compression test data (the value interval of strain is 0.05) for the construction of the constituted equation.
Figure 1.
Schematic of compression tests.
3. Results and Discussion
3.1. Flow Stress Characteristics
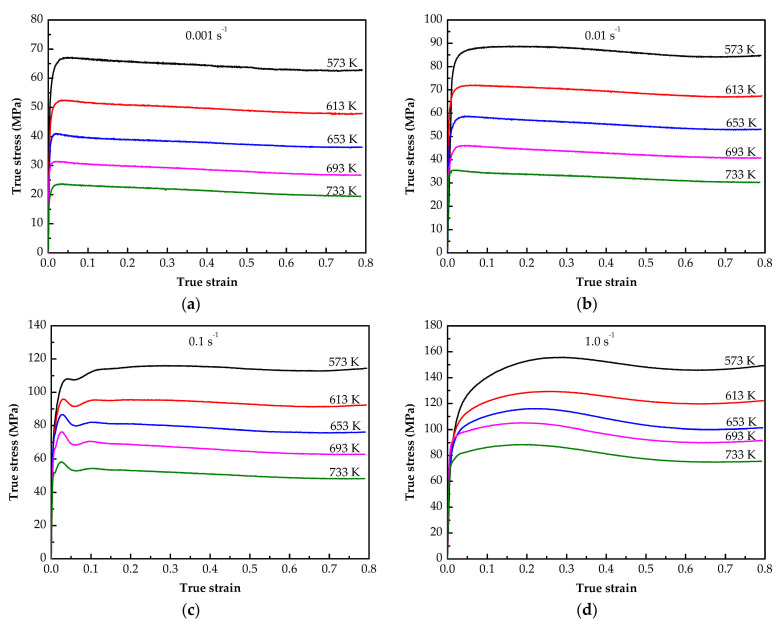
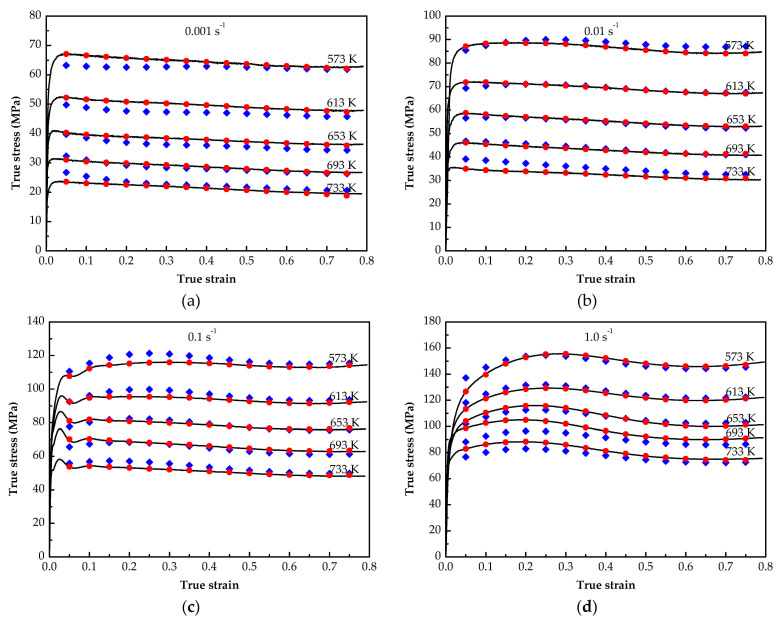
The results obtained under the predetermined experimental scheme (true stress-strain curves of the annealed 7075 Al alloy) are presented in Figure 2. For all the stress-strain curves, the flow stress increases rapidly in the initial stage of deformation, which indicates a strong work hardening phenomenon [9]. With the increase of strain, flow stress shows two flow characteristics: (1) At low strain rates conditions such as 0.001 and 0.01 s−1, it does not show obvious peak value, but maintains a steady flow. (2) At high strain rate conditions such as 0.1 and 1.0 s−1, the stress appears at an obvious peak value, then decreases slowly and finally reaches a stable state. This phenomenon is the result of work hardening and dynamic softening existing simultaneously in the hot deformation process, which compete with each other [9].
Figure 2.
True stress-strain curves of the annealed 7075 Al alloy with various deformation conditions: (a) 0.001 s−1; (b) 0.01 s−1; (c) 0.1 s−1; (d) 1.0 s−1.
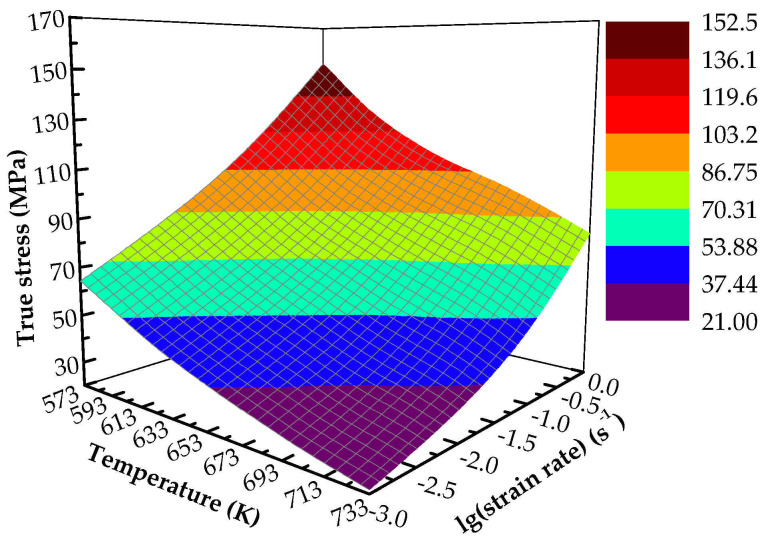
The flow stress level decreases with the increase of deformation temperature and increases with the increase of strain rate. To more intuitively reflect the influence of experimental variables on flow stress, Figure 3 shows the evolution of flow stress with different temperatures and strain rates at a strain of 0.4. It shows that the flow stress decreases with the increase of temperature at a constant strain rate, for example, at 0.001 s−1 with the temperature from 573 to 733 K, the stress value decreases from 64.42 to 21.38 MPa. The reason is that the increase of temperature means the increase of activation energy, which makes dislocation prone to slip [29]. In addition, when the deformation temperature increases, the critical shear stress required for the alloy to slip will decrease, which also easily leads to dislocation slip [29]. However, the flow stress increases with the increase of strain rate, for example, at 573 K, the stress value increases from 64.42 to 152.27 MPa when the strain rate ranges from 0.001 to 1.0 s−1. This is because the deformation time becomes shorter when the strain rate increases, which increases the deformation degree in unit time, and the softening process cannot be fully carried out, resulting in the increase of flow stress [30]. Although the flow stress of the alloy varies with temperature and strain rate, it is not a simple linear relationship.
Figure 3.
Evolution of flow stress with temperature and strain rate at true strain of 0.4.
3.2. Construction of SCAM Model
During the hot compression deformation, the flow stress of a material can be described by a constitutive equation. In the prediction of flow stress of materials, the well-known Arrhenius-type model is relatively common. In this model, the flow stress (σ) is calculated by strain rate () and temperature (T) [27]. The specific expression is as follows [31]:
| (1) |
where and σ represent strain rate (s−1) and flow stress (MPa), respectively. T and Q represent temperature (K) and activation energy (J mol−1), The R that appears here is gas constant of 8.314 J mol−1 K−1. Material constants including α, n1, β, n, A, α = β/n1. In general, temperature and strain rate can be expressed by an exponential equation called the Zener-Hollomon parameter (Z), mathematically expressed as follows [31]:
| (2) |
Thus, the constitutive equation including Z parameter can be described as:
| (3) |
It is not difficult to find that the original Arrhenius model neglected the effect of strain, which is detrimental to accurately describing flow stress. As mentioned in references [16,17,18,19,20], the change of strain will cause the change of material constants, so strain cannot be ignored. In this study, the constitutive model of the annealed 7075 Al alloy was constructed by the Arrhenius model with considering strain; the specific construction process is as follows.
3.2.1. Determination of Material Constants
According to the experimental data, the material constants under different strains were calculated to establish a constitutive equation. Here, the strain of 0.4 was selected as a demonstration for determining material constants.
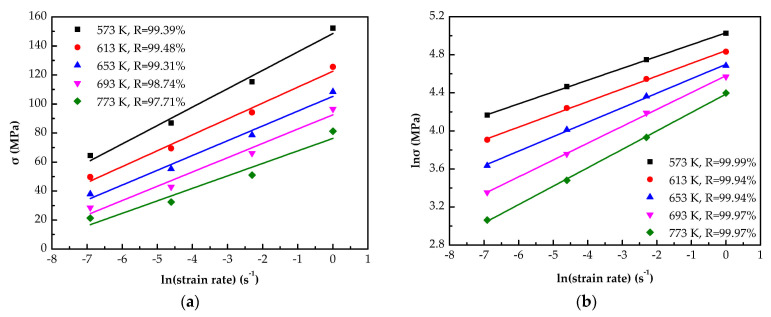
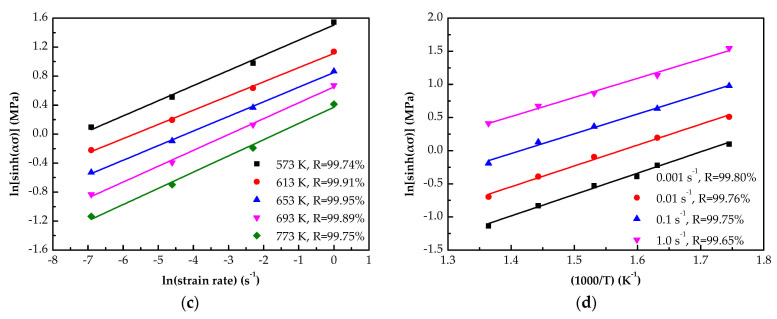
The method of solving the material constants can be found in References [16,17,18,19,20]. The relationship between σ-ln and lnσ-ln can be fitted by linear regression. The values of β and n1 can be solved by calculating the inverse of the slopes of each line in Figure 4a,b. The average is 0.0972 and 6.58, respectively. Thus, the value of α = β/n1 = 0.0148.
Figure 4.
Solving material constants by linear fitting: (a) σ—ln; (b) lnσ—ln; (c) ln[sinh(ασ)]—ln; (d) ln[sinh(ασ)]—1000/T.
By taking the logarithm of Equation (1) gives:
| (4) |
Differentiating Equation (4), and Q can be described by an equation as follows:
| (5) |
For a certain temperature, it can be obtained:
| (6) |
Figure 4c shows the linear fitting of ln[sinh(ασ)]−ln, the slope can be calculated for each line, and their average is n = 4.78.
Similarly, when the strain rate is constant, it can be derived:
| (7) |
Figure 4d is the ln[sinh(ασ)]−1000/T plots, the Q value fitted as 121.45 kJ mol−1 at the strain of 0.4.
Combining Equations (1) and (2), and taking the logarithm of both sides, it can be given:
| (8) |
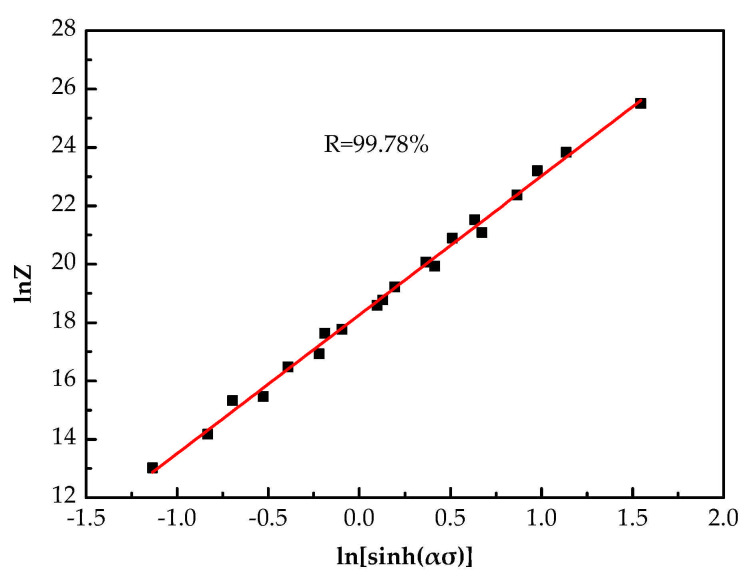
By fitting the relation between lnZ and ln[sinh(ασ)], the intercept of the fitting line is obtained, namely lnA, as shown in Figure 5, it equal to 18.27.
Figure 5.
Linear relationship of lnZ—ln[sinh(ασ)].
So far, all material constants at a strain of 0.4 have been obtained, as shown in Table 2. Material constants under other strains (the strains were set from 0.05 to 0.75 with an interval of 0.05) can also be obtained by using the similar method.
Table 2.
Material constants at the strain of 0.4.
| Parameter | α | n | Q (kJ mol−1) | A |
|---|---|---|---|---|
| Value | 1.48 × 102 | 4.78 | 121.45 | 8.5665 × 107 |
3.2.2. The Compensation of Strain for Material Constants
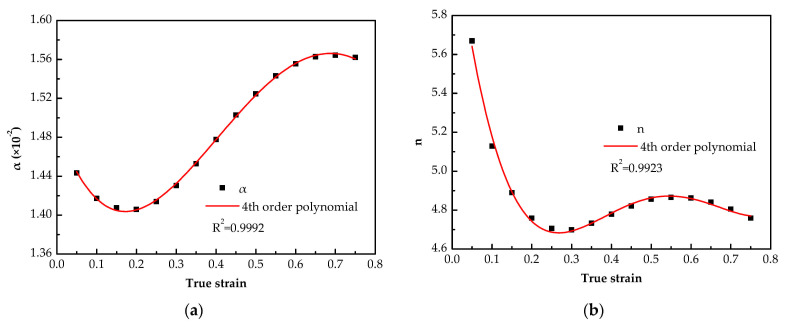
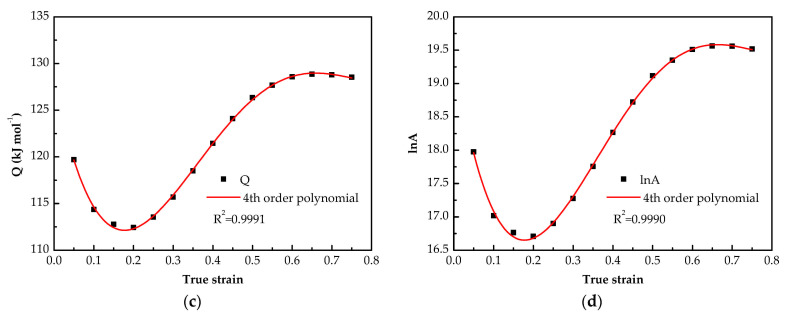
In the previous section, the material constants at different true strains were obtained, and they are shown as dots in Figure 6. It can be observed that each material constant varies significantly with the strain, and the activation energy varies between 112.43 and 128.85 kJ mol−1. Compared with solution-treated 7075 alloy (283–287 kJ mol−1) [32], solution-treated 7050 alloy (256.6 kJ mol−1) [33], homogenized 7150 alloy (229.75 kJ mol−1) [34], homogenized Al–7.5Zn–1.5Mg–0.2Cu–0.2Zr alloy (164.075 kJ mol−1) [35], over-aged 7012 and 7075 alloy (141–162 kJ mol−1 and 143–156 kJ mol−1) [36], the deformation activation energy of the alloy in this study is lower. It is well known that the deformation activation energy is greatly affected by the composition and initial structure of the alloy. In addition, the Q-value is usually obtained by fitting linear regression methods, which also contributes to the difference. In general, the deformation activation energy obtained in this study is indeed relatively low, which means that the alloy has relatively good formability.
Figure 6.
Polynomial fit between variation and true strain: (a) α—ε; (b) n—ε; (c) Q—ε; (d) lnA—ε.
In previous studies, the material constant is usually assumed as a polynomial function of strain [16,17,18,19,20]. The same method was used in this study. By polynomial fitting, it is found that each material constant and strain satisfy a fourth-order polynomial relationship (Figure 6), and the equation as (9),
| (9) |
where, C0, C1, C2, C3 and C4 are the coefficients of Equation (9), they are listed in Table 3, respectively, ε is the true strain and Y represents variation of α, n, Q and lnA, respectively.
Table 3.
The coefficients in Equation (9) for fitting α, n, lnA and Q.
| Parameter | C0 | C1 | C2 | C3 | C4 |
|---|---|---|---|---|---|
| α | 1.49 | −1.15 | 4.56 | −5.02 | 1.54 |
| n | 6.33 | −16.45 | 56.51 | −77.30 | 36.67 |
| lnA | 19.46 | −37.33 | 156.03 | −214.29 | 96.95 |
| Q | 128.30 | −214.57 | 896.39 | −1228.97 | 554.15 |
The strain-compensated Arrhenius constitutive model has been established, and Equation (3) can be written as Equation (10). According to Equations (9) and (10), the flow stress of the annealed 7075 Al alloy under various strains can be predicted.
| (10) |
3.3. Construction of BP-ANN Model
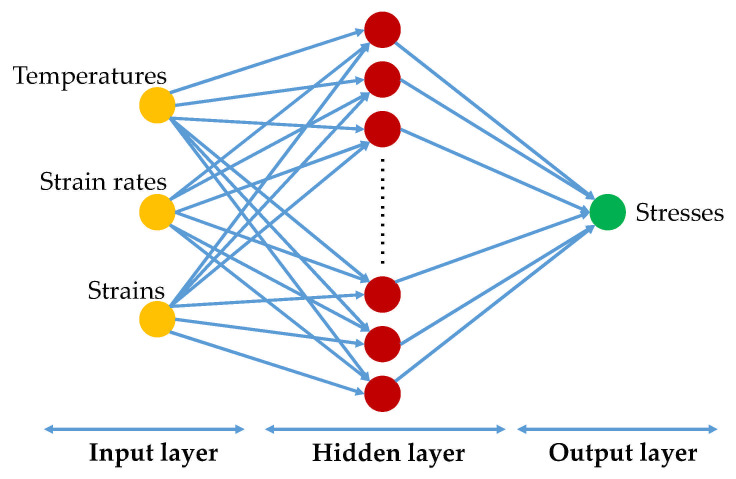
In all artificial neural networks, back-propagation artificial neural network (BP-ANN) is the most extensively employed. The algorithm consists of two parts: feed-forward neural network trained and error back propagation [37]. The basic idea is to minimize the error between the actual output value and the expected output value of the network through the gradient descent search technology [27]. A typical BP-ANN is usually composed of three parts, namely, the input layer, the hidden layer and the output layer (see Figure 7) [38]. In our study, the input layer contains three neurons corresponding to three deformation parameters (temperature, strain rate and strain), while the output layer has only one neuron, which is flow stress. In order to get the number of neurons in the hidden layer, the trial-and-error method was used to optimize the number of neurons [39]. After several attempts, the optimal number of neurons was determined to be 20. Thus, the network structure established was 3 × 20 × 1.
Figure 7.
Structure diagram of BP-ANN.
The construction of the BP-ANN model was carried out by a self-programmed program on MATLAB 2017a software. Among 300 experimental data, the data under the deformation conditions of 613 K/0.01 s−1, 653 K/0.1 s−1 and 693 K/1.0 s−1 (3 × 15 = 45) were taken as test data, and the rest of the data (255) were set as training data for the BP-ANN model. To avoid the influence of dimensional difference of input data on training efficiency, it is necessary to normalize these parameters. It should be pointed out that since the change of strain rate is an order of magnitude, logarithmic transformation is performed before normalization. Normalization of data adopts the mapminmax algorithm in MATLAB, and the formula is as follows:
| (11) |
where x and y are the data before and after normalization, respectively.
In this BP-ANN training, the maximum number of iterations was set to 1000 times, the learning rate was 0.001, and the desired training error was set to 10−6. After the training was completed, the BP-ANN model could be obtained to predict the flow stress under different deformation conditions.
3.4. Evaluation of Prediction Effect of Two Constitutive Models
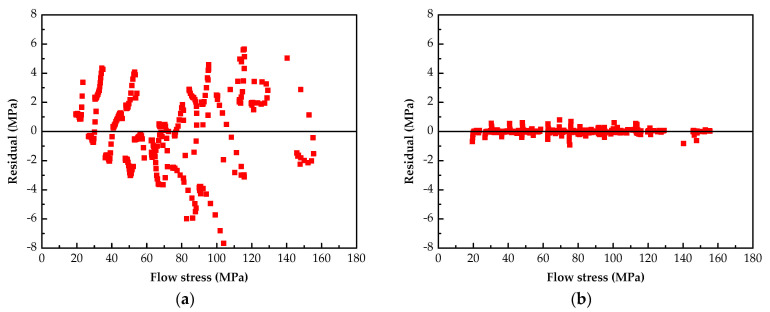
Figure 8 shows the comparison between the predicted values of the two models and the experimental values. The results reveal that the stress predicted by the SCAM model is less consistent with the test values than that predicted by the BP-ANN model. The residual results between the calculated values of the two models and the actual value are presented in Figure 9. It is clear that the residual for the SCAM model is about ±8 MPa, while it is less than ±1 MPa for the BP-ANN model.
Figure 8.
Comparison of flow stress predicted by SCAM model and BP-ANN model with experimental values: (a) 0.001 s−1; (b) 0.01 s−1; (c) 0.1 s−1; (d) 1.0 s−1.
Figure 9.
Residuals for different models: (a) SCAM model; (b) BP-ANN model.
To evaluate the quality of the established models, two important statistical indicators (R and AARE) were commonly used [26,37]. Corresponding calculation formulas are shown in Equations (12) and (13).
| (12) |
| (13) |
where represents the experimental results; is the results calculated according to the established constitutive model; and are the average values of and , respectively; N is the total number.
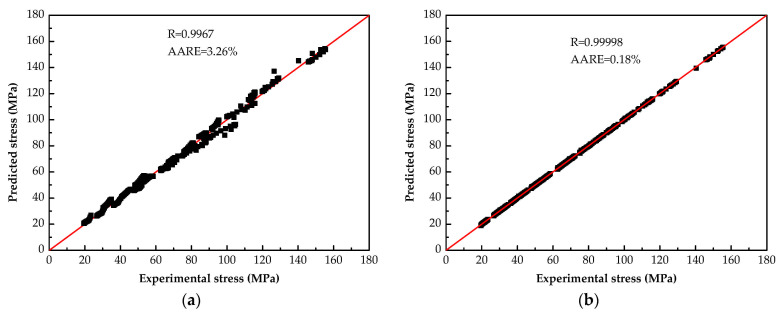
The correlation analysis results of calculated values based on the two models and experimental values are shown in Figure 10. It can be found that the data points predicted by BP-ANN model are more concentrated, with the R and AARE of 0.99998 and 0.18%, respectively (see Figure 10a.) For the SCAM model, R is 0.9967 and AARE is 3.26% respectively (see Figure 10b.) These data indicate that the BP-ANN model has a better precision in describing the hot deformation flow stress of annealed 7075 Al alloy.
Figure 10.
Correlation between the experimental values and predicted values: (a) SCAM model; (b) BP-ANN model.
Comparing between the SCAM model and BP-ANN model, the former uses linear fitting and polynomial fitting methods to derive the constants in the equation, but there were certain errors in each fitting process and it could not reach a more accurate state, so the prediction accuracy of the constitutive equation was low. On the other hand, the BP-ANN model predicts the flow stress through the network learning and pattern recognition method. It can deal with nonlinear problems well and has a strong adaptability and generalization ability [27]. Therefore, the established BP-ANN model has better performance and can be applied in the prediction of flow stress of the annealed 7075 Al alloy.
4. Conclusions
The deformation behavior of the annealed 7075 Al alloy at different compression conditions were investigated. For predicting its deformation behavior, constitutive equations based on SCAM model and BP-ANN model were established, and the prediction ability of the two models was evaluated and compared. According to the current research, several conclusions can be drawn:
The flow stress of the annealed 7075 Al alloy decreases as temperature increases and strain rate decreases.
The material constant (i.e., α, n, Q and lnA) in the SCAM model has a fourth-order polynomial relationship with the strain, and the activation energy varies in the range of 112.4312 and 128.8533 kJ mol−1.
The flow stress predicted by the BP-ANN model is more consistent with the experimental values than that predicted by the SCAM model. The residual for the BP-ANN model was controlled within 1 MPa, while it is about ±8 MPa for the SCAM model.
The R and AARE were obtained from the SCAM model are 0.9967 and 3.26%, respectively, while the R and AARE were superior in the BP-ANN model at 0.99998 and 0.18%, respectively, which reveals that the predicted accuracy of BP-ANN model is higher than that SCAM model.
Acknowledgments
The authors are grateful for the financial support from the Major Science and Technology Project of Yunnan Province (202002AB080001-4). Thanks to Materials for its recognition and help in our work.
Author Contributions
H.Y. and H.B. designed and performed the experiments; H.Y. analyzed data and wrote the paper; H.B. and M.L. conceived the central idea; M.L. and X.L. reviewed and edited the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the Major Science and Technology Project of Yunnan Province (202002AB080001-4).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Footnotes
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Zhang X.S., Chen Y.J., Hu J.L. Recent advances in the development of aerospace materials. Prog. Aerosp. Sci. 2018;97:22–34. doi: 10.1016/j.paerosci.2018.01.001. [DOI] [Google Scholar]
- 2.Shin J., Kim T., Kim D.E., Kim D., Kim K. Castability and mechanical properties of new 7xxx aluminum alloys for automotive chassis/body applications. J. Alloys Compd. 2016;698:577–590. doi: 10.1016/j.jallcom.2016.12.269. [DOI] [Google Scholar]
- 3.Ibrahim M.F., Samuel A.M., Samuel F.H. A preliminary study on optimizing the heat treatment of high strength Al-Cu-Mg-Zn alloys. Mater. Des. 2014;57:342–350. doi: 10.1016/j.matdes.2013.11.078. [DOI] [Google Scholar]
- 4.Wang H.R., Wang C.G., Li M.Y., Ma R., Zhao J. Constitutive equations for describing the hot compressed behavior of TC4-DT titanium alloy. Materials. 2020;13:3424. doi: 10.3390/ma13153424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Chen R.C., Zhang S.Y., Liu X.L., Feng F. A flow stress model of 300M steel for isothermal tension. Materials. 2021;14:252. doi: 10.3390/ma14020252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Guo Y.H., Xuanyuan Y.D., Ly X.N., Yang S. Hot Deformation behaviors of the Mg-3Sn-2Al-1Zn alloy: Investigation on its constitutive equation, processing map, and microstructure. Materials. 2020;13:312. doi: 10.3390/ma13020312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Luo L., Liu Z.Y., Bai S., Zhao J.G., Zeng D.P., Wang J., Cao J., Hu Y.C. Hot deformation behavior considering strain effects and recrystallization mechanism of an Al-Zn-Mg-Cu Alloy. Materials. 2020;13:1743. doi: 10.3390/ma13071743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Lin Y.C., Li L.T., Fu Y.X., Jiang Y.Q. Hot compressive deformation behavior of 7075 Al alloy under elevated temperature. J. Mater. Sci. 2012;47:1306–1318. doi: 10.1007/s10853-011-5904-y. [DOI] [Google Scholar]
- 9.Wu B., Li M.Q., Ma D.W. The flow behavior and constitutive equations in isothermal compression of 7050 aluminum alloy. Mater. Sci. Eng. A. 2012;542:79–87. doi: 10.1016/j.msea.2012.02.035. [DOI] [Google Scholar]
- 10.Xu L., Dai G.Z., Huang X.M., Zhao J.W., Han J., Gao J.W. Foundation and application of Al-Zn-Mg-Cu alloy flow stress constitutive equation in friction screw press die forging. Mater. Des. 2013;47:465–472. doi: 10.1016/j.matdes.2012.12.011. [DOI] [Google Scholar]
- 11.Zhang T., Zhang S.H., Li L., Lu S.H., Gong H. Modified constitutive model and workability of 7055 aluminum alloy in hot plastic compression. J. Cent. South Univ. 2019;26:2930–2942. doi: 10.1007/s11771-019-4225-1. [DOI] [Google Scholar]
- 12.Rezaei Ashtiani H.R., Shahsavari P. A comparative study on the phenomenological and artificial neural network models to predict hot deformation behavior of AlCuMgPb alloy. J. Alloys Compd. 2016;4:300. [Google Scholar]
- 13.Rezaei Ashtiani H.R., Shahsavari P. Strain-dependent constitutive equations to predict high temperature flow behavior of AA2030 aluminum alloy. Mech. Mater. 2016;100:209–218. doi: 10.1016/j.mechmat.2016.06.018. [DOI] [Google Scholar]
- 14.Chen L., Zhao G.Q., Yu J.Q. Hot deformation behavior and constitutive modeling of homogenized 6026 aluminum alloy. Mater. Des. 2015;74:25–35. doi: 10.1016/j.matdes.2015.02.024. [DOI] [Google Scholar]
- 15.Peng W.W., Zeng W.D., Wang Q.J., Yu H.Q. Comparative study on constitutive relationship of as-cast Ti60 titanium alloy during hot deformation based on Arrhenius-type and artificial neural network models. Mater. Des. 2013;51:95–104. doi: 10.1016/j.matdes.2013.04.009. [DOI] [Google Scholar]
- 16.Rezaei Ashtiani H.R., Parsa M.H., Bisadi H. Constitutive equations for elevated temperature flow behavior of commercial purity aluminum. Mater. Sci. Eng. A. 2012;545:61–67. doi: 10.1016/j.msea.2012.02.090. [DOI] [Google Scholar]
- 17.Haghdadi N., Zarei-Hanzaki A., Abedi H.R. The flow behavior modeling of cast A356 aluminum alloy at elevated temperatures considering the effect of strain. Mater. Sci. Eng. A. 2012;535:252–257. doi: 10.1016/j.msea.2011.12.076. [DOI] [Google Scholar]
- 18.Li J., Li F.G., Cai J., Wang R.T., Yaun Z.W., Xue F.M. Flow behavior modeling of the 7050 aluminum alloy at elevated temperatures considering the compensation of strain. Mater. Des. 2012;42:369–377. doi: 10.1016/j.matdes.2012.06.032. [DOI] [Google Scholar]
- 19.Gan C.L., Zheng K.H., Qi W.J., Wang M.J. Constitutive equations for high temperature flow stress prediction of 6063 Al alloy considering compensation of strain. Trans. Nonferrous Met. Soc. China. 2014;24:3486–3491. doi: 10.1016/S1003-6326(14)63492-0. [DOI] [Google Scholar]
- 20.Dai Q.S., Deng Y.L., Tang J.G., Wang Y. Deformation characteristics and strain-compensated constitutive equation for AA5083 aluminum alloy under hot compression. Trans. Nonferrous Met. Soc. China. 2019;29:2252–2261. doi: 10.1016/S1003-6326(19)65131-9. [DOI] [Google Scholar]
- 21.Ji G.L., Li F.G., Li Q.H., Li H.Q., Li Z. A comparative study on Arrhenius-type constitutive model and artificial neural network model to predict high-temperature deformation behaviour in Aermet100 steel. Mater. Sci. Eng. A. 2011;528:4774–4782. doi: 10.1016/j.msea.2011.03.017. [DOI] [Google Scholar]
- 22.Zhu Y.L., Cao Y., Liu C.J., Luo R., Li N., Shu G., Huang G.J., Liu Q. Dynamic behavior and modified artificial neural network model for predicting flow stress during hot deformation of Alloy 925. Mater. Today Commun. 2020:101329. doi: 10.1016/j.mtcomm.2020.101329. [DOI] [Google Scholar]
- 23.Zhao J.W., Ding H., Zhao W.J., Huang M.L., Wei D.B., Jiang Z.Y. Modelling of the hot deformation behaviour of a titanium alloy using constitutive equations and artificial neural network. Comp. Mater. Sci. 2014;92:47–56. doi: 10.1016/j.commatsci.2014.05.040. [DOI] [Google Scholar]
- 24.Sabokpa O., Zarei-Hanzaki A., Abedi H.R., Haghdadi N. Artificial neural network modeling to predict the high temperature flow behavior of an AZ81 magnesium alloy. Mater. Des. 2012;39:390–396. doi: 10.1016/j.matdes.2012.03.002. [DOI] [Google Scholar]
- 25.Sun Y., Zeng W.D., Han Y.F., Ma X., Zhao Y.Q., Guo P., Wang G., Dargusch M.S. Determination of the influence of processing parameters on the mechanical properties of the Ti-6Al-4V alloy using an artificial neural network. Comp. Mater. Sci. 2012;60:239–244. doi: 10.1016/j.commatsci.2012.03.047. [DOI] [Google Scholar]
- 26.Shokry A., Gowid S., Kharmanda G., Mahdi E. Constitutive models for the prediction of the hot deformation behavior of the 10%Cr steel alloy. Materials. 2019;12:2873. doi: 10.3390/ma12182873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Li K., Pan Q.L., Li R.S., Liu S.H., Huang Z.Q., He X. Constitutive modeling of the hot deformation behavior in 6082 aluminum alloy. J. Mater. Eng. Perform. 2019;28:981–994. doi: 10.1007/s11665-019-3873-5. [DOI] [Google Scholar]
- 28.Luo R., Cao Y., Qiu Y., Cui S.G., Zhou H.T., Zhou Y.M., Yuan F., Zhangxiao P.P., Cheng X.N. Investigation of constitutive model of as-extruded spray-forming 7055 aluminum alloy based on BP artificial neural network. J. Aeronaut. Mater. 2021;41:35–44. [Google Scholar]
- 29.Zhang B., Zhao F.F., Chen H.F., Yang Y., Ma Y.H., Qi K. Hot compression deformation of cobalt-based superalloy GH5605. Chin. J. Nonferrous Met. 2021;31:879–889. [Google Scholar]
- 30.Yang Q.Y., Deng Z.H., Zhang Z.Q., Liu Q., Jia Z.H., Huang G.J. Effects of strain rate on flow stress behavior and dynamic recrystallization mechanism of Al-Zn-Mg-Cu aluminum alloy during hot deformation. Mater. Sci. Eng. A. 2016;662:204–213. doi: 10.1016/j.msea.2016.03.027. [DOI] [Google Scholar]
- 31.Zener C., Hollomon J.H. Effect of strain rate upon plastic flow of steel. J. Appl. Phys. 1944;15:22–32. doi: 10.1063/1.1707363. [DOI] [Google Scholar]
- 32.Gupta R.K., Kumar V.A., Sarath Krishnan A., Niteshraj J. Hot Deformation Behavior of Aluminum Alloys AA7010 and AA7075. J. Mater. Eng. Perform. 2019;28:5021–5036. doi: 10.1007/s11665-019-04231-8. [DOI] [Google Scholar]
- 33.Hu H.E., Zhen L., Yang L., Shao W.Z., Zhang B.Y. Deformation behavior and microstructure evolution of 7050 aluminum alloy during high temperature deformation. Mater. Sci. Eng. A. 2008;488:64–71. doi: 10.1016/j.msea.2007.10.051. [DOI] [Google Scholar]
- 34.Jin N.P., Zhang H., Han Y., Wu W.X., Chen J.H. Hot deformation behavior of 7150 aluminum alloy during compression at elevated temperature. Mater. Charact. 2009;60:530–536. doi: 10.1016/j.matchar.2008.12.012. [DOI] [Google Scholar]
- 35.He J.L., Zhang D.T., Zhang W.W., Qiu C., Zhang W. Constitutive equation and hot compression deformation behavior of homogenized Al–7.5Zn–1.5Mg–0.2Cu–0.2Zr alloy. Materials. 2017;10:1193. doi: 10.3390/ma10101193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Cerri E., Evangelista E., Forcellese A., McQueen H.J. Comparative hot workability of 7012 and 7075 alloys after different pretreatments. Mater. Sci. Eng. A. 1995;197:181–198. doi: 10.1016/0921-5093(94)09714-3. [DOI] [Google Scholar]
- 37.Huang C.Q., Jia X.D., Zhang Z.W. A modified back propagation artificial neural network model based on genetic algorithm to predict the flow behavior of 5754 aluminum alloy. Materials. 2018;11:855. doi: 10.3390/ma11050855. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Han Y., Qiao G.J., Sun J.P., Zou D.N. A comparative study on constitutive relationship of as-cast 904L austenitic stainless steel during hot deformation based on Arrhenius-type and artificial neural network models. Comp. Mater. Sci. 2013;67:93–103. doi: 10.1016/j.commatsci.2012.07.028. [DOI] [Google Scholar]
- 39.Liu X.Y., Yang C., Yang X.R., Qiang M., Zhang Q.Q. A constitutive model of ultrafine grained pure titanium deformation at elevated temperature based on artificial neural network. Rare Met. Mater. Eng. 2018;47:3038–3044. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Not applicable.