Improved Discrimination of Disease States using Proteomics Data with the Updated Aristotle Classifier

Abstract

Mass spectrometry data sets from ‘omics studies are an optimal information source for discriminating patients with disease and identifying biomarkers. Thousands of proteins or endogenous metabolites can be queried in each analysis, spanning several orders of magnitude in abundance. Machine learning tools that effectively leverage these data to accurately identify disease states are in high demand. While mass spectrometry data sets are rich with potentially useful information, using the data effectively can be challenging because of missing entries in the data sets and because the number of samples is typically much smaller than the number of features, two challenges that make machine learning difficult. To address this problem, we have modified a new supervised classification tool, the Aristotle Classifier, so that ‘omics data sets can be better leveraged for identifying disease states. The optimized classifier, AC.2021, is benchmarked on multiple data sets against its predecessor and two leading supervised classification tools, Support Vector Machine (SVM) and XGBoost. The new classifier, AC.2021, outperformed existing tools on multiple tests using proteomics data. The underlying code for the classifier, provided herein, would be useful for researchers who desire improved classification accuracy when using their ‘omics data sets to identify disease states.

Graphical Abstract

INTRODUCTION

The combination of machine learning and mass spectrometry is burgeoning and offering new opportunities for disease diagnosis. In one example, the combination of clinical features and proteomics data of plasma samples from Alzheimer’s patients effectively predicted Alzheimer’s disease using a Support Vector Machine (SVM) classifier; the performance strongly depending on the patient’s race, reiterating the importance of including patients of different racial backgrounds in ‘omics data sets.¹ Machine learning and ‘omics data have also been used to identify leukemia in children with 90% accuracy by combining the supervised classification tool, XGBoost, with LC-MS data quantifying amino acids.² In another example, lipidomics data was analyzed with LASSO feature selection and an SVM classifier to accurately classify patients with renal cancer.³ The combination of the latest ‘omics techniques with emerging machine learning methods provides researchers with new opportunities to do a better job at identifying disease states.

While the term “machine learning” may be relatively new, the data science concepts that underly it have been around for a long time. The 100-year-old math algorithm Principal Components Analysis (PCA), is an unsupervised machine learning method still heavily in use today for analyzing ‘omics data.^4,5 Unfortunately, it typically underpredicts whether or not a difference in the disease state can be identified in the data. In fact, only if the disease related difference is the largest contribution to data variability will the disease group and healthy group separate on a PCA plot. To do a better job at classifying ‘omics data, many researchers have turned to supervised methods, such as partial least squares discriminant analysis (PLS-DA) and variants thereof.^5–9 This approach, originally developed around 1975,¹⁰ explicitly uses the disease status of a sample to eagerly identify the key differences in the data, which can be capitalized on to better separate the samples into a diseased group and a healthy one. PLS-DA, like all supervised machine learning methods, obtain improved classification performance specifically because the class labels are used in the model. The caveat with this strategy is that the two groups of samples are essentially forced apart in the underlying model, and without validation of the model with new data, this approach often becomes unreliable because it over-predicts the differences in the groups.^11,12

More recent supervised classification strategies that leverage the power and speed of modern computing, including Support Vector Machine (SVM)¹³ and decision tree-based classifiers, such as XGBoost¹⁴, show even greater promise for ‘omics researchers over these older methods. In several examples of studies using mass spectrometry data, SVM was the method of choice for performing supervised classification;^1,3 this approach outperformed methods like linear discriminant analysis and partial least squares discriminant analysis on multiple proteomics data sets.^{15, 16} Decision-tree based classifiers, including Random Forest, boosted decision trees, and XGBoost, have shown similar promise for accurate classification of ‘omics data.^{2, 17, 18} The development of new and better classifiers provides new opportunities to do a better job of supervised classification, which translates into enhanced ability to discriminate disease and ultimately, improved health outcomes.

We recently introduced a unique tool for supervised classification, the Aristotle Classifier.^19–21 Originally developed for small glycomics data sets with just 10–30 different glycan features per sample,¹⁹ the algorithm has proven also to be useful in classifying MALDI-MS data,^20–21 including intact proteins,²⁰ where the goal was bacterial typing, and lipids,²¹ where the analysis goal was to identify cells undergoing metabolic change after immunotherapy treatment. In both these cases, larger data sets of 1300²⁰ to 3500²¹ different m/z’s per sample were interrogated. The goal of this study is to further develop the classifier for proteomics data and other LC-MS experiments, particularly those that rely on isobaric labeling.

Isobaric tagging experiments are a very common choice for generating quantitative proteomics data,²² yet this approach introduces two unique challenges that should be considered when performing supervised classification: missing data and high dimensionality. Isobaric labeled peptides are only quantified when the precursors are selected for MS/MS experiments,²² and since the precursor ions selected for MS/MS are not the same from run-to-run, when multiple injections are needed to analyze a full data set (which is usually the case), this analysis strategy leads to missing data for some of the peptides on some of the samples; low-abundant peptides are particularly effected. For example, in a quantitative proteomics data set of brain proteins, 10,100 proteins were quantified in 40 samples using a TMT tagging strategy,²³ but of those, less than 7,000 proteins were quantified for all 40 samples. Classification algorithms need to be able to effectively handle the challenge of these missing data if they are to be adept at using the data to classify the samples.

The Aristotle Classifier has the potential to excel in classifying proteomics data because of the way it treats missing data. When test samples are being interrogated, if no peak abundance is present, the classifier simply ignores that particular m/z, so missing data has absolutely no impact on the final classification of the sample. This treatment of missing data is different than both SVM or decision tree-based classifiers like XGBoost.

XGBoost accepts data sets with missing data, but the algorithm makes an assignment in its decision trees, even when data is missing.¹⁴ The algorithm, using training data, attempts to predict whether missing data should be assigned to one group or the other -- the disease group or the healthy group for example -- and it invokes these rules on test data. For proteomics experiments, this treatment of missing data may be particularly illogical. When data is missing in the training set, it is often equally missing from both the healthy controls and the disease samples because missing data is commonly the result of a failure for the instrument to trigger MS/MS on the relevant precursor ion. Since, in a multiplexed isobaric tagging experiment, the precursor typically contains equitable numbers of samples from the healthy group and the diseased group, one would not usually want their machine learning algorithm to assign samples with missing data to a particular group, based on the fact that data is missing. In summary, XGBoost’s treatment of missing data is not well suited to the realities of proteomics experiments.

When using Support Vector Machine (SVM), missing data cannot be left missing and, instead, must be imputed, replaced with a real number in an unbiased way. In this case, the researcher is left scratching her head, trying to figure out what a reasonable imputing strategy may be. Replacing missing data with zeros is not a good choice, as the reason the data is missing is often not because the peptide of interest has no abundance, but rather, because the entire group of samples it was mixed with did not trigger an MS/MS experiment for that peptide. When using SVM for proteomics data, one effective choice in dealing with missing data is to calculate the average of all the training data for that particular feature and to use that value in place of the missing one.¹ In principle, this approach is also necessarily flawed as there is no reason why the peak with missing data would be equivalent to the average of the training data. But in practice, this procedure often negatively impacts the results the least, so it is adopted.

Aside from missing data, the second key challenge in applying supervised classification to proteomics data is the high-dimensional aspect of the data sets: the number of features is typically much higher than the number of samples. This problem, referred to in the data science field as ‘the curse of dimensionality’²⁴ makes generating an optimal model difficult, as the learning strategies often cannot differentiate between “a good model for this type of problem” vs “a good model for this particular group of samples”. Therefore, an unmet need exists in the machine learning field for solving problems that are plagued by the curse of dimensionality, or in mass spectrometry terms, cases where the number of m/z’s interrogated is much higher than the number of samples studied.

In the work presented herein, we have updated the Aristotle Classifier to optimally address classifying proteomics data from LC-MS experiments, which face both the two aforementioned challenges, of missing data and high-dimensionality. First, an explanation of the original scoring algorithm is provided, followed by a discussion of the updates made to it that improve the classifier’s performance for proteomics data. Finally, several experiments are conducted to determine the extent to which these enhancements improve classification on a variety of proteomics data sets over the field-dominating supervised classification methods of SVM and XGBoost. Most importantly, we provide in Supplemental Material, a working code example so others can use this tool directly or incorporate it into other machine learning and mass spectrometry pipelines.

EXPERIMENTAL

General considerations.

All calculations were executed in RStudio, using R version 4.0.3. The SVM and XGBoost algorithms were from the e1071 and xgboost packages, respectively. All AUC values reported herein were calculated using the package, pROC, and the function “auc”. Code from the original Aristotle Classifier was acquired from the Supplemental Data section of reference 20, and code from the updated version of the classifier, henceforth referred to as AC.2021, is provided in the Supplemental Data section of this report.

Data sets.

The brain proteomics data sets were acquired from reference 23. The first set, “Brain 1”, includes data acquired from samples removed from the dorsolateral prefrontal frontal cortex. The second set, “Brain 2”, contains proteomics data from samples originally extracted from the anterior cingulate gyrus. Both of these regions are known to undergo extensive dysregulation in Alzheimer’s patients. For both data sets, patients with Alzheimer’s Disease were treated as cases and the patients without Alzheimer’s Disease were treated as controls. There were twenty examples of each type in both data sets. All reported protein features and their abundances were used without any additional data processing.

The proteomics data from cerebral spinal fluid were acquired from reference 25. The three data sets, referred to in the original work as “Sweden,” “Magdeburg,” and “Berlin”, are numerically referred to herein, as set 1, set 2, and set 3. The same samples were selected for inclusion in each data set, and the same diagnostic criteria for demarcating the patients as Alzheimer’s (case) or not (control) were used as described in the original work. The number of cases and controls in the three data sets are: 29 and 31 for set 1; 26 and 28 for set 2; 33 and 50 for set 3. In all data sets, proteins whose abundance was reported to be “0” were not relabeled. Proteins whose abundance were labeled as “NA” were treated as missing numbers and processed differently than those labeled as zero abundance.

Classifications using SVM and XGBoost.

For both these classifiers, the original data matrices were transformed so that the samples appeared in columns and the features appeared in rows. For all SVM classifications, a linear kernel was used; the cost was set to 1; the accuracy was determined based on the class assignments without considering probability; and the AUC was determined based on the probabilities generated. Furthermore, prior to classification with SVM, all data sets were scaled, using the embedded function in R, and after that, all missing data were replaced with zeros, which is equal to the column mean after scaling. For XGBoost, the following parameters were set in every classification: booster = “gbtree”, objective = “binary:logistic”, eta=0.3, gamma=0, max_depth=6, min_child_weight=1, subsample=1, colsample_bytree=1. Furthermore, nrounds was set to 30 and the evaluation metric was set to “error”. During leave-one-out classifications, each sample in the data set was classified with its own model, built with all the remaining samples in that set.

Classification studies with the Aristotle Classifier.

The Aristotle classifier, both the original version and the AC.2021 update, accepts data matrices with features in rows and samples in columns. All data sets used herein were therefore imported without transformation for this classifier. The number of samples, the number of features, and the identities of the samples in the two classes “Low” and “Hi” were also input for each classification. Finally, the number of aggregating replicates, “k”, was chosen. This variable was renamed “Repeats” in AC.2021. The higher the “Repeats” value, the longer the classifier takes to complete a calculation, but the more reproducible the result becomes. For the work herein, 1000 repeats were used for every calculation using the original classifier as a higher number of repeats resulted in a very slow calculation. For AC.2021, tests were performed to determine the number of repeats necessary to achieve reproducible accuracy on three consecutive classifications. Using AC.2021, 1000 repeats was selected for the brain data sets and the Leave-One-Out (LOO) experiments on the first CSF data set. For LOO on the second CSF data set and all the train/test runs, 5000 repeats was used. Finally, 20,000 repeats was used on the LOO studies for the third data set. With these values selected, the number of misclassified samples from AC.2021 did not change for three repeated classifications. In both versions of the Aristotle classifier, the training data never include the sample being classified; therefore, the model produces output for a leave-one-out cross-validation each time it is run. In AC.2021, the variable, X, also needs to be set for each data set. For the leave-one-out experiments, X was set to 16 and 14 for the first two brain data sets respectively; it was set to 11, 7, and 12 for set 1, set 2, and set 3 of the CSF data sets. This value is manually optimized, and it represents the number training samples to select in each iteration of the model. In the original Aristotle classifier, this value is unmodifiable and equal to 4. Two examples are provided in Supplemental data showing how the training group size, X, impacts the accuracy and AUC of the classification. See Supplemental Tables 1 and 2.

Train/test experiments; all three classifiers.

The three CSF data sets were used for train/test experiments. In each case, the first 15 examples of each case (disease state or control) were used as a training set and the remainder of the samples were used as a test set. In this paradigm, test set 1 contained 29 samples; test set 2 contained 24 test samples; test set 3 contained 53 test samples. For both SVM and XGBoost, the parameters described above produced models with 100% training accuracy and AUC’s of 1 for all the training data for both classifiers. For AC.2021, the accuracy of the training samples was used to optimize the number of training samples per iteration, with values between 4 and 12 being tested iteratively. The value chosen for the final model was that which produced the smallest classification error for the training samples. In cases where the error for the training samples could not uniquely identify an optimal value for X, the AUC for the training data was used as a secondary evaluation metric. The selected number of training samples per iteration, X, was 8, 9, and 10 for set 1, set 2, and set 3 respectively.

RESULTS AND DISCUSSION

Classifier Overview.

The basic principles behind the scoring algorithm of the Aristotle Classifier are shown in Figure 1. First, a random set of four training samples from two different classes are used to determine which features --which m/z’s or which protein’s abundances-- to use in classification. To be selected as a usable feature, the eight training samples must partition into their respective classes based on the abundance of the feature in question. For example, all the training samples from group 1 need a higher (or lower) abundance than all the training samples from group 2, for each m/z that is to be saved as a scorable feature. In the figure, that condition is met for features 1 and 3, so they would be selected, but not features 2 and 4. Only those features that completely partition into their training groups are saved, while all other features are ignored. After feature selection, the border that discriminates the two groups is determined: This partition is the midpoint between the two most similar samples from the two groups, and it is depicted with a blue bar in the figure.

Figure 1.

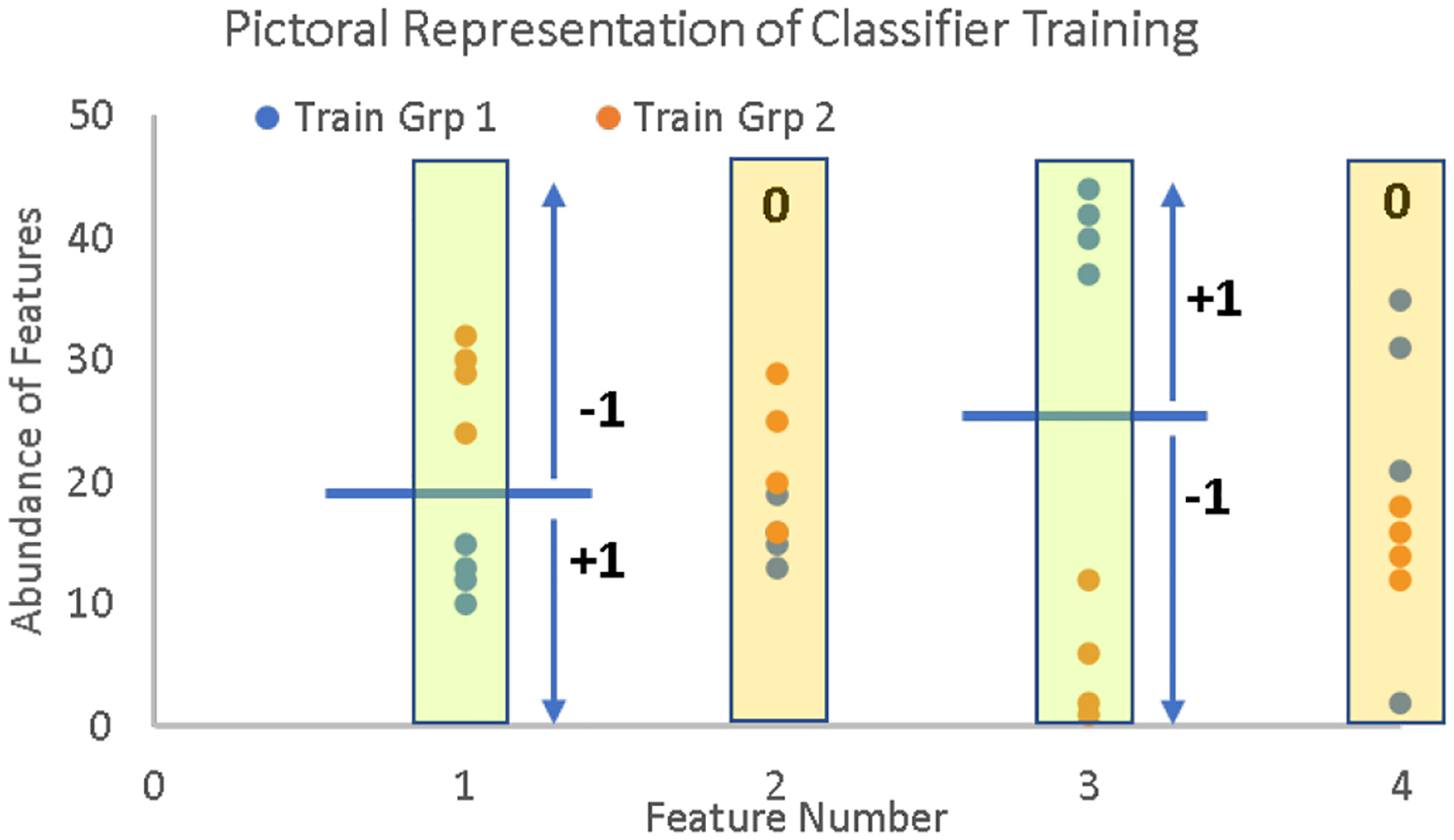
Pictorial description of the feature selection and scoring mechanism in the Aristotle Classifier. Training data from two different classes (blue dots and orange dots) are assessed, one feature at a time. The classifier selects the features in which the training data can be partitioned completely into their respective classes, ex: Features 1 and 3 in the figure are selected. Then a border (depicted by the blue line) is designated for the selected features. Samples that are not part of the training set are scored based on whether their selected features’ abundances are above or below the blue border, as shown in the figure and described more fully in the text. The final class assignment for test samples is based on the total point score for the sample.

Test samples are classified by awarding one point (+1) for each selected feature of the test sample whose abundance lies on the same side of the partition as the group 1 training samples; a (−1) is assigned for each feature when the test sample’s value for that feature is on the same side of the partition as the group 2 samples; a score of 0 is assigned for the selected features of the test sample if the abundance for the test sample is missing. Each saved feature is weighted equally in any given scoring round, and the sign of the sample’s final score, after all the points are summed, determines if it is ultimately classified as being from group 1 or group 2. Group 1 samples have a score greater than zero. To maximally leverage the training data, the entire feature selection and scoring process, starting with the random selection of eight training samples, is repeated many times, with 1000 replicates being a commonly implemented choice. The final score is the sum of all the scores from the individual rounds.

Classifier Updates.

Because the Aristotle Classifier handles missing data in a unique and optimal way, by completely ignoring it, we expected that it could potentially demonstrate itself to be a useful tool for classifying proteomics data, where missing values are common. Preliminary testing, however, demonstrated that the embedded feature selection step was typically weighting moderately useful features too similarly to the exceptional ones. In other words, marginally useful features were selected too frequently. We hypothesized that the classifier’s performance could be improved if the algorithm was more selective about the features that it selected for scoring.

As shown in Figure 1, the algorithm counts the outcome for each feature that has all eight training samples partitioned into their respective groups based on their abundance. If the number of randomly selected training samples is higher than eight, then the marginally useful features would be retained for scoring less often, as the larger set of training samples would fully partition into their respective classes less frequently. To test the hypothesis that a different initial group size could lead to better performance, the algorithm and underlying code was revised to allow the number of randomly selected training samples to be set as a user-adjustable parameter. This parameter, X, can now be set from 1 to any number that is equal or smaller than the training set’s minority class; however, testing on several data sets indicates that values from 4–10 are typically optimal, with occasional additional benefits gained when the value is higher for very high-dimensional data sets. See examples below.

In addition to allowing for flexibility in the stringency of the feature selection component, the scoring component of the algorithm was rewritten to be faster for high-dimensional data, where the number of features is much larger than the number of samples. The scoring algorithm did not change, but its implementation now more heavily leverages vector calculations, which are done more quickly than calculating single point values iteratively. A code example is provided in Supplemental Data.

Test 1 Brain Proteomics.

In the initial test of the updated classifier, two proteomics data sets, each from 40 human brains, were interrogated. Half the samples came from deceased individuals who had Alzheimer’s disease at the time of their death, and the other half were from non-Alzheimer’s patients in the same age group. These data sets were selected for several reasons: 1) They contain a large number of protein features (>10,000); 2) The data set contains a significant fraction of missing data: Brain 1 contains 17% missing data; Brain 2 contains 13%. 3) Because Alzheimer’s disease is a brain condition, and the proteins were from regions of the brain known to changes with Alzheimer’s disease, the data were expected to be classifiable with a reasonable degree of accuracy.

In this classification challenge, four different classifiers were used on both data sets, the original version of the Aristotle Classifier (AC.orig), the updated version, described in this manuscript (AC.2021), Support Vector Machine (SVM), and XGBoost. Details describing the hyperparameters used for each method are in the experimental section; different choices for the hyperparameters will yield slightly different results for the calculations, and the choice of settings herein are typical initial values used when applying these methods. Since these data sets were very limited in the number of samples available, a leave-one-out cross validation test was performed in each case. In this experiment, the sample being classified is left out of the training set, a model is developed with the remaining samples, and the left-out sample is classified with that model. This approach leverages all the available data while assuring that the test sample does not influence the model used to test it.

The results from this classification challenge are in Table 1, and results comparing AC.orig with AC.2021 using different training set sizes are in Supplemental Table 1. Here, one can plainly see that the updated Aristotle Classifier (AC.2021) proved to be a significant performance enhancement over the original version; furthermore, it edged out the other state-of-the-art classifiers in its ability to accurately classify these proteomics data. From the perspective of classification accuracy, the new classifier, AC.2021, beat all the other options on the first data set, derived from proteins isolated from the frontal cortex, and outperformed both the original Aristotle Classifier and SVM on the second data set, where proteins were obtained from the anterior cingulate gyrus. While AC.2021 tied XGBoost on this second data set, in terms of the overall accuracy achieved, AC.2021 had a very slight edge in its AUC, the area under the ROC curve, (where ROC stands for Receiver-Operating Characteristic); the AUC is a secondary measure of model quality.

Table 1:

Classification Results for Brain Proteomics Data

	Brain Set 1: 17% missing data				Brain Set 2: 13% missing data
Classifier	Accuracy	AUC	time	Classifier	Accuracy	AUC	time
Orig AC	82.50%	0.92	27m25s	Orig AC	87.5%	0.93	23m8s
AC.2021	97.50%	1	2m44s	AC.2021	97.50%	0.98	2m51s
SVM	90%	0.96	7m32s	SVM	85%	0.93	8m3s
XGB	95%	0.9	0m6s	XGB	97.50%	0.95	0m5s

The updated version of the classifier was also ten times faster than the original version and faster than SVM but not able to match the speed of XGBoost. One of the key design features of XGBoost is its ability to efficiently classify very large data sets,¹⁴ so its overall speed advantage is expected. All things considered, for proteomics data sets, the speed of the classifier is much less important than its accuracy. Acquiring the data for these samples, processing them, performing the proteomics experiments, and assigning the protein abundances can take months. At the end of the workflow, it doesn’t much matter if the classification step takes two minutes or ten minutes. However, in some applications, speed may be more important, so these data serve to benchmark this classifier against common competitors. Overall, these experiments serve to demonstrate that the 2021 updates to the Aristotle Classifier improve its performance compared to the original iteration and demonstrate its competitiveness versus existing state-of-the-art algorithms that have been under development for much longer.

Test 2 CSF Proteins.

In a second set of experiments, we sought data sets that were more difficult to classify than brain samples from Alzheimer’s patients. Furthermore, larger data sets were desirable, so both leave-one-out and train/test experiments could be conducted. For this purpose, three proteomics data sets that again studied Alzheimer’s patients were utilized, but this time, the proteins came from cerebral spinal fluid. By moving the sample source farther away from the impacted area, from brain to cerebral spinal fluid, we expected the classification difficulty to be somewhat higher but not impossible. A prior machine learning study on these data sets had been accomplished recently, and 85% of the patients were correctly classified.²⁵ However, one should note that in the former workflow, the full data sets (1180 to 1310 proteins) were not used. Instead, the group of proteins was radically downsized to include just 26 proteins that had the highest correlation to the disease state in these data, significantly simplifying the classification challenge. In the studies performed here, all the proteins for each data set are included in the study.

Using the same strategy as in experiment 1, each data set was classified with the four different classifiers mentioned earlier, and leave-one-out cross-validation was conducted. The classification results are shown in Figure 2, and example comparing AC.2021’s performance with different training group sizes appears in Supplemental Table 2. In Figure 2A, model accuracy of each method is depicted. While the original AC performed reasonably well on the first two data sets, its accuracy on data set 3 was only 60%, while the other methods’ accuracies were near 78–86% for this data set. This example shows that sometimes the ability to tune the training set size in the Aristotle Classifier makes a big difference. Supplemental Table 2 shows that as the training set size increases from 4 to 12, the accuracy steadily increases.

Figure 2.

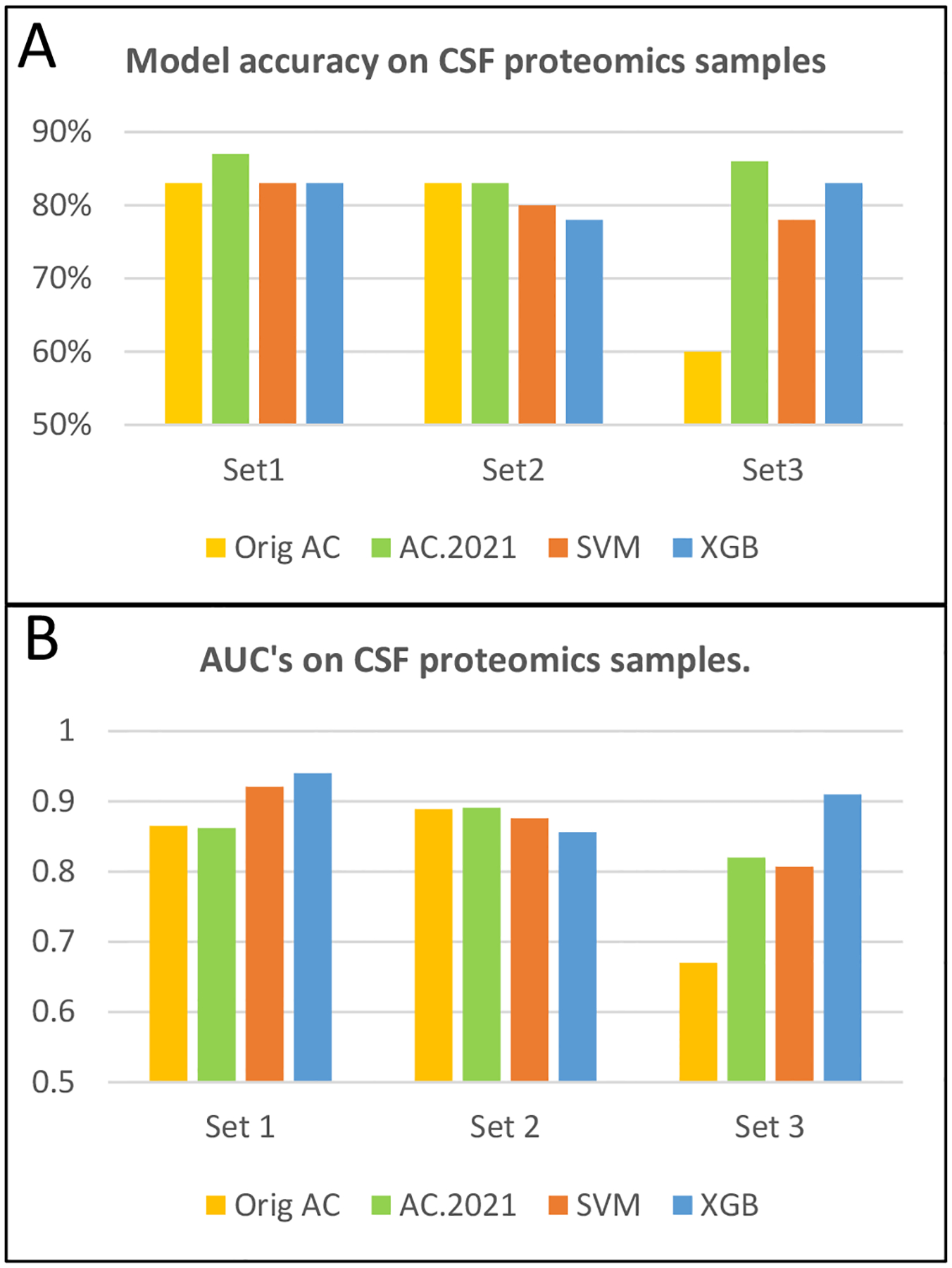
Leave-one-out cross validation data for proteomics data sets of CSF samples from Alzheimer’s patients. (A) Accuracy test for three data sets and four classifiers: Orig AC, AC.2021, SVM, and XGBoost. (B) Area Under the ROC Curve (AUC) for the same classifiers and data as in A.

For each data set, AC.2021, is the superior method: in two out of three tests, the accuracy of AC.2021 exceeded 85%; neither SVM nor XGBoost attained that level of accuracy on any of the three tests. Their accuracies were typically near 80%. While the percent differences are somewhat modest between the data sets, representing the results as percents somewhat obscures the actual benefit to patients. In considering the three data sets in aggregate, a total of 197 patients are tested. In all, AC.2021 misclassifies just 29 patients; XGB misclassifies 36, and SVM misclassifies 39.

Figure 2B shows the area under the receiver-operating characteristic (ROC) curves, the AUCs, for each method on these data sets. Here, XGBoost produced the largest AUC in two of the three examples, with AC.2021 edging it out on one data set. These data indicate that XGBoost is clearly a contender to consider when choosing a classifier to analyze proteomics data. Indeed, it has been the go-to method in past studies.^2,25 However, in the context of all the data presented herein, including Table 1 and Figure 2A, AC.2021 outperformed it more often than not.

Experiment 3: Train/test.

In the previous two experiments, the different models were assessed using a leave-one-out cross validation. Sometimes a better test of a model’s performance is to instead optimize and train the model on a subset of data and reserve the remaining data for a single test, done after all optimizations are complete. Thus, we additionally conducted train/test experiments on the three CSF proteomics data sets. In this paradigm, the first 15 samples from healthy controls and AD patients were used as training samples, for a total of 30 training samples, and the remaining data were used as test data.

The results for the train/test experiments for all four classifiers are in Figure 3. As expected, AC.2021 performed better than the original AC, due to the ability to optimize the training group size. Since the original AC sets the training group size at 4, features that do a moderate, but not optimal, job of separating the data are counted more frequently and therefore, the model underperforms. SVM and XGBoost, by contrast, generally perform somewhat better than the original AC but not quite as well overall as AC.2021. SVM performs well on the first and second data sets, but its performance on the third data set is rather poor. XGBoost does the opposite, performing relatively well only on the third data set. AC.2021 had the highest accuracy on each of the three data sets and, overall, the best AUC’s, when considering all three experiments. The reason for the performance differences between AC.2021, XGBoost, and SVM appears to be a combination of the way each one handles missing data and the way each one separates the classes. It would be difficult to predict in advance which of the three classifiers would perform the best on any given data set, but these results amplify the observation that AC.2021 is competitive with both XGBoost and SVM and should be considered in classification problems like these.

Figure 3.

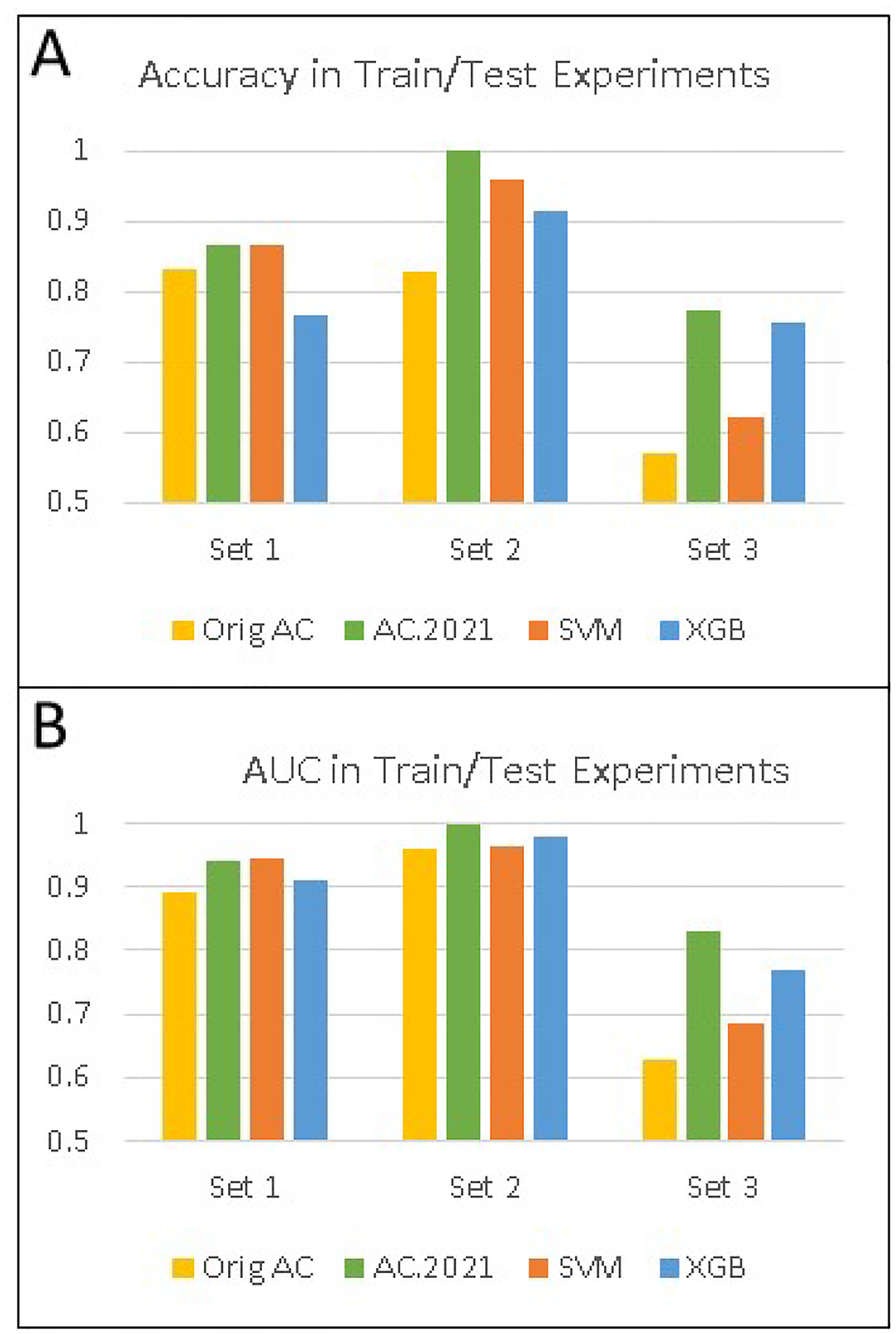
Classification results for independent test sets of proteomics data from Alzheimer’s patients. (A) Overall accuracy for three different data sets using Orig AC, AC.2021, XGBoost, and SVM. (B) AUC’s for the same test sets and classifiers as in A.

CONCLUSION:

Accurately classifying proteomics data with few samples, missing entries, and lots of features to consider, is an essential need of the proteomics community. The experiments in this manuscript demonstrate that AC.2021 has the potential to perform well on these types of sample-limited proteomics data sets, even against existing classifiers that have been around longer and are known for their strong performance. Based on the performance tests shown herein, we expect that AC.2021 will enable mass spectrometry researchers to more effectively identify patients in disease states; this tool will, therefore, meaningfully contribute to improving human health.