Assessment of the viscoelastic mechanical properties of the porcine optic nerve head using micromechanical testing and finite element modeling

Abstract

Optic nerve head (ONH) biomechanics is centrally involved in the pathogenesis of glaucoma, a blinding ocular condition often characterized by elevation and fluctuation of the intraocular pressure and resulting loads on the ONH. Further, tissue viscoelasticity is expected to strongly influence the mechanical response of the ONH to mechanical loading, yet the viscoelastic mechanical properties of the ONH remain unknown. To determine these properties, we conducted micromechanical testing on porcine ONH tissue samples, coupled with finite element modeling based on a mixture model consisting of a biphasic material with a viscoelastic solid matrix. Our results provide a detailed description of the viscoelastic properties of the porcine ONH at each of its four anatomical quadrants (i.e., nasal, superior, temporal, and inferior). We showed that the ONH’s viscoelastic mechanical response can be explained by a dual mechanism of fluid flow and solid matrix viscoelasticity, as is common in other soft tissues. We obtained porcine ONH properties as follows: matrix Young’s modulus E = 1.895[1.056, 2.391] kPa (median [min., max.]), Poisson’s ratio ν = 0.142[0.060, 0.312], kinetic time-constant τ = 214[89, 921] sec, and hydraulic permeability k = 3.854 × 10⁻¹[3.457 × 10⁻², 9.994 × 10⁻¹] mm⁴/(N.sec). These values can be used to design and fabricate physiologically appropriate ex vivo test environments (e.g., 3D cell culture) to further understand glaucoma pathophysiology.

1. Introduction

Glaucoma is the leading cause of irreversible blindness, with c. 78 million patients worldwide [1,2]. Glaucoma is an optic neuropathy characterized by chronic deterioration of vision due to gradual loss of retinal ganglion cells (RGC) [3]. The most common form of glaucoma is primary open-angle glaucoma (POAG), which is strongly associated with elevation of the intraocular pressure (IOP), thought to cause biomechanical insult to the RGC axons and the glial cells of the optic nerve head (ONH). This results in remodeling and often irreversible posterior deformation of the ONH (cupping) [3]. Therefore, ONH biomechanics is a key aspect of POAG pathophysiology. It is known that IOP fluctuates significantly [4–6], yet little is known about the viscoelastic mechanical behavior of the ONH.

Many soft tissues behave differently under static vs. dynamic loading (i.e., viscoelasticity), due to their high water content and the intrinsic viscoelastic behavior of the extracellular matrix (ECM) [7,8]. Tissue viscoelasticity strongly influences the magnitude and frequency of the mechanical loads on cells resident in the tissue, i.e., it influences the mechanobiological signals the cells receive from their environment. Further, fluid-dependent viscoelasticity (also known as poroelastic viscoelasticity) plays a key role in material transport (e.g., cellular nutrients and waste) to and from the cells. Therefore, viscoelasticity is an important aspect of understanding cell mechanobiology, which influences tissue remodeling [9].

We previously showed significant viscoelastic effects in the porcine and murine ONHs, as evident from a significant dependence of the biomechanical response on mechanical loading rate [10]. Additionally, Myers and co-workers showed that the posterior bovine sclera, a region of the ocular globe that includes the ONH, shows a nonlinear and viscoelastic mechanical response [11]. However, no studies report the viscoelastic material properties of the ONH.

We hypothesized that the ONH’s mechanical response could be explained using mixture theory based on a biphasic model with an inherently viscoelastic matrix. Therefore, this study’s objective was to assess the viscoelastic mechanical properties of the porcine ONH using micromechanical testing and finite element modeling. We chose to study the porcine ONH because porcine eyes are readily available and have been previously used to study glaucoma [12]; because porcine ocular anatomy is similar to human anatomy, particularly in the ONH possessing a collagenous lamina cribrosa [13,14]; and because the porcine optic disk size is similar to that in the human, making it appropriate for micromechanical testing [10]. Our results provide a detailed characterization of the mechanical properties of the ONH, which in turn provides new insight into the mechanophysiology of the ONH and further elucidates the role of ONH biomechanics in glaucoma.

2. Methods

2.1. Experimental sample preparation

For mechanical analyses of the ONH, 8 eyes were collected from 4 freshly sacrificed female pigs (Domestic Yorkshire Cross-bred Swine [common farm pig in the US], c. 5 months of age) by resection from the orbital cavity. Eyes were prepared for experimental testing on the same day as sacrifice while being stored in ice-cold PBS. Careful incisions were made through the extraocular muscles, the surrounding fascia, and the optic nerve to isolate the globe while keeping portions of the surrounding lid and skin attached, which were used as anatomical references (Fig. 1A).

Fig. 1.

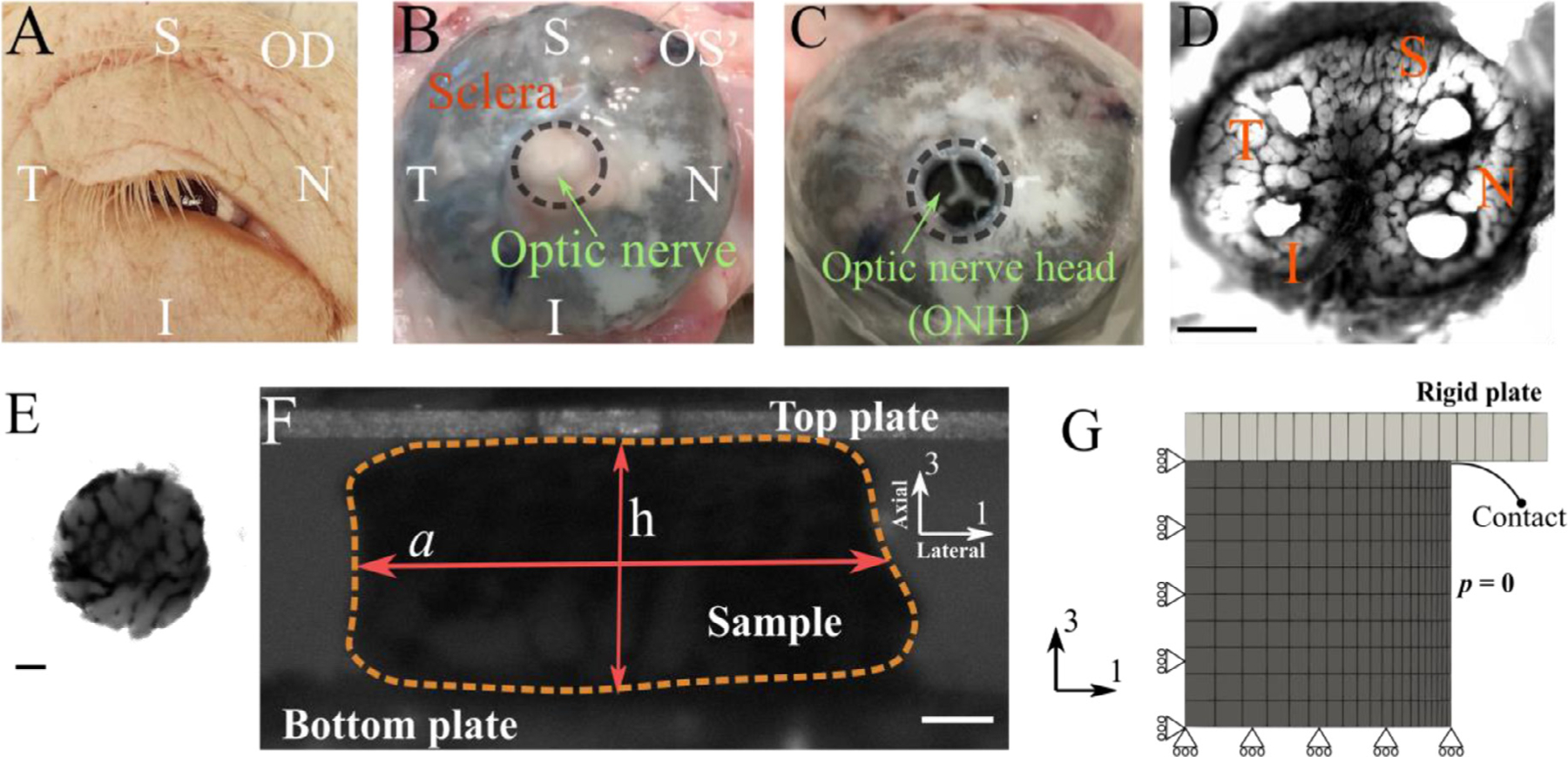
Overview of the experimental procedure used in this study. (A) an example of the harvested eye [OD] and surrounding tissue with labeling for anatomical orientation [I=inferior, N=nasal, S=superior, T=temporal]. (B) Posterior segment of an eyeball [OS] showing the four anatomical quadrants. (C) An eye with the optic nerve transected flush with the posterior scleral surface. (D) A tangential slice of an ONH (scale bar = 1 mm), from which four samples (E; scale bar = 0.1 mm) are harvested (one from each quadrant). (F) Each sample was tested using a micromechanical compression testing system, and the height [h] and width [a] of the sample were measured throughout the test (scale bar = 0.1 mm). From these measurements, the axial and lateral strains (engineering strains) were calculated as ϵ_axial =h/h₀ −1 and ϵ_lateral =a/a₀ −1, respectively, and the apparent Poisson’s ration was computed as ν_app = −ϵ_lateral/ϵ_axial; note that the axial direction is approximately normal to the optic disk (G) An axisymmetric finite element model was used to model the mechanical response of the ONH, where a rigid plate compresses the ONH sample in the axial (axis-3) direction. Rolling boundary conditions were utilized at the bottom and center-line to enforce model symmetry. The lateral face of the sample was prescribed to have zero pressure, which allowed outflow of fluid during compression.

The optic nerve head (ONH) was then dissected [10]. Briefly, the ONH was exposed by transection of the optic nerve flush with the sclera’s posterior aspect using a surgical blade (Fig. 1B and C). A 1 mm thick tangential slice posterior to this surface, and encompassing the peripapillary sclera, was then harvested by means of a scalpel blade (Fig. 1D). From each anatomical quadrant (i.e., inferior [I], nasal [N], superior [S], and temporal [T]), one cylindrical sample was collected using a 1 mm diameter surgical biopsy punch and placed in ice-cold physiological phosphate buffered saline solution (PBS). Each ONH sample’s cross-sectional image was acquired using brightfield microscopy (Leica DM6; Wetzlar, Germany), which was used later to measure sample diameter (Fig. 1E). The samples were then immediately studied via micromechanical testing.

2.2. Micromechanical incremental creep test

To measure the viscoelastic mechanical properties of the ONH, we conducted a dynamic mechanical test on each sample using a micromechanical testing device (CellScale Microsquisher, Waterloo, ON, Canada). This instrument measures the deflection of a tungsten cantilever beam with known diameter (0.5508 mm), length (54–57 mm), and elastic properties (Young’s modulus 411 GPa) as the tissue sample is compressed by the beam [10,15]. During mechanical testing, samples were bathed in PBS at 37 °C.

Samples were subjected to a force-controlled incremental creep protocol under unconfined compression between two rigid plates (Fig. 1F). To establish a consistent initial condition for the test, we first gradually loaded the samples to 200 μN (tare-load) over 60 sec, which ensured a complete but gentle contact between the rigid plate and the sample’s surface, immediately unloaded to zero force at the same rate, and then loaded to tare-load once more, after which the tare-load was maintained for one minute (recovery phase). The sample was imaged throughout the test using a CCD camera (Fig. 1F). The test protocol consisted of four incremental loading cycles to 524, 1047, 1470, and 2094 μN. At each force level, the sample was held for 5 min to allow creep deformation. Following the fourth creep cycle, the sample was unloaded to the tare-load level over 4 min and held there for 1 min, which concluded the micromechanical test.

2.3. Deformation analyses

We used the height of the sample during the test to calculate axial engineering strain as ϵ_axial = h/h₀ − 1, where h was the height of the sample during the test, and h₀ was the reference height of the sample, i.e. the height with the tare load on the sample. The sample’s reference height was measured by averaging the final 20 sec of the recovery phase before beginning the cycles of creep loading (h₀=0.5 ± 0.2 mm). To measure the lateral strain, we used image analysis. Specifically, we created a binarized mask that covered the sample, calculated the mask’s area, and calculated the sample’s average lateral width by dividing this area by the height of the mask (Fig. 1F). The lateral engineering strain was then calculated as ϵ_lateral = a/a₀ − 1, where a was the average lateral width of the sample and a₀ was its reference value, calculated as for h₀. Throughout the test, we also calculated the apparent Poisson’s ratio ν_app = −ϵ_lateral/ϵ_axial, which was used as measure of volumetric compressibility, with ν_app = 0.5 indicating incompressibility under the assumption of cylindrical axisymmetry.

2.4. Anatomical region heterogeneity in deformation responses

We compared the samples’ mechanical response from the four anatomical regions to determine whether the ONH’s heterogeneous structure affected the outcomes. Specifically, we calculated the ultimate creep strains and Poisson’s ratios (i.e., ϵ_axial, ϵ_lateral, and ν_app) at the end of each creep cycle by averaging data from the last 20 sec. We used two-way ANOVA to evaluate regional variance in the experimental results (see Statistics section). Data visualization was performed using Gramm [16].

2.5. Finite element model of the ONH

2.5.1. Mesh generation

To model deformation of the cylindrical ONH samples, we used an axisymmetric circular mesh subtending a 1-degree angle (Fig. 1G). Consistent with the experimental samples’ dimensions, the height and the radius of the samples were each set to 0.5 mm. 220 linear elements were used to tessellate the geometry in 3D (Fig. 1G); this mesh density was based on a preliminary convergence study (see supplementary Figure S2). The mesh was generated and the governing equations were solved using the FEBio software suite (FEBio v3.1; febio.org [17])

2.5.2. Boundary conditions

The boundary conditions were set to exploit the symmetry of the sample (Fig. 1G). The rigid plate’s contact with the sample was implemented by a surface-to-surface penalty-based algorithm active both in tension and compression that allows for lateral deformation of the contact surface [18]. Because one of the contact bodies was a rigid plate, we assigned the contact surface from the deformable body (ONH) to be the primary contact surface and the plate’s contact surface as the secondary. The sample’s lateral surface was prescribed as a zero-pressure boundary surface to allow for fluid exchange during mechanical loading.

2.5.3. Constitutive relations

To model the ONH’s mechanical behavior, we used a biphasic formulation with a viscoelastic matrix, similar to several existing studies considering other soft tissues [19–21]. Our approach was to use the fewest number of model parameters that could reasonably describe the biomechanical response of the ONH. The choice of a biphasic model was based on the compressibility observed in our samples; however, a classic biphasic model with a purely elastic matrix was not able to capture the complex viscoelastic mechanical response of the ONH. Therefore, we also included solid viscoelasticity. Here, we used a straightforward formulation of biphasic poroelasticity theory, using Darcy’s law to describe the solid-fluid interactions with an isotropic hydraulic permeability k, and a viscoelastic matrix to model the solid portion of the ECM using the reactive inelasticity (RIE) framework [22, 23]. RIE is a continuum mechanics framework based on the kinetics of molecular bonds to model the inelastic mechanical behaviors of tissue according to thermodynamics of observable state variables [23]. In RIE’s viscoelastic variant (reactive viscoelasticity), there are two types of bonds: permanent bonds (also called strong bonds) and formative bonds (also called weak bonds) [22, 23]. Consequently, the Helmholtz free energy of the solid material (Ψ) can be written as

$$\mathrm{\Psi }={\mathrm{\Psi }}_p+{\mathrm{\Psi }}_f$$ (1)

where Ψ_p and Ψf are the Helmholtz free energies of the permanent and formative bonds, respectively, and the subscripts ‘p’ and ‘f’ stand for permanent and formative, respectively. This notation will be used throughout the text.

Permanent bonds do not break-reform in response to external mechanical loading and thus confer hyperelastic mechanical behavior. In our model, Ψ_p was formulated using a compressible neoHookean relation:

$${\mathrm{\Psi }}_p=\psi \left(\mathbf{\text{F}}\right)=\frac{\mu }{2}\left(I_1-3\right)-\mu lnJ+\frac{\lambda }{2}{\left(lnJ\right)}^2$$ (2)

where F is the deformation gradient tensor, I₁ is the first invariant of the right Cauchy-Green strain tensor (i.e., I₁ = trace(C) = trace(F^TF)), and J = det(F). Further, μ is the shear modulus (μ = E/[2(1 + ν)]) and λ is the bulk modulus (λ = Eν/[(1 + ν)(1 − 2ν)]) of the matrix, where E is the matrix Young’s modulus and ν is the matrix Poisson’s ratio.

Formative bonds, on the contrary, break-reform in response to a differential external mechanical loading initiating a new generation of bonds (indicated by superscript α). The kinetics of these molecular bonds controls the amount of energy stored in them, resulting in viscoelastic behavior with a stress-free equilibrium condition. For this purpose, Ψf took the form

$${\mathrm{\Psi }}_f=\sum _{\alpha }{w}^{\alpha }\psi \left({\mathbf{\text{F}}}^{\alpha }\right)$$ (3)

where ψ is the intrinsic hyperelasticity relation for formative bonds, which is taken to be the same as for permanent bonds (Eq. (2)), F^α is the relative deformation gradient tensor, and w^α is the number fraction of a generation of bonds that was initiated in response to an increment of loading at time t = t^α. w^α is a scalar (0 < w^α < 1), which obeys the conservation law (assuming no damage):

$$\sum _{\alpha }{w}^{\alpha }=1$$ (4)

The kinetics of w^α controls the transient part of the mechanical response; here we assumed first-order kinetics:

$$\frac{d{w}^{\alpha }}{dt}=\frac{-w^{\alpha }}{\tau }$$ (5)

where τ is the time-constant of bond breaking-reforming. This form of the assumed kinetics results in an exponential stress-relaxation behavior [22,23].

In summary, there were a total of four model parameters: matrix Young’s modulus (E [kPa]), matrix Poisson’s ratio (ν), the time-constant of bond breaking-reforming (τ [sec]), and hydraulic permeability (k [mm⁴/(N.sec)]).

2.6. Parameter identification

To identify the model parameter values by the fitting of experimental data, we used a multi-start optimization method [24,25]. This Monte-Carlo-type approach eliminates the dependence of the data fitting results on the initial guess by conducting the optimization from randomly-generated initial guesses. We based the optimization on a constrained nonlinear least-squares algorithm (interior-point, fmincon, Matlab) and used Latin hypercube sampling with a grid size of 100 to sample the initial guesses. The bounds of the model parameter values were {E, ν, τ, k}_min={0.1 kPa, 0, 10 sec, 10⁻⁴ mm⁴/(N.sec)} and {E, ν, τ, k}_max {100 kPa, 0.49, 1000 sec, 1 mm⁴/(N.sec)}.

The cost function was designed to fit the axial and lateral strains simultaneously, as:

$$\begin{gathered} f=\sqrt{\frac{\left(f_{axial}^2+f_{lateral}^2\right)}{2}} \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=\sqrt{\sum _{i=1}^n\frac{{\left({ϵ}_{axial}^i-{ϵ}_{axial,0}^i\right)}^2+{\left({ϵ}_{lateral}^i-{ϵ}_{lateral,0}^i\right)}^2}{2n}} \end{gathered}$$ (6)

where f_axial and f_lateral are the root mean square of errors (RMSE) of the fits in the axial and lateral directions, respectively. ε_axial,0 and ε_lateral,0 are the experimental axial and lateral strains. The index i represents resampling intervals, which split the test duration into equal segments (n = 100). We have previously shown that using both axial and lateral strains in data-fitting maximizes the parameter identifiability from uniaxial tests [24]. Fits were preformed using a nonlinear constrained least-squares interior-point algorithm (fmincon, MATLAB), and the solutions were accepted if f_axial and f_lateral were less than 50% of the maximum experimental standard deviations of ϵ_axial,0 and ϵ_lateral,0, respectively [25]. To ensure local uniqueness of the parameter values, only the solutions where the Hessian matrix was full rank with a positive determinant were accepted, indicating convexity of the function at the solution point [26]. Due to the multi-start optimization’s stochastic nature, we conducted a confirmatory run, which resulted in the same results with minor, inconsequential differences that confirmed repeatability of the results (see supplementary Table S1 and Figures S3 and S4).

2.7. Model validation

To validate our model, we simulated existing experimental tests in which Boazak et al. [10] dynamically loaded porcine ONHs, including five cycles of mechanical loading between 0% and 15% compressive strain at loading rates of either 5%/min (slow) or 40%/min (fast). They reported a mean value of C₁ (the neoHookean constant) from the fifth cycle of 464 Pa for the slow loading rate, which increased to 725 Pa for the fast rate (p = 0.110). This is equivalent to the modulus increasing from 2.78 kPa to 4.35 kPa, which we calculated using the well-known equation E = 6C₁ incompressible neoHookean material (see for example [27]). Similar to Boazak et al., we used the fifth cycle to compare the mechanical response between the slow and fast loading cases based on the average tangent modulus, and we compared the results of our model prediction to experimental data. Since Boazak et al.’s experiments did not differentiate between anatomical regions, we used median values of model parameters over all the anatomical regions.

2.8. Statistics

For comparing the experimental deformation results from four anatomical regions we conducted a two-way ANOVA followed by a multiple comparison Tukey’s test on each of ϵ_axial, ϵ_lateral, and ν_app with the anatomical region (I, N, S, T) and the creep cycle number (Cycles 1–4) as independent variables. The statistical significance threshold was set at 5%.

To assess the experimental variation in the viscoelastic properties of the ONH, we conducted analyses of variance on each of the material parameters. Since the fit results were not Gaussian, we used a one-way non-parametric ANOVA test (Kruskal-Wallis test) for this purpose, followed by multiple comparison tests using Wilcoxon’s rank sum tests with Bonferroni correction. A significance level of 5% was used for these analyses.

3. Results

3.1. Anatomical region heterogeneity in deformation responses

To assess possible effects of tissue heterogeneity, we analyzed the effect of anatomical region on the mechanical response of the ONH during compression testing, considering compression cycle number and anatomical region as independent variables (Fig. 2). The anatomical region did not show an effect on axial strain (ϵ_axial; p = 0.7978); however, region was a significant factor for lateral strain (ϵ_lateral; p = 0.0091) and apparent Poisson ratio (ν_app; p<0.0001). Specifically, for ϵ_lateral the temporal region had a larger value compared to the nasal region (p<0.05), and for ν_app the temporal region had a larger value compared to both nasal and superior regions, but the inferior region only was larger relative to the nasal region (p<0.05; Fig. 2D–F). As expected, cycle number had a strong effect on axial (p = 0.0002) and lateral (p = 0.0046) strains. However, ν_app was not affected by the cycle number (p = 0.8224), i.e. ν_app was not dependent on the compression level. The p-values for the interaction between anatomical region and cycle number were almost unity for all the analyses, indicating that the anatomical heterogeneity was not affected by cycle number.

Fig. 2.

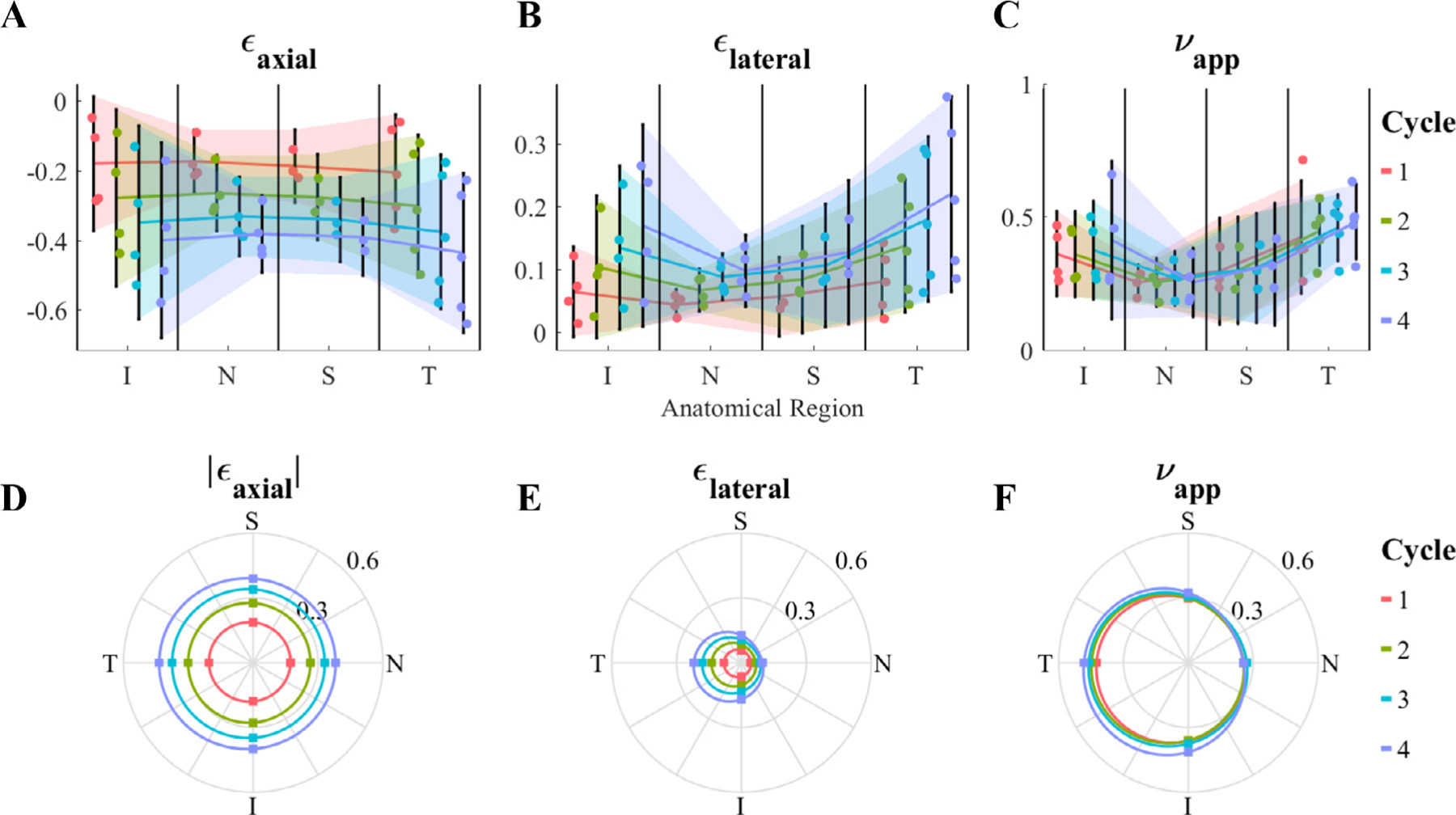
Regional dependence (analysis of variance) of (A and D) axial strain [ϵ_axial], (B and E) lateral strain [ϵ_lateral], and (C and F) apparent Poisson’s ratio [ν_app]. For each parameter, the first row (A-C) shows the individual data points, their means, and 95% confidence intervals (shaded region) for each anatomical region and cycle number, and the second row (D F) illustrates the mean values (dots) in a polar plot matching the anatomical orientations, where 0, 90, 180 and 270° correspond to nasal [N], superior [S], temporal [T], and inferior [I], respectively. Although there was no significant effect of anatomical region on ϵ_axial, both ϵ_lateral and ν_app were affected by the anatomical region, with the temporal and inferior quadrants having larger values compared to the nasal and superior quadrants. The cycle number significantly impacted ϵ_axial and ϵ_lateral; however, it did not affect ν_app. There was no interaction effect between the anatomical region and cycle number, i.e. heterogeneity was not affected by loading level.

3.2. Viscoelastic mechanical properties

The model fits the experimental data very well and captured both the axial and lateral strain behaviors for each of the anatomical regions with c. 75% of the fits passing the fit criteria (Fig. 3; for a detailed illustration of the residual objective function values vs. model parameters see supplementary Figure S1). The best-fit parameter values for the ONH were E = 1.895[1.056, 2.391] kPa (median [min., max.]), ν = 0.142[0.060, 0.312], τ = 213[89, 921] sec, and k = 3.854 × 10⁻¹[3.457 × 10⁻², 9.994 × 10⁻¹] mm⁴/(N.sec) (Fig. 4).

Fig. 3.

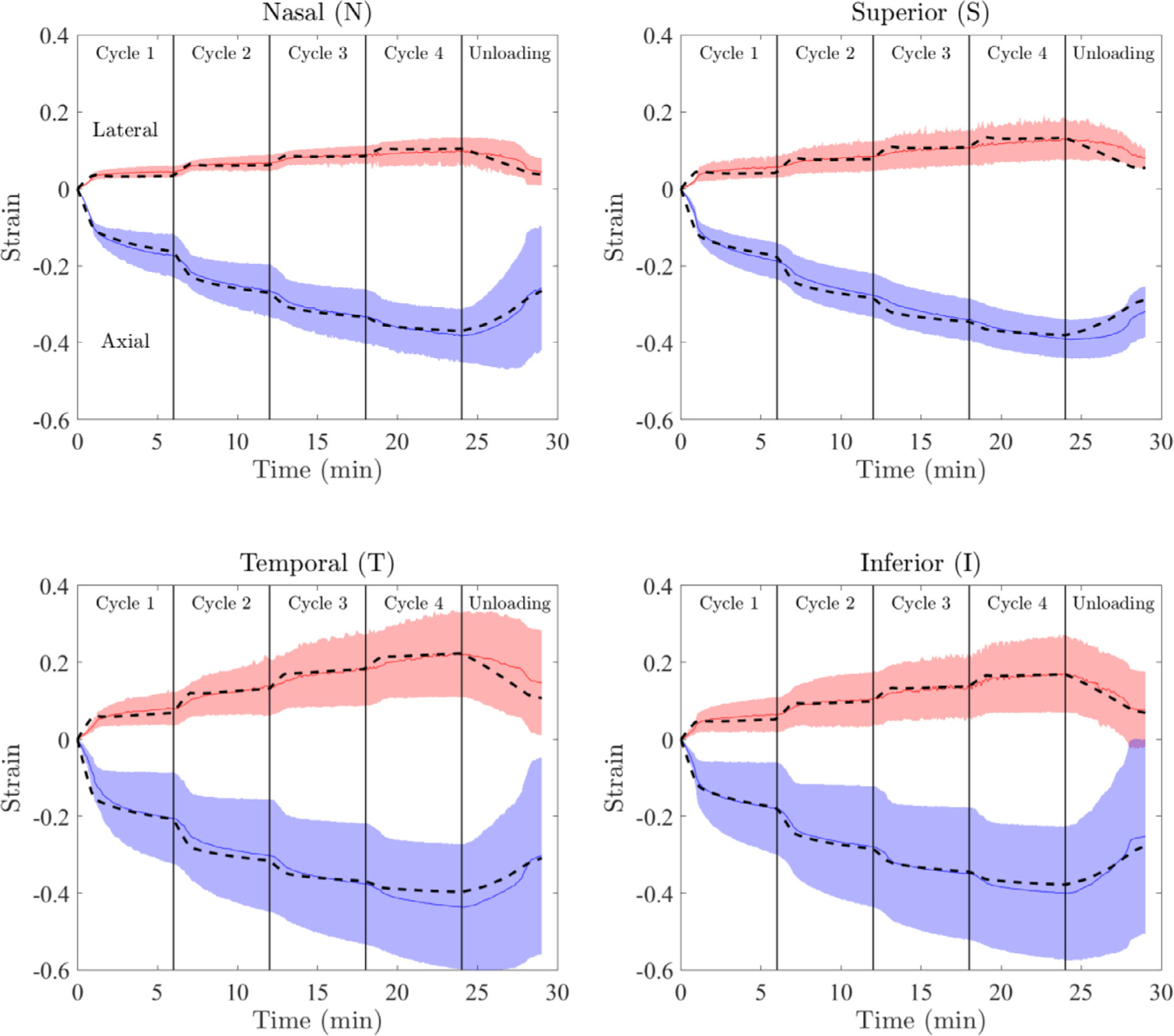
Results of data-fitting for each of the anatomical quadrants. The median and 95% confidence interval of the ex vivo experimental data are shown with solid lines and shading, respectively. Positive strains correspond to the lateral direction, while negative values are axial strains. For each region, the model response generated using the median of accepted fits is shown by the dashed lines. Note the good agreement between experimental (solid lines) and fitted (dashed lines) strains.

Fig. 4.

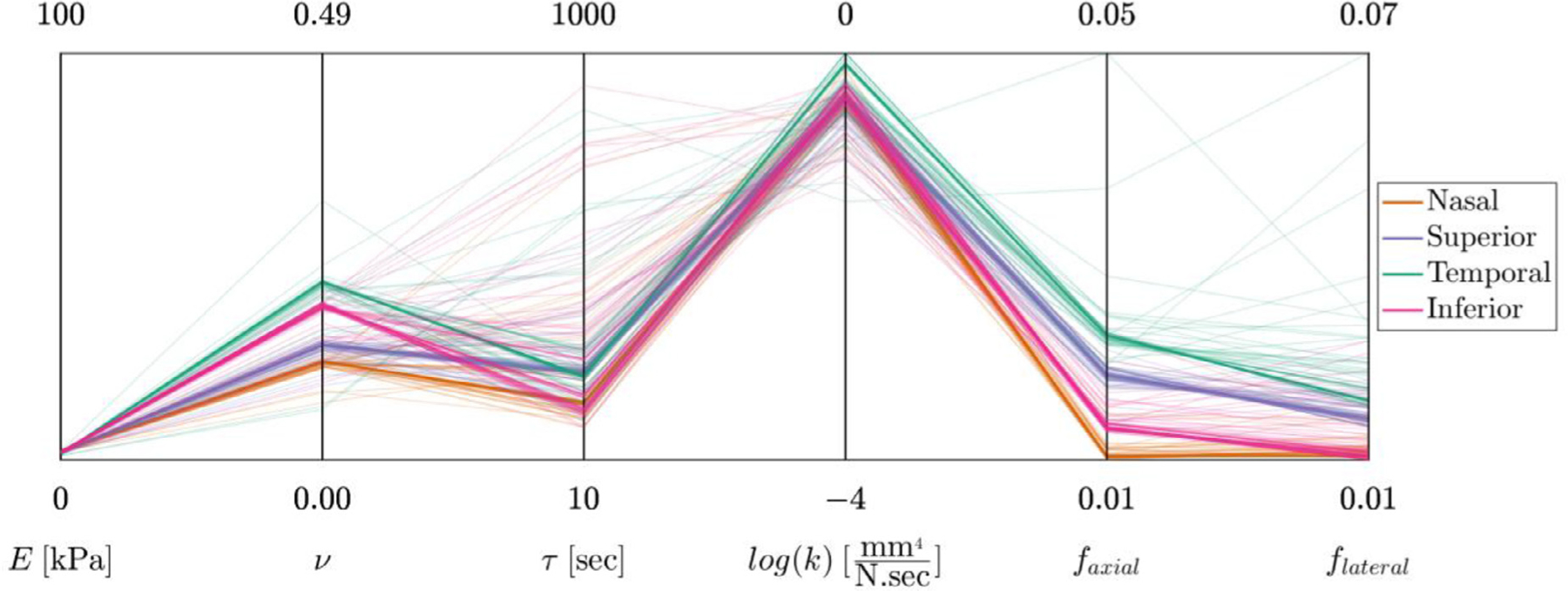
The data-fitting results shown in parallel coordinates format. The four coordinates on the left are the model parameters (E, ν, τ, andk). For each model parameter, the graphed range of the coordinate corresponds to the prescribed range of model parameter values. The two additional coordinates are the RMSE of the fits in the axial and lateral direction (i.e., f_axial and f_lateral).

To assess the regional heterogeneity in the viscoelastic material properties, we plotted the fitted material parameter values and conducted analysis of variance (Fig. 5). For each parameter, the median values had a nearly symmetrical distribution about the nasal-temporal axis, with either the nasal or temporal sides having the maximum/minimum values (Fig. 5). In more detail, the nasal region (N) had the highest value of the Young’s modulus (Fig. 5A and E) compared to the rest of the regions, while the temporal region (T) had the lowest value. (Here and below, when a difference is cited it indicates statistical significance with p<0.05). Conversely, the nasal region had the lowest value of Poisson’s ratio (ν) while the temporal region had the highest value (Fig. 5B&F). The variability was high for the time-constant (τ) with the distributions of the values of the regions being consistently skewed towards the range of 150–250 sec, and with the temporal and superior regions having slightly higher values (Fig. 5C&G). The permeability (k) value was highest in the temporal region (Fig. 5D and H).

Fig. 5.

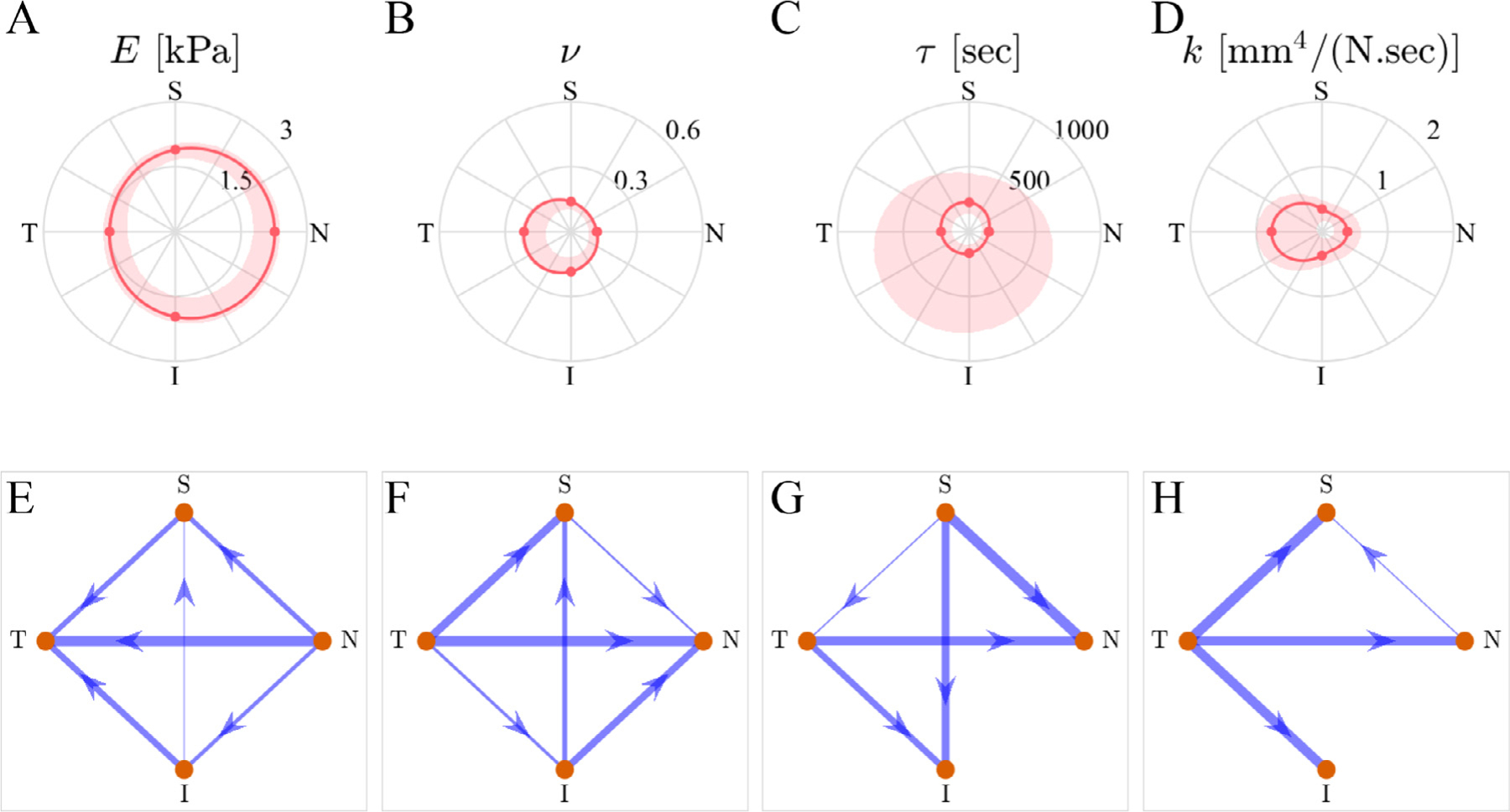
Anatomical distribution of the fit results. The first row shows the spatial distribution of each fitting parameter. The dots correspond to the median values, solid lines are the interpolated medians, and shaded areas are 95% confidence intervals for the acceptable fits (not the inter-sample variance). The second row shows the results of the multiple comparisons between the parameter values for each anatomical region using network graphs, where every arrow connecting two regions (start and destination) indicate that the “start” region has a statistically-significantly larger value compared to the “destination,” and the width of the lines is linearly proportional to the magnitude of the difference. The absence of a line implies that the difference was not statistically significant.”

3.3. Model validation

We used our model to predict the sensitivity of ONH mechanical response to loading rate, specifically comparing model results to the experimental observations of Boazak et al. [10]. They reported an increase in modulus from 2.78 kPa to 4.35 kPa (57% increase) as the compressive loading rate was increased from 5%/min to 40%/min. Our model also predicted an increase in modulus with loading rate, albeit by a smaller amount (5.15 kPa at 5%/min to 5.90 kPa at 40%/min, corresponding to a 14.5% increase).

4. Discussion

This study provides the first detailed evaluation of porcine optic nerve head (ONH) time-dependent biomechanical properties. Our results show that the ONH exhibits viscoelastic behavior, which can be quantitatively explained based on a combination of fluid-dependent and fluid-independent viscoelasticity. The former mechanism is a function of tissue porosity, while the latter is due to the biopolymeric structure of the ONH. Such a dual mechanism is common among other soft tissues exhibiting viscoelastic behavior [7,20].

In comparison to the previous literature, we showed that our model’s prediction of the dynamic modulus c. 5 kPa can be compared to previous measurements by Boazak et al. on the porcine ONH (c. 3 kPa [10]) and another study on the human lamina cribrosa (17.2 kPa [39]). Interestingly, our model also replicated the trend of compressive modulus increasing with increased loading, as previously reported [10], we were able to replicate the trend of an increased compressive modulus with a higher loading rate. However, the model’s predicted percentage increase in modulus for the faster vs. slower loading rate was smaller than seen experimentally (14.5% in model predictions vs. 57% in experiments). Some of this difference in magnitude could possibly be due to biological variability between animals; however, it is also not clear how the assumption of incompressibility used by Boazak et al. could have affected these differences, since our analyses showed that the ONH is compressible. Specifically, we found a fitted effective Poisson’s ratio (the neoHookean tissue Poisson’s ratio) of 0.142 [0.060, 0.312], and the apparent Poisson’s ratio ν_app was larger than ν (Fig. 3B). This difference further supports the possibility of fluid exudation upon mechanical loading, and illustrates the role of the fluid transport on the mechanical response of the tissue

Compressibility is only one determinant of tissue’s fluid-dependent viscoelasticity, with the other principal factor being the hydraulic permeability, which controls the transient pressure build-up during tissue deformation. A small hydraulic permeability translates into larger pressurization [40]. In this study, we report a porcine ONH hydraulic permeability of k = 3.854 × 10⁻¹[3.457 × 10⁻², 9.994 × 10⁻¹] mm⁴/(N.sec), which is the first account of ONH hydraulic permeability we are aware of. Although not the same tissue as ONH, the porcine peripapillary sclera, which is anatomically adjacent, has a somewhat smaller permeability (k = 0.86 × 10⁻² mm⁴/[N.sec]), and a stiffness of 10 kPa, which is larger than the stiffness we found for the ONH [15]. The lower permeability and higher stiffness are consistent with the denser fibrous structure of the peripapillary sclera compared to the ONH [28,29].

The viscoelastic properties, especially the time constant (characteristic time) and the dynamic loading (e.g., rate of mechanical loading) are two important factors in tissue remodeling through controlling cellular mechanotransduction pathways [30]. Our results indicate that the time constant of the solid matrix in the porcine ONH is in the range of 200 sec. Further, the median permeability of the ONH reported here corresponds to a biphasic characteristic time (τ_bp = a²/(H_ak), where a is the sample radius, H_a is its aggregate modulus, and k is the hydraulic permeability [31]) of ~5.4 min for a sample with diameter of 1 mm (as tested in this study) and ~87 min for a sample with diameter of 4 mm, which is close to a full-size ONH (Fig. 1D). It is likely that due to the effect of the surrounding tissue in vivo the fluid flow would be slower than the predictions based on unconfined compression tests; nonetheless, our observations indicate that the ONH’s mechanical response is likely to be sensitive to dynamic loading with fluctuation times on the order of minutes to hours. This is an important observation because it indicates that ONH’s viscoelastic response is within the range of IOP dynamic fluctuations (from seconds [blinking] [4] to hours [diurnal/nocturnal] [5, 32]). These fluctuations may contribute to ONH remodeling by ONH cells, such as astrocytes and lamina cribrosa cells [33,34]. Based on the time constants of the ONH it is likely that slower fluctuations (e.g., diurnal/nocturnal) are more relevant to remodeling in glaucoma than fast fluctuations, such as due to blinks, saccades and the ocular pulse; however, the IOP fluctuations occur at rates as high as 10,000 cycles per waking hour, which can also impact the effect of the slow and fast fluctuations [6]. Further studies, such as 3D cell culturing and controlled mechanical loading of ONH cells is required to confirm this hypothesis.

Another interesting observation was the ONH’s heterogeneity, which can have important implications for understanding glaucoma pathophysiology. Our observations indicated that the nasal region had a higher stiffness and lower permeability (Fig. 5), which was consistent with the observed axial strain responses, where the nasal region samples deformed less (Fig. 2). Further, the nasal-temporal axis was an approximate axis of material property symmetry for the porcine ONH. Interestingly, in human ONH, a similar symmetry is observed where the region along the nasal-temporal axis has a denser collagenous structure compared to the rest of the ONH, strongly hinting at a similar trend in human ONH mechanical properties [35], which can be correlated with the patterns of the progression of glaucoma [36]. We note that although the symmetry in heterogeneity is consistent between porcine and human samples, it is unclear whether the relative differences in mechanical properties between the regions, especially between the nasal and temporal regions, are consistent between human and pigs. An interesting next step would be to use the framework established in this study to assess the human ONH’s mechanical properties. Such data could help further evaluate the fidelity of current animal models of ONH biomechanics, specifically by providing comparative information in addition to what is already known about posterior pole fibrous architecture [14].

The loads imposed at each cycle of the mechanical test were motivated by physiological pressures, corresponding to approximately 5, 10, 15, and 20 mmHg acting on a circular surface area with diameter of 1 mm. However, the resulting axial deformations were somewhat higher than those measured in situ in the porcine eye, which are c. 13% at 30 mmHg relative to 6 mmHg [37]. It should be noted that the tissue is likely to be under residual stresses in situ, thus having a compressed reference state compared to the ex vivo conditions and resulting in smaller in vivo strains. Further, the lack of peripapillary sclera tissue in our tests and potential post mortem tissue softening [10] can cause these differences (Fig. 1F). Although the strains and the unconfined compression boundary conditions do not exactly replicate the in vivo situation, they were necessary simplifications to enable direct experimental evaluation of the viscoelastic mechanical properties of the ONH at each anatomical quadrant of the ONH.

Our study was subject to some limitations. For example, we modeled the ONH as an isotropic material with deformation-independent permeability. This assumption is justifiable based on the lack of dependence of apparent Poisson’s ratio on compression level (Fig. 2C); however, a strain-dependent permeability could improve the physiological relevance of the mathematical models. In addition, since we calculated tissue properties by data fitting, we attempted to model the ONH’s biomechanical response using the fewest possible number of parameters. Alternative models with a higher number of parameters, such as multiple time constants and reduced relaxation functions [38], could potentially improve the fidelity of the fits. Further, we used large samples from each quadrant of the ONH (Fig. 1D and E); this approach provides an average from each region, yet falls short of the spatial resolution required to appreciate the complex and fine laminar structure of the ONH. A potential future direction is to combine microstructural imaging, biochemical composition analyses, and mechanical modeling to better characterize regional differences in ONH biomechanics. Additionally, atomic force microscopy has been shown to be useful to assess the elastic properties of the ONH and lamina cribrosa [39], and a potential future approach for assessing the viscoelastic mechanical response and its physical mechanisms in the ONH is to use high-bandwidth AFM-based rheology on samples of various sizes to provide higher spatial resolution and to more directly investigate the fluid-dependent and -independent mechanisms of viscoelasticity in the ONH [7,8]. Further, the ONH is a complex tissue with both neural and connective tissue components, not differentiated in this model. In future, one could consider modeling these tissues separately to understand their individual mechanical behaviors in greater detail.

In conclusion, we evaluated ONH mechanical behavior using in vitro micromechanical testing and continuum mechanics modeling. We showed that the ONH’s viscoelastic mechanical response can be described by a combination of fluid-dependent and fluid-independent viscoelastic mechanisms. We also determined the viscoelastic mechanical properties of the porcine ONH for each of the four anatomical quadrants of the ONH. The material parameter values provided in this study can serve as benchmark values for future studies to replicate native tissue environments in ex vivo studies, such as using 3D cell cultures for studying mechanobiology and tissue engineering in glaucoma.

Statement of significance.

Optic nerve head (ONH) biomechanics is an important aspect of the pathogenesis of glaucoma, the leading cause of irreversible blindness. The ONH experiences time-varying loads, yet the viscoelastic behavior of this tissue has not been characterized. Here, we measure the time-dependent response of the ONH in porcine eyes and use mechanical modeling to provide time-dependent mechanical properties of the ONH. This information allows us to identify time-varying stimuli in vivo which have timescales matching the characteristic response times of the ONH, and can also be used to design and fabricate ex vivo 3D cultures to study glaucoma pathophysiology in a physiologically relevant environment, enabling the discovery of new generations of glaucoma medications focusing on neuroprotection.