Biomechanical consequences of compromised elastic fiber integrity and matrix cross-linking on abdominal aortic aneurysmal enlargement

Abstract

Abdominal aortic aneurysms (AAAs) are characterized histopathologically by compromised elastic fiber integrity, lost smooth muscle cells or their function, and remodeled collagen. We used a recently introduced mouse model of AAAs that combines enzymatic degradation of elastic fibers and blocking of lysyl oxidase, and thus matrix cross-linking, to study progressive dilatation of the infrarenal abdominal aorta, including development of intraluminal thrombus. We quantified changes in biomaterial properties and biomechanical functionality within the aneurysmal segment as a function of time of enlargement and degree of thrombosis. Towards this end, we combined multi-modality imaging with state-of-the art biomechanical testing and histology to quantify regional heterogeneities for the first time and we used a computational model of arterial growth and remodeling to test multiple hypotheses, suggested by the data, regarding the degree of lost elastin, accumulation of glycosaminoglycans, and rates of collagen turnover. We found that standard histopathological findings can be misleading, while combining advanced experimental and computational methods revealed that glycosaminoglycan accumulation is pathologic, not adaptive, and that heightened collagen deposition is ineffective if not cross-linked. In conclusion, loss of elastic fiber integrity can be a strong initiator of aortic aneurysms, but it is the rate and effectiveness of fibrillar collagen remodeling that dictates enlargement.

1. Introduction

Abdominal aortic aneurysms (AAAs) are defined by 50% or greater dilatations of the lumen of the infrarenal aorta. They are susceptible to rupture and thus are responsible for significant morbidity and mortality [1–3]. Notwithstanding their complex etiology, most AAAs are characterized histopathologically by compromised elastic fiber integrity, lost smooth muscle cells or their function, and remodeled collagen. Additionally, larger lesions often contain an intraluminal thrombus (ILT) that appears to have diverse biochemical and biomechanical effects on lesion enlargement and stability [4–6]. Much has been learned about the biochemomechanics of these lesions from data that are available clinically, mainly from in vivo imaging, as well as from detailed histological examinations and limited biomechanical testing following open surgery or death [7, 8]. Nevertheless, animal models provide critical insight into this disease, especially its progression as revealed by longitudinal studies that include tissue harvest for biomechanical assessment and histology. Among the many animal models considered, rodents have been favored for multiple reasons [9]. A particularly important advance was elastase infusion of the infrarenal abdominal aorta in the rat [10]; resulting lesions exhibit the aforementioned histopathological features, often including ILT. Yet, mouse models engender additional advantages, particularly given the myriad antibodies available for biological assays and the ease of genetic modification [11]. In most cases, however, elastase-induced lesions in mice tend not to progress to diameters sufficient to enable formation of ILT.

A second important advance in mouse models of AAAs was combination of elastase exposure with chronic administration of β-aminopropionitrile (BAPN), an inhibitor of lysyl oxidase and thus cross-linking of newly deposited elastin and collagen. Associated lesions enlarge significantly more than those following elastase exposure alone and often contain ILT [12], thus better mimicking the clinical condition since over 80% of human lesions contain ILT. We recently contrasted the time-course of lesion enlargement between elastase-only and elastase + BAPN in adult mice [13]. High-frequency ultrasound confirmed marked initial dilatations in both groups, but continual enlargement over 4 weeks in the elastase + BAPN group alone. The data further revealed marked reductions in aortic distensibility with lesion enlargement, yet the complex geometries necessitated additional experimental methods to assess the expected regional variations in biomaterial properties. Here, we combine a panoramic digital image correlation (pDIC) method with optical coherence tomography (OCT) to quantify in vitro the regional biaxial biomechanical properties of elastase + BAPN lesions for two durations of study, 4 and 8 weeks. We also use multiphoton microscopy and standard histology to correlate observed changes in properties with the underlying microstructure. Finally, we use a computational model to explore parametrically the longitudinal effects of lost elastic fiber integrity and collagen cross-linking, with special attention to rates of matrix turnover.

2. Methods

2.1. Animals

Following our prior study [13], sixteen 10-week old male C57BL/6J mice were anesthetized and porcine pancreatic elastase (10 mg/ml) was applied for 5 minutes to the adventitial surface of an approximately 4-mm long segment of the infrarenal aorta during an open surgical procedure. Beginning two days before surgery and continuing through the length of the study, the mice were given 0.2% BAPN in the drinking water ad libitum. At the appropriate end-point following surgery, 4 or 8 weeks, blood pressures were measured using a CODA tail-cuff system and the mice were imaged with high frequency ultrasound (Vevo 2100, FUJIFILM VisualSonics) to collect 3D datasets. The mice were then euthanized and the infrarenal aorta was excised by blunt dissection and prepared for in vitro biomechanical assessment. AAAs from two of the sixteen elastase + BAPN mice were so severe that they could not be subjected to the full battery of in vitro tests, and thus were excluded. The infrarenal aortas from six age- and sex-matched unperturbed C57BL/6J mice served as true controls. All animal procedures were approved by the Purdue University Animal Care and Use Committee.

2.2. Standard biaxial testing and analysis

AAAs from fourteen elastase + BAPN exposed mice were studied in vitro and results were compared with those from six untreated control aortas. The overall workflow (Fig. S1) began with standard biaxial testing [14]. Briefly, the excised aorta was cannulated on custom paired glass cannulas, placed within a Hank’s buffered salt solution (HBSS) at room temperature to ensure passive behaviors, and connected to a custom computer-controlled system to perform cyclic pressure-diameter tests at three fixed axial lengths (the estimated in vivo value and ±5% of this value) and cyclic axial force-length tests at four fixed pressures (10, 60, 100 and 140 mmHg). Note that the in vivo value of axial stretch is defined as that value at which the transducer-measured axial force does not change appreciably during cyclic pressurization, which appears to be energetically preferred [14]. A four-fiber family constitutive model was then used to fit simultaneously the unloading data collected during the last cycle of each of the seven testing protocols; the best-fit values of the model parameters were determined using nonlinear regression (Levenberg-Marquardt). This parameterization allowed biaxial wall stress and material stiffness to be computed from the associated stored energy function using validated methods (including the theory of small deformations superimposed on large to obtain in vivo relevant values of stiffness [15]), thus quantifying the bulk passive material behavior.

2.3. Optical coherence tomography (OCT)

Next, the aorta was re-cannulated on a custom blunt-ended triple-needle assembly to allow both pressurization and micrometer-controlled axial extension from one end [16, 17]. This needle assembly consisted of a large proximal blunt-ended needle through which was placed a small blunt-ended needle that was secured at its distal end within a medium-sized blunt-ended needle stub; the aortic sample was secured with ligatures on the proximal (large) and distal (medium) needles, thus allowing overall control of axial length by moving the inner needle within the large one. In this way, the aorta was set at a reference configuration defined by its specific in vivo axial stretch (determined from the standard biaxial testing) and a common pressure of 80 mmHg, then scanned with a commercial OCT system having an in-plane resolution of ~7 μm (Thorlabs, Inc.); 100 equally distributed cross-sectional images provided through-the-wall thickness information along the length of the specimen. To compute a complete map of the local thickness, each cross-sectional image was parameterized using polar coordinates and a locally weighted quadratic regression was used to automatically identify the inner and outer contours of the vessel wall [56]. Due to the size of the aneurysms, four rotational views (about the central axes of the sample) were required to obtain a full 3D reconstruction using an iterative multi-step registration scheme in 3DSlicer.

2.4. Multiphoton microscopy and image processing

Two-photon microscopy was then performed on the cannulated aortas (using the same triple needle assembly), again while held at the sample-specific in vivo stretch but an intraluminal pressure of 120 mmHg. The microscope (LaVision Biotec TriMScope) was powered by a Titanium-Sapphire Laser (Chameleon Vision II, Coherent) tuned at 840 nm and equipped with a 20X water immersion objective lens (N.A. 0.95). Signals from three major components of the aortic wall were acquired simultaneously: the second harmonic generation (SHG) signal arising from fibrillar collagens (390–425 nm), two-photon excited fluorescence from elastin (500–550 nm), and a fluorescent signal of cell nuclei (above 550 nm). Three-dimensional (3D) images were acquired with an in-plane (axial-circumferential) field of view of 500 μm x 500 μm at a consistent anatomical location. Numerical imaging resolution was 0.48 μm/pixel, while the out-of-plane (radial axis) step size was 1 μm/pixel. Each 3D image was acquired and processed as previously described [18]. Briefly, images of a portion of the aortic wall were numerically unfolded with respect to its pseudo-cylindrical geometry by transforming circumferential-radial slices from Cartesian to polar coordinates. The processed 3D images were analyzed to yield microstructural metrics for intramural constituents while wall thickness was defined by consistently averaging and thresholding intensity profiles of multiple subvolumes of each 3D transformed image in the radial direction. Collagen fiber bundle characterization focused on in-plane parameters: straightness, bundle width, primary orientation, and alignment. Straightness was computed as the ratio of end-to-end to total fiber length for 25 fibers, automatically selected at fixed depths for each image; bundle width (transversal section in the axial-circumferential plane) was measured directly; the in-plane primary orientation and alignment were estimated via a distribution of orientations for each circumferential-axial section using a 2D structure tensor analysis, namely OrientationJ plug-in for ImageJ. This distribution was averaged along the radial direction and normalized. Distributions were parameterized with a Von Mises circular probability density function F(θμ, κ) = exp(κ cos (θ−μ))/2πI₀(κ), where μ is the primary orientation, I₀ a modified Bessel function, and κ the alignment parameter, a measure of concentration that quantifies fiber alignment at the tissue level. Cell density was calculated as the number of cells per unit volume by counting the number of nuclei within defined subvolumes of the 3D image and normalizing by the appropriate sample-specific thickness. Three cell groups were considered based on characteristic shapes of their nuclei and radial location: endothelial (monolayer on intima), smooth muscle (SMCs, within the media), and other cells within the adventitia (likely fibroblasts and macrophages, among others). A semi-automatic algorithm selected multiple subunits of volume (100 μm x 100 μm x local layer-specific thickness, n = 25) for each 3D image, with conversion to binary form by filtering and thresholding. Luminal cell density was computed as number of cells per surface area and normalized by 0.01 mm²; medial and adventitial cell numbers were normalized by 0.001 mm³, each to allow consistent comparisons.

2.5. Panoramic digital image correlation (pDIC)

Our pDIC system and methods of data analysis have been described previously [19], and so too their utility in quantifying full-field deformations and material properties in murine arteries [17, 20]. Briefly, following biaxial testing, OCT scanning, and multiphoton imaging, the adventitia was stained with Evans blue dye and black India ink, then gently air-brushed with white India ink to form a unique white speckle pattern on a black background. The sample, still mounted on the triple-needle assembly, was then placed within a custom 45 degree-angle conical mirror, submerged within an HBSS-filled bath at room temperature, and connected to a pressure-controlled line. The reflection of the speckle pattern on the mirrored surface was captured by a vertically located digital camera (DALSA Falcon 4M30) from eight rotationally symmetric views. Data were collected at 42 quasi-static configurations: 14 pressures (10–140 mmHg, in 10 mmHg increments) and 3 axial stretches (as in standard biaxial testing), with 336 images acquired. The reference configuration was defined by a static pressure of 80 mmHg and specimen-specific in vivo axial stretch, consistent with that during OCT measurement. Custom MATLAB scripts were used to unwrap the pDIC images, such that the polar angle and radial coordinates in the acquired image were mapped onto a rectangular grid. Serial correlations were then performed between pairs of unwrapped images over all deformed configurations to reconstruct the 3D surface geometry at each deformed configuration as well as to compute full-field surface deformations. Once completed, the reference configuration geometry reconstructed using pDIC and the OCT-derived outer contours were co-registered via an optimal 3D rigid transformation by iteratively minimizing the sum of the squared nearest-neighbor distances between the pDIC and OCT points; the resulting co-registration was then used to map local thicknesses computed from OCT onto the pDIC-derived reconstruction of the reference configuration.

2.6. Inverse parameter estimation

Applied luminal pressures, axial stretch-associated axial forces, and measured full-field strains were used to determine best-fit values of material parameters in a nonlinear constitutive relation [20], thus allowing multiple mechanical metrics to be computed regionally, including biaxial wall stress, material stiffness, and elastic energy storage. Specifically, the surface of each pDIC-derived configuration was meshed with 40 four-noded circumferential patches (denoted Θ_m, m ∈ [1, 40]) x 25 axial (denoted Z_n, n ∈ [1, 25]), with a cylindrical coordinate system defined over Θ ∈ [−π, π] and Z ∈ [O, L] coordinates (where L is the reference length of the sample). Using the pDIC-derived displacement fields, Green strains were calculated at each Gauss point (using FEBio, an open source finite element package) for each surface patch assuming (for simplicity) an incompressible neo-Hookean strain energy function. Then, the material behavior at each Gauss point was modeled with a microstructurally-motivated strain energy function, accounting for the primary structural constituents of the wall: elastic fibers, SMCs, and multiple families of collagen fibers (see [16, 21]). The principle of virtual power was enforced at each Gauss point to achieve inverse characterization within each Θ_mZ_n element. The unknown material parameters were iteratively updated using a derivative-free genetic algorithm followed by a gradient-based local optimizer in order to maximize the log-likelihood of observing the experimentally measured pressures and axial loads [56]. Unconstrained optimization was performed with respect to logarithmically transformed values for all strictly non-negative parameters. Once completed, the final set of the identified parameters at each element was used to compute full-field distributions of various mechanical metrics. The relative uncertainties, quantified by geometric standard deviation (Fig. S16), in the material parameters as well as subsequent mechanical metrics were estimated from the Hessian of the log-likelihood function and using established uncertainty propagation techniques [56]. Note that the upper and lower 10% of the sample were excluded from the analysis to eliminate edge effects due to cannulation and suture ligation.

2.7. Histology

Following the multi-step testing, vessels were fixed overnight in a 10% neutral buffered formalin solution, then stored in 70% ethanol at 4 °C. Samples were embedded in paraffin and serially sectioned at 5 μm at three locations (due to the unique and heterogenous geometry and structure; Fig. S2). Stains included picrosirius red for collagen fibers and Movat’s pentachrome for elastin in black, aggregating glycosaminoglycans/proteoglycans (GAGs/PGs) in blue, and fibrin in pink/red. High-resolution images were acquired using an Olympus BX/51 microscope at 20X magnification. Custom MATLAB scripts were used to measure constituent-specific area fractions in each cross-section [20]. Similarly, for local comparison with mechanical properties, representative histological images were divided into 40 circumferential sections, thus allowing local constituent-specific area fractions to be calculated within each section. The thickness distribution of the histological image was then estimated as the sum of a pair of Eulerian solutions over the histological domain [16]. The 100 OCT cross-sections and histology-derived thicknesses were then normalized (to account for histological shrinkage and different loading conditions) and correlated at each position along the reconstructed surface to identify the optimal registration for the two modalities. Finally, using the maximal correlation coefficient, each histological section was spatially aligned with the reconstructed vessel geometry so that locally identified mechanical properties could be correlated with the different local constituent area fraction.

2.8. Statistics

Due to deviations from normality (Kolmogorov-Smirnov test), we used the non-parametric Kruskal Wallis test followed by Dunn’s post-hoc test for multiple comparisons to compare results across study groups. Correlations between the various mechanical metrics and histological area fractions were assessed using the non-parametric Spearman correlation coefficient, r. For all reported comparisons, a value of p < 0.05 was considered significant.

2.9. Computational simulations

Over the past twenty years, we have refined a constrained mixture model of arterial growth and remodeling [22]. Briefly, this model accounts for individual natural (stress-free) configurations, material properties, and rates of turnover of structurally significant constituents. Here, we extended a recent implementation [23] to include the presence of aggregating GAGs/PGs. Among the key equations, rates of production and removal of constituent α= 1, 2, …, n within layer Γ = M, A (media or adventitia) determine the apparent mass density per unit reference volume at the current time s > 0, with s = 0 defining the onset of insult under study (elastase-only, BAPN-only, or elastase + BAPN) through

$${\rho }_{\mathrm{\Gamma }\text{R}}^{\alpha }\left(S\right)={\rho }_{\mathrm{\Gamma }\text{R}}^{\alpha }\left(0\right)Q_{\mathrm{\Gamma }}^{\alpha }\left(S\right)+{\int }_0^s{m}_{\mathrm{\Gamma }\text{R}}^{\alpha }(\tau )q_{\mathrm{\Gamma }}^{\alpha }(s,\tau )\mathrm{d}\tau$$ (1)

where $m_{\mathrm{\Gamma }\text{R}}^{\alpha }(\tau )>0$ (with τ ∈ [0, s] the time at which constituent α is deposited) is the rate of referential mass density production and $q_{\mathrm{\Gamma }}^{\alpha }(s,\tau )\in [0,1]$ (with $Q_{\mathrm{\Gamma }}^{\alpha }(s)=q_{\mathrm{\Gamma }}^{\alpha }(s,0)$) is a first-order type decay that describes constituent removal due to either its normal half-life or accelerated loss in disease. The referential mass density for each layer is ${\rho }_{\mathrm{\Gamma }\text{R}}=\sum {\rho }_{\mathrm{\Gamma }\text{R}}^{\alpha }$ (for elastic fibers, SMCs, families of collagen fibers, and GAGs/PGs in the media, and minimal elastic fibers and families of collagen fibers in the adventitia), where ρ_ΓR = J_Γρ, with J_Γ = det F_Γ > 0 the layer-specific volume ratio, computed from the deformation gradient F_Γ from reference to current (in vivo) configurations for the mixture; ρ is the true mass density, assumed constant throughout. Similarly, the constituent-specific strain energy per unit reference volume is

$$\begin{gathered} W_{\mathrm{\Gamma }\text{R}}^{\alpha }(s)=\frac{{\rho }_{\mathrm{\Gamma }\text{R}}^{\alpha }(0)Q_{\mathrm{\Gamma }}^{\alpha }(s)}{\rho }{\widehat{W}}^{\alpha }\left({\mathbf{C}}_{{\mathrm{\Gamma }}_{\text{n}(0)}}^{\alpha }(s)\right) \\ +\frac{1}{\rho }{\int }_0^s{m}_{\mathrm{\Gamma }\text{R}}^{\alpha }(\tau )q_{\mathrm{\Gamma }}^{\alpha }(s,\tau ){\widehat{W}}^{\alpha }\left({\mathbf{C}}_{\mathrm{\Gamma }\text{n}(\tau )}^{\alpha }(s)\right)\text{d}\tau \end{gathered}$$ (2)

which admits a rule-of-mixtures relation $W_{\mathrm{\Gamma }\text{R}}=\sum W_{\mathrm{\Gamma }\text{R}}^{\alpha }$. Here, ${\widehat{W}}^{\alpha }\left({\mathbf{C}}_{{\mathrm{\Gamma }}_{\text{n}}(\tau )}^{\alpha }(s)\right)>0$, with ${\mathbf{C}}_{\mathrm{\Gamma }\text{n}(\tau )}^{\alpha }(s)={\mathbf{F}}_{\mathrm{\Gamma }\text{n}(\tau )}^{\alpha \text{T}}(s){\mathbf{F}}_{\mathrm{\Gamma }\text{n}(\tau )}^{\alpha }(s)$, is the stored elastic energy of constituent α that depends on the deformation gradient ${\mathbf{F}}_{{\mathrm{\Gamma }}^{(\tau )}}^{\alpha }(s)={\mathbf{F}}_{\mathrm{\Gamma }}(s){\mathbf{F}}_{\mathrm{\Gamma }}^{-1}(\tau ){\mathbf{G}}_{\mathrm{\Gamma }}^{\alpha }(\tau )$ experienced by that constituent at current time s relative to its potentially evolving natural configuration n(τ), with ${\mathbf{G}}_{\mathrm{\Gamma }}^{\alpha }(\tau )$ the pre-stretch at the time of deposition τ ∈ [ 0, s]. Let the stored energy function for the elastin-dominated matrix (α= e, with τ ≡ 0) and swollen GAGs/PGs (α= GAG) have a neo-Hookean form

$${\widehat{W}}^{\alpha }\left({\mathbf{C}}_{\mathrm{\Gamma }\text{n}(\tau )}^{\alpha }(s)\right)=\frac{c^{\alpha }}{2}\left({\mathbf{C}}_{\mathrm{\Gamma }\text{n}(\tau )}^{\alpha }(s):\mathbf{I}-3\right)$$ (3)

where c^α > 0 are respective shear moduli. Similarly, for collagen fibers (α = c, axially and diagonally oriented in the media as well as circumferentially, axially, and diagonally oriented in the adventitia) and a circumferentially oriented composite of medial collagen fibers and passive SMCs (α = m), consider a Fung-type exponential form

$${\widehat{W}}^{\alpha }\left({\mathbf{C}}_{\mathrm{\Gamma }\text{n}(\tau )}^{\alpha }(s)\right)=\frac{c_1^{\alpha }}{4c_2^{\alpha }}\left(\exp \left(c_2^{\alpha }{\left({\left({\lambda }_{\mathrm{\Gamma }n(\tau )}^{\alpha }(s)\right)}^2-1\right)}^2\right)-1\right)$$ (4)

where $c_1^{\alpha }>0$ and $c_2^{\alpha }>0$ are material parameters and ${\lambda }_{\mathrm{\Gamma }\text{n}(\tau )}^{\alpha }(s)$ is a corresponding stretch, which together constitute layer-specific “four-fiber family” models. Also let the rate of production of mass for SMCs, collagen fibers, and GAGs/PGs be

$$m_{\mathrm{\Gamma }\text{R}}^{\alpha }(\tau )=k_{\mathrm{\Gamma }\text{N}}^{\alpha }(\tau ){\rho }_{\mathrm{\Gamma }\text{R}}^{\alpha }(\tau ){\text{Y}}_{\mathrm{\Gamma }}^{\alpha }(\tau )$$ (5)

which are modulated by mechanobiological stimulus functions ${\text{Y}}_{\mathrm{\Gamma }}^{\alpha }$. Finally, $k_{\mathrm{\Gamma }\text{N}}^{\alpha }$ are evolving rate parameters that define the first-order kinetic decay

$$q_{\mathrm{\Gamma }}^{\alpha }(s,\tau )=\exp \left(-{\int }_{\tau }^s{k}_{\mathrm{\Gamma }\text{N}}^{\alpha }(t)\text{d}t\right).$$ (6)

For SMCs and collagen fibers, we let ${\text{Y}}_{\mathrm{\Gamma }}^{\alpha }=1+{\text{K}}_{\mathrm{\Gamma }\sigma }^{\alpha }\mathrm{\Delta }\sigma -{\text{K}}_{\mathrm{\Gamma }{\tau }_w}^{\alpha }\mathrm{\Delta }{\tau }_W$ to include deviations in mean pressure- and axial force-induced intramural stress Δσ = (σ – σ_o)σ_o and flow-induced wall shear stress Δτ_w = (τ_w − τ_wo)/τ_wo from homeostatic values (σ_o and τ_wo are homeostatic scalar metrics), with ${\text{K}}_{\mathrm{\Gamma }\sigma }^{\alpha }>0$ and ${\text{K}}_{\mathrm{\Gamma }{\tau }_w}^{\alpha }>0$ constituent- and layer-specific gain-type parameters. Similarly, let $k_{\mathrm{\Gamma }\text{N}}^{\alpha }=k_{\mathrm{\Gamma }o}^{\alpha }\left(1+\omega {(\mathrm{\Delta }\sigma )}^2\right)$ increase via (squared) deviations in intramural stress, with $k_{\mathrm{\Gamma }o}^{\alpha }$ baseline rate parameters and the gain ω = 1 herein. Mechanobiological stimuli for GAG/PG production remain unknown, thus we modeled their accumulation via a decreased removal/compensatory production process, with an energy-mediated decrease (cf. [24]) in the associated rate parameter in Eq. (6)

$$k_{\mathrm{\Gamma }\text{N}}^{GAG}(\tau )=k_{{\mathrm{\Gamma }}_o}^{GAG}{v}_{\mathrm{\Gamma }k}^{GAG}(\tau )=k_{{\mathrm{\Gamma }}_o}^{GAG}\left(1+K_{\mathrm{\Gamma }W}^{GAG}\mathrm{\Delta }W(\tau )\right)$$ (7)

where ΔW = (W − W_o)/W_o, with W the mean intramural stored energy per unit current volume and ${\text{K}}_{\mathrm{\Gamma }W}^{\text{GAG}}>0$ an associated gain. This decreased removal is hypothesized to be compensated, with a certain delay, via a rate of mass production per unit mass of GAGs/PGs (from Eq. (5))

$$\frac{m_{\mathrm{\Gamma }\text{R}}^{GAG}(\tau )}{{\rho }_{\mathrm{\Gamma }\text{R}}^{GAG}(\tau )}=k_{\mathrm{\Gamma }\text{N}}^{GAG}(\tau ){\text{Y}}_{\mathrm{\Gamma }}^{GAG}(\tau )=k_{\mathrm{\Gamma }o}^{GAG}{v}_{\mathrm{\Gamma }m}^{GAG}(\tau )$$ (8)

which, by introducing the modified stimulus function for mass production $v_{\mathrm{\Gamma }m}^{GAG}=v_{\mathrm{\Gamma }k}^{GAG}{\text{Y}}_{\mathrm{\Gamma }}^{GAG}$ (compare Eqs. (7) and (8)), conveniently allows us to determine $v_{\mathrm{\Gamma }m}^{GAG}$ at current time s (while advancing the computations) through the $v_{\mathrm{\Gamma }k}^{GAG}$-driven relaxation equation

$$\frac{d{v}_{\mathrm{\Gamma }m}^{GAG}(S)}{ds}=-\frac{1}{T^{GAG}}\left(v_{\mathrm{\Gamma }m}^{GAG}(s)-v_{\mathrm{\Gamma }k}^{GAG}(s)\right),$$ (9)

with T^GAG a characteristic time for the compensatory response. Note that for a (hypothetically) fully compensated production relative to removal, $v_{\mathrm{\Gamma }m}^{GAG}\to v_{\mathrm{\Gamma }k}^{GAG}=k_{\mathrm{\Gamma }\text{N}}^{CAG}/k_{\mathrm{\Gamma }o}^{GAG}$, hence $m_{\mathrm{\Gamma }\text{R}}^{GAG}\to k_{\mathrm{\Gamma }N}^{GAG}{\rho }_{\mathrm{\Gamma }\text{R}}^{GAG}$, with GAG/PG production balanced by removal in an evolved configuration.

3. Results

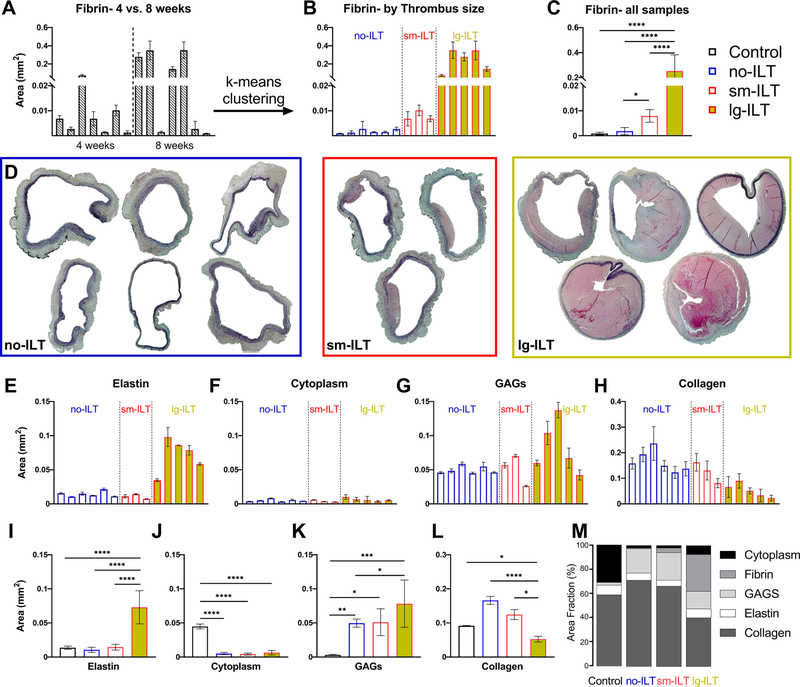
Thrombus, not time of enlargement, dictates characteristic histopathologic features.

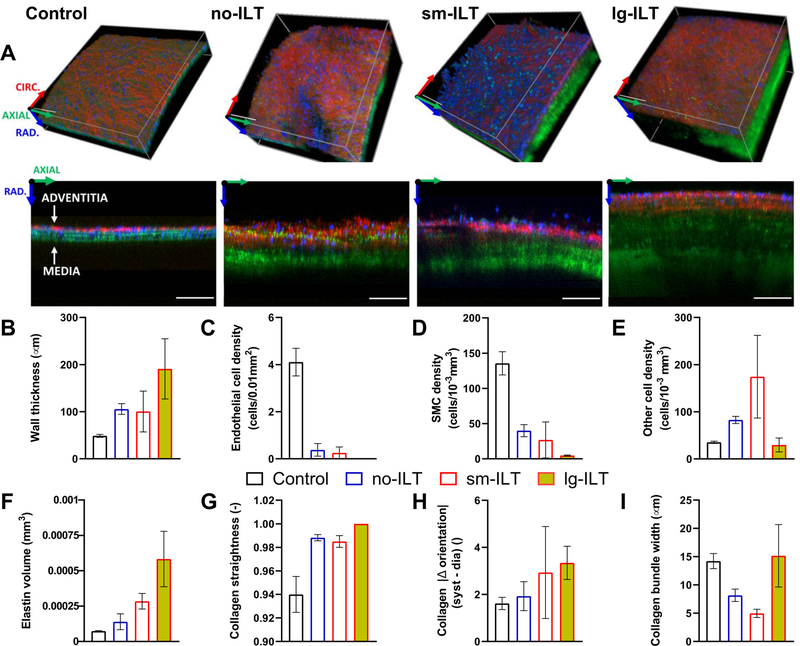
Independent of the duration of BAPN exposure (4 or 8 weeks), and consistent with our prior in vivo imaging [13], all 16 elastase + BAPN mice developed an AAA without rupturing in vivo (Fig. S2). ILT similarly manifested for both durations of BAPN, though generally greater in extent after 8 weeks (Fig. 1A). Using k-means clustering, with k = 3, the 14 fully tested AAAs separated naturally into one of three groups: “no-ILT” (i.e., not significant ILT, n = 6), “sm-ILT” (small, or modest, n = 3), or “lg-ILT” (large, or marked, n = 5), as seen in Fig. 1B,C, with the control group consisting of n = 6 age- and sex-matched normal aortas. Representative Movat-stained sections confirmed this classification for all 14 elastase + BAPN aortas (Fig. 1D), noting the distinct difference in fibrin (light pink) across groups. Notwithstanding intra- and interspecimen variability, quantitative histology revealed higher aortic cross-sectional areas of elastin and GAGs (Fig. 1E,I and G,K) and lower areas of collagen (Fig. 1H,L) with increasing amounts of fibrin; overall cell density (cytoplasm) was low in all three study groups (Fig. 1F,J), which was confirmed by multiphoton microscopy (Fig. 2A) and resulted in part from the increased wall thickness (Fig. 2B). In particular, elastase + BAPN reduced luminal (presumably endothelial) and medial (presumably smooth muscle) cell density significantly (Fig. 2C,D), especially for lg-ILT. By contrast, cell density increased dramatically in the adventitial layer in the no-ILT and sm-ILT groups compared with controls (Fig. 2E).

Fig. 1.

Study groups. (A) The planar area of fibrin (primary constituent in ILTs) in Movat’s pentachrome stained sections (light pink) was quantified in all seven 4-week and seven 8-week AAAs that were tested in vitro. (B) A k-means clustering separated these AAAs naturally into three groups based on fibrin: no-ILT (i.e., scarce fibrin, statistically similar to the six unperturbed control samples), sm-ILT (modest fibrin), and lg-ILT (marked fibrin), with (C) statistical significance noted. (D) Representative Movat’s pentachrome sections separated by study group, with associated (E-H) specimen-specific and (I-M) group-specific quantification. GAGs – mucoid material, likely glycosaminoglycan-dominant. Data are presented as mean ±SEM. ^****p < 0.0 0 01, ^***p < 0.0 01, ^**p < 0.01, *p < 0.05.

Fig. 2.

In situ microstructural organization of the intact aortic wall under in vivo loading conditions for the four primary groups: control, no-ILT, sm-ILT, and lg-ILT. (A) Representative volumes (top) and axial (z) – radial (r) slices (bottom) acquired using multi-photon microscopy in select regions of control and elastase + BAPN aortas. Shown are the second harmonic generation signal of collagen (red), two-photon fluorescence signal of elastin (green), and fluorescent signal of cell nuclei (blue). Scale bar: 100 μm. The color-coded coordinate system indicates circumferential (red), axial (green), and radial (blue) directions and is positioned at a point outside the samples. (B-I) Microstructural parameters reveal distinct group-specific elastase + BAPN effects. Values are evaluated at equivalent systolic luminal pressure and sample-specific in vivo axial stretch: mean ±SEM values of (B) wall thickness, (C) cell density at the luminal surface (presumably endothelial cells), (D,E) cell density within the media (presumably smooth muscle) and cell density within the adventitia (other cell types, likely including fibroblasts and macrophages), (F) elastin volume measured transmurally over an axial-circumferential area of 0.01 mm ^2, (G) in-plane (i.e., axial-circumferential) collagen fiber straightness, (H) difference in absolute value of collagen fiber orientation quantified from 80 to 120 mmHg at a fixed in vivo axial stretch, and (I) in-plane collagen fiber bundle width. Trends were assessed qualitatively since data are for representative regions, not full-field.

Albeit visible in most AAAs, the elastin was generally fragmented and not well-organized as laminae (Fig. 2A,F, Fig. S2). Collagen appeared less undulated/more stretched in the lg-ILT group compared to other groups, as evident from picrosirius red images (Fig. S2). Fibrillar collagen, mainly located in the adventitial layer, also differed among groups. In-plane straightness increased in all AAAs, resulting in nearly rectilinear fibers, particularly in the lg-ILT group (Fig. 2G). Collagen bundle width in the axial-circumferential plane was reduced in no-ILT samples compared with controls, and this width was reduced further in the sm-ILT groups (Fig. 2I). Yet, AAAs with lg-ILT had bundles of comparable mean width with controls. When comparing images of the same region distended from 80 to 120 mmHg without changing the axial stretch, the primary orientation of the collagen fiber bundles appeared to vary more in AAAs than in controls (Fig. 2H). Furthermore, the change in primary orientation increased gradually with ILT volume, likely reflecting the impossibility of the collagen fibers to undulate further.

Standard biaxial tests capture overall changes, not regional heterogeneities.

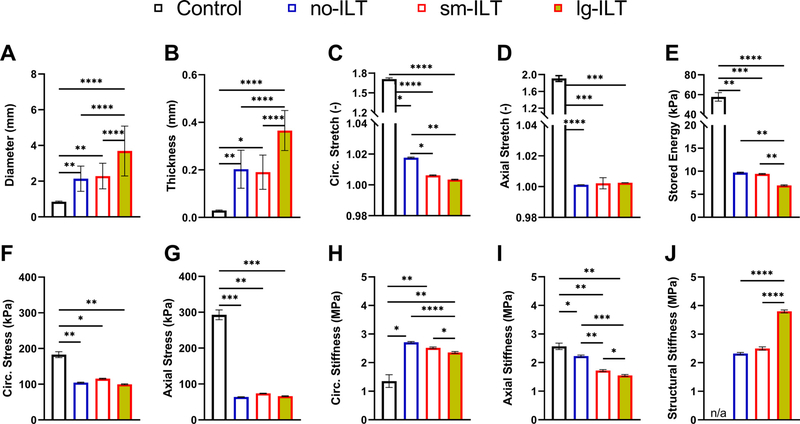
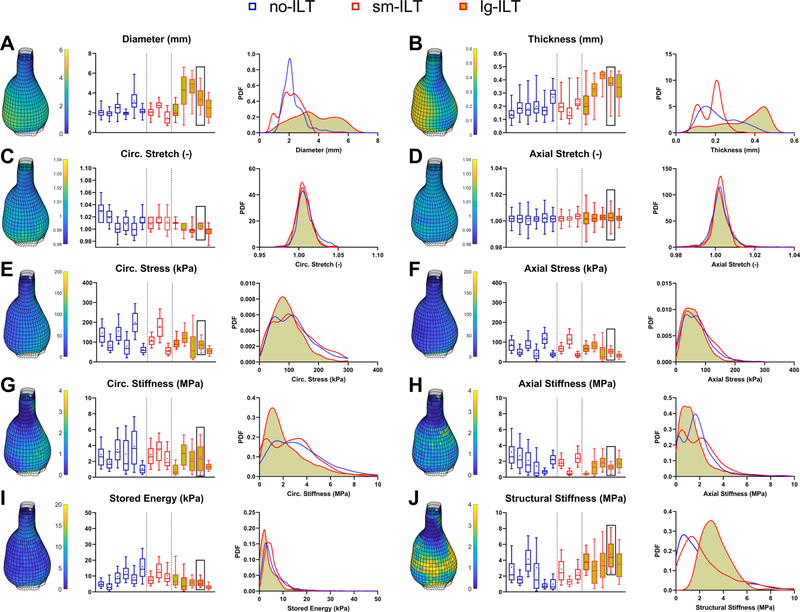
The marked histological changes suggested associated changes in biomechanical metrics. Despite luminal enlargement characteristic of AAAs, wall thickness increased significantly in all three groups of lesions, thus resulting in overall marked decreases in biaxial wall stretches and Cauchy stresses measured during standard tests, with elastic energy storage markedly decreased as well (Fig. S3). Despite a reduction in overall axial material stiffness, circumferential material stiffness tended to be preserved in the AAAs based on standard tests. Mean values of these many metrics changed similarly when assessed using pDIC + OCT (Fig. 3), with the exception of an apparent increase in circumferential material stiffness in the AAAs relative to controls. Quantitative differences between bulk measurements (Fig. S3) and mean results from pDIC + OCT (Fig. 3) suggested complex regional distributions in many of the metrics, as revealed in Figs. S4-S12 and summarized in Fig. 4 for all 14 AAAs, with overall probability distribution functions shown for the three aneurysmal groups (no-ILT, sm-ILT, and lg-ILT). Clearly, regional variations are complex in AAAs, emphasizing that local analyses are preferred.

Fig. 3.

Summary of mean ±SEM group-specific full-field biomechanical findings from pDIC + OCT measurements at a common pressure of 120 mmHg and specimen-specific axial stretch. Local (A) outer diameter, (B) wall thickness, (C,D) circumferential and axial stretch, (E) elastically stored energy, (F,G) circumferential and axial Cauchy stress, (H,I) circumferential and axial material stiffness, and (J) normalized structural stiffness. Here, biaxial material stiffness is computed directly from the stored energy function at the biaxial state of strain while structural stiffness is computed as the circumferential material stiffness times the ratio of local-to-mean wall thickness for that sample. The aneurysmal aortas associated with marked decreases in wall stress, due largely to the increased thickness, and dramatic losses of stored energy, likely due to the decreased axial stretch, loss of elastic fiber integrity, and increased deposition of other constituents, including GAGs. Axial stiffness decreased modestly despite the dramatic decrease in axial stretch while circumferential stiffness increased modestly. Compare results to those in Fig. S3 based on standard biaxial testing, which yields bulk behaviors. ^****p < 0.0 0 01, ^***p < 0.0 01, ^**p < 0.01, *p < 0.05.

Fig. 4.

Spatial distributions of key biomechanical metrics in all 14 aneurysmal aortas that were tested in vitro (same lesion order as in Fig. 1 B). (A-J) Box plots show multiple geometric and biomechanical metrics (mean denoted by ∗, median by horizontal line) evaluated at 120 mmHg and specimen-specific axial stretch within every subdomain (calculations in ~80 0–10 0 0 elements per sample) based on pDIC (diameter and stretches), OCT (thickness), and virtual fields-based inverse characterization (other metrics). The 3D reconstructed geometry of the reference configuration (80 mmHg and specimen-specific in vivo axial stretch) is shown for a representative lg-ILT sample (black box, second from last lesion) for each metric. Edges of the samples as well as patches with a poor coefficient of determination were neglected and left blank. Averaged probability density functions (pdf) compare entire distributions for each metric. Structural stiffness is defined as circumferential material stiffness times local thickness divided by the mean thickness for that sample. Compare with Figs. S4-S12. See also Fig. S3 for bulk results for the 6 control aortas, which do not exhibit marked regional variations and thus were not studied with pDIC.

Histomechanical correlations are revealing, but potentially misleading.

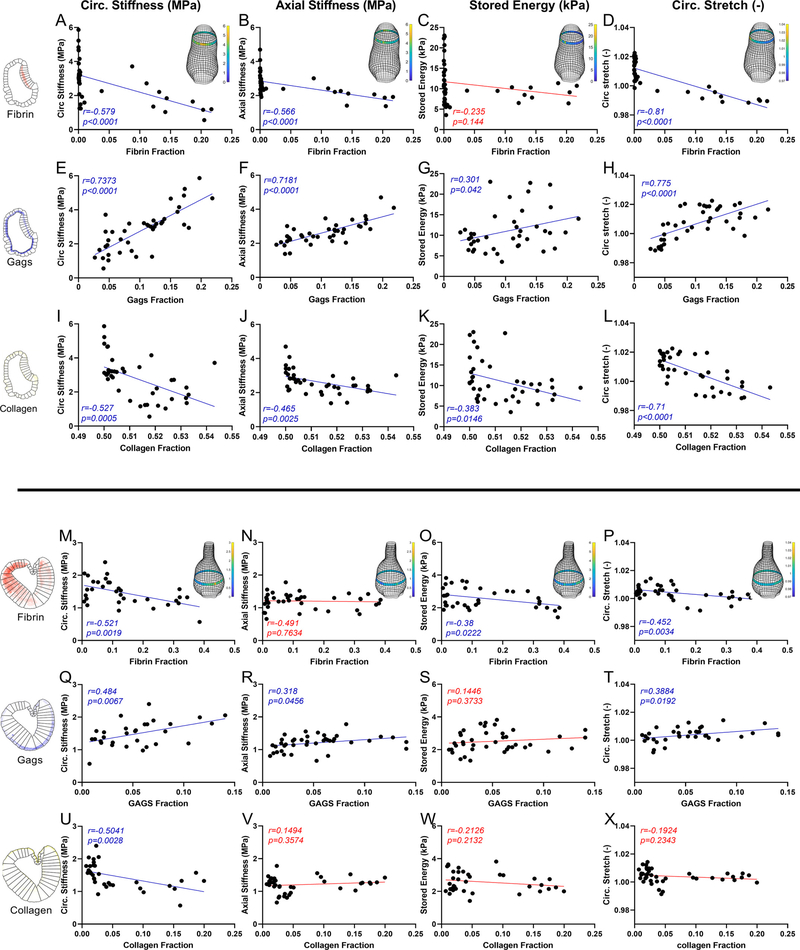
Figs. S13-S14 examine possible correlations, by AAA group (no-ILT, sm-ILT, lg-ILT), between local measurements of outer diameter D (pDIC) and wall thickness T (OCT), which suggested that a non-dimensional parameter D/T may be useful. Hence, further correlations were examined versus D/T, both by group and overall, for stored energy (a key metric indicating aortic functionality), circumferential material stiffness (a key mechano-regulated quantity), and axial material stiffness (to examine possible biaxial changes), with other possible correlations examined similarly, but not yielding significant results. Given the importance of accounting for local/regional variations in wall composition and associated biomechanical metrics, similar correlations are shown in Fig. 5 for two representative AAAs, one sm-ILT (Fig. 5A-L) and one lg-ILT (Fig. 5M-X). The regional histological area fractions were calculated as shown in Fig. S15, then associated with regional pDIC-determined metrics. A strong correlation emerged between increased circumferential material stiffness and increased GAG fraction (Fig. 5E,Q), which was initially surprising and potentially misleading given that GAGs engender little tensile stiffness. It appears, however, that this correlation arose due to a GAG-induced swelling/thickening of the wall that reduced collagen fiber undulation (cf. Fig. 2). Also potentially misleading, an inverse relationship emerged between circumferential material stiffness and collagen fraction (Fig. 5I,U). This finding likely arose, however, due to a considerable abundance of non-crosslinked collagen representative of frustrated deposition. Not surprisingly, stored energy, which is often a good metric for elastic fiber integrity and function, demonstrated weak correlations with all constituents. Albeit not shown, elastin correlated poorly with all mechanical metrics, likely due to the elastase disrupting the fibers and laminae, including those that remained visible histologically. Increased fibrin, that is, ILT, decreased the biaxial stiffness of the sm-ILT sample as well as the circumferential material stiffness of the lg-ILT sample.

Fig. 5.

Possible histomechanical correlations for a representative AAA having either (A-L) a sm-ILT or (M-X) a lg-ILT. See Figures S13-S14 for all correlations. Local regions for histological quantification are defined in Figure S15, noting that correlations were considered for all biomechanical metrics versus extent of fibrin (first rows, top and bottom lesions), GAGs (middle rows), and fibrillar collagen (bottom rows), but shown here are results for the four metrics having the best correlations and/or most biomechanical importance: circumferential (first column) and axial (second column) material stiffness, elastic energy storage (third column), and circumferential stretch (fourth column). Correlations were evaluated using a non-parametric Spearman correlation coefficient r, with non-significant correlations (p > 0.05) denoted in red. Of particular interest, circumferential stiffness correlated negatively with fibrin and positively with GAGs in both sm-ILT and lg-ILT samples. Interestingly, there was a negative correlation between circumferential stiffness and collagen, consistent with collagen presence not indicative of collagen integrity. Elastic energy storage (C,G and K for each sample), which is usually a good metric for elastic fibers integrity, exhibited weak correlations with all constituents, consistent with the elastase rendering the elastin incompetent though with some histological presence.

Computational modeling reveals fundamental roles of collagen turnover rates.

Given that the correlations revealed that one must be cautious in interpreting histological evidence for changes in biomechanical metrics, with elastase compromising elastic fiber integrity and BAPN preventing cross-linking of the newly deposited collagen, we turned to a computational growth and remodeling model to gain further insight. To avoid many uncertainties in the roles of ILT on wall structure and properties [6], we focused on the 6 AAAs that constituted the no-ILT group (Table S1). We first used our standard model (incorporating possible changes in elastic fibers, SMCs, and families of collagen fibers) to simulate the separate, and then combined, effects of elastase and BAPN. Consistent with experimental observations, elastase was assumed to affect mainly the structural integrity of elastic fibers, modeled via an acute 95% reduction in the modulus c^e in Eq. (3), with $Q_{\mathrm{\Gamma }}^e(s>0)\equiv 1$ (no mass degradation) and $m_{\mathrm{\Gamma }}^e(\tau >0)\equiv 0$ (no mass production) in Eqs. (1) and (2). Adverse effects of BAPN on the cross-linking of collagen were modeled via an acute 95% reduction in the parameter $c_1^c$ in Eq. (4) for all newly deposited collagen fibers (i.e., within the hereditary integral from τ = 0 and τ = s in Eq. (2)); hence, cross-linking of previously extant fibers (first term on the right-hand side in Eq. (2)) was not affected. In this way, the reduction in remnant cross-linking was gradual, mainly depending on the half-life of collagen. Additional effects, arising indirectly from these insults, were not considered at this stage.

For the case of elastase alone (Fig. S17A,B; dashed lines), the model predicted a modest aortic dilatation (~10% increase in inner radius; panel C), with enlargement constrained by a stiff intact adventitia that persisted over subsequent weeks. In this case the basal half-life of collagen was $T_{1/2}^c=70$ days [25], although shorter half-lives (to represent more rapid degradation and deposition of collagen in the face of lost elastin) yielded similar predictions over a simulated 8-week period. Other metrics experienced a similar trend, that is, an initial abrupt (modest-to-moderate) change due to the loss of elastin, which progressed with little-to-no change: total thickness initially decreased by incompressibility (F), circumferential stress (D) and circumferential (G) and axial (H) stiffness increased, and axial stress (E) and energy storage capability (marked, ~50%, consistent with severely compromised elastic fiber integrity; I) decreased. For the case of BAPN alone (Fig. S17A,B; dash-dotted lines), for which we also let $T_{1/2}^c=70$ days, the model predicted a reduction in remnant cross-linking of ~40% (~0.8*50%) by day 56 (0.8*70). This gradual decrease caused only mild gradual changes in geometry and mechanical properties, at least over the period of simulation. Both sets of findings were consistent with our prior in vivo observations [13]. When both cases were combined (Fig. S17A,B; dotted lines), with an assumed $T_{1/2}^c=70$ days, the independent responses added nearly linearly to produce an initially acute (elastase-driven) change in properties followed by mild (BAPN-driven) gradual changes over the simulated 8-week period.

Importantly, however, when the effects of elastase and BAPN were combined and the half-life of collagen was reduced to 1.5 days (Fig. S17A,B; solid lines), the model predicted a continued aortic dilatation that met the criterion of an AAA within 3 weeks (panel C), which resulted from the acute reduction in both elastic fiber integrity and effective collagen cross-linking (the latter only with the markedly increased turnover). This last pilot simulation revealed that the model could capture some of the qualitative changes observed experimentally, but not quantitatively. In particular, the standard model could not capture the greater dilatation or the marked thickening of the wall, which was expected since it did not model the marked accumulation of GAGs/PGs observed histologically. Moreover, axial stress and stiffness were underestimated while circumferential stress and (particularly) stiffness were overestimated; only stored energy was captured.

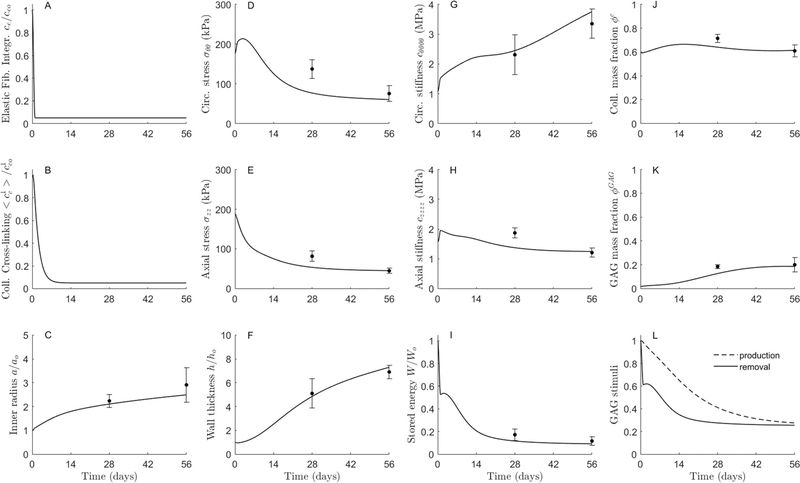
Thus, taking the pilot elastase + BAPN simulation in Fig. S17 with rapid turnover of collagen (solid line) as a starting point, we introduced three modifications. First, consistent with the experimental observation that collagen fibers, mostly oriented axially, were straightened significantly in the AAAs Fig. 2), we increased the deposition stretch of the axial family of collagen over the evolution, which compensated some for the lack of cross-linking and contributed to the reduced (though not negligible, particularly stiffness) mechanical properties in the axial direction (Fig. 3). Second, the rapid dilatation of the aorta stretched the continuously deposited collagen fibers in the circumferential direction (even with rapid turnover), leading to an exaggerated increase in mean circumferential stiffness (Fig. S17). This suggested that new collagen, at least that oriented circumferentially, was less stiff than the original. Noting that the parameter $c_1^c$ was already reduced significantly to describe BAPN-inhibited cross-linking, this additional effect was modeled via a decrease in the exponential parameter $c_2^c$ in Eq. (4) for the newly formed collagen in that direction. Third, the model was augmented to include GAG/PG turnover. We considered an initial presence of (otherwise negligible mechanically) GAGs/PGs within the media of the bilayered model (Fig. 1), which were subsequently removed more slowly (via Eq. (7)) than produced (via Eqs. (8) and ((9)), hence thickening the wall. Once these three features were included, the model captured well all of the experimentally inferred biomechanical metrics at both times, 4 and 8 weeks (Fig. 6). Finally, additional parametric studies confirmed that drastic reductions in the parameters c^e (for elastic fiber integrity; 95%) and $c_1^c$ (for collagen cross-linking; 95%) as well as in the half-life of collagen (≈98%) were required to capture the mean experimental data, including GAG/PG accumulation, within the first 8 weeks of aneurysmal enlargement (Figs. S18 and S19, respectively).

Fig. 6.

Computational predictions of the effects of (A,B) a prescribed elastase + BAPN exposure on (C-K) the subsequent evolution of normalized aortic geometry, biaxial mean wall stress and material stiffness, normalized elastic energy storage, and microstructural composition of the infrarenal aorta of an adult male C57BL/6J mouse under constant systolic blood pressure, flow, and axial length. (L) The evolution of GAGs/PGs was computed via an energy-mediated decrease in mass density with a delayed compensatory decrease in production (see Methods), which drove overall wall thickening. The symbols (circles with whiskers) show mean ±SEM values for the no-ILT group (see Fig. 1 D). Simulations include a simultaneous increase in axial (deposition) pre-stretch and decrease in circumferential stiffness for respective families of collagen fibers (Figs. 2 and 3; compare to Fig. S16). Model parameters are listed in Table S1. See, too, Figures S16-S18, which show pilot results that were fundamental to final model parameterization. Note, in particular, that the collagen half-life used here is 1.5 days, consistent with rapid turnover in the extreme situation of elastase and BAPN exposures.

4. Discussion

The aortic wall comprises hundreds of different glycoproteins, GAGs/PGs, and proteins [26], yet it is the elastic fibers (consisting of elastin and elastin-associated glycoproteins) and fibrillar collagens (especially collagens I and III and associated small leucinerich proteoglycans) that endow the healthy wall with much of its resilience (elastic fibers) as well as its stiffness and strength (collagen fibers). Lysyl oxidase is a copper-dependent enzyme essential for cross-linking newly synthesized elastic and collagen fibers; it is fundamental to the normal mechanical functionality and structural integrity of the aortic wall. We have known since at least the mid-1960s that, by blocking lysyl oxidase mediated matrix cross-linking, BAPN can compromise the structural integrity of the aorta, leading to aneurysms, dissections, and ruptures [27, 28]. Consistent with more recent studies using lysyl oxidase null (Lox^−/−) and Lox-mutant mice to focus on roles of matrix cross-linking in aortic development [29, 30], many of the prior studies delivered BAPN before the aortic wall had matured fully [31], which occurs by postnatal day 56 in mice [32, 33]. That is, considerable emphasis had focused on discovering effects of disrupting extracellular matrix during aortic development. Yet, AAAs tend to emerge in older individuals. There was, therefore, a need to study the mature aorta. Our study is significant in that it represents the first detailed regional assessment of the combined effects of elastase and BAPN on the abdominal aorta in adult mice.

Functional elastic fibers, especially in lamellar form, are formed and cross-linked during the perinatal period and they have a half-life on the order of decades [34]; thus, they are resistant to structural compromise in maturity except in cases of heightened elastolytic activity or mechanical fatigue over long periods, the latter of which does not occur naturally in mice [35]. It is for this reason that elastase has proven useful for compromising elastic fibers in models of AAA formation in mature mice. Conversely, collagen fibers have a much shorter half-life, on the order of 70–90 days under normal conditions, though this half-life can decrease by an order of magnitude in disease, including hypertension [25]. Given these differences in turnover rates, BAPN is thus expected to affect collagen fibers more than elastic fibers in maturity, though not over relatively short periods. It was thus expected that BAPN alone is ineffective in generating aneurysms over periods up to 100 days in mature mice [12]. By contrast, inducing hypertension [29] or compromising elastic fibers to dilate the aorta [12] stimulates increased collagen turnover by altering the mechanical state of stress in the mature aortic wall [23, 36], thus increasing the potency of BAPN-inhibition of cross-linking of newly deposited collagen fibers. An advantage of the elastase + BAPN model is that it addresses both of the key structural constituents of the aortic wall within the physiological constraints of maturity.

The infrarenal aorta can be exposed to elastase for short periods either intraluminally or peri-adventitially, which necessarily result in different degrees and spatial distributions of elastin breakdown. Indeed, despite adherence to experimental protocols, considerable variability is expected in the initial degree of elastin compromise in both cases. Any acute loss of elastic fibers also changes collagen fiber morphology [37], likely affecting its subsequent remodeling. Computational models of the progressive enlargement of human AAAs suggest that both the initial degree of elastolytic insult and the rate of collagen remodeling are critical determinants of lesion biomechanics [36, 38], the latter of which was demonstrated in vivo in an elastase-only mouse model by changing collagen synthesis rates by antagonizing miR29b [39]. Computational models of blood flow within human AAAs suggest further that lesion enlargement is critical for the development of an ILT [40], which the elastase + BAPN model admits in the mouse for the first time. There was, therefore, significant motivation to understand better the associated biomechanical properties of the aneurysmal wall in this mouse model, though with expected spatio-temporal variability. Standard methods for biomechanically testing the murine aorta were not sufficient, thus we also employed our pDIC + OCT system.

We previously used pDIC to study angiotensin II-induced lesions in the suprarenal aorta of mice [21, 41], but these lesions arise from a contained rupture of the media rather than aneurysmal enlargement [42]. We also used pDIC to study thoracic aortic aneurysms in three different mouse models [16], but these lesions also differ from AAAs. Our only prior use of pDIC to study a mouse model of AAA focused on an elastase-only model, which developed modest dilatations without ILT [43]. We focused therein on correlations between regional strains and histology, not inverse-based assessments of regional material properties. Hence, we are not aware of any prior comparable regional examination of biomechanical properties in any of these (elastase-only, BAPN-only, or elastase + BAPN) mouse models. The present experiments showed for the first time in this important mouse model that elastase + BAPN results in complex regional heterogeneities in composition and properties. A striking histopathological finding herein at 4 and especially 8 weeks of elastase + BAPN exposure was the marked accumulation of mucoid-staining material (likely aggregating GAGs/PGs) in both the media and adventitia, which our empirical correlations suggested and our computational simulations confirmed played a major role in dictating the pathologic wall properties.

With few exceptions (mainly enduring elastic fibers), extracellular matrix constituents undergo slow but continual turnover within the healthy arterial wall and such renewal is fundamental to tissue homeostasis [44]. Changes in the mass fraction of a particular constituent thus result from altered production, altered removal, or both. Accumulating evidence reveals the importance of aggregating GAGs/PGs in vascular mechanics and biology – they affect the mechanical properties of the wall, present various growth factors and cytokines to the cells, and directly affect cell proliferation, migration, and survival [45–47]. In particular, aggrecan and versican (often linked with hyaluronan) exhibit high negative fixed-charge densities, and the resulting hydration contributes to the viscoelasticity of the wall and, perhaps more importantly, creates a modest intra-lamellar swelling pressure within the media that appears to contribute to SMC mechanosensing [48]. Excessive accumulation of these GAGs/PGs can disrupt this mechanosensing, resulting in myriad phenotypic changes that may result in positive feedback, driving further accumulation, swelling, and perhaps cell death and dissection. Increased mechanical stress/stretch drives mesenchymal cell production of both fibrillar collagens and GAGs/PGs in vitro [49], and in vivo studies confirm that GAGs/PGs accumulate in cases of increased mechanical loading and injury [47, 50]. Nevertheless, quantification remains scant. GAGs/PGs are degraded by multiple proteases, particularly those of the ADAMTS (a disintegrin and metalloprotease with thrombospondin repeats) family [51]. Although there is little information on normal turnover rates of aggregating GAGs/PGs in arteries, these rates appear to be similar to those of fibrillar collagens [25], that is, with half-lives ranging from 1 (extreme) to 70 (maximum) days, with 23 days apparently typical in normalcy [50, 52].

Whereas increased GAGs/PGs have not been reported in elastase-induced aneurysm models [10, 11, 43], such increases are common in BAPN-induced models [27, 28, 53]. Importantly, Hosoda and Iri [27] reported that mucoid-positive material accumulated within the intra-lamellar spaces of the media in young rats, apparently first disrupting intra-lamellar connections between the SMCs and elastic laminae and then associating with SMC dropout with intra-lamellar widening and focal laminae fragmentation. Such a progressive damage process is consistent with computational simulations based on the high fixed charge density of aggregating GAGs/PGs [48]. Herein, we used a proven constrained mixture model of arterial growth and remodeling [23] to examine competing hypotheses on the effects of altered matrix turnover rates for aggregating GAGs/PGs as well as collagen. Under homeostatic conditions, it is straightforward to show that basal rates of turnover are related via $m_0^{\alpha }={\rho }_0^{\alpha }{k}_0^{\alpha }$, where $m_0^{\alpha }$ is the basal production rate, ${\rho }_0^{\alpha }$ the basal apparent mass density, and $k_0^{\alpha }$ the basal removal rate. Given a normal GAG/PG mass fraction of ~ 0.05, we find $m_0^{GAG/PG}$ ~ (0.05)(1050 kg/m³)(0.03 days⁻¹) ~ 1.575 kg/m³/day. Pilot simulations confirmed that GAGs/PGs can accumulate equally via increased production or decreased removal, though there remains a need for additional experimental data to identify the actual mechanism.

Recall that diffuse elastase exposure alone results in modest aortic dilatation in adult mice. We hypothesized that this finding results from a compensatory rapid deposition of fibrillar collagen to arrest the dilatation. Importantly, this hypothesis was supported by our computational model, which predicted the observed findings (Fig. S17). We hypothesized further that the lack of an effect of BAPN on the healthy aorta of older mice is due to long the half-life of vascular elastin (decades) plus the slow turnover of vascular collagen (two-to-three months) in the absence of a secondary stressor. Importantly, our model also predicted that BAPN alone does not affect the mature aorta over typical periods of observation (Fig. S17). Both of these results were obtained with modest re-parameterization of our prior model and they provide a biomechanical explanation for prior experimental findings [12, 13]. Most importantly here, however, we sought to simulate the case of elastase + BAPN without the additional complication of ILT; that is, we focused on the observed progressive dilatation that exceeds the threshold for an aneurysm [12, 13] and associated changes in biomechanical metrics. We hypothesized that the marked effect of BAPN on the aorta of young mice and similarly adult mice in the presence of a secondary stressor (elastase or angiotensin II) results from a marked decrease in half-life of collagen in these cases. Although our standard model captured many salient features of the experimental findings (Fig. S17), we needed to augment it to include a biomechanically stimulated production of GAGs/PGs (Fig. 6); without such an addition, the model could not capture the marked increase in diameter and especially the dramatic increase in wall thickness. Introducing such a contribution, combined with other experimentally motivated changes to the axial (increased straightness) and circumferential (decreased stiffness) families of collagen fibers, the model described the evolution of multiple biomechanical metrics well (Fig. 6). These findings support strongly the important role of rates of matrix turnover in dictating lesion enlargement. Finally, comparing our current results with related findings [54] suggests that the lack of a marked, continued aortic dilatation in the traditional elastase-only model is due to the diffuse, rather than focal, damage to the elastic fibers.

One limitation of the present simulations is that we were unable to prescribe the precise initial, likely heterogeneous, damagefield for elastin, hence our predictions represent mean results (cf. Figs. S3 and 3). Another limitation stems from the lack of information on stimuli of GAG/PG production in aortopathies. Additional data would allow us to improve the related aspects of our model. Another limitation of the modeling is that we did not include the effects of thrombus [55]. Rather, we focused on the effects of elastase and BAPN on wall mechanics and matrix turnover, with an emphasis on changing rates of turnover. For the first time, we included the effects of aggregating GAGs/PGs in the G&R model, which proved essential for capturing the dramatic changes in wall thickness and lumen. Future studies should include the diverse roles of ILT, which necessarily will require direct consideration of the evolving hemodynamics.

In summary, we presented experimental and computational findings on the rate and extent of AAA enlargement in an elastase + BAPN mouse model, which addresses contributions of the two primary structural constituents of the infrarenal aorta. Lesions separated naturally as a function of ILT presence and extent (Figs. 1 and 5), not duration of BAPN exposure. These findings confirm the need for more attention to the biochemomechanical effects of thrombus on the evolving wall and emphasize that it is the “biological” not “chronological” processes that are most important, which differ from mouse to mouse. Standard biomechanical testing captured overall changes, but advanced methods of testing were needed to delineate regional variations, which were dramatic. Local correlations between histological and biomechanical metrics revealed important findings, but highlighted the need for caution since histologically evident elastin fragments and collagen fibers need not be functional. Indeed, our experimental-computational findings suggested a heightened but frustrated deposition of collagen that attempted to limit lesion enlargement, but could not since cross-linking was inhibited. Finally, the computational model suggested that rates of collagen turnover increased many-fold and accumulation of presumably competent GAGs/PGs did not help to limit lesion enlargement or improve the biomechanical metrics. We submit that quantifying local functional (biomechanical) metrics is critical for understanding mechanisms of lesion enlargement though the need for a better understanding of the mechanobiological mechanisms remain.

Statement of Significance.

Precise mechanisms by which abdominal aortic aneurysms enlarge remain unclear, but a recent elastase plus β-aminopropionitrile mouse model provides new insight into disease progression. As in the human condition, the aortic degeneration and adverse remodeling are highly heterogeneous in this model. Our multi-modality experiments quantify and contrast the heterogeneities in geometry and biomaterial properties, and our computational modeling shows that standard histopathology can be misleading. Neither accumulating glycosaminoglycans nor frustrated collagen synthesis slow disease progression, thus high-lighting the importance of stimulating adaptive collagen remodeling to limit lesion enlargement.