Abstract
The cancer cell fraction (CCF), or proportion of cancerous cells in a tumor containing a single-nucleotide variant (SNV), is a fundamental statistic used to quantify tumor heterogeneity and evolution. Existing CCF estimation methods from bulk DNA sequencing data assume that every cell with an SNV contains the same number of copies of the SNV. This assumption is unrealistic in tumors with copy-number aberrations that alter SNV multiplicities. Furthermore, the CCF does not account for SNV losses due to copy-number aberrations, confounding downstream phylogenetic analyses. We introduce DeCiFer, an algorithm that overcomes these limitations by clustering SNVs using a novel statistic, the descendant cell fraction (DCF). The DCF quantifies both the prevalence of an SNV at the present time and its past evolutionary history using an evolutionary model that allows mutation losses. We show that DeCiFer yields more parsimonious reconstructions of tumor evolution than previously reported for 49 prostate cancer samples.
eTOC blurb
Analyses of tumor heterogeneity and evolution from bulk DNA sequencing data typically rely on the estimation of the cancer cell fraction (CCF) of a somatic single-nucleotide variant, defined as the fraction of cancer cells that contain the mutation. Estimation of the CCF is complicated for variants that overlap copy number aberrations, and current approaches make overly simplistic assumptions about the interactions between single-nucleotide variants and copy number aberrations. We introduce the descendent cell fraction (DCF), a novel statistic that accounts for loss of mutations during tumor evolution and derive the DeCiFer algorithm that jointly estimates DCFs and clusters mutations using a phylogenetic model.
Introduction
Cancer arises from an evolutionary process during which somatic mutations accumulate in the genome of different cells, yielding a heterogeneous tumor composed of different subpopulations of cells, or clones, that have distinct complements of mutations (Nowell 1976). Quantifying the heterogeneity within a tumor is essential for understanding carcinogenesis and devising personalized treatment strategies (Burrell et al. 2013, Andor et al. 2015, McGranahan & Swanton 2017). While recent single-cell DNA sequencing technologies enable high-resolution measurements of tumor heterogeneity (Navin 2015, Gawad et al. 2016, Kim et al. 2018, Gao et al. 2016, Laks et al. 2019, Myers et al. 2020, Zaccaria & Raphael 2021), the vast majority of cancer studies in research and clinical settings (The et al. 2020, Jamal-Hanjani et al. 2017, Dewey et al. 2014) rely on DNA sequencing of bulk tumor samples, where an individual sample comprises a mixture of thousands of different tumor cells. To quantify tumor heterogeneity using bulk sequencing data, most cancer sequencing studies analyze somatic single-nucleotide variants (SNVs) as these mutations are ubiquitous in cancer. The fundamental quantity used to quantify tumor heterogeneity from SNVs is the cancer cell fraction (CCF) – also known as the cellular prevalence or the mutation cellularity – which is the proportion of cancer cells that contain the SNV. CCFs form the basis for many cancer analyses, including: studying tumor heterogeneity (Jamal-Hanjani et al. 2017, Rajput et al. 2017, Dentro et al. 2020), reconstructing clonal evolution and metastatic progression (Gundem et al. 2015, Brastianos et al. 2015, Jamal-Hanjani et al. 2017, Cresswell et al. 2020), identifying selection (Williams et al. 2016, Lakatos et al. 2020, Bozic et al. 2010), and analyzing changes in mutational processes over time (Rubanova et al. 2020, Harrigan et al. 2020, Christensen et al. 2020). In these and other studies, the underlying assumption is that groups of SNVs with the same CCF are likely to be present in the same cancer cells and thus occurred on the same branch of the phylogenetic tree that describes the evolution of the tumor (Figure 1b).
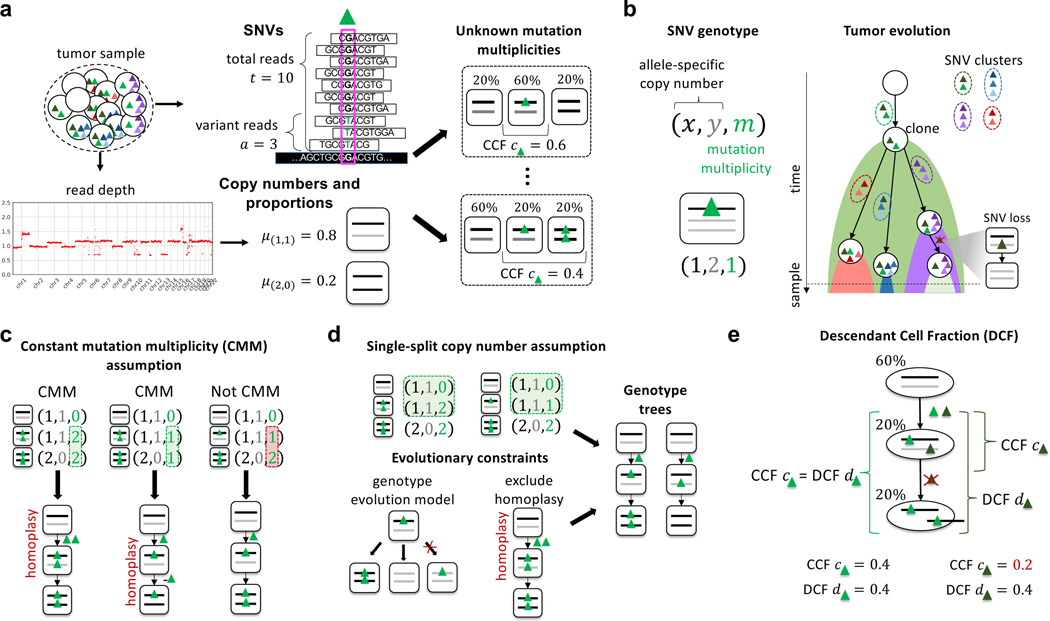
Figure 1: Quantifying tumor heterogeneity and evolution by computing cancer cell fractions (CCFs) and descendant cell fractions (DCFs) of SNVs that occur in genomic regions containing copy-number aberrations.
a, DNA sequencing of a bulk tumor sample yields two signals of somatic aberrations: (Top) at a position containing an SNV (green triangle), the number of total and variant sequencing reads provide an estimate of the variant allele frequency (VAF) of the SNV; (Bottom) the read depth (and B-allele frequency – not pictured) across genomics regions reveal allele-specific copy numbers (x, y) (black and gray lines) and their proportions μ(x, y). Bulk sequencing data does not measure the number of copies of an SNV in each cell/clone; these unknown mutation multiplicities complicate the estimation of the cancer cell fraction (CCF) of an SNV. b, Estimating the CCF of an SNV requires knowledge of the genotype at a locus defined as a triple (x, y, m) of integers indicating the allele-specific copy number at the locus and the mutation multiplicity m of the SNV. CCFs quantify heterogeneity within a tumor at the present time and are related to the past evolutionary history of a tumor. SNVs present in the same cells have the same CCF. Under some mild evolutionary assumptions the converse is also true and thus researchers typically group SNVs with similar CCFs. c, Nearly all existing methods to estimate CCFs rely on the Constant Mutation Multiplicity (CMM) assumption to constrain the possible genotypes at a locus. The constant mutation multiplicity assumption yields sets of genotypes with the property that all genotypes that contain the mutation have the same number M of copies of the mutation (highlighted in green). However, the constant mutation multiplicity assumption may admit sets of genotypes that are produced by unlikely evolutionary events such as homoplasy, and may also exclude other reasonable sets of genotypes, including copy-neutral loss of heterozygosity (right). d, We propose a less restrictive assumption on genotypes, the single split copy number assumption, as well as evolutionary constraints to enumerate potential biologically plausible sets of genotypes from a genotype tree. e, We introduce the Descendant Cell Fraction (DCF), a novel statistic that summarizes both the prevalence of the SNV and its evolutionary history. A pair of SNVs (light and dark green triangles) occurring on the same branch of a phylogenetic tree may have different CCF values if one of the SNVs (dark green) is later lost due to a copy-neutral loss of heterozygosity. This same pair of SNVs will have the same DCF value. Thus, clustering SNVs with similar DCFs groups mutations under an evolutionary model that allows mutation losses.
Importantly, the CCF of an SNV is not directly measured in bulk DNA sequencing data of a tumor sample. Rather, the CCF must be inferred from the DNA sequencing reads that align to the locus containing the SNV. Specifically, the CCF is calculated from the variant allele frequency (VAF), or proportion of copies of the locus in the sample that contain the SNV. The VAF in turn is estimated as the proportion of variant reads at the SNV locus (Figure 1a). For a heterozygous SNV in a diploid genomic region, the CCF is twice the VAF scaled by the proportion of cancer cells in the tumor sample, or tumor purity. However, somatic copy-number aberrations, including loss-of-heterozygosity events, that overlap at an SNV locus can alter the number of copies of the SNV in a cell, and these events substantially complicate the estimation of the CCF.
Calculation of CCF from the VAF requires knowledge of the mutation multiplicity, or the number of copies of the SNV in a cell or clone. Copy-number aberrations and loss-of-heterozygosity events alter the mutation multiplicities of SNVs. While copy-number aberrations and loss-of-heterozygosity events can be estimated from bulk sequencing data (Van Loo et al. 2010, Carter et al. 2012, Nik-Zainal et al. 2012, Oesper et al. 2013, 2014, Fischer et al. 2014, Zaccaria & Raphael 2020), knowledge of the copy numbers at a locus – even allele-specific copy numbers and subclonal copy-number proportions – is insufficient to determine mutation multiplicities. Indeed, there are often multiple possible values for the unobserved mutation multiplicities that provide equally plausible explanations for the observed read counts and copy numbers at an SNV locus. In statistical terms, the CCF is not identifiable from DNA sequencing data (Figure 1a). Since copy-number aberrations that amplify or delete large genomic segments, chromosomal arms, and even the whole genome (Zack et al. 2013, McPherson et al. 2016, Gerstung et al. 2020, Watkins et al. 2020) are frequent in cancer – particularly in solid tumors where up to ∼90% of tumors (Weaver & Cleveland 2006) may contain copy-number aberrations – it is imperative to have robust methods to calculate CCFs from bulk sequencing data.
Multiple computational methods have been developed in recent years to estimate CCFs in bulk sequencing data. These methods can be categorized into two different strategies. The first strategy is to severely restrict the possible mutation multiplicities of SNVs; specifically, many methods (Roth et al. 2014, Miller et al. 2014, McGranahan et al. 2015, Dentro et al. 2017, Jamal-Hanjani et al. 2017, Yuan et al. 2018, Cun et al. 2018, Dentro et al. 2020, Xiao et al. 2020, Gerstung et al. 2020, Lakatos et al. 2020, Tarabichi et al. 2021) assume that all cells harboring an SNV have the same mutation multiplicity. We refer to this assumption as the constant mutation multiplicity assumption (Figures 1c). Many methods rely on the constant mutation multiplicity assumption, as well as additional heuristics, to select a single value of the CCF for each SNV. These methods either calculate the CCF for each SNV separately (McGranahan et al. 2015, Dentro et al. 2017, Jamal-Hanjani et al. 2017, Cun et al. 2018, Dentro et al. 2020, Gerstung et al. 2020) or simultaneously infer CCFs and cluster SNVs across one or multiple samples, as done by PyClone (Roth et al. 2014), Ccube (Yuan et al. 2018), and others (Miller et al. 2014, Yuan et al. 2015, Caravagna et al. 2020, Xiao et al. 2020). While the constant mutation multiplicity assumption reduces the ambiguity in the calculation of the CCF, the assumption alone is insufficient to fully resolve such ambiguity. Moreover, the heuristics used to select the mutation multiplicity of an SNV – e.g., rounding the estimated average mutation multiplicity to the nearest integer (Dentro et al. 2017) – may introduce unexpected biases into the resulting analyses. More importantly, the constant mutation multiplicity assumption is often violated in practice. For example, an SNV occurring before an amplification may result in cancer cells with different mutation multiplicities: a group of cells without the amplification harboring a single copy of the SNV, and another group of cells with the amplification and multiple copies of the SNV. Scenarios such as this are frequent in solid tumors that often have subclonal copy-number aberrations (Carter et al. 2012, Zack et al. 2013, The et al. 2020, Watkins et al. 2020). Thus, the constant mutation multiplicity assumption is both too restrictive to model many real tumors and also too weak to overcome the issue of non-identifiability.
The second strategy to estimate CCFs is a phylogenetic approach using an evolutionary model that includes both SNVs and copy-number aberrations. Methods that use this strategy include PhyloWGS (Deshwar et al. 2015), SPRUCE (El-Kebir et al. 2016) and Canopy (Jiang et al. 2016). The evolutionary models employed in these methods do not make the constant mutation multiplicity assumption and thus allow more realistic scenarios such as mutation losses. However, this flexibility comes at a cost of computational efficiency: none of the current methods scale to the large numbers of SNVs measured in current cancer sequencing studies, and these methods may take days or weeks to process samples with a moderate number of mutations (≈1000). To address scalability, these methods group mutations into clusters where all mutations in a cluster are assumed to occur on the same branch of the phylogenetic tree describing the evolution of the tumor. Specifically, PhyloWGS (Deshwar et al. 2015) simultaneously clusters mutations and reconstructs a phylogeny, while Canopy (Jiang et al. 2016) and SPRUCE (El-Kebir et al. 2016) require mutation clusters in input. However, this pre-clustering approach is difficult because the CCFs of the mutations are not known in advance. If one clusters mutations using CCFs derived under the constant mutation multiplicity assumption then the restriction on mutation multiplicities reduces or eliminates the advantage of the phylogenetic approach. Because of these limitations, phylogenetic methods are not as widely used as methods that rely on the constant mutation multiplicity assumption.
In addition to the difficulties in estimating the CCF, there is another important limitation of the CCF itself: in many cases, the CCF is not the correct quantity to use for phylogenetic analysis. Specifically, the CCF measures only the prevalence of a mutation in the tumor at the present time and does not necessarily provide complete information about the past history of the mutation. Two mutations that occurred during the same cell division may have very different CCF values if one of these mutations is later lost due to a deletion (Figure 1e) (Tarabichi et al. 2021). In this case, one mutation may have a high CCF – suggesting that the mutation occurred early in the evolution of the tumor – while the other mutation has a low CCF value, misleadingly suggesting that the mutation occurred late during evolution. In fact, mutation losses are common in cancers that contain many copy-number aberrations (McPherson et al. 2016, Satas et al. 2020, El-Kebir 2018). Jamal-Hanjani et al. (2017) described this issue in the TRACERx sequencing study of non-small-cell lung cancer patients and proposed the “phyloCCF”, an ad hoc correction of the inferred CCF for SNVs in genomic regions affected by subclonal deletions. However, the phyloCCF still relies on the constant mutation multiplicity assumption and thus models only some of the effects of copy-number aberrations on CCFs; moreover, no standalone implementation of the method is currently available.
In this paper, we propose a new approach to analyze tumor heterogeneity and evolution in tumors that contain both SNVs and copy-number aberrations, addressing both limitations in current approaches to estimate CCF and limitations in the CCF quantity itself for phylogenetic analysis. We first show how to compute the CCF under the single split copy number assumption (Figures 1d), an assumption that relies on standard evolutionary models for SNVs and copy-number aberrations and is more realistic than the constant mutation multiplicity assumption. We then introduce a novel statistic, the descendant cell fraction (DCF) (Figures 1e), that generalizes the CCF to account for mutation losses. The DCF provides an elegant mapping between the quantities measured in bulk DNA sequencing data – copy-number aberrations and read counts of SNVs – and the evolutionary history of SNVs. Specifically, SNVs that co-occur on the same branch of the phylogenetic tree will have the same DCF. We utilize this mapping to derive a probabilistic model to estimate the CCF or DCF while accounting for uncertainties in DNA sequencing data. Finally, we address the issue of non-identifiability in the CCF and DCF by sharing information across multiple SNVs and samples. We implement our approach in an algorithm named DeCiFer (Figures 2). DeCiFer can be viewed as an intermediate between scalable approaches that compute CCFs using the restrictive constant mutation multiplicity assumption without an evolutionary model and phylogenetic approaches that simultaneously model the evolution of all SNVs and copy-number aberrations but do not scale to large numbers of mutations. DeCiFer combines the advantages of both approaches (e.g., clustering of mutations and joint evolution of SNVs and copy-number aberrations) while avoiding some of their major limitations (e.g., constant mutation multiplicity assumption and scalability). We show that that DeCiFer outperforms existing methods on simulated data. Finally, we use DeCiFer to analyze 49 metastatic prostate cancer samples (Gundem et al. 2015), and we show that DeCiFer infers DCFs that result in more realistic and more parsimonious evolutionary histories for these tumors compared to existing approaches.
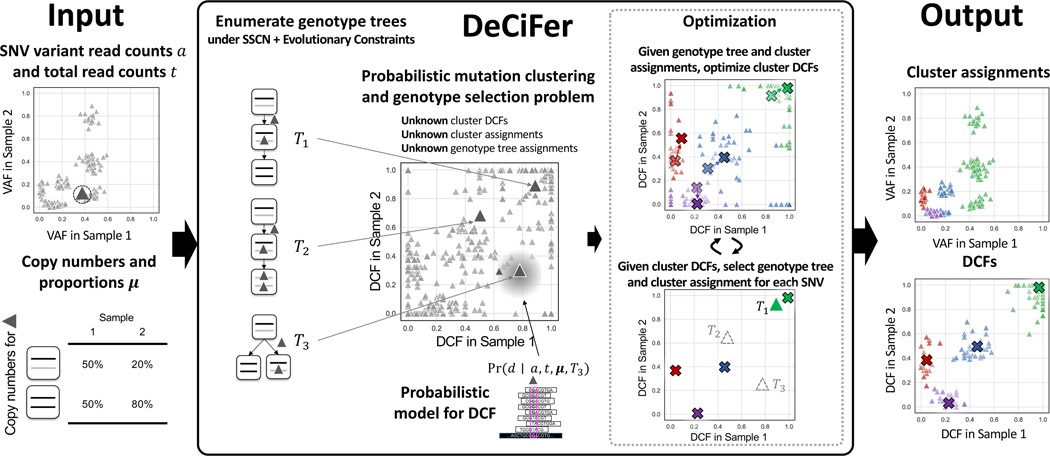
Figure 2: DeCiFer groups SNVs into clusters with shared evolutionary history, accounting for copy number aberrations and mutation loss.
(Left) Inputs to DeCiFer are variant a and total t read counts for SNVs identified in one or more tumor samples as well as the inferred copy numbers (x, y) and proportions μ(x, y) for each SNV locus. (Middle) DeCiFer examines possible genotype trees for each SNV conforming to the single split copy-number (SSCN) assumption and evolutionary constraints. Each genotype tree defines a transformation between the input data and a DCF value d in each sample. DeCiFer solves the probabilistic mutation clustering and genotype selection problem, simultaneously selecting a genotype tree for each SNV and clustering the DCF values determined by the selected genotype trees for all SNVs. DeCiFer uses a coordinate ascent approach, alternating between optimization of the DCF for each cluster given genotypes and cluster assignments followed by the selection of genotypes and cluster assignments given the DCF of each cluster. (right) Clusters output by DeCiFer often contain groups of SNVs with distinct VAFs (green points) but similar DCF values. These are a result of differing mutation multiplicities at SNV loci as well as loss of mutations in subpopulations of tumor cells.
Results
The Cancer Cell Fraction: Constant Mutation Multiplicity Assumption
The cancer cell fraction (CCF) c of an SNV is defined as the fraction of cancer cells in a sample that contain at least one copy of the SNV. The CCF is not directly observed from bulk sequencing data; rather, one observes the total number t of reads that align to the SNV locus and the corresponding number a of reads with the variant allele (Figure 1a). If the SNV locus is diploid (i.e., no copy-number aberrations), the standard approach (Roth et al. 2014, Miller et al. 2014, McGranahan et al. 2015, Dentro et al. 2017, Jamal-Hanjani et al. 2017, Yuan et al. 2018, Cun et al. 2018, Dentro et al. 2020, Xiao et al. 2020, Gerstung et al. 2020, Lakatos et al. 2020, Caravagna et al. 2020, Cresswell et al. 2020, Tarabichi et al. 2021) estimates the CCF c from the fraction of variant reads as , where ρ is the tumor purity – i.e., fraction of cancer cells in the sample – which also may be inferred from bulk sequencing data (Van Loo et al. 2010, Carter et al. 2012, Nik-Zainal et al. 2012, Oesper et al. 2013, 2014, Fischer et al. 2014, Zaccaria & Raphael 2020). Note that is the maximum likelihood estimate of the variant allele frequency (VAF) v – i.e., the proportion of copies of the locus in the sample that contain the SNV. More generally, if the SNV locus is aneuploid due to copy-number aberrations, nearly all existing methods (Roth et al. 2014, Miller et al. 2014, McGranahan et al. 2015, Dentro et al. 2017, Jamal-Hanjani et al. 2017, Yuan et al. 2018, Cun et al. 2018, Dentro et al. 2020, Xiao et al. 2020, Gerstung et al. 2020, Lakatos et al. 2020, Tarabichi et al. 2021) estimate the CCF by using the following generalization of the equation for diploid case:
| (1) |
where Ntot is the average total copy number in cancer cells and M is the number of copies of the SNV in cancer cells that contain the SNV.
While Eq. (1) has become the standard in the field, this equation incorporates strong assumptions about tumor clonal composition and evolution. To describe these assumptions, we define the genotype of an SNV locus in a cell as a triple (x, y, m) of non-negative integers, where the copy numbers (x, y) correspond to the number of maternal and paternal copies of the locus and the mutation multiplicity m ≤ x + y is the number of copies with the SNV. The CCF c is then the fraction of cancer cells that have genotypes (x, y, m) with m ≥ 1. Thus, we see that Eq. (1) assumes that m = M is fixed across all the cancer cells that contain the SNV (Figure 1c), which we state formally as follows.
Constant Mutation Multiplicity Assumption.
At every SNV locus, there exists an integer M ≥ 1 such that all genotypes at the locus have the form (x, y, m) where either m = 0 or m = M.
The Cancer Cell Fraction: Single Split Copy Number Assumption
The constant mutation multiplicity assumption severely limits the genotypes at a locus and is often violated in tumors with copy-number aberrations, as we will demonstrate in Results. Here, we define a less restrictive assumption on genotypes, the single split copy number assumption, that facilitates the computation of CCFs from bulk sequencing data under commonly used evolutionary models. Formally, we define a genotype set Γ as the set of genotypes at an SNV locus. Each genotype (x, y, m) in Γ has a corresponding genotype proportion g(x, y, m) that gives the prevalence of the genotype in the sample. Let denote the genotype proportions for genotypes in Γ, and note that the genotype proportions satisfy and . Given tumor purity ρ and a pair (Γ, g) of a genotype set and genotype proportions the CCF c is uniquely determined by the following equation:
| (2) |
where is the set of genotypes that contain the SNV.
Unfortunately, Eq. (2) is not directly applicable to bulk DNA sequencing data because neither the genotype set Γ nor the genotype proportions g are directly measured in bulk data. Rather from the aligned sequencing reads, one can estimate the VAF v of an SNV as well as the proportions μ(x, y) of cells with copy number (x, y) at the locus. The copy-number proportions may be inferred using current tools for copy number deconvolution (Van Loo et al. 2010, Carter et al. 2012, Nik-Zainal et al. 2012, Oesper et al. 2013, 2014, Fischer et al. 2014, Zaccaria & Raphael 2020). The key question is: what genotypes and genotype proportions are consistent with the estimated copy number proportions μ and VAF v? The relationship between these quantities is given by the following equations.
| (3) |
| (4) |
where F is the fractional copy number defined as . Note that F is the average copy number over all cells, including both cancer and normal cells; in contrast Ntot in Eq. (1) is the average copy number in cancer cells only. Thus, we have that for SNVs in autosomal chromosomes.
Given copy-number proportions μ and VAF v, there are often many pairs (Γ, g) that satisfy Eqs. (3) and (4); i.e., these equations are severely underdetermined. Thus, it is necessary to impose additional constraints on the pairs (Γ, g) that are considered. We make the following assumption.
Single Split Copy Number Assumption.
At every mutation locus, there is exactly one copy number with two distinct genotypes and .
We denote a genotype set as Γ* if it adheres to the single split copy number assumption. Genotype sets Γ* have two desirable properties: (1) They arise from standard evolutionary models for SNVs and copy-number aberrations (detailed in STAR Methods); (2) If genotype proportions g satisfying equations Eqs. (3) and (4) exist, then they are unique (see Eq. (13)). Note that these properties are not necessarily true for genotype sets derived from the constant mutation multiplicity assumption. We say that a genotype set Γ is consistent with v and μ provided there exist corresponding genotype proportions g satisfying Eqs. (3) and (4). STAR Methods describes necessary and sufficient conditions for consistency.
As the genotype proportions g for a single split copy number genotype set Γ* are uniquely determined given VAF v and copy-number proportions μ, the CCF c is uniquely determined as well (by Eq. (2)). Thus, we have the following relationship between CCF c and VAF v for a single split copy number genotype set Γ*.
Theorem 1.
Given tumor purity ρ, VAF v, copy-number proportions μ, and a single split copy number genotype set Γ* consistent with v and μ, the CCF c is uniquely determined by
| (5) |
where is the set of genotypes containing the mutation.
Further details and the proof for Theorem 1 are in STAR Methods. Note that similar to the constant mutation multiplicity Assumption, the CCF is non-identifiable under the single split copy number assumption since μ and v are not sufficient to determine Γ*. STAR Methods discusses how to enumerate and select genotype sets Γ*.
Recall that the VAF v is not directly measured from sequencing data; rather one observes only the total read count t and variant read count a. Thus, the affine transformation in Eq. (5) cannot be used directly to compute the CCF c from sequencing data. Many existing methods (Miller et al. 2014, McGranahan et al. 2015, Jamal-Hanjani et al. 2017, Dentro et al. 2017, Cun et al. 2018, Dentro et al. 2017, Xiao et al. 2020, Lakatos et al. 2020, Cresswell et al. 2020) calculate the CCF by assuming that the proportion of variant reads is an accurate estimate of the VAF and do not evaluate uncertainty due to sequencing errors and coverage. In STAR Methods, we introduce a probabilistic model to estimate the CCF from read counts of SNVs.
Descendant Cell Fraction
We derive a new quantity, the descendant cell fraction (DCF), a generalization of the CCF that accounts for potential SNV losses. The DCF of a mutation is the proportion of cells in a sample that are descendants of the ancestral cell where the mutation was first introduced. As an example, consider two SNVs that occurred at the same time in the same cell. If one of these SNVs is subsequently lost due to a deletion, these SNVs would have distinct CCFs at the time of sampling. However, the DCF for both SNVs would be the same, as they have the same set of descendent cells in the sample. Note that the DCF equals the CCF for SNVs that are not affected by deletions.
To define the DCF formally, we introduce the notion of a genotype tree , which is a rooted tree whose vertex set is a genotype set Γ and whose directed edges E encode evolutionary relationships between pairs of genotypes. While a tumor phylogeny models the evolutionary history of all SNVs in the tumor, a genotype tree describes the evolutionary history of only a single SNV. As such, inference of genotype trees of individual SNVs is a less challenging task than comprehensive phylogeny inference. We summarize a genotype tree TΓ and genotype proportions g by the DCF, which will enable us to assign a genotype tree to each SNV subject to a parsimony constraint regarding the number of distinct DCF values. Specifically, the DCF d of an SNV is defined as
| (6) |
where is the subset of genotypes that are descendants of the vertex corresponding to genotype (x*, y*, m*). Thus, while the CCF is the total prevalence of the subset of genotypes with mutation multiplicity m ≥ 1 at the present time, the DCF is total prevalence of genotypes that are descendants of the genotype (x*, y*, m*) where the mutation is first introduced. We have the following theorem.
Theorem 2.
Given tumor purityρ, VAF v, copy-number proportions μ, a single split copy number genotype set Γ* consistent with v and μ, and a genotype tree TΓ*, the DCF d is uniquely determined by
| (7) |
where is the set of genotypes in genotype tree that are descendants of the state (x*, y*, m*).
Observe that the only difference between Eqs. (7) and (5) is the use of ΓDCF rather than .
DeCiFer: Simultaneous Clustering and Genotype Selection using the DCF
Theorem 2 defines DCF d given VAF v, copy-number proportions μ and a genotype tree TΓ* for a single split copy number genotype set Γ*. However, neither Γ* nor TΓ* are directly observed by bulk data, and there frequently are multiple possible values that are consistent with the observed data. Examining SNVs individually, there is no way to distinguish between these values. However, by evaluating SNVs jointly and assuming that there are a small number of possible values of the DCF, we obtain constraints that reduce ambiguity in the selection of Γ* or TΓ* for individual SNVs. Specifically, we make the following assumption.
Assumption.
There exist DCF values d1, ..., dk such that for every SNV in a tumor sample at least one dj is a valid DCF for the SNV (i.e., solution of Equation (7)).
Under this assumption, SNVs may be partitioned into k groups according to their DCF. However, since SNVs may have more than one possible DCF value, the problem of identifying these groups entails the simultaneous selection of a genotype tree for each SNV (which determines the DCF value of the SNV) and the clustering of SNVs into k groups according to their DCF values.
Here, we describe this simultaneous selection and clustering problem in the more general setting where we have observations from p bulk sequencing samples from the same patient. Thus, we are given variant read counts , total read counts and copy-number proportions for each SNV i in each sample . Let be the set of genotype trees TΓ* for single split copy number genotype sets Γ* that are consistent with μi. Let be a selection of a genotype tree TΓ* for SNV i. Let be a cluster assignment for SNV i. We aim to find genotype selections s, cluster assignments z, and cluster DCFs where is the DCF of cluster j in sample that maximize the posterior probability of the parameters given the observed read counts. Eq. (30) in STAR Methods gives this posterior probability of the DCF for an individual SNV in one sample. We assume that given cluster assignments and DCFs, variant read counts are conditionally independent across samples and across SNVs. Thus, to compute the objective, we take the product across samples and SNVs. This leads to the following problem.
Probabilistic Mutation Clustering and Genotype Selection Problem.
Given a set of pairs of genotype sets and trees, variant read counts ai, total read counts ti and (iv) copy-number proportions μi for each SNV i as well as an integer k > 0 find (i) DCFs and for each SNV i, select (ii) and (iii) such that
| (8) |
is maximum.
While the hardness of this problem is open, the variant of the problem where every VAF v is observed instead of read counts a, t is NP-complete as it is equivalent to the well-studied Hitting Set problem (STAR Methods).
We introduce DeCiFer, an algorithm to solve the Probabilistic Mutation Clustering and Genotype Selection. DeCiFer uses a coordinate ascent approach to solve Eq. (8) by alternately optimizing (i) the cluster assignments z and genotype set assignments s for individual SNVs and (ii) the cluster DCFs D.
DeCiFer imposes stronger constraints on the allowed genotype sets than imposed by the single split copy number assumption, since some single split copy number genotype sets are not evolutionary plausible (for example, see the genotype set with homoplasy in Figure 1d). Specifically, we assume that the allowed genotype trees TΓ for an individual SNV conform to the following evolutionary model. First, each mutation is introduced exactly once but may be subsequently lost or amplified due to copy-number aberrations. Second, each allele-specific copy number (x, y) of the SNV locus is attained exactly once. Thus, viewing SNVs as two-state characters and copy-number aberrations as multi-state characters, we have the Dollo model for SNVs and the infinite alleles assumption for copy-number aberrations. Finally, any change in mutation multiplicity must be caused by a corresponding change in copy-number. These constraints were formally described by El-Kebir et al. (2016) (Definition 12, Supplementary Material). Note that all genotype sets Γ that meet these constraints are also single split copy number genotype sets. Under the evolutionary constraints, the mutation multiplicity m* for the split copy number (x*, y*) is m* = 1. DeCiFer enumerates using the same tree enumeration procedure introduced in SPRUCE (El-Kebir et al. 2016).
Further details of DeCiFer model selection and implementation are in STAR Methods. DeCiFer is available at https://github.com/raphael-group/decifer.
Simulations
We compared DeCiFer with PyClone (Roth et al. 2014), a commonly used method for clustering and estimation of CCFs, on simulated data. PyClone simultaneously infers mutation multiplicity for SNVs and clusters mutations based on CCF values computed from these multiplicities. However, PyClone does not include subclonal copy-number aberrations in its model. To analyze subclonal copy-number aberrations, we used two variations of PyClone. First, for mutations with subclonal copy-number aberrations, we estimate a clonal copy-number by computing the average allele-specific copy number at the locus over all clones and rounding to the nearest integers. Second, we used a procedure described in the TRACERx study (Jamal-Hanjani et al. 2017) to estimate CCFs before running PyClone. Specifically, we estimated CCFs for each SNV using a constant mutation multiplicity-based method that accounts for subclonal copy-number aberrations (Dentro et al. 2017). Then we adjusted the variant read counts input to PyClone to match the computed CCF for heterozygous variant on a diploid locus. Note that by pre-computing CCFs, this procedure pre-selects mutation multiplicities independently for each SNV. We refer to this procedure as adjusted PyClone in this section, or “Adj. Pyclone” in Figure 3). Further details are in the Quantification and Statistical Analysis section of STAR Methods.
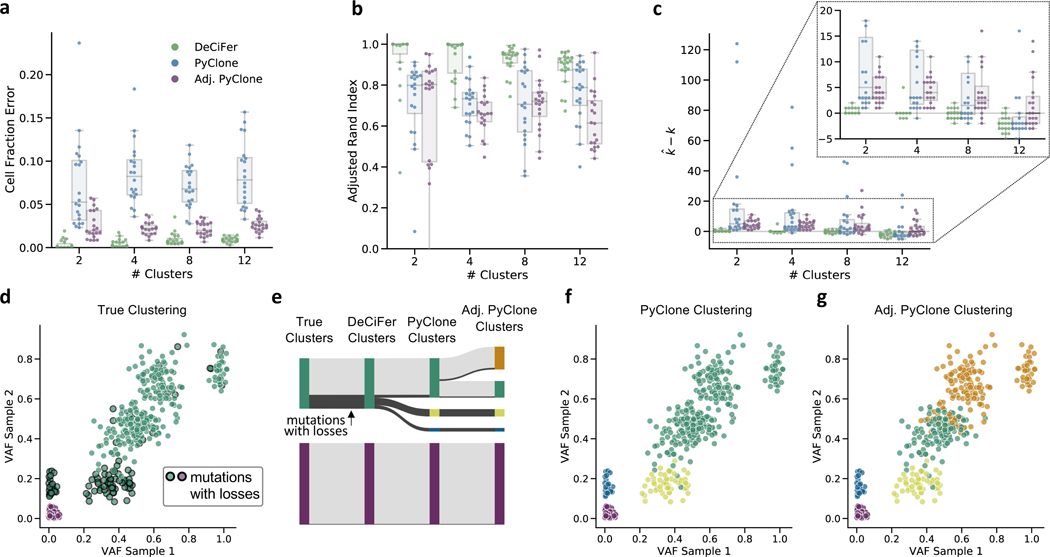
Figure 3: DeCiFer accurately infers cell fractions and clusters SNVs on simulated data with SNV losses.
a, The error in quantifying cell fractions (DCF for DeCiFer and CCFs for PyClone and Adjusted PyClone) on simulated data with 5 samples, 1000 mutations and varying number of clusters. Each jitter-boxplot gives results for twenty simulated data instances. b, The performance of each method in clustering SNVs as measured by adjusted Rand index. c, The difference between the inferred number of clusters and the true number k of clusters. d-g, Results from one simulation with k = 2 clusters demonstrates differences between CCF and DCF. d, Variant allele frequencies from two out of five samples: green mutations are the truncal cluster and the purple mutations are a subtruncal cluster that is absent in these two samples. Mutations that are lost in at least one sample are highlighted with a black outline. e. The relationship between the true clusters and the clusters inferred by DeCiFer and PyClone. DeCiFer infers two clusters and accurately recovers the true cluster assignments for all mutations. f, PyClone infers four clusters subdividing the truncal cluster into three separate clusters. The two additional clusters (yellow and blue) are defined by mutations that were lost in subpopulations of tumor cells. g, Adjusted PyClone infers five clusters subdividing the truncal cluster into four separate clusters.
We compared the three methods on simulated data with with 2, 4, 8, and 12 clusters of SNVs generated as follows. Each simulated instances contained 1000 SNVs, 5 samples and an expected read depth of 100X. We simulated input data by partitioning the SNVs into the given number of clusters and simulating an evolutionary process where cells accumulate clusters of SNVs as well as copy-number aberrations (whole chromosome, whole arm, and focal events) which may amplify or delete overlapping SNVs. To simulate the sequencing of every SNV in each sample, we draw the total number of reads from a Poisson distribution with rate equal to the coverage and the number of variant reads from a binomial distribution, as done in previous studies (Deshwar et al. 2015, Satas et al. 2020, Satas & Raphael 2017). For each number of clusters, we simulate 20 instances. The simulation process is described in detail in STAR Methods.
We find that DeCiFer outperforms both PyClone and the adjusted PyClone across all inputs according to three metrics. First, we compare methods using cell fraction error – the mean absolute difference between the inferred cell fraction (where cell fraction is DCF for DeCiFer and CCF for PyClone) and the true cell fraction over all SNVs in all samples (Figure 3a). Second, we evaluate the quality of clustering results by computing the adjusted Rand index across all pairs of SNVs (Figure 3b). We find that while the adjusted PyClone is more effective at inferring cluster CCFs, this adjustment does not improve and may worsen the accuracy of mutation clustering. This may be caused by the selection of mutation multiplicities when computing the input for adjusted PyClone. Finally, we observe that DeCiFer has highest accuracy in inferring the number of clusters (Figure 3c). Both versions of PyClone overestimate the number of clusters for these instances, with PyClone inferring between 40 to 120 clusters on several instances. In contrast, DeCiFer accurately estimates the number of clusters for most inputs and moderately underestimate the number of cluster for data with 12 clusters.
To further characterize the differences between methods, we examine one simulated instance (random seed s = 1) with k = 2 clusters (Figure 3d-g). In this example, the true clustering consists of a truncal cluster (green) and a subtruncal cluster (purple) which is present in 2 of 5 samples. DeCiFer infers two clusters(Figure 3e) accurately grouping all mutations in the truncal cluster. PyClone infers four clusters, subdividing the truncal cluster into three separate clusters (Figure 3e, f). In contrast, adjusted PyClone infers five clusters, subdividing the truncal cluster into four separate clusters (Figure 3e, g). The SNVs in two of the extra clusters inferred by Pyclone and Adj. Pyclone (yellow and blue clusters in Figure 3f, g) are affected by mutation losses, which DeCiFer correctly groups together by using the DCF. The extra cluster inferred by Adjusted Pyclone (orange cluster in Figure 3g) results from incorrect selection of mutation multiplicies. PyClone correctly groups together the SNVs in these clusters orange and green cluster because it selects mutation multiplicities while clustering. This example illustrates the importance of evaluating mutation multiplicities simultaneously while clustering SNVs and also accounting for mutation losses, key features of DeCiFer.
We performed further simulations to evaluate the performance of DeCiFer across a range of parameters (Figure S1). We simulate data with different numbers of SNVs (100, 250, 500, or 1000), samples (1, 3, 5, or 7) and varying expected read depth (25×, 100×, 200×, or 1000×). We see that performance generally increases with larger numbers of samples (Figure S1a) and higher read depth (Figure S1a). The number of SNVs minimally affects the performance of DeCiFer and PyClone (Figure S1b). We also compared DeCiFer with PhyloWGS (Deshwar et al. 2015), a method that infers tumor phylogenies while simultaneously clustering SNVs into clones. We ran PhyloWGS on simulated instances with 100 and 1000 SNVs. While reconstruction of a tumor phylogeny jointly from copy-number aberrations and all SNVs should in principle produce the most accurate mutation multiplicities, we found that on instances with 100 SNVs, PhyloWGS had the lowest performance (Figure S2). On instances with 1000 SNVs, we found that PhyloWGS did not converge in reasonable time (<3 days). These results suggest that phylogeny inference is challenging for large numbers of SNVs in the presence of copy-number aberrations, leading to convergence issues for approaches like PhyloWGS that attempt to simultaneously cluster SNVs and infer phylogenetic tree relating these clusters. In contrast, DeCiFer completed the largest instances in under 1.5 hours and produced highly accurate clusters. This suggests that the approach of simultaneous selection of genotype trees for individual SNVs while clustering DCF values retains many of the advantages of full phylogenetic inference.
Finally, we evaluated DeCiFer across varying sizes of mutation clusters. We simulated data with three clusters: a truncal cluster and two subtruncal clusters. The truncal cluster comprises 20% of mutations, and we simulate instances where the smaller cluster comprises 40%, 20%, 10% and 5% of mutations. For each value of prevalence, we generated 10 instances with 1000 mutations, 3 samples and an expected read depth of 100x. We find that while the cell fraction error increases and the adjusted Rand index decreases when the prevalence of the smaller cluster decreases, the drop in performance is modest (Figure S3) suggesting that DeCiFer’s results are fairly stable under varying distribution of SNVs across tumor clones.
Metastatic Prostate Cancer
We analyzed SNVs and copy-number aberrations identified in whole-genome sequencing data of 49 tumor samples from 10 metastatic prostate cancer patients from Gundem et al. (2015). The initial published analysis (Gundem et al. 2015) of these patients inferred CCFs for a subset of validated SNVs using the constant mutation multiplicity assumption, clustered these SNVs into tumor clones according to their CCF values, and built a phylogenetic tree describing the evolution of these clones. We analyzed SNVs and copy-number aberrations from another published analysis of these same samples (Zaccaria & Raphael 2020), computing the DCF of each SNV using DeCiFer and computing the CCF of each SNV using the method from Dentro et al. (2017) that relies on the constant mutation multiplicity assumption. Further details of the analysis are in the Quantification and Statistical Analysis section of STAR Methods.
We found that the DCFs computed by DeCiFer are substantially different from the constant multiplicity CCFs for a large number of SNVs (Figure 4 and Figure S4). We summarize these differences according to two commonly used classifications of SNVs. First, we classify SNVs as clonal if they are inferred to be present in all cells in a tumor sample (CCF ≈ 1) or subclonal if they are inferred to be present only in a subpopulation (CCF ≪ 1). The clonal/subclonal classification categorizes SNVs according to their presence in cancer cells at the time of sampling. Second, we classify SNVs as truncal if they are inferred to occur before the most recent common ancestor of all cancer cells in the sample, and subtrunal otherwise. Most previous studies (Roth et al. 2014, Miller et al. 2014, McGranahan et al. 2015, Dentro et al. 2017, Yuan et al. 2018, Cun et al. 2018, Dentro et al. 2020, Xiao et al. 2020, Gerstung et al. 2020, Lakatos et al. 2020, Caravagna et al. 2020, Cresswell et al. 2020) assume that clonal SNVs and truncal SNVs are identical. However, this assumption does not necessarily hold when SNVs are lost due to deletions in cancer cells. Using CCFs, one cannot distinguish such lost mutations from mutations that never occurred in a sample. However, the DCFs of these two cases will be different. Thus, by computing the DCF, DeCiFer has the ability to more precisely designate SNVs as truncal, especially those that were subsequently deleted and are subclonal. We classify SNVs as truncal if DCF ≈ 1 or subtruncal if DCF << 1 (Figure 4a).
Figure 4: DeCiFer changes the classification of a large number of SNVs.
a, The classification of SNVs depends on the values of their cell fractions (i.e., CCF or DCF). SNVs are classified as clonal/subclonal based on their CCF in a sample. SNVs are classified as truncal/subtruncal based on their DCF, which quantifies evolutionary history with respect to the cells in the sample. b, Numbers of SNVs with different classification across 49 samples from 10 prostate cancer patients.
Overall, >23000 SNVs across all samples had a change in classification (Figure 4a) when using constant multiplicity CCFs versus DCFs inferred by DeCiFer. Multiple factors contribute to such changes. First, we found that ∼8500 SNVs across all samples that were classified as subclonal using constant multiplicity CCFs are classified as truncal by DeCiFer (Figure 4b). This difference is due to the loss of mutations by deletions. Such losses affect a moderate percentage of SNVs across all patients (5–32%, Figure S4) consistent with other recent estimates of the frequency of mutation losses (McPherson et al. 2016). We also see a large number of classification differences that cannot be explained by losses of SNVs. For example, we found that ∼12000 SNVs across all samples are classified as clonal using constant multiplicity CCFs and as subtruncal by DeCiFer (Figure 4b). These correspond to a moderate percentage of SNVs across all patients (3–40%, Figure S4). These differences are explained by choices of different mutation multiplicities (and different genotype sets Γ), for these SNVs. We will show below that the genotypes selected by DeCiFer often result in more parsimonious explanations for the observed data.
Another key difference in classification of SNVs is the classification of mutations as absent in a sample. SNVs without any observed variant reads in a sample (VAF = 0) are typically classified as absent from the sample. As a result, current cancer sequencing studies generally assume in downstream analyses that these SNVs were never present in the observed cancer cells in that sample or their ancestors. However, SNVs can be deleted by copy-number aberrations during tumor evolution and, when all cancer cells in a sample have been affected by such deletions, truncal SNVs may appear as absent. We find that 1, 560 SNVs across all samples classified as absent using the constant multiplicity CCFs are classified as truncal or subtruncal by DeCiFer (Figure 4b), corresponding to 0–5% of the total number of SNVs across patients (Figure S4c).
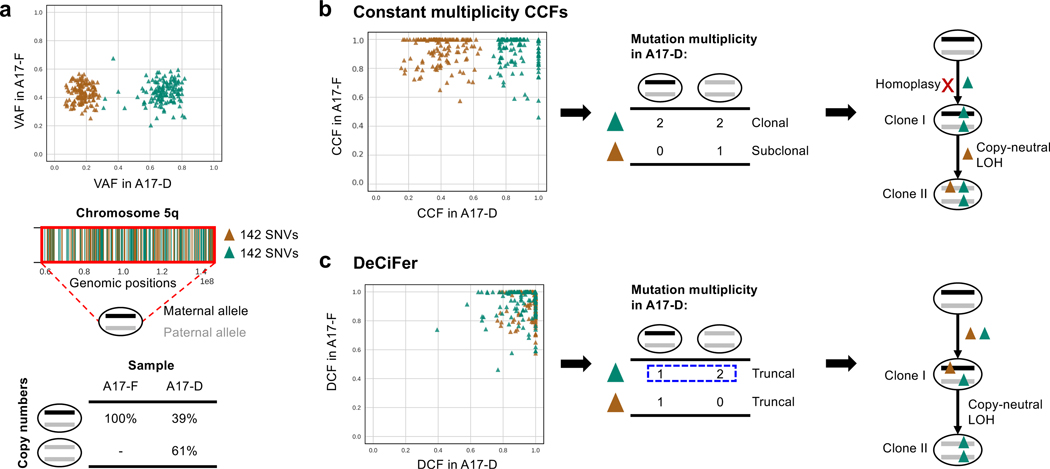
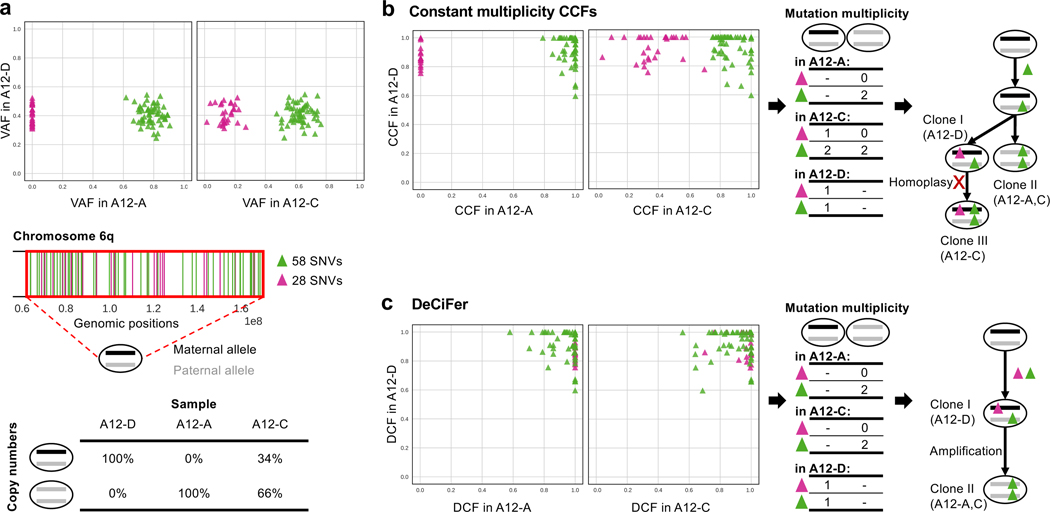
The differences between the inferred constant multiplicity CCFs and the DCFs do not simply result in different classifications of SNVs but also have a critical impact on downstream phylogenetic analysis. For example, on chromosome 5q in prostate cancer patient A17, we found two groups of 284 SNVs with different VAFs in sample A17-D that have been differently classified (Figure 5a, top). While one group (green) is classified as clonal and the other group (brown) as subclonal based on constant multiplicity CCFs, DeCiFer classifies both groups as truncal. A previous copy-number analysis (Zaccaria & Raphael 2020) identified the presence of cancer cells with different copy numbers in the same region (Figure 5a, bottom): 61% of cancer cells have a copy-neutral loss of heterozygosity (i.e., copy number (2, 0)), while the remaining cells are heterozygous diploid (i.e., copy number (1, 1)). Following the constant mutation multiplicity assumption, the mutation multiplicity of the clonal cluster (green) is 2 in all cancer cells (Figure 5b), indicating the presence of cells with genotype (1, 1, 2). As each of these SNVs are present on both the two copies of the locus, this implies that each of the 142 SNVs occured twice (homoplasy), once on each homologous chromosome. While recurrent mutations, or homoplasy, may occasionally happen in tumor evolution (Kuipers et al. 2017), observing homoplasy in 142 SNVs – all on the same chromosomal arm – seems highly unlikely.
Figure 5: DeCiFer reclassifies subclonal mutations from constant multiplicity CCFs as truncal resulting in simpler evolutionary scenarios on prostate cancer patient A17.
a, (Top) Two groups of 284 SNVs on chromosome 5q (brown and green) have similar VAFs in sample A17-F but different VAFs in sample A17-D, while being affected by the same copy-number aberration. (Middle) Positions of green and brown SNVs on chromosome 5q. (Bottom) Inferred copy numbers in samples: all cells in A17-F are heterozygous diploid, while 61% of cancer cells in A17-D have a copy-neutral loss of heterozygosity. b, A constant mutation multiplicity based method (Dentro et al. 2017) infers CCFs that separate the 284 SNVs into a clonal cluster (green) and a subclonal cluster (brown). Following the constant mutation multiplicity assumption, the clonal SNVs (green) are inferred to have mutation multiplicity of 2 in two distinct tumor clones (clone I and II). This leads to a phylogenetic reconstruction (right) with the unrealistic conclusion that each of the 142 SNVs occurred twice independently on both homologous chromosomes (i.e., 142 homoplasy events). c, DeCiFer infers DCF≈1 for all 284 SNVs by identifying different mutation multiplicities (blue dashed box) for SNVs in the green cluster across the two clones (I and II) and by identifying loss of brown SNVs in subset of tumor cells. Thus all SNVs in the green and brown cluster are truncal. This results in a realistic tumor phylogeny where the mutation multiplicities are consistent with the observed copy-neutral loss of heterozygosity.
On the same patient A17, DeCiFer infers DCFs that result in a much more realistic mutation multiplicies and phylogenetic reconstruction. In particular, DeCiFer infers that the two groups of SNVs (green and brown in Figure 5a) are part of the same truncal cluster (i.e., DCF≈ 1) but have different mutation multiplicities: the SNVs in the first group (green) have a multiplicity of 1 in one clone and a multiplicity of 2 in the other, a scenario that is not allowed under the constant mutation multiplicity assumption. DeCiFer’s results are consistent with a realistic evolutionary scenario where the two groups of SNVs occurred on different alleles of the chromosome: the first group (green) was amplified during the copy-neutral loss of heterozygosity event, while the second group (brown) was lost. Further supporting this reconstruction is the observation that the two groups of SNVs are randomly distributed over chromosome 5q (Figure 5a), indicating that the differences in VAF between the green and brown SNVs are not due to an error in the copy numbers for one group. Thus, DeCiFer’s classification of the SNVs in the brown group as truncal, but lost in a subpopulation of cancer cells results in a simpler and more realistic reconstruction of tumor evolution compared to the classification of these SNVs as subclonal according to their constant multiplicity CCFs.
On prostate cancer patient A12, we see an example of mutations that are classified as absent using constant multiplicity CCFs but classified as truncal by DeCiFer. Specifically, Chromosome 6q contains 86 SNVs that are split into two groups with different VAFs across three samples (Figure 6a, top): the first group (green) has VAFs between 0.4–0.8 in all samples, while the second group (magenta) has VAFs between 0.1–0.4 in samples A12-C and A12-D but VAFs ≈ 0 in the remaining sample A12-A. These two groups of SNVs have different constant multiplicity CCFs across samples and result in the inference of three distinct tumor clones with a complicated evolution characterized by recurrent mutation (homoplasy) of 58 SNVs in the magenta cluster (Figure 6b). However, a previous copy-number analysis (Zaccaria & Raphael 2020) revealed the presence of a copy-neutral loss of heterozygosity on chromosome 6q in these samples. The proportions of cancer cells that have the loss-of-heterozygosity event closely follow the VAFs of the SNVs in the magenta group of SNVs (Figure 6a, bottom): 100%, 66%, and 0% of cancer cells have a copy-neutral loss of heterozygosity in A12-A, A12-C, and A12-D, respectively. DeCiFer infers that all the 86 SNVs in the green and magenta groups are truncal with DCFs ≈ 1, and that the magenta group of SNVs were lost during the copy-neutral loss of heterozygosity event (Figure 6c). Indeed, in sample A12-A, where all cancer cells have the copy-neutral loss of heterozygosity, these SNVs have a VAF= 0. Note that the phyloCCF correction introduced in Jamal-Hanjani et al. (2017) to address issues of mutation loss would not have identified the magenta SNVs as truncal. Since phyloCCF is only applied to genomic regions affected by subclonal deletions and on each sample independently, it only considers SNVs with VAF > 0. Therefore, phyloCCF cannot distinguish between mutation losses and absences in a given sample as done by DeCiFer in this example. Thus DeCiFer yields a more parsimonious reconstruction of tumor evolution than obtained with constant multiplicity CCFs, with fewer tumor clones and no massive homoplasy.
Figure 6: DeCiFer accurately identifies losses of SNVs in prostate cancer patient A12.
a, Two groups of 87 SNVs on chromosome 6q (green and magenta) have different VAFs in samples A12-A and A12-C, with one group (magenta) having VAF = 0 in A12-A. (Middle) Positions of green and magenta SNVs on chromosome 6q. (Bottom): Inferred copy numbers in samples: sample A12-A only contains cancer cells with a copy-neutral loss of heterozygosity, A12-D only contains heterozygous diploid cells, and A12-C contains a mixture of both. b, A constant mutation multiplicity based method (Dentro et al. 2017) infers CCFs that separate the SNVs into a clonal cluster in all samples (green) and another cluster (magenta), which is clonal in A12-D, absent in A12-A, and subclonal in A12-C. Following the constant mutation multiplicity assumption, the mutation multiplicities in each sample indicate the presence of three distinct tumor clones (labeled I, II, and III). This leads to a phylogenetic reconstruction (right) with the unrealistic conclusion that 58 SNVs occurred twice independently on both homologous chromosomes in Clone III (58 homoplasy events). c, DeCiFer infers DCF ≈ 1 for all SNVs by identifying different mutation multiplicities (blue dashed box) for SNVs in green cluster in sample A12-C and by identifying the loss of 28 magenta SNVs in a subset of tumor cells due to a copy-neutral loss of heterozygosity. Thus, all SNVs in green and magenta clusters are truncal. Notably, these 28 SNVs have DCF ≈ 1 also in A12-A even though their VAF = 0; this is because all cancer cells have a copy-neutral loss of heterozygosity in sample A12-A. The inferred losses of these 28 SNVs are well supported by the fact that the proportion of cancer cells with the copy-neutral loss of heterozygosity (second row of table in (a)) closely follows their variations of VAF across samples (VAFs in (a)).
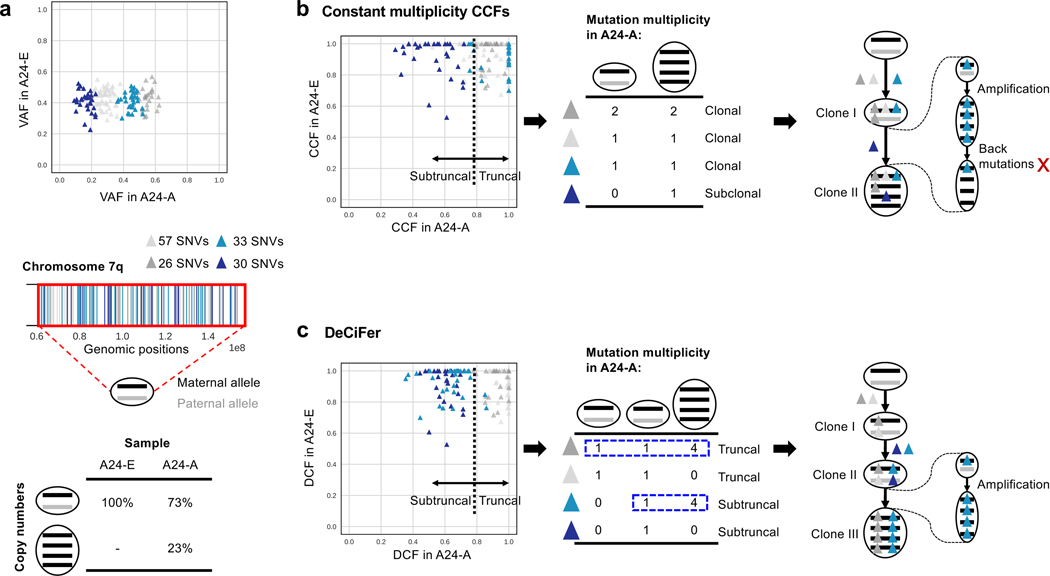
DeCiFer also classifies ∼12, 000 SNVs as subtruncal across all samples that are classified as clonal using constant multiplicity CCFs (Figure 4b). Such SNVs correspond to between 3–41% of the total number of SNVs in different patients (Figure S4c). We observe this on prostate cancer patient A24, where 167 SNVs in chromosome 7 of prostate cancer patient A24 form four distinct groups with different VAFs in sample A24-A. In this genomic region, there are two groups of cancer cells with different copy numbers (Figure 7a): 27% of cancer cells have a loss of heterozygosity with amplifications (i.e., allele-specific copy numbers {4, 0}), while the remaining cancer cells are diploid (i.e., allele-specific copy numbers {1, 1}). Using the constant multiplicity CCFs, these SNVs form two clusters (Figure 7b): one subclonal cluster composed of 30 SNVs, and one clonal cluster composed of the remaining 137 SNVs. Based on the constant mutation multiplicity assumption, all the clonal SNVs are inferred to have a constant SNV multiplicity of either 1 or 2. However, this solution is biologically unlikely: if an SNV was present in the cell where the amplification occurred, then the cell would have 4 copies of the SNV. Instead, only 1 or 2 copies are inferred to have the SNV, implying that back mutations simultaneously occurred for 33 SNVs (light blue) and homoplasy events simultaneously occurred for 26 SNVs (dark grey). DeCiFer identifies one group of 60 SNVs (light and dark blue) belonging to a subtruncal cluster (CCF≈ 0.7) while the remaining SNVs (light and dark grey) belong to the truncal cluster (Figure 7c). The DeCiFer solution corresponds to a more realistic reconstruction of tumor evolution, where differences in mutation multiplicities explain different cluster VAFs and are consistent with an amplification event.
Figure 7: DeCiFer accurately identifies subtruncal SNVs that are classified as truncal by the constant multiplicity CCFs with unrealistic evolutionary histories.
a, 167 somatic SNVs are located on chromosome 7 of prostate cancer patient A24. b, Four clusters of these SNVs have the same values of VAF in sample A24-E but different values in A24-A. c, Different cells have different copy numbers in the two samples for the genomic region harboring these SNVs: while all cells in A24-E are diploid in this region (i.e., copy numbers (1, 1)), the 20% of cells in A24-A have a loss of heterozygosity with an amplification (i.e., copy numbers (4, 0)). d, An existing method (Dentro et al. 2017) using the constant mutation multiplicity assumption infers that three clusters (cyan, and light and dark grey) of SNVs in (b) have CCF≈1 in both samples, corresponding to truncal SNVs. Instead, the method infers that the remaining cluster (dark blue) is subclonal in A24-A, which thus includes two tumor clones (clone I and II). Based on the values of VAF and the constant mutation multiplicity assumption, the method infers that each of the three clusters of clonal SNVs have the same SNV multiplicity: two of these clusters (light grey and cyan) have SNV multiplicity of 1 and the other cluster (dark grey) has an SNV multiplicity of 2. Since all the SNVs are affected by an amplification of the retained allele and since SNVs are also amplified with the corresponding allele, this result implies the unrealistic occurrence of back mutations for all the clusters; for example, three back mutations must have occurred for one of these clusters (cyan). e, DeCiFer infers that two (light and dark grey) of the clusters in (b) have DCF≈1 and correspond to truncal SNVs, while the other two remaining clusters (light and dark blue) have DCF≈0.6 and correspond to subtruncal SNVs. Specifically, DeCiFer obtains this result by identifying the loss of two clusters (light gray and dark blue) located on the same allele (black) and the presence of different mutation multiplicities in different clones (clones II and III) for the other two remaining clusters (dark grey and light blue), resulting in a realistic tumor phylogeny.
Discussion
The cancer cell fraction (CCF) is the cornerstone of tumor heterogeneity and evolution analysis using single-nucleotide variants (SNV). However, we demonstrated that current approaches to estimate CCFs suffer from major limitations and these limitations have striking consequences on real data. First, nearly all existing methods to estimate CCFs are based on the constant mutation multiplicity assumption that is violated in many tumors. Second, the CCF is not the correct quantity to group mutations for phylogenetic analysis in the case where SNV losses occur due to copy-number aberrations, a case that is common in solid tumors. In this work, we address these limitations by: (i) introducing the single split copy number assumption, a more realistic alternative to the constant mutation multiplicity assumption; (ii) defining the descendant cell fraction (DCF), a generalization of the CCF that accounts for SNV losses; (iii) developing DeCiFer, an algorithm that simultaneously estimates DCFs (or CCFs) of individual SNVs and clusters SNVs into a small number of groups according to these DCFs (or CCFs) across multiple tumor samples. We show that DeCiFer improves the identification of SNVs that co-occurred in the same tumor clone on both simulated and real cancer data, yielding more realistic reconstructions of tumor evolution compared to earlier approaches based on CCFs inferred using the constant mutation multiplicity assumption. DCF clusters account for mutation losses and differences in copy number, and thus can be used as input to standard tumor phylogeny methods (Popic et al. 2015, Qiao et al. 2014, El-Kebir et al. 2015, Malikic et al. 2015, Husic et al.´ 2019). This will enable phylogeny inference for realistic sized problems containing thousands of SNVs whose copy numbers may differ within and across tumor samples. DeCiFer can also be run with CCFs instead of DCFs, which may be preferable for certain applications such as neoantigen prediction (Cai et al. 2018) where identifying the clonal status of mutations is important.
While DeCiFer enables us to overcome some major limitations of previous studies, there are several venues for future improvements. First, we assume that the given copy numbers and proportions are exact. However, methods that infer copy numbers and proportions from bulk DNA sequencing data are subject to errors and may miss copy-number aberrations that are small or present at low proportion in a sample. This uncertainty could be incorporated into the DeCiFer model. Second, further improvements in SNV clustering are possible, such as better modeling of the tail of low prevalence SNVs that are expected due to neutral evolution (Caravagna et al. 2020). Third, breakpoints of structural variants could also be analyzed by DeCiFer since the prevalence of these mutations is proportional to read counts (Cmero et al. 2020). Finally, the genotype trees selected by DeCiFer for each SNV could be combined into tumor phylogenies, perhaps using consenus tree methods. DeCiFer provides a robust framework to decipher tumor heterogeneity in the presence of copy number aberrations providing a tool to improving understanding of tumor development and evolution.
STAR Methods
RESOURCE AVAILABILITY
Lead Contact
Requests for further information should be directed to and will be fulfilled by the lead contact, Ben Raphael (braphael@princeton.edu).
Data and Code Availability
DeCiFer code is available on GitHub at https://github.com/raphael-group/decifer(DOI 10.5281/zenodo.5082565) and it is distributed through Bioconda at https://bioconda.github.io/recipes/decifer/README.html. The simulations as well as the processed data and DeCiFer’s results for the prostate cancer patients analyzed in this study are available on GitHub at https://github.com/raphael-group/decifer-data. Whole-genome DNA sequencing data for all samples of the prostate cancer patients are available from the European Genome-phenome Archive (EGA) under accession number EGAS00001000262.
METHOD DETAILS
Derivation of Theorem 1
In this section, we derive in detail Main Text Theorem 1, which describes the relationship between CCF c and VAF v for an single split copy number genotype set Γ*. We will begin by restating several definitions provided in the main text. Given the tumor purity ρ, genotype set Γ and genotype proportions g uniquely determine the CCF c.
Definition 1.
The cancer cell fraction (CCF) c is defined in terms of a genotype set Γ and genotype proportions g and tumor purity ρ as
| (9) |
where ΓCCF is the subset of genotypes where m ≥ 1.
The genotype set Γ and genotype proportions uniquely determine the VAF v as follows.
Definition 2.
The variant allele frequency (VAF) v is defined in terms of a genotype set Γ and genotype proportions g as
| (10) |
where
| (11) |
is the fractional copy number of the locus as defined by Γ and g.
The genotype set Γ and genotype proportions uniquely determine the copy-number proportions μ as follows.
Definition 3.
The copy-number proportions μ is defined in terms of a genotype set Γ and genotype proportions g as
| (12) |
for all copy-number states (x, y).
We define consistency between the VAF v, copy-number proportions μ, genotype sets Γ and the underlying genotype states g in terms of the above equations.
Definition 4.
Genotype set and proportions (Γ, g) are consistent with VAF v and copy-number proportions μ provided that Eqs (10) and (12) are satisfied.
Definition 5.
Genotype set Γ is consistent with VAF v and copy-number proportions μ provided that there exist genotype proportions g such that Eqs. (10) and (12) are satisfied.
In the main text, we introduce the single split copy number assumption, which follows from simple evolutionary models on SNVs and copy-number aberrations: the Dollo model for SNVs, and infinite alleles model for allele-specific copy numbers.
Assumption 1. Single Split Copy Number.
At every SNV locus, there is exactly one copy-number state with two distinct genotypes and .
We make the claim for single split copy number genotype sets Γ* that provided consistent genotype proportions g exist, they are unique. Specifically they take the following form.
Lemma 1.
Given VAF v, copy-number proportions μ, and a single split copy number genotype set Γ*, if genotype proportions g exist such that are consistent with VAF v and copy-number proportions μ, they are uniquely determined as
| (13) |
where
| (14) |
This follows from the definition of consistency and Eqs. (10) and (12). A detailed proof of this and subsequent lemmas and theorems are provided in the Proofs section. Note that λ has a natural interpretation as the proportion of cells with copy-number state (x, y) that have the mutation, thus quantifying the “split” of the single split copy number state.
Lemma 1 gives the closed form of consistent genotypes but notes that there may not exist consistent genotype proportions for a given VAF v, copy-number proportions μ, and single split copy number genotype set Γ*. Below, we describe two conditions that together are necessary and sufficient for the existence of consistent genotype proportions.
Lemma 2.
Given VAF v, copy-number proportions μ, and a single split copy number genotype set Γ*, genotype proportions g such that / are consistent with VAF v and copy-number proportions μ exist if and only if
For all copy-number states (x, y) such that , there exists state for some m.
λ is in the range [0, 1] (Eq. (14)).
The constraint on also defines the range of VAFs that are possible for a given μ and Γ*.
Lemma 3.
A VAF v is feasible for copy-number proportions μ and a single split copy number genotype set Γ* consistent with μ provided v is in the range where
| (15) |
As the CCF is determined by genotype proportions, we can use Lemma 1 to characterize CCF c in terms of λ.
Lemma 4.
Given (i) copy-number proportions μ, (ii) a single split copy number genotype set Γ and (iii) the tumor purity ρ, the CCFs c resulting from genotype proportions g such that (Γ, g) is consistent with μ are uniquely determined as
| (16) |
for any value of the splitting parameter λ ∈ [0, 1].
These results jointly yield Theorem 1. For a detailed derivation, see Proofs.
Theorem 1.
Given tumor purity ρ, VAF v, copy-number proportions μ, and an single split copy number genotype set Γ* consistent with v and μ, the CCF c is uniquely determined by
| (17) |
where is the set of genotypes containing the mutation.
Derivation of the CCF formula under the Constant Mutation Multiplicity Assumption
We restate the constant mutation multiplicity assumption given in the main text.
Assumption 2. Constant Mutation Multiplicity.
At every SNV locus, there exists an integer M ≥ 1 such that all genotypes at the locus have the form (x, y, m) where either m = 0 or m = M.
Under this assumption, many methods approximate the CCF as
| (18) |
where is the average copy number of all cancer cells. By contrast, the fractional copy number F is the average copy number of all cells, tumor and normal cells alike. We have the following relationship for SNVs in autosomal chromosomes.
| (19) |
We will now show that the this equation approximates the CCF, as given by Definition 1.
Proposition 1.
Under the constant mutation multiplicity assumption with SNV multiplicity M and average copy number , variant allele frequency and tumor purity ρ, the CCF is approximated as
| (20) |
Proof.
We begin using Definition 1 that defines the CCF in terms of .
Next, we use the constant mutation multiplicity assumption, stating that for all where m > 0 it holds that m = M.
| (21) |
We use Definition 2 that defines the VAF in terms of (Γ, s).
Next, we use the constant mutation multiplicity assumption, stating that for all where m > 0 it holds that m = M.
Then, we rearrange terms.
| (22) |
We substitute (22) in (21), leading to
Finally, we use (19), leading to
□
Probabilistic model for CCF
Recall that the VAF v is not directly measured from sequencing data; rather one observes only the total read count t and variant read count a. Thus, the affine transformation in Eq. (5) cannot be used directly to compute the CCF c from the VAF v. Many existing methods (Miller et al. 2014, McGranahan et al. 2015, Jamal-Hanjani et al. 2017, Dentro et al. 2017, Cun et al. 2018, Dentro et al. 2017, Xiao et al. 2020, Lakatos et al. 2020, Cresswell et al. 2020) calculate the CCF by assuming that the proportion of variant reads is an accurate estimate of the VAF and do not evaluate uncertainty due to sequencing errors and coverage. Here we show how to derive a probability distribution Pr(c) for the CCF c from any probability distribution Pr(v) on the VAF v. Specifically, using a change-of-variable technique, we compute the posterior probability of the CCF given the observed data and a single split copy number genotype set as
| (23) |
where
| (24) |
is the inverse of Eq. (5).
To derive , we first apply Bayes’ Theorem, giving
| (25) |
We then assume that the VAF is conditionally independent of the total read count t given μ and Γ and that variant read count v is conditionally independent of μ and Γ given the VAF V (c) and total read count t. This yields the following posterior probability for V (c).
| (26) |
is the likelihood of the observed variant read counts for a given VAF value. is a prior over VAFs. is the prior probability of the VAF given copy-number proportion and a genotype set. In Lemma 3 in STAR Methods, we describe that not all VAFs are feasible given copy-number proportions μ and single split copy number genotype set Γ*. For example, 0.5 is an upper bound for VAFs v for heterozygous mutations in diploid regions. Thus, the prior has support only on the range of feasible VAFs as defined by Eq. (15).
One can use any reasonable distributions for the prior and likelihood. In practice, DeCiFer uses a binomial or beta-binomial distribution for the likelihood. For the prior, DeCiFer uses a uniform prior over the feasible range of VAFs, . Thus, DeCiFer has the following posterior distribution over the CCF c.
| (27) |
where B is the binomial or beta-binomial distribution and Z is a normalization constant. In Quantification and Statistical Analysis, we describe how we estimate parameters for the beta-binomial distribution from sequence data.
Probabilistic model for DCF
Using a similar procedure, we may obtain a posterior probability distribution over DCFs d. Here, the inverse transformation V (c) is replaced with
| (28) |
Note that ΓDCF is the set of genotypes in genotype tree TΓ* that are descendants of the state . Thus V (d) depends on both the genotype set Γ and the genotype tree TΓ. We thus have
| (29) |
The probability model for VAFs is unchanged. Thus, using a uniform prior and binomial or beta-binomial likelihood, we have
| (30) |
Mutation clustering and genotype selection
We formalize the theoretical problem of SNV clustering and selection when VAFs v are observed rather than read counts a, t. In this case, let be the set composed of pairs of single split copy number genotype sets and genotype trees that are consistent with μ. Note that when v and μ are observed, the DCF d is fully determined by a pair and the observed copy-number proportions μ and purity ρ (see 2 Eq. (7) in Theorem 2). Let be a selection of a genotype set and genotype tree pair for SNV i This leads to the following problem.
Problem 1 (Mutation Clustering and Genotype Selection Problem).
Given (i) an integer k > 0, and for each SNV i, (ii) a set of pairs of genotype sets and trees; find (i) a set of size k of DCF values and, for each SNV i, select (ii) such that where di is the DCF determined by si.
The Mutation Clustering and Genotype Selection problem is an instance of the well-known Hitting Set problem, which is known to be equivalent to the Set Cover problem and is NP-complete.
DeCiFer algorithm
DeCiFer aims to solve the Probabilistic Mutation Clustering and Genotype Selection problem, which optimizes the following function.
| (31) |
We use a coordinate ascent approach, where we alternatively optimize (i) cluster DCF values D and (ii) SNV cluster s and genotype tree assignments z. We begin by randomly initializing D(0) following k draws from a symmetric Dirichlet distribution. Note that given D, genotype tree and cluster assignments si and zi for an individual SNV are conditionally independent of the cluster and genotype set assignments of other SNVs. Thus, we optimize separately for each SNV i,
| (32) |
by considering all possible cluster and genotype set assignments. We then find the optimal cluster cell fraction values . Given and , a DCF value dℓ, j in sample for cluster j is conditionally independent of all other DCF values. Thus, we find
| (33) |
DeCiFer optimizes Eq. (33) using Brent’s algorithm to find a minimum in the range [0, 1], as implemented in the minimizescalar method of the SciPy optimize package (Virtanen et al. 2020). DeCiFer terminates upon convergence when cluster and genotype set assignments do not change between iterations, which indicates that the objective function does not change. Coordinate ascent is not guaranteed to converge to the global maximum. Thus, we use multiple restarts with different initializations.
Model selection
The number k of clusters is unknown, and thus we estimate it using a model-selection criterion. Specifically, we consider two different classes of clusters. The first class includes p + 2 fixed clusters, which we assume to be potentially present in every tumor. The second class includes a variable number of clusters, which is estimated using a model-selection criterion and whose cell fractions are estimated by DeCiFer. We describe the details of these clusters in the remaining of the section.
p + 2 fixed clusters, composed of three different groups. First, we include a ‘truncal’ cluster, such that the cell fraction values for this cluster are fixed to the purity of the samples. This is motivated by the common observation that in many tumors, there are a large number of SNVs that are present in all cells. Second, we include an ‘absent’ cluster, such that the cell fraction values for this cluster are fixed to zero. This cluster is necessary to guarantee feasiblity of solutions during optimization. That is, during early optimization steps, there exist mutations such that none of the cell fraction values are feasible. As such, the posterior probability for all cell fraction values would be zero, and the coordinate-ascent algorithm would be stuck. However, for single split copy number genotype trees meeting evolutionary constraints, there always exists a genotype tree for which d = 0 is a feasible cell fraction value. Thus, using an ‘absent’ cluster guarantees non-zero objective functions during optimization. Moreover, this ‘absent’ cluster may capture false positive variant calls in real data.
The cell fraction values for the ‘truncal’ and ‘absent’ clusters do not change during optimization. Last, we include p clusters which represent SNVs specific to each sample. This is motivated by the observations that frequently every sample has a certain number of unique SNVs. For a sample specific cluster in sample , we fix the cell fraction value of all other samples to be 0. We initialize to be the sample purity, but this value may change during optimization.
For the second class of clusters, we choose their number using a model-selection criterion based on the standard elbow method (Thorndike 1953). Specifically, we consider an increasing number k of clusters, starting from the minimum of p + 2 as described above until a given maximum number of clusters, and we apply DeCiFer to each of these values. As such, we evaluate how the objective value computed by DeCiFer changes with varying the number of clusters and we choose k as the elbow of the function, i.e., the value which improves the objective with respect to lower values but is not substantially improved by subsequent increases. Formally, we evaluate such improvements by using previous elbow methods (Zhang et al. 2017, Zaccaria & Raphael 2020), based on comparing the differences between the left and right derivatives of the objective function in each point.
Proofs
Lemma 1.
Given VAF v, copy-number proportions μ, and a single split copy number genotype set Γ*, if genotype proportions g exist such that (Γ*, g) are consistent with VAF v and copy-number proportions μ, they are uniquely determined as
where
Proof.
This follows from the definition of consistency and Eqs. (10) and (12). Consider the case where . By the single split copy number assumption, there exists a unique single with . Thus, to satisfy Eq. (12) we have that .
Next, consider the case where . Thus, we have that , or equivalently and for some , as copy-number proportions are non-negative. To derive λ, we substitute into Eq. (10) which must be satisfied for consistency.
Solving for λ, we obtain
Thus, any consistent genotype proportions will be fully determined by the above equations. □
Lemma 2.
Given VAF v, copy-number proportions μ, and a single split copy number genotype set Γ*, genotype proportions g such that / are consistent with VAF v and copy-number proportions μ exist if and only ifx
For all copy-number states (x, y) such that , there exists state for some m.
λ is in the range [0, 1] (Eq. (14)).
Proof.
To prove this, we must prove both directions of this statement. First, we will prove that if condition (1) and (2) are met, then the genotype proportions given by Eq. (13) are consistent, i.e., they satisfy Eqs. (10) and (12). In the proof for Lemma 1 we show that Eq. (10) is satisfied with . We will show here they satisfy Eq. (12). Consider copy-number state (x, y) such that . If condition (1) is met then there exists state , with , which satisfies Eq. (12). Next consider copy-number state (x, y) such that . Condition (1) is necessarily met by the definition of single split copy number genotype set. Thus , which satisfies Eq. (12).
Now we will prove the reverse direction, i.e., if the genotype proportions given by Eq. (13) are consistent, then conditions (1) and (2) are met. Consider condition (1) and assume, for the sake of contradiction, the converse: for some copy-number state (x, y) with , there does not exist any state . Thus and thus the genotype proportions are not consistent. Thus we have a contradiction. Consider condition (2), and assume, for the sake of contradiction, the converse: . If , then either or , which is not allowed by definition of genotype proportions. Thus, there do not exist consistent genotype proportions, and we have a contradiction. □
Lemma 3.
A VAF v is feasible for copy-number proportions μ and a single split copy number genotype set Γ* consistent with μ provided v is in the range [v−, v+] where
Proof.
We begin by finding v− such that
where g must be consistent with μ. We separate out the genotype proportions for the split state .
Recall from Eq. (13) that for all , . Thus, we have
Thus v is minimized when is minimized. By Eq. (13), we have that and . Thus is minimized when λ = 0 and . Therefore,
Following the same logic, we have that v is maximized when is maximized, i.e., when λ = 1.
Thus, we have that
□
Lemma 4.
Given (i) copy-number proportions μ, (ii) a single split copy number genotype set Γ and (iii) the tumor purity ρ, the CCFs c resulting from genotype proportions g such that (Γ, g) is consistent with μ are uniquely determined as
for any value of the splitting parameter .
Proof.
This follows directly from Lemma 3 and Definition 1. □
Theorem 1.
Given tumor purity ρ, VAF v, copy-number proportions μ, and a single split copy number genotype set Γ* consistent with v and μ, the CCF c is uniquely determined by
where is the set of genotypes containing the mutation.
Proof.
Substituting Eq. (13) into Eq. (10) to obtain the following.
We solve this for the term .
Substituting in for in Eq. (16) yields.
Note that m = 0 when and thus
From here, we obtain Theorem 1.
□
QUANTIFICATION AND STATISTICAL ANALYSIS
Estimating beta-binomial parameters
Read counts from bulk DNA sequencing are often affected by overdispersion, as noted in previous studies (Roth et al. 2014). We account for such overdispersion in DeCiFer by using a beta-binomial generative model similarly to the one proposed for PyClone (Roth et al. 2014). Specifically, we model the variant read count a with a Beta-Binomial distribution parameterized by mean v and precision s. However, in contrast to previous approaches (Roth et al. 2014) that define a prior distribution of s, in this work we estimate the value of s using germline single-nucleotide polymorphisms (SNPs). In particular, under the assumption that read counts from somatic SNVs and germline SNPs are affected by the same level of overdispersion (i.e., are drawn from beta-binomial distributions with the same parameters) we choose s to best fit germline SNPs with the same beta-binomial distributions parameterized by the mean v and s. Note that we know the value of v for germline SNPs, as this value is provided by the inferred allele-specific copy numbers: specifically, v corresponds to the proportion of allele-specific copy number, namely the B-allele frequency (Zaccaria & Raphael 2020). Moreover, we only consider SNPs with B-allele frequency = 0.5 or 0.5 to SNPs for which the computation of B-allele frequency is challenging (Zaccaria & Raphael 2020). We thus use the inferred value s and we substitute the likelihood with . Note that DeCiFer can use either generative model, according to different kinds of sequencing data.
Simulated data analysis details
We generate simulated data by jointly modeling the evolutionary process of SNVs and copy-number aberrations. Each tree simulated instance has n SNVs, k SNV clusters, m samples, expected read depth c and 3 copy-number clones. For each simulated instance, we generate a tree with k + 4 vertices. We grow a tree starting at the root. The root has exactly one child and each subsequent vertex added to the tree has equal probability of being a child to any existing vertex except the root. Each edge is then labeled either one of the k clusters of SNVs or one of the three sets of copy-number events.
SNVs are assigned to clusters using a multinomial distribution. As most tumors have a sizeable truncal cluster, each SNV has a probability p = 0.4 of being assigned to the truncal cluster, and p = 0.6/(k − 1) of being assigned to other clusters. To model copy-number evolution, we simulate a genome consisting of 5 chromosomes, with 10 segments each. Each segment initially has a copy-number of (1, 1). Each SNV is assigned to a segment and initially has a genotype of (x, y, m) = (1, 1, 0). We simulate an evolutionary process, which consists of amplifications and deletions (an increase or decrease in total copy number by 1) comprising 2 whole chromosome events, 5 chromosome arm events (affecting 5/10 segments of a chromosome) and 20 focal events (affecting 1 segment). These events are distributed into three groups uniformly. If a copy-number event affects a segment containing an SNV, the copy-number state for the SNV is updated accordingly. Moreover, the mutation multiplicity is updated, with probability to correspond to the probability of the affected segment containing the variant allele.
Clone proportions are generated as follows. Each sample is first assigned min(k, Poisson(3)) clusters. Then, to guarantee that all mutations are observed in at least one sample, we check that all leaf clones are assigned to at least one sample and if not, randomly assign them to a sample. Clone proportions are generated for clones present in a sample as a Dirichlet distribution with parameter α = [1]. Proportions less than 10% are rounded up to 10%, and clone proportions are renormalized. The variant read counts are then generated, where the total read depth d ∼ Poisson(c) with expected read depth c and the variant read counts are generated as a a ∼ Binomial(f, d) with f = max(v, 0.001) where v is the variant allele frequency of the mutation.
Below, we describe the parameter settings of the methods used in the simulated data comparison.
DeCiFer
On simulated data, DeCiFer was run using the following parameters:
| Parameter | Value |
|---|---|
| Likelihood model | Binomial |
| Min # of clusters | 2 |
| Max # of clusters | 15 |
| # of restarts | 10 |
| Max # of iterations | 50 |
| Elbow parameter | .2 |
| # of threads | 30 |
PyClone
PyClone does not consider subclonal copy-number aberrations and instead takes as input integer allele-specific copy number Nmaj, Nmin for each SNV. As the simulated data contains subclonal copy-number aberrations, we used two approaches to provide input for PyClone. In the first, we estimated the average allele-specific copy number for each SNV and rounded to the nearest integer value. That is,
| (34) |
and
| (35) |
In the second approach, we first compute CCFs using a constant mutation multiplicity-based method that accounts for subclonal copy-number aberrations (Jamal-Hanjani et al. 2017), and then use PyClone to cluster these CCFs based on scaled input VAFs. Then as input to PyClone, we use , the number of total reads t is the simulated total number of reads and the number of variant reads is .
PhyloWGS
PhyloWGS was run using default parameters.
Bioinformatic analysis of metastatic prostate cancer patients
DeCiFer requires two inputs for every sample in each patient: (1) sequencing read counts for SNVs and (2) allele-specific copy numbers for genomic regions harboring SNVs. We considered SNVs previously identified in these samples by Zaccaria & Raphael (Zaccaria & Raphael 2020) using Varscan 2 (v2.3.9) (Koboldt et al. 2012). To minimize false positives in SNV calls, we selected high confidence SNVs using the p-value computed by Varscan 2 (p < 10−4 in at least one sample). Varscan 2 analyzes each sample independently and does not report SNVs without a sufficiently high number of variant reads. As such, we used BCFtools (v1.9) (Li 2011) to obtain read counts across all samples for the set of SNVs called by Varscan 2 in at least one sample. We used the allele-specific copy numbers previously inferred by HATCHet for the same samples (Zaccaria & Raphael 2020). To enable the efficient enumeration of all possible state trees and to limit potential errors in regions with high copy numbers, we excluded any genomic region with allele-specific copy numbers (x, y) where max(x, y) > 4 and min(x, y) > 2. We applied DeCiFer to all patients using the default values of all parameters and by considering a beta-binomial generative model with precision parameter s ≈ 200, as estimated from germline SNPs.
Supplementary Material
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Antibodies | ||
| Bacterial and virus strains | ||
| Biological samples | ||
| Chemicals, peptides, and recombinant proteins | ||
| Critical commercial assays | ||
| Deposited data | ||
| Simulated Data | This Paper | https://github.com/raphael-group/decifer-data |
| Prostate cancer DNA sequencing | Gundem et al. (2015), EGA | https://ega-archive.org/studies/EGAS00001000262 |
| Prostate somatic single-nucleotide variants | Zaccaria & Raphael (2020), Github | https://github.com/raphael-group/hatchet-paper |
| Prostate allele and clone-specific copy numbers | Zaccaria & Raphael (2020), Github | https://github.com/raphael-group/hatchet-paper |
| Experimental models: Cell lines | ||
| Experimental models: Organisms/strains | ||
| Oligonucleotides | ||
| Recombinant DNA | ||
| Software and algorithms | ||
| DeCiFer | This Paper | https://github.com/raphael-group/decifer, DOI 10.5281/zenodo.5082565 |
| HATCHet | Zaccaria & Raphael (2020) | https://github.com/raphael-group/hatchet |
| PhyloWGS | Deshwar et al. (2015) | https://github.com/morrislab/phylowgs |
| PyClone | Roth et al. (2014) | https://github.com/Roth-Lab/pyclone |
| Varscan 2 | Koboldt et al. (2012) | http://varscan.sourceforge.net/ |
| Other | ||
Box 1: Progress and Potential.
The genomes of cancer cells contain numerous somatic mutations, errors that occur during DNA replication and are passed on to descendant cells. This accumulation of mutations yields a tumor that is a heterogeneous collection of cells that do not all have the same mutations. Quantifying this mutational heterogeneity is essential for identifying populations of cancer cells that are sensitive or resistant to treatment. In addition, mutations provide markers to infer the past evolutionary history of a tumor which is useful for timing events in tumor development such as the migrations between a primary tumor and distant metastases. High-throughput DNA sequencing allows cancer researchers to measure the mutations in a tumor. However, most cancer sequencing does not measure the mutations in an individual cancer cell but rather a mixture of the mutations that are present in thousands-millions of cells from a bulk tumor sample. An important and difficult challenge is to determine the fraction of cancer cells in a tumor that contain each mutation. This quantity is called the cancer cell fraction.
To understand the challenge faced in calculating the cancer cell fraction from bulk sequencing data, consider the following story of trick-or-treating on Halloween. Suppose that on Halloween the houses in your neighborhood hand out two types of candy bars, dark chocolate and milk chocolate. Some houses hand out a single bar while others hand out two, three, or more bars of different types. After a night of trick-or-treating your child returns with a bag filled with milk and dark chocolate bars. Can you determine the fraction of houses that gave your child at least one milk chocolate bar?
While this question about trick-or-treating might seem contrived, it is analogous to the problem of computing the cancer cell fraction (CCF) for a single-nucleotide variant (SNV), a type of mutation that alters a single position of the DNA sequence. The genome of a cancer cell typically contains thousands of SNVs, making them a reliable marker of heterogeneity and evolutionary studies. However, for each SNV bulk DNA sequencing measures only the proportion of copies of the DNA position in the tumor sample that contain the SNV. This quantity, called the variant allele frequency, is analogous to the proportion of candy bars in the trick-or-treating bag that are milk chocolate. Just as the proportion of milk chocolate bars in a trick-or-treating bag does not provide enough information to determine how many houses gave out milk chocolate, the variant allele frequency does not provide enough information to calculate the CCF. Instead, one must rely on some simplifying assumptions. For example, if one assumes that each house gives out exactly two chocolate bars and at most one milk chocolate bar, then the proportion of houses giving out milk chocolate bars is twice the proportion of milk chocolate bars in the bag. Similarly, since a normal human cell has exactly two copies of each chromosome if we assume that an SNV affects only one chromosome then in a pure tumor sample the CCF of an SNV is twice the variant allele frequency. However, cancer genomes often contain copy-number aberrations that duplicate or delete chromosomal segments. Thus the number of copies of an SNV in a cancer cell may vary – analogous to different houses in the neighborhood handing out different numbers of dark and milk chocolate candy bars. A less stringent assumption that is commonly used in cancer sequencing studies is to assume all cells containing a specific SNV contain the same number of copies of that SNV. This assumption is often violated in tumors with copy-number aberrations, as an SNV may be later duplicated due to a copy-number gain.
The key idea in this paper is to recognize that the number of copies of an SNV is not arbitrary, but rather is a consequence of an evolutionary process that involves both SNVs and overlapping copy-number aberrations. We develop an algorithm called DeCiFer that infers CCFs under a realistic evolutionary model. Moreover, we derive a more general quantity, the descendent cell fraction (DCF), that allows for loss of mutations during tumor evolution. We demonstrate the advantages of DeCiFer in the analysis of several prostate tumors, where we produce simpler and more reasonable explanations of the cancer sequencing data than previously reported. Going forward, DeCiFer will enable cancer biologists to accurately quantify present heterogeneity and past evolution in tumors that contain both SNVs and copy-number aberrations.
Highlights.
Current approaches estimate CCFs for SNVs using simplistic assumptions about genotypes
The descendent cell fraction (DCF) accounts for mutation loss in subsets of cells
DeCiFer infers plausible CCFs and DCFs under standard evolutionary models
DeCiFer yields more parsimonious tumor phylogenies in aneuploid tumors
Acknowledgements
We thank Yuanyuan Qi for help with the PhyloWGS simulation experiments. This work is supported by a US National Institutes of Health (NIH) grants U24CA211000 and U24CA248453 to B.J.R.
Footnotes
Declaration of Interests
B.J.R is a co-founder and consultant for Medley Genomics.
Code availability: Software is available at https://github.com/raphael-group/decifer
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Andor N, Graham TA, Jansen M, Xia LC, Aktipis CA, Petritsch C, Ji HP & Maley CC (2015), ‘Pan-cancer analysis of the extent and consequences of intratumor heterogeneity’, Nature Medicine 22(1), 105–113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bozic I, Antal T, Ohtsuki H, Carter H, Kim D, Chen S, Karchin R, Kinzler KW, Vogelstein B. & Nowak MA (2010), ‘Accumulation of driver and passenger mutations during tumor progression’, Proceedings of the National Academy of Sciences 107(43), 18545–18550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brastianos PK, Carter SL, Santagata S, Cahill DP, Taylor-Weiner A, Jones RT, Van Allen EM, Lawrence MS, Horowitz PM, Cibulskis K, Ligon KL, Tabernero J, Seoane J, Martinez-Saez E, Curry WT, Dunn IF, Paek SH, Park S-H, McKenna A, Chevalier A, Rosenberg M, Barker FG, Gill CM, Van Hummelen P, Thorner AR, Johnson BE, Hoang MP, Choueiri TK, Signoretti S, Sougnez C, Rabin MS, Lin NU, Winer EP, Stemmer-Rachamimov A, Meyerson M, Garraway L, Gabriel S, Lander ES, Beroukhim R, Batchelor TT, Baselga J, Louis DN, Getz G. & Hahn WC (2015), ‘Genomic Characterization of Brain Metastases Reveals Branched Evolution and Potential Therapeutic Targets.’, Cancer Discovery 5(11), 1164–1177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burrell RA, McGranahan N, Bartek J. & Swanton C. (2013), ‘The causes and consequences of genetic heterogeneity in cancer evolution’, Nature 501(7467), 338–345. [DOI] [PubMed] [Google Scholar]
- Cai W, Zhou D, Wu W, Tan WL, Wang J, Zhou C. & Lou Y. (2018), ‘Mhc class ii restricted neoantigen peptides predicted by clonal mutation analysis in lung adenocarcinoma patients: implications on prognostic immunological biomarker and vaccine design’, BMC genomics 19(1), 1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caravagna G, Heide T, Williams MJ, Zapata L, Nichol D, Chkhaidze K, Cross W, Cresswell GD, Werner B, Acar A. et al. (2020), ‘Subclonal reconstruction of tumors by using machine learning and population genetics’, Nature Genetics 52(9), 898–907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carter SL, Cibulskis K, Helman E, McKenna A, Shen H, Zack T, Laird PW, Onofrio RC, Winckler W, Weir BA, Beroukhim R, Pellman D, Levine DA, Lander ES, Meyerson M. & Getz G. (2012), ‘Absolute quantification of somatic DNA alterations in human cancer’, Nature Biotechnology 30(5), 413–421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christensen S, Leiserson MD & El-Kebir M. (2020), Physigs: Phylogenetic inference of mutational signature dynamics, in ‘Pacific Symposium on Biocomputing. Pacific Symposium on Biocomputing’, Vol. 25, World Scientific, pp. 226–237. [PubMed] [Google Scholar]
- Cmero M, Yuan K, Ong CS, Schroder J, Corcoran NM, Papenfuss T, Hovens CM, Markowetz F. & Macintyre G. (2020), ‘Inferring structural variant cancer cell fraction’, Nature communications 11(1), 1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cresswell GD, Nichol D, Spiteri I, Tari H, Zapata L, Heide T, Maley CC, Magnani L, Schiavon G, Ashworth A. et al. (2020), ‘Mapping the breast cancer metastatic cascade onto ctdna using genetic and epigenetic clonal tracking’, Nature communications 11(1), 1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cun Y, Yang T-P, Achter V, Lang U. & Peifer M. (2018), ‘Copy-number analysis and inference of subclonal populations in cancer genomes using sclust’, Nature protocols 13(6), 1488. [DOI] [PubMed] [Google Scholar]
- Dentro SC, Leshchiner I, Haase K, Tarabichi M, Wintersinger J, Deshwar AG, Yu K, Rubanova Y, Macintyre G, Demeulemeester J. et al. (2020), ‘Characterizing genetic intra-tumor heterogeneity across 2, 658 human cancer genomes’, bioRxiv. [DOI] [PMC free article] [PubMed]
- Dentro SC, Wedge DC & Van Loo P. (2017), ‘Principles of Reconstructing the Subclonal Architecture of Cancers.’, Cold Spring Harbor Perspectives in Medicine 7(8), a026625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deshwar AG, Vembu S, Yung CK, Jang GH, Stein L. & Morris Q. (2015), ‘PhyloWGS: Reconstructing subclonal composition and evolution from whole-genome sequencing of tumors’, Genome Biology 16(1), 35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dewey FE, Grove ME, Pan C, Goldstein BA, Bernstein JA, Chaib H, Merker JD, Goldfeder RL, Enns GM, David SP et al. (2014), ‘Clinical interpretation and implications of whole-genome sequencing’, Jama 311(10), 1035–1045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- El-Kebir M. (2018), ‘SPhyR: tumor phylogeny estimation from single-cell sequencing data under loss and error’, Bioinformatics 34(17), i671–i679. URL: https://academic.oup.com/bioinformatics/article/34/17/i671/5093218 [DOI] [PMC free article] [PubMed] [Google Scholar]
- El-Kebir M, Oesper L, Acheson-Field H. & Raphael BJ (2015), ‘Reconstruction of clonal trees and tumor composition from multi-sample sequencing data.’, Bioinformatics 31(12), i62–i70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- El-Kebir M, Satas G, Oesper L. & Raphael BJ (2016), ‘Inferring the Mutational History of a Tumor Using Multi-state Perfect Phylogeny Mixtures’, Cell Systems 3(1), 43–53. [DOI] [PubMed] [Google Scholar]
- Fischer A, Vazquez-Garcia I, Illingworth CJR & Mustonen V. (2014), ‘High-definition reconstruction of clonal composition in cancer.’, Cell Reports 7(5), 1740–1752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao R, Davis A, McDonald TO, Sei E, Shi X, Wang Y, Tsai P-C, Casasent A, Waters J, Zhang H. et al. (2016), ‘Punctuated copy number evolution and clonal stasis in triple-negative breast cancer’, Nature genetics 48(10), 1119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gawad C, Koh W. & Quake SR (2016), ‘Single-cell genome sequencing: current state of the science’, Nature Reviews Genetics 17(3), 175. [DOI] [PubMed] [Google Scholar]
- Gerstung M, Jolly C, Leshchiner I, Dentro SC, Gonzalez S, Rosebrock D, Mitchell TJ, Rubanova Y, Anur P, Yu K. et al. (2020), ‘The evolutionary history of 2, 658 cancers’, Nature 578(7793), 122–128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gundem G, Van Loo P, Kremeyer B, Alexandrov LB, Tubio JMC, Papaemmanuil E, Brewer DS, Kallio HML, Hogn as G, Annala M, Kivinummi K, Goody V, Latimer C, O’Meara S, Dawson KJ, Isaacs W, Emmert-Buck MR, Nykter M, Foster C, Kote-Jarai Z, Easton D, Whitaker HC, ICGC Prostate UK Group, Neal DE, Cooper CS, Eeles RA, Visakorpi T, Campbell PJ, McDermott U, Wedge DC & Bova GS (2015), ‘The evolutionary history of lethal metastatic prostate cancer.’, Nature 520(7547), 353–357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harrigan CF, Rubanova Y, Morris Q. & Selega A. (2020), Tracksigfreq: subclonal reconstructions based on mutation signatures and allele frequencies, in ‘Pacific Symposium on Biocomputing. Pacific Symposium on Biocomputing’, Vol. 25, World Scientific, p. 238. [PMC free article] [PubMed] [Google Scholar]
- Husic E, Li X, Hujdurovic A, Mehine M, Rizzi R, Makinen V, Milanic M. & Tomescu AI (2019), ‘Mipup: minimum perfect unmixed phylogenies for multi-sampled tumors via branchings and ilp’, Bioinformatics 35(5), 769–777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jamal-Hanjani M, Wilson GA, McGranahan N, Birkbak NJ, Watkins TBK, Veeriah S, Shafi S, Johnson DH, Mitter R, Rosenthal R, Salm M, Horswell S, Escudero M, Matthews N, Rowan A, Chambers T, Moore DA, Turajlic S, Xu H, Lee SM, Forster MD, Ahmad T, Hiley CT, Abbosh C, Falzon M, Borg E, Marafioti T, Lawrence D, Hayward M, Kolvekar S, Panagiotopoulos N, Janes SM, Thakrar R, Ahmed A, Blackhall F, Summers Y, Shah R, Joseph L, Quinn AM, Crosbie PA, Naidu B, Middleton G, Langman G, Trotter S, Nicolson M, Remmen H, Kerr K, Chetty M, Gomersall L, Fennell DA, Nakas A, Rathinam S, Anand G, Khan S, Russell P, Ezhil V, Ismail B, Irvin-sellers M, Prakash V, Lester JF, Kornaszewska M, Attanoos R, Adams H, Davies H, Dentro S, Taniere P, O’Sullivan B, Lowe HL, Hartley JA, Iles N, Bell H, Ngai Y, Shaw JA, Herrero J, Szallasi Z, Schwarz RF, Stewart A, Quezada SA, Le Quesne J, Van Loo P, Dive C, Hackshaw A, Swanton C. & TRACERx Consortium (2017), ‘Tracking the Evolution of Non-Small-Cell Lung Cancer.’, New England Journal of Medicine 376(22), 2109–2121. [DOI] [PubMed] [Google Scholar]
- Jiang Y, Qiu Y, Minn AJ & Zhang NR (2016), ‘Assessing intratumor heterogeneity and tracking longitudinal and spatial clonal evolutionary history by next-generation sequencing.’, Proceedings of the National Academy of Sciences of the United States of America 113(37), E5528–37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim C, Gao R, Sei E, Brandt R, Hartman J, Hatschek T, Crosetto N, Foukakis T. & Navin NE (2018), ‘Chemoresistance evolution in triple-negative breast cancer delineated by single-cell sequencing’, Cell 173(4), 879–893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koboldt DC, Zhang Q, Larson DE, Shen D, McLellan MD, Lin L, Miller C. a., Mardis ER, Ding L. & Wilson RK (2012), ‘VarScan 2: somatic mutation and copy number alteration discovery in cancer by exome sequencing.’, Genome Research 22(3), 568–576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuipers J, Jahn K, Raphael BJ & Beerenwinkel N. (2017), ‘Single-cell sequencing data reveal widespread recurrence and loss of mutational hits in the life histories of tumors’, Genome research 27(11), 1885–1894. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lakatos E, Williams MJ, Schenck RO, Cross WC, Househam J, Zapata L, Werner B, Gatenbee C, Robertson-Tessi M, Barnes CP et al. (2020), ‘Evolutionary dynamics of neoantigens in growing tumors’, Nature Genetics pp. 1–10. [DOI] [PMC free article] [PubMed]
- Laks E, McPherson A, Zahn H, Lai D, Steif A, Brimhall J, Biele J, Wang B, Masud T, Ting J. et al. (2019), ‘Clonal decomposition and DNA replication states defined by scaled single-cell genome sequencing’, Cell 179(5), 1207–1221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H. (2011), ‘A statistical framework for snp calling, mutation discovery, association mapping and population genetical parameter estimation from sequencing data’, Bioinformatics 27(21), 2987–2993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malikic S, McPherson AW, Donmez N. & Sahinalp CS (2015), ‘Clonality inference in multiple tumor samples using phylogeny.’, Bioinformatics 31(9), 1349–1356. [DOI] [PubMed] [Google Scholar]
- McGranahan N, Favero F, de Bruin EC, Birkbak NJ, Szallasi Z. & Swanton C. (2015), ‘Clonal status of actionable driver events and the timing of mutational processes in cancer evolution.’, Science Translational Medicine 7(283), 283ra54–283ra54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McGranahan N. & Swanton C. (2017), ‘Clonal Heterogeneity and Tumor Evolution: Past, Present, and the Future.’, Cell 168(4), 613–628. [DOI] [PubMed] [Google Scholar]
- McPherson A, Roth A, Laks E, Masud T, Bashashati A, Zhang AW, Ha G, Biele J, Yap D, Wan A, Prentice LM, Khattra J, Smith MA, Nielsen CB, Mullaly SC, Kalloger S, Karnezis A, Shumansky K, Siu C, Rosner J, Chan HL, Ho J, Melnyk N, Senz J, Yang W, Moore R, Mungall AJ, Marra M. a., Bouchard-Cotˆ e A, Gilks CB, Huntsman DG, McAlpine JN, Aparicio S. & Shah SP (2016), ‘Divergent modes of clonal spread and intraperitoneal mixing in high-grade serous ovarian cancer’, Nature Genetics. [DOI] [PubMed]
- Miller CA et al. (2014), ‘SciClone: inferring clonal architecture and tracking the spatial and temporal patterns of tumor evolution’, PLoS Comput Biol 10(8), e1003665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Myers MA, Zaccaria S. & Raphael BJ (2020), ‘Identifying tumor clones in sparse single-cell mutation data’, Bioinformatics 36(Supplement 1), i186–i193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Navin NE (2015), ‘The first five years of single-cell cancer genomics and beyond’, Genome research 25(10), 1499–1507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nik-Zainal S. et al. (2012), ‘The life history of 21 breast cancers’, Cell 149(5), 994–1007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nowell PC (1976), ‘The clonal evolution of tumor cell populations’, Science 194(4260), 23–8. [DOI] [PubMed] [Google Scholar]
- Oesper L, Mahmoody A. & Raphael BJ (2013), ‘THetA: inferring intra-tumor heterogeneity from high-throughput DNA sequencing data’, Genome Biol 14(7), R80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oesper L, Satas G. & Raphael BJ (2014), ‘Quantifying tumor heterogeneity in whole-genome and whole-exome sequencing data’, Bioinformatics 30(24), 3532–40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Popic V, Salari R, Hajirasouliha I, Kashef-Haghighi D, West RB & Batzoglou S. (2015), ‘Fast and scalable inference of multi-sample cancer lineages’, Genome biology 16(1), 91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qiao Y, Quinlan AR, Jazaeri AA, Verhaak RG, Wheeler DA & Marth GT (2014), ‘SubcloneSeeker: a computational framework for reconstructing tumor clone structure for cancer variant interpretation and prioritization’, Genome biology 15(8), 443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rajput A, Bocklage T, Greenbaum A, Lee J-H & Ness SA (2017), ‘Mutant-allele tumor heterogeneity scores correlate with risk of metastases in colon cancer’, Clinical colorectal cancer 16(3), e165–e170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roth A, Khattra J, Yap D, Wan A, Laks E, Biele J, Ha G, Aparicio S, Bouchard-Cotˆ e A. & Shah SP (2014), ‘PyClone: statistical inference of clonal population structure in cancer.’, Nature methods 11(4), 396–398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubanova Y, Shi R, Harrigan CF, Li R, Wintersinger J, Sahin N, Deshwar A. & Morris Q. (2020), ‘Reconstructing evolutionary trajectories of mutation signature activities in cancer using tracksig’, Nature communications 11(1), 1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Satas G. & Raphael BJ (2017), ‘Tumor phylogeny inference using tree-constrained importance sampling’, Bioinformatics 33(14), i152–i160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Satas G, Zaccaria S, Mon G. & Raphael BJ (2020), ‘Scarlet: Single-cell tumor phylogeny inference with copy-number constrained mutation losses’, Cell Systems 10(4), 323–332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tarabichi M, Salcedo A, Deshwar AG, Ni Leathlobhair M, Wintersinger J, Wedge DC, Van Loo P, Morris QD & Boutros PC (2021), ‘A practical guide to cancer subclonal reconstruction from DNA sequencing’, Nature Methods. URL: http://www.nature.com/articles/s41592-020-01013-2 [DOI] [PMC free article] [PubMed]
- The I, of Whole TP-CA, Consortium G. et al. (2020), ‘Pan-cancer analysis of whole genomes’, Nature 578(7793), 82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thorndike RL (1953), ‘Who belongs in the family?’, Psychometrika 18(4), 267–276. [Google Scholar]
- Van Loo P, Nordgard SH, Lingjærde OC, Russnes HG, Rye IH, Sun W, Weigman VJ, Marynen P, Zetterberg A, Naume B, Perou CM, Børresen-Dale A-L & Kristensen VN (2010), ‘Allele-specific copy number analysis of tumors’, Proceedings of the National Academy of Sciences 107(39), 16910–16915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Virtanen P, Gommers R, Oliphant TE, Haberland M, Reddy T, Cournapeau D, Burovski E, Peterson P, Weckesser W, Bright J, van der Walt SJ, Brett M, Wilson J, Millman KJ, Mayorov N, Nelson ARJ, Jones E, Kern R, Larson E, Carey CJ, Polat İ, Feng Y, Moore EW, VanderPlas J, Laxalde D, Perktold J, Cimrman R, Henriksen I, Quintero EA, Harris CR, Archibald AM, Ribeiro AH, Pedregosa F, van Mulbregt P. & SciPy 1.0 Contributors (2020), ‘SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python’, Nature Methods 17, 261–272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watkins TB, Lim EL, Petkovic M, Elizalde S, Birkbak NJ, Wilson GA, Moore DA, Gronroos E, Rowan A, Dewhurst SM et al. (2020), ‘Pervasive chromosomal instability and karyotype order in tumour evolution’, Nature 587(7832), 126–132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weaver BA & Cleveland DW (2006), ‘Does aneuploidy cause cancer?’, Current opinion in cell biology 18(6), 658–667. [DOI] [PubMed] [Google Scholar]
- Williams MJ, Werner B, Barnes CP, Graham TA & Sottoriva A. (2016), ‘Identification of neutral tumor evolution across cancer types’, Nature Genetics 48(3), 238–244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiao Y, Wang X, Zhang H, Ulintz PJ, Li H. & Guan Y. (2020), ‘Fastclone is a probabilistic tool for deconvoluting tumor heterogeneity in bulk-sequencing samples’, Nature Communications 11(1), 1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan K, Macintyre G, Liu W, Markowetz F, working group P−. et al. (2018), ‘Ccube: a fast and robust method for estimating cancer cell fractions’, bioRxiv p. 484402.
- Yuan K, Sakoparnig T, Markowetz F. & Beerenwinkel N. (2015), ‘BitPhylogeny: a probabilistic framework for reconstructing intra-tumor phylogenies’, Genome biology 16(1), 1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zaccaria S. & Raphael BJ (2020), ‘Accurate quantification of copy-number aberrations and whole-genome duplications in multi-sample tumor sequencing data’, Nature Communications 11(1), 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zaccaria S. & Raphael BJ (2021), ‘Characterizing allele-and haplotype-specific copy numbers in single cells with chisel’, Nature biotechnology 39(2), 207–214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zack TI, Schumacher SE, Carter SL, Cherniack AD, Saksena G, Tabak B, Lawrence MS, Zhang C-Z, Wala J, Mermel CH et al. (2013), ‘Pan-cancer patterns of somatic copy number alteration’, Nature genetics 45(10), 1134–1140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y, Mandziuk J, Quek CH & Goh BW (2017), ‘Curvature-based method for determining thé number of clusters’, Information Sciences 415, 414–428. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
DeCiFer code is available on GitHub at https://github.com/raphael-group/decifer(DOI 10.5281/zenodo.5082565) and it is distributed through Bioconda at https://bioconda.github.io/recipes/decifer/README.html. The simulations as well as the processed data and DeCiFer’s results for the prostate cancer patients analyzed in this study are available on GitHub at https://github.com/raphael-group/decifer-data. Whole-genome DNA sequencing data for all samples of the prostate cancer patients are available from the European Genome-phenome Archive (EGA) under accession number EGAS00001000262.