Bidirectional Mapping-Based Domain Adaptation for Nucleus Detection in Cross-Modality Microscopy Images

Abstract

Cell or nucleus detection is a fundamental task in microscopy image analysis and has recently achieved state-of-the-art performance by using deep neural networks. However, training supervised deep models such as convolutional neural networks (CNNs) usually requires sufficient annotated image data, which is prohibitively expensive or unavailable in some applications. Additionally, when applying a CNN to new datasets, it is common to annotate individual cells/nuclei in those target datasets for model re-learning, leading to inefficient and low-throughput image analysis. To tackle these problems, we present a bidirectional, adversarial domain adaptation method for nucleus detection on cross-modality microscopy image data. Specifically, the method learns a deep regression model for individual nucleus detection with both source-to-target and target-to-source image translation. In addition, we explicitly extend this unsupervised domain adaptation method to a semi-supervised learning situation and further boost the nucleus detection performance. We evaluate the proposed method on three cross-modality microscopy image datasets, which cover a wide variety of microscopy imaging protocols or modalities, and obtain a significant improvement in nucleus detection compared to reference baseline approaches. In addition, our semi-supervised method is very competitive with recent fully supervised learning models trained with all real target training labels.

I. INTRODUCTION

Microscopy and digital pathology image quantification plays a critical role in understanding the cellular mechanisms of life, exploring the biological association between pheno-types and diseases, and providing support for computer-aided diagnosis [1], [2]. Nucleus/cell detection is a fundamental task in microscopy image analysis, because it can facilitate many other quantitative studies such as nucleus/cell counting, segmentation, classification, tracking, phenotype identification, and so on [3]. Nucleus/cell detection can provide support for many downstream tasks such as quantification of clinically relevant nuclear biomarkers including estrogen receptor, progesterone receptor, and Ki67 labeling index [4], [5], [6], [7]. It can also be used to build cell graphs to model spatial distributions of nuclei/cells, which are very helpful for cancer grading, prediction of disease progression, discrimination between the different states of brain tissue, and so on [2], [8], [9].

At present, the amount and complexity of image data preclude manual nucleus detection, which might lead to in-efficiency and significant inter-observer variability. Computational methods, particularly convolutional neural networks (CNNs) and fully convolutional networks (FCNs) [10], [11], [12], have been used to locate individual cells/nuclei [13] and have produced excellent performance in specific (digital) microscopy images [13], [14]. For instance, Cires,an et al. [15] have presented a deep CNN to detect mitotic nuclei in hematoxylin and eosin (H&E) stained breast histology images, Sirinukunwattana et al. [16] have introduced a spatially constrained CNN to locate individual nuclei in colon cancer histopathology images, Kumar et al. [17] have proposed a three-class CNN to separate individual nuclei from image background for different-organ tissues, and Xing et al. [18] have learned multiple CNN models for nucleus detection in brain tumor, pancreatic neuroendocrine tumor and breast cancer pathology images. Recently, Gamper [19], [20] present a semi-automated approach to locate and label individual nuclei on H&E images and meanwhile introduce a large-scale dataset for nucleus segmentation and classification. The dataset consists of 19 different tissue types and can be a powerful resource for development of nucleus localization, segmentation and/or classification methods on H&E-stained histology image data.

CNN-based deep object detection models typically require a large amount of annotated training data. However, extensive annotations of individual cells in large-scaled datasets are prohibitively expensive or unavailable [14], [21]. In addition, CNN models trained on one microscopy image dataset (e.g., H&E stained) might not be applicable to another (e.g., immunohistochemistry (IHC) stained) because of domain or dataset shifts, as shown in Fig. 1. It is currently common to train specific CNN models on individual datasets [13], [22], and thus it requires a repetition of a tedious and costly image annotation process for each new dataset. Obviously, this strategy would significantly lower the data processing rate and hinder high-throughput image analysis. This situation would become worse when labeling target data is infeasible in some applications. On the other hand, one might want to fine-tune pretrained CNNs models on certain target datasets, but it may be difficult to collect enough target training images for proper fine-tuning [23]. Therefore, there is a need of methods that can transfer learned knowledge from one dataset or domain to another without additional target data annotations for nucleus/cell detection.

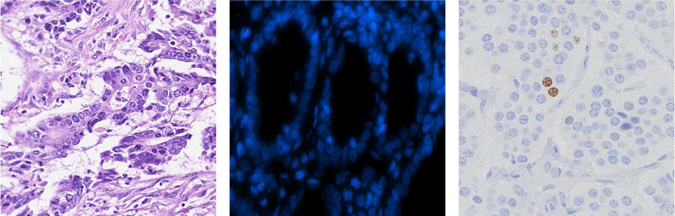
Fig. 1.

Example microscopy images. From left to right: hematoxylin and eosin (H&E) stained digital microscopy, DAPI stained fluorescence and Ki67 immunohistochemistry (IHC) stained tissue microarray images.

Unsupervised domain adaptation (UDA) is one type of method to address domain shifts without target data labeling [24], [25]. Most of the previous deep UDA methods align feature distributions from the source and target domains by reducing activation discrepancies between two domains [26], aligning second- or higher-order statistics of data distributions [27], or using adversarial learning [28], [23]. In particular, adversarial domain adaptation has been recently applied to medical image segmentation [29] and classification [30]. However, these approaches that conduct deep feature matching might not effectively capture low-level image appearance variance [31]. It might be also difficult to fully align feature distributions for structured output tasks such as nucleus/cell detection, which requires preserving spatial information in the prediction maps [32], [33]. On the other hand, some recent work [34], [35], [31] focuses on pixel-space adaptation for natural image translation, classification and segmentation using generative adversarial networks (GANs) [36]. These methods deal with relatively small domain shifts, which might not hold in cross-modality microscopy image datasets, or focus on source-to-target image generation and only train single-directional task models, which might be inferior to bidirectional learning [37]. In addition, none of these approaches are designed and evaluated with nucleus/cell detection in microscopy images.

In this paper, we present a bidirectional mapping-based generative adversarial domain adaptation method for cross-modality cell/nucleus detection (see Fig. 2). Specifically, we conduct bidirectional image-to-image mappings in the pixel space, converting raw source/target images (e.g., H&E stained) into target-/source-like ones (e.g., IHC stained). We then generate pseudo-labels by applying a source-domain detector to nucleus position estimation in the source-like, converted target training images, which share the same labels as corresponding real target images. We also learn a target-domain detector using both these real target data with pseudo-labels and the translated source images with real annotations. In this scenario, our domain adaptation method is able to take advantage of both accurate nucleus annotations in the source domain and real training images in the target domain for nucleus detection.

Fig. 2.

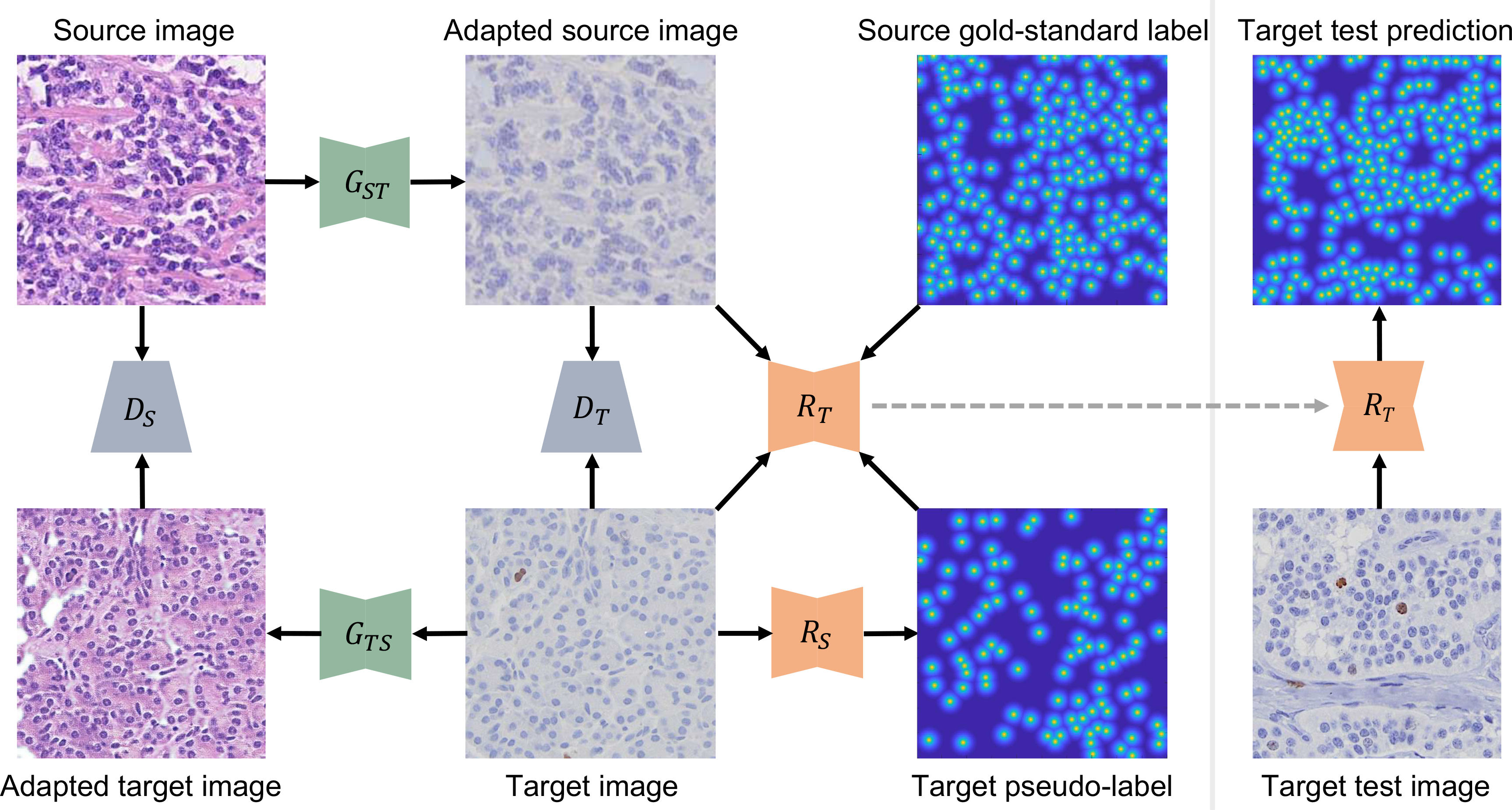
The overview of the proposed bidirectional adversarial domain adaptation method for nucleus detection. $G_{\mathcal{S}\mathcal{T}}/G_{\mathcal{T}\mathcal{S}}$ is the source-to-target/target-to-source generator and $D_{\mathcal{T}}/D_{\mathcal{S}}$ is its associated discriminator. $R_{\mathcal{S}}/R_{\mathcal{T}}$ is the source-/target-domain nucleus detector. Note that the target-domain detector $R_{\mathcal{T}}$ is learned with both gold-standard annotated, adapted source images and pseudo-labeled, real target images. The dashed gray arrow represents the transition from the training to testing stage. Here source and target data are H&E stained and IHC stained TMA microscopy images, respectively.

A preliminary version of this work was presented in the MICCAI-2019 conference [38]. Compared with the previous conference version that learns a one-directional detector with only target-like, adapted source images, this paper presents a bidirectional mapping-based adaptation algorithm specifically for nucleus detection, which trains an additional source-domain detector to assist with target-domain detector learning. Based on both source-to-target and target-to-source mappings, this method directly learns a target-domain detector using both source and target images on the fly, with no need of a second-stage model fine-tuning that is used in the previous work [38]. In addition, a novel pseudo-labeling algorithm is proposed to select highly-confident artificial annotations for target data self-labeling. Next, compared with our previous work, we explicitly extend our UDA method to semi-supervised domain adaptation (SSDA) so that it can take advantage of limited real, gold-standard target training annotations, if available. Finally, we further test the proposed method and evaluate its generalization ability on a new public fluorescence microscopy image dataset. We also conduct statistical t-tests for the experiments and provide a sensitivity analysis of important parameters in our method on different datasets. In summary, our contributions are four-fold:

• We present a bidirectional UDA-based nucleus detection method for cross-modality microscopy images. It conducts domain adaptation via image-to-image translation and uses both gold-standard annotated, transformed source images and pseudo-labeled, real target images for task model learning. Our method differs from many other GAN-based medical image analysis approaches (discussed in Section II), which require annotation of all target training data [39], [40], [41], [42], align feature distributions or task-specific output predictions from the source and target domains [29], [43], [44], [45], [46], [47], or learn a single-directional source-domain or target-domain task model [48], [49], [50], [51], [52], [53], [54], [55].

• We introduce a simple yet effective pseudo-labeling algorithm for target data self-labeling, which is achieved by applying a source-domain detector to transformed target training images. The pseudo-labels partner with gold-standard annotations in the source domain to learn a target-domain nucleus detector. Unlike the previous work [32] that fine-tunes a source model toward the target domain and creates pseudo-labels on real target data, our pseudo-label generation strategy creates artificial labels in a reverse direction, i.e., applying a source-domain detector to estimation of object positions on source-like converted target images. In addition, the work [32] requires image-level annotations of target data for pseudo-label generation, while ours needs no target label information. Our method ignores image pixels with low-confident predictions during pseudo-label generation, and this is different than [37], which generates fake labels for all unannotated target data for model training.

• We extend our UDA method to SSDA learning, where a small amount of annotated target data is available during model training. Our SSDA approach differs from the previous deep semi-supervised learning studies [48], [56] in its use of limited labeled target data: 1) our method emphasizes the contributions of these annotations during model training by activating the input from unlabeled target data for only every few iterations, because we find that it is not helpful for nucleus detection by simply pooling both annotated and unannotated images followed by random sampling, which is used by [48], [56]; 2) the annotated target images in our method coordinate with both pseudo-labeled target and translated source images for task model learning, while the work [48], [56] does not. Our method also differs from the studies [57], [58], which use more complicated attention mechanisms or consistency constraints for deep semi-supervised learning.

• We extensively evaluate the proposed method on 3 cross-modality microscopy image datasets, which covers a wide range of imaging modalities/protocols, including H&E stained brightfield, DAPI (4’,6-diamidino-2-phenylindole) stained fluorescence and Ki67 IHC stained tissue microarray (TMA) microscopy images. This distinguishes our work from many previous GAN-based microscopy or pathology image analysis studies [59], [60], [61], [62], [63], [64], [65], which conduct domain adaptation within one class of modality such as H&E, periodic acid-Schiff (PAS), or IHC stained. In addition, most of these approaches train a source- or target-domain task model with one type of image data, either transformed or not, for model prediction. This is different from our method that takes advantage of both gold-standard labeled source images and high-quality real target data for task model training.

II. RELATED WORK

Deep neural networks and particularly CNNs have been recently applied to medical image analysis, leading to compelling performance in various visual tasks such as object recognition, image segmentation, cell classification, and so on [13], [14], [22]. However, CNNs trained on one dataset might not be directly applicable to another due to dataset shifts. Domain adaptation is a popular method to tackle the dataset shift problem and has been applied to various visual tasks in computer vision [66], [67], [68]. In particular, deep domain adaptation that uses adversarial learning or GANs has recently attracted much attention in medical image computing [69], [70]. In Section II-A, we mainly review some related work of adversarial domain adaptation in non-microscopy or non-pathology image analysis, although GANs have been also reported for many other applications [69], [71], [72], [73]. In Section II-B, we survey deep domain adaptation methods specifically focusing on microscopy and digital pathology image analysis and also briefly discuss GAN-based image synthesis or translation approaches, which can be used for downstream tasks in a domain adaptation setting.

A. Adversarial Domain Adaptation in Medical Image Computing

Many adversarial learning and GAN based methods have been applied to image segmentation for different medical imaging modalities, such as computed tomography (CT) and magnetic resonance imaging (MRI). Chartsias et al. [39] have used a cycle-consistency GAN (CycleGAN) [74] to synthesize MR images from CT data for cardiac segmentation and have demonstrated that augmenting real MRI data with synthetic images can improve segmentation performance. Jiang et al. [40] have adopted a CycleGAN to generate hallucinated MRI images from CT scans and then combined these fake MR images and the real CT data to regularize training of a CT segmentation neural network. This method produces better lung tumor segmentation performance than the model trained with only CT images. Zhang et al. [41] have enhanced a CycleGAN with a shape consistency and applied it to image translation between CT and MRI data for cardiac segmentation; later, the authors have applied this method to pancreas segmentation in CT/MR images and breast lesion segmentation in mammogram X-ray images [42]. These methods require annotation of all training images in the target domain, i.e., dataset of interest, and this requirement might not be satisfied in some real applications.

Without relying on annotated target data, Kamnitsas et al. [29] have employed a domain discriminator [28] to learn domain-invariant features for brain lesion segmentation on MR images, which are acquired with different types of scanners. Similarly, Dou et al. [43] have used a domain critic module to differentiate source and target domains for adversarial learning, which aims to adapt a CNN trained with MR images to CT data for cardiac segmentation; afterward, this approach is extended for both CT and MR cardiac image segmentation [44]. Instead of aligning feature distributions, Wang et al. [45] have exploited a patch-based discriminator to encourage consistent output predictions from the source and target domains, and this output space-based adversarial learning method produces excellent performance for joint optic disc and cup segmentation on retinal fundus images. Chartsias et al. [46], [47] have also leveraged a discriminator to differentiate predicted masks of a segmentation network, which is incorporated into a disentangled representation learning framework [75] for multimodal cardiac segmentation in late gadolinium enhanced (LGE) and cine MRI image data.

Another approach of adversarial domain adaptation in medical image analysis is to directly map one domain to another at the image pixel level, mainly based on GANs [36]. Jiang et al. [48] have introduced a tumor-aware loss to a CycleGAN framework that converts labeled CT images to realistic MRI ones with tumor structure preservation; then, the synthesized MR images are combined with a small set of real annotated MRI data to learn a U-Net architecture [12] for lung tumor segmentation on real MR images. Pan et al. [49] have used a 3D CycleGAN to generate fake positron emission tomography (PET) images from corresponding MRI data such that each subject has a pair of MRI-PET images; next, the authors learn a multi-modal multi-instance learning network for Alzheimer’s disease classification. Yang et al. [50] have used a GAN network and a variational autoencoder (VAE) to decompose CT-source and MRI-target images into a shared content space and a domain-specific style space, and then they train a segmentation network with content-only images from the CT domain and apply it to liver segmentation on content-only images from the MRI domain. Instead of relying on two-stage data processing, Huo et al. [51] have unified a CycleGAN and a segmentor into a single framework, which can conduct simultaneous image translation and segmentation on CT/MRI data of abdominal organs and brains. Chen et al. [52] have conducted image and feature space adaptation within a single GAN-based framework, which is applied to heart and abdominal organ segmentation on CT/MR images.

Many GAN-based domain adaptation methods above adapt source data to the target domain and build a task-specific model with adapted source images for evaluation on real target data. By contrast, Mahmood et al. [53] have performed domain adaptation in a reverse direction for depth estimation from monocular endoscopy images. Specifically, they first transform real endoscopy images to synthetic-like data with adversarial learning and then feed these transformed data into a CNN model, which is trained with other annotated synthetic images, for depth estimation of real endoscopy data. Zhang et al. [54] have trained a segmentation neural network with digitally reconstructed radiographs (DRRs), which are generated from labeled CT images, and then have applied the network to multi-organ segmentation on fake DRR data, which are translated from corresponding real target X-ray images with an enhanced CycleGAN. Similarly, Chen et al. [55] have transformed target images into source-like data with a semantic-aware CycleGAN and then have trained a source-domain CNN to segment the source-like target images. This method provides good lung segmentation performance on cross-institution chest X-ray image datasets. These methods learn a task-specific model with transformed target data only, which are synthesized by a target-to-source mapping, and without using real target images, which can provide high-quality information for the content or structures of interest.

B. Deep Domain Adaptation in Microscopy and Digital Pathology Image Analysis

Compared with radiology image analysis, there is relatively less work focusing on deep domain adaptation in microscopy or digital pathology image computing, especially for those based on GANs. Several early studies exploit traditional machine learning methods including boosting and random forests to address microscopy dataset shifts for image segmentation [76], [77], [78], and some uses a Gaussian process based-Bayesian model to classify cross-tissue image patches [79]. Recently, two coupled U-Nets [80] are unified into a single framework and share part of network weights for domain adaptation, which is applied to segmentation of mitochondria and synapses in electron microscopy images. Huang et al. [81] have incorporated convolutional kernel adaptation into a conventional CNN, which is used to differentiate epithelium and stroma image patches cropped from pathology digital slides. This patch-based CNN model might take a high time cost for dense prediction. More recently, Liimatainen et al. [82] have iteratively fine-tuned a source U-Net-like network with target image data for cell detection. This approach provides promising performance for monolayer cultures of cancer cell lines, but it is evaluated on only one type of microscopy imaging modality, i.e., brightfield., and the dataset shift is relatively small.

Adversarial domain adaptation is drawing increasing interest in microscopy image analysis. A popular line of research is to learn domain-invariant feature representations with a domain classifier, which determines whether the representations are from the source or target domain/dataset. Ren et al. [30] have used a domain discriminator to adapt deep feature representations for prostate histopathology image classification, Javanmardi and Tasdizen [83] have applied a gradient reversal layer [28] to an FCN-CNN architecture for neuron membrane image segmentation, and Lafarge et al. [84] have presented a similar gradient reversal-based domain-adversarial neural network for mitosis identification in breast cancer images. However, they might have difficulty in fully aligning the distributions for structured outputs [32], [33], such as individual cell/nucleus localization, which is typically more challenging than image classification tasks [85]. Adversarial learning is also applied to gland segmentation in colon histology images [86] and cell segmentation in fluorescence microscopy images using limited training data [87], but without considering domain adaptation.

GAN-based image-to-image translation is recently used to deal with stain inconsistencies or color variations in pathology images. Bentaieb et al. [59] have employed a GAN model to perform stain transfer for cross-center or cross-scanner histopathology images, and then have used the stain transferred images to learn deep models for tissue segmentation and classification for different types of organs. Shaban et al. [60] have conducted CycleGAN-based stain style transfer for breast cancer histological image classification on different-laboratory data, de Bel et al. [61] have performed CycleGAN-based stain normalization for periodic acid-Schiff (PAS) stained renal tissue image segmentation, Zhou et al. [62] have improved a CycleGAN color normalization framework by using an auxiliary stain color matrix input for breast tumor classification in H&E images, and Zhang et al. [63] have used a CycleGAN to normalize staining intensities of cross-site Ki67 IHC-stained histopathological images for nucleus classification. Other applications of CycleGAN-based image synthesis include nuclei segmentation [64] and glomeruli segmentation [65], which convert images to the label domain. Most of these approaches translate one type of image data to another for stain normalization and train/test a task-specific model with the converted images. In addition, none of these methods are directly applicable to nucleus/cell detection in microscopy images, or they are focused on only one type of microscopy imaging modality/protocol, i.e., H&E, PAS or IHC stained.

There are some other work focusing on only stain normalization of histopathology images, which can support downstream tasks such as image segmentation or classification in a domain adaptation setting. Zanjani et al. [88] have used a GAN model to learn image-content structures and their relation to color attributes for stain normalization of cross-laboratory H&E images, and Nishar et al. [89] have introduced a direct skip connection from input to output into a GAN network for stain transfer in H&E histological images from different laboratories. Lahiani et al. [90] have incorporated a perceptual embedding loss into a CycleGAN framework, which can generate virtual fibroblast activation protein (FAP)-cytokeratin (CK) duplex tissue staining images from real H&E tissue data. Bayramo$\tilde{\text{g}}$lu et al. [91] have used a conditional GAN to convert hyperspectral lung histology images to virtual H&E stained data, and Han et al. [92] applied a conditional, cell mask-constrained GAN to image translation between phase contrast (PC) and differential interference contrast (DIC) microscopy data. Conditional GANs [92], [91] usually require image pairs of source and target training data, which are generally not available for the problem of nucleus detection in cross-modality microscopy images.

III. BIDIRECTIONAL ADVERSARIAL DOMAIN ADAPTATION

Fig. 2 shows the proposed domain adaptation method, which aims to learn a bidirectional nucleus detection model with GAN-based image-to-image translation. It trains a source-domain nucleus detector with annotated source images until convergence and applies this learned detector to pseudo-label generation on source-like, translated target images, which are generated from a target-to-source mapping at the pixel level. Additionally, it trains a target-domain nucleus detector with both pseudo-labeled, real target images and gold-standard annotated, target-like transformed source images, which are synthesized with a source-to-target mapping. This is different from those previous GAN-based medical image analysis approaches (see Section II), which are usually one-directional and do not take into consideration the fact that source-to-target adaptation might be easier than target-to-source for some cases, but the reverse might be true for others. Learning a nucleus detector based on both mappings can take advantage of accurate individual nucleus annotations in the source domain and high-quality training images in the target domain, thus potentially benefiting individual nucleus localization on cross-modality microscopy image datasets. Note that the proposed method does not require paired source-target training images.

Our study shares some similarities to the work [37], which introduces a bidirectional UDA-based image classification method. However, our method differs from [37] in terms of the following aspects: 1) the previous work [37] defines a class consistency loss and requires the target domain to share the same set of categories as the source domain, while our method uses a cycle-consistency GAN framework and also does not have this requirement (e.g., nucleus types of the source and target domain can be different); 2) the previous study [37] generates and uses pseudo-labels for all the annotated target samples, but our method ignores image pixels with low-confident predictions; 3) it is specifically designed for image classification and is only evaluated on digit and traffic sign images, while our approach focuses on a more challenging task that requires structured outputs [85]; 4) we extend and test our UDA method in an SSDA setting, while [37] does not.

A. Pixel-Level Image Adaptation

Let $\left({\mathit{X}}^s,{\mathit{Y}}^s\right)={\left\{\left({\mathit{x}}_i^s,{\mathit{y}}_i^s\right)\right\}}_{i=1}^{N^s}$ denote the source training data with N^s images ${\mathit{x}}_i^s\in {ℝ}^{w\times h\times c}$ and labels ${\mathit{y}}_i^s\in {ℝ}^{w\times h}$, where w, h and c are the width, height and channel of images or labels respectively, and ${\mathit{X}}^t={\left\{{\mathit{x}}_i^t\right\}}_{i=1}^{N^t}$ be the target training data with N^t unannotated images ${\mathit{x}}_i^t\in {ℝ}^{w^{\prime }\times h^{\prime }\times c^{\prime }}$. With (X^s, Y^s)and X^t, our goal is to learn mappings between source $\mathcal{S}$ and target $\mathcal{T}$ domains such that source/target images X^s/X^t can be translated to target-/source-style ones ${\widehat{X}}^s/{\widehat{X}}^t$, and build 1) a target-domain nucleus detector $R_{\mathcal{T}}$, which is applicable to real target data, based on these adapted source images ${\widehat{X}}^s$ and the real target images X^t, and 2) a source-domain nucleus detector $R_{\mathcal{S}}$, which is applicable to adapted target images ${\widehat{X}}^t$, using original source images X^s.

Given unpaired training data from source $\mathcal{S}$ and target $\mathcal{T}$ domains, the adversarial domain adaptation model learns two generators, $G_{\mathcal{S}\mathcal{T}}:\mathcal{S}\to \mathcal{T}$ and $G_{\mathcal{T}\mathcal{S}}:\mathcal{T}\to \mathcal{S}$. $G_{\mathcal{S}\mathcal{T}}$ adapts source images to the target domain so that its associated discriminator $D_{\mathcal{T}}$ is unable to distinguish between adapted source images $G_{\mathcal{S}\mathcal{T}}\left(X^s\right)$ and real target images X^t. Similarly, $G_{\mathcal{T}\mathcal{S}}$ maps data from the target to source domain, aiming to fool its corresponding discriminator $D_{\mathcal{S}}$. This is achieved by using the adversarial loss [36] in both mapping directions

$$\begin{gathered} {\mathcal{L}}_{GAN}\left(G_{\mathcal{S}\mathcal{T}},D_{\mathcal{T}}\right)={\mathbb{E}}_{x^t~X^t}\left[\log D_{\mathcal{T}}\left(x^t\right)\right] \\ +{\mathbb{E}}_{x^s~X^s}\left[\log \left(1-D_{\mathcal{T}}\left(G_{\mathcal{S}\mathcal{T}}\left(x^s\right)\right)\right)\right], \end{gathered}$$ (1)

$$\begin{gathered} {\mathcal{L}}_{GAN}\left(G_{\mathcal{T}\mathcal{S}},D_{\mathcal{S}}\right)={\mathbb{E}}_{x^s~X^s}\left[\log D_{\mathcal{S}}\left(x^s\right)\right] \\ +{\mathbb{E}}_{x^t~X^t}\left[\log \left(1-D_{\mathcal{S}}\left(G_{\mathcal{T}\mathcal{S}}\left(x^t\right)\right)\right)\right], \end{gathered}$$ (2)

where x^s/x^t is a sample from the source/target domain. In order to enforce the cycle consistency [74] such that the reconstructed images are identical to their original versions, i.e., $G_{\mathcal{T}\mathcal{S}}\left(G_{\mathcal{S}\mathcal{T}}\left(x^s\right)\right)\approx x^s$ and $G_{\mathcal{S}\mathcal{T}}\left(G_{\mathcal{T}\mathcal{S}}\left(x^t\right)\right)\approx x^t$, we apply an ℓ₁ penalty to the reconstruction error

$$\begin{gathered} {\mathcal{L}}_{cycle}\left(G_{\mathcal{S}\mathcal{T}},G_{\mathcal{T}\mathcal{S}}\right)={\mathbb{E}}_{x^s~X^s}\left[{\Vert G_{\mathcal{T}\mathcal{S}}\left(G_{\mathcal{S}\mathcal{T}}\left(x^s\right)\right)-x^s\Vert }_1\right] \\ +{\mathbb{E}}_{x^t~X^t}\left[{\Vert G_{\mathcal{S}\mathcal{T}}\left(G_{\mathcal{T}\mathcal{S}}\left(x^t\right)\right)-x^t\Vert }_1\right]. \end{gathered}$$ (3)

B. Bidirectional Detector Learning

1). Loss Function:

In addition to the aforementioned generators and discriminators, our domain adaptation framework also contains two deep regressors, $R_{\mathcal{S}}$ and $R_{\mathcal{T}}$, which map input images into corresponding label spaces for individual nucleus detection. Here we formulate nucleus detection with regression, because it shows better nucleus detection performance than classification modeling in some recent studies [93], [94]. We solve the regression problem with an end-to-end, pixel-to-pixel FCN model, which can directly predict pixel-level, dense output maps for nucleus position estimation. To train the regressors, we obtain the labels of training data based on gold-standard annotations as follows. For each source image ${\mathit{x}}_i^s\in X^s$, its corresponding label ${\mathit{y}}_i^s\in Y^s$ is defined as an identical-sized, continuous-valued and non-negative proximity map and each pixel value measures the proximity of this pixel to its closest real nucleus center (i.e., gold-standard annotation), higher values for closer positions, as shown in Fig. 2. Formally, we calculate the proximity map ${\mathit{y}}_i^s$ as

$$y_i^s(u,v)=\{\begin{array}{ll}\frac{e^{\alpha (1-\frac{E_i^s(u,v)}{ϵ})}-1}{e^{\alpha }-1}\hfill & \text{if}{E}_i^s(u,v)\le ϵ\hfill \\ 0,\hfill & \text{otherwise,}\hfill \end{array}$$ (4)

where $E_i^s(u,v)$ is the Euclidean distance between pixel (u, v) and its closest annotated nucleus center in image ${\mathit{x}}_i^s$, ϵ is a threshold to define the central regions of nuclei, and α controls the proximity decay. With this definition, only the pixels in nuclei’s central regions exhibit positive values, measuring how close they are to corresponding gold-standard annotations.

For source-domain detector $R_{\mathcal{S}}$, we directly train it with the accessible labeled source training data (X^s,Y^s). Due to lack of data annotations in the target domain, we can train its detector $R_{\mathcal{T}}$ with the adapted source images and corresponding labels $\left(G_{\mathcal{S}\mathcal{T}}\left(X^s\right),Y^s\right)$. Note that $G_{\mathcal{S}\mathcal{T}}\left(X^s\right)$ shares the same label Y^s with the original source images X^s. Because the cycle-consistency adversarial learning preserves the content of source images during image translation, while making the adapted source images as if drawn from the target domain, we expect that a detector trained with $\left(G_{\mathcal{S}\mathcal{T}}\left(X^s\right),Y^s\right)$ can be applicable to the target domain. We hypothesize that the source-to-target and target-to-source mappings might not be alternative but complementary. Learning a task model based on the source-to-target mapping might be easier than that using the other direction for some cases, but this might not be true for others. Instead, it might be helpful to learn a detector based on both mapping directions within a unified framework, where the learning can take advantage of both gold-standard annotated, transformed source data and pseudo-labeled, high-quality real target images. Thus we propose to learn the target-domain detector $R_{\mathcal{T}}$ with both source and target images. Specifically, we use the source-domain detector $R_{\mathcal{S}}$ to estimate pseudo-labels ${\tilde{Y}}^t$ on adapted target training images $G_{\mathcal{T}\mathcal{S}}\left(X^t\right)$, which share the same labels as real target images X^t, and learn $R_{\mathcal{T}}$ with a mixture of $\left(G_{\mathcal{S}\mathcal{T}}\left(X^s\right),Y^s\right)$ and $\left(X^t,{\tilde{Y}}^t\right)$. By defining a weighted mean squared error, we can write the objective function for detector learning as follows

$$\begin{gathered} {\mathcal{L}}_{reg}\left(G_{\mathcal{S}\mathcal{T}},G_{\mathcal{T}\mathcal{S}},R_{\mathcal{S}},R_{\mathcal{T}}\right)= \\ {\mathbb{E}}_{\left({\mathit{x}}^s,{\mathit{y}}^s\right)~\left(X^s,Y^s\right)}[{\Vert {\left({\mathit{y}}^s+\beta {\overline{y}}^{s}1\right)}^{\mathit{1}/2}\odot \left(R_{\mathcal{S}}\left({\mathit{x}}^s\right)-{\mathit{y}}^s\right)\Vert }_F^2 \\ +{\Vert {\left({\mathit{y}}^s+\beta {\overline{y}}^{s}1\right)}^{\mathit{1}/2}\odot \left(R_{\mathcal{T}}\left(G_{\mathcal{S}\mathcal{T}}\left(x^s\right)\right)-{\mathit{y}}^s\right)\Vert }_F^2] \\ +\lambda {\mathbb{E}}_{\left({\mathit{x}}^t,{\tilde{\mathit{y}}}^t\right)~\left(X^t,{\tilde{\mathit{Y}}}^t\right)}\left[{\Vert {\left({\tilde{y}}^t+\beta {\overline{\tilde{y}}}^t\mathit{1}\right)}^{1/2}\odot \left(R_{\mathcal{T}}\left(x^t\right)-{\tilde{\mathit{y}}}^t\right)\Vert }_F^2\right], \end{gathered}$$ (5)

where ${\overline{y}}^s/{\overline{\tilde{y}}}^t$ is the mean value of ${\mathit{y}}^s/{\tilde{\mathit{y}}}^t$ and allows the learning to automatically adjust the weight for each training image. 1 is a matrix with all entries equal to one. The parameter β controls the contributions from different image regions. ⊙ denotes element-wise multiplication and ‖ ‖_F represents the Frobenius norm. λ ∈ [0, 1] is used to weight the relative importance of source and target domains. With Equation (5), learning the target-domain detector $R_{\mathcal{T}}$ can take into consideration both accurate, fine-grained nucleus annotations in the source domain and real, high-quality training images in the target domain.

With the aforementioned loss functions, our full UDA objective is formulated as

$$\begin{gathered} \mathcal{L}\left(G_{\mathcal{S}\mathcal{T}},G_{\mathcal{T}\mathcal{S}},D_{\mathcal{S}},D_{\mathcal{T}},R_{\mathcal{S}},R_{\mathcal{T}}\right)={\mathcal{L}}_{GAN}\left(G_{\mathcal{S}\mathcal{T}},D_{\mathcal{T}}\right) \\ +{\mathcal{L}}_{GAN}\left(G_{\mathcal{T}\mathcal{S}},D_{\mathcal{S}}\right)+{\lambda }_{cycle}{\mathcal{L}}_{cycle}\left(G_{\mathcal{S}\mathcal{T}},G_{\mathcal{T}\mathcal{S}}\right) \\ +{\mathcal{L}}_{reg}\left(G_{\mathcal{S}\mathcal{T}},G_{\mathcal{T}\mathcal{S}},R_{\mathcal{S}},R_{\mathcal{T}}\right), \end{gathered}$$ (6)

where λ_cycle is a weighted hyperparameter for cycle consistency. We aim to learn the detectors $R_{\mathcal{S}}$ and $R_{\mathcal{T}}$ by solving the following optimization problem

$$\text{arg}\underset{\left\{\begin{array}{c}{G}_{\mathcal{S}\mathcal{T}},G_{\mathcal{T}\mathcal{S}},\\ R_{\mathcal{S}},R_{\mathcal{T}}\end{array}\right\}}{\min }\underset{\left\{D_{\mathcal{S}},D_{\mathcal{T}}\right\}}{\max }\mathcal{L}\left(G_{\mathcal{S}\mathcal{T}},G_{\mathcal{T}\mathcal{S}},D_{\mathcal{S}},D_{\mathcal{T}},R_{\mathcal{S}},R_{\mathcal{T}}\right).$$ (7)

2). Pseudo-Label Generation:

With a learned source-domain nucleus detector $R_{\mathcal{S}}$, we can generate pseudo-labels ${\tilde{Y}}^t$ for target images by applying $R_{\mathcal{S}}$ to nucleus position estimation on adapted target training images $G_{\mathcal{T}\mathcal{S}}\left(X^t\right)$. Based on the definition of the proximity map in Equation (4) and the loss used for detector learning in Equation (5), we expect pixels within central regions of nuclei to exhibit higher response values than other pixels in the prediction maps. Ideally, the pixel at each nucleus center in the foreground should exhibit the highest value within the local region, while pixels in the image background should have zero values.

Let the prediction be ${\widehat{Y}}^t=R_{\mathcal{S}}\left(G_{\mathcal{T}\mathcal{S}}\left(X^t\right)\right)$ of the transformed target training images $G_{\mathcal{T}\mathcal{S}}\left(X^t\right)$. For each predicted map ${\widehat{y}}_i^t\in {\widehat{Y}}^t$, we take local maxima as nucleus center candidates. In order to reduce the effects of false estimation, we only keep the nucleus center candidates that are located at the foreground regions with highly confident predictions, i.e., ${\widehat{y}}_i^t(u,v)\ge \eta \cdot max\left({\widehat{\mathit{y}}}_i^t\right)$, 0 ≤ η ≤ 1. With these selected center candidates, we can use Equation (4) to calculate the proximity map. For image background, we also choose only the highly confident regions, i.e., ${\widehat{\mathit{y}}}_i^t(u,v)\le 0.1\eta \cdot max\left({\widehat{\mathit{y}}}_i^t\right)$. Only those pixels located in the foreground and background regions with highly confident predictions are used for model training, and all the other pixels are discarded. Formally, the pseudo-label ${\tilde{\mathit{y}}}_i^t$ of target training image ${\mathit{x}}_i^t$ is defined as

$${\tilde{y}}_i^t(u,v)=\{\begin{array}{ll}\frac{e^{\alpha (1-\frac{E_i^t(u,v)}{ϵ})}-1}{e^{\alpha -1}}\hfill & \text{if}{E}_i^t(u,v)\le ϵ\hfill \\ 0\hfill & \text{if}{\widehat{\mathit{y}}}_i^t(u,v)\le 0.1\eta \cdot max\left({\widehat{\mathit{y}}}_i^t\right)\hfill \\ -1,\hfill & \text{otherwise,}\hfill \end{array}$$ (8)

where $E_i^t(u,v)$ is the Euclidean distance between pixel (u, v) and its closest selected nucleus center in the highly confident foreground regions of ${\mathit{x}}_i^t$. The 0 values in ${\tilde{\mathit{y}}}_i^t$ represent estimated background pixels, and the −1 values mean un-confident pixels, which are ignored during model training. In this scenario, we can alleviate the effect of false estimation and thus avoid degrading nucleus detection performance. Note that we do not use any real target data annotations but $\left(G_{\mathcal{S}\mathcal{T}}\left(X^s\right),Y^s\right)$ and $\left(X^t,{\tilde{Y}}^t\right)$, where ${\tilde{Y}}^t={\left\{{\tilde{y}}_i^t\right\}}_{i=1}^{N^t}$, to learn the target-domain detector $R_{\mathcal{T}}$.

C. Network Architecture, Training and Testing

The entire proposed framework consists of two generator-discriminator pairs and two nucleus detectors, as shown in Fig. 2. Similar to the CycleGAN [74], we adopt a residual learning block-based architecture to build the generators, each of which consists of two stride-2 convolutional layers, nine residual blocks [95] and two stride-2 transposed convolutional layers [96]. For the discriminators, we use a 70 × 70 PatchGAN [97] to determine whether each 70 × 70 patch in images is real or fake. This patch-based discriminator network is computationally efficient compared with a full-image discriminator. For the detectors, we adopt a U-Net-like network [98] with small modifications. Specifically, we use stride-2 convolutions to stack four residual blocks [95] in the downsampling path and bilinear interpolation followed by a convolution to connect another four residual blocks in the upsampling path. Additionally, it contains four long-range skip connections [12] from the downsampling to upsampling path and two context aggregation layers [99], which are linked to two stride-1 convolutional layers for output prediction.

We use a stage-wise training strategy [31], [100] to optimize the full objective in Equation (7), due to limited GPU memory. First, we train only the source-domain detector $R_{\mathcal{S}}$ with the existing labeled source data (X^s,Y^s), and then train the generators $G_{\mathcal{S}\mathcal{T}}$, $G_{\mathcal{T}\mathcal{S}}$ and discriminators $D_{\mathcal{S}}$, $D_{\mathcal{T}}$ by solving Equation (7) without the regression losses. Next, we use the learned generators to conduct pixel-level image translation and exploit the learned $R_{\mathcal{S}}$ to create pseudo-labels ${\tilde{Y}}^t$ in the target domain, as discussed in Section III-B2. With gold-standard annotations in adapted source images $\left(G_{\mathcal{S}\mathcal{T}}\left(X^s\right),Y^s\right)$ and pseudo-labels in real target images $\left(X^t,{\tilde{Y}}^t\right)$, we finally train the target-domain detector $R_{\mathcal{T}}$ by optimizing Equation (7) with keeping the other networks fixed. Following [35], [38], we add original source images and associated annotations to the training set to facilitate the learning of $R_{\mathcal{T}}$.

During the testing phase, we apply the learned target-domain detector $R_{\mathcal{T}}$ to dense prediction on target testing images $X_{test}^t$, i.e., ${\widehat{Y}}_{test}^t=R_{\mathcal{T}}\left(X_{test}^t\right)$. For each pixel (u, v) in prediction map ${\widehat{y}}_{test}^t\in {\widehat{Y}}_{test}^t$, we define a set of neighboring pixel predictions centered at (u, v) with a Chebyshev distance less than τ pixels and calculate an ensemble response value for pixel (u, v) by taking a weighted average of all predictions inside the neighboring region

$$F\left({\widehat{\mathit{y}}}_{test}^t(u,v)\right)=\sum _{\left(u^{\prime },v^{\prime }\right)\in \mathit{B}(u,v)}\gamma \left(u^{\prime },v^{\prime }\right){\widehat{\mathit{y}}}_{test}^t\left(u^{\prime },v^{\prime }\right),$$ (9)

$$\mathit{B}(u,v)=\left\{\left(u^{\prime },v^{\prime }\right)\in {\widehat{\mathit{y}}}_{test}^t:\max \left(\left|u-u^{\prime }\right|,\left|v-v^{\prime }\right|\right)\le \tau \right\},$$ (10)

where F(·) denotes the operation for neighboring ensemble prediction, B(u, v) defines the neighboring region for pixel (u, v) and γ(u^′, v^′) is the weight for pixel (u^′, v^′). Here we choose γ(u^′, v^′) = 1/|B(u, v)| for all the pixels in the neighboring region, where |B(u, v)| represents the cardinality of B(u, v). The selection of τ value depends on the nucleus size. This neighboring ensemble prediction can deal with the uncertainty in localization of nucleus centers [16].

With the prediction maps of target test images, we locate the nucleus positions with two different methods: 1) directly seek local maxima in the target prediction maps and 2) merge source- and target-domain prediction maps and then search for local maxima. For the second method, we apply the source-domain detector $R_{\mathcal{S}}$ to pixel-wise prediction on translated target test images, i.e., $R_{\mathcal{S}}\left(G_{\mathcal{T}\mathcal{S}}\left(X_{test}^t\right)\right)$, and aggregate neighboring predictions using Equation (9). Because $R_{\mathcal{S}}$ is trained on original, real source data and evaluated on adapted target images, while $R_{\mathcal{T}}$ is learned with adapted source data and tested on original, real target images, we expect these two detectors to complement each other and a prediction fusion might be able to boost nucleus detection. Hence we merge the predictions from both detectors with a linear combination

$$\rho F\left(R_{\mathcal{T}}\left(X_{test}^t\right)\right)+(1-\rho )F\left(R_{\mathcal{S}}\left(G_{\mathcal{T}\mathcal{S}}\left(X_{test}^t\right)\right)\right),$$ (11)

where ρ ∈ [0, 1] is a weight parameter. Finally, we suppress those low-valued pixels in each merged output map, i.e., not greater than 50η% of the maximum value, by assigning them zeros and then locate nuclei by searching for local maxima.

IV. SEMI-SUPERVISED DOMAIN ADAPTATION

Although large-scale data annotations are often prohibitively expensive in the target domain, it might be feasible to annotate only a small number of target images for semi-supervised model learning, which can improve model performance. For nucleus detection, labeling a nucleus is simply marking a single point (e.g., a mouse click) near the nucleus center [93] and thus it provides a small overhead for limited data annotation. Therefore, it is worth studying and evaluating the proposed framework in a semi-supervised learning situation, where a few target training images are manually annotated.

Suppose target images X^t = X^tl ∪ X^tu, where X^tl and X^tu are labeled and unlabeled images, respectively. Y^tl is the label for X^tl. We can rewrite Equation (5) for SSDA as

$$\begin{gathered} {\mathcal{L}}_{reg}^{SSDA}\left(G_{\mathcal{S}\mathcal{T}},G_{\mathcal{T}\mathcal{S}},R_{\mathcal{S}},R_{\mathcal{T}}\right)= \\ {\mathbb{E}}_{\left({\mathit{x}}^s,{\mathit{y}}^s\right)~\left({\mathit{X}}^s,{\mathit{Y}}^s\right)}[{\Vert {\left({\mathit{y}}^s+\beta {\overline{y}}^s\mathbf{1}\right)}^{1/2}\odot \left(R_{\mathcal{S}}\left({\mathit{x}}^s\right)-{\mathit{y}}^s\right)\Vert }_F^2 \\ +{\Vert {\left({\mathit{y}}^s+\beta {\overline{y}}^s\mathbf{1}\right)}^{1/2}\odot \left(R_{\mathcal{T}}\left(G_{\mathcal{S}\mathcal{T}}\left({\mathit{x}}^s\right)\right)-{\mathit{y}}^s\right)\Vert }_F^2] \\ +\lambda {\mathbb{E}}_{\left({\mathit{x}}^{tu},{\tilde{\mathit{y}}}^{tu}\right)~\left({\mathit{X}}^{tu},{\tilde{\mathit{Y}}}^{tu}\right)}[\Vert {\left({\tilde{\mathit{y}}}^{tu}+\beta {\overline{\tilde{y}}}^{tu}\mathbf{1}\right)}^{1/2} \\ \odot \left(R_{\mathcal{T}}\left({\mathit{x}}^{tu}\right)-{\tilde{\mathit{y}}}^{tu}\right){\Vert }_F^2] \\ +{\mathbb{E}}_{\left({\mathit{x}}^{tl},{\mathit{y}}^{tl}\right)~\left({\mathit{X}}^{tl},{\mathit{Y}}^{tl}\right)}\left[{\Vert {\left({\mathit{y}}^{tl}+\beta {\overline{y}}^{tl}\mathbf{1}\right)}^{1/2}\odot \left(R_{\mathcal{T}}\left({\mathit{x}}^{tl}\right)-{\mathit{y}}^{tl}\right)\Vert }_F^2\right], \end{gathered}$$ (12)

where the pseudo-label ${\tilde{\mathit{Y}}}^{tu}$ for unlabeled target training images is generated by applying the source-domain detector $R_{\mathcal{S}}$ to nucleus location estimation in corresponding source-style, adapted target images. Like unsupervised domain adaptation, we leverage the same stage-wise training strategy [31], [100] to learn the generators, discriminators and detectors. We find that it is not helpful to learn models for nucleus detection by simply pooling labeled and unlabeled target data followed by random sampling, which provide similar performance to the UDA counterpart. Here we emphasize the contributions of the set of labeled target data during model training by calculating ${\mathcal{L}}_{reg}^{SSDA}$ with Equation (12), but only activating the usage of adapted source training images and pseudo-labels on unannotated target images every 200 iterations. After model training, we detect individual nuclei using the model inference method discussed in Section III-C.

V. EXPERIMENTS AND DISCUSSION

A. Datasets

We extensively evaluate the proposed method on three microscopy image datasets, which are acquired using different staining techniques or imaging protocols/modalities. The first dataset [16] consists of 100 H&E stained colon cancer histology images (denoted by H&E in this paper), each of which is acquired at 20× objective magnification and has a dimension of 500 × 500 × 3. The second dataset [101] is a DAPI stained fluorescence microscopy image collection (denoted by DAPI), which contains 120 colon tissue images of size 612×452×3. The third dataset [102] contains 114 Ki67 IHC stained pancreatic neuroendocrine tumor (NET) images (denoted by IHC), which are created with TMA imaging at 20× magnification and have a dimension of 500×500×3. All the datasets have gold-standard annotations of nucleus centers. Following [93], [38], we randomly split each dataset into two halves, one for training and the other for testing. We further randomly select 20% of each training set as the validation set.

B. Implementation Details and Evaluation Metrics

We implement the proposed method using PyTorch. For hyperparameter values, we set d = 15, α = 3 in Equations (4), (8), β = 5, λ = 0.1 in Equations (5), (12) and λ_cycle = 10 in Equation (6). We closely follow [74] to train the generator and discriminator networks using the Adam solver with learning rate=0.0002, batch size=1, and number of epochs=75. We train the source-domain and target-domain detectors using stochastic gradient descent with Nesterov momentum and set the hyperparameters as: learning rate=0.001, momentum=0.99, weight decay=10⁻⁶, batch size=4 and number of iterations=10⁵. We scale the proximity map by a factor of 5 to facilitate training [93], [38], [103]. A small η (close to 0) might lead to incorrect pseudo-label generation, while a much larger η (close to 1) might miss real nuclei. We empirically set η = 0.85 in our experiments, aiming to reduce the influences of false pseudo-labels while retaining a certain number of correct pseudo-labels. We then evaluate a range of η values in sensitivity analyses in Section V-E. We apply data augmentation such as random cropping, rotation and flipping to model training. During training, we evaluate the model on the validation set every 200 iterations and stop the training if the exponential moving average curve of the validation loss does not improve for successive 100 checkpoints. For model inference, we set ρ = 0.7 for prediction map merging and τ = 1, 3, 5 for neighboring prediction fusion on the H&E, DAPI and IHC datasets, respectively.

Following previous nucleus/cell detection work [16], [94], [93], [38], we use precision, recall and F₁ score to evaluate the nucleus detection. Specifically, we define a region with a radius r = 16 centered at each annotated nucleus center as its gold-standard region. We use the Hungarian algorithm [104] to pair human annotations with the automatically detected nucleus centers. Each gold-standard annotation is matched with at most one automated detection, and vice versa. The matched detections are true positives (TP) and those not paired with any gold-standard annotations are false positives (FP). The gold-standard annotations that do not correspond to any detections are viewed as false negatives (FN). Based on these definitions, we can calculate the precision (P), recall (R) and F₁ score as: P = TP/(TP + FP), R = TP/(TP + FN) and F₁ = 2PR/(P + R).

C. Evaluation of Unsupervised Domain Adaptation

We first evaluate the proposed unsupervised learning-based domain adaptation with different experimental settings, as shown in Table I. Baseline means training a source-domain detector $R_{\mathcal{S}}$ with only original source images and directly applying it to nucleus detection in original target testing sets, while $\mathcal{S}$ represents applying the learned $R_{\mathcal{S}}$ to adapted target testing sets. ${\mathcal{T}}_{\mathcal{S}\to \mathcal{T}}$ denotes training a target-domain detector $R_{\mathcal{T}}$ with adapted source images and applying it in original target testing sets, ${\mathcal{T}}_{\mathcal{S}\leftarrow \mathcal{T}}$ means training $R_{\mathcal{T}}$ with original target images and pseudo-labels that are generated via the targetto-source mapping, ${\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$ represents the proposed method training $R_{\mathcal{T}}$ with both adapted source data and pseudo-labeled real target images with the first model prediction method for nucleus localization (see Section III-C), and $\mathcal{S}+{\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$ is the proposed method with the second nucleus localization method, i.e., merging the predictions from $\mathcal{S}$ and ${\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$ with Equation (11). The 5%-target and full-target means training with 5% of and all original annotated target images, respectively. In Table I, we repeat the above process for each model training five times, and report the average of each metric with different radii (i.e., r = 16 and 8) used to define the gold-standard region of each nucleus. In Table II, we list the p-values of two-sample t-tests (a significance level of 0.05), which compare $\mathcal{S}+{\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$ to other methods in terms of F₁ score.

TABLE I.

Evaluation of nucleus detection on different datasets in terms of precision (P), recall (R) and F₁ score (%). $\mathcal{S}$ and $\mathcal{T}$ denote the source and target domains, respectively. The first, second, third and forth panels represent the proposed method’s variants, proposed UDA methods, proposed SSDA methods with 5% gold-standard annotations available in each target dataset, and the target-only models respectively, for different radii (i.e., r = 16 and 8) used to define gold-standard regions.

Method		r = 16
		H&E ($\mathcal{T}$)						DAPI ($\mathcal{T}$)						IHC ($\mathcal{T}$)
		DAPI ($\mathcal{S}$)			IHC ($\mathcal{S}$)			H&E ($\mathcal{S}$)			IHC ($\mathcal{S}$)			H&E ($\mathcal{S}$)			DAPI ($\mathcal{S}$)
		P	R	F 1	P	R	F 1	P	R	F 1	P	R	F 1	P	R	F 1	P	R	F 1
1	Baseline	49.7	64.3	56.1	74.5	62.5	68.0	69.3	70.6	69.9	76.4	87.2	81.4	72.7	93.1	81.6	68.4	85.8	76.1
	$\mathcal{S}$	70.3	59.0	64.1	75.0	63.5	68.8	60.0	66.7	63.1	71.5	89.9	79.7	59.2	96.3	73.3	79.8	79.2	79.5
	${\mathcal{T}}_{\mathcal{S}\leftarrow \mathcal{T}}$	62.5	63.1	62.8	85.3	52.1	64.7	57.2	95.0	71.4	74.2	91.5	82.0	68.2	93.9	79.0	74.0	85.7	79.4
	${\mathcal{T}}_{\mathcal{S}\leftarrow \mathcal{T}}$	72.7	56.3	63.4	74.4	58.8	65.7	58.7	77.2	66.7	73.1	87.7	79.7	60.7	96.7	74.5	77.5	86.7	81.8
2	${\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$	70.1	61.2	65.3	82.8	59.3	69.1	65.3	84.6	73.7	74.7	90.4	81.8	76.2	93.0	83.7	77.8	83.3	80.5
	$\mathcal{S}+{\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$	71.8	60.5	65.7	82.9	60.2	69.7	65.9	81.0	72.6	74.8	90.4	81.8	75.8	94.2	84.0	79.4	82.0	80.7
3	${\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{SSDA}$	75.4	69.3	72.2	73.9	69.9	71.8	75.7	86.2	80.6	76.6	85.6	80.8	83.5	87.2	85.3	85.2	84.8	85.0
	$\mathcal{S}+{\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{SSDA}$	77.7	70.2	73.8	77.2	68.7	72.7	75.8	86.6	80.9	76.7	86.9	81.5	82.5	88.8	85.6	87.0	85.0	86.0
4	5%-target	73.6	66.0	69.9	73.6	66.0	69.9	75.7	86.0	80.8	75.7	86.0	80.8	85.8	82.2	84.3	85.8	82.2	84.3
	Full-target	75.7	90.8	82.5	75.7	90.8	82.5	77.2	89.3	82.8	77.2	89.3	82.8	87.7	89.5	88.6	87.7	89.5	88.6
Method		r = 8
		H&E ($\mathcal{T}$)						DAPI ($\mathcal{T}$)						IHC ($\mathcal{T}$)
		DAPI ($\mathcal{S}$)			IHC ($\mathcal{S}$)			H&E ($\mathcal{S}$)			IHC ($\mathcal{S}$)			H&E ($\mathcal{S}$)			DAPI ($\mathcal{S}$)
		P	R	F 1	P	R	F 1	P	R	F 1	P	R	F 1	P	R	F 1	P	R	F 1
1	Baseline	40.1	51.8	45.2	68.2	57.2	62.2	58.3	59.4	58.8	69.0	78.7	73.5	70.9	90.8	79.6	66.3	83.1	73.7
	$\mathcal{S}$	61.5	51.6	56.1	67.5	57.2	61.9	45.2	50.2	47.5	63.5	79.8	70.8	56.4	91.9	69.9	77.1	76.5	76.8
	${\mathcal{T}}_{\mathcal{S}\leftarrow \mathcal{T}}$	53.6	54.1	53.8	79.4	48.5	60.2	51.6	85.8	64.5	68.6	84.5	75.7	65.7	90.4	76.1	71.4	82.6	76.6
	${\mathcal{T}}_{\mathcal{S}\leftarrow \mathcal{T}}$	65.6	50.8	57.2	68.3	54.0	60.3	43.7	57.5	49.7	65.9	79.0	71.8	57.4	91.5	70.5	75.1	83.9	79.3
2	${\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$	62.5	54.5	58.2	77.0	55.2	64.3	55.5	71.9	62.6	68.8	83.2	75.3	73.8	90.1	81.1	75.3	80.7	77.9
	$\mathcal{S}+{\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$	64.4	54.2	58.9	77.2	56.1	65.0	54.8	67.4	60.4	68.5	82.9	75.0	73.3	91.0	81.2	77.1	79.6	78.3
3	${\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{SSDA}$	68.0	62.5	65.1	66.7	63.0	64.8	68.6	78.1	73.0	69.8	78.0	73.7	80.7	84.2	82.4	82.5	82.2	82.3
	$\mathcal{S}+{\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{SSDA}$	70.9	64.0	67.3	70.9	63.0	66.7	67.6	77.2	72.1	69.9	79.2	74.3	79.8	85.9	82.7	84.7	82.7	83.7
4	5%-target	66.7	59.8	63.3	66.7	59.8	63.3	68.9	78.5	73.7	68.9	78.5	73.7	82.9	79.5	81.5	82.9	79.5	81.5
	Full-target	71.1	85.3	77.6	71.1	85.3	77.6	72.0	83.3	77.2	72.0	83.3	77.2	86.0	87.8	86.9	86.0	87.8	86.9

TABLE II.

The p-values of two-sample t-tests (a significance level of 0.05) comparing $\mathcal{S}+{\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$ to other methods, in terms of F₁ score. $\mathcal{S}$ and $\mathcal{T}$ denote the source and target domains, respectively. The first, second, third and forth panels represent our method’s variants, proposed UDA methods, proposed SSDA methods with 5% gold-standard annotations available in each target dataset, and the target-only models respectively, for different radii (i.e., r = 16 and 8) used to define gold-standard regions.

Method		r = 16						r = 8
		H&E ($\mathcal{T}$)		DAPI ($\mathcal{T}$)		IHC ($\mathcal{T}$)		H&E ($\mathcal{T}$)		DAPI ($\mathcal{T}$)		IHC ($\mathcal{T}$)
		DAPI ($\mathcal{S}$)	IHC ($\mathcal{S}$)	H&E ($\mathcal{S}$)	IHC ($\mathcal{S}$)	H&E ($\mathcal{S}$)	DAPI ($\mathcal{S}$)	DAPI ($\mathcal{S}$)	IHC ($\mathcal{S}$)	H&E ($\mathcal{S}$)	IHC ($\mathcal{S}$)	H&E ($\mathcal{S}$)	DAPI ($\mathcal{S}$)
1	Baseline	2×10−6	0.081	0.095	0.198	1.9×10−3	1.2×10−5	10−6	0.014	0.357	0.012	0.015	1.3×10−5
	$\mathcal{S}$	0.018	5.9×10−3	0.0	10−6	0.0	8.8×10−3	1.3×10−3	10−6	0.0	3×10−6	0.0	1.1×10−3
	${\mathcal{T}}_{\mathcal{S}\leftarrow \mathcal{T}}$	1.8×10−3	10−6	0.114	0.442	5×10−6	1.5×10−3	4.3×10−5	3×10−6	1.8×10−3	0.05	2×10−6	1.9×10−4
	${\mathcal{T}}_{\mathcal{S}\leftarrow \mathcal{T}}$	1.5×10−3	0.0	5×10−6	0.442	0.0	2.3×10−3	9.2×10−3	0.0	0.0	4×10−6	0.0	0.011
2	${\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$	0.546	3.1×10−3	0.077	0.703	0.598	0.572	0.248	0.035	0.018	0.327	0.856	0.319
	$\mathcal{S}+{\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$	-	-	-	-	-	-	-	-	-	-	-	-
3	${\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{SSDA}$	4.3×10−5	7.7×10−4	1.1×10−5	1.4×10−3	0.071	1.7×10−5	5.7×10−5	0.594	4×10−6	5.6×10−3	0.150	4.6×10−5
	$\mathcal{S}+{\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{SSDA}$	6×10−6	10−6	9×10−6	0.222	0.042	3×10−6	5×10−6	1.5×10−4	6×10−6	0.068	0.072	4×10−6
4	5%-target	2.4×10−3	0.847	1.5×10−5	0.012	0.576	2.1×10−5	2.1×10−3	0.059	5×10−6	0.036	0.672	4×10−6
	Full-target	0.0	0.0	0.0	1.2×10−4	2×10−6	0.0	0.0	0.0	0.0	3.3×10−5	10−6	0.0

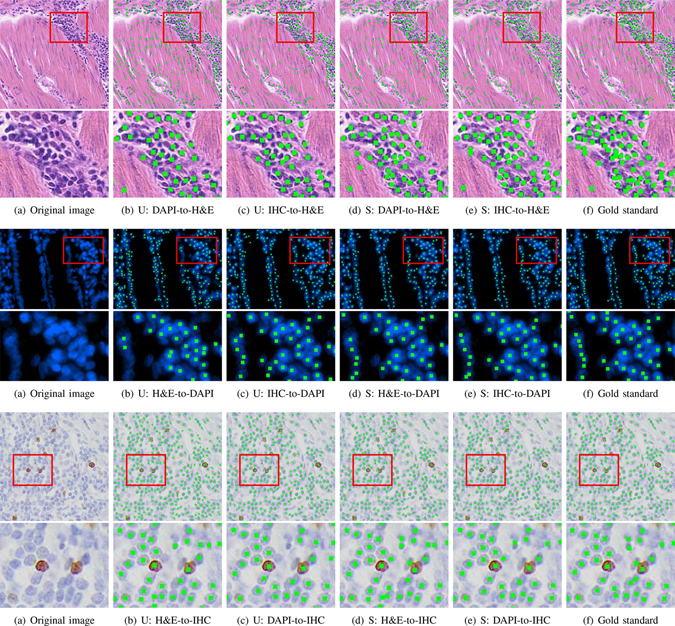
Based on Tables I and II, we note that when H&E or IHC is the target data, the proposed method that merges source and target predictions, $\mathcal{S}+{\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$, significantly outperforms the baseline and other variants (i.e., $\mathcal{S}$, ${\mathcal{T}}_{\mathcal{S}\to \mathcal{T}}$ and ${\mathcal{T}}_{\mathcal{S}\leftarrow \mathcal{T}}$) for almost all cases with p-values less than 0.05, except IHC-to-H&E with r = 16 for the baseline and DAPI-to-IHC with r = 16 and 8 for model ${\mathcal{T}}_{\mathcal{S}\leftarrow \mathcal{T}}$. The method $\mathcal{S}+{\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$ provides a lower F1 score than model ${\mathcal{T}}_{\mathcal{S}\leftarrow \mathcal{T}}$ for DAPI-to-IHC, perhaps because the source-to-target image translation does not produce reliable results. For DAPI as target and particularly the case of IHC-to-DAPI with r = 16, the baseline delivers close performance to the full-target model, leaving limited room for improvement and probably making domain adaptation difficult to further boost the performance. Compared to $\mathcal{S}+{\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$, the method using direct model inference for nucleus detection, ${\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$, produces a significantly lower F₁ score for IHC-to-H&E with r = 16 and 8 and a much better result for H&E-to-DAPI with r = 8. For the other cases, ${\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$ provides similar performance to $\mathcal{S}+{\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$. For most cases, bidirectional mapping-based detection model learning (i.e., ${\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$ and $\mathcal{S}+{\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$) outperforms the counterpart based on single-directional mapping (i.e., $\mathcal{S}$, ${\mathcal{T}}_{\mathcal{S}\to \mathcal{T}}$ and ${\mathcal{T}}_{\mathcal{S}\leftarrow \mathcal{T}}$). We also observe that for the same target dataset, using different source data produces different nucleus detection performance. For instance, it is better to use IHC instead of DAPI as the source for the H&E target data, probably because the IHC dataset exhibits relatively more divergent image appearance as compared to the other. Fig. 3 shows qualitative nucleus detection results of $\mathcal{S}+{\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$ on several example images.

Fig. 3.

Nucleus detection of the proposed methods, $\mathcal{S}+{\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$ and $\mathcal{S}+{\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{SSDA}$, on the H&E (rows 1 ~ 2), DAPI (rows 3 ~ 4) and IHC (rows 5 ~ 6) datasets. The red-rectangle regions in rows 1, 3, and 5 are zoomed in rows 2, 4 and 6, respectively. Columns (a) and (f) denote original images and gold standard annotations (green dots), respectively. Columns (b) and (c) represent the detection results of $\mathcal{S}+{\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$ in different experimental settings (source-to-target), and columns (d) and (e) are the results of $\mathcal{S}+{\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{SSDA}$ with 5% target training annotations.

D. Comparison with Other Methods

We compare our UDA methods, ${\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$ and $\mathcal{S}+{\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$, to several recent deep learning-based UDA approaches, such as adversarial discriminative domain adaptation (ADDA) [23], cycle-consistent adversarial domain adaptation (CyCADA) [31], iterative unsupervised domain adaptation (IUDA) [82] and generative adversarial domain adaptation (GADA) [63]. The IUDA and GADA are two domain adaptation methods specifically designed for nucleus/cell detection in microscopy images. Table III shows the results of these methods with different gold-standard radii, r = 16 and 8, on the H&E, DAPI and IHC datasets. We note that ADDA produces a lower F₁ score than CyCADA for all the cases except the H&E-to-IHC setting, suggesting the benefit of image pixel-level domain adaptation used in CyCADA; ADDA delivers better performance for H&E-to-IHC, probably because CyCADA does not obtain very reliable image translation results for that setting. Both CyCADA and IUDA produce a lower F₁ score than GADA for almost all the cases, except that CyCADA give a higher F₁ score for H&E-to-DAPI with r = 16. This might be because CyCADA uses a binary classification loss for object localization, which could potentially lead to degraded performance compared with regression modeling [94], [93] used in GADA, and IUDA fine-tunes source-trained nucleus detection models with artificial labels directly propagated from source to target datasets, which might exhibit significant variations such that fake target labels are not accurate enough for proper model fine-tuning. Our method outperforms GADA, perhaps due to the bidirectional mapping-based target model learning.

TABLE III.

Comparison with fully supervised and other domain adaptation models in terms of precision (P), recall (R) and F₁ score (%). $\mathcal{S}$ and $\mathcal{T}$ denote the source and target domains, respectively. The first, second, third and fourth panels denote fully supervised learning, other UDA methods, proposed UDA methods and proposed SSDA approaches with 5% gold-standard target annotations available respectively, for different radii (i.e., r = 16 and 8) used to define gold-standard regions.

Method		r = 16
		H&E ($\mathcal{T}$)						DAPI ($\mathcal{T}$)						IHC ($\mathcal{T}$)
		DAPI ($\mathcal{S}$)			IHC ($\mathcal{S}$)			H&E ($\mathcal{S}$)			IHC ($\mathcal{S}$)			H&E ($\mathcal{S}$)			DAPI ($\mathcal{S}$)
		P	R	F 1	P	R	F 1	P	R	F 1	P	R	F 1	P	R	F 1	P	R	F 1
1	FCN-8s [11]	57.3	79.5	66.6	57.3	79.5	66.6	86.1	65.6	74.5	86.1	65.6	74.5	97.0	55.0	70.2	97.0	55.0	70.2
	U-Net [12]	39.5	85.2	54.0	39.5	85.2	54.0	87.4	66.8	75.7	87.4	66.8	75.7	88.5	64.0	74.3	88.5	64.0	74.3
	FCRNA [103]	72.4	87.7	79.3	72.4	87.7	79.3	75.9	87.1	81.1	75.9	87.1	81.1	83.1	89.5	86.2	83.1	89.5	86.2
	FCRNB [103]	68.8	97.0	80.5	68.8	97.0	80.5	74.2	95.0	83.3	74.2	95.0	83.3	82.4	92.6	87.2	82.4	92.6	87.2
	FRCN [93]	76.4	87.2	81.4	76.4	87.2	81.4	76.4	90.3	82.8	76.4	90.3	82.8	86.3	88.5	87.4	86.3	88.5	87.4
	HoVer-Net [105]	86.3	79.9	83.0	86.3	79.9	83.0	83.2	75.7	79.3	83.2	75.7	79.3	87.9	85.0	86.5	87.9	85.0	86.5
	Full-target	75.7	90.8	82.5	75.7	90.8	82.5	77.2	89.3	82.8	77.2	89.3	82.8	87.7	89.5	88.6	87.7	89.5	88.6
2	ADDA [23]	55.0	31.7	40.2	74.6	39.9	52.0	56.9	17.1	26.3	72.4	27.4	39.8	80.8	78.2	79.5	56.4	46.2	50.8
	CyCADA [31]	63.1	40.2	49.1	81.3	45.3	58.2	63.3	92.4	75.1	78.1	60.4	68.1	67.0	85.8	75.3	86.6	51.6	64.7
	IUDA [82]	59.6	42.1	49.3	57.0	32.8	41.6	77.4	28.0	41.1	81.5	63.0	71.1	89.3	68.4	77.5	78.8	66.1	71.9
	GADA [63]	61.4	66.0	63.6	81.6	57.7	67.6	53.6	97.7	69.2	73.3	91.0	81.2	69.6	89.2	78.2	74.4	84.3	79.0
3	${\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$	70.1	61.2	65.3	82.8	59.3	69.1	65.3	84.6	73.7	74.7	90.4	81.8	76.2	93.0	83.7	77.8	83.3	80.5
	$\mathcal{S}+{\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$	71.8	60.5	65.7	82.9	60.2	69.7	65.9	81.0	72.6	74.8	90.4	81.8	75.8	94.2	84.0	79.4	82.0	80.7
4	${\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{SSDA}$	75.4	69.3	72.2	73.9	69.9	71.8	75.7	86.2	80.6	76.6	85.6	80.8	83.5	87.2	85.3	85.2	84.8	85.0
	$\mathcal{S}+{\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{SSDA}$	77.7	70.2	73.8	77.2	68.7	72.7	75.8	86.6	80.9	76.7	86.9	81.5	82.5	88.8	85.6	87.0	85.0	86.0
Method		r = 8
		H&E ($\mathcal{T}$)						DAPI ($\mathcal{T}$)						IHC ($\mathcal{T}$)
		DAPI ($\mathcal{S}$)			IHC ($\mathcal{S}$)			H&E ($\mathcal{S}$)			IHC ($\mathcal{S}$)			H&E ($\mathcal{S}$)			DAPI ($\mathcal{S}$)
		P	R	F 1	P	R	F 1	P	R	F 1	P	R	F 1	P	R	F 1	P	R	F 1
1	FCN-8s [11]	39.4	54.7	45.8	39.4	54.7	45.8	75.2	57.3	65.0	75.2	57.3	65.0	91.0	51.6	65.9	91.0	51.6	65.9
	U-Net [12]	27.3	59.0	37.4	27.3	59.0	37.4	73.2	55.9	63.4	73.2	55.9	63.4	77.0	55.7	64.7	77.0	55.7	64.7
	FCRNA [103]	66.8	80.9	73.2	66.8	80.9	73.2	65.4	75.1	70.0	65.4	75.1	70.0	80.9	87.1	83.9	80.9	87.1	83.9
	FCRNB [103]	66.1	93.2	77.4	66.1	93.2	77.4	68.5	87.7	77.0	68.5	87.7	77.0	80.4	90.3	85.0	80.4	90.3	85.0
	FRCN [93]	66.9	76.3	71.3	66.9	76.3	71.3	58.5	69.1	63.3	58.5	69.1	63.3	80.2	82.2	81.2	80.2	82.2	81.2
	HoVer-Net [105]	85.1	79.3	82.1	85.1	79.3	82.1	80.9	72.7	76.6	80.9	72.7	76.6	87.9	84.1	86.0	87.9	84.1	86.0
	Full-target	71.1	85.3	77.6	71.1	85.3	77.6	72.0	83.3	77.2	72.0	83.3	77.2	86.0	87.8	86.9	86.0	87.8	86.9
2	ADDA [23]	31.3	18.1	22.9	53.1	28.4	37.0	22.0	6.6	10.2	52.2	19.8	28.7	74.2	71.9	73.0	36.1	29.6	32.5
	CyCADA [31]	40.6	25.9	31.6	71.0	39.5	50.8	45.9	67.1	54.5	52.1	40.3	45.4	57.8	73.9	64.8	68.3	40.7	51.0
	IUDA [82]	40.3	28.5	33.4	42.3	24.4	31.0	53.6	19.4	28.5	68.9	53.2	60.1	85.7	65.7	74.4	75.0	62.9	68.4
	GADA [63]	52.0	55.9	53.9	75.0	53.1	62.2	49.9	90.9	64.4	67.5	83.8	74.8	66.6	85.3	74.8	71.4	80.9	75.8
3	${\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$	62.5	54.5	58.2	77.0	55.2	64.3	55.5	71.9	62.6	68.8	83.2	75.3	73.8	90.1	81.1	75.3	80.7	77.9
	$\mathcal{S}+{\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$	64.4	54.2	58.9	77.2	56.1	65.0	54.8	67.4	60.4	68.5	82.9	75.0	73.3	91.0	81.2	77.1	79.6	78.3
4	${\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{SSDA}$	68.0	62.5	65.1	66.7	63.0	64.8	68.6	78.1	73.0	69.8	78.0	73.7	80.7	84.2	82.4	82.5	82.2	82.3
	$\mathcal{S}+{\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{SSDA}$	70.9	64.0	67.3	70.9	63.0	66.7	67.6	77.2	72.1	69.9	79.2	74.3	79.8	85.9	82.7	84.7	82.7	83.7

Table III also compares the proposed UDA method to recent state-of-the-art fully supervised deep models, such as FCN-8s [11], U-Net [12], fully convolutional regression network (FCRN) A/FCRNB [103], fully residual convolutional network (FRCN) [93], and HoVer-Net [105], which are trained with all real, gold-standard annotated target images only. We see that the proposed approaches can provide a higher F₁ score than classification models such as FCN-8s and U-Net for most cases, and it also delivers competitive or even slightly better performance with those regression models including FCRNA/FCRNB, FRCN and/or HoVer-Net for IHC-to-DAPI and H&E-to-IHC. This suggests that adaptation from an appropriate source domain can be very helpful for nucleus detection when target data annotations are not available.

E. Parameter Sensitivity Analysis

The proposed method has an important parameter, λ in Equation (5), which controls the relative contributions from gold-standard annotated, adapted source data and artificially labeled, real target data. The top row of Fig. 4 shows the F₁ score of ${\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$ with different λ values for r = 16. For all experimental settings except IHC-to-DAPI, the F₁ score grows initially and then decreases with the increase in λ, suggesting the importance of pseudo-labeled, real target training images used for model learning. In addition, A small λ might not provide very informative content from the pseudo-labeled target data, while a much higher λ would make the target data dominate the training procedure and weaken the contributions from gold-standard annotated, converted source images. For the IHC-to-DAPI case, the nucleus detection performance does not show significant variation when λ ≤ 0.1 and drops dramatically for λ > 0.1, suggesting that learning with artificially annotated target images might not be helpful for this situation and this is consistent with the observation in Table II. For each case, the F₁ score with different λ values for r = 8 exhibits a similar trend to that for r = 16, so we do not show the results for r = 8 here.

Fig. 4.

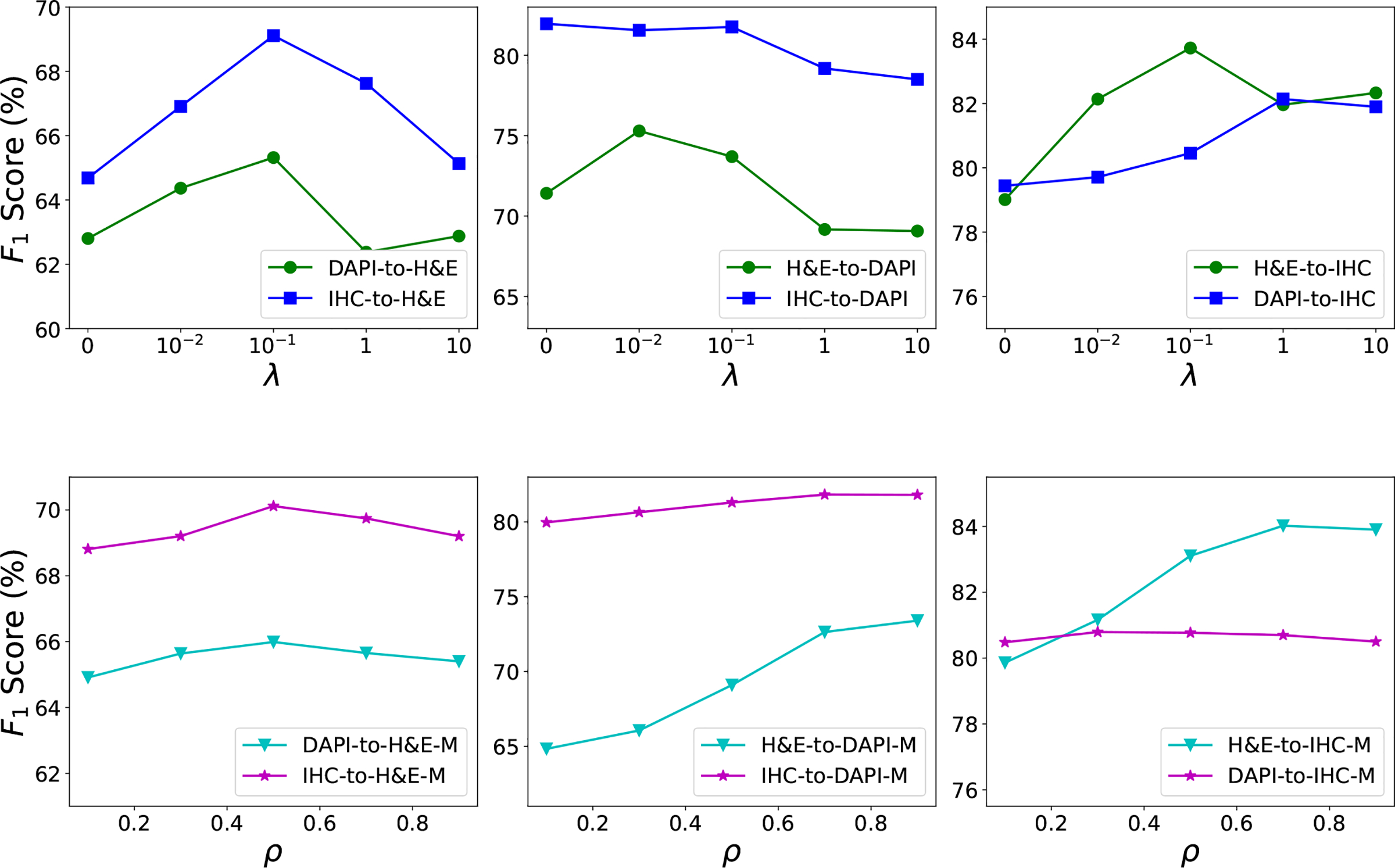
The F1 score of the proposed method ${\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$ with different λ’s (top row) and $\mathcal{S}+{\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$ with ρ’s (bottom row) on the H&E, DAPI and IHC datasets. $\mathcal{S}$ and $\mathcal{T}$ denote the source and target domains, respectively.

Another critical parameter is the ρ in Equation (11) for the proposed method with merging source and target predictions, $\mathcal{S}+{\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$. The bottom row of Fig. 4 displays the influence of ρ on nucleus detection, with λ = 0.1 and r = 16. The value of ρ has distinct effects for different domain adaptation settings. For H&E as the target with either DAPI or IHC as the source, the F₁ score improves as ρ increases but it keeps decreasing after ρ > 0.5, suggesting the benefit of merging source and target predictions for final nucleus localization. For cases of H&E-to-DAPI and H&E-to-IHC, the nucleus detection performance with ρ > 0.5 has a significant improvement compared to ρ < 0.5, showing that the target-domain detector provides more accurate nucleus localization than the source-domain detector. The IHC-to-DAPI case shows slight gain for large ρ values, and there is no significant variation for DAPI-to-IHC when varying ρ from 0 to 1.

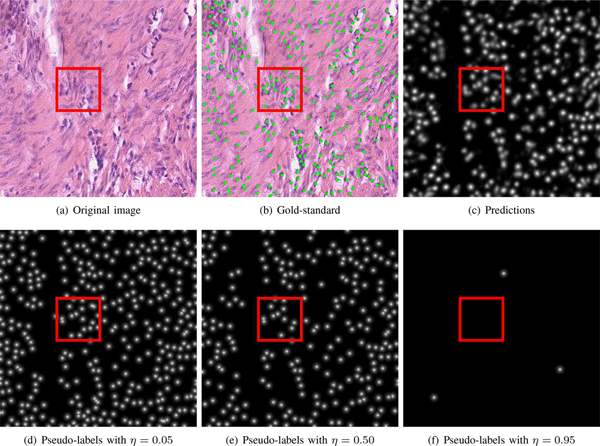
We also evaluate the effects of the η used for pseudo-label generation in Equation (8), as shown in Figs. 5 and 6. We find that for DAPI-to-H&E and H&E-to-DAPI, a high η value (e.g., 0.95) produces significantly less correct pseudo-labels than a relatively lower η value (e.g., 0.5), and thus this might cause a significant decrease in the F₁ score of ${\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$ with the increase of η value. For the IHC-to-H&E case, there are still a certain number of correct pseudo-labels when η = 0.95, so we do not observe a sharp performance drop when increasing the η value. For all the other cases and particularly H&E-to-IHC and DAPI-to-IHC, a small η leads to many incorrect pseudo-labels due to noisy model predictions and a relatively higher η value can eliminate a large proportion of these false pseudo-labels. Therefore, ${\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$ exhibits improved nucleus detection performance as the increase of η value. $\mathcal{S}+{\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$ has similar performance to ${\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$. The η shows different influences on nucleus detection in different datasets and experimental settings, and it would be challenging to automatically determine the optimal η value in advance. One potential solution is to determine the optimal η value based on a sufficiently representative validation set and then use that optimal value for model evaluation.

Fig. 5.

Pseudo-label generation with different η values on one example H&E image. Here DAPI and H&E are the source and target data, respectively. (a ~ f) denote an H&E image, gold-standard annotation, estimation of nucleus positions, and pseudo-labels with η = 0.05, η = 0.5 and η = 0.95, respectively. Some pseudo-labels in the red rectangle do not represent real nuclei with η = 0.05, while real nuclei in the rectangle are not correctly labeled with η = 0.95.

Fig. 6.

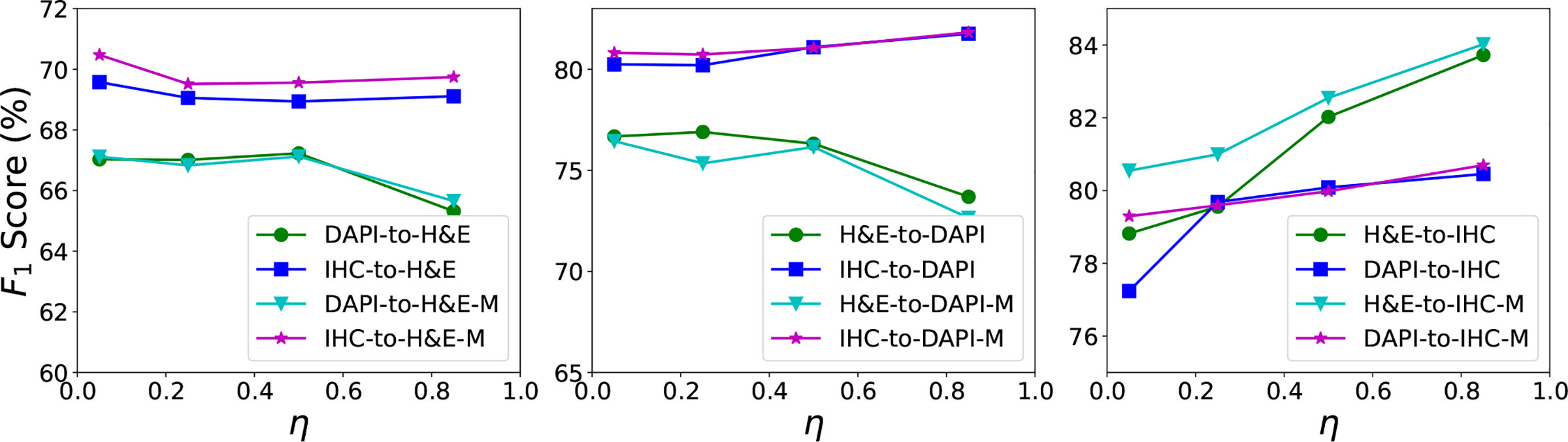
The F₁ score of the proposed methods, ${\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$ and $\mathcal{S}+{\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$ with different η values on the H&E, DAPI and IHC datasets. $\mathcal{S}$ and $\mathcal{T}$ denote the source and target domains, respectively. DAPI-to-H&E and DAPI-to-H&E-M represent ${\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$ and $\mathcal{S}+{\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$ respectively, for the experimental setting of DAPI as source and H&E as target. The same notations apply to other setting.

Fig. 7 shows the nucleus detection performance of the proposed methods, ${\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$ and $\mathcal{S}+{\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$, using different numbers of training images. Here, we use 5%, 20%, 60% and 100% of the source and target training data to train the proposed models. We see that except for H&E-to-DAPI with 5% and 20% of training data, both ${\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$ and $\mathcal{S}+{\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$ outperform the baseline methods for all the other cases. In particular, for DAPI-to-H&E, H&E-to-IHC and DAPI-to-IHC, domain adaptation obtains more gain when learning with less than 60% of the training data in each domain, and this demonstrates the importance of domain adaptation when only limited data are available. We also note that for most of cases, using more than 60% of the training data does not provide a significant improvement for nucleus detection, probably because the detector reaches its model capacity with more images used.

Fig. 7.

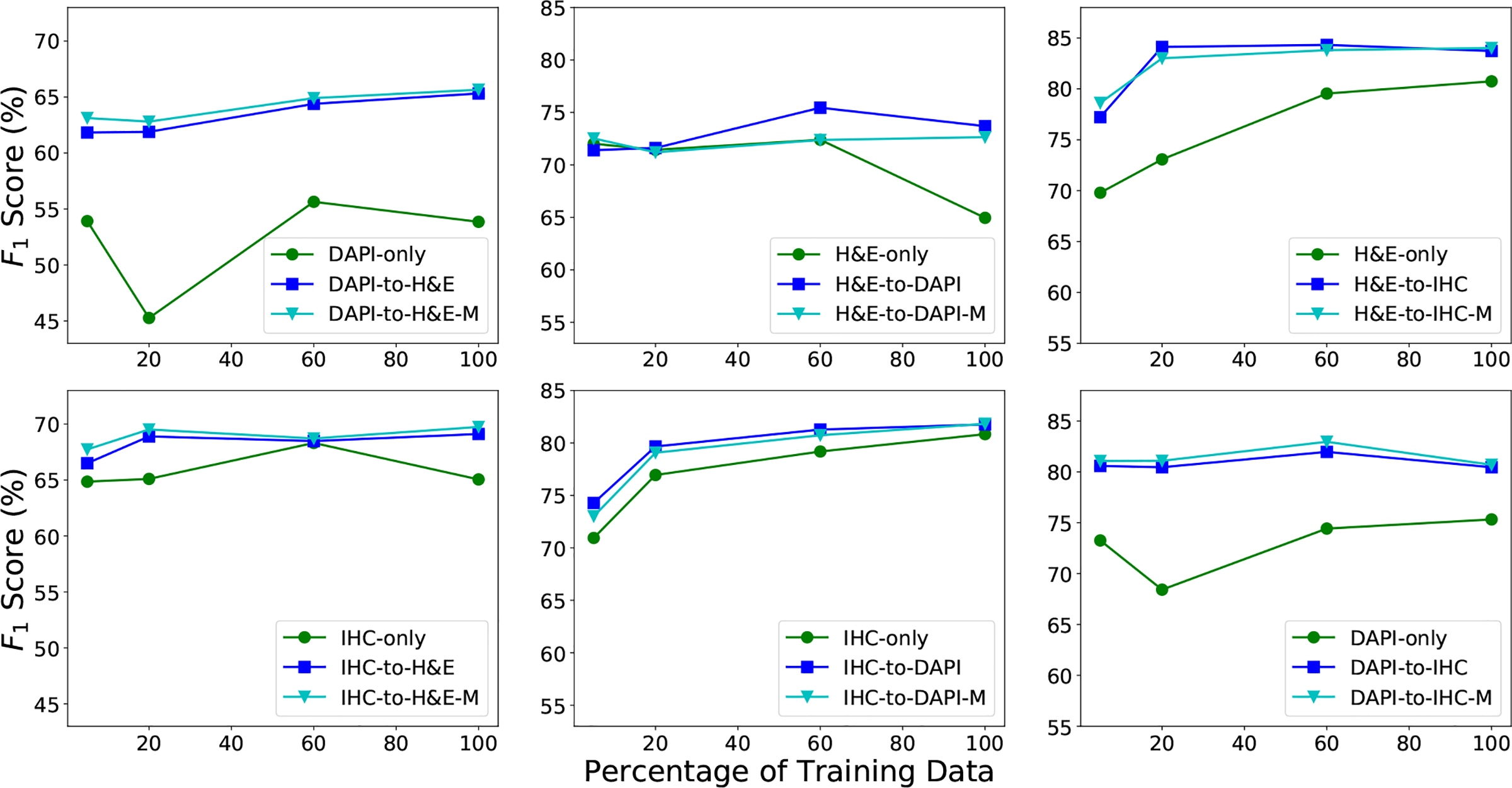
The F1 score of the proposed methods, ${\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$ and $\mathcal{S}+{\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$ with different numbers of training images on the H&E, DAPI and IHC datasets. $\mathcal{S}$ and $\mathcal{T}$ denote the source and target domains, respectively. DAPI-to-H&E and DAPI-to-H&E-M represent ${\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$ and $\mathcal{S}+{\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$ respectively, for the experimental setting of DAPI as source and H&E as target. The same notations apply to other settings.

We evaluate the effects of the radius r that is used to define gold-standard regions of manual annotations, as shown in Tables I, II, III and IV. As expected, nucleus detection with r = 16 produces better performance than that with r = 8, because a smaller r represents a stricter definition and more accurate nucleus localization. However, the performance of several competing methods drops considerably from r = 16 to r = 8 on the H&E or DAPI target data, while the proposed methods exhibits a relatively smaller decrease. For instance, $\mathcal{S}+{\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$ provides a slightly higher F₁ score than the baseline for IHC-to-H&E with r = 16, but significantly outperforms the baseline when r = 8, as shown in Table II. In addition, $\mathcal{S}+{\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$ is significantly better than the baseline and ${\mathcal{T}}_{\mathcal{S}\leftarrow \mathcal{T}}$ for IHC-to-DAPI with r = 8, and this is not true for r = 16. Similarly, the ADDA, CyCADA and IUDA methods as well as some fully supervised methods, such as FCN-8s, U-Net, FCRNA and FRCN, degrade performance dramatically from r = 16 to r = 8 for cases when H&E or DAPI is the target, but the proposed methods are relatively less affected by the radius parameter. This demonstrates that our methods locate individual nuclei more precisely as compared to others.

TABLE IV.

The p-values of two-sample t-tests (a significance level of 0.05) comparing the 5%-target model to the proposed SSDA methods trained with 5% gold-standard target data annotations, in terms of F₁ score with for different radii (i.e., r = 16 and 8). $\mathcal{S}$ and $\mathcal{T}$ denote the source and target domains, respectively.

Method	r = 16
	H&E ($\mathcal{T}$)		DAPI ($\mathcal{T}$)		IHC ($\mathcal{T}$)
	DAPI($\mathcal{S}$)	IHC($\mathcal{S}$)	H&E($\mathcal{S}$)	IHC($\mathcal{S}$)	H&E($\mathcal{S}$)	DAPI($\mathcal{S}$)
$\mathcal{S}+{\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{SSDA}$	0.042	0.157	0.515	0.467	0.036	8.7×10–4
5%-target	-	-	-	-	-	-
Method	r = 8
	H&E ($\mathcal{T}$)		DAPI ($\mathcal{T}$)		IHC ($\mathcal{T}$)
	DAPI($\mathcal{S}$)	IHC($\mathcal{S}$)	H&E($\mathcal{S}$)	IHC($\mathcal{S}$)	H&E($\mathcal{S}$)	DAPI($\mathcal{S}$)
$\mathcal{S}+{\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{SSDA}$	0.024	0.050	5.5×10–3	0.585	0.099	6.8×10–4
5%-target	-	-	-	-	-	-

F. Evaluation of Semi-Supervised Domain Adaptation

The third panels of Tables I and II show the nucleus detection performance of the proposed SSDA methods, ${\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{SSDA}$ and $\mathcal{S}+{\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{SSDA}$, which use only 5% of gold-standard labeled, real target data for model training. Compared with the UDA method $\mathcal{S}+{\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{UDA}$, the semi-supervised approach $\mathcal{S}+{\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{SSDA}$ produces significantly better performance for most domain adaptation settings except IHC-to-DAPI with r = 16 and 8 as well as H&E-to-IHC with r = 8. In addition, $\mathcal{S}+{\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{SSDA}$ obtains a higher F₁ score than the corresponding 5%-target model for almost all experimental settings except H&E-to-DAPI with r = 8 (Table I), and shows significant improvements for most cases when H&E and IHC as target (Table IV). Table III shows that ${\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{SSDA}$ and $\mathcal{S}+{\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{SSDA}$ outperform the fully supervised methods such as FCN-8s and U-Net by a large margin on all the three datasets, and meanwhile delivers very close or even better performance with other state-of-the-art fully supervised nucleus/cell models, such as FCRNA, FCRNB, FRCN and/or HoVer-Net, for the DAPI and IHC target datasets. This suggests that when training a deep nucleus detection model on a certain dataset, it might be sensible to annotate limited target data and conduct domain adaptation in a semi-supervised learning situation, because limited data annotation adds only a small overhead but might significantly boost the performance compared to completely unsupervised learning-based domain adaptation.

Fig. 8 shows the performance of the proposed SSDA methods trained with different percentages of labeled real target data. For the H&E and IHC target data, learning with a mixture of adapted source images and a few (no more than 20%) gold-standard annotated target images produces consistently better performance than training with available labeled target data only, particularly for DAPI-to-H&E and IHC-to-H&E. With more labeled target data used, there is not significant difference between learning with mixed data and using only the target data. This demonstrates that image translation is beneficial for nucleus detection when very limited target annotations are available, and the contribution of adapted source data gradually weakens with the increase in available manually labeled target data. Fig. 3 shows qualitative results of the proposed SSDA approaches on several example images.

Fig. 8.

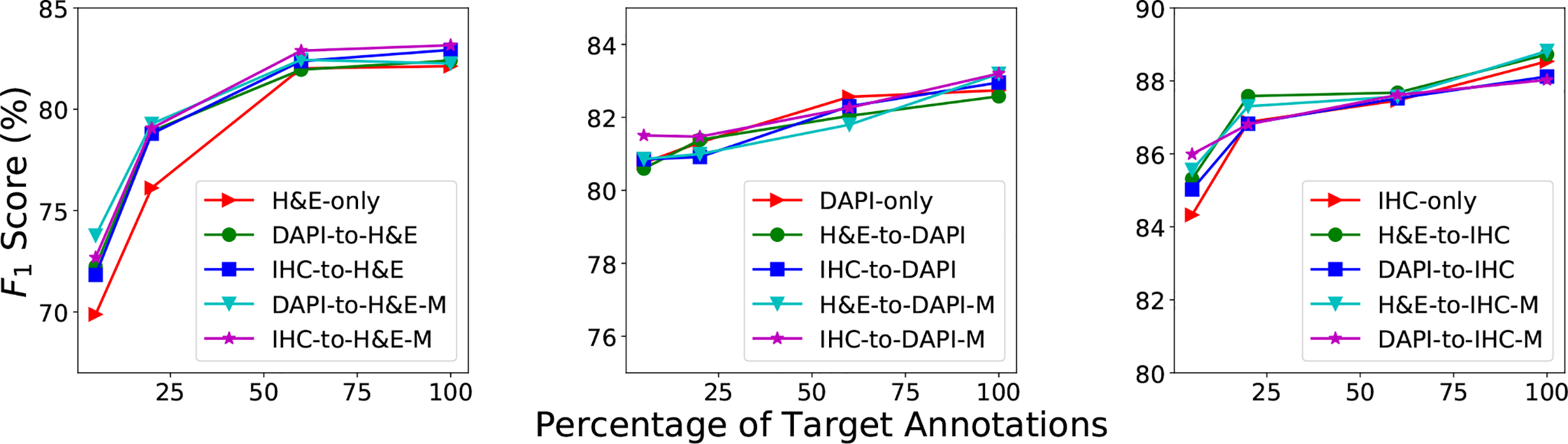
The F1 score of the proposed semi-supervised domain adaptation ${\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{SSDA}$ and $\mathcal{S}+{\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{SSDA}$ with different numbers of annotated target images on the H&E, DAPI and IHC datasets. $\mathcal{S}$ and $\mathcal{T}$ denote the source and target domains, respectively. DAPI-to-H&E and DAPI-to-H&E-M represent ${\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{SSDA}$ and $\mathcal{S}+{\mathcal{T}}_{\mathcal{S}\leftrightarrow \mathcal{T}}^{SSDA}$ respectively, for the experimental setting of DAPI as source and H&E as target. The same notations apply to other settings.

VI. CONCLUSION

In this paper, we propose a novel GAN-based UDA method for nucleus detection in cross-modality microscopy image data. Within an adversarial image-to-image translation framework, it learns a source-domain detector with existing labeled source data and exploits this detector to generate pseudo-labels on adapted target images. It also learns a target-domain detector using both adapted source data with gold-standard annotations and real target data with pseudo-labels, such that the detector learning can take advantage of source-to-target and target-to-source mappings by capturing different, complementary features. To further improve nucleus detection, our method merges predictions from both source- and target-domain detectors for final nucleus detection. The experiments demonstrate that the proposed UDA is beneficial when no data annotations are available in the target domain.

We also explicitly extend the UDA to SSDA learning, which has a small number of labeled target training data available. With only very limited labeled target data (e.g., 10%), the proposed SSDA method can significantly boost nucleus detection performance compared to the UDA counterpart, and can outperform the corresponding target-only model, which is trained with available annotated target data only. With more gold-standard target annotations used in model training, there is no significant performance improvement compared with the target only model. This suggests that it is very helpful to conduct SSDA when only a small amount of annotated target data is available. In addition, SSDA can produce very competitive performance with the full-target model but require less human effort for data annotation.

There are several examples of downstream tasks for nucleus detection on microscopy or pathology images. A principal use is the quantitation of nuclear biomarkers. Clinically relevant nuclear biomarkers include estrogen receptor and progesterone receptor [4], [5], both of which are required IHC biomarkers for invasive breast cancers. Ki67 labeling index is another clinically relevant example [6], and is required to grade pancreatic and gastrointestinal NETs. Quantitative IHC for Ki67 also has clinical utility in other NETs, follicular lymphoma, and breast carcinoma [106]. A number of other quantitative biomarkers, such as p53, are also of clinical interest, but have not yet received widespread use. In addition to IHC, nucleus detection is also important for quantitative chromogenic in situ hybridization (CISH) or fluorescence in situ hybridization (FISH) [107]. In either case, detection of nuclei is a key image analysis step as the signals to be quantified are located in the nuclei. In addition to biomarker quantitation, nucleus detection is essential in the characterization of the tumor microenvironment [108], [109]. In this capacity, nucleus detection is especially useful in multiplexed and/or multispectral fluorescence applications to establish the location of cells that can be further characterized in combination with other markers (such as PD-1, PDL-1, CD8, FoxP3, etc.) and quantified.

Some recent studies [110], [111] show that color augmentation is very helpful for classification tasks and outperforms some color normalization methods on H&E-stained histopathological image data. Extensive color perturbations for data augmentation encourage deep models to learn color-invariant features such that the models trained with one dataset are directly applicable to another. We expect that color augmentation could benefit within-modality downstream tasks such as nucleus detection on pathology images with the same type of staining, such as H&E. However, using the color augmentation techniques [110], [111] might not be very helpful for cross-modality detection tasks, e.g., models trained with DAPI fluorescence images probably do not perform well in H&E image data, because cross-modality microscopy images have significantly different preparation procedures and are not simply visual variations in stain. It is an interesting and important question how to conduct color augmentation for cross-modality microscopy image analysis tasks, and this is worth exploring in the future.