A Bonferroni mean considering Shapley fuzzy measure under hesitant bipolar-valued neutrosophic set environment for an investment decision

Abstract

Bonferroni mean (BM) operators have been established as a powerful tool for handling the interrelationship between the input arguments under various decision-making information. However, the existing BM operators do not take into account the overall interaction among decision makers or criteria. To overcome this limitation, this study considers the Shapley fuzzy measure (SFM) with the normalized weighted BM (NWBM) operator under a neutrosophic environment. In addition, the current research ignores the bipolarity and hesitancy during decision elicitations, resulting in the imprecise decision results. In this paper, the hesitant bipolar-valued neutrosophic set (HBNS) which is the extension of hesitant fuzzy set and bipolar neutrosophic set is employed. The main focus of this paper is in the development of an aggregation operator for HBNS. Based on the literature review, we would like to fill in the gaps by developing a hesitant bipolar-valued neutrosophic Shapley NWBM (HBN-SNWBM) operator where the overall interaction among decision makers can be considered. Besides that, a three-phase decision making framework is also proposed to show the applicability of the proposed aggregation operator to the real-world decision problems. The HBN-SNWBM operator and the decision making framework are applied to two examples of investment selection where evaluations are implemented using the proposed aggregations that based upon hesitant bipolar-valued neutrosophic sets. In the first example, it is found that a weapon company is the best alternative for investment followed by a food company. Sensitivity of parameters of the aggregation operator is also analysed and it is found that the ranking results are consistent despite of different parameter values used. This verifies the insensitivity of p,q parameters in the developed aggregation operator. The proposed decision making framework and hesitant bipolar-valued neutrosophic sets would be a great significance for the practical implementation of the aggregation operators.

Introduction

Multi-criteria decision making involves with several decision makers and multiple conflicting criteria. The use of real numbers is inaccurate in the real-world decision situations. To deal with shortcomings in real-number applications, Zadeh (1965) suggested fuzzy sets. The concept of fuzzy sets has been thoroughly investigated and is widely accepted in the field of decision-making. To date, fuzzy sets have been extended to intuitionistic fuzzy set (IFS) (Atanassov 1986), interval-valued IFS (Ye 2009), hesitant fuzzy set (HFS) (Torra 2010) and many more. However, fuzzy sets cannot handle the indeterminacy elements in the real-world problems. This motivates Smarandache (1998) to introduce the neutrosophic set (NS) by extending the IFS theory with indeterminacy membership. In contrast to IFSs, the indeterminacy degree of an element in a universe of discourse is expressed explicitly in NSs. On the other hand, the membership degree (T) and non-membership degree (F) of the IFSs are dependent, hence the incomplete information or indeterminacy degree in IFSs is given as 1-T- F. Smarandache (2005) has extensively discussed several distinctions between NS and IFS in his article entitled “Neutrosophic set—A generalization of the intuitionistic fuzzy set”. He also gave some examples of how the neutrosophic set generalises not only IFS but also fuzzy sets, classical sets, and paraconsistent sets. In recent study, Nagarajan et al. (2019) proposed some aggregation operators based on the triangular interval type-2 fuzzy set and interval neutrosophic set and applied them to traffic flow management. A comparison of traffic control management using classical, fuzzy, fuzzy type-2, neutrosophic set and interval-valued neutrosophic set was presented. Some limitations of using fuzzy sets were highlighted, such as the lack of adaptiveness when computing the connectedness of the interval-based input and the inability of fuzzy sets to handle uncertainty because they use crisp and accurate functions.

Later, the neutrosophic set has been extended to single-valued neutrosophic set (SVNS) (Wang et al. 2010) and interval neutrosophic set (INS) (Wang et al. 2005) to overcome the drawbacks in the non-standard subsets of neutrosophic set. SVNS is a useful representation of fuzziness, ambiguity, and indeterminacy of an element. Deli et al. (2015) extended the idea of SVNS to bipolar neutrosophic set (BNS). In BNS, decision makers could consider both positive and negative sides of the problem (Akram 2011). On the other hand, hesitancy concept which allows decision makers to state more than one judgment is also important. Torra (2010) extended a fuzzy set to a hesitant fuzzy set (HFS) so that decision makers would be less hesitant while making decisions. Both of the bipolar and hesitancy concepts are important in achieving a realistic and precise decision. Awang et al. (2019a; b) initiated to combine both BNS and HFS and introduced a hesitant bipolar-valued neutrosophic set (HBNS).

The multiple decision makers in multi-criteria decision making problems need to be aggregated by using the appropriate aggregation operators. The Bonferroni mean (BM) is known for its capability to handle the interrelationship among the input arguments. This aggregation operator has been widely studied and refined to weighted BM (WBM) (Xu and Yager 2011), normalized weighted BM (NWBM) (Zhou and He 2012), partitioned BM (PBM) (Dutta and Guha 2015) and geometric BM (GBM) (Zhang 2018). However, the existing BMs do not reflect the overall interrelationship of input arguments and their coalition, in which can be overcome by incorporating the Shapley fuzzy measure (SFM). Traditionally, SFM is used to get the importance value of each player in a cooperative game (Zhou et al. 2018). In decision making, SFM is incorporated not only to get the weightage of each decision maker, but also considering their individual contribution to the group decision (Nie et al. 2019). This fuzzy measure is more flexible than the probability in view of the fact that probability is constrained by its additivity property (Detyniecki 2001). Apart from that, SFM can handle the partial weight information of input arguments in which this measure can overcome the limitation of incomplete information of most of the multi-criteria decision making methods (MCDMs) (Peng et al. 2019).

Based on the literature survey, there are only two studies that incorporated both SFM and BM in their aggregation operator. Nie et al. (2019) studied the combination between PBM, NWBM and SFM with Pythagorean fuzzy set. Soon after, Awang et al. (2020) proposed the integration of NWBM and SFM considering the indeterminacy uncertainty information handled by the interval neutrosophic set (INS). However, the Pythagorean fuzzy set and INS in the existing combination of SFM and BM do not take into account the hesitancy and bipolarity information that are significant to acquire a precise decision making elicitation.

Considering these gaps, we aim to develop a hesitant bipolar-valued neutrosophic Shapley NWBM (HBN-SNWBM) operator that integrated SFM, NWBM and hesitant bipolar-valued neutrosophic set. The key contributions of this paper are listed as below:

• (i)Introduce the Shapley fuzzy measure which can take into account the overall interaction of criteria weights.
• (ii)Develop a new BM operator under hesitant bipolar-valued neutrosophic environment and propose a hesitant bipolar-valued neutrosophic Shapley normalized weighted BM operator.
• (iii)Formulate a MCDM method using the proposed HBN-SNWBM operator to effectively solve the hesitant bipolar neutrosophic problems.
• (iv)The proposed method is applied to investment problems with hesitant bipolar neutrosophic information.

The rest of this article is organized as follows: Sect. 2 reviews some existing aggregation operators. Section 3 provides the preliminary concepts of HBNS, SFM, and some existing BM operators. In Sect. 4, the HBN-SNWBM operator is defined and discuss several special cases of the proposed aggregation operator. Section 5 presents a decision-making model with HBN-SNWBM operator in hesitant bipolar-valued neutrosophic elements (HBNEs) form. Section 6 presents a simple illustrative example to verify its applicability in solving multi-criteria decision making problems. Next, a comparative study is conducted in Sect. 7 to verify the advantages of the proposed aggregation operator. Finally, Sect. 8 outlines the conclusion to this study and suggests several future research directions.

Literature review

Aggregation operators is an interesting research topic and significant in group decision making analysis. The classical aggregation operators are usually based on arithmetic and geometric mean methods, which also known as algebraic sum and algebraic product respectively. These basic aggregation operators were often assuming that the individual decision makers are equal importance. However, the evaluation made by multiple decision makers might carry different weights. Thus, Aczel and Saaty (1983) proposed a weighted geometric (WG) mean aggregation operator for the purpose of synthesizing ratio judgments in AHP method. Later, Dong and Wong (1987) introduced a weighted arithmetic (WA) aggregation operator using fuzzy set as its quantifier. Since then, there has been an increasing number of literatures on the extension to WA and WG mean aggregation operators in diverse kind of sets. Xu and Yager (2006) presented some WG aggregation operators based on IFSs.

Ordered weighted averaging (OWA) and ordered weighted geometric (OWG) are two popular extension of WA and WG respectively. OWA operator which originally introduced by Yager (1988) is a parameterized operator that provides aggregations between maximum and minimum. The weight vector of input arguments is according to the rearranged ordered position of all the input arguments. Later, Chiclana et al. (2000) presented OWG operator which grounded from WG and OWA operators. There are numerous extensions of OWA and OWG operators under different sets (Peng et al. 2016; Garg 2018; Vluymans et al. 2019).

In 2011, Wang and Liu (2011) introduced some Einstein operations on IFSs and further developed some extension to geometric aggregation operators based on the Einstein operations. There are countless extended aggregation operators that have been developed based on Einstein operations. For instance, Zhao and Wei (2013) developed the Einstein hybrid averaging and Einstein hybrid geometric for aggregating the intuitionistic fuzzy numbers. On the other hand, Peng et al. (2016) investigated Einstein aggregation operators under simplified neutrosophic information.

In the previous studies on aggregation operators, Choquet integral operator appears to be one of the favourite aggregation operators in aggregating decision information. Choquet integral which was first introduced by Choquet (1953) is a subadditive or superadditive to aggregate functions based on fuzzy measures. The Choquet integral is a generalization form to the weighted arithmetic mean and able to take into account the importance of a criterion, as well as the interactions between criteria. Its theories and applications have been extensively studied by scholars around the world. Ferreira et al. (2018) used Choquet integral in evaluating the ethical banking practices of four largest bank in Portugal. Pasi et al. (2019) applied fuzzy Choquet integral to evaluate the user-generated content.

Apart from that, Hamacher operator is also received extensive attention from researchers in the aggregation research direction. Hamacher was first introduced by Hamacher (1978) is a great alternative to the algebraic operators. The Hamacher t-norm and t-conorm are more flexible and a generalized form to the algebraic operators and Einstein t-norm and t-conorm respectively. Thus far, a number of studies have developed and improved the Hamacher aggregation operators to be applied in decision making problems (Chen et al. 2019; Darko and Liang 2020).

Most of the existing aggregation operators are known for their assumption that the criteria are mutually independent which is characterized by an independent axiom. Unlike previous aggregation operators, Bonferroni mean introduced by Bonferroni (1950) considers the interaction between criteria. Work on BM operator has progressed rapidly and a number of articles have been identified in extending BM. Zhang (2018) combined the traditional geometric mean and BM operator and defined the geometric Bonferroni mean (GBM) operator. The normalized weighted Bonferroni mean (NWBM) proposed by Zhou and He (2012) is a better extended version of BM that can overcome the limitations of assuming the same weights of input arguments in the traditional BM and the unsatisfied idempotency property of the WBM. Dutta and Guha (2015) proposed the partitioned BM (PBM) operator which are useful in partitioning the input arguments into several subparts as they assumed that the interrelationship is not always exist among all the attributes.

Work on BM operator has progressed rapidly and a number of articles have been identified in applying BM operator to solve multi-criteria decision making (MCDM) problems under all types of fuzzy and neutrosophic environments. Jamil and Rashid (2018) investigated weighted geometric Bonferroni mean and Choquet geometric Bonferroni mean operators for dual hesitant fuzzy set and applied in decision problem of energy policy for the society. Du and Yuan (2019) investigated some Bonferroni mean operators to aggregate the interval-valued intuitionistic 2-tuple linguistic information. On the other hand, Liu and Zhang (2019) aggregated the attributes of intuitionistic uncertain linguistic variables by using some extended BM operators. Liu and Wang (2014) extended NWBM operator based on single-valued neutrosophic sets. Later, Liang et al. (2018) studied the NWBM operator with single-valued trapezoidal neutrosophic information. Recently, Zhou et al. (2019) modified some NWBM operators and applied them to the sustainable selection of search and rescue robots.

In the literature, there are several aggregation operators that have been developed, motivated from the notion of Shapley fuzzy measure. Meng et al. (2013) defined the induced generalized interval-valued intuitionistic fuzzy hybrid Shapley averaging operator. Later, motivated by the idea of Shapley—Choquet integral operator by Meng et al. (2013). Qu et al. (2018) developed some generalized dual hesitant fuzzy generalized Choquet integral operators based on Shapley fuzzy measures. Nie et al. (2019) proposed an MCDM approach based on Shapley fuzzy measure and partitioned NWBM for Pythagorean fuzzy set.

There are a few other aggregation operators that have received considerable attention no less than the above mention aggregation operators, among them are Heronian mean operator (Beliakov et al. 2007), prioritized average operator (Yager 2008), Archimedean aggregation operator (Liu et al. 2019), and Frank operation-based aggregation operator (Yahya et al. 2021). The summary of literature review is given as below (Table 1).

Table 1.

Summary of literature review

Aggregation operators	Proposed by	Findings	Gaps
Weighted Geometric (WG)	Aczel and Saaty (1983)	Offer simple multiplicative weighting method Synthesizing ratio judgments in AHP method	Cannot capture the complex decision situations Did not consider the interdependencies among input arguments
Weighted Average (WA)	Dong and Wong (1987)	Offer simple additive weighting method
Ordered weighted average (OWA)	Yager (1988)	A parameterized operator that provides aggregations between maximum and minimum the arithmetic average, and the median criteria The weight vector of input arguments is according to the rearranged ordered position of all the input arguments	Did not consider the information when the relationship among input arguments are in the hesitant, indeterminant and bipolar situations
Ordered weighted geometric (OWG)	Chiclana et al. (2000)	Extended from WG and OWA
Einstein	Wang and Liu (2011)	Introduce the Einstein operations in WG and OWG for intuitionistic fuzzy set	Did not consider the interrelationship among input arguments
Choquet integral	Choquet (1953)	A generalization form to the WA and able to take into account the importance of a criterion, as well as the interactions between criteria	Did not consider the overall interaction among input decision makers The computation is long and complicated
Hamacher	Hamacher (1978)	The Hamacher t-norm and t-conorm are more flexible and a generalized form to the algebraic operators and Einstein t-norm and t-conorm respectively	Did not consider the interrelationship among input arguments Did not express decision makers’ hesitancy and bipolar judgmental thinking during evaluation process
Prioritized average (PA)	Xu and Yager (2006)	Modelling the importance of the relationship among criteria by knowing the priority among the criteria and unnecessary to provide weight vectors	Suppose that the input arguments are mutually independent
Heronian mean (HM)	Beliakov et al. (2007)	Capturing the correlations of the aggregated arguments	Did not consider the hesitant, bipolar and indeterminate informations
Bonferroni Mean (BM)	Bonferroni (1950)	An extension of the arithmetic means and geometric means Reflect the interdependence of the individual input arguments	Did not reflect the overall interaction among decision makers Did not consider the hesitant, bipolar and indeterminate informations

Preliminaries

This section provides the fundamental theories that are useful in the HBN-SNWBM operator development.

The hesitant bipolar-valued neutrosophic set (HBNS)

Definition 1

(Awang et al. 2019a, b) Let X be a reference set and with a generic element in X denoted by $x$. A hesitant bipolar-valued neutrosophic set $\widehat{H}$ in X is defined as:

$$\widehat{H}=\left\{x,〈h_T^{+}\left(x\right),h_I^{+}\left(x\right),h_F^{+}\left(x\right),h_T^{-}\left(x\right),h_I^{-}\left(x\right),h_F^{-}\left(x\right)〉\left|x\in X\right)\right\},$$ 1

where $h_T^{+}\left(x\right),h_I^{+}\left(x\right),h_F^{+}\left(x\right):X\to \left[0,1\right]$ and $h_T^{-}\left(x\right),h_I^{-}\left(x\right),h_F^{-}\left(x\right):X\to \left[-1,0\right]$. The positive elements $h_T^{+}\left(x\right)$,$h_I^{+}\left(x\right)$ and $h_F^{+}\left(x\right)$ denote the possible satisfactory degree of truth, indeterminacy and falsity of an element $x\in X$ with respect to a HBNS $\widehat{H}$ while the negative elements $h_T^{-}\left(x\right)$,$h_I^{-}\left(x\right)$ and $h_F^{-}\left(x\right)$ denote the possible satisfactory degree of truth, indeterminacy and falsity of an element $x\in X$ to the implicit counter property to the set $\widehat{H}$ respectively. Moreover, a HBNS $\widehat{H}$ must satisfy the conditions $0\le {\gamma }_T^{+},{\gamma }_I^{+},{\gamma }_F^{+}\le 1$, $-1\le {\gamma }_T^{-},{\gamma }_I^{-},{\gamma }_F^{-}\le 0$, $0\le max\left\{{\gamma }_T^{+}\right\}+max\left\{{\gamma }_I^{+}\right\}+max\left\{{\gamma }_F^{+}\right\}\le 3$, and $-3\le max\left\{{\gamma }_T^{-}\right\}+max\left\{{\gamma }_I^{-}\right\}+max\left\{{\gamma }_F^{-}\right\}\le 0$ in which ${\gamma }_T^{{}^{+}}\in h_T^{{}^{+}}\left(x\right)$,${\gamma }_I^{{}^{+}}\in h_I^{{}^{+}}\left(x\right)$, ${\gamma }_F^{+}\in h_F^{+}\left(x\right)$, ${\gamma }_T^{-}\in h_T^{{}^{-}}\left(x\right)$, ${\gamma }_I^{{}^{-}}\in h_I^{{}^{-}}\left(x\right)$ and ${\gamma }_F^{{}^{-}}\in h_F^{{}^{-}}\left(x\right)$ for $x\in X$. Throughout this paper, $\widehat{H}$ is used that denotes the HBNSs and $h=〈h_T^{+},h_I^{+},h_F^{+},h_T^{-},h_I^{-},h_F^{-}〉$ is used that denotes the hesitant bipolar-valued neutrosophic element (HBNE).

The operational laws of HBNSs are given as below:

Definition 2

(Awang et al. 2019a, b) Let $h=〈h_T^{+},h_I^{+},h_F^{+},h_T^{-},h_I^{-},h_F^{-}〉$, $h_a=〈h_{T_a}^{+},h_{I_a}^{+},h_{F_a}^{+},h_{T_a}^{-},h_{I_a}^{-},h_{F_a}^{-}〉$ and $h_b=〈h_{T_b}^{+},h_{I_b}^{+},h_{F_b}^{+},h_{T_b}^{-},h_{I_b}^{-},h_{F_b}^{-}〉$ be three HBNEs. Then,

(i) Addition

$$\begin{array}{cc}\hfill h_a\oplus h_b& =\left.〈\bigcup _{\begin{array}{c}{\gamma }_{T_a}^{+}\in h_{T_a}^{+},\hfill \\ {\gamma }_{T_b}^{+}\in h_{T_b}^{+}\hfill \end{array}}\left\{{\gamma }_{T_a}^{+}+{\gamma }_{T_b}^{+}-{\gamma }_{T_a}^{+}·{\gamma }_{T_b}^{+}\right\},\right)\bigcup _{\begin{array}{c}{\gamma }_{I_a}^{+}\in h_{I_a}^{+},\hfill \\ \gamma {}_{I_b}^{+}\in h_{I_b}^{+}\hfill \end{array}}\left\{\gamma {}_{I_a}^{+}·\gamma {}_{I_b}^{+}\right\},\bigcup _{\begin{array}{c}{\gamma }_{F_a}^{+}\in h_{F_a}^{+},\hfill \\ {\gamma }_{F_b}^{+}\in h_{F_b}^{+}\hfill \end{array}}\left\{{\gamma }_{F_a}^{+}·{\gamma }_{F_b}^{+}\right\},\bigcup _{\begin{array}{c}{\gamma }_{T_a}^{-}\in h_{T_a}^{-},\hfill \\ {\gamma }_{T_b}^{-}\in h_{T_b}^{-}\hfill \end{array}}\left\{-{\gamma }_{T_a}^{-}·{\gamma }_{T_b}^{-}\right\},\hfill \\ \hfill & \bigcup _{\begin{array}{c}{\gamma }_{I_a}^{-}\in h_{I_a}^{-},\hfill \\ {\gamma }_{I_b}^{-}\in h_{I_b}^{-}\hfill \end{array}}\left\{-\left(-{\gamma }_{I_a}^{-}-{\gamma }_{I_b}^{-}-{\gamma }_{I_a}^{-}·{\gamma }_{I_b}^{-}\right)\right\},\left(\bigcup _{\begin{array}{c}{\gamma }_{F_a}^{-}\in h_{F_a}^{-},\hfill \\ {\gamma }_{F_b}^{-}\in h_{F_b}^{-}\hfill \end{array}}\left\{-\left(-{\gamma }_{F_a}^{-}-{\gamma }_{F_b}^{-}-{\gamma }_{F_a}^{-}·{\gamma }_{F_b}^{-}\right)\right\}\right.〉\hfill \\ \hfill \end{array}$$ 2

(ii) Product

$$h_a\otimes h_b=\left.〈\bigcup _{\begin{array}{c}{\gamma }_{T_a}^{+}\in h_{T_a}^{+},\hfill \\ {\gamma }_{T_b}^{+}\in h_{T_b}^{+}\hfill \end{array}}\left\{{\gamma }_{T_a}^{+}·{\gamma }_{T_b}^{+}\right\},\bigcup _{\begin{array}{c}{\gamma }_{I_a}^{+}\in h_{I_a}^{+},\hfill \\ \gamma {}_{I_b}^{+}\in h_{I_b}^{+}\hfill \end{array}}\left\{\gamma {}_{I_a}^{+}+{\gamma }_{I_b}^{+}-{\gamma }_{I_a}^{+}·{\gamma }_{I_b}^{+}\right\},\right)\bigcup _{\begin{array}{c}{\gamma }_{F_a}^{+}\in h_{F_a}^{+},\hfill \\ {\gamma }_{F_b}^{+}\in h_{F_b}^{+}\hfill \end{array}}\left\{{\gamma }_{F_a}^{+}+{\gamma }_{F_b}^{+}-{\gamma }_{F_a}^{+}·{\gamma }_{F_b}^{+}\right\},$$

$$\bigcup _{\begin{array}{c}{\gamma }_{T_a}^{-}\in h_{T_a}^{-},\hfill \\ {\gamma }_{T_b}^{-}\in h_{T_b}^{-}\hfill \end{array}}\left\{-\left(-{\gamma }_{T_a}^{-}-{\gamma }_{T_b}^{-}-{\gamma }_{T_a}^{-}·{\gamma }_{T_b}^{-}\right)\right\},\left(\bigcup _{\begin{array}{c}{\gamma }_{I_a}^{-}\in h_{I_a}^{-},\hfill \\ {\gamma }_{I_b}^{-}\in h_{I_b}^{-}\hfill \end{array}}\left\{-{\gamma }_{I_a}^{-}·{\gamma }_{I_b}^{-}\right\},\bigcup _{\begin{array}{c}{\gamma }_{F_a}^{-}\in h_{F_a}^{-},\hfill \\ {\gamma }_{F_b}^{-}\in h_{F_b}^{-}\hfill \end{array}}\left\{-{\gamma }_{F_a}^{-}·{\gamma }_{F_b}^{-}\right\}\right.〉$$ 3

(iii) Power

$$\begin{array}{cc}\hfill h^{\rho }& =\left.〈\bigcup _{{\gamma }_T^{+}\in h_T^{+}}\left\{{\left({\gamma }_T^{+}\right)}^{\rho }\right\},\bigcup _{{\gamma }_I^{+}\in h_I^{+}}\left\{1-{\left(1-{\gamma }_I^{+}\right)}^{\rho }\right\},\right)\bigcup _{{\gamma }_F^{+}\in h_F^{+}}\left\{1-{\left(1-{\gamma }_F^{+}\right)}^{\rho }\right\},\hfill \\ \hfill & \bigcup _{{\gamma }_T^{-}\in h_T^{-}}\left\{-\left(1-{\left(1-\left(-{\gamma }_T^{-}\right)\right)}^{\rho }\right)\right\},\left(\bigcup _{{\gamma }_I^{-}\in h_I^{-}}\left\{-{\left(-{\gamma }_I^{-}\right)}^{\rho }\right\},\bigcup _{{\gamma }_F^{-}\in h_F^{-}}\left\{-{\left(-{\gamma }_F^{-}\right)}^{\rho }\right\}\right.〉\hfill \\ \hfill \end{array}$$ 4

where $\rho >0$. It is invalid for $\rho \le 0$ since the obtained set is not in HBNE form.

(iv) Scalar multiplication

$$\begin{array}{cc}\hfill \rho h& =\left.〈\bigcup _{{\gamma }_T^{+}\in h_T^{+}}\left\{1-{\left(1-{\gamma }_T^{+}\right)}^{\rho }\right\},\bigcup _{{\gamma }_I^{+}\in h_I^{+}}\left\{{\left({\gamma }_I^{+}\right)}^{\rho }\right\},\right)\bigcup _{{\gamma }_F^{+}\in h_F^{+}}\left\{{\left({\gamma }_F^{+}\right)}^{\rho }\right\},\bigcup _{{\gamma }_T^{-}\in h_T^{-}}\left\{-{\left(-{\gamma }_T^{-}\right)}^{\rho }\right\},\hfill \\ \hfill & \bigcup _{{\gamma }_I^{-}\in h_I^{-}}\left\{-\left(1-{\left(1-\left(-{\gamma }_I^{-}\right)\right)}^{\rho }\right)\right\},\left(\bigcup _{{\gamma }_F^{-}\in h_F^{-}}\left\{-\left(1-{\left(1-\left(-{\gamma }_F^{-}\right)\right)}^{\rho }\right)\right\}\right.〉\hfill \\ \hfill \end{array}$$ 5

where $\rho >0$. It is invalid for $\rho \le 0$ since the obtained set is not in HBNE form.

The following example is provided to illustrate scalar multiplication and what happen when $\rho =0$ and $\rho <0$ in the computation. Let us consider the following HBNE:

$$h=\left.〈0.5,\left\{0.1,0.3\right\},0.2,\left\{-0.2,-0.3\right\},\right)\left(-0.7,\left\{-0.4,-0.6\right\}\right.〉$$

Then by using the scalar multiplication in Definition 2 iv),

$$\begin{array}{cc}\hfill \rho h& =\left.〈\bigcup _{{\gamma }_T^{+}\in h_T^{+}}\left\{1-{\left(1-{\gamma }_T^{+}\right)}^{\rho }\right\},\bigcup _{{\gamma }_I^{+}\in h_I^{+}}\left\{{\left({\gamma }_I^{+}\right)}^{\rho }\right\},\right)\bigcup _{{\gamma }_F^{+}\in h_F^{+}}\left\{{\left({\gamma }_F^{+}\right)}^{\rho }\right\},\bigcup _{{\gamma }_T^{-}\in h_T^{-}}\left\{-{\left(-{\gamma }_T^{-}\right)}^{\rho }\right\},\hfill \\ \hfill & \bigcup _{{\gamma }_I^{-}\in h_I^{-}}\left\{-\left(1-{\left(1-\left(-{\gamma }_I^{-}\right)\right)}^{\rho }\right)\right\},\left(\bigcup _{{\gamma }_F^{-}\in h_F^{-}}\left\{-\left(1-{\left(1-\left(-{\gamma }_F^{-}\right)\right)}^{\rho }\right)\right\}\right.〉\hfill \\ \hfill \end{array}$$

where $\rho >0$.

When $\rho >0$ (let $\rho =0.5$),

$$\begin{array}{c}\rho h=\left.〈1-{\left(1-0.5\right)}^{0.5},\left\{{\left(0.1\right)}^{0.5},{\left(0.3\right)}^{0.5}\right\},{\left(0.2\right)}^{0.5},\left\{-{\left(--0.2\right)}^{0.5},-{\left(--0.3\right)}^{0.5}\right\},\right)\\ \left(-1\left(1-{\left(1-\left(--0.7\right)\right)}^{0.5}\right),\left\{-1\left(1-{\left(1-\left(--0.4\right)\right)}^{0.5}\right),-1\left(1-{\left(1-\left(--0.6\right)\right)}^{0.5}\right)\right\}\right.〉\\ \end{array}$$

$$\rho h=\left.〈0.29,\left\{0.32,0.55\right\},0.45,\left\{-0.45,-0.55\right\},\right)\left(-0.45,\left\{-0.23,-0.37\right\}\right.〉$$

The obtained $\rho h$ when $\rho >0$ is still a HBNE. Thus, the computation/definition is valid.

If $\rho =0$,

$$\begin{array}{c}\rho h=\left.〈1-{\left(1-0.5\right)}^0,\left\{{\left(0.1\right)}^0,{\left(0.3\right)}^0\right\},{\left(0.2\right)}^0,\left\{-{\left(--0.2\right)}^0,-{\left(--0.3\right)}^0\right\},\right)\\ \left(-1\left(1-{\left(1-\left(--0.7\right)\right)}^0\right),\left\{-1\left(1-{\left(1-\left(--0.4\right)\right)}^0\right),-1\left(1-{\left(1-\left(--0.6\right)\right)}^0\right)\right\}\right.〉\\ \end{array}$$

$$\rho h=\left.〈0,1,1,-1,\right)\left(0,0\right.〉$$

This is the obtained $\rho h$ when $\rho =0$, regardless of any HBNEs used. Thus, the computation/definition is invalid when $\rho =0$.

If $\rho <0$ (let $\rho =-0.5$),

$$\begin{array}{c}\rho h=\left.〈1-{\left(1-0.5\right)}^{-0.5},\left\{{\left(0.1\right)}^{-0.5},{\left(0.3\right)}^{-0.5}\right\},{\left(0.2\right)}^{-0.5},\left\{-{\left(--0.2\right)}^{-0.5},-{\left(--0.3\right)}^{-0.5}\right\},\right)\\ \left(-1\left(1-{\left(1-\left(--0.7\right)\right)}^{-0.5}\right),\left\{-1\left(1-{\left(1-\left(--0.4\right)\right)}^{-0.5}\right),-1\left(1-{\left(1-\left(--0.6\right)\right)}^{-0.5}\right)\right\}\right.〉\\ \end{array}$$

$$\rho h=\left.〈-0.41,\left\{3.16,1.83\right\},2.24,\left\{-2.24,-1.83\right\},\right)\left(0.83,\left\{0.29,0.58\right\}\right.〉$$

The obtained $\rho h$ when $\rho <0$ is definitely not a HBNE. Thus, the computation/definition is invalid when $\rho <0$.

The score function of HBNS is provided below to compare two HBNSs:

Definition 3

(Awang et al. 2019a, b) Let $h=〈h_T^{+},h_I^{+},h_F^{+},h_T^{-},h_I^{-},h_F^{-}〉$ be a HBNE, then the score function $s\left(h\right)$ is as below:

$$s\left(h\right)=\frac{\left(\frac{1}{{\ell }_{h_T}^{+}}\sum _{{\gamma }_T^{+}\in h_T^{+}}{\gamma }_T^{+}+1-\frac{1}{{\ell }_{h_I}^{+}}\sum _{{\gamma }_I^{+}\in h_I^{+}}{\gamma }_I^{+}+1-\frac{1}{{\ell }_{h_F}^{+}}\sum _{{\gamma }_F^{+}\in h_F^{+}}{\gamma }_F^{+}+1+\frac{1}{{\ell }_{h_T}^{-}}\sum _{{\gamma }_T^{-}\in h_T^{-}}{\gamma }_T^{-}-\frac{1}{{\ell }_{h_I}^{-}}\sum _{{\gamma }_I^{-}\in h_I^{-}}{\gamma }_I^{-}-\frac{1}{{\ell }_{h_F}^{-}}\sum _{{\gamma }_F^{-}\in h_F^{-}}{\gamma }_F^{-}\right)}{6}$$ 6

where $\ell {}_{h_T}^{+},\ell {}_{h_I}^{+},\ell {}_{h_F}^{+},\ell {}_{h_T}^{-},\ell {}_{h_I}^{-}$ and ${\ell }_{h_F}^{-}$ are the number of elements in $h_T^{+},h_I^{+},h_F^{+},h_T^{-},h_I^{-}$ and $h_F^{-}$, respectively. ${\gamma }_T^{{}^{+}}\in h_T^{{}^{+}}$,${\gamma }_I^{{}^{+}}\in h_I^{{}^{+}}$, ${\gamma }_F^{+}\in h_F^{+}$, ${\gamma }_T^{-}\in h_T^{{}^{-}}$, ${\gamma }_I^{{}^{-}}\in h_I^{{}^{-}}$ and ${\gamma }_F^{{}^{-}}\in h_F^{{}^{-}}$. If s ($h_1$) > s ($h_2$), then $h_1$ is bigger than $h_2$, represented by $h_1>h_2$ and if s ($h_1$) = s ($h_2$), then $h_1$ is equivalent to $h_2$, represented by $h_1=h_2$.

Shapley fuzzy measure (SFM)

Recently, the concept of SFM has showed a rapid interest among researchers where it has been recognized for measuring the overall interaction among the arguments and its coalition. In this regard, the concepts of $\lambda$-fuzzy measure and SFM are given as follows:

Definition 4

(Zhang et al. 2017) Let $N=\left\{C_i\left|i=1,2,...,n\right)\right\}$ be a set of criteria. Then a $\lambda$-fuzzy measure on N is:

$${\mu }_{\lambda }\left(N\right)=\left\{\begin{array}{c}\frac{1}{\lambda }\left(\prod _{C_i\in N}\left(1+\lambda {\mu }_{\lambda }\left(\left\{C_i\right\}\right)\right)-1\right),\text{if}\lambda \ne 0;\\ \sum _{C_i\in N}{\mu }_{\lambda }\left(\left\{C_i\right\}\right),\text{if}\lambda =0\end{array}\right)$$ 7

where ${\mu }_{\lambda }$ is a $\lambda$-fuzzy measure on N and the $\lambda$ values can be obtained by solving the following formula:

$$\prod _{C_i\in N}\left(1+\lambda {\mu }_{\lambda }\left(\left\{C_i\right\}\right)\right)=\lambda +1.$$ 8

On the basis of fuzzy mesures and fuzzy integral, Shapley (1953) introduced SFM. In the following, the SFM,$w_i\left(\mu ,N\right)$ is as follows:

$$w_i\left(\mu ,N\right)=\sum _{V\subseteq N/i}\frac{\left(\left|N\right|-\left|V\right|-1\right)!\left|V\right|!}{\left|N\right|!}\left(\mu \left(V\cup i\right)-\mu \left(V\right)\right),\forall i\in N$$ 9

where $\mu$ is a fuzzy measure on N. $\left|N\right|$ and $\left|V\right|$ indicates the cardinality of the set N and V respectively. $w_i\left(\mu ,N\right)$ represents the weight criteria on set N as $w_i\left(\mu ,N\right)>0$ and $\sum _{i=1}^n{w}_i\left(\mu ,N\right)=1$.

Bonferroni mean (BM)

Bonferroni mean is a powerful tool for handling the correlation among the individual input arguments. The definition of BM is provided as below:

Definition 5

(Bonferroni 1950) Let $p,q\ge 0$.$A_i\left(i=1,2,...,n\right)$ and $A_j\left(j=1,2,...,n\right)$ be a set of nonnegative numbers, then BM operator is defined as follows:

$$B{M}^{p,q}\left(A_i\right)={\left(\frac{1}{n\left(n-1\right)}\sum _{\underset{i\ne j}{i,j=1}}^n{A}_i^p{A}_j^q\right)}^{\frac{1}{p+q}}.$$ 10

The BM has satisfied the properties of monotonicity, idempotency, commutativity and boundedness. Later, Xu and Yager (2006) improved BM operator by introducing weight vectors of input arguments to BM, called the weighted BM (WBM) and its definition is as follows:

Definition 6

(Xu and Yager 2011) Let $p,q\ge 0$. $A_i\left(i=1,2,...,n\right)$ and $A_j\left(j=1,2,...,n\right)$ be a collection of nonnegative numbers. $w_i={\left(w_1,w_2,...,w_n\right)}^{{}^T}$ are the weight vectors of $A_i$ where $w_i$ represents the importance degree of $A_i$, satisfying $w_i>0$ and $\sum _{i=1}^n{w}_i=1$. $w_j={\left(w_1,w_2,...,w_n\right)}^{{}^T}$ are the weight vectors of $A_j$ where $w_j$ represents the importance degree of $A_j$, satisfying $w_j>0$ and $\sum _{i=1}^n{w}_j=1$. Then WBM is defined as follows:

$$WB{M}^{p,q}\left(A_i\right)={\left(\frac{1}{n\left(n-1\right)}\sum _{\underset{i\ne j}{i,j=1}}^n{\left(w_i{A}_i\right)}^p{\left(w_j{A}_j\right)}^q\right)}^{\frac{1}{p+q}}.$$ 11

The WBM operator does not satisfy the idempotency property. Thus, Zhou and He (2012) introduced the normalized weighted BM (NWBM). The definition of NWBM is given as below:

Definition 7

(Zhou and He 2012) Let $p,q\ge 0$. $p,q\ge 0$.$A_i\left(i=1,2,...,n\right)$ and $A_j\left(j=1,2,...,n\right)$ be a set of nonnegative numbers.$w_i={\left(w_1,w_2,...,w_n\right)}^T$ is the weight vector of $A_i$ where $w_i$ represents the importance degree of $A_i$, satisfying $w_i>0$ and $\sum _{i=1}^n{w}_i=1$. $w_j={\left(w_1,w_2,...,w_n\right)}^{{}^T}$ are the weight vectors of $A_j$ where $w_j$ represents the importance degree of $A_j$, satisfying $w_j>0$ and $\sum _{i=1}^n{w}_j=1$. Then,

$$NWB{M}^{p,q}\left(A_i\right)={\left(\sum _{\underset{i\ne j}{i,j=1}}^n\frac{w_i·w_j}{1-w_i}{A}_i^p{A}_j^q\right)}^{\frac{1}{p+q}}$$ 12

These definitions are prevalently used in the following proposed work.

Proposed hesitant bipolar-valued neutrosophic shapley normalized weighted bonferroni mean

This section develops the hesitant bipolar-valued neutrosophic Shapley NWBM (HBN-SNWBM) operator which is a combination between the SFM and BM concepts under the hesitant bipolar-valued neutrosophic environment. Before introducing the HBN-SNWBM in detail, we define the hesitant bipolar-valued neutrosophic Bonferroni mean (HBN-BM) as below:

Definition 8

Let ${\widehat{H}}_i=〈h_T^{+},h_I^{+},h_F^{+},h_T^{-},h_I^{-},h_F^{-}〉\left(i=1,2,...,n\right)$ and ${\widehat{H}}_j=〈h_T^{+},h_I^{+},h_F^{+},h_T^{-},h_I^{-},h_F^{-}〉\left(j=1,2,...,n\right)$ be a collection of HBNSs and $p,q\ge 0$. If

$$HBN-B{M}^{p,q}\left({\widehat{H}}_i\right)={\left(\frac{1}{n\left(n-1\right)}\sum _{\underset{i\ne j}{i,j=1}}^n\left({\widehat{H}}_i^p\otimes {\widehat{H}}_j^q\right)\right)}^{\frac{1}{p+q}},$$ 13

where $HBN-B{M}^{p,q}$ refers to the hesitant bipolar-valued neutrosophic BM (HBN-BM). In the following, we define the HBN-SNWBM operator as below:

Definition 9

Let ${\widehat{H}}_i=〈h_T^{+},h_I^{+},h_F^{+},h_T^{-},h_I^{-},h_F^{-}〉\left(i=1,2,...,n\right)$ and ${\widehat{H}}_j=〈h_T^{+},h_I^{+},h_F^{+},h_T^{-},h_I^{-},h_F^{-}〉\left(j=1,2,...,n\right)$ be a collection of HBNSs and $p,q\ge 0$. If

$$HBN-SNWB{M}^{p,q}\left({\widehat{H}}_i\right)={\left(\sum _{\underset{i\ne j}{i,j=1}}^n\frac{w_i\left(\mu ,N\right)w_j\left(\mu ,N\right)}{1-w_i\left(\mu ,N\right)}\left({\widehat{H}}_i^p\otimes {\widehat{H}}_j^q\right)\right)}^{\frac{1}{p+q}},$$ 14

where $w_i\left(\mu ,N\right)$ is the SFM of ${\widehat{H}}_i$ with its corresponding fuzzy measure $\mu$ on N and satisfies $w_i\left(\mu ,N\right)\in \left[0,1\right]$ and $\sum _{i=1}^n{w}_i\left(\mu ,N\right)=1$ while $w_j\left(\mu ,N\right)$ is the SFM of ${\widehat{H}}_j$ with its corresponding fuzzy measure $\mu$ on N and satisfies $w_j\left(\mu ,N\right)\in \left[0,1\right]$ and $\sum _{i=1}^n{w}_j\left(\mu ,N\right)=1$. Then $HBN-SNWB{M}^{p,q}$ is called the hesitant bipolar-valued neutrosophic Shapley NWBM (HBN-SNWBM).

The theorems that satisfied the proposed HBN-SNWBM are presented and followed by mathematical proofs. Theorem 3 shows the theorem of equality of HBN-SNWBM that is proved based on the arithmetic law of HBNSs. The proof is provided in the appendix.

Theorem 3

(Equality). Let $p,q\ge 0$ and ${\widehat{H}}_i=〈h_T^{+},h_I^{+},h_F^{+},h_T^{-},h_I^{-},h_F^{-}〉\left(i=1,2,...,n\right)$ be a set of HBNSs, then the aggregated value by the Eq. (14) is also a HBNS and.

$$\begin{array}{cc}\hfill HBN-SNWB{M}^{p,q}\left({\widehat{H}}_i\right)& =\left.〈\bigcup _{\begin{array}{c}\gamma {}_{T_i}^{+}\in h_{T_i}^{+},\hfill \\ \gamma {}_{T_j}^{+}\in h_{T_j}^{+}\hfill \end{array}}\left\{{\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(\gamma {}_{T_i}^{+}\right)}^p{\left(\gamma {}_{T_j}^{+}\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}\right)}^{\frac{1}{p+q}}\right\}\right),\hfill \\ \hfill & \bigcup _{\begin{array}{c}\gamma {}_{I_i}^{+}\in h_{I_i}^{+},\hfill \\ {\gamma }_{I_j}^{+}\in h_{I_j}^{+}\hfill \end{array}}\left\{1-{\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(1-{\gamma }_{I_i}^{+}\right)}^p{\left(1-{\gamma }_{I_j}^{+}\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}\right)}^{\frac{1}{p+q}}\right\},\bigcup _{\begin{array}{c}{\gamma }_{F_i}^{+}\in h_{F_i}^{+},\hfill \\ {\gamma }_{F_j}^{+}\in h_{F_j}^{+}\hfill \end{array}}\left\{1-{\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(1-{\gamma }_{F_i}^{+}\right)}^p{\left(1-{\gamma }_{F_j}^{+}\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}\right)}^{\frac{1}{p+q}}\right\},\hfill \\ \hfill & \bigcup _{\begin{array}{c}\gamma {}_{T_i}^{-}\in h{}_{T_i}^{-},\hfill \\ \gamma {}_{T_j}^{-}\in h{}_{T_j}^{-}\hfill \end{array}}\left\{-\left(1-{\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(1-\left(-\gamma {}_{T_i}^{-}\right)\right)}^p{\left(1-\left(-\gamma {}_{T_j}^{-}\right)\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}\right)}^{\frac{1}{p+q}}\right)\right\},\hfill \\ \hfill & \bigcup _{\begin{array}{c}\gamma {}_{I_i}^{-}\in h_{I_i}^{-},\hfill \\ {\gamma }_{I_j}^{-}\in h_{I_j}^{-}\hfill \end{array}}\left\{-{\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(-{\gamma }_{I_i}^{-}\right)}^p{\left(-{\gamma }_{I_j}^{-}\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}\right)}^{\frac{1}{p+q}}\right\},\left(\bigcup _{\begin{array}{c}\gamma {}_{F_i}^{-}\in h_{F_i}^{-},\hfill \\ \gamma {}_{F_j}^{-}\in h_{F_j}^{-}\hfill \end{array}}\left\{-{\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(-\gamma {}_{F_i}^{-}\right)}^p{\left(-\gamma {}_{F_j}^{-}\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}\right)}^{\frac{1}{p+q}}\right\}\right.〉\hfill \\ \hfill \end{array}$$ 15

where $i,j=1,2,...,n$ and ${\gamma }_T^{{}^{+}}\in h_T^{{}^{+}}\left(x\right)$,${\gamma }_I^{{}^{+}}\in h_I^{{}^{+}}\left(x\right)$, ${\gamma }_F^{+}\in h_F^{+}\left(x\right)$, ${\gamma }_T^{-}\in h_T^{{}^{-}}\left(x\right)$, ${\gamma }_I^{{}^{-}}\in h_I^{{}^{-}}\left(x\right)$ and ${\gamma }_F^{{}^{-}}\in h_F^{{}^{-}}\left(x\right)$ for $x\in X$. $w_i\left(\mu ,N\right)$ is the SFM of ${\widehat{H}}_i$ with its corresponding fuzzy measure $\mu$ on N and satisfies $w_i\left(\mu ,N\right)\in \left[0,1\right]$ and $\sum _{i=1}^n{w}_i\left(\mu ,N\right)=1$ while $w_j\left(\mu ,N\right)$ is the SFM of ${\widehat{H}}_j$ with its corresponding fuzzy measure $\mu$ on N and satisfies $w_j\left(\mu ,N\right)\in \left[0,1\right]$ and $\sum _{i=1}^n{w}_j\left(\mu ,N\right)=1$.

Next, we investigate the algebraic properties of HBN-SNWBM operator that are important when develop any new aggregation operator. Theorem 4 shows the reducibility property of the HBN-SNWBM.

Theorem 4.

(Reducibility) If $w_i\left(\mu ,N\right)={\left(\frac{1}{n},\frac{1}{n},...,\frac{1}{n}\right)}^T$, then

$$HBN-SNWB{M}^{p,q}\left({\widehat{H}}_i\right)=HBN-B{M}^{p,q}\left({\widehat{H}}_i\right).$$ 16

Further, the theorem of idempotency of HBN-SNWBM operator is given as follows:

Theorem 5.

(Idempotency) Let ${\widehat{H}}_i\left(i=1,2,...,n\right)$ be a set of HBNSs and are all equal, i.e., ${\widehat{H}}_i=\widehat{H}$, for all $i$. Then,

$$HBN-SNWB{M}^{p,q}\left({\widehat{H}}_i\right)=\widehat{H}.$$ 17

Commutativity is a theorem that can exchange order of numbers but still obtain the same value. This theorem is satisfied for the proposed HBN-SNWBM. Theorem 6 shows the commutativity and its proof.

Theorem 6.

(Commutativity) Let ${\tilde{\widehat{H}}}_i$ be any permutation of ${\widehat{H}}_i$, then.

$$HBN-SNWB{M}^{p,q}\left({\tilde{\widehat{H}}}_i\right)=HBN-SNWB{M}^{p,q}\left({\widehat{H}}_i\right).$$ 18

Monotonicity is a property to examine the proposed HBN-SNWBM to be either constant, or constantly increasing or constantly decreasing. Theorem 7 investigates this property.

Theorem 7.

(Monotonicity) Let ${\widehat{H}}_i=〈h_{T_i}^{+},h_{I_i}^{+},h_{F_i}^{+},h_{T_i}^{-},h_{I_i}^{-},h_{F_i}^{-}〉$ and ${\widehat{H}}_i^{\ast }=〈h_{T_i}^{+\ast },h_{I_i}^{+\ast },h_{F_i}^{+\ast },h_{T_i}^{-\ast },h_{I_i}^{-\ast },h_{F_i}^{-\ast }〉$ be any two sets of HBNSs where $i=1,2,...,n$. If ${\widehat{H}}_i\le {\widehat{H}}_i^{\ast }$, then.

$$HBN-SNWB{M}^{p,q}\left({\widehat{H}}_i\right)\le HBN-SNWB{M}^{p,q}\left({\widehat{H}}_i^{\ast }\right).$$ 19

Finally, we would like to verify the boundedness theorem of the proposed HBN-SNWBN operator. This theorem states that if the HBN-SNWBM is continuous over the closed and bounded interval, then the HBN-SNWBM is a bounded function. Theorem 8 discusses this property.

Theorem 8.

(Boundednesss) Let ${\widehat{H}}_i=〈h_{T_i}^{+},h_{I_i}^{+},h_{F_i}^{+},h_{T_i}^{-},h_{I_i}^{-},h_{F_i}^{-}〉\left(i=1,2,...,n\right)$ be a set of HBNSs and ${\widehat{H}}^{-}=〈min\left\{h_{T_i}^{+}\right\},min\left\{h_{I_i}^{+}\right\},max\left\{h_{F_i}^{+}\right\},max\left\{h_{T_i}^{-}\right\},max\left\{h_{I_i}^{-}\right\},min\left\{h_{F_i}^{-}\right\}〉$, ${\widehat{H}}^{+}=〈max\left\{h_{T_i}^{+}\right\},max\left\{h_{I_i}^{+}\right\},min\left\{h_{F_i}^{+}\right\},min\left\{h_{T_i}^{-}\right\},min\left\{h_{I_i}^{-}\right\},max\left\{h_{F_i}^{-}\right\}〉$, then

$${\widehat{H}}^{-}\le HBN-SNWB{M}^{p,q}\left({\widehat{H}}_i\right)\le {\widehat{H}}^{+}$$ 20

Subsequently, some special cases of $HBN-SNWBM$ operator is presented as below:

Case 1. If $q=0$, then HBN-SNWBM operator reduces as follows:

$$HBN-SNWB{M}^{p,q}\left({\widehat{H}}_i\right)={\left(\sum _{\underset{i\ne j}{i,j=1}}^n\frac{w_i{w}_j}{1-w_i}\left({\widehat{H}}_i^p\otimes {\widehat{H}}_j^q\right)\right)}^{\frac{1}{p+q}}={\left(\sum _{\underset{i\ne j}{i,j=1}}^n{w}_i{\widehat{H}}_i^p\right)}^{\frac{1}{p}}$$ 21

i.e.,

$$\begin{array}{cc}\hfill HBN-SNWB{M}^{p,0}\left({\widehat{H}}_i\right)& =\left.〈\bigcup _{{\gamma }_{T_i}^{+}\in h_{T_i}^{+}}\left\{{\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left({\gamma }_{T_i}^{+}\right)}^p\right)}^{w_i}\right)}^{\frac{1}{p}}\right\},\right)\hfill \\ \hfill & \bigcup _{{\gamma }_{I_i}^{+}\in h_{I_i}^{+}}\left\{1-{\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(1-{\gamma }_{I_i}^{+}\right)}^p\right)}^{w_i}\right)}^{\frac{1}{p}}\right\},\bigcup _{\gamma {}_{F_i}^{+}\in h_{F_i}^{+}}\left\{1-{\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(1-\gamma {}_{F_i}^{+}\right)}^p\right)}^{w_i}\right)}^{\frac{1}{p}}\right\},\hfill \\ \hfill & \bigcup _{\gamma {}_{T_i}^{-}\in h_{T_i}^{-}}\left\{-\left(1-{\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n\left(1-{\left(1-{\left(-\gamma {}_{T_i}^{-}\right)}^p\right)}^{w_i}\right)\right)}^{\frac{1}{p}}\right)\right\},\bigcup _{\gamma {}_{I_i}^{-}\in h_{I_i}^{-}}\left\{-{\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(-\gamma {}_{I_i}^{-}\right)}^p\right)}^{w_i}\right)}^{\frac{1}{p}}\right\},\hfill \\ \hfill & \left(\bigcup _{\gamma {}_{F_i}^{-}\in h_{F_i}^{-}}\left\{-{\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(-\gamma {}_{F_i}^{-}\right)}^p\right)}^{w_i}\right)}^{\frac{1}{p}}\right\}\right.〉.\hfill \\ \hfill \end{array}$$ 22

(a) If $p=1$ and $q=0$, then

$$\begin{array}{cc}\hfill HBN-SNWB{M}^{1,0}\left({\widehat{H}}_i\right)& =\left.〈\bigcup _{{\gamma }_{T_i}^{+}\in h_{T_i}^{+}}\left\{\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-\left({\gamma }_{T_i}^{+}\right)\right)}^{w_i}\right)\right\},\bigcup _{{\gamma }_{I_i}^{+}\in h_{I_i}^{+}}\left\{1-\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-\left(1-{\gamma }_{I_i}^{+}\right)\right)}^{w_i}\right)\right\}\right),\hfill \\ \hfill & \bigcup _{\gamma {}_{F_i}^{+}\in h_{F_i}^{+}}\left\{1-\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-\left(1-\gamma {}_{F_i}^{+}\right)\right)}^{w_i}\right)\right\},\bigcup _{\gamma {}_{T_i}^{-}\in h_{T_i}^{-}}\left\{-\left(1-\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-\left(1-\left(-\gamma {}_{T_i}^{-}\right)\right)\right)}^{w_i}\right)\right)\right\},\hfill \\ \hfill & \left(\bigcup _{\gamma {}_{I_i}^{-}\in h_{I_i}^{-}}\left\{-\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-\left(-\gamma {}_{I_i}^{-}\right)\right)}^{w_i}\right)\right\},\bigcup _{\gamma {}_{F_i}^{-}\in h_{F_i}^{-}}\left\{-\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-\left(-\gamma {}_{F_i}^{-}\right)\right)}^{w_i}\right)\right\}\right.〉.\hfill \\ \hfill \end{array}$$ 23

$$\begin{array}{cc}& \Rightarrow \left.〈\bigcup _{{\gamma }_{T_j}^{+}\in h_{T_j}^{+}}\left\{1-\prod _{j=1}^n{\left(1-{\gamma }_{T_j}^{+}\right)}^{w_j}\right\},\bigcup _{{\gamma }_{I_j}^{+}\in h_{I_j}^{+}}\left\{\prod _{j=1}^n{\left({\gamma }_{I_j}^{+}\right)}^{w_j}\right\},\right)\bigcup _{{\gamma }_{F_j}^{+}\in h_{F_j}^{+}}\left\{\prod _{j=1}^n{\left({\gamma }_{F_j}^{+}\right)}^{w_j}\right\},\bigcup _{{\gamma }_{T_j}^{-}\in h_{T_j}^{-}}\left\{-\prod _{j=1}^n{\left(-{\gamma }_{T_j}^{-}\right)}^{w_j}\right\},\hfill \\ \hfill & \bigcup _{{\gamma }_{I_j}^{-}\in h_{I_j}^{-}}\left\{-\left(1-\prod _{j=1}^n{\left(1-\left(-{\gamma }_{I_j}^{-}\right)\right)}^{w_j}\right)\right\},\left(\bigcup _{{\gamma }_{F_j}^{-}\in h_{F_j}^{-}}\left\{-\left(1-\prod _{j=1}^n{\left(1-\left(-{\gamma }_{F_j}^{-}\right)\right)}^{w_j}\right)\right\}\right.〉\hfill \\ \hfill \Rightarrow HBNW{A}_w\left(h_1,h_2,...,h_n\right)\\ \hfill \end{array}$$ 24

where HBNWA refers to the hesitant bipolar-valued neutrosophic WA operator.

(b) If $p=0,q=0$, then

$$HBN-SNWBM{}^{0,0}\left({\widehat{H}}_i\right)=\sum _{i=1}^n{\left(H_i\right)}^{w_i}$$

$$\Rightarrow \left.〈\bigcup _{{\gamma }_{T_i}^{+}\in h_{T_i}^{+}}\left\{\prod _{\underset{i\ne j}{i,j=1}}^n{\left({\gamma }_{T_i}^{+}\right)}^{w_i}\right\},\bigcup _{{\gamma }_{I_i}^{+}\in h_{I_i}^{+}}\left\{1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\gamma }_{I_i}^{+}\right)}^{w_i}\right\}\right),\bigcup _{\gamma {}_{F_i}^{+}\in h_{F_i}^{+}}\left\{1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-y{}_{F_i}^{+}\right)}^{w_i}\right\},$$

$$\bigcup _{\gamma {}_{T_i}^{-}\in h_{T_i}^{-}}\left\{-\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-\left(-\gamma {}_{T_i}^{-}\right)\right)}^{{\omega }_i}\right)\right\},\left(\bigcup _{\gamma {}_{I_i}^{-}\in h_{I_i}^{-}}\left\{-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(-\gamma {}_{I_i}^{-}\right)}^{{\omega }_i}\right\},\bigcup _{\gamma {}_{F_i}^{-}\in h_{F_i}^{-}}\left\{-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(-\gamma {}_{F_i}^{-}\right)}^{{\omega }_i}\right\}\right.〉$$

$$\Rightarrow HBNW{G}_w\left(h_1,h_2,...,h_n\right)$$ 25

where HBNWG refers to the hesitant bipolar-valued neutrosophic WG operator.

Case 2. If $p=q$, then HBN-SNWBM operator reduces to the following structure.

$$HBN-SNWB{M}^{p,p}\left({\widehat{H}}_i\right)={\left(\sum _{\underset{i\ne j}{i,j=1}}^n\frac{w_i{w}_j}{1-w_i}\left({\widehat{H}}_i^p\otimes {\widehat{H}}_j^p\right)\right)}^{\frac{1}{p+p}}={\left(\sum _{\underset{i\ne j}{i,j=1}}^n\frac{w_i{w}_j}{1-w_i}{\left({\widehat{H}}_i{\widehat{H}}_j\right)}^p\right)}^{\frac{1}{2p}}$$ 26

i.e.,

$$\begin{array}{cc}\hfill HBN-SNWB{M}^{p,p}\left({\widehat{H}}_i\right)& =\left.〈\bigcup _{\begin{array}{c}\gamma {}_{T_i}^{+}\in h_{T_i}^{+},\hfill \\ \gamma {}_{T_j}^{+}\in h_{T_j}^{+}\hfill \end{array}}\left\{{\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(\gamma {}_{T_i}^{+}\gamma {}_{T_j}^{+}\right)}^p\right)}^{\frac{w_i{w}_j}{1-w_i}}\right)}^{\frac{1}{2p}}\right\},\right)\bigcup _{\begin{array}{c}\gamma {}_{I_i}^{+}\in h_{I_i}^{+},\hfill \\ \gamma {}_{I_j}^{+}\in h_{I_j}^{+}\hfill \end{array}}\left\{1-{\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(1-\left(\gamma {}_{I_i}^{+}+\gamma {}_{I_j}^{+}-\gamma {}_{I_i}^{+}\gamma {}_{I_j}^{+}\right)\right)}^p\right)}^{\frac{w_i{w}_j}{1-w_i}}\right)}^{\frac{1}{2p}}\right\}\hfill \\ & \bigcup _{\begin{array}{c}{\gamma }_{F_i}^{+}\in h_{F_i}^{+},\hfill \\ {\gamma }_{F_j}^{+}\in h_{F_j}^{+}\hfill \end{array}}\left\{1-{\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(1-\left({\gamma }_{F_i}^{+}+{\gamma }_{F_j}^{+}-{\gamma }_{F_i}^{+}{\gamma }_{F_j}^{+}\right)\right)}^p\right)}^{\frac{w_i{w}_j}{1-w_i}}\right)}^{\frac{1}{2p}}\right\},\hfill \\ & \bigcup _{\begin{array}{c}\gamma {}_{T_i}^{-}\in h_{T_i}^{-},\hfill \\ \gamma {}_{T_j}^{-}\in h_{T_j}^{-}\hfill \end{array}}\left\{-\left(1-{\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(1-\left(-\gamma {}_{T_i}^{-}-\gamma {}_{T_j}^{-}-\gamma {}_{T_i}^{-}\gamma {}_{T_j}^{-}\right)\right)}^p\right)}^{\frac{w_i{w}_j}{1-w_i}}\right)}^{\frac{1}{2p}}\right)\right\}\hfill \\ & \left(\bigcup _{\begin{array}{c}\gamma {}_{I_i}^{-}\in h_{I_i}^{-},\hfill \\ {\gamma }_{I_j}^{-}\in h_{I_j}^{-}\hfill \end{array}}\left\{-{\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(\gamma {}_{I_i}^{-}{\gamma }_{I_j}^{-}\right)}^p\right)}^{\frac{w_i{w}_j}{1-w_i}}\right)}^{\frac{1}{2p}}\right\},\bigcup _{\begin{array}{c}\gamma {}_{F_i}^{-}\in h_{F_i}^{-},\hfill \\ \gamma {}_{F_j}^{-}\in h_{F_j}^{-}\hfill \end{array}}\left\{-{\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(\gamma {}_{F_i}^{-}\gamma {}_{F_j}^{-}\right)}^p\right)}^{\frac{w_i{w}_j}{1-w_i}}\right)}^{\frac{1}{2p}}\right\}\right.〉\hfill \end{array}$$ 27

If $p=q=1$, then

$$\begin{array}{cc}\hfill HBN-SNWB{M}^{1,1}\left({\widehat{H}}_i\right)& =\left.〈\bigcup _{\begin{array}{c}\gamma {}_{T_i}^{+}\in h_{T_i}^{+},\hfill \\ \gamma {}_{T_j}^{+}\in h_{T_j}^{+}\hfill \end{array}}\left\{{\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\gamma }_{T_i}^{+}\gamma {}_{T_j}^{+}\right)}^{\frac{w_i{w}_j}{1-w_i}}\right)}^{\frac{1}{2}}\right\}\right),\hfill \\ & \bigcup _{\gamma {}_{I_i}^{+}\in h_{I_i}^{+}}\left\{1-{\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(\gamma {}_{I_i}^{+}+\gamma {}_{I_j}^{+}-\gamma {}_{I_i}^{+}\gamma {}_{I_j}^{+}\right)}^{\frac{w_i{w}_j}{1-w_i}}\right)}^{\frac{1}{2}}\right\},\bigcup _{\begin{array}{c}{\gamma }_{F_i}^{+}\in h_{F_i}^{+},\hfill \\ {\gamma }_{F_j}^{+}\in h_{F_j}^{+}\hfill \end{array}}\left\{1-{\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left({\gamma }_{F_i}^{+}+{\gamma }_{F_j}^{+}-{\gamma }_{F_i}^{+}{\gamma }_{F_j}^{+}\right)}^{\frac{w_i{w}_j}{1-w_i}}\right)}^{\frac{1}{2}}\right\},\hfill \\ & \bigcup _{\begin{array}{c}\gamma {}_{T_i}^{-}\in h_{T_i}^{-},\hfill \\ \gamma {}_{T_j}^{-}\in h_{T_j}^{-}\hfill \end{array}}\left\{-\left(1-{\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(-\gamma {}_{T_i}^{-}-\gamma {}_{T_j}^{-}-\gamma {}_{T_i}^{-}\gamma {}_{T_j}^{-}\right)}^{\frac{w_i{w}_j}{1-w_i}}\right)}^{\frac{1}{2}}\right)\right\},\hfill \\ & \left(\bigcup _{\begin{array}{c}\gamma {}_{I_i}^{-}\in h_{I_i}^{-},\hfill \\ {\gamma }_{I_j}^{-}\in h_{I_j}^{-}\hfill \end{array}}\left\{-{\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-\gamma {}_{I_i}^{-}{\gamma }_{I_j}^{-}\right)}^{\frac{w_i{w}_j}{1-w_i}}\right)}^{\frac{1}{2}}\right\},\bigcup _{\begin{array}{c}\gamma {}_{F_i}^{-}\in h_{F_i}^{-},\hfill \\ \gamma {}_{F_j}^{-}\in h_{F_j}^{-}\hfill \end{array}}\left\{-{\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-\gamma {}_{F_i}^{-}\gamma {}_{F_j}^{-}\right)}^{\frac{w_i{w}_j}{1-w_i}}\right)}^{\frac{1}{2}}\right\}\right.〉\hfill \end{array}$$ 28

that we refer to as the hesitant bipolar-valued neutrosophic weighted interrelated average (HBNWIA) operator. In the following, the proposed aggregation operators are employed to solve the hesitant bipolar neutrosophic decision making problem.

A decision-making approach with HBN-SNWBM operator

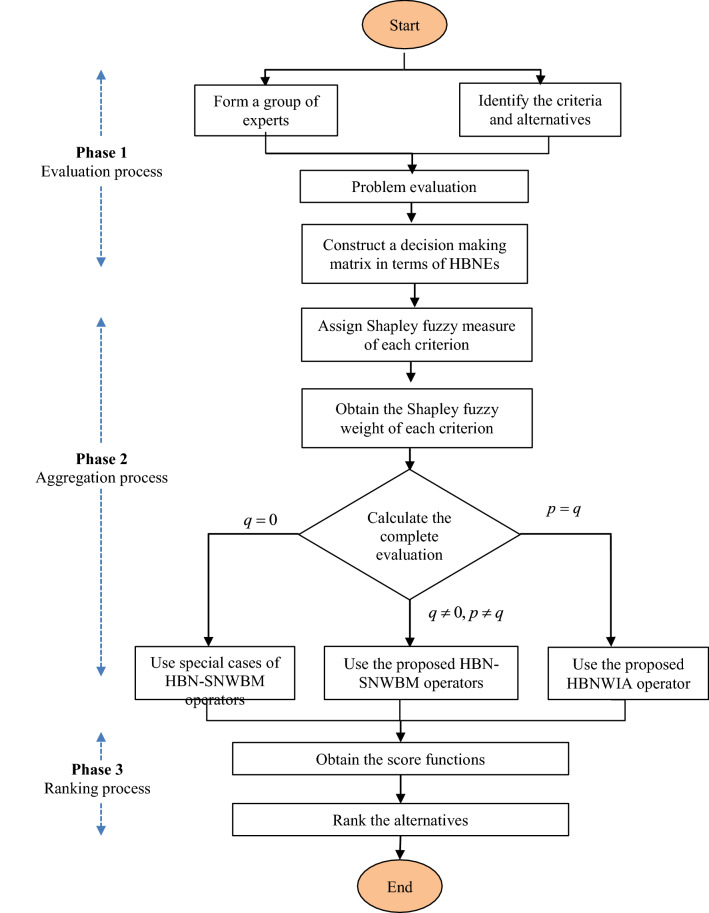
This section presents a decision-making approach employing the proposed HBN-SNWBM operator (Fig. 1). The developed decision-making approach is carried out in three main processes as shown in a general diagram below:

Fig. 1.

General diagram of the proposed decision approach

Phase 1: Evaluation process

By considering a problem with a set of alternatives $A_i=\left\{A_1,A_2,...,A_m\right\}$ and a set of criteria $c_j=\left\{c_1,c_2,...,c_n\right\}$, an assessment is carried out by pair-wisely comparing i-th alternative with respect to j-th criterion. A group of experts is chosen among the experts of the related problem. They are invited to discuss and give their consencus judgment values under hesitant bipolar-valued neutrosophic environment which are denoted as $h_{\mathit{ij}}=〈h_{T_{\mathit{ij}}}^{+},h_{I_{\mathit{ij}}}^{+},h_{F_{\mathit{ij}}}^{+},h_{T_{\mathit{ij}}}^{-},h_{I_{\mathit{ij}}}^{-},h_{F_{\mathit{ij}}}^{-}〉$. Then, the obtained information is transform into a matrix form of hesitant bipolar-valued neutrosophic elements. The general form of the decision matrix is as below:

$$D=\begin{array}{cc}& \begin{array}{cccc}{c}_1& c_2& \cdots & c_n\end{array}\\ \begin{array}{c}{A}_1\\ A_2\\ ⋮\\ A_m\end{array}& \left(\begin{array}{cccc}{h}_{11}& h_{12}& \cdots & h_{1m}\\ h_{21}& h_{22}& \cdots & h_{2m}\\ ⋮& ⋮& \ddots & ⋮\\ h_{n1}& h_{n2}& \cdots & h_{\mathit{nm}}\end{array}\right)\end{array}$$ 29

Phase 2: Aggregation process

In this phase, the proposed HBN-SNWBM aggregation operator is incorporated to get the complete evaluation. First of all, the Shapley fuzzy measure of each criterion is assigned by experts. Then, the Shapley fuzzy weights of criteria can be computed by Eqs. (7–9). Further, the complete evaluation rate of each alternative $A_i\left\{i=1,2,...,m\right\}$ can be computed using the proposed HBN-SNWBM operator provided in Eq. (14). Different values of p,q parameters is assign based on the experts’ preferences. When $q=0$, the complete evaluation of each alternatives is computed by the special cases of the proposed HBN-SNWBM operators as in Eq. (21–28). On the other hand, if $p=q$, use Eq. (26–28) to calculate the complete evaluation. The different p,q parameter values may influence the ranking results of alternatives. The general form of the obtained complete evaluation rate of each alternative can be written as:

$$\begin{array}{cc}& c_j\\ \begin{array}{c}{A}_1\\ A_2\\ ⋮\\ A_m\end{array}=& \left(\begin{array}{c}{h}_1\\ h_2\\ ⋮\\ h_m\end{array}\right)\end{array}$$ 30

Phase 3: Ranking process

Use the score function, $s\left(h_i\right)$ defined in Eq. (6) to get the rating of each alternative $A_i$. Then, the set of alternatives can be ranked according to the obtained values of score function. The highest score values will be the most preferable alternative. In general, the score values of each alternatives can be written as:

$$\begin{array}{cc}& c_j\\ \begin{array}{c}{A}_1\\ A_2\\ ⋮\\ A_m\end{array}=& \left(\begin{array}{c}s\left(h_1\right)\\ s\left(h_2\right)\\ ⋮\\ s\left(h_m\right)\end{array}\right)\end{array}$$ 31

Finally, the different values of parameters are analyzed to see the robustness of the final ranking results. The summary of the proposed decision making approach is given in Fig. 2.

Fig. 2.

Framework of the proposed decision approach

Illustrative examples

Two illustrative examples are given in this study to show the applicability of the proposed HBN-SNWBM aggregation operator.

Example 1

An illustrative example adapted from Ye (2014) is used to apply the proposed HBN-SNWBM operator. In choosing which company worth to be invested, the truth, indeterminacy and falsity elements exist during the decision process. The situations where investors are hesitating to state either truth or falsity is called the indeterminacy. The indeterminacy function in neutrosophic sets does not depend on truth or falsity functions unlike the IFS. Let us consider this investment problem. An investment firm intends to capitalize a sum of money into one of the most capable company. There are four possible alternatives: a transport company $\left(A_1\right)$, a food company $\left(A_2\right)$, an IT company $\left(A_3\right)$ and a weapons company $\left(A_4\right)$ with the following considered criteria: risk profile $\left(c_1\right)$, growth profile $\left(c_2\right)$ and environmental risk profile $\left(c_3\right)$. The four alternatives are judged by a group of experts with respect to the considered criteria under the HBNS information. The obtained information is transformed into a decision matrix as shown in Table 2.

Table 2.

The decision data in HBNS information

	$c_1$	$c_2$	$c_3$
$A_1$	$\left.〈\left\{0.4,0.5\right\},\left\{0.2,0.3\right\},\left\{0.3,0.4\right\},\right)$ $\left(-0.4,-0.2,\left\{-0.4,-0.5\right\}\right.〉$	$\begin{array}{c}\left.〈0.5,\left\{0.1,0.3\right\},0.2,\left\{-0.2,-0.3\right\},\right)\\ \left(-0.7,\left\{-0.4,-0.6\right\}\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈0.2,\left\{0.2,0.3\right\},\left\{0.5,0.6\right\},-0.5,-0.8,\right)\\ \left(\left\{-0.1,-0.3\right\}\right.〉\\ \end{array}$
$A_2$	$\begin{array}{c}\left.〈\left\{0.6,0.7\right\},\left\{0.1,0.2\right\},\left\{0.2,0.3\right\},\right)\\ \left(\left\{-0.2,-0.3\right\},-0.2,-0.7\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈\left\{0.6,0.7\right\},\left\{0.1,0.2\right\},\left\{0.2,0.3\right\}\right),\\ \left\{-0.2,-0.3\right\},\left(-0.8,-0.7\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈\left\{0.3,0.6\right\},\left\{0.3,0.5\right\},0.1,\right)\\ \left(-0.2,-0.4,-0.7\right.〉\\ \end{array}$
$A_3$	$\begin{array}{c}\left.〈\left\{0.3,0.6\right\},0.2,0.4,\left\{-0.3,-0.4\right\},\right)\\ \left(\left\{-0.2,-0.3\right\},-0.5\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈\left\{0.5,0.6\right\},\left\{0.2,0.3\right\},0.4,\right)\\ \left(-0.3,-0.7,-0.7\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈\left\{0.5,0.6\right\},0.3,0.2,\left\{-0.1,-0.3\right\},\right)\\ \left(-0.6,-0.4\right.〉\\ \end{array}$
$A_4$	$\begin{array}{c}\left.〈0.7,\left\{0.0,0.1\right\},\left\{0.1,0.2\right\},-0.2,-0.1,\right)\\ \left(\left\{-0.7,-0.8\right\}\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈0.6,0.1,\left\{0.1,0.3\right\},\right)\\ \left(-0.2,-0.8,\left\{-0.6,-0.7\right\}\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈0.4,0.3,\left\{0.1,0.2\right\},\left\{-0.1,-0.2\right\},\right)\\ \left(-0.7,-0.3\right.〉\\ \end{array}$

Based on the above table, the obtained data is analysed using the proposed HBN-SNWBM operator. First of all, experts gave the following SFM for each criterion:

$\mu \left(c_1\right)=0.4$, $\mu \left(c_2\right)=0.25$ and $\mu \left(c_3\right)=0.45$.

Next, by Eq. (8) the $\lambda$-value is obtained below:

$\lambda +1=\left(1+0.4\lambda \right)\left(1+0.25\lambda \right)\left(1+0.45\lambda \right)$,

$0.045{\lambda }^3+0.3925{\lambda }^2+0.1\lambda =0$,

$$\lambda =0,-0.263,-8.460$$

Since $\lambda \ge -1$ is only acceptable, we chose $\lambda =-0.263$. Then, the overall interaction of SFM of criteria is obtained by Eq. (7) as below:

$$\mu \left(c_1,c_2\right)=\frac{1}{\lambda }\left(\left(1+\lambda \mu \left(c_1\right)\right)\left(1+\lambda \mu \left(c_2\right)\right)-1\right)$$

$$\mu \left(c_1,c_2\right)=\frac{1}{-0.263}\left(\left(1-0.263(0.4)\right)\left(1-0.263(0.25)\right)-1\right)$$

$\mu \left(c_1,c_2\right)=0.624$;

By similar calculation, we get

$\mu \left(c_1,c_3\right)=0.803$,$\mu \left(c_2,c_3\right)=0.670$ and $\mu \left(c_1,c_2,c_3\right)=1$.

The Shapley fuzzy weight of criteria can be computed using the SFM in Eq. (9)

$$w_i=\sum _{V\subseteq N/i}\frac{\left(\left|N\right|-\left|V\right|-1\right)!\left|V\right|!}{\left|N\right|!}\left(\mu \left(V\cup i\right)-\mu \left(V\right)\right),\forall i\in N$$

$$w_1=\frac{\left(3-0-1\right)!0!}{3!}\left(\mu \left(c_1\right)-\mu \left(\varphi \right)\right)+\frac{\left(3-1-1\right)!1!}{3!}\left(\mu \left(c_1,c_2\right)-\mu \left(c_2\right)\right)+$$

$$\frac{\left(3-1-1\right)!1!}{3!}\left(\mu \left(c_1,c_3\right)-\mu \left(c_3\right)\right)+\frac{\left(3-2-1\right)!2!}{3!}\left(\mu \left(c_1,c_2,c_3\right)-\mu \left(c_2,c_3\right)\right)$$

$$w_1=\frac{2!0!}{3!}\left(0.4-0\right)+\frac{1!1!}{3!}\left(\left(0.624-0.25\right)+\left(0.803-0.45\right)\right)+\frac{0!2!}{3!}\left(1-0.670\right)$$

$$w_1=0.364$$

In similar manner, we get

$w_2=0.223$ and $w_3=0.413$.

After that, compute the complete evaluation rate of each alternative using the proposed HBN-SNWBM operators in Eqs. (14). The experts choose $p=q=1$, thus the proposed HBNWIA in Eq. (28) is used. The complete evaluation rate of each alternative $A_i\left\{i=1,2,...,m\right\}$ is attained as follows:

$$\begin{array}{cc}\hfill A_1& =\left.〈\left\{0.34,0.37\right\},\left\{0.17,0.21,0.21,0.22,0.25,0.26,0.26,0.3\right\},\left\{0.35,0.39,0.39,0.43\right\},\right)\hfill \\ \hfill & \left\{-0.41,-0.39\right\},-0.\left(54,\left\{-0.26,-0.29,-0.31,-0.34,-0.36,-0.39,-0.41,-0.44\right\}\right.〉\hfill \\ \hfill \end{array}$$

$$\begin{array}{cc}\hfill A_2& =\left.〈\left\{0.48,0.5,0.51,0.54,0.6,0.63,0.64,0.66\right\},\left\{0.17,0.2,0.21,0.24,0.24,0.28,0.29,0.32\right\},\right)\hfill \\ \hfill & \left(\left\{0.16,0.19,0.2,0.22\right\},\left\{-0.2,-0.22,-0.24,-0.26\right\},-0.41,-0.7\right.〉\hfill \\ \hfill \end{array}$$

$$\begin{array}{cc}\hfill A_3& =\left.〈\left\{0.42,0.45,0.46,0.48,0.54,0.56,0.57,0.6\right\},\left\{0.24,0.26\right\}\right),0.33,\hfill \\ \hfill & \left(\left\{-0.22,-0.26,-0.3,-0.34\right\},\left\{-0.47,-0.51\right\},-0.51\right.〉\hfill \\ \hfill \end{array}$$

$$\begin{array}{cc}\hfill A_4& =\left.〈0.55,\left\{0.13,0.17\right\},\left\{0.1,0.13,0.13,0.14,0.17,0.19,0.19,0.22\right\}\right)\left\{-0.16,-0.2\right\},-0.5,\hfill \\ \hfill & \left(\left\{-0.51,-0.54,-0.54,-0.57\right\}\right.〉\hfill \\ \hfill \end{array}$$

By Eq. (6), the score function values of each alternatives are as follows:

$s\left(h_1\right)=0.536$,$s\left(h_2\right)=0.669$,$s\left(h_3\right)=0.609$ and $s\left(h_4\right)=0.682$.

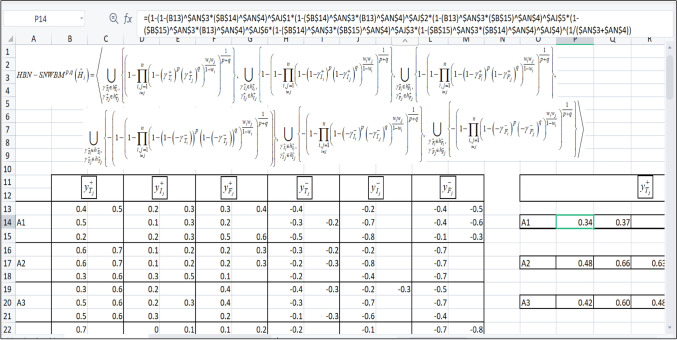
Based on the score function values, the alternatives is ranked as $A_4>A_2>A_3>A_1$. Thus, the best alternative is $A_4$ which is a weapon company. In this investment case, the best alternative to invest is a weapon company followed by a food company. The least favourable company to invest is a transport company. The execution of computation in this paper is made using a spreadsheet software. To illustrate the computation, an example of a spreadsheet computation is given in Fig. 3.

Fig. 3.

An example of excel spreadsheet computation

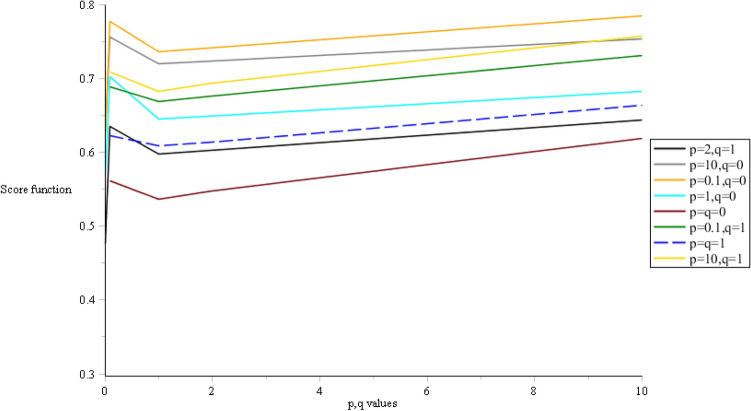
To see the sensitivity of the ranking result, a sensitivity analysis is implemented. The sensitivity analysis of $p,q$ parameters is carried out to see the influence of the parameters of the proposed HBN-SNWBM operator. Table 3 shows the ranking results after testing out different $p,q$ values.

Table 3.

The ranking results with different used of $p,q$ values

$p,q$	Score value	Ranking results
$p=0,q=0$	$s\left(h_1\right)=0.477,s\left(h_2\right)=0.629,s\left(h_3\right)=0.569,s\left(h_4\right)=0.621$	$A_4>A_2>A_3>A_1$
$p=0.1,q=0$	$s\left(h_1\right)=0.635,s\left(h_2\right)=0.756,s\left(h_3\right)=0.702,s\left(h_4\right)=0.777$	$A_4>A_2>A_3>A_1$
$p=1,q=0$	$s\left(h_1\right)=0.598,s\left(h_2\right)=0.719,s\left(h_3\right)=0.645,s\left(h_4\right)=0.736$	$A_4>A_2>A_3>A_1$
$p=10,q=0$	$s\left(h_1\right)=0.644,s\left(h_2\right)=0.753,s\left(h_3\right)=0.682,s\left(h_4\right)=0.785$	$A_4>A_2>A_3>A_1$
$p=q=1$	$s\left(h_1\right)=0.536,s\left(h_2\right)=0.669,s\left(h_3\right)=0.609,s\left(h_4\right)=0.682$	$A_4>A_2>A_3>A_1$
$p=0.1,q=1$	$s\left(h_1\right)=0.561,s\left(h_2\right)=0.688,s\left(h_3\right)=0.622,s\left(h_4\right)=0.708$	$A_4>A_2>A_3>A_1$
$p=2,q=1$	$s\left(h_1\right)=0.547,s\left(h_2\right)=0.676,s\left(h_3\right)=0.614,s\left(h_4\right)=0.694$	$A_4>A_2>A_3>A_1$
$p=10,q=1$	$s\left(h_1\right)=0.619,s\left(h_2\right)=0.731,s\left(h_3\right)=0.663,s\left(h_4\right)=0.757$	$A_4>A_2>A_3>A_1$

Based on the above table, it reveals that the obtained ranking order of alternatives is exactly same regardless of different values of parameters used. The parameters $p,q$ in the proposed HBN-SNWBM operator did not influence the decision ranking results. In other words, final ranking results did not sensitive to the changes of parameters p, q in our proposed aggregation operator. Generally, $p=q=1$ can be assigned to the proposed HBN-SNWBM operator as it is easy to be computed and also taking into account the interrelationship among criteria. The graph in Fig. 4 below unveils the similar pattern of the obtained score functions when different p,q values are tested out.

Fig. 4.

The sensitivity analysis of the proposed method

Example 2

This example is a real investment problem adapted from Du and Yuan (2019). An investor would like to invest a high-technology product in China. Four alternatives $A_i\left\{i=1,2,3,4\right\}$ are available and the panel of decision makers $E_k\left\{k=1,2,3\right\}$ whose Shapley fuzzy measure is $\mu \left(E_k\right)={\left(0.3,0.5,0.3\right)}^{\text{T}}$ are from various strategic decision-making areas. There are five considered criteria which are innovative capacity $\left(C_1\right)$, quality $\left(C_2\right)$, marketing capacity $\left(C_3\right)$, maintenance and after-sale service $\left(C_4\right)$ and risk taking capacity $\left(C_5\right)$ and their corresponding Shapley fuzzy measure is $\mu \left(C_j\right)={\left(0.3,0.4,0.3,0.1,0.3\right)}^{\text{T}},j=1,2,...,5$. The four alternatives are judged individually by three decision makers with respect to the considered criteria under the HBNS information. The obtained information is transformed into a decision matrix as shown in Table 4.

Table 4.

Decision matrix under HBNS information

$D_1$	$A_1$	$A_2$	$A_3$	$A_4$
$C_1$	$\begin{array}{c}\left.〈\left\{0.4,0.6\right\},0.2,0.3,\right)\\ \left\{-0.2,-0.4\right\},\left(-0.3,-0.5\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈\left\{0.6,0.7\right\},0.2,0.3,\right)\\ \left(\left\{-0.2,-0.3\right\},-0.7,-0.7\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈\left\{0.5,0.7\right\},0.3,0.2,\right)\\ \left(-0.2,-0.7,\left\{-0.5,-0.6\right\}\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈\left\{0.6,0.7\right\},0.2,0.3,\right)\\ \left(\left\{-0.2,-0.3\right\},-0.7,-0.7\right.〉\\ \end{array}$
$C_2$	$\begin{array}{c}\left.〈0.7,0.2,0.2,\right)\left\{-0.1,-0.2\right\}\\ \left(,-0.6,\left\{-0.7,-0.8\right\}\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈0.5,0.4,0.3,\right)\\ \left(\left\{-0.3,-0.4\right\},-0.6,-0.7\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈\left\{0.8,0.9\right\},0,0.1,\right)\\ \left(\left\{0,-0.1\right\},-0.7,-0.8\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈\left\{0.3,0.4\right\},0.2,0.3,\right)\\ \left\{-0.5,-0.6\right\},\left(-0.3,-0.5\right.〉\\ \end{array}$
$C_3$	$\begin{array}{c}\left.〈\left\{0.5,0.7\right\},0.3,0.2,\right)\\ \left(-0.2,-0.7,\left\{-0.5,-0.6\right\}\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈\left\{0.8,0.9\right\},0,0.1,\right)\\ \left(\left\{0,-0.1\right\},-0.7,-0.8\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈\left\{0.6,0.7\right\},0.2,0.3,\right)\\ \left(\left\{-0.2,-0.3\right\},-0.7,-0.7\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈0.7,0.2,0.2,\right)\left\{-0.1,-0.2\right\}\\ \left(,-0.6,\left\{-0.7,-0.8\right\}\right.〉\\ \end{array}$
$C_4$	$\begin{array}{c}\left.〈0.8,0.1,0.2,\right)\left\{0,-0.1\right\}\\ \left(,-0.6,\left\{-0.7,-0.9\right\}\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈0.7,0.2,0.2,\right)\left\{-0.1,-0.2\right\}\\ \left(,-0.6,\left\{-0.7,-0.8\right\}\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈\left\{0.6,0.8\right\},0.2,0.1,\right)\\ \left(-0.1,-0.7,\left\{-0.7,-0.8\right\}\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈0.7,0.2,0.2,\right)\left\{-0.1,-0.2\right\}\\ \left(,-0.6,\left\{-0.7,-0.8\right\}\right.〉\\ \end{array}$
$C_5$	$\begin{array}{c}\left.〈\left\{0.6,0.8\right\},0.2,0.1,\right)\\ \left(-0.1,-0.7,\left\{-0.7,-0.8\right\}\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈0.5,0.4,0.3,\right)\\ \left(\left\{-0.3,-0.4\right\},-0.6,-0.7\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈0.7,0.2,0.2,\right)\left\{-0.1,-0.2\right\}\\ \left(,-0.6,\left\{-0.7,-0.8\right\}\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈\left\{0.4,0.6\right\},0.2,0.3,\right)\\ \left\{-0.2,-0.4\right\},\left(-0.3,-0.5\right.〉\\ \end{array}$
$D_2$	$A_1$	$A_2$	$A_3$	$A_4$
$C_1$	$\begin{array}{c}\left.〈\left\{0.4,0.6\right\},0.2,0.3,\right)\\ \left\{-0.2,-0.4\right\},\left(-0.3,-0.5\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈\left\{0.6,0.7\right\},0.2,0.3,\right)\\ \left(\left\{-0.2,-0.3\right\},-0.7,-0.7\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈\left\{0.5,0.7\right\},0.3,0.2,\right)\\ \left(-0.2,-0.7,\left\{-0.5,-0.6\right\}\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈\left\{0.6,0.7\right\},0.2,0.3,\right)\\ \left(\left\{-0.2,-0.3\right\},-0.7,-0.7\right.〉\\ \end{array}$
$C_2$	$\begin{array}{c}\left.〈0.7,0.2,0.2,\right)\left\{-0.1,-0.2\right\}\\ \left(,-0.6,\left\{-0.7,-0.8\right\}\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈0.5,0.4,0.3,\right)\\ \left(\left\{-0.3,-0.4\right\},-0.6,-0.7\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈0.7,0.2,0.2,\right)\left\{-0.1,-0.2\right\}\\ \left(,-0.6,\left\{-0.7,-0.8\right\}\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈0.5,0.4,0.3,\right)\\ \left(-0.5,-0.2,-0.2\right.〉\\ \end{array}$
$C_3$	$\begin{array}{c}\left.〈\left\{0.5,0.7\right\},0.3,0.2,\right)\\ \left(-0.2,-0.7,\left\{-0.5,-0.6\right\}\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈0.5,0.4,0.3,\right)\\ \left(\left\{-0.3,-0.4\right\},-0.6,-0.7\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈0.7,0.2,0.2,\right)\left\{-0.1,-0.2\right\}\\ \left(,-0.6,\left\{-0.7,-0.8\right\}\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈0.4,0.4,0.5,\right)\\ \left(-0.5,-0.3,-0.4\right.〉\\ \end{array}$
$C_4$	$\begin{array}{c}\left.〈0.7,0.2,0.2,\right)\left\{-0.1,-0.2\right\}\\ \left(,-0.6,\left\{-0.7,-0.8\right\}\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈\left\{0.6,0.7\right\},0.2,0.3,\right)\\ \left(\left\{-0.2,-0.3\right\},-0.7,-0.7\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈\left\{0.6,0.8\right\},0.2,0.1,\right)\\ \left(-0.1,-0.7,\left\{-0.7,-0.8\right\}\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈\left\{0.5,0.7\right\},0.3,0.2,\right)\\ \left(-0.2,-0.7,\left\{-0.5,-0.6\right\}\right.〉\\ \end{array}$
$C_5$	$\begin{array}{c}\left.〈\left\{0.6,0.8\right\},0.2,0.1,\right)\\ \left(-0.1,-0.7,\left\{-0.7,-0.8\right\}\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈\left\{0.6,0.7\right\},0.2,0.3,\right)\\ \left(\left\{-0.2,-0.3\right\},-0.7,-0.7\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈\left\{0.8,0.9\right\},0,0.1,\right)\\ \left(\left\{0,-0.1\right\},-0.7,-0.8\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈0.5,0.4,0.3,\right)\\ \left(\left\{-0.3,-0.4\right\},-0.6,-0.7\right.〉\\ \end{array}$
$D_3$	$A_1$	$A_2$	$A_3$	$A_4$
$C_1$	$\begin{array}{c}\left.〈0.5,0.4,0.3,\right)\\ \left(\left\{-0.3,-0.4\right\},-0.6,-0.7\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈\left\{0.6,0.7\right\},0.2,0.3,\right)\\ \left(\left\{-0.2,-0.3\right\},-0.7,-0.7\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈\left\{0.5,0.7\right\},0.3,0.2,\right)\\ \left(-0.2,-0.7,\left\{-0.5,-0.6\right\}\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈\left\{0.6,0.7\right\},0.2,0.3,\right)\\ \left(\left\{-0.2,-0.3\right\},-0.7,-0.7\right.〉\\ \end{array}$
$C_2$	$\begin{array}{c}\left.〈0.7,0.2,0.2,\right)\left\{-0.1,-0.2\right\}\\ \left(,-0.6,\left\{-0.7,-0.8\right\}\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈0.5,0.4,0.3,\right)\\ \left(\left\{-0.3,-0.4\right\},-0.6,-0.7\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈0.7,0.2,0.2,\right)\left\{-0.1,-0.2\right\}\\ \left(,-0.6,\left\{-0.7,-0.8\right\}\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈0.4,0.5,0.6,\right)\\ \left(-0.6,-0.3,-0.4\right.〉\\ \end{array}$
$C_3$	$\begin{array}{c}\left.〈0.5,0.4,0.3,\right)\\ \left(\left\{-0.3,-0.4\right\},-0.6,-0.7\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈\left\{0.6,0.8\right\},0.2,0.1,\right)\\ \left(-0.1,-0.7,\left\{-0.7,-0.8\right\}\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈0.7,0.2,0.2,\right)\left\{-0.1,-0.2\right\}\\ \left(,-0.6,\left\{-0.7,-0.8\right\}\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈0.5,0.4,0.3,\right)\\ \left(-0.5,-0.2,-0.2\right.〉\\ \end{array}$
$C_4$	$\begin{array}{c}\left.〈0.7,0.2,0.2,\right)\left\{-0.1,-0.2\right\}\\ \left(,-0.6,\left\{-0.7,-0.8\right\}\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈\left\{0.6,0.7\right\},0.2,0.3,\right)\\ \left(\left\{-0.2,-0.3\right\},-0.7,-0.7\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈\left\{0.6,0.7\right\},0.2,0.3,\right)\\ \left(\left\{-0.2,-0.3\right\},-0.7,-0.7\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈\left\{0.6,0.7\right\},0.2,0.3,\right)\\ \left(\left\{-0.2,-0.3\right\},-0.7,-0.7\right.〉\\ \end{array}$
$C_5$	$\begin{array}{c}\left.〈\left\{0.6,0.8\right\},0.2,0.1,\right)\\ \left(-0.1,-0.7,\left\{-0.7,-0.8\right\}\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈0.7,0.2,0.3,\right)\\ \left(-0.3,-0.7,-0.8\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈\left\{0.8,0.9\right\},0,0.1,\right)\\ \left(\left\{0,-0.1\right\},-0.7,-0.8\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈0.5,0.4,0.3,\right)\\ \left(\left\{-0.3,-0.4\right\},-0.6,-0.7\right.〉\\ \end{array}$

First of all, calculate the $\lambda$ values based on the Shapley fuzzy measure of decision makers $\mu \left(E_k\right)={\left(0.3,0.5,0.3\right)}^{\text{T}}$ by Eq. (8):

$\lambda +1=\left(1+0.3\lambda \right)\left(1+0.5\lambda \right)\left(1+0.3\lambda \right)$,

$$\lambda =0,-0.264,-8.402$$

Since $\lambda \ge -1$ is only acceptable, we chose $\lambda =-0.264$. Then, the overall interaction of SFM of decision makers is obtained by Eq. (7) as below:

$$\mu \left(E_1,E_2\right)=\frac{1}{\lambda }\left(\left(1+\lambda \mu \left(E_1\right)\right)\left(1+\lambda \mu \left(E_2\right)\right)-1\right)$$

$$\mu \left(E_1,E_2\right)=\frac{1}{-0.264}\left(\left(1-0.264(0.3)\right)\left(1-0.264(0.5)\right)-1\right)$$

$\mu \left(E_1,E_2\right)=0.760$;

By similar calculation, we get

$\mu \left(E_1,E_3\right)=0.576$,$\mu \left(E_2,E_3\right)=0.760$ and $\mu \left(E_1,E_2,E_3\right)=1$.

The Shapley fuzzy weight of decision makers can be computed using the SFM in Eq. (9)

$$w\left(E_k\right)=\sum _{V\subseteq N/i}\frac{\left(\left|N\right|-\left|V\right|-1\right)!\left|V\right|!}{\left|N\right|!}\left(\mu \left(V\cup i\right)-\mu \left(V\right)\right),\forall i\in N$$

$$w\left(E_1\right)=\frac{\left(3-0-1\right)!0!}{3!}\left(\mu \left(E_1\right)-\mu \left(\varphi \right)\right)+\frac{\left(3-1-1\right)!1!}{3!}\left(\mu \left(E_1,E_2\right)-\mu \left(E_2\right)\right)+$$

$$\frac{\left(3-1-1\right)!1!}{3!}\left(\mu \left(E_1,E_3\right)-\mu \left(E_3\right)\right)+\frac{\left(3-2-1\right)!2!}{3!}\left(\mu \left(E_1,E_2,E_3\right)-\mu \left(E_2,E_3\right)\right)$$

$$w\left(E_1\right)=\frac{2!0!}{3!}\left(0.3-0\right)+\frac{1!1!}{3!}\left(\left(0.760-0.5\right)+\left(0.576-0.3\right)\right)+\frac{0!2!}{3!}\left(1-0.760\right)$$

$$w\left(E_1\right)=0.269$$

Thus, the Shapley fuzzy weights for second and third decision makers are $w\left(E_2\right)=0.462$ and $w\left(E_3\right)=0.269$.

In similar manner, we get the following combinations of Shapley fuzzy measure of criteria:

$\mu \left(C_1,C_2\right)=0.626$, $\mu \left(C_1,C_3\right)=0.544$, $\mu \left(C_1,C_4\right)=0.381$, $\mu \left(C_1,C_5\right)=0.544$, $\mu \left(C_2,C_3\right)=0.626$, $\mu \left(C_2,C_4\right)=0.4752$, $\mu \left(C_2,C_5\right)=0.626$, $\mu \left(C_3,C_4\right)=0.381$, $\mu \left(C_3,C_5\right)=0.544$, $\mu \left(C_4,C_5\right)=0.381$, $\mu \left(C_1,C_2,C_3\right)=0.809$,$\mu \left(C_1,C_2,C_4\right)=0.687$, $\mu \left(C_1,C_2,C_5\right)=0.809$, $\mu \left(C_1,C_3,C_4\right)=0.611$, $\mu \left(C_1,C_3,C_5\right)=0.743$, $\mu \left(C_1,C_4,C_5\right)=0.611$, $\mu \left(C_2,C_3,C_4\right)=0.687$, $\mu \left(C_2,C_3,C_5\right)=0.809$,$\mu \left(C_2,C_4,C_5\right)=0.687$, $\mu \left(C_3,C_4,C_5\right)=0.611$, $\mu \left(C_1,C_2,C_3,C_4\right)=0.859$, $\mu \left(C_1,C_2,C_4,C_5\right)=0.859$,$\mu \left(C_1,C_2,C_3,C_5\right)=0.959$, $\mu \left(C_1,C_3,C_4,C_5\right)=0.797$, $\mu \left(C_2,C_3,C_4,C_5\right)=0.859$, $\mu \left(C_1,C_2,C_3,C_4,C_5\right)=1$,

and the Shapley fuzzy weights of each criterion are as below:

$$w\left(C_1\right)=0.213,w\left(C_2\right)=0.293,w\left(C_3\right)=0.213,w\left(C_4\right)=0.068,w\left(C_5\right)=0.213$$

By using the proposed HBN-SNWBM operators in Eqs. (14), the aggregated decision matrix is obtained as below:

The obtained aggregated decision matrix in Table 5 has more than two hesitancy elements which makes it more complex for computations. To reduce the complexity, the aggregated decision matrix is reduce to BNS information. Then, the complete evaluation rate of each alternative $A_i\left\{i=1,2,...,m\right\}$ using the proposed HBN-SNWBM operators in Eqs. (14) with $p=q=1$ is as follows:

$$A_1=〈0.63,0.24,0.22,-0.19,-0.58,-0.69〉$$

$$A_2=〈0.59,0.26,0.26,-0.25,-0.65,-0.72〉$$

$$A_3=〈0.71,0.15,0.18,-0.14,-0.66,-0.71〉$$

$$A_4=〈0.53,0.31,0.33,-0.36,-0.48,-0.57〉$$

Table 5.

Aggregated decision matrix

	$A_1$	$A_2$	$A_3$	$A_4$
$C_1$	$\begin{array}{c}\left.〈\left\{0.42,0.48,...\right\},...\right),\\ \left(-0.37,-0.55\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈\left\{0.6,0.63,0.64,...\right\},...,\right)\\ \left(-0.7,-0.7\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈\left\{0.5,0.55,0.57,...\right\},...,\right)\\ \left(\left\{-0.5,-0.53-0.54,...\right\}\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈\left\{0.6,0.63,0.64,...\right\},...,\right)\\ \left(-0.7,-0.7\right.〉\\ \end{array}$
$C_2$	$\begin{array}{c}\left.〈0.7,0.2,0.2,\right)...,\\ \left(\left\{-0.7,-0.73,-0.74,...\right\}\right.〉\\ \end{array}$	$\left.〈0.5,0.4,0.3,\right)...,\left(-0.7\right.〉$	$\begin{array}{c}\left.〈\left\{0.74,0.77\right\},0.13,0.16,\right)...,\\ \left(...,\left\{-0.74,-0.76,-0.78\right\}\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈\left\{0.39,0.42\right\},0.37,0.42,\right)...,\\ ...,\left(-0.37,-0.51\right.〉\\ \end{array}$
$C_3$	$\begin{array}{c}\left.〈\left\{0.5,0.55,...\right\},0.34,0.24,\right)\\ \left(...,\left\{-0.57,-0.6,...\right\}\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈\left\{0.65,0.68,...\right\},0.17,\right)...,\\ \left(...,\left\{-0.74,-0.78\right\}\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈\left\{0.66,0.7\right\},0.2,0.24,\right)\\ \left(...,\left\{-0.7,-0.73\right\}\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈0.54,0.33,0.31,...\right)\\ \left(,...,\left\{-0.4,-0.42\right\}\right.〉\\ \end{array}$
$C_4$	$\begin{array}{c}\left.〈0.74,0.16,0.2,...\right),\\ \left(...,\left\{-0.7,-0.73,...\right\}\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈\left\{0.64,0.66,...\right\},0.2,0.26,\right)\\ \left(...,-0.66,\left\{-0.7,-0.74\right\}\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈\left\{0.6,0.64,...\right\},0.2,0.17,\right)\\ \left(...,\left\{-0.7,-0.73,...\right\}\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈\left\{0.61,0.65,...\right\},0.2,0.24,\right)...,\\ \left(...,\left\{-0.65,-0.67,...\right\}\right.〉\\ \end{array}$
$C_5$	$\begin{array}{c}\left.〈\left\{0.6,0.65,...\right\},0.2,0.1,\right)...,\\ \left(...,\left\{-0.7,-0.73,...\right\}\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈\left\{0.37,0.41,...\right\},0.27,0.3,\right)\\ \left(...,-0.66,-0.74\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈\left\{0.76,0.79,...\right\},0,0.13,\right)...,\\ \left(-0.66,\left\{-0.76,-0.8\right\}\right.〉\\ \end{array}$	$\begin{array}{c}\left.〈\left\{0.46,0.54\right\},0.33,0.3,\right)\\ ...,\left(-0.46,-0.63\right.〉\\ \end{array}$

By Eq. (6), the score function values of each alternatives are as follows:

$s\left(A_1\right)=0.71$,$s\left(A_2\right)=0.70$,$s\left(A_3\right)=0.77$ and $s\left(A_4\right)=0.60$.

Based on the obtained score values, the alternatives is ranked as $A_3>A_1>A_2>A_4$. The obtained results is consistent with Du and Yuan (2019). This could be due to the similarities between the proposed method and Du and Yuan’s method of employing the Bonferroni mean operator. In the following section, we address in depth the comparison of the proposed method with the existing literature.

Comparative analysis

A comparative analysis is carried out to confirm the efficacy of the proposed decision making method. The proposed decision-making method's validity is confirmed in the first subsection. The proposed method's advantages over existing methods are discussed in the second subsection.

Validity of the proposed method

Employing the Example 1 from Ye (2014), the proposed decision-making method based HBN-SNWBM operator is compared to the existing aggregation operators; arithmetic averaging, geometric averaging, weighted average (WA) (Dong and Wong 1987), weighted geometric (WG) (Aczel and Saaty 1983), generalised weighted average (GWA) and Bonferroni mean (BM) (Bonferroni 1950). For this purpose, we extend the mentioned aggregation operators under hesitant bipolar-valued neutrosophic environment and developed the hesitant bipolar-valued neutrosophic average (HBNA), hesitant bipolar-valued neutrosophic geometric (HBNG), hesitant bipolar-valued neutrosophic Bonferroni mean (HBN-BM) and generalised hesitant bipolar-valued neutrosophic weighted average (GHBN-WA). Hesitant bipolar-valued neutrosophic weighted average (HBNWA) and hesitant bipolar-valued neutrosophic weighted geometric (HBNWG) has been developed by Awang et al. (2019a,b). In the following, the definitions of HBNA, HBNG and GHBN-WA are given below:

Definition 10

Let ${\widehat{H}}_i=〈h_T^{+},h_I^{+},h_F^{+},h_T^{-},h_I^{-},h_F^{-}〉\left(i=1,2,...,n\right)$ be a collection of HBNSs, then HBNA operator is defined as follows:

$$HBNA\left({\widehat{H}}_i\right)=\sum _{i=1}^n\frac{1}{n}\left({\widehat{H}}_i\right)=\left.〈\bigcup _{\gamma {}_{T_i}^{+}\in h{}_{T_i}^{+}}\left\{1-\prod _{i=1}^n{\left(1-\gamma {}_{T_i}^{+}\right)}^{\frac{1}{n}}\right\},\bigcup _{\gamma {}_{I_i}^{+}\in h{}_{I_i}^{+}}\left\{\prod _{i=1}^n{\left(\gamma {}_{I_i}^{+}\right)}^{\frac{1}{n}}\right\},\bigcup _{{\gamma }_{F_i}^{+}\in h_{F_i}^{+}}\left\{\prod _{i=1}^n{\left({\gamma }_{F_i}^{+}\right)}^{\frac{1}{n}}\right\}\right)$$

$$\left(\bigcup _{\gamma {}_{T_i}^{-}\in h{}_{T_i}^{-}}\left\{-\prod _{i=1}^n{\left(-\gamma {}_{T_i}^{-}\right)}^{\frac{1}{n}}\right\},\bigcup _{\gamma {}_{I_i}^{-}\in h{}_{I_i}^{-}}\left\{-\left(1-\prod _{i=1}^n{\left(1-\left(-\gamma {}_{I_i}^{-}\right)\right)}^{\frac{1}{n}}\right)\right\},\bigcup _{\gamma {}_{F_i}^{-}\in h{}_{F_i}^{-}}\left\{-\left(1-\prod _{i=1}^n{\left(1-\left(-\gamma {}_{F_i}^{-}\right)\right)}^{\frac{1}{n}}\right)\right\}\right.〉$$ 32

Definition 11

Let ${\widehat{H}}_i=〈h_T^{+},h_I^{+},h_F^{+},h_T^{-},h_I^{-},h_F^{-}〉\left(i=1,2,...,n\right)$ be a collection of HBNSs, then HBNG operator is defined as follows:

$$HBNG\left({\widehat{H}}_i\right)=\prod _{i=1}^n{\left({\widehat{H}}_i\right)}^{\frac{1}{n}}=\left.〈\bigcup _{\gamma {}_{T_i}^{+}\in h{}_{T_i}^{+}}\left\{\prod _{i=1}^n{\left(\gamma {}_{T_i}^{+}\right)}^{\frac{1}{n}}\right\},\bigcup _{\gamma {}_{I_i}^{+}\in h{}_{I_i}^{+}}\left\{1-\prod _{i=1}^n{\left(1-\gamma {}_{I_i}^{+}\right)}^{\frac{1}{n}}\right\},\bigcup _{{\gamma }_{F_i}^{+}\in h_{F_i}^{+}}\left\{1-\prod _{i=1}^n{\left(1-{\gamma }_{F_i}^{+}\right)}^{\frac{1}{n}}\right\}\right)$$

$$\left(\bigcup _{\gamma {}_{T_i}^{-}\in h{}_{T_i}^{-}}\left\{-\left(1-\prod _{i=1}^n{\left(1-\left(-\gamma {}_{T_i}^{-}\right)\right)}^{\frac{1}{n}}\right)\right\},\bigcup _{\gamma {}_{I_i}^{-}\in h{}_{I_i}^{-}}\left\{-\prod _{i=1}^n{\left(-\gamma {}_{I_i}^{-}\right)}^{\frac{1}{n}}\right\},\bigcup _{\gamma {}_{F_i}^{-}\in h{}_{F_i}^{-}}\left\{-\prod _{i=1}^n{\left(-\gamma {}_{F_i}^{-}\right)}^{\frac{1}{n}}\right\}\right.〉$$ 33

Definition 12

Let ${\widehat{H}}_i=〈h_T^{+},h_I^{+},h_F^{+},h_T^{-},h_I^{-},h_F^{-}〉\left(i=1,2,...,n\right)$ be a collection of HBNSs, then generalized HBNWA (GHBN-WA) operator is defined as follows.

$$GHBN-WA\left({\widehat{H}}_i\right)={\left(\sum _{i=1}^n{\omega }_i{\widehat{H}}_i^{\rho }\right)}^{\frac{1}{\rho }}=\left.〈\bigcup _{\gamma {}_{T_i}^{+}\in h{}_{T_i}^{+}}\left\{{\left(1-\prod _{i=1}^n{\left(1-{\left(\gamma {}_{T_i}^{+}\right)}^{\rho }\right)}^{{\omega }_i}\right)}^{\frac{1}{\rho }}\right\},\right)$$

$$\bigcup _{\gamma {}_{I_i}^{+}\in h{}_{I_i}^{+}}\left\{1-{\left(1-\prod _{i=1}^n{\left(1-{\left(1-\gamma {}_{I_i}^{+}\right)}^{\rho }\right)}^{{\omega }_i}\right)}^{\frac{1}{\rho }}\right\},\bigcup _{{\gamma }_{F_i}^{+}\in h_{F_i}^{+}}\left\{1-{\left(1-\prod _{i=1}^n{\left(1-{\left(1-{\gamma }_{F_i}^{+}\right)}^{\rho }\right)}^{{\omega }_i}\right)}^{\frac{1}{\rho }}\right\},$$

$$\bigcup _{\gamma {}_{T_i}^{-}\in h{}_{T_i}^{-}}\left\{-\left(1-{\left(1-\prod _{i=1}^n{\left(1-{\left(1-\left(-\gamma {}_{T_i}^{-}\right)\right)}^{\rho }\right)}^{{\omega }_i}\right)}^{\frac{1}{\rho }}\right)\right\},\bigcup _{\gamma {}_{I_i}^{-}\in h{}_{I_i}^{-}}\left\{-{\left(1-\prod _{i=1}^n{\left(1-{\left(-\gamma {}_{I_i}^{-}\right)}^{\rho }\right)}^{{\omega }_i}\right)}^{\frac{1}{\rho }}\right\},$$

$$\left(\bigcup _{\gamma {}_{F_i}^{-}\in h{}_{F_i}^{-}}\left\{-{\left(1-\prod _{i=1}^n{\left(1-{\left(-\gamma {}_{F_i}^{-}\right)}^{\rho }\right)}^{{\omega }_i}\right)}^{\frac{1}{\rho }}\right\}\right.〉$$ 34

where $\rho >0$.

Table 6 shows the comparison analysis between the proposed aggregation operator with several existing aggregation operators in hesitant bipolar-valued neutrosophic set (HBNS) information.

Table 6.

The comparison with the existing aggregation operators

Method	Criteria Weight	Parameter	Score Function	Ranking Order
HBNA	No	No	$s\left(A_1\right)=0.585,s\left(A_2\right)=0.704,$ $s\left(A_3\right)=0.633,s\left(A_4\right)=0.735$	$A_4>A_2>A_3>A_1$
HBNG	No	No	$s\left(A_1\right)=0.528,s\left(A_2\right)=0.664,$ $s\left(A_3\right)=0.603,s\left(A_4\right)=0.658$	$A_2>A_4>A_3>A_1$
HBNWA (Awang et al. 2019a,b)	Yes	No	$s\left(A_1\right)=0.570,s\left(A_2\right)=0.695,$ $s\left(A_3\right)=0.629,s\left(A_4\right)=0.727$	$A_4>A_2>A_3>A_1$
HBNWG (Awang et al. 2019a,b)	Yes	No	$s\left(A_1\right)=0.477,s\left(A_2\right)=0.629,$ $s\left(A_3\right)=0.569,s\left(A_4\right)=0.621$	$A_2>A_4>A_3>A_1$
HBN-BM	No	Yes	$s\left(A_1\right)=0.554,s\left(A_2\right)=0.677,$ $s\left(A_3\right)=0.614,s\left(A_4\right)=0.694$	$A_4>A_2>A_3>A_1$
GHBN-WA	Yes	Yes	$s\left(A_1\right)=0.604,s\left(A_2\right)=0.730,$ $s\left(A_3\right)=0.670,s\left(A_4\right)=0.757$	$A_4>A_2>A_3>A_1$
HBN-SNWBM (Proposed method)	Yes	Yes	$s\left(A_1\right)=0.536,s\left(A_2\right)=0.669,$ $s\left(A_3\right)=0.609,s\left(A_4\right)=0.682$	$A_4>A_2>A_3>A_1$

From Table 6, it can be seen that the ranking order of the proposed HBN-SNWBM aggregation operator is in concordance with the existing aggregation operators of HBNA, HBNWA (Awang et al. 2019a, b), HBN-BM and GHBN-WA but slightly differ when compared to the geometric based aggregation operators, HBNG and HBNWG (Awang et al. 2019a, b). This is because the proposed aggregation operator was developed based on an arithmetic operator. There is a difference in ranking order between geometric and arithmetic operators due to their differing focal points. The arithmetic operators focus on the the group’s major points whereas the geometric operators focus the individual major points. This comparative analysis shows the validity of the proposed aggregation operator. However, due to the same ranking outcomes, it cannot demonstrate the benefits of the proposed method. The benefits of the proposed method is analysed in more detail in the next subsection.

Advantages of the proposed method

In this subsection, a comparative analysis is presented to demonstrate the advantages and flexibility of the proposed HBN-SNWBM decision making method over the existing methods. Therefore, different existing methods in the literature (Ye 2015; Garg et al. 2016; Liu and Li 2017; Liu and Zhang 2019; Yang et al. 2019) are used to solve the same example (Example 1). Table 7 summarizes the ranking results of the comparison analysis.

Table 7.

The comparison with the existing methods

Method	Ranking Order
SVNHFWA (Ye 2015)	$A_4>A_2>A_3>A_1$
SVNHFWG (Ye 2015)	$A_2>A_4>A_3>A_1$
CIFBM $\left(p=q=1\right)$ (Garg et al. 2016)	$A_1>A_4>A_3>A_2$
NNWBM $\left(p=q=1\right)$ (Liu and Li 2017)	$A_4>A_2>A_3>A_1$
NNWGBM $\left(p=q=1\right)$ (Liu and Li 2017)	$A_2>A_4>A_3>A_1$
IULWABM $\left(p=q=1\right)$ (Liu and Zhang 2019)	$A_2>A_4>A_1>A_3$
PFWBM $\left(p=q=1\right)$ (Yang et al. 2019)	$A_3>A_4>A_2>A_1$
HBN-SNWBM (Proposed method)$\left(p=q=1\right)$	$A_4>A_2>A_3>A_1$

The comparison condition parameter $p=q=1$ has been used by Garg et al. (2016), Liu and Li (2017), Liu and Zhang (2019) and Yang et al. (2019) which is similar to the parameter used in our proposed method. However, the comparison methods from Ye (2015) do not use any parameters. This is because p, q parameters are presented for the Bonferroni mean based aggregation operators. The ranking order of the proposed method is consistent to the operator SVNHFWA (Ye 2015) and NNWBM (Liu and Li 2017). This could be owing to the fact that both existing operators and the proposed operator shared some common comparison conditions. The SVNHFWA uses arithmetic averaging with hesitant and neutrosophic theory, while NNWBM uses the NWBM operator. However, when compared to the SVNHFWG (Ye 2015), CIFBM (Garg et al. 2016), NNWGBM (Liu and Li 2017), IULWABM (Liu and Zhang 2019), and PFWBM (Yang et al. 2019) operators, the proposed operator produces a completely different ranking order. Despite the fact that the common comparison condition of Bonferroni mean was employed, the ranking outcomes are influenced by the different set used and geometrically based operator. Yet, the proposed method is practical for dealing with problems involving the total interaction of criteria and decision makers' weights, as well as the ability to manage interaction between input arguments and hesitant bipolar indeterminacy.

Conclusion

The main objective of this paper is the development of a new BM operator in a hesitant bipolar-valued neutrosophic environment and its application to decision-making problems. This paper studied the appropriate characteristics of aggregation operators to handle the multiple indeterminacy, hesitancy and bipolar uncertainty data. Considering the notions of SFM and BM, this study developed the hesitant bipolar-valued neutrosophic Shapley NWBM (HBN-SNWBM) operator. Subsequently, some necessary properties were investigated and the special cases to the proposed HBN-SNWBM operator was studied. A multi-criteria decision making model was formulated using the proposed HBN-SNWBM operator to effectively solve the hesitant bipolar neutrosophic problems. Eventually, an illustrative example on an investment decision problem was provided under the hesitant bipolar-valued neutrosophic environment. The nature of the investment decision problem involves indeterminacy, hesitation and bipolarity during the decision-making process. The proposed method is advantageous to investors because it eliminates hesitation and allows bipolarity elements during decision elicitation. Furthermore, the problem with bipolarity information can be addressed effectively as the proposed aggregation operator considered both the negative and positive aspects of the problem. In our case, the proposed approach assisted investors in making more realistic and practical decisions. A comparative analysis is presented in two directions: to validate the proposed aggregation operator and to demonstrate its advantages. When compared to the previous operators, the analysis revealed that the proposed aggregation operator is more accurate and efficient.

The key contributions of this study can be summarized as follows. Firstly, this paper introduces the Shapley fuzzy measure which can take into account the overall interaction of criteria weights. Secondly, this study proposes a novel hesitant bipolar-valued neutrosophic aggregation operator that combines the NWBM operator and Shapley fuzzy measure to address the interrelationships between input arguments as well as the overall interaction among criteria. The proposed aggregation operator incorporated Shapley fuzzy measure, while most of the previous aggregation operators simply assumed the criteria’ weights. Finally, based on the proposed aggregation operator, this paper develops a decision-making method for investment selection. The new method is then proven to be useful in selecting which companies are worth investing in. The proposed MCDM method incorporating the HBN-SNWBM operator outperforms existing methods in dealing with situations involving dependent criteria with varying weightages, which occur in the majority of real-world problems. In other words, the proposed method employing the HBN-SNWBM operator is more practical than existing methods.

Several future research directions appear to be very interesting. Firstly, the aggregation operator proposed in this study can be extended into other neutrosophic sets such as vague neutrosophic set, neutrosophic soft set and many others. Secondly, it may be possible to consider the applications of the proposed method to tackle the current real issues such as in automatic ship classification (Połap et al. 2021), coastal erosion (Awang et al. 2019a, b), energy policy (Jamil and Rashid 2018) and covid-19 decision-making (Albahri et al. 2020). The common feature of these real-world problems is the interdependence of multiple criteria and different weights. In addition, in the case of the group MCDM problem, the Shapley fuzzy measure can be used to calculate the overall interaction of decision makers' weightages. Furthermore, the applications can be further extended to the development of new systems such as type-2 fuzzy control of non-linear system (Mohammadzadeh and Hashemzadeh 2015) and fractional-order chaotic system (Balootaki et al. 2020) of which the proposed operators could be used as a new aggregation method. Last but not least, with the help of integrated software, the complexity of the proposed method can be improved. In the future, we will focus on reducing the method's complexity while increasing its accuracy.

Abbreviations

T

Truth membership degree

I

Indeterminacy membership degree

F

Falsity membership degree

X

A reference set

$\widehat{H}$

Hesitant bipolar-valued neutrosophic set (HBNS)

h

Hesitant bipolar-valued neutrosophic element (HBNE)

$h_T^{+}\left(x\right)$

Possible satisfactory degree of truth of x to the set $\widehat{H}$

$h_I^{+}\left(x\right)$

Possible satisfactory degree of indeterminacy of x to the set $\widehat{H}$

$h_F^{+}\left(x\right)$

Possible satisfactory degree of falsity of x to the set $\widehat{H}$

$h_T^{-}\left(x\right)$

Possible satisfactory degree of truth of x to the implicit counter property to the set $\widehat{H}$

$h_I^{-}\left(x\right)$

Possible satisfactory degree of indeterminacy of x to the implicit counter property to the set $\widehat{H}$

$h_F^{-}\left(x\right)$

Possible satisfactory degree of falsity of x to the implicit counter property to the set $\widehat{H}$

${\gamma }_T^{+}$

Element of $h_T^{+}\left(x\right)$

${\gamma }_I^{+}$

Element of $h_I^{+}\left(x\right)$

${\gamma }_F^{+}$

Element of $h_F^{+}\left(x\right)$

${\gamma }_T^{-}$

Element of $h_T^{-}\left(x\right)$

${\gamma }_I^{-}$

Element of $h_I^{-}\left(x\right)$

${\gamma }_F^{-}$

Element of $h_F^{-}\left(x\right)$

$\rho$

A scalar value

$s\left(h\right)$

Score function of h

$\ell {}_{h_T}^{+}$

Number of elements of $h_T^{+}\left(x\right)$

$\ell {}_{h_I}^{+}$

Number of elements of $h_I^{+}\left(x\right)$

$\ell {}_{h_F}^{+}$

Number of elements of $h_F^{+}\left(x\right)$

$\ell {}_{h_T}^{-}$

Number of elements of $h_T^{-}\left(x\right)$

$\ell {}_{h_I}^{-}$

Number of elements of $h_I^{-}\left(x\right)$

${\ell }_{h_F}^{-}$

Number of elements of $h_F^{-}\left(x\right)$

$N=\left\{C_i\left|i=1,2,...,n\right)\right\}$

A set of criteria

${\mu }_{\lambda }$

$\lambda$-Fuzzy measure

$w_i\left(\mu ,N\right)$

Weight criteria on set N

$w_i={\left(w_1,w_2,...,w_n\right)}^{{}^T}$

The weight vectors of $A_i$

${\tilde{\widehat{H}}}_i$

Any permutation of ${\widehat{H}}_i$

$\begin{array}{c}{A}_i\left(i=1,2,...,n\right)\text{and}\\ A_j\left(j=1,2,...,n\right)\\ \end{array}$

A collection of nonnegative numbers

$w_i\left(\mu ,N\right)$

Shapley fuzzy measure of ${\widehat{H}}_i$

$A_i=\left\{A_1,A_2,...,A_m\right\}$

A set of alternatives

$c_j=\left\{c_1,c_2,...,c_n\right\}$

A set of criteria

$E_k\left\{k=1,2,3\right\}$

A panel of decision makers

Appendix

Proof of Theorem 3

Proof

Since ${\widehat{H}}_i=〈h_T^{+},h_I^{+},h_F^{+},h_T^{-},h_I^{-},h_F^{-}〉\left(i=1,2,...,n\right)$ and ${\widehat{H}}_j=〈h_T^{+},h_I^{+},h_F^{+},h_T^{-},h_I^{-},h_F^{-}〉\left(j=1,2,...,n\right)$, so by power rule of HBNSs in Eq. (4), we have

$$\begin{array}{cc}\hfill {\widehat{H}}_i^p& =\left.〈\bigcup _{\gamma {}_{T_i}^{+}\in h_{T_i}^{+}}\left\{{\left(\gamma {}_{T_i}^{+}\right)}^p\right\},\bigcup _{\gamma {}_{I_i}^{+}\in h_{I_i}^{+}}\left\{1-{\left(1-\gamma {}_{I_i}^{+}\right)}^p\right\},\bigcup _{{\gamma }_{F_i}^{+}\in h_{F_i}^{+}}\left\{1-{\left(1-{\gamma }_{F_i}^{+}\right)}^p\right\},\right)\hfill \\ \hfill & \left(\bigcup _{\gamma {}_{T_i}^{-}\in h{}_{T_i}^{-}}\left\{-\left(1-{\left(1-\left(-\gamma {}_{T_i}^{-}\right)\right)}^p\right)\right\},\bigcup _{\gamma {}_{I_i}^{-}\in h_{I_i}^{-}}\left\{-{\left(-\gamma {}_{I_i}^{-}\right)}^p\right\},\bigcup _{\gamma {}_{F_i}^{-}\in h_{F_i}^{-}}\left\{-{\left(-\gamma {}_{F_i}^{-}\right)}^p\right\}\right.〉\hfill \\ \hfill \end{array}$$

$$\begin{array}{cc}\hfill {\widehat{H}}_j^q& =\left.〈\bigcup _{\gamma {}_{T_j}^{+}\in h_{T_j}^{+}}\left\{{\left(\gamma {}_{T_j}^{+}\right)}^p\right\},\bigcup _{\gamma {}_{I_j}^{+}\in h_{I_j}^{+}}\left\{1-{\left(1-\gamma {}_{I_j}^{+}\right)}^p\right\},\bigcup _{{\gamma }_{F_j}^{+}\in h_{F_j}^{+}}\left\{1-{\left(1-{\gamma }_{F_j}^{+}\right)}^p\right\},\right)\hfill \\ \hfill & \left(\bigcup _{\gamma {}_{T_j}^{-}\in h{}_{T_j}^{-}}\left\{-\left(1-{\left(1-\left(-\gamma {}_{T_j}^{-}\right)\right)}^p\right)\right\},\bigcup _{\gamma {}_{I_j}^{-}\in h_{I_j}^{-}}\left\{-{\left(-\gamma {}_{I_j}^{-}\right)}^p\right\},\bigcup _{\gamma {}_{F_j}^{-}\in h_{F_j}^{-}}\left\{-{\left(-\gamma {}_{F_j}^{-}\right)}^p\right\}\right.〉\hfill \\ \hfill \end{array}$$

Using the product rule of HBNSs in Eq. (3), we have,

$$\begin{array}{cc}\hfill {\widehat{H}}_i^p\otimes {\widehat{H}}_j^q& =\left.〈\bigcup _{\begin{array}{c}\gamma {}_{T_i}^{+}\in h_{T_i}^{+},\hfill \\ \gamma {}_{T_j}^{+}\in h_{T_j}^{+}\hfill \end{array}}\left\{{\left(\gamma {}_{T_i}^{+}\right)}^p{\left(\gamma {}_{T_j}^{+}\right)}^q\right\},\bigcup _{\begin{array}{c}\gamma {}_{I_i}^{+}\in h_{I_i}^{+},\hfill \\ {\gamma }_{I_j}^{+}\in h_{I_j}^{+}\hfill \end{array}}\left\{1-{\left(1-\gamma {}_{I_i}^{+}\right)}^p{\left(1-\gamma {}_{I_j}^{+}\right)}^q\right\}\right),\hfill \\ & \bigcup _{\begin{array}{c}{\gamma }_{F_i}^{+}\in h_{F_i}^{+},\hfill \\ {\gamma }_{F_j}^{+}\in h_{F_j}^{+}\hfill \end{array}}\left\{1-{\left(1-{\gamma }_{F_i}^{+}\right)}^p{\left(1-{\gamma }_{F_j}^{+}\right)}^q\right\},\bigcup _{\begin{array}{c}\gamma {}_{T_i}^{-}\in h{}_{T_i}^{-},\hfill \\ \gamma {}_{T_j}^{-}\in h{}_{T_j}^{-}\hfill \end{array}}\left\{-\left(1-{\left(1-\left(-\gamma {}_{T_i}^{-}\right)\right)}^p{\left(1-\left(-\gamma {}_{T_j}^{-}\right)\right)}^q\right)\right\},\hfill \\ & \left(\bigcup _{\begin{array}{c}\gamma {}_{I_i}^{-}\in h_{I_i}^{-},\hfill \\ {\gamma }_{I_j}^{-}\in h_{I_j}^{-}\hfill \end{array}}\left\{-{\left(-\gamma {}_{I_i}^{-}\right)}^p{\left(-{\gamma }_{I_j}^{-}\right)}^q\right\},\bigcup _{\begin{array}{c}\gamma {}_{F_i}^{-}\in h_{F_i}^{-},\hfill \\ \gamma {}_{F_j}^{-}\in h_{F_j}^{-}\hfill \end{array}}\left\{-{\left(-\gamma {}_{F_i}^{-}\right)}^p{\left(-\gamma {}_{F_j}^{-}\right)}^q\right\}\right.〉\hfill \end{array}$$

Hence, by applying the scalar multiplication rule of HBNSs in Eq. (5), we have

$$\frac{w_i{w}_j}{1-w_i}\left({\widehat{H}}_i^p\otimes {\widehat{H}}_j^q\right)=\left.〈\bigcup _{\begin{array}{c}\gamma {}_{T_i}^{+}\in h_{T_i}^{+},\hfill \\ \gamma {}_{T_j}^{+}\in h_{T_j}^{+}\hfill \end{array}}\left\{1-{\left(1-{\left(\gamma {}_{T_i}^{+}\right)}^p{\left(\gamma {}_{T_j}^{+}\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}\right\},\bigcup _{\begin{array}{c}{\gamma }_{I_i}^{+}\in h_{I_i}^{+},\hfill \\ {\gamma }_{I_j}^{+}\in h_{I_j}^{+}\hfill \end{array}}\left\{{\left(1-{\left(1-{\gamma }_{I_i}^{+}\right)}^p{\left(1-{\gamma }_{I_j}^{+}\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}\right\}\right),$$

$$\bigcup _{\begin{array}{c}{\gamma }_{F_i}^{+}\in h_{F_i}^{+},\hfill \\ {\gamma }_{F_j}^{+}\in h_{F_j}^{+}\hfill \end{array}}\left\{{\left(1-{\left(1-{\gamma }_{F_i}^{+}\right)}^p{\left(1-{\gamma }_{F_j}^{+}\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}\right\},\bigcup _{\begin{array}{c}\gamma {}_{T_i}^{-}\in h{}_{T_i}^{-},\hfill \\ \gamma {}_{T_j}^{-}\in h{}_{T_j}^{-}\hfill \end{array}}\left\{-{\left(1-{\left(1-\left(-\gamma {}_{T_i}^{-}\right)\right)}^p{\left(1-\left(-\gamma {}_{T_j}^{-}\right)\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}\right\}$$

$$\left(\bigcup _{\begin{array}{c}\gamma {}_{I_i}^{-}\in h_{I_i}^{-},\hfill \\ {\gamma }_{I_j}^{-}\in h_{I_j}^{-}\hfill \end{array}}\left\{-\left(1-{\left(1-{\left(-\gamma {}_{I_i}^{-}\right)}^p{\left(-{\gamma }_{I_j}^{-}\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}\right)\right\},\bigcup _{\begin{array}{c}\gamma {}_{F_i}^{-}\in h_{F_i}^{-},\hfill \\ \gamma {}_{F_j}^{-}\in h_{F_j}^{-}\hfill \end{array}}\left\{-\left(1-{\left(1-{\left(-\gamma {}_{F_i}^{-}\right)}^p{\left(-\gamma {}_{F_j}^{-}\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}\right)\right\}\right.〉.$$

The following explanation is presented to obtain equation when incorporating summation.

Let $n=2$, then

$\sum _{\underset{i\ne j}{i,j=1}}^2\frac{w_i{w}_j}{1-w_i}\left({\widehat{H}}_i^p\otimes {\widehat{H}}_j^q\right)=\frac{w_1{w}_2}{1-w_1}\left({\widehat{H}}_1^p\otimes {\widehat{H}}_2^q\right)\oplus \frac{w_2{w}_1}{1-w_2}\left({\widehat{H}}_2^p\otimes {\widehat{H}}_1^q\right)$.

Note that, only the truth-membership part of the positive HBNS is shown, the rest is similar, thus omitted

$$\begin{array}{c}\frac{w_1{w}_2}{1-w_1}\left({\widehat{H}}_1^p\otimes {\widehat{H}}_2^q\right)\oplus \frac{w_2{w}_1}{1-w_2}\left({\widehat{H}}_2^p\otimes {\widehat{H}}_1^q\right)=\\ 〈\underset{\begin{array}{c}\gamma {}_{T_1}^{+}\in h_{T_1}^{+},\hfill \\ \gamma {}_{T_2}^{+}\in h_{T_2}^{+}\hfill \end{array}}{\cup }\left\{1-{\left(1-{\left(\gamma {}_{T_1}^{+}\right)}^p{\left(\gamma {}_{T_2}^{+}\right)}^q\right)}^{\frac{w_1{w}_2}{1-w_1}}\right\},...〉\oplus 〈\underset{\begin{array}{c}\gamma {}_{T_1}^{+}\in h_{T_1}^{+},\hfill \\ \gamma {}_{T_2}^{+}\in h_{T_2}^{+}\hfill \end{array}}{\cup }\left\{1-{\left(1-{\left(\gamma {}_{T_2}^{+}\right)}^p{\left(\gamma {}_{T_1}^{+}\right)}^q\right)}^{\frac{w_2{w}_1}{1-w_2}}\right\},...〉\\ \end{array}$$

By addition rule of HBNS in (2), we have

$$\Rightarrow 1-{\left(1-{\left(\gamma {}_{T_1}^{+}\right)}^p{\left(\gamma {}_{T_2}^{+}\right)}^q\right)}^{\frac{w_1{w}_2}{1-w_1}}+1-{\left(1-{\left(\gamma {}_{T_2}^{+}\right)}^p{\left(\gamma {}_{T_1}^{+}\right)}^q\right)}^{\frac{w_2{w}_1}{1-w_2}}-$$

$$\left(1-{\left(1-{\left(\gamma {}_{T_1}^{+}\right)}^p{\left(\gamma {}_{T_2}^{+}\right)}^q\right)}^{\frac{w_1{w}_2}{1-w_1}}\right)\left(1-{\left(1-{\left(\gamma {}_{T_2}^{+}\right)}^p{\left(\gamma {}_{T_1}^{+}\right)}^q\right)}^{\frac{w_2{w}_1}{1-w_2}}\right)$$

$$\Rightarrow 1-{\left(1-{\left(\gamma {}_{T_1}^{+}\right)}^p{\left(\gamma {}_{T_2}^{+}\right)}^q\right)}^{\frac{w_1{w}_2}{1-w_1}}{\left(1-{\left(\gamma {}_{T_2}^{+}\right)}^p{\left(\gamma {}_{T_1}^{+}\right)}^q\right)}^{\frac{w_2{w}_1}{1-w_2}}$$

$$\therefore 1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(\gamma {}_{T_i}^{+}\right)}^p{\left(\gamma {}_{T_j}^{+}\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}$$

Therefore,

$$\begin{array}{cc}\hfill \sum _{\underset{i\ne j}{i,j=1}}^n\frac{w_i{w}_j}{1-w_i}\left({\widehat{H}}_i^p\otimes {\widehat{H}}_j^q\right)& =\left.〈\bigcup _{\begin{array}{c}\gamma {}_{T_i}^{+}\in h_{T_i}^{+},\hfill \\ \gamma {}_{T_j}^{+}\in h_{T_j}^{+}\hfill \end{array}}\left\{1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(\gamma {}_{T_i}^{+}\right)}^p{\left(\gamma {}_{T_j}^{+}\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}\right\}\right),\hfill \\ & \bigcup _{\begin{array}{c}\gamma {}_{I_i}^{+}\in h_{I_i}^{+},\hfill \\ \gamma {}_{I_j}^{+}\in h_{I_j}^{+}\hfill \end{array}}\left\{\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(1-\gamma {}_{I_i}^{+}\right)}^p{\left(1-\gamma {}_{I_j}^{+}\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}\right\},\bigcup _{\begin{array}{c}{\gamma }_{F_i}^{+}\in h_{F_i}^{+},\hfill \\ {\gamma }_{F_j}^{+}\in h_{F_j}^{+}\hfill \end{array}}\left\{\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(1-{\gamma }_{F_i}^{+}\right)}^p{\left(1-{\gamma }_{F_j}^{+}\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}\right\},\hfill \\ & \bigcup _{\begin{array}{c}\gamma {}_{T_i}^{-}\in h_{T_i}^{-},\hfill \\ \gamma {}_{T_j}^{-}\in h_{T_j}^{-}\hfill \end{array}}\left\{-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(1-\left(-\gamma {}_{T_i}^{-}\right)\right)}^p{\left(1-\left(-\gamma {}_{T_j}^{-}\right)\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}\right\},\bigcup _{\begin{array}{c}\gamma {}_{I_i}^{-}\in h_{I_i}^{-},\hfill \\ {\gamma }_{I_j}^{-}\in h_{I_j}^{-}\hfill \end{array}}\left\{-1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(-\gamma {}_{I_i}^{-}\right)}^p{\left(-{\gamma }_{I_j}^{-}\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}\right\},\hfill \\ & \left(\bigcup _{\begin{array}{c}\gamma {}_{F_i}^{-}\in h_{F_i}^{-},\hfill \\ \gamma {}_{F_j}^{-}\in h_{F_j}^{-}\hfill \end{array}}\left\{-1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(-\gamma {}_{F_i}^{-}\right)}^p{\left(-\gamma {}_{F_j}^{-}\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}\right\}\right.〉\hfill \end{array}$$

Then, by power rule of HBNS in (4), we have

$$\begin{array}{cc}\hfill HBN-SNWB{M}^{p,q}\left({\widehat{H}}_i\right)=\left(\sum _{\underset{i\ne j}{i,j=1}}^n\frac{w_i{w}_j}{1-w_i}\left({\widehat{H}}_i^p\otimes {\widehat{H}}_j^q\right)\right)& \Rightarrow \left.〈\bigcup _{\begin{array}{c}\gamma {}_{T_i}^{+}\in h_{T_i}^{+},\hfill \\ \gamma {}_{T_j}^{+}\in h_{T_j}^{+}\hfill \end{array}}\left\{{\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(\gamma {}_{T_i}^{+}\right)}^p{\left(\gamma {}_{T_j}^{+}\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}\right)}^{\frac{1}{p+q}}\right\}\right),\hfill \\ & \bigcup _{\begin{array}{c}\gamma {}_{I_i}^{+}\in h_{I_i}^{+},\hfill \\ \gamma {}_{I_j}^{+}\in h_{I_j}^{+}\hfill \end{array}}\left\{1-{\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(1-\gamma {}_{I_i}^{+}\right)}^p{\left(1-\gamma {}_{I_j}^{+}\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}\right)}^{\frac{1}{p+q}}\right\},\hfill \\ & \bigcup _{\begin{array}{c}{\gamma }_{F_i}^{+}\in h_{F_i}^{+},\hfill \\ {\gamma }_{F_j}^{+}\in h_{F_j}^{+}\hfill \end{array}}\left\{1-{\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(1-{\gamma }_{F_i}^{+}\right)}^p{\left(1-{\gamma }_{F_j}^{+}\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}\right)}^{\frac{1}{p+q}}\right\},\hfill \\ & \bigcup _{\begin{array}{c}\gamma {}_{T_i}^{-}\in h_{T_i}^{-},\hfill \\ \gamma {}_{T_j}^{-}\in h_{T_j}^{-}\hfill \end{array}}\left\{-\left(1-{\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(1-\left(-\gamma {}_{T_i}^{-}\right)\right)}^p{\left(1-\left(-\gamma {}_{T_j}^{-}\right)\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}\right)}^{\frac{1}{p+q}}\right)\right\},\hfill \\ & \bigcup _{\begin{array}{c}\gamma {}_{I_i}^{-}\in h_{I_i}^{-},\hfill \\ {\gamma }_{I_j}^{-}\in h_{I_j}^{-}\hfill \end{array}}\left\{-{\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(-\gamma {}_{I_i}^{-}\right)}^p{\left(-{\gamma }_{I_j}^{-}\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}\right)}^{\frac{1}{p+q}}\right\},\hfill \\ & \left(\bigcup _{\begin{array}{c}\gamma {}_{F_i}^{-}\in h_{F_i}^{-},\hfill \\ \gamma {}_{F_j}^{-}\in h_{F_j}^{-}\hfill \end{array}}\left\{-{\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(-\gamma {}_{F_i}^{-}\right)}^p{\left(-\gamma {}_{F_j}^{-}\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}\right)}^{\frac{1}{p+q}}\right\}\right.〉.\hfill \end{array}$$

Thus, Theorem 3 holds.

Proof of Theorem 4

Proof

Since $w_i\left(\mu ,N\right)={\left(\frac{1}{n},\frac{1}{n},...,\frac{1}{n}\right)}^T$, then according to Eq. (14), we have

$$HBN-SNWB{M}^{p,q}\left({\widehat{H}}_i\right)={\left(\sum _{\underset{i\ne j}{i,j=1}}^n\frac{w_i\left(\mu ,N\right)w_j\left(\mu ,N\right)}{1-w_i\left(\mu ,N\right)}\left({\widehat{H}}_i^p\otimes {\widehat{H}}_j^q\right)\right)}^{\frac{1}{p+q}}={\left(\sum _{\underset{i\ne j}{i,j=1}}^n\frac{\left(\frac{1}{n}\right)\left(\frac{1}{n}\right)}{1-\left(\frac{1}{n}\right)}\left({\widehat{H}}_i^p\otimes {\widehat{H}}_j^q\right)\right)}^{\frac{1}{p+q}}$$

$\Rightarrow {\left(\sum _{\underset{i\ne j}{i,j=1}}^n\frac{1}{n\left(n-1\right)}\left({\widehat{H}}_i^p\otimes {\widehat{H}}_j^q\right)\right)}^{\frac{1}{p+q}}=HBN-B{M}^{p,q}\left({\widehat{H}}_i\right)$.$\square$.

Proof of Theorem 5

Proof

Since ${\widehat{H}}_i=\widehat{H}$ for all i, we have

$$HBN-SNWB{M}^{p,q}\left({\widehat{H}}_i\right)={\left(\sum _{\underset{i\ne j}{i,j=1}}^n\frac{w_i{w}_j}{1-w_i}\left({\widehat{H}}_i^p\otimes {\widehat{H}}_j^q\right)\right)}^{\frac{1}{p+q}}$$

$$={\left(\sum _{\underset{i\ne j}{i,j=1}}^n\frac{w_i{w}_j}{1-w_i}\left({\widehat{H}}^p\otimes {\widehat{H}}^q\right)\right)}^{\frac{1}{p+q}}\Rightarrow {\left(\sum _{\underset{i\ne j}{i,j=1}}^n\frac{w_i{w}_j}{1-w_i}\left({\widehat{H}}^{p+q}\right)\right)}^{\frac{1}{p+q}}$$

$=\widehat{H}{\left(\sum _{\underset{i\ne j}{i,j=1}}^n\frac{w_i{w}_j}{1-w_i}\right)}^{\frac{1}{p+q}}\Rightarrow \widehat{H}$.

Hence, the proof of Theorem 5 is completed.

Proof of Theorem 6

Proof

Since ${\tilde{\widehat{H}}}_i$ be any permutation of ${\widehat{H}}_i$, then

${\left(\sum _{\underset{i\ne j}{i,j=1}}^n\frac{w_i{w}_j}{1-w_i}\left({\tilde{\widehat{H}}}_i^p\otimes {\tilde{\widehat{H}}}_j^q\right)\right)}^{\frac{1}{p+q}}={\left(\sum _{\underset{i\ne j}{i,j=1}}^n\frac{w_i{w}_j}{1-w_i}\left({\widehat{H}}_i^p\otimes {\widehat{H}}_j^q\right)\right)}^{\frac{1}{p+q}}$.

Thus,

$$HBN-SNWB{M}^{p,q}\left({\tilde{\widehat{H}}}_i\right)=HBN-SNWB{M}^{p,q}\left({\widehat{H}}_i\right)$$

then it proves the Theorem 6.

Proof of Theorem 7

Proof

(1) For the truth-function part of positive bipolar

Since $h_{T_i}^{+}\le h_{T_i}^{+\ast }$ and $h_{T_j}^{+}\le h_{T_j}^{+\ast }$ for all i and j with $p,q>0$, then for the lower bound of truth membership function, we have

${\left(\gamma {}_{T_i}^{+}\right)}^p\le {\left(\gamma {}_{T_i}^{+\ast }\right)}^p,{\left(\gamma {}_{T_j}^{+}\right)}^q\le {\left(\gamma {}_{T_j}^{+\ast }\right)}^q$.

Hence,

$$1-{\left(\gamma {}_{T_i}^{+}\right)}^p{\left(\gamma {}_{T_j}^{+}\right)}^q\ge 1-{\left(\gamma {}_{T_i}^{+\ast }\right)}^p{\left(\gamma {}_{T_j}^{+\ast }\right)}^q$$

$$\Rightarrow \prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(\gamma {}_{T_i}^{+}\right)}^p{\left(\gamma {}_{T_j}^{+}\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}\ge \prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(\gamma {}_{T_i}^{+\ast }\right)}^p{\left(\gamma {}_{T_j}^{+\ast }\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}$$

$$\Rightarrow 1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(\gamma {}_{T_i}^{+}\right)}^p{\left(\gamma {}_{T_j}^{+}\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}\le 1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(\gamma {}_{T_i}^{+\ast }\right)}^p{\left(\gamma {}_{T_j}^{+\ast }\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}$$

$$\Rightarrow {\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left({\gamma }_{T_i}^{+}\right)}^p{\left({\gamma }_{T_j}^{+}\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}\right)}^{\frac{1}{p+q}}\le {\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left({\gamma }_{T_i}^{+\ast }\right)}^p{\left({\gamma }_{T_j}^{+\ast }\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}\right)}^{\frac{1}{p+q}}$$

$\Rightarrow 1-{\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(\gamma {}_{T_i}^{+}\right)}^p{\left(\gamma {}_{T_j}^{+}\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}\right)}^{\frac{1}{p+q}}\le 1-{\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(\gamma {}_{T_i}^{+\ast }\right)}^p{\left(\gamma {}_{T_j}^{+\ast }\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}\right)}^{\frac{1}{p+q}}$.

(2) For the indeterminacy-function part of positive bipolar

Since ${\gamma }_{I_i}^{+}\le \gamma {}_{I_i}^{+\ast }$ for all i and ${\gamma }_{I_j}^{+}\le \gamma {}_{I_j}^{+\ast }$ for all j and $p,q>0$, hence we have

${\left(1-{\gamma }_{I_i}^{+}\right)}^p\ge {\left(1-{\gamma }_{I_i}^{+\ast }\right)}^p$,${\left(1-{\gamma }_{I_j}^{+}\right)}^q\ge {\left(1-{\gamma }_{I_j}^{+\ast }\right)}^q$

$$\Rightarrow {\left(1-{\gamma }_{I_i}^{+}\right)}^p{\left(1-{\gamma }_{I_j}^{+}\right)}^q\ge {\left(1-{\gamma }_{I_i}^{+\ast }\right)}^p{\left(1-{\gamma }_{I_j}^{+\ast }\right)}^q$$

$$\Rightarrow 1-{\left(1-{\gamma }_{I_i}^{+}\right)}^p{\left(1-{\gamma }_{I_j}^{+}\right)}^q\le 1-{\left(1-{\gamma }_{I_i}^{+\ast }\right)}^p{\left(1-{\gamma }_{I_j}^{+\ast }\right)}^q$$

$$\Rightarrow \prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(1-{\gamma }_{I_i}^{+}\right)}^p{\left(1-{\gamma }_{I_j}^{+}\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}\le \prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(1-{\gamma }_{I_i}^{+\ast }\right)}^p{\left(1-{\gamma }_{I_j}^{+\ast }\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}$$

$$\Rightarrow 1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(1-{\gamma }_{I_i}^{+}\right)}^p{\left(1-{\gamma }_{I_j}^{+}\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}\ge 1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(1-{\gamma }_{I_i}^{+\ast }\right)}^p{\left(1-{\gamma }_{I_j}^{+\ast }\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}$$

$\Rightarrow 1-{\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(1-{\gamma }_{I_i}^{+}\right)}^p{\left(1-{\gamma }_{I_j}^{+}\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}\right)}^{\frac{1}{p+q}}\le$$1-{\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(1-{\gamma }_{I_i}^{+\ast }\right)}^p{\left(1-{\gamma }_{I_j}^{+\ast }\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}\right)}^{\frac{1}{p+q}}$.

(3) For the falsity-function part of positive bipolar.

Since $\gamma {}_{F_i}^{+}\ge \gamma {}_{F_i}^{+\ast }$ for all i and $\gamma {}_{F_j}^{+}\ge \gamma {}_{F_j}^{+\ast }$ for all j and $p,q>0$, therefore we have

${\left(1-\gamma {}_{F_i}^{+}\right)}^p\le {\left(1-\gamma {}_{F_i}^{+\ast }\right)}^p$,${\left(1-\gamma {}_{F_j}^{+}\right)}^q\le {\left(1-\gamma {}_{F_j}^{+\ast }\right)}^q$

$$\Rightarrow {\left(1-\gamma {}_{F_i}^{+}\right)}^p{\left(1-\gamma {}_{F_j}^{+}\right)}^q\le {\left(1-\gamma {}_{F_i}^{+\ast }\right)}^p{\left(1-\gamma {}_{F_j}^{+\ast }\right)}^q$$

$$\Rightarrow 1-{\left(1-\gamma {}_{F_i}^{+}\right)}^p{\left(1-\gamma {}_{F_j}^{+}\right)}^q\ge 1-{\left(1-\gamma {}_{F_i}^{+\ast }\right)}^p{\left(1-\gamma {}_{F_j}^{+\ast }\right)}^q$$

$$\Rightarrow \prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(1-\gamma {}_{F_i}^{+}\right)}^p{\left(1-\gamma {}_{F_j}^{+}\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}\ge \prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(1-\gamma {}_{F_i}^{+\ast }\right)}^p{\left(1-\gamma {}_{F_j}^{+\ast }\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}$$

$$\Rightarrow 1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(1-\gamma {}_{F_i}^{+}\right)}^p{\left(1-\gamma {}_{F_j}^{+}\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}\le 1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(1-\gamma {}_{F_i}^{+\ast }\right)}^p{\left(1-\gamma {}_{F_j}^{+\ast }\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}$$

$\Rightarrow 1-{\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(1-\gamma {}_{F_i}^{+}\right)}^p{\left(1-\gamma {}_{F_j}^{+}\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}\right)}^{\frac{1}{p+q}}\ge$$1-{\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(1-\gamma {}_{F_i}^{+\ast }\right)}^p{\left(1-\gamma {}_{F_j}^{+\ast }\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}\right)}^{\frac{1}{p+q}}$.

(4) For the negative bipolar

With similar proving, the proof for truth-function, indeterminacy-function and falsity-function parts of negative bipolar can be obtained as below:

$$-\left(1-{\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(1-\left(-\gamma {}_{T_i}^{-}\right)\right)}^p{\left(1-\left(-\gamma {}_{T_j}^{-}\right)\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}\right)}^{\frac{1}{p+q}}\right)\ge$$

$-\left(1-{\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(1-\left(-\gamma {}_{T_i}^{-\ast }\right)\right)}^p{\left(1-\left(-\gamma {}_{T_j}^{-\ast }\right)\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}\right)}^{\frac{1}{p+q}}\right)$,

$-{\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(-{\gamma }_{I_i}^{-}\right)}^p{\left(-\gamma {}_{I_j}^{-}\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}\right)}^{\frac{1}{p+q}}\ge -{\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(-\gamma {}_{I_i}^{-\ast }\right)}^p{\left(-\gamma {}_{I_j}^{-\ast }\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}\right)}^{\frac{1}{p+q}}$ and $-{\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(-\gamma {}_{F_i}^{-}\right)}^p{\left(-\gamma {}_{F_j}^{-}\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}\right)}^{\frac{1}{p+q}}\le -{\left(1-\prod _{\underset{i\ne j}{i,j=1}}^n{\left(1-{\left(-\gamma {}_{F_i}^{-\ast }\right)}^p{\left(-{\gamma }_{F_j}^{-\ast }\right)}^q\right)}^{\frac{w_i{w}_j}{1-w_i}}\right)}^{\frac{1}{p+q}}$.

(5) Comparing $HBN-SNWB{M}^{p,q}\left({\widehat{H}}_i\right)$ with $HBN-SNWB{M}^{p,q}\left({\widehat{H}}_i^{\ast }\right)$.

Let ${\widehat{H}}_i=〈h_{T_i}^{+},h_{I_i}^{+},h_{F_i}^{+},h_{T_i}^{-},h_{I_i}^{-},h_{F_i}^{-}〉=HBN-SNWB{M}^{p,q}\left({\widehat{H}}_i\right)$ and ${\widehat{H}}_i^{\ast }=〈h_{T_i}^{+\ast },h_{I_i}^{+\ast },h_{F_i}^{+\ast },h_{T_i}^{-\ast },h_{I_i}^{-\ast },h_{F_i}^{-\ast }〉=HBN-SNWB{M}^{p,q}\left({\widehat{H}}_i^{\ast }\right)$. Since $h_1\subseteq h_2$, if and only if $\forall \gamma {}_{T_1}^{+}\le \forall \gamma {}_{T_2}^{+},$ $\forall \gamma {}_{I_1}^{+}\le \forall \gamma {}_{I_2}^{+},$ $\forall \gamma {}_{F_1}^{+}\ge \forall \gamma {}_{F_2}^{+}$ and $\forall \gamma {}_{T_1}^{-}\le \forall \gamma {}_{T_2}^{-},$ $\forall \gamma {}_{I_1}^{-}\le \forall \gamma {}_{I_2}^{-},$ $\forall \gamma {}_{F_1}^{-}\ge \forall \gamma {}_{F_2}^{-}$ for all $x\in X$, then $\widehat{H}\le {\widehat{H}}^{\ast }$, i.e., $HBN-SNWB{M}^{p,q}\left({\widehat{H}}_i\right)\le HBN-SNWB{M}^{p,q}\left({\widehat{H}}_i^{\ast }\right)$.

Proof of Theorem 8

Proof

Since ${\widehat{H}}_i\ge {\widehat{H}}^{-}$, we have

$HBN-SNWB{M}^{p,q}\left({\widehat{H}}_i\right)\ge HBN-SNWB{M}^{p,q}\left({\widehat{H}}^{-},{\widehat{H}}^{-},...,{\widehat{H}}^{-}\right)={\widehat{H}}^{-}$.

Similarly, we can obtain

$HBN-SNWB{M}^{p,q}\left({\widehat{H}}_i\right)\le HBN-SNWB{M}^{p,q}\left({\widehat{H}}^{+},{\widehat{H}}^{+},...,{\widehat{H}}^{+}\right)={\widehat{H}}^{+}$.

Then,

${\widehat{H}}^{-}\le HBN-SNWB{M}^{p,q}\left({\widehat{H}}_i\right)\le {\widehat{H}}^{+}$ holds.

Then, the proof of the Theorem 8 is completed.

Data availability

The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.

Declarations

Conflict of interest

The authors declare that they have no conflict of interest.