THE INFLUENCE OF MOLECULAR STRUCTURE ON PFAS ADSORPTION AT AIR-WATER INTERFACES IN ELECTROLYTE SOLUTIONS

Abstract

Interfacial adsorption has been demonstrated to be an important retention process for per and polyfluoroalkyl substances (PFAS) in porous media with air or non-aqueous phase liquids (NAPLs) present. The objective of this study was to characterize the influence of PFAS molecular structure on air-water interfacial adsorption in electrolyte solutions. Measured and literature-reported surface-tension data sets were aggregated to generate the largest compilation of interfacial adsorption coefficients measured in aqueous solutions comprising environmentally representative ionic strengths. The surface activities and interfacial adsorption coefficients (K_i) exhibited chain length trends, with greater surface activities and larger K_i values corresponding to longer chain length. The impact of multiple-component PFAS solutions on the surface activity of a select PFAS was a function of the respective surface activities and concentrations. Quantitative structure-property relationship analysis (QSPR) employing a single molecular descriptor (molar volume) was used successfully to characterize the impact of PFAS molecular structure on air-water interfacial adsorption. A previously reported QSPR model based on PFAS data generated for deionized-water solutions was updated to include more than 60 different PFAS, comprising all head-group types and a wide variety of tail structures. The QSPR model developed for PFAS in electrolyte solution compared favorably to the model developed for deionized water. Additionally, the magnitude of ionic strength for non-zero ionic strength systems was determined to have relatively minimal impact on interfacial adsorption coefficients. The new QSPR model is therefore anticipated to be representative for a wide variety of PFAS and for a wide range of ionic compositions.

1. Introduction

Adsorption to fluid-fluid interfaces is an important retention mechanism to consider for per and polyfluoroalkyl substances (PFAS). Numerous surfactant-science studies reporting surface-tension measurements have demonstrated the strong air-water interfacial activity of PFAS (e.g., Hendricks, 1953; Downes et al., 1995; López-Fontán et al., 2005; Lunkenheimer et al., 2015). Brusseau and colleagues have demonstrated with modeling and miscible-displacement transport experiments that air-water interfacial adsorption is a significant retention mechanism for PFAS transport in unsaturated porous media (Brusseau, 2018; Lyu et al., 2018; Brusseau et al., 2019; Brusseau, 2020; Lyu and Brusseau, 2020; Guo et al., 2020; Yan et al., 2020). For example, Lyu et al. (2018) determined that air-water interfacial adsorption contributed approximately 50–75% of total retention for PFOA transport in unsaturated sand. Similarly, recent modeling and transport studies have demonstrated that adsorption at interfaces between non-aqueous phase liquid (NAPL) and water can serve as an additional PFAS retention process (Brusseau, 2018; Brusseau et al., 2019; Van Glubt and Brusseau, 2021). For example, PFOS adsorption to the decane-water interface contributed to more than 70% of the total retention for PFOS transport in a sand containing residual decane NAPL (Brusseau et al., 2019).

Understanding and quantifying the fluid-fluid interfacial adsorption of PFAS is crucial to characterizing PFAS transport, conducting accurate risk assessments, and developing effective mitigation and remedial-action plans. Brusseau (2018) discussed the many factors that can influence fluid-fluid interfacial adsorption of PFAS in porous-media systems. One such factor is the ionic strength of the aqueous solution. The impact of ionic strength on the surface/interfacial activity of PFAS has long been established in the field of surfactant science through surface-tension measurements (e.g., Talbot, 1959; Shinoda and Nakayama, 1963; Downes et al., 1995; An et al., 1996; López-Fontán et al., 2005). The influence of ionic strength on air-water interfacial adsorption and transport of PFAS in unsaturated porous media was recently demonstrated in a series of miscible-displacement experiments (Lyu and Brusseau, 2020).

Surfactant-science studies typically employ single-salt solutions, whereas soil pore-water comprises a mixture of salts consisting of both monovalent and divalent ions. The interfacial activity of PFAS is influenced by the ionic composition as well as ionic strength of the solution (Brusseau and Van Glubt, 2019). Hence, it is important to measure PFAS activities and interfacial adsorption coefficients (K_i) in aqueous solutions whose compositions are representative of natural subsurface systems. Surface-tension data for PFAS in electrolyte solutions that more closely reflect actual soil pore-water characteristics have been reported in recent environmental-focused studies (Brusseau et al., 2019; Brusseau and Van Glubt, 2019; Costanza et al., 2019; Silva et al., 2019). These studies all employed synthetic groundwater (SGW) solutions comprised of multiple monovalent and divalent salts. As would be expected, surface activities of PFAS measured in the SGW solutions were greater than those measured in deionized water. These studies employed different solution compositions, and it would be informative to compare the data sets to further evaluate ionic-composition effects.

As previously discussed, surface activity and interfacial adsorption coefficients need to be quantified to characterize PFAS retention and transport. However, measuring interfacial adsorption coefficients for each of the thousands of PFAS in existence is impractical. As an alternative, quantitative-structure/property-relationship (QSPR) models provide empirical-based functions for estimating compound properties based on molecular structure. Brusseau and colleagues have demonstrated the utility of using QSPR analyses for characterizing the fluid-fluid interfacial adsorption of PFAS and predicting interfacial adsorption coefficients (Lyu et al., 2018; Brusseau, 2019; Brusseau and Van Glubt, 2019).

The objective of this study is to characterize the influence of molecular structure on air-water interfacial adsorption of PFAS in aqueous solutions comprising environmentally representative ionic strengths. Surface tensions are measured for several PFAS in a 0.01 M synthetic groundwater solution and a 0.01 M NaCl reference solution. In addition, surface-tension data measured in environmentally representative ionic-strength solutions are compiled from the literature. Interfacial adsorption coefficients are determined from the measured and literature-reported surface-tension data. The data are evaluated through QSPR analysis and the impacts of solution ionic strength and composition on interfacial adsorption coefficients are evaluated. A previously reported QSPR model based on PFAS data generated for deionized-water solutions is updated to include more than 60 different PFAS, comprising all headgroup types and a wide variety of tail structures. The QSPR model developed for PFAS in electrolyte solution is compared to the model developed for deionized water.

2. Materials and Methods

2.1. Materials

Perfluorobutanoic acid (PFBA; CAS# 375–22-4, 98%) and perfluorobutane sulfonic acid (PFBS; CAS# 375–73-5, 98% purity) were purchased from TCI America. Perfluorooctanoic acid (PFOA; CAS# 335–67-1, 98%) was purchased from AIKE Reagent. Sodium perfluorooctanoate (Na-PFOA; CAS# 335–95-5, 97%) was purchased from Manchester Organics. Potassium perfluorooctane sulfonate (K-PFOS; CAS# 1763–23-1, 98%) was purchased from Matrix Scientific. Perfluorohexanoic acid (PFHxA; CAS# 307–24-4, 97%), perfluoroheptanoic acid (PFHpA; CAS#375–85-9, 99%), potassium perfluorohexane sulfonate (K-PFHxS; CAS# 3871–99-6, >98%), and perfluorooctane sulfonic acid (PFOS; CAS# 1763–23-1, 98%), were purchased from Sigma Aldrich.Perfluorononanoic acid (PFNA; CAS#375–95-1, 97%) was purchased from Shanghai Macklin Biochemical Co., Ltd. Perfluorodecanoic acid (PFDA; CAS#335–76-2, 98%) was purchased from Shanghai Aladdin Biochemical Technology Co., Ltd.

All background solutions were prepared with distilled, deionized water. Measurements were conducted with background solutions of 0.01 M NaCl or SGW. The SGW pH is 7.7 and ionic strength is 0.01 M, and it is comprised of the cations (concentration in mg/L) Na⁺¹ (50), Ca⁺² (36), and Mg⁺² (25), and anions NO₃⁻¹ (6), Cl⁻¹ (60), CO₃⁻²/HCO₃⁻¹ (133), and SO₄⁻² (99).

2.2. Methods

Surface tensions were measured for aqueous solutions of the selected PFAS to determine adsorption to the air-water interface. Measurements were conducted for individual compounds and some compound mixtures. Standard methods were followed using either a Fisher Scientific Surface Tensiomat 21 with a Du Nouy ring or a Biolin Scientific Sigma 701 precision force tensiometer using a Wilhelmy plate or Du Nouy ring. Comparisons of data collected for the same aqueous solutions using both instruments yielded consistent results. Solutions were prepared with a stock solution of the highest concentration to be measured, followed by dilutions to create subsequently lower concentrations. An automated method was employed for some measurements with the Sigma 701, where the software automatically controlled the addition of stock solution to the initial zero concentration solution to measure the entire concentration range. A minimum of 3–5 measurements were collected for each sample concentration. This constitutes one complete measurement set. Multiple sets were measured for the same PFAS over a period of 2–3 years to test for reproducibility. All measurements were conducted at room temperature (25±1 °C). The tensiometers were regularly calibrated with known masses and deionized water samples were regularly measured for surface tension to ensure proper instrument calibration.

Surface-tension data were aggregated from literature sources to combine with the measurements reported in the present study. A list of the literature data sets included in this work for electrolyte solutions is provided in Table 1. Additional surface-tension data sets were also collected from the literature for deionized-water systems to update the original QSPR model of Brusseau (2019). The additional data sources include the following: Boutevin et al., 2012; Hill et al., 2018; Lin et al., 2018a, 2018b; Ngo et al., 2010; Padoan et al., 2015; Rodriguez et al., 2001; Shen et al., 2018; Tadros, 1980; Wang et al., 2012; Yan et al., 2020; Zhai et al., 2019. The surface-tension data set of Ngo et al. (2010) was reported for an elevated temperature, and was temperature corrected based on the measurements reported by Tadros (1980). The literature data were digitized using the open-source Engauge program (Mitchell et al., 2017).

Table 1.

Experiments and literature data corresponding to solution molarity at or near 0.01 M included in this study

Analyte	Background Solutiona	Source
H-PFBA	0.01 M NaCl	This study
Na-PFPeA	0.01 M NaCl 0.01 M SGW	Brusseau and Van Glubt, 2019
H-PFHxA	0.01 M NaCl	This study
H-PFHpA	0.01 M NaCl	This study
H-PFOA	0.01M NaCl 0.01 M SGW	This study
Na-PFOA	0.01 M NaCl 0.01 M SGW	Brusseau and Van Glubt, 2019 & This study
H-PFNA	0.01 M NaCl	This study
H-PFDA	0.01 M NaCl	This study
H-PFTDA	0.01 M SGW	Brusseau and Van Glubt, 2019
NH4-GenX H-GenX	0.01 M NaCl 0.01 M SGW	Yan et al., 2020
H-PFBS	0.01 M SGW	This study
K-PFHxS	0.01 M SGW	This study
H-PFOS	0.01 M NaCl 0.01 M SGW	Brusseau and Van Glubt, 2019 & This study
K-PFOS	0.01 M NaCl 0.01 M SGW	Brusseau and Van Glubt, 2019 & This study
H-PFOS	0.01 M NaCl + 0.1 mg/L each PFBA, PFOA, PFTDA	This study
Na-PFPeA	DIW + 1 mg/L each Na-PFPeA, K-PFOS, PFTDA	This study
Na-PFOA	DIW + 1 mg/L each Na-PFPeA, K-PFOS, PFTDA	This study
K-PFOS	DIW + 1 mg/L each Na-PFPeA, K-PFOS, PFTDA	This study
PFTDA	DIW + 1 mg/L each Na-PFPeA, K-PFOS, PFTDA	This study
H-PFPeA	0.006 M SGW 0.023 M SGW	Silva et al., 2019
H-PFHxA	0.006 M SGW 0.023 M SGW	Silva et al., 2019
H-PFHpA	0.006 M SGW 0.023 M SGW	Silva et al., 2019
H-PFOA	0.006 M SGW 0.023 M SGW	Silva et al., 2019
H-PFOA	0.0125 M SGW 0.0375 M SGW	Costanza et al., 2019
H-PFNA	0.006 M SGW 0.023 M SGW	Silva et al., 2019
H-PFDA	0.006 M SGW 0.023 M SGW	Silva et al., 2019
K-PFBS	0.006 M SGW 0.023 M SGW	Silva, 2020
K-PFHxS	0.006 M SGW 0.023 M SGW	Silva, 2020
K-PFOS	0.0125 M SGW 0.0375 M SGW	Costanza et al., 2019
K-PFOS	0.006 M SGW 0.023 M SGW	Silva, 2020
SDS	0.01 M NaCl	This study
CTAB	0.01 M NaCl	Nakahara et al., 2011
Triton X45	0.01 M NaCl	Fainerman et al., 2009
CAPB	0.01 M NaCl	Staszak et al., 2015

^aSGW is synthetic groundwater and DIW is deionized water

2.3. Data Analysis

A summary of the data analysis is included here. Further details of the data analysis methods are included in the prior studies (Brusseau, 2019; Brusseau and Van Glubt, 2019; Brusseau, 2021). The Gibbs adsorption equation was used to calculate the surface excess Γ (mol/cm²) from the surface-tension function:

$$\Gamma =\frac{-1}{\text{xRT}}\frac{\partial \gamma }{\partial \mathit{lnC}}$$ (1)

where R is the universal gas constant (dyne-cm/mol °K), T is temperature (°K), γ is the surface tension (dyne/cm or mN/m), C is the aqueous concentration (mol/cm³), and x is a coefficient equal to 1 for nonionic surfactants or for ionic surfactants with excess solution electrolyte, and equal to 2 for ionic surfactants without excess solution electrolyte. The air-water interfacial adsorption coefficient (K_i; cm) was then determined as a function of concentration:

$$K_i=\frac{\Gamma }{C}=\frac{-1}{\text{xRT C}}\frac{\partial \gamma }{\partial \mathit{lnC}}$$ (2)

where the K_i can be quantified for any fluid-fluid system of interest, such as air-water or NAPL water.

The Szyszkowski equation was applied to all data sets to provide a uniform data-analysis method, and is represented by (e.g., Barnes and Gentle, 2011):

$$\gamma ={\gamma }_0\left[1-b\ln \left(1+\frac{C}{a}\right)\right]$$ (3)

where γ₀ is the surface tension when analyte aqueous solution concentration is zero, a (mol/cm³) is a parameter related to properties of the individual surfactant, and b is a parameter related to properties of the homologous series. Combining the differentiated form of equation 3 with equation 1 produces the Szyszkowski-Langmuir equation (e.g., Barnes and Gentle, 2011), which can be written in different forms to elucidate parameter identities:

$$\Gamma ={\gamma }_{0}b/RT\left(\frac{C}{C+a}\right)={\Gamma }_m\left(\frac{K_{L}C}{1+K_{L}C}\right)$$ (4)

where Γ_m is the maximum surface excess (=γ₀b/RT) and K_L is the Langmuir adsorption coefficient (a = 1/K_L). The “a” parameter is a function of the free energy of adsorption from solution. Combining equations 2 and 4 produces:

$$K_i=\frac{{\Gamma }_m}{C+a}$$ (5)

Equation 5 highlights the nonlinearity of K_i as a function of aqueous concentration, and that it approaches a constant maximum value at lower concentrations (C<<a). The K_i values were calculated corresponding to concentrations sufficiently low (i.e., 0.1 mg/L or lower) to represent essentially maximum values, as discussed in our prior studies (Brusseau, 2019; Brusseau and Van Glubt, 2019; Brusseau, 2021).

A full description of the QSPR methods used for the analyses are included in Brusseau (2019). Molar volume (V_m, cm³/mol) is used as the single molecular descriptor for the QSPR analysis. This is the same descriptor employed by Brusseau (2019) and Brusseau and Van Glubt (2019). Molar volumes were determined from reported measured values where available, or calculated using molecular weight and reported densities. A standard group-contribution analysis approach, employing the Schroeder (Baum, 1998) or Fedors (1974) method was used to calculate molar volumes for those compounds for which densities were unavailable. The latter method was employed for the zwitterionic PFAS to account for the presence of more complex functional groups.

3. Results and Discussion

3.1. Measured Surface Tensions

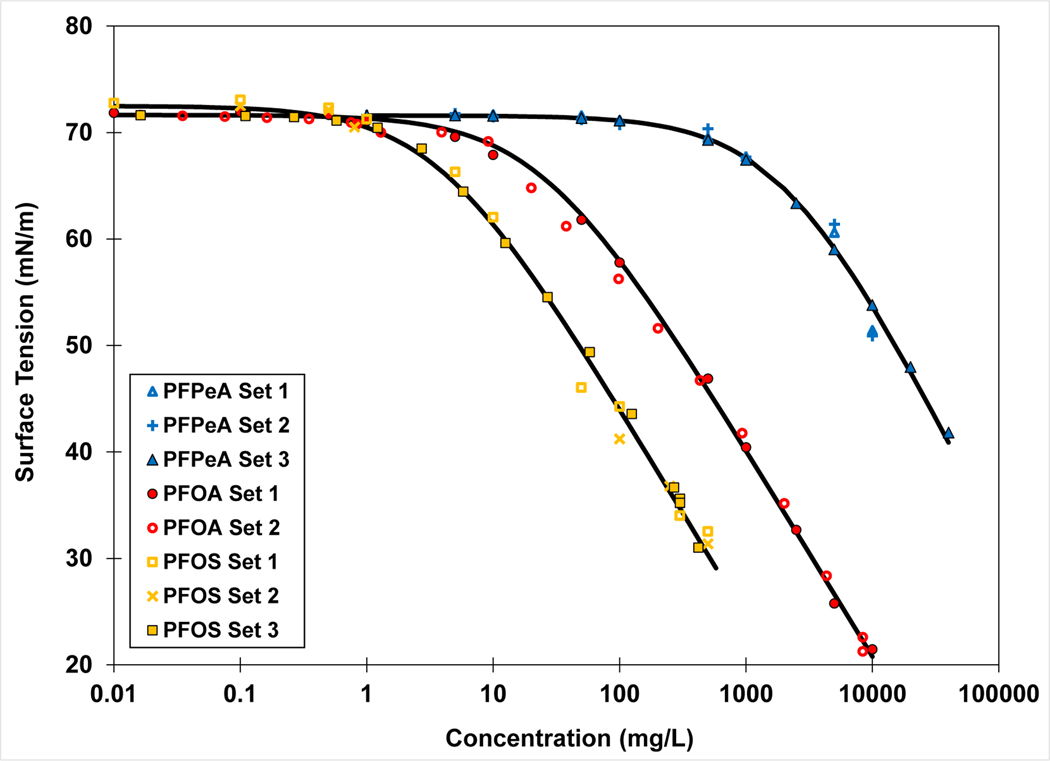
Measured surface tensions and fitted Szyszkowski functions for representative PFCAs and PFSAs are presented in Figures 1 and 2. The magnitudes of the surface activities are a function of chain length as expected. Greater surface activity is observed for compounds with longer chain lengths, with the decline in surface tension corresponding to lower concentrations compared to compounds of shorter chain length. This behavior is a manifestation of the greater hydrophobicity of longer carbon chains (e.g., Hendricks, 1953; Tamaki et al., 1989; Meissner et al., 1992; Campbell et al., 2009; Lunkenheimer et al., 2015). Good reproducibility is generally observed for the replicate measurement sets.

Figure 1.

Surface tension measurements and fitted Szyszkowski functions for Na-PFPeA, Na-PFOA, and K-PFOS in synthetic groundwater.

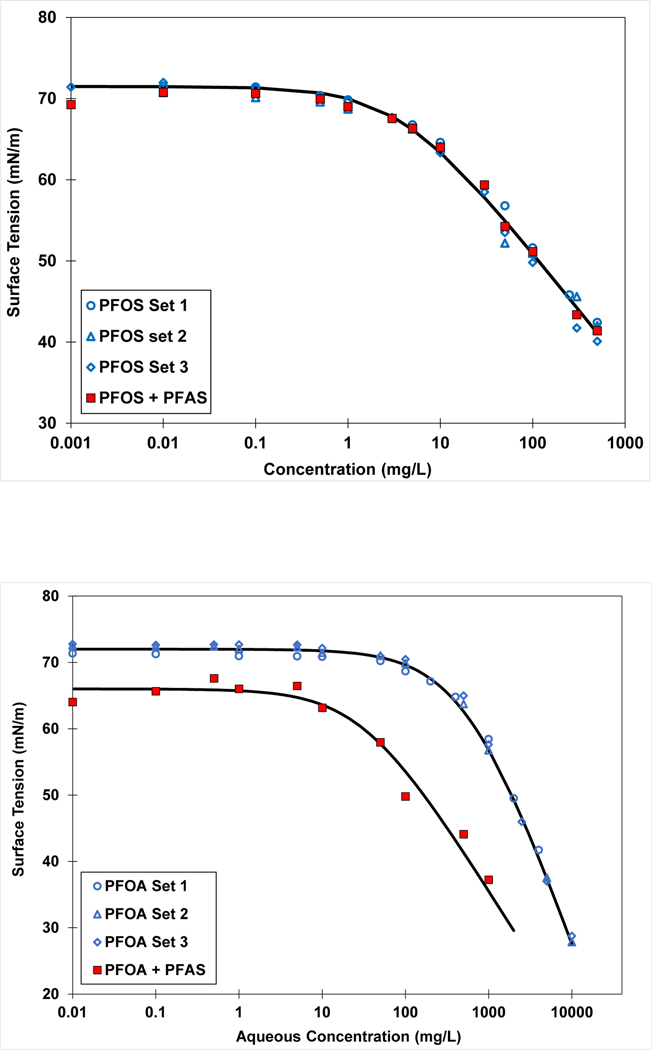
Figure 2.

Surface tensions for single and multiple-component solutions of PFAS. The solid curves represent Szyszkowski fits to the data. Top: Data for PFOS in 0.01 M NaCl solution. PFOS+PFAS solution contains 0.1 mg/L each of PFBA, PFOA, and PFTDA. Bottom: Data for Na-PFOA in deionized water solution. PFOA+PFAS solution contains 1mg/L each of Na-PFPeA, K-PFOS, and PFTDA.

PFAS-contaminated media generally contain mixtures of PFAS compounds. Therefore, understanding the adsorption behavior of mixtures is highly relevant to environmental systems. The impact of additional PFAS on the surface tension of PFOS was examined for a solution containing 0.1 mg/L each of PFBA, PFOA, and PFTDA in 0.01 M NaCl (Figure 2, Top). The results show that the surface-tension function for PFOS in the multiple-component solution is coincident with those of PFOS alone. The mean K_i value determined from the three individual surface-tension measurements is 0.033 (0.026–0.04) cm for a target concentration of 0.01 mg/L. The K_i value for PFOS in the multiple-component solution is 0.027 cm, which is within the 95% confidence interval of the PFOS-alone values. Consistent PFOS K_i values between the single and multiple-component solutions were also obtained for target concentrations of 0.1, 1, and 10 mg/L. These results indicate that the presence of relatively low concentrations of other PFAS had no measureable impact on PFOS activity and air-water interfacial adsorption.

Surface tensions were measured for another four-component mixture comprising Na-PFPeA, Na-PFOA, K-PFOS, and PFTDA in deionized water. Four sets of surface tensions were measured in this case, with concentration varying for one while the others remained at a constant background concentration of 1 mg/L each. An example data set is presented in Figure 2 (Bottom). The surface tensions for Na-PFOA are observed to be depressed at lower concentrations, resulting from the presence of relatively high concentrations of the other PFAS. Similar maximum K_i values were determined for K-PFOS for both the single-solute and multiple-component solutions. This indicates that there was no measurable impact of the other PFAS, consistent with the prior data set. Conversely, the maximum K_i value for Na-PFOA was 0.0024 cm for the multiple-component solution versus 0.00023 cm for the single-solute solution. Thus, the presence of the other PFAS had a significant impact on the K_i for Na-PFOA. The difference in impacts observed for PFOS and PFOA are consistent with the relative surface activities of the two (Vecitis et al., 2008; Brusseau and Van Glubt, 2019).

3.2. QSPR Analysis of Air-Water Interfacial Adsorption Coefficients

The QSPR analysis by Brusseau (2019) employed air-water (and a few NAPL-water) data sets with solutions of deionized water. The QSPR analysis by Brusseau and Van Glubt (2019) primarily used air-water data sets with solutions of deionized water, 0.01 M NaCl, and SGW. The data sets included in the present QSPR analysis all correspond to air-water systems with electrolyte solutions at or near 0.01 M. Specifically, the data comprise (1) PFAS and hydrocarbon surfactants for 0.01 NaCl, and (2) PFAS for 0.006 and 0.01 M SGW. The data sets employed in the analysis are listed in Table 1. The data from the multiple-component PFAS systems were not included in the QSPR analysis.

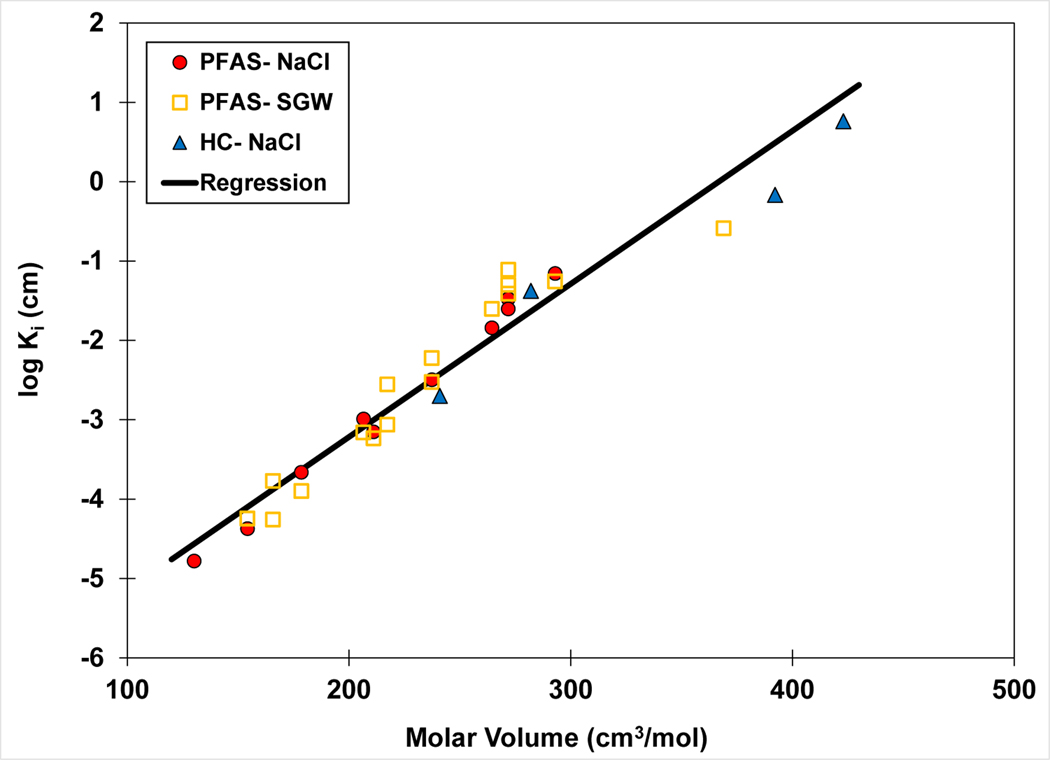
The results of the QSPR analysis are shown in Figure 3, including K_i values from this study and those calculated from the literature data. The V_m values span almost 300 cm³/mol and the K_i values span more than five log units. The QSPR regression has an r² of 0.946, indicating the analysis provides a good representation of the data despite differences in solution ionic strength and ion composition between the data sets. These results indicate that the molar-volume QSPR model has the potential to provide robust estimates of K_i values for PFAS in electrolyte solutions. This potential will be further evaluated below.

Figure 3.

QSPR model for air-water interfacial adsorption coefficient (K_i) versus molar volume. The K_i values are calculated from surface-tension data sets measured in 0.01 M NaCl or 0.006 and 0.01 M synthetic groundwater (SGW) solutions. Note that multiple values are reported for some PFAS. The regression equation is log K_i = 0.019 (±0.002) V_m − 7.1 (±0.45), r² = 0.946.

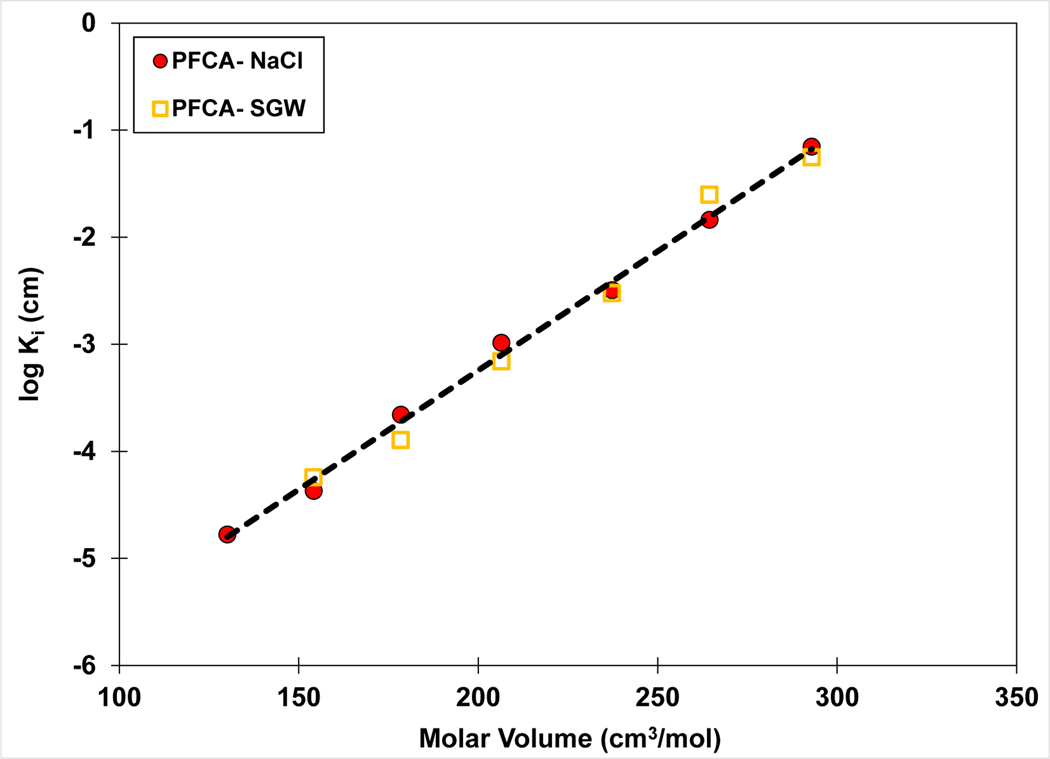
The similarity of K_i values for solutions of 0.01 M NaCl and 0.006 SGW observed in Figure 3 indicates similar PFAS surface activities for the two solutions. This is further demonstrated in Figure 4, wherein data are presented for only the homologous series of PFCAs in the two solutions. Concurrence of K_i values between the lower ionic-strength SGW solution and the higher ionic-strength NaCl solution is consistent with the presence of divalent ions in the SGW and their greater impact on activity (Brusseau and Van Glubt, 2019).

Figure 4.

QSPR model for air-water interfacial adsorption coefficient (K_i) versus molar volume of the C4-C10 homologous series of PFCAs. The K_i values are calculated from surface-tension data sets measured in 0.01 M NaCl or 0.006 M synthetic groundwater (SGW) solutions.

The similarity of K_i values measured for the 0.01 M SGW solution to values measured for the other two solutions indicates that ionic strength has a relatively small impact in this range of ionic strength. This was further tested by calculating K_i values for different ranges of ionic strength at five different PFAS target concentrations (0.01, 0.1, 1, 10, and 100 mg/L). Initially, four ionic-strength ranges were analyzed (<0.01, 0.01, >0.01 to <0.1, and ≥0.1 M). The actual ionic strengths are presented in Table 1. However, due to the nearly identical regressions for different ionic strengths at a given PFAS concentration, the number of ionic-strength ranges was decreased to two for simplicity and ease of comparison. Log K_i values corresponding to solution ionic strengths <0.1 M or ≥0.1 M were regressed with molar volume for each of the different PFAS concentrations. The regressions are essentially identical between the two ionic-strength ranges for a given PFAS target concentration. These results indicate that ionic strength has relatively minimal impact on the magnitude of PFAS interfacial adsorption coefficients for systems with non-zero ionic strength.

The ionic strength of soil pore-water is generally in the range of 0.005–0.01 M, spanning lower and higher values depending upon soil properties and conditions (e.g., Edmeades et al., 1985; Peverill et al., 1999). The ionic strengths for the data sets reported herein are similar to this range and therefore are representative of natural conditions. Additionally, the natural buffering capacity of soils reduces the likelihood of ionic strength changing significantly in a given system (e.g., Helyar and Porter, 1989; Sparks, 2003). Hence, it is anticipated that K_i values will exhibit relatively minimal changes due to solution ionic-strength effects under typical field conditions. The minimal impact of changes in ionic strength on PFAS air-water interfacial adsorption for non-zero ionic-strength systems observed in the present study is consistent with the results of prior surface-tension (Brusseau and Van Glubt, 2019; Silva et al., 2019) and transport studies (Lyu and Brusseau, 2020). These results indicate that the QSPR model presented in Figure 3 is likely to be representative for a broad range of natural pore-water systems with respect to ionic strength and composition.

3.3. Updated QSPR Model for PFAS in Deionized Water

The original QSPR model presented by Brusseau (2019) included air-water interfacial adsorption data for 42 individual PFAS representing anionic, cationic, and nonionic headgroups and a wide variety of tail structures. This data set was updated herein by adding 19 more PFAS, including several zwitterionic and additional cationic PFAS (Table 2). The new additions include PFAS of current significant interest such as precursors and replacements. The revised QSPR model is presented in Figure 5.

Table 2.

PFAS and hydrocarbon surfactants included in the revised QSPR model for deionized-water systems. Table revised from Brusseau (2019).

Acronym	Formula	Perfluorocarboxylates
PFAA	CF3CO2Na	Na-Perfluoroacetoate
PFPrA	C2F5CO2Na	Na-Perfluoropropanoate
PFBA	C3F7CO2Na	Na-Perfluorobutanoate
PFPeA	C4F9CO2Na	Na-Perfluoropentanoate
PFHxA	C5F11CO2Na	Na-Perfluorohexanoate
PFHpA	C6F13CO2Na	Na-Perfluoroheptanoate
PFOA	C7F15CO2Na	Na-Perfluorooctanoate
PFNA	C8F17CO2Na	Na-Perfluorononanoate
PFDA	C9F19CO2Na	Na-Perfluorodecanoate
PFUnA	C10F21CO2Na	Na-Perfluoroundecanoate
PFTDA	C12F25CO2H	H-Perfluorotridecanoic acid
		Branched PFCAs
Iso-PFOA	(CF3)2CF(CF2)4CO2Na	Na perfluoro-methyl-heptanoate
Iso-PFDA	(CF3)2CF(CF2)6CO2Na	Na-perfluoro-methyl-nonanoate
		Perfluorosulfonates
PFBS	C4F9SO3K	K-Perfluorobutanesulfonate
PFHxS	C6F13SO3K	K-Perfluorohexanesulfonate
PFHpS	C7F15SO3K	Na-Perfluoroheptanesulfonate
PFOS	C8F17SO3K	K-Perfluorooctanesulfonate
PFNS	C9F19SO3K	K-Perfluorononanesulfonate
		Polyfluoroalkyls
9H-PFNA	C8HF16CO2Na	Na-9H-hexadecafluorononanoate
7H-PFHpA	C6HF12CO2NH4	NH4-7H-dodecafluoroheptanoate
SHDBS	C9F17OC6H4SO3Na	Na-heptadecafluorononenyloxy benzene sulfonate
FC-53	CF3(CF2)5O(CF2)2SO3K	K-3-oxa-perfluorononane sulfonate
TDFHD	CF3(CF2)3CF(CF3)(CH2)10CO2Na	Na-tridecafluorohexadecanoate
UDFOS	CF3(CF2)3CH2CF2(CH2)2SO3H	H-undecafluorooctanesulfonate
NFHES	CF3CF2O(CF2)2(CH2)2SO3Na	Na-nonafluorohexylether sulfonate
UDFHES	CF3(CF2)2O(CF2)2(CH2)2SO3Na	Na-undecafluoroheptylether sulfonate
TDFP	CF3(CF2)2C(CF3)2CH2CO2Na	Na-tridecafluoropentanoate
TDHP	CF3(CF2)2C(CF3)2(CH2)2CO2Na	Na-tridecafluorohexanoate
HDFPEC	CF3(CF2)2OCF(CF3)CF2OCF(CF3)CO2Na	Na-heptadecafluoropolyether carboxylate
TDFPBP	CF3(CF2)2C(CF3)2CH2C6H4PO3Li2	Li-heptafluoro-bis-trifluoromethylpentylbenzene phosphonate
6:2 FTSA	CF3(CF2)5(CH2)2SO3H	6:2 fluorotelomer sulfonate
6:2 FtAoS	CF3(CF2)4(CH2)2S(CH2)2CONHC(CH3)2CH2SO 3Na	6:2 fluorotelomer thioether amido sulfonate
7H-6:2 monoPAP	H(CF2)6CH2OPO(ONa)2	disodium dodecafluoroheptyl phosphate
DFHOA	H(CF2)6COCCO2Na	Na-7H-dodecafluoroheptyloxyoate
GenX	CF3(CF2)2OCF3CFCO2NH4	NH4-perfluoromethyloxahexanoate
NFTFBA	CF3(CF2)3(CH2CF2)2CH2CO2H	H-nonafluoro-tetrafluorobutanoate
SNDBS	C10F19OC6H4SO3Na	Na-nonadecafluorononenyloxy benzene sulfonate
		Cationic PFAS
F9-CTAB	CF3(CF2)3(CH2)11N(CH3)3Br	Nonafluoropentadecyl-CTAB
F12-CTAB	(CF3)2(CF2)3(CH2)10N(CH3)3Br	Dodecafluoropentadecyl-CTAB
F17-CTAB	CF3(CF2)7(CH2)6N(CH3)3Br	Heptadecafluorotetradecyl-CTAB
HDFTAI	CF3(CF2)7CH2COHCH2N(CH3)3I	Heptadecafluoroundecan-2-oltrimethylammonium iodide
TDFTAI	CF3(CF2)5CH2COHCH2N(CH3)3I	Tridecafluorononan-2-oltrimethylammonium iodide
NFTAI	CF3(CF2)3CH2COHCH2N(CH3)3I	Nonafluorohepta-2-ol-trimethylammonium iodide
HDFSTAI	CF3(CF2)7SO2NH(CH2)3(CH3)3I	Heptadecafluoropropylaminosulfonetrimeth ylammonium iodide
TCFPATAI	CF3(CF2)10CONH(CH2)3N(CH3)3I	Tricosafluoropentaamidotrimethylammoniu m iodide
NDFPATAI	CF3(CF2)8CONH(CH2)3N(CH3)3I	Nonadecafluoropentaamidotrimethylammoni um iodide
		Zwitterionic PFAS
TDFAEB	CF3(CF2)2C(CF3)2CH2CONH(CH2)2N(CH3)2CH 2CO2	Tridecafluoroamide ethyl betaine
6:2 FTAB	CF3(CF2)5(CH2)2SO2NH(CH2)3N(CH3)2CH2CO 2	6:2 fluorotelomer sulfonamide betaine
HDFPEPB	CF3(CF2)2OCFCF3CF2OCFCF3CONH(CH2)3N(C H3)2CH2CO2	heptadecafluoropolyetheramide propyl betaine
TDFPBAO	CF3(CF2)2C(CF3)2CH2C6H4CONH(CH2)2NO(C H3)2	Tridecafluoropentylbenzamidodimethylamineoxide
TDFHBAO	CF3(CF2)2C(CF3)2CH2C6H4CONH(CH2)3NO(C H3)2	Tridecafluorohexylbenzamidodimethylamineoxide
		Nonionic PFAS
TDFTDE	CF3(CF2)5C2H4SC2H4(CH2CH2O)2OH	Tridecafluorothiodiethoxylate
TDFTTE	CF3(CF2)5C2H4SC2H4(CH2CH2O)3OH	Tridecafluorothiotriethoxylate
TDFTPE	CF3(CF2)5C2H4SC2H4(CH2CH2O)5OH	Tridecafluorothiopentaethoxylate
PFOA- amide	CF3(CF2)6CONHCH2CH3CHOH	N-(2-hydroxypropyl)perfluorooctane amide
NFTME	CF3(CF2)3CH2O(CH2CH2O)3CH3	Nonafluorotriethyleneoxide methyl ether
TDFTME	CF3(CF2)5CH2O(CH2CH2O)3CH3	Tridecafluorotriethyleneoxide methyl ether
HOFTME	CF2H(CF2)3CH2O(CH2CH2O)3CH3	H-octafluorotriethyleneoxide methyl ether
HDDFTME	CF2H(CF2)5CH2O(CH2CH2O)3CH3	H-dodecafluorotriethyleneoxide methyl ether
		Alcohol PFAS
8:1 FTOH	CF3(CF2)7CH2OH	8:1 Fluorotelomer alcohol
FC8diol	(CF2)6(CH2)2(OH)2	Perfluorooctane-1,8-diol
		Hydrocarbons
SDBS	C18H29SO3Na	Na-dodecylbenzene sulfonate
SDS	C12H25SO4Na	Na-dodecyl sulfate
CTAB	C19H42NBr	Hexadecyltrimethylammonium bromide
Triton 45	(CH3)3CCH2C(CH3)2C6H4-(OCH2CH2)nOH, n=4.5	Octylphenol Ethoxylate
CAPB		Cocamidopropyl betaine

Figure 5.

QSPR model for air-water interfacial adsorption coefficient (K_i) versus molar volume. The K_i values are calculated from PFAS and hydrocarbon-surfactant surface-tension data sets measured in deionized-water solutions. The regression equation is log K_i = 0.020 (±0.001) V_m − 8.2 (±0.30), r² = 0.965. The PFAS and hydrocarbon surfactants are identified in Table 2. Figure revised from Brusseau (2019).

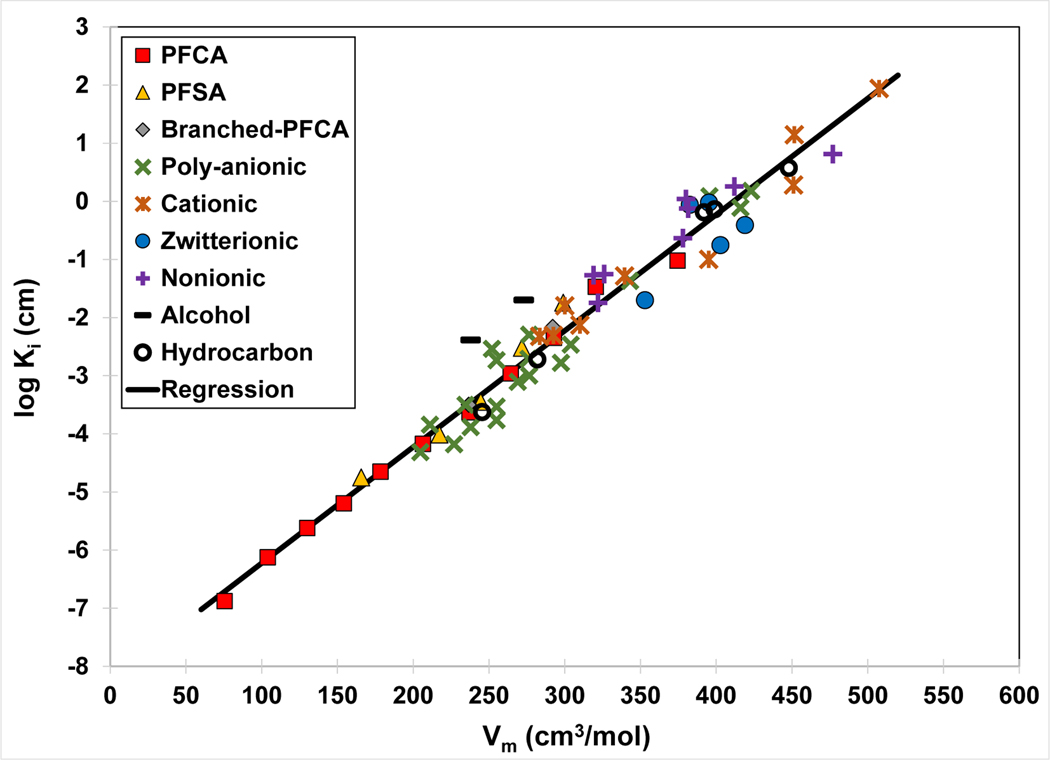
The log K_i-V_m regression is observed to provide an excellent representation of the measured data. Notably, the data span ~450 molar volume and 9 orders-of-magnitude for K_i, representing an extremely wide range of PFAS molecular sizes and tail lengths. As shown in Table 2, the data set includes anionic, cationic, zwitterionic, and nonionic head groups comprising different functional-group types. Additionally, a wide variety of tail structures is represented. Based on the robust high-resolution congruency demonstrated by the model for this highly diverse data set, it is anticipated that the QSPR model will be representative for many PFAS of interest.

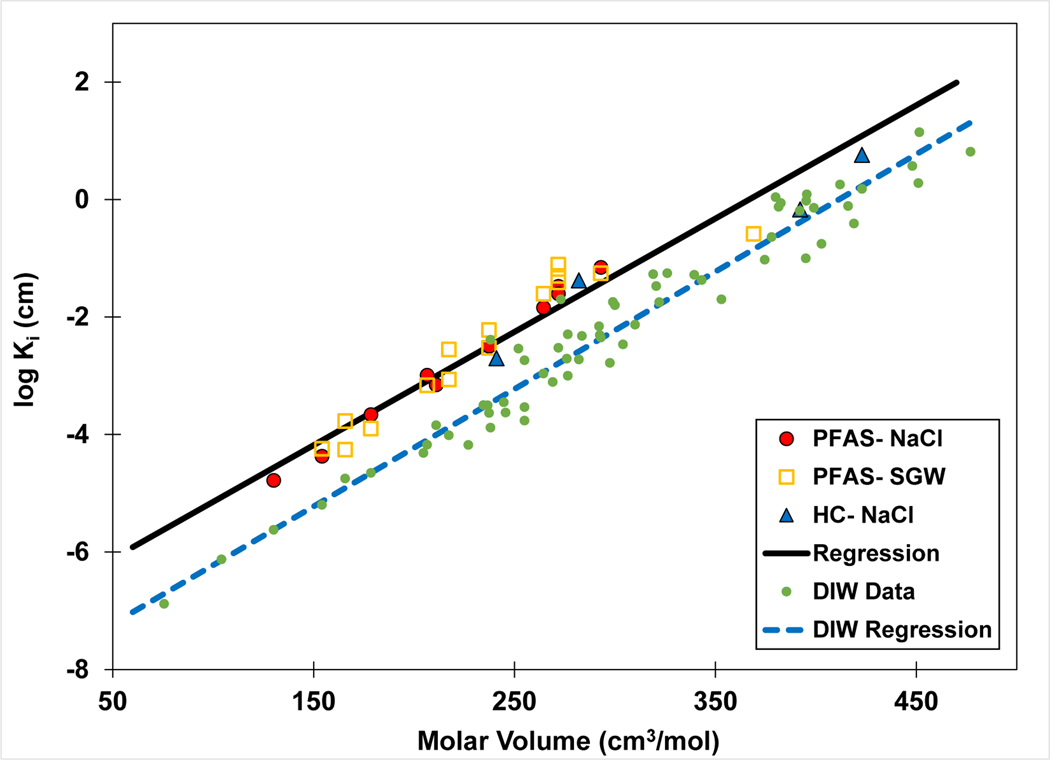
The measured data and QSPR model for electrolyte solutions is compared in Figure 6 to the model developed for deionized-water data. The regression slopes are statistically identical for the two data sets (see values reported in the respective figure captions). The coincident slopes indicate consistency in the relationship between log K_i and V_m for systems with differing solution characteristics. This reflects similarity of surface-activity behavior, which is expected given that interfacial adsorption is driven by the same hydrophobic-interaction process for both systems. The analysis presented here shows that molar volume is a good descriptor for characterizing surface activity, which is consistent with the findings of Brusseau (2019) and Brusseau and Van Glubt (2019). This is due to molar volume serving as an effective index of the influence of molecular size on solvation and hydrophobic interactions, as discussed by Brusseau (2019). The y-intercept for the electrolyte-solution data is greater than that of the deionized-water data, which reflects the influence of ionic strength on surface activity. The difference in intercepts produces an approximate factor of eight difference in K_i values.

Figure 6.

Comparison of QSPR models developed for PFAS in electrolyte (NaCl, SGW) and deionized-water (DIW) solutions. HC represents hydrocarbon surfactants.

Overall, the results presented in Figure 6 indicate consistency between the two QSPR models. One limitation of the QSPR model developed for the electrolyte solutions is that it is based on a moderate number of data sets representing a relatively narrow range of PFAS structures. Conversely, the QSPR model developed for the deionized-water data represents a wide range of PFAS structures. The similarity of the QSPR regression slopes for the two systems indicates that the QSPR model developed for electrolyte solutions should be representative for a wide variety of PFAS.

3.4. Reference Concentrations for PFAS Activity and Interfacial Adsorption

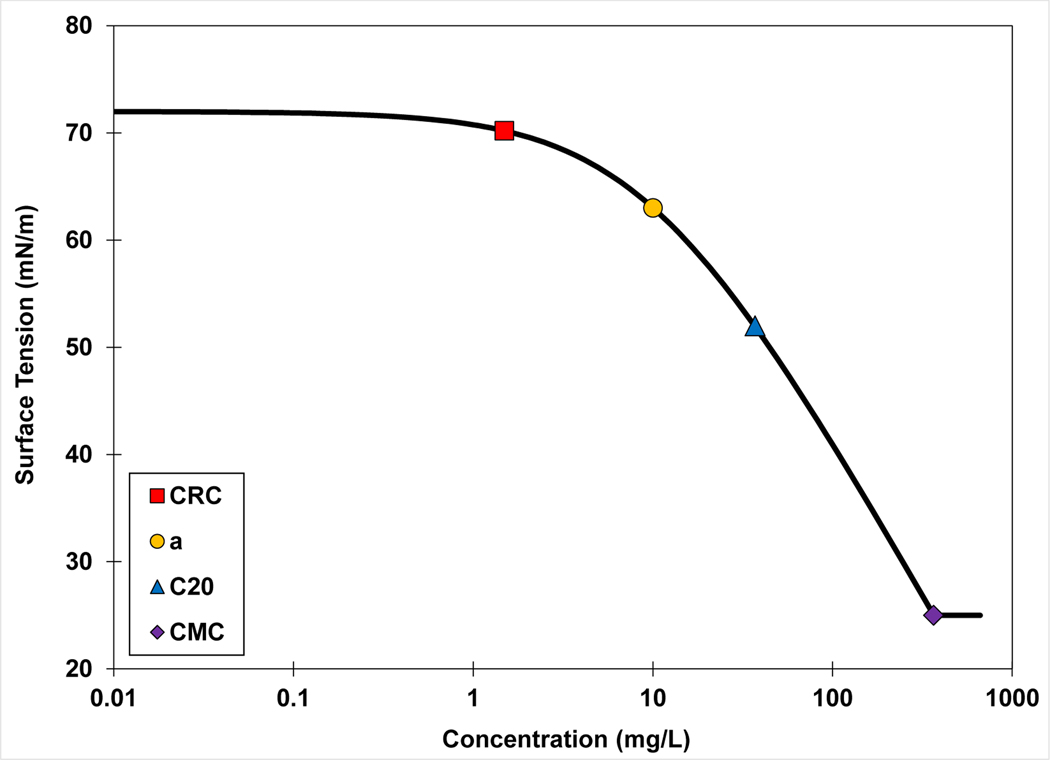
The γ-C function or surface-tension isotherm represents a characterization of the relationship between interfacial adsorption and solution activity of the surfactant, or equivalently a characterization of the surface activity of the surfactant. The γ-C function can be used to quantify surface activities and to compare and contrast among different surfactants. However, using the full γ-C function is cumbersome, and therefore single-value reference concentrations have been developed to serve as simplified indices of surfactant activity. The most commonly used reference concentration is the critical micelle concentration (CMC), representing the nominal concentration for onset of monomer aggregation. Another reference concentration is the C₂₀ concentration, which represents the concentration of surfactant required to reduce surface tension of the solvent by 20 mN/m (Rosen and Kunjappu, 2012). The “a” parameter from the Szyszkowski equation can be used as another reference concentration (e.g., Chang and Franses, 1995; Rosen and Kunjappu, 2012). This term is equivalent to the reciprocal of the Langmuir adsorption coefficient (equation 4) and represents the concentration at which interfacial adsorption is half of the maximum. Brusseau (2019a, 2021) introduced the critical reference concentration (CRC), which is defined as the concentration at which the slope of the γ-C function begins to increase significantly. For this work, the CRC was quantitatively defined as the concentration at which the surface tension is decreased by 2.5%. The different reference concentrations are illustrated in Figure 7.

Figure 7.

Representative surface-tension curve illustrating the four reference concentrations discussed in the main text. CRC is the critical reference concentration (quantitatively defined as the concentration at which the surface tension is decreased by 2.5%), “a” is the Szyszkowski parameter, C20 represents the concentration at which surface tension is decreased by 20 mN/m, and CMC is the critical micelle concentration.

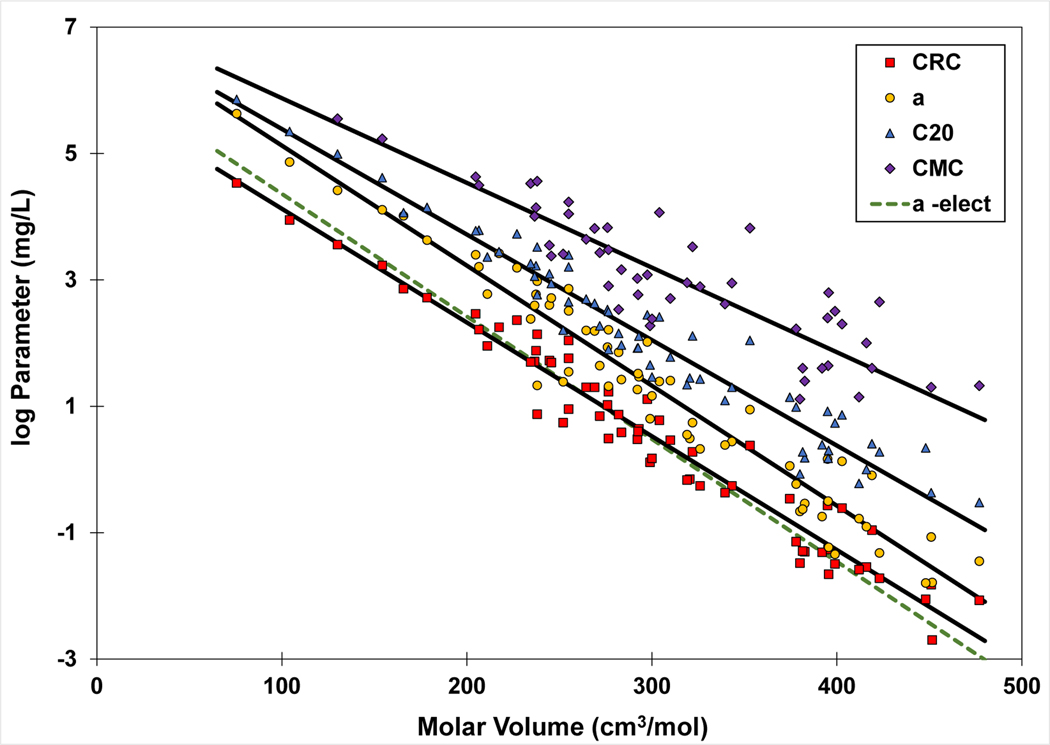
Each of the reference concentrations represents a specific and different condition with respect to the relative amount of surfactant adsorbed at the interface (the surface coverage) because of the nonlinearity of the γ-C function. For example, the CMC generally represents conditions of maximum surface coverage. Conversely, the CRC represents conditions of low surface coverage (< ~10%; Brusseau, 2021). The C₂₀ and a-parameter represent intermediate ranges of surface coverage. However, all of these reference concentrations are reflections of the free energy of adsorption from solution. As such, they all exhibit log-linear relationships to molar volume (Figure 8).

Figure 8.

Relationship of various reference concentrations (“Parameter”) to molar volume. The reference concentrations are defined in the caption for Figure 7. “a-elect” represents the regression for the “a” parameter determined for the electrolyte-solution data set (the measured K_i values are not shown to reduce clutter). The regression coefficients are CRC: slope = −0.018, intercept = 5.9, r² = 0.956; a: slope = −0.019, intercept = 7.0, r² = 0.946; a-elect: slope = −0.0194, intercept = 6.3, r² = 0.945; C20= slope = −0.0167, intercept = 7.0, r² = 0.948; CMC: slope = −0.0134, intercept = 7.2, r² = 0.788.

The slopes of the regressions for CRC and the a-parameter are very similar, whereas the slopes are somewhat smaller for the C₂₀ and CMC regressions. This reflects in part the impact of different slopes for the γ-C function for different PFAS at higher aqueous concentrations (different b and Γ_m values). The “b” values range from approximately 0.06 to 0.3, and exhibit a weak correlation to molar volume (slope=−0.00032, intercept=0.26, r²=0.3). The CRC is roughly 7-times lower than the a-parameter concentration. The a-parameter regression for the electrolyte-solution data has a lower intercept compared to that of the deionized-water data as would be expected. Similarly, the CRC-V_m regression for the electrolyte-solution data (slope=−0.018, intercept=5.26, r²=0.950) has a smaller intercept than the deionized-water data. The b-parameter for the electrolyte-solution data exhibits a correlation to molar volume that is very similar to that obtained for the deionized-water data.

Each of the reference concentrations provide a measure of the relative surface activity of a given surfactant. The key question is which is most relevant for the objectives of the target application. For applications concerning PFAS transport and fate in environmental systems, one objective would be to define conditions wherein air-water interfacial adsorption is essentially linear, such that K_i can be treated as practically constant. Characterizing and simulating PFAS retention and transport would be simplified under such conditions. Clearly, the CMC is not appropriate for this objective. Inspection of Figure 7 shows that surface tensions change significantly with small changes in concentration in the regions represented by the C₂₀ and a-parameter reference concentrations, meaning that air-water interfacial adsorption is nonlinear in those regions. In addition, use of the a-parameter is complicated by the fact that the “b” parameter varies across different PFAS. Conversely, surface tension changes minimally below the CRC. The CRC represents the condition of low surface coverage, wherein air-water interfacial adsorption is essentially linear and K_i values are essentially constant for concentrations lower than the CRC (Brusseau, 2019, 2021). Hence, the CRC would be the most relevant reference concentration for the designated target objective.

The QSPR model was developed using maximum K_i values, and is therefore applicable for PFAS concentrations that are lower than the respective CRCs. The CRC-V_m correlation can be used to determine the relevant CRC for a given PFAS, from which one can delineate the applicability of the model. An alternative approach can be used to estimate K_i values for cases wherein the concentration of interest is greater than the CRC, and air-water interfacial adsorption is nonlinear (i.e., K_i is a function of concentration). The a-V_m and b-V_m correlations can be used to estimate values for “a” and “b”, which can then be used with equations 4 and 5 to determine the K_i for the target concentration.

4. Conclusions

The influence of PFAS molecular structure on air-water interfacial adsorption in aqueous solutions comprising environmentally representative ionic strengths was investigated in this study. Surface tensions were measured for several PFAS in a 0.01 M synthetic groundwater solution and a 0.01 M NaCl reference solution. In addition, surface-tension data measured in environmentally representative ionic-strength solutions were compiled from the literature. Interfacial adsorption coefficients were determined from the measured and literature-reported surface/interfacial tension data.

It was demonstrated that changes in ionic strength within environmentally relevant ranges had minimal impact on air-water interfacial adsorption. The QSPR analysis provided a very good representation of the data sets and demonstrated consistent results with previous studies despite differences in solution properties. The results of the study indicate that the QSPR model developed herein should be applicable for a wide range of solution ionic strengths and compositions, and for a wide variety of PFAS. Hence, it is anticipated that the model will serve as a useful method for estimating air-water interfacial adsorption coefficients for characterizing and simulating PFAS transport and fate in environmental systems.

Highlights.

• Air-water interfacial adsorption coefficients for PFAS in electrolyte solution

• Adsorption coefficient trends with compound properties and solution characteristics

• Minimal ionic strength impact for non-zero ionic strength solutions

• QSPR model is developed to predict interfacial adsorption coefficients for PFAS