Automatic Pleural Line Extraction and COVID-19 Scoring From Lung Ultrasound Data

Abstract

Recent works highlighted the significant potential of lung ultrasound (LUS) imaging in the management of subjects affected by COVID-19. In general, the development of objective, fast, and accurate automatic methods for LUS data evaluation is still at an early stage. This is particularly true for COVID-19 diagnostic. In this article, we propose an automatic and unsupervised method for the detection and localization of the pleural line in LUS data based on the hidden Markov model and Viterbi Algorithm. The pleural line localization step is followed by a supervised classification procedure based on the support vector machine (SVM). The classifier evaluates the healthiness level of a patient and, if present, the severity of the pathology, i.e., the score value for each image of a given LUS acquisition. The experiments performed on a variety of LUS data acquired in Italian hospitals with both linear and convex probes highlight the effectiveness of the proposed method. The average overall accuracy in detecting the pleura is 84% and 94% for convex and linear probes, respectively. The accuracy of the SVM classification in correctly evaluating the severity of COVID-19 related pleural line alterations is about 88% and 94% for convex and linear probes, respectively. The results as well as the visualization of the detected pleural line and the predicted score chart, provide a significant support to medical staff for further evaluating the patient condition.

I. Introduction

Given its cost-effectiveness, portability, noninvasiveness, and safety, ultrasonography represents an extremely useful instrument to anatomically investigate the human body. Soft tissues are indeed characterized by very similar speeds of propagation of sound, hence allowing the exploitation of imaging protocols that assume quasi-homogeneous velocity (equal to 1540 m/s [1]) in the volume of interest. Furthermore, since the acoustic impedance of human tissues are also very similar [2], the different acoustic interfaces normally have a high transmission coefficient, thereby allowing the propagation of ultrasound waves.

Nevertheless, these assertions do not hold for the lung, where the presence of air complicates ultrasound propagation. In particular, the high mismatch between the acoustic impedance of intercostal tissues and the air contained in lungs creates an acoustic interface (pleural line) whose reflection coefficient tends to 1 [3], thus making the lung normally impenetrable to ultrasound. Therefore, alternative diagnostic strategies should be considered to examine this organ.

Nowadays, lung ultrasound (LUS) is based on the interpretation of imaging artifacts that appear in the reconstructed image below the pleural line. When a lung is healthy, it behaves as an almost perfect reflector and generates horizontal artifacts (known as A-lines), which are reverberations that appear at multiples of the distance between the probe and the pleural line [4]. In contrast, the vertical artifacts called B-lines correlate with various pathological conditions of the lung [5]–[9] and are likely associated with the formation of acoustic channels along the pleural surface [4]. Nonetheless, since the B-line genesis remains unclear [4], LUS is generally based on qualitative and subjective observations. However, some quantitative approaches have been recently proposed [10], [11], even if their use by clinicians is still limited [10], [11]. In contrast, semiquantitative approaches, mainly based on counting vertical artifacts in the image [12]–[14], are the most largely used. Furthermore, the automatic detection of characteristic LUS patterns, such as B-lines, is of growing interest because it provides clinicians with real-time important visual information [15]–[21].

Specific LUS patterns have been recently proposed for grading the condition of patients affected by COVID-19 pneumonia [22]–[24], which at present time affects more than 5 million people with about 345 thousand deaths worldwide [25]. Patterns of interest are: 1) thickening of the pleural line with pleural line irregularity; 2) various patterns, including focal and multifocal vertical artifacts; and 3) white lung consolidations. Other findings such as pleural effusions are uncommon, while A-lines could be helpful in signaling a recovery phase. In this work, we focus on the analysis of the pleural line characteristics, which are all affected by the significant patterns described above. Thickening of the pleural line with pleural line irregularity clearly affects directly the pleural line characteristics. The presence of vertical artifacts also influences the pleural line characteristic, as these patterns do originate from the pleural line itself. Ultimately, consolidations de facto break the pleural line, and strongly impact its intensity and continuity. Moreover, the presence of A lines implies a well reflecting pleural line, and thus correlate with a higher intensity of the pleural line. Of all the described alterations, pleural effusions are probably the least impactful on the pleural-line characteristics. In this context, the automatic analysis of the pleural line is thus particularly interesting. In fact, the pleural line appears completely continuous in a healthy lung, and becomes gradually more disrupted when the pathological condition worsen, as reported by the four-level scoring system defined in [24]. The scores range from 0 to 3, where score 0 means absence of pathological signs, and score 3 represents a severe condition. While score 0 represents a continuous and regular pleural line with the associated presence of A-lines, score 1 is associated with a slightly disrupted pleural line with the presence of vertical artifacts below the disruptions [24]. score 2 is associated with a broken pleural line that presents small or large consolidated areas (darker areas) below the breaking point, whereas score 3 denotes a completely permeable and discontinuous pleural line with large white areas underneath it (with or without large consolidations) [24].

Taking advantage of the abovementioned COVID-19 medical scoring procedure, this article addresses the problem of automatically and quickly performing the scoring task on LUS data. Although artificial intelligence diagnostic systems based on deep-learning [16], [18] might represent a straightforward choice for the development of very high accuracy automatic detection algorithms, their main drawback is that they require a very large set of annotated data samples that are currently not available for LUS data of COVID-19 patients.

Thus, it is required to define either unsupervised or supervised techniques based on “shallow” machine learning approaches that can properly operate with a limited number of labeled samples. In this article, we propose a novel system for the automatic estimation of COVID-19 severity (i.e., scoring) in LUS data by adapting and exploiting previous work developed for detecting and characterizing subsurface geological features in radar tomographic data [26], [27]. In detail, the proposed system is composed of two main parts. The first part is an unsupervised method for the automatic detection and characterization of the pleural line. The method is able to extract the pleural line geometric and intensity characteristics for each pixel of a given LUS image by exploiting a combination of a local scale hidden Markov model (HMM) and the Viterbi algorithm (VA). The second part leveraging on the information provided by the pleural line detection method is a supervised classification technique that provides the score for each image of the LUS video. It is based on ad hoc quantitative metrics based on COVID-19 pulmonary manifestations affecting the pleural line and the area below it and then on a support vector machine (SVM) classifier that performs the automatic scoring (i.e., COVID-19 severity assessment) of each LUS image.

The overall strategy is tested on in vivo LUS data recently acquired in several Italian hospitals. The data set is very heterogeneous and highlights different severity of the pathology. Moreover, the data are acquired with different probes, namely linear and convex, thus providing an excellent statistical variation of COVID-19 manifestations in LUS data.

This article is organized as follows. Section II illustrates the proposed method. Section III reports the experimental results on both automatic pleural line detection and scoring of LUS data. Finally, Section IV addresses the conclusions of this article.

II. Proposed Method

The proposed method analyzes, in an automatic way, LUS videos to detect and characterize the pleural line, on the basis of a scoring system specifically defined for LUS data obtained on COVID-19 patients. This is done by processing the video following an image-by-image approach. Note that in this article we refer to individual frames as images. Let be the LUS video where represents the th image (i.e., one video frame). Fig. 1 reports the block scheme of the proposed system for the automatic analysis of a generic image . This system is composed of two main parts: 1) automatic pleural line detection and 2) COVID-19 score classification. The first part aims at detecting on each image the pleural line by first discriminating it from the background and then reconstructing it by means of a combination of HMM and the VA. In this way, we obtain a set representing the geometric location of the pleural line at each image. The second part uses the pleural line to compute relevant features that describe both geometric and radiometric properties of the pleura and the area underneath it. A supervised SVM classifier is used to assign a COVID-19 score to each image . The result is a set of scores , where is the score of image . Set is used to make a binary decision on the positivity or negativity of the patient to COVID-19 LUS patterns. Moreover, it can be represented as a score histogram of the results for all the images in to provide a comprehensive patient overview of the score severity. In Sections II-A and II-B, the details of the method are presented.

Fig. 1.

Block scheme of the proposed method applied to one image of an LUS video.

A. Automatic Pleural Line Detection

To efficiently detect and characterize the pleural line in LUS data, an automatic detection method should possess the following requirements: 1) it should discriminate between the pleural line and other LUS data features such as the ribs; 2) it should efficiently detect the pleural line under noisy conditions; and 3) it should be able to perform inference and identify the pleural line position also when gaps occur in the LUS image (e.g., rupture of the pleura).

To this extent, we exploit and readapt a method previously developed for the characterization of radar tomographic data of the subsurface stratigraphy of Mars [26]. The method identifies all the linear or quasi-linear structures providing their intensity and geometrical characteristics by combining a local scale HMM and the VA.

In this framework, the LUS image of intensity with size can be seen as a trellis (see the example of Fig. 2 where an image portion is shown), where and are the image indexes of rows and columns, respectively. Note that to simplify the notation in the following the image index is omitted (i.e., ). The trellis properties are modeled by the HMM on which the VA performs the inference step. Starting from seeding points and based on the observed pixel intensities, the VA finds the most probable path, across the image that corresponds to any given linear structure present in the image (e.g., pleural line and ribs).

Fig. 2.

Visualization of a portion of the LUS image as a trellis. The geometrical position and intensity of the pleural line is retrieved by a combination of an HMM and the VA.

The pleural line detection is preceded by a two preliminary processing steps for image preparation and enhancement. The image preparation step is also required for the SVM classifier described in Section II-B, whereas the image enhancement is only relevant for the pleural line detection. The main purpose of the image enhancement processing is to reinforce the relevant features present in an LUS image and reduce the background noise thus easing unsupervised the pleural line detection procedure.

1). Image Preparation:

LUS data acquired by a convex probe are mapped into a linear grid moving from a polar to a Cartesian coordinate system. This is required for satisfying the assumption that the structures to be detected are linear or quasilinear. LUS data acquired by linear probes do not require this step.

2). Image Enhancement:

First, background noise in the image is smoothed out using a circular averaging filter of radius . The radius value is chosen considering the size of the relevant layering structures and the intensity of the background noise. This is to reduce the noise while preserving the shape and intensity values of the structures.

Second, relevant layering structures are separated from the background of the image by means of a statistical method. To this aim, we employ a Rician-based statistical model that is often applied to multiplicative-noise distributed data, especially in medical applications [28]–[30]. We model the statistical distribution of an LUS image as a mixture of background and foreground components, where the background is Rayleigh distributed (magnitude of 0-mean, diagonally covariated Gaussian) and the foreground (layered structures) is Rician distributed (magnitude of nonnull mean diagonally covariated Gaussian). Unsupervised parameter estimation of this model from data can be done as described in [31], where an automatic iterative implementation of the expectation maximization (EM) algorithm is devised specifically for the Rayleigh–Rice mixture. After parameter estimation, the optimal threshold is obtained by means of maximum-a posteriori approach, as described in [31]. This is done following the Bayes decision rule for minimum error that assigns each pixel to the class (i.e., background or layering structure) that maximizes the posterior conditional probability. Threshold represents the value of intensity that separates the relevant layering structure from the background noise. A pseudo-image is composed by setting to zero background values (i.e., values below ) and retaining foreground values (i.e., values above ), as shown in the example of Fig. 3.

Fig. 3.

Examples of results of different steps of the automatic pleural detection. (a) Original image . (b) Masked image by EM-based thresholding . (c) Enhanced LUS image . (d) Detected pleural line (black dotted line).

Finally, a skeleton representation of is obtained by convolution with a rectangular function as follows [26]:

where (*) is the convolution operator and the half-width of the rectangular function . The convolution described in (1) is performed to avoid nonphysical irregularities in the interface continuity along the -direction. These irregularities could arise from potential imprecisions due to noise in the peak detected values of . An example of the skeleton image in Fig. 5(c).

Fig. 5.

Example of the EM algorithm applied to an LUS image.

3). Pleural Line Detection With the VA:

In the LUS data context, we interpret the HMM parameters [26], [32] in the following way. The time step corresponds to the column variable . The hidden states correspond to the candidate linear structure in a particular row of the LUS image for each time step (see Fig. 2). The state transition matrix models the probability that the structure is located in a certain row at a given time step, given it was located at another particular row at the previous time step. For each time step, the observation vector is equal to the LUS image pixel intensities. Given these assumptions, the method described in [26] is applied to the LUS data in an image-by-image fashion of the standard VA approach to reduce the computational complexity by performing the inference on small image subblocks which are then chained together to produce the final result for any given tracked feature. Accordingly, multiple features identification can be obtained in near real-time.

Given the enhanced LUS image , the linear structures are sequentially tracked by the VA starting from intensity values denoted as seeding points taken from (i.e., values above threshold). For each time step, a number of states equal to around the seeding point is evaluated. Accordingly, also defines the maximum allowable variation, in terms of index , of the identified linear structure from one time step to another. The method identifies a set of linear structures [see the example of Fig. 2 based on a portion of ]. These objects in could correspond to any given actual linear structure present in the image. Each structure is characterized by its: 1) geometric position expressed as a set of couples (i.e., pixel wise detection) within the LUS image and 2) corresponding intensity extracted from .

With respect to [26], where all the identified structures are equally important, here, we aim to identify only the pleural line (see Fig. 2). To this purpose, ad hoc automatic detection conditions are specified as following. Let us define as follows: 1) the average deepness (in terms of row coordinates ) of the th structure; 2) and the average intensity of the th structure and the average intensity of all the structures in (i.e., ), respectively; and3) and the length of the th structure and the average length of all the structures, (i.e., ), respectively. First, we identify a subset of linear structures such that

to select only those having length and intensity above the average. Then, the pleural line is automatically identified within set as the deepest one, that is

In order to refine the estimate of geometric and intensity characteristics of , a second and finer iteration of the VA is applied only to the surroundings of . This is done directly on the image pleural portion, without enhancement, and by applying a circular filter with radius (instead of ).

The detected pleural line [see an example of detected pleural line in Fig. 5(d)] is described with the graph of a function defined over the domain of the columns of each image . The function is defined as , where and the general notation indicates the set of all integer numbers from to , inclusive. The function associates a given column index to a certain row . Therefore, the pair therefore identifies the pleural line in image coordinates. The condition on the column index bounds and is as such because the pleural line may not span the entire horizontal dimension of the LUS image for each given image.

By applying the proposed approach to all the images in the set of pleural lines is obtained. The automatic determination of the position and intensity characteristics of the pleural line described by allows us to quantitatively analyze its properties and to define a scoring procedure based on the classification approach that will be described in Section III.

B. Classification-Based COVID-19 Scoring Procedure

The geometric and intensity properties of the detected pleural line and the underneath region (i.e., the area below the pleural line) are further modeled by a set of features (i.e., metrics) to be analyzed by the means of a supervised classification approach. The classification goal is to provide a prediction on the score (i.e., the diagnosis) for each image. Indeed, the score value is directly connected to the presence of structures linked to COVID-19 and its severity. In this method, we consider the scoring system recalled in Section I and described in [24], which consists of four possible scores ranging from 0 to 3. Therefore, each score value can be seen as a class.

For each image, the feature vector is defined as . Features are related to the pleural line intensity, while features extract relevant statistical information on the intensity of below the pleural line. The features are novel and ad hoc defined for the COVID-19 scoring, while others are adapted from previous works in the radar domain. Given the above, we define each feature in as follows.

1). —Discontinuities in the Pleural Line:

Let us define a metric representing the intensity of the pleural line for each column normalized by the pleural line average intensity (across image columns)

Large variations of are potential indicators of pleural line discontinuities. A steady value of the metric across is representative of healthy patients. Accordingly, the feature is defined as the average value of , that is

2). —Presence of Consolidations:

The second feature quantifies the average intensity of the portion of the image below the pleural line with respect to the intensity value of the pleural line for each . Let be defined as follows:

where the number of pixels under the pleural line considered for integration is given by the constant . is defined as the average of the metric , that is

The feature quantifies phenomena such as white lungs and consolidations. Hence, steep peaks of this metric indicate consolidations in the lungs, while stable values are associated with lower scores.

3). —Total Variation:

This feature models strong variations in the pleural line intensity . It is defined as follows:

High values of correspond to strong variations in the pleural line possibly indicating large pleural disruptions.

4). —Statistical Characterization of the Image Area Below the Pleural Line:

Let us denote as the matrix containing the intensity values of below the pleural line. The area below the pleural line is of particular importance as it contains several indicators of the pathological conditions (e.g., A and B lines). Feature describes the distribution parameters that best model the intensity values in . As a preliminary step, is fit to several distributions [27] to identify the best-fitting distribution according to the value of the root mean square error (RMSE) and the Kullback–Leibler (KL) divergence between the original and the fit data. The fitting is performed by applying a sliding window to in both the horizontal and vertical directions. For each position of , the fitting is done by computing the statistical parameters of the previously estimated best fitting distribution of the pixels in the window. Accordingly, feature includes the average best-fit distribution parameters computed for each position of . The number of parameters depends on the best-fitting distribution: the Rayleigh distribution has one parameter, while the Gamma distribution has two parameters that defines the shape and the rate (i.e., the inverse of the scale) of the function. Features , and are defined as the first four statistical moments (i.e., average, standard deviation, skewness, and kurtosis) evaluated on the intensity values in for each image. High values of , and are related to pleural ruptures and consolidations as they provide a quantification of the amount of scattered ultrasound energy that originated from below the pleura as per definition of . For each available LUS image , the feature vector is computed and then normalized.

Then, it is given as input to an SVM classifier. The choice of an SVM over a deep learning approach is mainly related to the size of the training set required by the two types of classifiers. Indeed, a deep neural network requires a very large number of annotated samples in the training data set to estimate all the network parameters. This is not the case for LUS data of COVID-19 patients which, due to the recent nature of the virus, are to this date very scarce. A deep network trained on such few data is likely to show poor performance in terms of generalization capabilities, and thus, accuracy. In contrast, SVM classifiers show good generalization properties even when trained with a limited number of samples [33]. Furthermore, SVMs: 1) can solve strongly nonlinear problems in the feature space; 2) provide a sparse and unique solution to the learning problem; and 3) are fast in the training and testing phases and require low memory usage. To improve the discrimination performance and transform a nonlinear problem in a linear one, nonlinear kernel functions are applied to the input data. Here, we apply the Gaussian radial basis function (RBF) kernel as it is the most widely used one in general problems and has a better convergence time than the polynomial one [34].

By applying the scoring procedure to all the images of a video, a set of score is obtained.

III. Experimental Results

A. Data Set Description

The proposed method has been tested on a subset of the Italian COVID-19 LUS Database (ICLUS-DB) [35]. The data have been acquired in multiple clinical structures (BresciaMed, Brescia, Italy, Valle del Serchio General Hospital, Lucca, Italy, Fondazione Policlinico Universitario A. Gemelli IRCCS, Rome, Italy, Fondazione Policlinico Universitario San Matteo IRCCS, Pavia, Italy, Tione General Hospital, Tione (TN), Italy). Data have been acquired with different types of ultrasound scanners (Mindray DC-70 Exp, Esaote MyLabAlpha, Toshiba Aplio XV, WiFi Ultrasound Probes - ATL) using both linear and convex probes depending on the needs. Every image in an LUS video has been assigned a score ranging from 0 to 3 according to the severity of the illness, where 0 is a negative patient and 3 identifies a severe form of lung surface alteration connected to COVID-19 [24]. To guarantee objective annotation, the labeling process was stratified into four independent levels: 1) score assigned image-by-image by four master students with ultrasound background knowledge; 2) validation of the assigned scores performed by a PhD student with expertise in LUS; 3) second level of validation performed by a biomedical engineer with more than ten year of experience in LUS; and 4) third level of validation and agreement between clinicians with more than ten years of experience in LUS. The exploited data set is composed by 29 cases (10 negative, 15 confirmed positive to COVID-19 by swab technique, and four suspected positive to COVID-19), for a total of 58 videos. 20 videos have been acquired by a linear probe and 38 by a convex one. The data, for each acquisition, are provided as a sequence of images with intensity coded in the range [0–255]. The average number of processed images per video is about 60.

Table I shows the experimental setup of the parameters for the proposed method. Data acquired by either linear and convex probes have different characteristics. Here, we defined five groups as the data set that contains videos from linear and convex probes from the hospitals in Brescia and Rome and the data from the convex probe from the hospital in Lucca. We analyzed these five groups of video and generated five SVM models, called model , , , , and , where the letters , , and indicate the different hospitals (Brescia, Rome, and Lucca) and the subscript and designates the acquisition with the linear and convex probes, respectively. For each model, the number of samples (i.e., feature vectors ) denoted as is uniformly extracted from the overall available reference samples and exploited for the learning stage. The remaining samples are used for predicting the score of unseen patients and testing the generalization capability of the model. Here, we train the classifier with 50% of the reference samples (see Table II). To determine the parameters of the RBF kernel, we apply a tenfold cross-validation considering the range of the parameters and . is the regularization parameter that controls the tradeoff between having a low training accuracy and a low testing accuracy, hence, is related to the generalization capability of the model. is the inverse of the standard deviation of the Gaussian function, hence it indicates how much influence a training sample has in the classification phase. Table II shows the optimal kernel parameters and for the SVM models.

TABLE I. Parameters of the Proposed Method for Linear and Convex Probes.

Parameter	Linear	Convex
Filter radius	3	8
Filter radius	3	4
Rectangle Half Width	16	8
Viterbi State Bound	10	10
Pixels under the pleural line	100	100
Sliding windows size

TABLE II. Parameters of the Classification: Total Number of Samples, Numbers of the Training and Test Samples, and Best Parameters and for the RBF Kernelof the SVM Models.

Parameter	Model
	482	1246	102	102	278
	241	623	51	51	139
	32	32	256	16	16
	2	2	4	4	4

B. Automatic Pleural Line Detection

In this section, we discuss the results of the method described in Section II-A for pleural line detection.

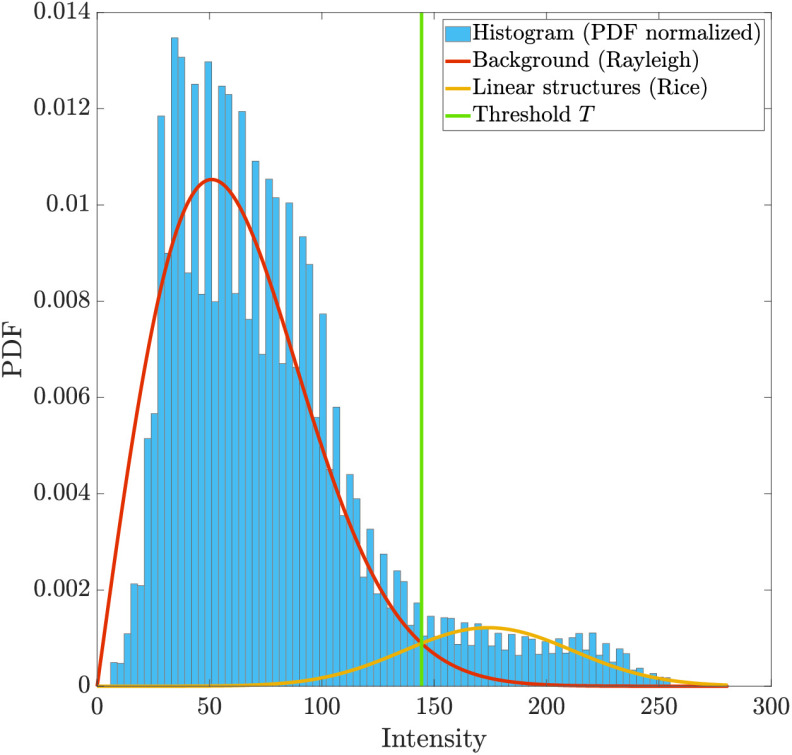
First, the preprocessing step is applied to the LUS image for feature highlighting and background noise suppression. Fig. 4 shows some examples of the results obtained by applying the circular filter with different values of the radius . Fig. 5 reports an example of probability density estimation by the EM algorithm. The algorithm models the LUS image intensity histogram as a mixture of two distributions, namely Rayleigh for the background and Rice for the putative features. An example of the results of the application of the threshold automatically derived by using the Bayes rule for minimum error is shown in Fig. 5(b), where a comparison of the obtained with the original image is provided [see Fig. 5(a)]. Fig. 5(c) reports the enhanced LUS image obtained by processing in Fig. 5(b). The thresholding procedure clearly highlights the image features. This reduces the background noise and is beneficial for the automatic pleural line detection performed with the VA.

Fig. 4.

Examples of results obtained by applying the circular filter with radius to a convex LUS image. (a) Unfiltered image. (b) . (c) . (d) .

The parameter settings for the actual pleural line detection method are summarized in Table I. The state transition matrix (see Section II-A) is assumed to be a triangular function with size equal to for each given hidden state [26]. Fig. 6 reports some examples of results of pleural line detection for both convex (after projection) and linear probes and for different scores. The figures display the detected pleural line, superimposed on the LUS image, and its associated intensity. The results highlight the method capability in accurately detecting the pleural line geometric position also in the presence of pleural fragmentation, which is typical of score 2 and 3. Indeed, the quantitative characterization of the pleural line allows the determination of its subtle variations in both intensity and size of the pleural gaps. score 0 patients (i.e., healthy patients) always show a stable value of the pleural line intensity in both the linear and convex case [see Fig. 6(a) and (e)].

Fig. 6.

Examples of experimental results on pleural line automatic detection (the pleural line detected by the method is shown in red) and intensity retrieval for linear and convex data. (a) Linear, score 0 (i.e., healthy patient). (b) Linear, score 1. (c) Linear, score 2. (d) Linear, score 3. (e) Convex, score 0. (f) Convex, score 1. (g) Convex, score 2. (h) Convex, score 3.

Table III reports the method accuracy for different types of probes and scores. The accuracy is computed as the number of images where the pleura is correctly detected over the total number of images for each analyzed acquisition (i.e., one video). The number of test cases is reported in Section III-A. The global accuracy (i.e., computed independently of the score value) is 0.92 for the linear case and 0.84 for the convex one. The method has a high accuracy for LUS images up to Score 2. The accuracy decreases for Score 3. This is expected as for some patients the severity of the pleural line anomaly (e.g., multiple large ruptures) is such that a meaningful detection becomes problematic. It is worth mentioning that in a very small number of experiments the proposed method was not able to correctly detect the pleural line for any given image of the video. The extremely poor image contrast resulted in a wrong estimation of the threshold by the EM as a result of the impossibility of modeling the background and the features intensity distribution as the sum of two separable distributions. As a lesson learned, a proper setting of the contrast before acquisition would be desirable for improving the algorithm detection performance.

TABLE III. Accuracy in the Unsupervised Detection of the Pleural Line (Overall and Separated by Score) Evaluated at a Single Image Level.

Type	Score				Overall Accuracy
	0	1	2	3
Linear	0.93	0.92	0.98	0.77	0.92
Convex	0.83	0.93	0.81	0.78	0.84

C. Classification-Based Scoring Procedure

This section describes the results of the automatic scoring procedure based on the supervised SVM classification. First, the results of the statistical analysis on the LUS images for the determination of the relevant distribution model of the intensity of the area below the pleural line (see Section II-B) as a function of the score are illustrated. Then, we present the classification results based on the SVM.

The statistical analysis is performed by fitting the Gamma, Nakagami, Rayleigh, and Weibull distributions to the distribution of the intensities in (i.e., the portion of below the pleural line). The KL distance and the RMSE are exploited as performance metrics for evaluating the quality of the fit. Table IV shows the results of this analysis. The Gamma distribution shows better performance than the other distributions for all the scores in terms of both the KL distance and the RMSE. Hence, for the computation of the feature , we assume that is Gamma-distributed.

TABLE IV. Fitting Performance of the Rayleigh, Gamma, Nakagami, and Weibull Distributions to the LUS Data.

Score	Metric	Rayleigh	Gamma	Nakagami	Weibull
0	KL distance	0.1653	0.1067	0.1683	0.1851
	RMSE	0.0075	0.005	0.0069	0.0068
1	KL distance	0.0441	0.0439	0.0457	0.0884
	RMSE	0.1535	0.0039	0.0044	0.0059
2	KL distance	0.0621	0.0197	0.0672	0.0834
	RMSE	0.0725	0.0081	0.0628	0.0262
3	KL distance	0.0086	0.0173	0.0536	0.0575
	RMSE	0.0125	0.0017	0.0024	0.0068

For each image of each video, we extracted the feature vector as per definition in Section II-B. As an example, Fig. 7 shows the values of the metrics and (exploited for defining and ) for the linear and convex probe data in Fig. 6. When the values of and are stable, the score associated with the image is 0. On the contrary, drops and peaks in the features indicate images with a higher score. While not explicitly exploited in this article, it is also interesting to note that a given sequence of peaks or drops in the metrics can be used for evaluating the size of the pleural line anomaly.

Fig. 7.

Values of and for the LUS data of Fig. 6. (a) Linear, score 0 (i.e., healthy patient). (b) Linear, score 1. (c) Linear, score 2. (d) Linear, score 3. (e) Convex, score 0. (f) Convex, score 1. (g) Convex, score 2. (h) Convex, score 3. Red dots indicate potential anomalies. relates to pleural line intensity, while provides information by comparing the pleural line intensity to the intensity of the image area below it.

Table V reports the SVM classification performance for each model in terms of the sensitivity (i.e., true positive), specificity (i.e., true negative), and overall accuracy (OA) for each score. The general effectiveness of the classification method is indicated by the high values of the sensitivity and the specificity of all the SVM models. Furthermore, the results show that the accuracies of correctly assigning the different scores are in the range of 80%–95%.

TABLE V. Classification Accuracy for Each the Model—Sensitivity, Specificity, and OA. B, R, and L Stands for Brescia, Rome, and Lucca Data, Respectively, While the Pedix L or C Indicates Either Linear or Convex Data.

Model	Metric	Score				Average
		0	1	2	3
	Sensitivity	0.8333	0.9394	0.9923	0.9663	0.9328
	Specificity	0.9979	0.9955	0.9641	0.9967	0.9885
	OA	0.8333	0.9394	0.9923	0.9663	0.9751
	Sensitivity	0.8010	0.8155	0.9667	0.8107	0.8507
	Specificity	0.9838	0.9779	0.8669	0.9831	0.9529
	OA	0.8010	0.8155	0.9667	0.8107	0.8484
	Sensitivity	0.9012	0.9079	0.9691	0.9326	0.9277
	Specificity	0.9979	0.9978	0.9103	0.9737	0.9699
	OA	0.9012	0.9079	0.9691	0.9326	0.9177
	Sensitivity	0.8824	0.9333	0.9508	0.8222	0.8971
	Specificity	0.9882	0.9885	0.8800	0.9881	0.9612
	OA	0.8824	0.9333	0.9508	0.8222	0.8971
	Sensitivity	0.9286	0.8696	0.9315	0.8874	0.9042
	Specificity	0.9712	0.9617	0.9189	0.9725	0.9560
	OA	0.9286	0.8696	0.9315	0.8874	0.9042

To better understand the potential of the proposed approach, we tested the method with the data of three patients, here called Patient B6, Patient R1, and Patient L2, all screened three times. Patient B6 is patient 6 in the Brescia data set and has been screened two times by a convex probe and one time with the linear probe. Patient R1 is patient number 1 of the Rome data set and has been screened one time by the convex probe and two times by the linear probe. Finally, Patient L2 is patient number 2 of the Lucca data set. Patient L2 was imaged with a convex probe. Table VI shows the OA for each video and the OA for each patient. Each video is processed and classified with the SVM model defined considering the specific probe and hospital. The overall video accuracy is defined as the average of the accuracies of each score in the video. By averaging the accuracies for the videos of the same patient, we can retrieve the OA for that patient. Fig. 8 shows the examples of the output of the scoring procedure based on the SVM classifier. The score is represented by the color of the square box around the image.

TABLE VI. OA of the Prediction of the Score for the Analysis of the Videos of Patients B6, R1, and L2.

Patient	Overall Accuracy
	Video 1	Video 2	Video 3	Patient accuracy
B6	0.873	0.876	0.941	0.896
R1	0.938	0.952	0.901	0.930
L2	0.913	0.926	0.907	0.915

Fig. 8.

Examples of the scoring procedure based on the SVM classifier. (a)–(d) Data are acquired by the linear probe. (e)–(h) Data are acquired by the convex probe. The columns and the color of the box around the image indicates the predicted score value. Colors green, yellow, orange, and red correspond to score 0, 1, 2, and 3, respectively.

The results for each patient can be further analyzed by evaluating the distribution of the predicted scores for each video (i.e., histogram of the set ). The first three columns of Fig. 9 report the distribution of the scores for the three patients and for each video separately. The predicted score and reference score are reported in blue and in red, respectively. The last column of Fig. 9 reports the histograms of the scoring as a result of the joint analysis of the three videos for each patient. The individual distribution of the predicted scores (i.e., one video) is a potential indicator of the average health status of the patient in the anatomical region where the video has been acquired. The sum of the scoring distribution indicates the overall health status with respect to COVID-19 LUS manifestations of the patient.

Fig. 9.

Scoring histograms of the frame of each video for patients (a) B6, (b) R1, and (c) L2. The first three columns show the distribution of the score values for each video. The last column shows the histogram of the scoring evaluated over three videos. Red bars represent the reference data, while the predicted labels are in blue and green.

IV. Conclusion

LUS imaging is a very promising technology for identifying and monitoring patients affected by COVID-19. The development of detection methods and techniques capable to automatically perform a fast and accurate diagnosis, without requiring the assistance of a trained expert, is still at an early stage. In this article, we have proposed a method for: 1) an unsupervised and automatic detection of the pleural line and the extraction of its geometric and intensity characteristics and 2) an automatic and supervised classification of each LUS image in terms of score (i.e., severity of COVID-19 pulmonary manifestation). For the task of the pleural line detection, we exploited a method based on an HMM and the VA. The pleural line and its underneath region information extracted by the method are then modeled by ad hoc metrics (i.e., features) that are given as input to the automatic scoring classification procedure.

The proposed scoring is based on a supervised SVM classifier that is applied to each image after the extraction of a proper feature vector.

The proposed method has been tested on the ICLUS-DB. The data set is very heterogeneous being acquired in different hospitals (thus different operators) and with different probes (i.e., linear and convex). The data are accompanied by the scoring information of each image that we exploit as reference data set. The experimental results show that the pleural line detector can accurately retrieve the pleural line characteristics (i.e., pixel by pixel geometric position and associated intensity) in an image with an OA of 92% and 84% for linear probes and convex probes, respectively. The SVM classifier provides an image-by-image evaluation of COVID-19 related LUS patterns, accompanied by the predicted score value with an average accuracy of 94% and 88% for linear and convex probes, respectively. The scoring results can both be visually displayed on each image and also provided in a histogram indicating the distribution of the predicted scores for the entire set of acquisitions of a patient in a video for further medical evaluation.

As a final remark, the proposed method has the potential for real-time implementation given the relatively low complexity of the proposed algorithms. The method has been implemented in MATLAB environment without any particular optimization. For each image, the algorithm identifies the pleural line in less than 2 s on a Dell XPS 9550 laptop. The algorithm for the scoring was tested on an ASUS F555UJ-XX006T laptop. The feature extraction on a frame and the testing phase of a sample take each less than 2 s, while the learning phase time depends on the number of samples. In our case, the learning time was in the range of few hours. However, this is an offline phase that is required only in the setup of the method. This opens the possibility of implementing the method directly on the ultrasound scanners, therefore, providing the user with both tools that support a postacquisition diagnosis and also a stream of enhanced information during the acquisition process.

As future work, we plan to extend the validation of the proposed method and the application to automatically identify other pulmonary diseases based on their appearance in LUS data.

Funding Statement

This work was supported by the VRT Foundation for this research (COVID-19 Call 2020) under Grant #1.