EVDHM-ARIMA-Based Time Series Forecasting Model and Its Application for COVID-19 Cases

Abstract

The time-series forecasting makes a substantial contribution in timely decision-making. In this article, a recently developed eigenvalue decomposition of Hankel matrix (EVDHM) along with the autoregressive integrated moving average (ARIMA) is applied to develop a forecasting model for nonstationary time series. The Phillips–Perron test (PPT) is used to define the nonstationarity of time series. EVDHM is applied over a time series to decompose it into respective subcomponents and reduce the nonstationarity. ARIMA-based model is designed to forecast the future values for each subcomponent. The forecast values of each subcomponent are added to get the final output values. The optimized value of ARIMA parameters for each subcomponent is obtained using a genetic algorithm (GA) for minimum values of Akaike information criterion (AIC). Model performance is evaluated by estimating the future values of daily new cases of the recent pandemic disease COVID-19 for India, USA, and Brazil. The high efficacy of the proposed method is convinced with the results.

I. Introduction

Future value forecasting is a crucial field of data science and automated systems in which a model is developed based on the past observations. The model is utilized to extrapolate the future values. Many methodologies have been developed in past for time-series forecasting. Previously, the autoregressive integrated moving average (ARIMA) has been used in several fields for statistical analysis and data prediction, such as electricity price [1], energy demand [2], vehicle velocity forecasting [3], and stock market price prediction [4]. Other methods, such as deep learning-based method, is also utilized for the time-series forecasting in [5]. Deep-learning-based methodologies need a huge amount of data for training the model. In case of small data set, there is a risk of overfitting for deep-learning-based forecasting models.

The ARIMA-based models are mainly suitable for linear time-series analysis [6]. Hence, the traditional ARIMA based approach is found less suitable to deal with real-world problems that possess nonlinear characteristics [4], [7]. Therefore, various hybrid models are proposed to improve the performance of ARIMA-based models for analyzing the real-world time series. In [4], a hybrid approach based on empirical mode decomposition (EMD), ARIMA, and support vector regression (SVR) is proposed. In [7], a complex neurofuzzy and ARIMA-based method is explored for the analysis of financial time series. A model based on ARIMA and support vector machine (SVM) techniques is utilized for the analysis of remaining useful life of aircraft engines [8]. A seasonal ARIMA- and SVM-based method is explored for the prediction of Taiwan’s machinery industry production [9]. Another study in [10] has utilized a hybrid methodology for financial data inspection. They integrated artificial neural networks (ANNs) with the ARIMA model in this work. All these studies show improved performance with the hybrid models. The singular spectrum analysis (SSA)- and ARIMA-based hybrid method is applied for time-series forecasting of ambient O₃ concentrations [11]. Moreover, the SSA is also extended for multisensor time series [12]. An autoregressive (AR) model is used for leak detection in transport pipeline [13] and sleep stage scoring using electroencephalogram [14].

Moreover, time-series forecasting methods are also found useful for the analysis of epidemiological data. In [15], a machine-learning-based method is used for modeling the dengue vector population. The results of the study show the effectiveness of the nonlinear methods compared with the linear methods. The statistical modeling of malaria time series is less suitable due to the presence of spatial nonstationarity [16]. Hence, a new approach to model the malaria time series is adopted using the genetic algorithm (GA). Therefore, linear models, such as ARIMA-based techniques, are not alone sufficient to model the real-world time series. Hence, adaptation of such techniques, which can also deal with the nonlinearity and nonstationarity of the underlying time series in combination with ARIMA model, may be more suitable for the modeling of the real-world time series.

Recently, COVID-19 has emerged as a potential threat to the health and safety of people globally. It was declared a public health emergency by the World Health Organization (WHO) on January 30, 2020 [17]. It is responsible to infect millions of people around the world. As per WHO, a total 8 708 008 confirmed cases and total 461 715 deaths are reported until June 21, 2020 all over the globe. Therefore, the study of future development trend of the novel COVID-19 epidemics is an emerging research topic at the current time. Moreover, COVID-19 time-series forecasting may play an important role in making the strategic planning for public health system. A deliberate plan assists government and health organizations to avoid a large number of deaths and help them to control the outbreak of the COVID-19. Hence, the development of efficient short-term forecasting models for COVID-19 is of prime importance.

Hence, various studies are performed for the COVID-19 time-series modeling and forecasting. The ARIMA model-based approach is explored for the analysis of COVID-19 time series in [18]. In this study, the mean of COVID-19 prevalence is stabilized using the first-order difference. Then, the second-order difference is also considered to make all the series to be stationary. In [19], a hybrid approach for the COVID-19 time-series forecasting is suggested. In this study, the authors have used ARIMA and wavelet-based forecasting techniques in combination. In [20], ARIMA and various machine learning methods are incorporated for the forecasting of the COVID-19 cases. In this work, stacking ensemble and SVR are found to be most suitable methods for COVID-19 time-series forecasting. A COVID-19 prediction study is performed using a deep learning framework in [21]. In this methodology, a COVID-19 Net is proposed, which is based on bidirectional gated recurrent units (GRUs) and convolutional neural network (CNN). In [22], a study is performed for the analysis of the temporal dynamics of COVID-19 outbreak in five different countries. The recurrence plot and mean-field kinetics are explored in this work. An improved model based on an adaptive neuro-fuzzy inference system is proposed for the forecasting of COVID-19 confirmed cases [23]. This method utilizes the pollination algorithm and the salp swarm algorithm to improve the effectiveness of the model.

In this article, an eigenvalue decomposition of Hankel matrix (EVDHM) and ARIMA-based automated model is developed for time-series forecasting. We have preferred the EVDHM-based method over EMD- and SSA-based method. As with EVDHM method, if the decomposed component does not satisfy the stationarity criterion, then it is possible to decompose it further using EVDHM. This is not possible with the SSA and EMD method. Hence, the performance of SSA- and EMD-based model is limited compared with the EVDHM methods, in the analysis of nonstationary time series. Moreover, the performance of the EMD-based model deteriorates due to the mode-mixing problem. The EVDHM-ARIMA model is applied to forecast the COVID-19 time series to test the effectiveness. The rest of this article is organized in the following manner. Section II describes the EVDHM and ARIMA. The proposed methodology is explained in Section III, and all the results related to the data series are given in Section IV. Finally, it is concluded in Section V.

II. Method

A. Eigenvalue Decomposition of Hankel Matrix

The EVDHM is a suitable method for nonstationary data processing, which is based on EVD applied over the Hankel matrix formed using time series [24]. The resulting components incorporate slowly varying trends, noise, and oscillatory trends. There are several applications of EVDHM, such as in cardiac signal analysis [25], [26], muscle signals [27], and complex data analysis [28].

A data series 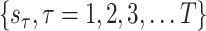can be used to shape a Hankel matrix of size 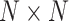as follows [24]:

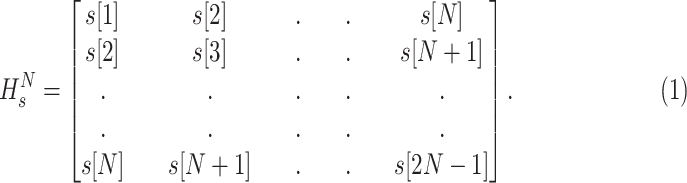The EVDHM is applied over 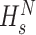matrix to secure the eigenvector matrix ( 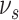) and eigenvalues matrix ( ) as follows [24]:

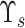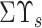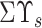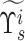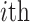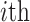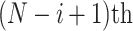In matrix , values other than diagonal elements are zero. The sum of magnitude of all the eigenvalues is . The vital eigenvalues pairs perform a crucial role in the decomposition process. Summation of magnitude of all the vital eigenvalue pairs should be at least 95% of . A new eigenvalue matrix can be formed using vital eigenvalue pair, which holds only the and eigenvalues and replaces the remaining eigenvalues pairs by zero. The matrix 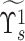is formed using the first vital eigenvalue pair and can be represented as follows [24]:

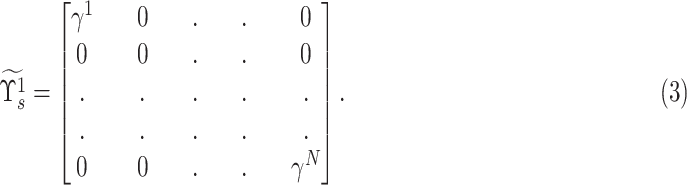The matrix 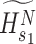is reconstructed by the use of matrix 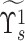and 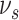as given follows [24]:

The first decomposed component, 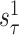, is computed from the 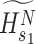by taking the average of skew-diagonal elements. The remaining components are computed using the subsequent vital eigenvalue pairs.

After getting all the decomposed components, the ARIMA method is applied. The detailed explanation of the ARIMA method is given in Section II-B.

B. ARIMA

The ARIMA was proposed by Box et al. [6] in year 1976. It is one of the crucial data-series estimation and analysis methods. The ARIMA structure is assumed to hold a linear functional relation with output. The ARIMA model is basically mentioned as ARIMA ( 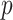, , 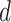and 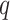) with the following consideration, where 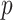is the order of the AR, 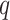is the order of moving average (MR), and 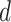is the order of integration which is the differenced series. All three parameters are nonnegative integer values. Consider a data series 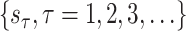. The conventional ARIMA ( 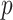, , 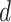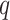) model of the data series 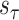can be expressed as follows [6]:

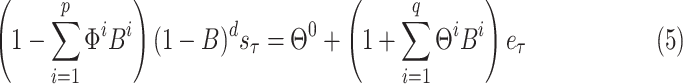where 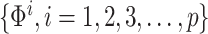are the coefficients of the AR component and 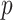is the order of the AR component. The back shift operator 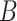is defined as 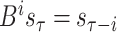; the order of differencing is also known as “integrated,” and 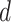is applied for transforming data from time-dependent mean to time independent mean. It is applied to find a stationary series in statistical sense. 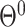represents the deterministic trend term. 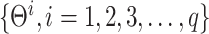are the coefficient parameters of MR component. 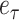is the independent identically distributed model error and referred to as white Gaussian noise with zero mean and 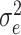variance [6]. On considering the differencing order 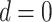, an ARIMA model reformed to an ARMA model.

On establishing the eigenvalue decomposition into ARIMA model, the linear ARIMA model can be promoted for nonlinear model that can be termed the EVDHM-ARIMA model.

III. Eigenvalue Decomposition of Hankel Matrix and ARIMA-Based Model

The ARIMA models cannot be estimated satisfactorily for nonlinear and nonstationary complex data series. However, none of the sole models is enough for estimating all types of data sets [6]. The EVDHM method is applied to decompose a nonstationary data series into subsequent monocomponent subseries. In this process, the nonstationarity of subseries is less compared with the main data series. Several unit-root tests are available to check the stationarity of data series [29]. The EVDHM is applied to transform a nonstationary series into multiple subseries that are more close to stationarity. This phenomenon assists the ARIMA method for better modeling and increases the estimation accuracy.

The use of ARIMA model requires to check the stationarity of input data series [30]. Moreover, if the input data series does not satisfy the stationarity criteria, a difference of the input data series has to be taken, and stationarity is evaluated on the differenced data series. A difference in the resulting data series is performed iteratively until the stationarity is satisfied. Assessing the stationary behavior of the input data series is a complex process, and the value of integration order parameter 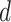should be as minimum as possible. The EVDHM-based decomposition is competent to avoid the higher values of 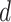, and decomposed subseries components satisfy with the lower values of 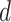compared with the original data series.

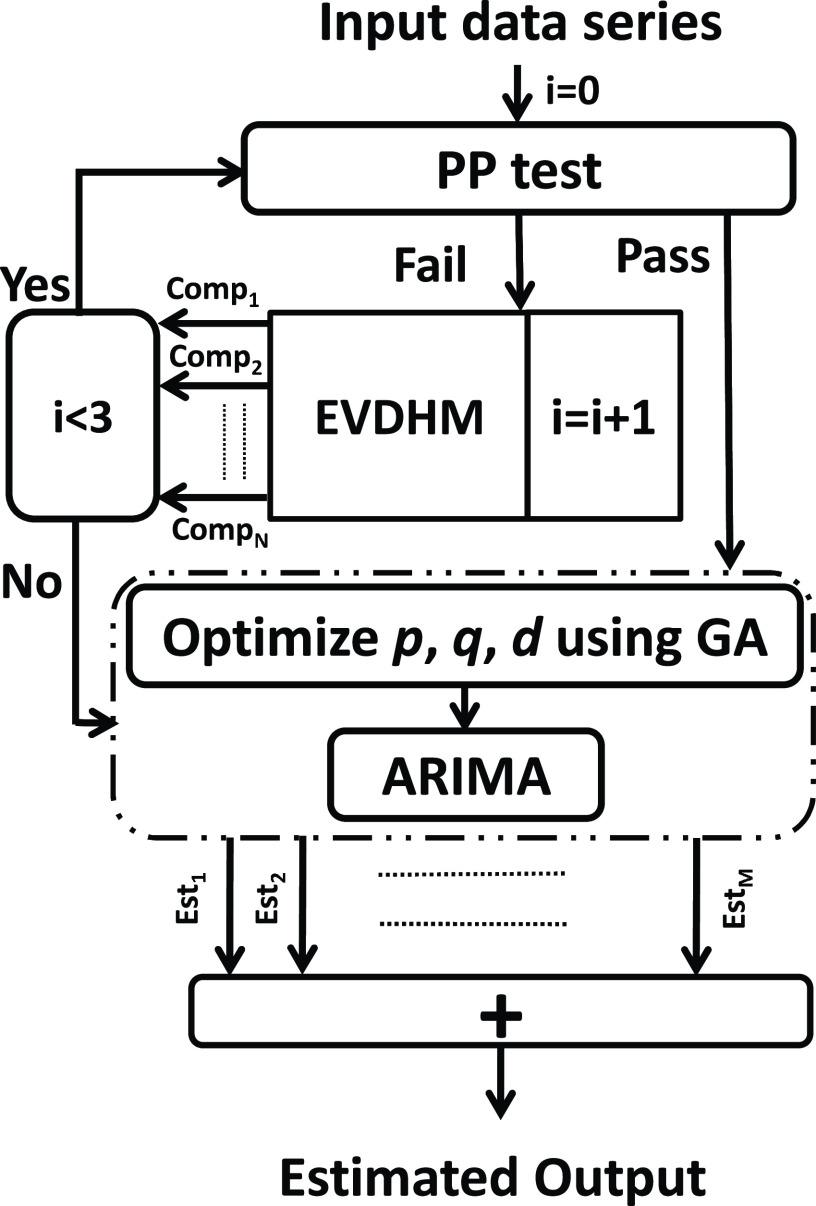
The EVDHM-ARIMA-based hybrid procedure is applied to derive a reliable prediction based on the past data series. Initially, the Phillips–Perron test (PPT) is applied to check the stationarity of the data series. If PPT fails, the EVDHM method is applied, and as a result, subseries are secured and called monocomponent series. Again, PPT is applied over all the monocomponents to check the stationarity. If some components fail the PPT, decomposition is performed using EVDHM. This process of decomposition and stationarity evaluation performed until all the components satisfy the PPT or up to maximum three iterations. After that, all the monocomponent series are modeled using the ARIMA model and their independent future estimation is conducted. In the end, all are combined to produce a composite forecasting outcome. The comprehensive procedure of the proposed EVDHM-ARIMA-based forecasting method is presented in Fig. 1 and its algorithm is given in Algorithm 1. The PPT is discussed in Section III-A, which is applied for stationarity evaluation in the proposed method.

Algorithm 1 Proposed EVDHM-ARIMA-Based Time-Series Forecasting Algorithm

• Input:Data series ( ),
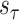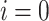
• Output:

  e,r

• 1Apply PPT

• (I) If Pass ( 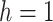, 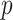-value < 0.05)

• switch to step 6.

• (II) If Fail,( 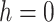, 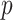-value )

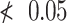• switch to step 2.

• 2Apply EVDHM over the data series

• 

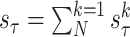
• 3Update i,

• 

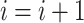
• 4Check, ,

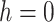• If Pass:

• switch to next step.

• If fails:

• switch to step 6

• 5Check, ,

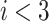• If Pass:

• switch to step 1.

• If fails:

• switch to next step

• 6Apply GA to optimize the 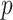, , 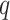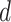parameters of ARIMA

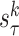• for for

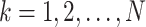
• 7Estimate the future value of 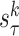for

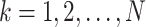
• using ARIMA

• 8Estimated components:

• Est₁, Est₂, ,

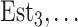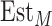
• 9
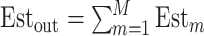
• 10Est_out is the Final output

Fig. 1.

Block diagram of the proposed EVDHM-ARIMA-based time-series forecasting method.

A. Unit Root Test for Stationarity Evaluation

The popular unit-root tests are Dickey–Fuller test (DFT), augmented DFT (ADFT), PPT, and others. In the proposed work, PPT is applied due to its automated characteristic, and it is the advanced version of DFT and ADFT [29]. The PPT is used to check the stationarity of each decomposed subsignal. For a univariate data series, the null hypothesis of unit root is tested with nonparametrically modified test statistics [31]. Due to the nonparametric property, model and lagged parameter are not required. In the present work, 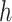is the Boolean decision vector for the tests. The left-tailed probabilities are noted by 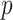-values. The maximum 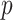-value is 0.999 and the minimum 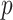-value is 0.001 in the proposed method. The PPT has the null hypothesis ( 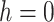) that the underlying time series is nonstationary against the alternative ( 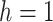) that the underlying time series is stationary. If the 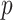-value is less than the statistically significant level (0.05), the null hypothesis 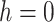is rejected and the alternate hypothesis 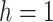can be accepted. Hence, the underlying time series is considered as stationary. If the 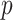-value is greater than 0.05, the null hypothesis is not rejected. Hence, the underlying time series cannot be considered as a stationary series.

B. Parameter Selection of ARIMA Model

The ARIMA parameters of the decomposed components are required for model fitting. In general, autocorrelation function (ACF) and partial autocorrelation function (PACF) are used to select the values of 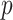and 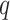. If there are many high positive ACF coefficients, the order of differentiation should be high. Moreover, the selection of 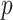, , 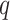and 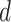using ACF and PACF is a manual process that is not suitable for the automated process. To overcome this issue, the GA-based ARIMA parameters optimization method is utilized. The three variables 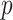, , 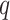and 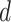are selected using the GA for the minimum value of Akaike information criterion (AIC). The minimization of AIC value is set as the objective function in GA. Three variables are varied between 0 and 5. The AIC is computed for each selected value of the 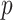, , 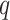and 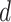. 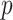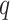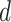Finally, we have selected the , , and values using GA for which the AIC showed the minimum value.

Generally, an estimated minimum error provides the optimal parameter for the formation of a suitable model. As the order of parameters is increased, the error is reduced, but complexity due to higher order is increased. To overcome this issue, AIC is utilized for the optimal parameter selection, which can best fit the model to the training data. The AIC is defined as [32]

where 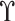is the maximum value of the likelihood function of the model and 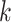represents the number of parameters of the model.

C. Role of EVDHM to Improve Estimation

The EVDHM method is based on the eigenvalues of the Hankel matrix formed using the data series. EVDHM is a nonparametric approach, and the ARIMA parameters selection process is automated in the present work. The PPT is also a nonparametric stationarity test that is used in this work. Hence, the complete method becomes a nonparametric approach for data-series forecasting.

The general process of estimation using ARIMA requires the input parameters selection, such as order of 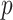, , 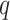and 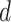. The ACF and PACF are well-known functions to find the values of these parameters. The major issue of using ACF and PACF is manual observation, which degrades the optimization process. Moreover, ARIMA can be applied over a stationary data series. If the data series is nonstationary, a difference operation has to be performed over the data, which increases the order of integration ( 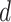). It makes the process complex. EVDHM is applied with ARIMA to enhance the estimation by decomposing the nonstationary data series to move toward the stationarity in the decomposed components. This approach is very useful in data analysis.

To evaluate the importance of EVDHM in the proposed model, we have taken the COVID-19 infected person data set of India in which daily new COVID-19 cases from January 22, 2020 to June 10, 2020 are opted. The data set is provided by the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University and available at [33]. The COVID-19 daily new cases for India ( 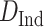) from January 22, 2020 to June 10, 2020 are shown in Fig. 2(a). Initially, PPT is applied over the main data series [see Fig. 2(a)], and it fails. Therefore, it is decomposed using EVDHM with 90% threshold criteria. Its decomposed components using EVDHM are shown in Fig. 2(b)–(k) and denoted as CP₁, CP₂, CP₃, …, CP₁₀. The trend of data series can be observed in CP₁ [see Fig. 2(b)], and variability is present in the remaining components and can be noticed in CP₂–CP₁₀ [see Fig. 2(c)–(k)]. Out of ten decomposed components, the first two components fail the PPT, as shown in Table I. Therefore, the second-stage decomposition is applied over CP₁ and CP₂, which results the component CP₁₁ for CP₁ and CP₂₁, CP₂₂, CP₂₃, CP₂₄, and CP₂₅ for CP₂.. The PPT is again applied over CP₁₁ and CP₂₁–CP₂₅, which shows that CP₁₁, CP₂₁, CP₂₂, and CP₂₄ fail the PPT and their 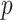-values are given in Table I.

Fig. 2.

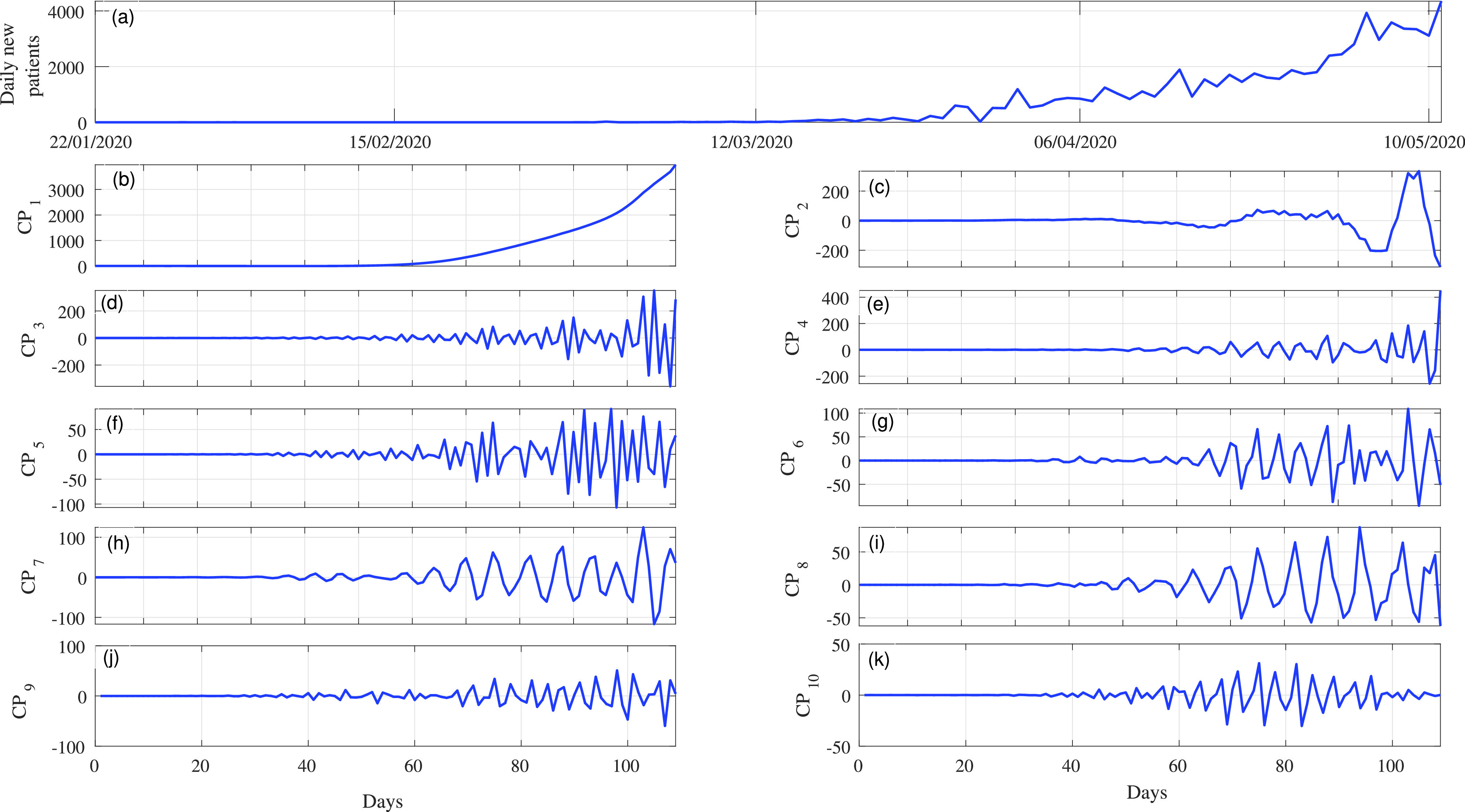
(a) COVID-19 time series (India data) and (b)–(k) its decomposed components using the EVDHM method represented as CP₁–CP₁₀.

TABLE I. 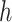-Values and 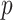-Values of PPT and SS Values for D_Ind Data and Its Decomposed Components Using the EVDHM Method.

Method	Iteration 1				Iteration 2				Iteration 3
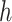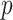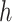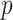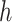	Components	-value	-value	SS value	Components	-value	-value	SS value	Components	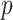-value	-value	SS value
EVDHM	CP1	0	0.9990		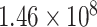CP11	0	0.9990		–	–	–	–
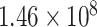	CP2	0	0.0764		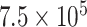CP21	0	0.1533		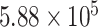CP211	0	0.141
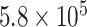									CP212	0	0.16
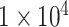					CP22	0	0.9926		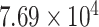CP221	0	0.99
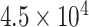									CP222	1	0.03
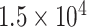									CP223	0	0.09	220.5
					CP23	1	0.0010		–	–	–	–
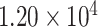					CP24	0	0.2477		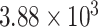CP241	0	0.40
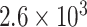									CP242	1	0.015	155.9
									CP243	1	0.006	43.47
					CP25	1	0.0047
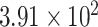	CP3	1	0.0010
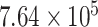	CP4	1	0.0010
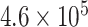	CP5	1	0.0010
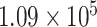	CP6	1	0.0010
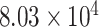	CP7	1	0.0010
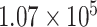	CP8	1	0.0010
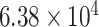	CP9	1	0.0010
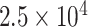	CP10	1	0.0010

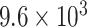The sum of squared (SS) values of the main data series and decomposed components is studied to evaluate the strength of the decomposed component. It is mathematically represented as

where 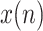is a data series having 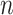samples. These values are shown in Table I, and it can be noticed that the SS value for the main signal is 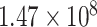, whereas the SS values for CP₂₁, CP₂₂, and CP₂₄ are 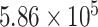, , 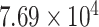and 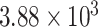, respectively. The strength of CP₂₁, CP₂₂, and CP₂₄ is less than 2% of the strength of the main signal. These components play insignificant role in model forming and forecasting. Therefore, further decomposition is not necessary. Moreover, the SS values of CP₁ and CP₁₁ are almost the same and it is a trend component that is generally nonstationary component. Therefore, we can select either CP₁ or CP₁₁, which is nearly the same components.

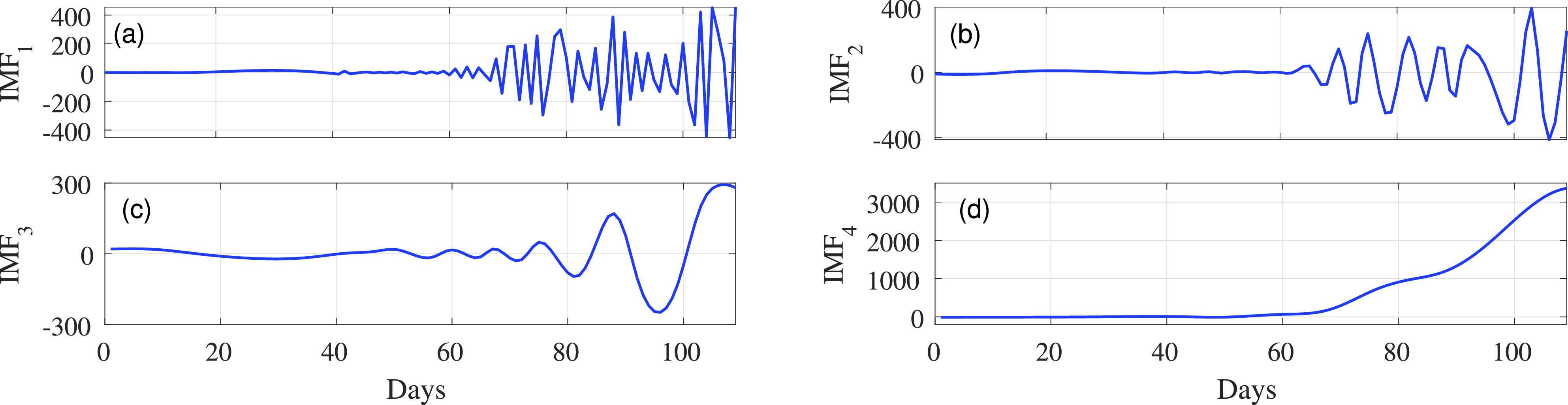
In order to check the effectiveness of the EVDHM-based decomposition in comparison with other methods, it is compared with the EMD-SSA-based decomposition for forecasting. The EMD-SSA-based decomposed components are shown in Figs. 3 and 4. The EMD decomposes 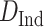into four components and out of which two components fail the PPT. There is more chance of nonstationarity in these components as EMD holds mode mixing between the components. The result of the PPT for the decomposed components obtained from the COVID-19 India data series using SSA and EMD is presented in Table II with the SS values corresponding to each decomposed component. Similarly, SSA also gives two components that do not satisfy PPT. The components that do not satisfy the PPT possess high SS value and contribute significantly in model forming and forecasting. Further decomposition cannot be applied to the components acquired using SSA and EMD as these methods result the same decomposed components as obtained in the first iteration. Therefore, using SSA and EMD, the nonstationarity can be reduced only up to a certain level. However, the EVDHM method can decompose a nonstationary time series in a better way and becomes more suitable in analyzing these kinds of signals.

Fig. 3.

Decomposed components of the COVID-19 time series (India data) using the EMD method represented as IMF₁–IMF₄.

Fig. 4.

Decomposed components of the COVID-19 time series (India data) using SSA represented as CP₁–CP₁₀.

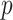TABLE II. -Values and -Values Secured by Applying PPT Over the Decomposed Components Obtained From the COVID-19 Daily New Cases Series for India Using the SSA and EMD Methods.

Method	Components	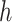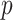-value	-value	SS value
SSA	CP1	0	0.9990
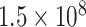	CP2	0	0.5820
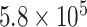	CP3	1	0.0010
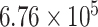	CP4	1	0.0010
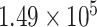	CP5	1	0.0010
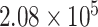	CP6	1	0.0010
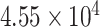	CP7	1	0.0010
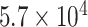	CP8	1	0.0010
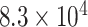	CP9	1	0.0010
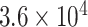	CP10	1	0.0010
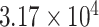EMD	IMF1	1	0.0010
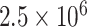	IMF2	1	0.0010
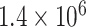	IMF3	0	0.584
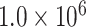	IMF4	0	0.999

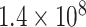IV. Results and Discussion

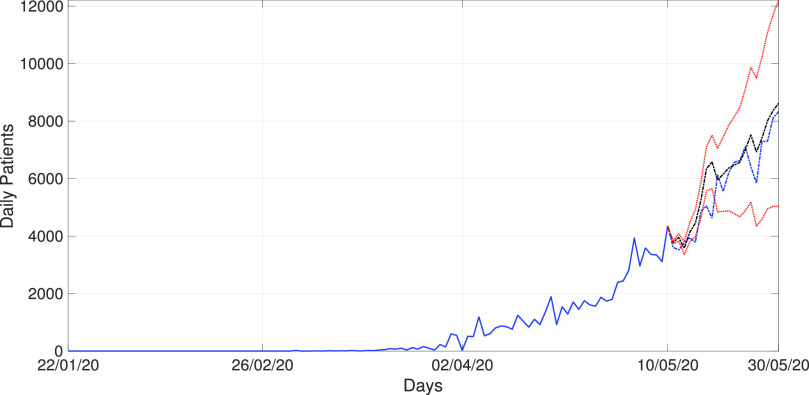
In this work, the proposed strategy is applied to predict the daily new patients affected by novel coronavirus disease (COVID-19) in India, USA, and Brazil. It is helpful to predict the daily new cases for recent days which in turn useful for in time strategic planning. Hence, essential steps can be executed for suppressing the effect of underlying disease. As discussed in Section III, for model formation, the Indian cases are considered from January 22, 2020 to May 10, 2020. Thus, the time series contains 109 days of data corresponding to the daily COVID-19 patients for India. Until May 10, 2020, there are total 67 161 persons affected by COVID-19 and new cases reach nearly 4300. The EVDHM-ARIMA model has fitted on 109 days of daily patients data, and furthermore, it is used for forecasting of daily cases for next 20 days, i.e., until May 30, 2020. First, the time series of daily number of COVID-19 patients is subjected to the EVDHM method. Hence, the time series is decomposed into the subcomponents, and stationarity is evaluated using PPT. Fig. 5 shows the COVID-19 daily new cases for India.

Fig. 5.

Predicted COVID-19 time series for India using the proposed method during May 11, 2020 to May 30, 2020. Note: In Figs. 5–8, the blue solid line shows the training period. The black dashed–dotted line shows the forecast values. The blue dotted line represents the actual data values in the forecast period. The red dotted lines represent the RMSE with 95% confidence interval.

To measure the forecasting performance of the proposed methodology, the root-mean-square error (RMSE) is computed. It is able to satisfy the triangle inequality criteria for metric distance [34]. It is defined as

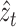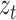where and denote the predicted and original COVID-19 time series, respectively. In general, RMSE is taken in ±95% observation interval to visualize the maximum possible range for predicted value. Next 20 days forecast values are computed using the proposed method. The mean of RMSE of forecast value for COVID-19 India data is 702.6. In Fig. 5, the RMSE values are shown in red dotted lines with 95% confidence interval and show the expected range of COVID-19 cases during these days.

The optimal values of 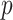, , 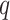and 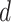for COVID-19 India data are summarized in Table III. For the trend component, CP₁ that is further decomposed and becomes CP₁₁, and the optimal values of 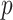, , 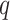and 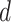are 2, 2, and 1, respectively. As component fails the stationarity property, it is differentiated and parameter 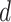is taken as 1. In Table III, it can be observed that the values of parameter 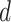are higher in most of the cases when components are close to the nonstationary property. Therefore, the 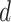value is higher for CP₁₁, CP₂₁₁, CP₂₁₂, CP₂₂₁, CP₂₂₃, and CP₂₄₁. The difference of greater order is required to fit the ARIMA model for these components compared with the stationary components. The original time series has 109 days of data. These 109 samples of time series are utilized to fit the ARIMA model to each of the decomposed components. Furthermore, the obtained model is explored to predict the next 20 samples of all the decomposed components. Thereafter, the final predicted samples of the original COVID-19 time series are acquired by summing all the predicted components obtained for the decomposed components.

TABLE III. Optimal Values of 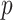, , 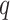and 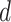Parameters for the Different Components Obtained Using the EVDHM Method for Covid-19 India Data.

Component
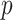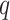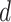CP3	3	2	0
CP4	2	2	0
CP5	2	1	0
CP6	2	2	0
CP7	2	3	0
CP8	3	2	0
CP9	2	2	0
CP10	3	2	0
CP11	2	2	1
CP211	2	2	1
CP212	2	2	1
CP221	2	1	1
CP222	2	2	0
CP223	2	1	1
CP241	2	2	1
CP242	2	2	0
CP243	2	2	0

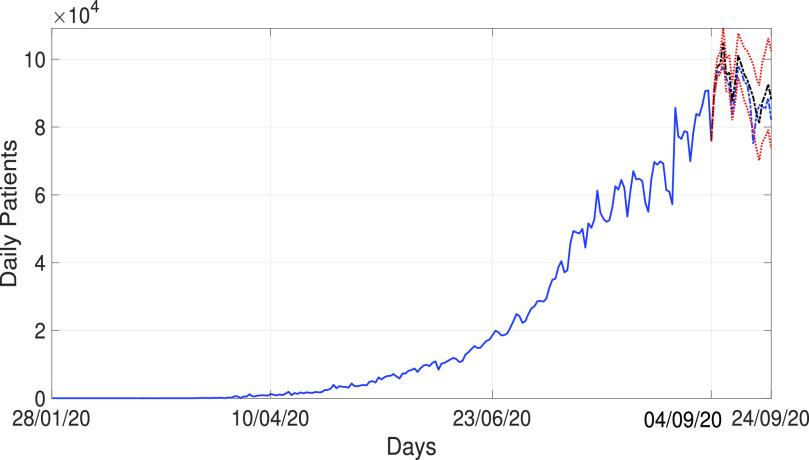
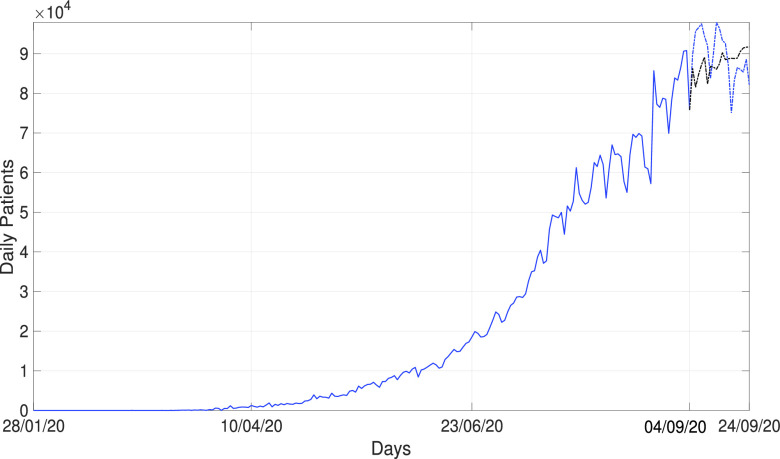
The EVDHM-ARIMA method is also applied for large COVID-19 data of India, which is taken from January 28, 2020 to September 4, 2020 for training the model. The predicted values are computed from September 5, 2020 to September 24, 2020, as shown in Fig. 6. These predicted values are very close to the original sequence. The local changes in daily new cases are also preserved using the proposed method. There will be 94 500±13 160 daily new cases and total 6 753 861±945 541 cases in India at the end of September 2020.

Fig. 6.

Predicted COVID-19 time series for India using the proposed method.

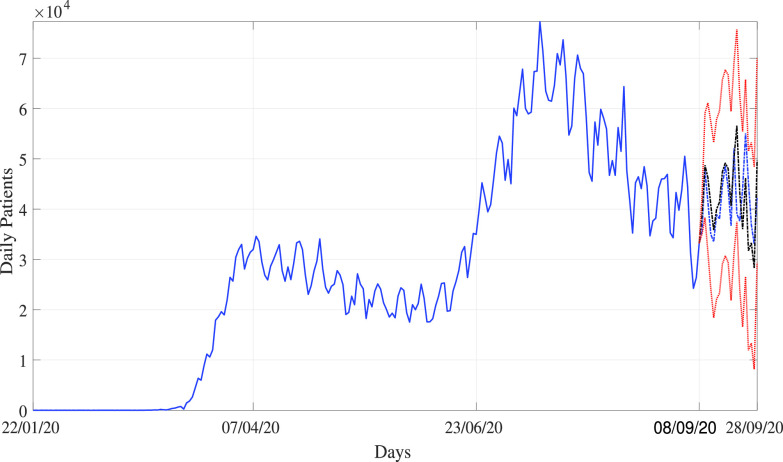
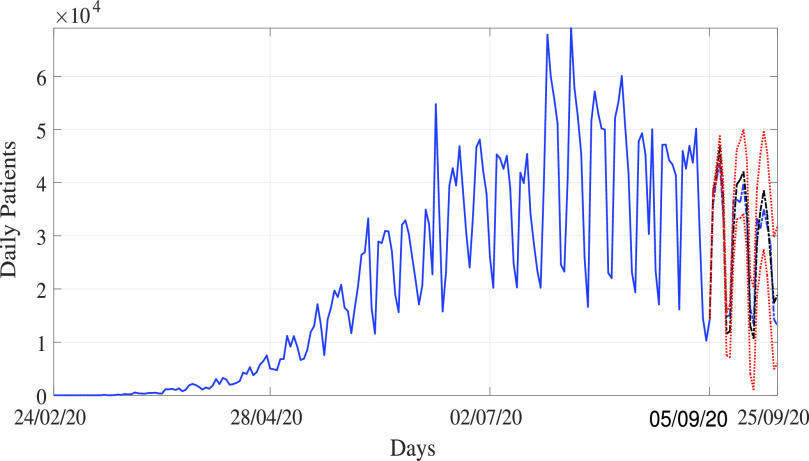
Moreover, the proposed method is also applied on the COVID-19 daily new cases of USA and Brazil country. Also, forecasting is done for the next 20 days similarly as done in the case of Indian data series. Predicted time series plots using the proposed methodology for COVID-19 USA and Brazil can be seen in Figs. 7 and 8, respectively. For USA on September 28, 2020, there will total 7 634 825±968 876 COVID-19 cases and approx 48 185 ± 6746 daily new cases on considering ±95% confidence interval. The Brazil daily new cases are very oscillatory in nature, which increases and decreases in a very short duration. In Brazil on September 25, 2020, there will be total 4 918 642±541 051 COVID-19 cases and nearly 35 247 ± 3877 daily new cases on taking ±95% confidence interval.

Fig. 7.

Predicted COVID-19 time series for USA using the proposed method.

Fig. 8.

Predicted COVID-19 time series for Brazil using the proposed method.

The EMD- and ARIMA-based models for the forecasting of time series are also proposed in [4] and [35]. In the EMD method, mixing of the modes is the major issue that causes a decline in the prediction performance. The wavelet and ARIMA-based prediction analysis is also preformed for the COVID-19 forecasting in [19]. In this method, wavelet is applied over residual to correct the local changes and overall performance is not improved that much due to dependence on residue. The predicted time series for COVID-19 data of India using wavelet-ARIMA method is presented in Fig. 9, in which it is noticed that the predicted values are far away from the actual values. In comparison to this, the EVDHM-ARIMA gives better results, which can be observed in Fig. 6. The performance of wavelet-ARIMA model depends on the accurate choice of mother wavelet that is a crucial problem [36]. Hence, the wavelet-ARIMA-based model performance may be affected due to the mother wavelet. The proposed method in our work is robust toward these kinds of limitations. Moreover, residual of the time series is used to fit the wavelet-ARIMA-based model. However, in our work, decomposed components of the time series using EVDHM are used to fit the ARIMA model, which is more suitable to deal with the nonstationarity present in the underlying time series.

Fig. 9.

Predicted COVID-19 time series for India data using the wavelet-ARIMA method [19]. The blue solid line shows the training period data. The black dashed–dotted line shows the forecast values. The blue dotted line represents the actual data values in forecast duration.

The present model is effective for short-term forecasting based on previous data. The availability of larger number of samples in the time series data provides better model fitting. In case of smaller time series, parameter selection for ARIMA model needs to perform carefully. Larger values of 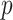make the ARIMA model unstable. In such a situation, lower values of 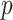are suggested or larger samples need to be taken in the time series. The proposed method can also be extended for short-term forecasting of stock exchange data for intraday and weekly projection of individual stock. The EVDHM-ARIMA-based forecasting model can also be applied for wind power, temperature, inertial navigation system error correction [37], solar radiation, electricity load, and many other time-series analysis. It can also be used in machine-learning-based models for performance enhancement. The results of the proposed method are more accurate for the forecasting of few future sample values. Increasing the number of forecast samples causes the larger values of forecasting error. To avoid this issue, further sample values can be forecast with correcting the short-term predicted values using the actual outcome. This process can be applied subsequently as more and more data are received. Therefore, an automated decision support system can be developed in various research fields.

V. Conclusion

In this work, a time-series forecasting model based on EVDHM and ARIMA is presented. The ability of EVDHM to decompose the nonstationary time series into stationary subcomponents is used in multiple iterations. ARIMA is applied over the decomposed subcomponents for model fitting, and short-term future values are forecasted based on the obtained model. The GA is applied to get the optimized values of the ARIMA parameters 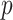, , 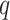and 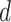with minimizing AIC values, which is correlated with the error. The proposed method is able to forecast the COVID-19 daily new cases for India, USA, and Brazil. In future, with slight modification, the proposed method can be implemented for other types of data, such as wind power, commodity supply and consumption data, electricity load, various systems error correction, and many others. A sensors data-based decision-making automated algorithms can also be developed using the proposed methodology. Moreover, the proposed method can also be extended for multivariate-series forecasting model.

Biographies

Rishi Raj Sharma received the M.Tech. degree from the ABV-Indian Institute of Information Technology and Management, Gwalior, India, in 2015 and the Ph.D. degree from IIT Indore, Indore, India, in 2018.

He has worked as an Assistant Professor with FET, R. B. S. College, Agra, India, and the Military College of Telecommunication Engineering, Mhow, India. He was a Research Scientist with the National Brain Research Centre, Gurgaon, India. He is currently working as an Assistant Professor with the Defence Institute of Advanced Technology, Pune, India. He was with the Product Development Team to develop ATULYA (microwave sterilizer), which neutralizes COVID-19 virus. His area of research covers time–frequency analysis, signal processing, artificial intelligence, and applications in various fields, especially human physiology and automotive radar.

Dr. Sharma received the IET Science, Measurement and Technology Premium Award in 2019. He is an active reviewer of several journals.

Mohit Kumar received the B.Tech. degree in electronics and communication engineering from Uttar Pradesh Technical University, Lucknow, India, in 2009, the M.E. degree in electronic instrumentation and control engineering from Thapar University, Patiala, India, in 2013, and the Ph.D. degree in electrical engineering from IIT Indore, Indore, India, in 2019. During his Ph.D. thesis, he worked on the analysis and classification of electrocardiogram (ECG) signals.

He is currently working as a Post-Doctoral Fellow with IIT Kanpur, Kanpur, India. His research interests include time series analysis and forecasting, classification of biomedical signals, signal processing, and nonstationary signal analysis.

Shishir Maheshwari (Member, IEEE) received the B.E. degree in electronics and communication engineering from Rajiv Gandhi Technological University, Bhopal, India, in 2010, the M.Tech. degree in signal and image processing from the National Institute of Technology, Rourkela, India in 2014, and the Ph.D. degree from IIT Indore, Indore, India, in 2020.

He is currently working as an Assistant Professor with the Birla Institute of Technology and Science, Pilani, India. His research interests include biomedical signal and image processing, time–frequency analysis, and machine–deep learning applications to various signals.

Dr. Maheshwari is an active reviewer of several journals.

Kamla Prasan Ray (Senior Member, IEEE) received the M.Tech. degree in microwave electronics from the University of Delhi, New Delhi, India, in 1985 and the Ph.D. degree from the Department of Electrical Engineering, IIT Bombay, Mumbai, India, in 1998.

He is currently a Professor, the Dean (Sponsored Research), and the Head of the Department of Electronics Engineering and Computer Science, Defence Institute of Advanced Technology (DIAT), DRDO, Pune, India. In 2016, he was the Program Director of SAMEER (MeitY), Mumbai, where he joined SAMEER (TIFR) in 1985 and worked for over 31 years in the areas of electromagnetics, RF, and microwave systems/components and developed expertise in the design of antenna elements/arrays and high-power RF/microwave sources for RADAR, scientific, and industrial applications. He has successfully executed over 50 projects sponsored by various government agencies (DRDO/MOD, ISRO/DOS, DAE, DST/DSIR/TIFAC, Meity, DBT, IMD, BHEL, and so on) and many industries in the capacity of main designer, a chief investigator, a project manager, and so on. Recently, he developed a microwave sterilizer, ATULYA, to neutralize COVID-19 virus. He was a Guest/Invited/Adjunct Faculty Member in electrical engineering with the Department of Electrical Engineering, IIT Bombay, the Goa Engineering College, Veling, India, the University of Mumbai, Mumbai, and CEERI (CSIR) Pilani, Pilani, India, for postgraduate courses. He has guided ten Ph.D. students and more than 100 M.Tech. students and evaluated more than 25 Ph.D. theses. He has coauthored a book with Prof G. Kumar for Artech House, USA, and published over 450 research papers in international/national journals and conference proceedings. He holds three patents, earned ten transfer of technology (ToT), and filed five patents. He has been in advisory capacity for many engineering colleges, polytechnic, and international/national conferences, chaired many sessions, and delivered more than 115 invited talks, which also includes “First Abdul Kalam Memorial Lecture” at Interim Test Range (ITR), DRDO, Chandipur, in 2018, and “Ram Lal Wadhwa Lectures” in 2018.

Dr. Ray is a member of many national-level scientific committees of various ministries and departments. He is a fellow of IETE, a Life Member of the Instrument Society of India, and an Engineer of the EMI/EMC Society of India. He received many awards, including most coveted IETE-Ram Lal Wadhwa Award in 2018, the IETE-Ranjna Pal Memorial Award in 2014, and several research paper awards. He is also an Associate Editor of International Journal on RF and Microwave Computer-Aided Engineering (John Wiley).