From Prediction to Prescription: Evolutionary Optimization of Nonpharmaceutical Interventions in the COVID-19 Pandemic

Abstract

Several models have been developed to predict how the COVID-19 pandemic spreads, and how it could be contained with nonpharmaceutical interventions, such as social distancing restrictions and school and business closures. This article demonstrates how evolutionary AI can be used to facilitate the next step, i.e., determining most effective intervention strategies automatically. Through evolutionary surrogate-assisted prescription, it is possible to generate a large number of candidate strategies and evaluate them with predictive models. In principle, strategies can be customized for different countries and locales, and balance the need to contain the pandemic and the need to minimize their economic impact. Early experiments suggest that workplace and school restrictions are the most important and need to be designed carefully. They also demonstrate that results of lifting restrictions can be unreliable, and suggest creative ways in which restrictions can be implemented softly, e.g., by alternating them over time. As more data becomes available, the approach can be increasingly useful in dealing with COVID-19 as well as possible future pandemics.

I. Introduction

The COVID-19 crisis is unprecedented in modern times, and caught the world largely unprepared. Since there is little experience and guidance, authorities have been responding in diverse ways. Many different nonpharmaceutical interventions (NPIs) have been implemented at different stages of the pandemic and in different contexts. On the other hand, compared to past pandemics, for the first time almost real-time data is collected about these interventions, their economic impact, and the spread of the disease. These two factors create an excellent opportunity for computational modeling and machine learning.

Most of the modeling efforts so far have been based on traditional epidemiological methods, such as compartmental models [1]. Such models can be used to predict the spread of the disease, assuming a few parameters, such as the basic reproduction number 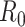can be estimated accurately. New ideas have also emerged, including using cell-phone data to measure social distancing [2]. These models have been extended with NPIs by modifying the transmission rates: each NPI is assumed to reduce the transmission rate by a certain amount [3]–[5]. Such models have received a lot of attention: in this unprecedented situation, they are our only source of support for making informed decisions on how to reduce and contain the spread of the disease.

However, epidemiological models are far from perfect. Much about how the disease is transmitted, how prevalent it is in the population, how many people are immune, and how strong the immunity is, is unknown, and it is difficult to parameterize the models accurately. Similarly, the effects of NPIs are unpredictable in that their effects vary based on the cultural and economic environment and the stage of the pandemic, and above all, they interact in nonlinear ways. To overcome the uncertainty, data is crucial. Model parameters can be estimated more accurately by fitting them to existing data. With enough data, however, it is also possible to use machine learning simply to model the data with few assumptions. The unknown epidemiological, cultural, and economic parameters and interactions are expressed in the time series of infections and NPIs. Machine learning can then be used to construct a model, such as a recurrent neural network, that predicts the outcomes accurately without having to understand precisely how they emerge.

The data-driven modeling approach is implemented and evaluated in this article. An LSTM neural network model [6], [7] is trained with publicly available data on infections and NPIs [8] in a number of countries and applied to predicting how the pandemic will unfold in them in the future. The predictions are cascaded one day at a time and constrained to a meaningful range. Even with the current limited data, the predictions are surprisingly accurate and well-behaved. This result suggests that the data-driven machine learning approach is potentially a powerful new tool for epidemiological modeling.

The main contribution of the article, however, is to demonstrate that machine learning can also be used to take the next step, i.e., to extend the models from prediction to prescription. That is, given that we can predict how the NPIs affect the pandemic, we can also automatically discover effective NPI strategies. The technology required for this step is different from standard machine learning. The goal is not to model and predict processes for which data already exists, but to create new solutions that may have never existed before. In other words, it requires extending AI from imitation to creativity.

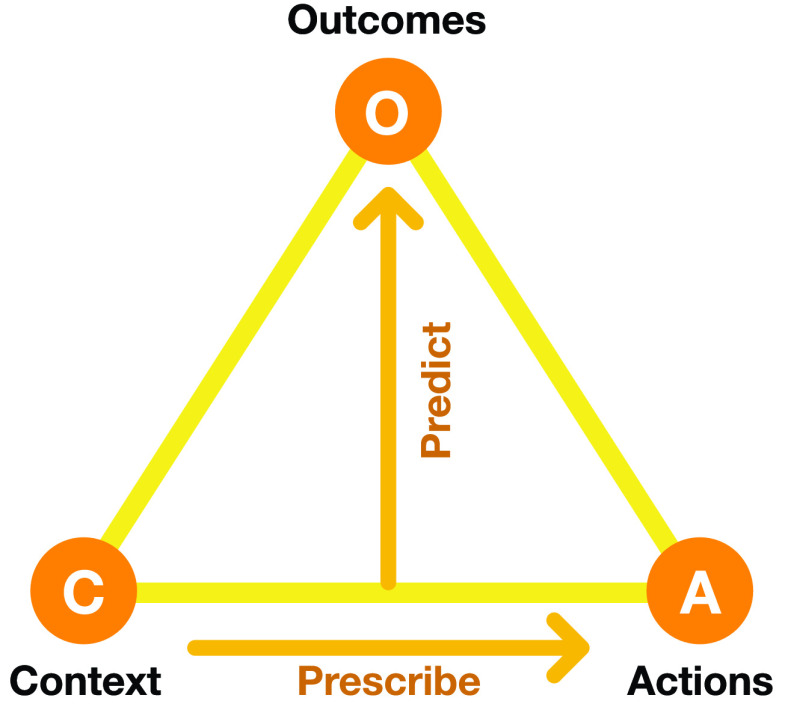
This extension is indeed underway in AI through several approaches, such as reinforcement learning, Bayesian parameter optimization, gradient-based approaches, and evolutionary computation [9]–[11]. The approach taken in this article is based on evolutionary surrogate-assisted prescription (ESP; [12]), a technique that combines evolutionary search with surrogate modeling (Fig. 1).

Fig. 1.

Elements of the ESP decision optimization method. A predictor is trained with historical data on how given actions in given contexts led to specific outcomes. For instance in the NPI optimization problem, given the state of pandemic in a particular country and the NPIs in effect, it predicts the future number of cases and the cost of the NPIs. The Predictor can be any machine learning model trained with supervised methods, such as a random forest or a neural network, or even a simulation, such as an epidemiological model. The Predictor is then used as a surrogate in order to evolve a Prescriptors, i.e., neural networks that implement decision policies (i.e., NPIs) resulting in best possible outcomes. With multiple conflicting objectives (such as cases and cost), evolution results in multiple Prescriptors, each representing a different tradeoff, from which a human decision maker can choose the ones that best matches their preferences.

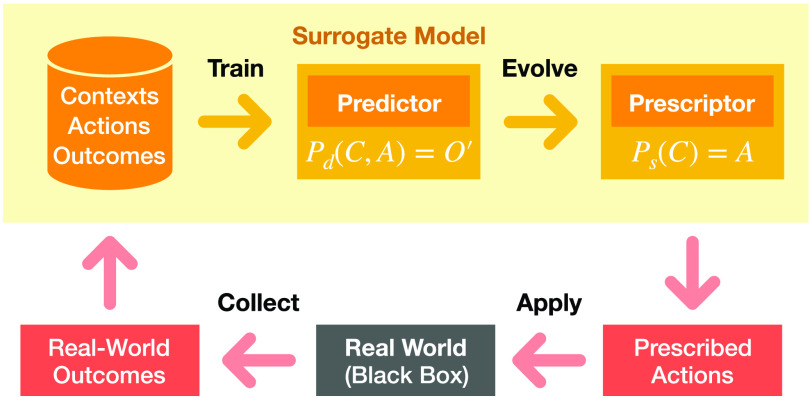
In ESP, a predictive model is first trained through standard machine learning techniques, such as neural networks. Given actions taken in a given context (such as NPIs at a given stage of the pandemic), it predicts what the outcomes would be (such as infections, deaths, and economic cost). A prescriptive model, another neural network, is then constructed to implement an optimal decision strategy, i.e., what actions should be taken in each context. Since optimal actions are not known, the Prescriptor cannot be trained with standard supervised learning. However, it can be evolved, i.e., discovered through population-based search. Because it is often impossible or prohibitively costly to evaluate each candidate strategy in the real world, the Predictor model is used as a surrogate. In this manner, millions of candidate strategies can be generated and tested in order to find ones that optimize the desired outcomes.

The ESP approach builds on prior work on evolutionary surrogate optimization [13]–[16]. Surrogate methods have been applied to a wide range of domains, ranging from turbomachinery blade optimization [17] to protein design [18] and trauma system optimization [19]. The current work extends the approach in complexity: the surrogate is not a blackbox function, but a recurrent neural network that integrates multiple time series of data; the solutions are not points that maximize the function, but are sequential decision strategies encoded in a neural network. Thus, while ESP is a case of evolutionary surrogate optimization, it pushes the boundaries of what is possible with it.

ESP has been used in several real-world design and decision optimization problems, including discovering growth recipes for agriculture [20] and designs for e-commerce websites [21]. It often discovers effective solutions that are overlooked by human designers. As a foundation for the current study, it was also applied to several sequential decision-making tasks where the ground truth is available, making it possible to evaluate its performance in comparison to standard reinforcement learning techniques, such as PPO, DQN, and direct evolution [12]. ESP was found to be more sample-efficient, reliable, and safe; much of these performance improvements were found to be due to a surprising regularization effect that incompletely trained Predictors and Prescriptors bring about.

Building on this foundation, this article focuses on a significant real-world application of evolutionary surrogate optimization, i.e., determining optimal NPIs for the COVID-19 pandemic. Using the data-driven LSTM model as the Predictor, a Prescriptor is evolved in a multiobjective setting to minimize the number of COVID-19 cases, as well as the number and stringency of NPIs (representing economic impact). In this process, evolution discovers a Pareto front of Prescriptors that represent different tradeoffs between these two objectives: 1) some utilize many NPIs to bring down the number of cases and 2) others minimize the number of NPIs with a cost of more cases. Therefore, the AI system is not designed to replace human decision makers, but instead to empower them: humans choose which tradeoffs are the best, and the AI makes suggestions on how they can be achieved. It therefore constitutes a step toward using AI not just to model the pandemic, but to help contain it.

The current implementation should be taken as a proof of concept i.e., a demonstration of the potential power of the approach. The currently available data is still limited in quantity, accuracy, and detail. However, the experiments already point to two general conclusions. First, school and workplace closings turn out to be the two most important NPIs in the simulations: they have the largest and most reliable effects on the number of cases. Second, partial or alternating NPIs may be effective. Prescriptors repeatedly turn certain NPIs on and off over time, for example. This is a creative and surprising solution, given the limited variability of NPIs that is available to the Prescriptors. Together these conclusions already suggest a possible focus for efforts on establishing and lifting NPIs, in order to achieve maximum effect and minimal cost.

The article begins with a background of epidemiological modeling and the general ESP approach. The datasets used, the data-driven predictive model developed, and the evolutionary optimization of the Prescriptor will then be described. Illustrative results will be reviewed in several cases, drawing general conclusions about the potential power of the approach. Future work on utilizing more detailed data and more advanced epidemiological and machine learning models, on improving reliability and creativity of solutions, and on making the system trustworthy and explainable will be discussed. An interactive demo, allowing users to explore the Pareto front of Prescriptors on multiple countries, is available at https://evolution.ml/esp/npi.

II. Background: Modeling Epidemics

In epidemiological modeling, mathematical and computational models are built to predict the progress of an infectious disease in order to inform intervention decisions to contain it. The models are based on basic assumptions about the disease as well as data about the population and disease and intervention history. In this section, different types of epidemiological models are characterized, followed by a review of existing COVID-19 modeling efforts, and the emerging opportunity for machine learning models.

A. Types of Epidemiological Models

Modern epidemic modeling started with the compartmental SIR model developed at the beginning of the 20th century [22]. The SIR model assumes susceptible individuals (S) can get infected (I) and, after a certain infectious period, die or recover (R), becoming immune afterwards. The model then describes global transmission dynamics at a population scale as a system of differential equations in continuous time. Depending on disease characteristics, these compartments and the flow patterns between them can be further refined: for instance in the case of HIV, mixing and contact depends on age groups [23]. The main limitation of such metapopulation models is that random mixing is limited between individuals within population subgroups, i.e., compartments.

Contact patterns can be represented more accurately through a network topology, taking into account geography, demographics, and social factors, and thus overcoming limitations of compartmental models [24]. The stochastic nature of transmissions was further demonstrated on five types of social and spatial networks for a population of 10 000 individuals [25]. Later studies focused on evolutionary and adaptive networks [26], aiming to model the dynamics of social links, such as frequency, intensity, locality, and duration of contacts, which influence the long term impacts of epidemics.

Indeed, multiple factors at different levels are now believed to influence how epidemics spread [27]. Models have become more detailed and sophisticated, relying on extensive computational power now available to simulate them. In addition to compartmental and network models, agent-based simulations have emerged as a third simulation paradigm. Agent-based approaches describe the overall dynamics of infection as a result of events and activities involving single individuals [28], resulting in potentially detailed but computationally demanding processes. For a more detailed review of the literature on epidemiological models and their mathematical insights see [29], [30].

B. Modeling the COVID-19 Pandemic

A variety of epidemiological simulations are currently used to model the COVID-19 pandemic. The focus is on simulating effects of NPIs in order to support decision making about response policies.

For instance, Stanford University [3] extended the SIR model up to nine compartments including susceptible, exposed, asymptomatic, presymptomatic, mild and severe symptomatic, hospitalized, deceased, and recovered populations, as well as a stochastic simulator for transitions between compartments, calibrated with MIDAS data [31]. At the time of this writing, the simulator supported up to three interventions at different times. In contrast, NPIs are implemented in a more granular fashion in the Bayesian inference model of Imperial College London [5]. Their model parameters are estimated empirically from ECDC data [32] for 11 countries. Deaths are then predicted as a function of infections based on the distribution of average time between infections and time-varying reproduction number 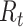. Further, the Institute for Health Metrics and Evaluation (IHME) of Washington University [4] combined compartmental models and mixed-effects nonlinear regression to predict cumulative and daily death rate as a function of NPIs. They also forecast health service needs using a micro-simulation model. As a further step, the University of Texas [2] developed a statistical model based on nonlinear Bayesian hierarchical regression with a negative-binomial model for daily variation in death rates. The novelty is to estimate social distancing using geolocation data from mobile phones, improving accuracy over the IHME model.

In general, most of COVID-19 forecast approaches use curve-fitting and ensembles of mechanistic SIR models with age structures and different parameter assumptions. Social distancing and NPIs are usually not represented directly, but approximated as changes in transmission rates. The main advantage is that running simulations require a few input parameters based on average data at population scale. In contrast, since contact dynamics in agent-based and network approaches results from events and activities of single individuals and their locations, they can be more accurate in modeling social distancing and NPIs. However, their parameters need to be calibrated appropriately, which is difficult to do with available data. Another challenge for current epidemiological modeling methods is that they require significant computing resources and sophisticated parallelization algorithms. COVID-19 pandemic has accelerated efforts to develop solutions to these challenges, and is likely to result in improved models in the future.

C. Opportunity for Machine Learning Models

Any of the above models that include NPI effects and generate long-term predictions could be used as the Predictor with ESP, even several of them together as an ensemble. Taking advantage of them is a compelling direction of future work (Section VIII). However, this article focuses on evaluating a new opportunity: building the model solely based on past data using machine learning. Given that data about the COVID-19 pandemic is generated, recorded, and made available more than any epidemic before, such a new approach may be feasible for the first time.

This data-driven approach has a lot of promise. The epidemiological models require several assumptions about the population, culture, and environment, depend on several parameters that are difficult to set accurately, and cannot take into account many possible nonlinear and dynamic interactions between the NPIs, and in the population. In contrast, all such complexities are implicitly included in the data. The data-driven models are phenomenological, i.e., they do not explain how the given outcomes are produced, but given enough data, they can be accurate in predicting them. This is the first hypothesis tested in this article; as shown in Section V, even with the limited data available at this point, data-driven models can be useful.

All the models discussed so far are predictive: Based on knowledge of the populations and the epidemic, and the data so far about its progress in different populations and efforts to contain it, they estimate how the disease will progress in the future. By themselves, these models do not make recommendations, or prescriptions, of what NPIs would be most effective. It is possible to set up hypothetical future NPI strategies manually and use the models to evaluate how well they would work. Such suggestions have been made in the COVID-19 pandemic as well [5], [33]–[35]. However, the space of potential strategies is huge (e.g., 10⁸³⁴ in this article). Only a few strategies can be tested in this manner, and the process is limited by the ability of human experts to create promising strategies. Given past experience with surrogate modeling and population-based search, automated methods may be more effective in this process. A method for doing so, ESP, will be described next.

III. Method: Evolutionary Surrogate-Assisted Prescription

ESP is a continuous black-box optimization process for adaptive decision-making [12]. In ESP, a model of the problem domain is used as a surrogate for the problem itself. This model, called the Predictor ( 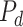), takes a decision as its input, and predicts the outcomes of that decision. A decision consists of a context (i.e., a problem) and actions to be taken in that context.

A second model, called the Prescriptor ( 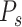), is then created. It takes a context as its input, and outputs actions that would optimize outcomes in that context. In order to develop the Prescriptor, the Predictor is used as the surrogate, i.e., a less costly and risky alternative to the real world.

More formally, given a set of possible contexts 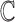and possible actions 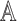, a decision policy 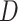returns a set of actions 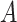to be performed in each context

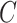
where 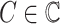and 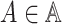. For each such 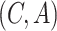pair there is a set of outcomes 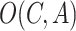, and the Predictor 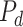is defined as

and the Prescriptor 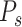implements the decision policy as

such that 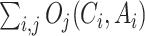over all possible contexts 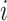and outcome dimensions 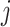is maximized (assuming they improve with increase). It thus approximates the optimal decision policy for the problem. Note that the optimal actions 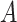are not known, and must therefore be found through search.

In the case of the NPI optimization problem, context 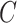consists of information regarding a region. This might include data on the number of available ICU beds, population distribution, time since the first case of the disease, current COVID-19 cases, and fatality rate. Actions 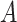in this case specify whether or not the different possible NPIs are implemented within that region. The outcomes 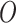measure the number of cases and fatalities within two weeks of the decision, and the cost of each NPI.

The ESP algorithm then operates as an outer loop that constructs the Predictor and Prescriptor models (Fig. 2).

• 1)Train a Predictor based on historical training data.
• 2)Evolve Prescriptors with the Predictor as the surrogate.
• 3)Apply the best Prescriptor in the real world.
• 4)Collect the new data and add to the training set.
• 5)Repeat.

In the case of the NPI optimization, there is currently no step 3 since the system is not yet incorporated into decision making. However, any NPIs implemented in the real world, whether similar or dissimilar to ESP’s prescriptions, will similarly result in new training data. As usual in evolutionary search, the process terminates when a satisfactory level of outcomes is reached, or no more progress can be made, or the system iterates indefinitely, continuously adapting to changes in the real world (e.g., adapting to the advent of vaccines or antiviral drugs).

Fig. 2.

ESP outer loop. The predictor can be trained gradually at the same time as the Prescriptor is evolved, using the Prescriptor to drive exploration. That is, the user can decide to apply the Prescriptor’s outputs to the real world, observe the outcomes, and aggregate them into the Predictor’s training set. However, any new prescriptions implemented in the real world, whether similar to the Prescriptors or not, can be used to augment the training dataset.

The Predictor model is built by modeling a 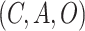dataset. The choice of algorithm depends on the domain, i.e., how much data there is, whether it is continuous or discrete, structured or unstructured. Random forests, symbolic regression, and neural networks have been used successfully in this role in the past [12], [20]. In some cases, such as NPI optimization, an ensemble of data-driven and simulation models may be useful, in order to capture expected or fine-grained behavior that might not yet have been reflected in the data (Section VIII).

The Prescriptor model is built using neuroevolution: neural networks because they can express complex nonlinear mappings naturally, and evolution because it is an efficient way to discover such mappings [36] and a natural way to optimize multiple objectives [37], [38]. Because it is evolved with the Predictor, the Prescriptor is not restricted by a finite training dataset, or limited opportunities to evaluate in the real world. Instead, the Predictor serves as a fitness function, and it can be queried frequently and efficiently. In a multiobjective setting, ESP produces multiple Prescriptors, selected from the Pareto front of the multiobjective neuroevolution run. The Prescriptor is the novel aspect of ESP: it makes it possible to discover effective solutions that do not already exist, even solutions that might be overlooked by human decision makers.

In the NPI optimization task, ESP is built to prescribe the NPIs for the current day such that the number of cases and cost that would result in the next two weeks is optimized. The details of the Predictor and Prescriptor will be described next, after an overview of the data used to construct them.

IV. Data on COVID-19

Even though COVID-19 is not the first global pandemic, it is the first that is recorded in significant detail, providing data that is made publicly available daily as the pandemic unfolds. From early on, data was available on the number of confirmed cases, number of hospitalizations, number of deaths, and number of recovered patients, per country, region, and day. Compiling data on NPIs turned out to be more difficult, and such datasets took longer to emerge. Each country takes different actions, at different levels, in different regions. These decision are reported in the press, but they are not easily aggregated and normalized.

The most comprehensive such dataset to date has been compiled by Oxford University’s Blavatnik School of Government [8], [39], [40]. They created a comprehensive representation of the different NPIs, characterized by type and different stringency, and encoded historical data in over 180 countries into this format since the beginning of the pandemic. The data also includes cases and deaths, and is updated continuously during the course of the pandemic. Such a common encoding is crucial for data-driven modeling to work. The NPI implementations at different countries must have significant overlap so that common principles can be learned. Although other datasets with more detailed NPI encodings exist (e.g., [41]), it would be more difficult to learn from them because such encodings result in less overlap.

The Oxford dataset was therefore used as a source for the current ESP study. The models were trained using the “ConfirmedCases” data for the cases and “Closure and Containment” data for the NPIs. At the time the experiments were run (in May 2020), there were eight such NPIs with granular intervention levels. The other NPI categories in the dataset, i.e., “Economic response”, “Public Heath” and “Miscellaneous” measures were not used because they have less direct impact on the spread of the epidemic. A summary of these NPIs is given in Table I. A detailed explanation of the data is provided in a codebook [42].

TABLE I. Definitions of the NPI Data Used in the Experiments.

NPI name	Level 0	Level 1	Level 2	Level 3	Level 4
hline C1_School closing	no measures	recommend closing	require closing some levels e.g., just high school, or just public schools)	require closing all levels
C2_Workplace closing	no measures	recommend closing (or recommend work from home)	require closing (or WFH) for some sectors or cate- gories of workers	require closing (or WFH) for all-but-essential workplaces (e.g., grocery stores, doctors)
C3_Cancel public events	no measures	recommend canceling	require canceling
C4_Restrictions on gatherings	no restrictions	restrictions on large gatherings (limit is above 1000 people)	restrictions on gatherings 101-1000 people	restrictions on gatherings 11-100 people	restrictions on gatherings 10 people or less
C5_Close public transport	no measures	recommend closing (or signifi- cantly reduce volume/route/means of transport available)	require closing (or prohibit most citizens from using it)
C6_Stay at home requirements	no measures	recommend not leaving house	require not leaving house with exceptions for daily exercise, grocery shopping, and 'essential' trips	require not leaving house with minimal exceptions (e.g., ok to leave once a week, or only one person at a time, etc)
C7_Restrictions on internal movement	no measures	recommend not to travel between regions/cities	internal movement restrictions in place
C8_International travel controls	no restrictions	screening arrivals	quarantine arrivals from some or all regions	ban arrivals from some regions	ban on all regions or total border closure

The data consists of daily ’Closure and containment’ measures in the ’Coronavirus Government Response Tracker’ by Oxford [8], [40], [42]. There are eight kinds of NPIs, each ranging in stringency from 0 (no measures) to 2, 3, or 4 (full measures). Together with daily cases, this data is used to train the Predictor model.

The number of cases was selected as the target for the predictions (instead of number of deaths, which is generally believed to be more reliable), because case numbers are higher and the data is smoother overall. The model also utilizes a full 21-day case history which it can use to uncover structural regularities in the case data. For instance, it discovers that many fewer cases are reported on the weekends in France and Spain. However, the data is still noisy for several reasons.

• 1)There are other differences in how cases are reported in each country.
• 2)Some countries, like the U.S., do not have a uniform manner of reporting the cases.
• 3)Cases were simply not detected for a while, and testing policy still widely differs from country to country.
• 4)Some countries, like China, U.S., and Italy, implemented NPIs at a state/regional level, and it is difficult to express them at the country level.
• 5)As usual with datasets, there are mistakes, missing days, double-counted days, etc.

It is also important to note that there is up to a two-week delay between the time a person is infected and the time the case is detected. A similar delay can therefore be expected between the time an NPI is put in places and its effect on the number of cases.

Despite these challenges, it is possible to use the data to train a useful model to predict future cases. This data-driven machine learning approach will be described next.

V. Data-Driven Predictive Model

With the above data sources, machine learning techniques can be used to build a predictive model. Good use of recent deep learning approaches to sequence processing can be made in this process, in particular recurrent neural networks. However, a method of cascading the predictions needs to be developed so that they can reach several steps into the future. Furthermore, methods are needed that keep the predictions within a sensible range even with limited data.

A. Predictor Model Design

This section describes the step-by-step design of the learned predictor. For a given country, let 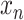be the number of new cases on day . The goal is to predict 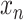in the future. First, consider the minimal epidemic model

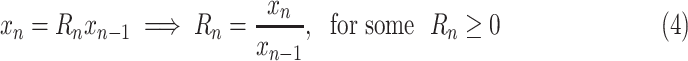where the factor 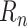is to be predicted. Focusing on such factors is fundamental to epidemiological models, and, when learning a predictive model from data, makes it possible to normalize prediction targets across countries and across time, thereby simplifying the learning task.

Training targets 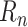can be constructed directly from daily case data for each country. However, in many countries case reporting is noisy and unreliable, leading to unreasonably high noise in daily . This effect can be mitigated by instead forming smoothed targets based on a moving average 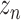of new cases

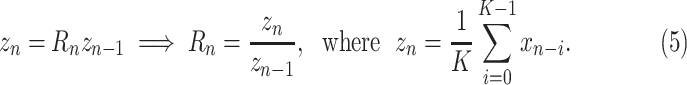In this article, for all models, i.e., prediction targets are smoothed over the preceding week.

To capture the effects of finite population size and immunity, an additional factor is included that scales predictions by the proportion of the population that could possibly become new cases

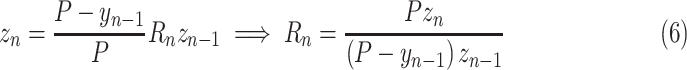where 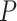is the population size, and 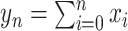is the total number of recorded cases by day 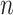. Notice that, when evaluating a trained model, the predicted 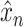can be recovered from a predicted 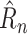by

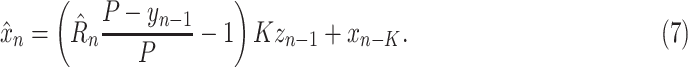Note that this formulation assumes that recovered cases are fully immune: when 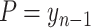, the number of new cases goes to 0. This assumption can be relaxed in the future by adding a factor to (6) (either taken from the literature or learned) to represent people who were infected and are no longer immune.

The trainable function implementing 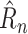can now be described. The prediction 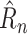should be a function of (1) NPIs enacted over previous days, and (2) the underlying state of the pandemic distinct from the enacted NPIs. For the models in this article, (1) is represented by the NPI restrictiveness values for the past 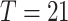days over all 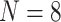available NPIs, and (2) is represented autoregressively by the 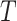previous values of 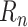(or, during forecasting, by the predicted when the true 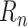is unavailable). Formally

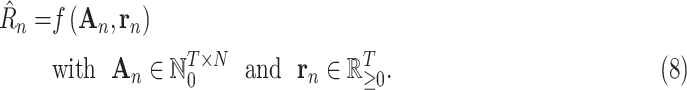In contrast to epidemiological models that make predictions based on today’s state only, this data-driven model predicts based on data from the preceding three weeks.

To help the model generalize with a relatively small amount of training data, the model is made more tractable by decomposing 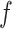with respect to its inputs

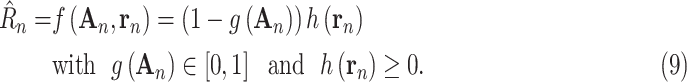Here, the factor 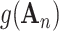can be viewed as the effect of social distancing (i.e., NPIs), and 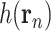as the endogenous growth rate of the disease.

To make effective use of the nonlinear and temporal aspects of the data, both 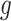and 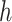are implemented as LSTM models [6], each with a single LSTM layer of 32 units, followed by a dense layer with a single output. To satisfy their output bounds, the dense layers of 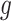and 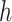are followed by sigmoid and softplus activation, respectively.

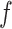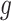Importantly, the factorization of into and 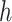makes it possible to explicitly incorporate the constraint that increasing the stringency of NPIs cannot decrease their effectiveness. This idea is incorporated by constraining 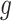to be monotonic with respect to each NPI, i.e.,

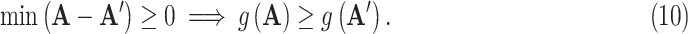This constraint is enforced by requiring all trainable parameters of 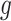to be non-negative, except for the single bias parameter in its dense layer. This non-negativity is implemented by setting all trainable parameters to their absolute value after each update.

Note that although the model is trained only to predict one day in the future, it can make predictions arbitrarily far into the future given a schedule of NPIs by autoregressively feeding the predicted 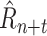back into the model as input.

For the experiments in this article, the model for 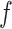was implemented in Keras [43]. The Keras diagram of the model is shown in Fig. 3. The model is trained end-to-end to minimize mean absolute error (MAE) with respect to targets 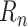using the Adam optimizer [44] with default parameters and batch size 32. MAE was used instead of mean squared error (MSE) because it is more robust to remaining structural noise in the training data. The last 14 days of data were withheld from the dataset for testing. For the remaining data, the 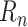were clipped to the range 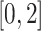to handle extreme outliers, and randomly split into 90% for training and 10% for validation during training. The model was trained until validation MAE did not improve for 20 epochs, at which point the weights yielding the best validation MAE were restored. Since the model and dataset are small compared to common deep learning datasets, the model is inexpensive to train. On a 2018 MacBook Pro Laptop with six Intel i7 cores, the model takes 276 ± 31 s to train (mean and std. err. computed over ten independent training runs).

Fig. 3.

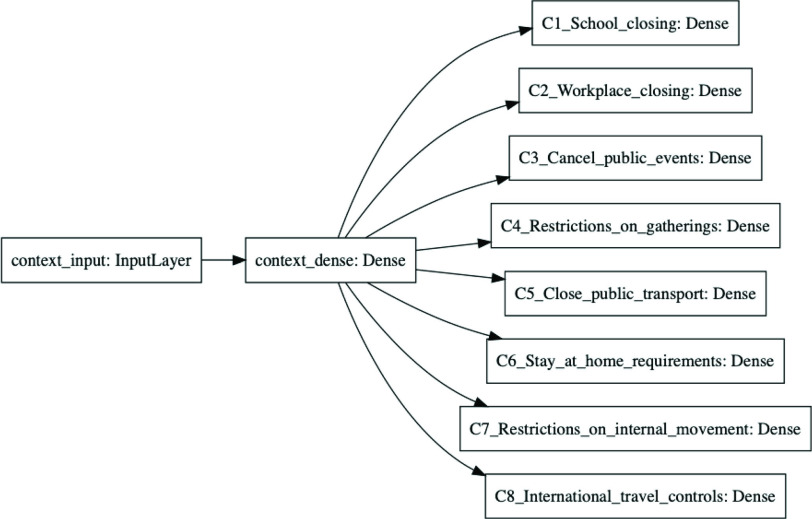
Predictor neural network. This diagram shows the Keras representation of the learnable predictor model. The previous 21 days of 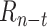are fed into the context_input; the previous 21 days of stringency values for the eight NPIs are fed into the action_input. The Lambda layer combines the context branch 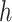and the action branch 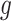as specified in (9) to produce a prediction 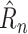. The effects of social distancing and endogenous growth rate of the pandemic are processed in separate pathways, making it possible to ensure that stringency has a monotonic effect, resulting in more regular predictions.

B. Predictor Empirical Evaluation

To validate the factored monotonic LSTM (NPI-LSTM) predictor design described above, it was compared to a suite of baseline machine learning regression models. These baselines included linear regression, random forest regression (RF), support vector regression (SVR) with an RBF kernel, and feed-forward neural network regression (MLP). Each baseline was implemented with sci-kit learn, using their default parameters [45]. Each method was trained independently 10 times on the training dataset described in Section V-A. The results on the test dataset (last days of the countries with the most cases) were evaluated with respect to four complementary performance metrics. In particular, for the comparisons in this section, training data consisted of data up until May 6, 2020, and test data consisted of data from May 7–20, 2020.

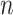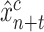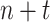Suppose training data ends on day . Let and be the model output and the corresponding predicted new cases [recovered via (7)] for the th country at day . The metrics were as follows.

1). 1-Step 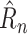MAE:

This metric is simply the loss the models were explicitly trained to minimize, i.e., minimize 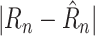given the ground truth for the previous 21 days

The remaining three metrics are based not only on single-step prediction but also the complete 14 day forecast for each country.

2). Raw Case MAE:

This is the most intuitive metric, included as an interpretable reference point. It is simply the MAE with respect to new cases over the 14 test days summed over all 20 test countries

3). Normalized Case MAE:

This metric normalizes the case MAE of each country by the number of true cases in the 14 day window, so that errors are in a similar range across countries. Such normalization is important for aggregating results over countries that have different population sizes, or are in different stages of the pandemic

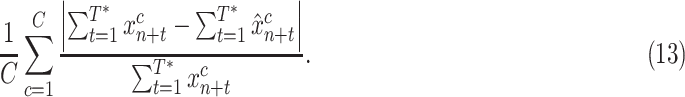4). Mean Rank:

This metric ranks the methods in terms of case error for each country, and then averages over countries. It indicates how often a method will be preferred over others on a country-by-country basis

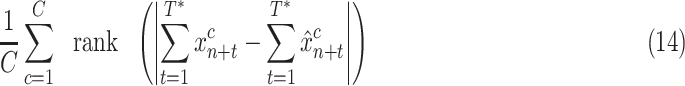where 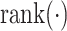returns the rank of the error across all five methods, i.e., the method with the lowest error receives rank of 0, the next-best method receives rank of 1, and so on.

Of these four metrics, normalized case MAE gives the most complete picture of how well a method is doing, since it combines detailed case information of Raw Case MAE with fairness across countries similar to Mean Rank. The results are shown in Table II. NPI-LSTM outperforms the baselines on all metrics. Interestingly, although RF and SVR do quite well in terms of the loss on which they were trained (1-step MAE), the simple linear model outperforms them substantially on the metrics that require forecasting beyond a single day, showing the difficulty that off-the-shelf nonlinear methods have in handling such forecasting.

TABLE II. Performance Comparison of NPI-LSTM Predictor With Baselines.

Method	Norm. Case	Raw Case	Mean Rank	1-step
MLP	2.47±1.22	1089126±540789	3.19±0.09	0.769±0.033
RF	0.95±0.05	221308±8717	1.98±0.10	0.512±0.000
SVR	0.71±0.00	280731±0	1.76±0.09	0.520±0.000
Linear	0.64±0.00	176070±0	1.63±0.09	0.902±0.000
NPI-LSTM	0.42±0.04	154194±14593	1.46±0.08	0.510±0.001

This table shows results along the four metrics described in Section V-B with mean and standard error over 10 trials. Interestingly, although RF and SVR do quite well in terms of the loss they were trained on (1-step 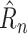MAE), the simple linear model outperforms them substantially on the metrics that require forecasting beyond a single day, showing the difficulty that off-the-shelf nonlinear methods have in handling such forecasting. In contrast, with the extensions developed specifically for the epidemic modeling case, the NPI-LSTM methods outperforms the baselines on all metrics.

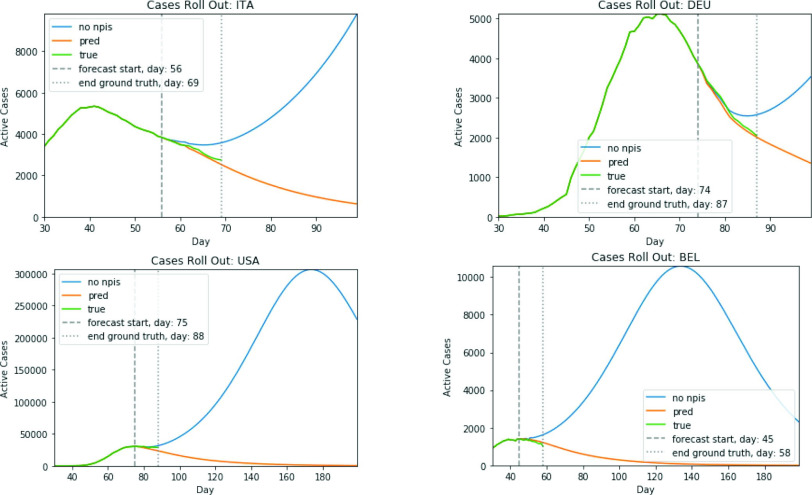
To verify that the predictions are meaningful and accurate, four example scenarios, i.e., four different countries at different stages of the pandemic, are plotted in Fig. 4 (active cases at each day is approximated as the sum of new cases over the prior 14 days). Day 0 represents the point in time when 10 total cases were diagnosed; in each case, stringent NPIs were enacted soon after. The predictor was trained on data up until April 17, 2020, and the predictions started on April 18, with 21 days of data before the start day given to the predictor as initial input. Assuming the NPIs in effect on the start day will remain unchanged, it will then predict the number of cases 180 days into the future. Importantly, during the first 14 days its predictions can be compared to the actual number of cases. For comparison, another prediction plot is generated from the same start date assuming no NPIs from that date on. The figures show that 1) the predictions match the actual progress well; 2) assuming the current stringent NPIs continue, the cases will eventually go to 0; and 3) with no NPIs, there is a large increase of cases, followed by an eventual decrease as the population becomes immune. The predictions thus follow meaningful trajectories.

Fig. 4.

Illustrating the predictive ability of the NPI-LSTM model. Actual and projected cases are shown for four sample countries. The model predicts the number of cases accurately for the first 14 days where it can be compared with the actual future data (between the vertical lines). The prolonged 180-day predictions are also meaningful, reducing the number of cases to zero with stringent NPIs, and predicting a major increase followed by an eventual decrease with less stringent NPIs. Thus, with proper constraints, data-driven machine learning models can be surprisingly accurate in predicting the progress of the pandemic even with limited data.

The main conclusion from these experiments is that the data-driven approach works surprisingly well, even with limited data. In particular, it makes it possible to build Prescriptors for ESP, as will be discussed in Section VI. The way confidence can be estimated in it will be described next.

C. Modeling Uncertainty in Predictions

An important aspect of any decision system is to estimate confidence in its outcomes. In prescribing NPIs, this means estimating uncertainty in the Predictor, i.e., deriving confidence intervals on the predicted number of future cases. In simulation models, such as those reviewed in Section II, variation is usually created by running the models multiple times with slightly different initial conditions or parameter values, and measuring the resulting variance in the predictions. With neural network predictors, it is possible to measure uncertainty more directly by combining a Bayesian model with it [46]–[48]. Such extended models tend to be less accurate than pure predictive models, and also harder to set up and train [49], [50].

A recent alternative is to train a separate model to estimate uncertainty in point-prediction models [51]. In this approach, called RIO, a Gaussian Process is fit to the original residual errors in the training set. The I/O kernel of RIO utilizes both input and output of the original model so that information can be used where it is most reliable. In several benchmarks, RIO has been shown to construct reliable confidence intervals. Surprisingly, it can then be used to improve the point predictions of the original model, by correcting them toward the estimated mean. RIO can be applied to any machine learning model without modifications or retraining. It therefore forms a good basis for estimating uncertainty also in the COVID-19 Predictor.

In order to extend RIO to time-series predictions, the hidden states of the two LSTM models (before the lambda layer in Fig. 3) are concatenated and fed into the input kernel of RIO. The original predictions of the predictor are used by the output kernel. RIO is then trained to fit the residuals of the original predictions. During deployment, the trained RIO model then provides a Gaussian distribution for the calibrated predictions.

To validate this process empirically with COVID-19 data, the data was preprocessed in four steps: 1) Among the 30 most affected countries in terms of cases, those with the most accurate predictions were selected, resulting in 17 countries with MAE less than 0.04; 2) the outlier days that had an 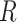larger than 2.0 were removed from the data; 3) the earliest ten days (after the first 21 days) were removed as well, focusing training on more recent data; and 4) for each country, 14 days were selected randomly as the testing data, and all the remaining days were used as the training data. The hyperparameters in these steps were found to be appropriate empirically. Table III shows the results. The conclusion is that RIO constructs reasonable confidence intervals at several confidence levels, and slightly improves the prediction accuracy. It can therefore be expected to work well in estimating confidence in the NPI prescription outcomes as well.

TABLE III. Results After Applying RIO to Predictor.

Dataset	Orig. MAE	RIO MAE	95% CI	90% CI	68% CI
Training	0.0319	0.0312	0.952	0.921	0.756
Testing	0.0338	0.0337	0.929	0.899	0.710

%CI = percentage of testing outcomes within estimated confidence intervals.

However, RIO will first need to be extended to model uncertainty in time series. Because NPI-LSTM forecasts are highly nonlinear and autoregressive, analytic methods are intractable. Instead, given that the predictor model with RIO returns both the mean and the quartiles for 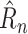, the quartiles after 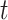days in the future can be estimated via Monte Carlo rollouts. Specifically, for each step in each rollout, instead of predicting and feeding it back into the model to predict the next step, is sampled from the Gaussian distribution returned by RIO, and this sample is fed back into the model. Thus, after steps, a sample is generated from the forecast distribution. Given several such samples (100 in the experiments in this article), the upper and lower quartile are computed empirically for all forecasted days .

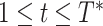Thus, RIO makes it possible to estimate uncertainty in the predictions, which in turn helps the decision maker interpret and trust the results, i.e., how reliable the outcomes are for the recommendations that the Prescriptors generate. The method for discovering good Prescriptors will be described next.

VI. Evolutionary Prescriptive Model

Whereas many different models could be used as a Predictor, the Prescriptor is the heart of the ESP approach, and needs to be constructed using modern search techniques. This section describes the process of evolving neural networks for this task. A number of example strategies are presented from the Pareto front, representing tradeoffs between objectives, as well as examples for countries at different stages of the pandemic, and counterfactual examples comparing possible versus actual outcomes. General conclusions are drawn on which NPIs matter the most, and how they could be implemented most effectively.

A. Prescriptor Model Design and Evolution

Any of the existing neuroevolution methods [36] could be used to construct the Prescriptor as long as it evolves the entire network including all of its weight parameters The most straightforward approach of evolving a vector of weights for a fixed topology was found to be sufficient in the current application. The Prescriptor model (Fig. 5) is a neural network with one input layer of size 21, corresponding to case information [as defined in (6)] for the prior 21 days. This input is the same as the context_input of the Predictor. The input layer is followed by a fully connected hidden layer of size 32 with the tanh activation function, and eight outputs (of size one) with the sigmoid activation function. The outputs represent the eight possible NPIs which will then be input to the Predictor. Each output is further scaled and rounded to represent the NPI stringency levels: within [0, 2] for “Cancel public events”, “Close public transport”, and “Restrictions on internal movement”; [0, 3] for “School closing”, “Workplace closing”, and “Stay at home”; [0, 4] for “Restrictions on gatherings” and “International travel controls”.

Fig. 5.

Prescriptor neural network. Given 21 days of past cases ( 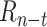in (6)) as input (context_input), the network generates recommended stringency values for each of the eight NPIs. The network is fully connected with one hidden layer. Because there are no targets, i.e., the optimal NPIs are not known, gradient descent cannot be used; instead, all weights and biases are evolved based on how well the network’s NPI recommendations work along the cases and cost objectives, as predicted by the Predictor.

The initial population uses orthogonal initialization of weights in each layer with a mean of 0 and a standard deviation of 1 [52]. The population size is 250 and the top 6% of the population is carried over as elites. Parents are selected by tournament selection of the top 20% of candidates using the NSGA-II algorithm [53]. Recombination is performed by uniform crossover at the weight-level, and there is a 20% probability of multiplying each weight by a mutation factor, where mutation factors are drawn from .

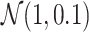Prescriptor candidates are evaluated according to two objectives: 1) the expected number of cases according to the prescribed NPIs and 2) the total stringency of the prescribed NPIs (i.e., the sum of the stringency levels of the eight NPIs), serving as a proxy for their economic cost. Both measures are averaged over the next 180 days and over the 20 countries with the most deaths in the historical data, which at the time of the experiment were United States, United Kingdom, Italy, France, Spain, Brazil, Belgium, Germany, Iran, Canada, Netherlands, Mexico, China, Turkey, Sweden, India, Ecuador, Russia, Peru, Switzerland. Both objectives have to be minimized.

Starting from the most recent day in the dataset for each country, each Prescriptor is fed with the last 21 days of case information. Its outputs are used as the NPIs at the evaluation start date, and combined with the NPIs for the previous 20 days. These 21 days of case information and NPIs are given to the Predictor as input, and it outputs the predicted case information for the next day. This output is used as the most recent input for the next day, and the process continues for the next 180 days. At the end of the process, the average number of predicted new cases over the 180-day period is used as the value of the first objective. Similarly, the average of daily stringencies of the prescribed NPIs over the 180-day period is used as the value for the second objective.

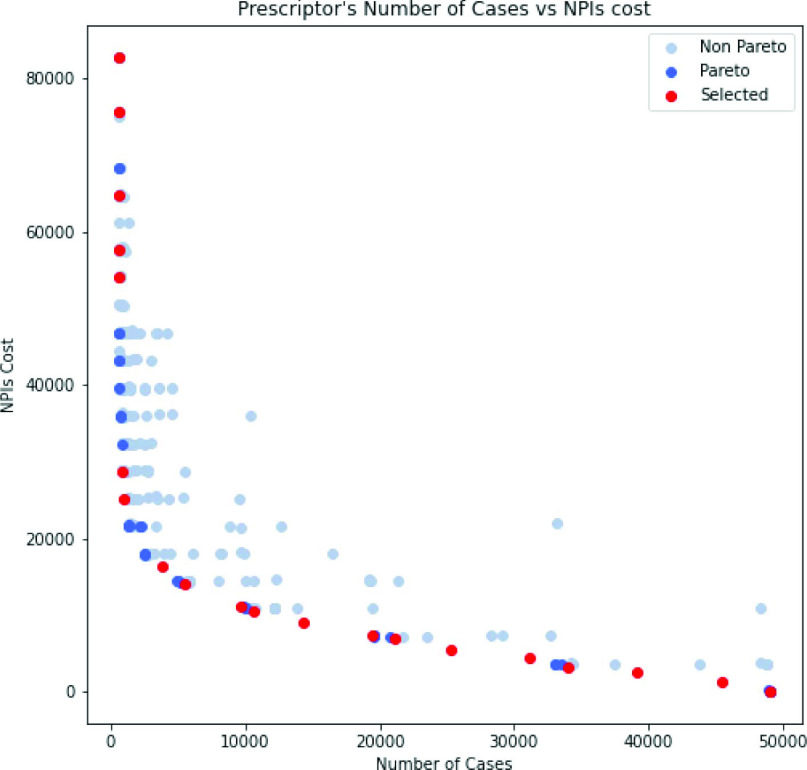
After each candidate is evaluated in this manner, the next generation of candidates is generated. Evolution is run for 100 generations, or approximately 18 h on an 8-CPU host. During the course of evolution, candidates are discovered that are increasingly fit along the two objectives. In the end, the collection of candidates that represent best possible tradeoffs between objectives (the Pareto front, i.e., the set of candidates that are better than all other candidates in at least one objective) is the final result of the experiment (Fig. 6). From this collection, it is up to the human decision maker to pick the tradeoff that achieves a desirable balance between cases and cost. Or put in another way, given a desired balance, the ESP system will find the best solution to achieve it (i.e., with the lowest cost and the lowest number of cases).

Fig. 6.

Fitness of the final population along the case and cost objectives. The candidates at the lower left side are on the Pareto front, representing the best tradeoffs. Those in red are used in the examples below and in the interactive demo (numbered 0–19 from left to right). They are the 20 candidates with the highest crowding distance in NSGA-II. The other candidates in the Pareto front are in dark blue and other final population candidates in light blue. An animation of how this population evolved can be seen at https://evolution.ml/esp/npi.

To illustrate these different tradeoffs, Fig. 7 shows the NPI Presprictions and the resulting forecasts for four different Prescriptors from the Pareto front for one country, Italy, on May 18th, 2020. The Prescriptor that minimizes cases prescribes the most stringent NPIs across the board, and as a result, the number of cases is minimized effectively. The Prescriptor that minimizes NPI stringency lifts all NPIs right away, and the number of cases is predicted to explode as a result. The third Prescriptor was chosen from the middle of the Pareto front, and it represents one particular way to balance the two objectives. It lifts most of the NPIs, allows some public events, and keeps the schools and workplaces closed. As a result, the number of cases is still minimized, albeit slightly slower than in the most stringent case. Lifting more of the NPIs, in particular workplace restrictions, is likely to cause the number of cases to start climbing. In this manner, the decision maker may explore the Pareto front, finding a point that achieves the most desirable balance of cases and cost for the current stage of the pandemic.

Fig. 7.

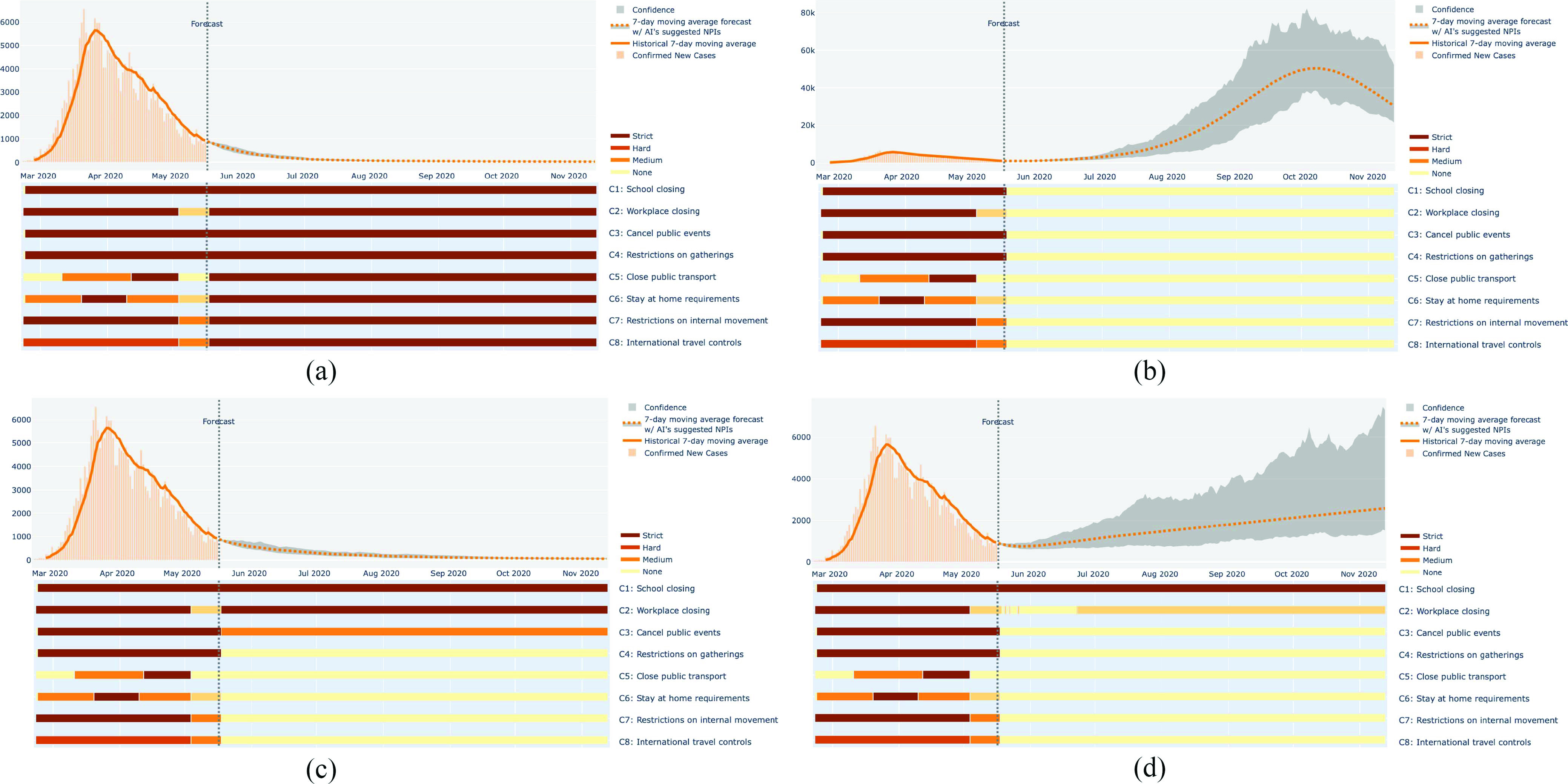
Comparison of different Prescriptors from the Pareto Front. The recommendations of four different Prescriptors are shown for Italy. Daily cases are shown as orange vertical bars and their seven-day moving average as the orange line. The vertical line indicates the start of the forecast, and the gray area represents uncertainty around the prediction. The NPI prescriptions are shown below the case plot as horizontal bars, with color representing stringency. (a) Prescriptor that minimizes the number of cases recommends a full set of NPIs at their maximum level of stringency. (b) Prescriptor that minimizes the NPI stringency recommends lifting all NPIs, which is likely to result in a high number of cases. (c) Prescriptor that tries to minimize the number of cases while lifting as many NPIs as possible recommends keeping restrictions mostly on schools and workplaces. (d) Prescriptor that tries to reduce the cost more by opening up workplaces completely may result in cases climbing up. In this manner, the human decision maker can explore the tradeoffs between cases and cost, and the ESP system will recommend the best ways to achieve it.

B. Discovered NPI Prescriptions

The shadowed area in Fig. 7(a)–(d) represents the uncertainty of the prediction, i.e., areas between 25th and 75th percentiles of the 100 Monte Carlo rollouts under uncertainty estimated through RIO. The width of the shadowed area is normalized to match the scale of the forecasts (dotted line). It is often asymmetric because there is more variance in how the pandemic can spread than how it can be contained. Whereas uncertainty is narrow with stringent Prescriptors [Fig. 7(a) and (c)], it often increases significantly with time with less stringent ones. The increase can be especially dramatic with Prescriptors with minimal NPIs, such as those in Fig. 7(b) and (d). Part of the reason is that at the time these forecasts were made, not much training data existed yet about this stage of the pandemic (i.e., the stage where countries are lifting most NPIs after the peak of the pandemic has passed). However, the result also suggests that such minimal-NPI prescriptions are fragile, making the country vulnerable to subsequent waves of the pandemic [see also Fig. 8(c) and (d)].

Fig. 8.

Comparison of tradeoff prescriptions for countries at different stages of the pandemic. The Prescriptors chosen represent a midrange in the balance between cases and cost, similar to that of Fig. 7(c). (a) For Brazil, where the pandemic is spreading rapidly at this point, Prescriptor 4 minimizes cases effectively while allowing some freedom of movement. (b) For Iran, where the pandemic appears to be entering a second wave, a more stringent Prescriptor 6 strikes a similar balance. (c) For U.S., where cases are relatively flat at this point, a less stringent Prescriptor 7 allows reducing cases gradually with minimal cost. (d) In contrast, an even slightly less stringent Prescriptor such as 9 would allow a high number of cases to return. Interestingly, in all these cases as well as in Fig. 7(c), schools and workplaces are subject to restrictions while others are lifted. Also, Prescriptor 7 often includes an alternation of stringency levels, suggesting a way to reduce the cost of the NPI while potentially keeping it effective. Thus, evolution discovers where NPIs may have the largest impact, and can suggest creative ways of implementing them.

To illustrate this process, Fig. 8 shows possible choices for three different countries at different stages of the pandemic on May 18, 2020. For Brazil, where the pandemic is still spreading rapidly at this point, a relatively stringent Prescriptor 4 allows some freedom of movement without increasing the cases much compared to full lockdown. For U.S., where the number of cases has been relatively flat, a less stringent Prescriptor 7 may be chosen, limiting restrictions to schools, workplaces, and public events. However, if NPIs are lifted too much, e.g., by opening up the workplaces and allowing public events, high numbers of cases are predicted to return. For Iran, where there is a danger of a second wave, Prescriptor 6 provides more stringent NPIs to prevent cases from increasing, still limiting the restrictions to schools, workplaces and public events.

Interestingly, across several countries at different stages of the pandemic, a consistent pattern emerges: in order to keep the number of cases flat, other NPIs can be lifted gradually, but workplace and school restrictions need to be in effect much longer. Indeed these are the two activities where people spend a lot of time with other people indoors, where it is possible to be exposed to significant amounts of the virus [54]–[56]. In other activities, such as gatherings and travel, they may come to contact with many people briefly and often outdoors, mitigating the risk. Therefore, the main conclusion that can already be drawn from these prescription experiments is that it is not the casual contacts but the extended contacts that matter. Consequently, when planning for lifting NPIs, attention should be paid to how workplaces and schools can be opened safely.

Another interesting conclusion can be drawn from Fig. 8(c): Alternating between weeks of opening workplaces and partially closing them may be an effective way to lessen the impact on the economy while reducing cases. This solution is interesting because it shows how evolution can be creative and find surprising and unusual solutions that are nevertheless effective. There is of course much literature documenting similar surprising discoveries in computational evolution [11], [20], [21], but it is encouraging to see that they are possible also in the NPI optimization domain. While on/off alternation of school and workplace closings may sound unwieldy, it is a real possibility [57]. Note also that it is a creative solution discovered in a highly limited search space: There are no options in the Prescriptor’s output for e.g., alternating remote and in-person work, extending school to wider hours, improving ventilation, moving classes outside, requiring masks, or other ways of possibly reducing exposure. How to best implement such distancing at schools and workplaces is left for human decision makers at this point; the model, however, makes a suggestion that coming up with such solutions may make it possible to lift the NPIs gradually, and thereby avoid secondary waves of cases.

C. Counterfactual and Retrospective Analysis

Thus, in the early stages, the ESP approach may suggest how to “flatten the curve,” i.e., what NPIs should be implemented in order to slow down the spread of the disease. At later stages, it may recommend how the NPIs can be lifted and the economy restarted safely. A third role for the approach is to go back in time and evaluate counterfactuals, i.e., how well NPI strategies other than those actually implemented could have worked. It may thus be possible to draw conclusions not only about the accuracy and limitations of the modeling approach but also lessons for future waves of the current pandemic, for new regions where it is still spreading, as well as for future pandemics.

For instance in the U.K. on March 16th, the NPIs actually in effect were the mild “recommend work from home” and “recommend cancel public events”. With only these NPIs, the predicted number of cases could have been quite high [Fig. 9(a)]. A lockdown was implemented on March 24th, and the actual case numbers were significantly smaller. However, it is remarkable that Prescriptor 8 would have required closing schools already on March 16th, and the predicted cases could have been much fewer even without a more extensive lockdown. Thus, the model suggests that an early intervention is crucial, and indeed other models have been used to draw similar conclusions [58]. What is interesting is that ESP suggests that it may be possible to control the pandemic with less than full lockdowns if acted early enough. Of course, the fully trained model was not available at that point, however these lessons may still be useful for countries and regions that are still in early stages, as well as for future pandemics.

Fig. 9.

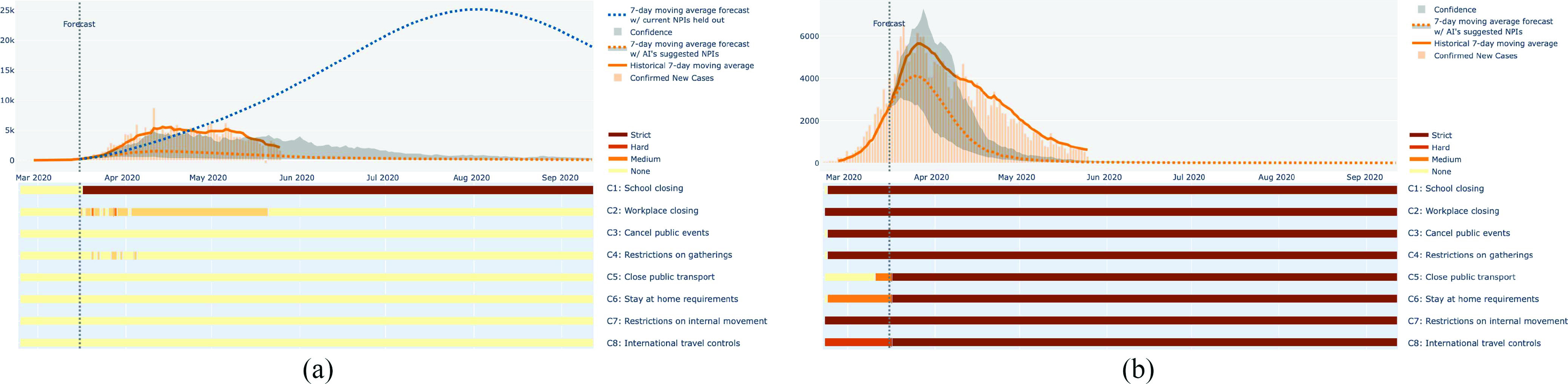
Evaluating the model with counterfactuals. Going back in time to make prescriptions makes it possible to evaluate how accurate the model is and to draw lessons for the remainder of this pandemic and future pandemics. (a) After an initial phase of mild NPIs, a lockdown in the U.K. averted a sharp rise in cases. However, Prescriptor 8 would have recommended earlier NPIs that could have resulted in an even better outcome without a full lockdown. (b) In Italy, a full lockdown in effect on March 16th should have resulted in much fewer cases than it did, suggesting that cultural and demographic factors were different than in other countries, and that the implementation of NPIs need to take such factors into account in order to be effective.

Some of the limitations of the data-driven approach also become evident in retrospective studies. For instance Italy, where the pandemic took hold before most of the rest of the world, was supposed to be in a lockdown on March 16th (which started already on February 23). Yet, the model predicts that under such a lockdown (suggested e.g., by Prescriptor 0 for that date), the number of cases should have been considerably smaller than they actually were [Fig. 9(b)]. The uncertainty is wide but the model’s prediction is remarkably different from those of many other countries. Part of the reason may be that the population in Italy did not adhere stringently to the NPIs at that point; after all, the full scale of the pandemic was not yet evident. The population may also have been older and more susceptible than elsewhere. The data used to train the model comes from 20 different countries and at a later stage of the pandemic spread, and these populations may have followed social distancing more carefully—therefore, the model’s predictions on the effectiveness of lockdowns may be too optimistic for Italy. Even with the uncertainty, this result suggests that local factors like culture, economy, population demographics, density, and mobility, may need to be taken into account in the models. It also suggests that the implementation of NPIs need to be sensitive to such factors in order to be effective.

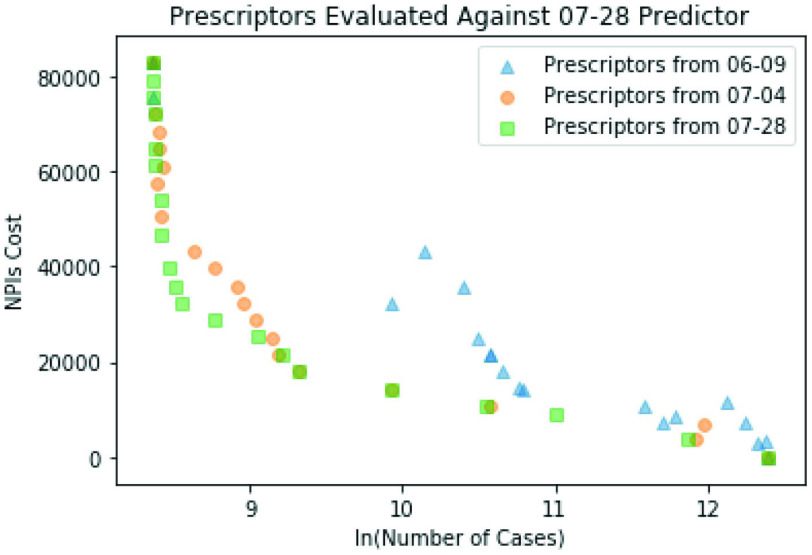
Retrospective studies also show that more data helps make better prescriptions: The Pareto front moves toward the bottom left corner over time, demonstrating that evolution finds Prescriptors that are able to minimize cases and stringency better (Fig. 10). The profile of the prescriptions also changes, for instance workplace restrictions and stay at home requirements become more important. These profiles partly reflect better decisions, and partly the changing nature of the pandemic. Eventually, once the pandemic has run its course, it should be possible to do a longitudinal study and separate those two factors, which is an interesting direction of future work.

Fig. 10.

Improvement of Prescriptors over time. The Prescriptors from the Pareto fronts on June 9th, July 4th, and July 28th were run for 180 days from July 28th against the Predictor from July 28th. The later Prescriptors are closer to the bottom left corner, indicating that when evolved with more experienced Predictors, they minimize cases and stringency better. The prescription profiles also change, suggesting that different NPI strategies are needed at different stages of the pandemic.

Overall, however, the data-driven ESP approach works surprisingly well even with the current limited data, and can be a useful tool in understanding and dealing with the pandemic. An interactive demo, available on the Web, that makes it possible to explore prescriptions and outcomes of the ESP model like those reviewed in this section, will be described next.

VII. Interactive Demo

To help understand the mechanisms and possibilities of ESP models, an interactive demo of the current state of the approach to NPI optimization is available at https://evolution.ml/esp/npi. The user can select a country by clicking on the map, and a Prescriptor from the Pareto front by clicking on the slider between Cases and NPIs. The number of cases and the recommended NPIs are then plotted over time, as in Figs. 7–9.

At the very left of the slider, the Presciptors prefer to minimize cases and therefore usually recommend establishing nearly all possible NPIs. At the very right, the Prescriptors prefer to minimize NPIs and therefore usually recommend lifting nearly all of them—usually resulting in an explosion of cases. The most interesting Prescriptors are therefore somewhere in the middle of this range. Some of them are able to keep the cases flat while lifting most of the NPIs, as was discussed in Section VI.

With the demo it is possible to explore the options for different countries at different stages of the pandemic. The demo will change as more data comes in and new functionality is added.¹ At the time of this writing, the Oxford dataset is updated in every few days, triggering a pipeline that retrains the Predictor and Prescriptors with the new data. In that sense, even though the prescriptions are not yet implemented in the real world, the demo already establishes the ESP update loop of Fig. 2. Thus, the demo can be seen as an illustration of the potential of the ESP approach. As a concrete implementation, it can hopefully also serve as a first step toward building a decision-support tool for real-world decision makers in the current pandemic, as well as in similar challenges in the future.

VIII. Discussion and Future Work

Given the encouraging results in this article, the most compelling direction of future work consists of updating the model with more data as it becomes available. The models can be extended to predicting and minimizing deaths and hospitalizations as well as cases. Such a multitask learning environment should make predictions in each task more accurate [59]. More data may make it possible to use more fine-grained NPIs as well as data on more fine-grained locations, such as U.S. counties. COVID-19 testing and treatment will hopefully improve as well so that the outcome measures will become more reliable. As vaccinations become available, the approach can be extended to include vaccination policies, such as prioritizing target populations, conducting campaigns, and implementing concurrent NPIs. In other words, data will improve in volume, relevance, accuracy, and extent, all of which will help make the predictors more precise, and thereby improve prescriptions throughout the pandemic.

Technically the most compelling direction is to take advantage of multiple prediction models, in particular more traditional compartmental and network models reviewed in Section II. General assumptions about the spread of the disease are built in to these models, and they can thus serve as a stable reference when data is otherwise lacking in a particular case. For instance, while the data was not comprehensive enough to generalize to Italy early in the pandemic [Fig. 8(c)], it might have been possible to parameterize a traditional model to perform more accurately. On the other hand, it is sometimes hard to estimate the parameters that these models require, and data-driven models can be more mode accurate in specific cases. A particularly good approach might be to form an ensemble from these models (as is often done in machine learning; [60], [61]), and thereby combine their predictions systematically to maximize accuracy.

Another way to make the system more accurate and useful is to improve the outcome measures. Currently the cost of the NPIs is proxied based on how many of them are implemented and at what stringency level. It may be possible to develop more accurate measures based on a variety of economic indicators, such as unemployment, consumer spending, and GNP. They need to be developed for each country separately, given different social and economic structures. With such measures, ESP would be free to find surprising solutions that, while stringent, may not have as high an economic impact.

The retrospective example of Italy in Fig. 9(b) suggests that it may be difficult to transfer conclusions from one country to another, and to make accurate recommendations early on in the epidemic. An important future analysis will be to analyze systematically how much data and what kind of data is necessary. For instance, if the model had been developed based on the data from China, would it have worked for Iran and Italy? Or after China, Iran, and Italy, would it have worked for the U.S. and the rest of Europe? That is, how much transfer is there between countries and how many scenarios does the model need to see before it becomes reliable? The lessons can be useful for the COVID-19 pandemic already, as well as for future pandemics.

A main consideration with the ESP approach in general is that the historical data needs to be comprehensive enough so that the predictor learns to evaluate even prescriptions that are novel. In other applications of ESP (such as growth recipes for agriculture and designs for Web interfaces; [20], [21]), a broad range of prescriptions were generated synthetically to make sure they covered the space broadly. Whereas such a process is not possible in the NPI optimization domain, it turned out not to be necessary: the over 180 countries in the dataset represented such a large variety of situations and responses at different stages of the pandemic that learning a robust predictive model was possible.

Ability to discover creative solutions, like alternating openings and closures in Fig. 8(c), is an important advantage of the evolutionary search approach, but care has to be taken to make sure they are safe. If the predictor cannot evaluate them accurately (because it has never seen them before), unexpected detrimental outcomes may result. In the NPI optimization domain, this problem is unlikely to arise, for three reasons: 1) such prescriptors are unlikely to fare well across several countries and several generations, and are likely to be eliminated from the population; 2) an isolated unreliable prescription would result in high uncertainty and be discarded; and 3) creativity in this application is limited to recombinations and time sequences of restrictions: as long as these elements exist in the data, evolution can combine and repeat them to discover a general principle (such as closing schools and workplaces, or repeating an opening and closing pattern). Thus, creativity is limited to a space that makes sense. More generally, ESP applications should include similar limits and sanity checks to avoid unwanted effects. Even in such a limited space there is often room to discover useful principles, as demonstrated in this article.

In applications where safety is paramount, it may be possible to use RIO to discount candidates with unsafe prescriptions, perhaps as an additional objective. It could be included late in the evolutionary search process so that evolution can explore and discover novel solutions for most of the run, with reliability and safety emphasized in the end.

The neural network models in the current implementation have relatively simple recurrent and feedforward architectures, compared to current deep learning models of image and language processing. Much of real-world decision-making is based on tabular data, and it is likely that such architectures will be sufficient in most applications. However, it would be interesting to apply recent metalearning and AutoML techniques, such as hyperparameter optimization and neural architecture search [10], [59], to such tabular networks as well. The processing needs may be different in these tasks, and metalearning may discover design choices that improve their performance.

Another interesting extension is to take into account that the Predictor and Prescriptor models in many applications are continually developed in the ESP outer loop, as described in Fig. 2. Instead of training the models from scratch each time the data is updated, it should be possible continue training with new data included. Such an approach is straightforward for the Predictor, but with the Prescriptor, it is necessary to ensure that prolonged evolution does not converge the population, making future innovations difficult. If done right, it may even increase the robustness of solutions [62]. Techniques for diversity maintenance, enhanced evolvability, and multiproblem transfer may prove useful in this role [63]–[65]

Any decision-support system, especially one in domains with many stakeholders with conflicting interests, needs to be trustworthy. More specifically, it needs to estimate confidence in its decisions and predictions, allow users to utilize their expert knowledge and explore alternatives, and explain the decision recommendations. The first step was already taken in this study by applying the RIO uncertainty estimation method (Section V-C) to the predictions. This approach may be improved in the future by grouping the countries according to original predictor performance, then training a dedicated RIO model for each group. In this way, each RIO model focuses on learning the predictive uncertainty of countries with similar patterns, so that the estimated confidence intervals become more reliable. As a further step, this uncertainty can be used by the Prescriptor to make safer decisions.

Second, a prescription “scratchpad” can be included, allowing the user to not only see the prescription details (as in the demo described in Section VII) but also modify them by hand. In this manner, before any prescriptions are deployed, the user can utilize expert knowledge that may not be available for ESP. For instance, some NPIs in some countries may not be feasible or enforceable at a given time. The interface makes it possible to explore alternatives, and see the resulting outcome predictions immediately. In this manner, the user may find more refined prescriptions than those proposed by ESP, or convince him/herself that they are unlikely to exist.

Third, currently the prescriptions are generated by an evolved neural network, which may perform well in the task, but does not provide an explanation of how and why it arrived at a given prescription. In the future, it may be possible to evolve explicit rule sets for this task [66], [67]. Rule sets are readable, specifying which feature values in the context lead to which prescriptions. They can be evolved as prescriptors themselves, or separately to imitate the neural network prescriptors. Thus, like RIO provides a model of uncertainty for the predictions, evolved rule sets can provide a model of explainability for the prescriptions, making it easier for human decision makers to understand and trust the system.

While this article demonstrates the potential value of ESP in coping with the COVID-19 pandemic, it may lead to a larger impact in the future. The general approach can be used to allow decision makers to minimize the impact of future pandemics, as well as improve responses to other natural and man-made disasters, and improve social policies in general. In many such domains, the first step toward adopting such AI-based decision support is likely to be simulations based on historical data. The implementation of ESP in the COVID-19 domain in this article constitutes such a step.

IX. Conclusion

Recent advances in AI have made it possible to not only predict what would happen but also prescribe what should be done. Also, widely available data has recently made it possible to build data-driven models that are surprisingly accurate in their predictions. This article puts these two advances together to derive recommendations for NPIs in the current COVID-19 crisis. The model leads to insights in which NPIs are most important to get right, as well as how they might be implemented most effectively. With further data and development, the approach may become a useful tool for policy makers, helping them to minimize impact of the current as well as future pandemics.

Biographies

Risto Miikkulainen (Fellow, IEEE) received the M.S. degree in engineering from the Helsinki University of Technology (currently, Aalto University), Espoo, Finland, in 1986, and the Ph.D. degree in computer science from the University of California at Los Angeles, Los Angeles, CA, USA, in 1990.

He is a Professor of Computer Science with the University of Texas at Austin, Austin, TX, USA, and an Associate VP of Evolutionary AI, Cognizant Technology Solutions, San Francisco, CA, USA, where he is scaling up these approaches to real-world problems. His current research focuses on methods and applications of neuroevolution, as well as neural network models of natural language processing and vision.

Olivier Francon received the Master of Science degree in cognitive science and artificial intelligence from EPITA, Paris, France, in 1999.

He is a Senior Director of Evolutionary AI, Cognizant Technology Solutions, San Francisco, CA, USA, where he leads the Evolutionary Surrogate-assisted Prescriptions offering of the Learning Evolutionary Algorithm Framework. Prior to Cognizant, he was a Principal Software Engineer with Sentient Technologies, San Francisco, where he was in charge of the applied neuroevolution and experimentation services of the distributed artificial intelligence platform.

Elliot Meyerson received the B.S. degree in computer science and mathematics from Wesleyan University, Middletown, CT, USA, and the Ph.D. degree in computer science from the University of Texas at Austin, Austin, TX, USA, in 2018.

He is a Senior Research Scientist of Evolutionary AI Team, Cognizant Technology Solutions, San Francisco, CA, USA. He works on AI and machine learning methods that can be applied across a broad range of application areas. His expertise is in two such broadly applicable technologies, deep learning and evolutionary computation, especially in methods that automatically discover useful regularities across seemingly disparate problems.

Xin Qiu received the B.E. degree from Nanjing University, Nanjing, China, in 2012, and the Ph.D. degree from the National University of Singapore, Singapore, in 2016.

He is a Senior Research Scientist of Evolutionary AI Team with Cognizant Technology Solutions, San Francisco, CA, USA. His research interests include evolutionary computation, probabilistic modeling, bandit algorithms, and reinforcement learning.

Darren Sargent received the B.Sc. degree in mathematics from the University of York, York, U.K, in 1991.

He is the Director of Evolutionary AI with Cognizant Technology Solutions, San Francisco, CA, USA, and previously a Principal Software Engineer with Sentient Technologies, San Francisco. Prior to joining Sentient he worked on big data and recommender systems for large retail customers. He is a seasoned software engineer with decades of experience in many platforms and languages.

Elisa Canzani received the B.S. and M.S. degrees in mathematics and applied mathematics from the University of Camerino, Camerino, Italy, and the Ph.D. degree in computer science from the Bundeswehr University Munich, Neubiberg, Germany, in 2017.

He is a Senior Data Scientist with Cognizant Technology Solutions, San Francisco, CA, USA, with expertise in supporting strategic decisions with data-driven insights and predictive models in aerospace, security, and defense. Her doctoral research focused on modeling dynamics of cyber-epidemics in interdependent critical infrastructure systems as Marie Curie Research Fellow within the NITIM European Graduate School.

Babak Hodjat received the Ph.D. degree in machine intelligence from Kyushu University, Fukuoka, Japan, in 2003.

He is a VP of Evolutionary AI with Cognizant Technology Solutions, San Francisco, CA, USA, leading an Research and Development team bringing advanced AI solutions to businesses. He is a serial entrepreneur, having started a number of Silicon Valley companies. They include Dejima, whose agent-oriented technology applied to intelligent interfaces is behind Apple’s Siri; Sentient Technologies, San Francisco, with technology behind the world’s largest distributed artificial intelligence system; and Sentient Investment Management, the world’s first AI-driven hedge-fund.