COVID-19 Optimizer Algorithm, Modeling and Controlling of Coronavirus Distribution Process

Abstract

The emergence of novel COVID-19 is causing an overload on public health sector and a high fatality rate. The key priority is to contain the epidemic and reduce the infection rate. It is imperative to stress on ensuring extreme social distancing of the entire population and hence slowing down the epidemic spread. So, there is a need for an efficient optimizer algorithm that can solve NP-hard in addition to applied optimization problems. This article first proposes a novel COVID-19 optimizer Algorithm (CVA) to cover almost all feasible regions of the optimization problems. We also simulate the coronavirus distribution process in several countries around the globe. Then, we model a coronavirus distribution process as an optimization problem to minimize the number of COVID-19 infected countries and hence slow down the epidemic spread. Furthermore, we propose three scenarios to solve the optimization problem using most effective factors in the distribution process. Simulation results show one of the controlling scenarios outperforms the others. Extensive simulations using several optimization schemes show that the CVA technique performs best with up to 15%, 37%, 53% and 59% increase compared with Volcano Eruption Algorithm (VEA), Gray Wolf Optimizer (GWO), Particle Swarm Optimization (PSO) and Genetic Algorithm (GA), respectively.

I. Introduction

In December 2019, the Chinese authorities notified the world that a virus was spreading quickly in Wuhan. Later, the virus spread to other countries with cases doubling within days. This virus is called Sever Acute Respiratory Syndrom-Related Coronavirus 2 (COVID-19) and is simply referred to as the coronavirus or COVID-19. Once this virus swarm the lungs after few days of infection, it can have devastating effects with manifesting cough, severe headache and high fever [1]–[3]. The majority of infected people will get through with relatively mild symptoms, but many cases become severe or even critical. Later, the World Health Organization (WHO) announced that this COVID-19 outbreak should be treated as a pandemic because of its rapid spread and the fact that most of the infected people are not immune to it [4], [5].

The coronavirus pandemic has put an end to the longest economic expansion in the world history. This is because people around the world are in mass quarantine and major parts of the world economy are in a complete standstill with many businesses shutting down. Economists believe that this economic recession is unlike any other witnessed in the recent history. Moreover, the economic challenges are massive if we do not deal with this pandemic immediately and provide necessary mitigation solutions [6], [7]. To deal with this unprecedented crisis, health companies and universities around the globe are working hard to produce appropriate vaccines. However, health professionals mentioning that the production of an effective vaccine may take a long time.

For the COVID-19 vaccine, people are wondering about the time when a vaccine will be ready. While a vaccine is not available yet, the average reproduction rate of coronavirus is between 1.4 to 2.5; meaning that with each infection, a further 2.5 people will be infected. In particular, the initial global infection rate was doubling daily in the first few weeks of 2020. In response, governments imposed lockdowns to slow the spread of the virus. Manual tracking of confirmed coronavirus cases is practiced by health officials. This manual contact tracing is labor intensive and requires more resources to manage large numbers of infected people [8]–[10]. In particular, infections spread more rapidly in large gatherings. Such scenarios will burden health agencies as well as authorities to their maximum potentials [11], [12]. The tireless process of finding and tracing infected people as well as the delay in test results can contribute in the increase the probability of coronavirus occurrence and infections.

In such situations of contagious viral infections, developing a good model is significant in making the appropriate decision on controlling the spread of the virus. Each type of virus infections has its own characteristics in terms of spreading and manifesting of symptoms. Derivation of a mathematical model to tackle the infection requires very thorough analysis of the biological characteristics of the virus [13]. In particular, a good mathematical model should consider the infection through someone with no symptoms of COVID-19 clinical presentation. Currently, there are currently a few existing mathematical models on the spreading pattern of COVID-19. Authors in [14] developed a real-time forecasting algorithm based on phenomenological models to evaluate short-term predictions of the cumulative number of confirmed reported cases. However, the coronavirus causes an emergency situation worldwide and needs a robust control model based on its specific characteristics. This article presents a COVID-19 optimizer Algorithm (CVA) that mimic the behavior of COVID-19 spreading across countries over the period of December 2019 to the time of writing this article. We also model the behavior of this pandemic transmission with its different stages that have been experienced so far and shows that how the model can be utilized for making decisions by governments and authorities in practicing optimum lockdowns. Further, the proposed CVA can cover almost all feasible regions of the optimization problems. We also simulated the coronavirus distribution process in several countries around the globe. The proposed mathematical model in this article formulates a coronavirus distribution process as an optimization problem to minimize the number of COVID-19 infected countries and with the aim to slow down the epidemic spread. Then, three scenarios are proposed to solve the optimization problem using the most effective factors in the distribution process. Simulation results show one of the controlling scenarios outperforms the others. Extensive simulations using several engineering optimization problems show the efficiency of the proposed CVA algorithm. Further, the proposed CVA technique can be applied in several research fields to solve constrained, unconstrained and engineering problems. In the existing literature, researchers use behavior of animals and insects to derive meta-heuristic algorithms whereas our proposed CVA is inspired from the COVID-19 infection process.

The rest of this article is organized as follows. Section II discusses the background and reviews the the literature on a developed CVA and controlling the spread of COVID-19. This is followed by presenting the CVA optimization algorithm and the proposed mathematical model to slow down the fast spread of the pandemic in section III. Finally, Section IV concludes the article.

II. Related Work

Recently, Meta-heuristic algorithms are widely used in optimizing the process of a wide-range of systems within different real-world scenarios. In the state-of-the-art, numerous number of optimization algorithms have been developed, which are mainly categorized into deterministic and stochastic algorithms. In a deterministic category, an algorithm constantly discovers a similar solution for a particular optimization problem when it starts from similar initial searching steps. This kind of algorithm is beneficial as it offers reliable performance due to its ability of obtaining a definite solution after each specific run. Nevertheless, such algorithms are also facing possibility of trapping within the local optima solution due to the lack of randomness manners, which could increase the possibility of exploring different promising rejoins while resolving a given optimization problem. On the other hand, as a second category, stochastic types of algorithms can fill-in the gap of a limited explored solution by gaining assistance from inherent stochastic operators that exist with such algorithms. As a result, various solutions could be obtained in return of each run, though the starting point is kept the same. However, the obtained results out of the stochastic algorithms are most likely to be unreliable compared with deterministic type approaches. This tradeoff drives the development of new algorithms to achieve more reliable and effective optimization methods. This was highly reflected by the wide-range of the proposed algorithms in the last decades, which are trying to find the best tuning method between randomness and quality of obtained solution over acceptable course of iterations.

Therefore, many related approaches have been developed, which are classified as a collective method that creates many random solutions and change them throughout the optimization process that follows a predefined strategy. By doing so, a more efficient method could be achieved in identifying a global optimum solution within a given search space of a problem. A set of well-known representatives of such algorithms are Genetic Algorithm (GA) [15], Particle Swarms Optimization (PSO) [16], Ant Colony Optimization (ACO), and Differential Evolution (DE). Obtaining wide-range of solutions normally reduce the chances of trapping with the local optimal solution of a given problem, which is considered one of the winning points of stochastic algorithms. Yet, achieving each solution enquires an evaluation function and finding the optimal collaboration between each solution, which is a challenging task. Nevertheless, such kind of algorithms introduces some challenges but they are widely used nowadays. This is due to the fact that their simplicity in solving problems by taking simple strategies inspired by some naive nature based collaborative behavior. Hence, several algorithms have been developed as a way to push further the advantages of such algorithms and lessen their limitation/drawbacks. We can name for example, Artificial Bee Colony (ABC) [17] optimization, Cuckoo Search (CS) [18], Firefly Algorithm (FA) [19], Gray Wolf Optimizer (GWO) [20], Salp Swarm Algorithm (SSA) [21], Whale Optimization Algorithm (WOA) [22], Laying Chicken ALgorithm [23], Big Bang Algorithm [24] and Swine Influenza Inspired Optimization (SIIO) [25].

From the above discussion, we can figure out that there is a high applicability of utilizing such inspiration from natural events or collaborative creatures in formulating an optimization algorithm that could improve the process of finding optimal solutions for a given problem. Therefore, in this article we propose a COVID-19 optimizer Algorithm (CVA), which we discuss in details in the rest of this article.

Klepac [26], who is a specialist professor in infection diseases’ modeling, has presented how COVID-19 spreads over a population within each country, its transmission speed and how to control such a spread. Assume that R represents a reproduction number, which is inferring the ability of this virus in infecting other people as a chain of contagious infections. Taking into account each person will typically infect a group of people over very short period of time, which then yields an outbreak. In contrast, if the probability gets closer to the fact that one person can infect less than one other person, the infection will taper off.

On the other hand, taking a simple correlation factor between the value of R and the transmission speed of an infection of any similar virus, the higher the R-value is the higher the number of infected people. Hence, from this point we can highlight the main concept behind the power of novel COVID-19's transmission speed in comparison with other similar pandemics. As was reported in [26], a seasonal flu can be transferred from one person to another within an average of 1.4, whereas COVID-19 transfers within an average of 2-3; which formed the initial stages of the outbreak.

It is important to highlight how likely the volume of infected people behaves. This relies on several factors, such as the number of vulnerable people in the population, the period of time that each person carries the virus asymptomatically, the probability of each person getting in contact with others (number of social contacts) and the possibility of transferring the virus to them as well as the frequency of having a group of people visiting a common place (such as shopping malls, airports, train stations, etc.) over a similar period of time. Taking the aforementioned factors into consideration, governments and authorities in charge can optimally plan the method of controlling the spread of such epidemic, which is highly related to maintaining the rate of value R (where R represents the reproduction rate). Accordingly, one can have a better understanding of the health ecosystem and thus manage to save more lives. Consider China, for instance, they had to immediately model the 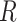rate and measure the transmission speed to take a quick decision within the right time and right measure.

As a way to limiting or controlling the transmission speed of the COVID-19, few recent research studies have been conducted to help governments and societies in ending this epidemic. Authors in [27] have investigated the role of confirmed cases isolation that could play in limiting the spread of such pandemic as well as tracing back their contacts. They have utilized a mathematical model to measure the effectiveness of this strategy in controlling the transmission speed of COVID-19. They have achieved that via the development of a stochastic transmission model to contain the virus outbreak. They have found that outbreaks were estimated to be controlled when the virus transmission is over within the first 12 weeks or by a threshold accumulation of 5000 cases. Though, the ability of controlling the spread of the infection using such kind of strategies is highly correlated to other factors such as pathogen.

On the other hand, a study was conducted in [28] to investigate the transmission behavior of the coronavirus and how it was varied over the time period of January 2020 to February 2020. The authors then introduced a combination of stochastic transmission model along with the captured data of COVID-19 cases in Wuhan as a way to categorize its transmission behavior. Then, they computed the probability of the initial cases, which may spawn outbreaks explored into other regions. They proposed model used to estimate the probability of exporting the virus out of Wuhan city. On the other hand, we believe that there may be some uncertainties and other issues that may affect the accuracy of the estimation process that were not considered. In particular, the issues are symptomatically exported cases and the probability of other unrecorded cases.

In a different study presented in [29], authors stressed on the essential need of an effective infection prevention and control measurement system that helps in stopping the spread. It was also reported that some of the existing and recently introduced measures lack in terms of scientific foundation as well as the ineffective measures as the outbreak has spread out of China to other countries rapidly.

On the other hand, such kind of measurement systems would highly help in educating the public health grounded on scientific evidence, hence it could effectively decrease the anxiety and stress triggered by misguided or inaccurate information. In other words, having these measures and information to be timely as well as being accurately reported to public, people can easily assess and interpret the situation without any panic. For instance, having the fact that the chance of transmitting the virus with a short face-to-face contact or contagion onset after roughly 14 days of contact to a person who tested positive has low possibility and should not be overstressed. The inaccurate measure and misguided information most likely will lead to a chaotic behavior among public and hence it is not beneficial implementing an epidemic control system relying on such information [30].

III. The Covid-19 Inspired Algorithm (CVA)

The details of our proposed CVA algorithm is discussed in this section. The details include mathematical equations, simulation of coronavirus distribution and other related steps. The exploration as well as exploitation processes of the CVA algorithm in finding the optimal solution of an optimization problem are outlined in this section.

Coronavirus in nature has started spreading rapidly due to its high transmission behavior and speed of the R-value (as stated within the initial estimates of reinfection average of 2-3), within each country and then outbreaks in that country. These outbreaks and export processes have inspired the proposed CVA algorithm in generating its initial solutions and population mimicking COVID-19 spreading behavior. During the process of COVID-19 spreading, some confirmed cases (solutions in CVA) may not spread in a specific region or export to other countries. This is due to the fact that those cases (solutions in CVA) have recovered or already passed away. Considering this scenario, these solutions will be removed from the feasible list in the next population and the algorithm will carry on exploring the remaining best solutions. Then, the CVA performs the spreading process of remaining best solutions to the rest of population.

A. COVID-19 Outbreak and Spreading

The initial solution is randomly set in a region of feasible space and initial population is generated based on the outbreak in that region. Possible solutions will also be exported to other regions, the same as coronavirus distribution process across cities and countries. We have defined the exporting process of the virus to other countries as the power of export, which could be different for each country based on its community's behavior and social activities. Here, for simplification this power is defined as a constant p for all countries, which is a percentage of the number of solutions in the initial population, 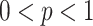. Let 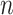is the number of solutions for initial population, so 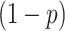of 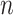are generated close to the initial solution based (1):

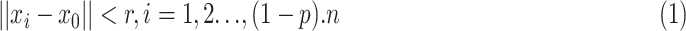where 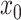is the initial solution, 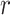is a positive constant number which restricts solutions in a specific region. When the generated number 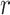exceeds its upper bound, the outbreak scenario will occur. As it was based on the inspiration of COVID-19 outbreak in a country, the CVA triggers the outbreak to reinforce the search by exploiting this part of population intensively; looking for the optimal solution. The parameter 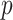is the percentage of the number of solutions in the initial population and generated far from the region of the initial solution in the feasible space based on (2):

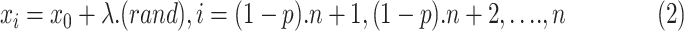Where rand is a real random number between 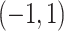and 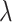is a large enough positive number. The above generation process has been inspired from the COVID-19 export to other countries; this part of population would not trigger the outbreak only after two iterations in our simulation. The reason behind this assumption is to obtain a more realistic simulation, where there is less possibility of having all people exposed/infected by the virus at the first instant. So there is an opportunity to control and quarantine infected cases before they could lead to an outbreak. In fact, the initial population of the CVA displays the first generation of people that were exposed to the virus. In the process of coronavirus distribution in our inspired algorithm, the population distributes the virus all over the region, so it uses this initial population to obtain more outbreak and export to cover all feasible regions in the optimization problems spaces.

B. Recovery, Remove and Transmission

In the distribution and infection process of the coronavirus, there are two categories of people: active cases that have the virus and can transmit it to others whereas closed cases is defined as the solutions that are either recovered from the COVID-19 symptoms or dead. In this context, in our COVID-19 optimizer and after generation of the initial population, there are two kinds of solutions in each population: closed cases that are not contributing to transmit to other regions of feasible space and are removed from the population. The second type of solutions, named active cases, can transmit the virus immediately or after a while (two iterations) of exported solutions.

In the CVA, the transmission power is a factor that enables spreading of the solutions to other feasible regions in the search space for generating the next population. This factor could be different for each solution (person) based on its communities compared with others. Furthermore, the transmission power is a positive integer constant, 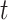, for all active solutions and it is zero for closed cases. Hence, the number of active solutions, 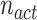, is obtained from (3):

where 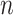is the number of solutions in the current population and 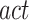is the rate of active solutions in the current population (we empirically set 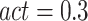). In the simulation, all solutions of the population are sorted based on their functions values and among 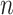solutions where the best 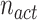will be selected as active cases. Then, the remaining solutions 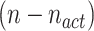will be removed. The remaining solutions are defined as the closed cases and are represented by (4):

where 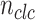is the number of closed cases that means all recovered and dead solutions.

In our proposed CVA algorithm, the best solution will be found out from the active cases, 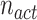and saved accordingly. This process will be repeated over throughout the course of iterations and eventually obtain the best solution 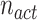, which will be announced as the optimal solution. For generating the next population, each solution of active cases can transmit the virus to new feasible solutions named 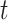, where 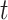is defined as the power of infection transmission. Hence, the number of solutions in the next population, 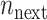, can be obtained from (5):

Using (3) and (5), we get:

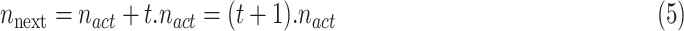Equation (6) calculates the number of solutions in the next population that has a direct relation with 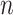, act, and 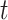. Thus, by increasing the number of solutions, the rate of active solutions and infection transmission power, the speed of distribution will be increased accordingly.

C. The Procedure of COVID-19 Inspired Algorithm

The principal steps of the coronavirus inspired algorithm in are proposed as follows:

• 1)The initial feasible solution is created randomly. This solution implies the initial region or country where the virus starts. The parameters of the algorithm are: number of solutions, 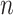; an arbitrary small positive number, 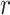; number of iterations, 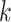with 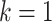at the first iteration; the power of export, 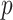; the percentage of the recovery, rec; the rate of active solutions, act; the infection transmission power, t; a positive small number, 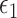, and the maximum number of iterations, 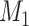. It is worth to mention that the parameters of the CVA technique are empirically set.
• 2)The initial population with n solutions is generated as follows: 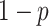percentage of solutions are generated very close to the solution with radius 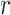and other 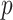percentage are generated far from the region of the initial solution in the feasible space. The coronavirus spreads some solutions from the initial attempt to other regions because of the human social interaction all over the world.
• 3)Based on the coronavirus termination process, some of the patients in step 2 that have been recovered or died, these solutions are removed from the population.
• 4)COVID-19 is spreading in a specific country initially and will be transmitted to other countries after sometime later. Likewise, the CVA technique is composed of two categorises of solutions that are contributed to find the optimal value. More precisely, solutions in the initial region transmit promptly (red points in Fig. 1) whereas the rest of solutions will be transmitted after two iterations (magnet points in Fig. 1).
• 5)The best solutions of each generation are found and saved. Then, the best solution among them will be selected as the optimal solution by the algorithm. If 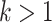, go to the next step, otherwise let 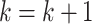and go back to step 3.
• 6)If 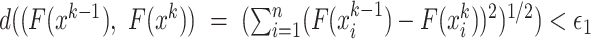or the number of iterations is more than 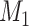, the algorithm will be terminated. 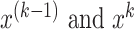are the best solutions in two consecutive generations. Otherwise, let 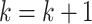and go to the step 2.

Fig. 1.

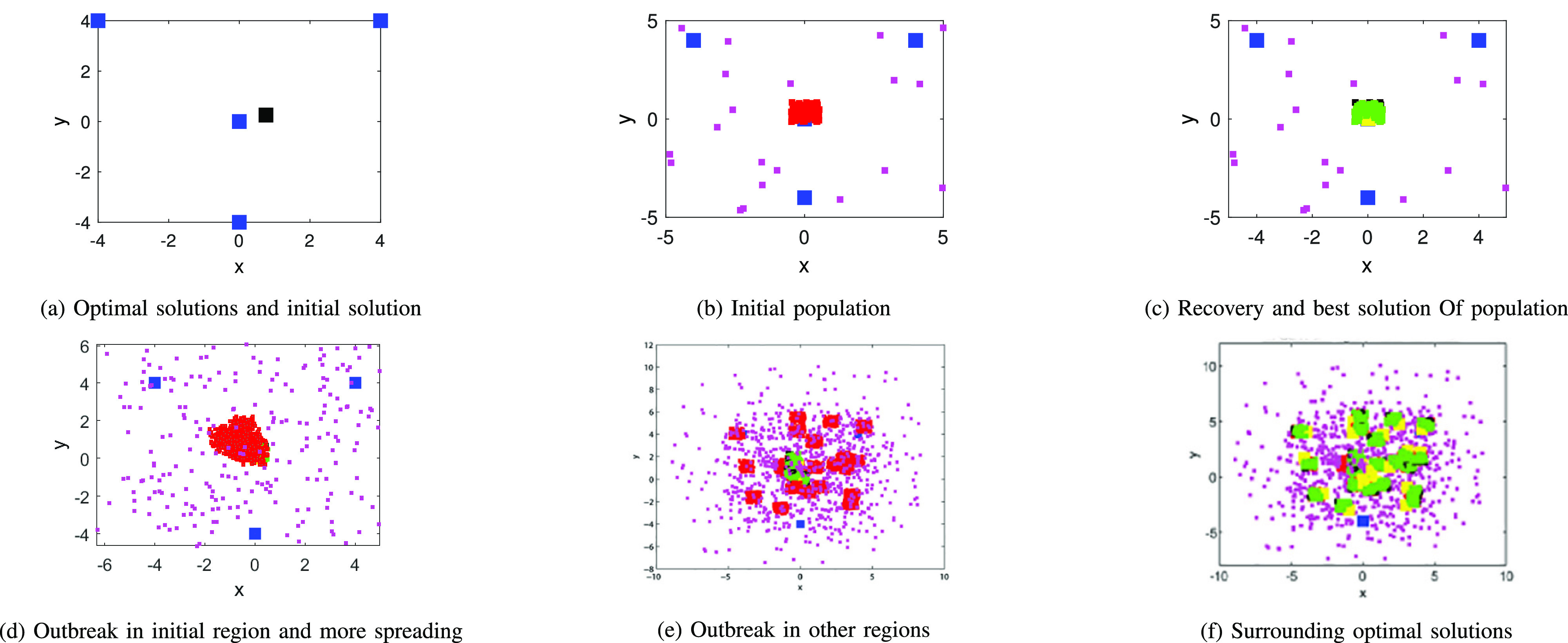
The process of COVID-19 spreading for a given optimization problem.

Fig. 1 shows the process of the CVA to find the optimal solutions, Fig. 1(a) shows the optimal solution (blue points) and the initial solution (black point) in a given optimization problem. As shown in Fig. 1(b), the initial population includes solutions, which can outbreak and spread (red points) as well as solutions exposed to be spread to other regions, but would not outbreak after two iterations (magnate points). The recovery process is illustrated in Fig. 1(c); it includes closed cases (green points, recovered, and black points, dead) and the best solution of the current population (large yellow points). Fig. 1(d) shows more outbreak and spreading from active solutions. Further, Fig. 1(e) shows the spreading solution outbreak in their regions and exporting to other districts. Eventually, Fig. 1(f) depicts the surrounding optimal solutions by population. More specifically, the yellow points are the best among the population and our proposed CVA selects the best among those best solutions. To show the performance of the proposed CVA, we use the benchmark functions of well-known optimization problems. Table I shows mathematical formulations of the problems, Table II presents the optimal values of the proposed algorithm and Figs. 2, 3 and 4 show the process of finding the optimal solution using the CVA algorithm for the given optimization problems. In all benchmark examples, we set the number of agents n to 100, the rate of active cases (act) to 0.3, the number of iterations (M) to 1; and the epsilon to 0.5. Fig. 2 presents the behavior of the original function, Fig. 2(b) finds the optimal solutions when the CVA is applied. Similarly, the proposed CVA can get the optimal solution shown in Figs. 2(d) and 2(f).

TABLE I. Optimization Test Functions Examples 1-8.

Examples	Equation
Example 1
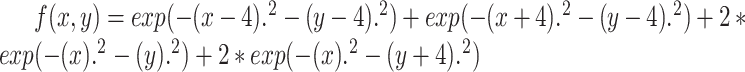
Example 2 - Deckkers-Aarts Function
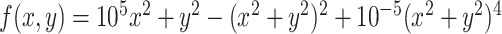
Example 3 - Himmelblau Function
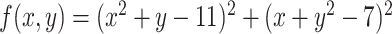
Example 4 - Sphere Function
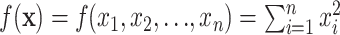
Example 5 - Rosenbrock Function
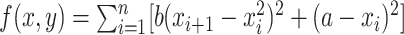
Example 6 - Bukin N. 6 Function
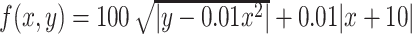
Example 7 - Holder-Table Function
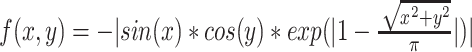
Example 8 - McCormick Function

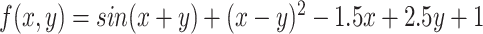
TABLE II. Results of the Proposed CVA for Examples 2-9.

	(x,y)	OS by CVA	Optimal Solution	IS
Example 1	(-0.0084, 0.0072)	1.9998	2	Random between (-1.5,1.5)
Example 2	(-0.0143, -10.7994)	-1.1615e+04	-24771.09375	Random between (0,1)
Example 3	(3.0039, 1.9995)	0.0005	0	Random between (-3,2)
Example 4	(-0.0077, 0.0166)	0.0003	0	Random between (-5,5)
Example 5	(0.9176, 0.8431)	0.0069	0	Random between (0,2)
Example 6	(-8.2987, 0.6886)	1.0044	0	Random between (-10,1)
Example 7	(-8.1329, -9.1749)	-16.9743	-19.2058	Random between (-8,-6)
Example 8	(-0.5481, -1.5564)	-1.9131	-1.9133	Random between (-2,1)

Fig. 2.

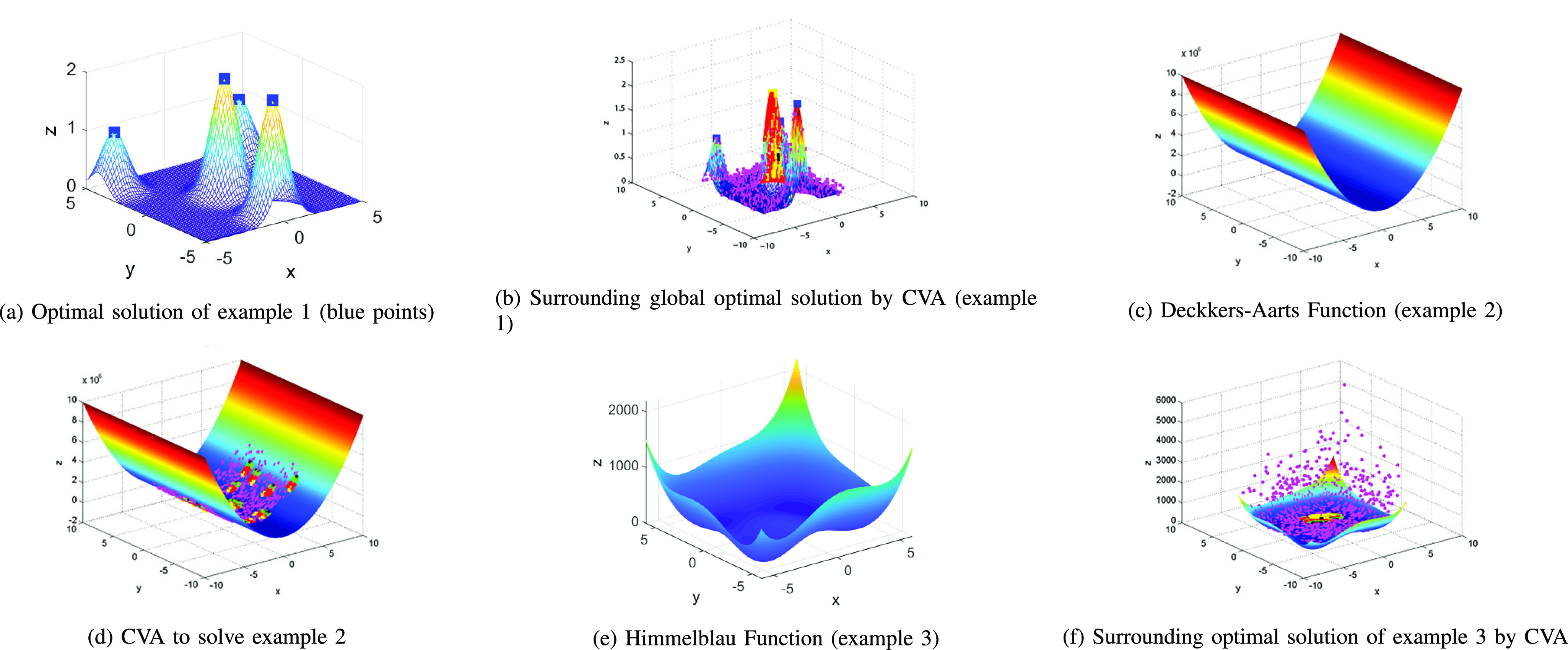
The results of example 1, 2 and 3 when original function (Left) and CVA are applied (right).

Fig. 3.

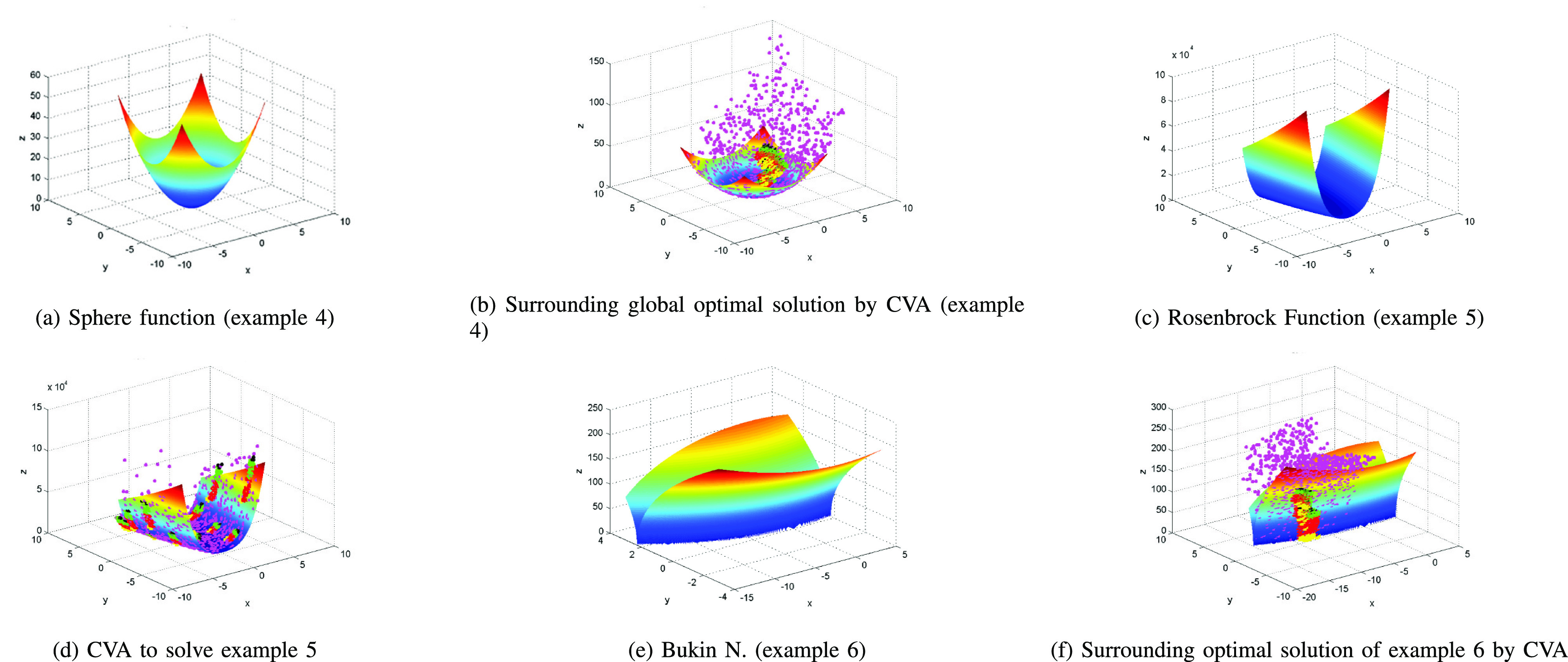
The results of example 4, 5 and 6 when original function (Left) and CAV are applied (right).

Fig. 4.

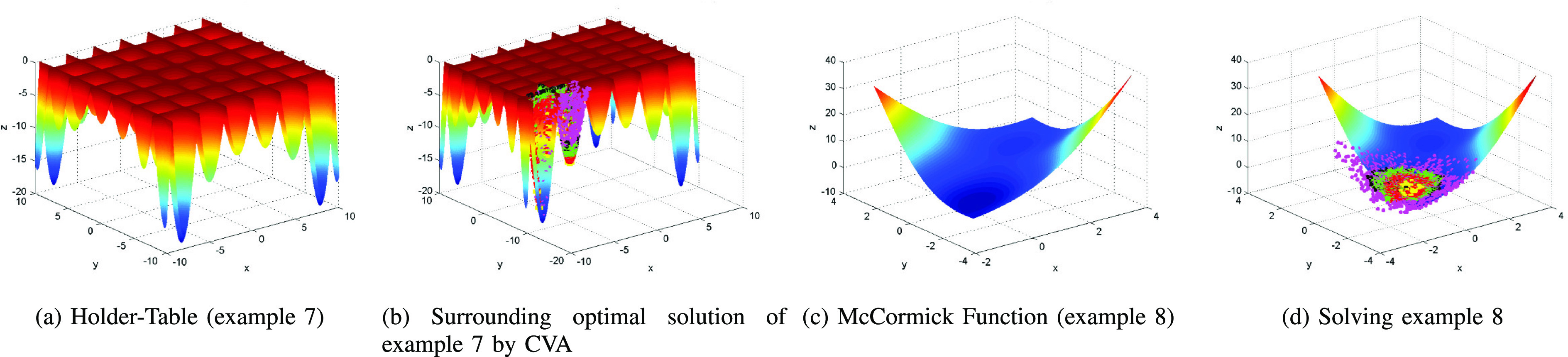
The results of example 7 & 8 when original function (Left) and CVA are applied (right).

In order to evaluate the performance of our CVA, we used the proposed algorithm to solve more optimization problems. In particular, Fig. 3(b), Fig. 3(d) and Fig. 3(f) show the results of the optimization problems which are presented in examples 4, 5 and 6, respectively. As can be seen, the proposed CVA could find the optimal solution with a short amount of time for all test functions in examples 4, 5 and 6.

The performance of the proposed algorithm is high since it can produce efficient solutions with only one iteration. Furthermore, the factor 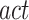is set to 0.3. Increasing this factor accelerates the convergence of the algorithm.

D. Performance Evaluation

This section presents the performance evaluation of the proposed CVA and most related meta-heuristic algorithms, such as the Volcano Eruption Algorithm (VEA) [31], the Grey Wolf Optimizer (GWO) [20], the PSO [16] and the GA [15]. Several well-known optimization problems have been used as benchmark test functions to verify the validity of the CVA performance evaluation. In particular, the CVA is used to solve two different categories of test functions: the unimodal and the multi-modal. The unimodal test functions that have just a global optimum, but the multi-modal test functions have a global optimum as well as multiple local optima.

In the experiments, we set the number of agents to 20, the maximum number of iterations to 100 and the epsilon to 0.1. In order to give credibility to the results, every value in Table III represents 50 runs of the algorithm. Further, the results in Table III show that the proposed algorithm is efficient on both the unimodal and the multi-modal test functions as compared to existing algorithms in the literature.

TABLE III. Comparison of CVA With VEA, GWO, PSO and GA Meta-Heuristic Techniques for Several Types of Optimization Problems.

F	CVA		VEA		GWO		PSO		GA
	Mean	Std.	Mean	Std.	Mean	Std.	Mean	Std.	Mean	Std.
Function 1	0.0107	0.0106	0.0142	0.0112	0.2080	0.1195	0.5774	0.3185	18.7254	4.9352
Function 2	1.9435	0.7396	1.7367	0.5892	2319.19	1237.109	3.5523	2.8537	27187.58	2745.82
Function 3	9.1690	6.8371	12.4784	8.3213	89.1347	37.9576	99.8320	24.6287	273.2519	29.5521
Function 4	1.0749	0.6921	1.3269	0.8263	9.4525	3.4676	4.2950	1.3083	18.5965	0.3517
Function 5	4.0734	2.9351	5.1245	3.2689	14.4316	5.9230	8.7162	4.9291	68.6618	6.0623

E. The Control of Coronavirus Spreading

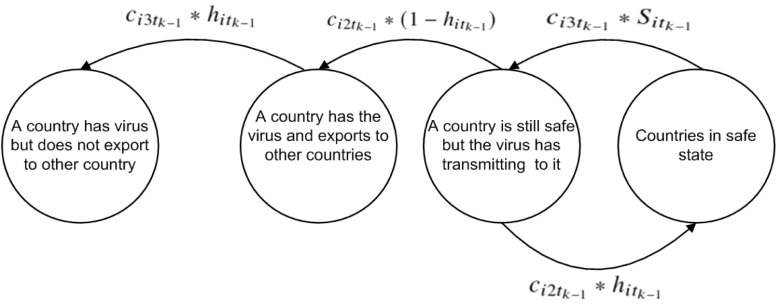
This section first presents the importance of preventing the spread of COVID-19 by developing a mathematical controlling model. The control of COVID-19 spreading is adopted for person-to-person infection and spreading among countries. The proposed mathematical model is derived to overcome the spread of COVID-19 among countries. The proposed control model maximizes the number of safe countries, while fulfilling the constraints of formulae 8 to 13.

The problem of COVID-19 spreading is defined as follow:

Definition: During the coronavirus spread, there are N regions (countries) with four states at k periods of time:

• 1)Countries are assumed in a safe state.
• 2)Countries are assumed to be safe, but they are susceptible to COVID-19 infection.
• 3)Countries are infected with COVID-19 that can be transmitted to other countries.
• 4)Countries can be infected with COVID-19, but do not transmit to other countries

In the aforementioned states, countries in state 4 do not need assistance from neighbouring regions due to the imposed lockdown to reduce and control of the disease spread. Countries in states 2 and 3 can still receive aid since they are still not in lockdown yet. However, in this article we ignore this assumption for simplicity purpose. Moreover, help can be made to countries in state 2 by finding and quarantine people who recently arrived from other countries in state 3. Finally, help for countries in state 3 can be made by testing people that have visited an infected country. For instance, applying COVID-19 test to all passengers who plan to leave such country. By this help, countries in state 3 would be quarantined and changed to state 4.

According to the aforementioned assumptions and states to control COVID-19 spreading, the objective is to maximize the number of countries being at state 1 during the fast spreading process. To achieve this goal, the control of COVID-19 spreading is modeled as a mixed binary-integer programming problem as follows:

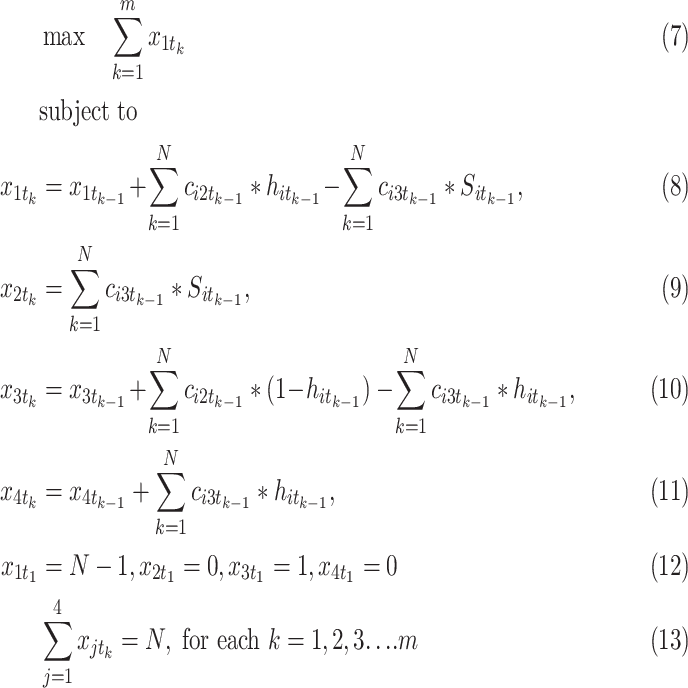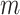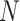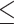
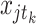
where is the time period, is the number of countries, 0 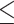N, 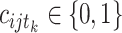, 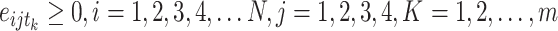. Variable 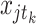is the number of countries in state j at a stipulated time period 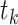, variable 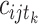is 1 if 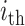country be in state j at stage 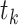, and it is 0 otherwise. Moreover, variable 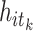is 1 if 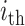country at stage 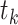gets help otherwise its value is 0. 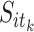is the spreading rate country i has at stage 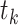. The value of 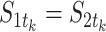=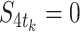, because only countries at state 3 can spread the COVID-19 to other countries for all 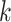, whereas the value of 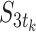is a positive integer. The objective function is utilized to maximize the number of countries stay in safe state in 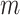periods of time. Constraint 8 to 13 are for 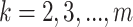number of safe countries (state 1) at the 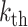stage = countries in state 1 plus countries in state 2, but they get help (help is a key measures to prevent COVID-19 spreading) minus the COVID-19 infected countries, which are responsible in spreading the virus to other countries in state 3 and stage 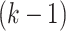. Further, constraint 9 originally is:

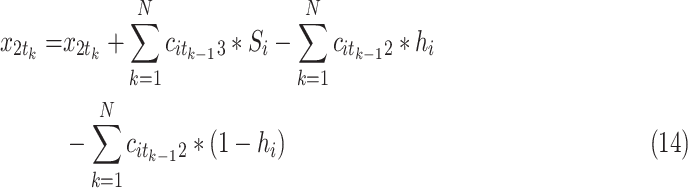As shown in formula 14, the number of countries in state 2 at the 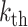stage are shrinking in case of getting help at 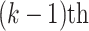stage, whereas this number is increasing if they don’t get help. So, all countries in this state will be changed to states 1 or 3. Furthermore, countries that are infected from countries at state 3 will transit their state to 2. Constraint 10 shows the number of countries in state 3 at the 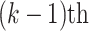stage. Constraint  10 is derived from the number of countries in state 3. Countries in state 2 don’t get help with excluding countries in state 3, where to get help at 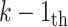stage. Further, constraint 11 is derived from the number of countries in state 4 (closed case) at stage k, which is derived from countries in state 4 and also countries in state  3, where to get help at stage . Constraint 12 shows the state of countries at the beginning of coronavirus which starts in a country. Constraint 12 indicates that the summation of the number of countries in all states should be equal to the number of countries, 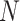, at all period of time. The state transition diagram of the proposed COVID-19 spreading control is illustrated in Fig. 5.

Fig. 5.

State transition diagram for COVID-19 spreading control.

F. Normal Distribution

In this sub-section, the process of coronavirus distribution is presented (Fig. 6(a)). A comparison has been conducted that shows the distribution of the results with different scenarios. Assuming a scenario with the number of countries (region or people) is N = 50, the number of agents (virus) is n = 50, the number of running iterations (stages or periods of time) is 5, the power of exporting to each country is 20 percent of solutions (this can be based on the communication in each country, but in this article, this is fixed for each country). Two main scenarios are simulated to illustrate the distribution of the virus among cities as detailed below.

Fig. 6.

The process of coronavirus distribution in normal state, Scenario I, Scenario II-A and Scenario II-B for 50 countries.

G. Scenario I

In this scenario, countries allocated in state 3 may get help and change to state 4. In fact, countries that are categorized under state 3, they could export the virus to other countries; hence helping them can be more effective in saving other countries. Help for state 3, based on the definition, is to control all commuting of the country. For example, testing passengers who exit from the country, so that they won’t export the virus to the destination country. By this kind of help, the country will be changed to the lockdown status (state 4). But, based on the obtained results and extensive simulation of this scenario, it is not recommended to control the spreading of the virus. The reason is that countries in state 3 can export the virus to other countries, because of asymptomatic transmission. Even before officials find out the start of infections in a country, the people who are infected with COVID-19 may have traveled to other regions. In Fig. 6(b), the large green points represent the safe countries (state 1), the green points with small magnet point in the center are countries in state 2 (exposed to getting the virus), the green points with red points in the center are countries in state 3 (with virus and can export), the green points with yellow points are for countries in state 4 (with virus but not exported).

H. Scenario II

1). Scenario II-A

In this scenario, not only countries with state 3 will be changed to state 4, but also countries that are exposed to get the virus in order to get help and change to state 1. Here, we assume that all countries in state 2 are recognized before, their state is changed to state 3. However, this consideration is a little hard and costly in reality. But, we could observe from the simulation that the results can be substantially effective. The reason obtained from the simulation is that, the most powerful factor of the coronavirus distribution is the power of exporting it to other countries. That in turn will move them to state 3 at the same time from the countries, where the just got the virus.

In Fig. 6(c), the large green points are safe countries (state 1), the green points with yellow points in the center are countries that got the virus already. But with getting help, their status can change to state 4 (not exporting the virus anymore). On the other hand, the green points with small magnet points in the center are countries in state 2 (exposed to getting the virus), the green points with white points in the center are countries in state 2, but with getting help, they will be changed to state 1.

• 

From Fig. 6(c), it is clear that all countries will converge to a safe state, (except the initial country), after only one iteration of the virus distribution. This is due to the fact that the initial country has been controlled such that it could not export the virus anymore. Hence, this country will be avoided from exporting the virus to some other countries as it is in state 3. Similarly, all countries in state 2 are infected and obtained help to be safe, so there will be no other countries to export the virus to others. The main challenge of this scenario is we may not recognize all countries that were exposed to the virus (state 2) before their status is changed to state 3. So to be realistic, we assume that the percentage of these countries can not be recognized right after starting the virus in the initial country.

2). Scenario II-B

In this scenario, we assume 50 percent of countries in state 2 will be recognized and get help before their states are changed to state 3. The power of export of countries in state 3 is also very effective in this scenario as well as in the power of distribution. The export power for each country is the rate of communication with other countries, so by increasing the number of countries (people) in our simulation, this power should be increased too, because the community of countries has a direct relation with the number of countries. Algorithm 1 illustrates the procedure of Scenario II-B.

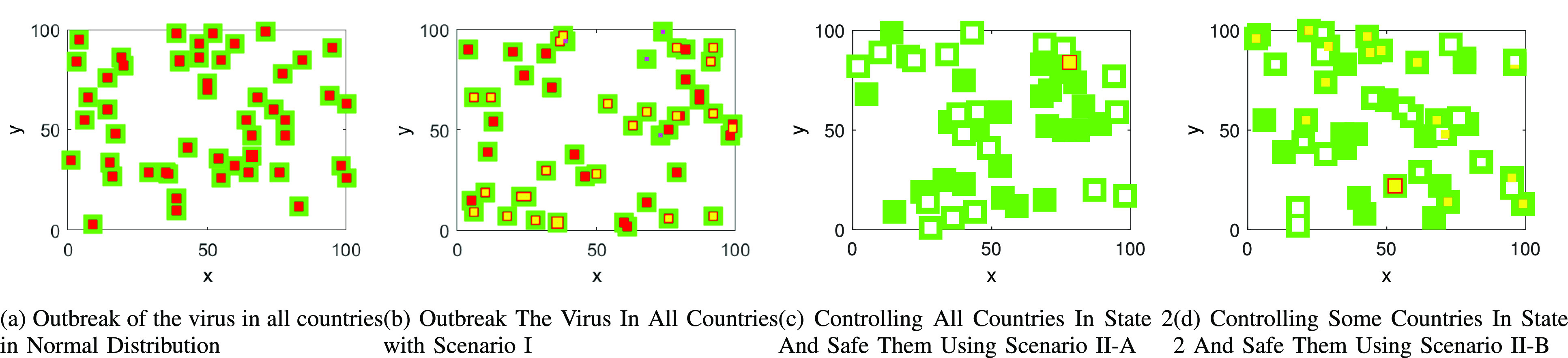
Fig. 6(d) shows the process of Scenario II-B in 5 iterations. Based on Fig. 6(d), 34 countries have been saved from being exposed to the virus, which can be a significant achievement. The results would be much better as much as recognizing a number of countries in state 2. In other words, during the coronavirus, we should focus on countries or people who have been exposed to the virus. Luckily, these achievements are valid for people too, so authors strongly suggest quarantining a recognized sick person and all people that had contact with a positive virus carrier recently. By this scenario, the virus cannot transmit to others and it will be controlled very soon, hence its dissemination will be substantially mitigated. Fig. 7 shows a comparison of a normal distribution, Scenario I, Scenario II-A and Scenario II-B with different numbers of people (country). We can observe from Scenario II-A that the virus distribution can be controlled with very high performance, while Scenario I presents the approximate behavior of the normal distribution of the virus.

Fig. 7.

Comparison of Scenario I and II normal distribution.

Scenario I represents the mass quarantine strategy in which the government authorities implement the appropriate measures to prevent the COVID-19 spread. However, practicing the lockdown strategy slams the economy and increases the unemployment rate. Therefore, it is strongly suggested to deploy actions of Scenario II-A, in which the results show that the virus could be controlled very quickly. Besides, the use of Scenario II-B that could also control the distribution process is much better than the conventional way presented in Scenario I.

Analyzing the complexity of an algorithm will quantify how fast it can run as a function of the input size. The run time of an algorithm depends on several factors: input size as well as the used hardware and software. Here, we are interested in the rate of time growth according to the input size and the algorithm used. In Algorithm 1, there are 17 assignments and several procedures in order to make countries stay safe. In particular, the complexity (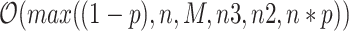) of the proposed algorithm can be derived as shown in (15):

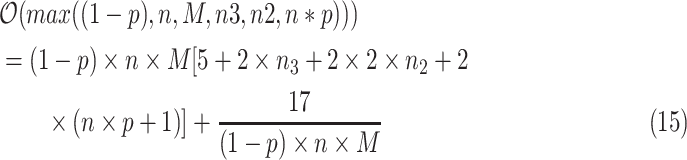Referring to (15), the maximum variable is n represents the number of countries. In worst case scenarios, the complexity of our proposed algorithm is .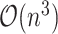

IV. Conclusion

This article answers an important question; how can governments and health authorities be able to protect people from the spread of of COVID-19? To achieve this goal, we modeled the coronavirus distribution process as an optimization problem to minimize the number of COVID-19 infected countries and hence slow down the epidemic spread. This will certainly ease the lockdown measures. Then, three scenarios are proposed to solve the optimization problem using the most effective factors in the distribution process. We also propose a novel COVID-19 optimizer Algorithm (CVA) to cover almost all feasible regions of the optimization problem. This is confirmed through a simulated coronavirus distribution process in several countries around the globe. Extensive simulations using several engineering optimization problems have shown the efficiency of the proposed CVA algorithm. For the future research directions, we plan to pursue the re-infection process where countries that have viruses and do not export to the other countries (state 4) may spread COVID-19 to other countries (state 3).