Multilevel Deep-Aggregated Boosted Network to Recognize COVID-19 Infection from Large-Scale Heterogeneous Radiographic Data

Abstract

In the present epidemic of the coronavirus disease 2019 (COVID-19), radiological imaging modalities, such as X-ray and computed tomography (CT), have been identified as effective diagnostic tools. However, the subjective assessment of radiographic examination is a time-consuming task and demands expert radiologists. Recent advancements in artificial intelligence have enhanced the diagnostic power of computer-aided diagnosis (CAD) tools and assisted medical specialists in making efficient diagnostic decisions. In this work, we propose an optimal multilevel deep-aggregated boosted network to recognize COVID-19 infection from heterogeneous radiographic data, including X-ray and CT images. Our method leverages multilevel deep-aggregated features and multistage training via a mutually beneficial approach to maximize the overall CAD performance. To improve the interpretation of CAD predictions, these multilevel deep features are visualized as additional outputs that can assist radiologists in validating the CAD results. A total of six publicly available datasets were fused to build a single large-scale heterogeneous radiographic collection that was used to analyze the performance of the proposed technique and other baseline methods. To preserve generality of our method, we selected different patient data for training, validation, and testing, and consequently, the data of same patient were not included in training, validation, and testing subsets. In addition, fivefold cross-validation was performed in all the experiments for a fair evaluation. Our method exhibits promising performance values of 95.38%, 95.57%, 92.53%, 98.14%, 93.16%, and 98.55% in terms of average accuracy, F-measure, specificity, sensitivity, precision, and area under the curve, respectively and outperforms various state-of-the-art methods.

I. Introduction

The recent coronavirus disease 2019 (COVID-19) epidemic has brought the whole world to the verge of destruction. On March 11, 2020, the World Health Organization (WHO) asserted COVID-19 infection to be a global pandemic [1]. According to their report, as of February 25, 2021, approximately 111762965 patients of COVID-19 virus have been confirmed, including 2479678 deaths with an average mortality rate of 2.22% [2]. Meanwhile, various trial vaccines are still undergoing development and clinical assessments to ensure their efficiency and safety before they can be officially approved. For the diagnosis of COVID-19, the reverse transcription-polymerase chain reaction (RT-PCR) test is considered the reference standard [3]. However, subjective evaluations and stringent testing requirements may restrict the speed and accuracy of screening people suspected to be infected with the virus. In this regard, radiological modalities, such as X-ray and computed tomography (CT), have exhibited effectiveness in the early diagnosis of COVID-19 [3], [4]. A recent clinical study [3] showed that chest CT image-based analysis achieved a 97% sensitivity for COVID-19 detection with reference to RT-PCR results. Similar observations have also been reported in [4], [5], implying that radiological imaging modalities may be useful in the early diagnosis of the disease. However, radiologists have to devote considerable time and effort to assess radiographic scans before effective diagnostic decisions can be made. Therefore, in epidemic regions with limited resources, this method may not be suitable.

Recent breakthroughs in artificial intelligence (AI) technology have significantly contributed to the advancement of tools for computer-aided diagnosis (CAD) [6]–[20]. In particular, the methods for deep learning-driven CAD have exhibited remarkable performance gains in various medical fields, including radiology. These state-of-the-art methods can mimic the human brain's capability to make effective diagnostic decisions similar to those of medical professionals. Moreover, these techniques can outperform real-time population screening applications where human assessment is not feasible. The generalized workflow cycle of a CAD tool is shown in Fig. 1 to illustrate its clinical usability in making diagnostic decisions.

Fig. 1.

Simple workflow diagram of computer-aided diagnosis (CAD) tool for visualizing clinical interpretation and usability in making effective diagnostic decisions.

In general, among the different deep learning algorithms, convolutional neural networks (CNNs) have attracted considerable attention in medical image processing applications. In the present COVID-19 outbreak, these CNN models can also be trained to differentiate between positive and negative cases in a real-time environment using radiographic data, such as X-ray or CT images. Though, to train CNN models, independent data are necessary—a requirement which can regarded as a major constraint in the deep learning domain. The internal structure of these models mainly includes a stack of convolutional and fully connected (FC) layers to extract deep features and then perform classification, respectively. Other layers are also present for different purposes, as defined in [21]; however, convolutional and FC layers are the core components that incorporate a number of trainable parameters. These parameters are initially trained using a dataset. Subsequently, a trained network capable of analyzing testing data and yielding desired results is derived.

Many researchers have recently proposed the use of different deep learning-based CAD methods to recognize COVID-19 pneumonia through radiological imaging modalities [6]–[20]. In most of the existing studies, deep classification networks act as black boxes that merely provide the final diagnostic decision (i.e., whether or not a patient is infected with COVID-19) without providing supplemental information that may assist radiologists in validating the CAD. To give visual insight about the decision of our model, the evolution of deep features was visualized as an additional output with the diagnostic decision. Moreover, these existing methods only employ single-modality data (either X-ray or CT scans) with including limited number of COVID-19 positive samples. In contrast, in this study, large-scale heterogeneous radiographic data, including both X-ray and CT scans, is considered by combining a total of six publicly available datasets [24]–[28]. Although, the total number of samples are not significantly large in context of a recent deep learning paradigm. However, in context of the recent pandemic of COVID-19 infection, our study included sufficient large number of positive samples in comparison with existing methods. Table I presents a brief comparison based on the number of positive and negative samples between proposed and various state-of-the-art methods. Finally, an efficient multilevel deep-aggregated boosted network (MDA-BN) including the optimal number of trainable parameters is proposed. Quantitative analysis shows the superior results of our model over various existing methods. The key contributions of this study are presented as follows:

• 1)To the best of our knowledge, this is the first study that simultaneously considers large-scale heterogeneous radiographic data from X-ray and CT images to diagnose COVID-19 infection without influencing the overall diagnostic. CT and X-ray images are not combined together to be fed into the MDA-BN model. Instead, either X-ray or CT image is used as input to our MDA-BN model. Originally, the proposed model is trained for heterogeneous radiographic data including both X-ray and CT images which can be obtained from different patients. It means that we do not consider the strict requirement of both X-ray and CT images from same patient. In addition, our trained model does not require both X-ray and CT images at the same time, but it uses only single modality data (either X-ray or CT image) in the testing phase.
• 2)For optimal memory consumption and fast execution speed, we utilize the strength of depth-wise (DW) convolution in our network design and propose an optimized deep network (with a total of 1.76 millions parameters) specifically for processing heterogeneous COVID-19 data.
• 3)Besides the use of existing blocks (Blocks A and B) in our network design, a new deep-aggregated block (Block C) is mainly introduced to incorporate the contribution of low-level and intermediate-level features with high-level deep features and provide an additional performance gain at a minimal increase in the total number of parameters. Additionally, our model leverages multistage training and multilevel deep-aggregated features in a mutually beneficial manner by performing individual training of both subnetworks named as boosted network (BN) and multilevel deep-aggregated network (MDA-N) to optimize the overall diagnostic performance.
• 4)Intermediate feature maps are visualized as a stack of multiple class activation map (CAM) images along with the diagnostic decision. Such additional output images provide visual insight into the conclusion reached by CAD and may assist radiologists in cross-validating the decision, particularly when such predictions are ambiguous.
• 5)Finally, to conduct future research and fair comparisons, the proposed model/code has been made publicly accessible freely via [22].

TABLE I. Comparison Based on Number of Positive and Negative Samples Between Proposed Multilevel Deep-Aggregated Boosted Network (MDA-BN) and Various State-of-the-Art Methods. “N/A” Means “not Available”.

Literature	Modality	#Scans(#Subjects)
		ive	ive
Minaee et al. [6]	X-Ray	184(N/A)	5000(N/A)
Khan et al. [7]	X-Ray	790(N/A)	802(N/A)
Martínez et al. [8]	X-Ray	120(120)	120(120)
Misra et al. [9]	X-Ray	184(N/A)	5824(N/A)
Farooq et al. [10]	X-Ray	68(45)	5873(2794)
Ardakani et al. [11]	CT	510(108)	510(86)
Oh et al. [12]	X-Ray	180(118)	322(322)
Singh et al. [13]	CT	345(N/A)	315(N/A)
Li et al. [14]	CT	305(251)	2370(2344)
Pereira et al. [15]	X-Ray	90(N/A)	1054(N/A)
Das et al. [16]	X-Ray	162(N/A)	6683(N/A)
Khan et al. [17]	X-Ray	284(N/A)	967(N/A)
Asnaoui et al. [18]	X-Ray	231(N/A)	5856(N/A)
Brunese et al. [19]	X-Ray	250(N/A)	6273(N/A)
Jaiswal et al. [29]	CT	1262(60)	1230(60)
Apostolopoulos et al. [30]	X-Ray	448(N/A)	2422(N/A)
Tsiknakis et al. [31]	X-Ray	122(122)	450(450)
Proposed	X-Ray CT	6550(1660)	6360(5272)

The remainder of this paper is organized as follows. Section II presents the background of different CAD methods related to COVID-19. Section III explains the proposed methodology by focusing on network architecture and optimal training scheme. Section IV briefly discusses the experimental setup and results. Finally, Section V summarizes the conclusion and future work.

II. Related Work

This section explores the literature on state-of-the-art methods related to AI-driven CAD [6]–[20] for the COVID-19 infection. In particular, the main objective of previous studies has been to analyze the given radiographic data and identify discriminative patterns that can differentiate between COVID-19 positive and negative patients. These studies mainly applied segmentation, detection, or classification algorithms to reach their final diagnostic decision. For example, in a recent study, Minaee et al. [6] prepared a binary class dataset consisting of 5184 chest X-ray images. Then, they performed transfer learning to four existing CNN models, DenseNet121 [44], SqueezeNet [39], ResNet18 [42], and ResNet50 [42], to check their individual results in detecting the COVID-19 infection. Similarly, Khan et al. [7] also analyzed the performance of four different models (i.e., VGG16 [40], VGG19 [40], ResNet50, and DenseNet121 [44]) for diagnosing patients as COVID-19 positive or negative based on X-ray scans. Given results demonstrated the superior performance of VGG16 and VGG19 compared with the other two networks above.

In another study, Martínez et al. [8] evaluated the performance of the NASNet [41], an existing deep network, in recognition of COVID-19 infection based on chest X-ray scans. Thereafter, Misra et al. [9], Farooq et al. [10], and Ardakani et al. [11] used different versions of the ResNet model in their studies to distinguish COVID-19 positive patients from negative patients and those with other types of disease. In [9], three ResNet models were combined and fine-tuned using X-ray dataset to discern COVID-19 positive and negative patients, and patients with pneumonia using a one-on-one framework. Subsequently, Farooq et al. [10] presented a three-step approach to fine-tune the ResNet50 architecture in three different stages. In each stage, the same data with different spatial sizes were used for network training. In [11], the performance of ten different CNN models was analyzed to discern COVID-19 patients based on their chest CT scans. According to the results, the ResNet101 [42] and Xception models achieved superior performance over all the other networks.

In the context of limited datasets, Oh et al. [12], Singh et al. [13], and Li et al. [14] devised methods to perform the optimal training of a deep network. In [12], the authors applied patch-level training rather than using the entire X-ray image at once. In the preprocessing stage, a FC dense network was used to segment the lung regions. Similarly, Singh et al. [13] presented a novel training method to obtain an optimal pre-trained CNN model. Subsequently, Li et al. [14] presented a self-supervised learning method to perform optimal training of a COVID-19 recognition model using CT dataset. In another study, Pereira et al. [15] combined handcrafted and deep features for diagnosis of COVID-19 positive patients using X-ray images. Additionally, a resampling algorithm was proposed to perform data augmentation and overcome the class imbalance problem.

In recent studies [16], [17], multiclass diagnostic methods were proposed to further make class-specific decisions in the case of negative prediction. For example, Das et al. [16] presented an optimized version of the standard InceptionNet model [45] to categorize input X-ray scan into one of the following four categories: 1) COVID-19 positive, 2) pneumonia, 3) tuberculosis, and 4) healthy case. Subsequently, Khan et al. [17] proposed another deep network, named CoroNet (including the Xception network and additional dense blocks), to categorize X-ray data samples into four different classes. To perform a comparative analysis of existing CNN models for COVID-19 infection detection, Asnaoui et al. [18] evaluated the collective response of seven different networks using X-ray images. All the networks were trained to classify the given X-ray scan into one of the following categories: 1) bacterial pneumonia, 2) COVID-19 positive, and 3) healthy case. The experimental results show the higher performance of InceptionResNet [43] compared with other networks. Thereafter, Brunese et al. [19] used two existing VGG16 networks in sequential order. The first VGG16 network differentiated between healthy and infected cases, and the second model further distinguished between COVID-19 and other type of infections. To reduce the number of trainable parameters, Owais et al. [20] utilized the capacity of DW convolution and proposed a light-weighted ensemble network using X-ray and CT data. However, in [20], the performance of each radiographic dataset was evaluated separately. Besides the automated diagnosis of COVID-19, there are some other studies [32]–[34] related to other medical diagnostic domains based on the fusion of different CNN models. These methods mainly utilized the concept of deep information fusion [35] to improve the overall CAD performance. We also utilized the strength of deep information fusion in this study and proposed an optimal MDA-BN model to recognize COVID-19 infection from large-scale heterogeneous radiographic data. Our method exhibits superior performance in terms of accuracy and computational cost over various state-of-the-art methods.

III. Proposed Method

This section presents the overall development cycle of the proposed framework. In the first step, the overall architecture of the proposed MDA-BN model is defined. Thereafter, the selected training mechanism for performing optimal training in this study is explained. A detailed explanation of each development stage is provided in the subsequent subsections.

A. Overview

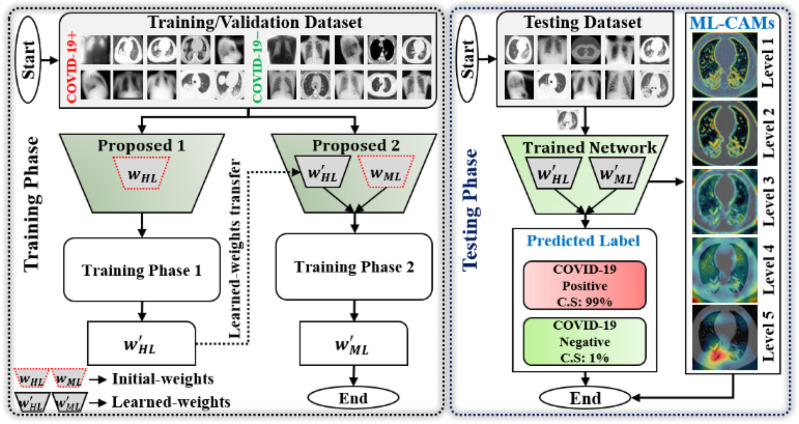
A comprehensive workflow of our method is presented in Fig. 2. The complete network architecture is designed based on the following two objectives: 1) optimal memory consumption and 2) fast execution speed at a minimal cost in terms of error. To achieve these two characteristics, the capacity of the basic building units (blocks A and B; Fig. 3) of MobileNet (MN) [23] was employed in developing the first subnetwork architecture called BN. Subsequently, a new deep-aggregated block (block C; Fig. 3) was introduced and a second subnetwork architecture, i.e., MDA-N, was defined. The proposed MDA-N incorporates low-level and intermediate-level structural information with high-level deep features (obtained from the first BN) for making the final diagnostic decision. The experimental results show that the conjunction of low-level, intermediate-level, and high-level features results in additional performance gain at a minimal computational cost. Additionally, in the testing phase, the defined deep-aggregated block generates the visual representation of multilevel features as a stack of multiple CAM images (levels 1–5; Fig. 2) for each input data sample. Such supplemental information can visually validate the CAD decision and further assist radiologists in identifying the lesion regions.

Fig. 2.

Comprehensive workflow diagram of proposed diagnostic framework in training and testing phases.

Fig. 3.

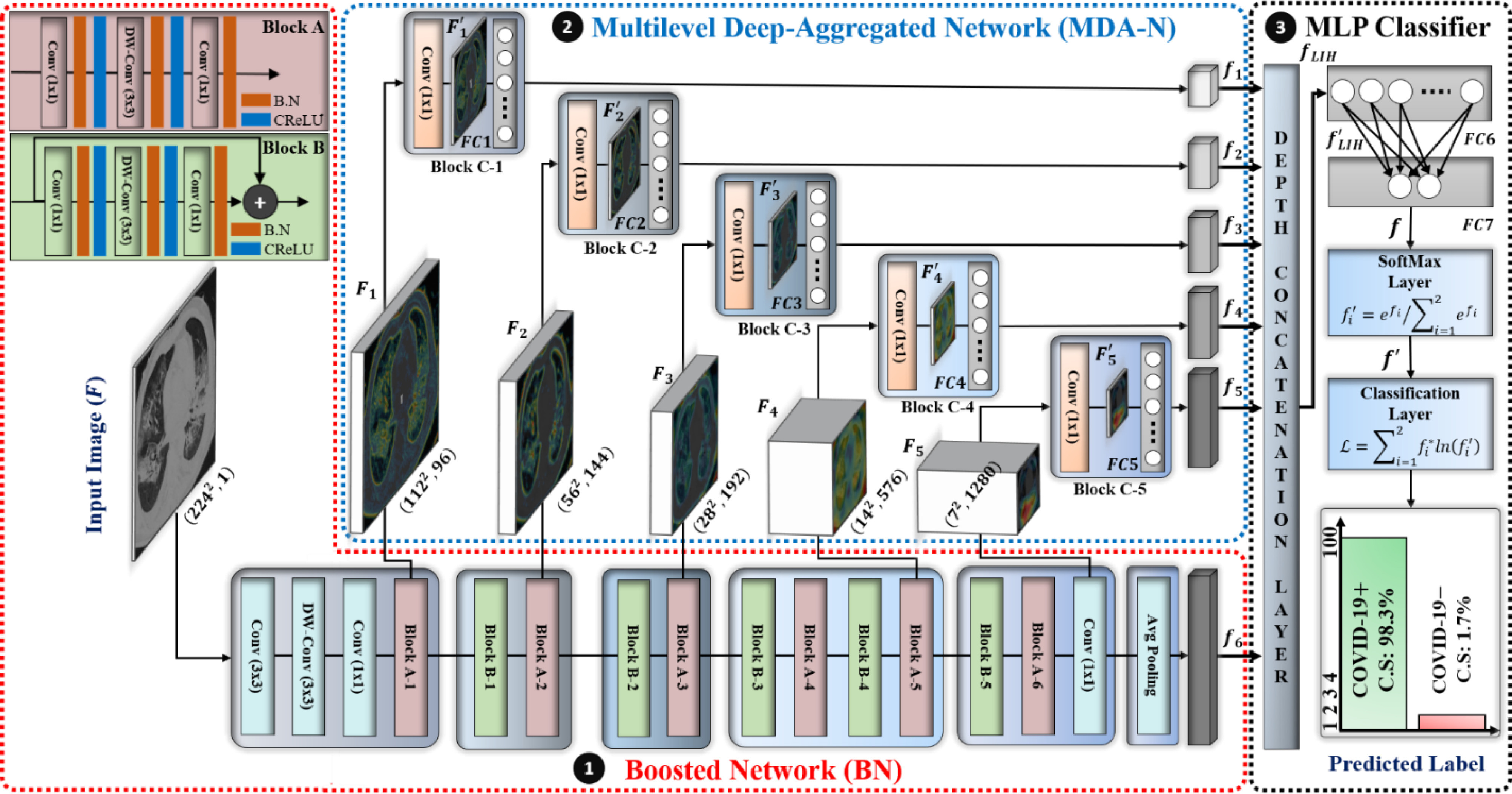
Overall architecture of proposed multilevel deep-aggregated boosted network (MDA-BN). (B.N: batch normalization layer; CReLU: clipped rectified linear unit layer).

B. Model Development

The comprehensive architecture and layer-wise configuration of the proposed MDA-BN model are presented and summarized in Fig. 3 and Table II, respectively. The MDA-BN architecture includes two subnetworks, namely BN and MDA-N, responsible for multilevel features extraction, and a multi-layer perceptron (MLP) classifier to reach the final diagnostic decision based on extracted features. Both subnetworks comprise a total of 16 building blocks (including 6, 5, and 5 blocks of A, B, C, respectively) with some additional layers (labeled as conv, DW-conv, and avg. pooling layers in Fig. 3). The structure and workflow of BN, MDA-N, and MLP-classifier are explained in detail in the following.

TABLE II. Layer-Wise Configuration Details of Our Proposed Model. (N: Number of Nodes in FC layer; Notations: 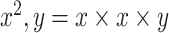, and ).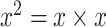

Layer Name	Input Dim.	Output Dim.	Filter Dim.	#Filter	Stride Info.
Input		-	-	-	-
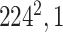
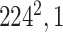
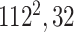
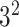
Conv				32	2
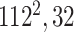
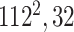
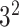
DW-conv				32	1
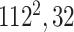
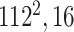
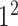
Conv				16	1
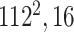
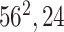
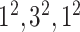
Block A-1				96,96,24	12,1
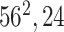
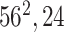
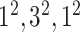
Block B-1				144144,24	11,1
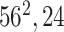
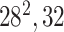
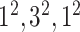
Block A-2				144144,32	12,1
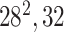
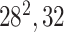
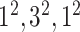
Block B-2				192192,32	11,1
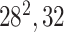
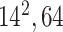
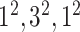
Block A-3				192192,64	12,1
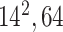
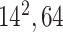
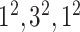
Block B-3				384384,64	11,1
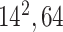
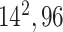
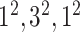
Block A-4				384384,96	11,1
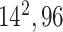
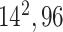
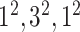
Block B-4				576576,96	11,1
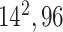
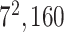
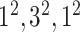
Block A-5				576576160	12,1
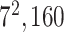
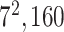
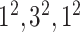
Block B-5				960960160	11,1
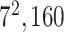
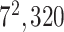
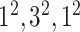
Block A-6				960960320	11,1
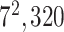
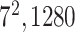
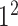
Conv				1280	1
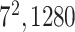
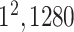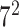
Avg. pool		*		1	1
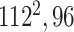
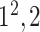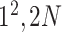
Block C-1		*		1	1
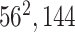
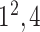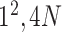
Block C-2		*		1	1
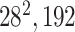
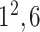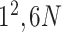
Block C-3		*		1	1
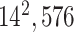
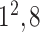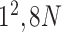
Block C-4		*		1	1
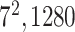
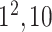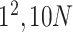
Block C-5		*		1	1
Depth con.	*		-	-	-
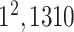
FC6			-	-	-
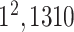
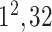
FC7			-	-	-
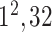
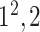
SoftMax			-	-	-
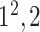
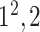
Class.	2	-	-	-	-

^*Input feature vectors fed to Depth con. layer.

1) BN Structure and Workflow: To exploit the high-level feature (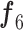; Fig. 3), the input image passes through BN, comprising a stack of multiple A and B building blocks and some additional layers. Blocks A and B (top left corner; Fig. 3) consist of three layers: 1) an expansion layer in which a 1 × 1 convolutional layer increases the depth of the input tensor by a factor of six; 2) a 3 × 3 DW convolutional layer that further processes the input tensor without changing its depth size; and 3) a projection layer (1 × 1 convolutional layer) that reduces the depth of the input tensor by a factor of six. The key difference between blocks A and B is the presence of a residual connection in block B to avoid the gradient-vanishing problem. 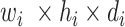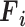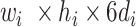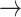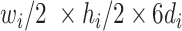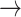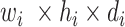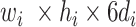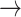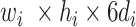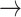Mathematically, these three layers transform the input tensor () as follows: (in block A) and 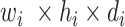(in block B).

In particular, the use of DW convolution in blocks A and B results in optimal memory consumption and fast execution speed; therefore, these building blocks are employed to develop the network architecture. In general, a standard convolutional layer [21] transforms a 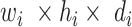input tensor (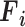) into a 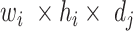output tensor (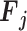) by applying a convolutional kernel, 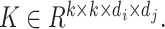In this operation, a total computational cost of 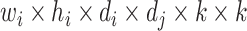is required [21]. In contrast, a similar operation is performed with a total computational cost of 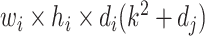in the DW convolutional layer. Thus, the DW convolution operation compared with the standard convolution operation reduces the average computational cost by a factor of 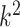. In the proposed model, each DW convolutional layer mainly includes a 3 × 3 kernel size 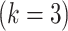; hence, the total computational cost is eight to nine times lower than that of the standard convolutional layer.

Initially, a simple convolutional layer followed by a DW convolutional layer (each layer has a total of 32 3 × 3 filters) processes the input image (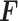) and generates output activation maps with a size of 112 × 112 × 32. Then, a projection layer (1 × 1 convolutional layer with a total of 16 filters) further processes this output (generated by the previous DW Conv layer) and transformed it into another output tensor with a size of 112 × 112 × 16.

After these layers, a stack of 11 building blocks (Blocks A-1–A-6 and B-1–B-5; Fig. 3) exploit more abstract features. These blocks process the output tensor of the preceding layer or block them one by one; ultimately, an output tensor with a size of 7 × 7 × 320 from the last building block (Block A-6; Fig. 3) is obtained. Thereafter, an expansion layer (a 1 × 1 convolutional layer with a total of 1280 filters) increases its (i.e., output of Block A-6) depth and converts into another 7 × 7 × 1280 activation map, which is further transformed into a single 1 × 1 × 1280 feature vector (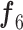; Fig. 3) after passing through a 7 × 7 average pooling layer.

2) MDA-N Structure and Workflow: To exploit the low-level and intermediate-level features (f₁–f₅; Fig. 3), the input image passes through MDA-N, comprising a total of five deep-aggregated blocks (Blocks C-1– C-5; Fig. 3). Block C is mainly designed to incorporate the contribution of low-level and intermediate-level features (f₁–f₅; Fig. 3) with high-level deep features (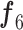; Fig. 3) in making more effective diagnostic decision. In an ablation study, experimental analysis has also proved that the aggregation of multilevel features offers an additional performance gain at a minimal increase in the total number of parameters.

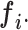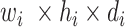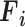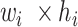
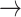
Block C includes a projection layer (1 × 1 convolutional layer) that transforms the three-dimensional input tensor into a two-dimensional (2D) activation map. Then, a FC layer identifies the larger patterns in the 2D activation map by combining all the feature values into a one-dimensional feature vector, Mathematically, this block processes the input tensor () as follows: 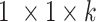. Here, 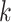is the growth rate hyperparameter that controls the weights of the low-level and intermediate-level features (i.e., f₁–f₅) and linearly increases from the low-level to high-level features. In addition, two additional layers, batch normalization (B.N) and clipped rectified linear unit (CReLU), are included after each convolutional layer.

In Fig. 3, the given input image is observed to be progressively downsampled into five different spatial sizes (i.e., 112 × 112, 56 × 56, 28 × 28, 14 × 14, and 7 × 7) after passing through multiple A and B building blocks. To benefit from the different resolutions, these intermediate tensors of five different spatial sizes were selected to extract additional low-level and intermediate-level features (f₁–f₅) by including a total of five deep-aggregated blocks (Blocks C-1– C-5; Fig. 3) in five different locations (Blocks A-1, A-2, A-3, A-5, and the last 1 × 1 convolutional layer in Fig. 3). Thus, MDA-N generated a weighted contribution of multiresolution feature maps (F₁–F₅; Fig. 3) as low-level and intermediate-level features (f₁–f₅; Fig. 3). In classification part, these multiresolution features (f₁–f₅) jointly contribute with high-level deep features (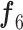) and make a diagnostic decision for input image.

3) MLP Classifier: In this stage, a depth concatenation layer combines all these low-level, intermediate-level, and high-level feature vectors (i.e., (f₁–f₆) along the depth direction and provides a feature vector, 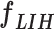, with a size of 1 × 1 × 1310. Furthermore, a MLP classifier consisting of a stack of four additional layers (FC6, FC7, SoftMax, and classification layers; Fig. 3) reach the final diagnostic decision based on 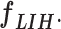The initial FC6 layer (including 32 nodes) further explore the more discriminative features in 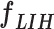and transform into a low-dimensional feature vector, 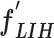, with a size of 1 × 1 × 32. Then, the FC7 layer, including two nodes (the same as the total number of classes), identify the larger patterns in 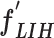by multiplying 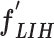by the trainable weights (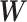) and adding a bias vector (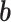) (i.e., 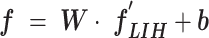, whereas 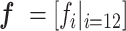). Subsequently, the SoftMax layer applies the softmax function as 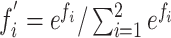[21] and transforms in terms of probability. Finally, the classification layer assigns each feature value () to one of the two mutually exclusive classes (i.e., COVID-19 positive or negative) using a cross-entropy loss function, 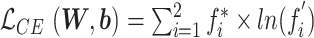[21]. Here, 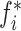indicates the actual class label of the 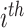class during the training procedure, and 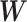and b represent all the trainable parameters.

C. Multistage Network Training

The multistage training of the network was performed to exploit multilevel deep-aggregated features and obtain the optimal learnable parameters of the proposed model. In the first phase, the BN model was independently trained with the defined training (denoted as 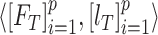) and validation (notated as 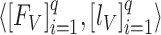) dataset having 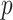training and 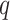validation images. After training, the optimal fine-tuned weights (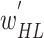) of the BN (first subnetwork) were obtained for the target domain. In the second phase, these optimal weights (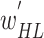) were used to initialize the weights of the BN in the proposed MDA-BN model. Additionally, the entire network was trained to obtain the optimal weights of the MDA-N (second subnetwork) while freezing all the BN weights by setting the learning rates to zero. The experimental results exhibit the superior performance of the adopted training approach compared with the conventional end-to-end training method. In addition, an independent validation dataset, 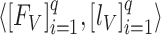, was used to stop the training after achieving optimal convergence in both the subnetworks. Upon satisfying this criterion and if there is no increase in the validation accuracy after a certain number of successive epochs, the network training is automatically stopped. Therefore, training is performed up to the optimal number of epochs (rather than completing a time-consuming training in all epochs) to avoid the overfitting problem. A simplified workflow of the defined training method is also presented as a pseudo-code in Algorithm 1. The total loss function of the proposed MDA-BN model can also be interpreted as follows:

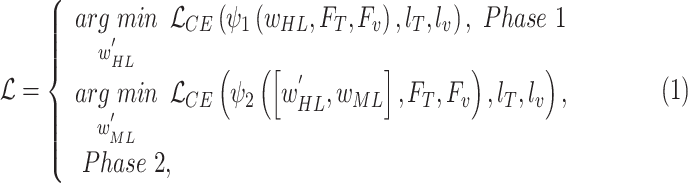where 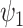and 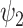denote the BN and MDA-BN as transfer functions, respectively; 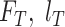, and 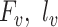represent the training set and validation data samples with their class labels, respectively and 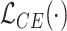is a cross-entropy loss function [21]. According to Eq. (1), the loss functions of BN and MDA-BN subnetworks were sequentially minimized for our selected training dataset 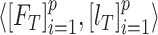to find their optimal weights 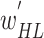(phase 1) and 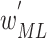(phase 2), respectively. In Eq. (1), the validation dataset 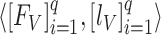was used to achieve the sufficient convergence of both BN and MDA-BN (as explained in Algorithm 1). In general, phase 1 training was carried out to exploit the contribution of high-level feature (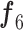) in class prediction. Then, phase 2 training further included the contribution of intermediate-level features (f₁–f₅) along with 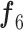and resulted in an additional performance gain. Thus, our multistage training performed the progressive training of a deep network (for target domain) under the constraint of limited training data and outperforms the conventional end-to-end training method.

Algorithm 1: Multistage Training Algorithm.

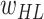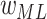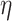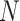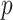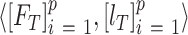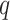• Input: trainable parameters, , ; learning rate ; maximum epoch, ; training data samples notated as ; and validation data samples notated as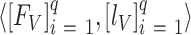

• Output: trained parameters ,

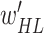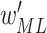
• 1Initialize parameters 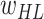(ImageNet pretrained weights), 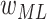(Gaussian random weights)
• 2/* Phase 1: Training of BN model */
• 3for 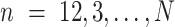do
• 4obtain: 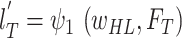and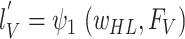
• 5 update:
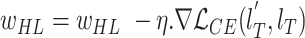
• 6check: if 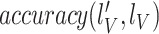converges do stop training end
• 7end
• 8Output 1: optimal weights 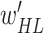for BN model
• 9/* Phase 2: Training of final MDA-BN model */
• 10for 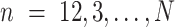do
• 11obtain: 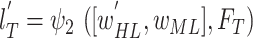and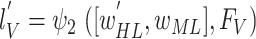
• 12update:
• 13check: if 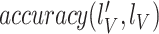converges do stop training end
• 14end
• 15Output 2: optimal weights 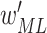and 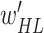for MDA-BN model

IV. Results And Analysis

A. Dataset and Experimental Setup

The quantitative analysis of the proposed method was made using a collection of six publicly available datasets (including X-ray and CT images) [24]–[28]. These were categorized into two main classes (i.e., COVID-19 positive and negative) based on their ground truth labels. Consequently, a considerable amount of heterogeneous radiographic data (including 12910 images) was obtained. The data consisted of COVID-19 positive and negative categories (including healthy as well as other viral and bacterial pneumonia cases). The COVID-19 positive collection included a total of 6550 images (including 3254 CT and 3296 X-ray images) of 1660 different patients. The COVID-19 negative collection consisted of a total of 6360 images (including 2217 CT and 4143 X-ray images) of 5272 different patients. Finally, in the data preprocessing stage, all the images were resized to 224  ×  224 as per the fixed size of the input layer in the proposed network.

For model development and simulation, the MATLAB R2019a coding framework (including a standard deep learning toolbox) was employed. All the simulations were performed using a desktop computer with an Intel Corei7 CPU, 16 GB RAM, NVIDIA GeForce GPU (GTX 1070), and Windows 10 operating system.

In our optimization scheme, we used a stochastic gradient descent (SGD) optimizer which has been used in most of the existing studies [36]–[38] with an initial learning rate of 0.001 with a 0.1 learning rate drop factor. For the optimization scheme for learning rate, we used the default scheme provided by MATLAB R2019a. In detail, each time the specified number of epochs elapses (in our experiments, we set it as 10 epochs), the initial learning rate of 0.001 is reduced by being multiplied with the learning rate drop factor of 0.1. For example, after 10 epochs, the learning rate becomes 0.0001 (0.001 × 0.1), after 20 epochs, it becomes 0.00001 (0.0001 × 0.1), etc.

In addition, the following hyperparameter settings were used for all deep learning-based networks: mini-batch size as 10, L2-regularization equal to 0.0001, and momentum factor as 0.9. In all experiments, a fivefold cross-validation was performed using 70% (9037 images), 10% (1291 images), and 20% (2582 images) of the data for training, validation, and testing, respectively. For a fair evaluation, different patient datasets were selected for training, validation, and testing. Finally, in the testing phase, the quantitative performance values of the proposed and baseline methods were measured based on the following five metrics: sensitivity (SEN), accuracy (ACC), precision (PRE), F-measure (F1), specificity (SPE), and area under the curve (AUC) [21].

B. Results of Proposed Method

The quantitative results (i.e., ACC, F1, SPE, SEN, PRE, and AUC) of the proposed method along with the performance of the MN (baseline network) were evaluated and compared [23]. In the list in Table III, the proposed MDA-BN is observed to outperform the MN model with average gains of 2.31%, 2.02%, 3.69%, 0.96%, 2.71%, and 1.12% in terms of ACC, F1, SPE, SEN, PRE, and AUC, respectively. In the 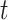-test analysis between the MDA-BN and MN, a significant improvement of the former 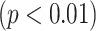over the latter (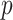-value 0.004) is observed. In addition, the 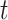-test performance between the BN (first subnetwork) and MN shows the significant gain of the former 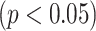over the latter (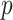-value 0.012). In addition to the quantitative performance gain, the number of trainable parameters of MDA-BN (1.76 million) is found to be approximately 21% lower than that of the MN model (2.24 million). Such a significantly lowered number of trainable parameters of the proposed MDA-BN model makes it compatible even for low-cost hardware resources, such as handheld devices. Although, it is not possible to obtain CT or X-ray images with low-cost handheld devices. However, our proposed solution can accomplish the following potential applications after getting CT or/and X-ray data: 1) can make an effective diagnostic decision at fast speed due to its reduced size of model, 2) can also be used in implementing a fast retrieval-based diagnostic framework for timely retrieval of relevant cases from existing large-scale databases. In spite of the reduced size of the proposed model, a detailed comparative study as shown in Table V also proved the superior diagnostic performance of our MDA-BN model over the existing large-sized networks such as ResNet18, ResNet50, ResNet101, DenseNet201, InceptionV3, etc.

TABLE III. Diagnostic Performance of Proposed Multilevel Deep-Aggregated Boosted Network (MDA-BN) Compared With Baseline Network MobileNet (MN) [23].

Model (#Par.)	#Fold	ACC	F1	SPE	SEN	PRE	AUC
MN [ 23 ] (2.24 million)	1	95.54	95.64	94.41	96.63	94.67	98.24
	2	94.58	94.83	91.04	98.02	91.85	98.08
	3	93.3	93.47	92.14	94.43	92.53	97.92
	4	95.43	95.57	93.72	97.1	94.09	98.78
	5	86.49	88.22	72.9	99.69	79.12	94.14
	Avg.(std)	93.07 (3.78)	93.55 (3.1)	88.84 (9.01)	97.18 (1.93)	90.45 (6.44)	97.43 (1.80)
MDA-BN (1.76 million)	1	95.92	96.03	94.65	97.17	94.91	98.74
	2	94.97	95.27	90.02	99.77	91.15	97.86
	3	95.08	95.25	93	97.1	93.47	98.57
	4	96.21	96.33	94.19	98.17	94.56	99.01
	5	94.7	94.96	90.81	98.47	91.69	98.55
	Avg. (std)	95.38 (0.65)	95.57 (0.58)	92.53 (2.05)	98.14 (1.1)	93.16 (1.68)	98.55 (0.43)

TABLE V. Detailed Comparative Performance Analysis Between Proposed Multilevel Deep-Aggregated Boosted Network (MDA-BN) and Various State-of-the-Art Methods.

Comparative Methods	Model Names	#Par (millions)	#TP	#TN	#FP	#FN	ACC	F1	SPE	SEN	PRE	AUC
Misra et al. [9]	ResNet18 [42]	11.18	1252	1026	246	58	88.24(7.48)	89.48(6.18)	80.7(14.31)	95.57(2.52)	84.54(10.17)	92.93(6.18)
Khan et al. [7]	VGG19 [40]	139.58	1274	1117	155	36	92.59(3.21)	93.09(2.72)	87.8(7.35)	97.24(2.06)	89.48(5.62)	95.19(4.62)
Minaee et al. [6]	SqueezeNet [39]	1.24	1181	1111	161	129	88.78(1.91)	88.99(2.17)	87.33(8.55)	90.18(8.89)	88.81(6.35)	95.39(1.18)
Brunese et al. [19]	VGG16 [40]	134.27	1261	1131	141	49	92.64(3.5)	93.04(3.15)	88.89(5.73)	96.29(1.99)	90.07(4.58)	95.91(4.38)
Ardakani et al. [11]	ResNet101 [42]	42.56	1280	1112	160	30	92.64(4.08)	93.2(3.43)	87.39(8.6)	97.74(1.43)	89.28(6.35)	96.14(4.04)
Martínez et al. [8]	NASNet [41]	4.27	1259	1134	138	51	92.68(4.49)	93.12(3.85)	89.12(9.62)	96.14(4.29)	90.66(6.9)	97.06(2.51)
Jaiswal et al. [29]	DenseNet201 [44]	18.11	1237	1113	159	73	91(3.21)	91.5(2.68)	87.5(8.41)	94.4(2.99)	89.08(6.2)	97.11(1.28)
Asnaoui et al. [18]	InceptionResNetV2 [43]	53.81	1267	1145	127	43	93.43(2.22)	93.73(2.07)	90.03(4.31)	96.72(3.27)	91.03(3.37)	97.36(0.58)
Apostolopoulos et al. [30]	MobileNetV2 [23]	2.24	1273	1130	142	37	93.07(3.78)	93.55(3.1)	88.84(9.01)	97.18(1.93)	90.45(6.44)	97.43(1.87)
Farooq et al. [10]	ResNet50 [42]	23.54	1277	1142	130	33	93.7(2.85)	94.07(2.52)	89.8(5.72)	97.5(1.09)	90.96(4.53)	97.82(1.18)
Tsiknakis et al. [31]	InceptionV3 [45]	21.81	1276	1180	92	34	95.11(1.28)	95.29(1.19)	92.75(2.28)	97.39(0.58)	93.29(1.98)	98.23(0.52)
Proposed	MDA-BN	1.76	1286	1177	95	24	95.38(0.65)	95.57(0.58)	92.53(2.05)	98.14(1.1)	93.16(1.68)	98.55(0.43)

Moreover, due to the following reasons, we selected an optimized version of the standard MobileNet model as backbone network: 1) comparable diagnostic performance for the target domain (COVID-19) compared to other large-sized networks [40]–[45] as shown in Table V, 2) reduced number of trainable parameters, 3) required low-cost hardware resources and applicable in real-time applications.

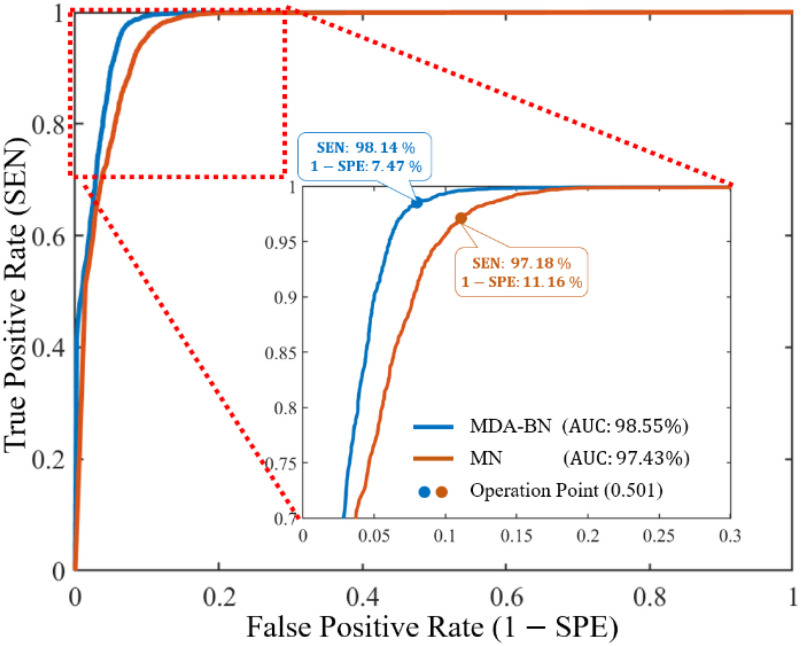
The performance differences between the MDA-BN and MN as receiver operator characteristic (ROC) curves are further highlighted in Fig. 4. For each model, the ROC curve presents a tradeoff between the true positive (TP) rate (SEN) and false positive (FP) rate (1 SPE) at different thresholds from 0 to 1 at 0.001 increments.

Fig. 4.

Receiver operating characteristic curves of proposed multilevel deep-aggregated boosted network (MDA-BN) versus baseline network MobileNet (MN) [23].

From the classification thresholds, 0.501 is taken as the operating point (Fig. 4); this indicates the optimal performance of both networks. In detail, this operating point implies that any radiographic image with a class probability greater than (or equal to) 0.501 is classified as a COVID-19 positive case whereas that less than 0.501 is classified as a COVID-19 negative case. To determine optimal threshold, we evaluated all the validation accuracies of our model for different thresholds from 0 to 1 at 0.001 increments. Then, based on the maximum validation performance, a classification threshold of 0.501 was selected as the operating point.

However, in contrast with the MN, the proposed MDA-BN model significantly reduced the FP rate (1 SPE) from 11.16% to 7.47% with an average gain of 3.69% and increased the TP rate (SEN) from 97.18% to 98.14% with an average gain of 0.96%. Additionally, the ROC performance of both networks was also evaluated for another operating point, resulting in the maximum TP rate (i.e., SEN 100%). The additional gain resulted in increases in the FP rates (1 SPE) from 7.47% to 12.75% and 11.16% to 18.12% for the MDA-BN and MN models, respectively. Nevertheless, the FP rate of the proposed method (12.75%) remains lower than that of the BN model (18.12%) with an average gain of 5.37%. The performance comparison between the MDA-BN and MN in terms of confusion matrices is shown in Fig. 5. In particular, these matrices summarize the predicted number of TP, true negative (TN), FP, and false negative (FN) data samples for the MDA-BN and BN models. In contrast with MN, the number of FP and number of FN samples for the proposed MDA-BN model are significantly reduced from 142 to 95 and from 37 to 24, respectively. The number of TP and number of TN samples also increased from 1273 to 1286 and from 1130 to 1177, respectively. On average, the proposed network (TP 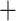TN 2463) compared with the baseline model (TP 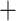TN 2403) correctly classified a total of 60 data samples.

Fig. 5.

Performance comparison of proposed multilevel deep-aggregated boosted network (MDA-BN) versus baseline network MobileNet (MN) [23] in terms of confusion matrices: (a) MN and (b) MDA-BN.

C. Ablation Study

An ablation study was conducted to highlight the significance of each subnetwork (i.e., the BN and MDA-N) in developing the final MDA-BN architecture. The feature-level performance was also progressively evaluated to show the significance of multilevel aggregated features. Table IV lists these ablated results (i.e., feature level performance of MDA-BN) in order. Based on the list, the concatenation of multilevel features (f₁–f₆) results in progressive performance gain. Finally, a high-performance MDA-BN model was obtained based on the aggregation of multilevel features. In addition, the aggregation of both subnetworks resulted in further performance gains compared with their individual results. On average, the performance difference between the MDA-BN and MDA-N (second subnetwork with aggregations f₁–f₅) was higher with average gains of 2.26%, 2.05%, 3.82%, 0.75%, 3.16%, and 1.19% in terms of ACC, F1, SPE, SEN, PRE, and AUC, respectively. Similarly, the performance gains of the MDA-BN versus BN (first subnetwork including 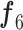) were 0.46%, 0.44%, 0.47%, 0.45%, 0.43%, and 0.68% in terms of ACC, F1, SPE, SEN, PRE, and AUC, respectively.

TABLE IV. Progressive Performance Gain of Proposed Model Based on Aggregation of Multilevel Features.

Model	#Features	#Par (millions)	ACC	F1	SPE	SEN	PRE	AUC
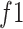
MDA-N		0.03	63.92	76.32	52.51	75.01	67.24	65.2
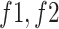
		0.06	83.41	84.97	75.14	91.43	79.54	90.55
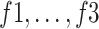
		0.09	87.55	88.26	83.19	91.78	85.22	93.14
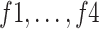
		0.41	88.51	89.44	82.2	94.64	85.01	94.4
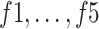
		1.72	93.12	93.52	88.71	97.39	90	97.36
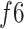
BN		1.68	94.92	95.13	92.06	97.69	92.73	97.87
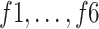
MDA-BN		1.76	95.38	95.57	92.53	98.14	93.16	98.55

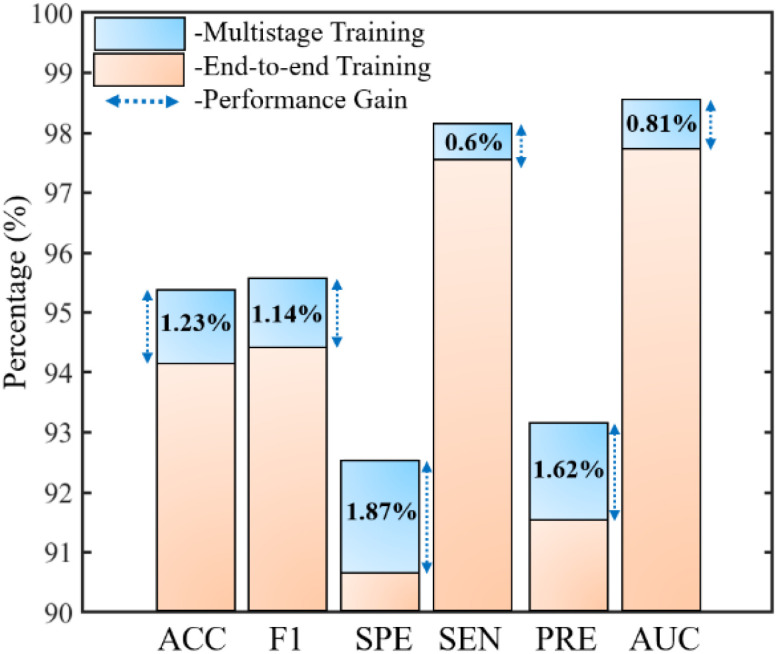
Moreover, an end-to-end training of the proposed network was also performed to demonstrate the significance of the adopted multistage training approach (Algorithm 1) in terms of the quantitative performance. These comparative results in terms of all the performance metrics are shown in Fig. 6. The results indicate that the training approach compared with the conventional end-to-end training method exhibits superior performance with average gains of 1.23%, 1.14%, 1.87%, 0.6%, 1.62%, and 0.81% in terms of ACC, F1, SPE, SEN, PRE, and AUC, respectively. Thus, an optimally trained network is derived by exploiting multilevel deep-aggregated features and employing multistage training via a mutually beneficial approach.

Fig. 6.

Performance comparison between adopted multistage network training and conventional end-to-end method.

D. Comparison

This section presents a detailed comparative analysis to highlight the superiority of the proposed solution over state-of-the-art methods. In recent literature, different attempts have been made to develop CAD-based solutions for the effective diagnosis of the COVID-19 infection. Though, this is our first study based on heterogeneous radiographic data. There are not standard benchmarks in the existing literature for our selected heterogeneous datasets. Therefore, for a fair comparison, we selected some recent deep learning-based CAD methods [6]–[11], [18], [19], [29]–[31] related to COVID-19 and evaluated their results with our experimental datasets based on same experimental protocols to ours rather than using their given results in comparison. Therefore, the comparison is more comprehensive than that in [6]–[20]; the results are summarized in Table V. It is observed that our method outperforms all of these baseline methods in terms of quantitative and computational performance. Tsiknakis et al. [31] proposed a solution whose results were comparable to those of the proposed technique and ranked second among those of the other current methods [6]–[11], [18], [19], [29], [30]. However, the number of trainable parameters of the proposed model is approximately 12.39 times lower than that in [31] (i.e., proposed MDA-BN: 1.76 million Tsiknakis et al. [31]: 21.81 million). Such an optimal number of trainable parameters of the proposed network makes it distinctive among all the baseline methods. In another related study, Minaee et al. [6] used an existing pre-trained network with an optimal number of trainable parameters (i.e., 1.24 million), which was 0.52 million less than those of the proposed MDA-BN method. Nevertheless, the quantitative results of the method in [6] were outperformed by those of the proposed method whose average gains were 6.6%, 6.58%, 5.2%, 7.96%, 4.35%, and 3.16% in terms of ACC, F1, SPE, SEN, PRE, and AUC, respectively. In terms of the confusion matrix of the proposed method versus that in [6], the proposed technique significantly reduced the total number of FPs and FNs from 161 to 95 and from 129 to 24, respectively; the total number of TPs and TNs also increased from 1181 to 1286 and from 1111 to 1177, respectively. In conclusion, the proposed method outperforms all existing methods [6]–[11], [18], [19], [29]–[31] in terms of various performance aspects; hence, it ranks first among all the models.

E. Discussion

This section discusses the key aspects of this study including a few limitations that may influence the overall performance of the system in a real-world scenario. An optimal deep network, whose performance is better and computational cost is lower compared with other methods, is mainly proposed to diagnose COVID-19 infection from heterogeneous radiographic data. Due to the following distinctive aspects, the proposed model outperforms various state-of-the-art methods [6]–[11], [18], [19], [29]–[31]: 1) considering the joint contribution of low-level, intermediate-level, and high-level features in making a final diagnostic decision, 2) considering the reduced number of training parameters with the use of DW convolution, 3) then, performing multistage training for efficient learning of these parameters. Experimental results (Table V) prove that our optimal network design leverages multilevel features and multistage training in a mutually beneficial manner to optimize the overall diagnostic performance and outperforms various baseline methods. In contrast, most of the existing studies [6]–[11], [18], [19], [29]–[31] performed end-to-end training with a limited number of training samples and considered only high-level features in making a diagnostic decision. However, we observed that for a limited dataset, the aggregation of multilevel features and multistage training can learn the target domain effectively and result in an additional gain in terms of high accuracy and/or low computational cost.

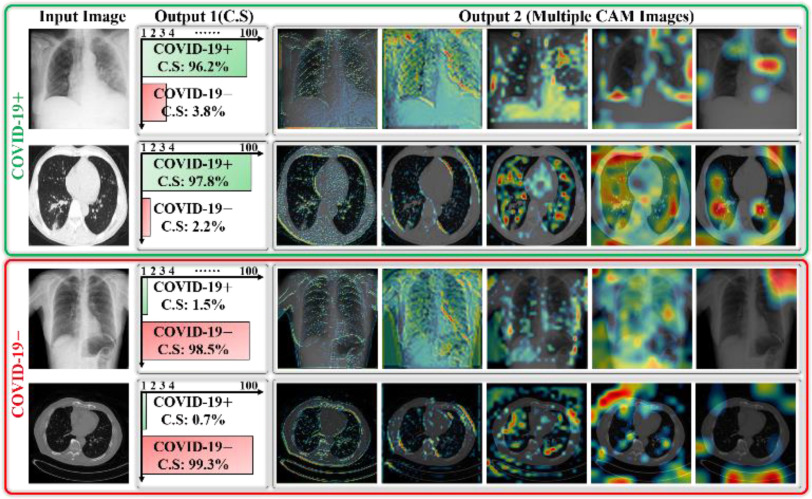
In most CAD methods, a deep classification network acts as a black box that only receives input and generates the output without providing a visual indication regarding the diagnostic decision. Accordingly, in this study, the progression of multilevel deep features was visualized as a stack of CAM images extracted from deep-aggregated blocks (Fig. 3) and added as output with the diagnostic decision. This additional output may provide a visual interpretation of the CAD decision and assist medical professionals in identifying the lesion regions more easily. These multiple CAM images (output 2) and predicted diagnostic decision (output 1) for a few testing data samples are shown in Fig. 7.

Fig. 7.

Visualization of predicted outputs of proposed network for given sample images including both COVID-19 positive and negative cases.

These results may assist radiologists in answering the following questions to reach a reasonable diagnostic decision. 1) In case of a positive prediction, which areas may include lesion patterns? 2) What is the confidence score (C.S of Fig. 7) of the model for CAD for a particular decision? 3) Does the CAD decision conform with that of a medical expert? The generated outputs (with optimal confidence score and multiple CAM images corresponding to each data sample) of the proposed network can answer the above queries to further support medical professionals in making an effective diagnostic decision.

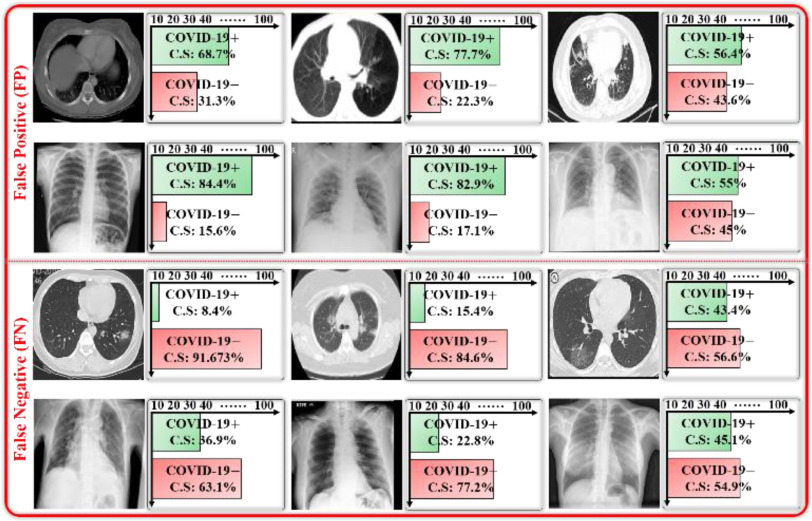
A few examples of misclassified data samples along with their predicted diagnostic decisions as confidence scores are shown in Fig. 8. First, these false predictions (i.e., FP and FN cases) may occur because of the presence of analogous lesion patterns in both COVID-19 positive and negative data samples. Second, the poor annotation of data samples can also result in false predictions by the CAD model. However, these can be minimized through the visual assessment of the input data samples and their predicted outputs (i.e., confidence score and multiple CAM images) by a medical professional.

Fig. 8.

Illustration of false positive (FP) and false negative (FN) data samples including predicted confidence scores.

Despite the significant gain of our method, there are a few challenges that may be encountered in the clinical setting. The first is the generalizability problem, which may result from the diversity of radiological imaging modalities. However, this is a data-driven constraint that can be overcome by adding more diversified and well-annotated COVID-19 infection datasets. Second, the inclusion of multiple CAM images does not always guarantee the identification of well-localized infectious regions. In our selected datasets, well-localized annotations (such as segmentation masks or boundary boxes) are not given, but only actual class labels are provided for all data samples as ground truths. Therefore, it is not possible to select and validate these multiple CAM images with correct lesion regions. To provide visual insight about the decision of our model, we just visualized multiple feature maps (extracted from five different layers of F₁ ∼ F₅ as shown in Fig. 3) corresponding to each testing sample. These multi-resolution feature maps simply highlight the possibility of infected regions and provide clues that can further assist radiologists in making effective diagnostic assessments. In a future study, we will explore well-localized datasets related to COVID-19 infection and intend to resolve these problems thoroughly.

V. Conclusion and Future Work

An optimal MDA-BN model to recognize the COVID-19 virus from chest radiographic scans (including X-ray and CT images) is proposed in this paper. The optimal size of the proposed network provides a cost-effective solution for real-time screening applications. The experimental analysis shows that the proposed solution outperforms various state-of-the-art methods in terms of quantitative performance as well as computational cost.

Even in the case that one patient has both CT and X-ray data, he or she can provide only one of these data to our system because our trained model does not require both X-ray and CT images at the same time. If one patient has both CT and X-ray data, and the diagnosing results of these two data sequentially obtained by our method are opposite, one of the results, which has higher C.S by our model, can be determined as a final result. Nevertheless, more sophisticated method would be researched to combine these two results in a future work. In addition, we aim to develop a more comprehensive CAD framework that can more precisely identify, localize, and quantify the infected regions from given chest radiographic scans. Moreover, it is intended to increase the number of multimodality datasets to enhance generalizability.

Funding Statement

This work was supported in part by the National Research Foundation of Korea (NRF) funded by the Ministry of Science and ICT (MSIT) through the Basic Science Research Program (NRF-2020R1A2C1006179), in part by the MSIT, Korea, under the ITRC (Information Technology Research Center) Support Program (IITP-2021-2020-0-01789) supervised by the IITP (Institute for Information & Communications Technology Planning & Evaluation), and in part by the NRF funded by the MSIT through the Basic Science Research Program (NRF-2019R1A2C1083813).