Abstract
A computational model with intelligent machine learning for analysis of epidemiological data, is proposed. The innovations of adopted methodology consist of an interval type-2 fuzzy clustering algorithm based on adaptive similarity distance mechanism for defining specific operation regions associated to the behavior and uncertainty inherited to epidemiological data, and an interval type-2 fuzzy version of Observer/Kalman Filter Identification (OKID) algorithm for adaptive tracking and real time forecasting according to unobservable components computed by recursive spectral decomposition of experimental epidemiological data. Experimental results and comparative analysis illustrate the efficiency and applicability of proposed methodology for adaptive tracking and real time forecasting the dynamic propagation behavior of novel coronavirus 2019 (COVID-19) outbreak in Brazil.
Keywords: Computational model, covid-19, epidemiological data, interval type-2 fuzzy systems, kalman filtering, machine learning
I. Introduction
In The last years, studies involving the integration of fuzzy systems and Kalman filters have been proposed in the literature [1]–[3]. In [4], fuzzy sets are combined with an optimization method based on extended Kalman filter with probabilistic-numerical linguistic information applied for tracking a maneuvering target. In [5], an optimization methodology of adaptive Unscented Kalman Filter (UKF) is presented by an evolutionary fuzzy algorithm named Fuzzy Adaptive Grasshopper Optimization Algorithm, and it is efficiently applied to different benchmark functions.
Recently, with the beginning of the Covid-19 epidemic outbreak, several researchers have proposed model based data analysis approaches applied to novel Coronavirus 2019 [6]–[8]. The objective of these studies is to characterize the evolution of pandemic in certain regions and, thus, to contribute for the requirements adopted to contain the contamination by virus and allocation of resources. In [9], a mathematical model based on SEIR model (Susceptible - Exposed - Infectious - Recovered) for forecasting the transmission dynamics of Covid-19 in Korea, is proposed. This study is able to predict the final size and the timing of the end of epidemic as well as the maximum number of isolated individuals using daily confirmed cases comparing epidemiological parameters between the national level and the Daegu/Gyeongbuk area. In [10], the role of asymptomatic carriers in transmission poses challenges for control of the Covid-19 pandemic, is addressed.
Differently from aforementioned approaches and others ones found from literature, the scope of this paper outlines a machine learning approach based on integration of Kalman filter and interval type-2 fuzzy systems for adaptive tracking and real time forecasting the COVID-19 dynamic propagation. The design of interval type-2 fuzzy Kalman filter, according to proposed methodology, is based on spectral unobservable components and uncertainty regions extracted from experimental data.
A. Motivation and Contributions of the Proposed Methodology
The impacts caused by novel coronavirus pandemic has motivated the analysis of epidemiological data, for support of political/health authorities and decision-making [11], [12]. In this context, several modeling methodologies has been proposed in literature for solving epidemiological problems [13]–[15]. However, the uncertainties inherent to experimental epidemiological data (underreporting, lack of information, incubation period of the virus, time to seek care and diagnosis) have open a new research field, in which the proposed methodology belongs to. The originality of the proposed methodology is outlined by following main contributions:
-
•
A new machine learning computational tool based on the successful integration of Kalman filters and type-2 fuzzy systems for adaptive tracking and real time forecasting of experimental epidemiological data, which is useful for analysis of COVID-19 dynamic propagation;
-
•
Formulation of new interval type-2 fuzzy clustering algorithm based on adaptive similarity distance mechanism ables to define specific operation regions in the epidemiological data associated to the behavior and uncertainty inherent to COVID-19 dynamic propagation;
-
•
Formulation of a new computational model with intelligent machine learning based on interval type-2 fuzzy Kalman filter, for adaptive tracking and real time forecasting the behavior and uncertainty inherent to COVID-19 dynamic propagation, from the specific operation regions in the epidemiological data.
II. Interval Type-2 Fuzzy Computational Model
In this section, the proposed methodology for designing the interval type-2 fuzzy Kalman filter computational model from experimental data, is presented.
A. Pre-Processing by Singular Spectral Analysis
1). Training Step
Let the initial experimental dataset referring to  time series under analysis, with
time series under analysis, with  samples, given by [16]:
samples, given by [16]:
 |
where 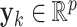 , with
, with 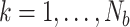 , is the time series vector at instant of time
, is the time series vector at instant of time  . From this initial dataset, a trajectory matrix
. From this initial dataset, a trajectory matrix 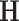 is defined, for each of the dimensions of
is defined, for each of the dimensions of 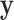 , considering a set of
, considering a set of 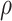 delayed vectors with dimension
delayed vectors with dimension 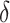 , which is an integer number defined by user with
, which is an integer number defined by user with  and
and 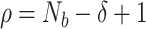 , given by:
, given by:
 |
and the covariance matrix  is obtained as follows:
is obtained as follows:
 |
Applying the Singular Value Decomposition (SVD) procedure to matrix  , is obtained a set of eigenvalues in decreasing order such that
, is obtained a set of eigenvalues in decreasing order such that 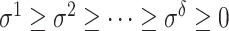 with their respective eigenvectors
with their respective eigenvectors 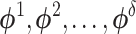 . Considering
. Considering  , and
, and 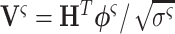 with
with  , the singular value decomposition of the trajectory matrix
, the singular value decomposition of the trajectory matrix  , can be rewritten as:
, can be rewritten as:
 |
where the matrix  is elementary (it has rank equal to 1), and is given by:
is elementary (it has rank equal to 1), and is given by:
 |
The regrouping of  into
into  linearly independent matrices terms
linearly independent matrices terms  , such that
, such that  , results in
, results in
 |
where  is the number of unobservable components extracted from experimental dataset. The unobservable spectral components
is the number of unobservable components extracted from experimental dataset. The unobservable spectral components  obtained from matrices
obtained from matrices  , are given by:
, are given by:
 |
where  ,
, 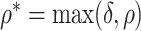 .
.
2). Recursive Step
The value of 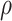 is increased by
is increased by  , with
, with 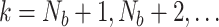 , and the covariance matrix is updated, recursively, as follows:
, and the covariance matrix is updated, recursively, as follows:
 |
where  with
with 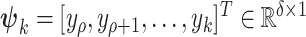 . Applying SVD procedure to covariance matrix
. Applying SVD procedure to covariance matrix  , the term
, the term  can be rewritten by:
can be rewritten by:
 |
where 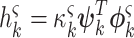 , with
, with 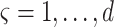 , such that
, such that  corresponds to the last element of the eigenvector
corresponds to the last element of the eigenvector 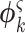 . Finally, the regrouping of the terms
. Finally, the regrouping of the terms 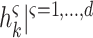 in
in  disjoint terms
disjoint terms 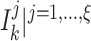 , results in
, results in
 |
such that 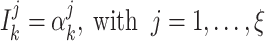 and
and  , represents the samples of extracted unobservable components at instant
, represents the samples of extracted unobservable components at instant  .
.
B. Parametric Estimation of Interval Type-2 Fuzzy Kalman Filter
The adopted structure of interval type-2 fuzzy Kalman filter presents the 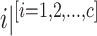 -th fuzzy rule, given by:
-th fuzzy rule, given by:
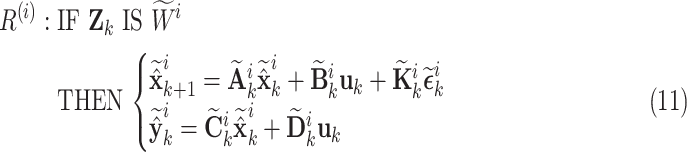 |
with 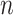 -th order,
-th order,  inputs,
inputs,  outputs, where
outputs, where  is the linguistic variable of the antecedent;
is the linguistic variable of the antecedent; 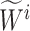 is the interval type-2 fuzzy set;
is the interval type-2 fuzzy set; 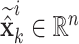 is the estimated interval states vector;
is the estimated interval states vector;  is the estimated interval output vector and
is the estimated interval output vector and  is the input signal. The matrices
is the input signal. The matrices  ,
, 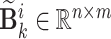 ,
,  ,
,  and
and  are, respectively, state matrix, input matrix, output matrix, direct transmission matrix and Kalman gain matrix. The residual error
are, respectively, state matrix, input matrix, output matrix, direct transmission matrix and Kalman gain matrix. The residual error 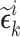 for
for 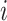 -th rule is defined as
-th rule is defined as  , where
, where  is the real time series and
is the real time series and 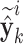 is the interval estimated time series by
is the interval estimated time series by  -th interval Kalman filter.
-th interval Kalman filter.
1). Parametric Estimation of Antecedent
The interval type-2 fuzzy version of Gustafson-Kessel clustering algorithm, is proposed, as formulated in the sequel. Given the experimental dataset  , choose the number of clusters
, choose the number of clusters 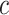 such that
such that 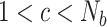 ; the initial partition matrix
; the initial partition matrix  , the termination tolerance
, the termination tolerance  and the interval weighting exponent
and the interval weighting exponent  , where
, where  and
and  correspond to, respectively, weighting exponent of upper and lower membership functions of the interval type-2 fuzzy set
correspond to, respectively, weighting exponent of upper and lower membership functions of the interval type-2 fuzzy set 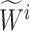 .
.
Repeat for 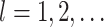
Step 1: Compute the centers of the clusters  :
:
 |
where  is the data at sample
is the data at sample  and
and  is the interval membership degree of
is the interval membership degree of 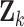 in the
in the  -th cluster.
-th cluster.
Step 2: Compute the covariance matrices  of the clusters:
of the clusters:
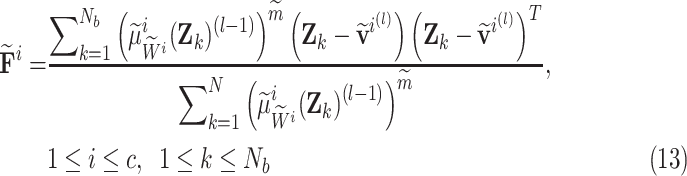 |
Step 3: Compute the distances  between the sample
between the sample 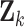 and the center
and the center  of the
of the  -th cluster:
-th cluster:
 |
Step 4: Update the interval partition matrix  :
:
If  for
for 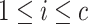 ,
, 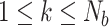
 |
where
 |
is the lower activation degree in 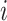 -th rule and
-th rule and
 |
is the upper activation degree in  -th rule. Otherwise,
-th rule. Otherwise, 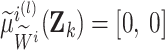 with
with 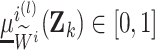 e
e 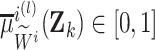
Until

2). Parametric Estimation of Consequent
The interval type-2 fuzzy OKID (Observer/Kalman Filter Identification) algorithm, is proposed, as formulated in the sequel. Let the experimental dataset 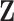 , such that
, such that 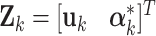 , where
, where  corresponds to spectral components extracted from the experimental dataset that presents higher eigenvalue and are more significant to represent the dynamics of experimental dataset. Choose an appropriate number of Markov parameters
corresponds to spectral components extracted from the experimental dataset that presents higher eigenvalue and are more significant to represent the dynamics of experimental dataset. Choose an appropriate number of Markov parameters  , through the following steps:
, through the following steps:
Step 1: Compute the matrix of regressors 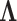 , given by:
, given by:
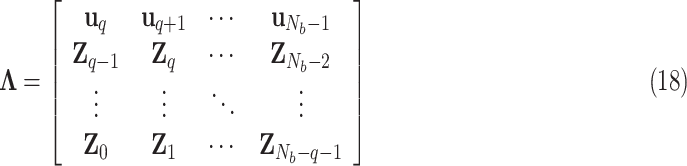 |
Step 2: Compute the interval Observer Markov Parameters:
 |
where  is the diagonal weighting matrix of the
is the diagonal weighting matrix of the 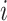 -th fuzzy rule obtained from the interval type-2 Gustafson-Kessel fuzzy clustering algorithm and
-th fuzzy rule obtained from the interval type-2 Gustafson-Kessel fuzzy clustering algorithm and
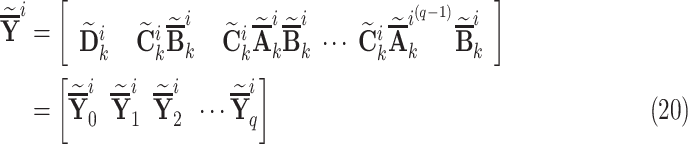 |
are the interval observer Markov parameters of  -th rule such that
-th rule such that  ,
, 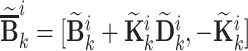 and
and 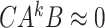 for
for  , where
, where  is the number of observer Markov parameters [17]. Manipulating the (19):
is the number of observer Markov parameters [17]. Manipulating the (19):
 |
Assuming 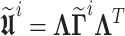 and
and 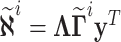 , Eq. (21) is rewriting as
, Eq. (21) is rewriting as 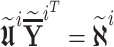 . Applying QR factorization to the term
. Applying QR factorization to the term 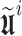 , it has:
, it has:
 |
Because the matrix 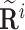 is upper triangular, Eq. (22) can be solved by backward replacement, obtaining the observer's Markov parameter vector
is upper triangular, Eq. (22) can be solved by backward replacement, obtaining the observer's Markov parameter vector  .
.
Step 3: Compute the observer gain and system Markov parameters:
 |
The system Markov parameters  are obtained as follows:
are obtained as follows:
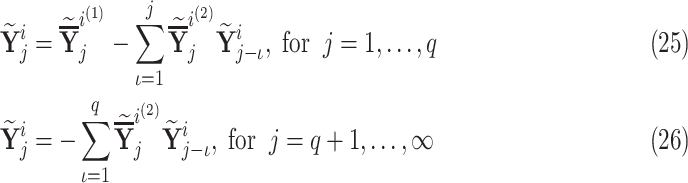 |
and the observer gain Markov parameters 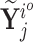 are obtained by:
are obtained by:
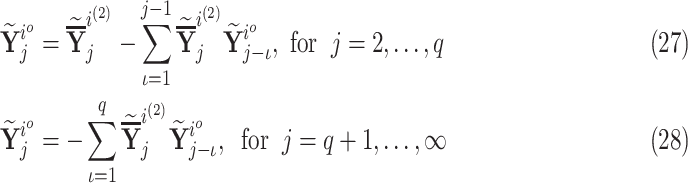 |
Step 4: Construct the Hankel matrix  :
:
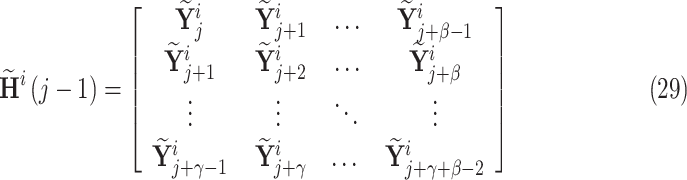 |
where 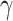 and
and  are arbitrary integers defined by user.
are arbitrary integers defined by user.
Step 5: For  , decompose the Hankel matrix
, decompose the Hankel matrix 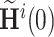 using Singular Value Decomposition:
using Singular Value Decomposition:
 |
where 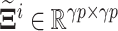 and
and  are orthogonal matrices and
are orthogonal matrices and 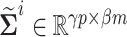 is the diagonal matrix of singular values.
is the diagonal matrix of singular values.
Step 6: Compute the observability matrix  and controllability matrix
and controllability matrix 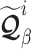 :
:
 |
Step 7: Compute the matrices that make up the consequent proposition of interval type-2 fuzzy Kalman filter:
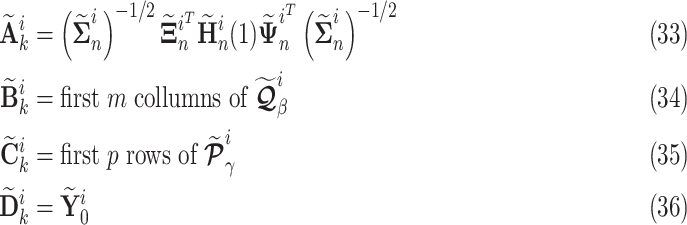 |
Step 8: Compute the interval Kalman gain matrix 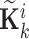 :
:
 |
Assuming 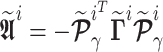 and
and 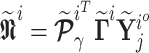 , Eq. (37) is rewriting
, Eq. (37) is rewriting 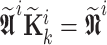 , which is solved by QR factorization method being applied to
, which is solved by QR factorization method being applied to 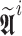 and obtaining the interval Kalman gain matrix
and obtaining the interval Kalman gain matrix 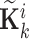 .
.
Recursive Updating of Interval Type-2 Fuzzy Kalman Filter Inference System: Considering the regressors vector  , at instant
, at instant  , given by
, given by
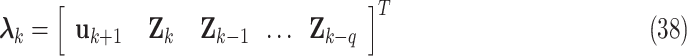 |
the interval observer Markov parameters  are obtained by recursive updating of
are obtained by recursive updating of 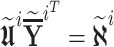 , as follows:
, as follows:
 |
The consequent proposition of the type-2 fuzzy Kalman filter is updated recursively by repeating the Step 3 to Step 7. Similarly, the interval type-2 fuzzy Kalman gain matrix 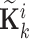 is obtained by recursive updating of
is obtained by recursive updating of 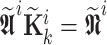 , as follows:
, as follows:
 |
In the sense to illustrate the sequential steps of the computational aspects for interval type-2 fuzzy Kalman filter design, for better understanding from readers, a flowchart of the proposed methodology is shown in Fig. 1. The code of interval type-2 fuzzy Kalman filter algorithm, based on the proposed methodology, is of open access from the link <https://drive.google.com/drive/folders/1BvzMnaZZhtleJ1dVggJJGWISpNfwdvqD?usp=sharing>.
Fig. 1.
The flowchart of the proposed methodology corresponding to computational aspects for designing the interval type-2 fuzzy Kalman filter.
III. Experimental Results
In this section, experimental results for forecasting analysis the COVID-19 dynamic propagation, including comparative analysis with the approaches in [18], [19] and with the machine learning models Least Absolute Shrinkage and Selection Operator (LASSO), Autoregressive Integrated Moving Average (ARIMA) and Long Short-Term Memory (LSTM) recurrent neural network, taking into account the experimental dataset of daily deaths reports caused by coronavirus disease in Brazil, are presented.
A. Interval Type-2 Fuzzy Kalman Filtering and Forecasting Analysis of the COVID-19 Dynamic Propagation in Brazil
The experimental dataset corresponding to daily deaths reports within the period ranging from 29 of February 2020 to 18 of May 2020, in Brazil, is shown in Fig. 2, which were extracted from official report by Ministry of Health of Brazil.1 The Variance Accounted For (VAF) was considered for evaluating the appropriate number of unobservable components, within a range from 2 to 15 ones for best representation of experimental dataset. Considering the cost-benefit balance for computational practical application of proposed methodology, the appropriated number of unobservable components was 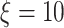 , with VAF value of 99.98%. For implementing the proposed type-2 fuzzy clustering algorithm, the following parameters were adopted: number of clusters
, with VAF value of 99.98%. For implementing the proposed type-2 fuzzy clustering algorithm, the following parameters were adopted: number of clusters 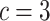 , interval weighting exponent
, interval weighting exponent 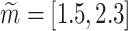 and termination tolerance
and termination tolerance 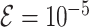 . The implementation of interval type-2 fuzzy OKID algorithm took into account the parameters values
. The implementation of interval type-2 fuzzy OKID algorithm took into account the parameters values  ,
,  and
and 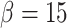 . The confidence region, as shown in Fig. 3, created by initial estimation of interval type-2 fuzzy Kalman filter, illustrates its efficiency for tracking the experimental dataset of daily deaths reports in Brazil.
From this confidence region, an interval normal distribution projections were estimated, delimiting upper and lower limits for forecasting the further daily deaths reports in Brazil. The efficiency of interval type-2 fuzzy Kalman filter based on its initial estimation by training step from experimental dataset of daily deaths reports, for forecasting the further (validation) experimental dataset of daily deaths reports, is shown in Fig. 4. The results of updating of interval type-2 fuzzy Kalman filter for tracking and forecasting the COVID-19 dynamic propagation related to the daily deaths reports, are shown in Figs. 4(b)–4(f). The efficiency of interval type-2 fuzzy Kalman filter, during its recursive updating for tracking and forecasting the COVID-19 dynamic propagation related to daily deaths reports in Brazil, was validated through Variance Accounted For (VAF) criterion, as shown in Fig. 5.
. The confidence region, as shown in Fig. 3, created by initial estimation of interval type-2 fuzzy Kalman filter, illustrates its efficiency for tracking the experimental dataset of daily deaths reports in Brazil.
From this confidence region, an interval normal distribution projections were estimated, delimiting upper and lower limits for forecasting the further daily deaths reports in Brazil. The efficiency of interval type-2 fuzzy Kalman filter based on its initial estimation by training step from experimental dataset of daily deaths reports, for forecasting the further (validation) experimental dataset of daily deaths reports, is shown in Fig. 4. The results of updating of interval type-2 fuzzy Kalman filter for tracking and forecasting the COVID-19 dynamic propagation related to the daily deaths reports, are shown in Figs. 4(b)–4(f). The efficiency of interval type-2 fuzzy Kalman filter, during its recursive updating for tracking and forecasting the COVID-19 dynamic propagation related to daily deaths reports in Brazil, was validated through Variance Accounted For (VAF) criterion, as shown in Fig. 5.
Fig. 2.
The experimental dataset of daily deaths reports within period from 29 of February 2020 to 18 of May 2020, in Brazil.
Fig. 3.
The confidence region generated by interval type-2 fuzzy Kalman filter for tracking the experimental dataset of daily deaths reports, from 29 of February 2020 to 18 of May 2020, in Brazil.
Fig. 4.

Performance of the interval type-2 fuzzy Kalman filter for adaptive tracking and real time forecasting the COVID-19 dynamic propagation related to daily deaths reports: (a) updating based on training data from 29 of February 2020 to 18 of May 2020; (b) recursive updating on 24 of June 2020; (c) recursive updating on 23 of July 2020; (d) recursive updating on 28 of August 2020; (e) recursive updating on 25 of September 2020; (f) recursive updating on 13 of October 2020.
Fig. 5.
Efficiency of interval type-2 fuzzy Kalman filter, in tracking and forecasting the COVID-19 dynamic propagation within period ranging from 18 of May to 20 of October 2020.
B. Comparative Analysis and Discussions
In this section, a more detailed discussion on the results shown in Section III-A, according to comparative analysis of proposed methodology with the approaches in [18], [19] as well as with the machine learning models LASSO, ARIMA and LSTM recurrent neural network, considering the metrics RMSE (Root Mean Square Error), MAE (Mean Absolute Error), RMSPE (Root Mean Square Percentage Error), R (coefficient of determination), MAD (Median Absolute Deviation) and MAPE (Mean Absolute Percentage Error), is presented.
(coefficient of determination), MAD (Median Absolute Deviation) and MAPE (Mean Absolute Percentage Error), is presented.
The approach in [18] is based on Wavelet-Coupled Random Vector Functional Link (WCRVFL) network for forecasting the COVID-19 dynamic propagation in Brazil, using normalized data. The efficiency of interval type-2 fuzzy Kalman filter, compared to approach in [18], is shown in Table I. As it can be seen, once that the approach in [18] uses different types of wavelets to process non-stationarity of experimental dataset, it presents competitive results compared to interval type-2 fuzzy Kalman filter, but the performance is slightly inferior due to its computing limitation from determination of the optimal number of nodes in the hidden layer of the WCRVFL network, tuning the scaling of the uniform randomization range for wavelet estimator and accurate data availability.The approach in [19] is based on ARIMA model for forecasting the COVID-19 dynamic propagation in Brazil. The efficiency of interval type-2 fuzzy Kalman filter, compared to approach in [19], is shown in Table II. The approach in [19] is fast in processing speed but presents performance more inferior than interval type-2 fuzzy Kalman filter due to consider only linear characteristics for modeling the COVID-19 dynamic propagation, which tends to increase forecasting errors in the time varying epidemiological data [20].Considering the prediction results available in approaches [18], [19], in the sense of clearly and intuitively illustrates the prediction performance of each method as compared to performance of proposed interval type-2 fuzzy Kalman filter, according to the number of cumulative cases of COVID-19 in Brazil, a comparative analysis is shown in Fig. 6.
TABLE I. Comparative Analysis Between the Interval Type-2 Fuzzy Kalman Filter and Approach in [18] for Forecasting the COVID-19 Dynamic Propagation in Brazil.
| Methodology | RMSE | MAE | RMSPE |
R
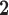
|
MAD | MAPE(%) |
|---|---|---|---|---|---|---|
| approach in [18] | 0.006 190 | 0.004 880 | 0.2359 | 0.999 450 | 0.176 | 0.00 745 |
| interval type-2 fuzzy Kalman filter | 0.003 388 | 0.000 701 | 0.00 339 | 0.999 677 | 0.1655 | 0.00 701 |
TABLE II. Comparative Analysis Between the Interval Type-2 Fuzzy Kalman Filter and Approach in [19] for Forecasting the COVID-19 Dynamic Propagation in Brazil.
| Methodology | RMSE | MAE | RMSPE |
R
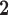
|
MAD | MAPE(%) |
|---|---|---|---|---|---|---|
| approach in [19] | 922.83 | 170.77 | 0.00 407 | 0.609 | 33 614 | 3.701 |
| interval type-2 fuzzy Kalman filter | 563.15 | 104.21 | 0.002 486 | 0.998 | 97 | 0.0 025 494 |
Fig. 6.
Comparative analysis of the prediction results between approaches [18], [19] and proposed interval type-2 fuzzy Kalman filter, according to the number of cumulative cases of COVID-19 in Brazil.
The comparative analysis between the interval type-2 fuzzy Kalman filter and the machine learning models LASSO, ARIMA and LSTM recurrent neural network, for forecasting the COVID-19 dynamic propagation in Brazil, within the horizon of 10 days, is shown in the Table III.A possible limitation of the interval type-2 fuzzy Kalman filter is the determination of some parameters (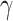 ,
, 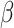 and
and 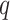 ), which requires some intuition by expert and depends on the experimental dataset. The parameters
), which requires some intuition by expert and depends on the experimental dataset. The parameters 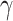 and
and  are related to dimension and rank of Hankel matrix in Eq. (29) so that a good conditioning can be guaranteed for parametric estimation of consequent proposition in interval type-2 fuzzy Kalman filter, whose most typical values are into the interval
are related to dimension and rank of Hankel matrix in Eq. (29) so that a good conditioning can be guaranteed for parametric estimation of consequent proposition in interval type-2 fuzzy Kalman filter, whose most typical values are into the interval  , where
, where 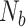 is the length of experimental dataset [17]. The numerical value of
is the length of experimental dataset [17]. The numerical value of  is related to the most representative factors of impulse response from experimental dataset and most typical values are into the interval
is related to the most representative factors of impulse response from experimental dataset and most typical values are into the interval 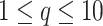 [21].
[21].
TABLE III. Comparative Analysis Between the Interval Type-2 Fuzzy Kalman Filter and Machine Learning Models LASSO, ARIMA and LSTM Recurrent Neural Network for Forecasting the COVID-19 Dynamic Propagation in Brazil.
| Model | RMSE | MAE | RMSPE |
R
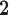
|
MAD | MAPE(%) |
|---|---|---|---|---|---|---|
| LASSO | 191.5600 | 163.4643 | 2.5081 | 0.7652 | 234.1 | 0.1283 |
| ARIMA | 203.0832 | 140.9561 | 2.6938 | 0.3680 | 245.7 | 0.1106 |
| LSTM | 116.0065 | 94.9875 | 1.3265 | 0.8290 | 193.4 | 0.0746 |
| interval type-2 fuzzy Kalman filter | 10.3586 | 3.9000 | 1.0542 | 0.9984 | 108.3 | 0.0427 |
IV. Conclusion
The results shown the applicability of machine learning approach based on interval type-2 fuzzy Kalman filter due to its recursive updating mechanism, for adaptive tracking and real time forecasting the COVID-19 dynamic propagation. For further works, the formulation and applicability of proposed methodology in the context of evolving interval type-2 fuzzy systems, is of particular interest.
Acknowledgment
The authors are grateful to Coordination for the Improvement of Higher Education Personnel (CAPES) and to the Master and Doctorate Program in Electrical Engineering at the Federal University of Maranhão (PPGEE-UFMA).
Footnotes
Available at: https://covid.saude.gov.br/
Contributor Information
Daiana Caroline dos Santos Gomes, Email: ginalber@ifma.edu.br.
Ginalber Luiz de Oliveira Serra, Email: daianagomes159@gmail.com.
References
- [1].Pires D. S. and Serra G. L. O., “Methodology for evolving fuzzy kalman filter identification,” Int. J. Control Automat. Syst., vol. 17, no. 3, pp. 793–800, Feb. 2019. [Google Scholar]
- [2].Eyoh I., John R., Maere G. D., and Kayacan E., “Hybrid learning for interval type-2 intuitionistic fuzzy logic systems as applied to identification and prediction problems,” IEEE Trans. Fuzzy Syst., vol. 26, no. 5, pp. 2672–2685, Oct. 2018. [Google Scholar]
- [3].Gil P., Oliveira T., and Palma L., “Adaptive neurofuzzy control for discrete-time nonaffine nonlinear systems,” IEEE Trans. Fuzzy Syst., vol. 27, no. 8, pp. 1602–1615, Aug. 2019. [Google Scholar]
- [4].Wang X., Xu Z., Gou X., and Trajkovic L., “Tracking a maneuvering target by multiple sensors using extended kalman filter with nested probabilistic-numerical linguistic information,” IEEE Trans. Fuzzy Syst., vol. 28, no. 2, pp. 346–360, Feb. 2020. [Google Scholar]
- [5].Asl R. M., Palm R., Wu H., and Handroos H., “Fuzzy-based parameter optimization of adaptive unscented kalman filter: Methodology and experimental validation,” IEEE Access, vol. 8, no. 1, pp. 54887–54904, 2020. [Google Scholar]
- [6].Zhong L., Mu L., Li J., Wang J., Yin Z., and Liu D., “Early prediction of the 2019 novel Coronavirus outbreak in the mainland China based on simple mathematical model,” IEEE Access, vol. 8, no. 1, pp. 51761–51769, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Lin Q. et al. , “A conceptual model for the Coronavirus disease 2019 (COVID-19) outbreak in wuhan, china with individual reaction and governmental action,” Int. J. Infect. Dis., vol. 93, no. 1, pp. 211–216, Apr. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Chintalapudi N., Battineni G., and Amenta F., “COVID-19 virus outbreak forecasting of registered and recovered cases after sixty day lockdown in italy: A. data driven model approach,” J. Microbiol. Immunol. Infect., vol. 53, no. 3, pp. 396–403, Jun. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Kim S., Seo Y. B., and Jung E., “Prediction of COVID-19 transmission dynamics using a mathematical model considering behavior changes,” Epidemiol. Health, Apr. 2020, Art. no. e2020026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Park S. W., Cornforth D. M., Dushoff J., and Weitz J. S., “The time scale of asymptomatic transmission affects estimates of epidemic potential in the COVID-19 outbreak,” Epidemics, vol. 31, Jun. 2020, Art. no. 100392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Huang Y. et al. , “SARS-CoV-2 viral load in clinical samples from critically ill patients,” Amer. J. Respir. Crit. Care Med., vol. 201, no. 11, pp. 1435–1438, Jun. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Kanagarathinam K. and Sekar K., “Estimation of reproduction number and early prediction of 2019 Novel Coronavirus Disease (COVID-19) outbreak in India using statistical computing approach,” Epidemiol. Health, May 2020, Art. no. e2020028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Piovella N., “Analytical solution of SEIR model describing the free spread of the COVID-19 pandemic,” Chaos Solitons Fractals, vol. 140, Nov. 2020, Art. no. 110243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Takele R., “Stochastic modelling for predicting COVID-19 prevalence in east africa countries,” Infect. Dis. Modelling, vol. 5, no. 1 pp. 598–607, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Varotsos C. A. and Krapivin V. F., “A new model for the spread of COVID-19 and the improvement of safety,” Saf. Sci., vol. 132, Dec. 2020, Art. no. 104962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Elsner J. B., “Analysis of time series structure: SSA and related techniques,” J. Amer. Statist. Assoc., vol. 97, no. 460, pp. 1207–1208, Dec. 2002. [Google Scholar]
- [17].Juang J. N., Applied System Identification. Hoboken, NJ, USA: Prentice Hall, 1994. [Google Scholar]
- [18].Hazarika B. B. and Gupta D., “Modelling and forecasting of COVID-19 spread using wavelet-coupled random vector functional link networks,” Appl. Soft Comput., vol. 96, Nov. 2020, Art. no. 106626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Sahai A. K., Rath N., Sood V., and Singh M. P., “ARIMA modelling & forecasting of COVID-19 in top five affected countries,” Diabetes Metab. Syndr.: Clin. Res. Rev., vol. 14, no. 5, pp. 1419–1427, Sep. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Zhang G., “Time series forecasting using a hybrid ARIMA and neural network model,” Neurocomputing, vol. 50, no. 1 pp. 159–175, Jan. 2003. [Google Scholar]
- [21].Callier F. M. and Desoer C. A., “Realization theory,” in Springer Texts in Electrical Engineering. Berlin, Germany: Springer, 1991. [Google Scholar]







