Efficient and Effective Training of COVID-19 Classification Networks With Self-Supervised Dual-Track Learning to Rank

Abstract

Coronavirus Disease 2019 (COVID-19) has rapidly spread worldwide since first reported. Timely diagnosis of COVID-19 is crucial both for disease control and patient care. Non-contrast thoracic computed tomography (CT) has been identified as an effective tool for the diagnosis, yet the disease outbreak has placed tremendous pressure on radiologists for reading the exams and may potentially lead to fatigue-related mis-diagnosis. Reliable automatic classification algorithms can be really helpful; however, they usually require a considerable number of COVID-19 cases for training, which is difficult to acquire in a timely manner. Meanwhile, how to effectively utilize the existing archive of non-COVID-19 data (the negative samples) in the presence of severe class imbalance is another challenge. In addition, the sudden disease outbreak necessitates fast algorithm development. In this work, we propose a novel approach for effective and efficient training of COVID-19 classification networks using a small number of COVID-19 CT exams and an archive of negative samples. Concretely, a novel self-supervised learning method is proposed to extract features from the COVID-19 and negative samples. Then, two kinds of soft-labels (‘difficulty’ and ‘diversity’) are generated for the negative samples by computing the earth mover's distances between the features of the negative and COVID-19 samples, from which data ‘values’ of the negative samples can be assessed. A pre-set number of negative samples are selected accordingly and fed to the neural network for training. Experimental results show that our approach can achieve superior performance using about half of the negative samples, substantially reducing model training time.

I. Introduction

Coronavirus Disease 2019 (COVID-19) has rapidly spread all over the world since first reported in December 2019. The disease is highly contagious and has infected over 14.4 million people worldwide to date (Jul 20th, 2020).¹ On March 11th, 2020, the World Health Organization (WHO) declared COVID-19 a pandemic. The reverse transcription polymerase chain reaction (RT-PCR) assay of sputum or nasopharyngeal swab is considered as the gold standard for confirmation of COVID-19 cases. However, several studies have reported insufficient sensitivities (i.e., high false negative rates) of RT-PCR for effective early diagnosis and subsequent treatment of presumptive patients [1]–[3]. Meanwhile, as most COVID-19 patients exhibit respiratory symptoms (mainly pneumonia) [4], the non-contrast thoracic computed tomography (CT) becomes an alternative solution to help diagnose COVID-19 positive patients from suspected cohorts.

Several studies [2], [5] described typical chest CT findings of COVID-19 as diffuse or focal ground-glass opacities, particularly bilateral and peripheral ground-glass, as well as consolidative pulmonary opacities. In addition, Bernheim et al. [5] noted the progression of chest CT manifestations from early to late stages, characterized by greater lung involvement, crazing paving and reverse halo signs, etc. Moreover, both Xie et al. [1] and Fang et al. [2] reported superior sensitivities of non-contrast chest CT to RT-PCR. However, due to the sudden outbreak of the COVID-19 pandemic, radiologists are now facing great pressure in reading the tremendous quantity of CT exams—a thin-slice CT sequence of 300 slices can take 5–15 minutes of a radiologist to make the diagnosis. Besides being time-consuming and painstaking, the reading process can become error- and omission-prone considering the extremely heavy workload. Also, identifying early signs of COVID-19 in CT can be difficult for junior radiologists. Therefore, automated algorithms that are able to consistently identify COVID-19 from CT exams are of great clinical value fighting the pandemic.

In recent years, deep learning (DL) based methods have been applied to various tasks in medical image analysis and achieved outstanding performance [6], [7], including diagnosis of pediatric pneumonia using chest X-ray images [8]. Nonetheless, DL-based methods are known to be data-hungry. For example, a recent work [9] showed that the DL method was able to distinguish COVID-19 from community acquired pneumonia (CAP) and non-pneumonia on chest CT exams, using 4,356 3D chest CT exams of 3,506 patients for development and validation of the DL method, of which 1,296 (30%) were confirmed COVID-19. Under most circumstances, however, it is difficult to collect a well-balanced dataset to train DL-based models for an emerging disease like COVID-19 for most medical centers, especially in the early stage of the outbreak. On one hand, the number of positive cases (e.g., COVID-19) is extremely low. On the other hand, it is more likely that these medical centers house a considerable archive of other cases such as CAP and non-pneumonia CT exams. This results in two practical challenges to the fast development of DL-based screening methods for rapid response to disease screening and control: insufficient positive training samples and seriously imbalanced classes.

In this work, we propose a novel solution to this dilemma, for effective and efficient training of DL-based methods to aid the COVID-19 diagnosis on chest CT exams—more specifically, to distinguish CT exams of COVID-19 from others. We have collected 305 CT exams for COVID-19 and 2,370 for CAP and non-pneumonia, resulting in a 1:8 positive to negative ratio. The common strategy for handling the imbalanced training data is either to under-sample the majority class or over-sample the minority class. However, the former may discard the potentially useful information in the majority class, whereas the latter may unnecessarily increase the computational overhead. Another line of solutions is to resample [10] or reweight [11] the training samples after forwarding them through the network, especially for those in the majority class. Notwithstanding, these solutions still require loss computation for all samples in each training epoch.

Different from these methods, we propose a dual-track ranking approach to explicitly measure the ‘value’ of negative samples for network training in an offline manner. The proposed approach ranks the negative samples in both terms of ‘difficulty’ and ‘diversity’. A novel self-supervised learning method (i.e., Rubik's cube Pro) is proposed to extract features from the COVID-19 and negative CT volumes. Then, two kinds of soft-labels (i.e., ‘difficulty’ and ‘diversity’) are generated for each negative sample by calculating the earth mover's distance (EMD) between its features and those of COVID-19 volumes. Using these generated soft-labels, the data ‘value’ of negative samples can be quantitatively evaluated. A pre-set number of negative samples are selected based on the joint ranking of ‘difficulty’ and ‘diversity,’ and fed to the neural network for training together with the COVID-19 volumes (Fig. 1).

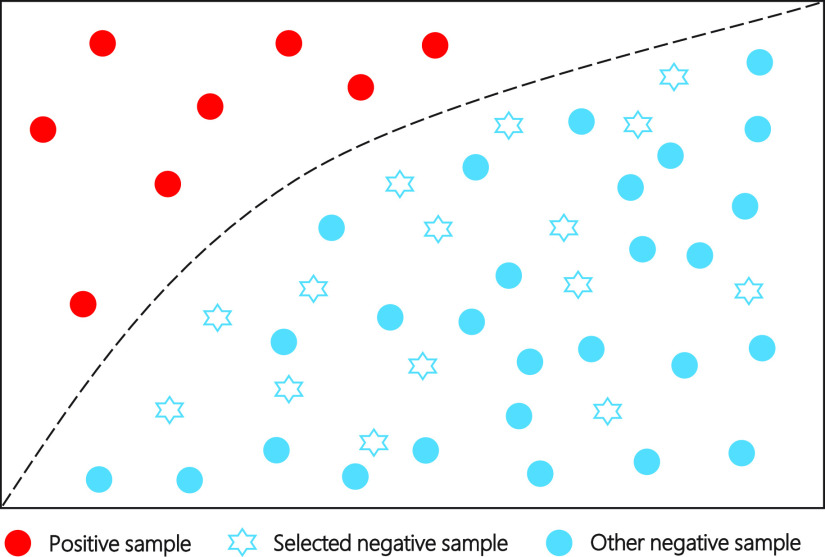
Fig. 1.

Imbalanced distribution of positive (red) and negative (cyan) samples. The proposed approach is encouraged to select a subset of samples (cyan stars), which are representative of the entire negative pool (cyan stars plus cyan circles). Therefore, we can maintain the performance of classifier and shorten the training period.

In summary, our contributions in this work are three folds:

• •We propose a novel self-supervised learning approach, namely Rubik's cube Pro, which is an extension of the approach proposed in our previous conference paper [12]. Compared to the common Rubik's cube [12], a random masking operation is added to the pretext task to improve self-supervised feature representation, which is more robust to deal with the multi-centre CT volumes used in this study.
• •A dual-track offline data selection approach is proposed to mine the informative negative samples for neural network training, which measures the data ‘value’ in two terms—‘difficulty’ and ‘diversity’. Compared to the online data selection and oversampling approaches, our offline method can significantly decrease the training period of deep learning models, which is crucial for the development of computer aided diagnosis system at the early stage of the COVID-19 outbreak.
• •We conduct extensive experiments to validate the efficiency and effectiveness of the proposed offline data selection approach. The experimental results show that, compared to the vanilla network training scheme using all available negative samples, our approach can achieve superior performance using only about half of the negative samples for training the COVID-19 classification network, substantially reducing model training time.

II. Related Work

In this section, we provide a systematic review of the literature related to our work. First, we review existing works on imaging-based diagnosis of pneumonia, including several concurrent works on COVID-19 diagnosis. Second, we review several topics closely related to our novel approach, including common strategies for imbalanced data, deep metric learning, and self-supervised training.

A. Imaging-Based Diagnosis of Pneumonia

A large body of literature focused on pneumonia diagnosis on chest X-ray images (e.g., [8], [13]–[16], to name a few). Notably, both Kermany et al. [8] and Rajarama et al. [14] applied DL methods to the diagnosis between bacterial and viral pneumonia in pediatric chest X-rays, which is similar to our goal of identifying COVID-19 (a type of viral pneumonia, indeed) from pneumonia of other etiologies (CAP) and non-pneumonia. For a cost-efficient solution, Zheng et al. [17] proposed a DL method for pneumonia diagnosis based on clinical lung ultrasound images, using CT as the gold standard. However, both X-ray and ultrasound images are insufficient for early diagnosis of COVID-19 because they may easily miss the subtle signs such as small regions of ground-glass opacities. Prior works on machine-learning driven imaging-based diagnosis of pneumonia are rare [18], until recently several concurrent works [9], [19], [20] appeared for the diagnosis of COVID-19. However, none of these works considered the problem of seriously imbalanced COVID-19 and archived chest CT data that may be encountered in practice when developing DL methods in the early stage of the outbreak.

B. Strategies for Imbalanced Data

Class imbalance is a problem with a long history in learning-based medical image analysis, and various solutions have been proposed to deal with it. Arguably, under-sampling the majority class and/or up-sampling the minority class to roughly equilibrate their instance numbers are the most straightforward and frequently used approaches. However, under-sampling with a simple random selection strategy may discard the samples potentially informative for training the DL model. Meanwhile, simply over-sampling the minority class may not increase the amount of effective information while substantially increasing the computational overhead. In other words, neither under-sampling nor over-sampling utilizes the inherent characteristics of the available training samples. Re-weighting class losses in inverse proportion to the numbers of class instances [21] is conceptually similar to the under- and over-sampling approaches, in that it only considers the instance numbers but not the properties of the data. Both the online hard example mining (OHEM) [10] and focal loss [11] tackled the class imbalance problem by estimating the difficulty levels of the training samples, thus requiring all the training samples to be processed by the current model in each training epoch. In contrast, our approach first picks the most informative negative samples from the big archive, and only uses the selected subset for more efficient training while achieving comparable performance. The sample selection is driven by sample difficulty and diversity, both of which are estimated by a model trained via metric learning.

C. Deep Metric Learning

Metric learning has been adopted in wide computer vision applications (see [22] for a survey). Recently, this concept has been revitalized in the realm of DL and became one of the central topics in few-shot learning [23]–[25]. In the general concept of metric learning, a learnable embedding function projects the input into an embedding space, where the projected samples of the same class should be closer to each other than those from different classes. To learn the embedding function, a distance metric (most often the squared Euclidean [23] or cosine distances [25]) is employed to measure the intra- and inter-class distances, and loss functions are defined accordingly (e.g., the triplet loss [26]) to encourage small intra-class and large inter-class distances. Unlike the typical deep metric learning, we learn the embedding using only a single class (the COVID-19) through a proxy task for self-supervised training. In addition, we employ the earth mover's distance [27] rather than the usual cosine or squared Euclidean distance due to the fact that EMD is considerably more robust especially in the task of comparing two histogram-based feature descriptors.

Specifically, the earth mover's distance is a distance measure between two sets of weighted objects or distributions, which is built upon the basic distance between individual objects. It has the form of the well-studied transportation problem from linear programming. Suppose that a set of suppliers are required to transport goods to a set of demanders. The goal of EMD is to find a least-expensive flow of goods from the suppliers to the demanders. In this study, EMD is adopted to measure the similarity between two histogram-based features. The calculation process is presented in Section IV C.

D. Self-Supervised Training

To deal with the deficiency of annotated data, researchers attempted to exploit useful information from the unlabeled data with unsupervised approaches [28], [29]. More recently, the self-supervised learning, as a new paradigm of unsupervised learning, attracts increasing attentions from the community. The pipeline consists of two steps: 1) pre-train a convolutional neural network (CNN) on a proxy task with a large unannotated dataset; 2) fine-tune the pre-trained network for the specific target task with a small set of annotated data. The proxy task enforces neural networks to deeply mine useful information from the unlabeled raw data, which can boost the accuracy of the subsequent target task with limited training data. Various proxy tasks had been proposed, which include grayscale image colorization [30], jigsaw puzzle [31], image inpainting [32], spatial position prediction [33], and object motion estimation [34].

For the applications with medical data, researchers took some prior-knowledge into account when formulating the proxy task. Zhang et al. [29] defined a proxy task that sorted the 2D slices extracted from the conventional 3D CT and magnetic resonance imaging (MRI) volumes, to pre-train the neural networks for the fine-grained body part recognition (the target task). Spitzer et al. [28] proposed to pre-train neural networks on a self-supervised learning task, i.e., predicting the 3D distance between two patches sampled from the same brain, for the better segmentation of brain areas (the target task). Zhuang et al. [12] proposed to pre-train 3D networks by playing a Rubik's cube game, which can be seen as an extension of 2D jigsaw puzzles [35]. Zhou et al. [36] formulated a content restoration pretext task for 3D medical volumes, which achieved impressive improvements on multiple medical image processing tasks. In this study, we extend the Rubik's cube approach by adding a random masking operation, which improves the robustness of the self-supervised feature representation.

III. Materials

A. Study Cohorts

This retrospective study was approved by the Institutional Review Boards of the participating hospitals, and informed consent was waived due to the retrospective nature of the study. It included 2,675 3D volumetric non-contrast thoracic CT exams from 2,595 patients acquired at over 10 medical centers between Nov. 11th, 2010 and Feb. 9th, 2020. The inclusion criteria included: (i) complete CT scans covering the whole lung, and (ii) acceptable image quality not affecting analysis. For CT exams with multiple reconstruction kernels at the same imaging session, we manually picked the one that was visually sharper. CT exams of the same subject acquired at different time points were all included. The dataset comprised 305 COVID-19 (11%), 872 CAP (33%), and 1,498 non-pneumonia (56%) exams. The data were anonymized before analysis.

All the COVID-19 data were confirmed RT-PCR positive cases, and further verified by experienced radiologists to confirm radiographical lung infections. The 305 COVID-19 CT exams were acquired on 251 patients from Jan. 18th, 2020 to Feb. 9th, 2020, using 18 scanner models made by four manufacturers (GE Medical Systems, MinFound Medical Systems, Philips, and Siemens). The CAP data comprised 872 CT exams acquired on 869 patients from Nov. 14th, 2010 to Nov. 4th, 2019, using nine scanner models made by four manufacturers (GE Medical Systems, Philips, Siemens, and Toshiba). Among them, 497 of the CAP exams were acquired at the same hospital as 80 of the COVID-19 exams. The non-pneumonia data comprised 1,498 CT exams acquired on 1,475 subjects between Nov. 11th, 2010 and Jul. 2^nd, 2019, using 18 scanner models made by four manufacturers (GE Medical Systems, Philips, Siemens, and Toshiba). The non-pneumonia cohort included subjects without any lung disease or with lung nodules (with and without complications).

B. Imaging Protocol

The CT examinations were performed using various scanners made by different manufacturers, presenting considerable variation in the imaging protocol (details presented in Table I). The exams were performed with the subjects instructed to hold the breath at full inspiration.

TABLE I. Imaging Protocols of the CT Exams.

	No. slices	Slice thickness (mm)	Matrix size	Pixel spacing (mm)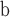	KVP (kV)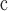	Collimation (mm)	Pitch
COVID-19	38–629	0.625–7.5	512×512	0.604–0.977	100–130	(4–128)×(0.6–3.75)	0.75–1.5
CAP	24–1,309	0.5–7	512×512	0.482–0.951	110–140	(8–128)×(0.6–1.25)	0.734–1.438
Non-pneumonia	24–879	0.75–10	512×512	0.5–0.977	100–140	(4–128)×(0.6–2.5)	0.75–1.5

The CT volumes are not of a uniform size, which makes the No. slices vary in a range.

Isotropic pixel sizes.

Automatic tube current was used.

IV. Method

A. Problem Formulation

There are two main challenges we encountered while developing the computer aided diagnosis system for COVID-19 using CT scans: 1) the quantity of COVID-19 CT volumes is deficient, compared to the available negative samples (i.e., non-pneumonia and CAP), suffering from the problem of class imbalance; and 2) due to the outbreak of COVID-19, there is limited time for the training and tuning of neural networks. Specifically, assuming we have 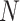COVID-19 and 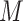negative CT volumes, where 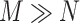, the neural network trained with such an imbalanced dataset may yield biased prediction. To alleviate the problem, many approaches have been proposed such as focal loss [11] and OHEM [10]. However, those online data selection approaches are extremely time-consuming, since they take the entire sample set (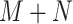) as the training set. Witnessed the fast outbreak of COVID-19, the tremendous time consumption caused by the online data selection approaches is unacceptable for the development of computer aided diagnosis systems.

To simultaneously address these two problems, we propose a dual-track ranking approach to explicitly measure the ‘value’ of negative samples for network training in an offline manner. As shown in Fig. 2, the proposed approach ranks the negative samples in both terms of ‘difficulty’ and ‘diversity’ by three steps. First, the proposed approach extracts features from the COVID-19 and negative CT volumes using a self-supervised learning method (i.e., Rubik's cube Pro). Then, a soft-label is generated for each negative sample by calculating the earth mover's distance (EMD) between the positive and negative features. Using these generated soft-labels, the data ‘value’ of negative samples can be assessed in two tracks (i.e., ‘difficulty’ and ‘diversity’). A pre-set number (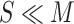) of negative samples are selected based on the joint ranking of two-tracks and fed to the neural network for training together with the positive volumes.

Fig. 2.

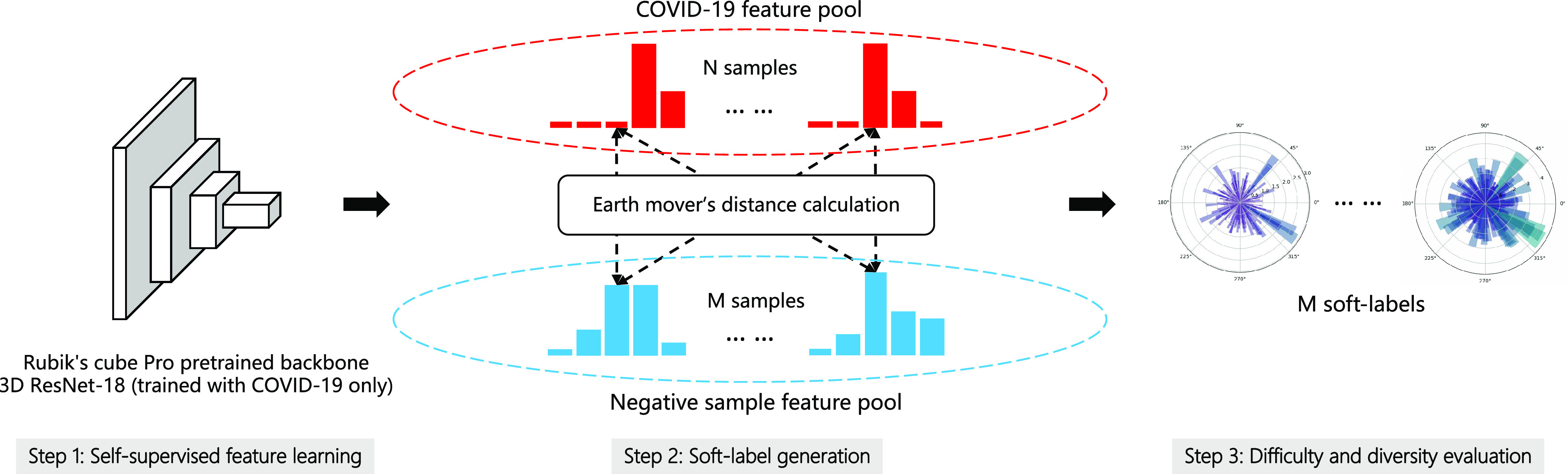
The pipeline of our dual-track ranking approach. The approach involves three steps: self-supervised feature learning, soft-label generation, and difficulty and diversity evaluation. The soft-labels are presented with polar histograms, where 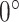is the first element.

B. Feature Extraction via Self-Supervised Learning

An improved version of the recently proposed self-supervised approach, namely Rubik's cube Pro, is adopted to extract discriminative features from CT volumes. Similar to [12], the 3D medical volume (original state) is seen as a 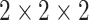Rubik's cube and accordingly partitioned into eight cubes. The cubes are then processed by a series of operations (i.e., rearrangement and rotation), which formulates a disarranged state of Rubik's cube. The aim of the Rubik's cube pretext task is to recover the original state of medical volume from the disarranged stage. To complete the pretext task, the 3D neural network is required to deeply mine the 3D anatomical information from the raw volume. In addition to the cube rearrangement and reorientation proposed in [12], our Rubik's cube Pro randomly masks the content of cube to increase the difficulty of the pretext task, which encourages the neural network to learn a more robust feature representation. The proposed Rubik's cube Pro involves three operations—cube permutation, cube rotation, and cube masking, which are introduced in details in the following.

1). Cube Permutation

Taking a pocket cube, i.e., 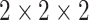Rubik's cube, as an example, we first select 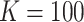permutations from the permutation pool (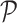), i.e., 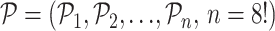, by maximizing the Hamming distance between each pair of permutations. Then, for each time of Rubik's cube recovery, the eight cubes are rearranged according to one of the 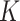permutations. To properly reorder the cubes, the network is trained to identify the selected permutation from the 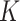options, which can be seen as a classification task with 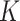categories. Assuming the 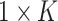network prediction as 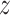and the one-hot ground-truth as 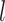, the permutation loss (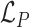) in this step can be defined as:

2). Cube Rotation

Additionally, the Rubik's cube Pro pretext task adopts the random cube rotation to encourage the network to extract rotation-invariant features. To reduce the complexity of the task, we limit the directions for cube rotation, i.e., only allowing 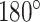horizontal and vertical rotations. To orientate the cubes, the network is required to recognize whether each of the input cubes has been rotated. It can be seen as a multi-label classification task using the 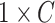( 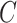is the number of cubes) ground truth (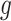) with 1 on the positions of rotated cubes and 0 vice versa. Hence, the predictions of this task are two 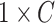vectors ( 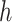and 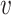) indicating the possibilities of horizontal (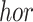) and vertical (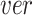) rotations for each cube. The rotation loss (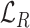) can be written as:

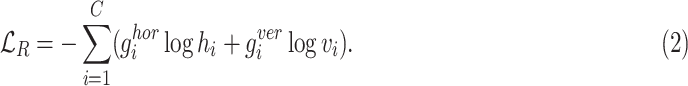3). Cube Masking

Inspired by the observation that learning from a harder task often leads to a more robust feature representation [37], [38], apart from the cube permutation and rotation proposed in [12], an additional operation, i.e., cube masking, is adopted in our Rubik's cube Pro to increase the difficulty of Rubik's cube recovery. Such a strategy can be seen as adding noise to the training data to avoid network overfitting. Many researches [39], [40] have proven the effectiveness of this strategy, but few of them integrate it into a self-supervised learning framework.

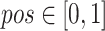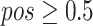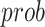The process of random masking strategy can be summarized as following. First, a random possibility () is generated for each cube to determine whether it should be masked or not. If the cube is to be masked (i.e., ), we generate a 3D matrix of the same shape of a cube to randomly block the content. The value of each voxel of is a probability () randomly captured from a uniform distribution [0, 1]. To obtain the mask, a thresholding operation (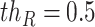) is performed to 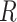, which leads the voxel value of 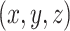to be 1 for 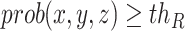and 0 vice versa, where 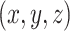is the 3D coordinate of a voxel. Assuming a cube after rearrangement and rotation as 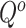, its masking state (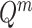) can be generated by multiplying the 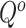and mask 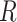in pixel-wise manner: 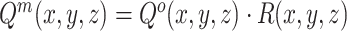. Since the objective of our Rubik's cube Pro is the same to [12] (i.e., 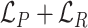), the neural networks recovering such partially masked Rubik's cubes can learn feature representations with robustness against disturbance of multi-centre data, compared to the original Rubik's cube.

C. Soft-Label Generation

After self-supervised learning, the pre-trained 3D neural network is then applied to extract features from both COVID-19 and negative samples (i.e., the features from the last convolutional layer of 3D ResNet-18). (Note that, to measure the distance from negative samples to the positive pool, only COVID-19 CT volumes are employed to pre-train the neural network for feature extraction.) We calculate the EMD between the features of each pair of positive and negative samples to construct an 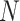-dimensional soft-label for each sample in the negative pool. The EMD is an actively used cross-bin distance metric due to its robustness, especially in the task of comparison between two histogram-based descriptors, such as the extracted features in our application. Denote the features of COVID-19 and negative CT samples as 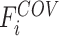(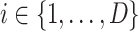) and 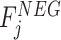(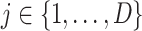), respectively, where 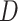is the number of elements contained in the extracted feature ( 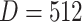of the last convolutional layer of ResNet-18). Referring to Section II C, the features of COVID-19 and negative CT samples can be seen as the sets of suppliers and demanders. The EMD between these two features can be defined as:

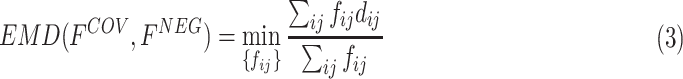subjected to the constraints:

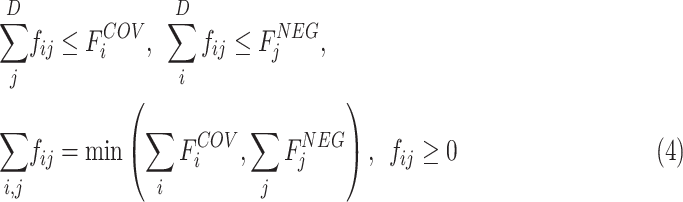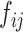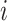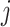where represents the amount of flow transported from element to , and 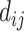represents its ground distance. The cost for transporting the unit amount from one element to another is determined by its ground distance. The EMD is obtained by measuring the minimum total cost to transform one feature into the other. Please refer to [41] for more details.

D. Difficulty and Diversity Evaluation

Using the generated soft-labels, we can explicitly evaluate the negative samples in terms of ‘difficulty’ and ‘diversity’ to the neural network.

1). Difficulty

Since the soft-label represents the distance from the negative sample to the COVID-19 feature pool, the sample with a smaller distance is perceptually more similar to the COVID-19. Hence, the average of EMD soft-label (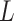) can be seen as a metric measuring the difficulty (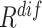) of each negative sample for the neural network to process, which can be defined as:

where 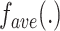is the average function and 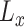is the 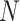-dimensional soft-label for sample .

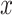2). Diversity

The diversity of training set directly influences the robustness of neural network—a more diverse training set may lead to more robust model performance. Therefore, beyond the ‘difficulty,’ we further measure the ‘diversity’ of negative samples using the generated soft-labels. For a sample 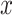, we first calculate the EMD between 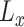and 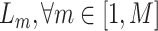where 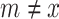, which forms an 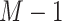dimensional EMD histogram. As the smaller EMD means the higher similarity of two features, the average of the obtained 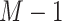EMD histograms can represent the overall dissimilarity of the negative sample to the other negative samples—the larger the averaged EMD, the higher diversity value of the negative sample. Therefore, the ‘diversity’ (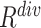) of sample 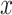can be written as:

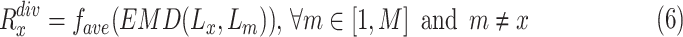where 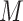is the number of negative samples.

3). Joint Ranking

To comprehensively assess the data ‘value,’ we reorder the ranking of negative samples by taking both 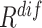and 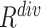into account. Let 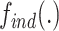represent the rank indexing function (taking an integer value starting from 1), the joint ranking (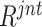) can be defined as:

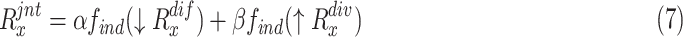where 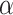and 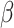are the weights for the two tracks (empirically set to 0.5 in our experiments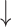); and and 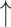express the operation of ascending and descending ordering. The smaller 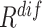means higher difficulty, which is vice verse for 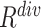; therefore, the two tracks are ordering in different directions.

E. Sample Selection

The obtained joint ranking (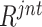) simultaneously measures the ‘difficulty’ and ‘diversity’ of negative samples, which can be used as guideline for negative sample selection for neural network training. There are many strategies for sample selection, such as hard example mining—assigning higher weights for the difficult samples. In our experiments, to involve a variety of negative samples for the robust feature representation learning, we apply a ‘long-tail’ distribution sampling [42] to the 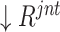, where a high-frequency sampling is performed to the top-ranked population, followed by a ‘tails off’ asymptotically sampling for the rest.

F. Implementation Details

All the experiments are conducted with the PyTorch package in Python 3.6.4 environment, using one Tesla V100 GPU.

1). Rubik's Cube Pro

Our Rubik's cube Pro is trained with a mini-batch size of 8. The initial learning rate is set to 0.001. The Adam solver [43] is used for network optimization. In our experiments, the 3D ResNet-18 [44] is adopted as the backbone. To reduce the time consumption of pretext task training, our Rubik's cube Pro is pre-trained with COVID-19 volumes only. The whole procedure of pre-training consumes about 20 minutes.

2). COVID-19 Classification Network

Straightforward data preprocessing is employed. First, we use an inhouse developed, DL-based algorithm to segment the lung masks for the 3D non-contrast CT volumes. The algorithm is robust and able to yield consistently high-quality lung masks even in the presence of severe pathological changes of the lungs. Next, we resample the CT volumes to have the unified voxel size of 1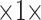5 mm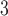. (We have conducted primitive experiments with thin-slice resampling of 1 mm thickness, which was exponentially slower but yielded similar performance.) Then, the CT volumes are cropped according to the lung masks, adding the buffers of 9 mm, 9 mm, and 5 mm in the 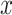, , 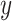and 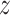directions both pre- and post the lung masks. The lung window setting with the window level set to 600 Hounsfield unit (HU) and window width set to 1500 HU is applied to the cropped CT volumes, whose voxel intensity values are subsequently rescaled to the range [0,1] linearly. Lastly, regions outside the lung masks are set to 0 value to eliminate interference from non-lung regions.

For input to the network, a center crop of 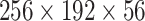voxels is taken from the preprocessed CT volume; a constant padding is performed around the volume for smaller lungs when needed. The input size is determined according to the mean size of the preprocessed CT volumes. To efficiently exploit the limited training data, two online data augmentation operations are performed during the training process, which acts as the regularization for our models: random intensity-jittering with the scale range in [0.9, 1.1] and random flipping. No data augmentation is performed for model testing.

The COVID-19 classification network adopts the same backbone and training protocol as Rubik's cube Pro. However, since the Rubik's cube Pro only uses the COVID-19 volumes for pre-training, which results in a biased network initialization, the COVID-19 classification network randomly initializes its weights, instead of using the Rubik's cube Pro pre-trained weights, at the beginning of network training. We notice that pre-training Rubik's cube Pro with all samples may boost the COVID-19 classification. However, the time consumption of pre-training increases to more than three hours, due to much more training samples (above 2,000 vs. 246). In consideration of development speed, the random initialization is preferred at the early stage of the development of computer aided diagnosis system.

V. Experiments

Due to the rapid outbreak of COVID-19, the main concerns of this study fall into two folds—the classification accuracy and training duration of the deep learning network. In this section, we conduct extensive experiments to validate the effectiveness of our offline negative sample mining approach in both terms.

A. Data Split

Examples of COVID-19, CAP (the hard sample) and non-pneumonia (the easy sample) from our dataset are presented in Fig. 3, respectively. According to patient IDs, the dataset is separated to training, validation, and test sets with the ratio of 75:5:20. The number of CT volumes contained in each set is listed in Table II.

Fig. 3.

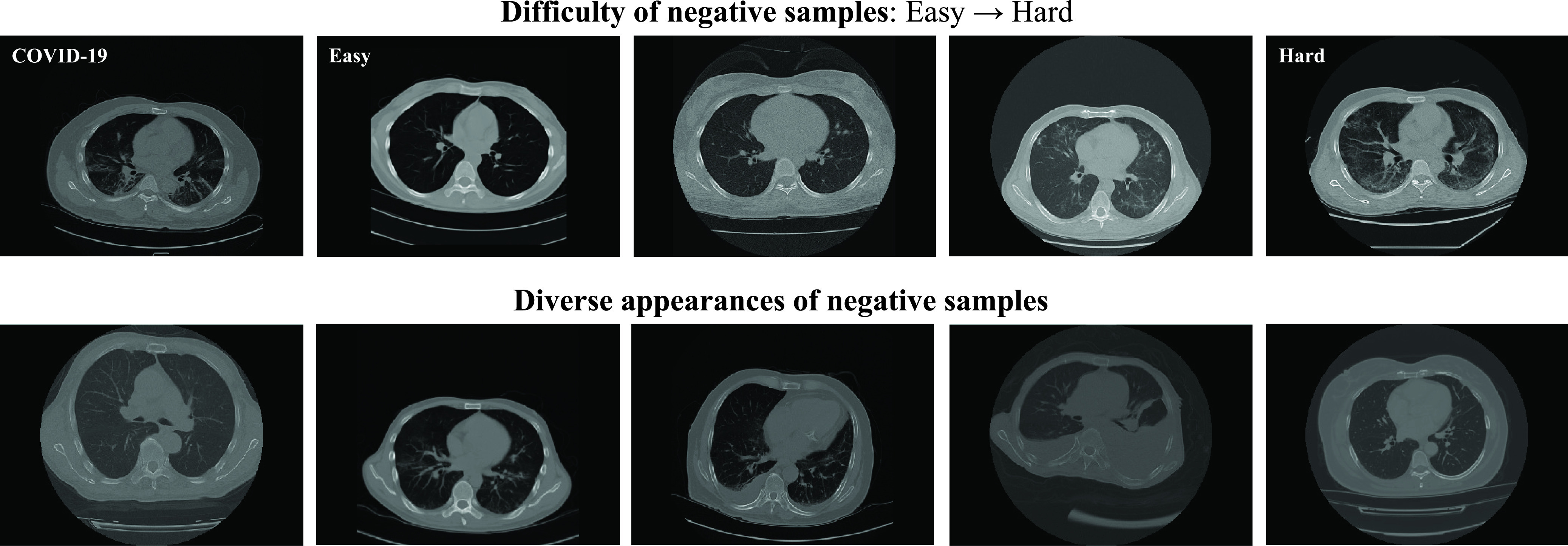
Exemplar samples of different levels of difficulty (the first row) and diversity (the second row) selected from the dataset. The COVID-19 sample is presented in the first row for comparison. The difficulty of the samples measured by our 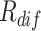gradually increases from the easy case to the hard case. The appearances of the hard samples are visually close to the COVID-19. The second row presents the negative samples with diverse appearances, which demonstrate the necessity of taking 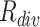into consideration.

TABLE II. Detailed Information of Data Split (The Number of CT Volumes).

	Training	Validation	Test
Positive	243	12	50
Negative	1,785	117	468

B. Evaluation Criterion

The F1 score, precision (PRE.), and recall (REC.) are adopted as the metric to evaluate the classification performance, which can be written as:

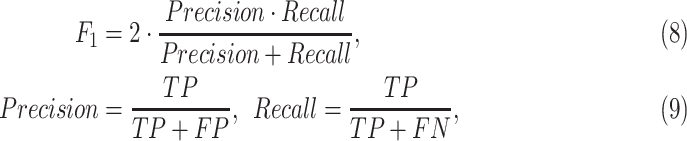where 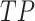, , 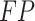and 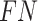represent the numbers of true positive, false positive, and false negative, respectively.

C. Difficulty and Diversity Samples Visualization

To visually compare the difficulty and diversity of different negative samples, we visualize samples of different levels of difficulty and diversity selected by our approach in Fig. 3. It can be observed that the hard cases (high difficulty) on the first row are visually close to the COVID-19 sample. Oppositely, the lung texture of the easy cases (low difficulty) is clear, which are easy for the classifier to identify. The samples with diverse appearances are presented in the second row of Fig. 3. To handle such a diverse dataset, 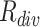is a useful criterion to tune the overall diversity of the set of selected samples.

D. Ablation Study

An ablation study is conducted to evaluate the contribution made by each ranking track of our approach. The evaluation result is presented in Table III. Compared to the random selection (i.e., the first row of Table III), the neural network trained with 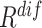or 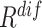-based selection approache achieves consistent improvements on F1 scores with different ratio of negative samples. The approach using the joint ranking () boosts the classification accuracy with the largest margin, which are 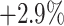, , 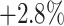and 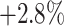higher than the random selection with 14%, 28%, and 56% negative samples, respectively.

TABLE III. Ablation Study of Our Two-Track Data Selection Approach. No Online Data Selection Approach is Adopted. (PRE.–Precision, REC.–Recall (%)) *The Training Period Using Offline Data Selection Approach Includes the Time Consumption of Self-Supervised Learning (0.3 Hour).

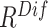
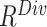
		Number of Negative Samples
			14% (246)			28% (500)			56% (1,000)			ALL (1,785)
			PRE.	REC.	F1	PRE.	REC.	F1	PRE.	REC.	F1	PRE.	REC.	F1
-	-	81.0	68.0	73.9	68.8	88.0	77.2	82.0	82.0	82.0	81.5	88.0	84.6
√	-	65.7	88.0	75.2	72.1	88.0	79.3	81.1	86.0	83.5	-	-	-
-	√	79.2	76.0	77.6	81.6	80.0	80.8	92.9	78.0	84.8	-	-	-
√	√	74.5	82.0	78.1	74.2	92.0	82.1	93.0	80.0	86.0	-	-	-
w/ Pre-training		60.3	88.0	71.5	65.2	90.0	75.6	74.6	88.0	80.7	-	-	-
Training period*		2.5 hour			4.6 hours			9.5 hours			19.6 hours

1). Quantity of Negative Samples

We investigate the trade-off between training period and classification accuracy by training the backbone network with different quantities of negative samples, which are 14%, 28%, and 56%. The corresponding training periods are also presented in Table III. Note that we use a Tesla V100 GPU in the experiments; therefore, the training period will be much longer under the same setting with some lower-speed GPUs such as Tesla P40.

As shown in Table III, fewer negative samples lead to the faster training iteration and network convergence, which shortens the period of training. However, the classification accuracy is observed to degrade in such a situation. Since our two-track data selection approach can comprehensively measure data ‘value,’ the neural network trained with the selected valuable negative samples achieves comparable classification accuracy to the one using the whole dataset (i.e., all 1,785 negative volumes). Furthermore, the neural network trained with 56% selected negative samples is observed to slightly outperform the one using all negative samples on precision and F1 score, which demonstrates that our approach can accurately measure the data ‘value’ for neural network and accordingly shorten the training period (i.e., a reduction of 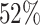of training time compared to the one using all samples).

2). Benefit for Shortening Development Period

We notice that the time reduction for training 3D ResNet-18 with 56% negative samples is about 10 hours compared to using all samples, which may not be significant compared to the other steps of computer aided diagnosis system development, such as backend (and possibly frontend) development. However, it is worthwhile to mention that the development of computer aided diagnosis system usually requires numerous experiments on testing different network architectures for the backbone selection, which are extremely time-consuming. In this regard, to demonstrate the generalization of the samples selected using the 3D ResNet-18, we adopt the selected samples to train a 3D ResNet-50 and evaluate its performances on the test set. The experimental results are presented in Table IV.

TABLE IV. COVID-19 Classification Accuracy of 3D ResNet-50 Trained With Different Quantities of Training Samples Selected by 3D ResNet-18. (PRE.–Precision, REC.–Recall (%); T. P.: Training Period).

	Number of Negative Samples
	14% (246)	28% (500)	56% (1,000)	ALL
PRE.	80.9	90.2	83.0	84.0
REC.	76.0	74.0	88.0	84.8
F1	78.4	81.3	85.4	84.8
T. P.	2.9 hours	5.4 hours	11.3 hours	23.5 hours

As shown in Table IV, the training period of 3D ResNet-50 (23.5 hours) is longer than 3D ResNet-18 (19.5 hours), due to the larger quantity of network parameters. It can be observed that the ResNet-50 trained with 56% negative selected samples achieves a consistently better F1 score (85.4%) than the one using all samples (84.8%), which demonstrates the generalization and effectiveness of the selected samples. To this end, as the number of testing network architectures increases during the process of backbone selection, the benefit of shortening development period provided by our offline data selection approach gradually becomes more significant.

3). Usage of Rubik's Cube Pro Pre-Trained Weights

Common self-supervised learning approaches use the pre-trained weights as the network initialization for the subsequent target task. To this end, we train a 3D ResNet-18 initialized with the Rubik's cube Pro pre-trained weights and present its result on test set for comparison. To save the time of self-supervised learning, only the COVID-19 volumes are involved for the Rubik's cube Pro pretext task, which may lead to biased predictions. The experimental results presented in Table III verify our intuition—the precision of COVID-19 classification networks using Rubik's cube Pro pre-trained weights is much lower than the random initialized ones.

E. Choice of Sampling Strategy

In Section IV E, we employed the long-tail distribution for negative sample selection from the pool after 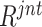ranking. Here, we further compare three sampling strategies (i.e., normal distribution, top-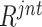, and long-tail distribution). The subsets of negative samples selected according to different distributions lead to varied improvements (deteriorations in some cases) in COVID-19 classification, as presented in Table V. Compared to the normal distribution sampling, the 1,000 negative samples selected by long-tail sampling contain more difficult and diverse cases, which benefit the accurate classification of COVID-19. However, when selecting smaller subsets (i.e., 246 and 500) of negative samples, the models trained with top- 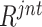selected samples yield extremely low classification performances. This may be because the neural network had difficulty in learning consistent information from only those samples which are most difficult and diverse. Different from that, the subsets sampled according to the long-tail distribution contain negative samples of varying ‘difficulty’ and ‘diversity,’ and outperform the others under most settings of negative sample quantity, validating the effectiveness of our choice of the sampling distribution.

TABLE V. Accuracy of COVID-19 Classification Network With Different Training Strategies. (PRE.–Precision, REC.–Recall (%)).

	Number of Negative Samples
	14% (246)			28% (500)			56% (1,000)
	PRE.	REC.	F1	PRE.	REC.	F1	PRE.	REC.	F1
Random	81.0	68.0	73.9	68.8	88.0	77.2	82.0	82.0	82.0
Normal distribution	77.6	76.0	76.8	70.8	92.0	80.0	85.7	84.0	84.8
Top-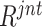	41.8	66.0	51.2	60.0	78.0	67.8	84.6	88.0	86.3
Long-tail distribution	74.5	82.0	78.1	74.2	92.0	82.1	93.0	80.0	86.0
Long-tail w/ Rubik's cube Pro*	75.9	88.0	81.5	78.9	90.0	84.1	97.7	84.0	90.3
* Rubik's cube Pro trained with all samples.

1). Pre-Training Rubik's Cube Pro With All Samples

To further exploit the benefit of self-supervised learning, we pre-train the backbone network on our Rubik's cube Pro pretext task with all training samples (1785 negative and 246 positive), and then finetune with the selected ones for the COVID-19 classification. The evaluation results are listed in the last row of Table V. It can be observed that the Rubik's cube Pro pre-trained weights consistently boost the accuracy of COVID-19 classification. However, it is worthwhile to mention that although pre-training on all samples can tackle the problem of biased predictions in the positive-sample-only Rubik's cube Pro, the time consumption of pre-training increases from 0.3 hour to more than three hours, due to the substantial increase in training samples.

In our practical application, the proposed offline data selection approach is adopted for extremely rapid response to the need for fast complete development cycle of computer aided diagnosis system, including tuning network architectures, data augmentation, and learning rate, etc, even within a day. After fulling the initial need and fixing the network architecture and hyper-parameters, the model can later adopts our Rubik's cube Pro pre-training pipeline for a better COVID-19 classification accuracy.

F. Combining Online Data Selection Strategies

Although the quantity of negative samples decreases from 1,785 to 1,000 using our offline data selection approach, the positive/negative ratio is still around 1:5. To further boost the accuracy of COVID-19 classification network, we combine the widely-used online data selection, such as OHEM [10] and focal loss [11], and over-sampling approaches to deal with the imbalanced positive/negative ratio. The accuracy of the hybrid methods is presented in Table VI, where the COVID-19 classification network trained with all samples is included for comparison.

TABLE VI. Comparison of Classification Performance Yielded by Networks Trained With Different Online Strategies Against Imbalanced Data. (Abbraviations: PRE.: Precision, REC.: Recall (%); Neg.: Negative, and Pos.: Positive; T. P.: Training Period).

COVID-19 classification network trained w/		No online strategy	Oversampling	OHEM [10]	Focal loss [11]
ALL Neg. (1785) + 246 Pos.	PRE.	81.5	86.3	91.3	86.0
	REC.	88.0	88.0	84.0	86.0
	F1	84.6	87.1	87.5	86.0
	T. P.	19.6 hours	34.3 hours	19.6 hours	19.6 hours
56% selected Neg. (1000) + 246 Pos.	PRE.	93.0	93.3	88.2	95.2
	REC.	80.0	84.0	90.0	80.0
	F1	86.0	88.4	89.1	87.0
	T. P.	9.5 hours	15.8 hours	9.5 hours	9.5 hours

It can be observed from Table VI that the online data selection approaches produce consistent improvements in the accuracy of the COVID-19 classification network. The OHEM yields the highest improvement in F1 score, i.e., around 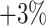compared to no online strategy. Although the oversampling approach achieves similar F1 score to OHEM, it enlarges the training set by oversampling the positive samples, which results in an expensive time cost for network training. Furthermore, it is worthwhile to mention that the COVID-19 classification network trained with our 1,000 selected negative samples yields higher accuracy to the one using all 1,758 negative samples, which demonstrate the effectiveness of our offline data selection approach.

VI. Discussions and Conclusion

In this work, we proposed an effective (in terms of better performance) and efficient (in terms of lower time cost) training strategy for COVID-19 classification networks using a relatively small number of COVID-19 CT exams and an archive of negative samples, empowered by self-supervised learning and informative data mining. Concretely, a novel self-supervised learning method (i.e., Rubik's cube Pro) was proposed to extract features from the COVID-19 and negative samples. Then, two kinds of soft-labels (i.e., ‘difficulty’ and ‘diversity’) were generated for the negative samples by computing the earth mover's distances between the features of the negative and COVID-19 samples. Using these soft-labels, data ‘values’ of the negative samples were comprehensively assessed. A pre-set number of negative samples were selected offline based on the joint ranking of difficulty and diversity, and fed to the neural network for training together with the COVID-19 samples. Experimental results show that, compared to the typical training scheme using all available negative samples, our approach achieved superior classification performance using only 56% of the negative samples for training the COVID-19 classification network, reducing model training time from 19.6 hours to 9.5 hours (a 52% reduction) for a rapid response to the disease outbreak.

A.

1). EMD-Driven Difficulty and Diversity Based Offline Sampling

We propose to select the most informative negative samples for COVID-19 classification according to the EMD-derived difficulty (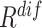) and diversity (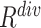). Table III showed a comparison of the performances using either or both of 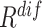and 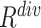, from which we noticed several interesting patterns. When using eithe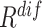r or 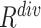separately, 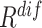consistently yielded superior recall to 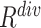, whereas 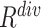consistently yielded superior precision to 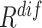. As expected, simultaneously using both of them produced more balanced results rendering the best F1 scores. We believe this property of our proposed offline sampling strategy can be utilized for desired adjustments to precision, recall, or F1 scores of the model.

2). Combining Online Sampling for Optimal Performance

After mining of the most informative negative samples offline, we further combined our proposed offline sampling strategy with several widely used online sampling strategies for imbalanced data for optimal performance. As shown in Table VI, the online sampling strategies all achieved varying improvements, but at vastly different time cost. Notably, OHEM achieved the best F1 scores while at the same time incurred the lowest time cost, which was optimal in terms of both effectiveness and efficiency. Therefore, our final joint sampling strategy incorporated OHEM.

3). Comparison of Different Pre-Training Weights

To demonstrate the effectiveness of our Rubik's cube Pro, we compare its performance with the conventional Rubik's cube [12]. To alleviate the influence caused by different selections of training samples, we pre-train and finetune the 3D ResNet-18 with the whole training set. The evaluation results are presented in Table VII. The self-supervised learning approaches yield consistent improvements to the COVID-19 classification accuracy, compared to the train-from-scratch. As the masking operation encourages the neural network to learn more robust feature representation, the Rubik's cube Pro is observed to outperform the conventional Rubik's cube with an improvement of 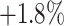for F1 score.

TABLE VII. Accuracy (%) of COVID-19 Classification Network With Different Self-Supervised Weights.

	Precision	Recall	F1
Train-from-scratch	81.5	88.0	84.6
Rubik's cube [12]	86.0	86.0	86.0
Rubik's cube Pro	89.6	86.0	87.8

4). Future Work

Our main contributions in this work focus on enabling rapid development of computer aided diagnosis systems for COVID-19 screening, given limited COVID-19 samples at the early stage of the outbreak, while maintaining a high classification performance. Therefore, we adopted a relatively small network (the ResNet-18) as our backbone. As the pandemic evolves, the focus shifts from development speed to classification accuracy. Accordingly, we will experiment with more complex backbones in the future with more COVID-19 data collected. Besides, there is a margin of improvement for the diversity criterion. To further ensure the diversity of selected samples, one of the options is to sequentially select samples, forcing the next sample to be different from the eralier selected ones. However, the sequential selection may cause an expensive computation as the number of selection increases. It is worthwhile to explore an advanced criterion balancing the diversity of selected samples and the computational cost in the future. Last but not least, the proposed offline data selection approach is currently only evaluated on the binary classification task (COVID-19 vs. negative). We will make our effort to extend the method to the multi-class classification problem in the future.

Funding Statement

This work was supported in part by the Key Area Research and Development Program of Guangdong Province, China under Grant 2018B010111001, in part by National Key Research and Development Project under Grant 2018YFC2000702, in part by the Natural Science Foundation of China under Grant 61702339, in part by the Science and Technology Program of Shenzhen, China under Grant ZDSYS201802021814180, and in part by Emergency Science and Technology Project on COVID-19 Pneumonia supported by the Department of Science and Technology of Hubei Province Project under Grant 2020FCA016.