Abstract
Early and accurate diagnosis of Coronavirus disease (COVID-19) is essential for patient isolation and contact tracing so that the spread of infection can be limited. Computed tomography (CT) can provide important information in COVID-19, especially for patients with moderate to severe disease as well as those with worsening cardiopulmonary status. As an automatic tool, deep learning methods can be utilized to perform semantic segmentation of affected lung regions, which is important to establish disease severity and prognosis prediction. Both the extent and type of pulmonary opacities help assess disease severity. However, manually pixel-level multi-class labelling is time-consuming, subjective, and non-quantitative. In this article, we proposed a hybrid weak label-based deep learning method that utilize both the manually annotated pulmonary opacities from COVID-19 pneumonia and the patient-level disease-type information available from the clinical report. A UNet was firstly trained with semantic labels to segment the total infected region. It was used to initialize another UNet, which was trained to segment the consolidations with patient-level information using the Expectation-Maximization (EM) algorithm. To demonstrate the performance of the proposed method, multi-institutional CT datasets from Iran, Italy, South Korea, and the United States were utilized. Results show that our proposed method can predict the infected regions as well as the consolidation regions with good correlation to human annotation.
Keywords: Computed tomography, COVID-19, segmentation, lung, deep learning, severity, consolidation, weak label
I. Introduction
Since November 2019, coronavirus disease 2019 (COVID-19) has in total 7.1 million confirmed cases and caused 363,000 deaths worldwide as of June 6th, 2020 [1]. Symptoms of COVID-19 include fever, cough, fatigue, with 17% to 29% of the patients showing acute respiratory distress syndromes (ARDS) [2]. Due to its high contagiousness (reproductive number = 3.28 [3]), early diagnosis of COVID-19 is critical so that mitigating steps such as patient isolation and contract tracing can be enforced to limit spread, and supportive treatment can be initiated. Reverse-transcription polymerase chain reaction (RT-PCR) assay is the gold standard for COVID-19 diagnosis. In early phase of infection (4-10 days), RT-PCR assays have low sensitivity (60-70%), which increases substantially over time [4]–[6]. Although initial studies suggested a sensitivity as high as 98% for computed tomography (CT) [5], later studies reported that about 18% of non-severe COVID-19 pneumonia have no imaging findings [7]. Per the prestigious Fleischner Society recommendations, chest CT is not indicted for mild COVID-19 infection but provides useful information in patients with moderate to severe disease as well as in those with worsening pulmonary functions [8]. Compared to RT-PCR, CT provides more information on the confirmed patients, e.g., the severity of their lung infection, the progression of the disease, and any complications such as the myocardial injury [9]. Relevant information is crucial for patient management and making treatment planning. Early CT imaging characteristics of COVID-19 are usually bilateral peripheral focal or multifocal ground-glass opacities (GGO). Crazy-paving patterns (GGO with superimposed inter- and intralobular septal thickening) and consolidation become the dominant CT findings in advanced or more severe disease forms [6], [10]–[12].
Prior studies have reported subjective grading of CT images by radiologists to calculate the severity score of COVID-19 pneumonia based on the type of pulmonary opacities (such as GGO, crazing paving pattern, or consolidation) and the extent of involvement of each lung lobe (based on visual perception of percentage of lung lobe involved) to assess disease severity and disease progression. However, such scoring system is inefficient, not part of standard diagnostic interpretation, and prone to inter- and intra-observer variations. For example, up to 25% lobar involvement is given a score of 2 and 26% lobar involvement gets a score of 3 for extent of opacities – such arbitrary classification is extremely challenging and inconsistent with visual or qualitative interpretation. Thus, developing an automated tool to quantify the severity of COVID-19 based on CT images is an urgent and unmet need to enhance diagnostic information and augment its prognostic value. [13].
With the initial success on computer vision tasks [14], deep learning methods have been widely applied to various medical imaging areas, e.g., denoising, reconstruction, detection, and segmentation. As for COVID-19 diagnosis, several groups have performed pioneering studies showing that deep learning can accurately detect COVID-19 and differentiate it from other lung disease [15]–[22]. Apart from COVID-19 diagnosis, semantic segmentation of the infected lung regions is crucial as it is a tool for further quantitative disease monitoring [23]. Deep learning methods have also been applied to COVID-19 CT image segmentation. Specifically, Huang et al. [23] have developed a segmentation network to perform serial quantitative CT assessment of Covid-19. Shan et al. [24] have devised a human-in-the-loop strategy during network training to reduce the manual labelling efforts. Chaganti et al. [25] has designed a deep learning pipeline to perform semantic segmentation and various severity measures together. Based on the semantic segmentation developed, assessment of features extracted from the infection regions can be used for further disease prediction [26], [27].
Most of the existing method focuses on segmenting the total infected areas without discriminating between GGO and consolidation. Chaganti et al. [25] used a threshold of -200 HU to separate consolidation from the predicted infected regions. Fan et al. [28] proposed a semi-supervised learning method to combine limited semantic annotations of consolidation with CT images not labeled for consolidation. In [28], a network was initially trained on a small set of images with consolidation annotations. The network was progressively tested on unlabeled CT images which was then included in the training dataset. Here we explored a different training strategy compared to [28], where only image-level labels for consolidation were used. Several noticeable methods have been proposed for weakly labeled segmentation, including multi-instance learning [29], localization maps [30], and expectation maximization (EM) [31], [32]. We employed the EM framework in this work because of its ability to easily incorporate prior functions on the target area.
In this work, we proposed a deep learning approach to learn the infection and consolidation information from CT images based on hybrid weak labels: patient-level multi-class information and manually labelled infection contours. A UNet was first trained with supervised learning to predict the infected regions based on strong semantic labels. Then it was fine-tuned to predict the consolidation regions based on patient-level labels only using EM algorithm. Since consolidation usually has higher Hounsfield unit (HU), a prior function was proposed to model the probability of a pixel being consolidation. The model was trained on CT images from Iran and validated on images from various datasets from Iran, Italy, South Korea, the United States and MedSeg.
Compared to existing studies, the main contributions of this work are as follows: (1) The EM algorithm was applied for weakly supervised learning of the segmentation of consolidation in COVID-19 CT datasets. Compared to the progressive learning framework [28], the proposed method does not need any starting semantic labels for the consolidation; (2) A novel prior function was proposed to model the consolidation in lung, which combined the data-driven network training with the expert-knowledge modeling; (3) More detailed derivation of the EM learning algorithm were derived compared to [31], which will be given in the appendix.
This paper is organized as follows. Section II introduces the proposed framework and implementation details. Experiment set-up and dataset details are presented in section III. Experimental results are shown in section IV, followed by discussions in section V. Finally, conclusions are drawn in Section VI.
II. Methodology
A. Overview
The proposed deep learning method1 consisted of the following two steps:
Step 1: training a semantic segmentation network for infected lung regions based on strong label.
Step 2: training a semantic segmentation network for consolidation based on patient-level weak label.
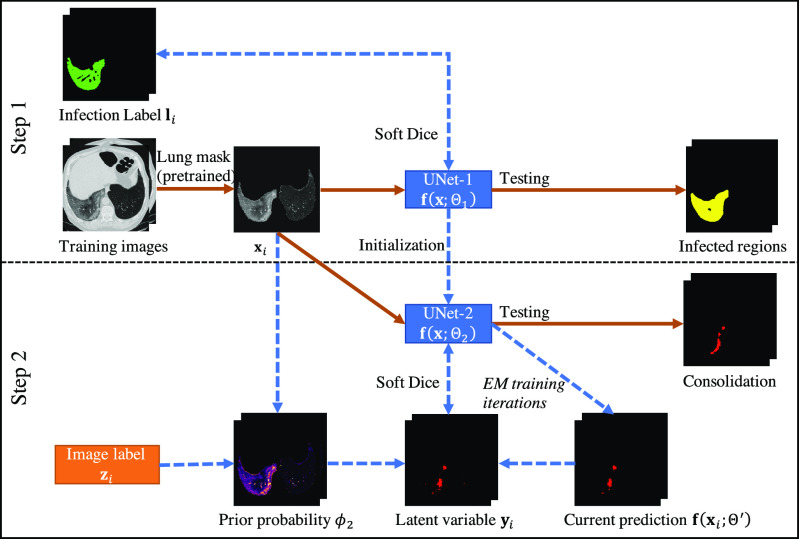
In step 1, a 2D UNet [33] was employed to segment the infection regions from the CT images (UNet-1). The training labels were CT images with pixel-level annotation of being infected or not. In step 2, UNet-1 was further finetuned to segment consolidation from the infected regions (UNet-2). A subset of the training images was annotated regarding the existence of consolidation for each patient. The consolidation network was trained in the framework of EM [31] to learn the segmentation of consolidation from patient-level annotations. A flowchart of the entire training process is given in Fig. 1.
Fig. 1.
Flowchart of the proposed hybrid label learning. Step 1 trains the infected region segmentation network UNet-1 using fully supervised learning. UNet-1 also provides initialization for the consolidation segmentation network UNet-2. Step 2 trains UNet-2 combining the image-level label 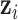 and prior probability
and prior probability 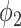 built from images
built from images 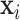 . The solid brown lines are the procedures that are involved in both training and testing, whereas the dashed blue lines are training procedures only.
. The solid brown lines are the procedures that are involved in both training and testing, whereas the dashed blue lines are training procedures only.
UNet-1 and UNet-2 had identical structures with 1-channel output activated by Sigmoid function. Both took 7 adjacent CT slices as input and output a two-class segmentation of the central slice. They used the standard UNet structure [33] and detailed parameters will be introduced in section III-B. To make the network concentrate on features inside the lung only, the lung masks were generated by a pretrained lung segmentation network [34] and applied to the CT images before being fed into the UNets.
B. Segmentation of the Infected Region With Strong Labels
We used 2D UNet with smooth Dice loss2 to learn the segmentation of infected regions. Denote the semantic label of the training image 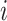 as
as 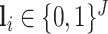 , where
, where 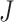 is the number of pixels in the labels. For pixel
is the number of pixels in the labels. For pixel 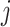 , we have:
, we have:
 |
Denote UNet-1 as 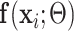 where
where 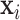 is the
is the 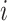 th training image and
th training image and 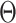 is the network parameters to be learned. The Dice loss was employed for the training as:
is the network parameters to be learned. The Dice loss was employed for the training as:
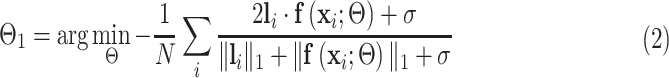 |
where 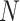 is the number of training images and
is the number of training images and 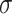 is the smoothing parameter which was set to 1 based on experience. After
is the smoothing parameter which was set to 1 based on experience. After  was learned, a binary segmentation of the infected regions was given for each image
was learned, a binary segmentation of the infected regions was given for each image 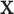 where pixel j was infected if
where pixel j was infected if 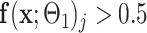 .
.
C. EM Framework for Weak Label Segmentation
We employed the EM framework [31] to solve the weakly labeled segmentation problem. Denote UNet-2 as 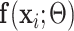 , which outputs the probability of each pixel belonging to consolidation. Denoting the image-level annotation as
, which outputs the probability of each pixel belonging to consolidation. Denoting the image-level annotation as 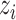 for image
for image 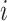 , where:
, where:
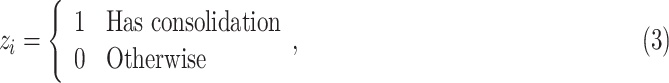 |
The object function was to minimize the following log-likelihood function:
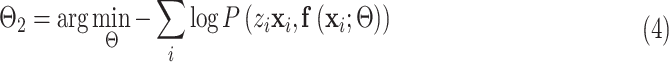 |
where 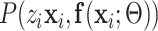 is the probability that image
is the probability that image 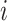 belongs to class
belongs to class 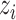 given the image
given the image 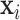 network output
network output 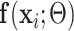 . The exact formula of the probability function is not required.
. The exact formula of the probability function is not required.
The EM algorithm introduced a latent discrete variable 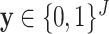 , which has meaning of pixelwise segmentation. Specifically, for pixel
, which has meaning of pixelwise segmentation. Specifically, for pixel 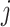 :
:
 |
For easier computation, the prior distribution of the image label 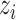 given image
given image 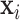 and the latent variable
and the latent variable 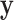 is considered to be pixelwise separable:
is considered to be pixelwise separable:
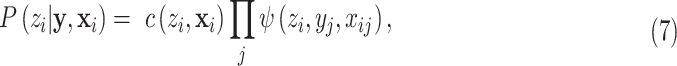 |
where 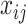 is the
is the 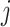 th pixel in image
th pixel in image  ;
; 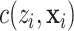 is a normalization factor so that
is a normalization factor so that 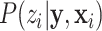 is a probability function, i.e.,
is a probability function, i.e.,
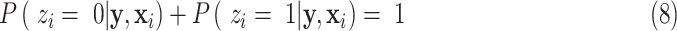 |
The basis function 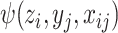 is defined as:
is defined as:
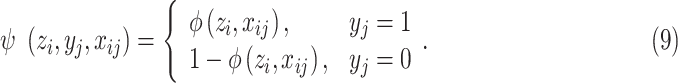 |
For the conciseness of the paper, we will directly give the final equations for the EM algorithm here. Detailed derivation can be found in the appendix as well as in [31]. The EM algorithm iteratively alternates between the following Expectation (E) and Maximization (M) steps:
E-Step: given network parameter 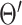 from the previous iteration, the latent variable
from the previous iteration, the latent variable 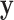 is solved pixelwise under the hard-EM approximation (using max instead of mean):
is solved pixelwise under the hard-EM approximation (using max instead of mean):
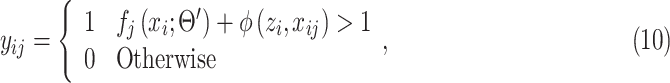 |
where 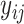 is the
is the 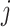 th pixel of
th pixel of 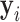 , which is the optimized latent variable for sample
, which is the optimized latent variable for sample 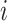 .
. 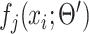 is the output of the current network at the
is the output of the current network at the 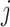 th pixel.
th pixel.
M-step: The network parameter 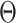 is optimized using the smooth Dice loss (2) by replacing the labels
is optimized using the smooth Dice loss (2) by replacing the labels 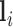 with
with  :
:
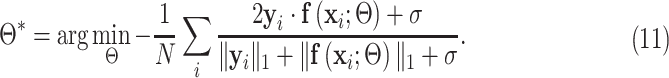 |
D. Prior Modeling for Consolidation
The key to the success of EM algorithm is the choice of prior probability model 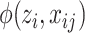 in (9). One choice of
in (9). One choice of 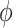 is to use a constant bias [31] for all the pixels according to the image-level label
is to use a constant bias [31] for all the pixels according to the image-level label 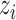 :
:
 |
where 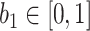 is the posterior probability of all pixels in image
is the posterior probability of all pixels in image 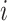 being consolidation if consolidation presents.
being consolidation if consolidation presents.
However, (12) does not model any prior knowledge of consolidation into the model and the performance may be limited. It is known that consolidation usually has higher HU compared to GGO. Hence, we proposed the HU-based probability model as:
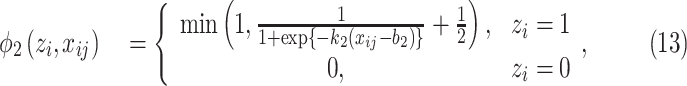 |
where 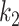 and
and 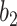 are hyperparameters to control the probability model. The probability of pixel
are hyperparameters to control the probability model. The probability of pixel 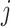 being consolidation increases with its HU value. When
being consolidation increases with its HU value. When 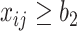 ,
, 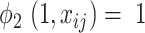 , which means that the pixel must be consolidation.
, which means that the pixel must be consolidation. 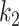 controls how steep the function increases. Larger
controls how steep the function increases. Larger 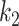 will make the function closer to a step function. There is also an offset of 0.5 to the Sigmoid function, which means that for images with label 1, all the pixels were considered to have at least half chance of being consolidation. Another reason to add this 0.5 bias was that according to [31], the posterior probability function should bias towards foreground (consolidation), otherwise it may suffer from underestimation.
will make the function closer to a step function. There is also an offset of 0.5 to the Sigmoid function, which means that for images with label 1, all the pixels were considered to have at least half chance of being consolidation. Another reason to add this 0.5 bias was that according to [31], the posterior probability function should bias towards foreground (consolidation), otherwise it may suffer from underestimation.
The overall training algorithm is given in Table I. We constrained the consolidation region within the infected region  predicted by UNet-1. The algorithm can be easily implemented based on the supervised learning framework. The only difference compared to a supervised training framework is the estimation of training label
predicted by UNet-1. The algorithm can be easily implemented based on the supervised learning framework. The only difference compared to a supervised training framework is the estimation of training label 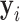 at each iteration. The estimation was done in the E-step (steps 3-7). The training images first went through the network to generate predictions
at each iteration. The estimation was done in the E-step (steps 3-7). The training images first went through the network to generate predictions  ; then it was combined with the posterior probability
; then it was combined with the posterior probability 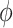 to generate the training label
to generate the training label 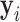 for the M-step. The M-step can be implemented using standard network training algorithms such as the Adam optimizer [35].
for the M-step. The M-step can be implemented using standard network training algorithms such as the Adam optimizer [35].
TABLE I. EM Training Algorithm.
| Algorithm 1. EM Training of UNet-2. |
INPUT
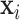 , , 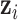 , infected region , infected region 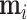 predicted from UNet-1. predicted from UNet-1. |
INITIALIZATION
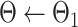 from UNet-1. from UNet-1. |
| 1 WHILE not stopped: |
| 2 Get a minibatch; |
| E-step: |
3 FOR 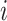 in the minibatch: in the minibatch: |
4 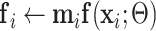 , consolidation prediction; , consolidation prediction; |
| 5 FOR each pixel j: |
6 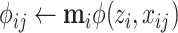 , posterior probability; , posterior probability; |
7 IF 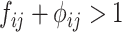 THEN THEN 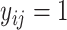 ELSE ELSE 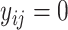 ; ; |
| M-step: |
8 Compute 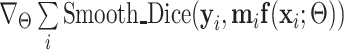 and update and update 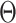 . . |
RETURN
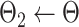 . . |
E. Severity and Consolidation Quantification
The severity and consolidation quantifications are given as:
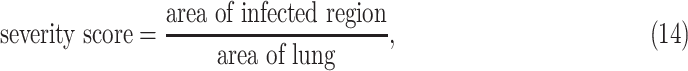 |
and
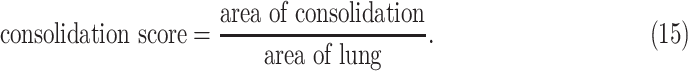 |
III. Experimental Setups
A. Dataset
This study was approved by the respective Institutional Review Boards (IRBs) at Massachusetts General Brigham under protocol number 2020P000819 and 2016P000767. Informed consent forms were waived due to the retrospective nature of this study. The dataset consists of 225 unenhanced CT examinations of RT-PCR assay positive COVID-19 patients performed between January 1, 2020 and March 30, 2020, from various hospitals in Iran, Italy, South Korea, and the United States. The chest CT examinations were acquired on 6-256 slice multidetector-row scanners from three CT vendors (GE Healthcare, Waukesha, Wisconsin, US; Philips Healthcare, Eindhoven, The Netherlands; Siemens Healthineers, Forchheim, Germany). To validate the segmentation of consolidation regions, we also incorporated a public dataset from MedSeg,3 where 9 CT images from Radiopeadia were annotated for regions of GGO and consolidation. A summary of the datasets is given in Table II. All the images were resampled to 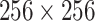 resolution in the axial plane. If an image has a slice thickness thinner than 4 mm, it was resampled to 5 mm.
resolution in the axial plane. If an image has a slice thickness thinner than 4 mm, it was resampled to 5 mm.
TABLE II. Dataset Information.
| Hospital | # CT images | # Semantic labels |
|---|---|---|
| Firoozgar Hospital, Tehran, Iran (Training) | 87 | 87 |
| Shahid Beheshti Hospital, Kashan, Iran (Testing) | 8 | 8 |
| Massachusetts General Brigham, Boston, United States (Testing) | 18 | 18 |
| Yeungnam University Hospital, Gyeongsan, South Korea (Testing) | 97 | 22 |
| Azienda Ospedaliera Universitaria Maggiore della Carità, Novara, Italy (Testing) | 15 | 14 |
| MedSeg, Radiopaedia (Consolidation Testing) | 9 | 9 |
Among the 225 CT images from our dataset, 149 were annotated for infected regions by two post-doctoral research fellows (with 1-2 years of experience in chest CT research), under the supervision of a subspecialty chest radiologist (13 years of clinical experience in thoracic imaging). The MedSeg dataset consists of 9 CT images from Radiopaedia with 829 slices in total. A radiologist segmented GGO and consolidation for each slice.
There were 22 out of 97 patients with semantic infection labels for the South Korean dataset. These 22 patients were randomly chosen before the development of the network. Annotating only part of the 97 patients saved valuable manual efforts due to the extensive works needed for the semantic annotation. The current testing dataset provided more than 7000 2D slices in total which is comparable to some of the existing studies [28]. A valid verification of UNet-1 was also reached with small p-value for the Pearson correlation between predicted and annotated infection areas. It also led to a more balanced testing dataset across different sites, so that the evaluation of UNet-1 will not be dominated by one single site.
The infection segmentation network (UNet-1) was trained on the images from Firoozgar Hospital (80 training and 7 validation) and tested on the 62 images with annotated infection areas from the other hospitals in our dataset.
To train the consolidation segmentation network (UNet-2), 19 patients from Firoozgar Hospital were confirmed by radiologists if the patient has only GGO or has both GGO and consolidation (15 had only GGO and 4 had both GGO and consolidation). UNet-2 was further validated on the MedSeg dataset to evaluate the accuracy of consolidation segmentation compared to the radiologist's annotation. It was also validated on the 138 testing CT images, where the prediction from UNet-2 was compared to the radiology reports. The patients were grouped to consolidation and non-consolidation groups using keywords including “consolidation” and “consolidated”. The consolidation scores (15) were calculated for each patient and statistical testing was done between the two groups.
B. Parameters
Both UNet-1 and UNet-2 have 5 down-sampling blocks and 4 up-sampling blocks. Each block consists of two convolution layers with batch normalization and leaky ReLU activation. The number of channels after the first convolutional layer is 32. The number of channels was doubled after each down-sampling block and halved before each up-sampling block. Stride-two and transposed convolutions were employed for down-sampling and up-sampling, respectively. Concatenation between encoder and decoder paths were replaced by adding operation to reduce training parameters. The output layer is a 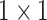 convolution layer with 1-channel output and Sigmoid activation.
convolution layer with 1-channel output and Sigmoid activation.
Both networks take 7 consecutive axial slices as the input and output the segmentation map of the central slice. The value in the images was normalized to 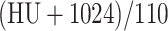 before being fed into the network. Various random transforms including rotation, translation, zooming, and flipping were incorporated during the training.
before being fed into the network. Various random transforms including rotation, translation, zooming, and flipping were incorporated during the training.
UNet-1 was trained on batches of 16 by the Adam algorithm for 200 epochs in total. The learning rate is 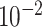 ,
, 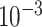 and
and 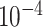 for epoch 1-50, 50-100, and 100-200.
for epoch 1-50, 50-100, and 100-200.
UNet-2 was initialized from UNet-1 and trained with batch size of 16. Adam algorithm was used in the M-step. 50 epochs were trained with learning rate of 0.0005. We implemented both 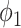 and
and 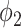 as in (12) and (13) as the prior function and tried various hyperparameters
as in (12) and (13) as the prior function and tried various hyperparameters 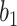 ,
, 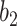 and
and 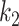 . For
. For 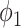 ,
, 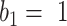 achieved the best Dice coefficient on the MedSeg dataset, which is equivalent to setting all the pixels in images with consolidation to consolidation. For
achieved the best Dice coefficient on the MedSeg dataset, which is equivalent to setting all the pixels in images with consolidation to consolidation. For 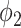 ,
, 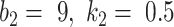 achieved the best Dice.
achieved the best Dice. 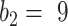 is equivalent to -34 HU before the gray value normalization.
is equivalent to -34 HU before the gray value normalization.
We also implemented thresholding as the baseline method [25], where pixels larger than -200 HU inside the predicted infected region were considered as consolidation.
C. Metrics
Performance of UNet-1 was evaluated on the 62 testing images by both the Dice coefficient and severity score defined in (14) compared to the radiologists’ annotation.
For UNet-2, the segmentation performance was evaluated on the 9 CT images from MedSeg dataset with the Dice coefficients. The pixelwise true positive and false positive rate were also calculated inside the predicted infected regions. It was also evaluated on the 138 testing CT images to distinguish consolidation and non-consolidation groups using the consolidation score defined in (15).
IV. Results
A. Severity Segmentation
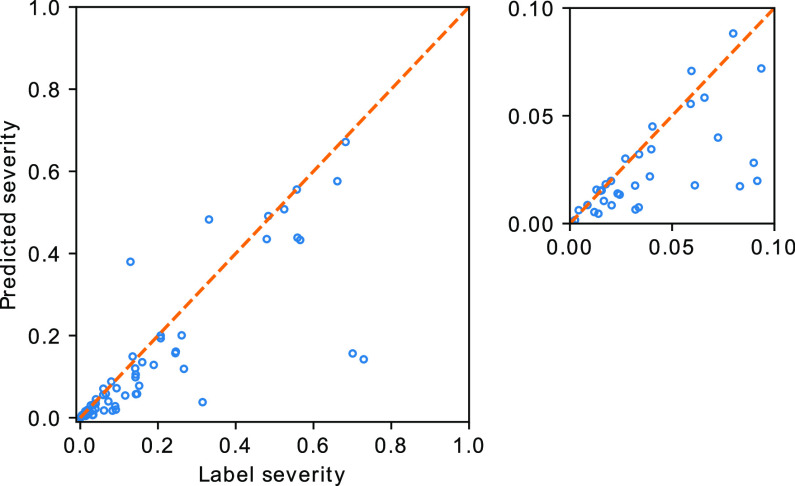
The severity quantification results are given in Fig. 2. A Pearson correlation coefficient of 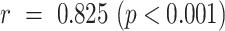 was achieved between the predicted and the labelled severity score. A mean Dice coefficient of 0.632 was achieved with the segmentation network, which was comparable to the value reported in [28]. A reasonable performance of UNet-1 is necessary since it provided the essential basis for the following weakly supervised learning of the consolidation segmentation.
was achieved between the predicted and the labelled severity score. A mean Dice coefficient of 0.632 was achieved with the segmentation network, which was comparable to the value reported in [28]. A reasonable performance of UNet-1 is necessary since it provided the essential basis for the following weakly supervised learning of the consolidation segmentation.
Fig. 2.
Severity based on manual segmentation (label severity) versus the predicted severity. The orange line plotted the ideal prediction curve where the predicted severity score equals to the labelled severity score. Label severity between [0, 0.1] is shown in the zoom-in plot.
B. Consolidation Segmentation
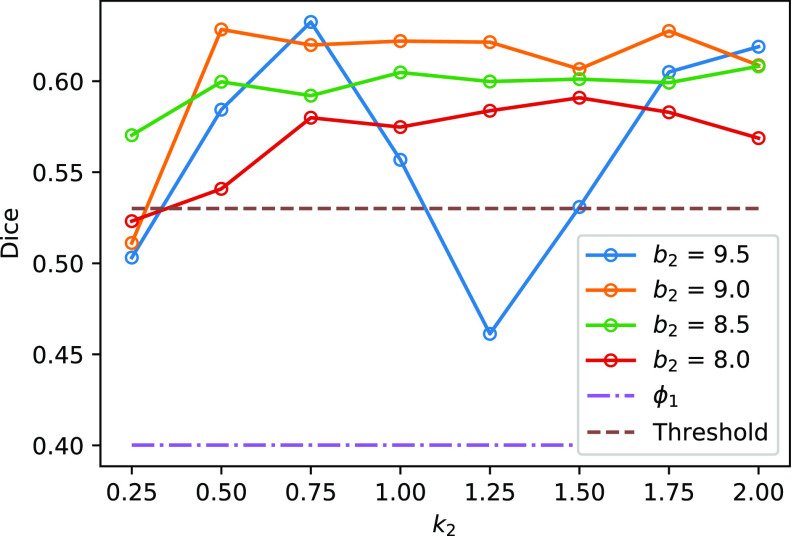
Fig. 3 shows the Dice coefficient of UNet-2 with 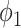 and
and 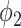 and the thresholding method on the MedSeg testing images. Thresholding by -200 HU could achieve a mean Dice coefficient of 0.530 of the consolidation regions. UNet-2 with
and the thresholding method on the MedSeg testing images. Thresholding by -200 HU could achieve a mean Dice coefficient of 0.530 of the consolidation regions. UNet-2 with 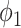 alone achieved a poor Dice coefficient of 0.400, which indicates that
alone achieved a poor Dice coefficient of 0.400, which indicates that 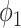 cannot efficiently extract features of consolidation from the weak labels. The proposed prior function
cannot efficiently extract features of consolidation from the weak labels. The proposed prior function 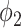 increased the Dice coefficient to 0.628 with
increased the Dice coefficient to 0.628 with 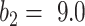 and
and 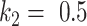 . The Dice coefficient generally increases with larger
. The Dice coefficient generally increases with larger 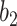 and keeps stable regarding
and keeps stable regarding 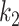 . However, the performance with
. However, the performance with 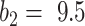 becomes not very stable.
becomes not very stable.
Fig. 3.
The Dice coefficient on the MedSeg dataset with different 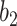 and
and 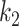 . The solid lines with hollow points show the results with prior function
. The solid lines with hollow points show the results with prior function 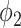 . The purple dash-dotted line is the result from
. The purple dash-dotted line is the result from 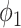 with
with 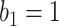 . The brown dashed line is the result from the thresholding with -200 HU. The
. The brown dashed line is the result from the thresholding with -200 HU. The 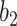 values 9.5, 9.0, 8.5, 8.0 correspond to 21, -34, -89, and -144 HUs respectively.
values 9.5, 9.0, 8.5, 8.0 correspond to 21, -34, -89, and -144 HUs respectively.
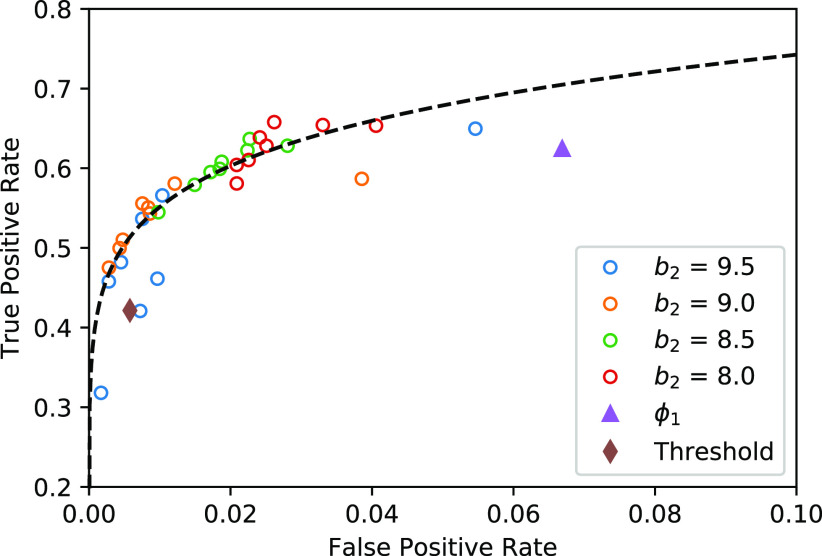
The trade-off between the true positive rate (TPR) and false positive rate (FPR) with different parameters are given in Fig. 4. The thresholding method will underestimate the consolidation regions, with a good specificity but relatively low sensitivity (TPR = 0.421, FPR = 0.006). EM algorithm with 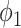 will overestimate the consolidation, with a higher sensitivity but low specificity (TPR = 0.624, FPR = 0.067). EM algorithm with
will overestimate the consolidation, with a higher sensitivity but low specificity (TPR = 0.624, FPR = 0.067). EM algorithm with 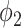 at
at 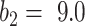 and
and 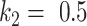 had TPR = 0.555 and FPR = 0.008. A receiver operator curve (ROC) was fitted by exponential function for all the data points from
had TPR = 0.555 and FPR = 0.008. A receiver operator curve (ROC) was fitted by exponential function for all the data points from 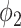 and is plotted as the black dashed line in Fig. 3. It can be observed that EM algorithm with the proposed
and is plotted as the black dashed line in Fig. 3. It can be observed that EM algorithm with the proposed 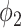 has better TPR-FPR trade-off compared to both thresholding and
has better TPR-FPR trade-off compared to both thresholding and 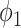 . Increasing
. Increasing 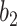 will reduce the FPR but also reduce the TPR. This is because that larger
will reduce the FPR but also reduce the TPR. This is because that larger 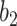 raises the threshold of consolidation in
raises the threshold of consolidation in 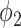 and the latent labels
and the latent labels 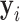 will bias towards GGO.
will bias towards GGO.
Fig. 4.
The TPR and FPR trade-offs on the MedSeg dataset. Black dashed line is a ROC fitted from results of UNet-2 with 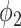 using different
using different 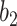 and
and 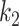 . Exponential function
. Exponential function 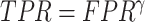 was used for the ROC fitting.
was used for the ROC fitting.
Fig. 5 shows two slices of testing images from the MedSeg dataset with the GGO and consolidation segmentation overlay. The MedSeg dataset had very detailed annotation where the vessels were excluded from the GGO. However, in the training dataset our annotation did not particularly excluded the vessels. Hence, the predicted infected regions (green lines) did not exclude the vessels as the annotation.
Fig. 5.
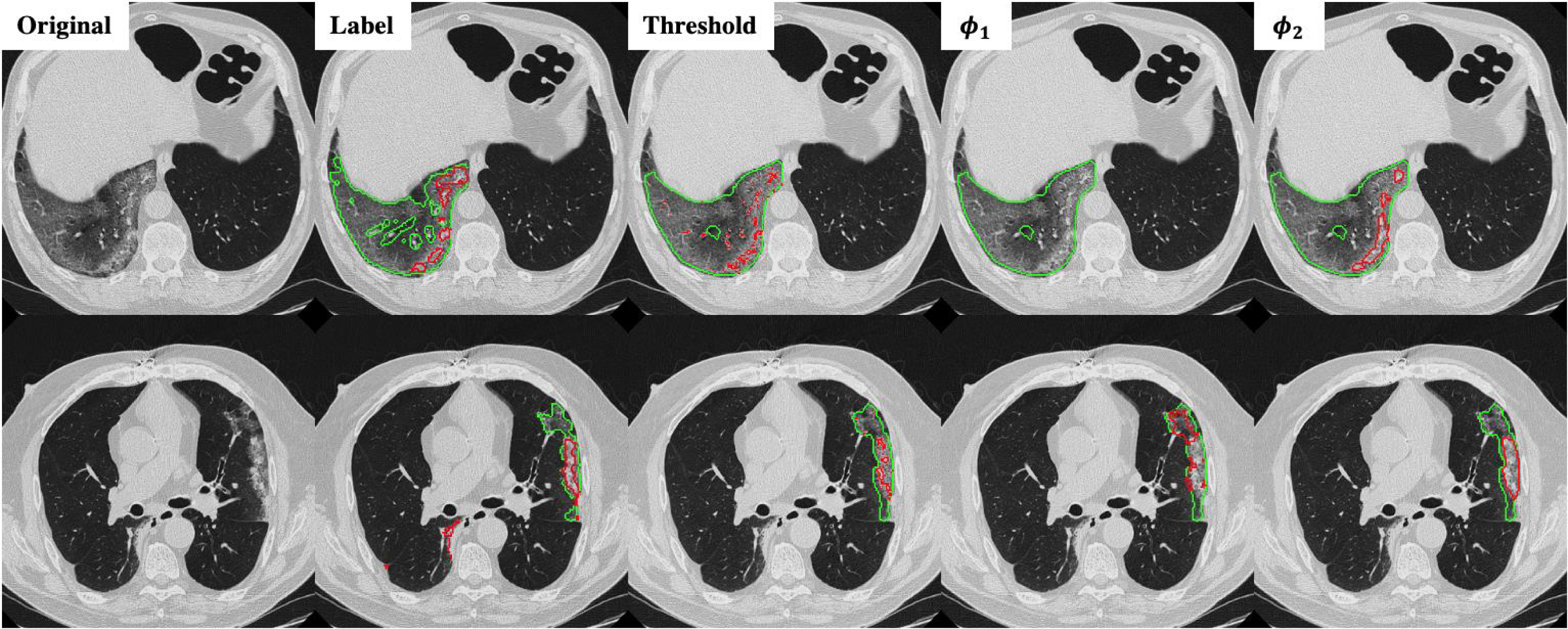
Infection and consolidation segmentation results on the MegSeg dataset for two different slices. Green lines show the boundary of GGO and read lines show the boundary of consolidation.
It can be observed from Fig. 5 that thresholding significantly underestimated the consolidations compared to the annotations. The predicted consolidation regions are also very scattered. Meanwhile, 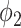 can generate continuous regions of consolidation that looks similar to the radiologists’ annotation, whereas
can generate continuous regions of consolidation that looks similar to the radiologists’ annotation, whereas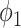 generally failed to stably predict the consolidation regions.
generally failed to stably predict the consolidation regions.
Fig. 5 also demonstrates that thresholding and 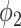 have different source of false positive (FP). The FP of thresholding mostly comes from the vessels which have higher HU compared to lung tissue. The FP of
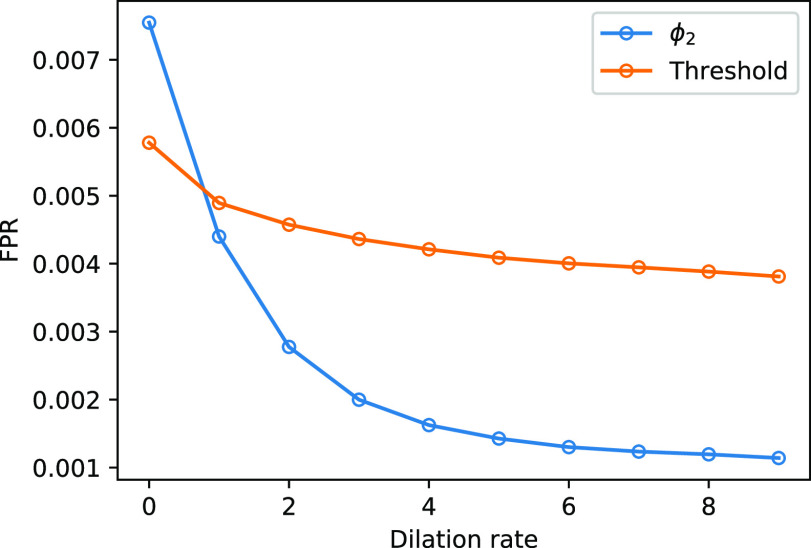
have different source of false positive (FP). The FP of thresholding mostly comes from the vessels which have higher HU compared to lung tissue. The FP of 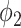 mostly comes from errors on the consolidation boundaries. To further verify this, we dilated the annotations with different dilation rates (0 to 9 pixels) and calculated the FPR at each dilation rate. The results are shown in Fig. 6. The FPR of both thresholding and
mostly comes from errors on the consolidation boundaries. To further verify this, we dilated the annotations with different dilation rates (0 to 9 pixels) and calculated the FPR at each dilation rate. The results are shown in Fig. 6. The FPR of both thresholding and 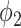 decreased with the increasing dilation rate. However, FPR of
decreased with the increasing dilation rate. However, FPR of 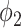 decreased much more than thresholding, and it was less than the FPR of thresholding for all the dilation rates larger than 0. This indicates that the FP pixels of
decreased much more than thresholding, and it was less than the FPR of thresholding for all the dilation rates larger than 0. This indicates that the FP pixels of 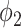 are closer to the labels compared to thresholding. These pixels are usually because of the slight errors on the boundaries of the same region, rather than segmentation of an incorrect region.
are closer to the labels compared to thresholding. These pixels are usually because of the slight errors on the boundaries of the same region, rather than segmentation of an incorrect region.
Fig. 6.
The FPR of thresholding and EM with 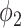 (
(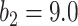 ,
, 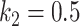 ) changing with different dilation rates of the labels.
) changing with different dilation rates of the labels.
It is also worth noticing that thresholding method with -200 HU as the threshold has already generated many FPs on the vessels. Further reducing the threshold may improve the TPR by including more pixels near the consolidation, but it will further deteriorate the FPR by including more vessels as consolidation.
C. Statistical Testing of Consolidation Score
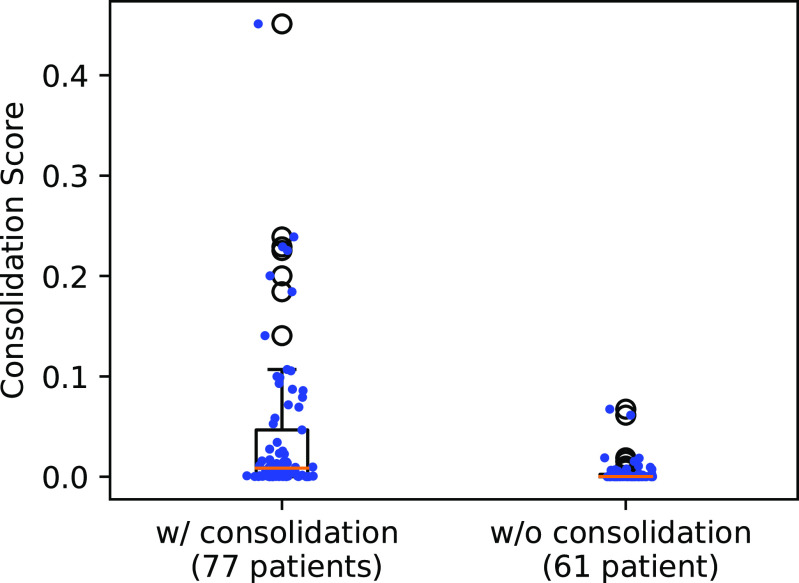
The 138 testing patients were divided into consolidation and non-consolidation groups according to their radiology reports. Fig. 7 shows the box plot of the consolidation score predicted by UNet-2 with 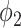 . The two groups were significantly different, with median value of 0.0403 versus 0.0043, and p-value of
. The two groups were significantly different, with median value of 0.0403 versus 0.0043, and p-value of 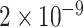 under Mann -Whitney U test.
under Mann -Whitney U test.
Fig. 7.
Box plot of the consolidation scores in the consolidation and non-consolidation groups. Blue dots show individual data points’ consolidation scores.
Most non-consolidation patients received lower consolidation scores when compared to patients with consolidation (p < 0.0001). There were two outliers which shows dramatically higher consolidation scores compared to the rest images in the non-consolidation group. Further investigation shows that these two images were overestimated because of the interlobular septal thickening, which had relatively higher HU compared to GGO. UNet-2 misclassified them into consolidation due to lack of training samples with interlobular septal thickening. As compared to groundglass opacities, both crazy-paving (groundglass opacities + septal thickening) and consolidation represent more advanced and severe disease, and therefore, this misclassification does not necessarily represent limitation of our algorithm.
V. Discussion
In this work, we proposed a deep learning method to predict the infection and consolidation regions of the COVID-19 pneumonia based on chest CT. It demonstrated improved segmentation of consolidation compared to the thresholding method [25] and EM training without the prior model [31].
The main contribution of this work is the combination of pixel-level labels with patient-level type information through the proposed hybrid weak label-based training. A novel prior function 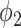 was proposed for the segmentation of consolidation in the EM framework. By incorporating the prior knowledge that consolidation usually has higher HU value into
was proposed for the segmentation of consolidation in the EM framework. By incorporating the prior knowledge that consolidation usually has higher HU value into 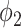 , the proposed network achieved improved performance compared to thresholding method and EM without such a prior. The proposed method also showed robustness for data coming from different sources, international sites, and protocols.
, the proposed network achieved improved performance compared to thresholding method and EM without such a prior. The proposed method also showed robustness for data coming from different sources, international sites, and protocols.
Although UNet-1 performs a standard segmentation task and is trained in a conventional supervised manner, a good performance is still crucial because UNet-1 is the basis for the following consolidation segmentation. UNet-1 also provides the total infected region to calculate the severity score (14), which is clinically important for the estimation of the lung function. According to Fig. 2, the predicted scores were underestimated compared to the label. One of the main causes is that the model tends to miss regions with very mild GGO infections, which are not very different from normal lung tissue. Furthermore, the annotations also tend to dilate from the visible boundaries of GGO. Meanwhile, the model predictions are closer to the boundaries, leading to smaller regions compared to the annotation.
We used the EM algorithm as the framework for the weakly labeled training. From the derivation of section C-2, the proposed prior function 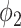 has clear physical meaning that it is the probability of a pixel belonging to consolidation given its pixel value and the image label, which was modeled by a Sigmoid function. We used
has clear physical meaning that it is the probability of a pixel belonging to consolidation given its pixel value and the image label, which was modeled by a Sigmoid function. We used 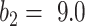 as the parameter of choice for
as the parameter of choice for 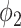 , which means that pixels larger than -34 HU inside the infected regions were considered as consolidation, and the pixels whose value were closer to -34 HU were considered to have higher probability of being consolidation.
, which means that pixels larger than -34 HU inside the infected regions were considered as consolidation, and the pixels whose value were closer to -34 HU were considered to have higher probability of being consolidation.
It was found that further increasing the threshold 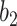 to 9.5 led to instable performance regarding
to 9.5 led to instable performance regarding 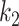 . Further inspection showed that at
. Further inspection showed that at 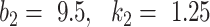 the model had low sensitivity and only included the densest consolidations. The most possible reason is that
the model had low sensitivity and only included the densest consolidations. The most possible reason is that 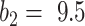 corresponds to 21 HU, which is higher than most consolidation pixels. When
corresponds to 21 HU, which is higher than most consolidation pixels. When 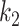 is small, the difference on
is small, the difference on 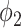 between less dense and denser consolidations is not too large, and less dense consolidations could be included into the latent label
between less dense and denser consolidations is not too large, and less dense consolidations could be included into the latent label 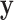 . When
. When 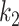 is large,
is large, 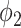 becomes very steep and since most consolidation pixels are below the changing point
becomes very steep and since most consolidation pixels are below the changing point 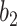 , the difference between their weights is small, which leads to similar weights between less dense and denser consolidations. However, when
, the difference between their weights is small, which leads to similar weights between less dense and denser consolidations. However, when 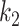 is at a certain value, the denser consolidations have considerably larger weights than the less dense ones. In consequence, only very dense consolidations are considered which leads to the low sensitivity and Dice.
is at a certain value, the denser consolidations have considerably larger weights than the less dense ones. In consequence, only very dense consolidations are considered which leads to the low sensitivity and Dice.
Currently the thresholding method is considered as a reliable method to separate GGO and consolidation [25]. We also observed a good Dice coefficient using thresholding only compared to the proposed weakly labeled learning. However, further investigation found that thresholding tends to misclassify vessels inside the infected regions to consolidation, as they have higher HU compared to GGO and other lung tissues. Most of the FPs in thresholding results came from these vessels, which are far from real consolidation regions. Although the proposed approach had similar FPR compared to thresholding, these FPs are mostly from difference between the boundaries of the labeled and predicted consolidation.
We believe that deep learning-based quantification can help address the need in patients with worsening respiratory status and moderate or severe infection where chest CT scan is recommended, and often performed [8]. The developed deep learning-based CT segmentation can serve as an important tool to help assess disease severity and progression as well as to predict prognosis. The predicted severity score of COVID-19 pneumonia along with other clinical and laboratory markers such as patient age, comorbidities, and oxygen saturation can help caretaking physicians determine patients in need of intubation or ICU admission. Although there are no known and approved treatment for COVID-19 pneumonia, multiple, ongoing clinical trials involving antiviral agents and antibodies can benefit from the proposed method which helps quantify the disease burden and thus, assess disease response or progression in an objective manner. Consistent scoring facilitated by the developed automatic tool can empower both cross-sectional and longitudinal comparisons, enable us better to understand the populational characteristics and the temporal evolution of the COVID-19 disease.
The proposed method has the benefit of segmenting consolidation regions without additional efforts to semantically annotate them on the CT images. Despite the limited number of weakly-labeled patients used to train the consolidation network, the network demonstrated promising performance on the MedSeg testing dataset which came from different sources with the training data. It can be used alone or combined with semantic labels for semi-supervised learning [28]. Inclusion of weakly labeled data can significantly increase the number of training data and generalizability to different protocols. The proposed method may also be applied to segmentation tasks beyond pulmonary consolidations, as long as the target has pixelwise features that can be modeled, e.g., higher/lower pixel values compared to the background.
VI. Conclusion
In this work we have proposed a deep learning method for infection and consolidation segmentation from CT images based on hybrid week labels. The network was initially trained with single-class contours and fine-tuned through weak patient-level labels. Evaluations based on datasets from multiple hospitals across the world demonstrate the effectiveness of the proposed framework. Future work will focus on more evaluations and score calculation for other infection types.
Appendix.
Here we give the detailed derivation of the EM algorithm (10) and (11). Compared to the original EM framework [30], our derivation supplemented some details such as the existence of the pixelwise separable basis 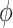 is (7).
is (7).
Given UNet-2 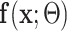 and the image labels
and the image labels 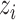 , we aim to minimize the following log-likelihood function
, we aim to minimize the following log-likelihood function
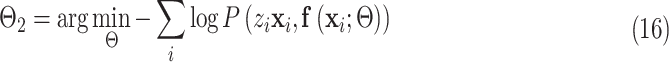 |
The following equation always holds regardless of the choice of the latent variable 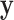 :
:
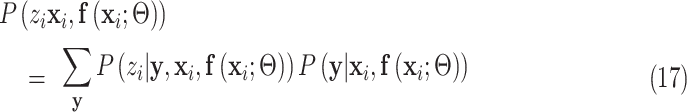 |
Here we selected 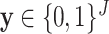 as in (6) with the following two assumptions:
as in (6) with the following two assumptions:
First, 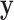 connects
connects 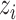 and
and 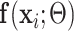 :
:
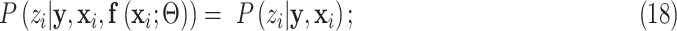 |
Second, 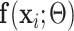 connects
connects 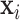 and
and 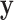 :
:
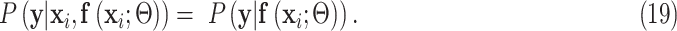 |
Substitute (18) and (19) into (17) and we have:
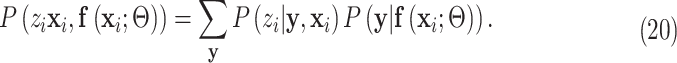 |
EM algorithm is essentially following the optimization transfer principle [36]. In the E-step, which builds a surrogate function of the original problem (16). The surrogate is then optimized during the M-step. E-step builds the surrogate function 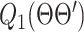 by taking the expectation of the log likelihood
by taking the expectation of the log likelihood 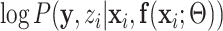 [37] as:
[37] as:
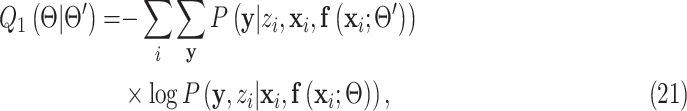 |
where 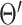 is the network parameters from the previous iteration. According to (18) and (19), the joint distribution can be written as:
is the network parameters from the previous iteration. According to (18) and (19), the joint distribution can be written as:
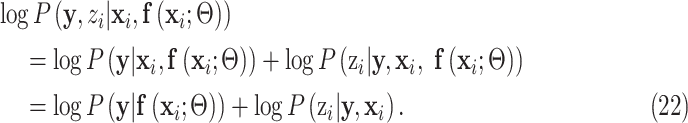 |
Substitute (22) into (21) and remove all the terms irrelevant to 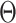 , the surrogate function becomes:
, the surrogate function becomes:
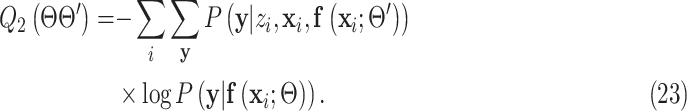 |
Because summation over all possible 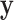 is not practical, the hard-EM approximation was taken, where the single point
is not practical, the hard-EM approximation was taken, where the single point 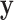 which maximizes
which maximizes 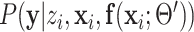 was taken instead of the expectation. Denote
was taken instead of the expectation. Denote 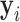 as the
as the 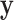 that maximize the probability for image
that maximize the probability for image 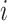 . It can be calculated as:
. It can be calculated as:
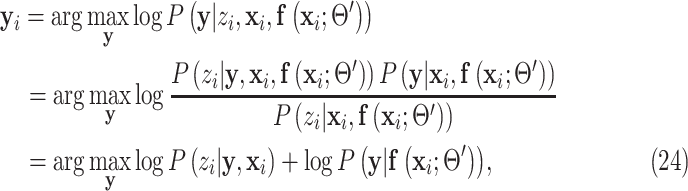 |
where in the last equality, the term without 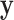 was dropped, and equations (18) and (19) were used to remove
was dropped, and equations (18) and (19) were used to remove 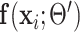 in the first term and
in the first term and 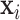 in the second term, respectively.
in the second term, respectively.
According to the definition of 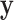 in (6),
in (6), 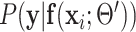 should be pixelwise separable, leading to:
should be pixelwise separable, leading to:
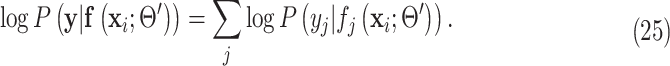 |
For the prior distribution 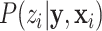 , according to Bayes’ theorem, we have:
, according to Bayes’ theorem, we have:
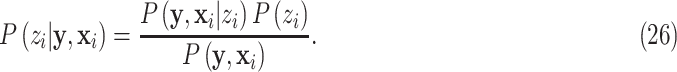 |
By modeling the joint (conditional) distributions as independent pixelwise, we have:
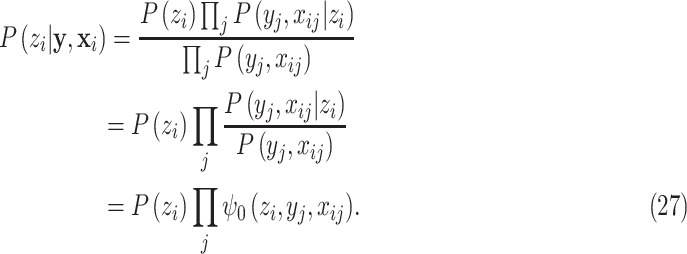 |
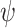 in (9) can be derived from
in (9) can be derived from 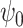 by multiplying proper normalization factors. Let
by multiplying proper normalization factors. Let
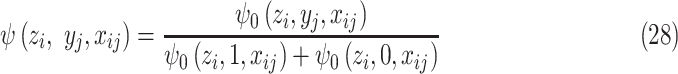 |
and 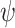 will satisfy the sum-to-one requirement in (9). Substitute (28) into (27) and we will reach
will satisfy the sum-to-one requirement in (9). Substitute (28) into (27) and we will reach
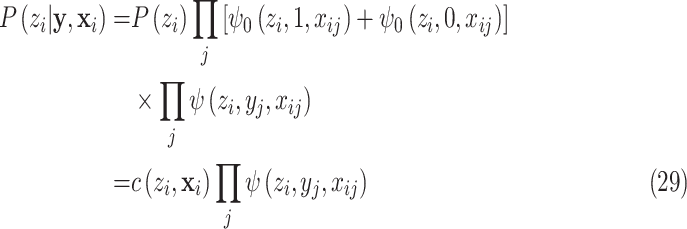 |
which gives equation (7).
Substitute (25) and (29) into (24) and remove the terms not relevant to 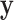 , we can get the separable distribution to be maximized as:
, we can get the separable distribution to be maximized as:
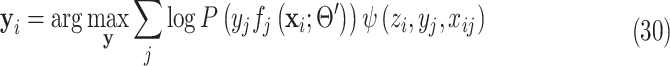 |
which can be solved pixelwise as
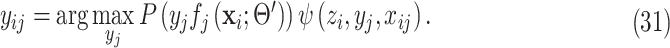 |
After 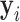 is solved, the hard-EM approximation of (23) becomes:
is solved, the hard-EM approximation of (23) becomes:
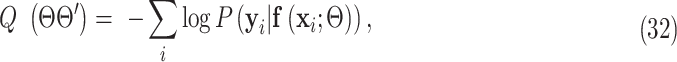 |
which is the final surrogate function from the E-step of the EM algorithm. Minimization of 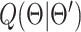 leads to the M-step given in (11).
leads to the M-step given in (11).
To solve (31), denote 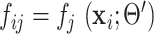 and
and 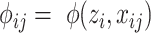 , we have
, we have
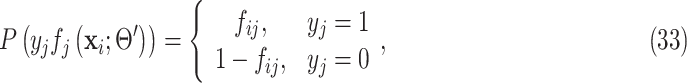 |
and
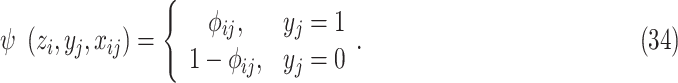 |
Note that (34) is the same with (9). The joint probability function becomes:
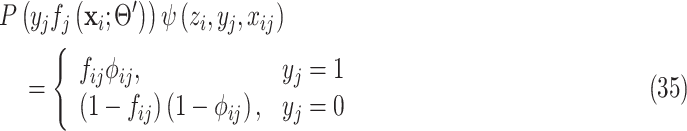 |
Hence, the solution to (31) is:
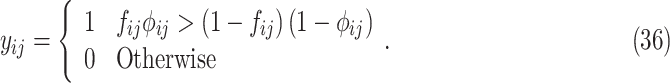 |
Because 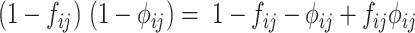 , (36) can be further reduced to:
, (36) can be further reduced to:
 |
which is the same with the E-step given in (10).
Funding Statement
This work was supported by NIH under Grant RF1 AG052653.
Footnotes
Contributor Information
Dufan Wu, Email: dwu6@mgh.harvard.edu.
Kuang Gong, Email: kgong@mgh.harvard.edu.
Chiara Daniela Arru, Email: carru@mgh.harvard.edu.
Fatemeh Homayounieh, Email: fhomayounieh@mgh.harvard.edu.
Bernardo Bizzo, Email: bbizzo@mgh.harvard.edu.
Varun Buch, Email: varun.buch@mgh.harvard.edu.
Hui Ren, Email: hren2@mgh.harvard.edu.
Kyungsang Kim, Email: kkim24@mgh.harvard.edu.
Nir Neumark, Email: nir.neumark@mgh.harvard.edu.
Pengcheng Xu, Email: pxu3@mgh.harvard.edu.
Zhiyuan Liu, Email: zliu40@mgh.harvard.edu.
Wei Fang, Email: wfang3@mgh.harvard.edu.
Nuobei Xie, Email: nxie@mgh.harvard.edu.
Won Young Tak, Email: wytak@knu.ac.kr.
Soo Young Park, Email: psy@knu.ac.kr.
Yu Rim Lee, Email: deblue00@naver.com.
Min Kyu Kang, Email: kmggood111@naver.com.
Jung Gil Park, Email: jgpark@ynu.ac.kr.
Alessandro Carriero, Email: profcarriero@virgilio.it.
Luca Saba, Email: lucasabamd@gmail.com.
Mahsa Masjedi, Email: mahsami141@gmail.com.
Rosa Babaei, Email: rosa.babaei@gmail.com.
Hadi Karimi Mobin, Email: hadi.karimimobin@gmail.com.
Shadi Ebrahimian, Email: sebrahimian@mgh.harvard.edu.
Ittai Dayan, Email: idayan@partners.org.
Mannudeep K. Kalra, Email: mkalra@mgh.harvard.edu.
Quanzheng Li, Email: quanzheng@mgh.harvard.edu.
References
- [1].Dong E., Du H., and Gardner L., “An interactive web-based dashboard to track COVID-19 in real time,” Lancet. Infect. Dis., vol. 20, no. 5, pp. 533–534, May 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Huang C. et al. , “Clinical features of patients infected with 2019 novel coronavirus in wuhan, china,” vol. 395, no. 10223, pp. 497–506, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Liu Y., Gayle A. A., Wilder-Smith A., and Rocklöv J., “The reproductive number of COVID-19 is higher compared to SARS coronavirus,” J. Travel Med., vol. 27, no. 2, pp. 1–4, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Ai T. et al. , “Correlation of chest CT and RT-PCR testing in coronavirus disease 2019 (COVID-19) in china: A report of 1014 cases,” Radiology, vol. 296, no. 2, pp. E32–E40, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Fang Y. et al. , “Sensitivity of chest CT for COVID-19: Comparison to RT-PCR,” Radiology, vol. 296, no. 2, pp. E115–E117, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Kanne J. P., Little B. P., Chung J. H., Elicker B. M., and Ketai L. H., “Essentials for radiologists on COVID-19: An update—Radiology scientific expert panel,” Radiology, vol. 296, no. 2, pp. E113–E114, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Wen Z. et al. , “Coronavirus disease 2019: Initial detection on chest CT in a retrospective multicenter study of 103 chinese subjects,” Radiol., Cardiothoracic Imag., vol. 2, no. 2, 2020, Paper e200092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Rubin G. D. et al. , “The role of chest imaging in patient management during the COVID-19 pandemic: A multinational consensus statement from the Fleischner society,” Chest, vol. 158, no. 1, pp. 106–116, Jul. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Driggin E. et al. , “Cardiovascular considerations for patients, health care workers, and health systems during the COVID-19 pandemic,” J. Amer. College Cardiol., vol. 75, no. 18, pp. 2352–2371, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Pan F. et al. , “Time course of lung changes on chest CT during recovery from 2019 novel coronavirus (COVID-19) pneumonia,” Radiology, vol. 295, no. 3, pp. 715–721, Jun. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Chung M. et al. , “CT imaging features of 2019 novel coronavirus (2019-nCoV),” Radiology, vol. 295, no. 1, pp. 202–207, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Li Y. and Xia L., “Coronavirus disease 2019 (COVID-19): Role of chest CT in diagnosis and management,” Amer. J. Roentgenol., pp. 1–7, 2020. [DOI] [PubMed]
- [13].Kim H., “Outbreak of Novel Coronavirus (COVID-19): What is the Role of Radiologists?,” Eur. Radiol., vol. 30, no. 6, pp. 3266–3267, Jun. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Krizhevsky A., Sutskever I., and Hinton G. E., “Imagenet classification with deep convolutional neural networks,” in Proc. Adv. Neural Inf. Process. Syst., 2012, pp. 1097–1105. [Google Scholar]
- [15].Li L. et al. , “Using artificial intelligence to detect COVID-19 and community-acquired pneumonia based on pulmonary CT: Evaluation of the diagnostic accuracy,” Radiology, vol. 296, no. 2, pp. E65–E71, Aug. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Wang B. et al. , “AI-assisted CT imaging analysis for COVID-19 screening: Building and deploying a medical AI system,” Appl. Soft Comput., Nov. 2020, Art. no. 106897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Gozes O., Frid-Adar M., Sagie N., Zhang H., Ji W., and Greenspan H., “Coronavirus detection and analysis on chest CT with deep learning,” 2020, arXiv:2004.02640. [Google Scholar]
- [18].Gozes O. et al. , “Rapid ai development cycle for the coronavirus (covid-19) pandemic: Initial results for automated detection & patient monitoring using deep learning ct image analysis,” 2020, arXiv:2003.05037. [Google Scholar]
- [19].Chen J. et al. , “Deep learning-based model for detecting 2019 novel coronavirus pneumonia on high-resolution computed tomography,” Sci. Rep., vol. 10, no. 1, 2020, Art. no. 19196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Hu S. et al. , “Weakly supervised deep learning for COVID-19 infection detection and classification from CT images,” IEEE Access, vol. 29, no. 8, pp. 118869–118883, 2020. [Google Scholar]
- [21].Zheng C. et al. , “Deep learning-based detection for COVID-19 from chest CT using weak label,” medRxiv, 2020. [Google Scholar]
- [22].Wang S. et al. , “A fully automatic deep learning system for COVID-19 diagnostic and prognostic analysis,” Eur. Respir. J., vol. 56, no. 2, Aug. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Huang L. et al. , “Serial quantitative chest CT assessment of COVID-19: Deep-learning approach,” Radiol., Cardiothoracic Imag., vol. 2, no. 2, 2020, Paper e200075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Shan F. et al. , “Lung infection quantification of COVID-19 in CT images with deep learning,” 2020, arXiv:.04655. [Google Scholar]
- [25].Chaganti S. et al. , “Automated quantification of CT patterns associated with COVID-19 from chest CT,” Radiol. Artif. Intell., vol. 2, no. 4, Jul. 2020, Art. no. e200048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Tang Z. et al. , “Severity assessment of COVID-19 using CT image features and laboratory indices,” Phys. Med. Biol., Oct. 2020. [DOI] [PubMed] [Google Scholar]
- [27].Yang R. et al. , “Chest CT severity score: An imaging tool for assessing severe COVID-19,” Radiol., Cardiothoracic Imag., vol. 2, no. 2, 2020, Paper e200047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Fan D.-P. et al. , “Inf-Net: Automatic COVID-19 lung infection segmentation from CT images,” IEEE Trans. Med. Imag., vol. 39, no. 8, pp. 2626–2637, Aug. 2020. [DOI] [PubMed] [Google Scholar]
- [29].Zhu W., Lou Q., Vang Y. S., and Xie X., “Deep multi-instance networks with sparse label assignment for whole mammogram classification,” in Proc. Int. Conf. Med. Image Comput. Comput.-Assisted Intervention, 2017, pp. 603–611. [Google Scholar]
- [30].Wei Y., Xiao H., Shi H., Jie Z., Feng J., and Huang T. S., “Revisiting dilated convolution: A simple approach for weakly-and semi-supervised semantic segmentation,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit., 2018, pp. 7268–7277. [Google Scholar]
- [31].Papandreou G., Chen L.-C., Murphy K. P., and Yuille A. L., “Weakly-and semi-supervised learning of a deep convolutional network for semantic image segmentation,” in Proc. IEEE Int. Conf. Comput. Vis., 2015, pp. 1742–1750. [Google Scholar]
- [32].Zhu W., Vang Y. S., Huang Y., and Xie X., “Deepem: Deep 3d convnets with em for weakly supervised pulmonary nodule detection,” in Proc. Int. Conf. Med. Image Comput. Comput.-Assisted Intervention, 2018, pp. 812–820. [Google Scholar]
- [33].Ronneberger O., Fischer P., and Brox T., “U-net: Convolutional networks for biomedical image segmentation,” in Proc. Int. Conf. Med. image Comput. Comput.-assisted intervention, 2015, pp. 234–241. [Google Scholar]
- [34].Hofmanninger J., Prayer F., Pan J., Röhrich S., Prosch H., and Langs G., “Automatic lung segmentation in routine imaging is primarily a data diversity problem, not a methodology problem,” Eur. Radiol. Exp., vol. 4, no. 1, p. 50, Dec. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Kingma D. P. and Ba J., “Adam: A method for stochastic optimization,” in Proc. 3rd Int. Conf. Learn. Representations (ICLR), San Diego, CA, USA, May 7–9, 2015. [Google Scholar]
- [36].Erdogan H. and Fessler J. A., “Monotonic algorithms for transmission tomography,” IEEE Trans. Med. Imag., vol. 18, no. 9, pp. 801–814, Sep. 1999. [DOI] [PubMed] [Google Scholar]
- [37].Little R. J. and Rubin D. B., in Statistical Analysis With Missing Data. New York, NY, USA: John Wiley Sons, 2019. [Google Scholar]