Abstract
The coronavirus disease 2019 (COVID-19) has swept all over the world. Due to the limited detection facilities, especially in developing countries, a large number of suspected cases can only receive common clinical diagnosis rather than more effective detections like Reverse Transcription Polymerase Chain Reaction (RT-PCR) tests or CT scans. This motivates us to develop a quick screening method via common clinical diagnosis results. However, the diagnostic items of different patients may vary greatly, and there is a huge variation in the dimension of the diagnosis data among different suspected patients, it is hard to process these indefinite dimension data via classical classification algorithms. To resolve this problem, we propose an Indefiniteness Elimination Network (IE-Net) to eliminate the influence of the varied dimensions and make predictions about the COVID-19 cases. The IE-Net is in an encoder-decoder framework fashion, and an indefiniteness elimination operation is proposed to transfer the indefinite dimension feature into a fixed dimension feature. Comprehensive experiments were conducted on the public available COVID-19 Clinical Spectrum dataset. Experimental results show that the proposed indefiniteness elimination operation greatly improves the classification performance, the IE-Net achieves 94.80% accuracy, 92.79% recall, 92.97% precision and 94.93% AUC for distinguishing COVID-19 cases from non-COVID-19 cases with only common clinical diagnose data. We further compared our methods with 3 classical classification algorithms: random forest, gradient boosting and multi-layer perceptron (MLP). To explore each clinical test item's specificity, we further analyzed the possible relationship between each clinical test item and COVID-19.
Keywords: COVID-19 diagnosis, clinical spectrum, indefiniteness elimination, neural network, quick screening
I. Introduction
Recently, the novel coronavirus disease 2019 (COVID-19) has rapidly spread into most countries in the world, and was defined as a new global pandemic by the World Health Organization (WHO) [1]. Up to December 28, 2020, COVID-19 has caused 80.8 million infections and 1.76 million deaths, with more than 590 thousand infections and 10 thousand deaths per day. It has become a great challenge for all over the world to stop the spread of the COVID-19 coronavirus. To slow down the rapid development of the epidemic situation, early identification, reporting, isolation, diagnosis and treatment is the best and most effective way to contain the pneumonia caused by the novel coronavirus. Therefore, how to quickly and effectively identify infected patients from the huge amount of suspected patients has become a worldwide problem. Reverse Transcription Polymerase Chain Reaction (RT-PCR) test has been the most critical approach for diagnosing COVID-19 [2], but it may require a long time for the specimen collection and analysis, and the related equipment was scarce in the early stage of the epidemic. Besides, due to the limited number of equipment and expensive cost, many suspected patients did not receive the RT-PCR test and a few of them cannot even afford other efficient detections like CT scans, especially in some developing countries [3], [4]. Instead, many of them can only receive some common clinical detections, such as blood tests, urine tests, etc. This motivates us to think about whether we can rapidly screen infected patients from suspected patients only with common clinical diagnosis, which will greatly reduce the burden of medical institutions and the cost of patients in certain countries and regions.
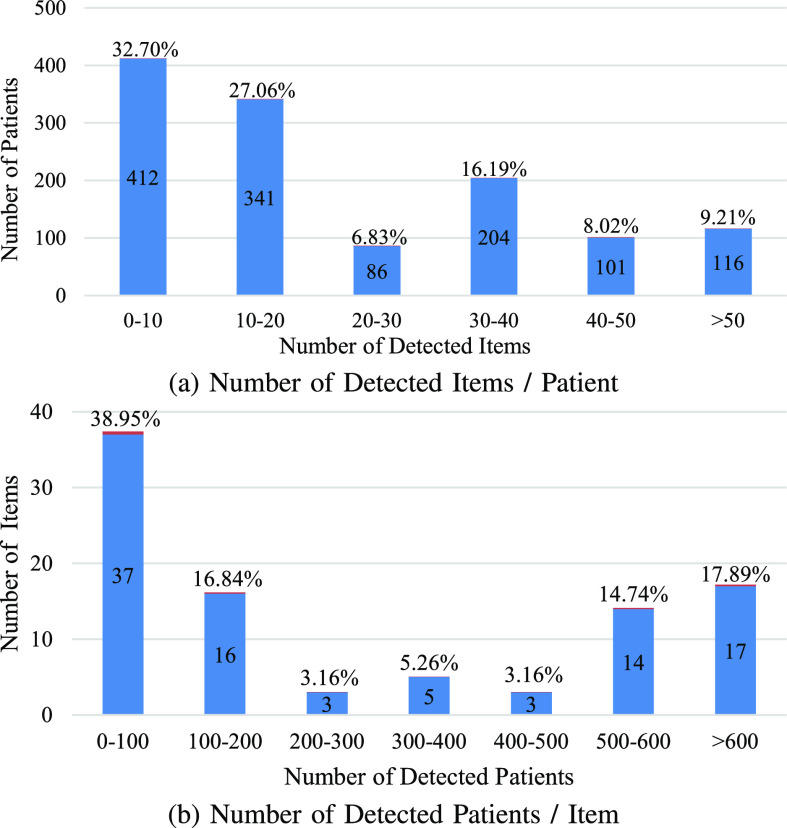
However, due to the difference in the detection and treatment processes, the detection items of each suspected patient vary greatly. For instance, in the modified COVID-19 Clinical Spectrum dataset [5], there is a total of 95 detection items and 1260 patients. As shown in Fig. 1, among all of the 1260 patients, 32.7% of the suspected patients have carried out less than 10% items. Among all of the 95 detection items, 38.9% of items are detected by less than 100 patients. Overall, in this dataset, 77.2% of the data are missing. Intuitively, we can fill the results of undetected items by zeros while processing the data, but the model will regard these items have been detected if we do so, which results in much additional noise. Moreover, many imputation methods have been proposed which aim at imputing missing data by various statistical or machine learning methods [6], [7]. However, previous work has shown that imputation methods are not suitable for handling clinical data with more than 40% missing [8]. Another common practice to deal with these clinical test results is to ignore the missing data.
Fig. 1.
Analysis of the used data. (a) represents for each patient, how many items has tested. (b) describes for each clinical test item, how many patients have been detected. These two figures show that the clinical data of each patient is very different.
However, ignoring the missing data will result in the detection result of each patient in different dimensions, which imposes further restrictions on the methods that can be used. For instance, since the neural networks have been proven to be of great advantages in dealing with big data, we want to design a neural network framework to handle these clinical data. However, a neural network based method requires at least one dimension of the input data needs to be consistent with the dimension of the network weights. For example, the fully connected layer which adopts a 1D vector as input requires the dimension of input data to be fixed, and the convolution layer requires the input data has the same channel number as the weight matrix. This characteristic makes it difficult for classical neural networks (e.g. [9]–[11]) to deal with the indefinite dimension data like the clinical spectrum. Therefore, an efficient method that can deal with the missing detection items problem is desperately needed if we want to develop a fast screening method with only common clinical test results.
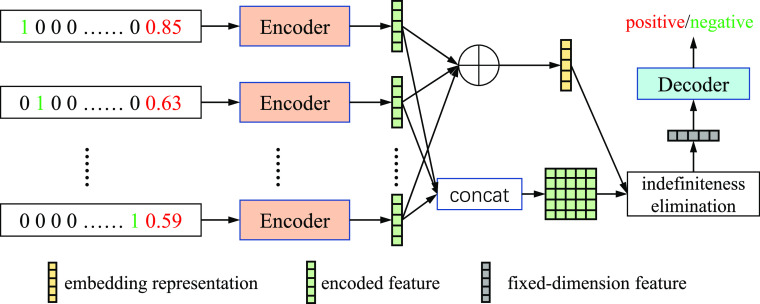
In this paper, we propose a novel neural network based method named Indefiniteness Elimination Network (IE-Net) to screen suspected cases by the common clinical detection results. An important advantage of the proposed IE-Net is that it can predict the diagnosis results from an indefinite dimension clinical spectrum. Specifically, the proposed IE-Net utilizes an encoder-decoder structure as shown in Fig. 2. To overcome the tested items inconsistent problem, the encoder encodes the data of each test item separately at first. After that, to deal with the dimensional uncertainty of the encoded feature matrix, we designed an indefiniteness elimination operation that can transform matrixes of different dimensions into vectors of the same dimension. In such a way, the IE-Net can diagnose the COVID-19 clinical detection results without introducing extra noise. What's more, the attention weight of the indefiniteness elimination operation could be further employed to analyze the relationship between each test item and COVID-19. This will help to pick up the significant clinical test items which highly correlated with COVID-19 and further reduce the cost and speed up the screening procedure. We tested the proposed IE-Net framework on the COVID-19 Clinical Spectrum dataset [5] which was collected from a hospital in Brazil. This dataset contains clinical testing results of 5644 peoples on 98 testing items. A few practical problems of this dataset make it cannot be used directly, and we adopted some appropriate preprocessing steps before using this dataset. We will give a detailed description in Section IV-B about why and how we preprocessed the dataset. Experimental results show that the proposed indefiniteness elimination operation significantly improves the model performance and the IE-Net achieves 94.80% accuracy, 92.79% recall, 92.97% precision and 94.93% AUC for distinguishing COVID-19 cases from non-COVID-19 cases with only common clinical diagnose data. Compared with traditional classification methods (random forest, gradient boosting, and multi-layer perceptron), the proposed IE-Net can bring at least 9.40% accuracy gains, 12.17% recall gains 3.66% precision and 9.71% AUC gains. Extensive results demonstrate the superiority of the proposed IE-Net framework in screening COVID-19 patients with only common clinical tests. Code and results have been released at https://github.com/gyguo/IE-Net.
Fig. 2.
Overview of the proposed framework. Our network consists of an encoder that encodes the results of each item separately, an indefiniteness elimination module which transforms the encoded feature into fixed dimension, and a decoder predicts whether a patient is infected by the COVID-19. 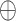 denotes the element-wise sum operation.
denotes the element-wise sum operation.
In general, the main contributions of this paper are:
-
•
We proposed a novel IE-Net to diagnose COVID-19 coronavirus with only some common clinical detection results, which is complementary to imaging-based methods and RT-PCR. This kind of method will be of great help to some developing countries and regions.
-
•
We propose a novel indefiniteness elimination operation which can transform the indefinite dimension matrices into fixed dimension vectors, which makes the deep neural networks can be applied to the clinical detection data with missing dimensions. It could also be applied to other indefinite dimension problems which are common in many fields.
-
•
We provide significant analysis and interpretation of the relationship between each clinical test item and COVID- 19 coronaviruses. This will help to pick up the significant clinical test items which highly correlated with COVID-19 and further reduce the cost and speed up the screening procedure.
II. Related Works
A. Artificial Intelligence Diagnosis for COVID-19
COVID-19 coronavirus has been spread fast all over the world due to its high infectivity. Although the virus can be directly identified by RT-PCR testing, the large number of suspected cases increased dramatically heavy burden on testing equipment and relevant staff. Since AI aided diagnosis system has made great progress in the past few years, and can greatly reduce the work of doctors and improve the speed of diagnosis [12]–[16], many AI-assisted algorithms have been proposed for COVID-19 diagnosis via clinical tests like X-ray and CT scans [3].
As far as we know, most of the X-ray based methods were proposed to screen COVID-19 from non-COVID-19 [17]–[20], and only a few X-ray based method was proposed to distinguish COVID-19 from other pneumonia [21]. However, the reliability of X-ray based methods are relatively low, this is mainly because that X-ray images are generally less sensitive than CT images [22]. Compared with X-ray based method, CT based methods can make much more precise diagnosis. In addition to the ability of classifying the COVID-19 and the non-COVID-19 [23]–[26], many CT based methods can distinguish COVID-19 from other pneumonia [27]–[29]. In addition, some CT based diagnosis methods can achieve severity assessment [30], [31], which could help medical institutions use resources more reasonably. Mei et al. integrate chest CT with clinical symptoms, exposure history and laboratory testing to diagnose positive patients for COVID-19 [32]. Harmon et al. trained AI model on multinational chest CT datasets to get higher detection accuracy [33]. Han et al. proposed a deep 3D multiple instance learning method to screen COVID-19 based on 3D chest CT. However, there are still a few developing countries and areas that are not able to afford these CT machines and it is also impossible to produce a sufficient number of CT scanners in a very short time. Therefore, in this paper, we proposed to adopt common clinical detection results, such as data of blood tests and urine tests to screen COVID-19 patients. This will help to further reduce the cost of COVID-19 test and achieve more effective use of existing medical resources.
B. Classification Algorithms in Machine Learning
Classification is one of the most basic tasks in machine learning, and it has been applied to many fields such as natural image classification [11], [34], handwriting recognition [35], medical image classification [36], etc. In the early days, some simple methods like logistic regression [37] and naive bayes classifier [38] were proposed to solve the linear classification problem. Logistic regression models can resolve classification problem by finding the best fitting model to describe the relationship between a set of independent variables and binary interest features [37]. Naive Bayes classifier is a simple linear classification technique based on Bayes Theorem, with an assumption of independence among predictors [38]. Besides, many non-linear classification algorithms were proposed to resolve more complex problems. Support vector machine (SVM) model represents instances as points mapped in space, so as to divide individual instances into a gap. SVM training algorithm builds a model to assign new samples to one or another category, making it capable of performing linear or nonlinear classification [39]. The decision tree establishes the classification model in the form of tree structure. It decomposes the input data into smaller subsets and incrementally generates a related decision tree [40]. Gradient boosting classifiers generate prediction models in the form of a set of weak prediction models. It builds models in a staged way and generalizes them by allowing optimization of any differentiable loss function [41]. Random forest constructs a multitude of decision trees at training and output the class the individual trees [42]. Besides, Multiple Instance Learning (MIL) has been widely used in medical image classification [43]–[45], Gaudioso et al. proven that multiple instance learning can helps to classify data belonging to similar categories [45]. Multi-Layer perceptron (MLP) [46] or neural network (NN) consists of multiple units neurons, arranged in layers, and trained by the backpropagation algorithm [47]. In recent years, deep neural networks (DNN) have been proven to be the most powerful classifier in dealing with big data [10], [11].
C. Missing Data Problem
Missing Data is a common problem in any kind of data-based research, which will bring extra difficulty for the researches [6]. There are three types of missing data problems, i.e. missing completely at random (MCAR), missing at random (MAR), missing not at random (MNAR) [7]. MCAR refers to that the missing data does not depend on any data, either observed or missing. MAR indicates that while given the observed data, the missing data does not depend on the data that are unobserved. And MNAR denotes the missing data depends on the value that would have been observed or other missing values in the dataset.
For dealing with the missing data problem, the simplest method is to use only a complete subset, but this approach would result in information loss and useful when a small number of data points are missing values [48]. Imputation methods aim at imputing missing data by various statistical methods like maximum likelihood [49], multiple imputation [50], fully Bayesian (FB) [51] etc., or machine learning techniques like k-Nearest Neighbor (KNN) [52]. However, imputation methods will introduce noise and cannot be used in case of too much missing data [8]. Besides, there are also a few machine learning algorithms, such as random forest [42], can deal with the situation of missing data without deleting the incomplete subset or imputing the missing values. In this case, there is no need to deal with the missing data.
In this paper, many suspected cases only took a few clinical tests which result in 77.2% of the data is missing compared with a whole completed test. To overcome this problem, we turned this missing data problem into a dimension transform problem that largely overcomes the limitation. That is, we directly ignore the missed data and design a special module to transform the data of different dimensions into the same dimension features, so as to solve the problem of data missing for training neural networks.
III. Methods
Given a series of diagnostic data with total 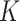 detected items, our goal is to diagnose whether each suspected case is infected with COVID-19. For an arbitrary suspected case,
detected items, our goal is to diagnose whether each suspected case is infected with COVID-19. For an arbitrary suspected case, 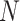 clinical test items are detected (
clinical test items are detected (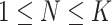 ). For a single detected item
). For a single detected item 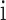 in all
in all 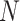 items, we use a vector
items, we use a vector 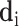 to represent the examination result of each detected item (
to represent the examination result of each detected item (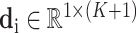 ), which consists of two parts. The first part is a one hot vector of dimension
), which consists of two parts. The first part is a one hot vector of dimension 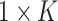 used to mark the detection item number, and the second part is the detected result. Therefore, the overall detection result of each suspected case is an indefinite dimension matrix (
used to mark the detection item number, and the second part is the detected result. Therefore, the overall detection result of each suspected case is an indefinite dimension matrix (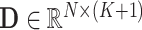 ).
).
As shown in Fig. 2, IE-Net uses the indefinite dimension matrix 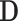 as the input to obtain the diagnosis results of suspected cases. IE-Net adopts an encoder-decoder framework, and we propose an indefiniteness elimination operation to transform the indefinite dimension encoded feature into a fixed-dimension feature for decoder.
as the input to obtain the diagnosis results of suspected cases. IE-Net adopts an encoder-decoder framework, and we propose an indefiniteness elimination operation to transform the indefinite dimension encoded feature into a fixed-dimension feature for decoder.
A. Encoder
The encoder takes the results of all detected items as input. Because each suspected case receives different examination items and the dimensions of the overall detection matrix 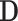 is inconsistent, we will not directly encode the whole detection results. On the contrary, the proposed IE-Net encodes the results of each item separately. For the test result of a single detected item
is inconsistent, we will not directly encode the whole detection results. On the contrary, the proposed IE-Net encodes the results of each item separately. For the test result of a single detected item 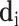 , the encoder outputs a 1D feature vector (
, the encoder outputs a 1D feature vector (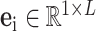 ) though two fully connected layers followed by Leaky ReLU activation function [53]
) though two fully connected layers followed by Leaky ReLU activation function [53]
 |
where 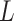 is the length of the encoded feature vector,
is the length of the encoded feature vector, 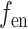 and
and 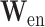 are the encoding operation and trainable weights of the encoder, respectively. Then we obtain the overall encoded feature matrix
are the encoding operation and trainable weights of the encoder, respectively. Then we obtain the overall encoded feature matrix 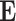 by concatenating all of the encoded feature vectors. (
by concatenating all of the encoded feature vectors. (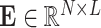 ).
).
B. Indefiniteness Elimination Operation
It is obvious that the overall encoded feature 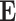 is an indefinite dimension matrix, which makes it hard for a neural network to handle, so we design an indefiniteness elimination operation in IE-Net to produce fixed dimension feature for decoder.
is an indefinite dimension matrix, which makes it hard for a neural network to handle, so we design an indefiniteness elimination operation in IE-Net to produce fixed dimension feature for decoder.
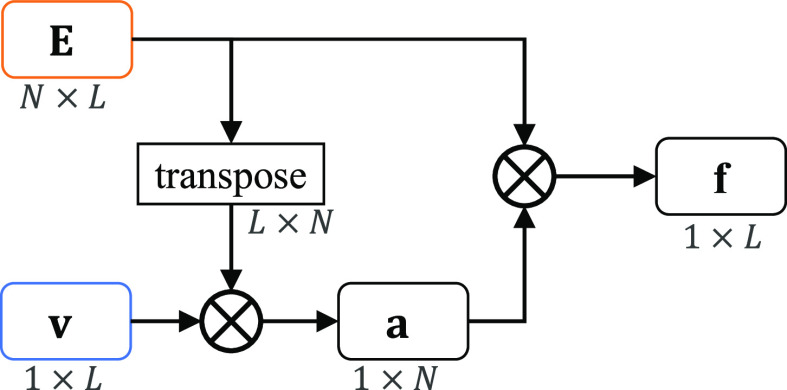
As shown in the Fig. 2 and Fig. 3, after the encode operation, we can get encoded feature matrix 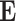 , and a embedding representation vector
, and a embedding representation vector 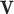 . Then we produce an attention vector
. Then we produce an attention vector 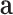 to filter items which are low related to COVID-19 (
to filter items which are low related to COVID-19 (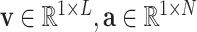 )
)
 |
where 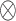 denotes matrix inner-product operation,
denotes matrix inner-product operation, 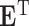 is the transposed feature matrix. After we got the attention vector, a fixed dimension feature vector
is the transposed feature matrix. After we got the attention vector, a fixed dimension feature vector 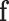 is generated (
is generated (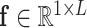 )
)
 |
we can see that 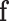 is a fixed dimension vector, which makes it possible to use the neural networks in the decoding operation.
is a fixed dimension vector, which makes it possible to use the neural networks in the decoding operation.
Fig. 3.
Detailed implementation of the indefiniteness elimination operation. 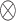 denotes matrix inner-product operation.
denotes matrix inner-product operation.
The indefiniteness elimination operation can be seen as an extension of the non-local mechanisms [54], [55] or some differential memory based spatio-temporal video recognition methods [56], [57]. But the indefiniteness elimination operation is designed for a different purpose as it aims at eliminating the effect of missing data in clinical detection.
C. Decoder
The decoder takes the fixed dimension feature vector 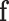 as input to predict whether the suspected case is infected with COVID-19
as input to predict whether the suspected case is infected with COVID-19
 |
where 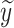 is the predicted results,
is the predicted results, 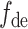 and
and 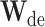 is the decoding operation and trainable weights of the decoder, respectively. The decoder is implemented by two fully connected layers, where the first layer is followed by the Leaky ReLU activation function and the second layer is followed by the sigmoid activation function, and dropout operation is used on the first fully connected layers [58].
is the decoding operation and trainable weights of the decoder, respectively. The decoder is implemented by two fully connected layers, where the first layer is followed by the Leaky ReLU activation function and the second layer is followed by the sigmoid activation function, and dropout operation is used on the first fully connected layers [58].
We optimize IE-Net by the binary cross entropy loss
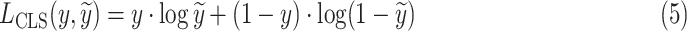 |
where 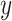 is the ground truth label, i.e.,
is the ground truth label, i.e., 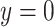 denotes a non-COVID-19 case and
denotes a non-COVID-19 case and 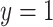 denotes a COVID-19 case.
denotes a COVID-19 case.
D. Implementation Details
We choose Adam as the optimizer [59], and the parameters of Adam are: 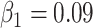 ,
, 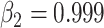 , the weight decay is set as 0.0005. The proposed model is trained through 200 epochs with learning rate 0.001.
, the weight decay is set as 0.0005. The proposed model is trained through 200 epochs with learning rate 0.001. 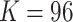 is determined by the dataset we used, and the dimension of the encoded feature is
is determined by the dataset we used, and the dimension of the encoded feature is 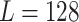 . We reported the results of 10-fold cross-validations during the classification process, which means the dataset is randomly divided into 10 parts, 9 of which were used for training and 1 for testing. The process can repeat 10 times, each time using different test data. The final performance of 10-fold cross-validation is the mean and variance of the results of 10 experiments. To prevent the overfitting, we designed a data augmentation strategy by shuffling the order of different detection vectors during training procedure. For three traditional methods, we utilize a widely used machine learning package Scikit-learn [60]. For GradientBoosting, we use learning
. We reported the results of 10-fold cross-validations during the classification process, which means the dataset is randomly divided into 10 parts, 9 of which were used for training and 1 for testing. The process can repeat 10 times, each time using different test data. The final performance of 10-fold cross-validation is the mean and variance of the results of 10 experiments. To prevent the overfitting, we designed a data augmentation strategy by shuffling the order of different detection vectors during training procedure. For three traditional methods, we utilize a widely used machine learning package Scikit-learn [60]. For GradientBoosting, we use learning  rate=0.05, n
rate=0.05, n  estimators=50 000, subsample=1.0. For Random Forest, we set n
estimators=50 000, subsample=1.0. For Random Forest, we set n  estimators=30, max
estimators=30, max  depth=10, min
depth=10, min  samples
samples split=2, min
split=2, min  samples
samples leaf=1. For Multi-Layer Perception, we set solver=’adam,’ activation=’logistic,’ alpha=1e-3, hidden
leaf=1. For Multi-Layer Perception, we set solver=’adam,’ activation=’logistic,’ alpha=1e-3, hidden  layer
layer sizes=(40, 4). For IE-Net, we use threshold 0.5 to determine the predicted results while evaluating. Our code is implemented on PyTorch platform [61], all experiments were run on a NVIDIA GTX 1080Ti GPU.
sizes=(40, 4). For IE-Net, we use threshold 0.5 to determine the predicted results while evaluating. Our code is implemented on PyTorch platform [61], all experiments were run on a NVIDIA GTX 1080Ti GPU.
IV. Experiments
In this section, we first give a detailed description of the evaluation metrics and the used COVID-19 Clinical Spectrum dataset. Then the COVID-19 Clinical Spectrum dataset is divided into training and validation sub-datasets to verify the performance of the proposed framework. The comparison experiments with traditional machine learning methods demonstrate the effectiveness of the proposed framework, especially for handling the indefinite dimension detection data. Finally, we carry on a detailed analysis of our methods.
A. Evaluation Metrics
For one thing, the classification accuracy can reveal the overall perception to the COVID-19 disease. For another thing, because we are dealing with an infectious disease, it is important to reduce the false negative rate. Any misdiagnosed virus carrier will help to spread the disease to others and cause much more infected patients. So we adopt recall as another evaluation metric in our paper. Besides, we also provide the results of precision and the area under the receiver operating characteristic curve (AUC). Since we used the 10-fold cross-validation strategy, for each method there will be 10 ROC curves, so we only provide the AUC value. PPrecision is another widely used evaluation metric that indicates the ability of the classifier not to label a negative sample as positive. The classification accuracy (ACC) can be calculated as equation 6, the Recall can be calculated as equation 7, and the Precision can be calculated as equation 8.
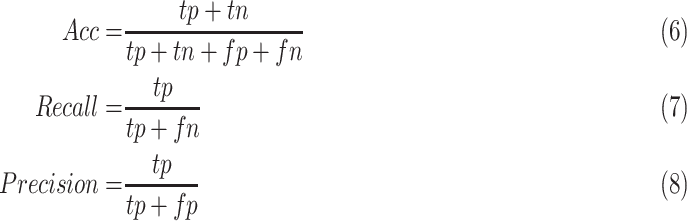 |
where 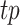 ,
, 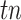 ,
, 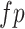 ,
, 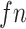 indicates the number of true positive, true negative, false positive and false negative, respectively.
indicates the number of true positive, true negative, false positive and false negative, respectively.
B. Dataset and Pre-Processing
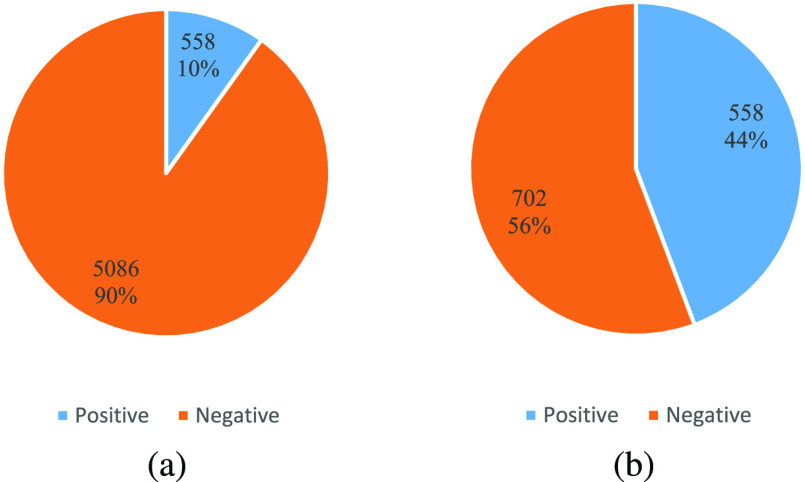
COVID-19 Clinical Spectrum dataset [5]. Data of this dataset is collected from the Hospital Israelita Albert Einstein, at Sao Paulo, Brazil. The original dataset contains the clinical diagnosis of 98 items and 5644 peoples. The patients are anonymous to protect the privacy. Most detection values are normalized to be zero-mean in the released raw data.
However, some practical issues make it difficult to directly use the raw dataset to train a diagnosing model. The first issue comes from the quantification of some test items. For example, the results of the “Urine-Aspect” test consists of four items: “clear,” “altered color,” “lightly cloud” and “cloud,” which should be digitized. Besides, the number of detected patients for some test items is too small, which makes those items meaningless for diagnosis. Moreover, The main problem is that the distribution of positive and negative cases is unbalanced. As shown in Fig. 4, positive cases only account for 10% of all data. A balanced dataset is more proper for revealing the real performance of a diagnose model. Precisely, when a model reports the classification accuracy of 90% on the raw data, it may simply regard all patients as healthy and still show high performance. To solve these problems, we disposed the raw data via the following steps according to previous preprocessing analysis pipeline to this dataset [62].
-
•
We represent boolean tags by numbers 0 and 1. To be specific, we use 1 to represent the positive patients and 0 to represent the negative patients. Moreover, For some items that diagnose other diseases like “Influenza A,”Influenza B,” 1 is used to represent “Detected,” and 0 is used to represent “Not Detected”.
-
•
We convert text tags to float numbers with the consideration of their correlation to disease. For a test item which has
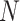 possible options, we use the numbers 0 to
possible options, we use the numbers 0 to  to represent the
to represent the 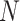 options. For example, as for the examination “Urine-Aspect,” there are four tags “clear,” “altered color,” “lightly cloud” and “cloud,” we convert them to “0,” “1,” “2,” “3” respectively. Even though one-hot coding may be better for some items, the data of those items will longer than others. Because IE-Net requires the data length of each item to be consistent, we use the numeric order for all the items.
options. For example, as for the examination “Urine-Aspect,” there are four tags “clear,” “altered color,” “lightly cloud” and “cloud,” we convert them to “0,” “1,” “2,” “3” respectively. Even though one-hot coding may be better for some items, the data of those items will longer than others. Because IE-Net requires the data length of each item to be consistent, we use the numeric order for all the items. -
•
For some results of “Urine-Leukocytes,” because “
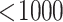 ” is not a specific number, we use value 999 to represent it.
” is not a specific number, we use value 999 to represent it. -
•
We remove the negative patients who have less than 20 tested items. For those patients, too little detected items makes their data not meaningful.
-
•
We remove two items which are not been tested by any patients.
Fig. 4.
Distribution of positive and negative cases of the raw COVID-19 Clinical Spectrum dataset (a) and modified dataset (b), respectively.
As shown in Fig. 4, the modified dataset contains the clinical diagnosis of 96 items and 1260 patients, and there are 558 positive cases and 702 negative cases in this modified dataset, which makes the distribution of positive and negative samples more balanced. To facilitate the subsequent research about COVID-19, the modified dataset will be made publicly available and they are all submitted in the supplementary materials along with the manuscript.
C. Experimental Results
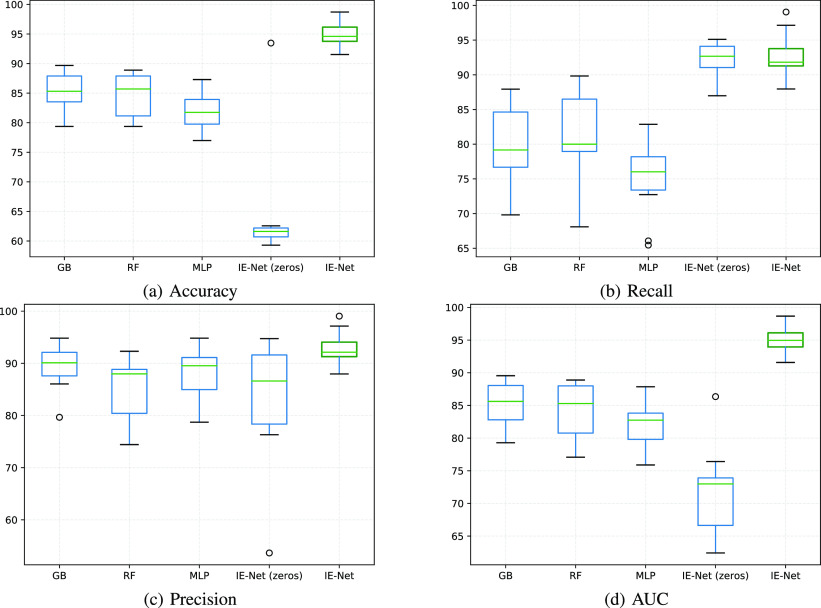
As shown in Table I and Fig. 5, we compared the proposed methods with three classification methods: Gradient Boosting (GB) [41], Random Forest (RF) [42], and Multi-Layer Perception (MLP) [46]. As the gradient boosting method and multi-layer perception method cannot dispose of variable-dimension inputs, we fill the absent tests with three data filling strategies in experiments. For each item, filling data of undetected patients of this item by (1) Zeros; (2) The average value of detected patients; (3) The median value of detected patients. The detailed results of different data filling strategies are shown in Table II, since three traditional methods perform better when the strategy is filling missed data by zeros, we use the result of this strategy as the default performance of the traditional algorithms in this paper.1 Moreover, to reflect the effect of filling blank items with 0 on the performance of a classifier, we also conduct IE-Net (zeros) which denotes the results of absent tests are filled with 0 and the proposed IE-Net framework is adopted at the same time. Because the number of cases is limited, we adopt the 10-fold cross-validation pipeline and report both the mean score and the standard deviation, so as to reveal the comprehensive performance of each method.
TABLE I. The Results for Random Forest, Gradient Boosting, MLP and Our IE-Net in Terms of Accuracy, Recall, Precision and AUC (%).
| 4]*Methods | Evaluation Metrics (mean  std) std) |
|||
|---|---|---|---|---|
| ACC | Recall | Precision | AUC | |
| GradientBoosting | 85.40 3.08 3.08 |
79.72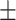 5.54 5.54 |
89.31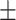 4.06 4.06 |
85.22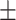 3.36 3.36 |
| Random Forest | 84.76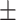 3.65 3.65 |
80.62 6.77 6.77 |
85.21 6.07 6.07 |
84.42 4.19 4.19 |
| MLP | 82.06 2.99 2.99 |
74.98 5.29 5.29 |
88.03 5.25 5.25 |
82.19 3.55 3.55 |
| IE-Net (zeros) | 64.41 9.74 9.74 |
92.35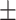 2.36 2.36 |
83.05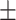 11.65 11.65 |
71.70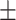 6.60 6.60 |
| IE-Net |
94.80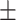 1.98 1.98
|
92.79 3.07 3.07
|
92.97 3.06 3.06
|
94.93 2.00 2.00
|
Fig. 5.
Box-plot for the results of IE-Net and other algorithms in terms of accuracy, recall, precision and AUC (%). GB, RF, MLP denote gradient boosting, random forest, and multi-Layer perception, respectively. IE-Net (zeros) denotes the results of absent tests are filled with 0.
TABLE II. Comparison of Different Missing Data Filling Strategy on Random Forest, Gradient Boosting, MLP and Our IE-Net, in Terms of Accuracy, Recall, Precision and AUC (%).
| 4]*Methods | 4]*Fill | Evaluation Metrics (mean  std) std) |
|||
|---|---|---|---|---|---|
| ACC | Recall | Precision | AUC | ||
| 2]*GradientBoosting | Zeros | 85.40 3.08 3.08 |
79.72 5.54 5.54 |
89.31 4.06 4.06 |
85.22 3.36 3.36 |
| Average | 85.94 3.86 3.86 |
78.85 5.14 5.14 |
89.21 5.13 5.13 |
84.96 2.02 2.02 |
|
| Median | 84.76 3.15 3.15 |
78.82 5.87 5.87 |
89.14 4.09 4.09 |
84.66 3.40 3.40 |
|
| 2]*Random Forest | Zeros | 84.76 3.65 3.65 |
80.62 6.77 6.77 |
85.21 6.07 6.07 |
84.42 4.19 4.19 |
| Average | 82.21 4.83 4.83 |
79.81 4.39 4.39 |
84.62 7.10 7.10 |
83.83 2.82 2.82 |
|
| Median | 84.44 3.66 3.66 |
79.99 6.967 6.967 |
85.46 5.68 5.68 |
84.10 4.18 4.18 |
|
| 2]*MLP | Zeros | 82.06 2.99 2.99 |
74.98 5.29 5.29 |
88.03 5.25 5.25 |
82.19 3.55 3.55 |
| Average | 55.71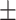 5.30 5.30 |
0.00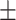 0.00 0.00 |
0.00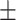 0.00 0.00 |
- | |
| Median | 55.71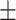 5.30 5.30 |
0.00 0.00 0.00 |
0.00 0.00 0.00 |
- | |
| 2]*IE-Net | Zeros | 64.41 9.74 9.74 |
92.35 2.36 2.36 |
83.05 11.65 11.65 |
71.70 6.60 6.60 |
| Average | 63.81 10.65 10.65 |
91.81 3.32 3.32 |
82.65 10.65 10.65 |
71.47 6.81 6.81 |
|
| Median | 63.45 9.41 9.41 |
92.51 2.15 2.15 |
83.46 10.71 10.71 |
71.97 6.16 6.16 |
|
Table I presents the classification results of all methods. Gradient Boosting achieves 85.4% accuracy, 89.31% precision, 85.22% AUC, performs best among three traditional methods in terms of accuracy, precision and AUC. However, the proposed IE-Net achieves 94.80% accuracy, 92.97% precision and 94.93% AUC, exceeds Gradient Boosting by 9.40% accuracy, 3.66% precision and 9.71% AUC. From the view of recall, Random Forest outperforms the other two traditional methods and achieves 80.62%. We can find that IE-Net can recall 92.79% positive cases, outperforms Random Forest by 12.17%. Jointly considering classification accuracy, recall, precision, and AUC, we can found that the proposed IE-Net is a better candidate for screening the COVID-19 patient.
Fig. 5 reports the accuracy, recall, precision and AUC of all the methods in box figures. The box figures are intuitive to show the overall performance of 10-fold cross-validation for each method. For a single box, the outlier values are denoted as circles. The highest and lowest lines represent the maximum and minimum values excluding any outliers, respectively. The middle green line denotes the median value, and the middle box represents the majority of all the scores, where the upper and lower boundaries of the box are the first quartile and third quartile, respectively. We can see that IE-Net consistently shows better performance than the other three traditional methods in both accuracy and recall.
From Table I and Fig. 5, we can observe that MLP performs worst in recall (74.98%) and IE-Net (zeros) performs worst in accuracy (64.41%) among these five methods. Particularly, even though IE-Net (zeros) has the same performance as IE-Net in terms of recall (92.35% vs. 92.79%), its accuracy is dramatically lower than that of the IE-Net (64.41% vs. 94.80%). This indicates that when the dimension of input data is fixed to use the neural network (filling data of undetected items by zeros), additional noise will be introduced, and this makes the neural network difficult to play its normal performance. The comparison between the MLP, IE-Net (zeros) and IE-Net demonstrates that the proposed method can better tackle the indefinite dimension problem. Moreover, the comparison between the IE-Net and random forest, gradient boosting shows that a well designed neural network has the potential to perform better than the traditional classification methods in dealing with clinical diagnosis data.
D. Model Analysis
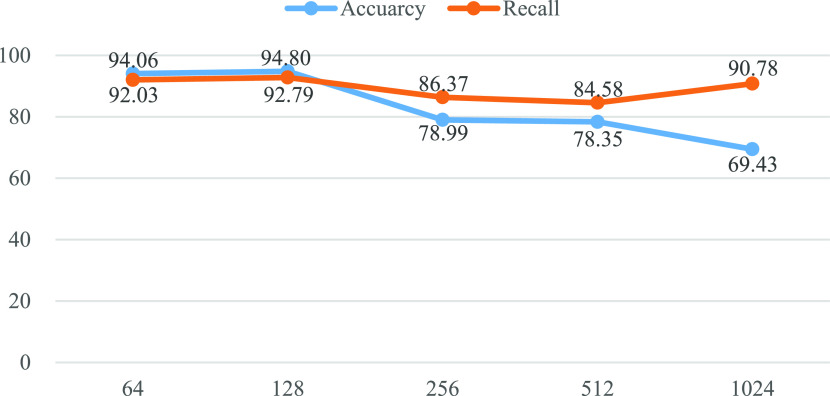
Effect of representation dimension. In the proposed IE-Net, we first project the raw detection data to a high dimension space to obtain more discriminative feature representation. It is an open question of what is a proper projection dimension. We verify the performance of IE-Net under different projection dimensions.
Fig. 6 compares the accuracy and recall of IE-Net with different representation dimensions. We can observe that the performance of IE-net first increases with the increase of the representation dimension, reaches the maximum when the dimension is 128, and then decreases with the increase of dimensions. In general, higher-dimensional representation provide better accuracy, which can explain why the performance increase from 64 to 128. However, with the increase of dimensions, the number of parameters of the model will also increase, and the overfitting problem will become more and more serious, which will lead to the decline of model performance.
Fig. 6.
Performance of IE-Net under different representation dimensions in terms of accuracy and recall (%).
Comparison of different data filling strategy for traditional methods. In Table II, we compare how different data filling strategies affect the results of the traditional methods. We compare three data filling strategies in experiments. For each item, filling data of undetected patients of this item by (1) Zeros. (2) The average value of detected patients. (3) The median value of detected patients. It is notable that the proposed IE-Net only used the data of detected items, so using different data filling strategies do not affect the final performance of our method. It is notable that the proposed IE-Net only used the data of detected items, so using different data filling strategies do not affect the final performance of our method.
As shown in Table II, different data filling strategies slightly affect the performance of Gradient Boosting, Random Forest and the proposed IE-Net. However, the performance of Multi-Layer Perception shows a sharp decline when the missed data is filled by the avarage or median values. Its recall becomes 0 means that it predicts all instances as negative while evaluation. The most likely reason is that filling missed data by the avarage or median values will increase the similarity between positive and negative samples, and makes Multi-Layer Perception unable to deal with this situation.
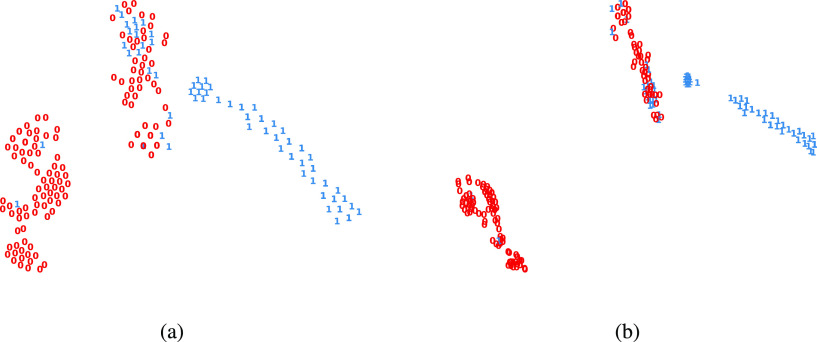
Representation visualization. Given a detection data, the proposed IE-Net first encodes each examination to a high-dimension feature via an encoder. Then these features are aggregated to a single feature vector. After that, IE-Net adopts the decoder network to judge whether this patient is infected by the COVID-19. Although IE-Net shows superior performance in terms of classification accuracy and recall, we step further and visualize the learned features to check whether the features are discriminative enough.
Fig. 7 shows the t-SNE [63] visualization of the aggregated features after the encoder layers, and the visualization of the feature before the final decision. Comparing the visualization of these two features, it can be found that the latter is more compact for each cluster and more separative for different clusters. This verifies the necessity of the decoder network. Besides, all cases are clustered into three groups. Most of the healthy people are clustered together and most of the COVID-19 infected patients are clustered together. Apart from these two distinct clusters, there is a mixed cluster, where both positive and negative cases show similar features. This is consistent with the medical common sense, as it is hard to diagnose some patients, even for an experienced doctor.
Fig. 7.
Representation visualizations by t-SNE [63]. Each case is visualized as one point, the infected and healthy cases are represented by 1 and 0, in color blue and red, respectively. (a) the visualization for the aggregated feature of each patient. (b) the visualization for the feature before final decision.
In addition, from the left part which is obviously clustered as negatives, we can see that there are still a small number of positive cases. This suggests that the clinical manifestations of these COVID-19 carriers are almost the same as those of uninfected people, as evidenced by the recent findings of many asymptomatic infected patients [64], [65]. This indicates that even if we reduce the screening criteria of positive cased, only simple clinical diagnosis is still insufficient to fully confirm all the carriers of COVID-19. Therefore, to reduce the damage of asymptomatic infected persons for controlling this epidemic, it is necessary to isolate and test the contact person of each known infected person.
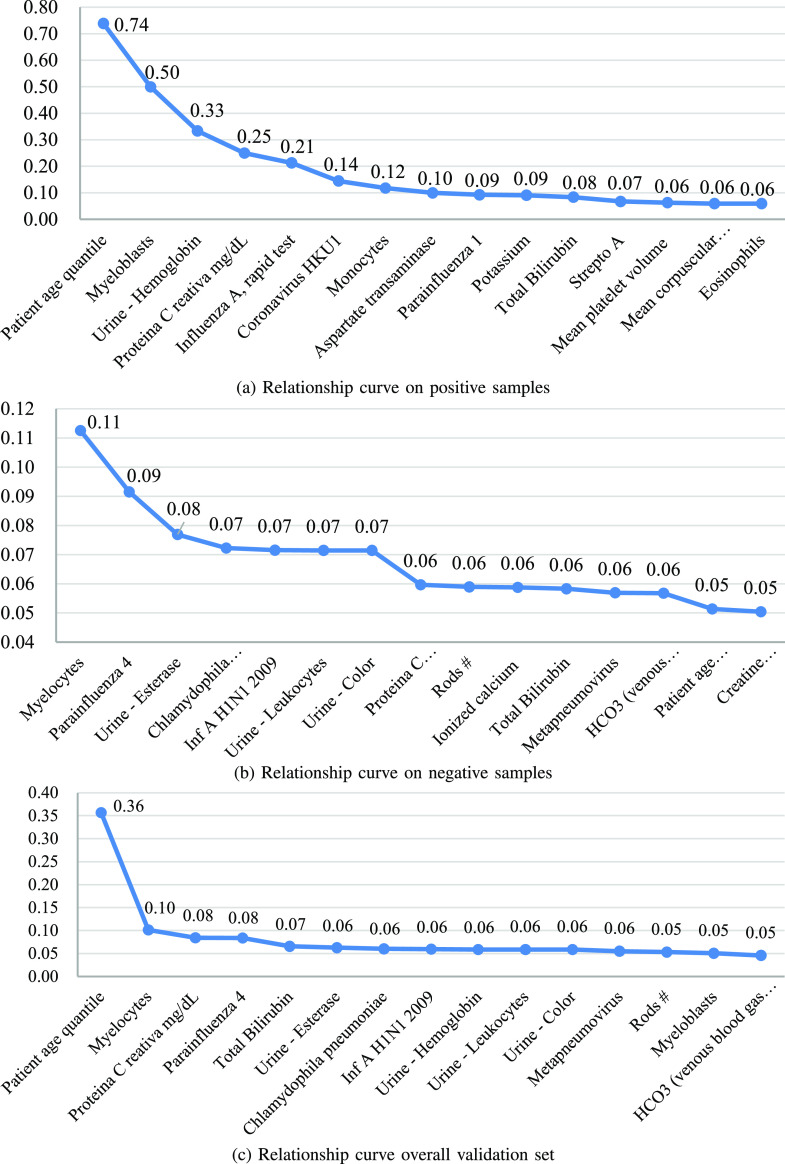
Analysis of the relationship between each test item and COVID-19. As mentioned in session III (B), the attention vector we obtained in the indefiniteness elimination operation is used to filter detections that are low related to COVID-19, so we can use it to analyze the relationship between each test item and COVID-19. Over the 10-fold cross-validation of IE-Net, we chose the model which achieves 98.72% accuracy and 99.05% recall to generate the attention weight vector for each case in the validation set. After obtaining these vectors, we calculated the average value of the weights for each detection, this value can be regarded as the correlation coefficient between the corresponding detection and the COVID-19. Then we normalize the correlation coefficients of all the test items. In order to better show the results in Fig. 8, we make the correlation coefficients of all items add up to 5 instead of 1 during normalization.
Fig. 8.
Relationship curves on positive cases (a), negative cases (b) and overall validation set (c), respectively. Values on the curves denote the normalized correlation coefficients of items.
Fig. 8 shows the most related 15 items for positive cases, negative cases and overall validation set, respectively. From the 3 curves, we can observe that:
-
1)
The correlation coefficient of “Patient age quantile” is significantly larger than other items, which is caused by its high correlation to positive cases (ranked first in the correlation of positive cases and 14th in the negative cases). This shows that there is a great relationship between age and infection. This has been proven by the existing data [66]–[68]. It is reported in [68] that among all the confirmed cases in the United States, 31% of cases, 45% of hospitalizations, 53% of ICU admissions, and 80% of deaths occurred among adults aged lager 65 years.
-
2)
Besides of the age, “Myeloblasts,” “Urine-Hemoglobin,” and “Proteina C reativa mg/dL” are most related to the positive cases. This means that we need to pay more attention to the results of these three tests when screening infected patients. Moreover, this result is consistent with the description in the previously published coronavirus prevention handbook [69]. As the 34th tip of coronavirus prevention handbook said, in the early stage of COVID-19, the total number of white blood cells is normal or decreased (”Myeloblasts” is a kind of white blood cell), and in most patients, c-reactive protein rate were elevated [69].
-
3)
Besides of the age, “Myeloblasts” is the most related item for both the positive cases and negative cases.
-
4)
The most relevant items of positive and negative cases are not the same. For example, the second and third related items on the negative cases are “Parainfluenza 4” and “Urine - Esterase,” which have a low correlation with the positive cases. This means that some test results may be able to exclude uninfected people, while the existing research mainly focuses on confirming the infected patients.
V. Discussions and Conclusion
In this paper, we have presented a novel IE-Net architecture for better screening COVID-10 patients with only common clinical diagnosis results. Particularly, to eliminate the indefiniteness caused by the different detected items for each single suspected cases, we encoded data of each test item into vectors at first, then we transformed the encoded feature matrix into a vector of fixed dimension by a series of matrix transposition and inner product operations. In such a way, we can use neural networks here to screen COVID-19 cases without filling the data of undetected items. 10 fold cross-validation experiments were conducted on a real COVID-19 clinical test dataset to demonstrate the effectiveness of IE-Net. Performance improvements can be clearly observed when comparing to other classification algorithms.
The proposed method could be useful in under-developed countries and areas where there is no sufficient advanced diagnosis tools such as CT and RT-PCR test available. The major limitations of the proposed method is that the IE-Net can only eliminate the indefiniteness of one dimension which indicates the number of the detected items, and require the results of different detection items have to be coded into the same dimension. This makes data of some items cannot be coded in the one-hot form due to the length of the coded data will be longer than the other. Moreover, IE-Net requires the data form of the detection items should be unified, which makes it hard for IE-Net to introduce more complex clinical diagnoses like CT scans or X-ray. In the future work, we will improve the way we encoding the data, and makes our method can process medical images of different modality and other clinical detection data whenever these types of data are available as discussed in [3]. This will make the proposed eliminating indefiniteness strategy can be applied to more complex scenarios, such as simultaneously processing of medical images of CT, X-ray and other clinical tests like blood test and urine test, even if each patient only had some of these tests. Besides, applying the proposed method in more complex scenarios makes it possible for us to compare the proposed eliminating indefiniteness strategy with other COVID-19 screening approaches based on clinical data.
Funding Statement
This work was supported by in part the Key-Area Research and Development Program of Guangdong Province (2019B010110001), in part by the Guangdong Provincial Key Laboratory of Medical Image Processing (2017B030314133), in part by the National Science Foundation of China under Grants 61806167, 82060336, 61936007 and U1801265, in part by the Natural Science Basic Research Plan in Shaanxi Province of China (2019JQ-630), and in part by the Fundamental Research Funds for the Central Universities and the research funds for interdisciplinary subject, NWPU.
Footnotes
The codes for our method and the comparison methods have been published in https://github.com/gyguo/IE-Net.
Contributor Information
Guangyu Guo, Email: gyguo95@gmail.com.
Zhuoyan Liu, Email: lzy8962@gmail.com.
Shijie Zhao, Email: shijiezhao666@gmail.com.
Lei Guo, Email: lguo@nwpu.edu.cn.
Tianming Liu, Email: tianming.liu@gmail.com.
References
- [1].Organization W. H., “Coronavirus disease 2019 (COVID-19): Situation report, 76,” Tech. Doc., Mar. 5, 2020. [Google Scholar]
- [2].Ai T. et al. , “Correlation of chest CT and RT-PCR testing in coronavirus disease 2019 (COVID-19) in china: A report of 1014 cases,” Radiology, vol. 296, no. 2, pp. E32–E40, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Shi F. et al. , “Review of artificial intelligence techniques in imaging data acquisition, segmentation and diagnosis for COVID-19,” IEEE Rev. Biomed. Eng., vol. 14, pp. 4–15, 2021. [DOI] [PubMed] [Google Scholar]
- [4].Lloyd-Sherlock P., Ebrahim S., Geffen L., and McKee M., “Bearing the brunt of COVID-19: Older people in low and middle income countries,” 2020. [DOI] [PubMed] [Google Scholar]
- [5].Einstein D., “Diagnosis of COVID-19 and its clinical spectrum,” 2020. [Online]. Available: https://www.kaggle.com/einsteindata4u/covid19
- [6].Ibrahim J. G., Chu H., and Chen M.-H., “Missing data in clinical studies: Issues and methods,” J. Clin. Oncol., vol. 30, no. 26, 2012, Art. no. 3297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Howell D. C., “The treatment of missing data,” Sage Handbook Social Sci. Methodol., pp. 208–224, 2007. [Google Scholar]
- [8].Jakobsen J. C., Gluud C., Wetterslev J., and Winkel P., “When and how should multiple imputation be used for handling missing data in randomised clinical trials-a practical guide with flowcharts,” BMC Med. Res. Methodol., vol. 17, no. 1, pp. 1–10, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Karen S. and Andrew Z., “Very deep convolutional networks for large-scale image recognition,” in Proc. Int. Conf. Learn. Representations, 2015, pp. 1–14. [Google Scholar]
- [10].Szegedy C. et al. , “Going deeper with convolutions,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit., 2015, pp. 1–9. [Google Scholar]
- [11].He K., Zhang X., Ren S., and Sun J., “Deep residual learning for image recognition,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit., 2016, pp. 770–778. [Google Scholar]
- [12].Andreu-Perez J., Poon C. C., Merrifield R. D., Wong S. T., and Yang G.-Z., “Big data for health,” IEEE J. Biomed. Health Inform., vol. 19, no. 4, pp. 1193–1208, Jul. 2015. [DOI] [PubMed] [Google Scholar]
- [13].Ravì D. et al. , “Deep learning for health informatics,” IEEE J. Biomed. Health Inform., vol. 21, no. 1, pp. 4–21, Jan. 2017. [DOI] [PubMed] [Google Scholar]
- [14].Schlemper J., Caballero J., Hajnal J. V., Price A. N., and Rueckert D., “A deep cascade of convolutional neural networks for dynamic mr image reconstruction,” IEEE Trans. Med. Imag., vol. 37, no. 2, pp. 491–503, Feb. 2018. [DOI] [PubMed] [Google Scholar]
- [15].He Z., Zhu L., Li M., Li J., Chen Y., and Luo Y., “Rapid and high-quality 3 d fusion of heterogeneous ct and mri data for the human brain,” Sci. China Inf. Sci., vol. 62, no. 10, 2019, Art. no. 204101. [Google Scholar]
- [16].Liu F. and Li H., “Joint sparsity and fidelity regularization for segmentation-driven ct image preprocessing,” Sci. China Inf. Sci., vol. 59, no. 3, 2016, Art. no. 32112. [Google Scholar]
- [17].Hemdan E. E.-D., Shouman M. A., and Karar M. E., “COVIDX-net: A framework of deep learning classifiers to diagnose COVID-19 in X-ray images,” 2020, arXiv:2003.11055.
- [18].Zhang J., Xie Y., Li Y., Shen C., and Xia Y., “COVID-19 screening on chest X-ray images using deep learning based anomaly detection,” 2020, arXiv:2003.12338.
- [19].Apostolopoulos I. D. and Bessiana T. A., “COVID-19: Automatic detection from X-ray images utilizing transfer learning with convolutional neural networks,” Phys. Eng. Sci. Med., vol. 43, no. 2, pp. 635–4640, 2020. [DOI] [PMC free article] [PubMed]
- [20].Farooq M. and Hafeez A., “COVID-ResNet: A deep learning framework for screening of COVID-19 from radiographs,” 2020, arXiv:2003.14395.
- [21].Wang L., Lin Z. Q., and Wong A., “COVID-net: A tailored deep convolutional neural network design for detection of COVID-19 cases from chest radiography images,” Sci. Rep., vol. 10, no. 1, pp. 1–12, 2020. [DOI] [PMC free article] [PubMed]
- [22].Wong H. Y. F. et al. , “Frequency and distribution of chest radiographic findings in COVID-19 positive patients,” Radiology, vol. 296, no. 2, pp. E72–E78, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Chen J. et al. , “Deep learning-based model for detecting 2019 novel coronavirus pneumonia on high-resolution computed tomography: A prospective study,” Sci. Rep., vol. 10, no. 1, pp. 1–11, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Wang X. et al. , “A weakly-supervised framework for COVID-19 classification and lesion localization from chest CT,” IEEE Trans. Med. Imag., vol. 39, no. 8, pp. 2615–2625, 2020. [DOI] [PubMed] [Google Scholar]
- [25].Jin C. et al. , “Development and evaluation of an AI system for COVID-19 diagnosis,” Nature Commun., vol. 11, no. 1, pp. 1–14, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Fang M. et al. , “CT radiomics can help screen the coronavirus disease 2019 (COVID-19): A preliminary study,” Sci. China Inf. Sci., vol. 63, no. 7, pp. 1–8, 2020. [Google Scholar]
- [27].Barstugan M., Ozkaya U., and Ozturk S., “Coronavirus (COVID-19) classification using CT images by machine learning methods,” 2020, arXiv:2003.09424.
- [28].Wang S. et al. , “A deep learning algorithm using CT images to screen for corona virus disease (COVID-19),” Eur. Radiol., to be published. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Xu X. et al. , “A deep learning system to screen coronavirus disease 2019 pneumonia,” Engineering, vol. 6, no. 10, pp. 1122–1129, 2020. [DOI] [PMC free article] [PubMed]
- [30].Tang Z. et al. , “Severity assessment of COVID-19 using CT image features and laboratory indices,” Phys. Med. Biol., vol. 66, no. 3, Jan. 2021. Art. no. 035015. [DOI] [PubMed]
- [31].Shi F. et al. , “Large-scale screening of COVID-19 from community acquired pneumonia using infection size-aware classification,” Phys. Med. Biol., to be published. [DOI] [PubMed]
- [32].Mei X. et al. , “Artificial intelligence-enabled rapid diagnosis of patients with COVID-19,” Nature Med., vol. 26, no. 8, pp. 1224–1228, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Harmon S. A. et al. , “Artificial intelligence for the detection of COVID-19 pneumonia on chest CT using multinational datasets,” Nature Commun., vol. 11, no. 1, pp. 1–7, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Cheng G., Li R., Lang C., and Han J., “Task-wise attention guided part complementary learning for few-shot image classification,” Sci. China Inf. Sci., vol. 64, no. 2, pp. 1–14, 2021. [Google Scholar]
- [35].LeCun Y. et al. , “Handwritten digit recognition with a back-propagation network,” in Proc. Adv. Neural Inf. Process. Syst., 1990, pp. 396–404. [Google Scholar]
- [36].Wang H. et al. , “Recognizing brain states using deep sparse recurrent neural network,” IEEE Trans. Med. Imag., vol. 38, no. 4, pp. 1058–1068, Apr. 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Kleinbaum D. G., Dietz K., Gail M., Klein M., and Klein M., Logistic Regression. Berlin, Germany: Springer, 2002. [Google Scholar]
- [38].Rish I. et al. , “An empirical study of the naive bayes classifier,” Proc. Int. Joint Conf. Artif. Intell. Workshop Empirical Methods Artif. Intell., vol. 3, no. 22, 2001, pp. 41–46. [Google Scholar]
- [39].Suykens J. A. and Vandewalle J., “Least squares support vector machine classifiers,” Neural Process. Lett., vol. 9, no. 3, pp. 293–300, 1999. [Google Scholar]
- [40].Murthy S. K., “Automatic construction of decision trees from data: A multi-disciplinary survey,” Data Mining Knowl. Discov., vol. 2, no. 4, pp. 345–389, 1998. [Google Scholar]
- [41].Friedman J. H., “Greedy function approximation: A gradient boosting machine,” Ann. Statist., vol. 29, pp. 1189–1232, 2001. [Google Scholar]
- [42].Liaw A. and Wiener M., “Classification and regression by randomforest,” R News, vol. 2, no. 3, pp. 18–22, 2002. [Google Scholar]
- [43].Astorino A., Fuduli A., Gaudioso M., and Vocaturo E., “Multiple instance learning algorithm for medical image classification,” in Proc. 27th Italian Symp. Adv. Database Syst., 2019. [Google Scholar]
- [44].Vocaturo E. and Zumpano E., “Dangerousness of dysplastic nevi: A multiple instance learning solution for early diagnosis,” in Proc. IEEE Int. Conf. Bioinf. Biomed., 2019, pp. 2318–2323. [Google Scholar]
- [45].Gaudioso M., Giallombardo G., Miglionico G., and Vocaturo E., “Classification in the multiple instance learning framework via spherical separation,” Soft Comput., vol. 24, no. 7, pp. 5071–5077, 2020. [Google Scholar]
- [46].Pal S. K. and Mitra S., “Multilayer perceptron, fuzzy sets, classifiaction,” IEEE Trans. Neural Netw., vol. 3, no. 5, pp. 683–697, 1992. [DOI] [PubMed] [Google Scholar]
- [47].Rumelhart D. E., Hinton G. E., and Williams R. J., “Learning representations by back-propagating errors,” Nature, vol. 323, no. 6088, pp. 533–536, 1986. [Google Scholar]
- [48].Choudhury S. J. and Pal N. R., “Imputation of missing data with neural networks for classification,” Knowl.-Based Syst., vol. 182, 2019, Art. no. 104838. [Google Scholar]
- [49].White H., “Maximum likelihood estimation of misspecified models,” Econometrica: J. Econometric Soc., vol. 50, pp. 1–25, 1982.
- [50].Chen T. and Fienberg S. E., “The analysis of contingency tables with incompletely classified data,” Biometrics, vol. 32, pp. 133–144, 1976.
- [51].Scharfstein D. O., Halloran M. E., Chu H., and Daniels M. J., “On estimation of vaccine efficacy using validation samples with selection bias,” Biostatistics, vol. 7, no. 4, pp. 615–629, 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Dixon J. K., “Pattern recognition with partly missing data,” IEEE Trans. Syst., Man, Cybern., vol. 9, no. 10, pp. 617–621, Oct. 1979. [Google Scholar]
- [53].Glorot X., Bordes A., and Bengio Y., “Deep sparse rectifier neural networks,” in Proc. 14th Int. Conf. Artif. Intell. Statist., 2011, pp. 315–323. [Google Scholar]
- [54].Wang X., Girshick R., Gupta A., and He K., “Non-local neural networks,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit., 2018, pp. 7794–7803. [Google Scholar]
- [55].Wu C.-Y., Feichtenhofer C., Fan H., He K., Krahenbuhl P., and Girshick R., “Long-term feature banks for detailed video understanding,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit., 2019, pp. 284–293. [Google Scholar]
- [56].Miller A., Fisch A., Dodge J., Karimi A.-H., Bordes A., and Weston J., “Key-value memory networks for directly reading documents,” in Proc. Conf. Empirical Methods Natural Lang. Process., Nov. 2016, pp. 1400–1409. [Google Scholar]
- [57].Oh S. W., Lee J.-Y., Xu N., and Kim S. J., “Video object segmentation using space-time memory networks,” in Proc. IEEE Int. Conf. Comput. Vis., 2019, pp. 9226–9235. [Google Scholar]
- [58].Xu B., Wang N., Chen T., and Li M., “Empirical evaluation of rectified activations in convolutional network,” 2015, arXiv:1505.00853.
- [59].Kingma D. P. and Ba J., “Adam: A method for stochastic optimization,” in Proc. Int. Conf. Learn. Representation, 2015, pp. 1–14. [Google Scholar]
- [60].Pedregosa F. et al. , “Scikit-learn: Machine learning in python,” J. Mach. Learn. Res., vol. 12, pp. 2825–2830, 2011. [Google Scholar]
- [61].Paszke A. et al. , “Pytorch: An imperative style, high-performance deep learning library,” Advances in Neural Information Processing Systems, vol. 32, H. Wallach, H. Larochelle, A. Beygelzimer, F. d’Alché-Buc, E. Fox, and R. Garnett, Eds. Curran Associates, Inc., 2019, pp. 8024–8035. [Online]. Available: http://papers.neurips.cc/paper/9015-pytorch-an-imperative-style-high-performance-deep-learning-library.pdf [Google Scholar]
- [62].Isabela T. and Thamiris C., “COVID-19 classifier,” 2020. [Online]. Available: https://www.kaggle.com/isabelatelles/covid-19-classifier-auc-95-41-recall-93-51
- [63].Maaten L. v. d. and Hinton G., “Visualizing data using t-SNE,” J. Mach. Learn. Res., vol. 9, pp. 2579–2605, 2008. [Google Scholar]
- [64].Bai Y. et al. , “Presumed asymptomatic carrier transmission of COVID-19,” JAMA, vol. 323, no. 14, pp. 1406–1407, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [65].Hu Z. et al. , “Clinical characteristics of 24 asymptomatic infections with COVID-19 screened among close contacts in Nanjing, China,” Sci. China Life Sci., vol. 63, no. 5, pp. 706–711, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [66].Novel C. P. E. R. E. et al. , “The epidemiological characteristics of an outbreak of 2019 novel coronavirus diseases (COVID-19) in China,” Zhonghua Liu Xing Bing Xue Za Zhi= Zhonghua Liuxingbingxue Zazhi, vol. 41, no. 2, p. 145, 2020. [DOI] [PubMed] [Google Scholar]
- [67].Remuzzi A. and Remuzzi G., “COVID-19 and Italy: What next?,” Lancet, vol. 395, no. 10231, pp. 1225–1228, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [68].COVID C. and Team R., “Severe outcomes among patients with coronavirus disease 2019 (COVID-19)-U.S., february 12-march 16, 2020,” MMWR Morb Mortal Wkly Rep., vol. 69, no. 12, pp. 343–346, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [69].Zhou W., The Coronavirus Prevention Handbook: 101 Science-Based Tips That Could Save Your Life, Skyhorse, 2020. [Google Scholar]