Abstract
In December 2019, China announced the breakout of a new virus identified as coronavirus SARS-CoV-2 (COVID-19), which soon grew exponentially and resulted in a global pandemic. Despite strict actions to mitigate the spread of the virus in various countries, COVID-19 resulted in a significant loss of human life in 2020 and early 2021. To better understand the dynamics of the spread of COVID-19, evidence of its chaotic behavior in the US and globally was evaluated. A 0–1 test was used to analyze the time-series data of confirmed daily COVID-19 cases from 1/22/2020 to 12/13/2020. The results show that the behavior of the COVID-19 pandemic was chaotic in 55% of the investigated countries. Although the time-series data for the entire US was not chaotic, 39% of individual states displayed chaotic infection spread behavior based on the reported daily cases. Overall, there is evidence of chaotic behavior of the spread of COVID-19 infection worldwide, which adds to the difficulty in controlling and preventing the current pandemic.
Keywords: Chaotic behavior, COVID-19 pandemic, spread of infections, 0–1 test
I. Introduction
In December 2019, the coronavirus SARS-CoV-2 (COVID-19) broke out in China and soon grew into a global pandemic affecting almost every country worldwide [1]. The virus is transmitted through human-to-human contact, and infected individuals present with symptoms such as cough, fever, headache, and breathing difficulties [2]. Several elements facilitate the spread of infection and severity of disease: (1) close contact with infected individuals, (2) contact with individuals who have been to locations with a considerable number of confirmed COVID-19 cases, (3) efficiency and speed of COVID-19 transmission, (4) susceptibility of individuals over 65, and (5) having underlying health conditions (e.g., respiratory problems, hypertension, cardiovascular disease, and diabetes) [2].
Governments around the world have imposed different polices and undertaken preventive public health measures, such as social distancing orders, travel restrictions, local or national lockdown, and partial or complete border closures, to control the spread of the pandemic [3]. However, the COVID-19 pandemic remains one of the main sources of death worldwide at the time of writing this article. A better understanding of the underlying processes affecting COVID-19 pandemic dynamics and related infection patterns will help to improve the effectiveness of public health interventions worldwide.
Even though many different aspects of the COVID-19 pandemic have already been investigated, including the mechanisms and rate of infection transmission, how fast it reaches its peak, and how long it will last, it is difficult to accurately assess its dynamics [4]. Since the COVID-19 pandemic started in one or more specific places in China and quickly spread worldwide, it is reasonable to assume that it represents a nonlinear complex phenomenon. One of the main factors of complex systems is chaotic behavior, in which elements of the system align and compete for survival [5]. Sensitivity to initial conditions renders chaotic systems unpredictable, especially long-term; however, chaotic systems can be described by a few variables and equations [6]. Recently, Jones and Strigul [6] concluded that the chaotic behavior of the spread of COVID-19 represents a deterministic chaotic system. Such knowledge will help to better understand the unpredictable impact of small changes in a multitude of social, behavioral, economic, and political conditions on the dynamics of infection, which should be considered when creating public health management policies and mitigation strategies.
II. Objectives
To investigate the chaotic behavior of the COVID- 19 pandemic, we analyzed data from a total of 214 counties and territories globally. Specifically, we aimed to confirm that the COVID-19 epidemic displays chaotic behavior based on the analysis of time-series data of reported daily infections. Firstly, we investigated the spread of infection in different US states, followed by its behavior in other countries around the world. The present article is structured as follows: the background section discusses the objectives and conclusions of published articles concerning the chaotic behavior of pandemics; the methodology section explains the binary 0–1 test for chaos using time-series data; the results section represents the outcomes of the 0–1 test; and the discussion section explains the results.
III. Background
The dynamics of the spread of pandemics are similar to the behavior of other nonlinear systems including chaotic maps and turbulent flows [7]. In such systems, a small seed increases exponentially and then saturates; in general, chaotic behavior indicates that the system is extremely sensitive to the initial conditions. Some of the distinguishing features of nonlinear behavior can be used to analyze human pandemics. Many studies have investigated the deterministic chaotic dynamics of pandemics. Matouk [8] developed a susceptible-infected model with multi-drug resistance (SIMDR) and its fractional-order counterpart to predict the spread of the COVID-19 infection. In this compartmental model, the dynamics of one class of susceptible population and three classes of infected populations were investigated. The fractional-order counterpart of the model was considered with a view to achieving a higher degree of freedom and accuracy of modeling. Numerical tools of Lyapunov exponents (LEs), Lyapunov spectrum, and bifurcation diagrams were used to study the complex dynamics of the system. LE can be used to assess chaotic behavior by calculating the divergence rate of trajectories in the phase space; positive LE may indicate chaotic behavior, while negative LE does not generally represent stability [9]. The study by Matouk [8] verified the existence of chaotic attractors for the integer-order model and its fractional-order, and indicated that the fractional-order model was more realistic than its integer-order SIMDR model in explaining real epidemics data.
Other studies have investigated the chaotic behavior of different epidemics such as Rift Valley fever, childhood diseases, and epizootic outbreaks. Pedro et al. [10] developed a susceptible-asymptomatic-infectious-recovered compartmental model to investigate the Rift Valley fever epidemic. The study used a variety of nonlinear analysis tools, including bifurcation diagrams, maxima return maps, Poincaré maps, and LEs to investigate the nonlinear dynamics of the system. Billings and Schwartz [11] developed a susceptible-exposed-infectious-recovered (SEIR) model to forecast outbreaks of childhood diseases by adding stochastic perturbations to model parameters and LEs to identify chaotic behavior. Sun et al. [12] proposed a susceptible-infectious-recovered-susceptible (SIRS) model, and demonstrated the model’s chaotic properties based on LE indices. Eilersen et al. [13] described an eco-epidemiological model with a two-prey one-predator ecosystem, where one carries a disease. To assess whether the dynamic model is chaotic, the study determined the LE. Following an epizootic outbreak, chaotic behavior occurred in the system at different ranges of model parameters. The study indicated that chaos mostly occurs when the disease spreads into more prey species. Interestingly, the study verified chaotic behavior in a relatively minimal eco-epidemiological system [13].
Several articles have investigated chaotic behavior under specific environmental and geographic conditions, including the presence of noise, presence of seasonality, impacts of locations (small and big cities), and impacts of compartmental models. He and Banerjee [14] analyzed a fractional-order susceptible-infectious-recovered (SIR) epidemic system under the conditions of external noise and parametric seasonality. Although an integer-order SIR system exhibited stable behavior, the fractional-order SIR epidemic model in the presence of noise and seasonality forces showed strong patterns of nonlinear dynamic changes. This study utilized numerical tools, such as MFuzzyEn and the largest positive LE, and reported rich dynamic behaviors based on system parameters, degree of noise and seasonality, and fractional derivative order. The study concluded that the infectious disease outbreak could be controlled by applying efficient health and medical measures [14]. Yi et al. [15] investigated the dynamic behavior of an SEIR compartmental model with seasonality in relation to the transmission rate. The study applied bifurcation diagrams, Poincaré maps, LEs, and Lyapunov diagrams to investigate the periodic, chaotic, and hyperchaotic behaviors of the system. Grenfell et al. [16] used a time-series-susceptible-infected-removed (TSIR) model to determine the dynamic features of measles epidemics in various cities.
The study indicated that the epidemic model could accurately determine the dynamic features of the long-term behavior of measles in big cities. Based on LEs, the results indicated that small cities are more predictable and stable than larger cities. Li et al. [17] applied a numerical simulation and qualitative analysis to investigate a discrete-time susceptible-infectious (SI) compartmental model using the Euler scheme to transform the continuous model into a discrete epidemic model. The complex dynamics of the system were investigated through transcritical bifurcation, Hopf bifurcation, and flip bifurcation. The results indicated that the discrete-time epidemic model has a richer dynamic behavior than the corresponding continuous-time model [17].
Several of the reviewed studies utilized an assessment of LE to draw conclusions regarding evidence of chaotic system behavior. In general, a positive LE value is an indicator of the potential for deterministic chaos in a system whose equations are known; however, for the examined time-series data used in the present study, an LE >0 may not be a sufficient indicator of chaotic behavior since the system equations are unknown [18]. It should also be noted that other studies applied fractal analysis to assess the spread of COVID-19 around the world [19]–[21].
A powerful computational alternative to confirm chaotic system properties is a 0–1 test. This test, first proposed by Gottwald and Melbourne [22], [23] and later improved by Gottwald and Melbourne [24], does not rely on the underlying equation of a system. Also, the 0–1 test is not computationally intensive and does not require phase space reconstruction of the investigated system. The test results close to 1 indicate the presence of chaos, while closer to 0 indicates lack of chaos.
He et al. [25] used an SEIR compartmental model and applied a particle swarm optimization (PSO) algorithm to determine parameters of the model representing the evolution of the COVID-19 pandemic in Hubei province, China. The study also used the 0–1 test to verify the presence of chaos in the system, indicating that the system could produce chaotic behavior in the presence of seasonality and stochastic infection. Recently, Ahmed and Matouk [26] developed an antimicrobial resistance (AMR) model containing both classes of susceptible and resistant features. The study investigated complex dynamics including the existence of homoclinic connections, flip bifurcations, multiple closed invariant curves, and coexistence of multiple attractors. The 0–1 test was successfully applied to verify the existence of chaotic behavior in the system.
IV. Methodology
This section outlines the methodology for the determination of deterministic chaos using the 0–1 test and discusses relevant COVID-19 infection time-series data.
A. Determination of Deterministic Chaos Using the 0–1 Test
The applied 0–1 test procedure using the notation outlined by Gottwald and Melbourne [24] is provided in Appendix.
B. COVID-19 Data Source and Processing
The data used in the present study were collected from Johns Hopkins University (JHU) Center for Systems Science and Engineering (CSSE) COVID-19 Data [27], available in the GitHub online publication by Dong et al. [28]. The files used were ‘time_series_covid19_confirmed_US.csv’ (i.e., US data), containing county-level confirmed cases of COVID for all US states and territories, and ‘time series_covid19_deaths_global. csv’ (i.e., global data), containing similar data for countries and territories worldwide.
The aggregated data sources for these data included World Health Organization (WHO), European Centre for Disease Prevention and Control (ECDPC), US Center for Disease Control (CDC), BNO News, WorldoMeters, COVID Tracking Project, Los Angeles Times, and The Mercury News. In addition, the data provided by the entities authorized to release COVID-19-related data in each country worldwide were utilized. For US states and territories, data released by the county-level authorized bodies were used as the source of the COVID-19 data. These data were adjusted accordingly if any discrepancy was observed or reported. As of 4/26/2021, Google Scholar revealed a total of 4,170 cited data sources [28] when a search using the phrase “An interactive web-based dashboard to track COVID-19 in real-time” was used. Hence, we were able to assure the desired level of data quality control and the upkeep of the data used in the present study.
Data processing was performed using MATLAB (ver. R2020) and pandas (ver. 1.2.0), an open-source data analysis and manipulation library in Python programming language. The two databases used in this study provide the cumulative confirmed cases of COVID-19 by date. For example, daily cumulative COVID-19 time series data can be mathematically shown as:
 |
where
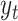 is the cumulative count of COVID-19 confirmed cases for day
is the cumulative count of COVID-19 confirmed cases for day
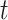 ,
,
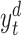 is the daily count of confirmed COVID-19 cases at any day
is the daily count of confirmed COVID-19 cases at any day
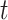 , and
, and
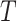 is the number of days contained in the duration of the time series data, i.e.,
is the number of days contained in the duration of the time series data, i.e.,
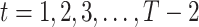 ,
,
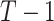 ,
,
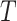 . To calculate
. To calculate
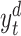 , one can simply use the following mathematical operation.
, one can simply use the following mathematical operation.
 |
In this study, the US data between 1/22/2020 and 12/13/2020 (a day before the COVID vaccination started in the US) were selected for analysis. These county-level cumulative data were first converted into the daily count of confirmed cases using (2) for each county and later grouped by state and territory to secure one time-series data per state/territory for the date range mentioned above. A similar approach was utilized for the global data to identify the daily count of confirmed COVID-19 cases.
V. Results
The results of the 0–1 test for chaotic behavior of the spread of COVID-19 infection based on the daily count of confirmed cases in the US and globally are discussed below.
A. Spread of COVID-19 Infection in the US
For the US, the time-series data for each state from the day of the first confirmed case (COVID-19 infection) were used. The K-median values from the 0–1 test were used to signify whether the time-series infection data exhibited deterministic chaos. The time-series data with K-median values at or greater than 0.9 were classified as chaotic, and those with K-median values less than 0.9 were classified as non-chaotic.
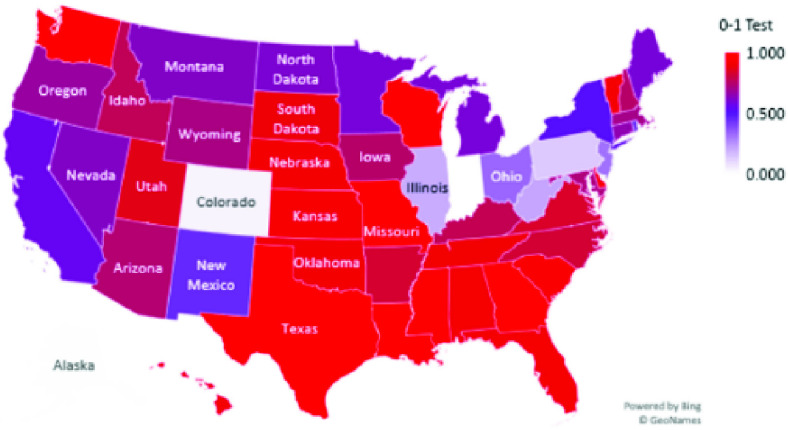
The results show that the spread of COVID-19 infection in 19 out of 50 states was chaotic (39.2%). The states that showed chaotic behavior in the examined time-series data for daily infections were Alabama, Delaware, District of Columbia, Florida, Georgia, Hawaii, Kansas, Louisiana, Mississippi, Missouri, Nebraska, Oklahoma, South Carolina, South Dakota, Tennessee, Texas, Vermont, Washington, and Wisconsin. Table 1 shows the K-median values from the 0–1 test for the confirmed daily COVID-19 cases by US state. In addition, Figure 1 illustrates a geographical map of US states, with the red color signifying chaotic behavior of the time-series data representing daily spread of infections.
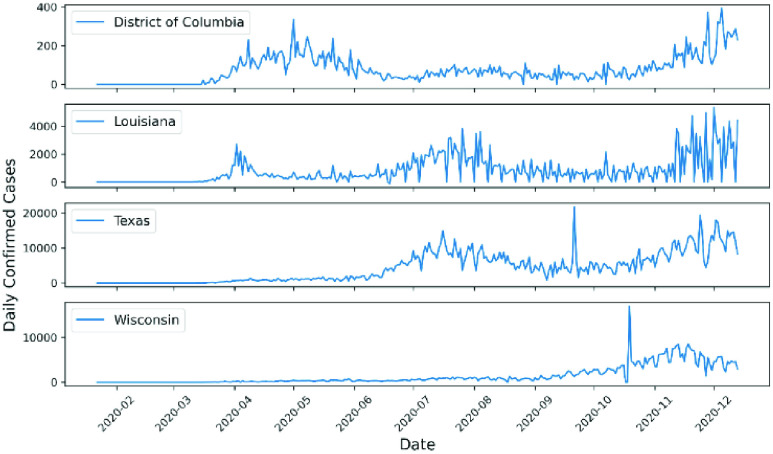
FIGURE 2.
Examples of confirmed daily COVID-19 cases for states showing chaotic behavior.
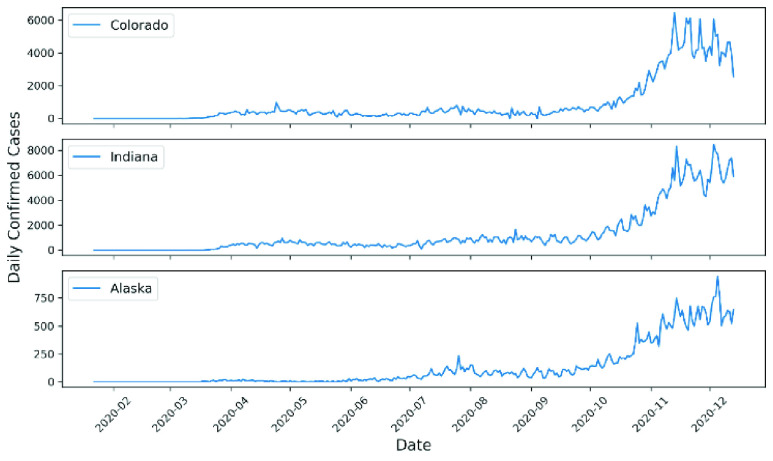
FIGURE 3.
Examples of confirmed daily COVID-19 cases for states showing non-chaotic behavior.
TABLE 1. K-Median Values From the 0–1 Test for Confirmed Daily COVID-19 Cases in the US by State.
| States | K-median | Population Estimate | Total Confirmed Cases |
|---|---|---|---|
| Georgia | 1 | 10,617,423 | 54,284 |
| DC. | 0.9761 | 705,749 | 2,487 |
| Texas | 0.9721 | 28,995,881 | 140,911 |
| Wisconsin | 0.9666 | 5,822,434 | 46,896 |
| Louisiana | 0.9664 | 4,648,794 | 26,861 |
| Missouri | 0.962 | 6,137,428 | 35,318 |
| Washington | 0.9583 | 7,614,893 | 20,206 |
| Mississippi | 0.9511 | 2,976,149 | 17,945 |
| South Carolina | 0.935 | 5,148,714 | 25,221 |
| Delaware | 0.9277 | 973,764 | 4,546 |
| Kansas | 0.921 | 2,913,314 | 18,846 |
| Nebraska | 0.9161 | 1,934,408 | 14,886 |
| Alabama | 0.9152 | 4,903,185 | 29,563 |
| Vermont | 0.9145 | 623,989 | 575 |
| Florida | 0.9133 | 21,477,737 | 112,593 |
| Oklahoma | 0.9088 | 3,956,971 | 23,767 |
| Hawaii | 0.9086 | 1,415,872 | 1,959 |
| Tennessee | 0.9051 | 6,829,174 | 45,431 |
| South Dakota | 0.901 | 884,659 | 9,104 |
| Utah | 0.86 | 3,205,958 | 23,390 |
| Virginia | 0.8332 | 8,535,519 | 28,191 |
| Arkansas | 0.8224 | 3,017,804 | 18,570 |
| North Carolina | 0.817 | 10,488,084 | 43,660 |
| Kentucky | 0.7762 | 4,467,673 | 22,310 |
| Idaho | 0.7711 | 1,787,065 | 12,118 |
| Iowa | 0.7473 | 3,155,070 | 25,625 |
| New Hampshire | 0.747 | 1,359,711 | 3,096 |
| Arizona | 0.7394 | 7,278,717 | 40,844 |
| Maryland | 0.728 | 6,045,680 | 23,465 |
| Wyoming | 0.7137 | 578,759 | 3,936 |
| Massachusetts | 0.7057 | 6,892,503 | 29,058 |
| Oregon | 0.6744 | 4,217,737 | 9,385 |
| Connecticut | 0.6512 | 3,565,287 | 14,676 |
| Nevada | 0.6224 | 3,080,156 | 18,683 |
| Montana | 0.6222 | 1,068,778 | 7,330 |
| North Dakota | 0.607 | 762,062 | 8,787 |
| Minnesota | 0.5992 | 5,639,632 | 37,882 |
| Michigan | 0.5982 | 9,986,857 | 46,516 |
| Maine | 0.5969 | 1,344,212 | 1,592 |
| California | 0.5585 | 39,512,223 | 158,538 |
| New York | 0.5145 | 19,453,561 | 77,516 |
| New Mexico | 0.4502 | 2,096,829 | 11,980 |
| Rhode Island | 0.4467 | 1,059,361 | 7,082 |
| Ohio | 0.3307 | 11,689,100 | 56,273 |
| New Jersey | 0.3113 | 8,882,190 | 40,065 |
| West Virginia | 0.212 | 1,792,147 | 6,322 |
| Illinois | 0.1971 | 12,671,821 | 84,890 |
| Pennsylvania | 0.1349 | 12,801,989 | 49,510 |
| Colorado | 0.0323 | 5,758,736 | 28,819 |
| Alaska | 0.0024 | 731,545 | 4,114 |
| Indiana | 0 | 6,732,219 | 42,543 |
FIGURE 1.
K-Median Values From the 0–1 Test for Confirmed Daily COVID-19 Cases in the US.
B. Spread of COVID-19 Infection on a Global Scale
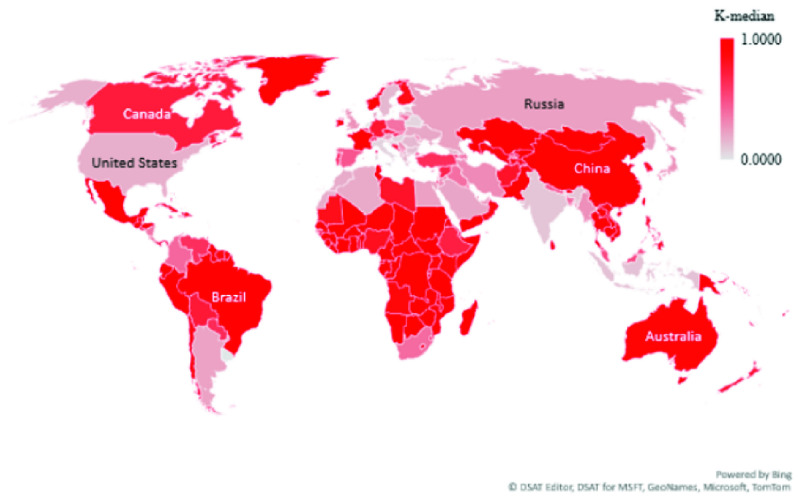
The results of the 0–1 test with K-median values for the daily count of confirmed cases of COVID in different continents, countries and territories on the global scale are depicted in Tables 2 and 3 and are illustrated in Figures 4–5. Figure 4 shows the geographical map with red color signifying chaotic behavior. Overall, 118 countries out of a total of 213 countries/territories (55%) exhibited chaotic behavior of the spread of COVID-19 infections. The Department of Economic and Social Affairs of the United Nations Secretariat (UN/DESA) classifies all countries and territories into three broad categories: 1) developed economies, 2) economies in transition, and 3) developing economies based on various econometric measures [29]. Table 4 shows that the proportion of developing countries or territories showing chaotic time series of daily confirmed COVID-19 cases was 68.3% (110 out of 161). In contrast, the same proportion for the developed and ‘in-transition countries or territories was 13.9% (5 out 36) and 18.8% (3 out of 16), respectively. This data indicates that Europe still was better off in terms of the proportion of countries with chaotic spread of infections (11 out of 32 or 34.4%). In contrast, the same figure was 86% for Sub-Sharan Africa and 70% for Latin America and the Caribbean (Table 5). The above provides convincing evidence that the likelihood of these countries and territories to have chaotic behavior in COVID-19 daily infection number is greater than that of their Asian counterpart, where this proportion was only 46.4% (13 out of 28), with Japan being designated as ‘developed’ country and removed from the calculation shown in Table 2.
TABLE 2. Results From 0–1 Test for Chaos for Daily COVID-19 Confirmed Cases Globally (Excluding the United States).
| Continent/Subcontinent | Number of countries and territories | K-median >0.90 | Percentage out of the group |
|---|---|---|---|
| Australia/New Zealand | 2 | 1 | 50% |
| Central and Southern Asia | 13 | 5 | 38% |
| Eastern and South-Eastern Asia | 16 | 8 | 50% |
| Europe | 48 | 14 | 29% |
| Latin America And the Caribbean | 47 | 33 | 70% |
| Northern Africa And Western Asia | 24 | 4 | 17% |
| Northern America | 5 | 3 | 60% |
| Oceania (Excluding Australia And New Zealand) | 8 | 7 | 88% |
| Sub-Saharan Afica | 50 | 43 | 86% |
| Total: | 213 | 118 | 55% |
TABLE 3. Results of the 0–1 Test for Specific Countries/Territories (N = 213).
| Country/Region | K-median |
|---|---|
| Solomon Islands | 1 |
| Antigua and Barbuda | 0.999 |
| Holy See | 0.999 |
| Kyrgyzstan | 0.999 |
| Saint Vincent and the Grenadines | 0.999 |
| Marshall Islands | 0.999 |
| Equatorial Guinea | 0.999 |
| Timor-Leste | 0.999 |
| Seychelles | 0.998 |
| Bhutan | 0.998 |
| Kazakhstan | 0.998 |
| Samoa | 0.998 |
| St. Martin | 0.998 |
| Barbados | 0.997 |
| Burundi | 0.997 |
| Sao Tome and Principe | 0.997 |
| Congo (Brazzaville) | 0.997 |
| Mayotte | 0.997 |
| Saint Barthelemy | 0.997 |
| Ecuador | 0.997 |
| Benin | 0.997 |
| Dominica | 0.997 |
| Guinea | 0.996 |
| Cambodia | 0.996 |
| South Sudan | 0.996 |
| Cameroon | 0.996 |
| Zimbabwe | 0.996 |
| Liberia | 0.996 |
| Comoros | 0.995 |
| Eritrea | 0.995 |
| Lesotho | 0.995 |
| Somalia | 0.995 |
| Mongolia | 0.994 |
| Saint Pierre and Miquelon | 0.994 |
| Cayman | 0.994 |
| Sudan | 0.994 |
| Sint Maarten | 0.994 |
| Peru | 0.994 |
| Togo | 0.994 |
| Tanzania | 0.993 |
| Burkina Faso | 0.993 |
| Sierra Leone | 0.992 |
| British Virgin Islands | 0.992 |
| Guadeloupe | 0.992 |
| Rwanda | 0.992 |
| Bahamas | 0.992 |
| Cuba | 0.992 |
| Fiji | 0.991 |
| Vietnam | 0.991 |
| Bonaire and Saba | 0.991 |
| Monaco | 0.99 |
| New Caledonia | 0.99 |
| Turks and Caicos Islands | 0.99 |
| Ghana | 0.99 |
| Gabon | 0.99 |
| Chad | 0.99 |
| Zambia | 0.989 |
| Gambia | 0.989 |
| Papua New Guinea | 0.989 |
| Laos | 0.989 |
| Congo (Kinshasa) | 0.988 |
| Faroe Island | 0.988 |
| Martinique | 0.987 |
| Guinea-Bissau | 0.987 |
| Trinidad and Tobago | 0.987 |
| Malawi | 0.986 |
| Gibraltar | 0.986 |
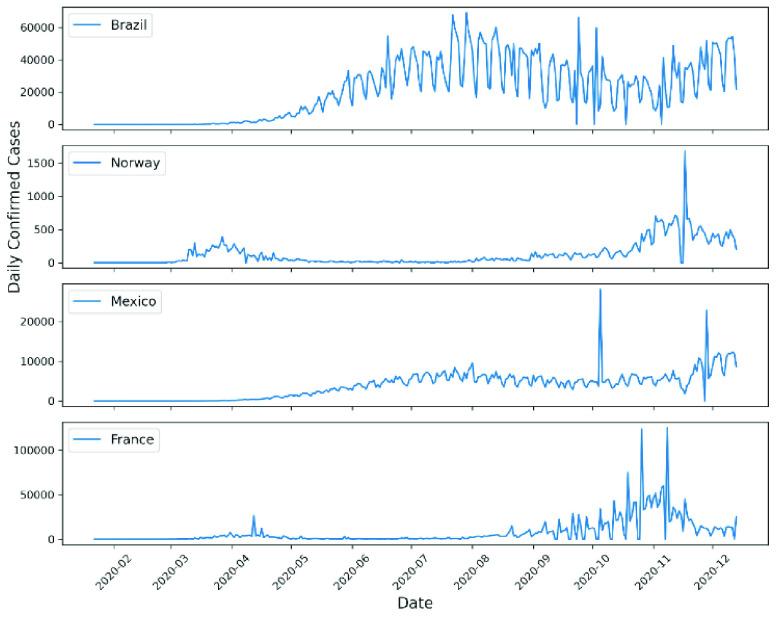
| Mexico | 0.985 |
| Yemen | 0.984 |
| Grenada | 0.984 |
| Central Afican Republic | 0.984 |
| Haiti | 0.983 |
| Pakistan | 0.983 |
| Norway | 0.983 |
| Guatemala | 0.982 |
| Djibouti | 0.982 |
| Botswana | 0.982 |
| Mali | 0.982 |
| Guyana | 0.981 |
| Jamaica | 0.979 |
| France | 0.978 |
| El Salvador | 0.978 |
| France | 0.978 |
| Taiwan | 0.978 |
| French Guiana | 0.976 |
| Cabo Verde | 0.976 |
| San Marino | 0.975 |
| Dominican Republic | 0.973 |
| Tunisia | 0.972 |
| Mauritius | 0.972 |
| Maldives | 0.97 |
| Brazil | 0.969 |
| Senegal | 0.968 |
| Bermuda | 0.967 |
| Honduras | 0.967 |
| French Polynesia | 0.965 |
| Madagascar | 0.965 |
| Greenland | 0.965 |
| Kosovo | 0.963 |
| Saint Kitts and Nevis | 0.962 |
| Eswatini | 0.962 |
| China | 0.957 |
| Saint Lucia | 0.955 |
| Andorra | 0.954 |
| Channel Islands | 0.953 |
| Namibia | 0.949 |
| Cote d’lvoire | 0.949 |
| Montserrat | 0.949 |
| Mozambique | 0.94 |
| Thailand | 0.935 |
| Iceland | 0.927 |
| Liechtenstein | 0.925 |
| Niger | 0.919 |
| Israel | 0.917 |
| Australia | 0.914 |
| Montenegro | 0.907 |
| Ireland | 0.903 |
| Panama | 0.903 |
| Uganda | 0.901 |
| Suriname | 0.892 |
| Malta | 0.889 |
| Belize | 0.888 |
| Kenya | 0.888 |
| Falkland Islands (Malvinas) | 0.875 |
| Diamond Princess | 0.874 |
| Uzbekistan | 0.873 |
| Angola | 0.866 |
| Sri Lanka | 0.86 |
| Tajikistan | 0.859 |
| Singapore | 0.851 |
| Oman | 0.849 |
| Chile | 0.845 |
| Philippines | 0.839 |
| Bahrain | 0.835 |
| Brunei | 0.831 |
| Finland | 0.83 |
| Kuwait | 0.826 |
| Curacao | 0.824 |
| Mauritania | 0.815 |
| Reunion | 0.811 |
| Luxembourg | 0.8 |
| Korea South | 0.8 |
| Nigeria | 0.795 |
| New Zealand | 0.775 |
| Libya | 0.774 |
| Afghanistan | 0.772 |
| Bosnia and Herzegovina | 0.759 |
| Germany | 0.757 |
| Czechia | 0.747 |
| Armenia | 0.738 |
| Bolivia | 0.73 |
| Slovakia | 0.713 |
| Canada | 0.71 |
| Ethiopia | 0.693 |
| Syria | 0.668 |
| Anguilla | 0.644 |
| MS Zaandam | 0.639 |
| Paraguay | 0.636 |
| Turkey | 0.63 |
| Venezuela | 0.618 |
| Portugal | 0.615 |
| Switzerland | 0.606 |
| Belgium | 0.598 |
| Malaysia | 0.51 |
| Cyprus | 0.48 |
| Spain | 0.467 |
| Nepal | 0.457 |
| Lebanon | 0.436 |
| Bangladesh | 0.419 |
| Lithuania | 0.417 |
| Moldova | 0.415 |
| Spain | 0.407 |
| Colombia | 0.405 |
| South Africa | 0.392 |
| Iraq | 0.378 |
| Poland | 0.377 |
| Qatar | 0.367 |
| Nicaragua | 0.367 |
| Costa Rica | 0.353 |
| Azerbaijan | 0.351 |
| Jordan | 0.301 |
| Iran | 0.299 |
| Serbia | 0.292 |
| United Arab Emirates | 0.289 |
| Burma | 0.279 |
| United Kingdom | 0.277 |
| Japan | 0.269 |
| Austria | 0.245 |
| Russia | 0.231 |
| Egypt | 0.228 |
| Argentina | 0.223 |
| Saudi Arabia | 0.213 |
| Ukraine | 0.209 |
| Algeria | 0.193 |
| Morocco | 0.19 |
| US | 0.183 |
| Denmark | 0.177 |
| Vanuatu | 0.173 |
| Latvia | 0.171 |
| North Macedonia | 0.161 |
| Georgia | 0.157 |
| Albania | 0.157 |
| Sweden | 0.155 |
| Romania | 0.152 |
| Greece | 0.148 |
| Slovenia | 0.137 |
| Bulgaria | 0.125 |
| Indonesia | 0.121 |
| India | 0.114 |
| Croatia | 0.091 |
| Hungary | 0.083 |
| Estonia | 0.068 |
| Italy | 0.066 |
| Belarus | 0.065 |
| West Bank and Gaza | 0.057 |
| Netherlands | 0.017 |
| Uruguay | 0 |
FIGURE 4.
Results of the 0–1 test for confirmed daily COVID-19 cases globally.
FIGURE 5.
Examples of confirmed daily COVID-19 cases for countries showing chaotic behavior.
TABLE 4. Economic Status of the Countries and Time Series Data of Daily-Confirmed Cases (Excluding the United States).
| Economic Status | Number of countries or territories in the economic development category | K-Median > 0.9 | |
|---|---|---|---|
| Count | % within category | ||
| Developed countries | 36 | 5 | 13.9% |
| Economy-in-Transition | 16 | 3 | 18.8% |
| Developing countries | 161 | 110 | 68.3% |
| Total | 213 | 118 | 54.9% |
VI. Discussion
In the present study, only confirmed daily COVID-19 cases were subjected to nonlinear dynamics analysis. The available data for the number of hospitalizations, daily number of deaths, and number of recoveries were not considered here. While the time-series data for daily infections in the entire US were not found to be chaotic, results of the state-level analysis indicate that the confirmed COVID-19 infections for more than 35% of the states showed chaotic behavior. It should be noted that the US is one of the largest countries in the world and many of its states are comparable with other countries with respect to population size.
Given the fact that Italy, Spain, and the United Kingdom were greatly affected at the beginning of the pandemic in Europe, we also expected that such countries would also exhibit chaotic behavior in their reported daily infection data; however, this was not the case. It can be hypothesized that if the spread of infection in these countries was analyzed on a smaller scale— by recognized regions— the results may be different. For example, England (part of the UK) has nine recognized regions, and if London were to be considered separately, England alone would have ten-fold more data as compared with, for example, merged infection data for Northern Ireland and Scotland. In Asia, a similar situation could occur in countries such as India due to their large geographic size (28 states and 8 Union Territories) and massive population.
VII. Limitations of the Study
We note several limitations of our methodology and results. The present study did not consider other important factors that may play a vital role in providing the ability to assess dynamics of the spread of COVID-19 infection, including for example, demographic and socioeconomic data such as income, education, employment, proportion of people under the poverty line, total population, population density, or urban vs. non-urban population. In addition, data regarding the relevant sociopolitical factors, government regulations, and public health policies should also be considered to improve our understanding of the nonlinear dynamics of the spread of COVID-19 infection worldwide and develop effective countermeasures. In future work, the largest Lyapunov exponent of each time-series data for daily infections should also be assessed to verify the current results.
VIII. Conclusion
In the present study, time-series data representing the spread of infections based on the confirmed daily cases of COVID-19 during the period of 1/22/2020 to 12/13/2020 were investigated for the presence of chaos. The results showed that in most countries and territories irrespective of the continent, the data spread of COVID-19 infection exhibited chaotic behavior. The nature of deterministic chaos data renders it difficult to predict the dynamics of a pandemic in the long term [30].
Finally, our results confirm the conclusions made by Jones and Stirgul [6], who suggested that the COVID-19 epidemic demonstrates chaotic behavior that should inform future public health policies. Clearly, other data regarding the relevant sociopolitical factors, government regulations, and public health policies should be considered to improve our understanding of the nonlinear dynamics of the spread of COVID-19 infection worldwide and develop effective countermeasures. In addition, an evolutionary self-organizing map (ESOM) methodology [31] should be applied in the future to test the predictability of infection spread models.
Biographies

Nabin Sapkota received the M.S. and Ph.D. degrees in industrial engineering from the University of Central Florida, Orlando, FL, USA, in 2003 and 2006, respectively. He is currently an Associate Professor with the Department of Engineering Technology, Northwestern State University of Louisiana. His research interests include applications of soft computing and nonlinear dynamics, advanced application of statistics, optimization problem generations, and applications of digital simulation.

Waldemar Karwowski (Senior Member, IEEE) received the M.S. degree in production engineering and management from the Technical University of Wroclaw, Poland, in 1978, and the Ph.D. degree in industrial engineering from Texas Tech University, in 1982. He is currently the Pegasus Professor and the Chairman of the Department of Industrial Engineering and Management Systems and the Executive Director of the Institute for Advanced Systems Engineering, University of Central Florida, Orlando, FL, USA. He has over 500 publications focused on mathematical modeling and computer simulation with applications to human–systems engineering, human-centered-design, safety, neuro-fuzzy systems, nonlinear dynamics and chaos, and neuroergonomics. He also serves as the Co-Editor-in-Chief for the Journal Theoretical Issues in Ergonomics Science (Taylor and Francis Ltd.), the Editor-in-Chief for the Human-Intelligent Systems Integration Journal (Springer), and the Field Chief Editor for the Frontiers in Neuroergonomics Journal.

Mohammad Reza Davahli received the B.S. degree in civil engineering from the Isfahan University of Technology, Iran, in 2008. He is currently pursuing the Ph.D. degree with the Industrial Engineering and Management Systems Program, University of Central Florida. For five years, he worked as a Data Analyst with Kayson Company, which is one of the leading engineering, procurement, and construction companies. He is also a Research Assistant, advised by Prof. W. Karwowski. His current research interests include time-series data analysis and sequence-learning predictive models.

Awad Al-Juaid received the B.S. degree in systems engineering from the King Fahd University of Petroleum and Minerals, Saudi Arabia, in 2003, the M.S. degree in industrial engineering from King Abdulaziz University, Saudi Arabia, in 2009, and the Ph.D. degree in industrial engineering from the University of Central Florida, USA, in 2016. He is currently an Associate Professor with the Industrial Engineering Department, Taif University (TU), Saudi Arabia. He was working as a Safety Engineer with SABIC, in 2003, and a Planning Engineer with SCECO, for seven years. He is also the former Dean of the University Development Deanship, TU, and the Director of the Strategic Planning and Information Department, TU. He has several publications focused on, neuroergonomic, safety, quality assurance, planning, neuro-fuzzy systems, and supply chain management. He also serves as an Editor for the Journal Theoretical Issues in Ergonomics Science (Taylor and Francis Ltd.), and a reviewer and a consultant for institutional accreditation in Saudi Arabia.

Redha Taiar is currently a Professor with the University of Reims Champaign, France. His past and present positions include the Head of the European Master of Biomechanics, Ergonomics and Clinical Research; the Head of the University Diploma of Podiatrics; the Head of the University Diploma of Ergonomics; the Head of the Laboratory of Biomechanics, University of Reims; the Vice Head of the Department of Sport Science; the Head of Redha Taiar Biomechanical Engineering (RTBE) Society developed for Sport and medical advice for industry; and the Vice Head of the Congress of Physical Medicine and Rehabilitation Society (SOFMER) Reims, France. His research interests include the industry engineering for medicine and high-level sport.

Atsuo Murata received the M.E. and Ph.D. degrees in industrial engineering from the University of Osaka Prefecture, in 1985 and 1987, respectively. From 1997 to 2006, he was a Professor with Hiroshima City University. Since 2006, he has been a Professor with the Department of Intelligent Mechanical Systems, Okayama University. His current research interests include accident analysis and safety management, and automotive ergonomics.

Grzegorz Wróbel received the M.S. degree in finance and banking from the Cracow University of Economics, Poland, in 1998, and the Ph.D. degree in production engineering from the Warsaw University of Technology, Poland, in 2003. He is currently an Assistant Professor with the Department of Logistics and Process Engineering, University of Information Technology and Management in Rzeszow, Rzeszow, Poland. He has over 30 publications focusing on object modeling, computer simulation, and management systems. He is also a Certified Professional Specialist with Kaizen Institute Poland. He also manages the Laboratory of Business Process Simulation and Optimization, University of Information Technology and Management in Rzeszow.

Tadeusz Marek is currently a Professor of psychology with Jagiellonian University, Krakow, Poland, and the Chairman of the Department of Cognitive Neuroscience and Neuroergonomics, Institute of Applied Psychology. He is the past Vice Rector (Vice Chancellor) of Jagiellonian University and the past President of the Committee on Ergonomics, Polish Academy of Sciences. He is the author/coauthor of over 300 research publications. His research interests include cognitive neuroscience, chronopsychology, neuroadaptive technologies, neuroergonomics, and human factors.
Appendix: Procedure for 0–1 Test
The 0–1 test procedure using the notation outlined by Gottwald and Melbourne [24] is as follows:
-
Step 1.
Define a time series
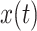 for t = 1,
for t = 1,
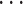 , N, where
, N, where
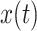 is the time-series value at time t. Additionally, define a set
is the time-series value at time t. Additionally, define a set
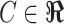 of non-negative random values. Gottwald and Melbourne [24] suggested random values for
of non-negative random values. Gottwald and Melbourne [24] suggested random values for
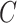 in the interval (0,
in the interval (0,
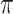 ); therefore, in the present study, values for
); therefore, in the present study, values for
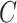 are in the interval (
are in the interval (
 /5,
/5,
 /5) to avoid resonances distorting the statistics. While
/5) to avoid resonances distorting the statistics. While
 must be avoided, and exclusion of
must be avoided, and exclusion of
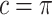 , is not necessary, the authors found the above procedure helpful.
, is not necessary, the authors found the above procedure helpful. -
Step 2.For each
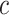 :
:
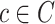 , and
, and
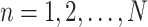 , compute the translation variables
, compute the translation variables
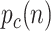 and
and
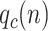 as follows:
as follows: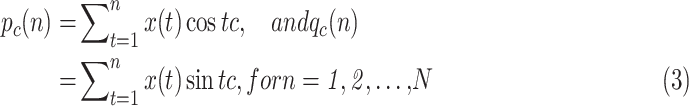
After step 2, this procedure generates
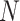 sets
sets
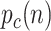 and
and
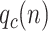 for each
for each
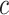 :
:
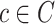 considered.
considered. -
Step 3.Compute the mean square displacement for the translation variables (i.e., Fourier coefficients)
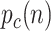 and
and
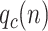 as follows:
as follows: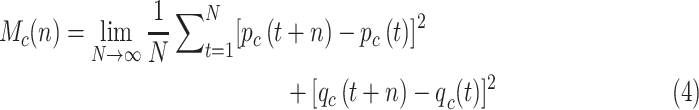
According to Gottwald and Melbourne [23], [24], for the time series with regular dynamics, the mean square displacement is a bounded function in time whereas it scales linearly with time (
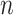 ) if the time series is chaotic. In such a case, the plot of
) if the time series is chaotic. In such a case, the plot of
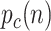 vs.
vs.
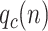 looks like an irregular not bounded function in time. Gottwald and Melbourne [24] suggested that this definition of mean square displacement requires that be much less than
looks like an irregular not bounded function in time. Gottwald and Melbourne [24] suggested that this definition of mean square displacement requires that be much less than
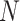 or
or
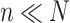 . Gottwald and Melbourne [24] also suggested selection of
. Gottwald and Melbourne [24] also suggested selection of
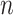 such that
such that
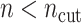 where
where
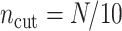 , and reported that this scheme of selecting
, and reported that this scheme of selecting
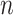 produced good results (plots) showing regular dynamics and chaotic dynamics clearly in a
produced good results (plots) showing regular dynamics and chaotic dynamics clearly in a
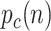 vs.
vs.
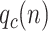 graph.
graph. -
Step 4.The
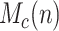 vs.
vs.
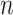 plot shows increasing linearity with
plot shows increasing linearity with
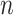 ; however, there is an oscillation confounded with
; however, there is an oscillation confounded with
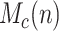 . To smooth this oscillation, Gottwald and Melbourne [24] suggested using the modified mean square displacement for the translation variables, which can be defined as follows:
. To smooth this oscillation, Gottwald and Melbourne [24] suggested using the modified mean square displacement for the translation variables, which can be defined as follows:
where
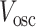 (
(
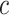 ,
,
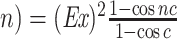 and Et
and Et
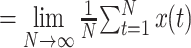
-
Step 5.Finally,
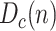 s values from step 4 were used to estimate the asymptotic growth rate,
s values from step 4 were used to estimate the asymptotic growth rate,
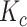 . Using the correlation method, the asymptotic growth rate
. Using the correlation method, the asymptotic growth rate
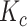 can be calculated as follows:
can be calculated as follows:
where
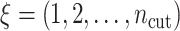 and
and
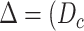 (1),
(1),
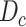 (2),
(2),
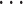 ,
,
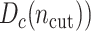 and cov(
and cov(
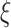 ,
,
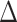 ) is the covariance between vectors
) is the covariance between vectors
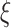 and
and
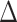 . Finally, Gottwald and Melbourne [32] also provided theoretical proof that their test yields a value of 0 for periodic and quasi-periodic dynamics and a value of 1 for nonlinear (chaotic) systems.
. Finally, Gottwald and Melbourne [32] also provided theoretical proof that their test yields a value of 0 for periodic and quasi-periodic dynamics and a value of 1 for nonlinear (chaotic) systems.
Funding Statement
This work was supported in part by the Research Grant from the Taif University Researchers Supporting Project, Taif University, Taif, Saudi Arabia, under Grant TURSP-2020/229.
References
- [1].Mangiarotti S., Peyre M., Zhang Y., Huc M., Roger F., and Kerr Y., “Chaos theory applied to the outbreak of COVID-19: An ancillary approach to decision making in pandemic context,” Epidemiol. Infection, vol. 148, p. e95, May 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Davahli M. R., Karwowski W., Sonmez S., and Apostolopoulos Y., “The hospitality industry in the face of the COVID-19 pandemic: Current topics and research methods,” Int. J. Environ. Res. Public Health, vol. 17, no. 20, p. 7366, Oct. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Nicola M., Alsafi Z., Sohrabi C., Kerwan A., Al-Jabir A., Iosifidis C., Agha M., and Agha R., “The socio-economic implications of the coronavirus pandemic (COVID-19): A review,” Int. J. Surg., vol. 78, pp. 185–193, Jun. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Postavaru O., Anton S. R., and Toma A., “COVID-19 pandemic and chaos theory,” Math. Comput. Simul., vol. 181, pp. 138–149, Mar. 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Zheng H. and Bonasera A., “Chaos, percolation and the coronavirus spread: A two-step model,” Eur. Phys. J. Plus, vol. 135, no. 10, pp. 1–24, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Jones A. and Strigul N., “Is spread of COVID-19 a chaotic epidemic?” Chaos, Solitons Fractals, vol. 142, Jan. 2021, Art. no. 110376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Bonasera A. and Zhang S., “Chaos, percolation and the coronavirus spread,” Frontiers Phys., vol. 8, p. 171, Apr. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Matouk A. E., “Complex dynamics in susceptible-infected models for COVID-19 with multi-drug resistance,” Chaos, Solitons Fractals, vol. 140, Nov. 2020, Art. no. 110257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Raj V., Renjini A., Swapna M. S., Sreejyothi S., and Sankararaman S., “Nonlinear time series and principal component analyses: Potential diagnostic tools for COVID-19 auscultation,” Chaos, Solitons Fractals, vol. 140, Nov. 2020, Art. no. 110246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Pedro S. A., Abelman S., Ndjomatchoua F. T., Sang R., and Tonnang H. E. Z., “Stability, bifurcation and chaos analysis of vector-borne disease model with application to rift valley fever,” PLoS ONE, vol. 9, no. 10, Oct. 2014, Art. no. e108172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Billings L. and Schwartz I. B., “Exciting chaos with noise: Unexpected dynamics in epidemic outbreaks,” J. Math. Biol., vol. 44, no. 1, pp. 31–48, Jan. 2002. [DOI] [PubMed] [Google Scholar]
- [12].Sun G.-Q., Jin Z., Liu Q.-X., and Li L., “Chaos induced by breakup of waves in a spatial epidemic model with nonlinear incidence rate,” J. Stat. Mech., Theory Exp., vol. 2008, no. 8, Aug. 2008, Art. no. P08011. [Google Scholar]
- [13].Eilersen A., Jensen M. H., and Sneppen K., “Chaos in disease outbreaks among prey,” Sci. Rep., vol. 10, no. 1, pp. 1–7, Mar. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].He S. and Banerjee S., “Epidemic outbreaks and its control using a fractional order model with seasonality and stochastic infection,” Phys. A, Stat. Mech. Appl., vol. 501, pp. 408–417, Jul. 2018. [Google Scholar]
- [15].Yi N., Zhang Q., Mao K., Yang D., and Li Q., “Analysis and control of an SEIR epidemic system with nonlinear transmission rate,” Math. Comput. Model., vol. 50, nos. 9–10, pp. 1498–1513, Nov. 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Grenfell B. T., Bjørnstad O. N., and Finkenstädt B. F., “Dynamics of measles epidemics: Scaling noise, determinism, and predictability with the TSIR model,” Ecol. Monographs, vol. 72, no. 2, pp. 185–202, May 2002. [Google Scholar]
- [17].Li L., Sun G.-Q., and Jin Z., “Bifurcation and chaos in an epidemic model with nonlinear incidence rates,” Appl. Math. Comput., vol. 216, no. 4, pp. 1226–1234, Apr. 2010. [Google Scholar]
- [18].Thiel M., Kurths J., Romano M. C., Károlyi G., and Moura A., Eds., Nonlinear Dynamics and Chaos: Advances and Perspectives. New York, NY, USA: Springer, 2010. [Online]. Available: https://link.springer.com/content/pdf/10.1007%2F978-3-642-04629-2.pdf [Google Scholar]
- [19].Castillo O. and Melin P., “Forecasting of COVID-19 time series for countries in the world based on a hybrid approach combining the fractal dimension and fuzzy logic,” Chaos, Solitons Fractals, vol. 140, Nov. 2020, Art. no. 110242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Abbasi M., Bollini A. L., Castillo J. L. B., Deppman A., Guidio J. P., Matuoka P. T., Meirelles A. D., Policarpo J. M. P., Ramos A. A. G. F., Simionatto S., Varona A. R. P., E. Andrade, II, Panjeh H., and Trevisan L. A., “Fractal signatures of the COVID-19 spread,” Chaos, Solitons Fractals, vol. 140, Nov. 2020, Art. no. 110119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Păcurar C.-M. and Necula B.-R., “An analysis of COVID-19 spread based on fractal interpolation and fractal dimension,” Chaos, Solitons Fractals, vol. 139, Oct. 2020, Art. no. 110073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Geory G. A. and Melbourne I., “A new test for chaos in deterministic systems,” Proc. Roy. Soc. London A, Math., Phys. Eng. Sci., vol. 460, no. 2042, pp. 603–611, Feb. 2004. [Google Scholar]
- [23].Gottwald G. A. and Melbourne I., “Testing for chaos in deterministic systems with noise,” Phys. D, Nonlinear Phenomena, vol. 212, nos. 1–2, pp. 100–110, Dec. 2005. [Google Scholar]
- [24].Gottwald G. A. and Melbourne I., “On the implementation of the 0–1 test for chaos,” SIAM J. Appl. Dyn. Syst., vol. 8, no. 1, pp. 129–145, Jan. 2009. [Google Scholar]
- [25].He S., Peng Y., and Sun K., “SEIR modeling of the COVID-19 and its dynamics,” Nonlinear Dyn., vol. 101, no. 3, pp. 1667–1680, Jun. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Ahmed E. and Matouk A. E., “Complex dynamics of some models of antimicrobial resistance on complex networks,” Math. Methods Appl. Sci., vol. 44, no. 2, pp. 1896–1912, Jan. 2021. [Google Scholar]
- [27].Hopkins J.. (2020). COVID-19 Dashboard by the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University (JHU). Johns Hopkins University, Baltimore, MD, USA. [Online]. Available: https://github.com/CSSEGISandData/COVID-19 [Google Scholar]
- [28].Dong E., Du H., and Gardner L., “An interactive Web-based dashboard to track COVID-19 in real time,” Lancet Infectious Diseases, vol. 20, no. 5, pp. 533–534, May 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].United Nations. The World Economic Situation and Prospects 2014. Accessed: 2017. [Online]. Available: https://www.un.org/en/development/desa/policy/wesp/wesp_current/wesp2014.pdf [Google Scholar]
- [30].Karwowski W., Sapkota N., Servi L. D., Schmorrow D., and Gutierrez E., “Evidence of chaos in human emotions expressed in tweets,” Nonlinear Dyn. Psychol. Life Sci., vol. 24, no. 4, pp. 475–497, Oct. 2020. [PubMed] [Google Scholar]
- [31].Sapkota N., Karwowski W., and Ahram T., “Application of evolving self-organizing maps for analysis of human adverse events in the context of complex socioeconomic infrastructure interactions,” IEEE Trans. Human-Mach. Syst., vol. 45, no. 4, pp. 500–509, Aug. 2015. [Google Scholar]
- [32].Gottwald G. A. and Melbourne I., “On the validity of the 0–1 test for chaos,” Nonlinearity, vol. 22, no. 6, p. 1367, May 2009. [Google Scholar]