Abstract
The spread of epidemics and diseases is known to exhibit chaotic dynamics; a fact confirmed by many developed mathematical models. However, to the best of our knowledge, no attempt to realize any of these chaotic models in analog or digital electronic form has been reported in the literature. In this work, we report on the efficient FPGA implementations of three different virus spreading models and one disease progress model. In particular, the Ebola, Influenza, and COVID-19 virus spreading models in addition to a Cancer disease progress model are first numerically analyzed for parameter sensitivity via bifurcation diagrams. Subsequently and despite the large number of parameters and large number of multiplication (or division) operations, these models are efficiently implemented on FPGA platforms using fixed-point architectures. Detailed FPGA design process, hardware architecture and timing analysis are provided for three of the studied models (Ebola, Influenza, and Cancer) on an Altera Cyclone IV EP4CE115F29C7 FPGA chip. All models are also implemented on a high performance Xilinx Artix-7 XC7A100TCSG324 FPGA for comparison of the needed hardware resources. Experimental results showing real-time control of the chaotic dynamics are presented.
Keywords: Chaos, chaotic circuits, epidemic models, FPGA implementations
I. Introduction
Deterministic chaos is a common behavior in continuous-time dynamical systems of differential equations with nonlinear terms, which exhibit aperiodicity, ergodicity and sensitivity to initial conditions [1]. These properties of chaotic systems are needed in many applications such as modeling of robots [2], motion control [3], Random Number Generation and encryption applications [4]. This demand on chaotic systems in various applications has encouraged the exploration of different methods for their analog and digital hardware realizations [5]–[7]. Meanwhile, mathematical models of biological systems have been associated with chaotic behavior long before the emergence of chaos theory and dates back to the logistic equation model of population growth [8]. Epidemics and infectious diseases modeling is a relatively difficult problem, since their dynamics vary largely from one outbreak to another. For such emerging and reemerging diseases, the causes and transfer processes are often poorly known and understood. Susceptible, infected, recovered and possibly also exposed classes of a given population need to be considered. Many models have been developed for viral infectious diseases such as Influenza and Ebola [9]–[14] and nearly all of them show chaotic dynamics even after vaccination is administrated [15]. The emergence of chaotic behavior can be attributed mostly to predator-prey and competition dynamics [16]–[18] as well as nonlinear interactions between cell populations such as in cancer models [19]–[22] and Parkinson’s disease [23], [24].
Recently, following the COVID-19 epidemic crisis, more attention has been directed towards epidemics and infectious diseases modeling and the study of their state behavior against different factors [25]. These models usually contain many parameters and are sensitive to variations in their values. Therefore the implementation of these model should be attempted with caution. In this regards it is known that fixed-point implementation of chaotic models is generally more reliable and reproducible than floating-point ones [26], [27]. In fixed-precision fixed-point addition, there is no mantissa alignment and hence, no rounding errors in addition operations. A fixed-point representation was used in [27] to implement modified versions of the product integration rules; which are used to solve differential equations. Moreover, fixed-point operations can be performed efficiently in any Hardware Description Language (HDL) and realized on FPGA modules providing the advantages of re-programmability, reduced hardware cost, high speed, noise immunity and reliability. Many chaotic systems have already been digitally realized and tested on FPGA platforms [28]–[30] and also using Field Programmable Analog Arrays (FPAAs) [31]. One major advantage of FPGA realizations is that they facilitate experimenting with various chaos control schemes and real-time chaotic time-series prediction algorithms [32].
In this work we show the feasibility of implementing complex chaotic epidemic models using fixed-point architectures on FPGAs on two different FPGA platforms to explore the utilization of resources. We present the realization process of three virus spreading models and one disease progress model. Sensitivity of the chaotic dynamics to parameter variation is explored through continuous bifurcation diagrams prior to implementation. Difficulty arises from several aspects: (i) all the considered models have many parameters (17 parameters in the case of the Ebola model for example) and (ii) the sensitivity of chaotic behavior with respect to all these parameters needs to be carefully investigated before implementation. (iii) All models require several multiplication operations (7 multiplications and 1 division in the Cancer model for example). While it is possible for chaotic systems implemented on FPGAs for the purposes of encryption applications to be deigned such that they contain very few parameters and a limited number of multiplication/division operations [29], this is clearly not the case in epidemic models. It is worth noting that an analog circuit realization of a tumor growth model was recently presented in [33]. To the best of our knowledge, no FPGA realization of an epidemic or disease model on an FPGA platform has yet been reported in the literature. This article shows the feasibility of implementing these complex models efficiently on FPGAs for real-time simulation, control and prediction purposes.
This article is organized as follows: section II presents the investigated models and explores their chaotic dynamics. Section III presents the first proposed FPGA design procedure based on an Altera Cyclone IV EP4CE115F29C7 FPGA chip. A second implementation based on a Xilinx Artix-7 XC7A100TCSG324 chip is also reported. Section IV shows the FPGA resource utilization facts and experimental results.
II. Selected Models
In this section, we describe the four models that are considered in this work. The details of these models and their respective derivation assumptions can be found in [11], [13], [25] and [34].
A. Ebola Model
In [13], a 4-D model for the spread of the Ebola virus in West Africa between 2013 and 2016 was proposed. This deterministic model suggests that societal and environmental conditions were conducive to the propagation of Ebola. Once the epidemic had broken out, its propagation was driven by a few predominant processes. The spread model based on recorded time series data of 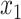 and its higher order derivatives
and its higher order derivatives  optimally fit the following model
optimally fit the following model
 |
where  is a nonlinear function with 14 terms given by
is a nonlinear function with 14 terms given by
 |
This model can be easily discretized using an Euler method with a suitable step size  . Figure 1(a) shows the simulation results of the discretized system with
. Figure 1(a) shows the simulation results of the discretized system with  and for the parameter values
and for the parameter values  . Prior to considering an implementation of this system, the type of response obtained at different values of the parameters and the sensitivity to parameter variations needs to be studied. This was done by considering variations in narrow steps of one parameter at a time while fixing the other parameters using bifurcation diagrams. A bifurcation diagram reveals periodic windows and examines the robustness of the chaotic behavior versus parameter variations. For this system, the bifurcation diagram versus a chosen parameter was generated through plotting the value of the state
. Prior to considering an implementation of this system, the type of response obtained at different values of the parameters and the sensitivity to parameter variations needs to be studied. This was done by considering variations in narrow steps of one parameter at a time while fixing the other parameters using bifurcation diagrams. A bifurcation diagram reveals periodic windows and examines the robustness of the chaotic behavior versus parameter variations. For this system, the bifurcation diagram versus a chosen parameter was generated through plotting the value of the state  , every time it reaches a local maximum after discarding two thirds of the total number of points. Following extensive simulations of the system (2), we found that some parameters correspond to chaotic behavior only in very narrow ranges of their values, such as
, every time it reaches a local maximum after discarding two thirds of the total number of points. Following extensive simulations of the system (2), we found that some parameters correspond to chaotic behavior only in very narrow ranges of their values, such as 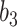 . Other parameters can generate chaos for wider ranges such as
. Other parameters can generate chaos for wider ranges such as  . In addition, some parameter variations drift the model into quasi-periodic state (donut-shaped attractor) such as when
. In addition, some parameter variations drift the model into quasi-periodic state (donut-shaped attractor) such as when  and
and  .
.
FIGURE 1.
Numerical simulations of the discretized (a) Ebola model with initial conditions  showing projection in the
showing projection in the  plane and (b) Influenza model with initial conditions
plane and (b) Influenza model with initial conditions  and
and  projected in the
projected in the  plane (the total number of birds (
plane (the total number of birds ( ) is 10,000).
) is 10,000).
B. Influenza Model
The influenza model considered here was proposed in [11] for avian influenza in a seabird colony and is given by
 |
This model is obviously a non-autonomous periodically forced model where 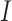 and
and  respectively correspond to the infected and recovered individuals.
respectively correspond to the infected and recovered individuals.  may be interpreted as the recruitment rate of infectious individuals,
may be interpreted as the recruitment rate of infectious individuals,  is the transmission rate constant,
is the transmission rate constant,  is the recovery rate constant and
is the recovery rate constant and  is the natural death rate constant. The driving forcing function
is the natural death rate constant. The driving forcing function  oscillates with a period of 1 year corresponding to the annual breeding season. It is also straight forward to discretize this model using Euler’s backward method and the simulation results in this case are shown in Fig. 1(b) for
oscillates with a period of 1 year corresponding to the annual breeding season. It is also straight forward to discretize this model using Euler’s backward method and the simulation results in this case are shown in Fig. 1(b) for 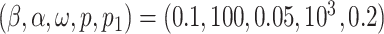 and using a step size
and using a step size 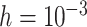 . The effect of the parameter variations on the state variables in this system was also carefully examined using bifurcation diagrams. The best two parameters that result in the widest range of chaotic behavior were found to be
. The effect of the parameter variations on the state variables in this system was also carefully examined using bifurcation diagrams. The best two parameters that result in the widest range of chaotic behavior were found to be  and
and  and the corresponding bifurcation diagrams are plotted in Fig. 2 versus
and the corresponding bifurcation diagrams are plotted in Fig. 2 versus  .
.
FIGURE 2.
Bifurcation diagrams of the discretized Influenza model against (a)  and (b)
and (b)  with the same initial conditions as in Fig. 1(b).
with the same initial conditions as in Fig. 1(b).
C. COVID-19 Model
A recent model of the COVID-19 pandemic was proposed in [25] taking into consideration data from China, Japan, South Korea and Italy. This model is given by
 |
where  is the daily number of new cases,
is the daily number of new cases,  is the daily additional severe cases and
is the daily additional severe cases and  is the daily number of new deaths. The model contains three multiplier-type nonlinearities (
is the daily number of new deaths. The model contains three multiplier-type nonlinearities ( ) in addition to two quadratic terms. Simulation results of this model after being discretized with an Euler method are shown in Fig. 3 with
) in addition to two quadratic terms. Simulation results of this model after being discretized with an Euler method are shown in Fig. 3 with  ). For system (4), all parameters correspond to chaotic behavior only for narrow ranges or specific values. Hence, the solution exhibits extra sensitivity to the parameters values and extra care with the FPGA implementation is needed.
). For system (4), all parameters correspond to chaotic behavior only for narrow ranges or specific values. Hence, the solution exhibits extra sensitivity to the parameters values and extra care with the FPGA implementation is needed.
FIGURE 3.
Numerical simulations of the discretized COVID-19 model with initial conditions  and discretization step
and discretization step  (a) projection in the
(a) projection in the  plane and (b) projection in the
plane and (b) projection in the  plane.
plane.
D. Cancer Model
Many models of cancer growth are available in the literature from which we selected the 3-D model introduced in [34] and given by
 |
where  is the number of tumor cells,
is the number of tumor cells,  is the number of healthy host cells, and
is the number of healthy host cells, and  is the number of effector immune cells.
is the number of effector immune cells.  and
and  are constants obtained by rescaling the original system model, which are described in [34], to obtain the dimensionless equations (5). These constants are related respectively to the loss of the tumor cell population, the tumor cell killing rate by the effector cells, the rate by which the tumor cells inactivate the healthy cells, the rate by which the tumor cells inactivate the effector cells, the death rate of the effector cells, the growth rate of the healthy tissue cells and the direct dependence of the stimulation of the immune system on the number of tumor cells. This model contains 7 multiplier operations and one division operation making it hardware demanding.
are constants obtained by rescaling the original system model, which are described in [34], to obtain the dimensionless equations (5). These constants are related respectively to the loss of the tumor cell population, the tumor cell killing rate by the effector cells, the rate by which the tumor cells inactivate the healthy cells, the rate by which the tumor cells inactivate the effector cells, the death rate of the effector cells, the growth rate of the healthy tissue cells and the direct dependence of the stimulation of the immune system on the number of tumor cells. This model contains 7 multiplier operations and one division operation making it hardware demanding.
Simulation results of this model after being discretized with an Euler method are shown in Fig. 4 with  . For this system, the study of the effects of the parameter variations on the state variables using bifurcation diagrams revealed interestingly that it exhibits a period doubling route to chaos against
. For this system, the study of the effects of the parameter variations on the state variables using bifurcation diagrams revealed interestingly that it exhibits a period doubling route to chaos against  and reverse bifurcation against both
and reverse bifurcation against both  and
and  , as shown in Fig. 5.
, as shown in Fig. 5.
FIGURE 4.
Numerical simulations of the discretized Cancer model with initial conditions  and
and  (a) projection in the
(a) projection in the  plane and (b) projection in the
plane and (b) projection in the  plane.
plane.
FIGURE 5.
Bifurcation diagrams of the discretized Cancer model against (a)  , (b)
, (b)  , (c)
, (c)  and (d)
and (d)  with the same initial conditions of Fig. 4.
with the same initial conditions of Fig. 4.
III. FPGA Implementations
A. Using Altera Cyclone IV
Figure 6 depicts the FPGA design process applied to implement three of the studied models (Ebola, Influenza and Cancer). This process consists of two parallel phases, namely the Verilog Design and the Design Verification phases. The two phases run in parallel to ensure that the hardware implementation meets all the specifications of the system at different key points during the process. The design steps allow for an iterative mechanism.
FIGURE 6.
FPGA Design flowchart.
1). Fixed-Point Architecture
Floating-point units typically need more than one clock cycle to produce an output and consequently, synchronizing fixed-point results is much easier and usually produces a simpler and faster hardware design [35]. In fixed-point architectures, memory and bus widths are smaller, contributing significantly to a lower cost and power consumption [36]. That is why a fixed-point architecture is used to implement the hardware components of the three models. The fixed-point signed notation of  is used to represent the number of bits allocated to the integer part
is used to represent the number of bits allocated to the integer part  and the fraction part
and the fraction part  of the number. The number of bits was determined by taking into account the maximum possible value of all state variables in the chaotic models. Both the Ebola and Cancer models use an internal architecture of 64-bit signed fixed-point whereas, the Influenza model requires more precision in the fractional part and hence a 256-bit signed fixed-point architecture is used. A typical histogram of the distribution of values for the four-state variables in the Ebola model is shown in Fig. 7. The more spread the values are, the less the required precision to discriminate among successive values.
of the number. The number of bits was determined by taking into account the maximum possible value of all state variables in the chaotic models. Both the Ebola and Cancer models use an internal architecture of 64-bit signed fixed-point whereas, the Influenza model requires more precision in the fractional part and hence a 256-bit signed fixed-point architecture is used. A typical histogram of the distribution of values for the four-state variables in the Ebola model is shown in Fig. 7. The more spread the values are, the less the required precision to discriminate among successive values.
FIGURE 7.
Frequency histograms showing the distribution of values in the four states of the Ebola model.
2). Hardware
Here the details of implementing the Cancer model (as an example) are discussed. This model is the most complex from an implementation perspective. Figure 8(a) shows the architecture of the top-level module of the Cancer model. One of the main components of this module is the phase-locked loop which is responsible for generating the clock frequency required to run the model blocks. This clock frequency is fed to the control unit which is responsible for controlling the number of iterations through a state machine. The Cancer_top module, shown in Fig. 8(b), is responsible for generating the values of the next state from the existing state values in the model. The selection logic enables the user to route any two-state variables to a digital-to-analog converter for external observation on an oscilloscope.
FIGURE 8.

Architecture of (a) Cancer model top-level module and (b) the module Cancer_top.
Figure 9 shows the internal architecture of the combinational cancer module particularly the arithmetic and shift operations needed. The arithmetic operations are implemented using IP cores from Intel. To optimize the multiplication operation for example by a constant equal to 2.5, we first shift by 2 bits, which is a multiplication of 4, then we add the result to the original value resulting in a multiplication by 5. Finally, we shift the product 1 bit to the right in order to divide by 2. This enables us to compute a multiplication by 2.5 without the need to use the resource-consuming multiplication operation. The dotted lines in the figure are the state registers used to store the values of the three state variables of the model. These state registers enable synchronize the inputs and outputs with the clock cycles.
FIGURE 9.
Internal architecture of the Cancer module.
3). Timing Analysis
Timing analysis is performed using the Timing Quest Timing Analyzer tool in Intel Quartus Prime software to find the maximum frequency at which the realized models can operate. The minimum input and output delays are set to 2ns, whereas the maximum input and output delays are set to 3ns. The maximum frequencies at which we can operate our three modules are found to be 17.02MHz, 10.86MHz, and 1.62MHz for the Ebola, Influenza, and Cancer models, respectively. The reduction in operating frequency in the Influenza model is mainly attributed to the necessary higher precision when compared to the Ebola model (256-bits vs. 64-bits). The drastic reduction in frequency in the Cancer model mainly results from the complex division operation needed to create  . The PLL in all three designs was used to provide the clocks at maximum frequencies.
. The PLL in all three designs was used to provide the clocks at maximum frequencies.
B. Using Xilinx ARTIX-7
Figure 10 shows the general block diagram used where a 3D chaotic system is considered with outputs 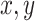 and
and  stored in three registers. Three combinational circuits are used to compute the numerical solution for
stored in three registers. Three combinational circuits are used to compute the numerical solution for 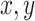 and
and  . Taking the Covid 19 chaotic system as an example for this design procedure, Fig. 11 displays the three combinational circuits required to calculate the numerical solution of
. Taking the Covid 19 chaotic system as an example for this design procedure, Fig. 11 displays the three combinational circuits required to calculate the numerical solution of  which correspond respectively to
which correspond respectively to  , and
, and  . Different arithmetic blocks are used to compute the numerical solution including adders, subtractors, and multipliers. 32-bit fixed points are used for the implementation each with 4-bits for the integer part and 28-bits for the fractional part. For the Cancer model, Fig. 12 presents the three combinational circuits needed to compute the numerical solution of
. Different arithmetic blocks are used to compute the numerical solution including adders, subtractors, and multipliers. 32-bit fixed points are used for the implementation each with 4-bits for the integer part and 28-bits for the fractional part. For the Cancer model, Fig. 12 presents the three combinational circuits needed to compute the numerical solution of 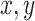 , and
, and  which represent
which represent 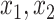 and
and 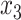 for this model respectively. The term
for this model respectively. The term  is computed based on a linear approximation method. The linear binomial coefficients are generated based on MATLAB curve fitting. Since the range of
is computed based on a linear approximation method. The linear binomial coefficients are generated based on MATLAB curve fitting. Since the range of  is [1:2], the linear approximation is applied for an input interval [1:2]. Four uniform segments are used for the approximation. Here 64 bits fixed point are used each with 16-bits for the integer part and 48-bits for the fractional part. The outputs are truncated to 12-bits and hence the three registers
is [1:2], the linear approximation is applied for an input interval [1:2]. Four uniform segments are used for the approximation. Here 64 bits fixed point are used each with 16-bits for the integer part and 48-bits for the fractional part. The outputs are truncated to 12-bits and hence the three registers  , and
, and 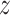 use 12 bits.
use 12 bits.
FIGURE 10.
General block diagram for a 3D dynamical system, where a three combinational circuits are used to compute  and
and  .
.
FIGURE 11.

Combinational circuits block diagram for the numerical solution of 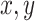 and
and  for the Covid 19 model.
for the Covid 19 model.
FIGURE 12.

Combinational circuits block diagram for the numerical solution of  and
and  for the proposed cancer chaotic system.
for the proposed cancer chaotic system.
IV. Results
The first implementation described in section III-A was based on the DE2-115 development board equipped with Altera Cyclone IV EP4CE115F29C7 FPGA device. This board includes many input/output (I/O) peripherals including switches and a High-Speed Mezzanine Card (HSMC) connector. A Texas Instruments high-speed Digital to Analog Converter (TI DAC5672) was connected to the HSMC connector on the DE2-115 board. The TI DAC5672 is a 14-bit dual-channel DAC, hence the main outputs of the three models needed to be scaled down to 14 bits in order to be displayed on the oscilloscope (RIGOL DS4012). Figure 13 shows the final experimental setup while the FPGA is running the Ebola model code. Table 1 summarizes the FPGA resource utilization for each of the three implemented models with this FPGA.
FIGURE 13.
Experimental setup running the Ebola model on the Altera Cyclone IV FPGA board and showing the  chaotic attractor.
chaotic attractor.
TABLE 1. FPGA Resources Utilization on Altera Cyclone IV.
| Resource | Ebola | Influenza | Cancer |
|---|---|---|---|
| Logic elements | 4462/114480 (4%) | 3874/114480 (4%) | 5182/114480 (5%) |
| Registers | 300 | 533 | 246 |
| Embedded multiplier (9-bit) | 96/532 (18%) | 127/532 (24%) | 48/532 (9%) |
| Pins | 37/529 (7%) | 34/529 (6%) | 36/529 (7%) |
| PLL | 1/4 (25%) | 1/4 (25%) | 1/4 (25%) |
| Frequency (MHz) | 17 | 10.8 | 1.6 |
For the second implementation described in section III-B the Xilinx XC7A100TCSG324 FPGA was used. Table 2 presents a summary of the resources needed to implement the Covid-19 and Cancer models. The Covid 19 model is the most resource demanding of all models. Figure 14 shows the oscilloscope output from all epidemic models using this FPGA.
TABLE 2. Hardware Resources Summary for COVID 19 and Cancer Chaotic Systems Using a Xilinx XC7A100TCSG324 FPGA. The Throughput is Computed for 12 bits Output.
| Logic Utilization | Total No. Slices | Total No. Slices Registers | Maximum Frequency MHz | Throughput |
|---|---|---|---|---|
| Covid 19 | 605 | 288 | 23.263 | 0.279 |
| Cancer | 157 | 152 | 37.927 | 0.455 |
FIGURE 14.
Experimental results using the Xilinx Artix-7 FPGA board and showing from left to right (in sequence) the chaotic attractor projection:  of the Ebola model,
of the Ebola model,  of the Influenza model,
of the Influenza model,  of the Covid-19 model,
of the Covid-19 model,  of the Covid-19 model,
of the Covid-19 model,  of the Cancer model and
of the Cancer model and  of the Cancer model.
of the Cancer model.
V. Conclusion
We reported on the feasibility of implementing four complex chaotic models for virus spreading (Ebola, Influenza and Covid 19) and disease progress (Cancer) on two different FPGA platforms using fixed-point architectures. Although these models require a large number of multiplier blocks and have many parameters, their efficient realization on FPGAs is possible. Future work on applying and investigating the robustness of chaos control techniques to these epidemic models in real-time is ongoing.
Biographies

M. Elnawawy (Student Member, IEEE) was born in Giza, Egypt. He received the B.Sc. degree (summa cum laude) in computer engineering and the M.Sc. degree in computer engineering from the American University of Sharjah, United Arab Emirates, in 2017 and 2019, respectively. In 2020, he joined as a Lab Instructor with the Computer Science and Engineering Department, American University of Sharjah. His research interests include machine learning, field-programmable gate arrays, and embedded systems. He received several awards including the American University of Sharjah graduate student research, scholarly, and creative work excellence award, the Sharjah Islamic Bank research award, and the Outstanding Cambridge Learner awards. He is a member of the Upsilon Pi Epsilon Honor Society.

F. Aloul (Senior Member, IEEE) received the B.S. degree (summa cum laude) in electrical engineering from Lawrence Technological University, Michigan, USA, and the M.S. and Ph.D. degrees in computer science and engineering from the University of Michigan, Ann Arbor, USA. He is currently a Professor and the Department Head of computer science/engineering and the Director of the HP Institute, American University of Sharjah (AUS), United Arab Emirates. He has more than 130 publications in international journals and conferences, in addition to one U.S. patent. His current research interests include cyber security, mobile applications, and design optimization.
Dr. Aloul received a number of awards including the Global Engineering Deans Council (GEDC) Airbus Engineering Diversity Award, the Sheikh Khalifa Award for Higher Education, AUS Excellence in Teaching Award, the Abdul Hameed Shoman Award for Young Arab Researchers, and the Sheikh Rashid’s Award for Outstanding Scientific Achievement. He is a regular invited speaker and panelist across a number of international conferences related to Cyber Security, Technology, Innovation, and Education. He is a Certified Information Systems Security Professional (CISSP).

A. Sagahyroon (Senior Member, IEEE) received the B.Sc. degree in electrical engineering from the University of Khartoum, the M.Sc. degree in electrical engineering from Northwestern University, Evanston, IL, USA, and the Ph.D. degree from The University of Arizona, Tucson, AZ, USA. From 1993 to 1999, he has been a member of the Department of Computer Science and Engineering, Northern Arizona University. In 1999, he joined the Department of Math and Computer Science, California State University. In 2003, he joined the Department of Computer Science and Engineering, American University of Sharjah, where he served as the Department Head for seven years. He is currently a Professor of computer science and engineering and the Associate Dean of undergraduate affair with the American University of Sharjah. He has many publications in international conferences and journals. His research interests include innovative applications of emerging technology in the medical field, power consumption of portable electronics, and FPGAs based design. He was an Invited Technical Reviewer for National Science Foundation Programs, and served in technical program committees of many international conferences.

A. S. Elwakil (Senior Member, IEEE) was born in Cairo, Egypt. He received the B.Sc. and M.Sc. degrees in electronics and communications from Cairo University, Egypt, and the Ph.D. degree in electrical and electronic engineering from the National University of Ireland, University College Dublin. He also held visiting positions at Istanbul Technical University, Turkey; Queens University, Belfast, U.K.; the Technical University of Denmark, Lyngby, Denmark; and the King Abdullah University of Science and Technology, Saudi Arabia. He is currently a Full Professor with the University of Sharjah, United Arab Emirates; also with the University of Calgary, AB, Canada; and also with the Nanoelectronics Integrated Systems Center (NISC) Research Center, Nile University, Cairo. He has authored or coauthored more than 350 publications in these areas (current H-index 45). His research interests include circuit theory, nonlinear dynamics, chaos theory, and fractional-order circuits and systems with diverse applications ranging from the modeling of oscillatory networks and nonlinear behavior in electronic circuits and plasma physics to modeling of energy storage devices, bio-materials, and biological tissues. He has been a member of the IEEE Technical Committee on Nonlinear Circuits and Systems, since 2000. He was a recipient of the Egyptian Government First Class Medal for achievements in engineering sciences, in 2015, and the UAE president award (Khalifa Award), in 2020. He is an International Observer in the European Cooperation in Science and Technology (COST) action on fractional-order system-analysis synthesis and their importance for future design (CA15225) and an Expert with the United Nations Development Program (UNDP). He was on the Editorial Board of the IEEE Journal on Emerging and Selected Topics in Circuits and Systems and an Associate Editor for the IEEE Transaction on Circuits and Systems—I: Regular Papers. He currently serves as an Editor-in-Chief for the International Journal of Circuit Theory and Applications (Wiley) and an Associate Editor for the International Journal of Electronics and Telecommunications (AEUE, Elsevier).

Wafaa S. Sayed received the B.Sc. degree (Hons.) from the Electronics and Communications Engineering Department and the M.Sc. degree from the Engineering Mathematics Department, Faculty of Engineering, Cairo University, Egypt, in 2012 and 2015, respectively. She is currently pursuing the Ph.D. degree with Cairo University. She is currently an Assistant Lecturer with Cairo University. She has 31 publications in international journals and international conferences in addition to five book chapters. Her research interests include chaos theory, chaotic cryptography, fractional dynamics, mathematical software and adaptive personalized e-learning.
Ms. Sayed was awarded the 1st place prize in the Masters Forum competition of the 22nd International Conference on Electronics, Circuits, and Systems (ICECS 2015) and her paper entitled “What are the correct results for the special values of the operands of the power operation” was cited in the 2019 - IEEE Standard for Floating-Point Arithmetic (Revision of IEEE Std 754-2008). The article proposed a formal definition of pow(x,y) for special values of the operands, which is used in the revised standard to define missed cases of pow(x,y) in the earlier version.

Lobna A. Said (Senior Member, IEEE) received the B.Sc., M.Sc., and Ph.D. degrees in electronics and communications from Cairo University, Egypt, in 2007, 2011, and 2016, respectively. She is currently a full-time Assistant Professor with the Faculty of Engineering and Applied Science and the Nano-Electronics Integrated System Research Center (NISC), Nile University (NU). She has more than 100 publications including journals, conferences, and book chapters. Her research interests include interdisciplinary, including system modeling, control techniques, optimization techniques, analog and digital integrated circuits, fractional-order circuits and systems, non-linear analysis, and chaos theory.
She was selected as a member of the Egyptian Young Academy of Sciences (EYAS) to empower and encourage young Egyptian scientists. In 2020, she was selected as an affiliate member of the African Academy of Science (AAS). She received the State Encouragement Award from the Egyptian Government, in 2019. She has been the Vice-Chair of research activities at the IEEE Computational Intelligence Egypt Chapter, since 2018, and is the Counselor of the IEEE NU Student Branch.

S. M. Mohamed received the B.Sc. degree in electronics and communication engineering from Cairo University, in 2020. She is currently a Research Assistant with the Nanoelectronics Integrated Systems Center, Nile University. Her research interest includes the digital design implementations of chaotic systems.

Ahmed G. Radwan (Senior Member, IEEE) was the Former Director of the Nanoelectronics Integrated Systems Center (NISC), Nile University, and was a former Member of the Egyptian Young Academy of Science (EYAS), ASRT. He was a Visiting Professor with the Computational Electromagnetic Lab (CEL), McMaster University, Canada, and also with the King Abdullah University of Science and Technology (KAUST), Saudi Arabia. He had many short academic stays in several countries including Malaysia, Czech Republic, Brazil, France, Tunis, United Arab Emirates (UAE), Sweden, China, Germany, Portugal, Spain, Hong Kong, Austria, and Italy. Recently, he was selected as an Observer to COST Action CA15225. He is currently the Vice President of research with Nile University, Egypt, and also a Professor of engineering mathematics and physics with Cairo University, Egypt. Based on the Scival database, he is one of the top authors worldwide in two research tracks “Capacitors — Networks(circuits) — Fractional-order capacitor (T.21555)” and “Chaos theory — Chaotic systems — Multi-scroll chaotic (T.8806).” He has more than 340 articles, H-index 43, and more than 5600 citations based on Scopus database. He has six U.S. patents in several interdisciplinary topics. His research interests include interdisciplinary concepts between mathematics and engineering applications such as fractional-order systems, chaos, memristors, and encryption.
Dr. Radwan received the State Achievements Award for research in mathematical sciences, in 2012, the Scopus Award in engineering and technology, in 2019, from Elsevier as the top researcher in Egypt, from 2014 to 2018, the Abdul Hameed Shoman Award for Arab researchers in basic sciences (Information/Data Security), in 2015, the Cairo University Excellence Award for research in engineering sciences, in 2016, the Prof. Mohamed Amin Lotfy Award from ASRT in the mathematical sciences, in 2016, the state first class medal of science and arts, the State Excellence Award in advanced technological sciences, in 2018, and several other awards. He was awarded the best paper/poster awards in several international conferences such as Modern Circuits and Systems Technologies (MOCAST) 2017-Greece, ICECS2015-Egypt and ECTI-CON2016-Thailand. He received the international publications award endowed by Cairo University for the top researchers in all fields through the years 2011, 2012, 2013, 2014, 2015, 2016, 2017, and 2018 individually. He is the Founder and the General Chair of the Novel Intelligent and Leading Emerging Sciences conference (NILES2019, NILES2020) and was the Technical Program Co-Chair of the 28th IEEE International Conference in Microelectronics (ICM2016), Cairo. He organized many special sessions in international conferences and was a Counselor of the IEEE Nile University Student Branch, from 2014 to 2016. He was a Lead/Guest Editor of several special issues in multiple journal including the Journal of Circuits, Systems and Signal Processing, Mathematical Problems in Engineering, Complexity, International Journal of Electronics and Communications (AEUE), Microelectronics Journal, and Journal of Advanced Research.
References
- [1].Strogatz S. H., Nonlinear Dynamics and Chaos With Applications to Physics, Biology, Chemistry, and Engineering. Boca Raton, FL, USA: CRC Press, 2018. [Google Scholar]
- [2].ElSafty A. H., Tolba M. F., Said L. A., Madian A. H., and Radwan A. G., “A study of the nonlinear dynamics of human behavior and its digital hardware implementation,” J. Adv. Res., vol. 25, pp. 111–123, Sep. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Gohari P. S., Mohammadi H., and Taghvaei S., “Using chaotic maps for 3D boundary surveillance by quadrotor robot,” Appl. Soft Comput., vol. 76, pp. 68–77, Mar. 2019. [Google Scholar]
- [4].Elsafty A. H., Tolba M. F., Said L. A., Madian A. H., and Radwan A. G., “Enhanced hardware implementation of a mixed-order nonlinear chaotic system and speech encryption application,” AEU, Int. J. Electron. Commun., vol. 125, Oct. 2020, Art. no. 153347. [Google Scholar]
- [5].Elwakil A. S., Salama K. N., and Kennedy M. P., “An equation for generating chaos and its monolithic implementation,” Int. J. Bifurcation Chaos, vol. 12, no. 12, pp. 2885–2895, Dec. 2002. [Google Scholar]
- [6].Tlelo-Cuautle E., Pano-Azucena A. D., Guillén-Fernández O., and Silva-Juárez A., Analog/Digital Implementation of Fractional Order Chaotic Circuits and Applications. Cham, Switzerland: Springer, 2020, doi: 10.1007/978-3-030-31250-3. [DOI] [Google Scholar]
- [7].Soliman N. S., Tolba M. F., Said L. A., Madian A. H., and Radwan A. G., “Fractional X-shape controllable multi-scroll attractor with parameter effect and FPGA automatic design tool software,” Chaos, Solitons Fractals, vol. 126, pp. 292–307, Sep. 2019. [Google Scholar]
- [8].Kermack W. O. and McKendrick A. G., “A contribution to the mathematical theory of epidemics,” Proc. R. Soc. Lond. A, Math. Phys. Sci., vol. 115, no. 772, pp. 700–721, 1927. [Google Scholar]
- [9].Viboud C., “Prediction of the spread of influenza epidemics by the method of analogues,” Amer. J. Epidemiol., vol. 158, no. 10, pp. 996–1006, Nov. 2003. [DOI] [PubMed] [Google Scholar]
- [10].Casagrandi R., Bolzoni L., Levin S. A., and Andreasen V., “The SIRC model and influenza A,” Math. Biosci., vol. 200, no. 2, pp. 152–169, Apr. 2006. [DOI] [PubMed] [Google Scholar]
- [11].O’Regan S. M., Kelly T. C., Korobeinikov A., O’Callaghan M. J. A., Pokrovskii A. V., and Rachinskii D., “Chaos in a seasonally perturbed SIR model: Avian influenza in a seabird colony as a paradigm,” J. Math. Biol., vol. 67, no. 2, pp. 293–327, Aug. 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Mangiarotti S., “Low dimensional chaotic models for the plague epidemic in Bombay (1896–1911),” Chaos, Solitons Fractals, vol. 81, pp. 184–196, Dec. 2015. [Google Scholar]
- [13].Mangiarotti S., Peyre M., and Huc M., “A chaotic model for the epidemic of ebola virus disease in West Africa (2013–2016),” Chaos, Interdiscipl. J. Nonlinear Sci., vol. 26, no. 11, Nov. 2016, Art. no. 113112. [DOI] [PubMed] [Google Scholar]
- [14].Barrientos P. G., Rodríguez J. Á., and Ruiz-Herrera A., “Chaotic dynamics in the seasonally forced SIR epidemic model,” J. Math. Biol., vol. 75, nos. 6–7, pp. 1655–1668, Dec. 2017. [DOI] [PubMed] [Google Scholar]
- [15].Herrera A. R., “Paradoxical phenomena and chaotic dynamics in epidemic models subject to vaccination,” Commun. Pure Appl. Anal., vol. 19, no. 5, p. 2533, 2020. [Google Scholar]
- [16].Tang S. and Chen L., “Chaos in functional response host–parasitoid ecosystem models,” Chaos, Solitons Fractals, vol. 13, no. 4, pp. 875–884, Mar. 2002. [Google Scholar]
- [17].Gakkhar S. and Naji R. K., “Existence of chaos in two-prey, one-predator system,” Chaos, Solitons Fractals, vol. 17, no. 4, pp. 639–649, Aug. 2003. [Google Scholar]
- [18].Vano J., Wildenberg J., Anderson M., Noel J., and Sprott J., “Chaos in low-dimensional Lotka–Volterra models of competition,” Nonlinearity, vol. 19, no. 10, p. 2391, 2006. [Google Scholar]
- [19].Letellier C., Denis F., and Aguirre L. A., “What can be learned from a chaotic cancer model?” J. Theor. Biol., vol. 322, pp. 7–16, Apr. 2013. [DOI] [PubMed] [Google Scholar]
- [20].Gallas M. R., Gallas M. R., and Gallas J. A. C., “Distribution of chaos and periodic spikes in a three-cell population model of cancer,” Eur. Phys. J. Special Topics, vol. 223, no. 11, pp. 2131–2144, Oct. 2014. [Google Scholar]
- [21].Galindo M. C., Nespoli C., and Messias M., “Hopf bifurcation, cascade of period-doubling, chaos, and the possibility of cure in a 3D cancer model,” Abstract Appl. Anal., vol. 2015, pp. 1–11, 2015. [Google Scholar]
- [22].Shahzad M., “Chaos control in three dimensional cancer model by state space exact linearization based on lie algebra,” Mathematics, vol. 4, no. 2, p. 33, May 2016. [Google Scholar]
- [23].Yulmetyev R. M., Demin S. A., and Hänggi P., “Manifestation of chaos in real complex systems: Case of Parkinson’s disease,” in The Logistic Map Route to Chaos. Berlin, Germany: Springer, 2006, pp. 175–196. [Google Scholar]
- [24].Dash S., Abraham A., Luhach A. K., Mizera-Pietraszko J., and Rodrigues J. J., “Hybrid chaotic firefly decision making model for Parkinson’s disease diagnosis,” Int. J. Distrib. Sensor Netw., vol. 16, no. 1, 2020, Art. no. 1550147719895210. [Google Scholar]
- [25].Mangiarotti S., Peyre M., Zhang Y., Huc M., Roger F., and Kerr Y., “Chaos theory applied to the outbreak of COVID-19: An ancillary approach to decision making in pandemic context,” Epidemiol. Infection, vol. 148, pp. 1–29, May 2020, doi: 10.1017/S0950268820000990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Sayed W. S., Radwan A. G., Fahmy H. A., and El-Sedeek A., “Software and hardware implementation sensitivity of chaotic systems and impact on encryption applications,” Circuits, Syst., Signal Process., vol. 39, no. 11, pp. 5638–5655, 2020. [Google Scholar]
- [27].Abdelaty A. M., Roshdy M., Said L. A., and Radwan A. G., “Numerical simulations and FPGA implementations of fractional-order systems based on product integration rules,” IEEE Access, vol. 8, pp. 102093–102105, 2020. [Google Scholar]
- [28].Sayed W. S., Radwan A. G., Elnawawy M., Orabi H., Sagahyroon A., Aloul F., Elwakil A. S., Fahmy H. A., and El-Sedeek A., “Two-dimensional rotation of chaotic attractors: Demonstrative examples and FPGA realization,” Circuits, Syst., Signal Process., vol. 38, no. 10, pp. 4890–4903, Oct. 2019. [Google Scholar]
- [29].Tolba M. F., Elwakil A. S., Orabi H., Elnawawy M., Aloul F., Sagahyroon A., and Radwan A. G., “FPGA implementation of a chaotic oscillator with odd/even symmetry and its application,” Integration, vol. 72, pp. 163–170, May 2020. [Google Scholar]
- [30].Pano-Azucena A. D., Ovilla-Martinez B., Tlelo-Cuautle E., Muñoz-Pacheco J. M., and de la Fraga L. G., “FPGA-based implementation of different families of fractional-order chaotic oscillators applying Gränwald–Letnikov method,” Commun. Nonlinear Sci. Numer. Simul., vol. 72, pp. 516–527, Jun. 2019. [Google Scholar]
- [31].Silva-Juárez A., Tlelo-Cuautle E., de la Fraga L. G., and Li R., “FPAA-based implementation of fractional-order chaotic oscillators using first-order active filter blocks,” J. Adv. Res., vol. 25, pp. 77–85, Sep. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Pano-Azucena A., Tlelo-Cuautle E., Tan S., Ovilla-Martinez B., and de la Fraga L., “FPGA-based implementation of a multilayer perceptron suitable for chaotic time series prediction,” Technologies, vol. 6, no. 4, p. 90, Oct. 2018. [Google Scholar]
- [33].Sabarathinam S. and Thamilmaran K., “Controlling of chaos in a tumour growth cancer model: An experimental study,” Electron. Lett., vol. 54, no. 20, pp. 1160–1162, Oct. 2018. [Google Scholar]
- [34].Itik M. and Banks S. P., “Chaos in a three-dimensional cancer model,” Int. J. Bifurcation Chaos, vol. 20, no. 01, pp. 71–79, Jan. 2010. [Google Scholar]
- [35].Vahid F., Digital Design with RTL Design, Verilog and VHDL. Hoboken, NJ, USA: Wiley, 2010. [Google Scholar]
- [36].Menard D., Chillet D., and Sentieys O., “Floating-to-fixed-point conversion for digital signal processors,” EURASIP J. Adv. Signal Process., vol. 2006, no. 1, Dec. 2006, Art. no. 096421. [Google Scholar]













