Abstract
This study focuses on modeling, prediction, and analysis of confirmed, recovered, and death cases of COVID-19 by using Fractional Calculus in comparison with other models for eight countries including China, France, Italy, Spain, Turkey, the UK, and the US. First, the dataset is modeled using our previously proposed approach Deep Assessment Methodology, next, one step prediction of the future is made using two methods: Deep Assessment Methodology and Long Short-Term Memory. Later, a Gaussian prediction model is proposed to predict the short-term (30 Days) future of the pandemic, and prediction performance is evaluated. The proposed Gaussian model is compared to a time-dependent susceptible-infected-recovered (SIR) model. Lastly, an analysis of understanding the effect of history is made on memory vectors using wavelet-based denoising and correlation coefficients. Results prove that Deep Assessment Methodology successfully models the dataset with 0.6671%, 0.6957%, and 0.5756% average errors for confirmed, recovered, and death cases, respectively. We found that using the proposed Gaussian approach underestimates the trend of the pandemic and the fastest increase is observed in the US while the slowest is observed in China and Spain. Analysis of the past showed that, for all countries except Turkey, the current time instant is mainly dependent on the past two weeks where countries like Germany, Italy, and the UK have a shorter average incubation period when compared to the US and France.
Keywords: COVID-19, deep assessment methodology (DAM), fractional calculus, least squares, long short-term memory, modeling, prediction of pandemics, SIR model
I. Introduction
Public health programs and capacity planning are essential for tracing and managing health risks. These programs focus on prevention more than diagnosing, detection, and responding to the cases, including infectious disease outbreaks [1]. To plan successful preventive activities, solid estimates are needed about the spread and localization of the disease, and the possible path and case numbers. Therefore, reliable mathematical predictive modeling for any kind of diseases (especially for communicable diseases) is an essential tool for public health policies. European countries were not particularly successful in combating the COVID-19 outbreak due to the insufficiency of such predictions.
The spread of COVID-19 could not be effectively avoided at its origin and has become a pandemic that infects more than 8 million people in 215 countries and territories as of 2020 [2]. It is important to understand the behavior of the pandemic in order to prepare health care workers and other related parties. The modeling and prediction of COVID-19 have crucial importance for planning hospital resources [3]. To combat with further progression of the COVID-19 infection requires predictive modeling. The authorities can take required precautions regarding the staff and/or hospital resources to overcome the epidemic-like difficulties they may encounter in the future by predicting the progression of the infection [3].
Recent developments in digital technology and informatics in parallel with the development of data science lead the companies, institutions, universities and especially, the countries to give priority to evaluating the data and predicting what can be forthcoming [3]. Computational mathematical methods have a significant role in understanding the dynamics of an epidemic and application of such methods on biological systems has been an interest to many researchers throughout decades [4]–[7]. Because of the current outbreak of COVID-19, many mathematical methodologies are being investigated on predicting the trend, estimating the peak, and modeling the course of the pandemic. The models can be used separately or in combination, [8] adopts three types of mathematical models for fitting COVID-19 data: the logistic model, Bertalanffy model, and Gompertz model. The least-square method is used for fitting and the final cumulative number of confirmed cases is predicted. Another study, [9], combines ARIMA and wavelet-based predicting techniques for 5 countries. In [10] a method to predict the spread of COVID-19 based on dictionary learning and online nonnegative matrix factorization is proposed and evaluated for one-step predictions and extrapolated near future. In [11], a stochastic transmission dynamic model is fitted to multiple publicly available datasets by using sequential Monte Carlo simulation and resulting number of cases, transmission rate over time, and basic Reproduction number (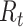 ) is inferred. Besides, Schüttler et al.
[12] proposed a Gauss Model to map time to the Gauss function to model the daily deaths per day and country. In [13], authors show that simple mean-field models can be used to interpret epidemic spreading and to forecast time of the peak of confirmed cases. Another mathematical method based on the data analysis of logistic growth equations describing the process on the macroscopic level is used in an attempt to calculate the expected end of the outbreak in Italy [14]. Also, [15] carries out a time series analysis using a mixed-effect model of lagged, log-linear case counts for each province and predicts a province-level growth rate in China.
) is inferred. Besides, Schüttler et al.
[12] proposed a Gauss Model to map time to the Gauss function to model the daily deaths per day and country. In [13], authors show that simple mean-field models can be used to interpret epidemic spreading and to forecast time of the peak of confirmed cases. Another mathematical method based on the data analysis of logistic growth equations describing the process on the macroscopic level is used in an attempt to calculate the expected end of the outbreak in Italy [14]. Also, [15] carries out a time series analysis using a mixed-effect model of lagged, log-linear case counts for each province and predicts a province-level growth rate in China.
Another well-known model that is widely applied by researchers is the susceptible-infected-recovered (SIR) model [16]–[18] which uses mainly three variants of infection: susceptible, infected, and recovered. Nesteruk [19] used the SIR model to predict the epidemic characteristics in mainland China while Batista [20] applied it to estimate the final size of the Covid-19 epidemic. However, in the original SIR model transmission rate 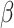 and recovering rate
and recovering rate  remain as time-invariant variables. As a result, such models are unable to include the impacts of specific state interventions to control and avoid the spreading of the virus in different periods into the SIR-modelling. Therefore, Ping-En Lu used an extended version of SIR called Time-dependent SIR model, in which both transmission rate
remain as time-invariant variables. As a result, such models are unable to include the impacts of specific state interventions to control and avoid the spreading of the virus in different periods into the SIR-modelling. Therefore, Ping-En Lu used an extended version of SIR called Time-dependent SIR model, in which both transmission rate 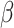 and recovering rate
and recovering rate 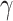 are also functions of time so that model could adapt and adequately predict the trend of COVID-19 in China [21]. Before that, the SIR epidemic model had also been used to describe the spread of other diseases such as influenza and measles [22], [23].
are also functions of time so that model could adapt and adequately predict the trend of COVID-19 in China [21]. Before that, the SIR epidemic model had also been used to describe the spread of other diseases such as influenza and measles [22], [23].
One of the mathematical approaches to model a physical phenomenon is setting up a differential equation where the dependent variable satisfies a differential equation with respect to the independent variable. Integer order differential equations cannot model processes with memory and non-locality because of their locality property. On the other hand, Fractional Calculus is a branch of mathematics that focuses on fractional-order differential and integral operators and can be used to address the limitations of integer-order differential models. Fractional operators convert the integer-order differential equations into the non-integer order differential equation and lead to a very essential advantage: the memory property. Fractional order derivatives are the generalization of the integer order counterparts and represent the intermediate states between two known states. For example, zero order-derivative of the function represents the function itself while the first-order derivative represents the first derivative of the function. Between these known states, there are infinitely many intermediate states [24]. Therefore, fractional operators provide more accurate models in many branches of science and engineering including mechanics, biology, biomedical devices, nanotechnology, diffusion, diffraction, and economics [25]–[43].
Memory property of fractional calculus has been employed for modeling and prediction on epidemics such as Measles, Malaria, Dengue, and Ebola [44]–[47]. Recently, [48] illustrated that the memory feature of the fractional derivative explores the hidden dynamics of infection in contrast to an integer type of derivative by analyzing the data of India. Furthermore, in our previous studies, methods based on fractional calculus (FC) that work for modeling and prediction of time series were introduced. In these studies, the children’s physical growth, subscriber numbers of operators, GDP per capita were modeled and compared with other modeling approaches such as Fractional Model-1 and Polynomial Models [3], [7], [49], [50]. According to the results, proposed fractional models had better results compared to the results obtained from Linear and Polynomial Models [3], [7], [49], [50]. As a result, the existing applications of the fractional differential approach on various biological studies and success of our prior work on modeling and prediction of time series using fractional approach are the foundations of our motivation to analyze COVID-19 with fractional calculus.
This study focuses on modeling and predicting the trend of COVID-19 pandemic for eight countries including China, France, Germany, Italy, Spain, Turkey, the UK, and the US. The first main focus of this study is modeling and the one-step prediction of the pandemic. After modeling and having the mathematical expression for the dataset, a short-term future (30-Days) prediction is investigated. In this study, we mainly apply our “Deep Assessment Methodology (DAM)” [3] for predicting the case numbers and death numbers related to the coronavirus pandemic. DAM is a method that is derived from the fractional differential equations for modeling and prediction purposes and uses the properties of fractional calculus. The method utilizes the corresponding Laplace transform properties. Here, the data is modeled with an approach that considers the effect of a finite number of previous values and the derivatives. Further, the prediction is obtained by assuming a value in a specific time can be expressed as the summation of the previous values weighted by unknown coefficients and the function to be modeled is continuous and differentiable. In this way, DAM takes previous values and variation rates between different time samples (derivative) of the dataset into account while modeling the data itself and predicting upcoming values. Combining the previous values with the variations weighted by the unknown coefficients lead to calling this method as “deep assessment”. There are two advantages of the method regarding other approaches mentioned in this section. First, the proposed method uses the generalization of the derivative operator. The generalization of the derivative operator provides flexibility when modeling the structure of the data. In this way, the modeling has one more parameter to control and optimize the error between the proposed modeling and real data. Second, the deep assessment method has the ability of both modeling and prediction. During modeling, the present value is expressed as a summation of the previous values and changes of the function with unknown weights, which is then optimized by the Least Squares Method. Thus, combining the fractional derivative and defining the instant value as the summation of the weighted previous values and changes, the prediction can be obtained since the epidemic can be assumed as a system with memory. In other words, previous values and the increase between the intervals can affect the present and the future. To overcome the limitation of the locality which presents in integer-order derivates, the fractional differential equation is utilized which includes the hereditary and non-locality properties of the non-integer order derivatives.
In a recent study [51], a mathematical model is presented by incorporating the isolation class to model the dynamical behavior of COVID-19. Their model employs a Nonstandard Finite Difference (NSFD) scheme and Runge-Kutta fourth-order method. In [52], outcomes of various models such as SIR, SEIR, and ARIMA are discussed. Further, [53] develops two models to capture the trend of dynamic: A mathematical model that accounts for various parameters related to the spread of the virus and a non-parametric model that uses the Fourier Decomposition Method (FDM).
The number of confirmed cases (prevalence), the intensity of cases in a specific location (incidence), and the number of deaths can be used as a proxy of the effectiveness of a country’s fight against the pandemic. In general, it is a reasonable measurement of a country’s health system strength and public health strategy against COVID-19 [54]. Some researchers used the date of the first recorded case and cumulative case numbers as a criterion for evaluating coronavirus pandemic in certain countries [1], [2]. Therefore, the prediction of case numbers and death numbers is very essential not only for the researchers but also for governments and institutions to take action against an uncontrolled spreading. The reliable number of case predictions defined by modeling based on scientific foundations is vital for the relevant institutions and organizations to determine their road maps.
As shown in our previous study [3], DAM successfully models and predicts time series data. In this study, we predicted the total number of confirmed cases, death, and recovered case numbers for 8 countries including China, France, Germany, Italy, Spain, Turkey, the UK, and the US using our previously proposed work, Deep Assessment Methodology. To assign performance of DAM on the COVID-19 dataset we compared the model with Long Short-Term Memory (LSTM), a special type of artificial neural network used in analyzing time series problems. Later, a Gaussian fitting approach based on DAM is proposed for predicting the short-term future of the pandemic and compared to the Time-dependent SIR model [21]. Lastly, an analysis of model coefficients is made with wavelet denoising and correlation coefficients to understand the effect of the past.
The structure of the study is the following. Section II explains the Formulation of the Modeling Approaches where two methods that utilize fractional calculus are introduced. After that, Section III, namely the Proposed Approaches, are devoted to explaining how to obtain modeling, simulation, testing, and prediction. In this section, Deep Assessment Methodology, the prediction with Deep Assessment, Time-dependent SIR model, Modeling Based on Gaussian Distribution with DAM, and Prediction with LSTM are explained. Then, in Section IV, the results are presented and compared. Section V discusses the limitations of the study. Lastly, Section VI highlights the conclusion of the study.
II. The Proposed Approaches
A. Modeling and Prediction with Deep Assessment Methodology
This section is dedicated to our previously proposed modeling and prediction approach Deep Assessment Methodology (DAM) [3]. The two main goals of DAM are to find a function representing the dataset optimally and to predict the unknown upcoming values. To achieve these goals, DAM exploits fractional calculus and Taylor series expansion. It is suggested for the readers to see more detail by referring [3].
To express or infer an event or a phenomenon that depends on its previous values and states, the effects of previous values and change over time on the current time instant should be understood. With this motivation, DAM represents a function  with finite summations of its previous values and derivatives of the previous values weighted with unknown coefficients
with finite summations of its previous values and derivatives of the previous values weighted with unknown coefficients  and
and 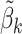 , as shown in (1).
, as shown in (1).
 |
Here, 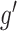 stands for the first-order derivative of
stands for the first-order derivative of 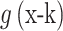 with respect to
with respect to  . Approximating the function in such a way leads to achieving the memory property. Later, assuming that
. Approximating the function in such a way leads to achieving the memory property. Later, assuming that 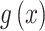 is a differentiable and continuous function, DAM expands
is a differentiable and continuous function, DAM expands 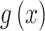 as Taylor Series with unknown constant coefficients
as Taylor Series with unknown constant coefficients  ’s as given in (2).
’s as given in (2).
 |
Similarly, a previous time instant is expressed as
 |
Using (1) and (3), the form of the function 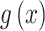 is obtained as follows.
is obtained as follows.
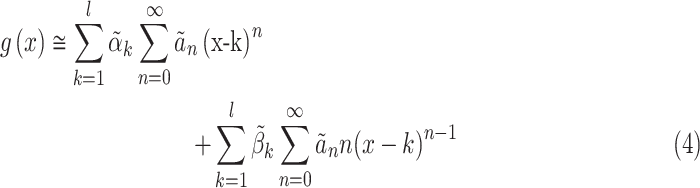 |
Truncating 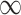 to
to  for the numerical calculations and expressing unknown coefficients
for the numerical calculations and expressing unknown coefficients 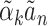 as
as 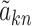 ,
, 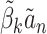 as
as  yield the final form of the approximated
yield the final form of the approximated 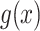 function and its first derivative:
function and its first derivative:
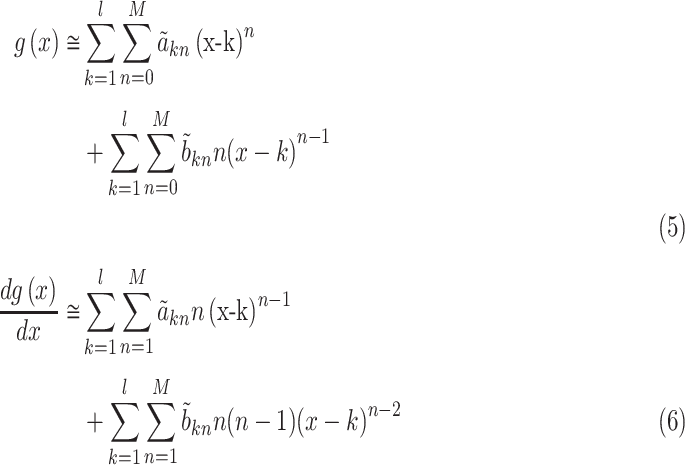 |
After this step, the next step is to include the heritability property [5], [35], [41]. Therefore, first, the fractional derivative of 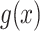 function needs to be defined. Throughout the study, Caputo’s description of the fractional derivative is employed as in (7)
[18].
function needs to be defined. Throughout the study, Caputo’s description of the fractional derivative is employed as in (7)
[18].
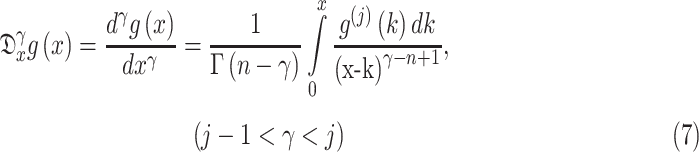 |
In (7), 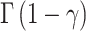 is the Gamma function. Here, the fractional derivative is taken with respect to
is the Gamma function. Here, the fractional derivative is taken with respect to 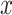 in the order of
in the order of 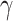 and
and 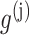 corresponds to the
corresponds to the 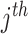 order derivative with respect to
order derivative with respect to 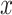 . The derivative is generalized by changing the first-order derivative in (6) to fractional derivative in the order of
. The derivative is generalized by changing the first-order derivative in (6) to fractional derivative in the order of  as in (7)
[3], [7], [49], [50]. In DAM,
as in (7)
[3], [7], [49], [50]. In DAM, 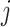 is set to 1, and the fractional-order changes between [0, 1]. Using the fractional derivative operator which is inserted into the fractional differential equation contributes to the hereditary property [3], [7], [49], [50]. Throughout the paper it is assumed that function
is set to 1, and the fractional-order changes between [0, 1]. Using the fractional derivative operator which is inserted into the fractional differential equation contributes to the hereditary property [3], [7], [49], [50]. Throughout the paper it is assumed that function 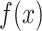 stands for the total number of COVID-19 confirmed cases, recovery from the infection, cumulative deaths over time with the order of
stands for the total number of COVID-19 confirmed cases, recovery from the infection, cumulative deaths over time with the order of  is equal to (8).
is equal to (8).
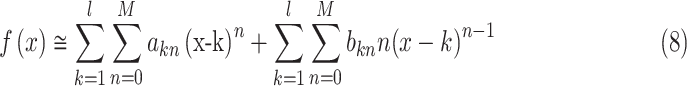 |
The function 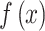 satisfies the fractional differential equation (9) and models the discrete dataset related to COVID-19 as it is given above for
satisfies the fractional differential equation (9) and models the discrete dataset related to COVID-19 as it is given above for 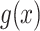 for a general approach.
for a general approach.
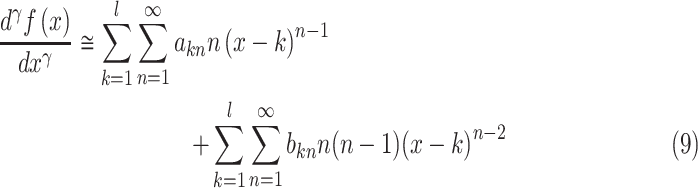 |
Here,  denotes the time. Note that, different from (6), introducing the variable fractional order between 0 and 1 in the derivative operator at the left-hand side of (6) for
denotes the time. Note that, different from (6), introducing the variable fractional order between 0 and 1 in the derivative operator at the left-hand side of (6) for 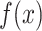 gives a more general, flexible model given in (9)
[27]. Also, this brings one additional parameter,
gives a more general, flexible model given in (9)
[27]. Also, this brings one additional parameter,  , the fractional-order to model the dataset optimally. To solve the differential equation, (9) is transformed into the Laplace domain which converts the equation into an algebraic form. After taking the inverse Laplace Transform of the transformed algebraic equation, we get the final form of
, the fractional-order to model the dataset optimally. To solve the differential equation, (9) is transformed into the Laplace domain which converts the equation into an algebraic form. After taking the inverse Laplace Transform of the transformed algebraic equation, we get the final form of 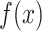 as (10)
[18].
as (10)
[18].
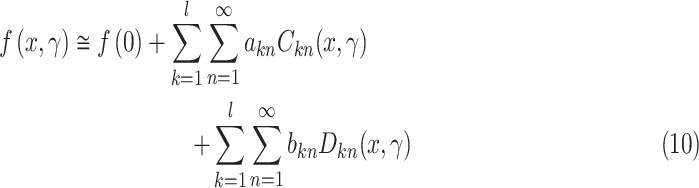 |
where,
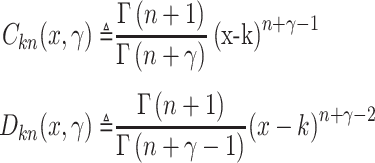 |
The infinite summation of polynomials is approximated as a finite summation given in (11).
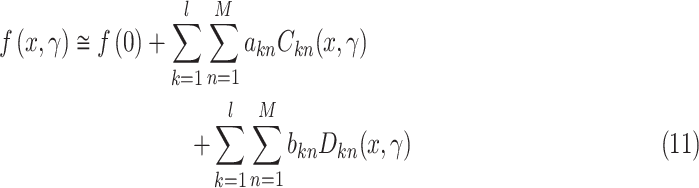 |
Note that, 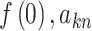 , and
, and 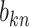 are unknown coefficients that need to be found. For the Laplace Transform (
are unknown coefficients that need to be found. For the Laplace Transform ( ), the following properties are utilized to find (9)
[18].
), the following properties are utilized to find (9)
[18].
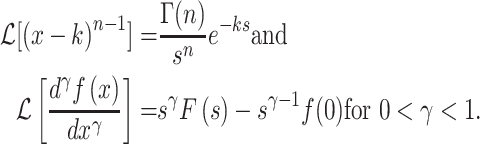 |
where  stands for the Laplace transform and
stands for the Laplace transform and  .
.
To reduce the error between the proposed function 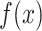 obtained by DAM and real data, the Least Square Method is employed. The unknown coefficients
obtained by DAM and real data, the Least Square Method is employed. The unknown coefficients  , and
, and  and parameters such as
and parameters such as  , are optimized by minimizing the squared total error. The squared total error
, are optimized by minimizing the squared total error. The squared total error 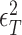 is defined as the error between the approximated function
is defined as the error between the approximated function 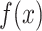 and the actual data and shown in (12):
and the actual data and shown in (12):
 |
The error 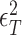 is minimized by a gradient-based approach as the following.
is minimized by a gradient-based approach as the following.
 |
and
 |
where, 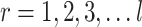 and
and 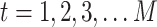 .
.
Then, a system of linear algebraic equations (SLAE) given in (13) is created where 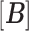 the matrix contains all unknowns
the matrix contains all unknowns 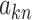 ,
,  and
and 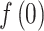 .
.
 |
[ ], [
], [ ], and [
], and [ ] are shown in (14), (15), and (16), as shown at the bottom of the next page, respectively. Optimum values of
] are shown in (14), (15), and (16), as shown at the bottom of the next page, respectively. Optimum values of 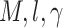 are found by grid search. As mentioned above,
are found by grid search. As mentioned above,  is constrained in (0, 1) region.
is constrained in (0, 1) region.
 |
 matrix consists of the four main blocks below. Note that, in the matrix, the abbreviations are used as
matrix consists of the four main blocks below. Note that, in the matrix, the abbreviations are used as  and
and  .
.
With a data sequence vector  ] that contains
] that contains 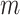 points, DAM divides the range of the data into 4 regions in total including the prediction range. This is shown in Fig. 1 where the horizontal axis represents time.
points, DAM divides the range of the data into 4 regions in total including the prediction range. This is shown in Fig. 1 where the horizontal axis represents time. 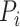 denotes the data for
denotes the data for 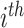 date where
date where  . Since the beginning of infection is different for each country, the length of the dataset used for modeling varies. For example,
. Since the beginning of infection is different for each country, the length of the dataset used for modeling varies. For example,  is the COVID-19 infected case numbers of a country in the second recorded day of their dataset. The region division is required because of parameters given in the previous section (10) such as
is the COVID-19 infected case numbers of a country in the second recorded day of their dataset. The region division is required because of parameters given in the previous section (10) such as  need to be found separately for modeling and prediction. Here the first three regions consist of the actual data where region 4 contains unknown future values predicted by the method itself. DAM models any time instant in terms of previous
need to be found separately for modeling and prediction. Here the first three regions consist of the actual data where region 4 contains unknown future values predicted by the method itself. DAM models any time instant in terms of previous 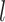 values, therefore the first
values, therefore the first 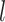 value is taken as “historical data”. The second region is the “modeling region”. Then, Region 3 comes as the “Testing Region” which is used to understand the performance of modeling. Finally, Region 4 is the “prediction region” where the aim is to predict the next upcoming data, in our case, COVID-19 infected case numbers.
value is taken as “historical data”. The second region is the “modeling region”. Then, Region 3 comes as the “Testing Region” which is used to understand the performance of modeling. Finally, Region 4 is the “prediction region” where the aim is to predict the next upcoming data, in our case, COVID-19 infected case numbers.
FIGURE 1.
The regions of the dataset [3].
For modeling Region 2, the optimum values of coefficients 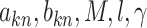 , and
, and  are determined by employing Least Squares Method.
are determined by employing Least Squares Method.
After modeling the Region 2, the performance of the method is measured with Region 3. DAM makes a one-step prediction at a time because every time instant 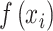 depends on anterior values including
depends on anterior values including 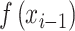 . When there are no actual previous data for calculating a particular time instant, previously predicted values are used. Otherwise, parameters are updated in an online fashion according to the data at hand. With the help of function
. When there are no actual previous data for calculating a particular time instant, previously predicted values are used. Otherwise, parameters are updated in an online fashion according to the data at hand. With the help of function  , the first value of the testing region,
, the first value of the testing region,  of Figure 1, is calculated. Here
of Figure 1, is calculated. Here  corresponds to the modeling of actual data
corresponds to the modeling of actual data  . Then, since the testing region has actual data, point x
. Then, since the testing region has actual data, point x 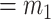 and its corresponding value
and its corresponding value  are included in the modeling region and
are included in the modeling region and 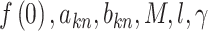 values are adjusted before the next point is calculated (i.e.
values are adjusted before the next point is calculated (i.e.  ,
,  . After value
. After value  was obtained from modeling, the value is stored and the same procedure is followed to find
was obtained from modeling, the value is stored and the same procedure is followed to find  . These operations are repeated until the last value of the testing region, is calculated. In our experiments,
. These operations are repeated until the last value of the testing region, is calculated. In our experiments, 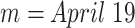 .
.
The last region is called the “Prediction Region” where there are no actual data. In this region, the first prediction 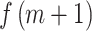 is found by using the coefficients and unknowns obtained by the tuning approach in the testing region. After that, the first predicted value (
is found by using the coefficients and unknowns obtained by the tuning approach in the testing region. After that, the first predicted value ( is included in Region 3 (testing) for the consecutive prediction
is included in Region 3 (testing) for the consecutive prediction 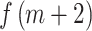 . This procedure is iterative and continues up to
. This procedure is iterative and continues up to 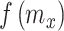 .
.
The algorithm for the prediction with DAM is given in Fig. 2. The first step is initializing the parameters ( and
and  and
and 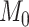 ). Here,
). Here,  and
and 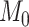 are predefined values and determine how many steps should be taken in the optimization of
are predefined values and determine how many steps should be taken in the optimization of 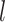 and
and 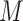 values. Then, the counter variable
values. Then, the counter variable 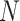 is introduced, which sets the number of prediction steps.
is introduced, which sets the number of prediction steps.
FIGURE 2.
The algorithm for the prediction [3].
The total number of prediction steps is given as 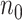 . The fractional-order
. The fractional-order 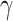 starts from 0 to 1 with the increment is 0.01 for each loop trying to find the optimized value. Note that,
starts from 0 to 1 with the increment is 0.01 for each loop trying to find the optimized value. Note that,  corresponds to the integer-order derivative and it is included in the search region of optimization. For each value of
corresponds to the integer-order derivative and it is included in the search region of optimization. For each value of  between 0 and 1, matrix
between 0 and 1, matrix 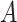 given as (14) is formed, and then, the unknown constant coefficients are given in (10) are evaluated together with the parameters
given as (14) is formed, and then, the unknown constant coefficients are given in (10) are evaluated together with the parameters 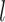 and
and 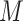 . After modeling, for each testing data, the value of the error is analyzed and compared to previously obtained values. If it is smaller than the previous one, the corresponding fractional-order value is memorized. At the end of Loop II, the optimal value of the fractional-order, which corresponds to the optimal modeling in the test region is obtained and the coefficients given in (10) are found. Subsequently, the prediction for the next upcoming value is made with the same equation. Afterward, all the iterative procedures starting from the increment for N is repeated so that the previously predicted value is included in the initial data for the next step prediction. This process continues up to the end of Loop I. Finally,
. After modeling, for each testing data, the value of the error is analyzed and compared to previously obtained values. If it is smaller than the previous one, the corresponding fractional-order value is memorized. At the end of Loop II, the optimal value of the fractional-order, which corresponds to the optimal modeling in the test region is obtained and the coefficients given in (10) are found. Subsequently, the prediction for the next upcoming value is made with the same equation. Afterward, all the iterative procedures starting from the increment for N is repeated so that the previously predicted value is included in the initial data for the next step prediction. This process continues up to the end of Loop I. Finally, 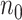 the number of predictions is obtained. Keep in mind that, for the parameters l and M, there exist two loops starting from 1 to
the number of predictions is obtained. Keep in mind that, for the parameters l and M, there exist two loops starting from 1 to  and 1 to
and 1 to 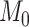 trying to find the optimum values of the coefficients to get the outcomes with a minimum error for the testing region 4, 8.
trying to find the optimum values of the coefficients to get the outcomes with a minimum error for the testing region 4, 8.
DAM is a general framework and can be applied to many time series modeling problems. Here we apply it to model and predict the ongoing pandemic, COVID-19. In this study, the COVID-19 case numbers of countries are modeled until the 19th of April, 2020. The date 19th of April is in Region 3 as testing to predict for next values.
B. Time-Dependent Sir Modelling and Prediction Approach
We employ the Time-dependent susceptible-infected-recove- red model (SIR) that is described in detail by Lu et al.
[21] to compare it with DAM. It is a common and well-known pandemic model, upgraded by using variables as functions of time. From ordinary differential equations of the traditional SIR model, with most recent data of that day, we have with  (total population):
(total population):
 |
The formulas for 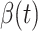 and
and 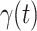 are derived from the above equations and the followings are obtained:
are derived from the above equations and the followings are obtained:
 |
The approach is using Finite Impulse Response (FIR) and Ridge Regression to track and predict the transmission rate and recovering rate based on historical numbers with elements of machine learning algorithms. This tracking and the predicting process is programmed on Python, see more in [21]. In general,  and
and  at time
at time 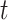 are predicted based on previous data of themselves as below:
are predicted based on previous data of themselves as below:
 |
where 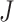 and
and 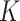 are the orders of the two FIR filters,
are the orders of the two FIR filters, 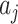 and
and 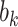 are the coefficients of the impulse responses of these two FIR filters. These coefficients
are the coefficients of the impulse responses of these two FIR filters. These coefficients 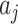 and
and  are estimated by the Ridge Regression method:
are estimated by the Ridge Regression method:
 |
where  and
and  are the regularization parameters,
are the regularization parameters, 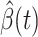 and
and  are the predicted transmission rate and recovering rate. After predicting the value for
are the predicted transmission rate and recovering rate. After predicting the value for 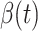 and
and 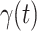 , we substitute them into (18) and (19) to find out the estimated number of infected and recovered cases of the next days.
, we substitute them into (18) and (19) to find out the estimated number of infected and recovered cases of the next days.
C. Modeling and Prediction of the Peak with Gaussian Distribution
This section briefly explains how to model and predict the peak time and value for the daily confirmed COVID-19 cases using DAM. After modeling the discrete finite data, the prediction of the peak value for the total confirmed cases can be found by assuming that the derivative of the total confirmed cases has Gaussian distribution. The number of daily confirmed cases follows an increasing trend in the first period of the pandemic and it is expected that this number decreases by time with precautions and the immune system. Therefore, it is reasonable to assume the number of daily confirmed cases curve has a bell shape. This way, the future of total confirmed cases and the peak time of the infection can be modeled and predicted. Using this approach, one can model the discrete data at the early stages of the pandemic and find an analytical expression that represents the dataset with minimum error.
In our case, the dataset which is modeled with DAM has the analytical expression 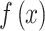 as given in (10) for the total confirmed data in a specific interval. Since the discrete dataset now has a continuous form, the change of the total confirmed case over time is represented as
as given in (10) for the total confirmed data in a specific interval. Since the discrete dataset now has a continuous form, the change of the total confirmed case over time is represented as 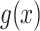 :
:
 |
where, 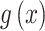 is assumed to be a Gaussian distribution
is assumed to be a Gaussian distribution  with unknown constant coefficients
with unknown constant coefficients 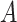 ,
, 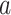 , and
, and 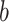 . Here,
. Here, 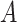 ,
, 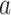 , and
, and 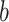 are related to the peak of the Gaussian, the variance, and the mean, respectively. For our discrete data,
are related to the peak of the Gaussian, the variance, and the mean, respectively. For our discrete data, 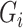 is defined as:
is defined as:
 |
Then, from (11), 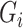 is obtained as (28).
is obtained as (28).
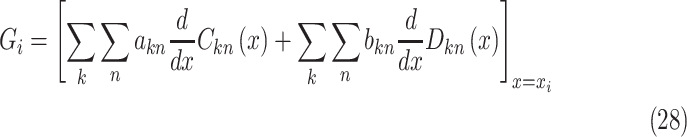 |
The final expression for 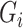 becomes (29):
becomes (29):
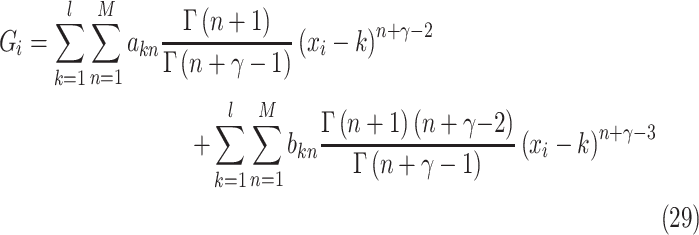 |
The same procedure implemented in DAM for optimization, the Least Squares Method is employed where  corresponds to a total error between the proposed Gaussian distribution
corresponds to a total error between the proposed Gaussian distribution  and the derivative of the curve representing actual data found by DAM and is as given in (30).
and the derivative of the curve representing actual data found by DAM and is as given in (30).
 |
A gradient-based error minimization approach is followed to find constant coefficients  , and
, and  .
.
 |
By distributing the exponential term over the terms within the brackets and substituting  , (32) is obtained.
, (32) is obtained.
 |
After obtaining (32),  is introduced as (33),
is introduced as (33),
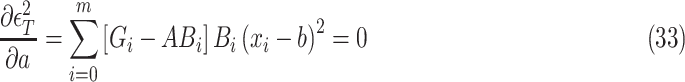 |
The final expression for (33) is as follows:
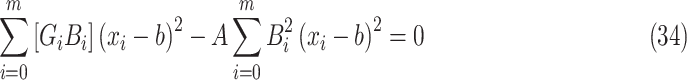 |
After applying the same procedure to 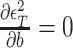 , we get (35):
, we get (35):
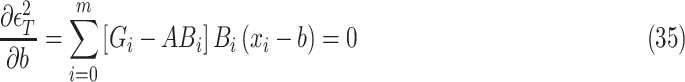 |
Then,
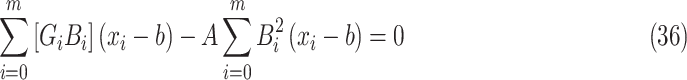 |
We have 3 equations as (32), (34), and (36) with three unknowns. Therefore, unknown coefficients can be found optimally using the Least Square Method.
After obtaining the unknown coefficients, optimal 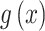 can be found. Note that,
can be found. Note that, 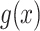 is the derivative of the
is the derivative of the 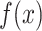 in the data region. The integration of
in the data region. The integration of 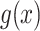 gives the prediction related to peak value and time of the total confirmed cases.
gives the prediction related to peak value and time of the total confirmed cases.
In Fig. 3, 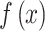 and
and 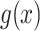 are illustrated. Here, the actual dataset that contains
are illustrated. Here, the actual dataset that contains 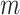 values, the finite dataset from
values, the finite dataset from 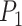 to
to  , is shown. Under the assumption of the derivative of
, is shown. Under the assumption of the derivative of 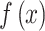 is equal
is equal  , we can predict for the upcoming values of the function
, we can predict for the upcoming values of the function 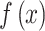 by employing the Least square method. Note that, to find
by employing the Least square method. Note that, to find 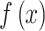 for
for 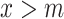 , optimum
, optimum 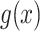 should be integrated as in (37).
should be integrated as in (37).
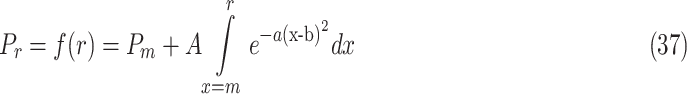 |
In Fig. 3,  is the predicted value of total confirmed cases at
is the predicted value of total confirmed cases at 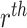 day and
day and 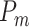 is the known last value of total confirmed cases at
is the known last value of total confirmed cases at 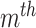 day. Area of region S is equal to
day. Area of region S is equal to 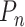 . Keep in mind that, the values
. Keep in mind that, the values 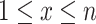 corresponds to the historical data (Region-1) in DAM. Consequently, by integrating the Gaussian function, the prediction for
corresponds to the historical data (Region-1) in DAM. Consequently, by integrating the Gaussian function, the prediction for  day is obtained.
day is obtained.
FIGURE 3.
The algorithm for the peak prediction.
A prediction with Gaussian modeling can be summarized as follows. First, the continuous function, which is obtained through DAM that approximates the real dataset 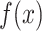 is used to find the daily changes in confirmed cases. Then, by assuming that the daily changes curve is a Gaussian function, unknown parameters (
is used to find the daily changes in confirmed cases. Then, by assuming that the daily changes curve is a Gaussian function, unknown parameters ( , and
, and 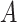 ) of the Gaussian are obtained by Least Square Method that minimizes
) of the Gaussian are obtained by Least Square Method that minimizes  . Finally, by integrating the area under the fitted Gaussian curve, the prediction is obtained as given in (37).
. Finally, by integrating the area under the fitted Gaussian curve, the prediction is obtained as given in (37).
The Gaussian approach models the derivative of the continuous total confirmed cases which are obtained by DAM modeling. Unlike this approach, the SIR model employs discrete total confirmed cases directly. SIR model predicts upcoming days with modeled function while the proposed approach calculates total cases by integrating the modeled curve.
D. Prediction with Long Short-Term Memory
Conventional Neural Networks that operate on vectors fail to capture time dependencies on sequential data. Recurrent Neural Networks are a family of models that address this issue and are capable of processing over time series. In this study, to compare the performance of DAM on the COVID-19 dataset, we used a special type of recurrent neural network, Long Short-Term Memory (LSTM), that is widely popular in predicting and modeling the content of time series. An LSTM cell in layer- 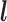 and step-
and step- 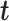 has two kinds of inputs, one from the previous time step (
has two kinds of inputs, one from the previous time step (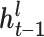 ) and another from the previous layer (
) and another from the previous layer (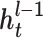 ). Information from previous time steps are stored in cell state
). Information from previous time steps are stored in cell state 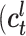 ) and updated with gated inputs. There are four gates in an LSTM cell: input, forget, output, and gate. Gate
) and updated with gated inputs. There are four gates in an LSTM cell: input, forget, output, and gate. Gate 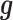 is a hyperbolic tangent (tanh) and takes values between −1 and 1. All other gates are sigmoid functions and are between 0 and 1. LSTMs optionally inherit information from previous time steps with the help of gates. Gate equations are listed below in Equation (38)–(43). Each gate learns its own set of parameters
is a hyperbolic tangent (tanh) and takes values between −1 and 1. All other gates are sigmoid functions and are between 0 and 1. LSTMs optionally inherit information from previous time steps with the help of gates. Gate equations are listed below in Equation (38)–(43). Each gate learns its own set of parameters 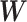 ’s and
’s and  ’s. In equations (42) and (43),
’s. In equations (42) and (43), 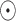 is the Hadamard Product.
is the Hadamard Product.
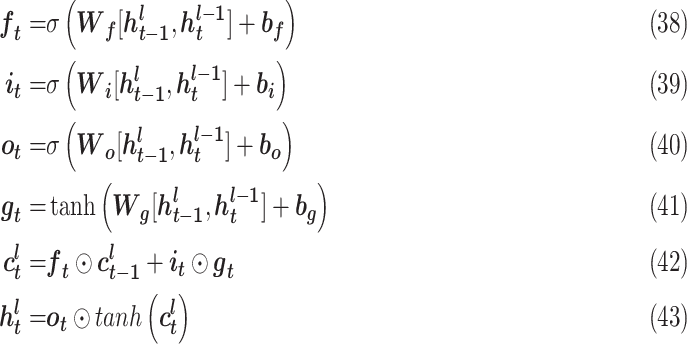 |
An LSTM unit may consist of one or multiple cells where each cell updates its state with the previous state 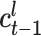 . Therefore gates, the cell state (
. Therefore gates, the cell state (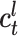 ) and hidden state
) and hidden state 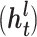 are vectors that contain information from all cells of an LSTM unit. Equation (42) shows how an LSTM cell is updated. Here, f gate decides how much of previous knowledge should participate in the current state while
are vectors that contain information from all cells of an LSTM unit. Equation (42) shows how an LSTM cell is updated. Here, f gate decides how much of previous knowledge should participate in the current state while  gate decides how much of new input should be acquired. Then LSTM neuron updates its internal hidden state by multiplying output and squashed version of
gate decides how much of new input should be acquired. Then LSTM neuron updates its internal hidden state by multiplying output and squashed version of 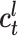 . An LSTM unit only outputs its hidden state information
. An LSTM unit only outputs its hidden state information 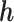 , cell states are utilized internally. To compare our previously proposed approach to the COVID-19 dataset, we employed a Vanilla LSTM network with two stacked LSTM layers and a linear prediction layer. Each LSTM layer contains 50 units. The model is trained with the Adam Optimizer and the learning rate is set to 0.001 [55].
, cell states are utilized internally. To compare our previously proposed approach to the COVID-19 dataset, we employed a Vanilla LSTM network with two stacked LSTM layers and a linear prediction layer. Each LSTM layer contains 50 units. The model is trained with the Adam Optimizer and the learning rate is set to 0.001 [55].
III. Numerical Results
In this section, we report modeling, prediction, and incubation period analysis of COVID-19 cases for 8 countries using the proposed approaches in comparison to Time-Dependent SIR and LSTM models. COVID19 dataset used in this study is retrieved from [56] and contains numbers of confirmed, recovered, and death cases. Proposed approaches are implemented on MATLAB and publicly available at [57] and [58]. First, the performance of Deep Assessment Methodology on modeling and prediction are investigated. Later, the peak of COVID-19 infection is predicted using the Gaussian Distribution modeling approach. Further, we compared DAM prediction performance to other prediction approaches, Time-Dependent SIR Model and LSTM. Results are reported using the Mean Average Precision Error (MAPE) metric which is calculated as follows:
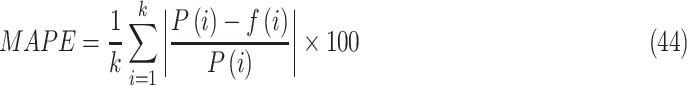 |
where  is the total number of samples,
is the total number of samples,  is the actual value and
is the actual value and  is the predicted value for
is the predicted value for  sample.
sample.
A. Modeling Results with Deep Assessment Methodology
In this part, we illustrate the modeling performance of Deep Assessment on COVID-19 cases.
Modeling results for the number of confirmed cases, deaths, and recoveries using Deep Assessment, are shown in Table 1. With DAM,  value (the number of required previous data) is optimized with grid search and varies across countries. For the modeling of the COVID-19 infected case numbers of each country, the required previous data
value (the number of required previous data) is optimized with grid search and varies across countries. For the modeling of the COVID-19 infected case numbers of each country, the required previous data  of past years used in the algorithm differs after optimization and reported in the second column. Optimized
of past years used in the algorithm differs after optimization and reported in the second column. Optimized 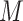 values can be found in the first column. The Deep Assessment model has a 0.6671%, 0.6957%, and 0.5756% average MAPEs for confirmed cases, deaths, and recoveries, respectively. For confirmed and death cases Turkey is the best-modeled country with the smallest MAPE being 0.13% and 0.0092%, while for recovered cases USA is modeled best with 1.62e-12% MAPE. As mentioned in the previous section, the grid search of the fractional-order parameter includes 1, where it is equal to the integer-order derivative. Column 4 shows that none of the experiments optimized fractional-order as 1. This finding demonstrates the benefit of fractional calculus.
values can be found in the first column. The Deep Assessment model has a 0.6671%, 0.6957%, and 0.5756% average MAPEs for confirmed cases, deaths, and recoveries, respectively. For confirmed and death cases Turkey is the best-modeled country with the smallest MAPE being 0.13% and 0.0092%, while for recovered cases USA is modeled best with 1.62e-12% MAPE. As mentioned in the previous section, the grid search of the fractional-order parameter includes 1, where it is equal to the integer-order derivative. Column 4 shows that none of the experiments optimized fractional-order as 1. This finding demonstrates the benefit of fractional calculus.
 |
TABLE 1. Modeling Results ( ,
,  , and MAPE Values) of 8 Countries Including China, France, Germany, Italy, Turkey, the UK, and the USA for COVID-19 Dataset Using Deep Assessment Methodology.
, and MAPE Values) of 8 Countries Including China, France, Germany, Italy, Turkey, the UK, and the USA for COVID-19 Dataset Using Deep Assessment Methodology.
| Modeling Results | DAM Results | ||||
|---|---|---|---|---|---|
| M |  |
MAPE | 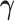 |
||
| Confirmed | China | 7 | 20 | 0.5683 | 0.18 |
| France | 7 | 19 | 1.0726 | 0.07 | |
| Germany | 7 | 20 | 0.6013 | 0.18 | |
| Italy | 7 | 20 | 0.2756 | 0.18 | |
| Spain | 5 | 20 | 0.5941 | 0.01 | |
| Turkey | 6 | 20 | 0.1300 | 0.03 | |
| UK | 7 | 20 | 1.2367 | 0.03 | |
| USA | 5 | 20 | 0.8589 | 0.2 | |
| Death | China | 7 | 20 | 0.8669 | 0.39 |
| France | 7 | 20 | 2.1636 | 0.39 | |
| Germany | 7 | 20 | 0.5136 | 0.43 | |
| Italy | 7 | 19 | 0.2783 | 0.03 | |
| Spain | 7 | 20 | 0.1541 | 0.32 | |
| Turkey | 7 | 20 | 0.0092 | 0.39 | |
| UK | 7 | 20 | 0.4310 | 0.43 | |
| USA | 5 | 20 | 1.1496 | 0.11 | |
| Recovery | China | 7 | 20 | 0. 5683 | 0.18 |
| France | 7 | 20 | 0.0004 | 0.32 | |
| Germany | 6 | 20 | 0.9463 | 0.22 | |
| Italy | 6 | 20 | 0.8944 | 0.03 | |
| Spain | 7 | 19 | 0.3488 | 0.07 | |
| Turkey | 7 | 20 | 3.04E-10 | 0.43 | |
| UK | 4 | 20 | 1.8471 | 0.39 | |
| USA | 7 | 20 | 1.61E-12 | 0.07 | |
Fig. 4 illustrates the modeling performance of each country. As can be seen from the figures, countries with smooth actual data curves like Turkey and Italy result in smaller MAPEs. As expected, jumps in the dataset result in relatively higher MAPEs as in confirmed cases of China and recovered cases of Germany.
FIGURE 4.

COVID-19 modeling on confirmed, death, and recovered cases for China, France, Italy, Germany, Spain, Turkey, UK, and the USA with DAM Methodology.
B. One-Step Prediction With DAM and LSTM
This section illustrates the prediction performance of Deep Assessment Methodology on the COVID-19 dataset and compares DAM with LSTM. For all experiments, the test region is set to the 19th of April. Table 2 reports optimized 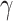 ,
,  ,
,  values, and the corresponding performance of both DAM and LSTM models. Here, column 3 reports the performance of DAM while column 6 represents LSTM. Column 3 shows that DAM predicts COVID-19 with an average 0.1343% error while LSTM yields a 0.6393% error. The best-predicted country is Italy for confirmed cases and deaths while France has the smallest MAPE on recoveries. For all three settings, DAM yields the highest MAPE for Spain. Table 2 demonstrates that in the implemented setting, DAM outperforms LSTM by 0.5050% average error and produces fair results.
values, and the corresponding performance of both DAM and LSTM models. Here, column 3 reports the performance of DAM while column 6 represents LSTM. Column 3 shows that DAM predicts COVID-19 with an average 0.1343% error while LSTM yields a 0.6393% error. The best-predicted country is Italy for confirmed cases and deaths while France has the smallest MAPE on recoveries. For all three settings, DAM yields the highest MAPE for Spain. Table 2 demonstrates that in the implemented setting, DAM outperforms LSTM by 0.5050% average error and produces fair results.
 |
Table 3 reports the prediction of COVID-19 confirmed cases, deaths, and recoveries on April 20th for both DAM and LSTM methods. It can be seen that except for the prediction of recovered cases of Spain, both models produce similar results.
TABLE 2. Test (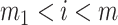 ) Results (
) Results ( ,
,  ,
, 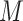 , and MAPE) of COVID-19 Confirmed Cases, Deaths, and Recoveries for Corresponding Countries.
, and MAPE) of COVID-19 Confirmed Cases, Deaths, and Recoveries for Corresponding Countries.
| Test Results | DAM | LSTM | |||||
|---|---|---|---|---|---|---|---|
| M |  |
MAPE(%) * | 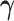 |
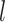 |
MAPE(%) | ||
| Confirmed | China | 3 | 20 | 0.0295 | 0.39 | 23 | 0.0085 |
| France | 6 | 11 | 0.0098 | 0.22 | 8 | 0.0157 | |
| Germany | 6 | 5 | 0.2199 | 0.11 | 21 | 0.0775 | |
| Italy | 3 | 13 | 0.0089 | 0.39 | 11 | 0.0536 | |
| Spain | 4 | 13 | 0.2577 | 0.18 | 13 | 0.0916 | |
| Turkey | 4 | 9 | 0.0435 | 0.03 | 11 | 0.1796 | |
| UK | 2 | 18 | 0.0801 | 0.18 | 24 | 0.1283 | |
| USA | 6 | 13 | 0.0209 | 0.22 | 14 | 0.0063 | |
| Death | China | 3 | 20 | 0.0295 | 0.76 | 8 | 7.9000 |
| France | 3 | 8 | 0.0196 | 0.32 | 10 | 0.1014 | |
| Germany | 6 | 10 | 0.0879 | 0.18 | 12 | 0.3231 | |
| Italy | 6 | 15 | 0.0146 | 0.07 | 14 | 0.1564 | |
| Spain | 6 | 14 | 0.0531 | 0.07 | 8 | 0.0830 | |
| Turkey | 3 | 7 | 0.0187 | 0.03 | 20 | 0.000 | |
| UK | 3 | 16 | 0.0356 | 0.22 | 10 | 3.0697 | |
| USA | 4 | 16 | 0.0210 | 0.22 | 22 | 0.5126 | |
| Recovery | China | 4 | 9 | 0.0194 | 0.39 | 15 | 0.0865 |
| France | 4 | 7 | 0.0065 | 0.22 | 7 | 0.0543 | |
| Germany | 5 | 5 | 2.0290 | 0.13 | 8 | 0.1124 | |
| Italy | 6 | 6 | 0.0180 | 0.07 | 13 | 0.1190 | |
| Spain | 2 | 4 | 0.0603 | 0.03 | 12 | 0.0440 | |
| Turkey | 3 | 12 | 0.1418 | 0.32 | 8 | 2.2211 | |
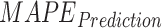 values
values
TABLE 3. Prediction Results of the Confirmed, Death, and Recovery Cases of the Countries for 20 April 2020.
| 20.04.2020 | Model | China | France | Germany | Italy | Spain | Turkey | UK | USA |
|---|---|---|---|---|---|---|---|---|---|
| Confirmed | DAM | 83716 | 155905 | 148498 | 181317 | 199134 | 90763 | 125567 | 789503 |
| LSTM | 82738 | 156297 | 147522 | 181695 | 200117 | 89434 | 120434 | 788457 | |
| Real | 82747 | 150278 | 147065 | 181228 | 200210 | 90980 | 124743 | 798227 | |
| Death | DAM | 4901 | 20036 | 4402 | 23956 | 21007 | 2145 | 16920 | 42223 |
| LSTM | 4057 | 20915 | 4752 | 24098 | 20820 | 2140 | 16370 | 40783 | |
| Real | 4632 | 20265 | 4862 | 24114 | 20852 | 2140 | 16509 | 42853 | |
| Recovery | DAM | 77077 | 37779 | 90398 | 49559 | 82227 | 12744 | – | – |
| LSTM | 77335 | 36592 | 89785 | 48950 | 78086 | 13673 | – | – | |
| Real | 77386 | 37681 | 91500 | 48877 | 81894 | 13430 |
C. Modelling and Short-Term Prediction With Sir Model
Following Lu et al.
[21], for the prediction, we set  and
and 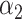 to be 0.03 and 10−6 respectively for all 8 countries. However, to avoid noising data and due to the trend of each country, we set the orders of the FIR filters
to be 0.03 and 10−6 respectively for all 8 countries. However, to avoid noising data and due to the trend of each country, we set the orders of the FIR filters 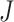 and
and  as well as choose training data for conditioning and predicting
as well as choose training data for conditioning and predicting 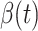 and
and 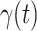 differently. The performance, parameters, and settings are reported in Table 4. The first row of the table reports the starting date of training data for prediction. The orders of the FIR filters are illustrated in the second and third rows. The next three rows show MAPE of active cases, recovered cases, and total confirmed cases respectively within training periods for all countries. Note that we exclude data of the 17th of April for China because Wuhan had revised its official death to increase by 1290 deaths. Also, a special note for Spain and U.K is that they stopped updating the recovered number since the 19th of May and 11th of April respectively. Regard to active cases, the lowest MAPE is obtained for the US as 0.64% while China yields the highest value as 3.9945%. In contrast, the lowest MAPE regarding recovered cases is obtained for China as 0.4102% while the US yields the highest value as 1.9007%. However, the MAPE of total confirmed cases, which is the sum of active and recovered number, are just below 0.8% for all countries. Finally, the last three rows report active, recovered and total confirmed cases for each country on date 19th of July, 2020.
differently. The performance, parameters, and settings are reported in Table 4. The first row of the table reports the starting date of training data for prediction. The orders of the FIR filters are illustrated in the second and third rows. The next three rows show MAPE of active cases, recovered cases, and total confirmed cases respectively within training periods for all countries. Note that we exclude data of the 17th of April for China because Wuhan had revised its official death to increase by 1290 deaths. Also, a special note for Spain and U.K is that they stopped updating the recovered number since the 19th of May and 11th of April respectively. Regard to active cases, the lowest MAPE is obtained for the US as 0.64% while China yields the highest value as 3.9945%. In contrast, the lowest MAPE regarding recovered cases is obtained for China as 0.4102% while the US yields the highest value as 1.9007%. However, the MAPE of total confirmed cases, which is the sum of active and recovered number, are just below 0.8% for all countries. Finally, the last three rows report active, recovered and total confirmed cases for each country on date 19th of July, 2020.
TABLE 4. MAPE of Training Period (Until 19 June) and Prediction Results of the Countries.
| Results | China* | France | Germany | Italy | Spain* | Turkey | U.K* | U.S | |
|---|---|---|---|---|---|---|---|---|---|
| Starting date | 13 Feb | 18 Mar | 22 Mar | 7 Mar | 21 Mar | 28 Mar | 18 Mar | 26 Mar | |
| J | 3 | 4 | 4 | 5 | 4 | 5 | 4 | 3 | |
| K | 3 | 5 | 6 | 5 | 4 | 4 | 4 | 3 | |
| MAPE (%) | Active case | 3.9945 | 1.5090 | 1.9115 | 1.0586 | 1.3998 | 0.8976 | 0.8643 | 0.6400 |
| Recovered | 0.4102 | 1.2024 | 1.6285 | 0.9687 | 0.9580 | 1.1190 | 1.2242 | 1.9007 | |
| Total confirmed | 0.0520 | 0.7552 | 0.3022 | 0.3556 | 0.3387 | 0.2359 | 0.7898 | 0.2690 | |
| 19.07.2020 | |||||||||
| - Active case | 52 | 56961 | 4119 | 7216 | 71403 | 11949 | 276610 | 1547882 | |
| - Recovered case | 83475 | 110090 | 195951 | 235225 | 225315 | 188886 | 46680 | 1683074 | |
| - Total confirm | 83527 | 167051 | 200071 | 242442 | 296718 | 200835 | 323290 | 3230956 | |
*China: We exclude data of the 17th of April when Wuhan revised its official death to increase by 1290 deaths.
*Spain: It stopped updating the recovered number since the 19th of May.
*UK: It stopped updating the recovered number since the 11th of April.
The modeled and predicted active and recovered cases are illustrated in Fig. 5.
FIGURE 5.

COVID-19 modeling on active and recovered cases for China, France, Italy, Germany, Spain, Turkey, UK, and the USA with SIR Model.
D. Peak and Short-Term Prediction With Gaussian
In this section, the peak of daily confirmed new cases and short-term trends of COVID-19 (30-days ahead) are predicted using Gaussian modeling with DAM. As explained in Section III-C, Deep Assessment Methodology is required for peak estimation. First, the data is modeled using DAM, then the derivative of the modeled data is fitted to a Gaussian by Least Square Method, and relevant parameters such as  , and
, and 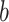 are optimized. Once, the parameters of Gaussian are determined, the future prediction is made based on the model at hand. In this setting, for the modeling with DAM, the total confirmed cases and daily new confirmed cases until the 19th of June are used. The Prediction range is 30 days, from the 19th of June to the 19th of July. In Table 5, the performance, parameters, and settings are reported for Gaussian peak modeling. The first row of the table, reports the Cut value, the number of points eliminated during Gaussian fitting to achieve better optimization because taking the derivative of the edge points in a finite domain causes jumps. For all countries, M, number of terms in the equation, is set to 3, as reported in the second row. Fractional order
are optimized. Once, the parameters of Gaussian are determined, the future prediction is made based on the model at hand. In this setting, for the modeling with DAM, the total confirmed cases and daily new confirmed cases until the 19th of June are used. The Prediction range is 30 days, from the 19th of June to the 19th of July. In Table 5, the performance, parameters, and settings are reported for Gaussian peak modeling. The first row of the table, reports the Cut value, the number of points eliminated during Gaussian fitting to achieve better optimization because taking the derivative of the edge points in a finite domain causes jumps. For all countries, M, number of terms in the equation, is set to 3, as reported in the second row. Fractional order  ’s are illustrated in the third row. The largest fractional order is obtained for the UK. For Germany and Spain,
’s are illustrated in the third row. The largest fractional order is obtained for the UK. For Germany and Spain, 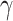 is determined equally, being 0.54. Performance of DAM on modeling the data until the 19th of June is shown in the fifth row. The lowest MAPE is obtained for Italy as 0.0229% while Germany yields the highest value as 1.2281%. The average MAPE on modeling is 0.5429%. After taking the derivative of modeled data, Gaussian’s parameters are found by Least Squares Method and the parameter related to variance (
is determined equally, being 0.54. Performance of DAM on modeling the data until the 19th of June is shown in the fifth row. The lowest MAPE is obtained for Italy as 0.0229% while Germany yields the highest value as 1.2281%. The average MAPE on modeling is 0.5429%. After taking the derivative of modeled data, Gaussian’s parameters are found by Least Squares Method and the parameter related to variance (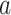 ), can be seen in row 5. In row 6,
), can be seen in row 5. In row 6,  value is reported, which represents the time of peak after the beginning of the infection. For instance, China reached a peak 10 days after the first confirmed case. The latest peak is modeled for the USA as 66. The number of daily changes for the peak date is
value is reported, which represents the time of peak after the beginning of the infection. For instance, China reached a peak 10 days after the first confirmed case. The latest peak is modeled for the USA as 66. The number of daily changes for the peak date is  in the Gaussian modeling and shown in the seventh row. The highest change is predicted for the USA. Finally, the last row reports total confirmed cases for each country on date 19th of July 2020. The determined parameters
in the Gaussian modeling and shown in the seventh row. The highest change is predicted for the USA. Finally, the last row reports total confirmed cases for each country on date 19th of July 2020. The determined parameters 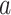 and
and  of gaussian are on row 5 and 6, respectively. One can see from the 8th column, the latest peak date is observed in the USA and the fastest peak date is obtained for China. It is illustrated that, for modeling, the Gaussian model produces superior results with smaller M value when compared to plain Deep Assessment Methodology. With
of gaussian are on row 5 and 6, respectively. One can see from the 8th column, the latest peak date is observed in the USA and the fastest peak date is obtained for China. It is illustrated that, for modeling, the Gaussian model produces superior results with smaller M value when compared to plain Deep Assessment Methodology. With 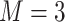 , Gaussian yields smaller MAPE compared to
, Gaussian yields smaller MAPE compared to  in DAM.
in DAM.
TABLE 5. Prediction Results of the Confirmed and Daily Changes in the Countries.
| Gauss Results | China | France | Germany | Italy | Spain | Turkey | UK | USA |
|---|---|---|---|---|---|---|---|---|
| Cut | 7 | 11 | 9 | 5 | 9 | 4 | 8 | 10 |
| M | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
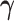 |
0.01 | 0.65 | 0.65 | 0.75 | 0.09 | 0.32 | 0.33 | 0.38 |
| MAPE(%) | 0.0875 | 0.0172 | 1.2281 | 0.0229 | 1.1671 | 0.6667 | 0.5586 | 0.5956 |
 |
0.004 | 0.0023 | 0.0027 | 0.0012 | 0.0012 | 0.0014 | 0.000927 | 0.000426 |
 |
10 | 41 | 38 | 42 | 42 | 37 | 59 | 66 |
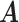 |
6535.5 | 3946.4 | 5179.5 | 4862.2 | 6208.9 | 3833.0 | 5302.1 | 30292.6 |
| 19.07.2020 | 83325 | 159452 | 190660 | 238023 | 245575 | 185299 | 304237 | 2459714 |
The modeled and predicted confirmed cases are illustrated in Fig. 6. The left-hand side figures show the original data, the modeling, and the prediction curves of total confirmed cases. The modeling curve is obtained using DAM, after that, the prediction curve is obtained by fitting the derivative of modeled data to the Gaussian function. Right-hand side figures illustrate the actual data and fitted Gaussians which are the predicted values. Fig. 6 show that peak predictions are reasonably close to real data except for the US. When analyzed together with Table 5, it is seen that Germany yields the highest MAPE due to fluctuations in the actual data. However, the daily change curve of France is the best-fitted one. When compared with the prediction results of the SIR model reported in Table 4, the Gaussian approach underestimates the trend of the pandemic and yields lower values of predictions. The reason for that is two-folded. First, the time-dependent SIR model takes the dynamics of pandemic into accounts such as transmission rate, recovering rate, and the reproduction numbers. On the other hand, Gaussian modeling relies on directly confirmed cases data without using any variant related to pandemic. Secondly, on Gaussian modeling, a Gaussian function is fitted to the daily changes in confirmed cases by optimizing two parameters. However, daily changes in confirmed cases do not follow a perfect Gaussian. Therefore, while fitted Gaussian fades away quickly, daily changes have oscillations on the right-hand side tail caused by the dynamic nature of the pandemic.
FIGURE 6.

COVID-19 modeling on confirmed and daily changes for China, France, Italy, Germany, Spain, Turkey, UK, and the USA. Left-hand side figures demonstrate total confirmed case numbers, while the right-hand side figures illustrate daily changes in confirmed cases.
E. Understanding the Effect of History By Analyzing the Short-Term Memory Weight Vector
It is important to understand the effect of the previous number of cases on current cases to assess the severity and the future of a pandemic. Analyzing the past helps to understand the net incubation period, the effect of regulations against the pandemic, whether the virus mutates or not, and the effect of a particular collective behavior in a country. Therefore, in this section, we analyze the memory property through optimized coefficients of previous time instances. As explained in Section II, at any time instant, we can express a function  as a weighted summation of its previous values and its derivative:
as a weighted summation of its previous values and its derivative:
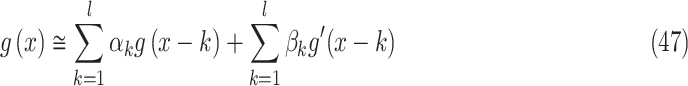 |
Here, the second term in equation (47) can be expanded as:
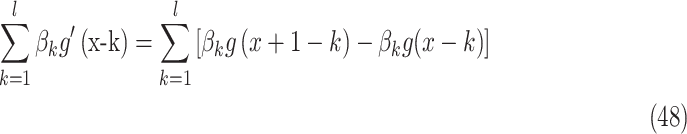 |
To directly see the effect of any previous instant, we substitute (48) into (47). In this case,  becomes:
becomes:
 |
where the weight coefficient of any previous instant  is calculated as follows:
is calculated as follows:
 |
In equation (49), 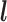 determines the number of previous steps considered in the modeling. The coefficients
determines the number of previous steps considered in the modeling. The coefficients 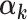 and
and 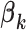 are found using the Taylor expansion, fractional derivative, and Least Square Method as explained in section II. Once these coefficients are found, the effect of any previous time instant can be understood by calculating
are found using the Taylor expansion, fractional derivative, and Least Square Method as explained in section II. Once these coefficients are found, the effect of any previous time instant can be understood by calculating 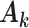 by equation (50). Together with
by equation (50). Together with 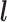 steps considered in the past,
steps considered in the past, 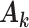 coefficients form an
coefficients form an 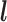 -dimensional memory weight vector
-dimensional memory weight vector 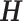 :
:
 |
Any element 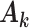 of
of 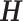 represents how important the
represents how important the 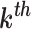 previous step in regards to the current instance. To achieve better modeling and inference, experiments are carried out with
previous step in regards to the current instance. To achieve better modeling and inference, experiments are carried out with 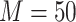 . In this section, normalized
. In this section, normalized  vectors are analyzed using wavelet-based denoising and correlation coefficients.
vectors are analyzed using wavelet-based denoising and correlation coefficients.
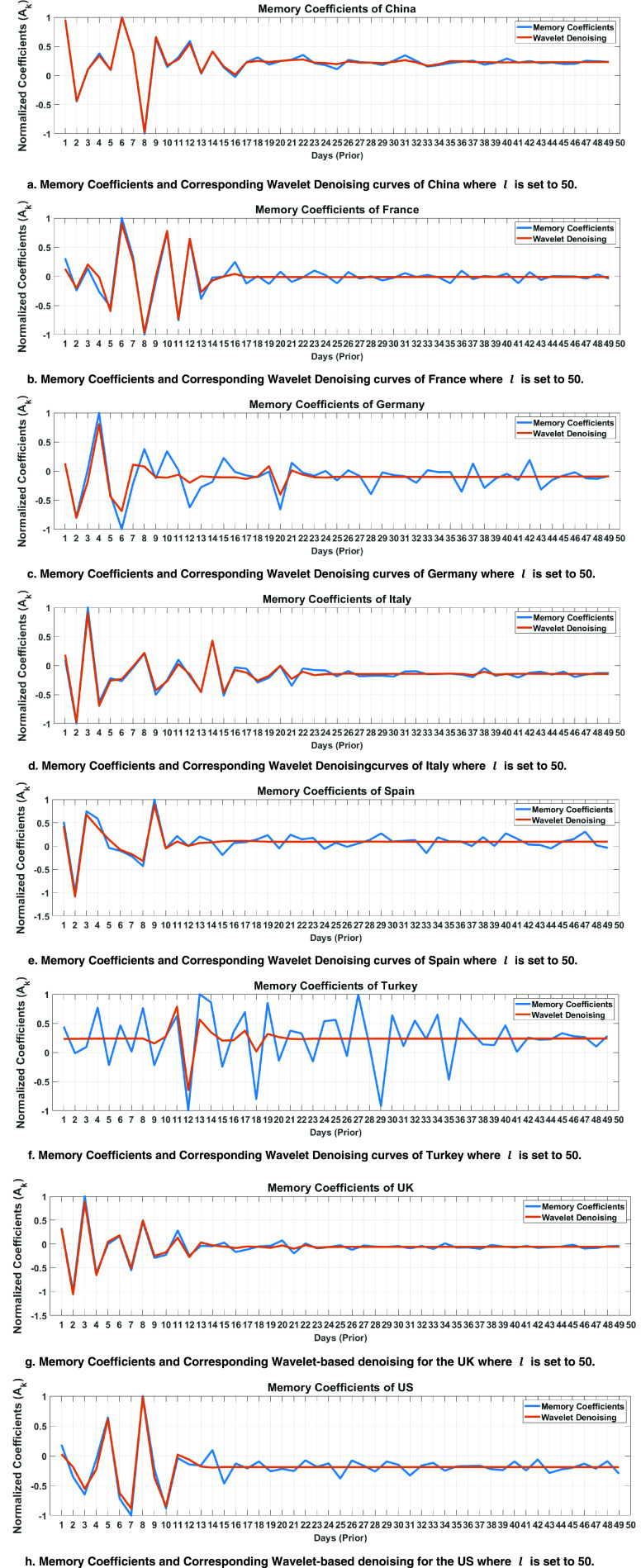
Fig. 7 illustrates the normalized memory vectors for China, France, Germany, Italy, Spain, Turkey, the UK, and the US. To eliminate oscillations, wavelet-based denoising is applied to each memory vector, 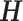 . For each figure, the blue curve denotes the original memory signal, while the red curve denotes the denoised signal. Figures indicate that, for all countries, except Germany and Turkey, coefficients after day 14–20 washes out and has oscillations. When wavelet-based denoising is applied, coefficients after 14–20 days are zeroed out. This means that any time instant can be mainly expressed in terms of the last two weeks. This is consistent with the incubation period of COVID-19, the number of confirmed cases today are mainly dependent on the number of cases in the last 14-days [1]. In countries like Germany, Italy, and the UK, the highest memory coefficients are observed within the first week. In the US and France, the highest peaks of coefficients span the second week. Based on this observation, Germany, Italy, and the UK have shorter average incubation periods when compared to the US and France.
. For each figure, the blue curve denotes the original memory signal, while the red curve denotes the denoised signal. Figures indicate that, for all countries, except Germany and Turkey, coefficients after day 14–20 washes out and has oscillations. When wavelet-based denoising is applied, coefficients after 14–20 days are zeroed out. This means that any time instant can be mainly expressed in terms of the last two weeks. This is consistent with the incubation period of COVID-19, the number of confirmed cases today are mainly dependent on the number of cases in the last 14-days [1]. In countries like Germany, Italy, and the UK, the highest memory coefficients are observed within the first week. In the US and France, the highest peaks of coefficients span the second week. Based on this observation, Germany, Italy, and the UK have shorter average incubation periods when compared to the US and France.
FIGURE 7.
Normalized memory coefficients and corresponding wavelet-based denoised signals for China, France, Germany, Italy, Spain, Turkey, U.K., and the U.S.
Among all the countries, Turkey is the one with the largest non-zero memory period. In contrast to other countries, memory coefficients of Turkey include non-zero values up to the 40th day. Considering COVID-19 has an incubation period up to 14 days, the reason behind this figure can be the noise on the existing data, the strategy against the pandemic, and the collective behavior of the country.
Fig. 8 shows the correlation coefficients (given in Table 6) between memory vectors by a color map. Correlation coefficient  takes values between [−1, 1] and the sign of
takes values between [−1, 1] and the sign of  indicates the direction of a relationship. Positive
indicates the direction of a relationship. Positive  means that, if any value for a country increases, the other country also increases. Negative
means that, if any value for a country increases, the other country also increases. Negative  means that if the value of one country increases, the value of the other country decreases. In this figure, the red color indicates a strong positive correlation while blue color indicates a strong negative correlation. The color bar is given on the right-hand side of the figure. One can see that the strongest correlation is observed in the UK– Italy pair, while the strongest negative correlation is observed for France and the US. France is negatively correlated with Germany and Turkey while China possesses highly positive correlations with France and Spain. Both China and France has a strong negative correlation with the US. On the other hand, the US and Germany do not have any positive correlation with another country, while Turkey does not maintain any relevant affair at all. Also, Spain has weak positive correlations with the UK, Germany, and Italy. Germany is negatively correlated with France. Lastly, two countries that have a strong positive correlation between them, the UK and Italy, have a similar pattern of correlation coefficient values. Both countries have a weak positive correlation with China, France, and Germany.
means that if the value of one country increases, the value of the other country decreases. In this figure, the red color indicates a strong positive correlation while blue color indicates a strong negative correlation. The color bar is given on the right-hand side of the figure. One can see that the strongest correlation is observed in the UK– Italy pair, while the strongest negative correlation is observed for France and the US. France is negatively correlated with Germany and Turkey while China possesses highly positive correlations with France and Spain. Both China and France has a strong negative correlation with the US. On the other hand, the US and Germany do not have any positive correlation with another country, while Turkey does not maintain any relevant affair at all. Also, Spain has weak positive correlations with the UK, Germany, and Italy. Germany is negatively correlated with France. Lastly, two countries that have a strong positive correlation between them, the UK and Italy, have a similar pattern of correlation coefficient values. Both countries have a weak positive correlation with China, France, and Germany.
FIGURE 8.
Correlation Coefficient,  , of Memory vectors between 8 countries: China, France, Germany, Italy, Spain, Turkey, U.K., and the U.S.more explicit integration into the modeling.
, of Memory vectors between 8 countries: China, France, Germany, Italy, Spain, Turkey, U.K., and the U.S.more explicit integration into the modeling.
TABLE 6. Correlation Coefficients Between Country Pairs.
| Correlation Coefficient, R | China | France | Germany | Italy | Spain | Turkey | UK | USA |
|---|---|---|---|---|---|---|---|---|
| China | 1 | 0.62640685 | −0.1795882 | 0.02134012 | 0.50360116 | −0.1232921 | 0.01180925 | −0.3709889 |
| France | 0.62640685 | 1 | −0.3059618 | 0.02498707 | 0.04795931 | −0.2380957 | −0.0916445 | −0.6562742 |
| Germany | −0.1795882 | −0.3059618 | 1 | 0.08040289 | 0.34262272 | 0.24667393 | 0.07811075 | 0.20395324 |
| Italy | 0.02134012 | 0.02498707 | 0.08040289 | 1 | 0.30283785 | 0.11679214 | 0.79029593 | 0.0983885 |
| Spain | 0.50360116 | 0.04795931 | 0.34262272 | 0.30283785 | 1 | 0.03679665 | 0.35842576 | −0.0286716 |
| Turkey | −0.1232921 | −0.2380957 | 0.24667393 | 0.11679214 | 0.03679665 | 1 | 0.12739537 | 0.10123804 |
| UK | 0.01180925 | −0.0916445 | 0.07811075 | 0.79029593 | 0.35842576 | 0.12739537 | 1 | 0.21701357 |
| US | −0.3709889 | −0.6562742 | 0.20395324 | 0.0983885 | −0.0286716 | 0.10123804 | 0.21701357 | 1 |
IV. Limitations of the Study
In this study, the curve of daily changes is assumed to be a Gaussian function, however, in reality, it does not follow a perfect Gaussian for every country. Also, the model relies on the data without considering any prevention measures taken by governments and social distancing policies directly. Investigating the direct effect of preventions are left for future study. However, daily confirmed cases, active cases, and deaths show the strategies, politics, and preventions such as curfews, wearing masks, social distancing of each country indirectly. The change in the daily confirmed cases, active cases, and deaths overtime inherently keep the information about each country. Further, the time-dependent SIR model takes the dynamics of pandemic and thereby the effectiveness of government interventions over time into account, still, the impact e.g. of the reproduction factor (R-Value) needs a
V. Conclusion
This document is aimed to provide practical suggestions on how to predict case numbers for a better strategy for planning health resources for patients under the current pandemic conditions. This modeling is not only for today’s COVID-19 reality, but it can also be used for future local or worldwide outbreaks. In this study, the number of confirmed cases, deaths, and recoveries of the COVID-19 outbreak is modeled and predicted for 8 countries including China, France, Germany, Italy, Spain, Turkey, the UK, and the USA.
First, we modeled the COVID-19 data, from the first confirmed case date to the 19th of April by using our previously presented Deep Assessment Methodology which relies on Fractional Calculus. Then, a one-step prediction was made using the DAM and Long-Short Term Memory (LSTM) to assess the performance of DAM. The third part of the study focused on the short-term prediction of the pandemic where the following 30 days are predicted with the Time-Dependent SIR model and Gaussian model that relies on the derivative of the continuous number of confirmed cases obtained from DAM. The purpose of the Gaussian modeling was to predict the future of the pandemic through the daily changes of pandemic data and to estimate the peak number of cases. Employed Time-dependent SIR model effectively predicted the number of infected and recovered cases in the future up to the 19th of July. We showed that DAM successfully modeled the COVID19 dataset with 0.6671%, 0.6957%, and 0.5756% average MAPEs for confirmed cases, deaths, and recoveries, respectively. Also, results illustrated that DAM is superior to LSTM for a one-step prediction of the pandemic. Based on the analysis, it can be seen that fitting a Gaussian function on the dataset underestimates the future trend of the pandemic. The proposed Gaussian prediction method can be used in peak prediction, however, underestimates the future. Better prediction results can be achieved by taking the different distributions (generalized inverse Gaussian, Maxwell-Boltzmann, Nakagami, F and Fréchet distributions) into account that model the daily change of the number of patients for the future studies.
Lastly, an analysis of the past is made by applying wavelet-based denoising on memory coefficient vectors and calculating correlation coefficients between countries’ vectors obtained with the DAM. The experiments showed that, for all countries except Turkey, the current number of confirmed cases of the pandemic was mainly determined by the last 14 days which was consistent with the incubation period of COVID-19. Results point out that, countries like Germany, Italy, and the UK have a shorter average incubation period when compared to the US and France.
Evaluation of multivariable and multifunctional problems, analyzing time windows, randomness, noise, and error changes are also left to future work. Implementations of the DAM and Gaussian Prediction are publicly available at [57] and [58].
Conflicts of Interest: The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Biographies

Ertuğrul Karaçuha graduated from the Electronics and Telecommunication Engineering Department, Istanbul Technical University, in 1986. He received the master’s and Ph.D. degrees from Istanbul Technical University, Çukurova University, and Istanbul University, in 1990, 1992, 1993, and 1996, respectively. From 1988 to 1989, he was a Research and Development Engineer with Teletaş. From 1989 to 1996, he was a Research Assistant with Istanbul Technical University. From 1994 to 2001, he was an Assistant Professor with the Gebze Advanced Technology Institute. From 2002 to 2013, he was the Head of the Tariffs Department and the Vice-President of the Information and Communication Technologies Authority. He was also with the Informatics Institute, Istanbul Technical University, where he was a Professor. He is currently the Dean of the Graduate School of Science Engineering, Istanbul Technical University.

Nisa Özge Önal graduated from the School of Business, Istanbul University, in 2016. She received the M.Sc. degree from the Department of Applied Informatics, Istanbul Technical University, Turkey, in 2018, where she is currently pursuing the Ph.D. degree with the Department of Applied Informatics, Informatics Institute. She is also a Research Assistant with Istanbul Technical University. Her research interests include computational and applied mathematics.

Esra Ergün received the bachelor’s degree in electronics and communications engineering from Istanbul Technical University, in 2017, where she is currently pursuing the M.Sc. degree. She is also a Research Assistant with Istanbul Technical University. Her research interests include continual learning, representation learning, and domain adaptation for deep neural networks.

Vasil Tabatadze was born in 1982. He received the B.Sc., M.Sc., and Ph.D. degrees from the Physics Department, Tbilisi State University, Tbilisi, in 2003, 2005, and 2009, respectively. He was an Academic Staff with Akhaltsikhe State University, Samtskhe-Javaxethi State University, and Tbilisi State University, Georgia. He is currently an Invited Associate Professor with Istanbul Technical University. His research interests include computer simulations of the electromagnetic radiation and scattering phenomena, direct and inverse problems in electrodynamics, and computational electromagnetics.

Hasan Alkaş received the Diplom-Volkswirt degree from the University of Bonn, the Master of Science degree from the University of Sussex, and the Ph.D. degree from the University of Cologne. From 2001 to 2006, he held leading positions with Deutsche Telekom, responsible for regulatory economics, strategy, and pricing. From 2006 to 2010, he was a Principal Economist with the European Commission and the Enterprise and Industry Directorate-General. He was the Dean of the Faculty Society and Economics in 2015. He was also a Senior Economist with the Scientific Institute for Infrastructure and Communication (WIK) and leading projects in regulatory economics and pricing, Bonn. He is currently a Professor of microeconomics (international markets). His main teaching areas are micro, regulatory, institutional and organizational economics, applied game theory, and innovation management. He is also a Specialist in regulatory and industrial economics, especially in telecoms, postal, and energy markets. His main research interests include pricing strategies in network industries (telecoms, post, and energy), regulation, costing, and new investment theory of real options, industrial policies for key enabling technologies (KETs), quantitative economic modeling on e-solutions, and ICT productivity.

Kamil Karaçuha (Graduate Student Member, IEEE) was born in Istanbul, Turkey, in 1993. He received the B.Sc. and double major degrees from the Electrical and Electronics and Physics Departments, Middle East Technical University, Ankara, in 2017 and 2018, respectively. He is currently a Research Assistant with Istanbul Technical University. His research interests include electromagnetic theory, scattering and diffraction problems in electromagnetics, antenna design, and mathematical modeling.

Haci Ömer Tontuş was a Deputy Dean of the Medical Faculty from 2011 to 2013. He has worked extensively as the director, a consultant, and an executive committee member with different divisions, Ministry of Health, including the CEO of the Health Promotion. He is currently a Lecturer with the Department of Molecular Biology and Genetics, Faculty of Science and Letter, Istanbul Technical University. He was involved in many projects in public and private institutions. Since the outbreak of Covid-19, he has been conducting studies on predictions for the post-covid-19 period. He has published 11 books in medical tourism and one book in Future of Healthcare. His main research interests include undergraduate medical education, increasing the level of health literacy of the population, medical tourism, assessment in medical education, and future of healthcare. He serves as the Editor for Medical Tourism-Focused Destination Health magazine.

Nguyen Vinh Ngoc Nu received the bachelor’s degree in economics from Foreign Trade University, Ho Chi Minh City, Vietnam, in April 2019. She is currently a Teaching Assistant with the Rhine-Waal University of Applied Science, Germany.
Funding Statement
This work was supported by the Vodafone Future Laboratory, Istanbul Technical University (ITU), under Grant ITUVF20180901P11.
References
- [1].Kandel N., Chungong S., Omaar A., and Xing J., “Health security capacities in the context of COVID-19 outbreak: An analysis of international health regulations annual report data from 182 countries,” Lancet, vol. 395, no. 10229, pp. 1047–1053, Mar. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Callaway E., “Time to use the P-word? Coronavirus enters dangerous new phase,” Nature, vol. 579, no. 12, p. 1038, Feb. 2020, doi: 10.1038/d41586-020-00551-1. [DOI] [PubMed] [Google Scholar]
- [3].Remuzzi A. and Remuzzi G., “COVID-19 and Italy: What next?” Lancet, vol. 395, no. 10231, pp. 1225–1228, Mar. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Gómez F., Bernal J., Rosales J., and Cordova T., “Modeling and simulation of equivalent circuits in description of biological systems–A fractional calculus approach,” J. Electr. Bioimpedance, vol. 3, no. 1, pp. 2–11, Jul. 2019. [Google Scholar]
- [5].Magin R. L., “Fractional calculus models of complex dynamics in biological tissues,” Comput. Math. with Appl., vol. 59, no. 5, pp. 1586–1593, Mar. 2010. [Google Scholar]
- [6].Chen Y., Xue D., and Dou H., “Fractional calculus and biomimetic control,” in Proc. IEEE Int. Conf. Robot. Biomimetics, Shenyang, CHINA, 2004, pp. 901–906. [Google Scholar]
- [7].Önal N., Karaçuha K., Erdinç G. H., Karaçuha B. B., and Karaçuha E., “A mathematical model approach regarding the children’s height development with fractional calculus,” Int. J. Biomed. Biol. Eng., vol. 13, no. 5, pp. 252–260, 2019. [Google Scholar]
- [8].Jia L., Li K., Jiang Y., Guo X., and zhao T., “Prediction and analysis of coronavirus disease 2019,” 2020, arXiv:2003.05447. [Online]. Available: http://arxiv.org/abs/2003.05447
- [9].Chakraborty T. and Ghosh I., “Real-time forecasts and risk assessment of novel coronavirus (COVID-19) cases: A data-driven analysis,” Chaos, Solitons Fractals, vol. 135, Jun. 2020, Art. no. 109850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Lyu H., Strohmeier C., Menz G., and Needell D., “COVID-19 time-series prediction by joint dictionary learning and online NMF,” 2020, arXiv:2004.09112. [Online]. Available: http://arxiv.org/abs/2004.09112
- [11].Kucharski A. J., Russell T. W., Diamond C., Liu Y., Edmunds J., Funk S., Eggo R. M., Sun F., Jit M., Munday J. D., and Davies N., “Early dynamics of transmission and control of COVID-19: A mathematical modelling study,” Lancet Infectious Diseases, vol. 20, pp. 553–558, Mar. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Schüttler J., Schlickeiser R., Schlickeiser F., and Kröger M., “Covid-19 predictions using a gauss model, based on data from April 2,” Physics, vol. 2, no. 2, pp. 197–212, Jun. 2020. [Google Scholar]
- [13].Fanelli D. and Piazza F., “Analysis and forecast of COVID-19 spreading in China, Italy and France,” Chaos, Solitons Fractals, vol. 134, May 2020, Art. no. 109761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Vattay G., “Predicting the ultimate outcome of the COVID-19 outbreak in Italy,” 2020, arXiv:2003.07912. [Online]. Available: http://arxiv.org/abs/2003.07912
- [15].Kraemer M. U. G., Yang C.-H., Gutierrez B., Wu C.-H., Klein B., Pigott D. M., du Plessis L., Faria N. R., Li R., Hanage W. P., Brownstein J. S., Layan M., Vespignani A., Tian H., Dye C., Pybus O. G., and Scarpino S. V., “The effect of human mobility and control measures on the COVID-19 epidemic in China,” Science, vol. 368, no. 6490, pp. 493–497, May 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Calafiore G. C., Novara C., and Possieri C., “A modified SIR model for the COVID-19 contagion in Italy,” 2020, arXiv:2003.14391. [Online]. Available: http://arxiv.org/abs/2003.14391 [DOI] [PMC free article] [PubMed]
- [17].Sinkala M., Nkhoma P., Zulu M., Kafita D., Tembo R., and Daka V., “The COVID-19 pandemic in Africa: Predictions using the SIR model indicate the cases are falling,” medRxiv, 2020, doi: 10.1101/2020.06.01.20118893. [DOI]
- [18].Wangping J., Ke H., Yang S., Wenzhe C., Shengshu W., Shanshan Y., Jianwei W., Fuyin K., Penggang T., Jing L., Liu M., and Yao H., “Extended SIR prediction of the epidemics trend of COVID-19 in Italy and compared with Hunan, China,” SSRN Electron. J., May 2020, doi: 10.2139/ssrn.3556691. [DOI] [PMC free article] [PubMed]
- [19].Nesteruk I., “Statistics based predictions of coronavirus 2019-nCoV spreading in mainland China,” medRxiv, Feb. 2020, doi: 10.1101/2020.02.12.20021931. [DOI]
- [20].Batista M., “Estimation of the final size of the coronavirus epidemic by the SIR model,” medRxiv, Feb. 2020, doi: 10.1101/2020.02.16.20023606. [DOI]
- [21].Chen Y.-C., Lu P.-E., Chang C.-S., and Liu T.-H., “A time-dependent SIR model for COVID-19 with undetectable infected persons,” 2020, arXiv:2003.00122. [Online]. Available: http://arxiv.org/abs/2003.00122 [DOI] [PMC free article] [PubMed]
- [22].Osthus D., Hickmann K. S., Caragea P. C., Higdon D., and Del Valle S. Y., “Forecasting seasonal influenza with a state-space SIR model,” Ann. Appl. Stat., vol. 11, no. 1, pp. 202–204, Mar. 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Bjørnstad O. N., Finkenstädt B. F., and Grenfell B. T., “Dynamics of measles epidemics: Estimating scaling of transmission rates using a time series SIR model,” Ecol. Monographs, vol. 72, no. 2, pp. 169–184, May 2002. [Google Scholar]
- [24].Podlubny I., Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications. Amsterdam, The Netherlands: Elsevier, Oct. 1998. [Google Scholar]
- [25].Magin R. L., “Fractional calculus in bioengineering, part 1,” Crit. Rev. Biomed. Eng., vol. 32, no. 1, pp. 1–104, 2004. [DOI] [PubMed] [Google Scholar]
- [26].Scalas E., Gorenflo R., and Mainardi F., “Fractional calculus and continuous-time finance,” Phys. A, Stat. Mech. Appl., vol. 284, nos. 1–4, pp. 376–384, Sep. 2000. [Google Scholar]
- [27].Machado J. T., Kiryakova V., and Mainardi F., “Recent history of fractional calculus,” Commun. Nonlinear Sci. Numer. Simul., vol. 16, no. 3, pp. 1140–1153, Mar. 2011. [Google Scholar]
- [28].Tarasov V. E., “On history of mathematical economics: Application of fractional calculus,” Mathematics, vol. 7, no. 6, p. 509, Jun. 2019. [Google Scholar]
- [29].Baleanu D., Güvenç Z. B., and Machado J. A. T., New Trends in Nanotechnology and Fractional Calculus Applications. New York, NY, USA: Springer, Jan. 2010. [Google Scholar]
- [30].Tenreiro Machado J. A. and Mata M. E., “Pseudo phase plane and fractional calculus modeling of western global economic downturn,” Commun. Nonlinear Sci. Numer. Simul., vol. 22, nos. 1–3, pp. 396–406, May 2015. [Google Scholar]
- [31].Moreles M. A. and Lainez R., “Mathematical modelling of fractional order circuit elements and bioimpedance applications,” Commun. Nonlinear Sci. Numer. Simul., vol. 46, pp. 81–88, May 2017. [Google Scholar]
- [32].Tabatadze V., Karaçuha K., and Veliev E. I., “The fractional derivative approach for diffraction problems: Plane wave diffraction by two strips with fractional boundary conditions,” Prog. Electromagn. Res. C, vol. 95, pp. 251–264, 2019, doi: 10.2528/PIERC19062505. [DOI] [Google Scholar]
- [33].Sierociuk D., Dzieliński A., Sarwas G., Petras I., Podlubny I., and Skovranek T., “Modelling heat transfer in heterogeneous media using fractional calculus,” Phil. Trans. Roy. Soc. A, Math., Phys. Eng. Sci., vol. 371, no. 1990, May 2013, Art. no. 20120146. [DOI] [PubMed] [Google Scholar]
- [34].Bogdan P., Jain S., Goyal K., and Marculescu R., “Implantable pacemakers control and optimization via fractional calculus approaches: A cyber-physical systems perspective,” in Proc. IEEE/ACM 3rd Int. Conf. Cyber-Phys. Syst., Beijing, China, Apr. 2012, pp. 23–32. [Google Scholar]
- [35].Dimeas I., Petras I., and Psychalinos C., “New analog implementation technique for fractional-order controller: A DC motor control,” AEU-Int. J. Electron. Commun., vol. 78, pp. 192–200, Aug. 2017. [Google Scholar]
- [36].Sierociuk D., Skovranek T., Macias M., Podlubny I., Petras I., Dzielinski A., and Ziubinski P., “Diffusion process modeling by using fractional-order models,” Appl. Math. Comput., vol. 257, pp. 2–11, Apr. 2015. [Google Scholar]
- [37].Tarasova V. V. and Tarasov V. E., “Elasticity for economic processes with memory: Fractional differential calculus approach,” Fractional Differ. Calculus, vol. 6, no. 2, pp. 219–232, 2016. [Google Scholar]
- [38].Tarasov V. E. and Tarasova V. V., “Macroeconomic models with long dynamic memory: Fractional calculus approach,” Appl. Math. Comput., vol. 338, pp. 466–486, Dec. 2018. [Google Scholar]
- [39].Tejado I., Pérez E., and Valério D., “Fractional calculus in economic growth modelling of the group of seven,” Fractional Calculus Appl. Anal., vol. 22, no. 1, pp. 139–157, Feb. 2019. [Google Scholar]
- [40].Škovránek T., Podlubny I., and Petráš I., “Modeling of the national economies in state-space: A fractional calculus approach,” Econ. Model., vol. 29, no. 4, pp. 1322–1327, Jul. 2012. [Google Scholar]
- [41].Tejado I., Valério D., Pérez E., and Valério N., “Fractional calculus in economic growth modelling: The Spanish and Portuguese cases,” Int. J. Dyn. Control, vol. 5, no. 1, pp. 208–222, Mar. 2017. [Google Scholar]
- [42].Ming H., Wang J., and Fečkan M., “The application of fractional calculus in Chinese economic growth models,” Mathematics, vol. 7, no. 8, p. 665, Aug. 2019. [Google Scholar]
- [43].Blackledge J., Kearney D., Lamphiere M., Rani R., and Walsh P., “Econophysics and fractional calculus: Einstein’s evolution equation, the fractal market hypothesis, trend analysis and future price prediction,” Mathematics, vol. 7, no. 11, p. 1057, Nov. 2019. [Google Scholar]
- [44].Islam M. R., Peace A., Medina D., and Oraby T., “Integer versus fractional order SEIR deterministic and stochastic models of measles,” Int. J. Environ. Res. Public Health, vol. 17, no. 6, p. 2014, Jan. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Area I., Batarfi H., Losada J., Nieto J. J., Shammakh W., and Torres Á., “On a fractional order Ebola epidemic model,” Adv. Difference Equ., vol. 2015, no. 1, p. 278, Dec. 2015. [Google Scholar]
- [46].Almeida R., Brito da Cruz A. M. C., Martins N., and Monteiro M. T. T., “An epidemiological MSEIR model described by the caputo fractional derivative,” Int. J. Dyn. Control, vol. 7, no. 2, pp. 776–784, Jun. 2019. [Google Scholar]
- [47].Haq F., Shahzad M., Muhammad S., Wahab H. A., and ur Rahman G., “Numerical analysis of fractional order epidemic model of childhood diseases,” Discrete Dyn. Nature Soc., vol. 2017, pp. 1–7, Jan. 2017. [Google Scholar]
- [48].Shaikh A. S., Shaikh I. N., and Nisar K. S., “A mathematical model of COVID-19 using fractional derivative: Outbreak in India with dynamics of transmission and control,” Adv. Difference Equ., vol. 373, pp. 1–19, Apr. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Önal N., Karaçuha K., Erdinç G. H., Karaçuha B. B., and Karaçuha E., “A mathematical approach with fractional calculus for the modelling of children’s physical development,” Comput. Math. Methods Med., vol. 2019, Sep. 2019, Art. no. 3081264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Önal N. O., Karacuha K., and Karacuha E., “A comparison of fractional and polynomial models: Modelling on number of subscribers in the Turkish mobile telecommunications market,” Int. J. Appl. Phys. Math., vol. 10, no. 1, pp. 41–48, 2020. [Google Scholar]
- [51].Zeb A., Alzahrani E., Erturk V. S., and Zaman G., “Mathematical model for coronavirus disease 2019 (COVID-19) containing isolation class,” Biomed Res. Int., vol. 2020, Jun. 2020, Art. no. 3452402, doi: 10.1155/2020/3452402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Anirudh A., “Mathematical modeling and the transmission dynamics in predicting the Covid-19–what next in combating the pandemic,” Infectious Disease Model., vol. 5, pp. 366–374, Jan. 2020, doi: 10.1016/j.idm.2020.06.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Singhal A., Singh P., Lall B., and Joshi S. D., “Modeling and prediction of COVID-19 pandemic using Gaussian mixture model,” Chaos, Solitons Fractals, vol. 138, Sep. 2020, Art. no. 110023, doi: 10.1016/j.chaos.2020.110023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Maddison A., “A comparison of levels of GDP per capita in developed and developing countries, 1700–1980,” J. Econ. Hist., vol. 43, no. 1, pp. 27–41, Mar. 1983. [Google Scholar]
- [55].Kingma D. P. and Ba J., “Adam: A method for stochastic optimization,” 2014, arXiv:1412.6980. [Online]. Available: http://arxiv.org/abs/1412.6980
- [56].(Jun. 18, 2020). Coronavirus Cases. Accessed: Jun. 18, 2020. [Online]. Available: https://www.worldometers.info/coronavirus/
- [57].Tabatadze V.. (Aug. 16, 2020). Vasilitabatadze/Deep-Assesment-Methodology. Accessed: Aug. 16, 2020. [Online]. Available: https://github.com/vasilitabatadze/Deep-Assesment-Methodology [Google Scholar]
- [58].Tabatadze V.. (Aug. 16, 2020). Vasilitabatadze/Gaussian-Prediction-for-Covid-19. Accessed: Aug. 16, 2020. [Online]. Available: https://github.com/vasilitabatadze/Gaussian-Prediction-for-Covid-19 [Google Scholar]