Spontaneous helielectric nematic liquid crystals: Electric analog to helimagnets

Significance

The recent discovery of the emerging ferroelectric nematics opens an avenue not only for exploring exotic polar matter states in condensed matter physics but also for providing opportunities toward brand new liquid crystal technologies. Here, we revealed the existence of a helielectric nematic state by introducing the chirality into the ferroelectric nematics. Combining multiple intercorrelated measurements, we confirmed a helicoidal-type polar vector field in the helielectric nematics. The emergent polar symmetry triggers distinctions in topology to the dielectric cholesterics. Via proper doping of chiral generators, the helielectric state can survive down to room temperature, retaining excellent nonlinear optical and dielectric properties. Hence, it offers a stable material platform for exploring unidentified polarity–chirality–coupled textures and developing functional electrooptical devices.

Abstract

Recently, a type of ferroelectric nematic fluid has been discovered in liquid crystals in which the molecular polar nature at molecule level is amplified to macroscopic scales through a ferroelectric packing of rod-shaped molecules. Here, we report on the experimental proof of a polar chiral liquid matter state, dubbed helielectric nematic, stabilized by the local polar ordering coupled to the chiral helicity. This helielectric structure carries the polar vector rotating helically, analogous to the magnetic counterpart of helimagnet. The helielectric state can be retained down to room temperature and demonstrates gigantic dielectric and nonlinear optical responses. This matter state opens a new chapter for developing the diverse polar liquid crystal devices.

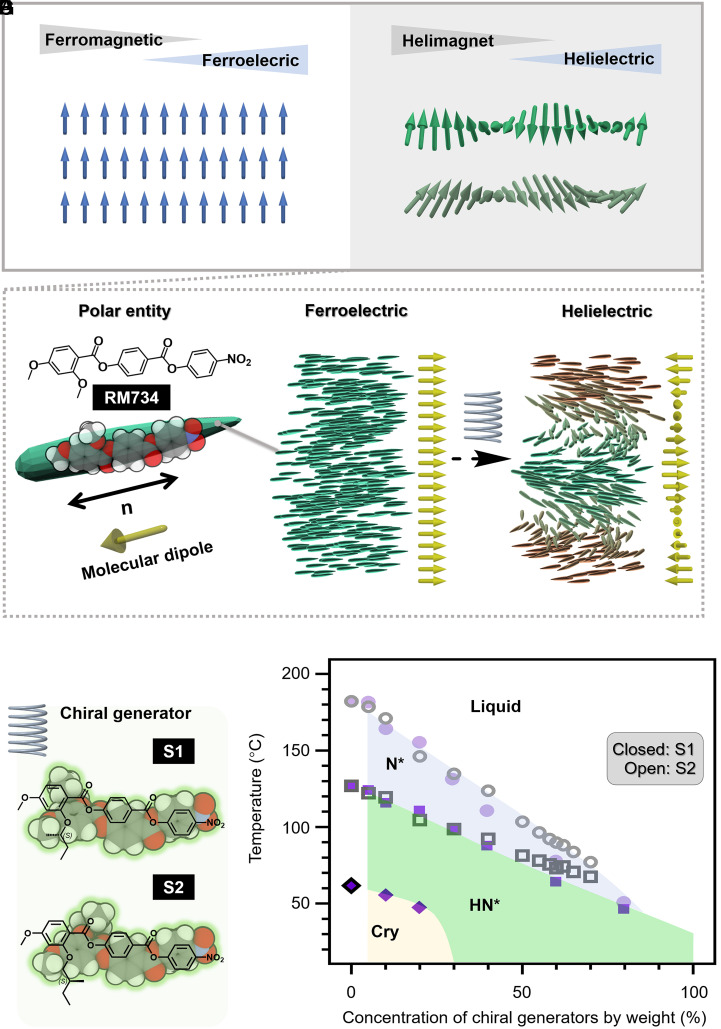
In nature , a new matter state usually arises as a result of unexpected combinations of hierarchical orderings. Helicity is one of the most essential nature of matter states for organizing superstructures in soft matters, spanning many length scales from the atomic to the macroscopic biological levels. When constructed from building blocks with inherent polarity, three hierarchical orderings could coexist in a helical structure: 1) the head-to-tail or polar symmetry of each building block (e.g., Fig. 1C), 2) the orientational order of a swarm of building blocks (Fig. 1A), and 3) the emergent helicity (Fig. 1B). While a simultaneous realization of these three orderings could lead to extraordinary material properties, such highly hierarchical structures are often challenging to achieve in man-made systems. Probably the most familiar example is the chiral magnet or helimagnet (Fig. 1B) in quantum systems, where the magnetic spins form two- or three-dimensional spiral structures (1, 2). The polar magnetic helical structures are considered mainly to originate from either the breaking of the space-inversion symmetry in crystal structures (3) or the magnetic frustration (1, 4, 5). Their strong magnetism-chirality coupling triggers enormous interests in condensed matter physics, leading to many unique quantum and information functionalities (6–9). From the mirror relationship between the magnetism and electricity, we anticipate the incidence of a possible electric version of the helimagnets, namely helielectrics. However, the diverse magnetic topological states rarely show up in electric systems, except a few recent breakthroughs (e.g., the observation of the electric skyrmions, polar vortices, and merons in metal-organic crystals) (10–12). The special electric states at nanoscale exhibit extraordinary properties such as local negative dielectric permittivity (13) and strain-polarization coupling (14, 15). Nevertheless, nearly all the aforementioned chiral magnet or electric-analog systems are based on elaborately fabricated inorganics. It is expected that the revolutionary realization of these topologies in a soft matter system would bring the advantages of flexibility, simple preparation, large-area film formation, and ease of integration into electric devices.

Fig. 1.

Topological analogy: electric versus magnetic states. (A) Uniform magnetization or polarization. (B) Helimagnet or helielectric states. Possible helicoidal (top) and heliconical (bottom) textures are shown. (C) Molecular structure of the polar anisotropic entity, RM734. The molecular polar dipole is nearly parallel to the long molecular axis. (D) The ferroelectric nematic state with spontaneous polarization. (E) HN* state with heli realized by adding chiral generators into the polar chiral nematic state. One-dimensional polarization fields are also depicted in D and E for clarity. (F) The molecular structures of the chiral generators S1 and S2. (G) The state diagram of the two HN* materials by mixing RM734 with S1 or S2.

Among the soft matter systems, liquid analogs of ferromagnet and helimagnet have been reported in liquid crystal (LC) colloids recently (16–20). For the electric versions, there already exist a category of materials possessing all the aforementioned three hierarchical orderings (i.e., the ferroelectric smectic LCs) (21–26). The smectic C* (SmC*) has layered heliconical structure with its local polarity aligning perpendicular to the long molecular axis. Confinement to thin LC cells leads to the unwound ferroelectric state of SmC* with microsecond switching time, thereby being a promising candidate for LC display applications. However, the unavoidable defect generation in the devices originated from the crystal-like structure has been one of the main technical difficulties. Moreover, the SmC* has intrinsically low fluidity and polarity (spontaneous polarization P_s < 1 μC). Here, we report a discovery of a helimagnetic analog state in polar LC materials, dubbed helielectric nematic (HN*). The spontaneous polar nematic ordering is coupled to the chiral orientational helicity (Fig. 1B), taking the form with a nearly helicoidal orientational field. Thanks to its much higher fluidity than the traditional SmC* ferroelectrics, uniform structures can be easily obtained by the typical thermal annealing process. The simultaneous observation of the traditional nonlinear second-harmonic generation (SHG) and SHG interferometry microscopies, as well as the optical observations of the selective reflection from HN* state, allow us to directly visualize the helical polar field. In contrast to the traditional nanoscopic helimagnetic or helielectric inorganics, a wide tunability of the periodic distance ranging from micrometers to near ultraviolet wavelength is achieved in the fluidic structure. Besides, the ability of switching between the polar and nonpolar helical LC states enables complementary physics study for the topology features in HN*. As gifts of the chirality–polarity interaction, the matter state uniquely expresses giant dielectric and SHG optical response, especially interesting SHG amplification when the SHG wavelength coincides with the reflection band of the HN* state.

Results and Discussion

Creation and Observation of Helielectric Nematic Order.

Fluids with the traditional nematic order exhibit the orientational cooperativity but lose the intermolecular positional regularity. The average direction of the local molecular orientation is characterized by the director, n, with the head-to-tail invariant nature. Though a single anisotropic entity (usually a molecule) has a preferred directional dipole (Fig. 1C), the equivalent number of upwards and downward dipole vectors in the nematic state results in the zero spontaneous polarization. Introducing strong molecular dipole and geometrical asymmetry into the entity is an effective root for breaking this symmetry, realizing a fluidic ferroelectric or the so-called splay nematic [N_F (27–31) or N_s (32–34); the naming of the new materials state is still under debate] state. It takes a local ferroelectric ordering with orientated polarity (Fig. 1 A and D) (27–30, 33–35). Critically, the head-to-tail invariance breaks down, so n ≠ −n. Learning from that the helimagnet is a helically modulated ferromagnetic state (Fig. 1B), we conceive the idea of incorporating a chiral generator to induce helicity in the N_F state, leading to the creation of the corresponding helielectric state (Fig. 1E). To test this possibility, we used a reported RM734 molecule as the ferroelectric nematic material (27, 33, 36, 37) and synthesized S1, S2, E1, and E2 as chiral generators (Fig. 1F and SI Appendix, Fig. S2). The four chiral generators incorporate chiral groups at various positions on the RM734 molecular scaffold and share similarity with a recently reported chiral LC material (32). In addition, we also examined a commercial chiral generator R811 as a reference molecule that is structurally distinct from RM734.

The doping of the commercial apolar chiral generator R811 is expected to exhibit relatively low eminent polarity at high doping ratio and a strong preference to form crystals (SI Appendix, Fig. S10). The dissolution limit of R811 in RM734 matrix is only 9 wt%. On the contrary, the doping of S1, S2, E1, or E2 facilitates the formation of a helielectric state that could exist across a wide temperature window (Fig. 1G and SI Appendix, Fig. S2). Our chiral generators have excellent miscibility (up to 70%) into RM734 while retaining the helielectric state, suggesting that the macroscopic polarity is achieved by long-range polar interactions. Fig. 1G demonstrates the matter state diagram as a function of temperature and the weight percentage of the chiral generators (S1 and S2; Materials and Methods). Interestingly, the state diagrams are independent on the molecular structure of the chiral generators (SI Appendix, Supplementary Discussion 1). A general trend of the matter phase sequence could be identified: isotropic liquid → nonpolar helical nematic state (N*) → HN* state → crystal. This phase sequence could easily be observed from the differential scanning calorimetry (DSC) study (SI Appendix, Fig. S4). It is worth noting that the X-ray diffraction of the HN* state is similar to that for the N* state, excluding the possibility of other LC phases such as smectics (SI Appendix, Figs. S14 and S15). Similar to the traditional N and N_F state transition in a single ferroelectric nematic material (27–30, 33–35), the helical state can also exhibit the nonpolar–polar transition as discussed later. The temperature range of the N* phase is linearly reduced with increasing the chiral doping percent. When the content of the chiral generators exceeds ∼30% in weight, the crystal phase is suppressed and the HN* phase becomes stable at room temperature.

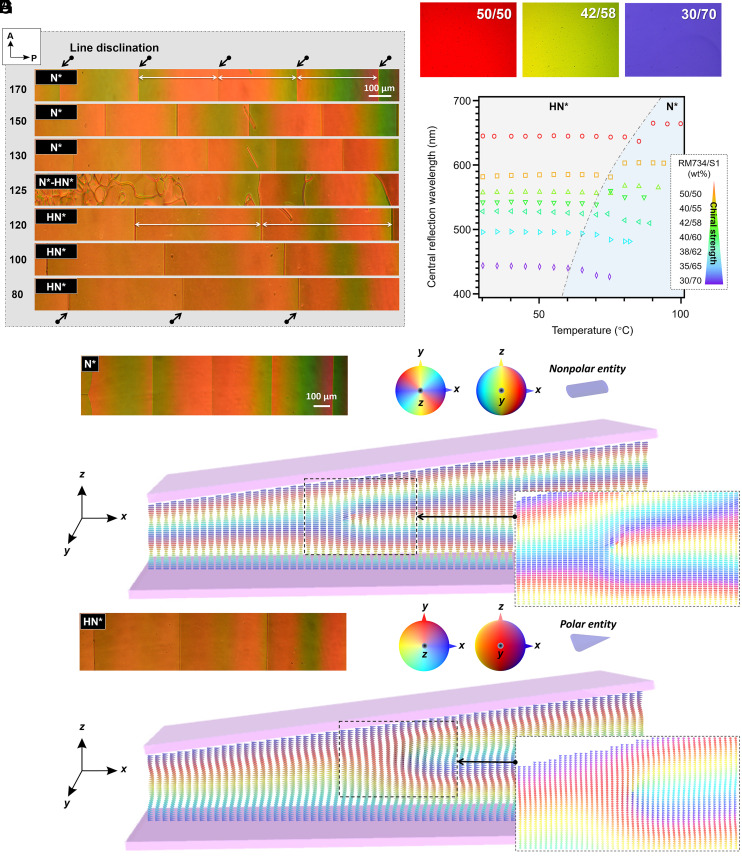
Polarized light microscopy (PLM) enables us to directly visualize the transition from N* state to HN*. Fig. 2A shows the evolution of PLM images for RM734/S1 = 95/5 near the N*–HN* transition in a wedged LC slab, where the upper and bottom surfaces are parallel-rubbed to give rise the unidirectional planar alignment. The so-called Grandjean–Cano lines appear, which represent the disclinations separating aligned helical structures with differed number of the helix (38). In an α degree–wedged LC slab, the periodicity L of the Grandjean–Cano lines and the helical pitch p of the nonpolar helical structure follow the relationship P = 2Ltanα (38). Near the N*–HN* transition, the L value was observed to double from the N* to HN* state. However, the real helical pitch p remained almost the same (not doubled), according to the reflection wavelength measurements (Fig. 2 B–E and SI Appendix, Figs. S5, S6, and S8B), optical rotation power measurement (SI Appendix, Fig. S13 and Supplementary Discussion 3), and microscopy observations of fingerprint texture (Upper of Fig. 3D, vide infra). Therefore, the observed doubling of L suggested that the relationship P = 2Ltanα does not apply to the HN* state. In the N* state, the relationship P = 2Ltanα originates from the insertion of a half helical pitch from domain to domain (Fig. 2F, Top) to form the Grandjean–Cano lines. In contrast, the same insertion mode would lead to surface defects in HN* materials given the mismatch between the neighboring vectorized field of the polarization. We hypothesized that HN* materials form the Grandjean–Cano lines by inserting a full helical pitch in neighbors to avoid a free energy penalty caused by additional surface defects. Fig. 2 F and G demonstrate the simulated topological structures in both the N* and HN* states confined in the wedge LC slab (Materials and Methods). The HN* state carries a λ^−1/2λ^+1/2 pair-type of disclination (39–41). Learning from the recent discussion on the control of surface polarity by the rubbing direction (29), the present parallel [i.e., synpolar in (29)] rubbing results in the uniform polar field on both the surfaces with the same polarity direction (e.g., polar vectors uniformly orient toward right on both the upper and bottom surfaces). Indeed, this situation is confirmed by confocal SHG interferometry (SI Appendix, Fig. S11). Therefore, we conclude that the equation describing the relationship between the helical pitch and periodicity of Grandjean–Cano lines transmutes into P = Ltanα in the HN* state. Such an anomaly arises from the symmetry variation (from n ≡ −n to n ≢ −n) from the N* to HN* state. It inspires the importance for further exploring localized chiral topologies like skyrmions in the new polar chiral state and comparing the physics with the existing apolar counterparts in future (42).

Fig. 2.

General properties of HN*. (A) The textural evolution of RM734/S1 = 95/5 mixture in a wedge cell with an inclination angle of tanα = 0.0079. The numbers on the left of the photographs mean the temperature in Celsius. While there is no net polarization in the N* state, a helically wound polarity field appears in the HN* state. The line disclinations are indicated by black arrows. In B–D, the PLM images of the selective reflection in the HN* state of RM734/S1 = 50/50 at 62 °C (B), 42/58 at 59 °C (C), and 30/70 at 49 °C (D) are shown. (E) The temperature dependencies of the mean visible-light reflection peaks for RM734/S1 mixtures. The reflection experiments were made in 5-μm LC slabs. Interestingly, in contrast to traditional N* materials, the reflection wavelength in a wide temperature range over about 80 °C barely changes (maximally within 20 nm). (F) PLM and simulated director field in a wedged cell in the N* state. The line disclinations are indicated by black arrows. (G) PLM and simulated polarization field in the HN* state in the same wedged cell as in F. The expanded views of near the disclinations are shown on the right bottom for G and F.

Fig. 3.

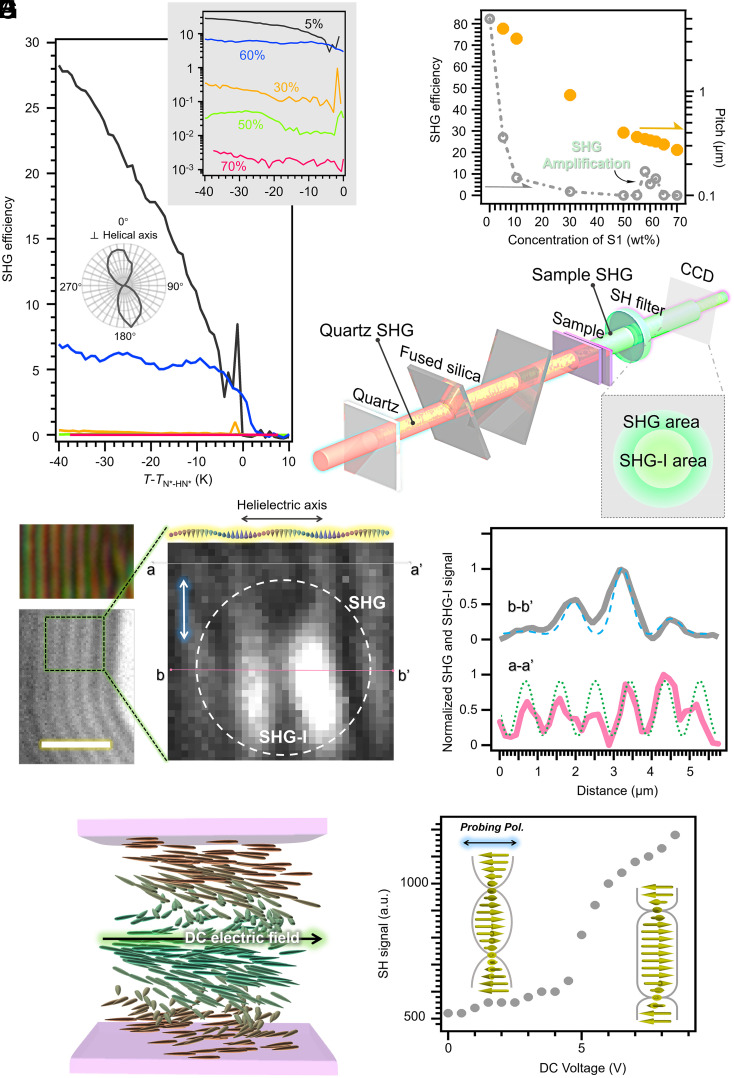
SHG amplification and observation of the HN* structure. (A) The temperature dependencies of SH signal for RM734/S1 = 95/5, 70/30, 50/50, 40/60, and 30/70 mixtures. The SH signal is amplified in RM734/S1 = 40/60 (also refer to B). The horizontal axis is the reduced temperature. T_N*-HN* is the transition temperature between the N* and HN* states. The SHG efficiency, defined as the SH signal intensity ratio of the HN* materials to that of a Y-cut quartz plate. The Inset on the right top shows the SH signal in a log scale in the HN* state. The polar plot clearly shows the strongest SHG occurs perpendicular to the helical axis of the helielectric structure, suggesting the helical structure is helicoidal-like. (B) The saturated SHG efficiency in the HN* state and helical pitch of the HN* state as a function of the weight percentage of S1. (C) Optical setup for the simultaneous observation of SHG and SHG-I images. In the SHG-I imaging area, the quartz, and sample SH signals overlap, causing the interference of SHG. The SH signal of the polar domains interferes with that of the quartz plate constructively or destructively depending on the rotation angle of the fused silica plate. In the imaging, we choose the proper angle for best contrast of the SHG interferometry. (D) PLM (Upper) and traditional (Lower) microscopy observations of the “fingerprint” helical structure (scale bar, 5 μm). The latter was made without polarizers during the SHG measurement. (E) Simultaneous observation of SHG and SHG-I microscopies. The SHG-I area, where a Gaussian reference SH beam from a Y-cut quartz plate is overlapped with the sample SH signal, is indicated by a white dotted circle. The incident polarization is indicated by a white arrow. The width of the image is 5.6 μm. (F) The SHG and SHG-I signal plots along a-a′ and b-b′ lines. The blue chain and green dotted line are the fitting curves to the spatial variation of the SH and SHG-I signals. The corresponding polarity field is depicted in E. (G) The schematic of the HN* structure under an IPE field application. (H) The SH signal as a function of the applied DC voltage. Over 9 V_DC, electrohydrodynamic convection occurs.

To investigate the emergent polar property of the HN* state materials, we conducted the SHG measurement. It probes the breaking of the inversion center in the system, characterizing the static polar ordering. Fig. 3A demonstrates the temperature dependencies of the SH signal strength for the HN* state with different chiral generator S1 concentration. For all the mixtures irrespective of the helical pitch, the SH signal shows up slightly above the N*–HN* transition and increases with decreasing the temperature. The SH signal in the HN* state is steady or slightly increasing for most of the mixtures, suggesting the emergent polarity is stable in the HN* temperature range. With a lower concentration of S1, the HN* state shows stronger SH signal (e.g., maximally 83, 32, and 0.4 times of SH signal of a Y-cut quartz plate at S1 weight percent of 0%, 5%, and 30%, respectively). Increasing the concentration of S1 results in a rapid decrease of the SH signal (Fig. 3B). This is attributed to the decrease of both the helical pitch and the inherent polarity of the systems by increasing the ratio of the less polar chiral generators (SI Appendix, Fig. S3). Especially, as the helical pitch becomes shorter compared to the wavelength of the fundamental ray, the net polarity for the fundamental ray decreases and the SH signal weakens. Surprisingly, a clear SHG enhancement up to ∼500 times was observed when the concentration of S1 locates in a limited window of 58 to 62 wt% (Inset on right top in Fig. 3 A and B, compare the enhanced signal with that in the 50 to 55 wt% mixtures). In this range, the helical pitch is about 510 to 550 nm (SI Appendix, Fig. S5), comparable to the SH wavelength of 532 nm. Besides, the SHG light is circularly polarized following the handedness of the helielectric structure. The absolute value of the so-called dissymmetry factor g value, defined as $g=2({\eta }_{\text{L}}-{\eta }_{\text{R}})/({\eta }_{\text{L}}+{\eta }_{\text{R}})$ expressing the purity of the circular polarization, is ∼1.7 for all the tested material. This g value indicates the excellent handedness selectivity in the spontaneous SH light generation.

It is known that the polarity vector of RM734 is almost along the local director (43). Meanwhile, there exists good correspondence between the polarity vector and the magnitude of the SH signal. The SHG measurement is thus a robust method to determine the polarity structure of the HN* state. To visualize the polar helicity, we designed SHG interference (SHG-I) microscopy. SHG-I is the sole technique able to probe the polar properties in bulk fluidic materials and sensitive to the orientation of the polarity (44–47). Fig. 3 C–F demonstrate the simultaneous observation of SHG and SHG-I microscopies. In a 5-μm homeotropically aligned slab, the helical axis is aligned parallel to the LC slab surface, thus showing the fingerprint texture confirmed by PLM (Fig. 3D). The fingerprint textures are characteristic in both the N* and HN* states and they look the same. It should be noted that such a fingerprint texture can only appear at the homeotropic surface anchoring, whereas only the uniform and smooth texture with the helical axis along the surface normal direction could be observed at the planar surface anchoring (Fig. 2 B–D; no periodic pattern was observed). These facts mean the observed periodic fingerprint is surely distinct to the stripe (27, 30, 33, 34) and banded (27, 30) textures observed in SH images of pure ferroelectric nematics (e.g., RM734 and DIO). Therefore, the realization of the fingerprint textures allows us to directly determine how the polarity vector modulates along the helical axis.

The SHG microscopy image reveals that the periodicity of the fine, dark bright stripes is consistent to the width, ∼1.1 μm, of the finger texture of both the N* and HN* state. The periodicity is the half of the helical pitch, 2.2 μm, of the HN* state. The simultaneous SHG and SHG-I observation in an image clarifies that the adjacent bright stripes have a mutual phase difference of π (i.e., the alternation of dark and bright in interfered SH signal intensity) (Fig. 3E). Fig. 3F demonstrates the intensity plots of the cross sections for SHG (line a-a′) and SHG-I (line b-b′) microscopies. The spatial distributions of both the signals are well-fitted, where the two beams are assumed to be impinged onto a charged coupled device (CCD) as Gaussian spots. Here, we emphasize two experimental facts: 1) SHG signal is highest when the excitation polarization is parallel to n but extincted when perpendicular to n (the Inset of Fig. 3A); and 2) the downward and upward polarizations exhibit minimum and maximum SHG-I intensities. After carefully comparing the spatial distributions of the SHG and SHG-I in a single image (Fig. 3 E and F), we conclude that the helicity of the polarity vector field is as calculated in the top of Fig. 3E. Particularly, the aforementioned means that the present helieletric structure is helicoidal-like. Furthermore, such a helielectric polar vector field can respond to an electric field. An SHG measurement was carried out in a planar aligned LC slab under an in-plane electric field (IPE field; refer to Fig. 3G). The polarization of the incident fundamental beam is set to be parallel to the direction of the IPE field. Upon increasing the electric field, the increase of SH signal was detected, indicating the reorientation of the polar vector toward the IPE field direction (Fig. 3H and SI Appendix, Fig. S16 and Supplementary Discussion 4). The electrohydrodynamic convection flow occurs exceeding 9 direct current voltage. Overall, the evidence for the existence of the HN* state is solid. We believe this state would be a general matter state and consistent with those polar chiral nematic phases as reported very recently in several other systems (29, 32, 48).

Theoretical Consideration on Stability of HN*.

To explain the emergence of the polarity through the N*–HN* phase transition, we learn from the computational models of magnetic systems. We describe a Landau–de Gennes type free energy density near the phase transition as follows, by assuming the polarity $\mathit{P}$ as the primary order parameter:

$$f=a\left(T-T_c\right)P_0{}^2+b{P}_0{}^4+1/2K_{11}{\left(\nabla \cdot \mathit{n}\right)}^2+1/2K_{22}{\left(\mathit{n}\cdot \left(\nabla \times \mathit{n}\right)\right)}^2+1/2K_{33}{\left(\mathit{n}\times \left(\nabla \times \mathit{n}\right)\right)}^2-1/2K_{22}^{\prime }\mathit{n}\cdot \left(\nabla \times \mathit{n}\right)+\text{J}{\left(\nabla \mathit{P}\right)}^2+D\mathit{P}\cdot (\nabla \times \mathit{P}),$$

where $T_c$, $P$, $K_{22}$ and $K_{22}^{\prime }$, $q_0$, and $\mathit{n}$ denote the transition temperature, polarization strength, twist elastic coefficient, wave number of the helical pitch, and the director vector. The first two terms represent the Landau free energy, describing the stability of the polar state. The third to fifth terms are the Frank elastic energies from the contribution from splay, twist, and bend deformations, and the sixth term is the twisting energy from the chiral nematics. Since the local polarity favors the uniform polarization field, the second-to-last term penalizes the free energy from the spatial variation of the polarization field with the coefficient $\text{J}$. The last term corresponds to the electric counterpart of the Heisenberg and Dzyaloshinskii–Moriya interactions that represents the tendency of the polarity winding with the coefficient $D$. ${\left(\nabla \mathit{P}\right)}^2$ means ${\sum }_{j=x,y,z}({\sum }_{i=x,y,z}{\partial }_i{P}_j)$. As discussed above, the polarization vector is parallel to the director, so $\mathit{P}=P_0\mathit{n}$ as confirmed by SHG measurement. Now, we consider the experimentally observed state that the helical axes of both the N* and HN* state are oriented along the surface normal, say, the z-direction. Therefore, we use the ansatz for the director field with the wavenumber of helical structure,$q$,

$$\mathit{n}=\left(\cos q,\sin q,0\right).$$

The difference of the free energy between the nonpolar–polar helical structures is $\mathrm{\Delta }f=f\left(\mathit{P}\right)-f\left(0\right)$. By putting the director field into the free energy density, $\mathrm{\Delta }f$ reads

$$\mathrm{\Delta }f=a\left(T-T_c\right)P_0{}^2+b{P}_0{}^4+P_0{}^{2}q(Jq-D).$$

By minimizing the free energy ($\partial \mathrm{\Delta }\text{f}/\partial P_0=0, {\partial }^2\mathrm{\Delta }\text{f}/\partial P_0{}^2>0$), we obtain the solutions for $P_0$ as

$$\mid \mathit{P}\mid =0, \sqrt{Dq-J{q}^2-a\left(T-T_c\right)}/\sqrt{2b}.$$

When $T<T_c+\left(Dq-J{q}^2\right)/a$, nonzero spontaneous polarization $\mathit{P}$ appears and the free energy for the HN* state is always lower than that in the N* state by ${(Dq-J{q}^2-a\left(T-T_c\right))}^2/4b$. This suggests the incidence of the HN* would be a general phenomenon if the existence of the polarity is allowed in fluidic systems.

LC Capacitor with Extraordinary Dielectric Properties.

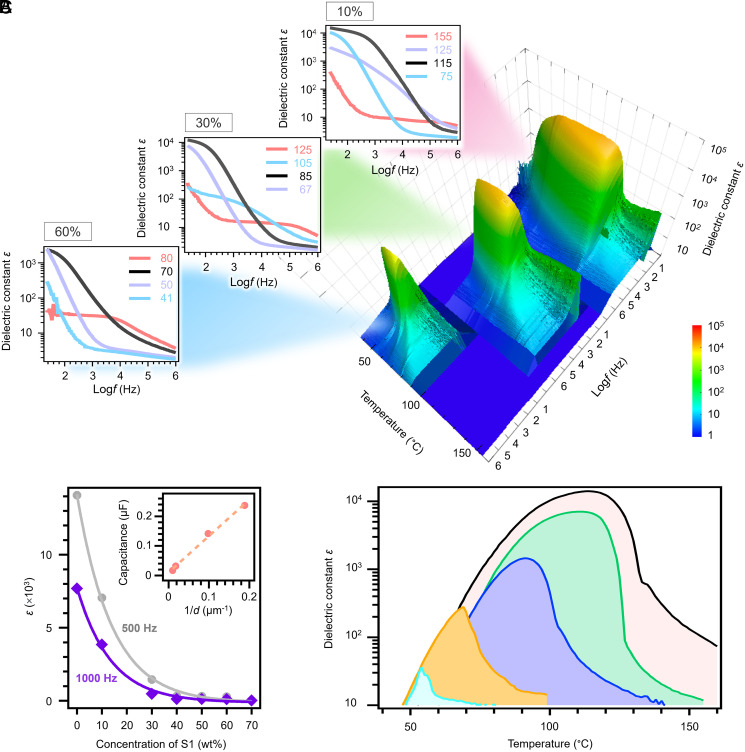
The HN* materials can be easily filled between flexible substrates and deformed, possibly serving as a promising flatform for flexible LC capacitors. Considering the strong polarity of the HN* materials reflected in the SHG response, it is of great interest to measure what magnitude the dynamic dielectric response is, and in what range the capacitance can be controlled as electronic elements. We investigated the temperature dependence of the dielectric response for materials with different concentrations of the chiral generator S1 (Fig. 4A). The giant dielectric constant values in the range of 1,000 to 10,000 at 1,000 to 500 Hz were detected for the mixtures with S1 below 20 wt% (Fig. 4B). Similar to the SHG measurement results, the maximum dielectric constant decreases upon increasing the chiral doping ratio (Fig. 4B). Thanks to the huge dielectric constant, the capacitance of the HN* state is in the range of nano-farad. For example, the effective capacitance of a HN* capacitor at RM734/S1 = 90/10 contacting with 1 × 1 cm electrodes is as huge as 0.02 μF when the film thickness is ∼100 μm. The capacitance value can be dramatically tuned up to ∼0.2 μF by decreasing the film thickness down to ∼5 μm (Inset of Fig. 4B). The dielectric constant for the mixtures increases when approaching the N*–HN* transition and then decreases (Fig. 4C) (i.e., a bell-shape temperature variation). It is worth noting that the polarity never weakens in the HN* by lowering temperature, which is manifested in the steady increase of the SH signal (Fig. 3A). Therefore, the bell-shape temperature variation of dielectricity would be interpreted as below. First, the nucleation and growth of microscopic polar domains embedded in the nonpolar background proceed with lowering temperature, giving rise to the increase of both the SHG and dielectric constant. Under this circumstance, the average polar vector in each polar domain is small and can be switched by the probe voltage (typically 10 to 100 mV and electric field ∼1 to 10 mV/μm). At lower temperatures, each polar domain becomes too big. Thereby, the relaxation frequency becomes lower and the effective dielectric response becomes worse. This is consistent with the scenario of the relaxor-like behaviors (49, 50) as frequently observed in inorganic ferroelectric materials.

Fig. 4.

Extraordinary large dielectric constant and relaxor-like response. (A) The Three-dimensional and two-dimensional plots of the dielectric spectroscopy for RM734/S1 = 90/10, 70/30, and 40/60 mixtures in their HN* state. The numbers in the two-dimensional–plotted figures indicate the measurement temperatures. (B) The maximum dielectric constant at 500 Hz and 1,000 Hz as a function of the concentration of S1. The Inset demonstrates the capacitance of the HN* capacitor (RM734/S1 = 90/10) contacting with 1 × 1 cm electrodes at different thickness d. The frequency of the probe electric field is 500 Hz. (C) The dielectric constant measured at 500 Hz as a function temperature for RM734/S1 = 100/0 (black), 90/10 (green), 70/30 (blue), 40/60 (orange), and 30/70 (light blue) mixtures.

In summary, we report real-space observation of polar helielectric state with the local nematic ordering. The realization of such a state with the homochiral helical arrangement of the polarity vector is made possible through the coupling between the strong local polarity and chirality. This unique electric structure in fluids resembles the helimagnets in the context of magnetic systems, but distinct in their high tunability of the helielectric pitch in a wide range from hundred nanometers up to several tens of micrometer. Furthermore, our findings confirm three important features of the helielectric nematics: 1) Contrary to the high-temperature nature of ferroelectric nematic found previously, the helielectric nematics preserve their presence down to room temperature; 2) the stabilization gifts the materials the giant dielectric effect and optical nonlinearity to be used at low temperatures; and 3) the optical nonlinear response is amplified at helielectric pitch close to the SHG wavelength. These discoveries open the door for exploring physics of polar topological structures previously inaccessible in fluidic materials and for engineering room temperature flexible device by utilizing the excellent electrooptic properties.

Materials and Methods

Sample Preparation.

The polar helical materials were realized by mixing a ferroelectric nematic LC (RM734 in Fig. 1D) with the commercial or four homemade chiral generators (R811, E1, E2, S1 and S2; Fig. 1G and SI Appendix, Fig. S2) independently by weight. The mixtures were made by dissolving the materials in chloroform solvent. After mechanical mixing, the solvent was mildly evaporated at 55 °C. S1 and S2 were designed to have the same backbone of mesogen with N_F LC. The mixtures were introduced to homemade or commercial LC slabs with controlled thickness and alignment conditions. As planar and homeotropic alignment materials, we used KPI-3000 (Shenzhen Haihao Technology Co., Ltd) and KPI-9811 (Shenzhen Haihao Electronic Co., Ltd) or JALS204 (JSR Corporation), respectively. For the observation of Cano lines, we used commercial wedge LC slabs (KCRS-03, EHC) with parallel-rubbed planar alignment. The slab thickness is continuously varied from 0 to 300 μm in the wedge slabs. Homemade planar slabs with the slab thickness in the range of 4 to 10 μm were used for the observation of reflection imaging and spectroscopy. Homemade 5-μm–thick slabs with planar alignment were used for measuring the SH signals as a function of temperature. Homemade 10-μm–thick and 5-μm–thick slabs with homeotropic alignment layer were used for measuring the dielectric properties and SHG microscopies, respectively. It is noted that the complete homeotropic anchoring is difficult in the polar materials. The use of the homeotropic alignment layer produces large polar tilting of the neat RM734 materials and smaller tilting in the helieletric materials. Therefore, the fingerprint texture is observed.

Optical Spectroscopy.

The optical spectroscopy is measured in the reflection mode by using an upright optical microscopy (BX51, Olympus). The input light is unpolarized and focused to the samples by a 10× objective (numerical aperture NA = 0.25). The reflected light is guided into a spectroscopy (Ocean optics, USB4000) through an optical fiber. The reflected light is detected without placing a polarizer before the spectroscopy. During these measurements, the intensity of the input light is controlled to be weak to avoid the temperature increase of the sample. Also, to measure the polarization state of the reflected light, a quarter-wave plate is put before the detector.

SHG-I Measurement.

An SHG-I measurement system is built as discussed in Fig. 3C and SI Appendix, Fig. S12 and Supplementary Discussion 2. The fundamental beam is emitted from a Q-switched pulsed laser (MPL-277 III-1064–20µJ) with a central wavelength of 1,064 nm, pulse duration of 5 ns, and 100 Hz repetition. The SH light is detected in the transmission or reflection (backward) geometry by a photomultiplier tube (DH-PMT-D100V, Daheng Optics) or a scientific complementary metal-oxide-semiconductor (CMOS) camera (Zyla-4.2P-USB3, Andor). For the SHG interferometry, we used two fused silica plates for generating the phase difference between the SH signal from the sample and the reference Y-cut quartz plate. The fused silica plates are rotated in opposite directions to avoid the variation of the optical path during their rotation. With larger rotating angle of the fused silica plates, the induced phase difference is larger. For the SHG-I microscopy, we choose several interference conditions for the best imaging contrast by finding the corresponding rotating angles of the fused silica plates.

Dielectric Spectroscopy.

The dielectric spectroscopy was conducted by using an LCR meter (4284A, Agilent). The data collections of the frequency and temperature sweeping are automated by a homemade software written in Labview.

X-Ray Diffraction Measurement.

The samples were melted on a hot stage, then loaded into glass tubes with diameter of 0.3 mm. X-Ray diffraction measurement was executed by Rigaku Nanopix-SP with an ultrahigh intensity microfocus rotating anode X-ray generator. The wavelength X-ray is 0.154 nm.

Calculation of the Director and Polarity Orientation Profile in the Wedge Slab.

To simulate both the structures of N* and HN* states in wedge slabs, we perform the relaxation minimization of the Ginzburg–Landau functional based on a Landan-de Gennes modeling (51, 52). For the N* state, we wrote the free energy as expansions in the orientational order in terms of a symmetric and traceless tensor $Q_{\text{ij}}=S(n_{\text{i}}{n}_{\text{j}}-{\text{δ}}_{\text{ij}}/3)$, where i, j are the Cartesian coordinates and $S$ is the scalar order parameter. The head-to-tail invariance is guaranteed here. To the lowest relevant orders, the free energy density is written as

$$f=f_L+f_e+f_s,$$

$$f_L=A_0(1-U/3)Q_{\alpha \beta }^2/2-A_{0}U{Q}_{\alpha \beta }{Q}_{\beta \zeta }{Q}_{\zeta \alpha }/3+A_{0}U{(Q_{\alpha \beta }^2)}^2/4,$$

$$f_e=L{({\partial }_{\beta }{Q}_{\alpha \beta })}^2/2+2q_{0}L{ϵ}_{\alpha \zeta \delta }{Q}_{\alpha \beta }{\partial }_{\zeta }{Q}_{\delta \beta },$$

$$f_s=W{(Q_{\alpha \beta }-Q_{\alpha \beta }^0)}^2/2,$$

where $f_L$, $f_e$, and $f_s$ are the Landau, the elastic and surface anchoring free energies. $A_0$ and $U$ are phenomenological parameters depending on temperature and pressure. $U$ controls the magnitude of the order. $L$, ${ϵ}_{\alpha \zeta \delta }$, $W$, and $Q_{\alpha \beta }^0$ are the elastic constant, Levi–Civita tensor, anchoring coefficient, and surface Q-tensor component. We used typical material parameters for the calculation: $A_0$, $U$, and $W$ are 1, 6, and $100$, respectively. $L$ is used in the range of 0.02 to 1.

For the calculation of the topological structure for the HN* state, we start with the topological structure of the N* structure obtained as described above. To include the vectorized polar nature that breaks the head-to-tail invariance, we write the free energy density as expansions of the director orientation, $n$, as follows:

$$f=\frac{1}{2} K_{11}{\left(\text{div} \mathbf{n}\right)}^2+\frac{1}{2} K_{22}{\left(\mathbf{n}\cdot \left(\text{curl} \mathbf{n}\right)\right)}^2+\frac{1}{2} K_{33}{\left(\mathbf{n}\times \left(\text{curl} \mathbf{n}\right)\right)}^2-\frac{1}{2}{K}_{22}^{\text{′}}\mathbf{n}\cdot \left(\nabla \times \mathbf{n}\right).$$

Based on the result of the SHG-I measurement in the backward geometry where the birefringence effect is minimized, the surface polarization in the adjacent domains align in the same direction (SI Appendix, Fig. S11). Therefore, we set the surface polarity orientation, equivalent to the director vector, to be identical for all the bottom and top surfaces. For simplicity, we relax the above director-based free energy to get the equilibrium structure. Though the assumption is rough, still the simulated orientational pattern captures the essential structural difference between the N* and HN* state.

Data Availability

Data and simulations have been deposited in the Open Science Framework (OSF) database of Helielectric nematic liquid crystals (DOI: 10.17605/OSF.IO/ZFUS8).