Parallel Transmit Optimized 3D Composite Adiabatic Spectral-Spatial Pulse for Spectroscopy

Abstract

Purpose

To develop a 3D composite adiabatic spectral-spatial pulse for refocusing in spin-echo spectroscopy acquisitions and to compare its performance against standard acquisition methods.

Methods

A 3D composite adiabatic pulse was designed by modulating a train of parallel transmit (pTx) optimized 2D sub-pulse with an adiabatic envelope. The spatial and spectral profiles were simulated and validated by experiments to demonstrate the feasibility of the design in both single and double spin echo spectroscopy acquisitions. Phantom and in-vivo studies were performed to evaluate the pulse performance and compared to semi-LASER with respect to localization performance, sequence timing, signal suppression and specific absorption rate (SAR).

Results

Simultaneous 2D spatial localization with water and lipid suppression was achieved with the designed refocusing pulse, allowing high quality spectra to be acquired with shorter minimum TE/TR, reduced SAR deposition, as well as adaptation to spatially varying B₀ and B₁⁺ field inhomogeneities in both prostate and brain studies.

Conclusion

The proposed composite pulse can serve as a more SAR efficient alternative to conventional localization methods such as semi-LASER at ultra-high field for spin-echo based spectroscopy studies. Sub-pulse pTx optimization provides the flexibility to manage the tradeoff between multiple design criteria to accommodate different field strengths and applications.

INTRODUCTION

Magnetic resonance spectroscopy (MRS) has been widely used as a non-invasive tool to characterize in-vivo metabolites of interest in biological tissues. Standard acquisition strategies include single-voxel spectroscopy (SVS) and its spatially encoded variant known as magnetic resonance spectroscopic imaging (MRSI) or chemical shift imaging (CSI). To achieve spatial localization and spectral suppression of unwanted water or lipid signals, multiple orthogonal spatial selective pulses and additional spectral selective suppression pulses are typically used. In terms of localization, two common acquisition methods historically have included Stimulated Echo Acquisition Mode (STEAM) and Point Resolved Spectroscopy (PRESS) (1). While STEAM has its advantages in terms of peak power, specific absorption rate (SAR) and shorter minimum echo times, the double spin-echo approach of PRESS and its variants are typically favored over STEAM due to the two-fold increase in signal to noise ratio (SNR) (2).

Despite the improvements in SNR, spectral dispersion (3) and quantification (4) at ultra-high field (UHF), increased chemical shift artifacts, transmit B₁ (B₁⁺) inhomogeneities and B0 inhomogeneities impose additional requirements on the acquisition methods which make PRESS undesirable when considered for both SVS and CSI applications. Appropriate spin-echo methods to address these issues include Localization by Adiabatic Selective Refocusing (LASER) or semi-LASER techniques which use high bandwidth, B₁⁺-insensitive adiabatic RF pulses for refocusing. To address the spatially quadratic phase that results from a single slice-selective adiabatic pulse, both LASER and semi-LASER methods use pairs of adiabatic refocusing pulses leading to increased minimum echo times (TE) and to increased SAR which in turn requires longer repetition times (TR). In addition to chemical-shift and B₁ inhomogeneities, greater B₀ variations at UHF impact the spectral selectivity of suppression methods both inside, and more prominently, outside the volume of interest (VOI) when a strong localized B₀ shimming is imposed. This results in compromised spectral quality either from incomplete suppression of undesired signals or unintended suppression of desired signals, and potentially spatially varying effects on coupled spin systems within the VOI due to the unintended shift of the selective window when using chemical-shift selective RF pulses.

An alternative to using RF pulses which are solely spatially selective, spatial-spectral (SPSP) pulses have been introduced to provide both spatial and spectral selectivity, where a series of sub-pulses define the spatial selectivity and an “envelope”, or “parent pulse”, defines the spectral selectivity by modulating the amplitude and phase of the sub-pulses. Despite its early introduction and later extended work (5-10), one limiting drawback of such pulses is their long duration due to the limitations in peak RF amplitude and gradient slew rate especially at UHF, although a recent study presented an optimized SPSP pulse that mitigated these issues (11). In general, SPSP pulses were usually constrained to be 2D selective with applications demonstrated in brain, prostate and other targets (11-17).

As opposed to 1D pulses, a unique advantage of 2D and 3D spatially selective pulses is the ability to compensate for B0 and B1 field inhomogeneities (8,10) (18), while 2D SPSP pulses are affected by off-resonance effects the same way as 1D pulses (18). While 2D spatially selective pulses have potential advantages for use as sub-pulses to make a 3D SPSP pulse, such use has been limited to date due to their increased duration and limited bandwidths although introduced shortly after 2D pulses (18-21).

More recently, parallel transmit (pTx) has been introduced and provides capabilities of accelerating multi-dimensional RF pulses by employing the spatial encoding power of multi-channel transmit sensitivities (22,23). With pTx, tailored 3D pulses have been demonstrated in several imaging studies for selective excitation, magnetization preparation, and field compensation (24-30). Despite the limited use of pTx tailored pulses in spectroscopy to date (27,31-33), the potential exists to use multidimensional pTx optimized spatially selective pulses as sub-pulses in composite SPSP pulse designs thus capitalizing on their unique advantages.

In this work, we proposed replacing multiple refocusing and spectral suppression pulses in a typical localized spectroscopy acquisition by a 3D SPSP pulse or pulses, comprised of an adiabatic parent pulse and 2D selective pTx optimized sub-pulses. The potential gains include reducing minimum echo times (TE), repetition times (TR) and total power deposition as defined by the specific absorption rate (SAR). The pTx optimization of the sub-pulses are critical in order to obtain the spectral bandwidths required for different in vivo applications. The tradeoff of spatial and spectral selectivity is explored in both phantoms and in vivo for applications in the prostate and brain. Several design and optimization considerations are also discussed to help facilitate its use in future applications at 7T and above.

METHODS

3D SPSP Pulse Design

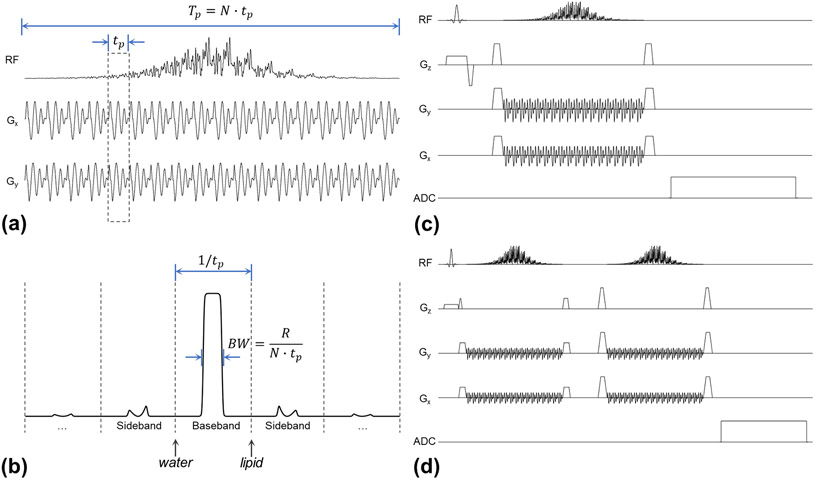
As previously described by Jang et. al. (34), the design of the 3D SPSP pulse follows a two-step approach. First, a sub-pulse is designed with an inherently refocused spiral gradient and measured field maps using the spatial domain method (35). Second, a total of N sub-pulses are modulated by a hyperbolic secant (HS1) adiabatic envelope, referred to here as the “parent pulse”, with a time-bandwidth product R given by:

$$R=T_p\cdot \text{BW}=N\cdot t_p\cdot \text{BW}$$

where T_p is the total duration of the 3D pulse, BW is the spectral bandwidth of the parent pulse, and t_p is the sub-pulse duration. The sub-pulse duration t_p is also the discretization resolution of the parent pulse that determines separation of the baseband and sidebands (1/t_p) of the 3D pulse, given the sub-pulse serves as a Dirac comb function in the time domain, and produces periodic sidebands in the spectral domain. To satisfy the Nyquist criterion, N ≥ R needs to be satisfied for the HS pulse (36). To avoid sideband excitation/refocusing of water and lipid, the sub-pulse should produce stopbands including the 4.7 ppm (water) and 1.3 ppm (methylene) lipid signals when properly centering the pulse on the metabolites of interest. At 7T, this requires that the sub-pulse should be no longer than 1 ms. In practice, the 95% passband (i.e. the “flat top”) is a better indicator to characterize the usable spectral bandwidth of the pulse and improves with increasing R assuming a constant BW. Dependent on the R of the parent pulse and the sub-pulse duration, the stopband may also include additional fat resonances such as the 0.9 ppm (methyl) and 5.3 ppm (methine) signals. Illustrations of the 3D SPSP pulse and the relationship between these design parameters are provided in Figure 1.a, 1.b. With this two-step approach, the design of refocusing is simplified by using an adiabatic parent pulse. The sub-pulse is designed using pTx pulse design methods (22,23,35), where the magnitude least-squares optimization (37) can also be employed to reduce the peak power by relaxing phase constraints within tolerable levels. Directly designing a refocusing pulse with pTx is often more challenging since additional constraints and optimizations need to be imposed on the design (30,38-41).

Figure 1.

Examples of the 3D SPSP pulses and acquisition sequences used in the study. (a) The waveforms of the RF pulses (only the first channel plotted) and spiral gradients of the 3D SPSP pulses are shown. (b) The relationship between design parameters as described in the methods are depicted where a simulated spin echo frequency profile of an adiabatic parent pulse is shown. (c) The minimum pulse sequence for spectroscopy acquisition using the 3D SPSP pulse is shown, where water and lipid suppression are achieved by the inherent spectral selectivity of the 3D SPSP pulse. (d) A double spin echo variant of the sequence is shown with improved localization and the ability to rewind spatial phase variations introduced by the 3D SPSP pulse in high spectral bandwidth excitations.

Pulse Optimization & Peak Power Reduction

For a given parent pulse and R value, pushing the gradient slew rate can shorten each sub-pulse thus increasing the spectral bandwidth at the cost of a greater peak RF amplitude and higher SAR. There are, however, several strategies that can be employed to limit the peak amplitude while maintaining the desired spectral bandwidth. For example, one can use a HS1 pulse with a larger R and N to reduce the peak power at the cost of a longer TE. Additional flexibility is provided by the degrees of freedom made possible through pTx. In the composite pulse, each sub-pulse is expected to perform a certain rotation according to its location within the parent pulse. In cases where the sub-pulses are required to perform relatively large rotations (i.e. near the center of the parent pulse), it is preferable to design the sub-pulse using large-tip-angle methods (38,39,42,43) in addition to the standard small-tip-angle (STA) method. In this study we use a large-tip-angle pulse design with optimal control theory (40) while imposing a hard constraint on peak RF amplitude. The steps for sub-pulse design include the following:

1) Use the spatial domain method to design an initial STA pulse. A Tikhonov regularization on the total RF power is optional but recommended.

2) Scale the pulse to get a nominal flip angle of 90 degree and denote its peak voltage as (V₀).

3) Determine the maximum peak voltage to constrain optimization (V_max). This could be the known maximum peak voltage of the MRI system or an empirical reduction factor such as V_max = αV₀, where α ranges from 0.5 to 0.75.

4) Scale the candidate pulse by half or lower so that its peak amplitude is now below V_max.

5) Use the scaled pulse as an initial input for the optimal control algorithm and iterate. An explicit regularization term can be added to penalize for total RF power.

6) In each iteration, clip the updated pulse for all time points that exceed V_max.

7) Continue with iterations until the convergence condition is met (such as when the change in NRMSE is below certain threshold), or maximum iterations have been reached.

8) Run Bloch simulation to check the excitation profile.

Design of Maximized Spectral Bandwidth

An inherent tradeoff between spatial and spectral bandwidth must be made for a 3D SPSP pulse. Improved spatial selectivity (i.e. sharper VOI boarders) requires traversal of higher spatial frequencies in excitation k-space, resulting in a longer spiral sub-pulse (typically constrained by gradient slew rate) that decreases the achievable spectral bandwidth and therefore limits the usability of the pulse especially at UHF. By accelerating the sub-pulse with pTx, such spatial-spectral constraints can be alleviated, thus increasing the flexibility needed for tailoring the 3D SPSP pulse. Note that the adiabatic behavior of the 3D SPSP pulse is attributed to its parent adiabatic pulse, whereas its sub-pulse does not have or need any adiabatic behavior. Although one can use both sub-pulse and adiabaticity of the parent pulse to improve B1+/excitation homogeneity, the sub-pulse does not have to be uniform. To further maximize the spectral bandwidth, additional acceleration of the sub-pulse can be achieved by relaxing the spatial profile of the sub-pulse while taking advantage of the adiabaticity of the parent pulse to still produce a uniform refocusing. For example, instead of using a typical homogeneous excitation target in the sub-pulse design, an inhomogeneous excitation profile such as a 2D Gaussian profile can be used. Since a Gaussian profile has a relatively compact k-space representation and no sidelobes, it can be relatively short supporting larger spectral bandwidths with few excitation artifacts arising from under-sampling when using pTx acceleration. Once the 3D SPSP pulse satisfies adiabatic conditions at all locations within the target VOI, a homogeneous inversion can be achieved despite each sub-pulse being designed with a spatially inhomogeneous excitation profile. Therefore, uniform refocusing can be achieved with relaxed spatial profile constraints on the sub-pulse coupled with pTx acceleration to provide the flexibility needed to tailor bandwidths for specific applications and field strengths.

For the design of maximized spectral bandwidth, however, a double spin-echo acquisition is advantageous and desired. First, the significant spatial phase variation arises from the intended inhomogeneous excitation profile of the sub-pulse can be refocused by using the double spin-echo approach. Second, by using two consecutive 3D SPSP pulses, the transition bands of the spatial and spectral profile become sharper, the latter making it feasible to increase the 95% passband by using a higher R without compromising stopband performance, thus allowing the pulse to be used at even higher field strengths.

Pulse Sequence & Quadratic Phase Correction

The adiabatic envelope in the 3D SPSP pulse introduces a quadratic phase to the spectral domain instead of the spatial domain as in LASER and semi-LASER where a second pulse is used per localization direction to cancel the quadratic phase. Considering the finite sampling has a much higher resolution in the spectral domain than in the spatial domain, signal losses due to quadratic phase in the spectral domain are negligible, making it possible to use a single 3D SPSP pulse for refocusing in a spin-echo MRS experiment provided the spatial phase variations of the 3D SPSP pulse can be controlled. As such, the resulting minimal sequence consists of a single slice-select excitation pulse and a 3D SPSP refocusing pulse as shown in Figure 1.c. Ideally, no additional spectrally selective water or lipid suppression pulses are required.

Regarding the quadratic phase in the spectral domain, there are several options available to rewind it if necessary. The easiest approach is to use a pair of the 3D SPSP pulses in a double spin-echo setup similar to PRESS as shown in Figure 1.d, which provides additional benefits including improved spatial and spectral selectivity, rewinding of residual spatial phase variations and mitigation of gradient imperfections. A second approach is to use a 2D SPSP excitation pulse so that its parent adiabatic pulse and that of the 3D SPSP refocusing pulse form an adiabatic spin-echo pair and thus cancel the quadratic phase as previously described (44). Alternatively, the quadratic phase in the spectral domain may be corrected during post-processing, as the phase profile of the adiabatic pulse is known a priori.

MRI Experiments

All experiments were conducted on a Siemens Magnetom 7T scanner with a whole-body gradient system (Siemens Healthineers, Erlangen, Germany) and a full 16x1kW parallel transmission system. The magnet is actively shielded, 60 cm in subject bore, with a maximum gradient amplitude of 70 mT/m and slew rate of 200 T/m/s. As a proof of principle without loss of generality, an 8-channel transmit, 32-channel receive head coil (Nova Medical, Wilmington, MA) is used throughout the study. For the in-vivo human brain study, signed informed consent was provided to participate in an IRB approved study. To demonstrate the refocusing spatial profile and frequency response, crushed spin-echo experiments were simulated with a custom GPU accelerated Bloch simulator using an EXORCYCLE (45) phase cycling. Two phantom studies were performed to demonstrate the use of the pulse in single SE and double SE configurations. The single SE study was performed on a prostate phantom, where a relatively narrow passband is required compared to neuro applications. The double SE approach was performed on a “Braino” phantom (GE Medical Systems, Milwaukee, WI) and in-vivo as it supported the larger spectral bandwidths required.

For the single SE study, a prostate spectroscopy phantom was immersed in a larger cylindrical container filled with saline to properly load the RF coil and consisted of two separate compartments where the inner one contained metabolites including citrate, choline, creatine and spermine (46) and the outer one was filled with cooking oil representing periprostatic lipids. For the 3D SPSP pulse, the sub-pulse was designed using a 1 ms spiral gradient of resolution 12 mm, FOV 192 mm, radial acceleration of 3, maximum slew rate 170 T/m/s. Calibration data was acquired as required for the pTx pulse design. Channel-wise B₁⁺ mapping was acquired and calculated using the previously described hybrid method (47,48). The B₀ field mapping was acquired using a standard dual-echo gradient echo (GRE) approach. Both field maps were acquired with FOV 192x192 mm² and voxel-size 1.5x1.5x3 mm³. The spiral gradient and rewinder were designed following known methods (49,50). The parent pulse used a HS1 pulse of R = 9, N = 18, T_p = 18 ms to minimize TE. Spectroscopic imaging was first acquired with the excitation and 3D SPSP RF pulses centered on water to demonstrate the on-resonance spatial localization performance. To suppress water and fat, and to selectively refocus the prostate metabolites between 2.6 and 3.2 ppm, the center frequency of the acquisition was then shifted by −1.8 ppm from water. No additional water suppression technique was used due to the inherent spectral selectivity of the 3D SPSP pulse. Acquisition parameters were as follows: TR/TE 2000/31ms, FOV 128x128 mm², VOI 48x36x10 mm³, acquisition matrix 24x24, interpolated size 32x32, Hamming-windowed sinc excitation pulse (2.60 ms in duration, time-bandwidth product of 8.65). For comparison, another set of spectra were acquired with semi-LASER using the following parameters adapted from a previous study: TR/TE 2500/76, FOV 128x128 mm², VOI 48x36x10 mm³, acquisition matrix 24x24 interpolated to 32x32, standard excitation pulse (2.60 ms in duration) and a hyperbolic secant (HS1) pulses (R = 20, 10 ms in duration) for refocusing. For lipid and water suppression MEGA (51) and VAPOR (52) were used, respectively. For spectra acquired with the 3D SPSP pulse, the quadratic phase was corrected by using the simulated adiabatic pulse phase. A custom software in MATLAB (The MathWorks, Inc., Natick, MA) was used to perform manual adjustment of constant, linear and predicted quadratic phase terms.

For the double SE study, the Braino phantom was used to demonstrate two examples of 3D SPSP pulse design with the following specs:

1) a square sub-pulse profile (mimicking semi-LASER), VOI 48x48 mm², parent pulse HS1 with R = 16, N = 24, T_p = 19.2 ms, using a 0.8 ms spiral gradient of resolution 16 mm, FOV 192 mm, radial acceleration of 3 and maximum slew rate 150 T/m/s;

2) a 2D Gaussian sub-pulse profile, VOI 48x48 mm² (defined by the full width at half maximum), parent pulse HS1 with R = 16, N = 32, T_p = 19.2 ms, using a 0.6 ms spiral gradient of resolution 24 mm, FOV 192 mm, radial acceleration of 2 and maximum slew rate 180 T/m/s.

Calibration data was again acquired using the same B0 mapping approach while, due to a software upgrade, channel-wise B₁⁺ mapping was acquired using a product sequence consisting of a pre-saturated Turbo-FLASH acquisition (47,48,53,54). Both field maps were again acquired with FOV 192x192 mm² and voxel-size 1.5x1.5x3 mm³. As with the single SE method, no additional water suppression was used given the inherent spectral selectivity of the 3D SPSP pulse. The spectroscopy acquisition parameters included: a center frequency shift of −1.9 ppm from water, TR 2500 ms, TE 59 ms (for 3D SPSP) and 62 ms (for semi-LASER), FOV 168x168 mm², VOI 48x48x10 mm³, acquisition matrix 24x24 interpolated to 32x32, a Hamming-windowed sinc excitation pulse (2.60 ms in duration, time-bandwidth product of 8.65). For semi-LASER, flattened HS (HS4) pulses (R = 40, 10 ms in duration) were used for refocusing along with VAPOR for water suppression. To optimize the performance of VAPOR, delay timings and flip angles were optimized experimentally using an SVS acquisition to best minimize the residual water signal. The acquisition parameters were chosen to permit a relatively short TR to reduce scan times given the large encoding matrix used in the study.

For the in-vivo brain studies, the same Gaussian design was used for the 3D SPSP pulse along with the same measurement parameters for double spin echo acquisition and semi-LASER. Both single voxel spectroscopy (SVS) and chemical shift imaging (CSI) acquisition were performed with each localization method from the same VOI. The only difference between the two were that SVS acquisitions were performed with 16 averages and the CSI were acquired with a single average and 2D phase encoding. The VOI covered the posterior cingulate cortex and the double SE spectroscopy with 3D SPSP pulse was acquired with and without the addition of outer volume suppression. The spectra acquired went through the same spatial and spectral reconstruction steps including a spatial Hamming windowing, exponential filtering in the time domain, fast Fourier transform, frequency shift adjustment and zero / first order phase corrections.

SAR Comparison

For the Braino phantom and in-vivo studies a default circularly polarized B1+ shim (known as the “TrueForm” mode) was used for all non-pTx pulses. The transmitter reference voltage was determined by finding the maximum signal during an SVS acquisitions arrayed over a series of excitation flip angles. Power calibration for the 3D SPSP pulse was determined by simulation to match the FWHM of its excitation profile to correspond with the VOI similar to that of the refocusing pulses in semi-LASER. Experimental validation was done by using flip angle mapping with a pre-saturated Turbo-FLASH sequence using the designed sub-pulse for excitation and ensuring the nominal flip angle was reached. The global SAR during acquisition was measured by the scanner (known as the time-averaged RF power on the console computer), which was normalized by TR and then compared between sequences. To account for the potentially lower transmit efficiency in semi-LASER due to a sub-optimal B1+ shim, a phase shimming solution was calculated for the VOI using the same measured per-channel B1+ mappings as used for pTx pulse design (55). The ratio of the mean B1+ within the VOI before and after the shim, was used to scale the measured SAR to obtain the predicted SAR with the optimized transmit efficiency.

RESULTS

Prostate Phantom Study

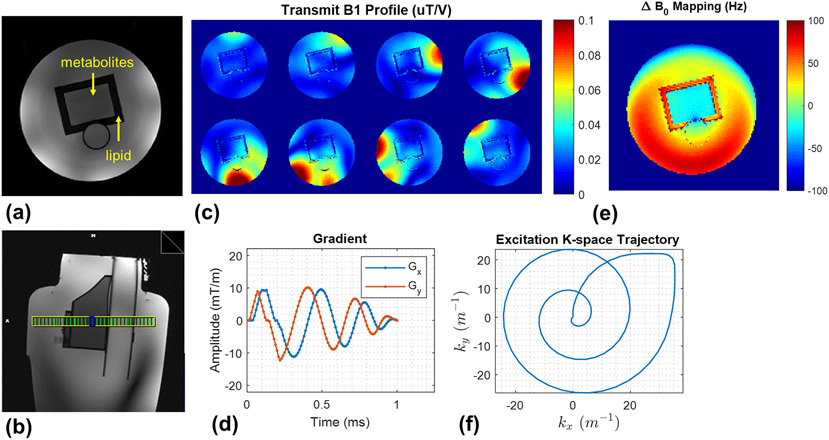
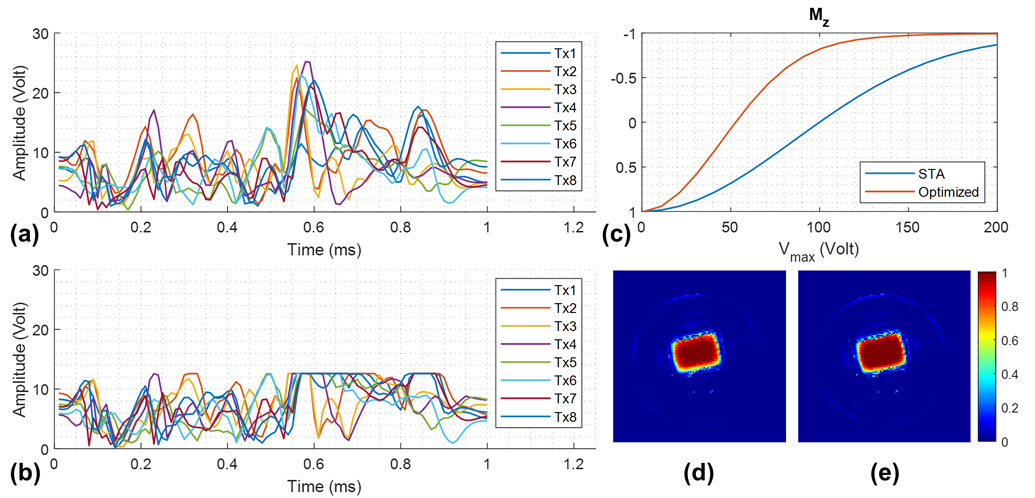
The prostate phantom setup, measured B₁⁺ and B₀ field maps, spiral gradient waveforms and excitation k-space trajectories are shown in Figure 2. The designed sub-pulse and its version designed with the optimal control theory approach were simulated (Figure 3), where the peak amplitude was reduced by 50% while maintaining a comparable excitation profile. Excitation imperfections could be observed in the outer volume and appeared in the pattern of side lobes resulting from a limited excitation k-space coverage. Experimental excitation profiles of the sub-pulse are shown in Figure 4.b which match closely with simulation.

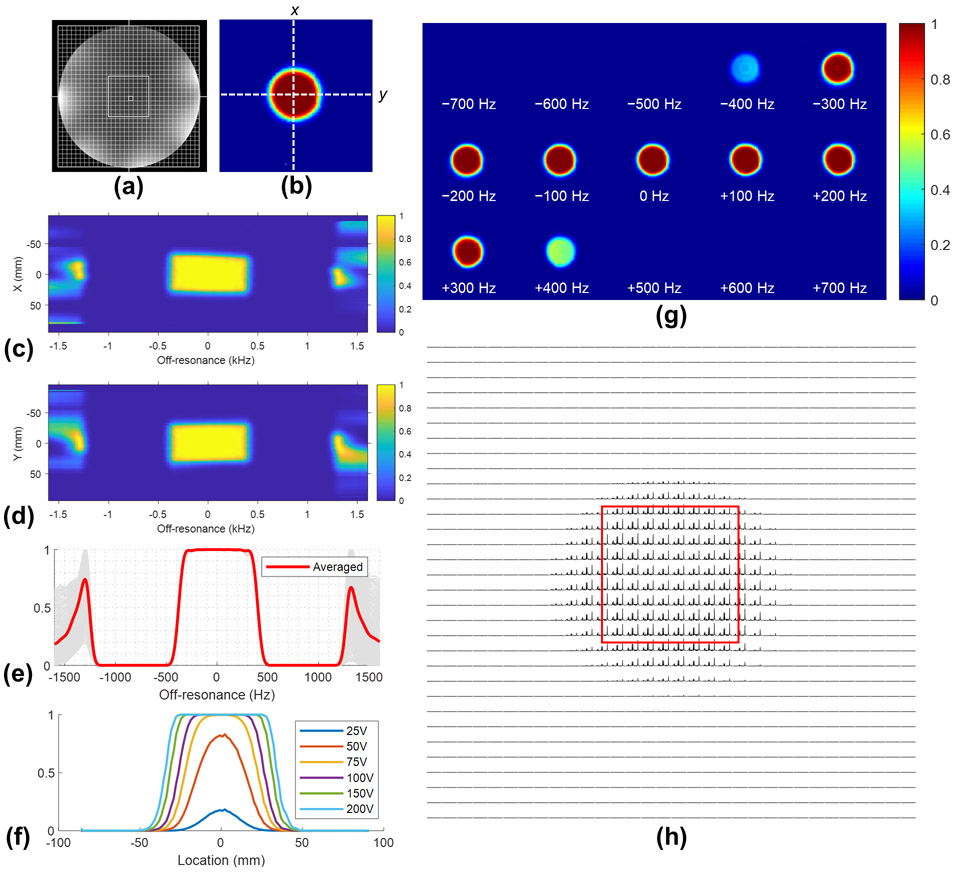
Figure 2.

The experiment setup for the 7T phantom study was demonstrated by: (a) axial and (b) sagittal 2D GRE images. (c) Measured per-channel transmit B₁ (B₁⁺) maps of the coil used. (d) Measured field maps using dual-echo GRE methods. (e) The spiral gradient waveforms used for sub-pulse design and (f) the corresponding excitation K-space trajectory.

Figure 3.

Per-channel waveforms of the sub-pulse (nominal flip angle 10°) designed by (a) spatial domain method assuming small tip angles (STA) and (b) optimal control method with peak RF amplitude constraints, and (c) the corresponding inversion profiles within the ROI to show the peak voltage needed to achieve adiabaticity for the 3D SPSP pulse. (d) Simulated crushed spin-echo profile of the 3D SPSP pulse on resonance with V_max = 200 V for STA design, and (e) V_max = 125 V for optimal control design, both assuming an ideal 90° excitation. The latter approach imposes a hard limit on the peak amplitude while enabling the pulse to be used for large-tip-angle excitation and maintaining its excitation profile.

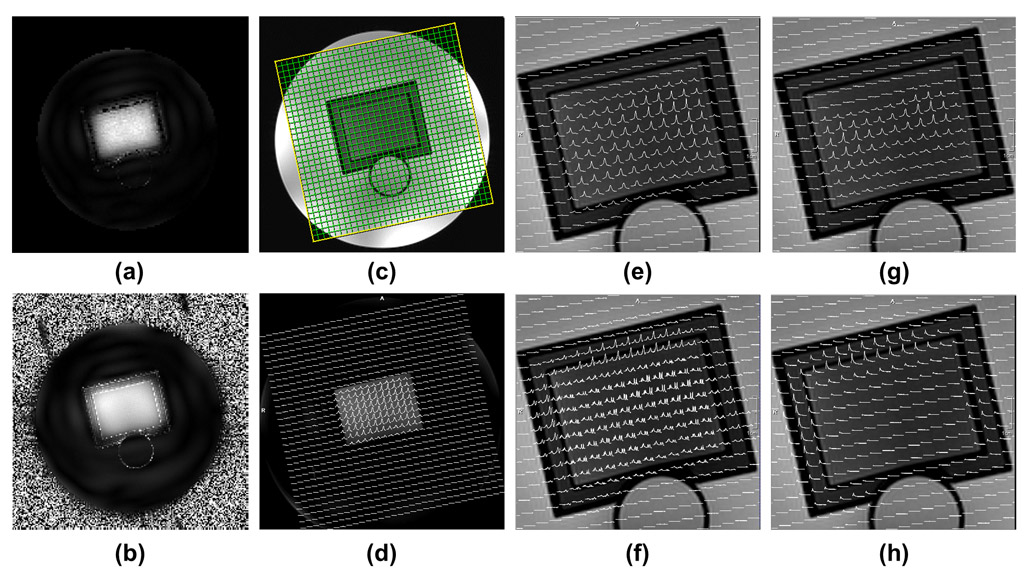
Figure 4.

Spatial and spectral profiles of the designed 3D SPSP pulse. (a) Simulated excitation profile of the 2D sub-pulse. (b) Experimental excitation profile estimated from low flip angle GRE images. (c) The planning of an axial 24x24 CSI grid on a sagittal scout through the prostate phantom. (d) Spatially resolved water spectra (df = 0) acquired with the 3D SPSP pulse sequence. (e) Zoomed-in version of (d). (f) Spatially resolved metabolite spectra from citrate to choline (df = −1.8 ppm). (g) Residual water spectra (df = −1.8 ppm). (h) Residual lipid spectra (df = −1.8 ppm). df: offset (delta) frequency in ppm of the stated RF pulse with respect to water.

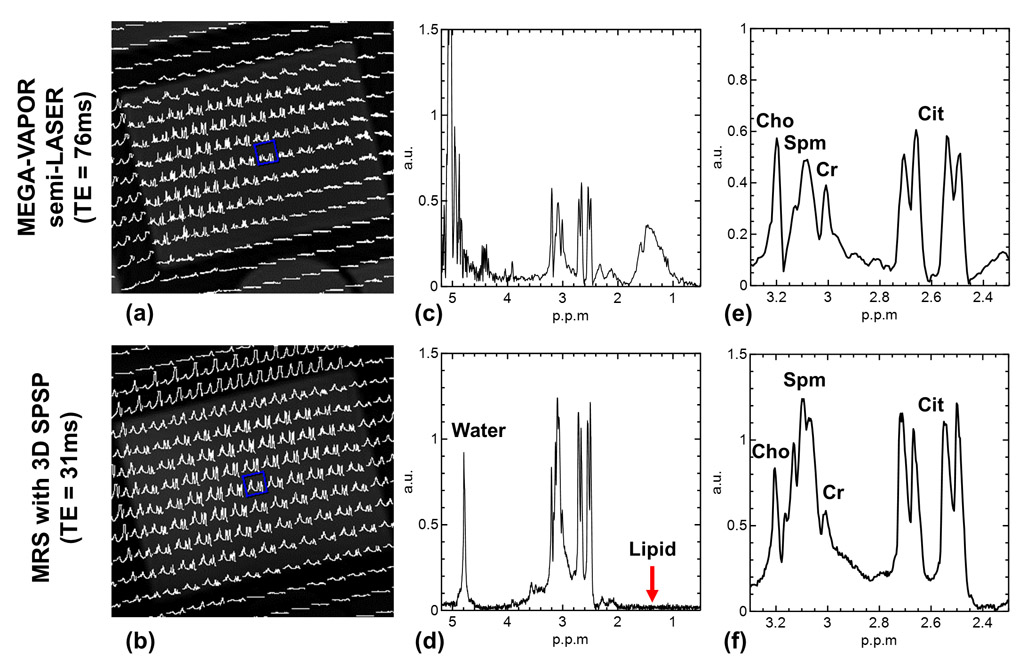
The spatial excitation profile of the 3D SPSP pulse was demonstrated by the spatially resolved water spectra (0 ppm in frequency offset) and metabolite spectra (−1.8 ppm in frequency offset), as shown in Figure 4.c and 4.d, respectively. Both spectra showed good agreement with the spatial profile of the sub-pulse. Residual water and lipid signals which are designed to be suppressed by the spectral profile of the 3D SPSP pulse are shown in Figure 4.e and 4.f, demonstrating an effective suppression. As a comparison, spatially resolved spectra acquired with MEGA-VAPOR semi-LASER and with the 3D SPSP pulse are shown in Figure 5, where the central voxel of the VOI is displayed. When compared, the spectra acquired with the 3D SPSP pulse demonstrates superb water and lipid suppression and a more pronounced spermine signal centered at 3.1 ppm due to the shorter TE.

Figure 5.

Comparison of spectra acquired with MEGA-VAPOR semi-LASER versus the proposed method with the 3D SPSP pulse. Spatially resolved metabolite spectra of the two methods are shown in (a) and (b), respectively. The spectra of the selected voxel (blue box) were shown in (c) and (d) to demonstrate the water and lipid suppression of the 3D SPSP pulse. The respective zoomed-in metabolite spectra are shown in (e) and (f). All spectra were shown in magnitude. The higher peak amplitudes for the 3D SPSP acquisition are due to a shorter TE and the varying spectral shapes for spermine and citrate between the two acquisitions are due to differences in J-modulation from these coupled spin systems. Cho: choline; Spm: spermine; Cr: creatine; Cit: citrate.

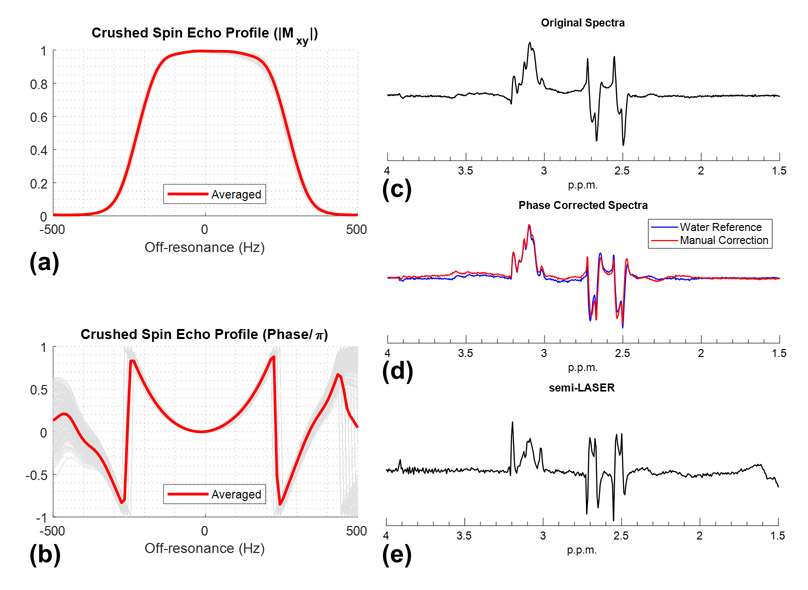
A simulation of the crushed spin-echo profile of the 3D SPSP pulse within the VOI is depicted in Figure 6 where both voxel-wise and averaged plots show consistent magnitude and quadratic phase profiles as determined by the adiabatic parent pulse. Quadratic phase correction by post-processing yielded spectra well matched with that when using the water spectra as a phase reference.

Figure 6.

Simulated voxel-wise (gray) and averaged (red) spectral profiles within the localization volume in the phantom study are shown in (a) magnitude and (b) phase. To account for the phase variations due to B1+ and B0 fields, each voxel-wise profile has been phase corrected by its on-resonance echo for better visualization. The acquired spectra (real part) of the central voxel in the excitation ROI are shown in (c) and can be phase-corrected by using water spectra as reference (blue) or by adding a predicted quadratic phase term (red) in post-processing, as shown in (d). The spectra from semi-LASER were shown in (e), which was acquired with TR/TE = 2500/76 ms, whereas spectra acquired with proposed method used TR/TE = 2000/31 ms. Both spectra were acquired with the minimized echo time of the sequence and not optimized with respect to the J-modulation of citrate.

Braino Phantom Study

For the 3D SPSP pulse, the simulated spatial and spectral double spin echo profiles and the chemical shift along X and Y directions were shown in Figure 7, Figure S1 (see Supporting Information). Upon reaching adiabaticity, both spatial and spectral profiles show a flat response within VOI as expected with a conventional adiabatic pulse resulting in a 600Hz spectral passband with at least 95% efficiency. The spatially resolved spectra acquired with 3D SPSP pulses overall matched with their simulated spatial profiles. As a comparison, the SVS and CSI data acquired using the 3D SPSP pulse were compared to that acquired with semi-LASER as shown in Figure 8, where the zoomed-in plots of spectra of the former showed a spatially uniform baseline within the nominal VOI. An additional result is available in the Supporting Information (Figure S2, Figure S3) showing a water-suppression only version of the 3D SPSP pulse that provides approximately 800 Hz for the 95% passband with an even shorter total pulse duration (14.4 ms). Chemical shift images of NAA were provided in Supporting Information (Figure S4) for 3D SPSP pulses with different designs.

Figure 7.

A brief summary of the 3D SPSP pulse performance using a gaussian VOI. Slice planning of the Braino phantom is shown in (a) and compared with the simulated double spin echo profile of the 3D SPSP pulse (b). The chemical shift profiles of the pulse along x and y directions across the center of the VOI as indicated by white dashed lines in (b) are shown in (c) and (d), respectively. The voxel-wise spectral profiles and their average within the VOI are plotted in (e) and provide approximately 600 Hz of at least 95% passband. The spatial profiles with respect to the peak amplitude and off-resonance are shown in (f) and (g), respectively. Spatially resolved spectra (displayed from 1.5 to 4.5 ppm in magnitude) acquired with the 3D SPSP pulse using double spin echo method are shown in (h) and overall matched simulated spatial profiles.

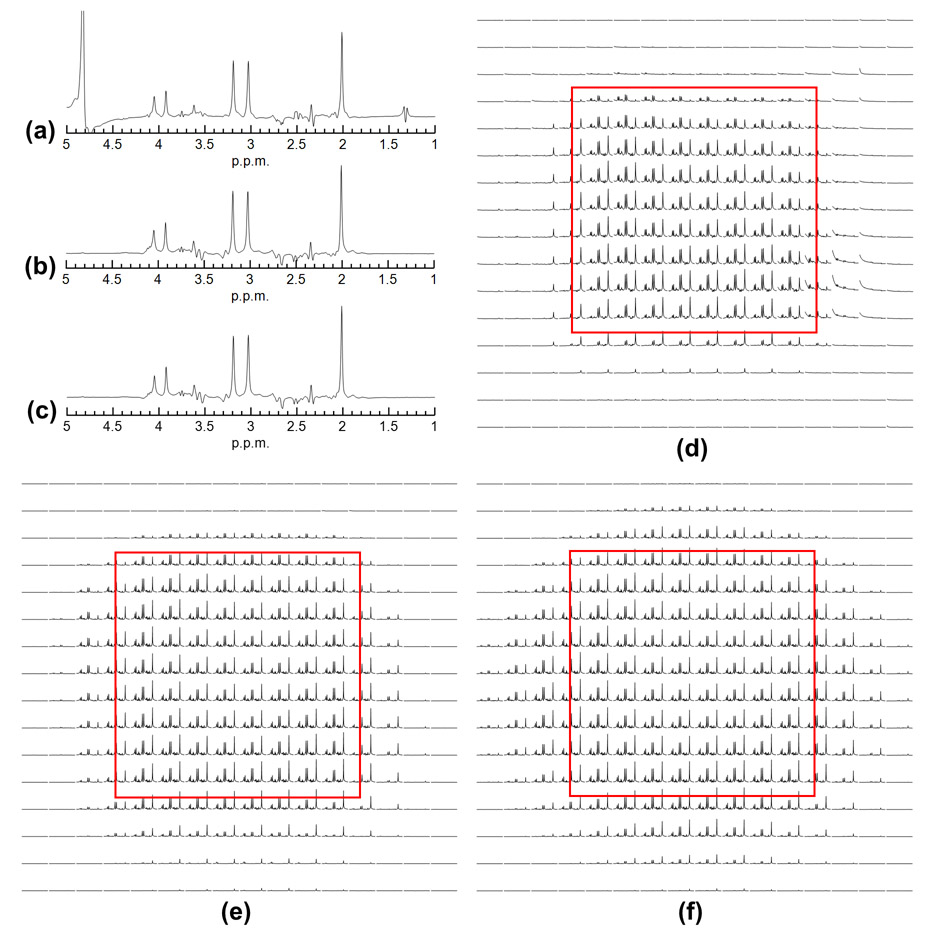
Figure 8.

Comparison of spectra acquired by semi-LASER and double spin echo sequence with 3D SPSP pulses on the Braino phantom. Real part of the SVS spectra acquired with 16 averages using (a) semi-LASER, (b) 3D SPSP pulses with square VOI, and (c) gaussian VOI. The spatially resolved spectra (displayed from 1.5 to 4.5 ppm in magnitude) acquired with the same measurement parameters as SVS are shown in (d), (e), (f), respectively.

In-Vivo Study

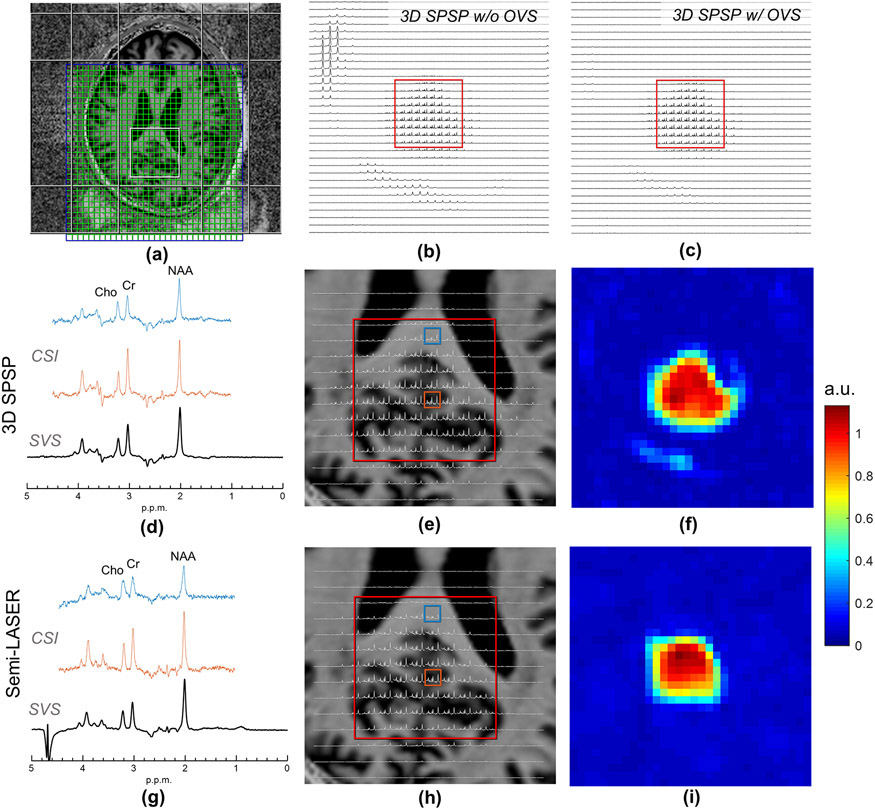
For in-vivo studies, a summary of the experimental results is shown in Figure 9. As with the phantom results, a spatially uniform water suppression by the 3D SPSP pulse resulted in a cleaner spectral baseline supported by the B0-following properties of the 3D SPSP pulse. Residual lipid signal was observed near the periphery of the brain, arising from the lipid peaks at around 1.59 ppm (56), as a result of being close to the NAA thus not within the optimal stopband and the excitation imperfection of the pulse, which can be mitigated by using outer volume suppression.

Figure 9.

In-vivo spectra acquired by semi-LASER and the double spin echo 3D SPSP pulses. (a) Spectroscopic imaging slice planning on MP2RAGE anatomic images of the brain of a volunteer where the VOI is shown in the posterior cingulate cortex. OVS pulses are also shown as planned for use in the 3D SPSP acquisition. The spatially resolved spectra acquired using 3D SPSP pulses without and with OVS are shown from 1.0 to 4.5 ppm in (b), (c), respectively. Residual lipid peaks in (b) were located at approximately 1.59 ppm. Single voxel spectra (SVS) and selected CSI spectra collected from the VOI are shown for the 3D SPSP pulses designed using a Gaussian spatial profile with OVS in (d) and semi-LASER (g). The upper (blue) and lower (orange) selected CSI spectra come from primarily white and gray matter from the indicated voxels on the zoomed in CSI datasets for the 3D SPSP (e) and semi-LASER (f) acquisitions, both shown from 1.5 to 4.5 ppm. Chemical shift images of NAA calculated by integrating the magnitude of the spectra are shown in (f) for 3D SPSP pulses and (i) for semi-LASER. The effective VOI in (f) appears slightly larger than (i) due to a broader transition band in Gaussian profile. Spectra in (d), (g) are shown in real, whereas (b), (c), (e), (h) are displayed in magnitude.

SAR Comparison

For the prostate phantom study, the single SE acquisition with the 3D SPSP pulse only deposited 22% of the SAR compared with that of semi-LASER when taking into account differences in TR. For double SE acquisitions, the global SAR comparison between semi-LASER and 3D SPSP pulses is given in the Table 1. While the double SE method uses two refocusing pulses that afford a higher spectral bandwidth, an overall significant SAR reduction is still expected in several different designs compared with semi-LASER even when using a transmit efficiency optimized RF shim.

Table 1:

Global SAR comparison between semi-LASER and double SE with 3D SPSP pulses in phantom and in-vivo studies.

Study	Sequence	TR/TE (ms)	Refocusing Pulses / Design Specs	Pulse Duration (ms)	OVS	Global SAR (W/kg)
						CP Mode	B1 Shim
Braino Phantom	semi-LASER	2500/62	HS, n = 4, R = 40	10	Off	2.3	2.3
	double SE with 3D SPSP Pulse	2500/59	Gaussian (0.6 ms), R = 16, N = 32	19.2	Off	0.43
		2500/59	Square (0.8 ms), R = 16, N = 24	19.2	Off	0.67
		2500/49	Hanning (0.6 ms), R = 16, N = 24	14.4	Off	0.60
In-Vivo	semi-LASER	2500/62	HS, n = 4, R = 40	10	Off	3.16	1.18
	double SE with 3D SPSP Pulse	2500/59	Gaussian, (0.6 ms), R = 16, N = 32	19.2	Off	0.41
		2500/59	Gaussian (0.6 ms), R = 16, N = 32	19.2	On	0.57

DISCUSSION

In this study, we demonstrated by simulation and experimentally the feasibility of designing 3D SPSP pulses with pTx to replace the refocusing pulses for localized spin echo spectroscopy. With increased design flexibility enabled by pTx, a 3D SPSP pulse can be accelerated to increase its spatial and spectral bandwidth while simultaneously being able to control peak and total RF power, making it feasible to be used for refocusing in spectroscopy even at UHF. Benefits of the proposed method include reduced SAR deposition, a shorter minimum TE, tracking of B₀ variations and the potential for reduced TRs and acquisition times, although one does need to consider the additional time for calibration scans and pulse design. Note that the significant SAR reduction by the 3D SPSP pulse is accompanied by a compromised spatial bandwidth due to the need of shortening 2D sub-pulse to increase the spectral bandwidth. Therefore, one disadvantage of the 3D SPSP pulse is its inferior sharpness with respect to spatial localization compared with LASER or semi-LASER. Demonstration of such spectral-spatial constraints is provided in Supporting Information (Figure S5).

For the 3D SPSP pulse, the ability to compensate for field inhomogeneities is achieved by properly weighting the central excitation K-space during its traversal, given that field inhomogeneities are, in general, slowly varying spatially. Enhanced by the distinct frequency components carried by each transmit channel, this unique feature creates spatially varying frequencies that adapt to the local field (18,28), and therefore achieves “B₀-following” characteristics. As a result, the spectral selectivity of the 3D SPSP pulse is also spatially adaptive, making the pulse less sensitive to off-resonance effects as demonstrated by the spatial consistency in water suppression (i.e. spectra baseline). One possible application of such field adaptive spectral selectivity is to use the pulse for mapping a single metabolite over a large VOI (57), whereas a conventional 1D selective pulse will suffer from a shift in the selective window due to field inhomogeneities at UHF. Additional insensitivities to B1+ inhomogeneities are provided by the adiabatic parent pulse that allows the use of an inhomogeneous excitation profile for the sub-pulse to achieve further acceleration and thus a higher spectral bandwidth which otherwise cannot be obtained by an amplitude-modulated pulse. Such increased bandwidth also enables the 3D SPSP pulse to be used in other alternative sequences at UHF such as in UTE-SPECIAL (58).

While HS pulses were used as the parent pulses in the study, other variants of adiabatic full passage pulses are also viable options. For example, improvements can be made to the parent adiabatic pulse by using Shinnar Le Roux (59) and optimal control method (60) to achieve a better spectral profile for the same pulse duration along with reduced peak amplitude and total SAR. However, an exception is the Gradient Offset Independent Adiabatic (GOIA) pulse, which uses a modulated gradient waveform to reduce peak and total RF power and therefore cannot be used as the parent pulse for the 3D SPSP pulse. When using GOIA pulses for semi-LASER, we estimate that the global SAR will be reduced by approximately 20% compared with HS pulses (36,61). However, to minimize chemical shift displacement for HS pulses, a higher bandwidth is typically used and therefore the SAR comparison presented here is still deemed conservative. Note that the SAR efficiency of the pTx pulse may vary dependent on how its power is regulated in its design. A common method as employed in the study is to use L-curve criterion in Tikhonov regularization which provides an empirically balanced tradeoff between the RF power and its excitation fidelity. In terms of peak power management, we have adopted the optimal control method to enforce a hard limit on the peak power while still achieving nearly equivalent excitation. For body imaging, the ability to set a hard limit on peak power is critical as the peak B₁⁺ achievable in the torso is more limited than in the brain. Another critical concern at UHF with pTx is the local RF heating effects as measured by local SAR deposition, which can also be regulated by incorporating virtual observation points (62) in the pulse design. While local SAR was not actively managed in the study, it is still expected that the pTx tailored pulse has a reduced local SAR compared with a phase-magnitude shim for semi-LASER where there are fewer degrees of freedom in the optimization space.

As with other pTx tailored pulses, the 2D sub-pulse inherently comes with a certain amount of excitation errors, depending on the solver used for pulse design, the spatial encoding capabilities of the multi-channel RF coils (i.e. transmit equivalent to g-factors for parallel imaging on receive), as well as the under-sampling employed in the excitation k-space. Such excitation imperfections are more noticeable outside of the VOI and manifests as signals outside the targeted region. However, when the pulse is used for refocusing along with proper crushing or phase cycling, these unwanted signals are suppressed and even more so in double spin-echo acquisitions. Despite this fact, residual lipid signals outside the VOI were still observed in our in-vivo brain studies as demonstrated in Figure 9. In addition, while the pulse itself is capable of compensating for B₀ and B₁⁺ inhomogeneity, the residual errors arising from imperfect compensations may still cause some amount of non-linear spatial phase variation. Therefore, when used in single spin-echo spectroscopy, the pulse is more suitable for CSI than SVS considering the potential SNR loss in the latter case due to volume averaging across the VOI. Due to the use of spiral gradients (63), off-resonance effects cause distortion and blurring of the VOI for the 3D SPSP pulse instead of a linear displacement in the slice select direction as is typically found when using 1D selective pulses. While pTx tailored pulses tend to have a narrow bandwidth in general, the chemical shift errors are mitigated by including a B0 field mapping in the pulse design and by the spiral gradients which are two-dimensional and have a greater total amplitude on average than slice select gradients.

As demonstrated by the results, the 3D SPSP pulse provided a B0-following spectral selectivity allowing a more robust and spatially consistent water suppression compared with VAPOR. For lipid suppression, however, outer volume suppression may be needed, considering the fat resonances that are close to or within the passband are not optimally suppressed and are sensitive to excitation imperfections of the sub-pulse due to the great abundance of lipid compared with metabolites of interest. Note that for semi-LASER lipid suppression may not be needed at all if the localization VOI is not placed near the subcutaneous fat. In general, to afford simultaneous water and lipid suppression by maximizing the 95% passband and minimizing the transition band, a higher time-bandwidth product is needed by the parent pulse which comes at the cost of a longer total pulse duration and consequently increased minimum TE. When a shorter pulse duration or TE is preferred, one may use water-suppression only 3D SPSP pulses along with outer volume suppression for lipid suppression at the cost of increased SAR while maintaining other advantages.

Compared with SASSI (11), where two well optimized SPSP adiabatic pulses are used for refocusing, the proposed 3D SPSP pulse provides inherent B0-following spectral selectivity, whereas SASSI needs a wider bandwidth to provide a margin so that the selective window will still refocus metabolites when shifted by a spatially varying B0, which in turn leads to a slightly broader transition band and may also affect water or lipid suppression. The optimization of the parent pulse in SASSI can also be employed in the 3D SPSP pulse to gain the same improvement in pulse performance such as reduced peak amplitude and SAR, and possibly a sharper spectral profile or a shorter pulse duration. As with other SPSP pulses, it may be more challenging to increase the bandwidth of the SPSP pulses to minimize chemical shift displacements at even higher field strengths, whereas the proposed 3D SPSP pulse provides more flexibility to allow a tradeoff in pulse performance.

CONCLUSION

In this study we demonstrated the design of a pTx tailored 3D adiabatic SPSP pulse and proposed its use to replace the refocusing pulse train in spectroscopy. By simulation and experiments we showed the advantages of the method including simultaneous 2D spatial selectivity with water and lipid suppression, reduction in minimum TE/TR and SAR, as well as adaptations to B₀ and B₁⁺ field inhomogeneities. Compared with semi-LASER, the proposed method may serve as an alternative acquisition strategy for spectroscopy that is more SAR efficient especially at UHF, where to minimize field inhomogeneities and chemical shift effects by increasing pulse bandwidths are more limiting. With the design flexibility afforded by pTx, more optimization approaches may be explored in future studies to facilitate its use in future applications at 7T and above.

Supplementary Material

Supplementary Material

Figure S1. A brief summary of the 3D SPSP pulse performance using a square VOI. Slice planning of the Braino phantom is shown in (a) and compared with the simulated double spin echo profile of the 3D SPSP pulse (b). The chemical shift profiles of the pulse along x and y directions across the center of the VOI as indicated by white dashed lines in (b) are shown in (c) and (d), respectively.). The voxel-wise spectral profiles and their average within the VOI are plotted in (e) and provide approximately 600 Hz of at least 95% passband. The spatial profiles with respect to the peak amplitude and off-resonance are shown in (f) and (g), respectively. Spatially resolved spectra (displayed from 1.5 to 4.5 ppm in magnitude) acquired with the 3D SPSP pulse using double spin echo method are shown in (h) and overall matched simulated spatial profiles.

Figure S2. A brief summary of the excitation profiles of the 3D SPSP pulse using a hanning VOI. Slice planning of the braino phantom is shown in (a) and compared with the simulated double spin echo profile of the 3D SPSP pulse (b). The chemical shift profiles of the pulse along x and y directions across the center of the VOI as indicated by white dashed lines in (b) are shown in (c) and (d). The voxel-wise spectral profiles and their average within the VOI are plotted in (e) and provide approximately 800 Hz of at least 95% passband. The spatial profiles with respect to the peak amplitude and off-resonance are shown in (f) and (g), respectively. Spatially resolved spectra (displayed from 1.5 to 4.5 ppm in magnitude) acquired with the 3D SPSP pulse using double spin echo method are shown in (h) and overall matched simulated spatial profiles.

Figure S3. Demonstration of spectra acquired by semi-LASER and double spin echo with 3D SPSP pulses using the braino phantom. Real part of the SVS spectra acquired with 16 averages using semi-LASER, 3D SPSP pulses with hanning VOI, are shown in (a), (c), respectively. The spatially resolved spectra (displayed from 1.0 to 4.5 ppm in magnitude) acquired with the same measurement parameters as SVS are shown in (b), (d), respectively. For the 3D SPSP pulse, the sub-pulse duration is 0.6 ms, and the parent pulse used was HS1, R = 16, N = 24. Spectra were acquired with the transmitter frequency shifted by −2.4 ppm from water. This is a water suppression only version of the 3D SPSP pulse, as indicated by the refocused lactate.

Figure S4. Chemical shift imaging of NAA calculated from spectra acquired with (a) semi-LASER, (b) SPSP pulse with square VOI, (c) 3D SPSP pulse with hanning VOI, (d) 3D SPSP pulse with gaussian VOI. For (b), (c), (d), spectra were acquired using double spin echo method. Each image was normalized by the value of its central voxel. Spectra processing steps included a spatial hamming filtering, exponential filtering in the time domain, fast Fourier transform, frequency shift adjustment, and integral of the spectra magnitude. For square VOI and gaussian VOI, the 3D SPSP pulses were designed with water and lipid suppression, whereas for hanning VOI the 3D SPSP pulse was designed with water suppression only.

Figure S5. Demonstration of the spatial phase variation with respect to the sub-pulse duration when using the 3D SPSP pulse in a single SE setup. Simulated spatial profiles of crushed spin echo are shown in (a) magnitude and (b) phase. From left to right, the sub-pulse durations are 0.8 ms, 1 ms, 1.2 ms, 1.5 ms. All 3D SPSP pulses used the same parent pulse (HS1, R = 16, N = 24), each having a nominal bandwidth of 833 Hz, 667 Hz, 556 Hz, 444 Hz, respectively, as shown in (c). While spectroscopy was performed at 7T in the study, the single SE method with the 3D SPSP pulse is less constrained by the spectral bandwidth needed at lower fields and therefore has fewer spatial phase variations, making it possible to be used if a comparable pTx system is equipped at lower fields.