Applying Spatio-temporal Scan Statistics and Spatial Autocorrelation Statistics to identify Covid-19 clusters in the world - A Vaccination Strategy?

Abstract

With the whole world being affected by the pandemic, it is a matter of great importance that studies about spatial and spatio-temporal aspects of the COVID-19 (Sars-Cov-2) pandemic should be conducted, therefore the main goal of this paper is to present the Global Moran's I and the Local Moran's I used to evaluate spatial association in the number of deaths and infections by COVID-19, and a spatio-temporal Poisson scan statistic used to identify emerging or “alive” clusters of infections by Sars-Cov-2 in space and time. As of January 2021 vaccination against COVID-19 already started, since the use of spatial clustering methods to identify non-vaccinated populations is not new among studies on vaccination coverage strategies, this paper also aims to discuss the implementation of spatial and spatio-temporal clustering methods in early vaccination.

1. Introduction

At the end of 2019, the situation of infections by COVID-19 (Sars-Cov-2) was already being considered an epidemic in the city of Wuhan in China (Shereen et al., 2020), although it was difficult at first to identify the virus’ origin, it is known that the Severe Acute Respiratory Syndrome (SARS) and the Middle East Respiratory Syndrome (MERS) usually need intermediate hosts (Zhang et al., 2020), there is a possibility that bats and pangolins were the first carriers. After several public organizations called for caution relating to COVID-19, on March 11 of 2020 the pandemic state was recognized by the World Health Organization (WHO) (Brodeur et al., 2020).

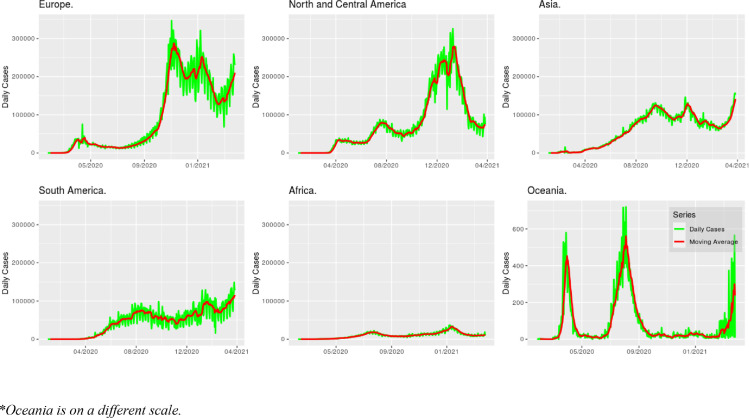
Even though a great number of social restrictions ranked as effective, some of them more intrusive such as restricting access to most places where people could gather in small or larger groups, and others that were less intrusive such as border restrictions and governmental support to vulnerable populations (Haug et al., 2020), were adopted to diminish the number of daily infections caused by COVID-19, the moving average of daily cases rose in almost all continents in the end of 2020, but at the time vaccination started there was a noticeable dip in the moving average of the daily number of infections (Fig. 1 ) in Europe, Asia and North and Central America, similar to the ones that were seen before in Oceania in 2020, which always had a lower number of daily infections when compared to other continents.

Fig. 1.

Moving average of daily infections by COVID-19 in 2020.

With the whole world being affected by the pandemic, it is a matter of great importance that studies about the spatio-temporal aspects of the COVID-19 pandemic should be conducted, the main goal of this paper is to present methods used to identify spatial and spatio-temporal dependence in the number of infections and deaths caused by Sars-Cov-2 among different countries in 2020, so these techniques may be used in future or hypothetical situations where is necessary to investigate the behavior of a pathogen agent in space and time or to better assist decision making in disease outbreaks.

The spatial method was calculated by using the Global Moran's I and the Local Moran's I (Cardoso, 2007), which is also known as a LISA statistic (Local indicator of spatial association), both being used as indicators of spatial association. Spatio-temporal association was evaluated by computing a spatio-temporal Poisson scan statistic, proposed by Kulldorff (2001) to identify emerging or “alive” clusters in space and time. As of January 2021 vaccination against COVID-19 already started, since the use of spatial clustering methods to identify non-vaccinated populations is not new among studies on vaccination coverage strategies (Truelove et al., 2019; Brownwright et al., 2017) and a study done on spatial clustering in medical vaccine exemptions on kindergartens in the state of California in the United States (Gromis and Liu, 2020) showed that spatial clustering of vaccination exemptions is a threat to local herd immunity, this paper also aims to discuss the implementation of spatial and spatio-temporal clustering methods in early vaccination, which could be useful to accelerate herd immunity or prevent further disease outbreaks.

2. Methods

The statistical software R (version 4.0.3) was used to calculate the spatial and the spatio-temporal association, the COVID-19 database used in the study is also available in R, in a package called “COVID-19” built by the COVID-19 Data Hub (Guidotti and Ardia, 2020), the database begins in January 2020 and is constantly updated, it also gathers data from various sources of information for all countries in which it was possible to obtain data. The database provides data about political measures adopted by each country during the pandemic, even though that information is not available for all countries included, which is one of the limitations of the database, that lack of data is also seen in variables such as the number of recovered cases, where some countries had no recovered cases during the analysis’ period of time, since the reason for this was not explicit in the website of COVID-19 Data Hub, this paper supposes it was not possible to access data for countries which the information was lacking in the unified database.

The cumulative number of deaths, infections and recovered cases is given by the database, but since these numbers are only available in its daily cumulative form, it was necessary to calculate monthly quantities for each one of the variables in the period of time considered in this paper between January and December 2020. The population of each country is also available in the database, so in order to better understand the spatial and the spatio-temporal effects of COVID-19 in each location, it was necessary to calculate the ratio between the number of infections, the number of recovered cases and the quantity of deaths in the population.

2.1. Moran's I

To evaluate spatial association during the first year of the pandemic, a knn method was used to create spatial polygons and to build spatial weight matrices, which are necessary to calculate the Global Moran's I and the LISA. The Global Moran's I is widely used and gathers all spatial dependence in one value (BRAGA et al., 2010), while the use of the Local Moran's I is important to identify patterns of spatial association, hence the LISA should be used with the Global Moran's I, as it is stated by MAIA et al. (2018) “while the global Moran's I may suggest, in general, that there is little spatial autocorrelation in the data, LISA values can identify smaller geographic areas where positive or negative clustering occurs”.

The Global Moran's I is calculated as shown in Eq. (1), where $w$ is the spatial weight matrix, $x$ is the value of the studied variable, $n$is the number of identified polygons and $\overline{x}$ is the mean or average

$$J=\frac{n{\sum }_{i=1}^n{\sum }_{j=1}^n(x_i-\overline{x})(x_j-\overline{x})w_{\mathit{ij}}}{\mathrm{W}{\sum }_{i=1}^n{(x_i-\overline{x})}^2}$$ (1)

W is defined by the following equation $W=\sum _{i=1}^n\sum _{j=1}^n{w}_{ij}$

The values range from - 1 to 1, with the 0 value indicating an absence of spatial autocorrelation, positive values are indicators of positive spatial association, while negative values mean there is an inverse association, since this work seeks to find positive spatial association, the hypothesis tests were built within a 95% confidence level, so that the alternative hypothesis (H1) corresponds to an index higher than zero and the null hypothesis (Ho) to a lack of spatial association, both of which can be written mathematically as H0: I = 0 and H1: I > 0. The monthly quantities were important to avoid problems of non-stationarity when computing the Global Moran's I, according to Cardoso (2007) (translated from portuguese). “The index loses its validity when calculated for non-stationary data.”, in order to validate the index 10,000 simulations were computed in a test of random permutations (Monte-Carlo) (Seffrin et al., 2018).

Whereas the Local Moran's I (LISA) is calculated by the following Eq. (2)

$$I\left(i\right)=\frac{x_i-\overline{x}}{s_i^2}\sum _{j=1}^n{w}_{\mathit{ij}}(x_j-\overline{x}),i=1,...,n,j\ne i$$ (2)

Where $s_i^2$ is the variance of the studied variable $x_i$

$$s^2\left(i\right)=\sum _{j=1}^n\frac{{\left(x_j-\overline{x}\right)}^2}{n-1},i=1,...,n,j\ne i$$

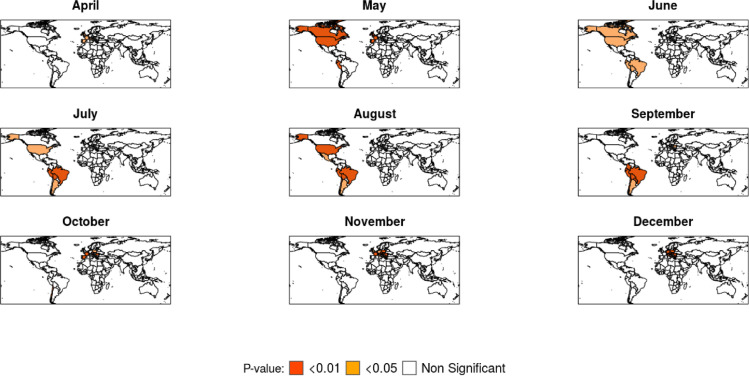
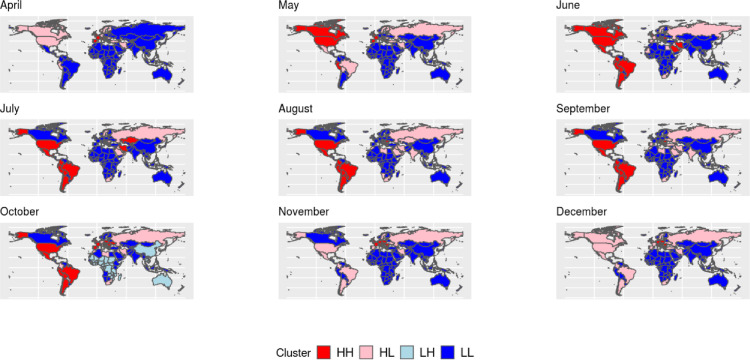
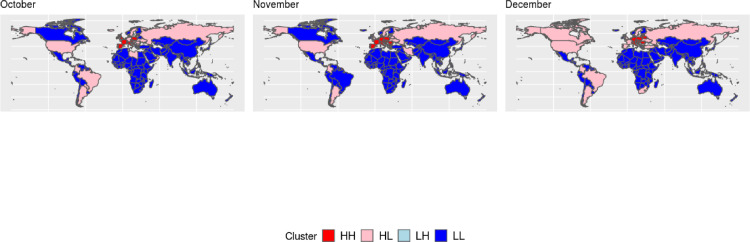
Local Moran's I maps, Boxmaps, and Global Moran's I tables, were built for variables (number of cases and deaths) which achieved a global index IM > 0.50 at least in one month during 2020, the orange-colored regions in the LISA maps (Fig. 2, Fig. 3 ) show regions with P-value < 0.001 whereas the light orange-colored regions represent locations with P-value < 0.05, although some regions may also be light orange-colored when only clusters with P-value < 0.001 were found. Boxmaps are cartographic representations of the Moran scatter plot, in which according to Seffrin et al. (2018) the HH means that the identified locations have high index values and are close to other areas of high value, the LL value means that areas identified with low values are surrounded by areas with low values, the LH value represents areas with a low value surrounded by other areas with high values, while HL is the opposite, they are regions with high values close to locations with low values, in the built Boxmaps (Fig. 4, Fig. 5 ) HH values were red-colored, LL blue-colored, LH light blue-colored and HL light red-colored.

Fig. 2.

Local Moran's I on the number of deaths per inhabitant.

Fig. 3.

Local Moran's I on the number of cases per inhabitant.

Fig. 4.

Boxmaps of the number of deaths per inhabitant (For interpretation of the references to color in this figure, the reader is referred to the web version of this article).

Fig. 5.

Boxmaps of the number of cases per inhabitant (For interpretation of the references to color in this figure, the reader is referred to the web version of this article).

2.2. The Poisson scan statistic

The prospective scan statistic proposed by Kulldorff (2001) was chosen to identify emerging spatio-temporal clusters in the cumulative number of cases for each month, to apply the technique it was considered that the data follows a Poisson distribution. The purely spatial scan statistic creates a wide variety of circular windows in different locations throughout the map, each one with a specific group of neighboring areas, all of these circular windows are also flexible in their two dimensions, size and locality, and may or not contain a cluster of events. A scan statistic is defined as the likelihood ratio over all possible circles and when maximized identifies the one which constitutes the most likely cluster, the P-value is obtained through the Monte-Carlo hypothesis test.

For the purely spatial scan statistic we have that the definition of the scan statistic $S$ is given by Eq. (3)

$$S=\underset{Z}{\text{max}}\left\{\frac{L\left(Z\right)}{L_0}\right\}$$ (3)

Where $Z$ is defined as a possible circle, $L\left(Z\right)$ is the maximum likelihood for $Z$ and it tells how likely the observed data are given a differential rate of events inside and outside the zone, $L_0$ is the likelihood function under the null hypothesis of spatial randomness, therefore

$$\frac{L\left(Z\right)}{L_0}={\left\{\frac{n_Z}{\mu \left(Z\right)}\right\}}^{n_Z}{\left\{\frac{N-n_Z}{N-\mu \left(Z\right)}\right\}}^{N-n_Z},if{n}_Z>\mu \left(Z\right),\text{otherwise}\frac{L\left(Z\right)}{L_0}=1$$

Given that $N$ is the observed total number of cases, $n_Z$ is the number of cases in the circle $Z$ and for the Poisson model $\mu \left(Z\right)$ is the expected number under the null hypothesis, so $\mu$($A$) = $N$ where A is the total region under study, which could be the world, a country or a higher area with our circles $Z$, if the null hypothesis is rejected then the approximate location of the cluster that caused rejection can be specified.

In opposition to the purely spatial scan statistic, the spatio-temporal scan statistic creates cylindrical windows in three dimensions, so our previously defined circle $Z$ for the purely spatial scan statistic becomes a cylinder, where the height is a representation of time, the cylinders are flexible in their circular bases and initial dates, hence only “alive” clusters, the ones which cylinders achieved the end of the study period are considered, the maximum likelihood ratio tests are conducted the same way as they are in the purely spatial scan statistic, so if the null hypothesis is rejected not only the approximate location of the cluster can be specified but also its beginning.

Spatio-temporal scan statistics are useful to identify emerging clusters, since purely spatial scan statistics have a few limitations as it is pointed by Kulldorff (2001), there is little power to detect emerging clusters when conducting a purely spatial analysis for a long period of time, therefore the solution would be to use a spatio-temporal scan statistic.

3. Results

When calculated for the number of deaths per inhabitant in each country (Table 1 ), the highest index of global spatial association was achieved in April (IM = 0.72; P-value < 0.05), other months identified with high Global Moran's I values were November (IM = 0.69; P-value < 0.05) and December (IM = 0.70; P-value < 0.05). Whereas when computed for the number of infections per inhabitant caused by COVID-19 (Table 2 ), the highest values for the Global Moran's I were found in October (IM = 0.60; P-value < 0.05), November (IM = 0.67; P-value < 0.05) and December (IM = 0.58; P-value < 0.05).

Table 1.

Global Moran's I on the number of deaths per inhabitant.

Month	Moran Global	P-value (Monte-Carlo)
January	- 0.0238	0.2215
February	- 0.0129	0.2264
March	0.2789	0.0005
April	0.7199	0.0001
May	0.4843	0.0001
June	0.2308	0.0041
July	0.3172	0.0006
August	0.4295	0.0001
September	0.4229	0.0001
October	0.3514	0.0001
November	0.6974	0.0001
December	0.7091	0.0001

Table 2.

Global Moran's I on the number of cases per inhabitant.

Month	Global Moran	P-value (Monte-Carlo)
January	- 0.0353	0.3253
February	0.0200	0.2843
March	0.3975	0.0001
April	0.3625	0.0001
May	0.3796	0.0001
June	0.4516	0.0001
July	0.3400	0.0001
August	0.2803	0.0001
September	0.3089	0.0001
October	0.6038	0.0001
November	0.6742	0.0001
December	0.5809	0.0001

Considering the number of deaths per inhabitant, when identifying local spatial autocorrelation with the Local Moran's I (Fig. 2) after April, month with the highest Global Moran's I, spatial dependence was strong in Europe, South America and North America, with little difference in maps throughout the year. For the number of infections per inhabitant, after October, which was the first month with a high global dependence, local association was strong in Europe until the end of the year (Fig. 3).

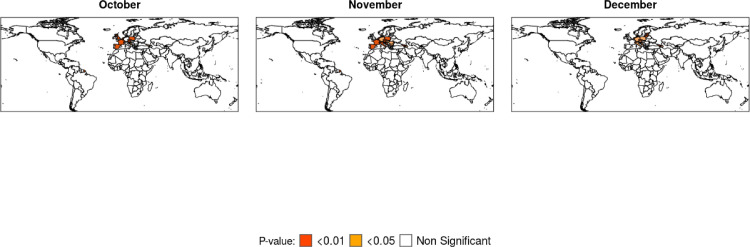
The spatio-temporal scan statistic was only computed for the number of cumulative cases during the pandemic (Table 3 ), the method to calculate spatio-temporal clusters showed itself to be way more computer intensive than the calculation of the Global Moran's I and the LISA. But the spatio-temporal scan statistic also was efficient to identify emerging clusters in space and time, with most of the locations in October and November also identified in the Local Moran's I both for the number of infections per inhabitant and for the number of deaths per inhabitant in these months.

Table 3.

COVID-19 case clusters identified by the spatio-temporal Poisson scan statistic.

Month	Duration	Localities	Risk	P-value (Monte-Carlo)
February	4	South Korea	3.4422	0.001
March	6	Bahamas, Canada, Colombia, Costa Rica, Cuba, Dominican Republic, Guatemala, Honduras, Haiti, Jamaica, Mexico, Nicaragua, Panama, El Salvador, United States.	1.5693	0.001
April	8	Russia, Mongolia, Kazakhstan.	1.5687	0.001
May	9	Bolivia, Brazil, Paraguay, Suriname, Guyana, Uruguay, Chile, Peru, Argentina, Trinidad and Tobago, Venezuela.	1.3208	0.001
June	12	Bolivia, Brazil, Paraguay, Uruguay, Chile, Peru, Argentina.	1.1212	0.001
July	9	India.	1.1808	0.001
August	10	India, Nepal.	1.1186	0.001
September	12	India, Nepal.	1.0667	0.001
October	9	Austria, Belgium, Switzerland, Czech Republic, Germany, Denmark, France, United Kingdom, Ireland, Liechtenstein, Luxembourg, Monaco, Netherlands, Norway, Poland.	1.2416	0.001
November	12	Austria, Bosnia and Herzegovina, Switzerland, Czech Republic, Germany, Croatia, Hungary, Italy, Liechtenstein, Poland, San Marino, Serbia, Slovakia, Slovenia	1.1183	0.001
December	22	Turkey	1.1116	0.001

4. Discussion

In April global cases of COVID-19 reached 1 million, in the same month the world also reached 3 million cases (Brodeur et al., 2020), with an exponential growth in the number of infections, the Global Moran's I was also very high for the number of deaths per inhabitant, while local spatial association was strong only in Europe, the Boxmap (Fig. 4) shows that all areas identified with local dependence for the number of deaths per inhabitant were either HH (High-High) clusters in April or HL (High-low) clusters after April, which means that in general locations with a high number of deaths were close to other areas that also had a high number of deaths. Even though April was a very concerning month to the international community, global spatial autocorrelation on the number of cases per inhabitant only started to grow higher than IM > 0.50 in October, but the boxmaps for the number of infections (Fig. 5) show the same trend that happened for the number of deaths, when looking them together with the LISA maps (Fig. 3) all locations identified with spatial association were either HH or HL clusters.

The Poisson scan statistic calculated for the number of cumulative cases identified the duration of emerging clusters in the number of infections throughout the year, in a comparison between a timeline of events that occurred in the pandemic (Brodeur et al., 2020) and the observed clusters, since March 25th the US was identified as an emerging cluster by the Scan Statistic and one day later turned out to be the country with most cases of COVID-19 in the World, in May 22th Brazil was identified as a cluster and in the same day surpassed Russia turning out to be the 2nd country with most cases in the world. Other patterns can be verified when comparing results given by the scan statistics against the locations identified as HH and HL clusters in the Boxmaps of infections per inhabitants (Fig. 5), all clusters of the Scan Statistic were also HH or HL clusters in the months they have been identified (October, November and December).

When comparing both methods, the Poisson spatio-temporal scan statistic and the Moran's I, the Scan Statistic was efficient not only to detect emerging clusters of COVID-19 cases in space and time by identifying their duration, but also in showing “hidden” clusters not visible in LISA maps, such as small European countries like San Marino and Liechtenstein, since the implementation of a Poisson scan statistic demands too much computational power, the Moran's I is a better alternative inasmuch as it is easier to calculate and does not demand too much computational power.

A study on the clustering of cases and deaths of COVID-19 in countries throughout the world (which the ones with high mortality or incidence rate may also be called hotspots) (Shariati et al., 2020), have pointed out southern, northern and Western Europe as HH clusters of COVID-19 cases in April, this same region was identified as HH cluster for the number of deaths in our evaluation in the same period of time, a few months later European regions were also identified as clusters by the Poisson scan statistic, including San Marino which could not be specified by the Local Moran's I. In another study (Melin et al., 2020) the clustering of countries with similar behavior according to their coronavirus cases, classified either as very high or high, up to May 13 included different countries like Turkey, Brazil and Russia, that were also identified either by the Poisson scan statistic in the number of cases or by the Local Moran's I in the number of deaths.

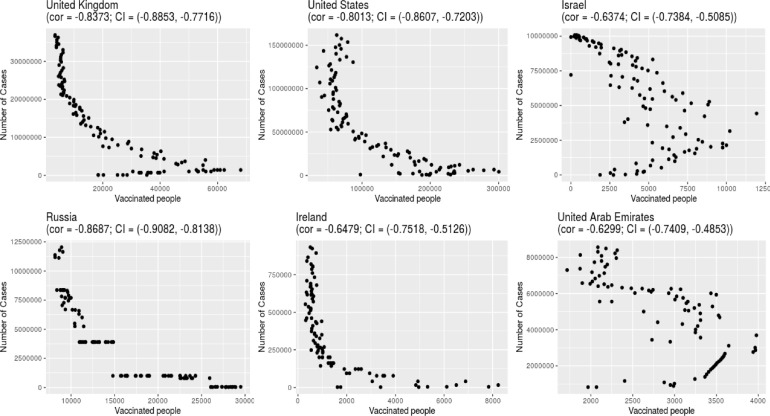
Spatial clustering methods are a powerful tool to control disease outbreaks and assist in decision making, these methods were used before in studies regarding vaccination coverage strategies against measles, in these studies it is pointed that in countries with high average vaccination coverage rates, the difference of vaccination coverage in certain locations can delay disease elimination (Brownwright et al., 2017) and that in accord to Truelove et al. (2019) “Even minimal clustering of non-vaccination, and resultant susceptibility, can produce substantial increases in outbreak risk, particularly”. As of February 2021, COVID-19 vaccination campaigns in various countries are showing a great correlation (higher than 0.60) between the beginning of vaccination and the diminishing of daily infections (Fig. 6 ), therefore, in early vaccination the use of spatio-temporal scan statistics would be useful to identify “alive” clusters and start vaccination campaigns in areas where COVID-19 outbreaks are occurring or are about to occur that would be useful not only to avoid collapse of public health systems but also to prevent a worsening of the outbreak, in situations where there is a lack of computational power instead of a Scan Statistic the use of the Local Moran's I which was used to find non-vaccination clusters in Brownwright et al. (2017) would be interesting.

Fig. 6.

Correlation plots (with P-value < 0.00001) between the number of daily cases and vaccinated people until 2021-04-03.

5. Conclusion

Both the Poisson scan statistic proposed by Kulldorff (2001), the Global and the Local Moran's I were already used before in studies about spatial and spatio-temporal characteristics of Sars-CoV-2, whereas the Scan Statistic for instance was used once in studies about the spatio-temporal behavior of COVID-19 in the state of Sergipe in Brazil (Andrade et al., 2020), while both the Global Moran's I and the LISA were used in Chinese studies regarding the spatial characteristics of the pandemic in China (Kang et al., 2020), in this paper these methods showed themselves to be useful when there is a need to study spatial and spatio-temporal characteristics of a virus.

While the Global Moran's I could be used with great success to identify the spatial association in smaller areas affected by the virus and help in decision making while dealing with local outbreaks, the LISA would be useful not only to identify with more precision where the spatial association is occurring but it also should be used when the goal is to control COVID-19 outbreaks in larger areas. The spatio-temporal scan statistic should be used when trying to identify “alive” clusters and their initial date, therefore it would be a great tool in decision making when dealing not only with COVID-19 outbreaks but also with other diseases.

Since a lot of vaccination campaigns are still in early stage throughout the world and there is a correlation between the number of vaccinated people and fewer daily cases of COVID-19 in a variety of countries, after all the use of spatial clustering methods to identify non-vaccination clusters in late stages of disease elimination is advised to prevent outbreaks, more thought should be given to spatio-temporal clustering and spatial clustering of risk areas in early stage vaccination strategies in order to better use limited vaccination resources and stop local COVID-19 outbreaks preserving public and private health systems.

Limitations

It should be pointed out that this work needs to be amplified, since there are a few limitations in it, such as some corrections that have happened in the database since it is built with real-time updated data, and the great heterogeneity we're dealing with when working with data from all over the world, even though the provided database had information about political measures adopted, it had no information about different health systems, variants of COVID-19, case definitions, or other important measures, which means that some of the correlations found may not be reliable.

Since we could not control these limitations, because of the real-time nature of our data and the lack of information that could diminish the effect of this heterogeneity in the data we worked with, it is important to think about the techniques applied here in a “local” level, like hospitals, schools, workplace, or even cities, states, or other types of administrative divisions, where there is information about possible confounders, and in the case of COVID-19 or other disease outbreaks, uniformity in the measures adopted to combat its spreading and other external factors that could bring more homogeneity to its clustering evaluation.

Funding

This work was supported by The Brazilian National Council for Scientific and Technological Development (CNPQ) under Grant 144790/2020–3.

All authors attest they meet the ICMJE criteria for authorship.