MARCOS technique under intuitionistic fuzzy environment for determining the COVID-19 pandemic performance of insurance companies in terms of healthcare services

Abstract

Assessing and ranking private health insurance companies provides insurance agencies, insurance customers, and authorities with a reliable instrument for the insurance decision-making process. Moreover, because the world’s insurance sector suffers from a gap of evaluation of private health insurance companies during the COVID-19 outbreak, the need for a reliable, useful, and comprehensive decision tool is obvious. Accordingly, this article aims to identify insurance companies’ priority ranking in terms of healthcare services in Turkey during the COVID-19 outbreak through a multi-criteria performance evaluation methodology. Herein, alternatives are evaluated and then ranked as per 7 criteria and assessments of 5 experts. Experts’ judgments and assessments are full of uncertainties. We propose a Measurement of Alternatives and Ranking according to the Compromise Solution (MARCOS) technique under an intuitionistic fuzzy environment to rank insurance companies. The outcomes yielded ten insurance companies ranking in terms of healthcare services in the era of COVID-19. The payback period, premium price, and network are determined as the most crucial factors. Finally, a comprehensive sensitivity analysis is performed to verify the proposed methodology’s stability and effectiveness. The introduced approach met the insurance assessment problem during the COVID-19 pandemic very satisfactory manner based on sensitivity analysis findings.

1. Introduction

Insurance has an important place in modern society’s daily life [1]. Insurers play a fundamental role in economies since they manage risks for individuals and firms, and countries. Thanks to insurance, further, people do not have to worry about unexpected events [2].

Health insurance ensures the expenses for the treatment of policyholders in case of illness and/or injuries resulting from an accident during the insurance period [3]. In private health insurance, one of the alternative financing methods of healthcare services, the reimbursement institution is private health insurance, and individuals or institutions insure their health risks [4].

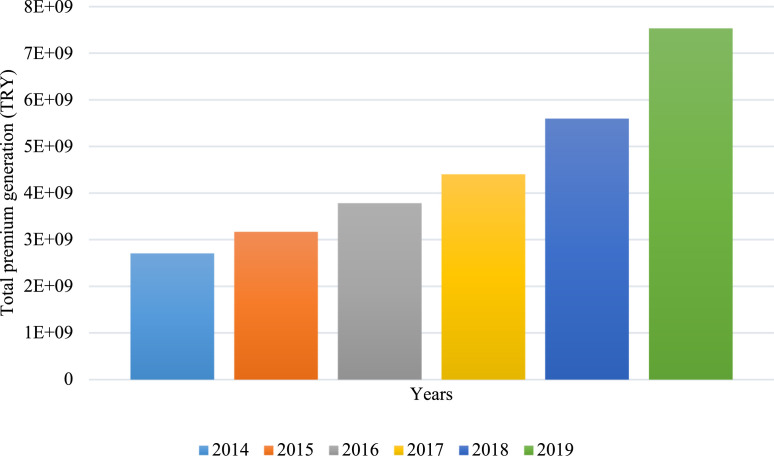
Turkey’s health insurance covers illness, private health, health for foreigners, emergency health, health, and travel health products [5]. Since the beginning of the 1990s, there have been some crises in Turkey regarding health financing. As a result, radical changes were made in the health system with the Health Transformation Program, which started in 2003, and one of them was the Social Security Reform. With this reform, the general health insurance system was implemented as well as access of all citizens to health services has become more comfortable. Thus, the regulations associated with the delivery and financing of health services have gained momentum, especially after 2003, and financing and the provision of services, both radical changes, have taken place [6]. In 2012, all citizens in Turkey had been general health insurance coverage. In Turkey, further, public health insurance is made mandatory against the risk of illness that may arise, regardless of the people’s economic power and will. Thereby, all members of society benefit from general health insurance. However, no matter how the scope of the basic coverage package is determined, it is natural that there is a difference between the health services provided within the scope of the state’s social security and the optimal conditions in systems based on public finance. As of 2018, the share of private health insurance in Turkey’s insurance sector is 10.9%, which corresponds to 3.8% of the population [5]. Fig. 1 presents the development of private health insurance in Turkey.

Fig. 1.

Development of private health insurance in Turkey.

https://www.tsb.org.tr/official-statistics.aspx?pageID=1003.

Nowadays, increasing average life expectancy, developingtechnology, and changes in the structure of diseases have increased private health insurance. Recently, many epidemics such as Middle East respiratory syndrome coronavirus (MERS) [7], severe acute respiratory syndrome (SARS) [8], bird flu [9], swine flu [10], etc. have emerged. Since late 2019, The COVID-19 outbreak caused by the virus named SARS-CoV-2 has been spreading at an increasing rate and threatening the whole world. As of 16th January 2021, as per Johns Hopkins University report [11], 94,078,427 individuals were infected, and 2,014,436 people died due to this pandemic worldwide. In Turkey, the first COVID-19 case has been officially confirmed on 11th March 2020. Moreover, based upon Turkey’s health ministry, the total number of tests administered was 27,223,445, of which 2,380,665 returned positive, with 23,832 passing away, whereas the total number of 2,254,052 patients are recovered [12].

As a result, The COVID-19 epidemic, which directly affects the lifestyle of billions of people, has begun to transform the insurance industry and many other industries in the world. In this challenging period in Turkey, full treatment costs for COVID-19 illness were covered under private health insurers’ policy. Thus, analyzing the performance of insurance companies in such a challenging process is a quite significant issue. As a result, this paper aims to propose an effective and reliable decision-tool named intuitionistic fuzzy Measurement of Alternatives and Ranking according to Compromise Solution (IF-MARCOS) for measuring the performance of insurance companies in Turkey in terms of health services during the COVID-19 outbreak. The alternatives’ utility functions are stated according to the relationships defined in the MARCOS method, which is a simple and efficient multi-criteria technique and based on determining the relationship between ideal and anti-ideal alternatives. A consensus ranking is then realized concerning ideal and non-ideal solutions. Although the MARCOS method is relatively new, many papers have been performed about it [13], [14], [15], [16], [17]. Intuitionistic fuzzy sets (IFSs) have also been performed successfully in real-world problems to employ inconsistent, vague, ambiguous, and incomplete information. It has attracted more and more attention since its introduction and researchers achieved satisfactory results. For example, Li et al. [18] integrated QFD and TOPSIS for selecting a knowledge management system under IFSs. Xue et al. [19] developed a novel approach for solving IFSs-based MCDM problems with incomplete weight information. Büyüközkan and Göçer [20] studied the MCDM problem through AHP and axiomatic design approach for IFSs. Schitea et al. [21] employed WASPAS, COPRAS, and EDAS multi-criteria methods to solve site selection problems under IFSs. Recently, Kumari and Mishra [22] studied a green supplier selection problem based on parametric measures of IFSs. Rouyendegh et al. [23] discussed an IF-based TOPSIS technique for evaluating green suppliers. Though MARCOS is a robust tool, it cannot express DMs’ vagueness, ambiguity, and incomplete information. Thanks for extending the MARCOS method to IFSs; therefore, the introduced IF-MARCOS methodology can handle imprecise, indeterminate, vague, and incomplete information successfully in real situations.

Evaluation of health insurance companies, especially regarding customer-oriented factors, has become a vital research area of plenty of insurance research centers during the COVID-19 pandemic. This is mainly due to the undeniable importance of health insurance on the capital market and the critical role of service quality in customer satisfaction. This issue has remained one of the major topics associated with the insurance industry, which has not been sufficiently studied in the literature. In summary, this study is structured around the following main objectives:

• •To assess ten insurance companies operating in Turkey regarding health services during the COVID-19 pandemic and determine which one is the best.
• •While making this assessment, it is the first time in the literature to handle a novel approach called MARCOS method under an intuitionistic fuzzy environment.
• •To determine the importance of the evaluation criteria used in evaluating insurance companies. The contributions of this work can be pointed out as follows:
• •Although the MARCOS technique is a powerful decision-making tool, it cannot express fuzziness and ambiguity information.
• •Combined with the intuitionistic fuzzy sets, we posit the IF-MARCOS model, which can better describe decision-makers’ evaluation information.
• •We extend assessments of decision-makers to the intuitionistic fuzzy sets to extract criteria weights and rank the alternatives.
• •IF-MARCOS approach is suggested to apply to multiple criteria group decision making (MCGDM) problems.
• •A real-world problem of insurance companies’ assessment is given for the extended MARCOS methodology to MCGDM problems.

To achieve the mentioned objectives, the rest of this work is organized as follows. A literature review is performed in Section 2. In the third section of the study, IF-MARCOS is presented in detail. Application and sensitivity analysis is carried out in Section 4. The fifth section of the paper is about managerial implications. Finally, the concluding observations with directions for future works and limitations are presented in Section 6.

2. Literature review

In this paper, the literature section is divided into two subsections. The first is the studies that applied the MARCOS method, while the second is the insurance studies conducted multiple criteria decision making (MCDM) techniques.

2.1. Studies applied the MARCOS method

MARCOS represents a new multi-criteria technique developed by Stević et al. [24]. They showed that the advantages of the MARCOS methodology with traditional multi-criteria techniques: Multi-Attributive Border Approximation area Comparison (MABAC) [25], Additive Ratio Assessment (ARAS) [26], Weighted Aggregated Sum Product ASsessment (WASPAS) [27] and technique for order of preference by similarity to ideal solution (TOPSIS) [28]. The advantages of the MARCOS methodology were confirmed through a case study in which the evaluation of sustainable supplier selection in healthcare industries was performed. After the initial study, in just a few months, several studies have appeared in the literature that exploit the advantages of the MARCOS methodology [13], [14], [16], [17], [29], [30].

The MARCOS method has undergone several extensions using fuzzy theories, gray theories, and D numbers [13], [14], [16]. An extension of the MARCOS methodology in a fuzzy environment was presented by Stankovic et al. [14] and Ilieva et al. [13]. In their study, Stankovic et al. [14] used fuzzy triangular numbers to represent the uncertainties that exist when analyzing road traffic risks. Ilieva et al. [13] also used fuzzy triangular numbers to represent uncertainty in the MARCOS model and demonstrated the application of the fuzzy MARCOS methodology for cloud service selection. Chakraborty et al. [16] extended the MARCOS method using D numbers for supplier selection in an iron and steel industry. D numbers were used to represent the uncertainties in the expert evaluation of the decision matrix criteria. In addition to extending the MARCOS method using fuzzy and D numbers, Badi and Pamucar [17] extended the MARCOS method using gray numbers and demonstrated the possibilities of applying the MARCOS-G methodology for supplier selection for a steelmaking company. In addition to application in an uncertain environment, Puška et al. [29] developed a multi-criteria framework for project management software evaluation. In the study [29], the MARCOS methodology was used to assess alternatives, while the weighting coefficients of the criteria were defined based on subjective assessments of experts.

2.2. MCDM in insurance

Since the importance of insurance is evident for each country, various studies have been carried out in this area. Doumpos et al. [31] argued that the papers related to the financial performance of insurance companies could be generally classified into the following four groups: (i) papers that consider individual financial ratios, (ii) papers that examine the credit ratings of firms, (iii) failure prediction works, and (iv) studies on the efficiency of insurers [32], [33], [34], [35]. In recent years, however, studies using MCDM methods to select, evaluate, and rank insurance companies have been increasing exponentially [3], [36], [37], [38], [39], [40], [41]. Table 1 demonstrates some recent MCDM works in the field of insurance.

Table 1.

MCDM studies in the field of insurance.

Author/s	Criteria used	Aim	Method
Saeedpoor et al. [42 ]	Tangibility, reliability, assurance, responsiveness, empathy	Ranking life insurance firms based upon the SERVQUAL model.	Fuzzy AHP and fuzzy TOPSIS integrated model
Yücenur and Demirel [43 ]	Price, profitability, portfolio structure, portfolio size, sales channel structure, brand equity, organizational quality, solvency ratio	Selection of an insurance company for a foreign investor who wants to buy a local insurance company.	Fuzzy VIKOR
Mandić et al. [44 ]	Equity and reserves, business assets, provision and liabilities, financial incomes, cost of insurance	Evaluation of the efficiency of insurance companies	Fuzzy AHP and TOPSIS integrated model
Puelz [45 ]	Net payment index, contractual flexibility, financial strength, cash value accumulation	Selection of the best life insurance firm	AHP
Khodaei Valahzaghard and Ferdousnejhad [46 ]	Assets, cash flow, income, capital adequacy	Ranking insurance firms	AHP and factor analysis
Chang [47 ]	Financial structure, profitability, equity repayment capacity, management, and overall operational efficiency	Assessment of Taiwanese insurance firms	GRA
Tsai et al. [48 ]	Business index, a whole company operating index, an entire company operating index	Evaluating Taiwanese insurance companies	ANP and TOPSIS hybrid framework
Sehhat et al. [49 ]	Productivity, sales network, development, information technology, customer satisfaction, composition, and growth, after-sales service	Ranking Iranian insurance firms	AHP and TOPSIS hybridization
Sabet and Fadavi [50 ]	Operating costs, insurance costs, number of employees/branches/agents/issued insurance/complimentary insurances, profit, market share, investment return	Determining the efficiency of insurance companies	DEA
Fan et al. [51 ]	Image, service, relationship, trust, payment equity, experience, price, product variety	Evaluating the intentions of consumers’ cross-buying bancassurance	TOPSIS
Venkateswarlu and Bhishma Rao [52 ]	Loss ratio, expense ratio, combined ratio, underwriting results ratio, net retention ratio, investment income ratio, operating ratio, net earnings ratio, the return of equity	Evaluating the profitability of non-life insurance companies in India	GRA and TOPSIS model
Tuş Işık [53 ]	Insurance premium, coverage, discounts applied, recognition, service quality	Selecting the most suitable insurance firm	QUALIFLEX and ORESTE
Doumpos et al. [31 ]	Equity to assets, solvency ratio, technical reserves ratio, liquid assets to total liabilities ratio, operating expense ratio, loss ratio, return on assets, total assets, risk retention ratio, inflation rate, inequality of income (GINI), GDP	Determining the performance of non-life insurers	PROMETHEE II and regression analysis
Kazemi and Bardeji [54 ]	Branch manpower skill, general and administrative costs of the branch, the grade of the branch, premiums, employees’ wages	Ranking the insurance branches in Iran	Fuzzy AHP and PROMETHEE integrated model
Torbati and Sayadi [55 ]	Cost of insurance, other costs, premium income, deferred claims, market share, customer satisfaction, customer education level, amount of investment, facility to employees, manpower skills	Measuring the performance of insurance branches	Best-Worst Method (BWM) and Fuzzy Inference System
Nourani et al. [56 ]	Service expenses, debt capital, equity, total investment, earned premiums, claims, profit, investment income	Determining the technical efficiency of insurance firms	DEA
Wang et al. [40 ]	Commissions, investment income, earned premium, management expense	Evaluating the efficiency of general insurance companies	Neutrosophic data AHP and TOPSIS combined approach
Mishra et al. [57 ]	Confidence, responsiveness, reliability, tangibles	Determining the service quality in vehicle insurance companies	Fuzzy TODIM

As shown in Table 1, these works have applied various methods like AHP, TOPSIS, DEA, Gray relational analysis (GRA),PROMETHEE, etc. Each one of these methods has its advantages as well as disadvantages. However, it is a fact that there is a need for reliable and robust models to better cope with ambiguity and vagueness for evaluating private health insurers in the age of COVID-19. Accordingly, unlike the others, this work posits an extension to MARCOS under the intuitionistic fuzzy environment (IF-MARCOS) methodology for the first time in the literature.

3. Research methodology

3.1. Preliminary knowledge

The fuzzy set proposed by Zadeh [58] employs uncertainty in a mathematical format. Nonetheless, it can merely concentrate on the membership degree of ambiguous situations [59], [60]. It does not succeed in dealing with the non-membership degree of vague conditions. To fill this gap, Atanassov [61] introduced Intuitionistic Fuzzy Sets (IFS) as an effective way of coping with vagueness and imprecision due to the degree of hesitation in the system. To understand the following section, IFS is explained below [21], [62], [63].

Let a set X be a fixed universe of discourse and its subset $A=\left\{\left(x,{\mu }_A\left(x\right),{\nu }_A\left(x\right)\right|xϵX\right\}$ which is assigned by the membership function ${\mu }_A\left(x\right)=[0,1]$ and non-membership function ${\nu }_A\left(x\right)=[0,1]$, satisfying $0\le {\mu }_A\left(x\right)+{\nu }_A\left(x\right)\le 1$. Moreover, for each IFS A, ${\pi }_A=1-{\mu }_A\left(x\right)-{\nu }_A\left(x\right)$ which corresponds to the degree of hesitancy. It is evident that $0\le {\pi }_A\left(x\right)\le 1$.

3.2. Intuitionistic fuzzy MARCOS (IF-MARCOS)

In this paper, we are utilized to MCDM method to obtain the weight of each criterion with respect to the intuitionistic fuzzy method and intuitionistic fuzzy weighted averaging (IFWA) operator introduced by Xu [64], and the linguistic variables are converted into intuitionistic fuzzy numbers (IFNs).

The MARCOS technique introduced by Stevic et al. [65] is based on the measurement of choices and their ranking as a compromise solution. Although the MARCOS method is a powerful decision-making tool, it cannot express fuzziness and uncertainty information. It is, therefore, necessary to make the technique more capable with a fuzzy extension. The description IF-MARCOS method is defined as follows.

(i) e $=$ {1,2,…,f} is the set of decision makers (DMs) and their weights are $\phi =\left[{\phi }_1,{\phi }_2,\dots ,{\phi }_f\right]$ and ${\sum }_{e=1}^f{\phi }_e=1$.

$${\phi }_e=\frac{\left({\mu }_e+{\pi }_e.\left(\frac{{\mu }_e}{{\mu }_e+{\vartheta }_e}\right)\right)}{\sum _{k=1}^l\left({\mu }_e+{\pi }_e.\left(\frac{{\mu }_e}{{\mu }_e+{\vartheta }_e}\right)\right)}$$ (1)

(ii) $C_m$ is the number of criteria, and their weights are W $=$ [${\mathit{w}}_1$, ${\mathit{w}}_2$,…, ${\mathit{w}}_n$]

$$\sum _{m=1}^n{w}_m=1(m=1,2,\dots ,n)$$

Step 1. Assessment of criteria by experts

The linguistic assessments for the criteria and DMs are realized using Table 2.

Table 2.

Linguistic variables for a rating of criteria and DMs.

Expression	IFNs ($\mu ,\vartheta$)
Very important (VI)	(0.88, 0.08)
Important (I)	(0.75, 0.20)
Medium (M)	(0.50, 0.45)
Unimportant (UI)	(0.35, 0.60)
Very unimportant (VU)	(0.08, 0.88)

For example, let the ratings for three DMs (DM1, DM2, DM3) are M, I, M, respectively. Then, the weight of the first DM is computed by using Eq. (1) as follows:

$${\phi }_{D{M}_1}=\frac{0.5+0.05\left(\frac{0.5}{0.5+0.45}\right)}{0.5+0.05\left(\frac{0.5}{0.5+0.45}\right)+0.75+0.05\left(\frac{0.75}{0.75+0.2}\right)+0.5+0.05\left(\frac{0.5}{0.5+0.45}\right)}=0.285$$

We, therefore, obtain the weights of DMs as 0.285, 0.430, and 0.285, respectively.

Step 2. Construct aggregated IF decision matrix

Let $D={\left[P_{me}\right]}_{n\ast f}$ $\left(e=1,2,\dots ,f;m=1,2,\dots ,n\right)$ be the IF decision matrix of decision-makers. Here, $P_{me}$ indicates the assessment of dth about DM the $j$th criteria. $P_{me}$ is utilized by IFN, and it could be expressed that $P_{me}=\left({\mu }_{P_{me}},{\vartheta }_{P_{me}},{\pi }_{P_{me}}\right)$ where ${\pi }_{P_{me}}$ is the hesitation degree of ${\pi }_{me}$ is calculated as follows:

$${\pi }_{me}=1-{\mu }_{P_{me}}-{\vartheta }_{P_{me}}e=1,2,\dots ,f;m=1,2,\dots ,\mathit{n}.$$

The aggregated IF decision matrix is presented as $\hat{R}={\left[{\hat{P}}_{me}\right]}_{n\ast f}$

$${\hat{P}}_m=IFW{A}_w\left(P_{m1},P_{m2},\dots ,P_{me}\right)=\left[1-\prod _{e=1}^f{\left(1-{\mu }_{P_{me}}\right)}^{{\phi }_e},\prod _{e=1}^f{\left({\nu }_{P_{me}}^{\left(k\right)}\right)}^{{\phi }_e},\prod _{e=1}^f{\left(1-{\mu }_{P_{me}}\right)}^{{\phi }_e}\right)\left(-\prod _{e=1}^f{\left({\vartheta }_{P_{me}}\right)}^{{\phi }_e}\right]$$ (2)

where ${\hat{P}}_m=\left({\mu }_{{\hat{P}}_m},{\vartheta }_{{\hat{P}}_m},{\pi }_{{\hat{P}}_m}\right)$.

For example, suppose that DMs rate the first criterion (C1) as I, M, M, respectively. Then, aggregated $\mu ,\vartheta$, and $\pi$ of C1 are computed as follows:

$$\mu =1-\left({\left(1-0.75\right)}^{0.285}\times {\left(1-0.5\right)}^{0.430}\times {\left(1-0.5\right)}^{0.285}\right)=0.590$$

$$\vartheta =0.2^{0.285}\times 0.45^{0.430}\times 0.45^{0.285}=0.356$$

$$\pi =1-\left(0.590+0.356\right)=0.054$$

The linguistic evaluations for the alternatives are carried out utilizing Table 3.

Table 3.

Linguistic variables for a rating of alternatives.

Expression	IFNs [$\mu ,\nu$]
Extremely good (EG)	[1.00, 0.00]
Very very good (VVG)	[0.85, 0.10]
Very good (VG)	[0.80, 0.15]
Good (G)	[0.70, 0.20]
Medium good (MG)	[0.60, 0.30]
Fair (F)	[0.50, 0.40]
Medium bad (MB)	[0.40, 0.50]
Bad (B)	[0.25, 0.60]
Very bad (VB)	[0.10, 0.75]
Very very bad (VVB)	[0.10, 0.90]

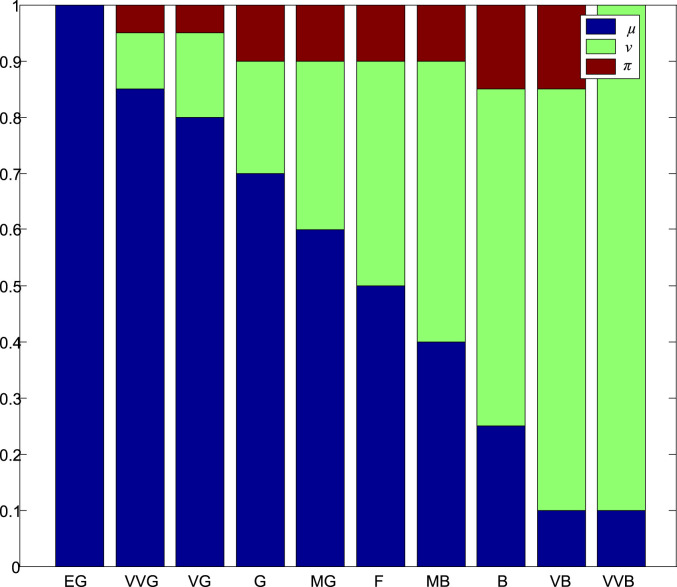
Membership functions of the linguistic variables presented in Table 3 are illustrated in Fig. 2.

Fig. 2.

Plots of IFNs [$\mu$, v, $\Pi$].

Step 3. Determine the IF ideal solutions

The IF has positive (IFPIS), which is ${\tau }^{+}=(1,0,0)$ and negative ideal solution (IFNIS), which is ${\tau }^{-}=(0,1,0)$. While IFNIS and IFPIS are defined by max and min operators, it is stated that there is no significant difference in their results [21].

Step 4. Calculate the distance measures

A fuzzy normalized Euclidean distance equation is used for determining the distance measure [66]. ${\delta }_m^{+}$ and ${\delta }_m^{-}$ are utilized in these equations below to demonstrate positive and negative distance measures, respectively.

$${\delta }_m^{+}=\sqrt{{({\mu }_{{\hat{P}}_m}-{\tau }^{+})}^2+{({\vartheta }_{{\hat{P}}_m}-{\tau }^{+})}^2+{({\pi }_{{\hat{P}}_m}-{\tau }^{+})}^2}$$ (3)

$${\delta }_m^{-}=\sqrt{{({\mu }_{{\hat{P}}_m}-{\tau }^{-})}^2+{({\vartheta }_{{\hat{P}}_m}-{\tau }^{-})}^2+{({\pi }_{{\hat{P}}_m}-{\tau }^{-})}^2}$$ (4)

For instance, ${\delta }_1^{+}$, ${\delta }_1^{-}$ and ${\mathit{CC}}_1$ for C1 is calculated as follows:

$${\delta }_1^{+}=\sqrt{{(0.590-1)}^2+{(0.356-0)}^2+{(0.054-0)}^2}=0.546$$

$${\delta }_1^{-}=\sqrt{{(0.590-0)}^2+{(0.356-1)}^2+{(0.054-0)}^2}=0.875$$

Step 5. Determine the closeness coefficient (CC) values

$C{W}_m$ is the CC of the mth criterion, and it is defined utilizing IFPIS ${\delta }_m^{+}$ and IFNIS ${\delta }_m^{-}$ as follows:

$$C{W}_m=\frac{{\delta }_m^{-}}{{\delta }_m^{-}+{\delta }_m^{+}}$$ (5)

CC value of C1 can be calculated as follows:

$$C{W}_1=\frac{0.875}{0.875+0.546}=0.616$$

Step 6. Calculate the weights of criteria and alternatives

The importance of each criterion is obtained from the CC values. It is noted that the total weights should be equal to 1, and normalization is applied to compute the finalized weights.

After Steps 5 and 6, we get a decision matrix $\stackrel{⌣}{D}$.

$$\left[\begin{array}{cccc}\hfill {\stackrel{⌣}{w}}_1\hfill & \hfill {\stackrel{⌣}{w}}_2\hfill & \hfill \dots \hfill & \hfill {\stackrel{⌣}{w}}_n\hfill \end{array}\right]$$

$$\stackrel{⌣}{D}=\left[\begin{array}{cccc}\hfill {\stackrel{⌣}{x}}_{11}\hfill & \hfill {\stackrel{⌣}{x}}_{12}\hfill & \hfill \dots \hfill & \hfill {\stackrel{⌣}{x}}_{1n}\hfill \\ \hfill {\stackrel{⌣}{x}}_{21}\hfill & \hfill {\stackrel{⌣}{x}}_{22}\hfill & \hfill \dots \hfill & \hfill {\stackrel{⌣}{x}}_{2n}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill {\stackrel{⌣}{x}}_{m1}\hfill & \hfill {\stackrel{⌣}{x}}_{m2}\hfill & \hfill \dots \hfill & \hfill {\stackrel{⌣}{x}}_{mn}\hfill \end{array}\right]$$

Let CW values of benefit-type evaluation criteria be 0.616, 0.735, and 0.824, respectively. We use normalization to gain the relative weight of C1 as follows:

$$w_{C1}=\frac{0.616}{0.616+0.735+0.824}=0.283$$

Step 7. Construct an extended IF decision matrix

An extended decision matrix $\stackrel{⌣}{E}$ is built by computing the anti-ideal $\stackrel{⌣}{A}AI$ and ideal $\stackrel{⌣}{A}I$ solution.

$$\left[\begin{array}{cccc}\hfill {\stackrel{⌣}{w}}_1\hfill & \hfill {\stackrel{⌣}{w}}_2\hfill & \hfill \dots \hfill & \hfill {\stackrel{⌣}{w}}_n\hfill \end{array}\right]$$

$$\stackrel{⌣}{E}=\begin{array}{c}\hfill {\stackrel{⌣}{A}}_1\hfill \\ \hfill {\stackrel{⌣}{A}}_2\hfill \\ \hfill ⋮\hfill \\ \hfill {\stackrel{⌣}{A}}_m\hfill \\ \hfill \stackrel{⌣}{A}AI\hfill \\ \hfill \stackrel{⌣}{A}I\hfill \end{array}\left[\begin{array}{cccc}\hfill {\stackrel{⌣}{x}}_{11}\hfill & \hfill {\stackrel{⌣}{x}}_{12}\hfill & \hfill \dots \hfill & \hfill {\stackrel{⌣}{x}}_{1n}\hfill \\ \hfill {\stackrel{⌣}{x}}_{21}\hfill & \hfill {\stackrel{⌣}{x}}_{22}\hfill & \hfill \dots \hfill & \hfill {\stackrel{⌣}{x}}_{2n}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill {\stackrel{⌣}{x}}_{m1}\hfill & \hfill {\stackrel{⌣}{x}}_{m2}\hfill & \hfill \dots \hfill & \hfill {\stackrel{⌣}{x}}_{mn}\hfill \\ \hfill {\stackrel{⌣}{x}}_{ai1}\hfill & \hfill {\stackrel{⌣}{x}}_{ai2}\hfill & \hfill \dots \hfill & \hfill {\stackrel{⌣}{x}}_{ain}\hfill \\ \hfill {\stackrel{⌣}{x}}_{id1}\hfill & \hfill {\stackrel{⌣}{x}}_{id2}\hfill & \hfill \dots \hfill & \hfill {\stackrel{⌣}{x}}_{idn}\hfill \end{array}\right]$$ (6)

The $\stackrel{⌣}{A}AI$ is the worst alternative, whereas the $\stackrel{⌣}{A}I$ is an alternative with the most acceptable performance. They are computed by applying Eqs. (7), (8), respectively.

$$\stackrel{⌣}{A}AI=\underset{i}{min}{\stackrel{⌣}{x}}_{ij},ifj\in Band\underset{i}{max}{\stackrel{⌣}{x}}_{ij},ifj\in C$$ (7)

$$\stackrel{⌣}{A}I=\underset{i}{max}{\stackrel{⌣}{x}}_{ij},ifj\in Band\underset{i}{min}{\stackrel{⌣}{x}}_{ij},ifj\in C$$ (8)

It is noted that B consists of benefit-type criteria, while C consists of cost-type criteria.

For example, let C1 be a benefit criterion, and CW values of three alternatives be 0.635, 0.216, and 0.756, respectively. Then we get:

$$\stackrel{⌣}{A}AI=min\left\{0.635,0.216,0.756\right\}=0.216$$

$$\stackrel{⌣}{A}I=max\left\{0.635,0.216,0.756\right\}=0.756$$

Step 8. Build the normalized IF decision matrix

The normalized value ${\stackrel{⌣}{\zeta }}_{ij}\mathrm{of}$ alternatives are obtained as follows.

$${\stackrel{⌣}{\zeta }}_{ij}=\left\{\begin{array}{c}\frac{{\stackrel{⌣}{x}}_{aij}}{{\stackrel{⌣}{x}}_{idj}},j\in B\hfill \\ \frac{{\stackrel{⌣}{x}}_{idj}}{{\stackrel{⌣}{x}}_{aij}},j\in C\hfill \end{array}\right)$$ (9)

For example, the normalized value of C1 in relation to A1 is obtained as follows:

$${\stackrel{⌣}{\zeta }}_{11}=\frac{0.635}{0.756}=0.840$$

Similarly, the normalized values of other alternatives are found to be 0.286 and 1.000, respectively.

Step 9. Build the weighted IF decision matrix

The weighted values for each alternative are calculated as follows.

$${\stackrel{⌣}{\Omega }}_{ij}={\stackrel{⌣}{\zeta }}_{ij}{\stackrel{⌣}{w}}_j$$ (10)

In Eq. (10), ${\stackrel{⌣}{w}}_j$ represents the relative importance of jth criterion.

For example, the weighted value of A1 as per C1 is computed as follows:

$${\stackrel{⌣}{\Omega }}_{ij}=0.840\times 0.283=0.238$$

Step 10. Create the ${\stackrel{⌣}{S}}_i$ matrix

To obtain the values of ${\stackrel{⌣}{S}}_i$ matrix, Eq. (11) is applied.

$${\stackrel{⌣}{S}}_i=\sum _{i=1}^n{\stackrel{⌣}{\Omega }}_{ij}$$ (11)

For example, should the weighted decision matrix values of alternative A1 according to three criteria are 0.238, 0.107, and 0.143, respectively, ${\stackrel{⌣}{S}}_1$ is obtained by some of these values, i.e. 

$${\stackrel{⌣}{S}}_1=0.238+0.107+0.143=0.488$$

Step 11. Determine the utility degrees of alternatives

The utility degrees of alternatives are determined through Eqs. (12), (13).

$${\stackrel{⌣}{K}}_i^{-}=\frac{{\stackrel{⌣}{S}}_i}{{\stackrel{⌣}{S}}_{ai}}$$ (12)

$${\stackrel{⌣}{K}}_i^{+}=\frac{{\stackrel{⌣}{S}}_i}{{\stackrel{⌣}{S}}_{id}}$$ (13)

Let the sum of AI and AAI values be 1.000 and 0.438, respectively. Afterward, the utility degree of A1 is computed as follows:

$${\stackrel{⌣}{K}}_1^{-}=\frac{0.488}{0.438}=1.114$$

$${\stackrel{⌣}{K}}_1^{+}=\frac{0.488}{1.000}=0.488$$

Step 12. Identify the utility function of alternatives

By using Eq. (14), the utility functions of alternatives are computed.

$$f\left({\stackrel{⌣}{K}}_i\right)=\frac{{\stackrel{⌣}{K}}_i^{+}+{\stackrel{⌣}{K}}_i^{-}}{1+\frac{1-f\left({\stackrel{⌣}{K}}_i^{+}\right)}{f\left({\stackrel{⌣}{K}}_i^{+}\right)}+\frac{1-f\left({\stackrel{⌣}{K}}_i^{-}\right)}{f\left({\stackrel{⌣}{K}}_i^{-}\right)}}$$ (14)

In Eq. (14), $f\left({\stackrel{⌣}{K}}_i^{+}\right)$ represents the utility function of the ideal solution, whereas $f\left({\stackrel{⌣}{K}}_i^{-}\right)$ represents the utility function as per the anti-ideal solution. $f\left({\stackrel{⌣}{K}}_i^{+}\right)$ and $f\left({\stackrel{⌣}{K}}_i^{-}\right)$ are calculated using Eqs. (15), (16).

$$f\left({\stackrel{⌣}{K}}_i^{+}\right)=\frac{{\stackrel{⌣}{K}}_i^{-}}{{\stackrel{⌣}{K}}_i^{-}+{\stackrel{⌣}{K}}_i^{+}}$$ (15)

$$f\left({\stackrel{⌣}{K}}_i^{-}\right)=\frac{{\stackrel{⌣}{K}}_i^{+}}{{\stackrel{⌣}{K}}_i^{-}+{\stackrel{⌣}{K}}_i^{+}}$$ (16)

For example, the ideal and anti-ideal solutions of A1 are calculated as follows, respectively:

$$f\left({\stackrel{⌣}{K}}_i^{+}\right)=\frac{1.114}{1.114+0.488}=0.695$$

$$f\left({\stackrel{⌣}{K}}_i^{-}\right)=\frac{0.488}{1.114+0.488}=0.305$$

Finally, the utility function of A1 can be determined as follows:

$$f\left({\stackrel{⌣}{K}}_1\right)=\frac{1.114+0.488}{1+\frac{1-0.695}{0.695}+\frac{1-0.305}{0.305}}=0.431$$

The utility functions of the remaining alternatives are calculated similarly.

Step 13. Rank the alternatives

Ranking the alternatives is realized in the last step based on the final values of utility functions. That is to say, and the most preferred alternative is the one with the highest utility value.

4. Case study

Due to its contribution to economic stability and the environment of trust it emerged, the insurance industry has become an essential part of the financial sector in recent years. Additionally, the health insurance market, which is the subject of this study, is a large market and economic resource. About the literature review of Acharya et al. [67], Adebayo et al. [68], Alhassan et al. [69], Habib et al. [70], Choi et al. [71], and Erlangga et al. [72], the number of research on health insurance has remarkably increased recently, which emphasize the significance of this issue.

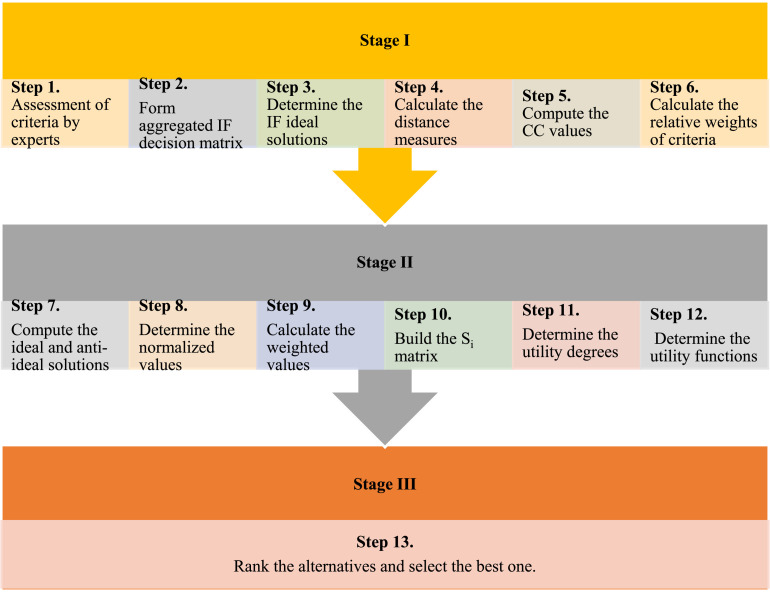
Therefore, in this paper, we propose an IF MARCOS framework for selecting the best private health insurance company among those having the largest market share in Turkey. The flowchart of the proposed method is illustrated in Fig. 3.

Fig. 3.

The flowchart of the proposed approach.

Although health insurance covers illness, private health, health for foreigners, emergency health, supplementary health, andtravel health products, this study is restricted to merely private health insurance. In this sense, ten private health insurance companies are examined for the present work. Based on the extensive literature review summarized in Table 1, as well as the opinions and experience of five experts in the health care insurance sector, the most relevant criteria are specified as follows:

• $-$Effectiveness (C1): It refers to the effectiveness of contracted clinics, hospitals, and doctors.
• $-$Responsibility (C2): It depicts responsibility in caring for COVID-19 patients and their families.
• $-$Network (C3): It defines the number of healthcare providers like clinics and hospitals for patients with COVID-19.
• $-$Support (C4): It refers to customer service providing 24/7 service for problems related to COVID-19.
• $-$Age (C5): It depicts to age limits covered by COVID-19-related treatments.
• $-$Payback period (C6): It means quick reimbursement forillness-related procedures (COVID-19 tests, intensive care, hospitalizations, etc.).
• $-$The premium price (C7): It defines the price of the private health insurance policy.

The experts were: a health insurance director, a market development manager, a business development manager, a technical coordinator, and a marketing communication expert.

As of 2019, the top 10 insurance companies in Turkey in terms of total premium production were included in the alternatives set and analyzed. In 2019, these companies carried out 94% of the total premium production in Turkey. The names of these insurance companies were kept confidential; thus, they were named A1, A2,… , A10. By the end of June 2020, in the field of health and sickness, they have had a market share of 4.11%, 1.83%, 7.91%, 5.24%, 34.32%, 2.16%, 0.54%, 22.44%, 0.78%, and 9.56%, respectively [73].

The solution steps using the proposed methodology are explained in detail below.

Step 1 and 2. The survey questionnaire used to evaluate the criteria and alternatives is presented in the appendix (Table A.1). The seven criteria’ linguistic assessments are realized by the decision-makers (DMs) using rating scales in Table 2, which assess the ten insurer alternatives as per the seven criteria using the rating scale in Table 3. The linguistic evaluations for the criteria and alternatives are presented in Table 4, Table 5.

Table A.1.

Questionnaire form.

Please express the significance levels of the following criteria.
	Very important	Important	Medium	Unimportant	Very unimportant
Effectiveness (C1)
Responsibility (C2)
Network (C3)
Support (C4)
Age (C5)
Payback period (C6)
Premium price (C7)

Please evaluate the alternatives below according to the criteria using extremely good (EG), very very good, very good (VG), good (G), medium good (MG), fair (F), medium bad (MB), bad (B), very bad (VB), very very bad (VVB).
	C1	C2	C3	C4	C5	C6	C7
A1
A2
A3
A4
A5
A6
A7
A8
A9
A10

Table 4.

Linguistic assessments for the rating of the evaluation criteria.

	DM1	DM2	DM3	DM4	DM5
C1	M	I	M	M	I
C2	I	I	I	M	M
C3	VI	I	VI	I	I
C4	I	I	I	I	M
C5	M	I	I	VI	I
C6	VI	VI	VI	VI	VI
C7	VI	VI	VI	I	VI

*M: Medium, I: Important, VI: Very important.

Table 5.

Linguistic assessments for the rating of the alternatives.

Alternatives	Experts	Evaluation criteria
		C1	C2	C3	C4	C5	C6	C7
	DM1	G	F	MB	F	B	F	MG
	DM2	MG	F	MB	F	B	F	G
A1	DM3	F	MG	F	F	MB	MB	F
	DM4	F	MG	F	G	MB	B	F
	DM5	F	MG	F	G	MB	F	G
	DM1	B	F	B	B	VG	B	VB
	DM2	B	F	B	B	VG	B	VB
A2	DM3	MB	B	F	B	VG	B	B
	DM4	B	B	F	G	G	B	B
	DM5	B	MB	MB	F	G	B	VB
	DM1	MG	G	F	MG	MG	MG	F
	DM2	MG	F	F	MG	VG	MG	F
A3	DM3	G	F	MG	G	G	G	G
	DM4	G	G	F	G	F	G	G
	DM5	G	F	MG	MG	MG	F	MG
	DM1	VG	VVG	VG	G	F	VG	G
	DM2	VG	VVG	VG	G	F	VG	G
A4	DM3	G	G	VVG	G	MG	VVG	MG
	DM4	G	G	VVG	VG	MG	EG	G
	DM5	VG	G	VVG	G	G	EG	MG
	DM1	EG	G	EG	VG	VG	VVG	G
	DM2	VG	EG	EG	VG	VG	EG	EG
A5	DM3	VVG	EG	VVG	EG	VG	EG	VG
	DM4	EG	VG	EG	VVG	G	VG	EG
	DM5	VG	VVG	VVG	VG	G	EG	VVG
	DM1	MB	F	F	F	MG	G	G
	DM2	MB	MG	F	F	MG	G	MG
A6	DM3	F	F	MG	F	F	MG	VG
	DM4	MB	MG	MG	MB	MG	G	G
	DM5	MB	F	MG	F	MG	MG	VG
	DM1	B	MB	VB	F	VGG	B	MG
	DM2	B	MB	B	B	EG	B	G
A7	DM3	VB	MB	B	F	EG	VB	G
	DM4	B	B	VB	F	EG	B	MG
	DM5	B	B	B	B	EG	VB	F
	DM1	VVG	VG	VVG	G	B	VVG	G
	DM2	VG	VVG	EG	VVG	B	VVG	VG
A8	DM3	VVG	VVG	VG	VVG	VB	VVG	VVG
	DM4	VG	VG	VVG	VG	VVB	VG	EG
	DM5	G	VVG	VVG	VVG	VB	VVG	VVG
	DM1	MB	B	F	F	B	MB	G
	DM2	MB	B	F	G	MB	B	G
A9	DM3	B	MB	B	F	B	MB	G
	DM4	B	B	VB	F	B	B	F
	DM5	B	B	MB	G	F	B	F
	DM1	G	MG	MG	G	VG	G	MG
	DM2	G	MG	F	MG	VG	MG	G
A10	DM3	G	F	MG	VG	VG	VG	G
	DM4	VG	G	F	G	VVG	VG	G
	DM5	VG	MG	G	G	VVG	G	VG

Step 3. The ratings for the DMs are defined by the committee utilizing Table 4. Then Eq. (1) is applied to extract the weight of each DM. These weights are given in Table 6. For example, the importance of the first DM is calculated in Box I.

Table 6.

Decision-makers’ weights.

	DM1	DM2	DM3	DM4	DM5
Linguistic variables	VI	VI	I	M	M
Weight	0.249	0.249	0.215	0.143	0.143

Box I.

$${\phi }_{D{M}_1}=\frac{0.88+0.04\left(\frac{0.88}{0.88+0.08}\right)}{0.88+0.04\left(\frac{0.88}{0.88+0.08}\right)+0.88+0.04\left(\frac{0.88}{0.88+0.08}\right)+0.75+0.05\left(\frac{0.75}{0.75+0.2}\right)+0.5+0.05\left(\frac{0.5}{0.5+0.45}\right)+0.5+0.05\left(\frac{0.5}{0.5+0.45}\right)}=0.249$$

Step 4. The aggregated IF decision matrix demonstrated in Table 7 is obtained using Eq. (2). For example, aggregated $\mu ,\vartheta$, and $\pi$ of the first criterion are computed as follows:

$$\mu =1-\left({\left(1-0.5\right)}^{0.249}\times {\left(1-0.75\right)}^{0.249}\times {\left(1-0.5\right)}^{0.215}\right)\left(\times {\left(1-0.5\right)}^{0.143}\times {\left(1-0.75\right)}^{0.143}\right)=0.619$$

$$\vartheta =0.45^{0.249}\times 0.2^{0.249}\times 0.45^{0.215}\times 0.45^{0.143}\times 0.2^{0.143}=0.327$$

$$\pi =1-\left(0.619+0.327\right)=0.054$$

Table 7.

Aggregated IF decision matrix.

	$\mu$	$\vartheta$	$\pi$
C1	0.619	0.327	0.054
C2	0.695	0.252	0.053
C3	0.840	0.115	0.045
C4	0.724	0.225	0.051
C5	0.732	0.215	0.053
C6	0.880	0.080	0.040
C7	0.867	0.091	0.042

Step 5. By using Table 7, ${\delta }_m^{+}$, ${\delta }_m^{-}$ and the IF weights of each criterion are computed with the help of Eqs. (3)–(5) as shown in Table 8. For example, while the IFPIS and IFNIS are ${\tau }^{+}=(1,0,0)$ and ${\tau }^{-}=(0,1,0)$, respectively, ${\delta }_1^{+}$, ${\delta }_1^{-}$ and ${\mathit{CC}}_1$ for C1 is calculated as follows:

$${\delta }_1^{+}=\sqrt{{(0.619-1)}^2+{(0.327-0)}^2+{(0.054-0)}^2}=0.505$$

$${\delta }_1^{-}=\sqrt{{(0.619-0)}^2+{(0.327-1)}^2+{(0.054-0)}^2}=0.916$$

$$C{W}_1=\frac{0.916}{0.916+0.505}=0.645$$

Table 8.

The weights of criteria.

	${\delta }_m^{+}$	${\delta }_m^{-}$	$CW$	Normalized weights
C1	0.505	0.916	0.645	0.117
C2	0.399	1.022	0.719	0.131
C3	0.202	1.221	0.858	0.156
C4	0.360	1.062	0.747	0.136
C5	0.347	1.075	0.756	0.137
C6	0.150	1.274	0.895	0.163
C7	0.167	1.257	0.883	0.160

Step 6. As in Step 4, utilizing Table 5, firstly, the values $\mu ,\vartheta$, and $\pi$ are found in this step. These values are given in Table 9.

Table 9.

Aggregated $\mu ,\vartheta ,$ and $\pi$ values of alternatives as per each criterion.

	C1			C2			C3			C4
	$\mu$	$\vartheta$	$\pi$	$\mu$	$\vartheta$	$\pi$	$\mu$	$\vartheta$	$\pi$	$\mu$	$\vartheta$	$\pi$
A1	0.584	0.020	0.396	0.553	0.018	0.429	0.452	0.029	0.518	0.568	0.012	0.420
A2	0.285	0.577	0.138	0.407	0.478	0.116	0.372	0.506	0.123	0.379	0.484	0.137
A3	0.654	0.245	0.101	0.591	0.305	0.104	0.538	0.361	0.101	0.639	0.259	0.101
A4	0.769	0.166	0.065	0.788	0.142	0.071	0.827	0.122	0.051	0.717	0.192	0.091
A5	1.000	0.000	0.000	1.000	0.000	0.000	1.000	0.000	0.000	1.000	0.000	0.000
A6	0.423	0.477	0.100	0.542	0.357	0.101	0.553	0.346	0.101	0.487	0.413	0.100
A7	0.220	0.629	0.150	0.360	0.527	0.113	0.194	0.655	0.151	0.414	0.469	0.117
A8	0.815	0.129	0.056	0.832	0.117	0.051	1.000	0.000	0.000	0.814	0.126	0.060
A9	0.329	0.548	0.123	0.285	0.577	0.138	0.391	0.493	0.116	0.591	0.305	0.104
A10	0.733	0.184	0.083	0.597	0.301	0.102	0.581	0.317	0.102	0.705	0.208	0.087
	C5			C6			C7
	$\mu$	$\vartheta$	$\pi$	$\mu$	$\vartheta$	$\pi$	$\mu$	$\vartheta$	$\pi$
A1	0.329	0.043	0.627	0.449	0.029	0.522	0.584	0.011	0.404
A2	0.775	0.163	0.062	0.250	0.600	0.150	0.157	0.692	0.151
A3	0.673	0.241	0.086	0.627	0.270	0.102	0.597	0.300	0.104
A4	0.571	0.327	0.102	1.000	0.000	0.000	0.667	0.231	0.101
A5	0.775	0.163	0.062	1.000	0.000	0.000	1.000	0.000	0.000
A6	0.580	0.319	0.101	0.667	0.231	0.101	0.721	0.200	0.079
A7	1.000	0.000	0.000	0.199	0.650	0.151	0.639	0.259	0.102
A8	0.178	0.689	0.133	0.844	0.106	0.050	1.000	0.000	0.000
A9	0.331	0.541	0.128	0.324	0.551	0.125	0.653	0.244	0.103
A10	0.816	0.134	0.051	0.721	0.200	0.079	0.696	0.212	0.092

Second, by using Table 9 and Eqs. (3)–(5), Table 10 is obtained.

Table 10.

Aggregated IF decision matrix for alternatives.

	C1			C2			C3			C4
	${\delta }_m^{+}$	${\delta }_m^{-}$	CW	${\delta }_m^{+}$	${\delta }_m^{-}$	CW	${\delta }_m^{+}$	${\delta }_m^{-}$	CW	${\delta }_m^{+}$	${\delta }_m^{-}$	CW
A1	0.575	1.207	0.677	0.620	1.206	0.660	0.755	1.190	0.612	0.603	1.215	0.668
A2	0.929	0.528	0.363	0.770	0.672	0.466	0.816	0.631	0.436	0.799	0.655	0.451
A3	0.436	1.004	0.697	0.521	0.918	0.638	0.595	0.842	0.586	0.456	0.983	0.683
A4	0.292	1.136	0.795	0.265	1.167	0.815	0.218	1.207	0.847	0.354	1.084	0.754
A5	0.000	1.414	1.000	0.000	1.414	1.000	0.000	1.414	1.000	0.000	1.414	1.000
A6	0.755	0.680	0.474	0.590	0.847	0.590	0.574	0.862	0.600	0.666	0.769	0.536
A7	1.014	0.456	0.311	0.836	0.605	0.420	1.049	0.424	0.288	0.760	0.683	0.473
A8	0.233	1.193	0.837	0.211	1.214	0.852	0.000	1.414	1.000	0.232	1.196	0.837
A9	0.875	0.573	0.396	0.929	0.528	0.363	0.792	0.651	0.451	0.521	0.918	0.638
A10	0.335	1.100	0.767	0.513	0.925	0.643	0.535	0.903	0.628	0.372	1.064	0.741
	C5			C6			C7
	${\delta }_m^{+}$	${\delta }_m^{-}$	CW	${\delta }_m^{+}$	${\delta }_m^{-}$	CW	${\delta }_m^{+}$	${\delta }_m^{-}$	CW
A1	0.919	1.191	0.564	0.760	1.190	0.610	0.580	1.218	0.677
A2	0.284	1.143	0.801	0.972	0.495	0.337	1.101	0.377	0.255
A3	0.415	1.018	0.711	0.472	0.968	0.672	0.513	0.926	0.644
A4	0.549	0.889	0.618	0.000	1.414	1.000	0.418	1.023	0.710
A5	0.284	1.143	0.801	0.000	1.414	1.000	0.000	1.414	1.000
A6	0.537	0.900	0.627	0.418	1.023	0.710	0.352	1.080	0.754
A7	0.000	1.414	1.000	1.042	0.430	0.292	0.456	0.984	0.683
A8	1.080	0.383	0.261	0.195	1.230	0.863	0.000	1.414	1.000
A9	0.870	0.580	0.400	0.881	0.567	0.392	0.437	1.004	0.697
A10	0.233	1.191	0.836	0.352	1.080	0.754	0.382	1.055	0.734

Step 7. With the help of Eqs. (7), (8) and using CW values from Table 10, we construct an extended decision matrix as presented in Table 11.

Table 11.

Extended IF decision matrix.

	C1	C2	C3	C4	C5	C6	C7
A1	0.677	0.660	0.612	0.668	0.564	0.610	0.677
A2	0.363	0.466	0.436	0.451	0.801	0.337	0.255
A3	0.697	0.638	0.586	0.683	0.711	0.672	0.644
A4	0.795	0.815	0.847	0.754	0.618	1.000	0.710
A5	1.000	1.000	1.000	1.000	0.801	1.000	1.000
A6	0.474	0.590	0.600	0.536	0.627	0.710	0.754
A7	0.311	0.420	0.288	0.473	1.000	0.292	0.683
A8	0.837	0.852	1.000	0.837	0.261	0.863	1.000
A9	0.396	0.363	0.451	0.638	0.400	0.392	0.697
A10	0.767	0.643	0.628	0.741	0.840	0.754	0.734
AI	1.000	1.000	1.000	1.000	1.000	0.292	0.255
AAI	0.311	0.363	0.288	0.451	0.261	1.000	1.000

For example, since C1 is a benefit-type criterion, AI and AAI values for it are calculated as follows:

$$A{I}_{C1}=Max\left\{0.677,0.363,0.697,0.795,1.000,0.474,0.311,\right)\left(0.837,0.396,0.767\right\}=1.000$$

$$AA{I}_{C1}=Min\left\{0.677,0.363,0.697,0.795,1.000,0.474,0.311,\right)\left(0.837,0.396,0.767\right\}=0.311$$

For C6, as a cost-type criterion, AI and AAI values are determined as follows:

$$A{I}_{C6}=Min\left\{0.610,0.337,0.672,1.000,1.000,0.710,0.292,\right)\left(0.863,0.392,0.754\right\}=0.292$$

$$AA{I}_{C6}=Max\left\{0.610,0.337,0.672,1.000,1.000,0.710,0.292,\right)\left(0.863,0.392,0.754\right\}=1.000$$

Step 8. Using Eq. (9), the normalized values for each criterion are computed. The normalized IF decision matrix is demonstrated in Table 12.

Table 12.

Normalized IF decision matrix.

	C1	C2	C3	C4	C5	C6	C7
A1	0.677	0.660	0.612	0.668	0.564	0.479	0.376
A2	0.363	0.466	0.436	0.451	0.801	0.866	1.000
A3	0.697	0.638	0.586	0.683	0.711	0.435	0.396
A4	0.795	0.815	0.847	0.754	0.618	0.292	0.359
A5	1.000	1.000	1.000	1.000	0.801	0.292	0.255
A6	0.474	0.590	0.600	0.536	0.627	0.411	0.338
A7	0.311	0.420	0.288	0.473	1.000	1.000	0.373
A8	0.837	0.852	1.000	0.837	0.261	0.339	0.255
A9	0.396	0.363	0.451	0.638	0.400	0.746	0.366
A10	0.767	0.643	0.628	0.741	0.840	0.387	0.347
AI	1.000	1.000	1.000	1.000	1.000	1.000	1.000
AAI	0.311	0.363	0.288	0.451	0.261	0.292	0.255

For example, the normalized value of C1 as per the A1 alternative is obtained as follows:

$${\stackrel{⌣}{\zeta }}_{11}=\frac{0.677}{1.000}=0.677$$

Step 9. With the help of Eq. (10), the weighted values for each alternative are computed. Also, Table 8, Table 12 are considered to obtain these weighted values. The weighted IF decision matrix is shown in Table 13.

Table 13.

Weighted IF decision matrix.

	C1	C2	C3	C4	C5	C6	C7	Total
A1	0.079	0.086	0.095	0.091	0.078	0.078	0.060
A2	0.042	0.061	0.068	0.061	0.110	0.141	0.160
A3	0.082	0.083	0.091	0.093	0.098	0.071	0.064
A4	0.093	0.107	0.132	0.102	0.085	0.048	0.058
A5	0.117	0.131	0.156	0.136	0.110	0.048	0.041
A6	0.056	0.077	0.094	0.073	0.086	0.067	0.054
A7	0.036	0.055	0.045	0.064	0.137	0.163	0.060
A8	0.098	0.111	0.156	0.114	0.036	0.055	0.041
A9	0.046	0.047	0.070	0.087	0.055	0.121	0.059
A10	0.090	0.084	0.098	0.101	0.115	0.063	0.056
AI	0.117	0.131	0.156	0.136	0.137	0.163	0.160	1.000
AAI	0.036	0.047	0.045	0.061	0.036	0.048	0.041	0.314

For example, the weighted value fro position A1-C1 is computed as follows:

$${\stackrel{⌣}{\Omega }}_{ij}=0.677\times 0.117=0.079$$

Step 10. In this step, ${\stackrel{⌣}{S}}_i$ value of each alternative is determined by using Eq. (11). For example, ${\stackrel{⌣}{S}}_1$ value of A1 is calculated as follows:

$${\stackrel{⌣}{S}}_1=0.079+0.086+0.095+0.091+0.078+0.078+0.060=0.568$$

Accordingly, the ${\stackrel{⌣}{S}}_i$ values found are given in the first column of Table 14.

Table 14.

Utility degrees and utility functions of alternatives.

	Si	${\breve{K}}_i^{-}$	${\breve{K}}_i^{+}$	$f\left({\breve{K}}_i^{-}\right)$	$f\left({\breve{K}}_i^{+}\right)$	$f\left({\breve{K}}_i\right)$	Rank
A1	0.568	1.807	0.568	0.239	0.761	0.528	7
A2	0.644	2.050	0.644	0.239	0.761	0.599	2
A3	0.581	1.850	0.581	0.239	0.761	0.540	6
A4	0.624	1.987	0.624	0.239	0.761	0.581	3
A5	0.738	2.349	0.738	0.239	0.761	0.686	1
A6	0.506	1.611	0.506	0.239	0.761	0.471	9
A7	0.560	1.784	0.560	0.239	0.761	0.521	8
A8	0.611	1.945	0.611	0.239	0.761	0.568	4
A9	0.486	1.546	0.486	0.239	0.761	0.452	10
A10	0.606	1.930	0.606	0.239	0.761	0.564	5

Step 11. Via Eqs. (12), (13), the utility degree of alternatives are computed. For example, the utility degree of A1 is obtained as follows:

$${\stackrel{⌣}{K}}_1^{-}=\frac{0.568}{0.314}=1.807$$

$${\stackrel{⌣}{K}}_1^{+}=\frac{0.568}{1.000}=0.568$$

Thus, the utility degrees of alternatives are given in the second and third columns of Table 14.

Step 12. In order to get the utility functions of alternatives, one should first compute the utility functions as per ideal and anti-ideal solutions through Eqs. (15), (16). For example, the ideal and anti-ideal solutions of A1 are calculated as follows, respectively:

$$f\left({\stackrel{⌣}{K}}_i^{+}\right)=\frac{1.807}{1.807+0.568}=0.761$$

$$f\left({\stackrel{⌣}{K}}_i^{-}\right)=\frac{0.568}{1.807+0.568}=0.239$$

Afterward, the utility functions of each alternative are calculated with the help of Eq. (14). The utility function of A1, for example, can be determined as follows:

$$f\left({\stackrel{⌣}{K}}_1\right)=\frac{1.807+0.568}{1+\frac{1-0.761}{0.761}+\frac{1-0.239}{0.239}}=0.528$$

As a result, Table 14 presents an ideal solution, an anti-ideal solution, and the utility functions of alternatives evaluated.

Step 12. Lastly, alternatives are ranked in descending order according to their utility functions. Put another way, the alternative having the most significant utility function is the best. As a result, alternative A5 is the best alternative, i.e., the most preferred insurance company. It is followed by A2, A4, A8, A10, A3, A1, A7, A6, and A9.

4.1. Sensitivity analysis and validation of the results

After obtaining the initial results in the MCMD model, the question arises of how subjectively defined input parameters affect the model results and what results are obtained by applying other multi-criteria models [74]. Therefore, an indispensable step in multi-criteria decision-making is to check the results’ robustness and analyze the sensitivity of the obtained results to changes in the input parameters of the MCDM model [75]. Keeping in mind the literature’s recommendations [76], [77], [78], [79], [80], [81], in the following part, the sensitivity analysis and validation of the results were performed through three sections. In the first section, the influence of the change of weight coefficients of the decision-maker was performed. In the second section, the analysis of the impact of the change of the most important criterion on the ranking results was performed, and in the third section, the robustness of the obtained solution was checked by comparison with other MCMD techniques.

4.1.1. Influence of the change of weight coefficients of decision-maker on ranking results

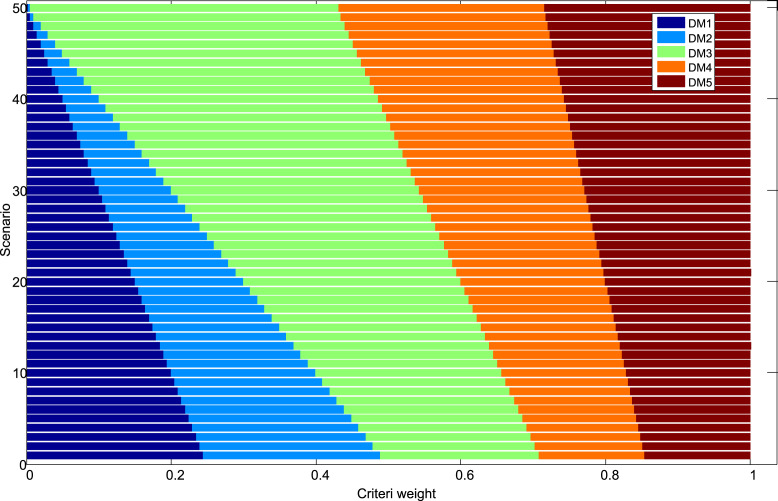
The decision-makers’ weighting coefficients were definedbased on subjective assessments and were used for the fusion of the weighting coefficients of the criteria. Since the decision-makers’ (DMs) weights directly influence the determination of the criteria weight’s values, it is necessary to perform an analysis of the impact of changes in their values on the final ranking results. In the following part, an experiment is presented. The changes in the value of the weight coefficients of the DM that have the greatest influence on decision making, i.e., those with the highest values of weight coefficients, are simulated. The importance of the DM was defined earlier as follows: $w_1^{DM}=w_2^{DM}=0.249$, $w_3^{DM}=0.215$ and $w_4^{DM}=w_5^{DM}=0.143$. Based on the presented values, we notice that DM1 and DM2 have the most significant influence on the multi-criteria model’s final results since they have the greatest values of weight coefficients.

The change in the weight coefficients’ values was performed through 50 scenarios, wherein in each scenario, the importance of the weight coefficients DM1 and DM2 were reduced by 2%. At the same time, the values of the remaining weighting coefficients were corrected by applying the expression $w_n:\left(1-w_B\right)=w_n^{\ast }:\left(1-w_B^{\ast }\right)$, where $w_B^{\ast }$ represents the updated value of the weighting coefficient DM1 and DM2, $w_n^{\ast }$ represents the reduced value of the considered criterion, $w_n$ represents the original value of the considered criterion, and $w_B$ represents the original value of the criterion DM1 and DM2. Thus, 50 new vectors of weight coefficients were obtained according to the following rules: (1) The change of the values of the weight coefficients DM1 and DM2 in the interval $w_1^{DM},w_2^{DM}\in \left[0.0025,0.2444\right]$ was simulated through 50 scenarios, and (2) The change of the remaining values of the weight coefficients in the intervals $w_3^{DM}\in \left[0.2148,0.4264\right]$ and $w_4^{DM},w_5^{DM}\in \left[0.1432,0.2843\right]$ is simulated. The new vectors of weight coefficients through the scenarios are shown in Fig. 4.

Fig. 4.

DM’s weights through 50 scenarios.

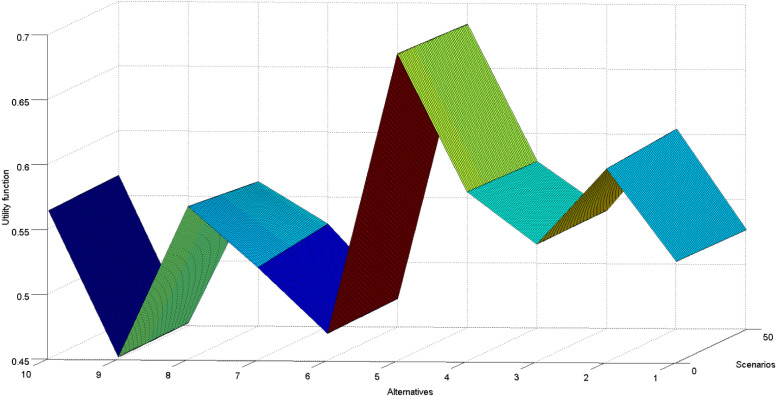
After forming new 50 vectors of weight coefficients, their influence on the change of the value of utility functions in MCMD methodology was analyzed. The shift in weight coefficients DMs on the change of utility functions is shown in Fig. 5.

Fig. 5.

Influence of change of weight coefficients DM1 and DM2 on change of utility functions.

The results show that the first three alternatives (A5, A2, and A4) have a good advantage over the remaining alternatives through all 50 scenarios, i.e., they represent a set of dominant alternatives. The worst alternative from the group (A9) remained the last ranked through all 50 scenarios. Alternatives A8 and A10 retained their ranks through scenarios S1–S24, respectively, for the interval $w_1^{DM},w_2^{DM}\in \left[0.1297,0.2444\right]$. For interval $w_1^{DM},w_2^{DM}\in \left[0.0025,0.1247\right]$, alternatives A8 and A10 exchanged their places, i.e. A10 took the fourth rank, while A8 became the fifth-ranked. Similar changes occurred with alternatives A1 and A7 (seven-ranked and eighth-ranked alternatives). For interval $w_1^{DM},w_2^{DM}\in \left[0.0698,0.2444\right]$, alternatives A1 and A7 retained their initial rank, while changes in weight coefficients in interval $w_1^{DM},w_2^{DM}\in \left[0.0025,0.0648\right]$ led to a change in their positions by giving preference to alternative A7 over alternative A1.

Based on the presented analysis, we can generally conclude that the change in the decision-makers’ weight coefficients’ value may affect the final ranking results in the multi-criteria models. In this experiment, changes in the weight of the decision maker’s criteria lead to minor changes in the alternative ranks, which shows that the obtained solution is stable and that there is a good advantage of a set of dominant alternatives over other alternatives.

4.1.2. Influence of the change of weight coefficients on ranking results

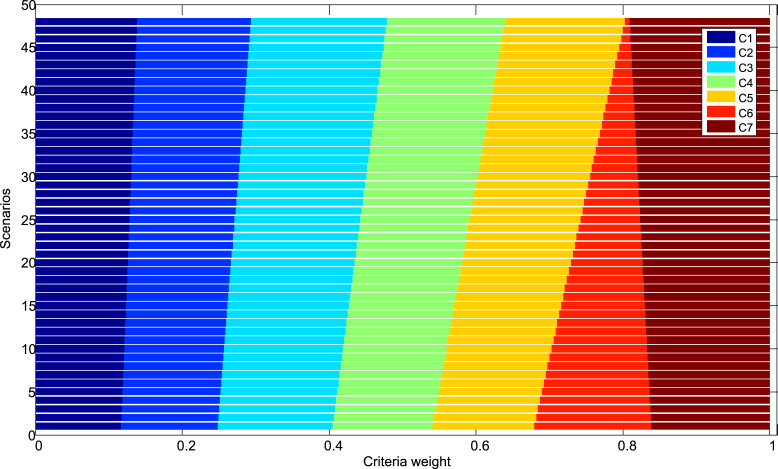
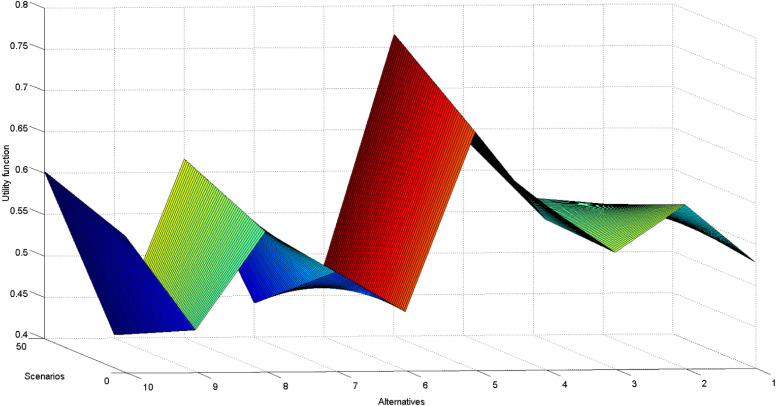
The influence of the change of weight coefficients on the ranking results was analyzed through an experiment in which 50 scenarios were formed. Through each of the scenarios, the value of the criteria weight of the most influential criterion (C6) was reduced by 2%, thus simulating the weighting factor’s change in the interval $w_6\in \left[0.0016,0.1626\right]$. The values of the remaining criteria in the scenarios were proportionally adjusted to meet the condition ${\sum }_{j=1}^n{w}_j=1$. Therefore, new vectors of weight coefficients of the criteria were obtained (Fig. 6), and their influence on the change of utility functions was analyzed in Fig. 7.

Fig. 6.

Criteria weights through 50 scenarios.

Fig. 7.

Influence of change of criterion weights on change of utility functions.

Based on the presented analysis (Fig. 7), it can be noticed that the changes in the value of the weight coefficient of criterion C6 mostly affect the change in the rank of alternative A2, which is the second-ranked alternative in terms of initial rank. For the values of the weighting factor $w_6\in \left[0.1334,0.1626\right]$, alternative A2 retained the second position among the considered alternatives. However, for the values of $w_6\in \left[0.0016,0.1301\right]$, there are significant changes in the rank of alternative A2, according to the following: (1) Scenario S10–17: for the values of $w_6\in \left[0.1073,0.1301\right]$, alternative A2 took the third rank; (2) Scenario S18–S21: for the values of $w_6\in \left[0.0228,0.0911\right]$, alternative A2 changed its rank and took the fourth position from the third place; (3) Scenario S22–S43: for values $w_6\in \left[0.0228,0.0911\right]$, alternative A2 replaced the rank with alternative A10 and moved from the fourth place to the fifth position in the overall rank; and (4) In the remaining scenarios S44–S50: for the values of $w_6\in \left[0.0016,0.0195\right]$ alternative A2 is moved from the fifth to the sixth position in the overall ranking. Alternatives A3, A4, A8, and A10 adjusted their ranks according to the changes in the rank of alternative A2 through the 50 scenarios considered. Minor changes in ranks also occur with alternatives A7 and A6 (eighth-ranked and nine-ranked). For values $0.0781\le w_6\le 0.1626$ alternatives, A7 and A6 kept their initial rank, while for values $0.0016\le w_6\le 0.0748$ the alternatives changed their places. Changes in the value of the most influential criterion’s weighting factor did not affect the difference in the remaining alternatives’ ranks.

Based on the presented analysis, we can conclude that the first-ranked alternative (A5) remained dominant through all 50 scenarios. It represents the best solution regardless of the changes in the weighting coefficients of the evaluation criteria. The A4 alternative retained its position in dominant options, as it ranked second-ranked or third-ranked through 50 scenarios. Simultaneously, it was confirmed that alternatives A6, A7, and A9 represent the worst solutions through all 50 scenarios. We can conclude that the alternative’s initial rank is confirmed and credible despite the changes in some alternatives’ positions. This statement is confirmed by Spearman’s rank correlation coefficient, which shows a significant statistical correlation between the initial set of ranks and the ranks obtained through the scenarios. Spearman’s correlation coefficient’s average value through scenarios is 0.940, which shows a high correlation and confirms the initial solution’s stability.

4.1.3. Comparison with intuitionistic fuzzy MCDM methodologies

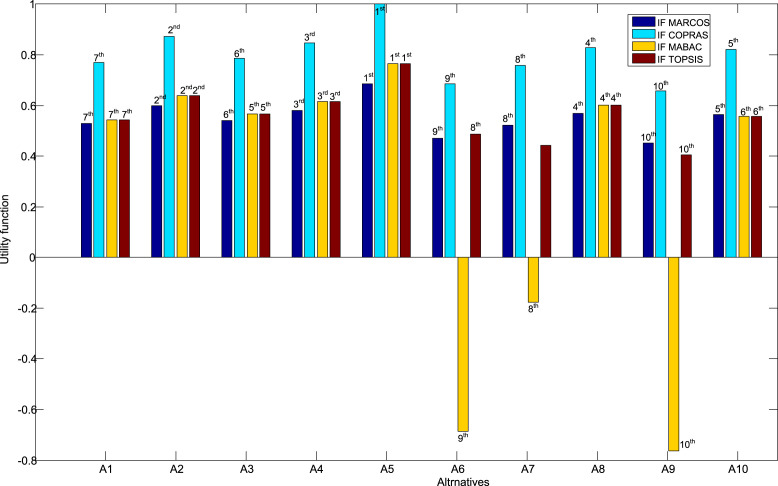
Since intuitionistic fuzzy sets were used in this paper to deal with uncertainty and inaccuracy, three IF multi-criteria techniques were chosen to compare the results: intuitionistic fuzzy COPRAS (COmplex PRoportional ASsessment) technique [22], intuitionistic fuzzy MABAC (Multi-Attributive Border Approximation area Comparison) technique [19], intuitionistic fuzzy TOPSIS (Technique for Order Preference by Similarity to Ideal Solution) technique [23]. A comparative overview of the application of these intuitionistic fuzzy MCMD methodologies is shown in Fig. 8.

Fig. 8.

Ranks of the alternatives based on different IF methodologies.

Based on the obtained results, it was confirmed that alternative A5 represents the best solution according to all MCDM methodologies. The results showed that the application of IF MARCOS and IF COPRAS multi-criteria techniques gives the same rank. Small differences in rank occurred with IF MABAC, and IF TOPSIS methods. However, these changes are not drastic, which is confirmed by Spearman’s rank correlation coefficient, which is 0.976 for IF TOPSIS, and 0.988 for IF MABAC. The presented analysis proves the validity of the methodology proposed in this paper and that the proposed choice of alternative A3 is credible.

5. Managerial implications and limitations

This paper posits a multiple-criteria group decision-making methodology called IF-MARCOS, which aims to select the most acceptable insurance company in terms of health services among diverse alternatives considering several conflicting criteria. The proposed framework allows decision-makers to express their opinions and assessments with linguistic variables and enables various people to join by a robust technique to come to a final decision. Since MARCOS provides a compromise solution as per ideal and non-ideal solutions, satisfactory performance is achieved in a fuzzy environment. The main contributions of the work are summarized below:

• •The proposed approach ensures the selected insurance company meets the requirements of decision-makers.
• •The study suggested a novel MCGDM framework for modeling and analyzing evaluation information with a high degree of ambiguity.
• •Due to its intuitionistic fuzzy sets basis, the proposed model can better capture the inconsistency, deficiency, and uncertainty of human judgment.
• •Some approaches based on intuitionistic fuzzy sets could be seen from relevant literature; however, as far as the authors’ knowledge, applying these methodologies within the context of insurance company evaluation and selection has not been conducted.
• •The salient characteristic of the proposed approach is that it considers the importance of each decision-maker. In most decision support tools, the decision-makers’ importance is ignored, i.e., their knowledge, opinions, and experience are equally important.
• •In this work, criteria weights were assigned by the decision-makers through linguistic variables. Then, linguistic criteria weights were transformed into suitable intuitionistic fuzzy numbers. Via the IFWA operator, each decision-maker judgment was merged to calculate the aggregated criteria weight. Finally, these weights were directly used in IF-MARCOS along with the aggregated IF rating of criteria.
• •The IF-MARCOS framework is based on experts’ opinions in which evaluation information is exceptionally crucial. Therefore, it can be used in problems where experts have enough information on the issue.

Although this study contributes to the literature, it also has some limitations. The limitations of this work are emphasized below:

• •The difficulty accessing the information and data needed to implement this approach could be one of the limitations.
• •In this paper, the ranking order of insurance companies has been validated by some MCDM methods under only IF environments. The lack of comparison with other fuzzy set extensions (hesitant, spherical, neutrosophic, picture, etc.) may be limited.
• •The ranking results obtained in this study are based on the opinions and assessments of five experts. Different ranking results may arise in the analysis to be conducted according to various experts’ considerations.

It is evident that decision-making tools that enable the processing of uncertain group information require complex mathematical formulations, which, to some extent, makes them challenging to understand. This group of tools includes the multi-criteria model presented in this paper. The development of such models goes through two phases. In the first phase, after the mathematical formulation of the model, the model is tested through the conceptual version of the software and implementation to solve complex real-world problems. This study represents the first phase of model development. The software was developed within the Microsoft Excel program, while Matlab 2018 was used to visualize the sensitivity analysis results. The Excel program was used as a database in which expert assessments of alternatives were processed. Visual Basic (VB) code for validation of results and sensitivity analysis of multi-criteria Methodology implemented within the Excel program. Visual Basic code for analyzing the impact of changes in weight coefficients on ranking results is presented in Appendix B. In addition to the proposed VB code, a unique VB code was developed to analyze the impact of experts’ weight coefficients on ranking results. As this is the first phase of development that involves testing and implementing a decision support system, the authors have not yet developed a user-oriented interface.

The development of a user-oriented interface is planned for the second phase of model development. Within that stage, the full implementation of the multi-criteria framework in the decision-making system will be achieved. It is planned to develop an online decision-making system that will be easy to use without requiring detailed knowledge of the model’s mathematical formulations. That will make this tool acceptable for use by a large number of users. The model’s adaptability is planned in terms of the number of experts who can participate in the research. Also, adaptability can be updated in terms of the number of criteria and alternatives for evaluation.

One of the significant limitations of the proposed multi-criteria model is the impossibility of online learning of the IF MARCOS algorithm. One possibility to improve this model’s adaptability is to adapt the IF membership functions of the linguistic variables used to represent expert preferences. This improvement would allow a more objective presentation of individual expert preferences depending on the problem’s knowable level. Therefore, it is necessary to focus future research on increasing the adaptability of linguistic variables’ membership functions depending on the changing of experts’ weight coefficients. Future research should also focus on developing artificial intelligence (AI) based algorithm trained by the IF MARCOS algorithm. Such an AI-based algorithm would have the ability to generalize future decisions efficiently.

6. Conclusions

Increasing health needs and health expenses with the aging population, the increase in average life expectancy, and patient expectations in parallel with technology development increase the pressure on financing health expenses. In the age of COVID-19, the importance of private health insurance has been better understood. From this perspective, analyzing insurance companies’ performance in this process is an essential issue for customers, managers of insurance companies, and politicians. In this respect, this study aims to provide a decision support tool. Combined the intuitionistic fuzzy sets with the MARCOS method, a useful, efficient, easy to use, flexible, and robust decision tool is developed to measure insurance companies’ performance in health services.

In this paper, ten insurance companies in Turkey are evaluated by five experts from the insurance sector as per seven criteria determined by the extensive literature review and expert opinions through the IF-MARCOS approach. The findings execute that the payback period (0.163), premium price (0.160), and network (0.156) are the most significant factors for the insurance sector to select the most acceptable insurance company. In this research, a sensitivity analysis is performed as well. The sensitivity analysis indicates the validity of the introduced IF-MARCOS model. As per this analysis, the proposed methodology is also well-consistent with existing ones (IF-COPRAS, IF-MABAC, and IF-TOPSIS).

Further, the ease of calculation and increase of the approach’s steadiness is the proposed framework’s superiorities over the other methods. The sensitivity analysis also states and identifies the effect of various weights of criteria and decision-makers on the insurance company evaluation. Likewise, its outcomes also prove the stability and validity of the introduced framework. Thus, it has been gathered that the IF-MARCOS methodology is relatively successful in assessing evaluation criteria and alternatives in real-world problems and reflecting human judgments in the best way. Finally, the introduced approach can be a reliable decision technique for other compelling issues faced by managers, politicians, and shareholders. Managerial implications are also offered to carry out the suggested methodology better.

Through the above analysis as well as sensitivity and validation tests, we can indicate that the proposed IF-MARCOS methodology has the following advantages: (1) It not only takes the imprecise information into account but also deals with different importance of decision-makers; (2) With different criteria weights, we can obtain various ranking outcomes and the most acceptable alternative; and (3) Because the criteria weights are determined as per the opinions of experts, firms can improve their evaluation process through the proposed IF-MARCOS approach.

MARCOS technique with intuitionistic fuzzy set information has a considerable chance of success for MCDM problems. Future research may be applied to various decision-making problems such as supplier selection, renewable energy sources’ evaluation, project selection, sustainability assessments, etc., in engineering, finance, management science, and other scientific applications. It could be recommended to consider different criteria for evaluating insurance companies. The proposed model could be attempted to operate under interval-valued IFS. In the future, interval-valued IFNs or trapezoidal IFNs could be employed by researchers. Moreover, D numbers, Z numbers, spherical fuzzy sets, hesitant fuzzy sets, and picture fuzzy sets can be applied for future works. The introduced framework can be implemented under uncertainty sets such as gray numbers, rough numbers, D numbers, Z numbers, and other extensions of fuzzy sets (spherical, hesitant, neutrosophic, picture, etc.).

Ethics declarations

All participants were asked to sign an online informed consent. If a participant did not sign the consent, the questionnaire was automatically closed; consequently, an ethics committee’s approval was not required. Serbian legislation indicates that ethics approval is not required for anonymous interviews/questionnaires.

CRediT authorship contribution statement

Fatih Ecer: Design and implementation of the research, to the analysis of the results and to the writing of the manuscript. Dragan Pamucar: Design and implementation of the research, to the analysis of the results and to the writing of the manuscript.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A.

See Table A.1.

Appendix B.

See next.

Appendix C. Supplementary data

The following is the Supplementary material related to this article.

MMC S1

The Excel file with VBA code.